A New Method of the Pattern Storage and Recognition in Oscillatory Neural Networks Based on Resistive Switches
Abstract
1. Introduction
2. Materials and Methods
2.1. General Principle
2.1.1. Vector Storage and ONN Training
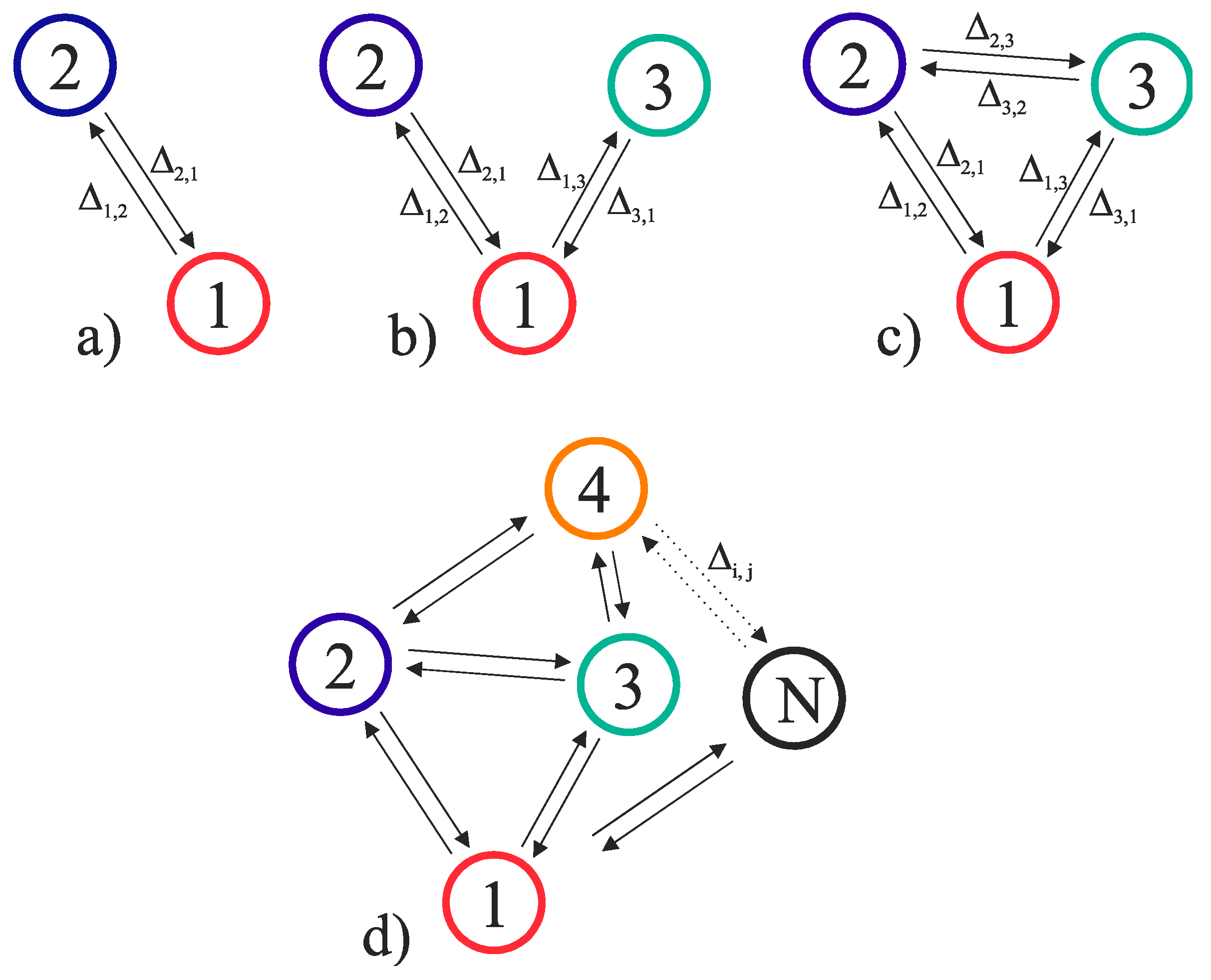
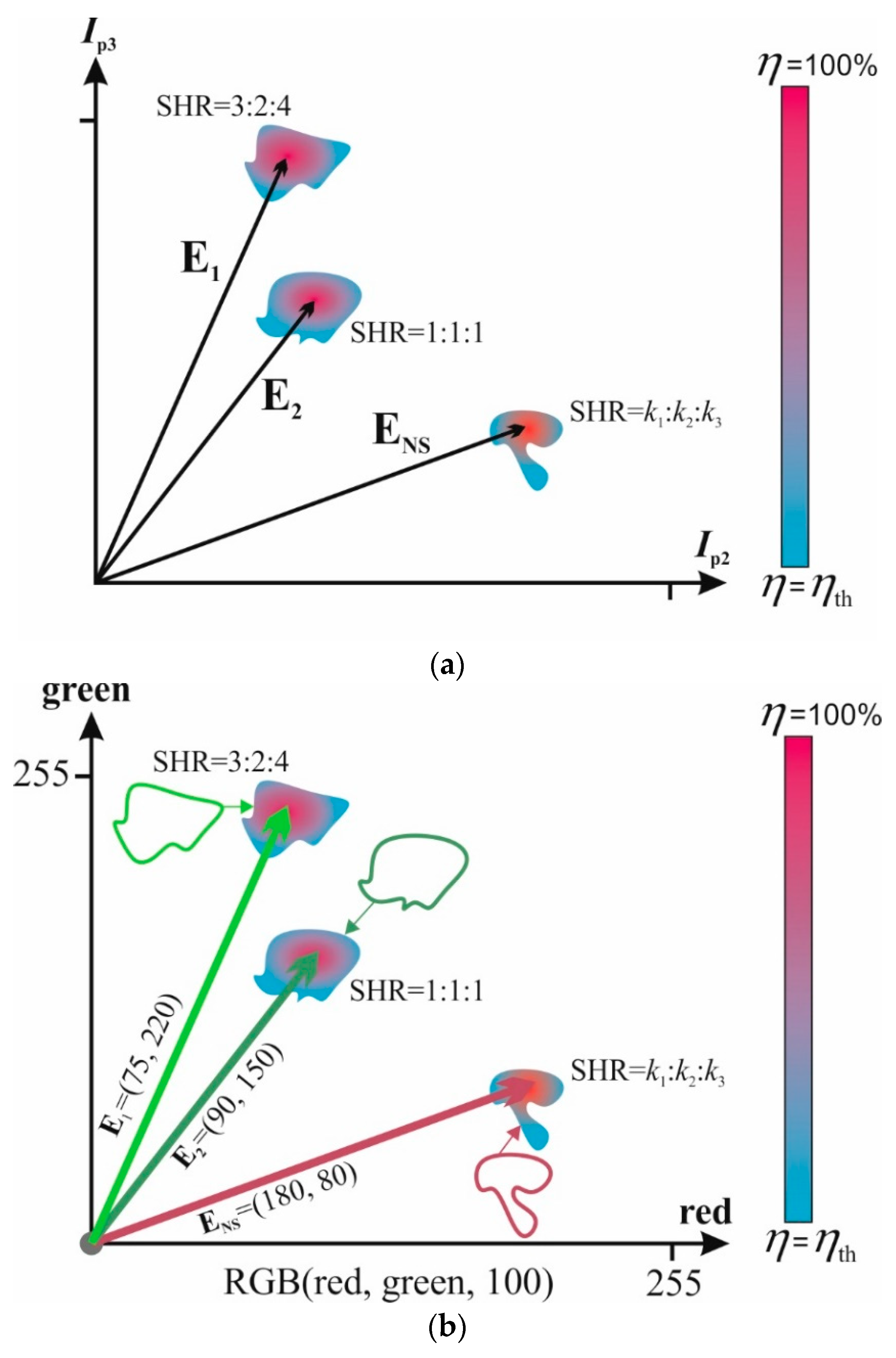
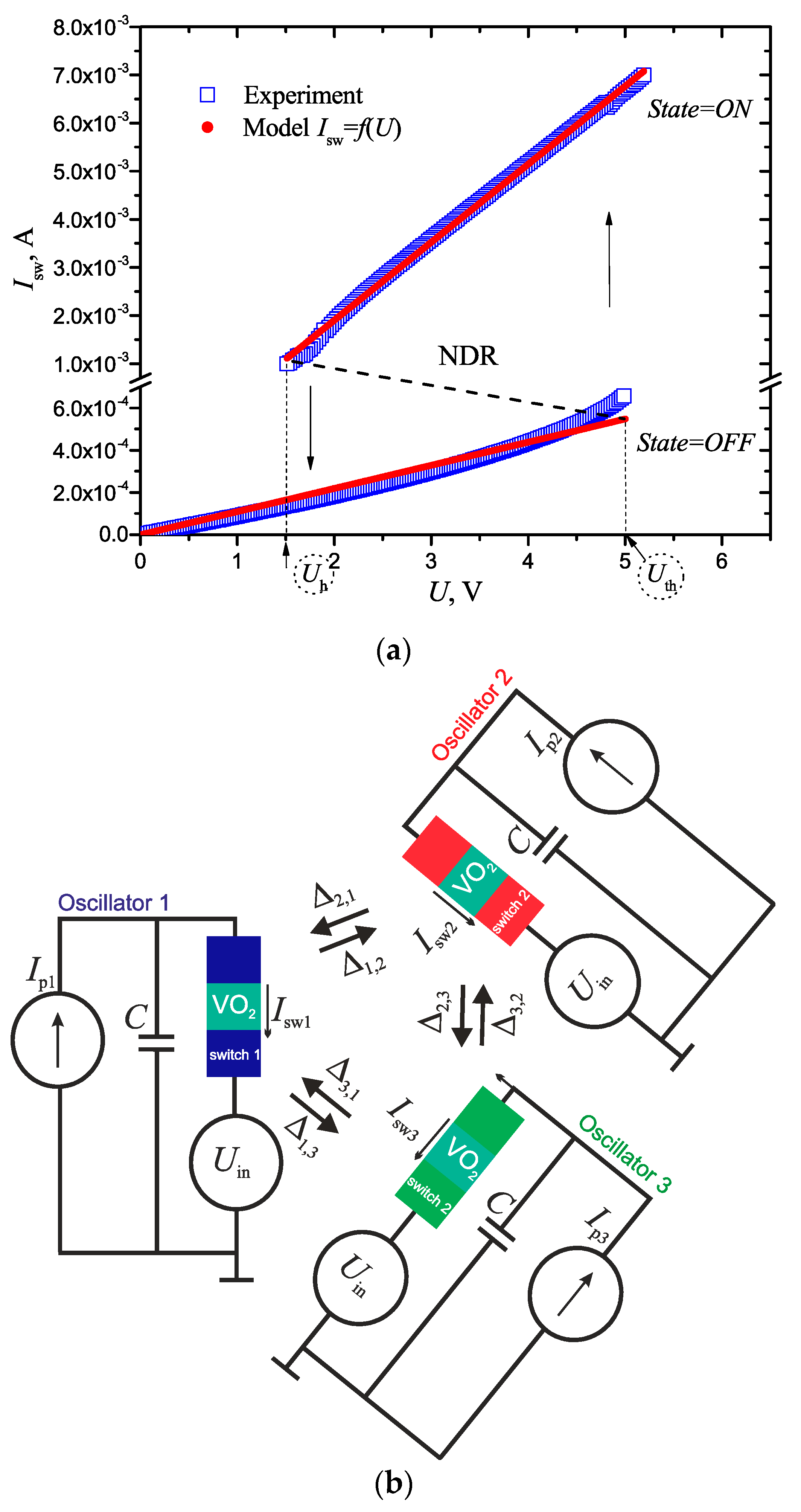
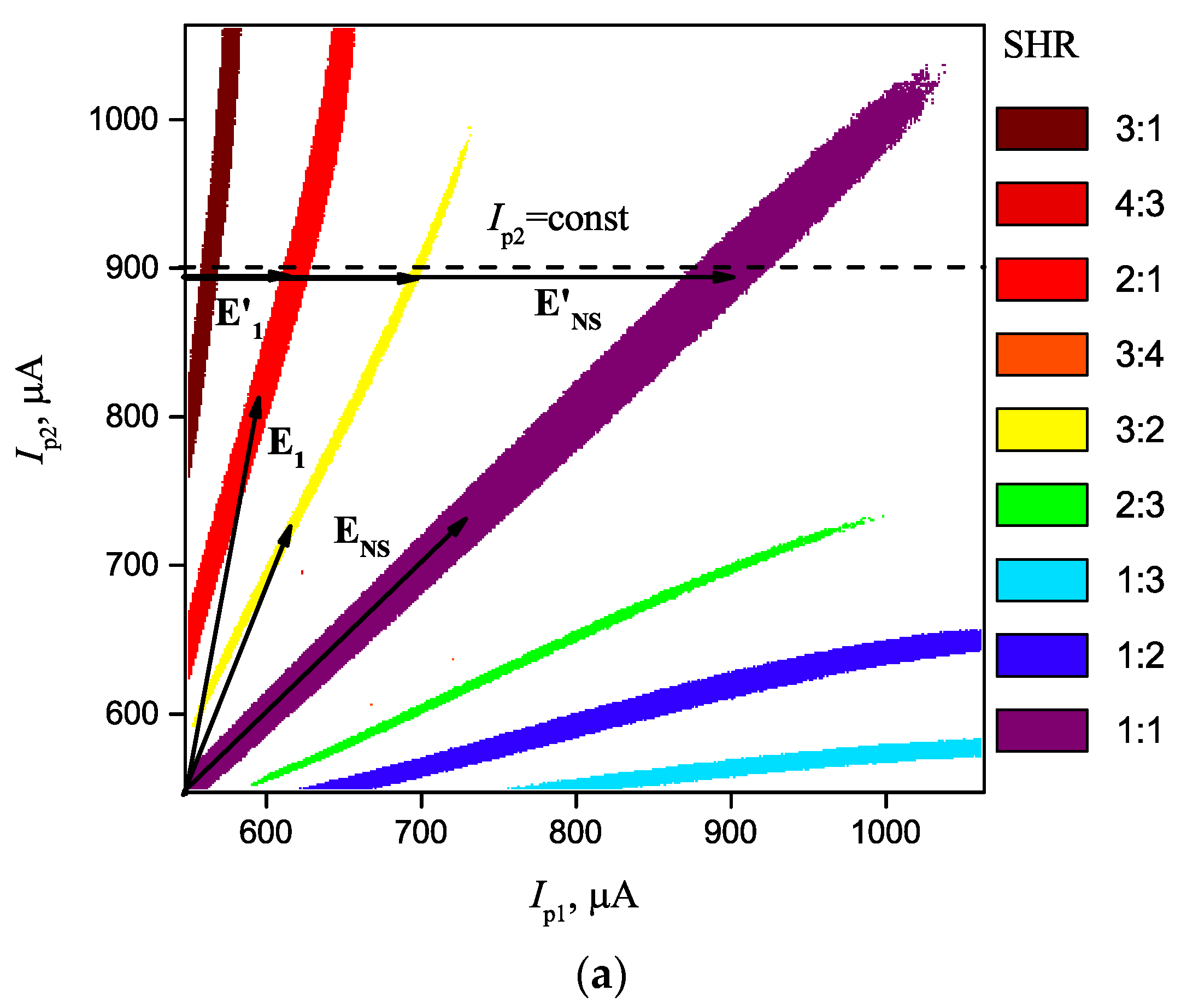
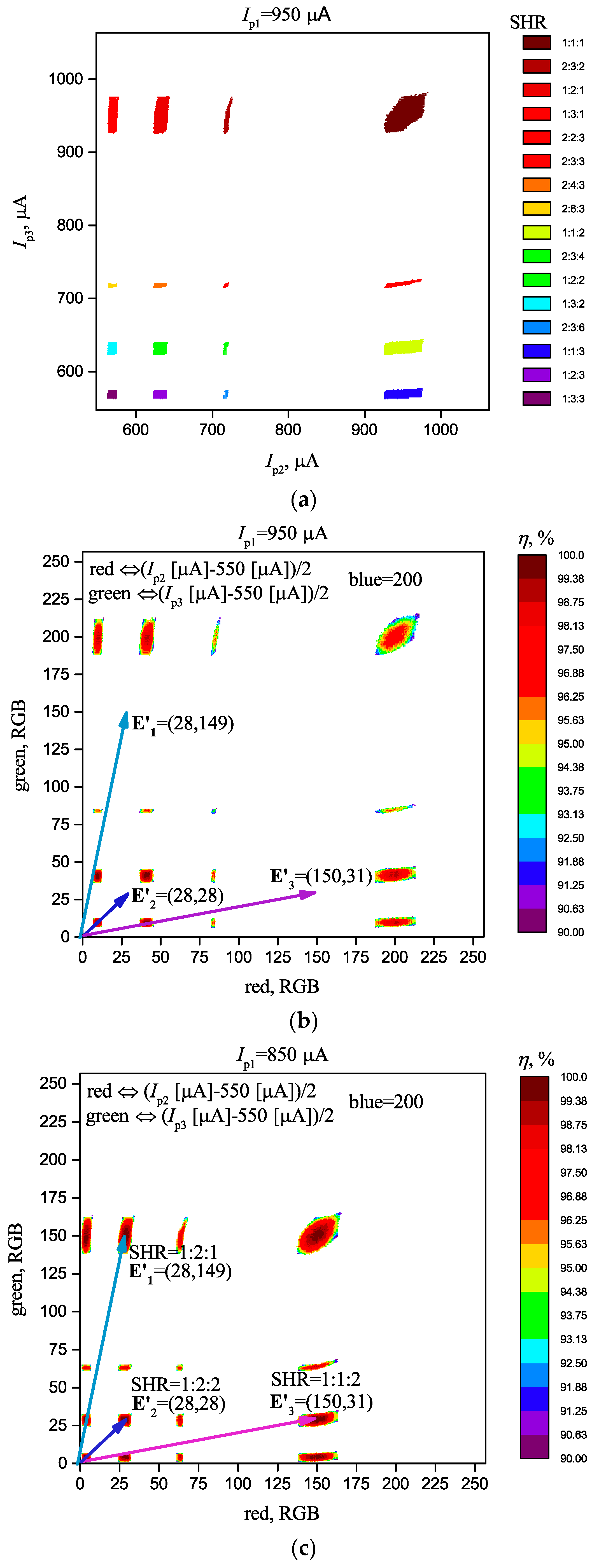
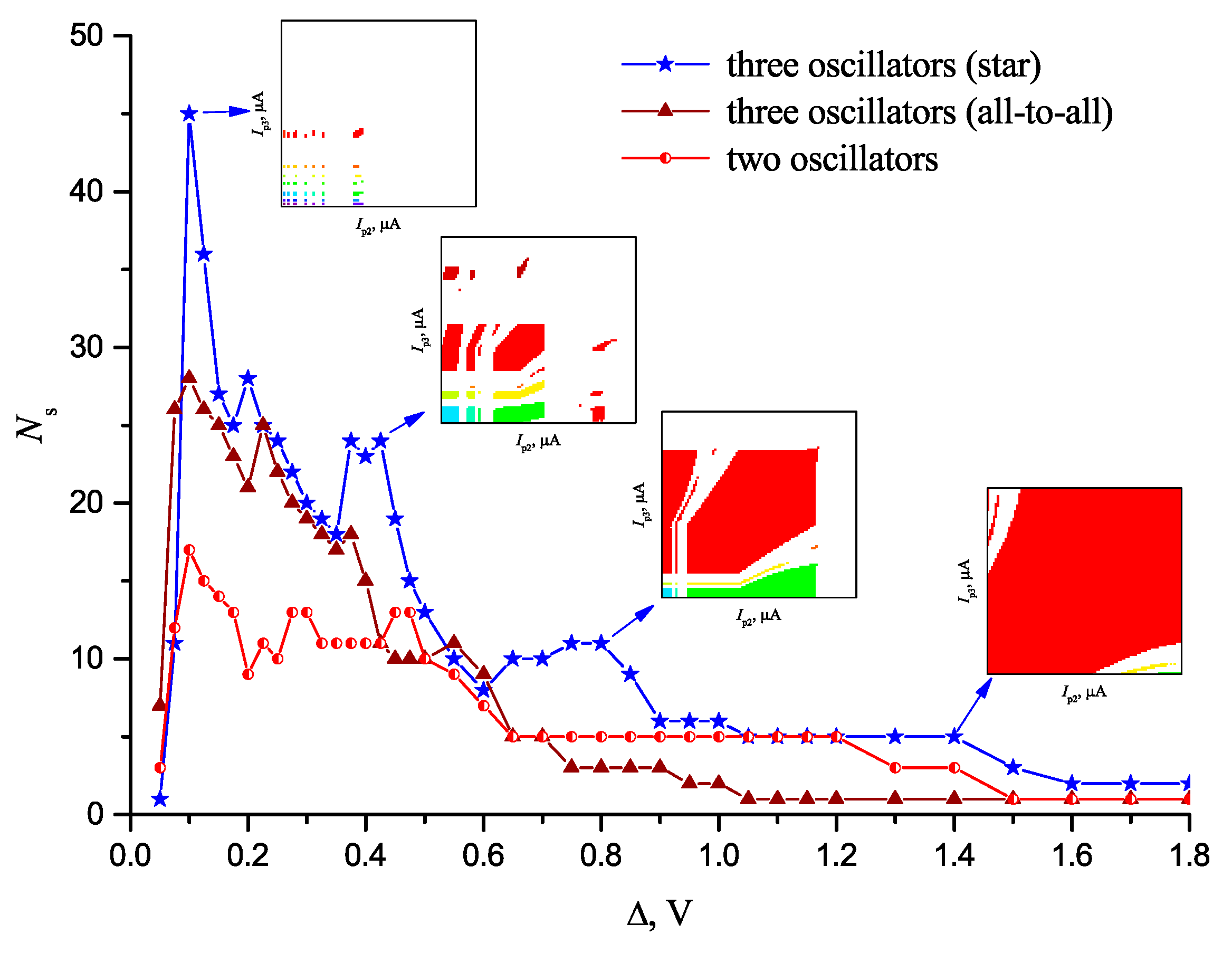
- For storage, arbitrary vectors E1, E2, …, Ei, ..., ENs should be specified. If necessary, control parameters should be transformed into the corresponding coordinate system (for example, a color one, see Figure 3b,c). In general, vectors have dimensionality M and appear as a set of a network parameters that affects the system SHR. For example, they can be either currents, as shown in Figure 3 E = (δIp1(1), δIp2(2), …, δIpN(M)), or they can be coupling strengths between some definite oscillators E = (δΔi,j(1), δΔi,j(2), …, δΔi,j(M)), or mixed parameters E = (δIp1(1), δΔi,j(2), …, δΔi,j(M)) (see Figure 4).
- Then, the network should be trained by the adjustment of the ONN parameters that are not used for the vectors’ determination (coupling strengths, currents of other oscillators in the network, noise level, and synchronization effectiveness threshold ηth). The adjustment is performed until the synchronization areas coincide with the vectors’ ends at the point of maximum value of synchronization effectiveness η (similar network training was used in the work [15]). The adjustment can be performed in two steps.
- First, by using random search until the vectors enter the synchronization area.
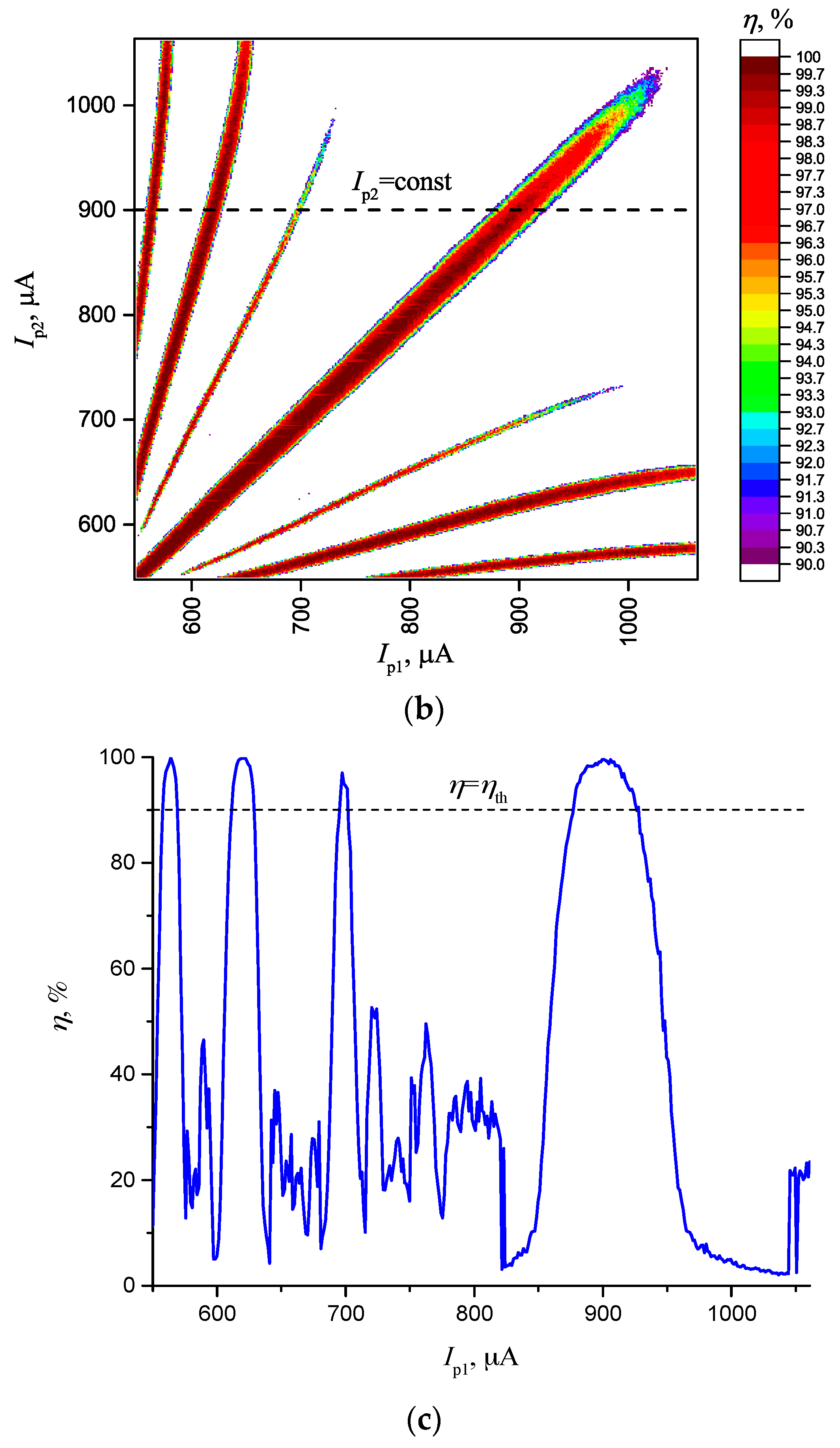
- Then, one of gradient methods [29] may be applied to search the maximum η. As a result, each stored vector corresponds to its unique value of SHR and maximum of η(E).
- If the training does not provide a positive result, one more oscillator should be included into the system and coupled with all oscillators already present, thus increasing the number of varied parameters and the number of possible synchronous states Ns. Then, the training should be repeated (see step 2).
2.1.2. Vectors Recognition
- Set the test vector T to the system input through applying shifts to the control parameters (see Figure 4). The vector’s coordinates may be either shifts of currents, or coupling strengths or their combination, as it has been indicated above.
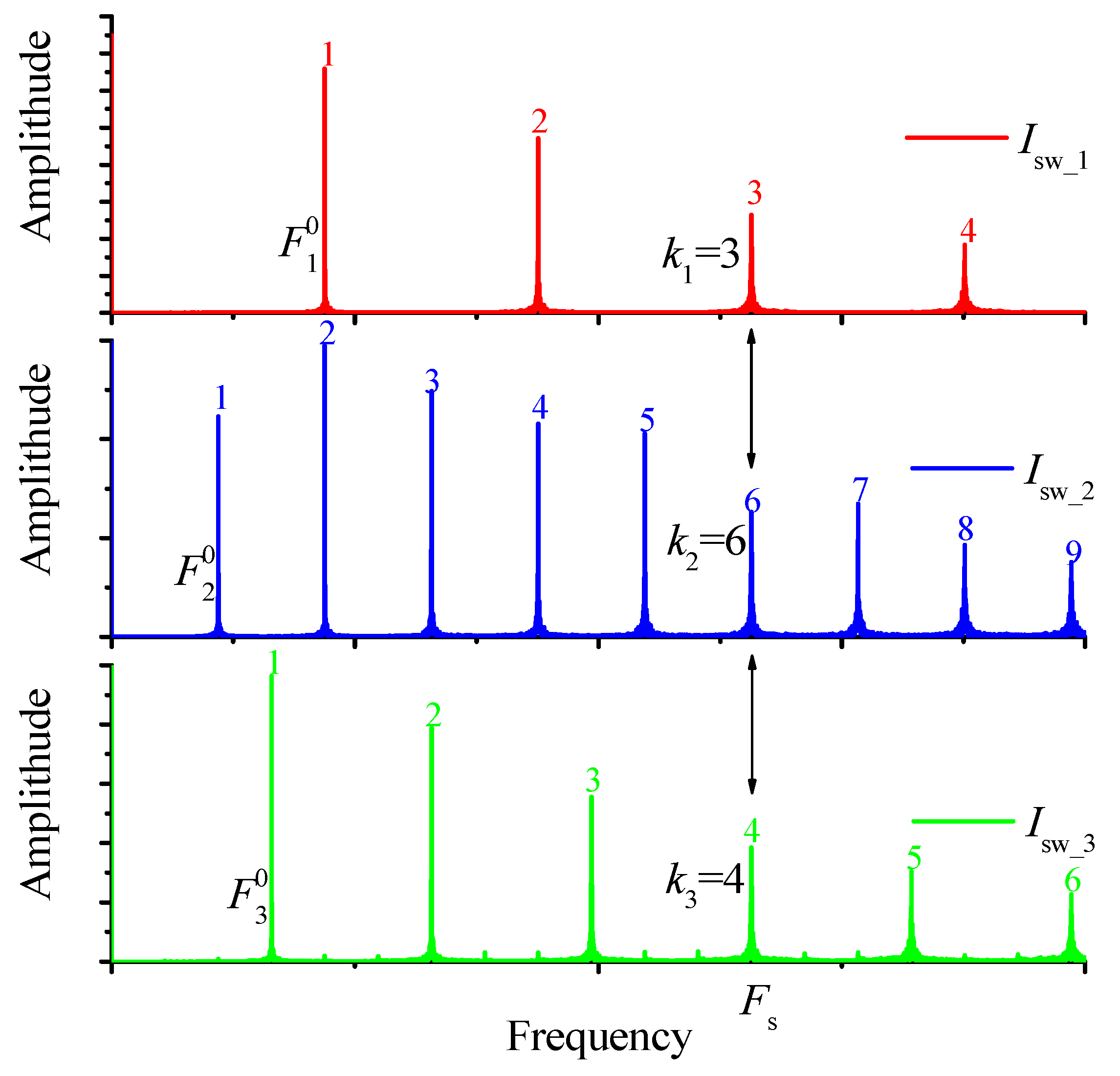
- If one of the conditions is met (T ≈ E1 or T ≈ E2 or … or T ≈ ENS), i.e., coordinates values of T are equal to one of the stored patterns, a transition to the synchronous state will occur and, actually, the act of the corresponding pattern recognition will take place. Which patterns have been exactly recognized can be determined by the value of SHR. The existence of the synchronization areas ensures the vector recognition even at its coordinates’ insignificant displacement from the stored pattern.
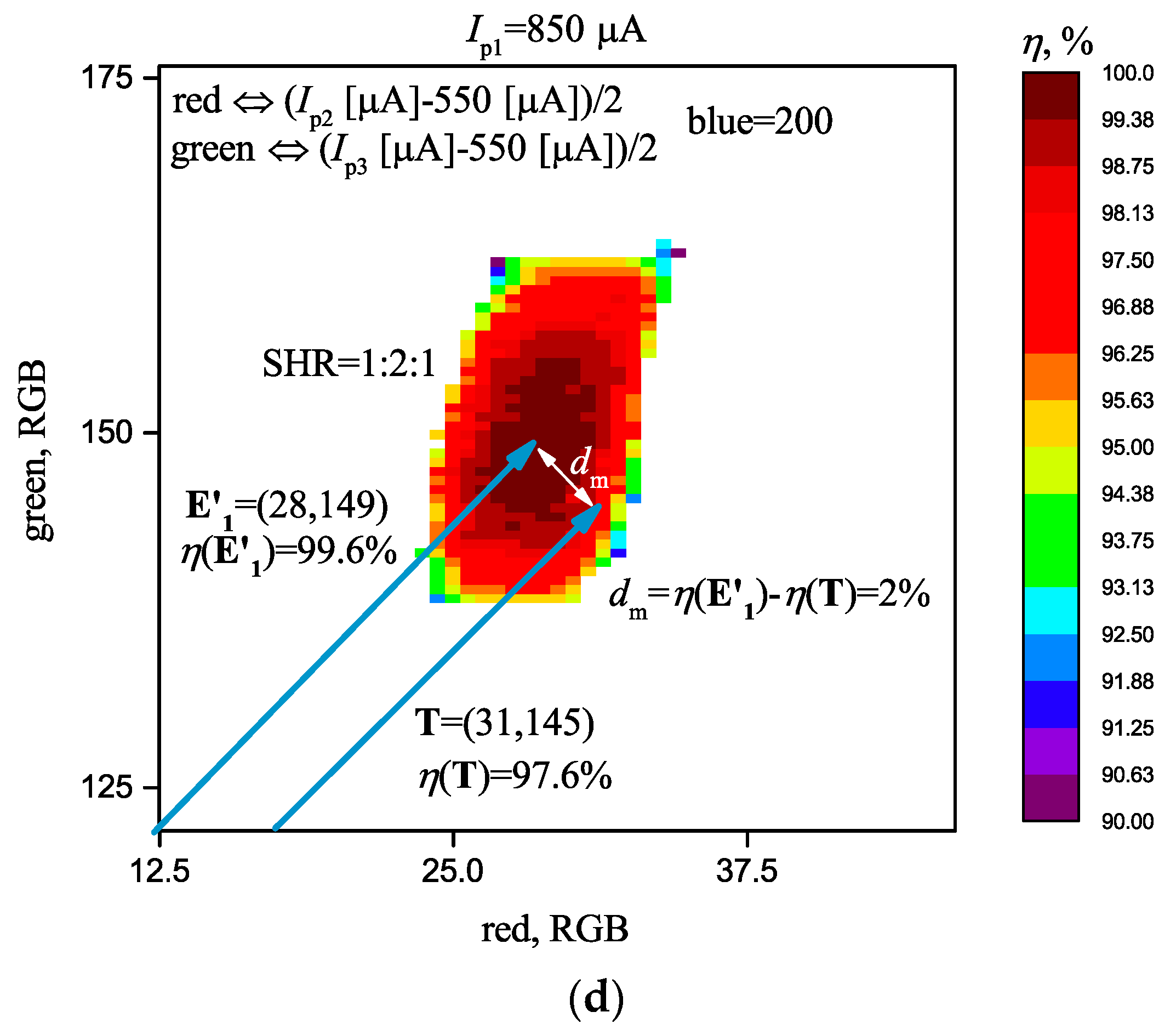
- The degree of match dm between the objects may be such magnitude as the difference between the synchronization effectiveness of the stored and the test vectors dm = η(E) − η(T). If the magnitude of η(E) is not known, then to compare the degree of match, the formula dm = 100% − η(T) can be used. The less dm is, the closer vector T is to vector E.
2.2. Model Object
2.3. Method of Calculating a Family of Metrics
3. Results
3.1. Vector Storage and ONN Training
3.2. Vectors Recognition
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Heaton, J. Artificial Intelligence for Humans; Createspace Independent Publishing: Scotts Valley, CA, USA, 2015; ISBN 9781505714340. [Google Scholar]
- Bishop, C.M. Neural Networks for Pattern Recognition; Clarendon Press: New York, NY, USA, 1995; ISBN 0198538642. [Google Scholar]
- Hopfield, J.J.; Tank, D.W. Computing with neural circuits: A model. Science 1986, 233, 625–633. [Google Scholar] [CrossRef] [PubMed]
- Strogatz, S.H. From Kuramoto to Crawford: Exploring the onset of synchronization in populations of coupled oscillators. Phys. D Nonlinear Phenom. 2000, 143, 1–20. [Google Scholar] [CrossRef]
- Vodenicarevic, D.; Locatelli, N.; Abreu Araujo, F.; Grollier, J.; Querlioz, D. A Nanotechnology-Ready Computing Scheme based on a Weakly Coupled Oscillator Network. Sci. Rep. 2017, 7, 44772. [Google Scholar] [CrossRef] [PubMed]
- Nakano, H.; Saito, T. Grouping Synchronization in a Pulse-Coupled Network of Chaotic Spiking Oscillators. IEEE Trans. Neural Netw. 2004, 15, 1018–1026. [Google Scholar] [CrossRef] [PubMed]
- Velichko, A.; Belyaev, M.; Putrolaynen, V.; Pergament, A.; Perminov, V. Switching dynamics of single and coupled VO2-based oscillators as elements of neural networks. Int. J. Mod. Phys. B 2017, 31, 1650261. [Google Scholar] [CrossRef]
- Shukla, N.; Parihar, A.; Cotter, M.; Barth, M.; Li, X.; Chandramoorthy, N.; Paik, H.; Schlom, D.G.; Narayanan, V.; Raychowdhury, A.; Datta, S. Pairwise coupled hybrid vanadium dioxide-MOSFET (HVFET) oscillators for non-boolean associative computing. In Proceedings of the 2014 IEEE International Electron Devices Meeting, San Francisco, CA, USA, 15–17 December 2014; pp. 28.7.1–28.7.4. [Google Scholar]
- Khitun, A.G.; Geremew, A.K.; Balandin, A.A. Transistor-Less Logic Circuits Implemented With 2-D Charge Density Wave Devices. IEEE Electron. Device Lett. 2018, 39, 1449–1452. [Google Scholar] [CrossRef]
- Khitun, A.; Liu, G.; Balandin, A.A. Two-dimensional oscillatory neural network based on room-temperature charge-density-wave devices. IEEE Trans. Nanotechnol. 2017, 16, 860–867. [Google Scholar] [CrossRef]
- Liu, G.; Debnath, B.; Pope, T.R.; Salguero, T.T.; Lake, R.K.; Balandin, A.A. A charge-density-wave oscillator based on an integrated tantalum disulfide-boron nitride-graphene device operating at room temperature. Nat. Nanotechnol. 2016, 11, 845–850. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S. Generation of high-frequency power oscillation by astable mode arcing with SCR switched inductor. IEEE J. Solid-State Circuits 1984, 19, 269–271. [Google Scholar] [CrossRef]
- Chen, C.; Mathews, R.; Mahoney, L.; Calawa, S.; Sage, J.; Molvar, K.; Parker, C.; Maki, P.; Sollner, T.C.L. Resonant-tunneling-diode relaxation oscillator. Solid. State. Electron. 2000, 44, 1853–1856. [Google Scholar] [CrossRef]
- Sharma, A.A.; Bain, J.A.; Weldon, J.A. Phase Coupling and Control of Oxide-Based Oscillators for Neuromorphic Computing. IEEE J. Explor. Solid-State Comput. Devices Circuits 2015, 1, 58–66. [Google Scholar] [CrossRef]
- Romera, M.; Talatchian, P.; Tsunegi, S.; Araujo, F.A.; Cros, V.; Bortolotti, P.; Yakushiji, K.; Fukushima, A.; Kubota, H.; Yuasa, S.; et al. Vowel recognition with four coupled spin-torque nano-oscillators. arXiv, 2018; arXiv:1711.02704. [Google Scholar]
- Belyaev, M.A.; Boriskov, P.P.; Velichko, A.A.; Pergament, A.L.; Putrolainen, V.V.; Ryabokon’, D.V.; Stefanovich, G.B.; Sysun, V.I.; Khanin, S.D. Switching Channel Development Dynamics in Planar Structures on the Basis of Vanadium Dioxide. Phys. Solid State 2018, 60, 447–456. [Google Scholar] [CrossRef]
- Velichko, A.; Belyaev, M.; Putrolaynen, V.; Perminov, V.; Pergament, A. Thermal coupling and effect of subharmonic synchronization in a system of two VO2 based oscillators. Solid State Electron. 2018, 141, 40–49. [Google Scholar] [CrossRef]
- Sakai, J. High-efficiency voltage oscillation in VO2 planer-type junctions with infinite negative differential resistance. J. Appl. Phys. 2008, 103, 103708. [Google Scholar] [CrossRef]
- Hoppensteadt, F.C.; Izhikevich, E.M. Oscillatory Neurocomputers with Dynamic Connectivity. Phys. Rev. Lett. 1999, 82, 2983–2986. [Google Scholar] [CrossRef]
- Hoppensteadt, F.C.; Izhikevich, E.M. Pattern recognition via synchronization in phase-locked loop neural networks. IEEE Trans. Neural Netw. 2000, 11, 734–738. [Google Scholar] [CrossRef] [PubMed]
- Izhikevich, E.M. Weakly pulse-coupled oscillators, FM interactions, synchronization, and oscillatory associative memory. IEEE Trans. Neural Netw. 1999, 10, 508–526. [Google Scholar] [CrossRef] [PubMed]
- Nikonov, D.E.; Csaba, G.; Porod, W.; Shibata, T.; Voils, D.; Hammerstrom, D.; Young, I.A.; Bourianoff, G.I. Coupled-Oscillator Associative Memory Array Operation for Pattern Recognition. IEEE J. Explor. Solid-State Comput. Devices Circuits 2015, 1, 85–93. [Google Scholar] [CrossRef]
- Pikovsky, A.; Rosenblum, M.; Kurths, J. (Jürgen) Synchronization: A Universal Concept in Nonlinear Sciences; Cambridge University Press: Cambridge, UK, 2003; ISBN 9780521533522. [Google Scholar]
- Theodoridis, S.; Koutroumbas, K. Pattern Recognition; Academic Press: Cambridge, MA, USA, 2009; ISBN 9781597492720. [Google Scholar]
- Kumar, A.; Mohanty, P. Autoassociative Memory and Pattern Recognition in Micromechanical Oscillator Network. Sci. Rep. 2017, 7, 411. [Google Scholar] [CrossRef] [PubMed]
- Shukla, N.; Parihar, A.; Freeman, E.; Paik, H.; Stone, G.; Narayanan, V.; Wen, H.; Cai, Z.; Gopalan, V.; Engel-Herbert, R.; et al. Synchronized charge oscillations in correlated electron systems. Sci. Rep. 2014, 4, 4964. [Google Scholar] [CrossRef]
- Hoppensteadt, F.C.; Izhikevich, E.M. Synchronization of laser oscillators, associative memory, and optical neurocomputing. Phys. Rev. E 2000, 62, 4010–4013. [Google Scholar] [CrossRef]
- Velichko, A.; Putrolaynen, V.; Belyaev, M. Effects of Higher Order and Long-Range Synchronizations for Classification and Computing in Oscillator-Based Spiking Neural Networks. arXiv, 2018; arXiv:1804.03395. [Google Scholar]
- Gill, P.E.; Murray, W.; Wright, M.H. Practical Optimization; Emerald Group Publishing: Bingley, UK, 1982; ISBN 0122839528. [Google Scholar]
- Velichko, A.; Belyaev, M.; Putrolaynen, V.; Perminov, V.; Pergament, A. Modeling of thermal coupling in VO2-based oscillatory neural networks. Solid State Electron. 2018, 139, 8–14. [Google Scholar] [CrossRef]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velichko, A.; Belyaev, M.; Putrolaynen, V.; Boriskov, P. A New Method of the Pattern Storage and Recognition in Oscillatory Neural Networks Based on Resistive Switches. Electronics 2018, 7, 266. https://doi.org/10.3390/electronics7100266
Velichko A, Belyaev M, Putrolaynen V, Boriskov P. A New Method of the Pattern Storage and Recognition in Oscillatory Neural Networks Based on Resistive Switches. Electronics. 2018; 7(10):266. https://doi.org/10.3390/electronics7100266
Chicago/Turabian StyleVelichko, Andrei, Maksim Belyaev, Vadim Putrolaynen, and Petr Boriskov. 2018. "A New Method of the Pattern Storage and Recognition in Oscillatory Neural Networks Based on Resistive Switches" Electronics 7, no. 10: 266. https://doi.org/10.3390/electronics7100266
APA StyleVelichko, A., Belyaev, M., Putrolaynen, V., & Boriskov, P. (2018). A New Method of the Pattern Storage and Recognition in Oscillatory Neural Networks Based on Resistive Switches. Electronics, 7(10), 266. https://doi.org/10.3390/electronics7100266






