2. Methods
Traditionally, SAR imaging is conducted from moving aircraft or spacecraft. However, the key to synthetic aperture imaging is the collection of data with different antenna displacements and signal processing to construct an image from the displaced antenna radar observations. The motion creating the antenna displacement need not be continuous as evident in the derivation of the commonly used “stop and hop” approximation in radar signal modeling [
1]. Radar platform motion during LFM-CW operation has some effect but can be compensated for [
3,
4]. The data must be collected with antenna displacements spaced no farther apart than one-half of the real-aperture antenna size in order to avoid grating lobes and aliasing. The synthetic aperture processing enables image formation at much higher resolution than possible with a real-aperture antenna [
1].
Conventional SAR with its one-dimensional (1D) synthetic aperture generates 2D images of the surface backscatter. Interferometric SAR uses an additional antenna that is vertically and/or horizontally displaced by a baseline to enable estimation of the surface vertical displacement [
1]. Since the SAR signal penetrates vegetation canopies, multiple baselines can enable tomographic reconstruction of scattering within the vegetation canopy [
5,
6,
7,
8,
9,
10,
11,
12]. Multi-baseline SAR is a special case of a 2D synthetic aperture where the elevation dimension is sparsely sampled [
10].
A 2D synthetic aperture is formed by coherently collecting radar echoes over a 2D grid of antenna displacements where the antenna is displaced in both azimuth and elevation. With a uniform rectangular sampling grid (that is, the observations using real-aperture antennas are collected at each point of an evenly spaced grid—a fully sampled aperture) within a rectangular 2D synthetic aperture, some of the complexities that arise in multi-baseline SAR are ameliorated. While full sampling of a 2D synthetic aperture in space is probably impractical from orbit, ground-based 2D SAR is both practical and useful for vegetation studies, and the subject of this paper.
For a full 2D synthetic aperture, the synthetic azimuth beamwidth φ
A and elevation beamwidth φ
E are given by
where
mA and
mE are the projected synthetic aperture dimensions in the azimuth and elevation directions and λ is the radar wavelength. However, it should be noted that the synthetic aperture length can be arbitrarily truncated, with the penalty of loss in synthetic aperture resolution. For a truncated synthetic aperture, the effective imaging resolution in azimuth and elevation is given by the slant range
R times the beamwidth, i.e.,
These expressions differ from SAR with a full synthetic aperture where resolution is independent of range, i.e., the azimuth resolution is
r = l/2 where
l is the real-aperture antenna size [
1].
From the 2D synthetic aperture radar data, a 3D matched filter that accounts for range walk in the azimuth and elevation directions can be employed to generate a backscatter image of the target. Having both azimuth and elevation displacements, as well as range resolution, means that the resulting backscatter image can be created in 3D. The picture elements of a 3D image are termed volume elements or “voxels” in contrast to the picture elements (“pixels”) of 2D images. With a fully filled 2D synthetic aperture, phase unwrapping is not required nor is a target model needed.
While a variety of approximate methods (e.g., modified range-Doppler filtering) can be used to create the voxel images, for this study, we prefer the use of true 3D matched filtering via time-domain backprojection. The 3D matched filtering is aided by formulating the SAR backprojection algorithm in strictly spatial variables [
4,
13]. Ignoring apodization windows and the 1/
R4 slant range dependence, 3D backprojection formulated in spatial variables can be expressed as [
4]
where
,
v (x, y, z) is the complex-valued backscatter at the voxel centered at (
x,
y,
z), and
is the interpolated range-compressed radar signal for the (
n,m)
th synthetic aperture sampling location at the slant range distance
dn,m computed as
where (
xn,m,
yn,m,
zn,m) is the location of the radar for the (
n,m)
th sampling location. Backprojection implicitly compensates for range migration, which is particularly significant for short-range SAR. The voxels are evaluated at a 3D grid of (
x,
y,
z) values to form a 3D backscatter image. The voxel spacing is typically set to be consistent with the resolution values given in Equations (3) and (4) and with the range resolution associated with the range pulse compression. In this paper, the voxel size is set to be 10 cm in azimuth by 10 cm in elevation by 10 cm in range. The range dimension oversamples the range resolution, although, in this application, the range migration, coupled with the short-range operation, results in an improved effective range resolution in the voxel image from that obtained by range compression alone. The apodization window trades sidelobe suppression for mainlobe resolution. In this work, simple 1D Hamming apodization windows are used for range-compression, as well as for azimuth and elevation compression.
Note that the simple time-domain back projection image formation algorithm described in Equation (5) does not account for the attenuation of the signal through the vegetation. This is required for estimation of the vegetation backscatter at each voxel.
At the C-band, the tree vegetation (leaves, twigs, and branches) can be treated as a 3D volume scattering region [
14,
15]. The radar signal penetrates the vegetation and some of it scattered back to the radar. Additional signal is scattered in other directions and is lost to the radar. This scattering loss attenuates the signal as it passes through the vegetation [
1]. Nevertheless, the attenuation through the vegetation of a single tree is adequate for observing backscatter from vegetation elements at the backside of the tree. This is not the case at higher radar frequencies.
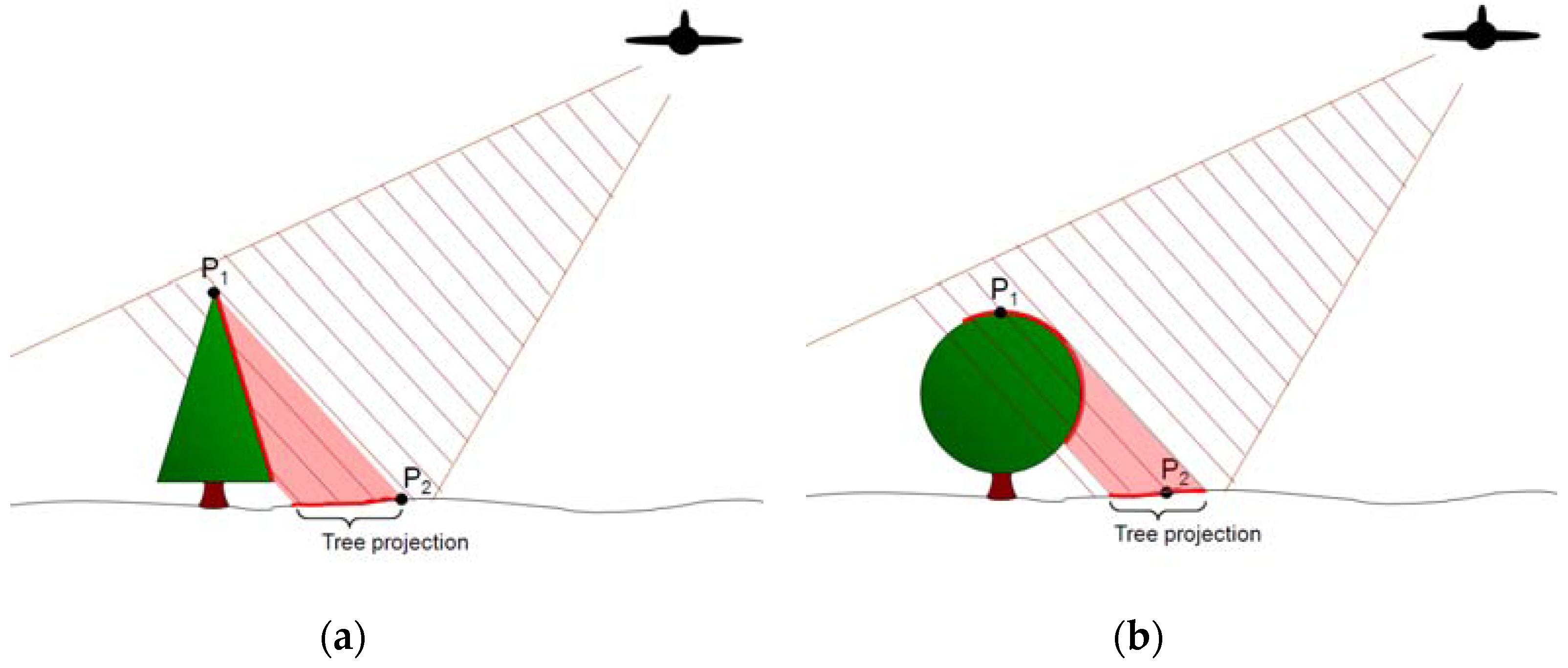
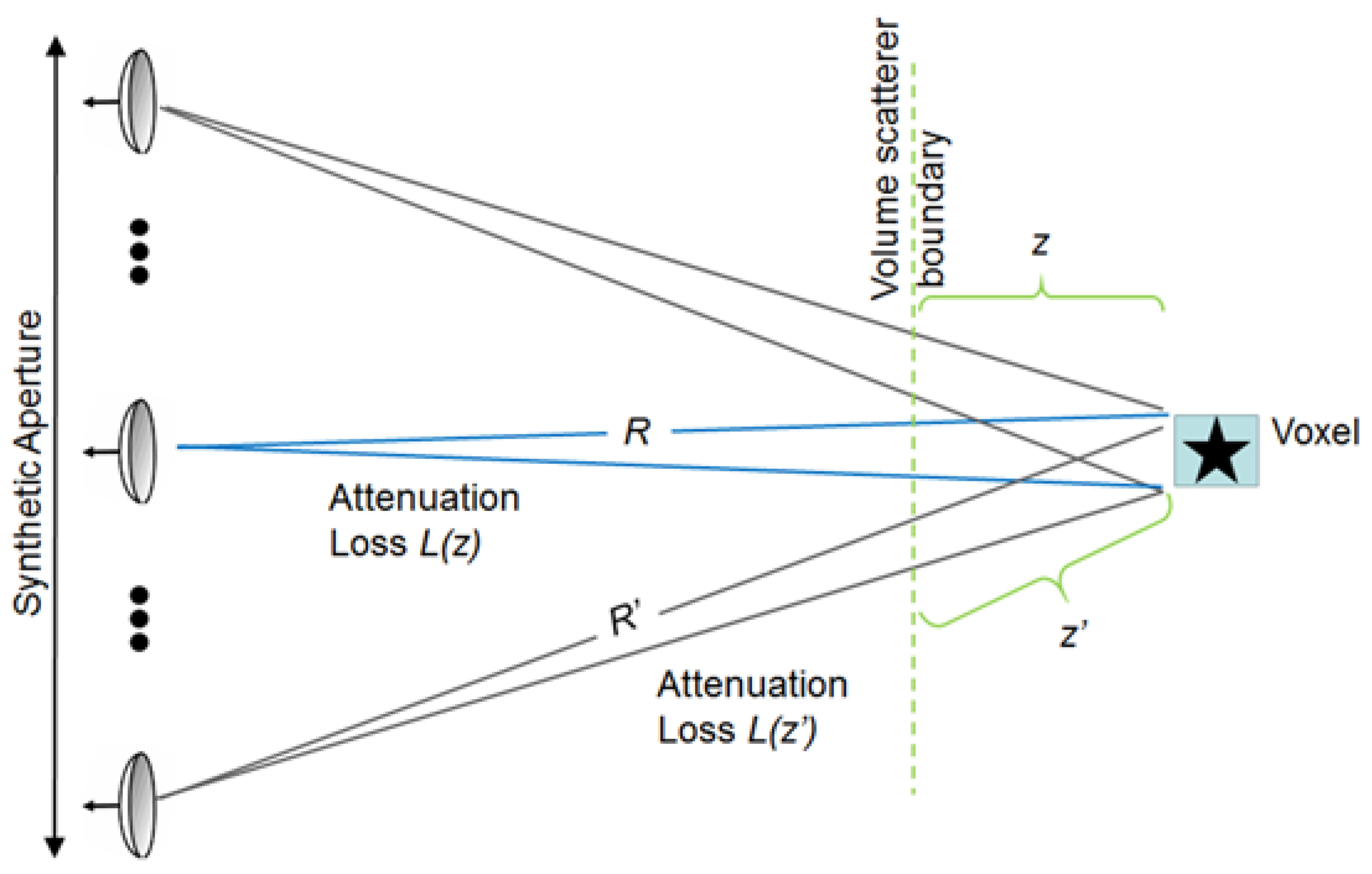
As illustrated in
Figure 4, the two-way attenuation of the signal reflecting from backscattering elements at a given voxel location depends on the characteristics of the intervening vegetation that vary throughout the tree volume. For simplicity in this paper, the vegetation path is treated as composed of discrete volume elements, and the effects of multipath within the volume scatterer are neglected when they result in path length extension longer than a single radar range bin.
Since the radar does not resolve individual leaves and branches, within each voxel, the volume scattering is modeled as a backscattering cross-section σ and an extinction cross-section κ
e. The cross-sections are assumed to be azimuthally fixed [
14] over the angles associated with the synthetic aperture observations. The attenuation
L(
z) along the signal propagation path is given by
For 3D imaging consistent with the backprojection algorithm given in Equation (5), the polar form of the attenuation equation in Equation (7) is converted to a rectangular discrete formulation
where
x’ = x/z’ and
y’ = y/z’. For convenience in this expression, κ
e has been scaled by the voxel volume. If the assumption is made that κ
e is proportional to the σ, i.e., κ
e = Aσ, a rough approximation for the attenuation is
In this paper, the constant
A is estimated from the actual data. Once the attenuation is known, the attenuation-corrected image
is computed as
In practice, the image is computed from the front of the tree to the back. Note that the attenuation term is squared due to the two-way propagation of the signal. Note that once voxel images of
I and
L are available, this model can be reversed to synthesize the appearance of the tree as viewed from other incidence angles, for example, when observed from an aircraft SAR. In this case,
L(x, y, z) is computed using Equation (9) and
I(x, y, z) using Equation (10). The synthesized 2D SAR image
S(x′′, y′′) is computed by summing the integrated path-attenuated backscatter for the voxels at the same slant range and azimuth. Ignoring 1/
R4 slant range dependence and a constant scale factor, the projected backscatter image can be approximately computed as
where
r(x’’
,y’’
) denotes the voxels at the appropriate azimuth and a fixed slant range.
The value of A is estimated by first computing the unattenuated v using Equation (9). The vegetation density is assumed to be roughly uniform when averaged over azimuth and elevation, i.e., the average attenuation versus range is roughly constant. With this assumption, the A estimate is the value of A that minimizes the slope of the root-mean-square attenuated image over the extent of the foliage. This attenuation model is only approximate but has the advantage of simplicity and requires no a priori knowledge about the tree.
A weakness of the computation shown in Equation (11) is that it does not account for changes in scattering behavior with elevation incidence angle: i.e., changes in σ can be expected as a function of incidence angle. For example, the trunk is less normal-facing when viewed from overhead, and thus has a less specular reflection compared to viewing it from the side. In addition, since the core branches have a relatively vertical orientation, they have a more favorable upward scattering than the sideward scattering observed by the ground-based radar. Adjustment for incidence angle effects is not addressed in this paper, but is reserved for a future paper.
In summary, controlled displacement and data collection in multiple dimensions using small real-aperture antennas enables formation of large 2D synthetic apertures, which, when coupled with the radar range resolution, can enable true 3D radar imaging for a distributed target such as a tree when coupled with backprojection image formation and a simple attenuation model.
3. 3D Imaging Sensor
The major elements of the ground-based radar system include a high-precision 2D scan mechanism, the radar electronics, and the image formation processing. These components are briefly described below. The synthetic aperture approach to imaging is particularly effective for short range application as the processing algorithm accounts for the fact that the target is in the near-field of the synthetic aperture while the target is in the far field of the small real-aperture antennas. To achieve similar resolution with a single real aperture antenna, a much larger antenna would be required, placing the target in the near-field of the antenna, which would make focusing more difficult.
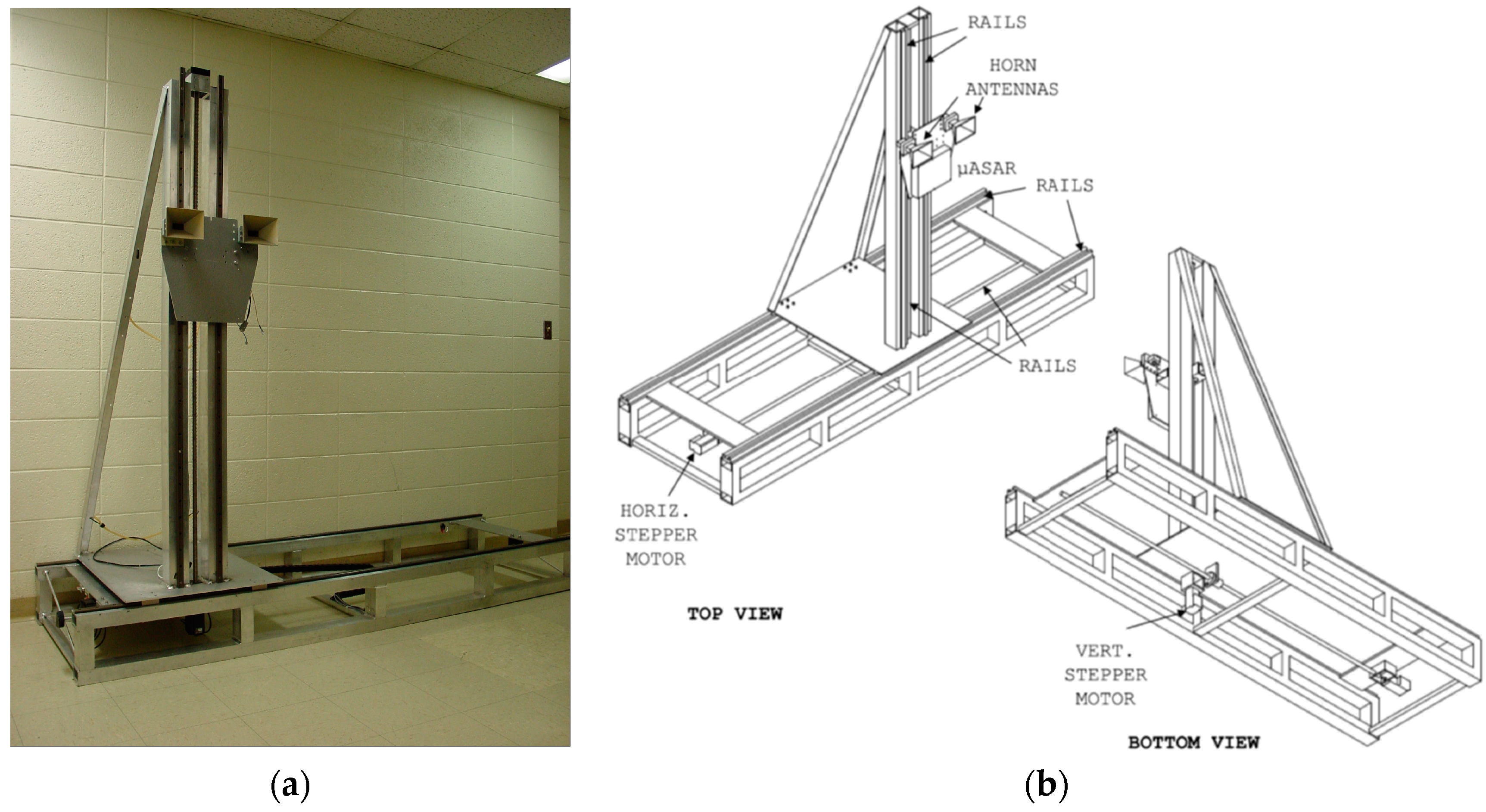
A photograph and design drawings of the student-built scan mechanism are shown in
Figure 5 [
16]. The scanner is capable of precise motion over approximately 1.7 m in the vertical and horizontal dimensions. It supports the transmit and receive antennas and the radar electronics, stopping in 5 cm increments to support Nyquist spatial sampling with dual 13.5 cm by 10 cm horns. Separate transmit and receive horns, spaced 25 cm apart, in a pseudo mono-static mode are used. The separation distance is included in the image formation processing. For this experiment, two Waveline model 5999 standard gain horns (Waveline Inc., Fairfield, NJ, USA, 2011) with 30° beamwidth in both axes were used.
For tree imaging, the scanner is typically placed 15 m to 30 m from the tree with the scanner plane orthogonal to the trunk. The scanner takes approximately 1 h to complete a full scan with short stops during radar data collection at each position. The scanner control system provides a serial data stream to the radar to report the position of the antenna assembly, which is recorded with the data. The position information is used in the image formation.
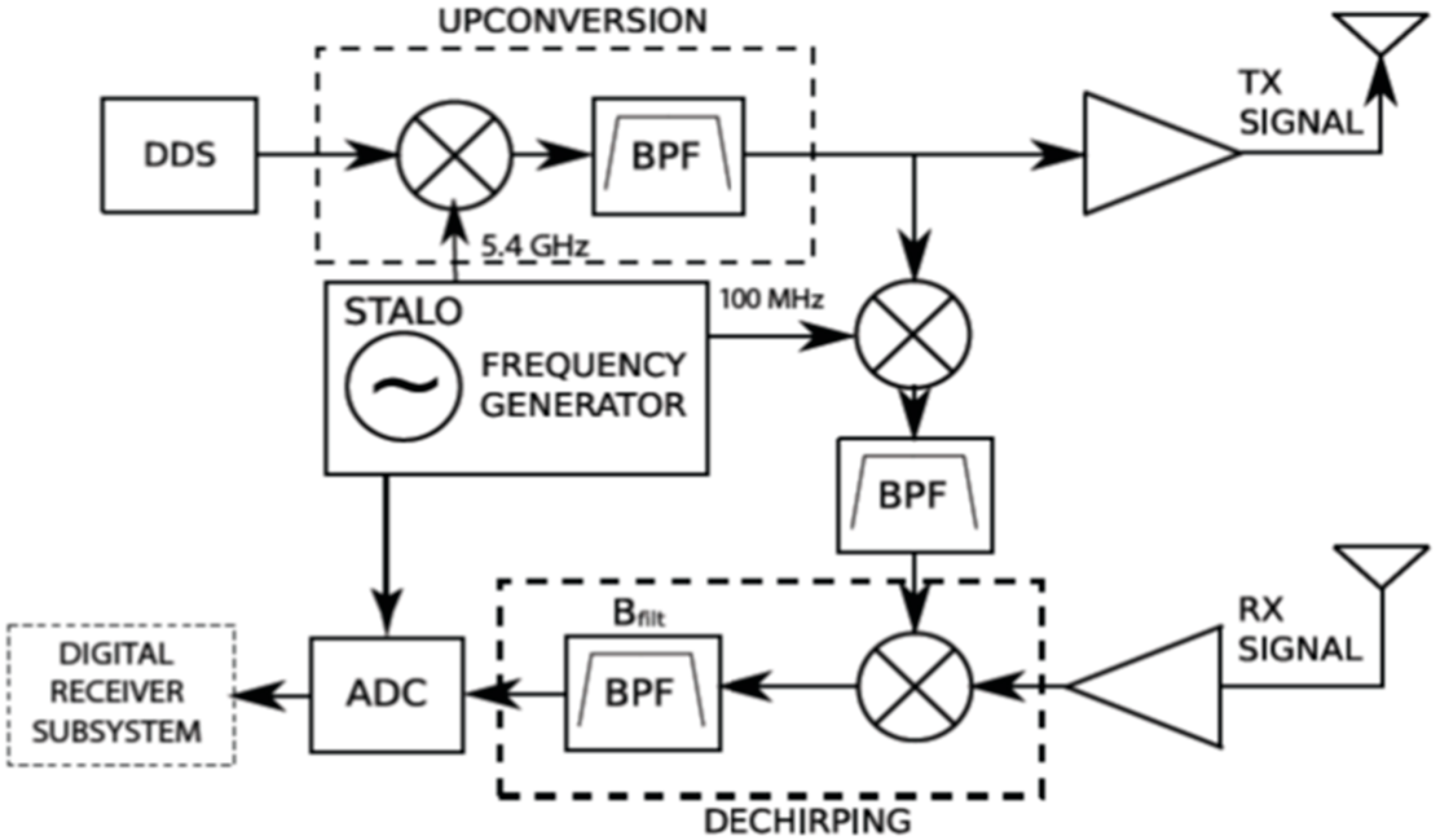
Radar data collection is accomplished using a microASAR programmed for very short-range operation. The microASAR is a compact, flexible, self-contained SAR system designed for operation in a small aircraft. It is described in detail in [
2,
3]. A block diagram of the RF subsystem is shown in
Figure 6. An LFM-CW SAR operating at C-band (5.4 GHz) with 120 MHz of bandwidth, it has a range resolution of 1.25 m. The self-contained data collection system collects raw SAR data on a compact flash disk. For the short-range operation in this application, the transmit power is set to 10 mW. Because of its small size and weight, the self-contained microASAR can be mounted adjacent to the antennas on the scanner to reduce RF losses. The bistatic microASAR continuously transmits and receives signals using two separate standard C-band horn antennas (see
Figure 5a). The two antennas have about 40 dB of isolation. Feedthrough leakage is further suppressed by the bandpass filter in the dechirping stage (see
Figure 6) of the microASAR hardware [
2]. The location of the antennas are recorded in the data. Only data collected from when the scanner is stopped at one of the scan positions on the 5 cm by 5 cm position measurement grid are used in the image formation. Multiple pulses at each location are averaged to improve the signal-to-noise ratio. In this experiment, measurements were collected at vertical (VV) polarization.
In processing the data, the raw microASAR data is first range-compressed by windowing and computing the fast Fourier transform (FFT). The range-compressed data is used in the 3D backprojection algorithm to create 3D voxel images of radar backscatter from the target over a 3D grid centered on the target tree. As indicated earlier, in this study, the voxel size is set to 10 cm horizontal by 10 cm vertical by 10 cm in ground range. Note that, due to the large relative range migration involved in short-range operation, the effective range resolution in the synthetic aperture image is finer than the radar bandwidth would normally support. The positions and separation distance between the transmit and the receive antennas are accounted for in the backprojection processing geometry. While graphics processing unit (GPU)-based processing algorithm to form images could have been used [
17], for this study, the processing is done in Matlab (Mathworks, Sunnyvale, CA, USA, 2011) without attempting formal calibration of
A or σ, i.e., the images are uncalibrated [
16]. Unfortunately, radar calibration is hindered by the loss of critical calibration data due to a human error. Calibration was to be based on observations of an isolated 20 cm diameter aluminum sphere hanging from a thin nylon line.
Note that a similar 2D synthetic aperture setup has been successfully used for observing volume and layer scattering within a snowpack [
18,
19]. The resulting 3D imaging capability enables tracking the evolution of the backscatter within the key snow layers associated with the risk of avalanches.
4. Results
A number of 3D SAR images of different tree types have been collected. Data collections were done on calm days to minimize leaf motion.
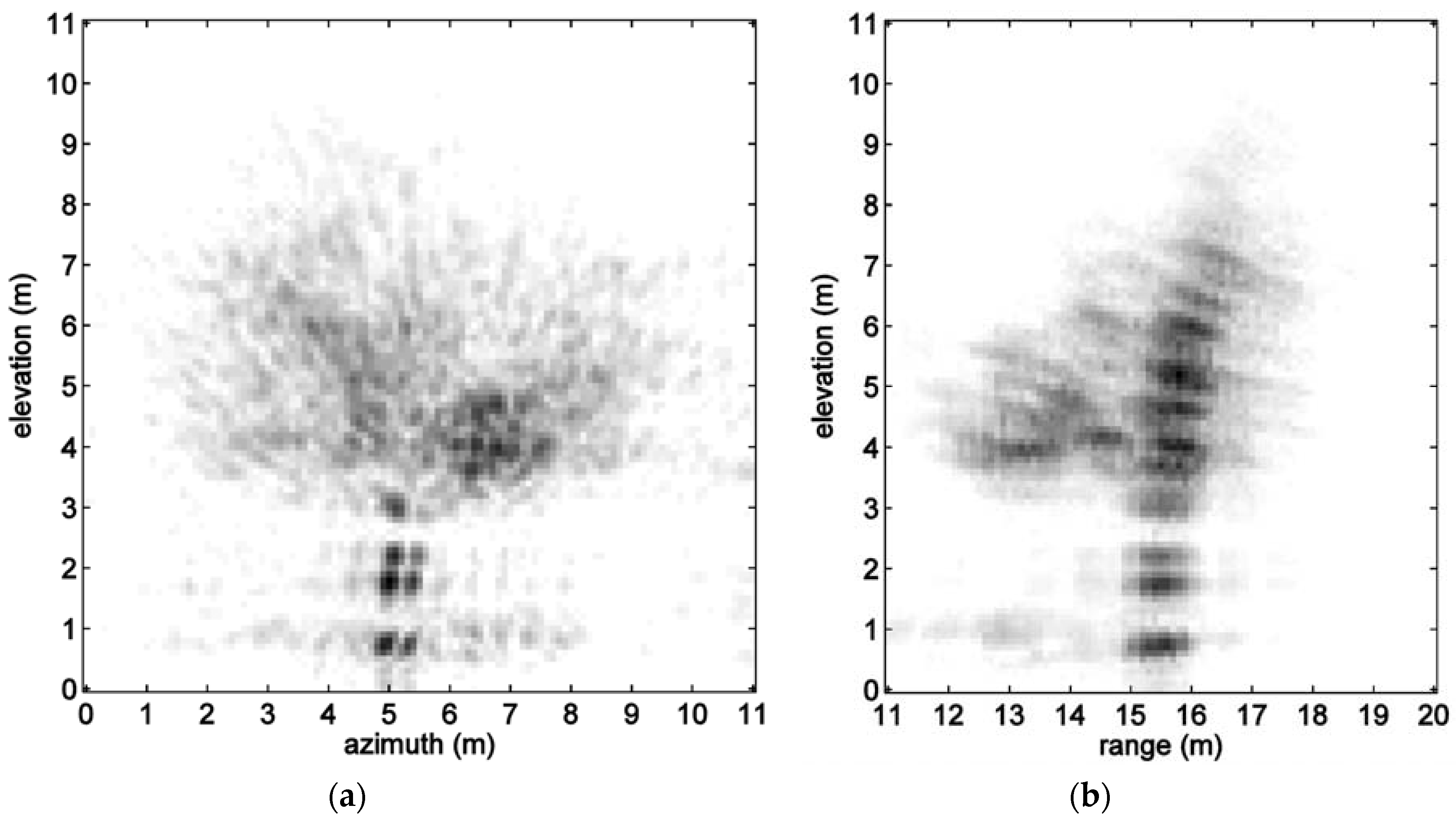
Figure 7 shows an optical image of a small Norway Maple tree, and corresponding radar views of it are provided in
Figure 8 where the radar operated at a distance of about 30 m from the tree base. Unfortunately, the multipath from the ground limits the accuracy of the near-ground imaging of the trunk. Because of the difficulties of visualizing the 3D voxel image, only integrated 2D slices through the 3D image are presented [
16]. The arbitrarily-scaled linear grayscale has been selected to eliminate background noise. Images from two additional trees are shown in
Figure 9 and
Figure 10. The features and their sizes in the radar images are validated from manual measurements of the tree [
16].
The tree in
Figure 7 and
Figure 8 has dense foliage on the left, but is sparse on the right and is missing foliage at its rear due to storm damage. As expected, at 10 cm by 10 cm by 10 cm, the resolution of the 3D voxel images is too coarse to resolve individual leaves or small branches. However, the images clearly reveal the large-scale structure of the tree canopy. Though attenuated by its passage through the foliage, the radar signal successfully passes through the forward part of the canopy to enable imaging of the rear part of the tree canopy. This is more evident in later tree images in
Figure 9 and
Figure 10 where the trees have full rear foliage. Note that there is a close resemblance of the optical and radar images, though the radar image includes backscatter values from within the canopy, while the optical image is unable to see significantly into the foliage.
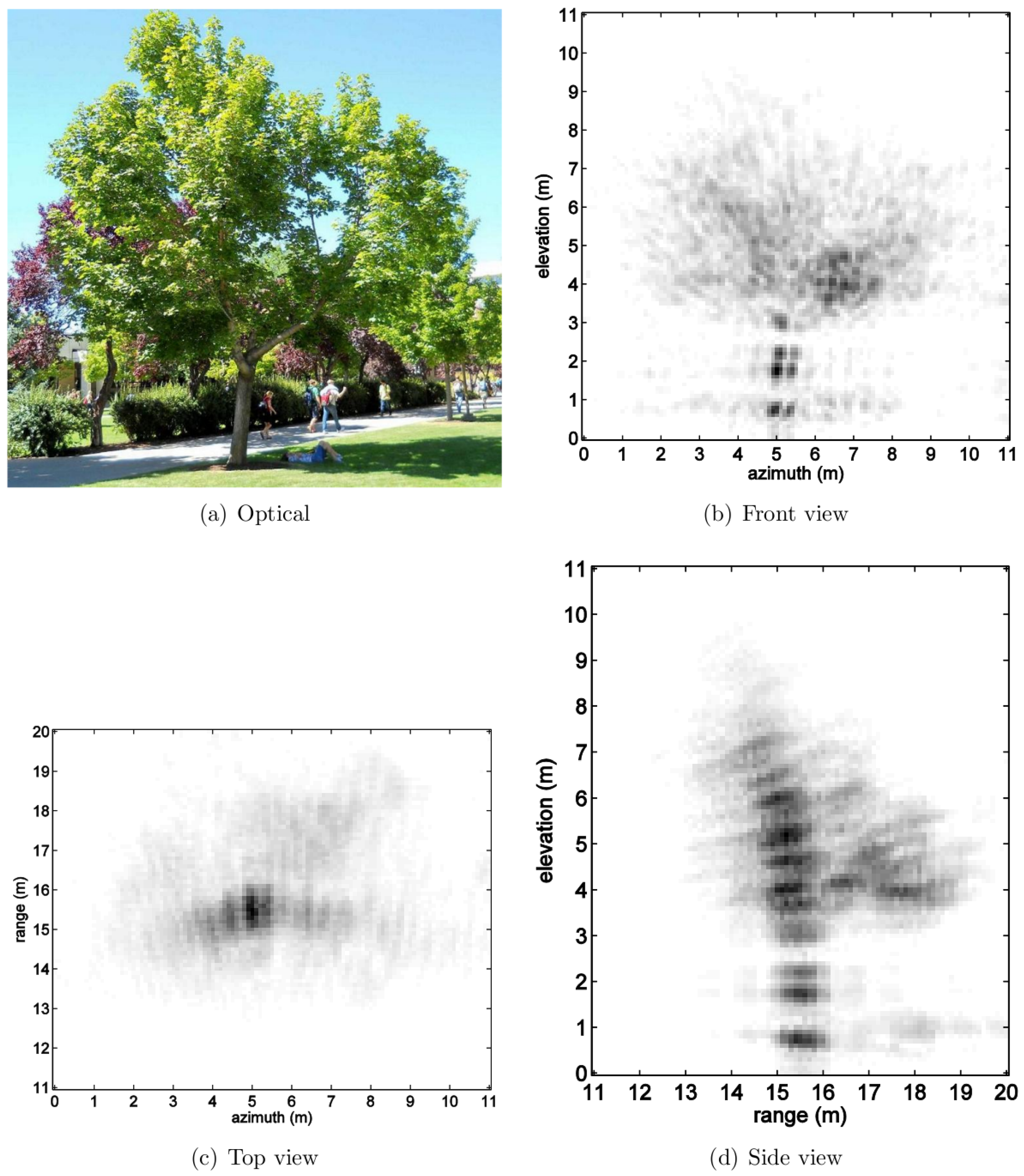
The radar images of trees shown in
Figure 9 and
Figure 10 help provide insight into the 3D structure of the trees, including observation of a wayward branch on the right side of the tree in
Figure 9. While it is clear from the optical image that the branch is extending far to the right, the side view from the radar image also shows that the branch is extending forward toward the radar. This side view is, in effect, a synthesized depth image since the radar only observes from the front. Note that smaller patches of leaves held by unresolved branches extend forward and backward from the trunk. From the top view, which is also a synthesized image, the tree foliage extends closer to the radar than it does to the rear, something validated by direct manual measurement of the tree [
16].
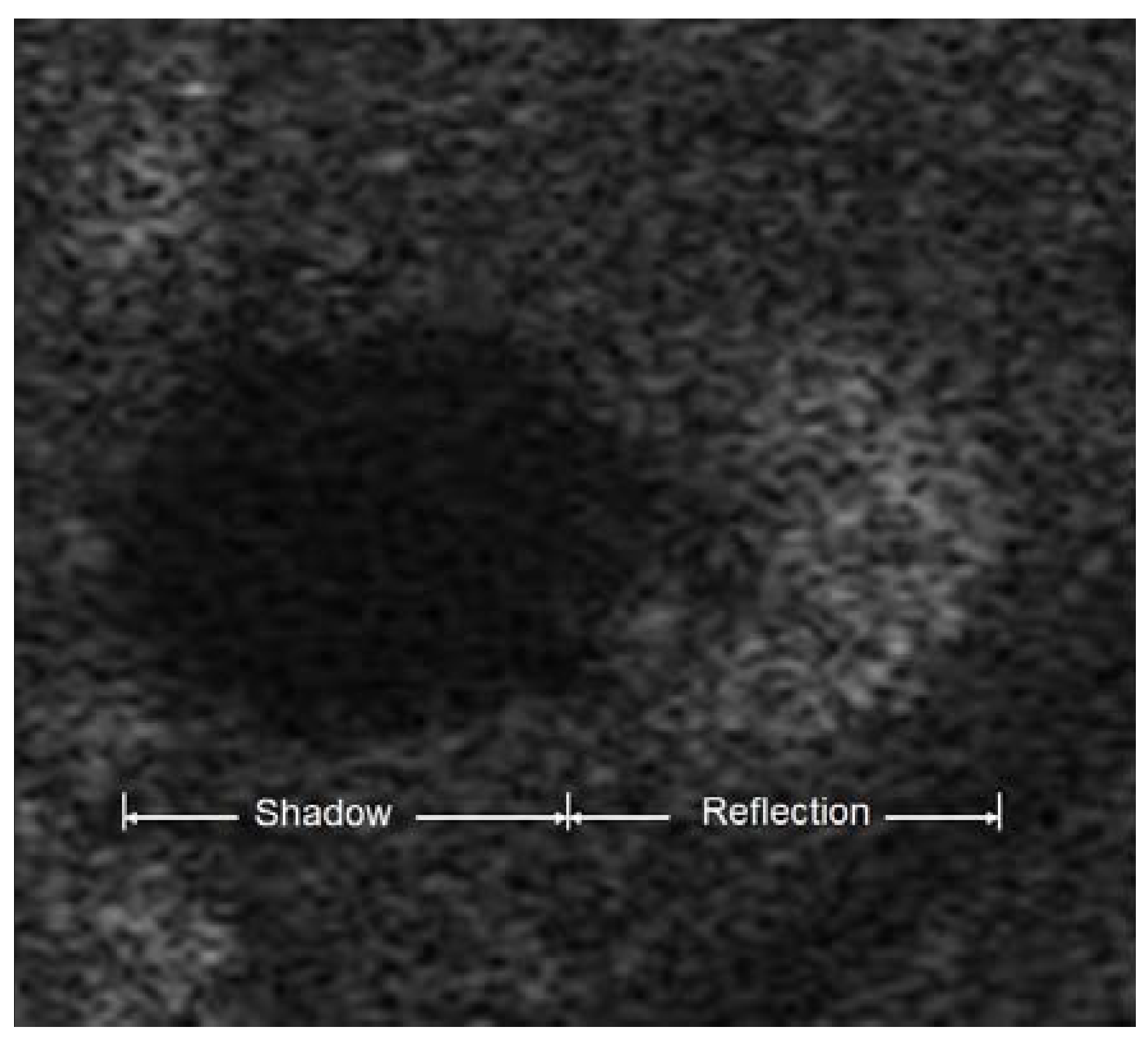
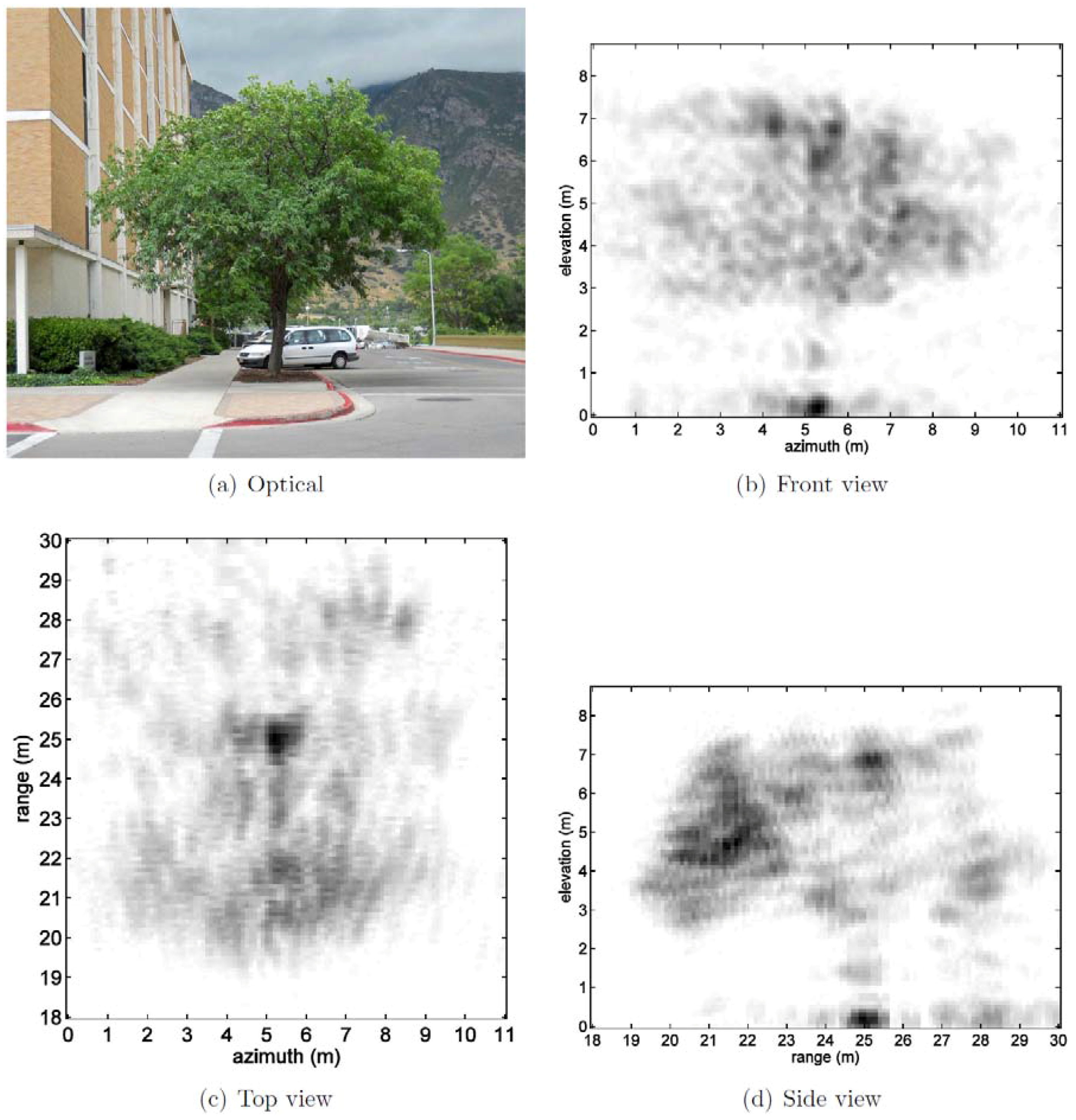
Figure 10 shows a tree next to a large building. By imaging only the volume corresponding to the location of the tree, the building is excluded from the image. As expected, no volume imaging from within the building was observed. This tree is a healthy, symmetric specimen. The total attenuation through the tree was appreciable, leading to some loss in image quality of the dense foliage at the rear of the tree.
From the 3D voxel images of
I and the estimated
A value, the appearance of this tree in a conventional C-Band SAR image with the same range resolution is computed using Equation (11) and shown in
Figure 11. Unfortunately, airborne SAR images of these trees during the growing season are not available for comparison. Instead, the image is compared with a conventional airborne SAR image of a different tree shown in
Figure 3. The synthetic SAR image uses an incidence angle of 50°, which corresponds to the incidence angle of the SAR image of the tree in
Figure 3. Though the tree shadow is not included in the synthetic image, the modelled backscatter from the synthetic tree image resembles the backscattering from the SAR image, confirming the viability of the approach.