Group Counterfactual Explanations: A Use Case to Support Students at Risk of Dropping Out in Online Education

Abstract

This paper proposes the novel application of group counterfactual explanations to the problem of predicting students at risk of dropout. Our objective is to explain how to recover the largest possible number of students while minimizing effort and cost. Using group counterfactuals, instructors and institutions could recover large groups of students with minimal remedial actions. For testing, we used the well-known public educational Open University Learning Analytics Dataset (OULAD), which contains students’ clicks made throughout interactions with online courses. We modified and adapted the only existing algorithm for the generation of group counterfactuals, named GROUP-CF. We also used the Diverse Counterfactual Explanations (DiCE) individual counterfactual algorithm with the K-means clustering method and new options in discovering the most representative counterfactuals for a group of students. The results obtained are very promising; our approach can be successfully applied to recover 99.3% of students at risk of failing in a shorter time in comparison to traditional individual counterfactuals. Moreover, although a group counterfactual proposes to change a greater number of students’ features, the values are lighter and therefore seem easier to apply than the ones obtained with individual counterfactuals. This work opens up a new line of research in education.

1. Introduction

In the current era of rapidly expanding real-world artificial intelligence (AI) applications, the transparency and interpretability of machine learning (ML), data mining (DM), and deep learning (DL) models have become critical. However, often, these models are considered ‘black boxes’ because of the difficulty in understanding the reasons behind their decisions [1]. This lack of clarity is of particular concern in sectors where automated decisions have a significant impact on people’s lives, such as education, health, or finance. In this context, explainable artificial intelligence (XAI) has emerged as a key discipline, seeking to unravel the inner workings of ML models and provide clear and understandable explanations for end users. One of the most prominent approaches in the field of XAI is the generation of counterfactual scenarios or explanations [2]. These are hypothetical scenarios that show the reality of what would have happened if other decisions had been made. Counterfactuals provide an intuitive way to understand how small changes in a model’s inputs can change its decisions. For example, a counterfactual scenario might answer the question, ‘What should be different in the student X’s learning behavior so that he/she would not be predicted as at risk of dropping out?’. This ability to provide clear, action-oriented explanations has led counterfactuals to feature prominently in the XAI literature and especially in the education domain [3]. Additionally, the current increasing interest in generating counterfactual scenarios arises not only because of their easy interpretability but also because various legal analyses suggest that these counterfactual scenarios meet the requirements of the General Data Protection Regulation (GDPR), as they provide clear and understandable explanations of automated decisions without compromising the privacy of individuals [4].

However, all research on and applications of counterfactuals focus on individual scenarios, i.e., each instance receives a unique prediction and explanation. This approach, while useful for each particular instance or student, does not address cases where multiple instances or students may share common characteristics and thus benefit from a group counterfactual scenario. The generation of group counterfactuals allows for the creation of a single explanation for a set of similar instances or students, facilitating the identification of patterns and promoting efficiency in decision making. There are only a few works that deal with the problem of generating group counterfactuals, seeking to provide more information about patterns than individual counterfactuals [5], despite the fact that this approach poses psychological advantages because it reduces stakeholders’ memory load and facilitates pattern finding [6].

In the domain of education, group counterfactuals may have endless applications. Academic failure is a major challenge nowadays, since it may have highly negative effects for educational institutions and students [7]. For example, a group of students with similar academic characteristics could benefit from the same counterfactual explaining how to prevent academic failure, rather than generating a separate explanation for each student. The identification of students at risk of academic failure is essential for timely instructional interventions [8,9], since students who fail at some point during their studies are 4.2 times more likely to drop out and leave their educational institutions [10]. There are many causes behind academic failure, among which we can find some related to aspects such as time management, family, learning, assessment, and subjects [11]. Some authors have recognized that uncooperative and hostile environments can lead to academic failure and have linked it to low motivation, low engagement, and alienation from school, suggesting that positive relations with teachers can thus be a protective factor against academic failure [12]. In addition, early academic failure, recently addressed in the literature [13], can lead to consequences such as limited job opportunities; increased risks of unemployment, inequality, and cycles of poverty; lower incomes; barriers to personal development; increased risks of social problems; and even impacts on health and well-being. It is essential to recognize the consequences of early school leaving and to work towards the implementation of education policies and programs that promote school retention, support at-risk students, and promote equal educational opportunities.

The main contribution of this paper is the proposal of a framework for generating group counterfactual scenarios in the domain of education. The purpose is to identify common patterns among students at risk of failing and provide explanations and recommendations that can guide more effective interventions to help teachers to support these at-risk students. This approach does not intend to eliminate individualized types of interventions, which are sometimes indispensable in education, but to provide a complementary approach when stakeholders need or prefer group-focused interventions. It should also be noted that this paper only addresses the generation of these group counterfactuals, and not their translation into effective actions to be applied by educators, which would be a topic for further research. Finally, to validate our framework, we defined two research questions:

• RQ1: Is it feasible to generate successful group counterfactuals for the problem of recovering students at risk of failing in a reasonable time?
• RQ2: What is the performance of group counterfactual explanations compared to individual counterfactuals according to standard indicators in this problem?

To answer these RQs, we developed a comprehensive validation process using a public educational dataset and adopted a quantitative perspective to complement the mostly qualitative validation performed by Warren and colleagues [5]. As described at the end of this paper, the results obtained from this validation process indicate that our approach can be successfully applied to generate useful group counterfactual explanations in our reference problem. These results show some clear advantages over individual counterfactuals in terms of execution time and the number of changes to be implemented in features to prevent at-risk students from failing.

The rest of the manuscript is structured as follows: Section 2 presents the background of this work and the literature related to it; the use case is presented in Section 3; Section 4 presents the validation of the proposed approach; the limitations of our study are presented in Section 5; finally, Section 6 summarizes the conclusions and presents some future lines to be addressed.

2. Background

Three areas are directly pertinent to the problem under investigation: counterfactual explanations, counterfactuals in education, and group counterfactuals. The core literature across these areas is reviewed in the following section. Figure 1 delineates the three domains and their principal works, situating our use case at the intersection of these.

2.1. Counterfactual Explanations

Counterfactuals are hypothetical scenarios or alternative situations that illustrate possible outcomes if a specific event or intervention had not taken place. They allow us to answer questions such as ‘What would have happened if instead a certain feature took the value “x” instead of “y”?’ Counterfactuals are particularly useful when randomized controlled experiments, considered the ‘gold standard’ in establishing causal relationships, are not possible. Instead, observational studies and causal analysis algorithms are used to identify and evaluate counterfactuals [17].

In recent years, different methods have been developed for the generation of (individual) counterfactual explanations. Some of the most representative ones are propensity score matching (PSM) [18], difference-in-differences (DID) [19], regression discontinuity (RD) [20], and instrumental variables (IVs) [21], as well as others based on axiomatic attribution [4] and multiobjective minimization ideas [22].

However, the most popular method is DiCE or diverse counterfactual explanations [14]. This is a post hoc explainability tool designed to generate diverse counterfactual explanations for machine learning models. Unlike other methods that focus on assessing the importance of features in individual predictions, DiCE focuses on creating alternative scenarios (known as ‘what-ifs’) in which the model’s predictions would change if certain attributes of the input were altered, making it easier to interpret for those without prior computational knowledge. Another difference from most existing methods is that, while they seek to generate explanations through the importance of variables or the visualization of graphs, DiCE seeks to generate explanations through examples, which is considered the most relevant means of generating explanations. An example of an explanation generation framework with DiCE is MMDCritic [23], which selects both prototypes and critiques from the original data points.

More recently, explanations have been proposed as a way to provide alternative perturbations that would have changed the prediction of a model [24]. In other words, given an input feature x and the corresponding output of an ML model f, a counterfactual explanation is a perturbation of the input to generate a different output y using the same algorithm. In most existing methods, the objective is to find a counterfactual explanation that minimizes both the distance to the original instance x and the loss associated with not achieving the desired prediction y. This is the standard process, which normally looks for a single counterfactual close to the original entry point that can change the decision of the model. However, the approach used in DiCE is different and focuses on generating a set of counterfactuals that not only change the decision of the model but also offer various alternatives for the user.

2.2. Counterfactuals in Education

Counterfactuals have been increasingly applied in education to improve interpretability, decision making, and intervention design, but no prior review has systematically examined their methodological, algorithmic, and presentation aspects within this domain. Counterfactual explanations can be applied in the educational field to answer important questions—for example, what should be the value of a specific characteristic/variable/factor for a student to move from being at risk of dropout to not being at risk? [25]. Understanding the interaction of factors to identify a student as at risk of dropout could help decision makers to interpret the situation and determine the necessary corrective actions to reduce or eliminate this risk [15].

Most of the research on counterfactuals in education focuses on predicting academic performance and student dropout and improving learning outcomes. For instance, the studies by Tsiakmaki and Ragos [16], Smith et al. [26], and Afrin et al. [27] use counterfactuals to identify small, actionable changes that could transform a failing prediction into a passing one. Similarly, Swamy et al. [28] and Garcia-Zanabria et al. [15] apply counterfactual reasoning to detect dropout risks and design targeted interventions, while other studies explore broader challenges such as fairness in admissions or optimizing cognitive learning experiences [29,30]. Collectively, these works demonstrate that counterfactuals not only improve the interpretability of AI models but also foster data-driven decision making and personalized educational interventions.

Regarding the specific methods and algorithms used when generating counterfactuals in education, it is possible to identify three main categories: optimization-based, instance-based, and heuristic search categories following Guidotti [2]. Optimization-based methods, such as diverse counterfactual explanations (DiCE) and the contrastive explanation method (CEM), are the most common, focusing on balancing validity, proximity, diversity, and sparsity. Instance-based approaches (e.g., NICE and CORE) identify similar real examples in the data to construct plausible counterfactuals, while heuristic approaches like MOC rely on genetic algorithms to find optimal solutions. Additionally, several studies explore causality-aware methods, such as the path-specific counterfactual (PSC) [29] and structural causal models (SCMs) [31], which explicitly model cause–effect relationships among educational factors. The authors highlight emerging research integrating large language models (LLMs) and generative adversarial networks (GANs) for counterfactual generation [32,33], as well as the use of group-based and path-based counterfactuals, which could help to design more interpretable and context-aware educational interventions.

An important problem when generating counterfactuals in education is how counterfactuals are presented to stakeholders. The way in which these findings are presented can influence the interpretation and understanding of the results by the audience, including their capacity to discern major patterns and trends. There are five main forms when presenting counterfactuals in education: textual, tabular, visual static, visual interactive, and flow-/process-based presentations. Textual explanations (e.g., Afzaal et al. [34]; Ramaswami et al. [35]) use natural language to provide recommendations, while tabular formats [16,36] organize feature changes systematically. Visual static forms (e.g., [29]) include graphs and causal diagrams, whereas interactive dashboards [15,37] enable users to explore counterfactual outcomes dynamically. The authors argue that integrating multiple presentation modes—textual for interpretability, visual for clarity, and interactive for engagement—can significantly improve how educators understand and apply counterfactual insights in practice. However, they note that many studies still lack advanced visualization or user-centered presentation approaches.

Thus, counterfactual explanations hold significant potential to transform educational analytics, promoting transparency, fairness, and personalized learning. Some current research challenges and directions for future work are as follows: integrating prescriptive analytics and personalized feedback, extending counterfactual reasoning to underexplored areas such as student motivation and engagement, incorporating causal inference and reinforcement learning, and designing interactive, multimodal visualization frameworks. While current research demonstrates substantial progress, the educational field of applying/generating counterfactuals is still in the early stages in terms of fully harnessing counterfactual reasoning to support informed, equitable, and actionable decision making.

2.3. Group Counterfactuals

Despite the recent boom in AI, there are still few papers related to the generation of (individual) counterfactuals and even fewer with regard to group counterfactual generation. To the best of our knowledge, there is only one paper proposing an algorithm for the generation of group counterfactuals, namely that by Warren et al. [5]. The main objective is to provide users with an understanding of how the model’s decision would change if certain characteristics of the group were modified, which is particularly relevant in scenarios where decisions collectively affect multiple instances or users.

In order to generate these group counterfactuals, Warren et al. [5] developed an algorithm whose starting point is a set of related instances that have been classified by the model as being of the same class. Taking these inputs, the four main steps of the method are as follows.

• Identification of key features: For each instance, multiple individual counterfactual explanations are generated using DiCE. They then analyze the differences in features that produce the classification change in these individual counterfactuals, identifying those features that are most effective in altering the model’s prediction. These features are candidates for inclusion in the group counterfactuals.
• Sampling of feature values: Once the key features have been identified, values for these features are sampled from data points in the counterfactual class. These sampled values are more likely to generate valid counterfactual transformations, as they come from real data points.
• Counterfactual candidate generation: Key feature values, obtained from sampling in the counter class, are substituted into the original instances to generate candidate counterfactuals for the group. These modifications are counterfactual transformations that could potentially change the classification of the entire group.
• Selection of the best explanation: Finally, the feature value substitutions in the candidate counterfactuals are evaluated for validity and coverage. Validity refers to whether changes in features effectively alter the classification of instances to the opposite class, while coverage assesses whether this change applies to all instances in the group. The counterfactual with the highest coverage is selected as the best explanation for the group.

In their work, group counterfactuals were tested and compared to individual counterfactuals by a group of 207 individuals with no prior knowledge of AI. The evaluation concluded that group counterfactuals produced modest but definite improvements in users’ understanding of an AI system, and they reached the conclusion that group counterfactuals are more accurate and trustable than individual counterfactuals; therefore, users are more satisfied and confident.

Note that the work presented by Warren et al. [5] is of major relevance due to being the first (to the best of our knowledge) tool for the generation of group counterfactuals. However, it also poses some open problems because this is achieved in an isolated way for a particular group of instances, failing to address the problem of taking a whole population and establishing different clusters or groups of instances for which counterfactuals can be generated. Moreover, the authors do not present comprehensive experimentation on how many instances should be taken to build them or the percentage of features to be changed.

The use case presented in this paper seeks to shed some light on how to apply Warren et al.’s ideas, and it is unique since it is the only one that takes a whole population of instances, clusters them, and generates group counterfactuals for each group, comprising a series of in-depth experiments to extract conclusions on the application of Warren et al.’s ideas in real, complex scenarios like academic failure in education.

In our case, we modified Warren’s approach by providing a context for it, considering the following:

(a)

The criteria used to define potential groups of individuals for which a group counterfactual can be built;

(b)

The assignment of individuals from a whole population into groups by means of a clustering process;

(c)

The selection of the main features to be modified in the group counterfactuals;

(d)

The efficient selection of individuals to be used to build the group counterfactual for each group.

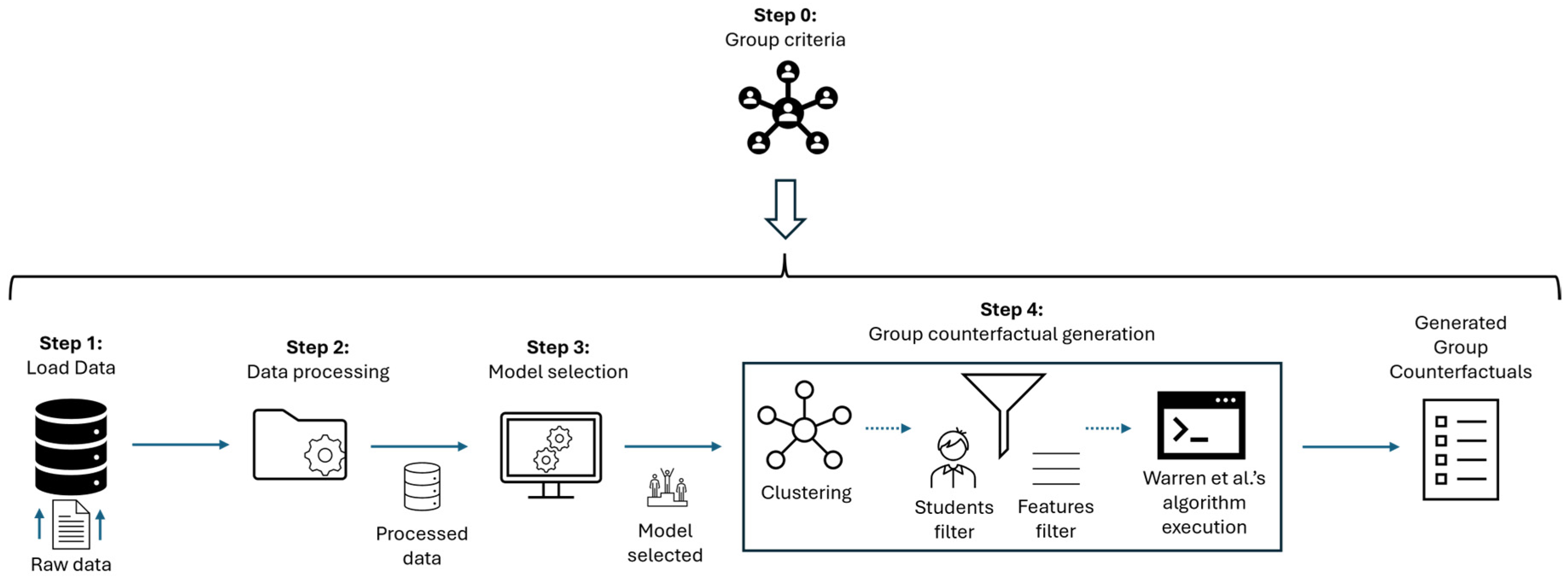
3. Materials and Methods

The main purpose of this section is to describe the methodology used to discover group counterfactuals from educational data. To do so, a series of four sequential steps are taken, as graphically depicted in Figure 2. This process begins with data loading (step 1) and finalizes with group counterfactual generation (step 4), obtaining the group counterfactuals as results.

Note that the final purpose is to obtain a group counterfactual for each of the groups of interest into which our population is divided. Therefore, it is first necessary to define the criteria to obtain these groups, which occurs in a previous task that can be considered step 0 in our approach. In our use case, we divide the student population into groups according to their activity-level behavior (i.e., clicks on different educational resources, as explained later), since it is expected that highly active students will need different group counterfactuals compared to those who show more inactive behavior during the course. In addition, these attributes are actionable and easily altered in interventions; therefore, it is reasonable to include them in counterfactual explanations. This strategy can vary depending on the analyst’s area of focus.

Once these criteria are defined, the steps of our approach, depicted in Figure 2, are as follows:

• Data loading (step 1): Data are loaded into the pipeline.
• Data processing (step 2): Data are conveniently processed so that machine learning algorithms can obtain predictive models from them.
• Model selection (step 3): The best model is selected based on the results obtained.
• Group counterfactual generation (step 4): From the model obtained and the dataset itself, a process is conducted to obtain a group counterfactual for each of the groups defined in our problem. As illustrated, this step begins with a clustering process to divide the population according to the criteria defined in step 0. It also defines values for some parameters related to the features to be used and the students to consider in each cluster, before finally applying Warren’s algorithm.

These steps, formally presented in Algorithm 1, are adopted since this is the natural way to build counterfactuals. It is crucial that the data are loaded and cleaned so that we can obtain a representative predictive model, which is the starting point in making predictions and, therefore, building counterfactual scenarios. In the following subsections, we will explain in detail each of these steps.

Algorithm 1: Group counterfactual generation

Input: RD                 //Raw dataset Output: GC                //Group counterfactuals 1: Load(RD)                 //Load data onto the pipeline 2: PD ← Data_Processing(RD)         //PD denotes processed data 3: BM ← Model_Selection(PD)         //BM denotes best model 4: C = {Ci} ← Clustering(PD), I = 1..k         //Ci denotes each of the obtained clusters; k = n. clusters 5: Determine %f and %st           //% of features and students to be considered 6: Determine m               //m is the most suitable method of selecting students 7: For each i 8:  C’i ← Subset(PD,Ci,%st,m)       //We select only %st of students 9:  GCi ← Warren_Alg(PD,BM,C’i,%f)      //See [5] for all details of Warren et al.’s algorithm 10: Return GC = {GCi}, I = 1..k

3.1. Data Loading

In our use case, we choose to use the public Open University Learning Analytics Dataset (OULAD) [38], which contains information about 22 courses, 32,593 students, their assessment results, and records of their interactions with the virtual learning environment. It was collected at the Open University in 2013 and 2014. We use the dataset for a STEM course, named DDD in the original data source, conducted in 2013 and 2014 with 2296 students.

The data consist of 473 variables, of which only the columns related to student interactions (clicks) in the virtual learning environment are loaded, reducing the number to 457 columns (as our strategy is to analyze activity behavior, we decided not to include features that reflect other characteristics of students, such as demographic, registration information, or assessment data). The columns reflect different categories, distributed across 41 weeks (4 weeks before starting the course and the 37 weeks that the course spans). The categories are the following: externalquiz, forumng, glossary, homepage, oucollaborate, oucontent, ouwiki, resource, subpage, url, total_clicks. The target variable is final_result, which is a binary variable that can take the values of pass (1620 students) and fail (676 students).

A graphical summary of the data used is presented in Figure 3.

3.2. Data Processing

Once the described dataset is loaded, the next step consists of preparing the data for modeling development. We perform two data processing tasks to summarize all features (to reduce the problem from sequential data to tabular data) and to address the issue of class imbalance.

First, we summarize the click columns by category so that the new columns will be composed of the clicks of all weeks added together according to each category. Thus, finally, the new 10 features/attributes are the following: n_clicks_externalquiz, n_clicks_forum, n_clicks_glossary, n_clicks_homepage, n_clicks_oucollaborate, n_clicks_oucontent, n_clicks_ouwiki, n_clicks_resource, n_clicks_subpage, and n_clicks_url. These represent the total number of clicks performed during the course by each student on the different educational resources, such as external quizzes, forums, glossaries, etc. See [38] for detailed descriptions of all attributes. We decided to adopt this approach, which deals with fewer attributes, for two reasons: first, it reduces the time required to create the model and the counterfactuals; second, it results in more concise counterfactuals that are easier to interpret and, therefore, more trustable.

Second, given the nature of the data, there is some imbalance between the two classes. Therefore, the SMOTE class balancing technique was used [39]. This technique generates random samples of the minority class until it matches the size of the majority class, with the aim of improving the model’s predictive performance. To conduct this task, we used the SMOTE functionality of Python 3.9 included in the library imblearn.over_sampling [40] with the following settings: sampling = auto (default); random_state = 42 (initial seed); k_neighbors = 5 (default).

3.3. Model Selection

Once the data had been processed, the next step was to select a predictive model built with the whole population and with all features defined in the data processing step. For this purpose, we explored two different approaches: on one hand, a classical machine learning model, random forest, in its standard configuration; on the other hand, an AutoML tool called AutoGluon [41].

Random forest was chosen as a starting point because of its robustness and ability to handle nonlinear features without excessive preprocessing. It was configured with the default parameters to establish a baseline and evaluate the initial performance. Moreover, AutoGluon was selected to explore an automated approach, taking advantage of its ability to perform hyperparameter optimization and model selection efficiently. This approach allows the comparison of the results obtained with a traditional model versus those provided by a system that seeks to maximize performance with as little manual effort as possible.

Note that the selection of the best model will be performed mainly on the basis of the F2-Score, since this metric prioritizes recall (although it also considers accuracy), which is crucial in this context, where correctly identifying students at risk of failing is more important than minimizing the number of false positives. By maximizing the F2-Score, we seek to ensure that the model captures as many true positives as possible (students who will actually fail) while maintaining an acceptable balance with respect to false positives. This will allow for effective interventions to reduce academic failure, prioritizing those cases that the model considers most likely to fail and, therefore, where support actions will have a greater impact.

For the random forest, the base hyperparameters were used. The only modification made was to increase the iterations to 1000 in order to increase the likelihood of obtaining a better model. Figure 4 presents the confusion matrix generated by the model, which displays the number of correct and incorrect predictions for each class (NF = No Fail; F = Fail). As can be seen, out of the 486 students who did not fail, 400 were correctly classified as not failing students and 86 were mistakenly classified as failing; moreover, out of the 202 students who failed, 69 were mistakenly classified as not failing students, while 133 were correctly classified as failing. The value obtained for the F2-Score metric was 0.65.

Regarding AutoGluon, the ‘best_quality’ preset was used, which seeks to obtain the best results regardless of the training/inference cost and time spent. AutoGluon tests multiple models, seeking the best model and its hyperparameter combination.

Table 1. AutoGluon best models.

Model	F2-Score
ExtraTrees_r4_BAG_L1	0.688
RandomForest_r34_BAG_L1	0.683
ExtraTrees_r172_BAG_L1	0.675
ExtraTrees_r126_BAG_L1	0.668
ExtraTrees_r178_BAG_L1	0.663
RandomForest_r15_BAG_L1	0.649
RandomForestGini_BAG_L1	0.645
RandomForest_r166_BAG_L1	0.645
RandomForest_r39_BAG_L1	0.642
RandomForest_r127_BAG_L1	0.641

presents the top 10 best-performing models selected by AutoGluon from those tested according to the F2-Score metric. For the sake of reproducibility, note that 10-fold cross-validation was the approach employed to obtain the quality metrics of the models considered, on which model selection was based.

As can be seen, ‘ExtraTrees_r4_BAG_L1’ is the best model obtained by AutoGluon, obtaining an F2-Score of 0.688 in the test data. Note that the F2 metric places a greater emphasis on recall (students that fail are the focus of our research), but, in OULAD, the number of students who fail is smaller than the number of those who do not. The F2-Score of 0.688 is therefore tied to the data used, but, given the imbalance, we consider the model feasible. In addition, the model obtained a value of 0.81 for the area under the ROC curve (AUC ROC) metric, which indicates that the model is useful, particularly in domains where it is crucial to separate classes, as in education or medicine [42]. AutoGluon’s ‘ExtraTrees_r4_BAG_L1’ obtains an approximately 5% greater F2-Score than random forest (0.683); therefore, this model is selected to produce the predictions and generate the counterfactuals. Its confusion matrix is shown in Figure 5 (NF = No Fail; F = Fail). In this case, out of the 486 students who did not fail, 361 were correctly classified as not failing, and 125 were mistakenly classified as failing students; moreover, out of the 202 students who failed, 53 were mistakenly classified as not failing, while 149 were correctly classified as failing students.

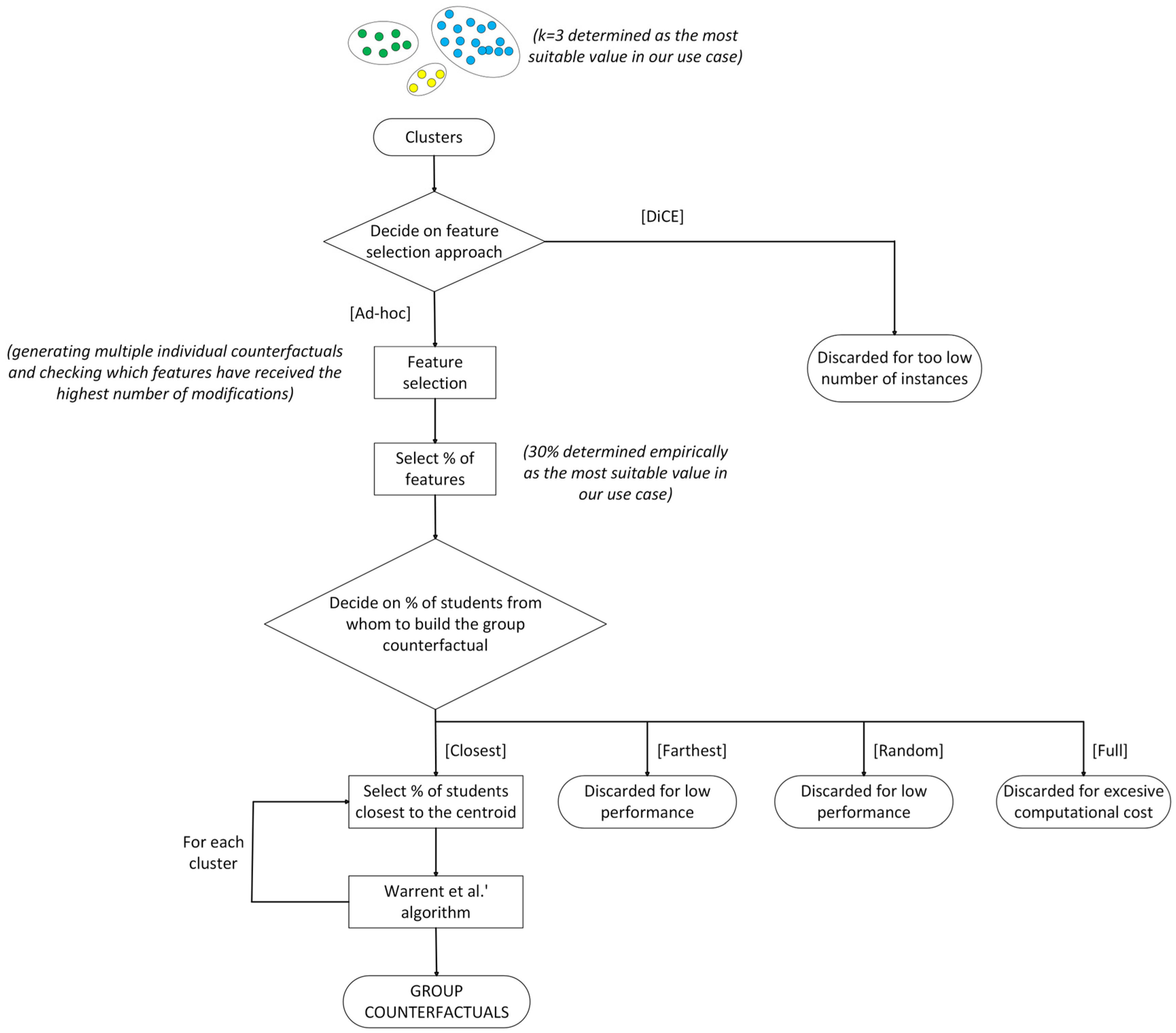
3.4. Group Counterfactual Generation

As explained previously in this paper, the generation of group counterfactuals utilizes the algorithm presented by Warren and colleagues. This algorithm takes a series of (homogeneous) instances and generates a group counterfactual for them. The mentioned algorithm has a series of parameters, mainly related to the features to consider and the number of them that can be altered in the resulting counterfactuals.

Our approach must deal with a whole heterogeneous population, where Warren’s ideas cannot be directly applied. Previously, it was necessary to split the population into groups of interest composed of homogeneous individuals, where Warren’s approach could be implemented. In addition, in a real scenario, it is not practical to build counterfactuals using all the available features, since it is difficult to identify interventions from them. It is therefore necessary to find a balanced number of features to be varied in the counterfactuals generated. Finally, the number of individuals in these groups may be huge, and there may be a high computational cost in building counterfactuals from all of them. It is therefore of interest to explore different alternatives that consider only some representative instances from whom the counterfactual can be generated in each cluster.

Considering these aspects, before applying Warren’s algorithm to the problem of students’ academic failure, we must address three issues:

• The split of the whole population into groups, for which we will use clustering techniques;
• The selection of features to be modified by the group counterfactuals;
• The selection of the instances (students) of each group from whom we will build the group counterfactual.

The solutions presented for each of the above issues are described in Section 3.4.1, Section 3.4.2 and Section 3.4.3, respectively, and formally presented in the flow diagram depicted in Figure 6. Once the clusters are defined, the features selected, and the students identified, we can apply Warren’s algorithm, for which we do not provide an additional explanation since it has been already described in Section 2.3 and in Warren et al. [5]. However, we present the counterfactuals resulting from the application of this algorithm in Section 3.4.4.

3.4.1. Clustering

As previously explained, it is important to decide which groups of interest to analyze in advance. In this paper, we focus on the activity levels shown by the students according to their interactions (clicks) with the different resources. Once this aspect is clarified, the students are divided into groups so that we can obtain a representative group counterfactual for each group.

In our approach, we obtain these groups by means of a clustering process, since this is the most feasible way to obtain groups from a series of students. First, we select only those students who are labeled with a ‘fail’ class value. The final goal is to build a counterfactual for each group of students who fail, so the focus must be placed only on these students.

Given the numerical nature of the data, we decided to use the K-means algorithm [43,44] for clustering, since this algorithm is particularly efficient for numerical data, minimizing the sum of the squared distances between the points and the cluster centroid (the point located at the center of the cluster). For the sake of reproducibility, the normalized Euclidean distance was employed to compute the distance between instances. However, K-means has a disadvantage whereby the number of clusters must be defined in advance. To resolve this issue, we used the elbow method to determine the desired number of clusters. This method consists of calculating the inertia (the sum of the squared distances between the points and their centroids) for different values of k, the number of clusters. This method allows us to identify the optimal value of k by observing the point where the reduction in inertia begins to decrease less steeply, forming an ‘elbow’ in the graph, as depicted in Figure 7. This figure represents the within-cluster sum of squares (WCSS) value, depending on the value of ‘k’ considered for the number of clusters. It is observed that, starting from the value k = 3 on the x-axis, the peak in the elbow begins, which indicates an adequate number of clusters. Therefore, we proceed to run K-means specifying 3 clusters. The elbow method is based on quantitative calculations (WCSS); thus, despite applying visual heuristic principles, it has attracted the attention of the academic community in the last few years [45,46].

Once K-means is executed, we obtain the three clusters summarized in

Table 2. Cluster analysis.

0	n_Students		n_Clicks_Externalquiz	n_Clicks_Forumng	n_Clicks_Glossary	n_Clicks_Homepage	n_Clicks_Oucollaborate	n_Clicks_Oucontent	n_Clicks_Ouwiki	n_Clicks_Resource	n_Clicks_Subpage	n_Clicks_Url
0	499	mean	3.5	59.38	4.53	92.75	3.35	86.57	11.85	22.3	58.76	7.02
		stdev	4.8	59.9	13.41	61.16	6.84	78.56	24	19.44	51.43	7.9
1	12	mean	20.91	1239.41	11.08	978.83	29.75	215.41	130.25	114.41	491.75	52.16
		stdev	13.48	607.38	19.2	332.84	21.61	168.3	105.75	56.66	261.24	30.7
2	165	mean	10.02	302.52	8.66	293.34	13.67	186.01	59.81	70.97	217.37	29.6
		stdev	10.24	164.73	36.57	112.15	17	131.97	60.56	62.9	130.58	28.42

. In the table, the first column represents the cluster ID, the second column represents the number of students assigned to each cluster, and the rest of the columns represent the values (mean and standard deviation) for each of the features considered in our problem.

Looking at the values of the clusters in Table 2, the following conclusions can be reached:

• Cluster 0 is the most represented cluster, with 499 individuals. It is formed by those students who have had less interaction throughout the academic year, since most attributes have relatively low values in comparison with other clusters.
• Cluster 1 is the least represented cluster, with only 12 individuals. It is formed by those students who have interacted the most but still ended up failing.
• Cluster 2 is formed by 165 students who had more interaction than the students in cluster 0 but still exhibited a low level of interaction.

In order to ensure that the obtained clusters have sufficient quality to feed the rest of the process, we evaluate them using some standard metrics, all implemented using the scikit-learn library [47]. The results are presented in

Table 3. Metrics for evaluation of the obtained clusters.

Name	Explanation	Value	Interpretation
Silhouette [48]	It takes values between −1 and 1; the closer to 1, the better. It evaluates the quality of the clusters by indicating how well each data point within its own cluster compares to other clusters. Values close to 1 indicate that the points in the cluster are similar to each other, while a value close to −1 indicates that the points are closer to a different cluster than the one that was initially assigned.	0.49	This value indicates that the clusters are moderately well defined. While most points seem reasonably assigned to their clusters, some overlap between clusters might be present.
Davies–Bouldin [49]	It takes values greater than or equal to 0, with the lowest value being the best. It evaluates the quality of the clusters by focusing on the relationship between the dispersion within clusters (intra-cluster) and the separation between clusters (inter-cluster). It is constructed as the quotient of both values. Thus, when the clusters are separated and compact, the value of this index is minimized. A value close to 0 indicates good separation between clusters, while high values indicate an overlap between clusters.	0.65	This suggests that the clusters have moderate internal dispersion and that the separation between clusters may not be very distinct, pointing to a less compact cluster structure.
Calinski–Harabasz [50]	It takes values greater than or equal to 0; the higher, the better. It evaluates the quality of clusters based on the ratio of intra-cluster dispersion to inter-cluster dispersion. A high value indicates better-defined clusters, where the points within each cluster are more grouped and the clusters are well separated from each other, while a lower value suggests worse quality, with high intra-cluster dispersion.	494.16	This score suggests that the clusters exhibit moderate cohesion and separation. A higher score typically indicates better-defined clusters, while this value points to somewhat looser cluster formation.

, where we provide, for each metric, its name, its explanation, its bibliographic reference, the value obtained in our problem, and an interpretation of these values, justifying the selection of the clusters obtained to feed the rest of the process.

3.4.2. Selection of Features

One of the main reasons for applying Warren’s algorithm is the set of features that can be modified and, therefore, can be part of the group counterfactuals. As can be seen in previous sections, the data processing task filtered all features (demographics, social, etc.) except those related to the interactions of students with the resources (clicks). All click features are actionable and therefore are candidates to be included in the group counterfactuals. As a consequence, no further filtering on the features must be performed at this stage.

Another important issue is the number of features to vary in each group counterfactual. In real scenarios, such as the one presented in our use case, there may be dozens or hundreds of potential actionable features. However, it is important to select the most representative ones for the sake of pragmatism and trust. Note that counterfactuals affecting many features may not be easy to apply and users may be reluctant to use them. To address this issue, we decided to prioritize the candidate features and select only a certain percentage of them to be considered in the execution of Warren’s algorithm.

To select candidates, we explored two alternatives:

• Choosing the features based on the importance provided by DiCE—note that DiCE orders features according to their relevance;
• An ad hoc approach consisting of generating multiple individual counterfactuals and checking which features have received the highest number of modifications.

The former has already been implemented and appears efficient and logical. However, DiCE requires a minimum number of students from whom to obtain a feature ranking and cannot be applied in problems like ours, where there may be clusters with few students, as will be seen later. Therefore, we selected the latter approach.

Once we have defined the criteria with which to prioritize the features, we must define the percentage of them (starting from the ones with the highest priority) that will be modified in each counterfactual. As will be seen later in this paper, 30% is the most appropriate value in our case use.

3.4.3. Selection of Students

In Warren’s work, the authors present some examples of generating group counterfactuals from a small group of individuals. However, in real scenarios like ours, we can find hundreds or even thousands of individuals, and it can be a high-consuming task to build counterfactuals using all instances. To address this, in our use case, we explore different alternatives that are more efficient than using a sample of students for each cluster, as well as the approach that considers all of them.

When selecting a sample of students for each cluster, we focus on the centroid of each cluster, which is the central point of the cluster. If a selection must be made, it is logical to use the centroid and its neighborhood as the most representative elements in each cluster and build the counterfactual from them, giving less relevance to the individuals in the cluster who are located further from the centroid. However, to confirm that this is the most convenient approach, we defined and explored the following four choices:

• Selecting the % of students closest to the centroid (named ‘closest’ throughout the remainder of the paper);
• Selecting a % of students farther away from the centroid (‘farthest’);
• Selecting a random % of students (‘random’);
• Selecting all students in the cluster (‘full’).

As will be seen later, the ‘full’ approach is the one that generates more representative counterfactuals, but the computational cost of creating them is too high in comparison to the ‘closest’ approach, which seems to be a more balanced approach, providing also almost perfect performance in terms of representativeness.

3.4.4. Execution of Warren’s Algorithm

After executing the algorithm with the selected settings (k = 3, 30% of features and the ‘closest’ approach for student selection), the output obtained is structured as shown in

Table 4. Group counterfactuals generated.

Cluster	n_Clicks_Externalquiz	n_Clicks_Forumng	n_Clicks_Glossary	n_Clicks_Homepage	n_Clicks_Oucollaborate	n_Clicks_Oucontent	n_Clicks_Ouwiki	n_Clicks_Resource	n_Clicks_Subpage	n_Clicks_Url
0	13	-	-	-	27	-	-	281	-	-
1	17	788	-	-	25	-	-	-	-	-
2	-	-	182	498	-	-	-	76	-	-

. The values in the table indicate the minimum number of clicks that students should make in each of the categories to change their prediction from failing to not failing. Here, ‘-’ means that it is not necessary to modify this variable as part of the counterfactual. Note that the counterfactuals generated normally indicate that the number of clicks should be increased, which is aligned with other researchers’ findings, particularly on OULAD, and therefore constitutes pedagogical support for the counterfactual recommendations obtained in our work. Specifically, in [51], a predictive model is presented that effectively identifies students at risk of withdrawing based on an analysis of the number of clicks.

Some important information can be obtained from the three group counterfactuals obtained:

• The counterfactual for cluster 0 indicates that it would be useful for students of this type (those who failed, having very low interaction levels) to have more clicks (higher activity) on three types of resources: external quizzes, collaboration (although not explicitly explained in the dataset, we presume that these are clicks on collaborative tasks), and resources—see all details in [38].
• For cluster 1 (students with high levels of activity, but still failing), the counterfactual appears to recommend fewer interactions, which seems paradoxical. This is likely to indicate that there are too few students in this cluster, and it is challenging to obtain a valuable general recovery pattern. In this case, other personalized interventions could be more useful. For instance, in small and potentially unstable clusters like this, where unrealistic counterfactuals may be obtained, it would be interesting to integrate simple monotonicity constraints or even individual-level counterfactuals.
• For cluster 2 (students with moderately low interaction levels), there is a recommendation to increase the activity, particularly in glossaries, as well as homepages and resources.

Although not the focus of this paper, apart from tabular formats, there are other, more understandable methods of representing counterfactuals, being mostly graphical. In our view, the greedy representation is the most intuitive. It is a graph that shows the greediest path (the path with the highest impact towards the opposite class) from the original instance until it reaches the final prediction of the counterfactual. While not exhaustive, intending only to provide an example, Figure 8 graphically shows the group counterfactual for cluster 0. It starts from the original prediction (‘Factual Score’) and ends with the prediction after applying the entire counterfactual (‘Counterfactual Score’). We can see that the counterfactuals could be translated into an intervention aligning with three recommendations: first, to increase clicks (3 to 281) for resources, which is the recommendation with the highest impact in terms of changing from ‘Fail’ to ‘Not Fail’; then, an increase in clicks (2 to 27) for collaboration, which almost leads to a class change; and, finally, an increase in clicks (2 to 13) for external quizzes, that completes the change in class.

4. Results and Discussion

In this section, we present the tests conducted as part of our use case on the dataset to provide answers to the research questions proposed at the beginning of the paper. The implementation code and the results obtained are publicly available in the following GitHub repository: https://github.com/0Kan0/Group-Counterfactuals-in-the-prediction-and-recovery-of-students-at-risk-of-academic-failure (accessed on 18 December 2025)—Supplementary Materials. We analyze the results obtained and discuss them. This section is structured into two subsections, each focused on the first and second research questions of our work.

4.1. Group Counterfactual Success (RQ1)

The first research question proposed in this paper is whether it is possible to build successful group counterfactuals with the approach described in a reasonable time. Thus, there are two major aspects behind this research question: success and time. Therefore, to address this question, we carried out a set of experiments employing metrics aligned with these two principal aspects. These metrics are defined below.

• Validity: This represents a success rate that reflects the relationship between the number of instances in a group that have changed class by using a certain counterfactual with respect to the total instances of that group, according to Equation (1), as formally defined in Mothilal et al., 2020 [14]. In the context of this section, it represents the percentage of students that have transitioned from failing to passing by using the group counterfactual obtained for this cluster, with respect to the total number of students in the cluster.

$$Validity={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n\mathbb{I}(\widehat{f}\left(c,x_i\right)>t)$$

(1)

where

n: the total number of instances in the group;

x_i: each original instance;

c: the counterfactual employed;

$\mathbb{I}\left(·\right):$ a function that returns 1 if the condition is true or 0 otherwise;

$\widehat{f}(c,x_i)$: a model that makes a prediction for x_i, applying to x_i the changes suggested by the counterfactual c;

t: the minimum threshold for which the above prediction is considered good enough (in our case, 0.8). Considering higher values such as 0.9 or 1 would be too restrictive, and a reduced number of instances would be considered as changing from one class to another. Meanwhile, choosing lower values, particularly those slightly higher than 0.5, would be an overly lax approach, since a model that is closer to random would be considered good. Therefore—and in the absence of a more formal study to determine confidence intervals for this parameter—we assume the value of 0.8, which provides reasonably good preliminary results.

Regarding this and other metrics for group counterfactuals used later in this manuscript (except the execution time), it is important to clarify that aspects such as sign conventions or orders of magnitude are defined as presented in [14], which is the standard reference used in this area. Therefore, all details of these aspects can be found there.

• Execution time: This measures the time (in seconds) to generate a certain counterfactual. In the context of this section, it represents the time needed to generate a group counterfactual for a certain cluster.

Note that these are metrics associated with each cluster, but an average can be calculated for them considering all clusters. In fact, we employ this average-based approach for the sake of simplicity in this part of the manuscript, as we do not focus on saving students from a particular cluster but on all of them.

As stated in the previous section, the most convenient number of clusters ‘k’ in our case study is 3, a value obtained with the elbow method. After obtaining the clusters, the following quality to define is the percentage of features that will form the group counterfactual. To define the most convenient value in our use case, we adopt an approach consisting of experimenting with different percentage values, ranging from 10% to 50%. In our use case, 10% is the minimum value that yields success, since we have 10 potential features, and it represents the inclusion of only one feature in the counterfactual. We also considered other multiples of 10, i.e., 20%, 30%, 40%, and 50%. The results obtained are presented in

Table 5. Results obtained with different % features (average values considering all clusters).

% Features	Validity	Execution Time
10	0.953	232.24
20	0.963	32.39
30	0.993	30.33
40	0.993	19.86
50	0.996	28.01

.

As we can see from the table, there is a positive trend from 10% to 30% in validity, which seems to stop at 40%. For the 50% value, the improvement is minimal compared to the results obtained for the 30% value, so we chose this as the most convenient value, as it provides simpler and more manageable counterfactuals and because there is no clear improvement with higher values. This trend is also the reason for not considering values higher than 50%, since this seems to lead to more complex and less cost-effective counterfactuals with no real performance improvement in terms of validity.

Regarding the execution time, we can see that higher % values of features lead to lower execution times, since the number of combinations decreases. Again, the values of this metric for 30% are in a similar range to the other values considered, so this metric confirms the selection made.

After selecting 30% as the most convenient value for the number of features to be included in the group counterfactuals, the next aspect to experiment with is the approach used to select the students in the cluster from whom the group counterfactual will be built. We experimented with the four alternatives defined in Section 3.4.3, varying the percentage of students to be used, ranging from small values such as 1% or 5% up to the value of 50%. The idea behind this test is to obtain the most appropriate strategy among the four available ones and determine a percentage of students that permits us to build successful counterfactuals within a reasonable time. Since we deal with many different combinations of several aspects in this test, and given the intrinsically random nature of some of the strategies used, we conducted 30 runs to avoid any statistical bias. The results obtained are presented in

Table 6. Results obtained with different student selection approaches and different % of students (average values considering all clusters and 30 runs).

Technique	% Students	Validity	Average Time (s)
Closest	1.0%	0.969	4.37
	5.0%	0.966	18.3
	10.0%	0.962	35.35
	15.0%	0.922	22.67
	20.0%	0.986	44.43
	25.0%	0.993	92.13
	50.0%	1.0	192.8
Farthest	1.0%	0.959	7.91
	5.0%	0.963	36.05
	10.0%	0.957	58.64
	15.0%	0.990	34.54
	20.0%	0.980	44.22
	25.0%	0.999	112.18
	50.0%	1.0	204.17
Random	1.0%	0.937	4.51
	5.0%	0.967	38.05
	10.0%	0.987	42.49
	15.0%	0.977	32.86
	20.0%	0.984	44.54
	25.0%	1.0	117.32
	50.0%	1.0	189.27
Full	100.0%	1.0	364.18

.

Regarding the percentage of students, in all configurations, we can see that 25% leads to a minimum validity rate of 0.99, which means that virtually all students are saved with their group counterfactuals. Among all alternatives, the one that achieves this value the fastest is the ‘closest’ approach. While 25% of students in the ‘random’ configuration led to high validity, the time value was higher than in the ‘closest’ approach. The value of 50% led to validity of 1.0 in all cases, but the time was also longer. Considering the above, the most balanced approach seems to be the ‘closest’ one with 25% of students.

Having experimented with different strategies and values for the features and students, we can conclude that, in our case study of academic failure, and according to our approach, the most convenient strategy consists of selecting three cohesive clusters, with 30% of the most relevant features according to the priority policy defined, and using only the 25% of students in each cluster who are closest to the centroid. With these settings, our group counterfactuals are able to change 99.3% of students from failing to passing, and they are built within a reasonable average time of 92.13 s. This recovery rate, being close to 100%, may seem unusually high, but, in counterfactual explanation tasks, especially those aimed at designing actionable interventions, the goal is precisely to achieve counterfactuals with very high validity, meaning that almost all target instances flip to the desired class when the suggested changes are applied. Prior work on counterfactual explanations [14] explicitly frames validity as a core requirement, since low-validity counterfactuals would translate into ineffective or unreliable recommendations for real learners. In our context, where the counterfactuals are intended to guide interventions to prevent academic failure, a high recovery rate is not only expected but necessary to ensure that the recommendations meaningfully support the vast majority of at-risk students.

Thanks to the obtained counterfactuals, if, in the future, a new student appears with signs of failing according to the predictive model, it would be necessary to determine which cluster he/she belongs to and apply the group counterfactual explanation to help him/her. However, the practical transformation of these counterfactuals into effective actions must be performed by educators, and this aspect is beyond the scope of this paper.

Analyzing the results, we can provide an answer to the first research question, and it is positive. Our approach can be effectively used to generate group counterfactuals that are able to potentially and theoretically save almost all students who fail (according to the considered dataset), and these counterfactuals are obtained in approximately 1.5 min.

4.2. Comparison of Group and Individual Counterfactuals (RQ2)

Until now, most of the literature has focused on generating one individual counterfactual for each instance (e.g., students) of a target population. In fact, this is the standard and most used approach. However, in this work, we propose an approach to building one group counterfactual that can be successfully applied to several instances. Therefore, to analyze the potential benefits of group versus individual counterfactuals, some experiments must be conducted. This is the topic of the second research question stated in the Introduction, which will be answered here.

The most common approach employed in the literature to validate counterfactuals consists of measuring a series of standardized metrics that represent counterfactuals’ quality in terms of some desirable properties [14]. These metrics are explained next, excluding the validity and execution time (in creating either an individual or group counterfactual), which have already been explained in Section 4.1.

• Sparsity: This measures the relationship between the number of features modified in a counterfactual and the total amount of features in the original instance, as formally defined in Equation (2), according to Mothilal et al. [14].

$$Sparsity=1-{\displaystyle \frac{1}{d}}{\sum }_{i=1}^d\mathbb{I}(c_i\ne x_i)$$

(2)

where

d: the total number of features in each instance;

c: the counterfactual employed;

x: each original instance;

c_i: the value of the i-th feature in the counterfactual c;

x_i: the value of the i-th feature in the instance x;

$\mathbb{I}\left(·\right):$ a function that returns 1 if the condition is true or 0 otherwise.

• Proximity: This measures the average of the feature-wise distances between the counterfactual and the original instance, as formally described in Equation (3), according to Mothilal. Note that the formula used is only valid for continuous features such as the ones used in our use case and would need to be adapted in problems with categorial features [14].

$$Proximity=-{\displaystyle \frac{1}{d}}{\sum }_{i=1}^d{\displaystyle \frac{\left|c_i\ne x_i\right|}{{MAD}_i}}$$

(3)

where

d: the total number of features in each instance;

c: the counterfactual employed;

x: each original instance;

c_i: the value of the i-th feature in the counterfactual c;

x_i: the value of the i-th feature in the instance x;

MAD_i: the median absolute deviation for the i-th feature. The MAD represents a robust indicator of the variability in features’ values; therefore, when dividing by the MAD, we are considering the relative prevalence of observing the feature at a certain value [14].

We have compared the performance of the group counterfactuals built with our approach versus the individual counterfactuals generated using the default settings of DiCE as stated by the authors [14], which is probably the most well-known approach. Note that we have used the settings with the best results for group counterfactuals according to the explanation provided in Section 4.1 (three clusters, 30% of features, and 25% of students closest to the centroid). In this validation, note that the individual (e.g., students) is the center of the analysis. This means that every student will be analyzed with his/her corresponding individual counterfactual and also with the group counterfactual obtained for his/her cluster. After this, an average for all students in each cluster is calculated for each type of counterfactual (individual and group), and the results obtained are presented in

Table 7. Comparison of group and individual counterfactuals (average values considering all instances in each cluster for each type of counterfactual—individual and group).

Cluster	Cluster Students	Counterfactual Type	Validity	Sparsity	Proximity	Execution Time (s)
0	499	Individual	1.0	0.816	−21.93	239.50
		Group	1.0	0.7	−10.748	62.94
1	12	Individual	1.0	0.848	−9.814	5.77
		Group	1.0	0.7	−0.914	1.58
2	165	Individual	1.0	0.848	−5.835	79.85
		Group	0.98	0.7	−0.781	26.46

.

Analyzing the above table, some important aspects must be discussed:

• Regarding validity, as expected, all students are successfully recovered with individual counterfactuals (validity = 1.0), since each student has been provided with a concrete, customized counterfactual, which has been specifically built for him/her. However, the group counterfactuals do not lag behind and also reach a 1.0 validity value in clusters 0 and 1, as well as 0.98 in cluster 2. Note that this is a very positive result considering that only one counterfactual has been used to recover all students in each cluster.
• With respect to sparsity, it is observed that individual counterfactuals change fewer variables on average (higher sparsity). Although the number of features to be changed is an aspect that can be adjusted as a parameter, in this case, more variables need to be changed in the group counterfactuals in comparison to individual ones to obtain similar validity values. This is also expectable behavior, because it is easier to find a combination of actionable features for a particular individual rather than a combination of features that work for all individuals in a cluster.
• Regarding proximity, it is observed that group counterfactuals have values closer to 0, which indicates that, although they modify more variables on average than individual counterfactuals, the changes in terms of the features’ values (clicks) are lighter and less abrupt. Therefore, the variations suggested by the counterfactual explanations seem more feasible compared to individual counterfactuals.
• Finally, it can be observed that less time is required (within a factor of 3 to 4) to generate a group counterfactual for all instances of a cluster than to generate an individual counterfactual for each learner in the cluster.

From the results obtained and the above discussion, we can now provide an answer to the second research question of our study: group counterfactuals seem to be a successful approach to recovering almost all students from failing, and, although more features need to be changed to adapt to the majority of the individuals in the cluster, group counterfactuals are an interesting approach as they propose feasible, lighter changes and do so in a shorter time than individual counterfactuals. The validity of these findings has been confirmed with a series of statistical tests (described in Appendix A) carried out to compare the different types of counterfactuals (group and individual) for all students.

A final remark can be made regarding the ease of applying group counterfactuals to students in real time when they are predicted to be failing in a real environment. While generating an individual counterfactual requires the student’s data to be entered into DiCE and then the individual counterfactual generated (which is also an issue for teachers with limited AI knowledge), with the group counterfactual, it is sufficient to determine to which cluster the student belongs by analyzing their characteristics; then, once identified, we can apply the previously defined group counterfactual for the cluster.

5. Limitations

In this paper, we have presented a use case for the generation of group counterfactual explanations in an educational context, particularly in the problem of academic dropout. To the best of our knowledge, this is the first use case of this type in education.

Despite the contribution that it represents, this preliminary work has some limitations that need to be mentioned. First, note that it is based on only one dataset in one reference domain. Therefore, we do not present a definitive solution but an approach that can be used in a complementary way with others, particularly when there is an interest in capturing group patterns for intervention at a larger scale.

Moreover, note that we have not addressed the problem of translating the group counterfactuals into real effective actions to be implemented by experts; we merely provide these experts with group counterfactuals, including some potential clues for intervening in certain problems in their domains.

As we only used one dataset, there may be limitations in terms of model reliability, significance, and uncertainty, affecting important aspects such as robustness. Moreover, in our research, some parameters, such as the number of features to be altered, have been defined empirically, which could also affect the sensitivity and validation of the results obtained.

Regarding obtaining groups from a population, we employed a single clustering method (K-means) with good results, but other approaches could be explored depending on the nature of the data used in other use cases. Regarding clustering, another limitation is that one of the clusters obtained was quite small, which could lead to problems such as implausibility in some attributes and a lack of stability in the cluster, and this may threaten the strength and reproducibility of the results.

As indicated in the next section, it would be interesting to explore other datasets and provide preliminary software implemented with functionalities to perform real-time analysis, allowing the user to determine quality indicators (reliability, significance, certainty, robustness, sensitivity, plausibility, or stability) during the process and decide accordingly.

6. Conclusions and Future Work

In this paper, we have presented a case study in which we have proposed and used an approach for the generation of group counterfactuals that can be used for intervention in students at risk of academic failure. Our approach draws from the work by Warren et al. and it is based on their algorithm for group counterfactual generation. This algorithm, although very important in this area, has some limitations in terms of applicability. In particular, the authors built one group counterfactual for a concrete group of homogeneous instances, experimenting with a group formed of very few instances, but the reality is more complex. Our approach takes a whole heterogeneous population, defines criteria to split it, and obtains groups by means of a formal clustering process. In addition, we have experimented with different values for some parameters in their algorithm, such as the percentage of features to be altered in the counterfactuals, and analyzed different alternatives when using a sample of students in each cluster from whom to build the group counterfactual in an efficient manner.

We have conducted a comprehensive quantitative validation process to analyze the benefits of our proposal in our use case. The results obtained show that (a) it is feasible to generate successful group counterfactuals for the problem of recovering students at risk of failing in a reasonable time and (b), in this environment, the use of these group counterfactuals has some advantages over traditional individual counterfactuals, mainly in terms of the time needed to create them and because the changes to be applied according to group counterfactuals are less abrupt than the ones suggested by individual counterfactuals.

The main implication is that this use case opens the door for the application of the proposed approach to other environments beyond education, where there is a need for explanations about multiple instances in which to intervene. In this way, instances with similar characteristics can benefit from a unique explanation, which may imply more efficient decision making. In addition, when a new instance (e.g., ‘student’) is classified into an undesired class (for instance, ‘fail’ in education), there would be no need to create a new individual counterfactual for this particular student, which is a costly and non-trivial task, but only to determine the cluster to which he/she belongs and immediately apply the group counterfactual related to that cluster.

A broader examination of the clustering results in our study reveals that the three student groups exhibit distinct patterns of engagement, which carry meaningful implications for educational practice. The largest cluster consists of students with persistently low interaction, suggesting a pattern of disengagement that may stem from a lack of motivation, limited digital study, or early feelings of academic inadequacy. A second cluster, although very small, is composed of highly active students who nevertheless fail, indicating that high activity alone is not synonymous with effective learning and may mask deeper issues such as poor self-regulation, inefficient study strategies, or confusion that leads to repeated but unproductive platform use. The third cluster reflects moderately active students who still fall short, hinting at a threshold effect in which partial engagement is insufficient for success unless directed toward the most pedagogically meaningful resources. These patterns collectively imply that failure is not tied to a single behavioral profile but emerges from qualitatively different trajectories of interaction. Consequently, group counterfactuals do more than optimize technical efficiency: they provide interpretable behavioral archetypes that can inform targeted pedagogical interventions, helping educators to discern when students need motivation, strategic guidance, or conceptual support rather than a generic increase in activity.

This analysis offers tutors a useful way to interpret students’ digital footprints by showing that different patterns of engagement reflect different underlying needs. Very low activity often signals early disengagement, while moderate activity suggests that students are trying but not focusing on the most meaningful resources, and very high activity may indicate confusion rather than mastery. These insights can be translated into course- or program-level actions such as highlighting key materials, integrating guided study pathways, or embedding timely prompts that redirect students toward high-impact resources. By viewing click patterns as indicators of broader learning behaviors, instructors can design courses that proactively support students before individual problems escalate.

This paper does not address the ethical, psychological, and behavioral implications of applying group counterfactuals to students. From background knowledge, applying group counterfactuals in educational settings raises significant concerns across multiple dimensions. Ethically, using group-based counterfactual reasoning can perpetuate harmful stereotypes and reinforce systemic biases, particularly when algorithms make predictions about student performance based on demographic group membership rather than individual characteristics [52]. Psychologically, exposure to group counterfactuals may trigger stereotype threats, where students underperform due to anxiety about confirming negative group stereotypes, as demonstrated in educational contexts [53]. Behaviorally, students may internalize group-based predictions, leading to self-fulfilling prophecies that limit their academic aspirations and effort [54]. Recent research has highlighted how algorithmic fairness in education must consider not only statistical parity but also the psychological impacts on students’ sense of agency and self-efficacy [55]. Furthermore, the use of group counterfactuals in educational AI systems can undermine principles of individualized learning and may violate students’ rights to be assessed based on their own merits rather than group membership [56].

Future Work

While this was a preliminary study, there are some aspects that could be addressed by the community as potential future lines of research:

• The main idea for further research is the proposal of new ways for creating a certain group counterfactual from a given set of instances in a particular cluster. The current solution opts for an instance-based approach, in which explanations are created by modifying the original instances in a uniform way, applying the same counterfactual transformation repeatedly (i.e., substituting the same target value in several predictive instances). However, there are other possible alternatives; for example, counterfactual groups could be formed by showing ranges of values or generalizations of feature differences computed from sets of similar instances.
• A promising line would be to add simple monocity constraints for the features to be included in the counterfactuals or even use individual-level counterfactuals, particularly when small clusters are generated, in order to gain plausibility.
• In this research, we have used K-means for the clustering of instances. It could be interesting to try other clustering approaches, such as rule-based clustering analysis, using neural networks to improve instance clustering, or even simply applying other clustering tools such as DBSCAN. In particular, DBSCAN seems interesting since it permits us to capture the density of the population and obtain groups of similar instances with no need to specify the number of clusters. Regardless of the clustering approach used, it would also be interesting to improve the approach presented by providing the functionality to perform clustering sensitivity analyses, so that the user is aware of the quality of the clusters generated.
• While our validation used only OULAD, this remains the most widely used and recognized benchmark in educational data mining, with countless studies relying on it for dropout prediction, engagement analysis, and explainable AI research [57]. Nonetheless, it would be interesting to generalize to diverse datasets from other domains in order to confirm the preliminary results obtained in our use case or even to identify some improvable aspects in our approach. In particular, it would be interesting to focus on more complex datasets with more features and instances so as to assess the scalability of the proposal presented in this paper.
• Following on from the previous point, the used dataset’s quality may impact the results obtained when generating counterfactuals. For this reason, it would be interesting to implement a mechanism to automatically inform the user about different aspects depending on the dataset used in each case, such as model reliability, uncertainty quantification, significance, and confidence intervals in data splits so as to assess robustness, stability when small clusters appear, and sensitivity for parameters. It would also be useful to apply fine-tuning mechanisms for parameters.
• Moreover, it would be interesting to determine whether group counterfactuals can substitute or have to co-exist with individual counterfactuals in certain domains, particularly those that are critical, such as education, medicine, or safety. It would also be interesting to perform a large-scale study in each of these domains to clearly measure the impact of group counterfactuals in the decision-making process.
• An additional direction for future work is to complement the current algorithmic evaluation with human-centered or pedagogical evaluation. Although we measured the validity, sparsity, proximity, and execution time, these metrics do not capture how instructors interpret the explanations or whether the suggested changes are meaningful in real teaching contexts. User studies with tutors and students, or small-scale classroom pilots, would allow us to evaluate the clarity, usefulness, and practical relevance of group counterfactuals and better understand how they can support decision making in authentic educational settings.