VexNet: Vector-Composed Feature-Oriented Neural Network
Abstract
1. Introduction
- Refined vexel representation: we introduce the vexel concept, which eliminates pose scalars and improves computational efficiency.
- Non-iterative voting algorithm: we develop a single-pass voting mechanism for vexels, reducing complexity compared to CapsNet while enhancing predictive performance.
- Weight-sharing operators: we propose specialized weight-sharing operators for vexels to balance computational complexity and generalization ability.
- Extensive validation: we conduct comprehensive experiments, showing our method’s improved accuracy, robustness to adversarial attacks, and reductions in parameter count and computational cost.

2. Literature Review
3. Problem Definition
4. Proposed Method
4.1. Preliminaries
- Notation
- : input/output channels (for convolutional layers)
- : height and width of feature maps
- : height and width of the kernel
- : number of vexels in fully connected layers (input/output)
- : dimensionality of input/output vexels
- : indices of input/output channels
- : spatial indices in the input
- : spatial indices in the output
- : matrix–vector multiplication
- : scalar–vector product
4.2. Adaptive and Biased Mixed Weights
| Algorithm 1 Vexel voting algorithm |
Input: features coefficient, weights . Output: adaptive scalar weights . ▹, .
|
| Algorithm 2 Vexel propagation algorithm |
Input: features , bias matrix weights , coefficient weights . Output: features . ▹ Note that for convolution, , .
|
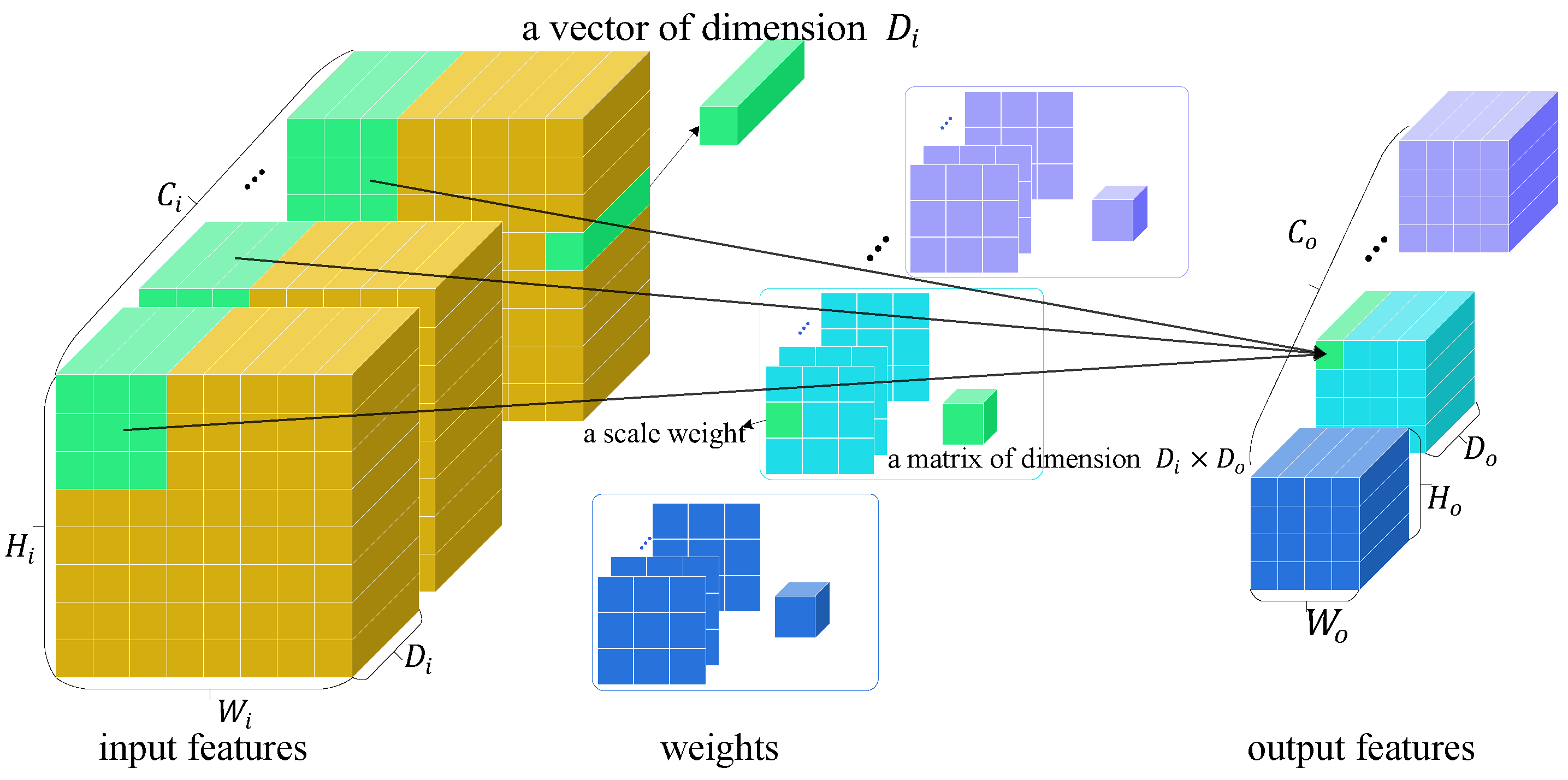
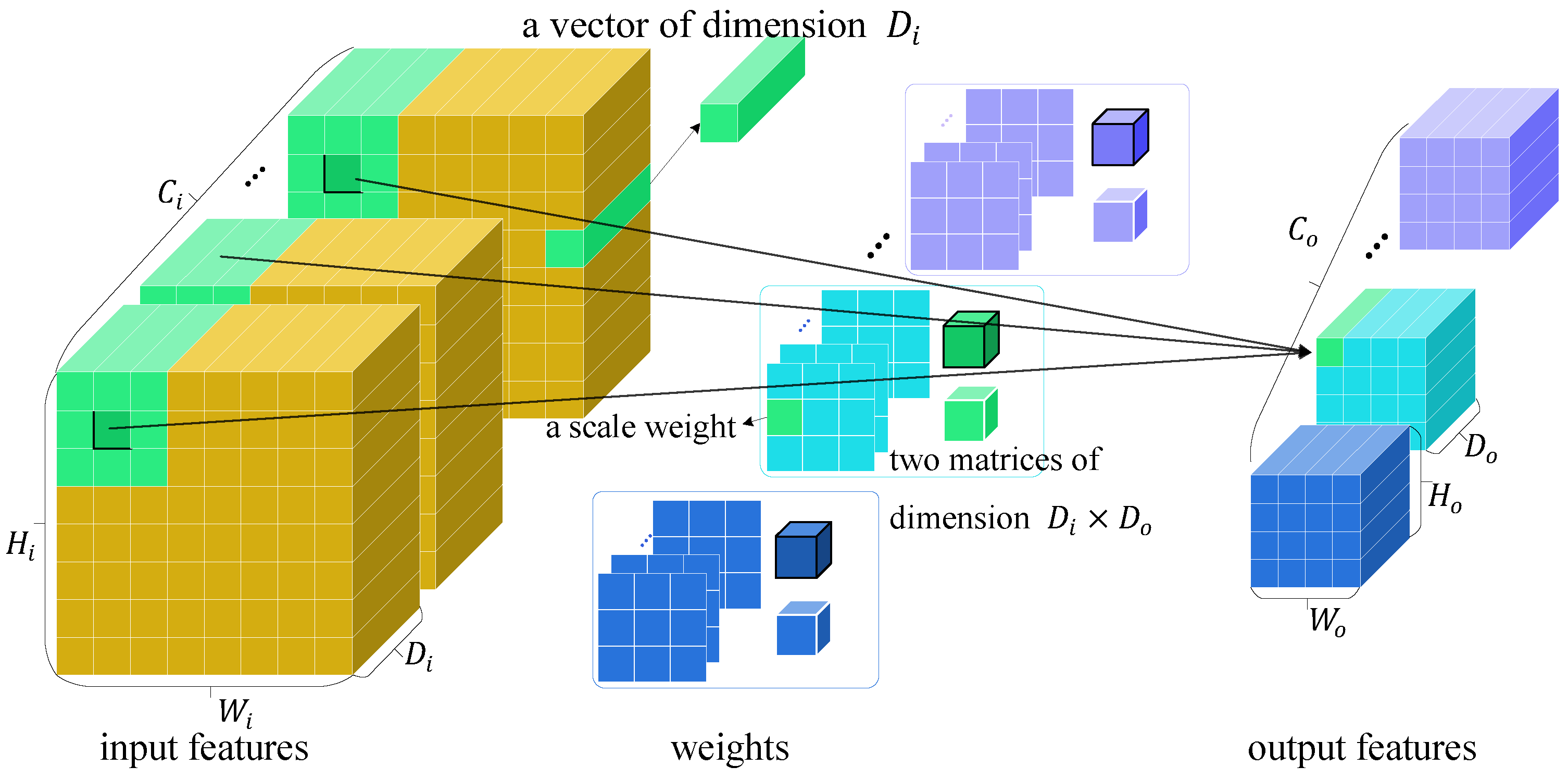
4.3. Vexel Operators
4.4. Relation to CapsNets
5. Results
5.1. Implementation Details
- FashionMNIST comprises 60,000 training and 10,000 test grayscale images of size , spanning 10 fashion categories.
- SVHN contains 73,257 training and 26,032 test RGB images of size , depicting house numbers.
- CIFAR-10 consists of 50,000 training and 10,000 test RGB images of size , covering 10 object classes.
- smallNORB is a 3D object recognition dataset with grayscale images of five object categories, captured under varying lighting, azimuth, and elevation conditions.
- For CIFAR-10 and SVHN: 19 convolutional layers organized into eight residual blocks;
- For smallNORB: six convolutional layers;
- For FashionMNIST and affineMNIST: a single convolutional layer.
5.2. Image Classification Results
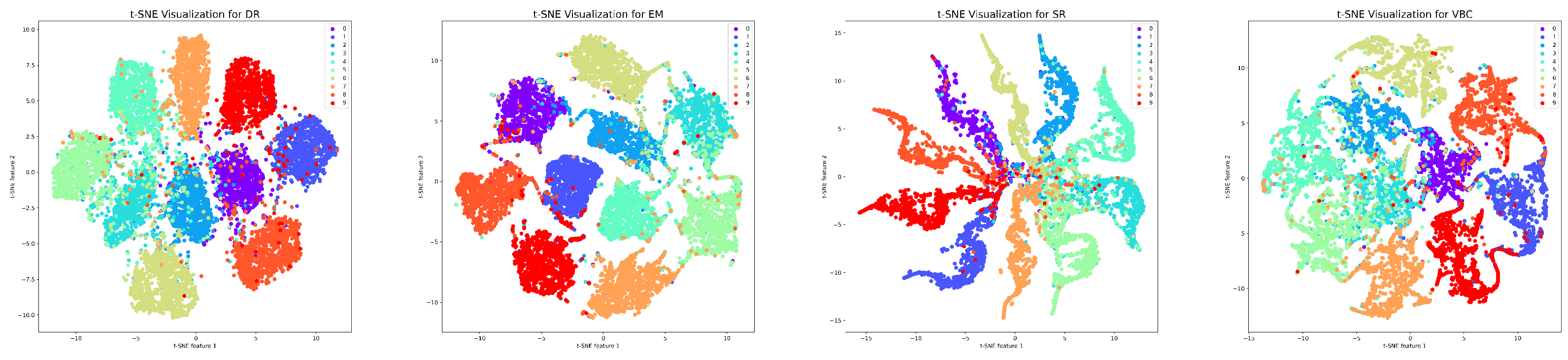
5.3. Visualization of Classification
5.4. Robustness Experiments
5.4.1. Robustness to Affine Transformation
5.4.2. Robustness to Adversarial Attack
5.5. Ablation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Graves, A.; Graves, A. Long short-term memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–45. [Google Scholar]
- Tran, D.; Bourdev, L.; Fergus, R.; Torresani, L.; Paluri, M. Learning spatiotemporal features with 3d convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 4489–4497. [Google Scholar]
- Bordes, A.; Usunier, N.; Garcia-Duran, A.; Weston, J.; Yakhnenko, O. Translating embeddings for modeling multi-relational data. Adv. Neural Inf. Process. Syst. 2013, 26, 2787–2795. [Google Scholar]
- Baltrušaitis, T.; Ahuja, C.; Morency, L.P. Multimodal machine learning: A survey and taxonomy. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 423–443. [Google Scholar] [CrossRef] [PubMed]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Lin, T.Y.; Maire, M.; Belongie, S.; Bourdev, L.; Girshick, R.; Hays, J.; Perona, P.; Ramanan, D.; Zitnick, C.L.; Dollár, P. Microsoft COCO: Common Objects in Context. arXiv 2014, arXiv:1405.0312. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Linnainmaa, S. The Representation of the Cumulative Rounding Error of an Algorithm as a Taylor Expansion of the Local Rounding Errors. Ph.D. Thesis, University Helsinki, Helsinki, Finland, 1970. Master’s Thesis (in Finnish). [Google Scholar]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Robbins, H.; Monro, S. A stochastic approximation method. In The Annals of Mathematical Statistics; Institute of Mathematical Statistics: Hayward, CA, USA, 1951; pp. 400–407. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. arXiv 2013, arXiv:1312.6199. [Google Scholar]
- Nguyen, A.; Yosinski, J.; Clune, J. Deep neural networks are easily fooled: High confidence predictions for unrecognizable images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 427–436. [Google Scholar]
- Kurakin, A.; Goodfellow, I.J.; Bengio, S. Adversarial examples in the physical world. In Artificial Intelligence Safety and Security; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018; pp. 99–112. [Google Scholar]
- Su, J.; Vargas, D.V.; Sakurai, K. One pixel attack for fooling deep neural networks. IEEE Trans. Evol. Comput. 2019, 23, 828–841. [Google Scholar] [CrossRef]
- Ribeiro, F.D.S.; Leontidis, G.; Kollias, S. Capsule routing via variational bayes. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 3749–3756. [Google Scholar]
- Hahn, T.; Pyeon, M.; Kim, G. Self-routing capsule networks. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Pechyonkin, M. Understanding Hinton’s Capsule Networks Part I: Intuition. 2017. Available online: https://medium.com/ai%C2%B3-theory-practice-business/understanding-hintons-capsule-networks-part-i-intuition-b4b559d1159b (accessed on 11 October 2023).
- Sabour, S.; Frosst, N.; Hinton, G.E. Dynamic routing between capsules. arXiv 2017, arXiv:1710.09829. [Google Scholar]
- Lenc, K.; Vedaldi, A. Understanding image representations by measuring their equivariance and equivalence. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 991–999. [Google Scholar]
- Baeldung. Translation Invariance and Equivariance in Computer Vision. Online Forum Comment. 2022. Available online: https://www.baeldung.com/cs/translation-invariance-equivariance (accessed on 1 September 2023).
- Duval, L. What Is the Difference Between “Equivariant to Translation” and “Invariant to Translation”. Online Forum Comment. 2017. Available online: https://datascience.stackexchange.com/questions/16060/what-is-the-difference-between-equivariant-to-translation-and-invariant-to-tr (accessed on 1 September 2023).
- Hinton, G.E.; Krizhevsky, A.; Wang, S.D. Transforming auto-encoders. In Proceedings of the International Conference on Artificial Neural Networks, Espoo, Finland, 14–17 June 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 44–51. [Google Scholar]
- Hinton, G.E.; Sabour, S.; Frosst, N. Matrix capsules with EM routing. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the 27th International Conference on Machine Learning (ICML), Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Bridle, J. Training stochastic model recognition algorithms as networks can lead to maximum mutual information estimation of parameters. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 27–30 November 1989; Volume 2. [Google Scholar]
- Liu, Y.; Cheng, D.; Zhang, D.; Xu, S.; Han, J. Capsule networks with residual pose routing. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 2648–2661. [Google Scholar] [CrossRef] [PubMed]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-mnist: A novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; Ng, A.Y. Reading digits in natural images with unsupervised feature learning. In Proceedings of the NIPS Workshop on Deep Learning and Unsupervised Feature Learning, Granada, Spain, 12–17 December 2011. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- LeCun, Y.; Huang, F.J.; Bottou, L. Learning methods for generic object recognition with invariance to pose and lighting. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2004), Washington, DC, USA, 27 June–2 July 2004; Volume 2, pp. II–104. [Google Scholar]
- Ye, X. calflops: A FLOPs and Params Calculate Tool for Neural Networks in Pytorch Framework. 2023. Available online: https://github.com/MrYxJ/calculate-flops.pytorch (accessed on 2 May 2025).
- Olshen, F.M.; Stone, L.G.; Weiss, L.A. A new approach to classification problems. IEEE Trans. Inf. Theory 1978, 24, 670–679. [Google Scholar]
- MacQueen, G.H. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Statistics; University of California Press: Berkeley, CA, USA, 1967; pp. 281–297. [Google Scholar]
- van der Maaten, L.J.P.; Hinton, G.E. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- The PyTorch Lightning Team. PyTorch Lightning 2.1.0. 2023. Available online: https://github.com/PyTorchLightning/pytorch-lightning (accessed on 4 September 2024).
- NVIDIA Corporation. CUDA Toolkit 11.8.0. 2023. Available online: https://developer.nvidia.com/cuda-11-8-0-download-archive (accessed on 9 September 2024).
- ISO/IEC 14882:2011(E); Programming Language C++. ISO: Geneva, Switzerland, 2011.
- GNU Project. GCC, the GNU Compiler Collection, Version 9.4.0 with Partial C++14 Support. 2021. Available online: https://al.io.vn/no/GNU_Compiler_Collection (accessed on 2 May 2025).
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]






| Dynamic Routing [23] | EM Routing [28] | Self-Routing [21] | Variational Bayes [20] | |
|---|---|---|---|---|
| Iterative cluster | True | True | False | True |
| Extra scalar activation | False | True | True | True |
| Loss Function | Accuracy (%) |
|---|---|
| Marginal loss | 92.52 |
| NLL loss | 91.51 |
| CrossEntropy Loss | 92.47 |
| Abbreviation | Method |
|---|---|
| CapsNets | |
| DR | Dynamic Routing CapsNet [23] |
| EM | EM Routing CapsNet [28] |
| SR | Self-Routing CapsNet [21] |
| VB | Variational Bayes CapsNet [20] |
| ResRouting | Residual Dynamic Routing [33] |
| VexNets | |
| Vex-VW | VexNet with vexel-wise operator |
| Vex-CW | VexNet with channel-wise operator |
| Vex-AC | VexNet with all-channel operator |
| Vex-Cyclic | VexNet with cyclic vexel operator |
| Vex-CyclicSR | VexNet with self-routing |
| Methods | CIFAR-10 (%) | SVHN (%) | Params (M) | FLOPs (M) |
|---|---|---|---|---|
| Vex-VW | 92.48 | 96.40 | 2.60 | 91.41 |
| Vex-CW | 92.47 | 96.44 | 1.37 | 88.95 |
| Vex-AC | 92.52 | 96.39 | 1.29 | 88.79 |
| Vex-Cyclic | 92.44 | 96.40 | 1.45 | 89.03 |
| DR [23] | 92.21 | 96.33 | 2.59 | 91.23 |
| EM [28] | 91.46 | 95.78 | 1.40 | 89.86 |
| SR [21] | 92.31 | 96.12 | 1.40 | 89.96 |
| VB [20] | 88.49 | 94.80 | 0.32 | 38.27 |
| ResRouting [33] | 92.38 | 96.16 | 1.40 | 89.86 |
| AvgPool | 92.06 | 96.45 | 0.30 | 41.30 |
| Conv | 89.99 | 96.02 | 0.90 | 61.00 |
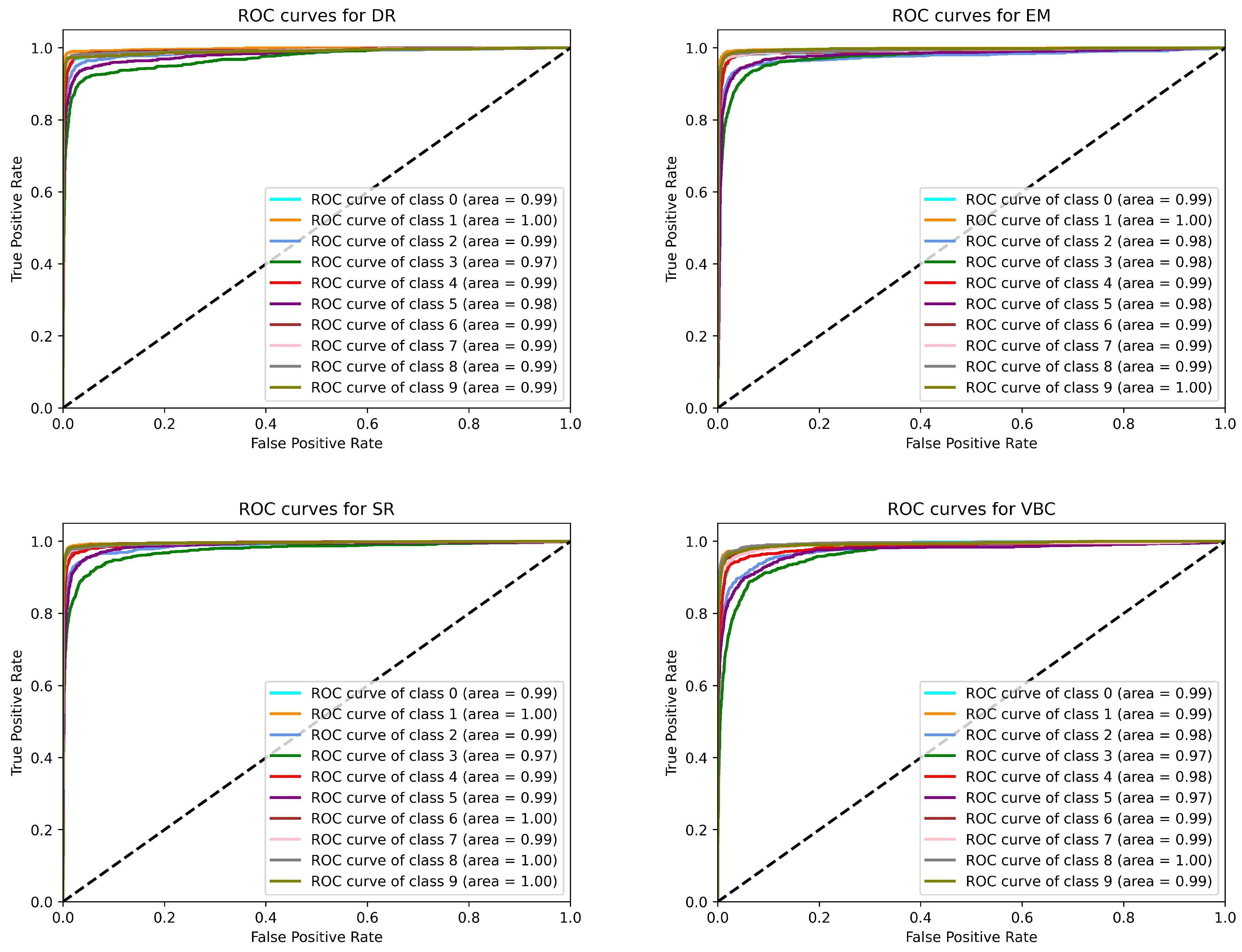
| Capsule Networks | |
|---|---|
| DR | 0.988 |
| EM | 0.989 |
| SR | 0.992 |
| VB | 0.985 |
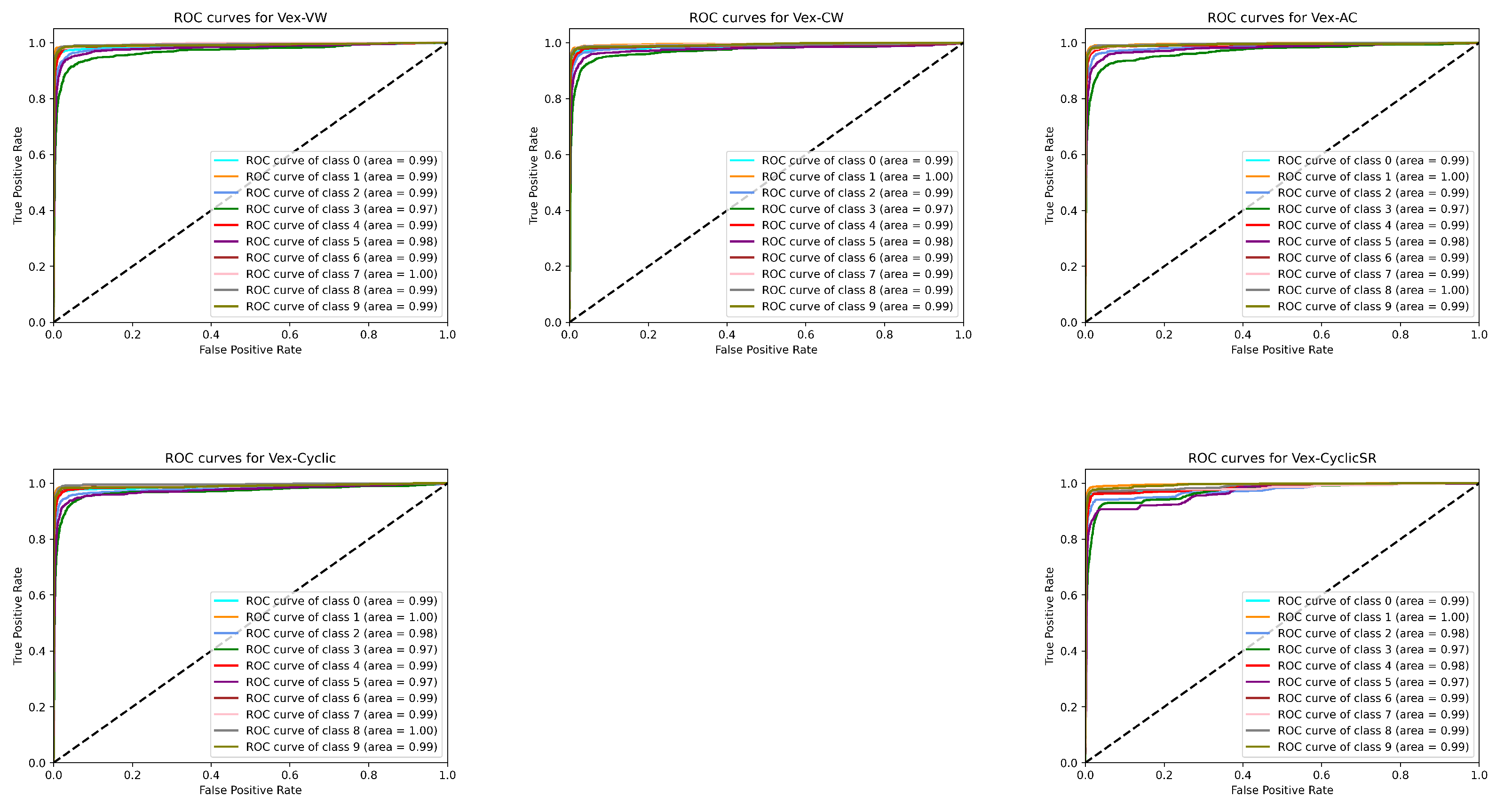
| VexNets | |
| Vex-VW | 0.988 |
| Vex-CW | 0.988 |
| VEx-AC | 0.989 |
| Vex-Cyclic | 0.987 |
| Vex-CyclicSR | 0.985 |
| Method | Elevation Familiar | Novel | Azimuth Familiar | Novel |
|---|---|---|---|---|
| Vex-VW | 94.85 | 83.83 | 93.20 | 81.94 |
| Vex-CW | 95.15 | 81.78 | 93.60 | 81.72 |
| Vex-RW | 95.22 | 82.11 | 92.86 | 81.67 |
| Vex-Cyclic | 95.61 | 82.51 | 93.44 | 81.60 |
| DR | 94.50 | 81.90 | 92.67 | 80.85 |
| EM | 93.84 | 80.64 | 92.94 | 80.65 |
| SR | 94.25 | 82.74 | 92.85 | 81.67 |
| AvgPool | 94.32 | 82.28 | 91.51 | 78.24 |
| Conv | 92.49 | 81.22 | 91.61 | 77.93 |
| CIFAR-10 | SVHN | |||
|---|---|---|---|---|
| Targeted | Untargeted | Targeted | Untargeted | |
| Vex-VW | 4.39 | 15.62 | 2.77 | 21.82 |
| Vex-CW | 4.15 | 14.93 | 2.35 | 12.04 |
| Vex-RW | 4.37 | 20.32 | 2.78 | 15.68 |
| Vex-Cyclic | 5.51 | 24.75 | 2.71 | 24.69 |
| DR [23] | 6.33 | 39.76 | 2.93 | 20.50 |
| EM [28] | 9.85 | 45.94 | 7.65 | 33.61 |
| SR [21] | 5.36 | 37.64 | 4.93 | 25.53 |
| AvgPool | 18.46 | 62.65 | 15.38 | 44.44 |
| Conv | 21.61 | 60.57 | 17.94 | 44.47 |
| CIFAR-10 | SVHN | |||
|---|---|---|---|---|
| Targeted | Untargeted | Targeted | Untargeted | |
| Vex-VW | 15.75 | 14.79 | 8.45 | 22.75 |
| Vex-CW | 8.90 | 12.13 | 6.89 | 8.88 |
| Vex-RW | 11.41 | 14.63 | 9.50 | 11.40 |
| Vex-Cyclic | 13.57 | 20.70 | 9.79 | 15.41 |
| DR [23] | 15.36 | 45.47 | 8.83 | 30.63 |
| EM [28] | 36.57 | 66.74 | 20.87 | 44.62 |
| SR [21] | 17.61 | 55.96 | 14.82 | 37.58 |
| AvgPool | 45.40 | 84.90 | 42.60 | 62.20 |
| Conv | 42.80 | 82.00 | 41.80 | 62.60 |
| Vex-VW | Vex-CW | Vex-RW | Vex-Cyclic | Vex-CyclicSR | |
|---|---|---|---|---|---|
| , Vex-1 | 92.33 ± 0.23 | 92.33 ± 0.12 | 92.20 ± 0.18 | 92.23 ± 0.29 | 91.93 ± 0.10 |
| , Vex-2 | 92.20 ± 0.16 | 92.22 ± 0.10 | 92.54 ± 0.24 | 92.30 ± 0.26 | 91.70 ± 0.47 |
| , Vex-1 | 92.25 ± 0.26 | 92.12 ± 0.11 | 92.02 ± 0.22 | 92.21 ± 0.20 | 91.85 ± 0.15 |
| , Vex-1 | 92.25 ± 0.15 | 92.30 ± 0.16 | 92.22 ± 0.27 | 92.13 ± 0.19 | 91.63 ± 0.34 |
| , Vex-1 | 92.06 ± 0.14 | 92.20 ± 0.12 | 92.14 ± 0.10 | 92.33 ± 0.20 | 91.89 ± 0.16 |
| , Vex-1 | 92.17 ± 0.23 | 92.32 ± 0.12 | 92.34 ± 0.14 | 92.22 ± 0.35 | 91.92 ± 0.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, X.; Guo, Z.; Li, Z.; Cao, Y.; Chen, X.; Wu, T. VexNet: Vector-Composed Feature-Oriented Neural Network. Electronics 2025, 14, 1897. https://doi.org/10.3390/electronics14091897
Du X, Guo Z, Li Z, Cao Y, Chen X, Wu T. VexNet: Vector-Composed Feature-Oriented Neural Network. Electronics. 2025; 14(9):1897. https://doi.org/10.3390/electronics14091897
Chicago/Turabian StyleDu, Xiao, Ziyou Guo, Zihao Li, Yang Cao, Xing Chen, and Tieru Wu. 2025. "VexNet: Vector-Composed Feature-Oriented Neural Network" Electronics 14, no. 9: 1897. https://doi.org/10.3390/electronics14091897
APA StyleDu, X., Guo, Z., Li, Z., Cao, Y., Chen, X., & Wu, T. (2025). VexNet: Vector-Composed Feature-Oriented Neural Network. Electronics, 14(9), 1897. https://doi.org/10.3390/electronics14091897







