Abstract
Traditional sparse code multiple access (SCMA) systems, which transmit user codewords through fixed subcarrier allocations, exhibit vulnerability to external jamming and interference. To address this challenge, we propose a novel SCMA codebook design incorporating the frequency-hopping (FH) technique in this paper. The construction of FH-SCMA codebooks is developed by applying cyclic shifting operations to the factor graph matrix of the conventional SCMA codebooks, where the cyclic shifting patterns are governed by chaotic Bernoulli FH sequences. Through a comprehensive case study, the critical properties of the proposed FH-SCMA codebooks—the uniformity and the sparsity, along with its error-rate performance—are illustrated in detail. Through the proposed FH-SCMA codebooks, the subcarriers of FH-SCMA are randomly hopped over within the resource-block group, while retaining the sparsity requirement, thereby facilitating the multi-user detection at the receiver. The proposed FH-SCMA system (codebooks) achieves superior performance under jamming scenarios compared to both the traditional SCMA and the previous pseudo-random FH-SCMA.
1. Introduction
As a promising enabler for next-generation wireless systems, non-orthogonal multiple access (NOMA) is a transformative multiple-access paradigm, which mainly includes power-domain and code-domain schemes. Among these variants, a code-domain sparse code multiple-access (SCMA) achieves massive connectivity within limited time-frequency resource blocks through multi-dimensional constellation spreading and sparse codeword allocation [1,2,3]. The SCMA codebooks are the most critical component in SCMA systems, which determine both the capacity and error-rate of the system. The capacity of the SCMA system depends mainly on the overload rate of the SCMA codebooks. Furthermore, the sparsity structure of the SCMA codebooks can guarantee the (near) optimal and low-complexity multi-user detection at receivers.
However, existing SCMA systems employ statically predefined codebooks where non-zero entries in codewords persistently occupy fixed subcarriers within resource block (RB) groups. This static subcarrier allocation mechanism, inherent to conventional SCMA implementations, renders systems susceptible to both intentional jamming and interference [2,3]. To address these challenges, we propose a new codebook design incorporating the dynamic subcarrier allocations, which enhances the reliability and the security of SCMA under adversarial jamming.
Frequency-hopping (FH) is a typical physical-layer security technique during signal transmission. The active carrier frequencies of the transmitted symbol are hopped within the given frequency bands according to an FH strategy (FH sequence), thus avoiding the spectral bands contaminated by the jammer. The FH sequence is the key component that determines the anti-jamming/interference capability of the system. In previous studies, various types of FH sequences targeting specific goals have been proposed, such as no-hit and low-hit FH sequences [4,5], chaotic FH sequences [5,6,7], wide-gap FH sequences [4], and other pseudo-random FH sequences [8,9,10]. The FH integrated with the SCMA codebook (FH-SCMA codebook) presents a novel methodology to overcome the intrinsic limitations of conventional SCMA architectures. The prototype of FH-SCMA was first introduced in our previous study [11], where the central frequency of the entire SCMA codebook is hopped over the extra RB-groups according to the preset FH sequence, but such an FH-SCMA scheme incurred significant spectral waste.
In contrast to the prototype SCMA and the existing FH-SCMA schemes, this paper proposes a new design scheme integrating the FH and SCMA codebook. Based on this new design, the active subcarrier of the codebooks is hopped over by the given RB group according to the specific FH sequence. Thus, it could enhance the jamming resistance capability and the spectral efficiency, which is the first contribution of this paper. It is well known that the sparsity of the developed FH-SCMA codebooks determines the optimal performance of the multi-user detection at receivers. However, the hopped-subcarriers with the random-manner cannot ensure the sparsity of the FH-SCMA codebooks. Thus, in this paper, we propose the idea of performing the FH on the factor graph matrix to retain the sparsity, and the FH sequence is generated by the p-ary chaotic sequence based on the Bernoulli mapping function. This is another contribution of this paper. Compared to other chaotic mapping functions (e.g., the Logistic function) [6,7], the Bernoulli mapping function can generate the sequence with better uniform characteristics. To the best of our knowledge, there have been no studies on the integrated design of the FH and SCMA codebook to combat jamming/interference in SCMA systems.
The remainder of this paper is organized as follows. In Section 2, the traditional SCMA codebooks (system) and the drawbacks due to the jamming are introduced. Also, the existing solutions to the anti-jamming are extensively reviewed. In Section 3, the property requirements of the new FH-SCMA codebooks are introduced firstly; then, a construction algorithm of the FH-SCMA codebook set is developed. In Section 4, as a case study, the construction process and the properties of the proposed FH-SCMA codebooks are presented step-by-step. In Section 5, the bit-error-rate (BER) performance of the proposed FH-SCMA codebooks (system) is evaluated by simulations. Finally, the conclusions and the future work are drawn in Section 6.
2. Problem Description and Related Work
In this section, we will firstly introduce the model of the traditional SCMA system (codebooks), and its technical drawbacks and issues are obviously drawn when the jamming attack exists. Then, the existing solutions to combating jamming/interference in SCMA systems are reviewed comprehensively.
2.1. Problem Descriptions of Traditional SCMA
We consider traditional SCMA uplinks with J users (UEs), of which symbols are multiplexed to connect to the base station (BS) on a resource block group containing K orthogonal subcarriers (SCs). The SCMA codebook set with J codebooks is properly designed, which can be denoted by [2].
where the j-th UE’s codebook is arranged as a matrix, satisfying . The column vector with entries is called a codeword with low density. At the transmitter, the SCMA coder of user j selects a codeword from (i.e., a column-vector ) based on the instantaneously transmitted M-ary symbol . The detailed codebook design method can be readily found in previous studies, which will be extensively reviewed in the next subsection.
Assuming that the channel-gains of the j-th user are denoted as , corresponding to these pre-assigned K subcarriers and the transmitted M-ary symbol m is encoded as the SCMA codeword , the K-dimensional received signal of these J users can be expressed as [11]
where denotes the transmit power of the j-th user, and it is assumed that for all js. is a vector, with each element following the additive white Gaussian noise (AWGN). denotes the jamming signals that are emitted at the portion of K sub-carriers and the portion of time intervals during the entire transmission. We assume that , where is a vector with the dimension . There are non-zero elements in , and each element follows the complex Gaussian distribution. Thus, it indicates that there are subcarriers contaminated by the jammer (), and the signal-to-jamming ratio (SJR) is .
A flat Rayleigh fading channel is considered in this paper, and the probability-of-density (pdf) of the amplitude of channel gain can be written as follows with parameter .
where the mean square value .
For a given SCMA codebook , the usage of the active subcarriers of and can be represented by the mapping matrix . Thus, the factor graph matrix corresponding to this SCMA codebook set is denoted as
where the element belongs to . If , it indicates that the k-th subcarrier is occupied by the transmitted data; otherwise, the subcarrier is vacant.
Assume that the number of “1”s in each row of the factor graph matrix is denoted as , and the number of “1”s in each column is denoted as . To achieve the optimal performance of multi-user detection at the SCMA receiver, the specific sparsity requirement of the SCMA codebook set should be met [3], as shown below.
In traditional SCMA systems, the codebooks and corresponding factor graph matrix are pre-assigned to J SCMA users, enabling data transmission through fixed subcarriers. This fixed transmission scheme renders specific users susceptible to performance degradation when their designated SCs experience persistent jamming or interference. The drawback of traditional SCMA is illustrated clearly in Figure 1, where the mapping matrix of the user is preset as . As demonstrated in Figure 1, the shaded areas indicate active subcarriers at which the non-zero data are sent. The transmission of this user can be completely devastated when the and active subcarriers are continuously attacked by the jammer.
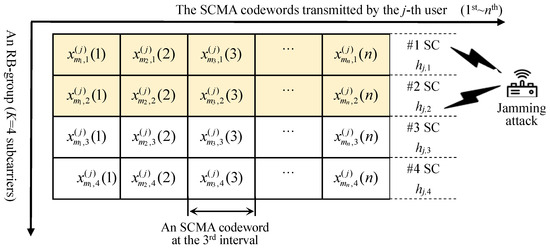
Figure 1.
The diagram of the data transmission of the traditional SCMA user using the fixed mapping matrix .
2.2. Related Work
In SCMA systems, the SCMA codebook set is the most critical component, which determines the overload capability, the multi-user detection performance, and so forth. Up to now, plenty of constructions of SCMA codebooks have been extensively reported [12,13,14,15,16,17,18]. For example, some studies have concentrated on implementing interleaving and rotation techniques in mother codebooks [14,15]. Others have optimized the process of codebook design utilizing various algorithms (i.e., genetic algorithm and differential evolution) [16,17]. In addition, some specific codebooks have been designed for wireless channels (i.e., AWGN and Rayleigh fading channels) [18]. However, these current codebooks lack the explicit mechanisms of jamming/interference suppression.
Regarding the aspect of jamming/interference suppression, FH technology has received tremendous research attention owing to its strong resilience to jamming/interference and thus significantly enhanced robustness in various harsh communication environments [19,20]. The FH sequences (also called FH patterns) are some of the most important components to determine the entire system performance. In past engineering practice, traditional (pseudo-)random FH sequences, with which the frequency-hits follow a near uniform-distribution over arbitrary access delays, were extensively studied in [21,22,23]. These traditional pseudo-random FH sequences unfortunately retain frequency-hits due to the uniform-distribution. However, in some practical scenarios, several emerging FH sequences have been proposed to meet the specific requirements in transmissions. The quasi-orthogonal FH sequence, which has the lower frequency-hits over the restricted time-shifts, is proposed for quasi-synchronous FH multi-access systems [24,25,26,27]. The chaotic FH sequence based on the nonlinear function is usually developed for FH systems targeting higher security and longer periodicity [5,6,7]. As for the following jamming, the wide-gap FH sequences and their construction algorithms have been proposed in [4,27]. The wide-gap FH sequence allows the frequencies at adjacent slots to hop over the wider band-gap, to avoid the wideband following jamming.
To combat the jamming/interference in SCMA systems, most of the previous studies have mainly focused on the signal processing of anti-jamming, the channel coding, and the SCMA receiver design (the new message-passing-algorithm (MPA) design). For example, a new FH-based SCMA system is proposed in [28], which adopts the FH technique to increase the system diversity and to promote extrinsic information interaction between users. In Ref. [29], the FH technique and the low-rate Turbo-Hadamard codes are jointly applied to suppress the jamming attack in SCMA systems. The SCMA receiver design is a crucial issue to improve the performance. Since the high computational complexity of MPA is unacceptable for the actual hardware processing ability, several simplified MPA algorithms are investigated. Ref. [2], associating MPA with multidimensional interference cancellation, leads to fewer iterations. Ref. [30] establishes the interference model of the single-carrier SCMA system in fading channels, and the Gaussian approximate interference-based belief propagation algorithm processing is proposed to realize efficient detection and complexity reduction.
Similar to this paper, some FH-SCMA systems have been proposed in previous studies [11,31], where the entire subcarriers of SCMA are hopped over the wider spectral band according to the FH sequence. The exiting FH-SCMA could improve the capability of jamming suppression but lead to the waste of the spectrum. In our previous study [32], an inter-RBs hopping SCMA system was proposed to combat jamming attacks. The prime sequence is utilized to govern the changes of SCMA codebooks; thus, its period is restricted by the prime number.
Overall, there have not been any studies on the joint design of the FH and SCMA codebook to suppress the anti-jamming/interference in SCMA systems. The codebook design is the most efficient solution to combat the jamming and interference.
3. The Integrated Design of the FH Sequence and SCMA Codebooks
Firstly, we will introduce the basic requirements of FH-SCMA codebook design, which guarantee the performance of MPA in multi-user detector. Then, a construction algorithm integrating the FH sequence and the SCMA codebook is proposed.
3.1. Requirements of FH-SCMA Codebook Design
To address the problem that the traditional SCMA is subject to external jamming, a new SCMA codebook-based FH technique is proposed, where the codebooks are changed according to the FH sequence. To achieve optimal performance, the technical challenges of the proposed FH-SCMA codebook design are concluded as follows:
- Challenge 1: To achieve the (near) optimal MPA performance at the SCMA receiver, the sparsity of the factor graph matrix of the proposed FH-SCMA codebooks should be satisfied.
- Challenge 2: To ensure the security of the FH-SCMA codebooks, the FH sequence and FH-SCMA codebook should have a sufficiently long period and good randomness.
- Challenge 3: The proposed FH-SCMA codebooks should avoid additional collisions of subcarriers because it could result in the deterioration of the MPA performance at the SCMA receiver.
To address Challenges 1 and 3, the FH-SCMA codebooks proposed in this paper are implemented by performing the cyclic shifting operation on a given factor graph matrix. For Challenge 2, the FH sequence, which governs the cyclic shifting operation, is generated by a nonlinear chaotic p-ary sequence based on the Bernoulli function. The details of FH-SCMA codebook design will be presented in Section 3.2.
3.2. Construction Algorithm of FH-SCMA Codebooks
The construction algorithm of FH-SCMA codebooks consists of four steps: (1) the generation of chaotic sequence, (2) mapping to the p-ary FH sequence, (3) the cyclic shifting operation, and (4) the generation of FH-SCMA codebooks.
Step 1 (The generation of the chaotic sequence): The analog sequence is generated based on the Bernoulli mapping function,
where the parameter and the initial value are preset.
Step 2 (Mapping to the p-ary FH sequence): The analog sequence is mapped to a p-ary sequence (i.e., to ) as follows:
- The continuous interval is divided into p non-overlapping sections,where .
- The algorithm mapping the analog sequence to the p-ary sequence is shown as
Thus, a p-ary FH sequence with the period L is presented as
Compared to other nonlinear chaotic mapping functions, e.g., the Logistic function, Cubic function, and so forth, the sequence generated by the Bernoulli mapping function exhibits better uniform-distribution characteristic, and its period could be sufficiently long [5,6,7]. These features boost the randomness/uniformity, and the unpredictability of the proposed FH-SCMA codebooks.
Step 3 (The cyclic shifting operation): Given an SCMA codebook set (or a factor graph matrix ), which can be readily obtained from previous studies [12,13,14,15,16,17,18], the column-wise vectors in perform the cyclic -digit(s) shifting operation. Then, the instantaneous factor graph matrix at the l-th interval is written as
where is the element in and the parameters should satisfy that .
Step 4 (The generation of FH-SCMA codebooks): For different time intervals ls, a series of factor graph matrices corresponding to the new FH-SCMA codebooks can be expressed as
From the above steps, it is observed that the factor graph matrix is changed according to the sequence , which ensures that the originally fixed SCMA codebooks become the hopped-SCMA codebooks by the integrated design of the chaotic FH sequence and . The construction complexity is moderate, as these four steps can be realized through elementary mathematical transformations. The computational complexity of the algorithm mainly stems from the demand for higher numerical precision in Steps 1 and 2.
4. A Case Study: An Example of FH-SCMA Codebooks and Their Properties
In this section, the construction process and properties are presented by a case study. It is worth noting that the following analysis and results can also be extended to general cases with various values of parameters .
For easy explanation, we select a previous SCMA codebook with , and its factor graph matrix is denoted as [1]
In addition, the parameters of the construction algorithm are preset as: , and . Then, the analog chaotic sequence is generated according to Step 1. The elements of during the intervals are denoted as
Based on the mapping algorithm in Step 2, a 6-ary chaotic sequence is generated, where the segment of over is illustrated here
Based on Step 3 and , the hopped mapping matrices for these six UEs at the intervals are obtained as follows by performing the cyclic shifting operations on :
Finally, according to the hopped mapping matrices, as shown in (17), we obtain the hopped rule of the subcarriers and its corresponding FH-SCMA codebooks.
- Test 1: Functional testing
We take #1 UE and # 2 UE as examples to illustrate the hopped-subcarrier (hopped-SC) of the FH-SCMA codewords, as shown in Figure 2. From these figures, it can be observed that the active subcarriers of UEs are changed randomly according to the hopped mapping matrices and the generated p-ary chaotic FH sequence . The hopped-SC scheme can efficiently avoid the jamming attack. Therefore, the proposed FH-SCMA codebooks (systems) can enhance the security and the performance reliability, owing to the integration of the chaotic FH sequence , which exhibits good randomness, a long period, and high unpredictability.
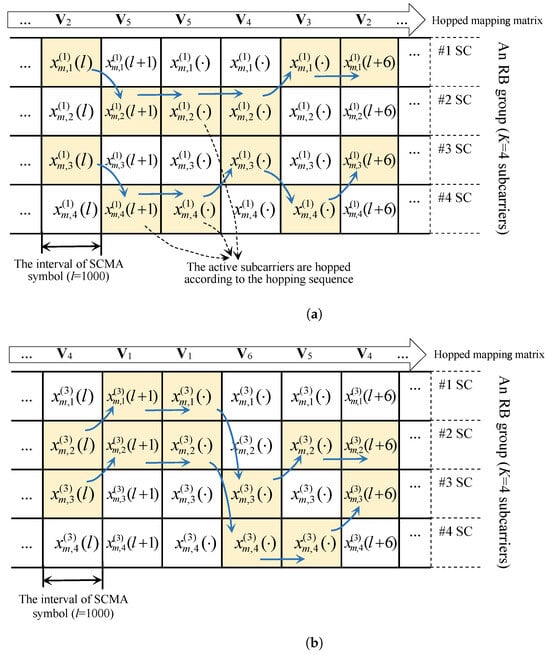
Figure 2.
The diagram of the proposed FH-SCMA codebooks and the hopped sub-carriers (the shaded areas are the active subcarriers, at which non-zero symbols are sent): (a) UE and (b) UE.
- Test 2: Sparsity and uniformity testings of the FH-SCMA codebooks
The sparsity of the codebooks can be easily verified by the characteristics of the elements in , as shown in Equation (13). At different time intervals ls, the column-vectors in are composed of the various permutations of ; meanwhile, all elements and their positions in remain unchanged as those in . The sparsity of the developed FH-SCMA codebooks is consistent with the original factor graph matrix, i.e.,
The above property can also be verified by the example, as shown in Equation (17). The proposed FH-SCMA codebooks do not alter the sparsity of the codebooks, which is beneficial to the multi-user MPA detection at the FH-SCMA receiver, without introducing extra decoding errors.
Then, the uniformity of FH-SCMA codebooks (i.e., the randomness of the active subcarriers) over the intervals is checked in Table 1, where , , and UEs are considered here as the example. The distribution number of the various subcarrier (SC) combinations, i.e., SC + SC, SC + SC, SC + SC, SC + SC, SC + SC, and SC + SC, follow a near-uniform distribution, which lies between the range of 314 and 349. In addition, various users attain the small values of the standard deviations, i.e., 5.38 for UE, 11.36 for UE, and 12.49 for UE, which implies that various SC-combinations are employed uniformly by different UEs.

Table 1.
The number of the usage of various SC-combinations for the FH-SCMA users over intervals.
5. The BER Performance of the Proposed FH-SCMA Codebooks
In this section, the BER improvement of the proposed FH-SCMA system (codebooks) is evaluated by Monte Carlo simulations using Matlab software. The parameters of the system and the wireless channels are set as follows: the employed FH-SCMA codebooks with are as shown in Equation (17), and the mean square value of Rayleigh fading channels . We assume that one jammer emits the adverse signal on two dimensional time-frequency resources. Specially, one subcarrier (i.e., , there are 25% SCs jammed) and some time-intervals (TIs) during the entire transmission are attacked by the jammer with various SJRs. Also, the performance of the traditional SCMA system without FH, and the SCMA system with the random FH-SCMA codebooks, are plotted as the benchmark. The classic Max-Log-MPA multi-user detector is employed at SCMA receivers.
The BER comparisons of the proposed FH-SCMA system with other SCMA systems are presented in Figure 3. The jammer emits the hostile signal with SJR = 0 dB on 25% SCs, and 50% and 100% TIs. It this well known that 100% TIs jammed is the worst case. From this figure, we can observe that the proposed FH-SCMA codebooks can attain superior performance under the jamming attacks. Although the random FH-SCMA system employs the FH technique, the random FH strategy may introduce additional collisions of subcarriers in the FH-SCMA codebooks (i.e., the extra decoding errors at the MPA receiver), thus ruining the sparsity of the FH-SCMA codebooks and degrading the system performance. The traditional SCMA without FH obtains an unacceptable BER performance due to the lack of the mechanism of jamming suppression.
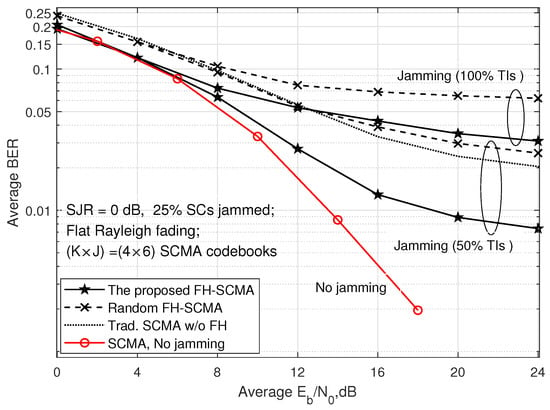
Figure 3.
BER comparisons among the previous SCMA systems and the proposed FH-SCMA system.
The BERs of the proposed FH-SCMA system with various SJRs are plotted in Figure 4. The parameters of the jammer and SCMA system are set the same as those in Figure 3 except for the value of SJR. We find that the proposed FH-SCMA obtains the worse BER as the value of SJR decreases but still attains an acceptable performance even though the system suffers from a strong jamming attack (25% SCs and 50% TIs jammed) and Rayleigh fading.
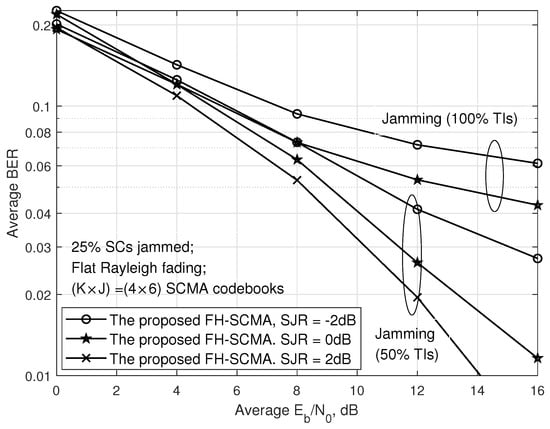
Figure 4.
BERs of the proposed FH-SCMA system under jamming attack with various SJRs.
As illustrated in Figure 3 and Figure 4, the error-floors remain at the level of due to the effects of both Rayleigh fading and strong jamming, but we can infer that the BER performance could be further improved by introducing channel coding schemes in FH-SCMA systems. In addition, it is notable that the BER improvements in these simulations are obtained without increasing subcarrier resources; that is, the number of sub-carriers utilized by SCMA users is consistently maintained at 4 () during the entire transmission. This feature renders the proposed FH-SCMA suitable for band-limited scenarios.
6. Conclusions and Discussions
In this paper, we have proposed a new design of SCMA codebooks integrated with FH technology, which helps the SCMA system enhance its anti-jamming capability and transmission reliability. The hopped-SCMA codebooks are implemented by performing the cyclic shifting operation on the factor graph matrix of the SCMA codebooks, and the cyclic shifting operation is governed by the chaotic Bernoulli FH sequence. Through the proposed construction algorithm and performance analysis, the advantages of the proposed FH-SCMA codebooks and their system are concluded as follows:
- The proposed FH-SCMA codebooks attain a long period and good randomness/ uniformity, since the hopped-SCMA codebooks are controlled by the chaotic FH sequence based on the Bernoulli mapping function. The usage distributions of various SC-combinations obtain the small value of standard deviations. The active sub-carriers are hopped over a given RB group, which enhances the spectral efficiency.
- The sparsity of the proposed FH-SCMA codebooks is maintained perfectly so that the classic MPA multi-user detection can be directly applied to the FH-SCMA receiver without any adjustment. This feature guarantees that FH-SCMA codebooks attain favorable performance with low complexity.
- In aid of the FH technique, the FH-SCMA codebooks (system) can efficiently combat the strong jamming attack (25% SCs and 50% TIs jammed), and the BER performance achieves an acceptable level of compared to other SCMA systems, which is more suitable for the massive user access under the severe electromagnetic environment.
Overall, the main contents of this paper include: (i) a heuristic algorithm for constructing the FH-SCMA codebooks, and (ii) a simulation-based evaluation of properties, including the uniformity and the BER performance. However, the construction complexity of the proposed FH-SCMA codebooks mainly arises from the numerical precision of generating elements in the analog chaotic sequence with long periods. This complexity may pose implementation limitations in practice. Following this paper, we can draw forth several interesting directions in our future work. For example, more flexible construction algorithms of FH-SCMA codebooks will be developed via various mathematical methods. The theoretical BER expression of the FH-SCMA system employing the proposed FH-SCMA codebooks and the multi-user detection will be derived. In addition, the BER performance could be further improved by introducing emerging channel coding schemes, such as Polar code and low-density parity check code.
Author Contributions
Conceptualization, Q.Z.; methodology, P.Z. and Q.Z.; validation, P.Z., Z.X. and Q.Z.; formal analysis, P.Z., Z.X. and Q.Z.; investigation, P.Z. and Z.X.; data curation, P.Z., Z.X. and Q.Z.; writing—original draft preparation, P.Z.; writing—review and editing, Q.Z.; supervision, Q.Z.; project administration, Q.Z.; funding acquisition, Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Open Fund for Key Laboratory of Internet of Things Standards and Applications in Ministry of Industry and Information Technology under grant number 202303.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ding, Z.; Lei, X.; Karagiannidis, G.K.; Schober, R.; Yuan, J.; Bhargava, V.K. A survey on non-orthogonal multiple access for 5G networks: Research challenges and future trends. IEEE J. Sel. Area Commun. 2017, 35, 2181–2195. [Google Scholar] [CrossRef]
- Vameghestahbanati, M.; Marsland, I.; Gohary, R.; Yanikomeroglu, H. Multidimensional constellations for uplink SCMA systems a comparative study. IEEE Commun. Surv. Tutor. 2019, 21, 2169–2194. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, L.L. Sparse or dense: A comparative study of code domain NOMA systems. IEEE Trans. Wirel. Commun. 2021, 20, 4768–4780. [Google Scholar] [CrossRef]
- Zeng, Q.; Chen, J.; Niu, X.; Zhou, L.; Liu, X. Optimal no-hit-zone sequences with wide-gap for improved FHMA systems under follower jamming. IEEE Trans. Commun. 2025, 73, 1493–1495. [Google Scholar] [CrossRef]
- Zeng, Q.; Liu, X. Chaos theory-based NHZ-FH sequence set for quasi-synchronous FHMA system. Electron. Lett. 2017, 53, 1493–1495. [Google Scholar] [CrossRef]
- Lin, C.; Sun, S. Chaotic frequency hopping sequences. IEEE Commun. Lett. 1998, 46, 1433–1437. [Google Scholar]
- Jung, J.; Lim, J. Chaotic standard map based frequency hopping OFDMA for low probability of intercept low probability of intercept. IEEE Commun. Lett. 2011, 15, 1019–1021. [Google Scholar] [CrossRef]
- Bao, J.; Ji, L. New families of optimal frequency hopping sequence sets. IEEE Trans. Inf. Theory 2016, 62, 5209–5224. [Google Scholar] [CrossRef]
- Xu, S.; Mi, J. New constructions for near-optimal sets of frequency-hopping sequences via the Gaussian periods in finite fields. IEEE Access 2022, 10, 18463–18469. [Google Scholar] [CrossRef]
- Niu, X.; Xing, C.; Liu, Y.; Zhou, L. A construction of optimal frequency hopping sequence set via combination of multiplicative and additive groups of finite fields. IEEE Trans. Inf. Theory 2020, 66, 5310–5315. [Google Scholar] [CrossRef]
- Zeng, Q.; Liu, Z.; Liu, X.; Zhong, J.; Xiao, P. Frequency-hopping based SCMA for massive connectivity in multi-cell networks. In Proceedings of the IEEE Vehicle Technology Conference 2021 Fall (VTC 2021-Fall), Helsinki, Finland, 27 September–28 October 2021; pp. 1–6. [Google Scholar]
- Luo, Q.; Liu, Z.; Chen, G.; Xiao, P.; Ma, Y.; Maaref, A. A design of low-projection SCMA codebooks for ultra-low decoding complexity in downlink IoT networks. IEEE Trans. Wirel. Commun. 2023, 22, 6608–6623. [Google Scholar] [CrossRef]
- Huang, C.; Su, B.; Lin, T.; Huang, Y. Downlink SCMA codebook design with low error rate by maximizing minimum Euclidean distance of superimposed codewords. IEEE Trans. Veh. Technol. 2022, 71, 5231–5245. [Google Scholar] [CrossRef]
- Cai, D.; Fan, P.; Lei, X.; Liu, Y.; Chen, D. Multi-dimensional SCMA codebook design based on constellation rotation and interleaving. In Proceedings of the 2016 IEEE 83rd Vehicular Technology Conference ( VTC 2016-Spring), Nanjing, China, 15–18 May 2016; pp. 1–5. [Google Scholar]
- Klimentyev, V.P.; Sergienko, A.B. SCMA codebooks optimization based on genetic algorithm. In Proceedings of the European Wireless 2017, Dresden, Germany, 17–19 May 2017; pp. 1–5. [Google Scholar]
- Deka, K.; Priyadarsini, M.; Sharma, S.; Beferull-Lozano, B. Design of SCMA codebooks using differential evolution. In Proceedings of the 2020 IEEE International Conference on Communications Workshops (ICC Workshops), Dublin, Ireland, 7–11 June 2020; pp. 1–7. [Google Scholar]
- Yu, L.; Fan, P.; Cai, D.; Ma, Z. Design and analysis of SCMA codebook based on star-QAM signaling constellations. IEEE Trans. Veh. Technol. 2018, 67, 10543–10553. [Google Scholar] [CrossRef]
- Vikas, V.; Rajesh, A.; Deka, K.; Sharma, S. A comprehensive technique to design SCMA codebooks. IEEE Commun. Lett. 2022, 26, 1735–1739. [Google Scholar] [CrossRef]
- Bluetooth Special Interest Group (SIG). Bluetooth Specification, 683 Version 5.0. 2016. Available online: http://www.bluetooth.org (accessed on 1 January 2016).
- Torrieri, D.; Talarico, S.; Valenti, M.C. Analysis of a frequency-hopping millimeter-wave cellular uplink. IEEE Trans. Wirel. Commun. 2016, 15, 7089–7098. [Google Scholar] [CrossRef]
- Lin, M.; Yang, M.; Chang, G.C.; Liu, C.Y.; Kwong, Y.S.; C, W. Frequency-hopping CDMA with Reed-Solomon code sequences in wireless communications. IEEE Trans. Commun. 2007, 55, 2052–2055. [Google Scholar] [CrossRef]
- Al-Dweik, A.J.; Sharif, B.S. Exact performance analysis of synchronous FH-MFSK wireless networks. IEEE Trans. Veh. Technol. 2009, 58, 3771–3776. [Google Scholar] [CrossRef]
- Guan, L.; Li, Z.; Si, J.; Hao, B. Analysis of asynchronous frequency hopping multiple-access network performance based on the frequency hopping sequences. IET Commun. 2015, 9, 117–121. [Google Scholar] [CrossRef]
- Ye, W.; Fan, P.; Pengf, D.; Suehiro, N. Theoretical bound on no hit zone of frequency hopping sequences. In Proceedings of the Fifth International Workshop on Signal Design and Its Applications in Communications, Guilin, China, 10–14 October 2011; pp. 115–117. [Google Scholar]
- Guan, L.; Li, Z.; Si, J.; Hao, B. Strong no-hit-zone sequences for improved quasi-orthogonal FHMA systems: Sequence design and performance analysis. IEEE Trans. Commun. 2019, 67, 5336–5345. [Google Scholar]
- Liu, X.; Zhou, L.; Zeng, Q. No-hit-zone frequency hopping sequence sets with respect to aperiodic Hamming correlation. Electron. Lett. 2018, 54, 212–213. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, C.; Zeng, Q.; Liu, X.; Wu, H. Optimal low-hit-zone frequency-hopping sequence sets with wide-gap for FHMA systems under follower jamming. IEEE Commun. Lett. 2022, 26, 969–973. [Google Scholar] [CrossRef]
- Su, H.; Zhao, M.; Fang, X.; Zhang, P. Frequency hopping non-orthogonal multiple access. In Proceedings of the 2023 International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 2–4 November 2023; pp. 990–995. [Google Scholar]
- Li, W.; Zheng, Z.; Luan, S.; Pan, G. An anti-jamming SCMA method using Turbo-Hadamard codes for satellite communications. In Proceedings of the 2024 International Conference on the Frontiers of Electronic, Electrical and Information Engineering (ICFEEIE), Huangshan, China, 21–23 June 2024; pp. 1–6. [Google Scholar]
- Qin, T.; Yang, Z.; Liang, J.; Han, K.; Hu, J. Receiver Designs for SC-SCMA Systems Over Frequency Selective Channels. In Proceedings of the IEEE 99th Vehicular Technology Conference 2024 Spring (VTC2024-Spring), Singapore, 24–27 June 2024; pp. 1–6. [Google Scholar]
- Bai, Z.; Li, B.; Yang, M.; Yan, Z.; Zuo, X.; Zhang, Y. FH-SCMA: Frequency hopping based sparse code multiple access for next generation internet of things. In Proceedings of the IEEE Wireless Communications and Networking Conference (IEEE WCNC), San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar]
- Yang, K.; Zeng, Q.; Liu, X.; Fang, K.; Niu, X. Design and Analysis of Inter-RBs Hopping SCMA System under Jamming Attacks. In Proceedings of the IEEE 22nd International Conference on Communication Technology, Nanjing, China, 11–14 November 2022; pp. 1–6. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).