Comparative Analysis of Post Hoc Explainable Methods for Robotic Grasp Failure Prediction
Abstract
1. Introduction
- RQ1: Do the explanation methods agree on selecting the most responsible feature for grasp failures?
- RQ2: How similar are their results on ranking important features and their contributions in explaining the failures?
- RQ3: How does the choice of ML model (Decision Tree vs. Random Forest) affect feature importance rankings?
- RQ4: How do different explanation methods compare in terms of computational efficiency?
2. Background
2.1. Grasp Stability Prediction in Robotics
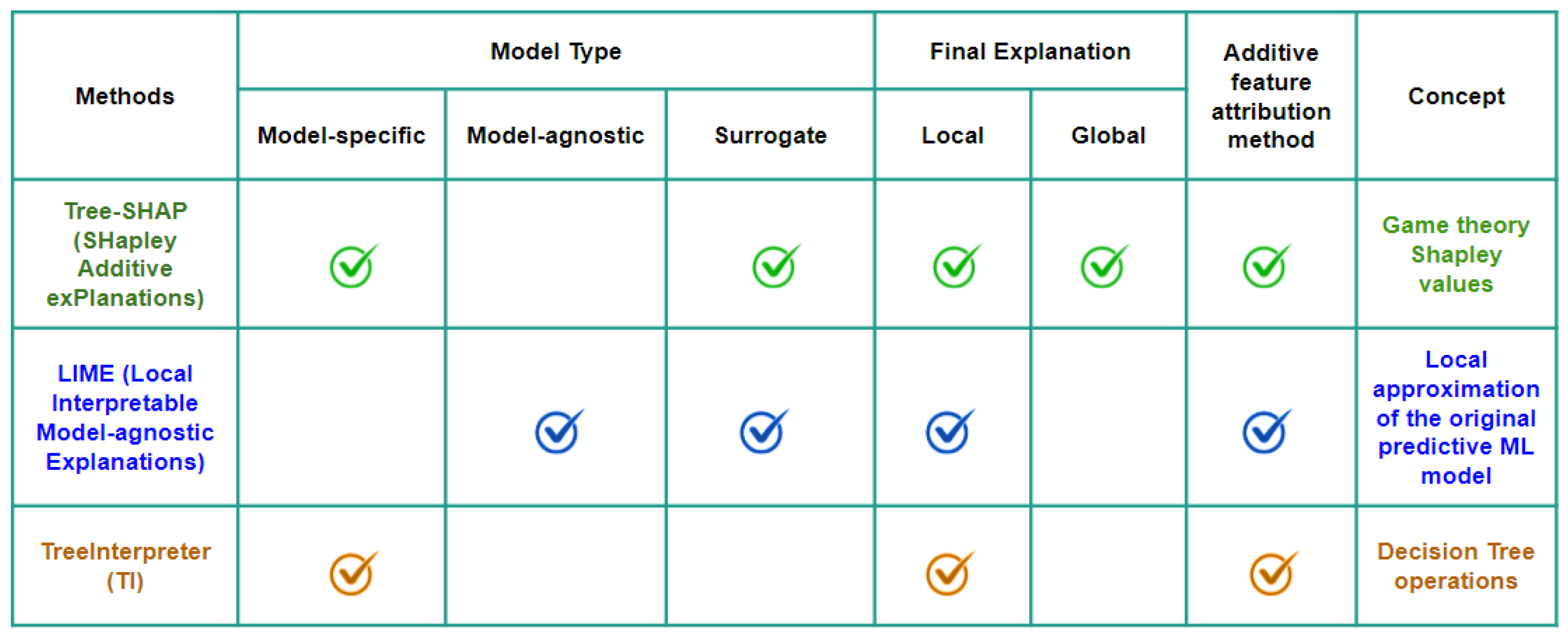
2.2. Post Hoc Explanation Methods
- Additive Feature Attribution: Some methods express explanations as a sum of feature effects [22].
- Underlying Concept: The theoretical foundation behind the explanation approach.
2.2.1. Local Interpretable Model-Agnostic Explanations (LIME)
2.2.2. SHAP and Tree-SHAP
2.2.3. TreeInterpreter (TI)
- The expected prediction value at the parent node (based on all training samples that reached that node).
- The expected prediction value at the child node the sample moves to.
- The difference between these values, which represents the contribution of the feature that defined the split.
2.3. Feature Importance in Decision Tree and Random Forest Classifiers
2.4. Rank Similarity Metrics
2.4.1. Kendall’s Tau Correlation Coefficient
2.4.2. Rank-Biased Overlap (RBO)
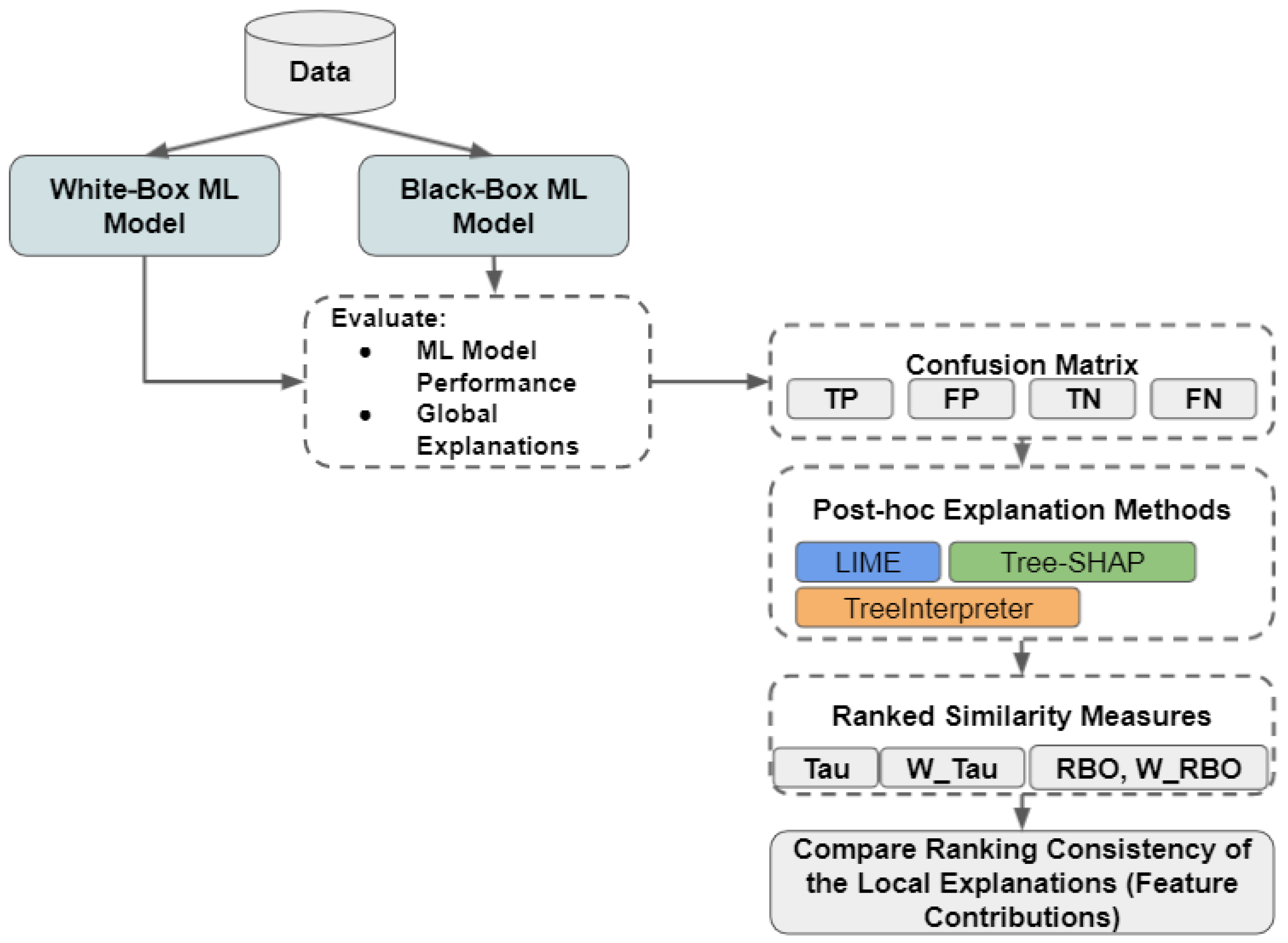
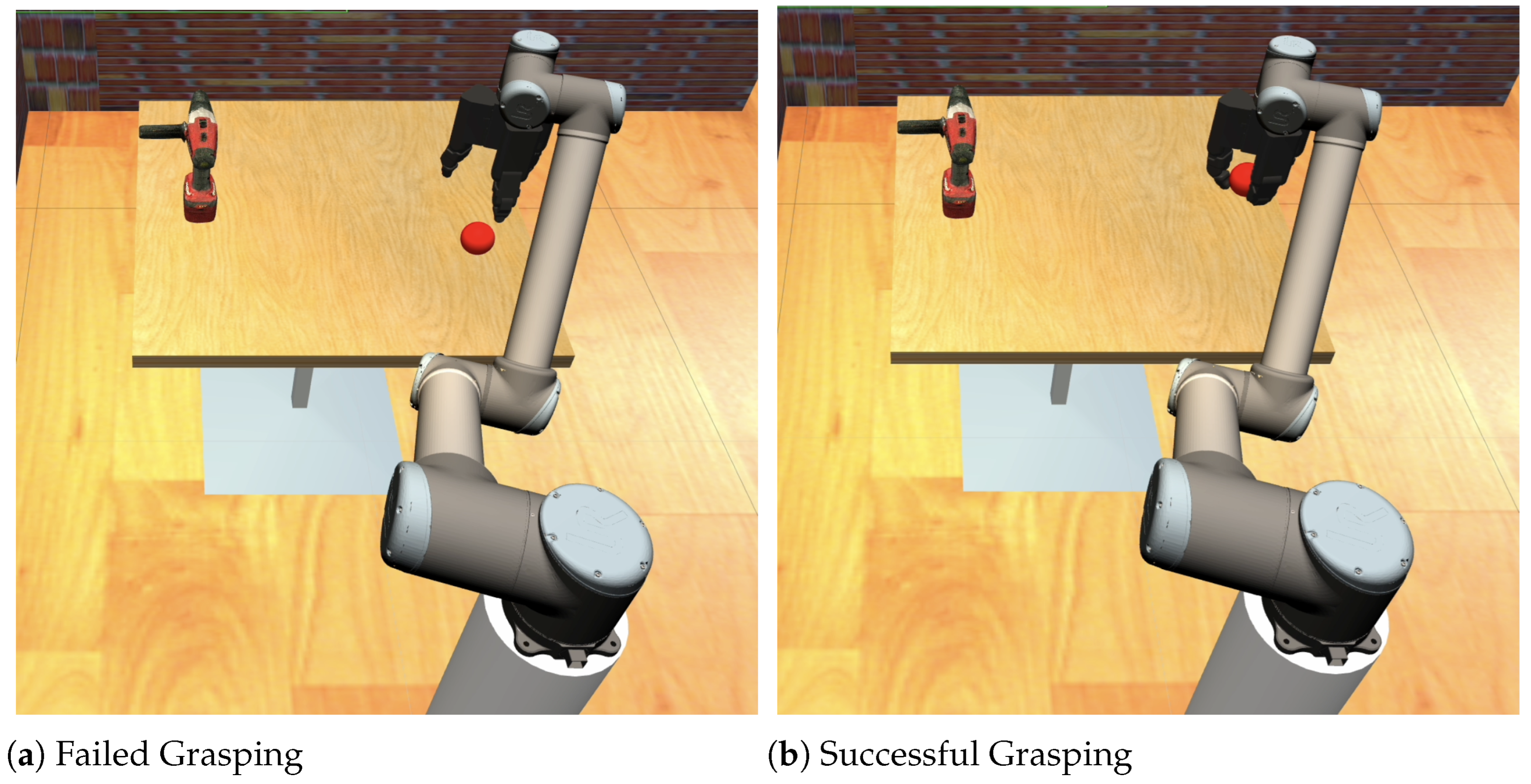
3. Methodology: Application to Robotics Grasping Failure Detection
- : Hand 1, indicating the only hand used in the simulation.
- : Fingers on the hand, where each finger has three joints.
- : Joints in each finger, with each joint having measurements for position (), velocity (), and effort ().
4. Results
4.1. Experimental Setup
4.2. ML Model Performance Comparison
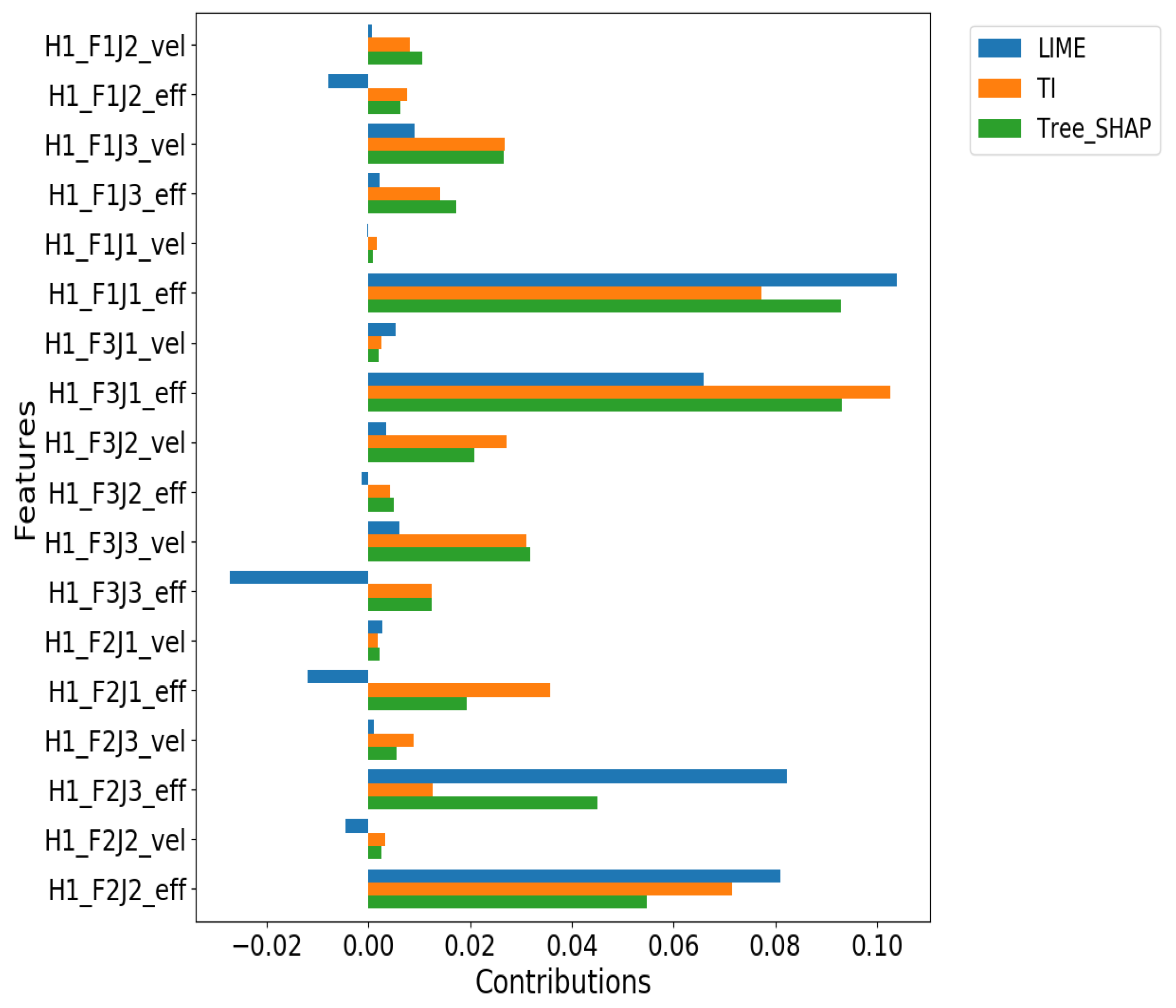
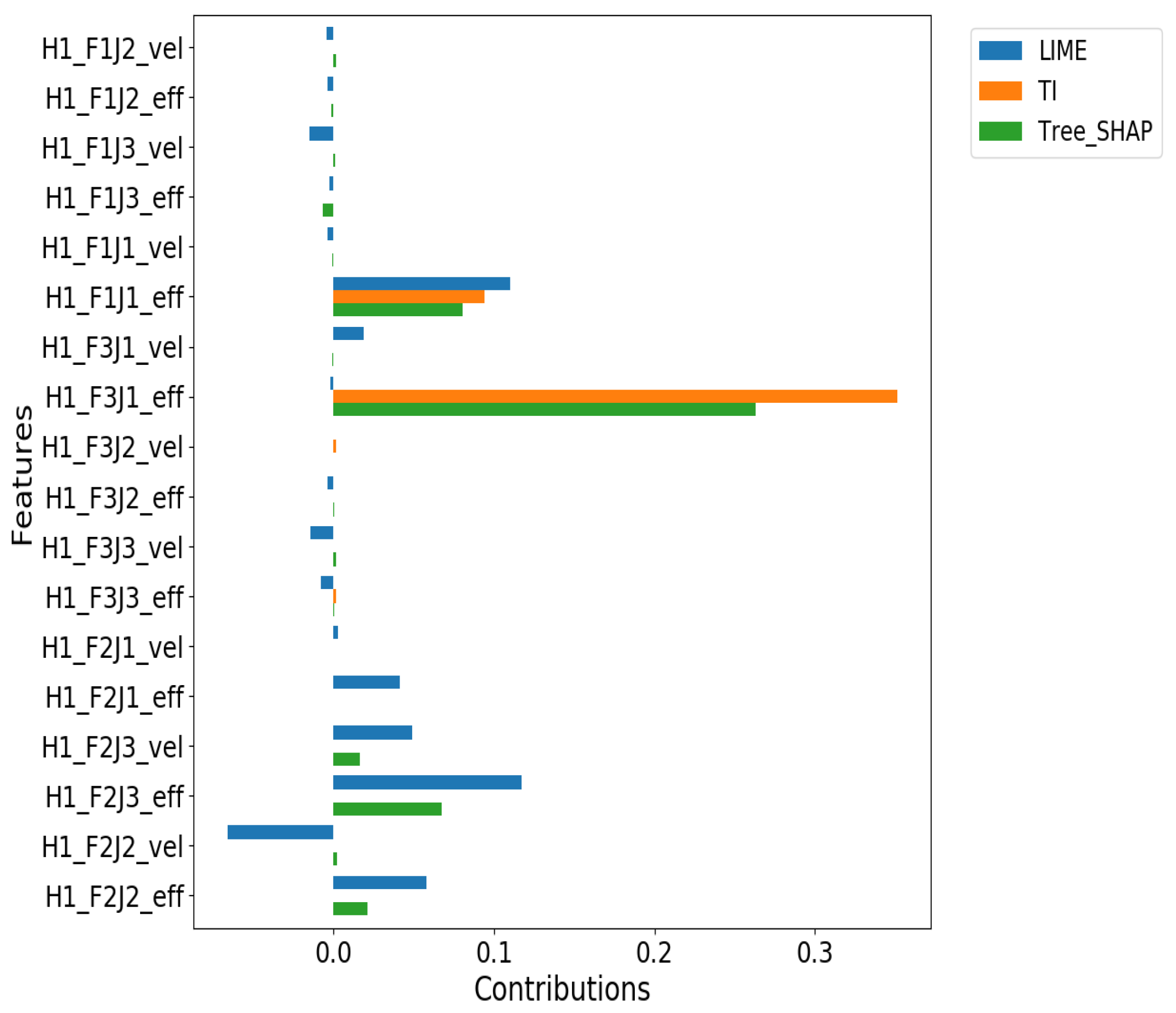
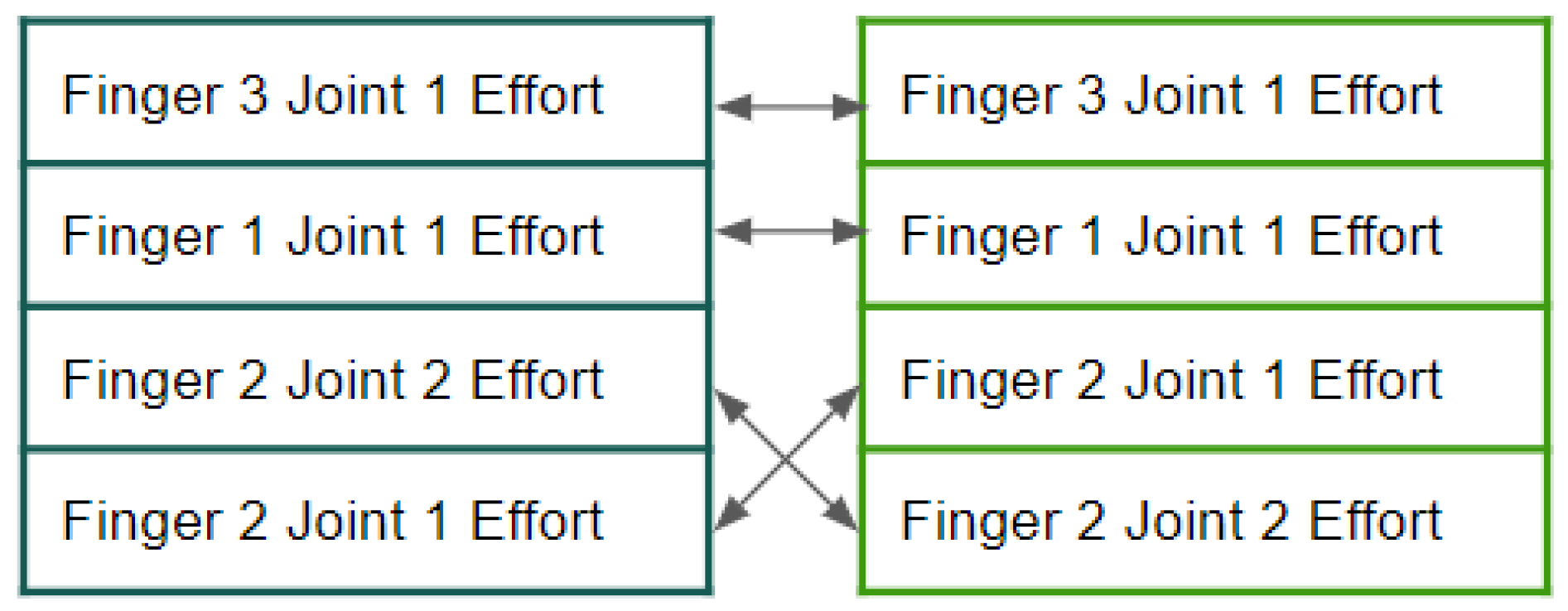
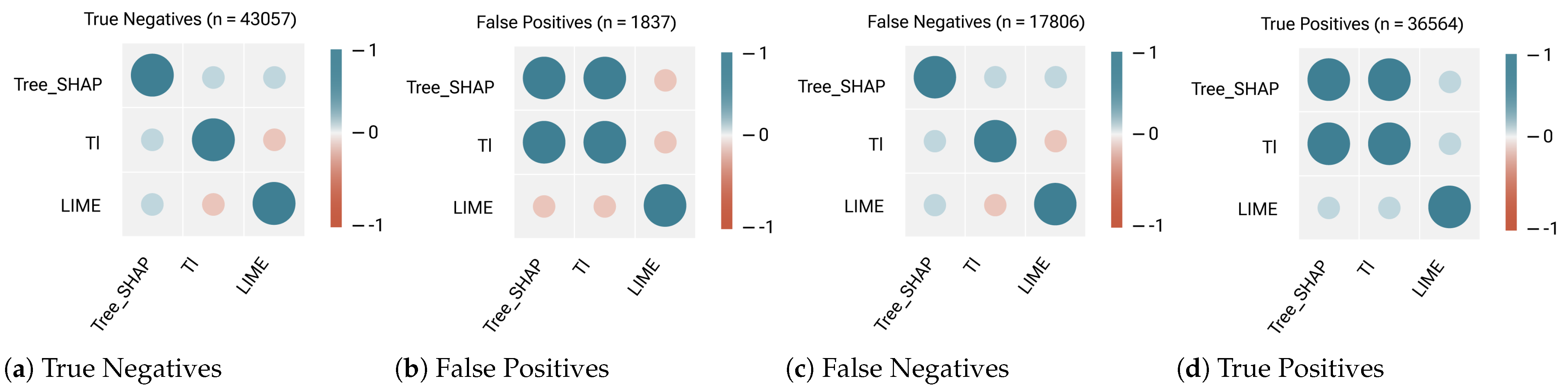
4.3. RQ1: Do the Explanation Methods Agree on Selecting the Most Responsible Feature for Grasp Failures?
4.4. RQ2: How Similar Are Their Results on Ranking Important Features and Their Contributions in Explaining the Failures?
4.5. RQ3: How Does the Choice of ML Model (Decision Tree vs. Random Forest) Affect Feature Importance Rankings?
4.6. RQ4: How Do Different Explanation Methods Compare in Terms of Computational Efficiency?
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ML | machine learning |
| DT | Decision Tree |
| RF | Random Forest |
| SHAP | SHapley Additive exPlanations |
| LIME | Local Interpretable Model-agnostic Explanations |
| TI | TreeInterpreter |
| AUC | Area Under the Curve |
| ROC | Receiver Operating Characteristic |
| RBO | Rank-Biased Overlap |
| FN | False Negative |
| FP | False Positive |
| TN | True Negative |
| TP | True Positive |
| FI | feature importance |
| MSE | Mean Squared Error |
| MAE | Mean Absolute Error |
| CART | Classification and Regression Trees |
References
- Kitagawa, S.; Wada, K.; Hasegawa, S.; Okada, K.; Inaba, M. Multi-stage learning of selective dual-arm grasping based on obtaining and pruning grasping points through the robot experience in the real world. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; IEEE: New York, NY, USA, 2018; pp. 7123–7130. [Google Scholar]
- Della Santina, C.; Arapi, V.; Averta, G.; Damiani, F.; Fiore, G.; Settimi, A.; Catalano, M.G.; Bacciu, D.; Bicchi, A.; Bianchi, M. Learning from humans how to grasp: A data-driven architecture for autonomous grasping with anthropomorphic soft hands. IEEE Robot. Autom. Lett. 2019, 4, 1533–1540. [Google Scholar] [CrossRef]
- Dixon, W.E.; Walker, I.D.; Dawson, D.M.; Hartranft, J.P. Fault detection for robot manipulators with parametric uncertainty: A prediction-error-based approach. IEEE Trans. Robot. Autom. 2000, 16, 689–699. [Google Scholar] [CrossRef]
- Cho, C.N.; Hong, J.T.; Kim, H.J. Neural network based adaptive actuator fault detection algorithm for robot manipulators. J. Intell. Robot. Syst. 2019, 95, 137–147. [Google Scholar] [CrossRef]
- Shin, J.H.; Lee, J.J. Fault detection and robust fault recovery control for robot manipulators with actuator failures. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation, Detroit, MI, USA, 10–15 May 1999; IEEE: New York, NY, USA, 1999; Volume 2, pp. 861–866. [Google Scholar]
- Damak, K.; Boujelbene, M.; Acun, C.; Alvanpour, A.; Das, S.K.; Popa, D.O.; Nasraoui, O. Robot failure mode prediction with deep learning sequence models. Neural Comput. Appl. 2025, 37, 4291–4302. [Google Scholar] [CrossRef]
- Muradore, R.; Fiorini, P. A PLS-based statistical approach for fault detection and isolation of robotic manipulators. IEEE Trans. Ind. Electron. 2011, 59, 3167–3175. [Google Scholar] [CrossRef]
- Molnar, C. A Guide for Making Black Box Models Explainable. 2018. Available online: https://christophm.github.io/interpretable-ml-book (accessed on 15 January 2024).
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Cramer, J.S. The origins of logistic regression. In Tinbergen Institute Working Paper; Tinbergen Institute, Amsterdam and Rotterdam: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Chung, K. On Model Explainability, from LIME, SHAP, to Explainable Boosting. 2019. Available online: https://everdark.github.io/k9/notebooks/ml/model_explain/ (accessed on 30 April 2024).
- Lou, Y.; Caruana, R.; Gehrke, J.; Hooker, G. Accurate intelligible models with pairwise interactions. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; ACM: New York, NY, USA, 2013; pp. 623–631. [Google Scholar]
- Caruana, R.; Lou, Y.; Gehrke, J.; Koch, P.; Sturm, M.; Elhadad, N. Intelligible models for healthcare: Predicting pneumonia risk and hospital 30-day readmission. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 1721–1730. [Google Scholar]
- Acun, C.; Nasraoui, O. In-Training Explainability Frameworks: A Method to Make Black-Box Machine Learning Models More Explainable. In Proceedings of the 2023 IEEE/WIC International Conference on Web Intelligence and Intelligent Agent Technology (WI-IAT), Venice, Italy, 26–29 October 2023; pp. 230–237. [Google Scholar] [CrossRef]
- Acun, C.; Ashary, A.; Popa, D.O.; Nasraoui, O. Enhancing Robotic Grasp Failure Prediction Using A Pre-hoc Explainability Framework*. In Proceedings of the 2024 IEEE 20th International Conference on Automation Science and Engineering (CASE), Puglia, Italy, 28 August–1 September 2024; pp. 1993–1998. [Google Scholar] [CrossRef]
- Lipton, Z.C. The mythos of model interpretability. Queue 2018, 16, 31–57. [Google Scholar] [CrossRef]
- Craven, M.; Shavlik, J.W. Extracting tree-structured representations of trained networks. Adv. Neural Inf. Process. Syst. 1996, 8, 24–30. [Google Scholar]
- Baehrens, D.; Schroeter, T.; Harmeling, S.; Kawanabe, M.; Hansen, K.; MÞller, K.R. How to explain individual classification decisions. J. Mach. Learn. Res. 2010, 11, 1803–1831. [Google Scholar]
- Strumbelj, E.; Kononenko, I. An efficient explanation of individual classifications using game theory. J. Mach. Learn. Res. 2010, 11, 1–18. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should i trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Fisher, A.; Rudin, C.; Dominici, F. All models are wrong, but many are useful: Learning a variable’s importance by studying an entire class of prediction models simultaneously. J. Mach. Learn. Res. 2019, 20, 1–81. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4765–4774. [Google Scholar]
- Lundberg, S.M.; Erion, G.G.; Lee, S.I. Consistent individualized feature attribution for tree ensembles. arXiv 2018, arXiv:1802.03888. [Google Scholar]
- Saabas, A. Interpreting random forests. Data Dive 2014. Available online: http://blog.datadive.net/interpreting-random-forests (accessed on 10 February 2024).
- Saabas, A. TreeInterpreter Library. 2019. Available online: https://github.com/andosa/treeinterpreter (accessed on 10 February 2024).
- Villani, V.; Pini, F.; Leali, F.; Secchi, C. A survey on human–robot collaboration in industrial settings: Safety, intuitive interfaces and applications. Mechatronics 2018, 55, 248–266. [Google Scholar] [CrossRef]
- Hoffman, R.R.; Mueller, S.T.; Klein, G.; Litman, J. Explaining explanation, part 1: Theoretical foundations. IEEE Intell. Syst. 2019, 34, 72–79. [Google Scholar] [CrossRef]
- Lasota, P.A.; Fong, T.; Shah, J.A. A survey of methods for safe human-robot interaction. Found. Trends Robot. 2017, 5, 261–349. [Google Scholar] [CrossRef]
- Robla-Gómez, S.; Becerra, V.M.; Llata, J.R.; Gonzalez-Sarabia, E.; Torre-Ferrero, C.; Perez-Oria, J. Working together: A review on safe human-robot collaboration in industrial environments. IEEE Access 2017, 5, 26754–26773. [Google Scholar] [CrossRef]
- Andriella, A.; Siqueira, H.; Fu, D.; Magg, S.; Barros, P.; Wermter, S.; Dautenhahn, K.; Rossi, S.; Mastrogiovanni, F. Explaining semantic human-robot interactions. Curr. Robot. Rep. 2022, 3, 1–10. [Google Scholar]
- Kok, J.N.; Boers, E.J. Trust in robots: Challenges and opportunities. Curr. Robot. Rep. 2020, 1, 297–309. [Google Scholar] [CrossRef]
- Datta, S.; Kuo, T.; Liang, H.; Tena, M.J.S.; Celi, L.A.; Szolovits, P. Integrating artificial intelligence into health care through data access: Can the GDPR act as a beacon for policymakers? J. Med. Internet Res. 2020, 22, e19478. [Google Scholar]
- Asan, O.; Bayrak, A.E.; Choudhury, A. Artificial intelligence and human trust in healthcare: Focus on clinicians. J. Med. Internet Res. 2020, 22, e15154. [Google Scholar] [CrossRef]
- Alvanpour, A.; Das, S.K.; Robinson, C.K.; Nasraoui, O.; Popa, D. Robot Failure Mode Prediction with Explainable Machine Learning. In Proceedings of the 2020 IEEE 16th International Conference on Automation Science and Engineering (CASE), Hong Kong, China, 20–21 August 2020; pp. 61–66. [Google Scholar]
- Shadow Robot Company. Smart Grasping Sandbox. GitHub Repository. 2023. Available online: https://github.com/shadow-robot/smart_grasping_sandbox (accessed on 15 December 2023).
- Cecati, C. A survey of fault diagnosis and fault-tolerant techniques—Part II: Fault diagnosis with knowledge-based and hybrid/active approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar]
- Isermann, R. Fault-Diagnosis Systems: An Introduction from Fault Detection to Fault Tolerance; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Raza, A.; Benrabah, A.; Alquthami, T.; Akmal, M. A Review of Fault Diagnosing Methods in Power Transmission Systems. Appl. Sci. 2020, 10, 1312. [Google Scholar] [CrossRef]
- Sapora, S. Grasp Quality Deep Neural Networks for Robotic Object Grasping. Ph.D. Thesis, Imperial College London, London, UK, 2019. [Google Scholar]
- Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R.; et al. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Giannotti, F.; Pedreschi, D. A survey of methods for explaining black box models. Acm Comput. Surv. (CSUR) 2018, 51, 1–42. [Google Scholar] [CrossRef]
- Doshi-Velez, F.; Kim, B. Towards A Rigorous Science of Interpretable Machine Learning. arXiv 2017, arXiv:1702.08608. [Google Scholar]
- Fujimoto, K.; Kojadinovic, I.; Marichal, J.L. Axiomatic characterizations of probabilistic and cardinal-probabilistic interaction indices. Games Econ. Behav. 2006, 55, 72–99. [Google Scholar] [CrossRef]
- Haddouchi, M.; Berrado, A. A survey and taxonomy of methods interpreting random forest models. arXiv 2024, arXiv:2407.12759. [Google Scholar]
- Rokach, L.; Maimon, O. Decision Trees. In Data Mining and Knowledge Discovery Handbook; Maimon, O., Rokach, L., Eds.; Springer: Boston, MA, USA, 2005; pp. 165–192. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation importance: A corrected feature importance measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: Berlin/Heidelberg, Germany, 2013; Volume 26. [Google Scholar]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Ronaghan, S. The Mathematics of Decision Trees, Random Forest and Feature Importance in Scikit-Learn and Spark. 2018. Available online: https://medium.com/data-science/the-mathematics-of-decision-trees-random-forest-and-feature-importance-in-scikit-learn-and-spark-f2861df67e3 (accessed on 12 January 2024).
- Louppe, G.; Wehenkel, L.; Sutera, A.; Geurts, P. Understanding variable importances in forests of randomized trees. Adv. Neural Inf. Process. Syst. 2013, 26, 431–439. [Google Scholar]
- Huggett, M. Similarity and Ranking Operations. In Encyclopedia of Database Systems; Liu, L., Özsu, M.T., Eds.; Springer: Boston, MA, USA, 2009; pp. 2647–2651. [Google Scholar] [CrossRef]
- Kendall, M.G. The treatment of ties in ranking problems. Biometrika 1945, 33, 239–251. [Google Scholar] [CrossRef] [PubMed]
- Webber, W.; Moffat, A.; Zobel, J. A similarity measure for indefinite rankings. Acm Trans. Inf. Syst. (TOIS) 2010, 28, 1–38. [Google Scholar] [CrossRef]
- Gibbons, J.D.; Chakraborti, S. Nonparametric Statistical Inference, 4th ed.; revised and expanded; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberl, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Vigna, S. A weighted correlation index for rankings with ties. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18–22 May 2015; pp. 1166–1176. [Google Scholar]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Anchors: High-precision model-agnostic explanations. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Cupcic, U. How I Taught My Robot to Realize How Bad It Was at Holding Things, Shadow Robot Company. 2019. Available online: https://www.shadowrobot.com/blog/how-i-taught-my-robot-to-realize-how-bad-it-was-at-holding-things/ (accessed on 13 January 2024).
- Cupcic, U. A Grasping Dataset From Simulation Using Shadow Robot’s Smart Grasping Sandbox, Shadow Robot Company. 2019. Available online: https://www.kaggle.com/ugocupcic/grasping-dataset (accessed on 15 December 2023).
- Quigley, M.; Gerkeyy, B.; Conleyy, K.; Fausty, J.; Footey, T.; Leibsz, J.; Bergery, E.; Wheelery, R.; Ng, A. Robotic Operating System. Version ROS Melodic Morenia. 2018. Available online: https://www.ros.org (accessed on 27 April 2025).
- Koenig, N.; Howard, A. Design and use paradigms for Gazebo, an open-source multi-robot simulator. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No.04CH37566), Sendai, Japan, 28 September–2 October 2004; Volume 3, pp. 2149–2154. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]

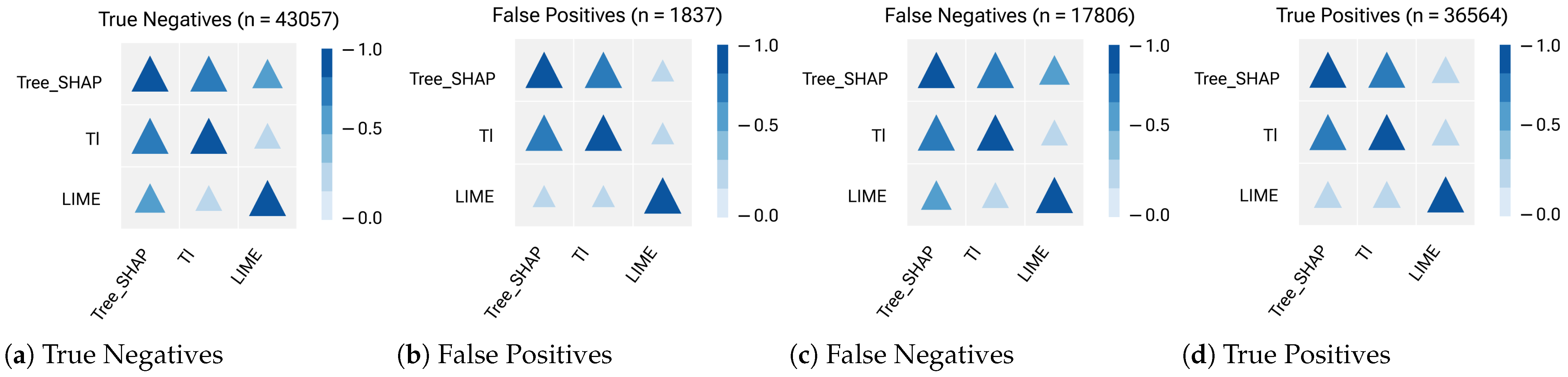

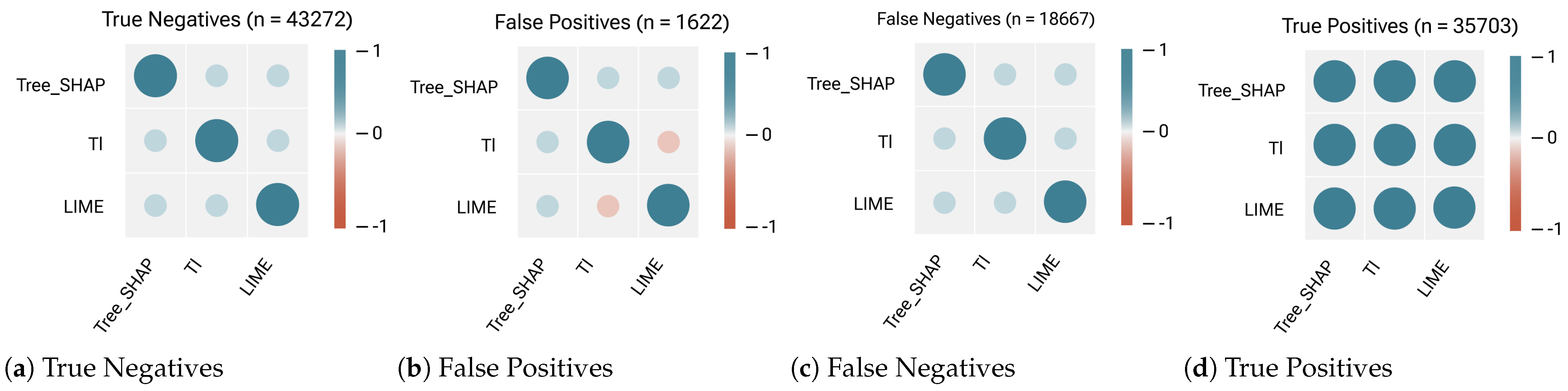

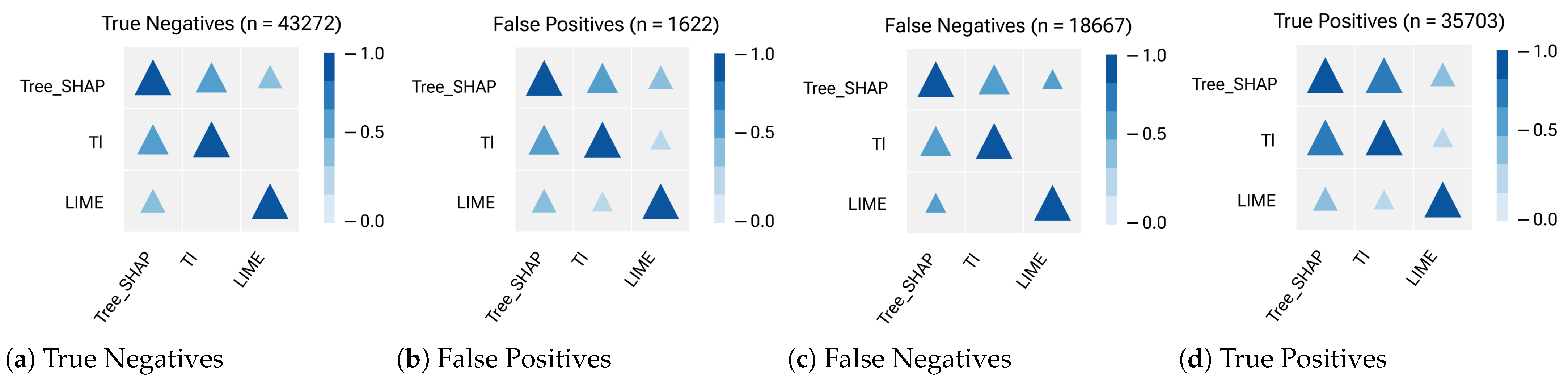


| 0 | 1 | ||
|---|---|---|---|
| Kendall’s Tau | similar in reverse order | disjoint (no similarity) | identical (similar) |
| Weighted Kendall’s Tau | similar in reverse order | disjoint | identical |
| RBO | NA | disjoint | identical |
| Weighted RBO | NA | disjoint | identical |
| Feature | Definition |
|---|---|
| effort in joint 1 in finger 1 | |
| velocity in joint 1 in finger 1 |
| Metric | Random Forest | Decision Tree |
|---|---|---|
| Accuracy | 0.8020 (±0.0001) | 0.7947 (±00030) |
| F1 | 0.7879 (±0.0004) | 0.7816 (±0.0062) |
| Precision | 0.9530 (±0.0015) | 0.9369 (±0.0124) |
| Recall | 0.6715 (±0.0013) | 0.6707 (±0.0151) |
| AUC | 0.8712 (±0.0002) | 0.8524 (±0.0053) |
| True Negatives | ||||||||
|---|---|---|---|---|---|---|---|---|
| Decision Tree | Random Forest | |||||||
| Kendall Tau | Weighted K-Tau | RBO | Weighted RBO | Kendall Tau | Weighted K-Tau | RBO | Weighted RBO | |
| Tree-SHAP & TI | 0.3 | 0.2 | 0.7 | 0.7 | 0.3 | 0.5 | 0.8 | 0.8 |
| Tree-SHAP & LIME | 0.3 | 0.2 | 0.3 | 0.2 | 0.3 | 0.2 | 0.6 | 0.3 |
| LIME & TI | 0.3 | 0.2 | 0.0 | 0.0 | −0.3 | −0.4 | 0.4 | 0.2 |
| False Negatives | ||||||||
| Decision Tree | Random Forest | |||||||
| Kendall Tau | Weighted K-Tau | RBO | Weighted RBO | Kendall Tau | Weighted K-Tau | RBO | Weighted RBO | |
| Tree-SHAP & TI | 0.3 | 0.2 | 0.7 | 0.7 | 0.3 | 0.5 | 0.9 | 0.8 |
| Tree-SHAP & LIME | 0.3 | 0.2 | 0.3 | 0.2 | 0.3 | 0.2 | 0.6 | 0.3 |
| LIME & TI | 0.3 | 0.2 | 0.0 | 0.0 | −0.3 | −0.4 | 0.4 | 0.2 |
| True Positives | ||||||||
| Decision Tree | Random Forest | |||||||
| Kendall Tau | Weighted K-Tau | RBO | Weighted RBO | Kendall Tau | Weighted K-Tau | RBO | Weighted RBO | |
| Tree-SHAP & TI | 1 | 1 | 0.9 | 0.8 | 1 | 1 | 0.9 | 0.8 |
| Tree-SHAP & LIME | 1 | 1 | 0.4 | 0.2 | 0.3 | 0.5 | 0.4 | 0.2 |
| LIME & TI | 1 | 1 | 0.3 | 0.2 | 0.3 | 0.5 | 0.4 | 0.2 |
| False Positives | ||||||||
| Decision Tree | Random Forest | |||||||
| Kendall Tau | Weighted K-Tau | RBO | Weighted RBO | Kendall Tau | Weighted K-Tau | RBO | Weighted RBO | |
| Tree-SHAP & TI | 0.3 | 0.2 | 0.6 | 0.7 | 1 | 1 | 0.9 | 0.8 |
| Tree-SHAP & LIME | 0.3 | 0.3 | 0.4 | 0.2 | −0.3 | −0.4 | 0.3 | 0.2 |
| LIME & TI | −0.3 | −0.2 | 0.3 | 0.2 | −0.3 | −0.4 | 0.3 | 0.2 |
| Tree-SHAP (s) | TreeInterpreter (s) | LIME (s) | |
|---|---|---|---|
| Decision Tree | 0.00024 | 0.00001 | 3.33447 |
| Random Forest | 0.07646 | 0.00234 | 4.66648 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alvanpour, A.; Acun, C.; Spurlock, K.; Robinson, C.K.; Das, S.K.; Popa, D.O.; Nasraoui, O. Comparative Analysis of Post Hoc Explainable Methods for Robotic Grasp Failure Prediction. Electronics 2025, 14, 1868. https://doi.org/10.3390/electronics14091868
Alvanpour A, Acun C, Spurlock K, Robinson CK, Das SK, Popa DO, Nasraoui O. Comparative Analysis of Post Hoc Explainable Methods for Robotic Grasp Failure Prediction. Electronics. 2025; 14(9):1868. https://doi.org/10.3390/electronics14091868
Chicago/Turabian StyleAlvanpour, Aneseh, Cagla Acun, Kyle Spurlock, Christopher K. Robinson, Sumit K. Das, Dan O. Popa, and Olfa Nasraoui. 2025. "Comparative Analysis of Post Hoc Explainable Methods for Robotic Grasp Failure Prediction" Electronics 14, no. 9: 1868. https://doi.org/10.3390/electronics14091868
APA StyleAlvanpour, A., Acun, C., Spurlock, K., Robinson, C. K., Das, S. K., Popa, D. O., & Nasraoui, O. (2025). Comparative Analysis of Post Hoc Explainable Methods for Robotic Grasp Failure Prediction. Electronics, 14(9), 1868. https://doi.org/10.3390/electronics14091868








