High-Precision and Efficiency Hardware Implementation for GELU via Its Internal Symmetry
Abstract
1. Introduction
- We propose the internal symmetry piecewise approximation (ISPA). Instead of using the symmetry of the entire GELU activation function, we use the symmetry of the GELU’s internal Gauss error function (erf) to achieve a piecewise approximation of the positive and negative parts.
- We propose an Error Peak Search Strategy (EPSS), an automated framework for determining optimal segmentation schemes in piecewise approximation tasks. Extensive experimental results demonstrate that EPSS achieves superior performance compared to conventional optimization methods, including but not limited to the Nelder-Mead simplex algorithm and Newton-CG (Newton Conjugate Gradient) method.
- The proposed method is verified on three ViT models (Res-ViT, VIT-B, and VIT-L) with different configurations and demonstrated lossless precision.
- Hardware implementation on the FPGA platform achieves lower resource costs (LUT, Register and BRAM) and higher work frequency compared with the existing advanced method.
2. Background and Prior Research
3. Algorithm Design
3.1. Internal Symmetry Piecewise Approximation Method
3.2. Error Peak Search Strategy
| Algorithm 1 Error Peak Search Strategy |
|
4. Hardware Architecture and Implementation Details
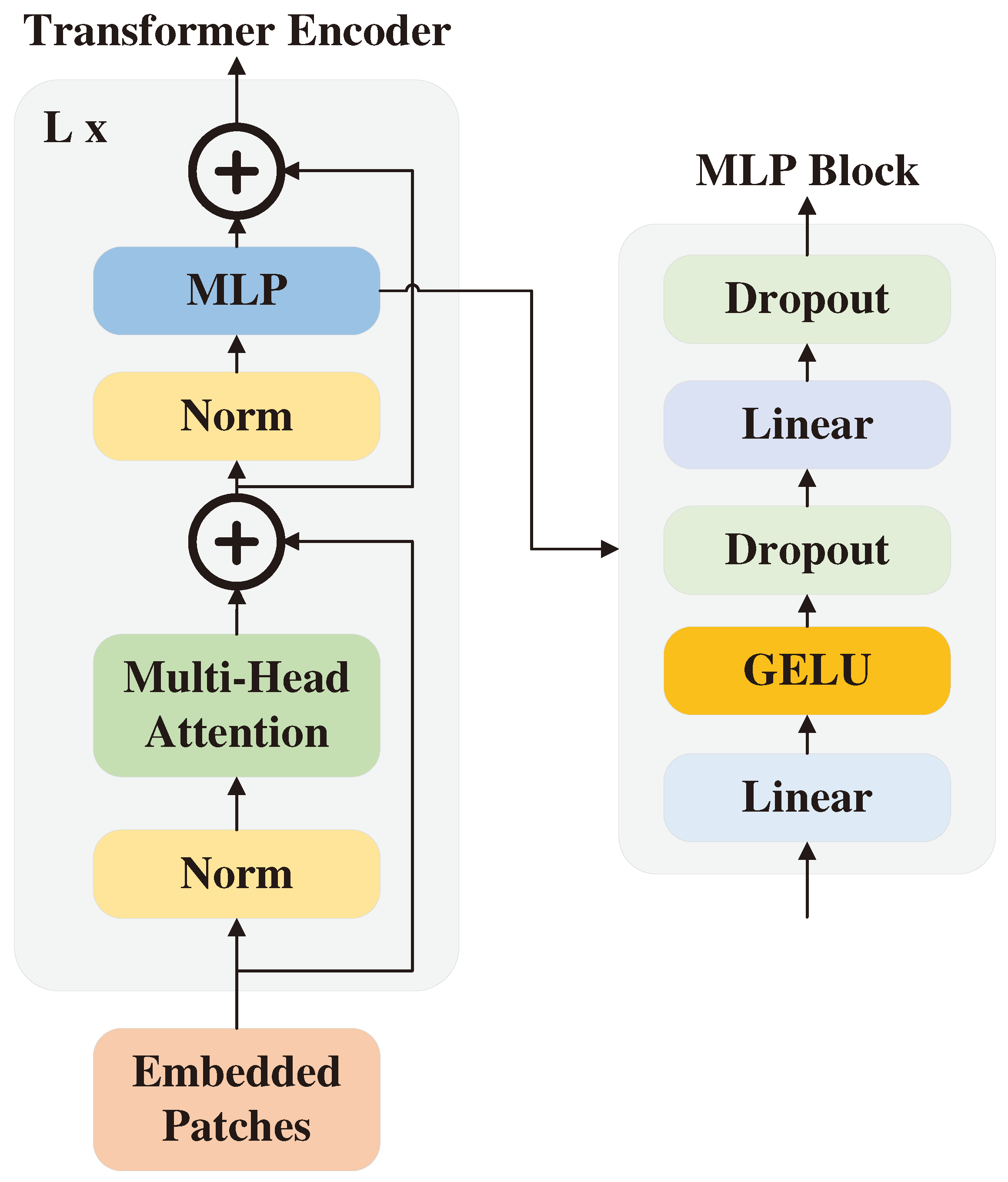
4.1. Overall Architecture
4.2. Basic Calculate Unit
5. Experiments and Performance Evaluation
5.1. Quantitative Error Characterization
5.2. DNN Accuracy Test
5.3. Hardware Resource Evaluation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hendrycks, D.; Gimpel, K. Gaussian error linear units (gelus). arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Lee, M. Mathematical analysis and performance evaluation of the gelu activation function in deep learning. J. Math. 2023, 2023, 4229924. [Google Scholar] [CrossRef]
- Dubey, S.R.; Singh, S.K.; Chaudhuri, B.B. Activation functions in deep learning: A comprehensive survey and benchmark. Neurocomputing 2022, 503, 92–108. [Google Scholar]
- Devlin, J.; Chang, M.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the Proc. NAACL-HLT, Albuquerque, NM, USA, 29 April–4 May 2019; pp. 4171–4186. [Google Scholar]
- Raffel, C.; Shazeer, N.; Roberts, A.; Lee, K.; Narang, S.; Matena, M.; Zhou, Y.; Li, W.; Liu, P.J. Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer. J. Mach. Learn. Res. 2020, 21, 140:1–140:67. [Google Scholar]
- Radford, A.; Wu, J.; Child, R.; Luan, D.; Amodei, D.; Sutskever, I. Language models are unsupervised multitask learners. OpenAI Blog 2019, 1, 9. [Google Scholar]
- Zhang, P.; Dai, X.; Yang, J.; Xiao, B.; Yuan, L.; Zhang, L.; Gao, J. Multi-Scale Vision Longformer: A New Vision Transformer for High-Resolution Image Encoding. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 2978–2988. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer using Shifted Windows. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision, ICCV 2021, Montreal, QC, Canada, 10–17 October 2021; pp. 9992–10002. [Google Scholar]
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J.; et al. Learning Transferable Visual Models From Natural Language Supervision. In Proceedings of the 38th International Conference on Machine Learning, ICML 2021, Virtual Event, 18–24 July 2021; Meila, M., Zhang, T., Eds.; PMLR: Westminster, UK, 2021; Volume 139, pp. 8748–8763. [Google Scholar]
- Radford, A.; Kim, J.W.; Xu, T.; Brockman, G.; McLeavey, C.; Sutskever, I. Robust Speech Recognition via Large-Scale Weak Supervision. In Proceedings of the International Conference on Machine Learning, ICML 2023, Honolulu, HI, USA, 23–29 July 2023; PMLR: Westminster, UK, 2023; Volume 202, pp. 28492–28518. [Google Scholar]
- Wang, T.; Gong, L.; Wang, C.; Yang, Y.; Gao, Y.; Zhou, X.; Chen, H. ViA: A Novel Vision-Transformer Accelerator Based on FPGA. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2022, 41, 4088–4099. [Google Scholar] [CrossRef]
- Nag, S.; Datta, G.; Kundu, S.; Chandrachoodan, N.; Beerel, P.A. ViTA: A Vision Transformer Inference Accelerator for Edge Applications. In Proceedings of the 2023 IEEE International Symposium on Circuits and Systems (ISCAS), Monterey, CA, USA, 21–25 May 2023; pp. 1–5. [Google Scholar]
- You, H.; Sun, Z.; Shi, H.; Yu, Z.; Zhao, Y.; Zhang, Y.; Li, C.; Li, B.; Lin, Y. ViTCoD: Vision Transformer Acceleration via Dedicated Algorithm and Accelerator Co-Design. In Proceedings of the 2023 IEEE International Symposium on High-Performance Computer Architecture (HPCA), Montreal, QC, Canada, 25 February–1 March 2023; pp. 273–286. [Google Scholar]
- Dumoulin, J.; Houshmand, P.; Jain, V.; Verhelst, M. Enabling Efficient Hardware Acceleration of Hybrid Vision Transformer (ViT) Networks at the Edge. In Proceedings of the 2024 IEEE International Symposium on Circuits and Systems (ISCAS), Singapore, 19–22 May 2024; pp. 1–5. [Google Scholar]
- Marino, K.; Zhang, P.; Prasanna, V.K. ME-ViT: A Single-Load Memory-Efficient FPGA Accelerator for Vision Transformers. In Proceedings of the 2023 IEEE 30th International Conference on High Performance Computing, Data, and Analytics (HiPC), Goa, India, 18–21 December 2023; pp. 213–223. [Google Scholar]
- Dong, P.; Zhuang, J.; Yang, Z.; Ji, S.; Li, Y.; Xu, D.; Huang, H.; Hu, J.; Jones, A.K.; Shi, Y.; et al. EQ-ViT: Algorithm-Hardware Co-Design for End-to-End Acceleration of Real-Time Vision Transformer Inference on Versal ACAP Architecture. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2024, 43, 3949–3960. [Google Scholar] [CrossRef]
- Parikh, D.; Li, S.; Zhang, B.; Kannan, R.; Busart, C.; Prasanna, V. Accelerating ViT Inference on FPGA through Static and Dynamic Pruning. In Proceedings of the 2024 IEEE 32nd Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Orlando, FL, USA, 5–8 May 2024; pp. 78–89. [Google Scholar]
- Tian, S.; Szafranski, C.; Zheng, C.; Yao, F.; Louri, A.; Chen, C.; Zheng, H. VITA: ViT Acceleration for Efficient 3D Human Mesh Recovery via Hardware-Algorithm Co-Design. In Proceedings of the 61st ACM/IEEE Design Automation Conference, DAC ’24, San Francisco, CA, USA, 23–27 June 2024. [Google Scholar]
- Han, Y.; Liu, Q. HPTA: A High Performance Transformer Accelerator Based on FPGA. In Proceedings of the 2023 33rd International Conference on Field-Programmable Logic and Applications (FPL), Gothenburg, Sweden, 4–8 September 2023; pp. 27–33. [Google Scholar]
- Zhou, M.; Xu, W.; Kang, J.; Rosing, T. TransPIM: A Memory-based Acceleration via Software-Hardware Co-Design for Transformer. In Proceedings of the 2022 IEEE International Symposium on High-Performance Computer Architecture (HPCA), Seoul, Republic of Korea, 2–6 April 2022; pp. 1071–1085. [Google Scholar]
- Luo, Y.; Yu, S. H3D-Transformer: A Heterogeneous 3D (H3D) Computing Platform for Transformer Model Acceleration on Edge Devices. ACM Trans. Des. Autom. Electron. Syst. 2024, 29, 1–19. [Google Scholar] [CrossRef]
- Wang, H.Y.; Chang, T.S. Row-wise Accelerator for Vision Transformer. In Proceedings of the 2022 IEEE 4th International Conference on Artificial Intelligence Circuits and Systems (AICAS), Incheon, Republic of Korea, 13–15 June 2022; pp. 399–402. [Google Scholar]
- Nilsson, P.; Shaik, A.U.R.; Gangarajaiah, R.; Hertz, E. Hardware implementation of the exponential function using Taylor series. In Proceedings of the 2014 NORCHIP, Tampere, Finland, 27–28 October 2014; pp. 1–4. [Google Scholar]
- Qin, Z.; Qiu, Y.; Sun, H.; Lu, Z.; Wang, Z.; Shen, Q.; Pan, H. A Novel Approximation Methodology and Its Efficient VLSI Implementation for the Sigmoid Function. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3422–3426. [Google Scholar] [CrossRef]
- Xie, Y.; Joseph Raj, A.N.; Hu, Z.; Huang, S.; Fan, Z.; Joler, M. A Twofold Lookup Table Architecture for Efficient Approximation of Activation Functions. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2020, 28, 2540–2550. [Google Scholar] [CrossRef]
- Leboeuf, K.; Namin, A.H.; Muscedere, R.; Wu, H.; Ahmadi, M. High Speed VLSI Implementation of the Hyperbolic Tangent Sigmoid Function. In Proceedings of the 2008 Third International Conference on Convergence and Hybrid Information Technology, Busan, Republic of Korea, 11–13 November 2008; Volume 1, pp. 1070–1073. [Google Scholar]
- Chiluveru, S.R.; Gyanendra; Chunarkar, S.; Tripathy, M.; Kaushik, B.K. Efficient Hardware Implementation of DNN-Based Speech Enhancement Algorithm With Precise Sigmoid Activation Function. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 3461–3465. [Google Scholar] [CrossRef]
- Choi, K.; Kim, S.; Kim, J.; Park, I.C. Hardware-Friendly Approximation for Swish Activation and Its Implementation. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 4516–4520. [Google Scholar] [CrossRef]
- Sadeghi, M.E.; Fayyazi, A.; Azizi, S.; Pedram, M. PEANO-ViT: Power-Efficient Approximations of Non-Linearities in Vision Transformers. In Proceedings of the 29th ACM/IEEE International Symposium on Low Power Electronics and Design, Newport Beach, CA, USA, 5–7 August 2024; pp. 1–6. [Google Scholar]
- Hong, Q.; Liu, Z.; Long, Q.; Tong, H.; Zhang, T.; Zhu, X.; Zhao, Y.; Ru, H.; Zha, Y.; Zhou, Z.; et al. A reconfigurable multi-precision quantization-aware nonlinear activation function hardware module for DNNs. Microelectron. J. 2024, 151, 106346. [Google Scholar] [CrossRef]
- Li, L.; Zhang, S.; Wu, J. An Efficient Hardware Architecture for Activation Function in Deep Learning Processor. In Proceedings of the 2018 IEEE 3rd International Conference on Image, Vision and Computing (ICIVC), Chongqing, China, 27–29 June 2018; pp. 911–918. [Google Scholar]
- Liu, K.; Shi, W.; Huang, C.; Zeng, D. Cost effective Tanh activation function circuits based on fast piecewise linear logic. Microelectron. J. 2023, 138, 105821. [Google Scholar] [CrossRef]
- Li, Y.; Cao, W.; Zhou, X.; Wang, L. A Low-Cost Reconfigurable Nonlinear Core for Embedded DNN Applications. In Proceedings of the 2020 International Conference on Field-Programmable Technology (ICFPT), Maui, HI, USA, 9–11 December 2020; pp. 35–38. [Google Scholar]
- Li, T.; Zhang, F.; Xie, G.; Fan, X.; Gao, Y.; Sun, M. A high speed reconfigurable architecture for softmax and GELU in vision transformer. Electron. Lett. 2023, 59, e12751. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. In Proceedings of the 9th International Conference on Learning Representations, ICLR, Vienna, Austria, 4 May 2021. [Google Scholar]
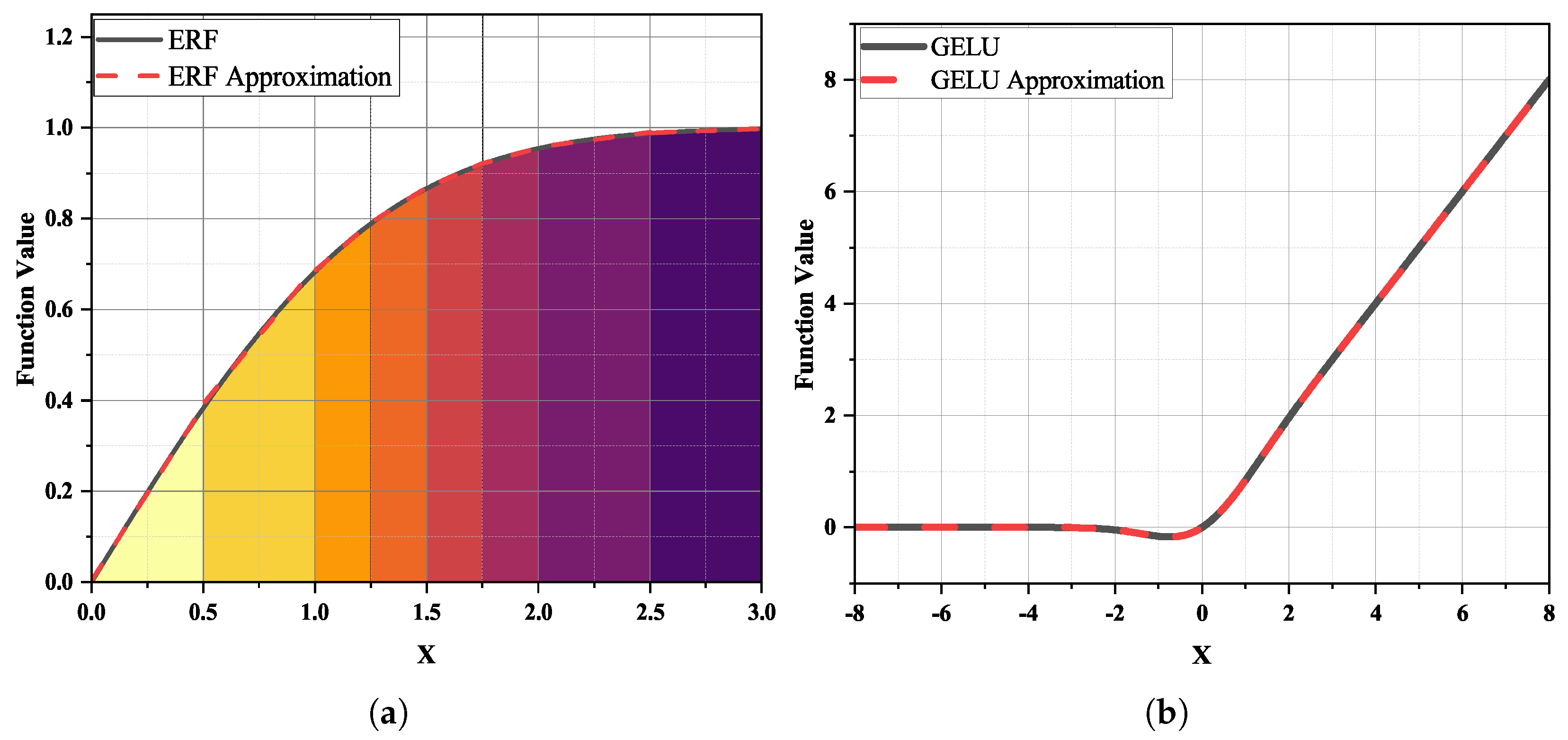
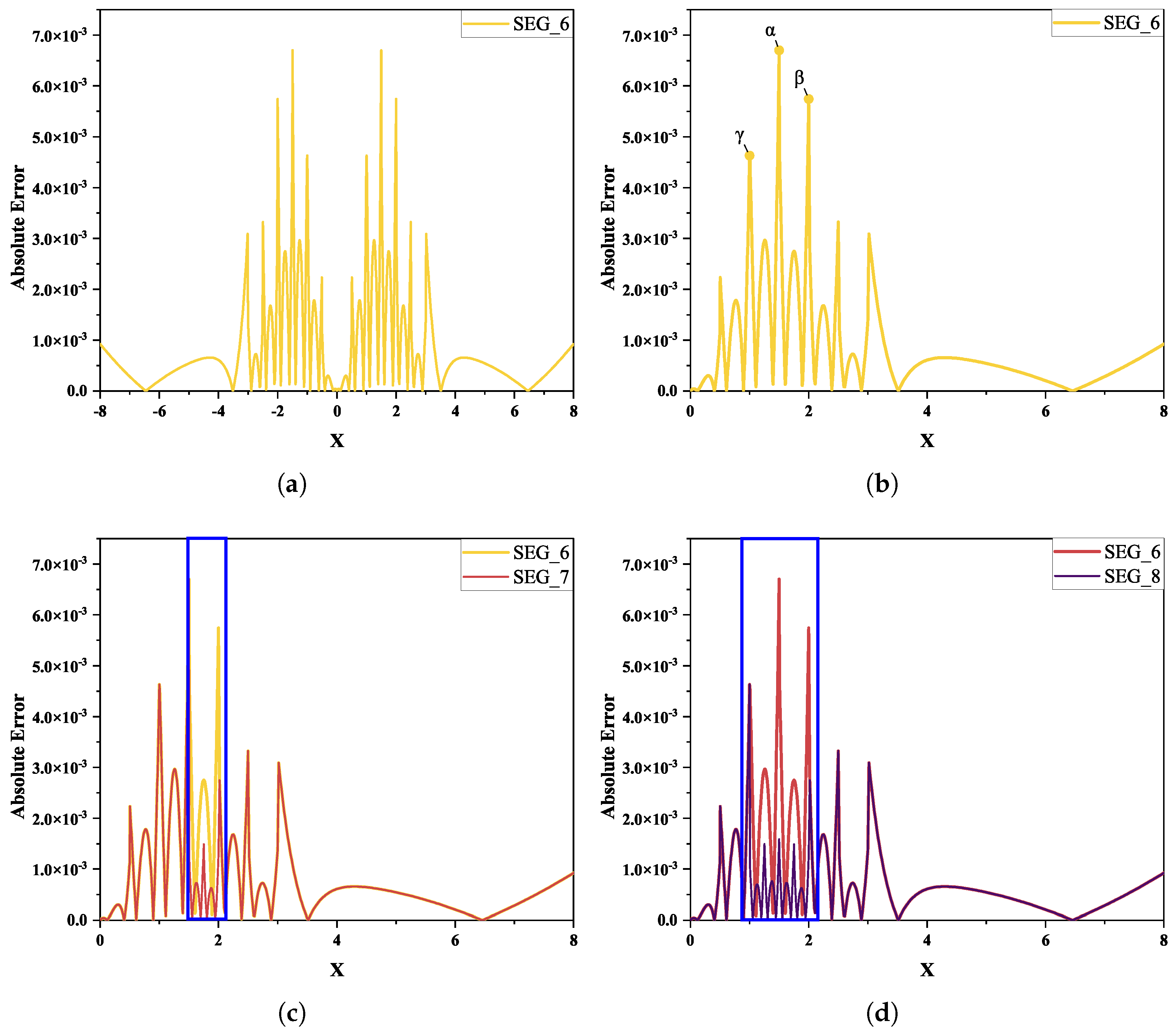
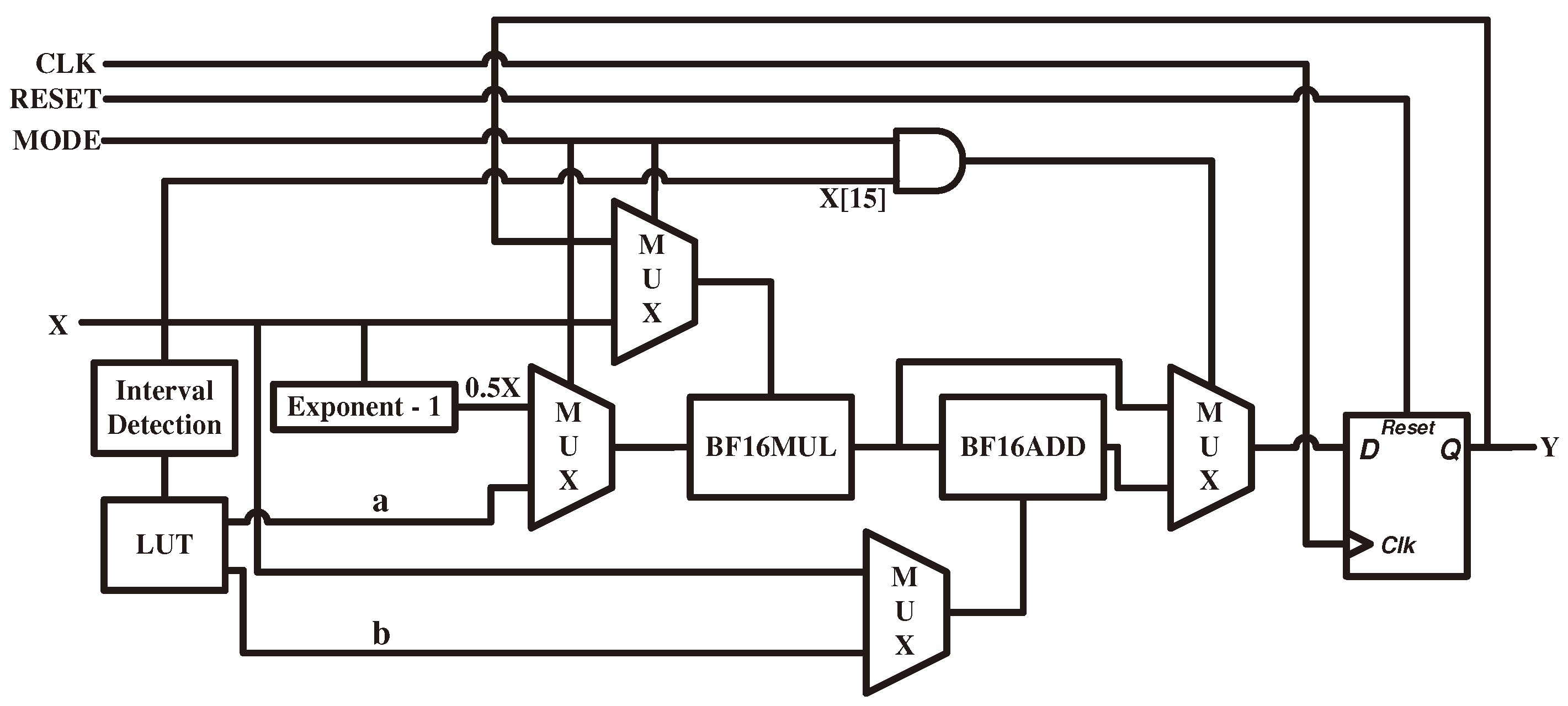

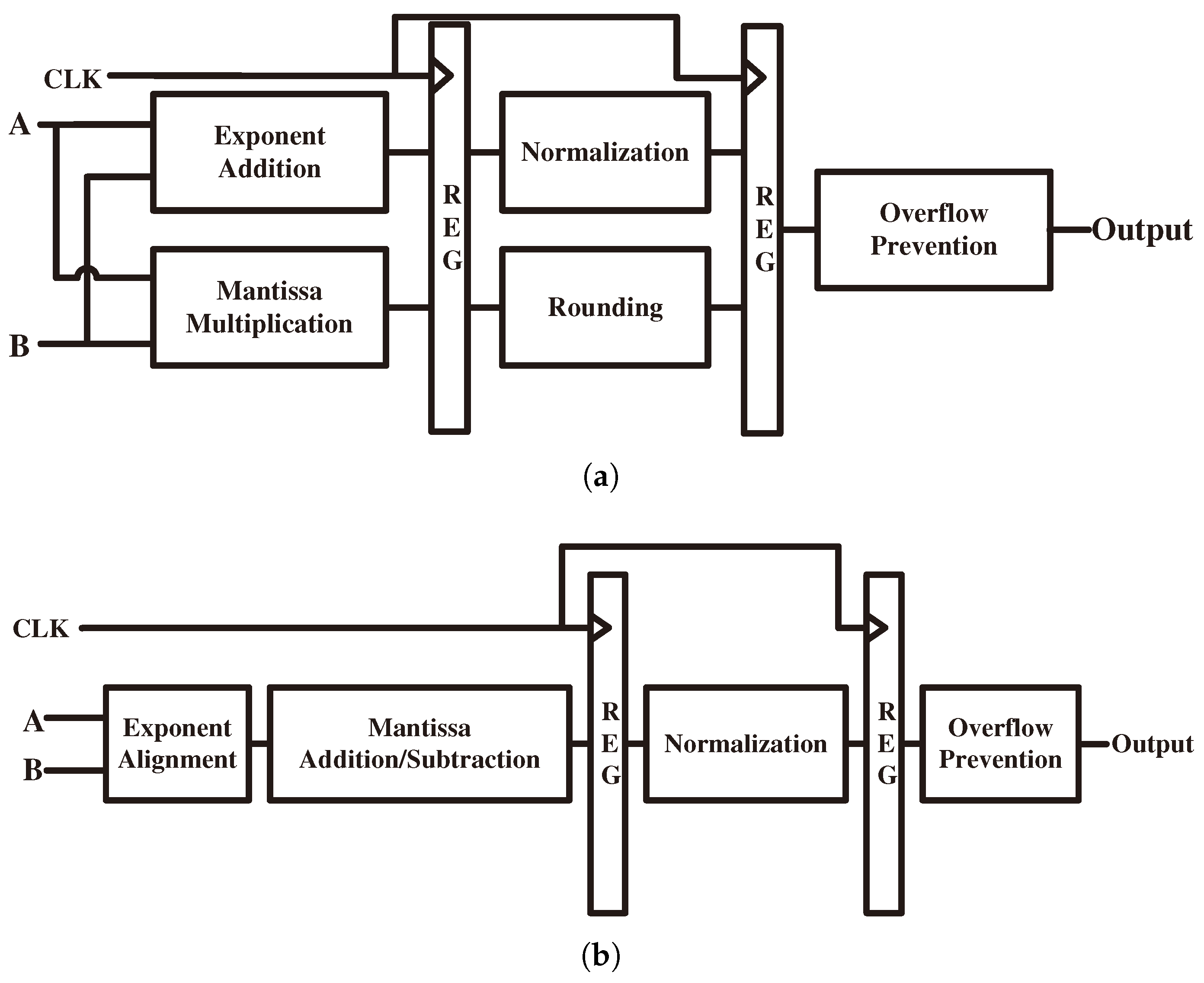
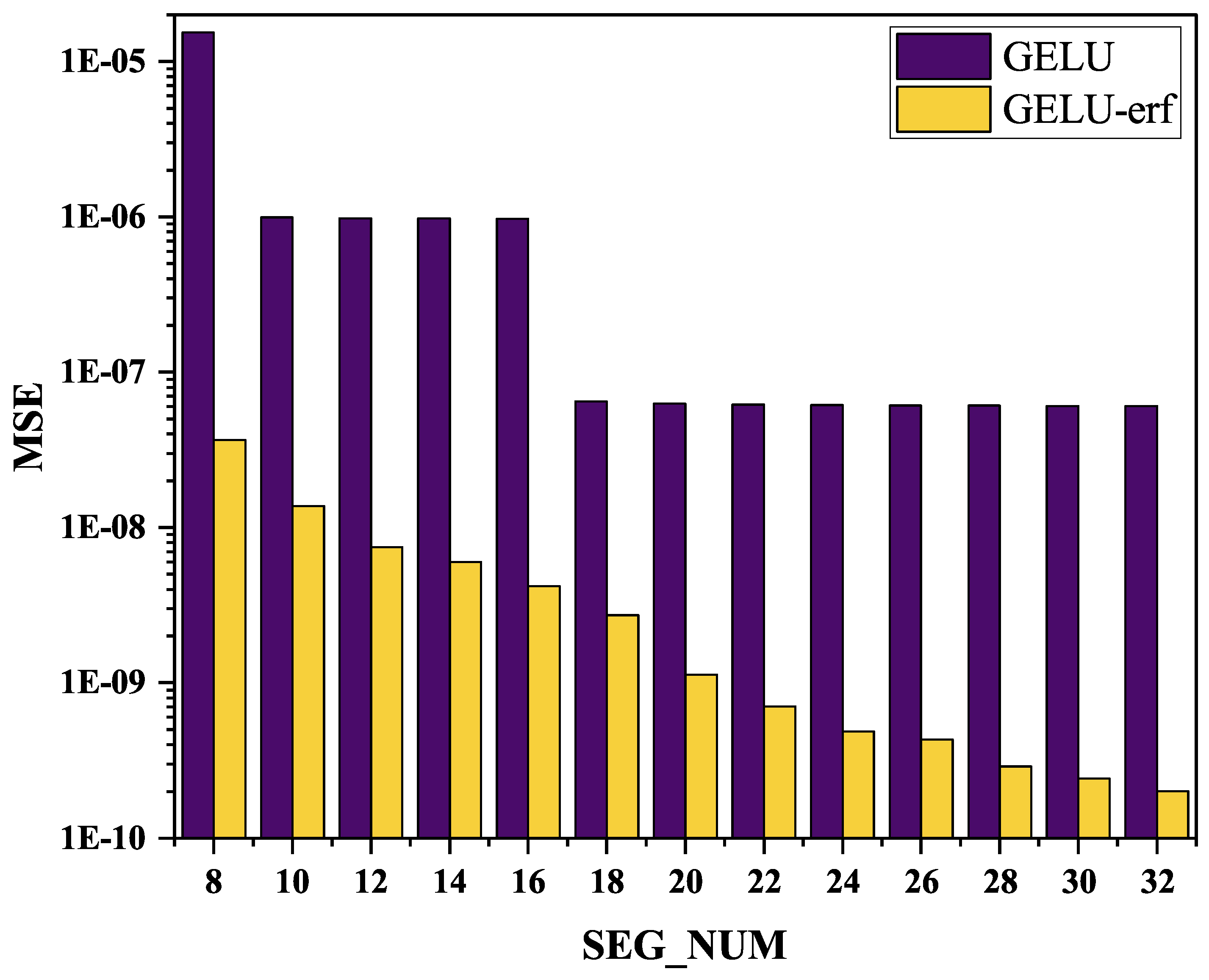
| Method | Input Interval | Segment Number | MSE | MAE |
|---|---|---|---|---|
| [25] | [−8,8] | 16 | 1.19 | 1.95 |
| [29] | [−4,4] | 10 | 8.31 | N/A |
| [33] | [−4,4] | N/A | 7.10 | 1.13 |
| [30] | [−8,8] | 8 | 1.54 | 4.06 |
| ISPA-8 | [−8,8] | 8 | 3.97 | 2.74 |
| ISPA-16 | [−8,8] | 16 | 4.29 | 1.07 |
| Res-ViT | ViT-B | ViT-L | ||||
|---|---|---|---|---|---|---|
| TOP-1 | TOP-5 | TOP-1 | TOP-5 | TOP-1 | TOP-5 | |
| Baseline | 90.97 | 99.03 | 92.17 | 99.10 | 93.32 | 99.30 |
| Fitted NN | 90.94 | 99.03 | 92.16 | 99.10 | 93.29 | 99.30 |
| Acc. Loss | −0.03 | 0.00 | −0.03 | 0.00 | −0.03 | 0.00 |
| Res-ViT | ViT-B | ViT-L | ||||
|---|---|---|---|---|---|---|
| TOP-1 | TOP-5 | TOP-1 | TOP-5 | TOP-1 | TOP-5 | |
| Baseline | 90.97 | 99.03 | 92.17 | 99.10 | 93.32 | 99.30 |
| Fitted NN | 90.97 | 99.03 | 92.17 | 99.10 | 93.32 | 99.30 |
| Acc. Loss | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Device | LUT | Slice Register | DSP | BRAM (Mb) |
|---|---|---|---|---|
| XCZU9EG | 274,080 | 548,160 | 2520 | 32.1 |
| Method | Device | LUT | Slice Register | DSP | BRAM (Bits) | Frequency (MHz) |
|---|---|---|---|---|---|---|
| [25] | XC7S50 | 176 * | 0 | 0 | 11,264 | 50 |
| [29] | XCVU9P | 2940 | 2951 | 16 | 0 | 250 |
| [33] | XC7Z045 | 324 | 318 | 1 | 0 | 410 |
| [30] | XC7Z010 | 219 | 247 | 0.5 | 0 | 312.5 |
| ISPA-8 | XCZU9EG | 295 | 194 | 0 | 0 | 450 |
| ISPA-16 | XCZU9EG | 337 | 185 | 0 | 0 | 450 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Wu, Y.; Zhuang, M.; Zhou, J. High-Precision and Efficiency Hardware Implementation for GELU via Its Internal Symmetry. Electronics 2025, 14, 1825. https://doi.org/10.3390/electronics14091825
Huang J, Wu Y, Zhuang M, Zhou J. High-Precision and Efficiency Hardware Implementation for GELU via Its Internal Symmetry. Electronics. 2025; 14(9):1825. https://doi.org/10.3390/electronics14091825
Chicago/Turabian StyleHuang, Jianxin, Yuling Wu, Mingyong Zhuang, and Jianyang Zhou. 2025. "High-Precision and Efficiency Hardware Implementation for GELU via Its Internal Symmetry" Electronics 14, no. 9: 1825. https://doi.org/10.3390/electronics14091825
APA StyleHuang, J., Wu, Y., Zhuang, M., & Zhou, J. (2025). High-Precision and Efficiency Hardware Implementation for GELU via Its Internal Symmetry. Electronics, 14(9), 1825. https://doi.org/10.3390/electronics14091825






