Abstract
Grid-forming (GFM) converters play a vital role in future power systems due to their ability to independently establish voltage and frequency. However, their interaction with AC circuits may give rise to synchronous oscillations, which pose a threat to system stability and dynamic performance. This paper investigates the issue of synchronous oscillations and proposes an ultra-local model predictive control strategy for their suppression. First, a small-signal power dynamic model is developed to analyze the mechanism behind these oscillations. It is revealed that this problem is related to the electromagnetic dynamics of power transfer and is strongly influenced by the line impedance characteristics. Then, a predictive control framework is formulated, which incorporates oscillation suppression into the control objective and enables the real-time optimization of the active power reference. To avoid reliance on detailed system models, an ultra-local modeling approach is introduced. In this framework, a fixed-time sliding mode observer is employed to estimate the system power dynamics in real time, enabling the prediction of future states without requiring grid-side parameters and facilitating the design of a model-free controller. Simulation results verify that the proposed method effectively mitigates synchronous oscillations while significantly enhancing system stability and robustness.
1. Introduction
Renewable energy sources represent a key solution for achieving carbon neutrality. Power electronic converters serve as essential interfaces for integrating these sources into the power grid. Among various converter control strategies, grid-forming (GFM) control has attracted increasing attention due to its ability to provide voltage and frequency support proactively and independently. Unlike the widely adopted grid-following (GFL) control in current practical applications [1], which relies on a phase-locked loop (PLL) to synchronize with the grid frequency, grid-forming (GFM)-controlled converters operate as voltage sources and achieve self-synchronization based on the principle of active power balance. This emulates the behavior of conventional synchronous generators (SGs) and enables stable operation under weak grid conditions or even in islanded modes. As a result, GFM control has emerged as a promising solution for enhancing grid stability and accelerating the transition toward 100% renewable power systems [2].
Grid-forming (GFM) converters, while offering advanced grid support functionalities, introduce stability challenges that are different from those encountered in both GFL converters and traditional SGs. Unlike GFL converters, which rely on external voltage references for synchronization, GFM converters establish synchronization internally and can operate independently. Consequently, under strong grid conditions, where the system behaves similarly to two voltage sources being electrically close, the stability control of grid-tied GFM converters becomes more challenging. In addition, compared to SGs, GFM converters feature a significantly wider power control loop bandwidth, owing to their high switching frequencies and fast-acting digital control systems. Although this facilitates a faster dynamic response, it also increases the risk of synchronous oscillations [3], also known as synchronous frequency resonance (SFR) [4].
Synchronous oscillations, typically manifests as power oscillations near the fundamental grid frequency (50 Hz or 60 Hz) during power transmission [5]. Fundamentally, they are induced by the power transfer through electrical networks. The phenomenon becomes more pronounced in transmission lines with low resistance-to-inductance () ratios. In addition, the coupling between active and reactive power, as well as improperly tuned control parameters, can further aggravate the occurrence and severity of synchronous oscillations in GFM converter systems [6].
To mitigate the phenomenon of synchronous oscillations, numerous studies have been conducted from various perspectives, including the modification of virtual impedance, the decoupling of active and reactive power, the restructuring of power synchronization loops, and other advanced control strategies. Among the various proposed methods, virtual resistor-based control strategies have been widely studied for their simplicity and their ability to reshape line impedance, effectively introducing damping to attenuate the resonance peak near the synchronous frequency [5,7]. In practice, a high-pass filter (HPF) is often added to the virtual resistor to avoid impacting the system’s steady-state gain. However, this also introduces a pair of complex-conjugate poles into the control loop. Under strong grid conditions and with a large virtual resistance, these poles may shift into the right half of the complex plane, leading to oscillations and potential instability [8]. Moreover, such methods tend to increase the coupling between active and reactive power and make the design of control parameters more difficult. Another approach to mitigating synchronous oscillations is to decouple active and reactive power using cross feedforward compensation, as proposed in refs. [4,8,9]. By introducing cross-regulation branches derived from small-signal power dynamics into the outer control loops, this method not only reduces active–reactive power coupling but also suppresses oscillations by eliminating conjugate poles associated with resonance. However, the design of these decoupling components is complex and highly sensitive to the accuracy of operating point and parameter estimation. In addition to the aforementioned methods, modifying the power synchronization control (PSC) loop is another effective approach. In refs. [10,11], power derivative terms are incorporated into the PSC to provide virtual inertia and suppress oscillations. However, such methods inherently reduce the dynamic responsiveness of the power control loop. To overcome this limitation, Liu et al. [12] present a model predictive control (MPC)-based auxiliary controller integrated into the PSC, formulated from an optimization-based control perspective, and specifically designed for synchronous oscillation suppression. This method predicts future system behavior using a dynamic model and computes control inputs by solving an optimization problem over a receding horizon, thereby achieving effective damping without compromising the system’s dynamic performance. Nevertheless, accurately modeling the power dynamics in practice is challenging, as the parameters of the grid-side network are often difficult to obtain, posing limitations to the practical implementation of this method. As a potential alternative, other emerging advanced control strategies, such as model-free control [13] and reinforcement learning-based control [14], have been receiving increasing attention in the field of converter control. These approaches reduce or even eliminate reliance on detailed mathematical models. Compared with reinforcement learning-based control, which typically requires extensive historical data for training, mode-free-based methods offer better real-time implementability and robustness, making them a promising candidate for mitigating the problem of synchronous oscillations.
This paper proposes a model-free predictive controller to assist the PSC and suppress synchronous oscillations without compromising dynamic performance. Firstly, a power dynamic model of GFM converters is developed by incorporating the electromagnetic dynamics of AC transmission lines, based on which the fundamental mechanism underlying synchronous oscillations is identified. Subsequently, the concept of predictive control is introduced, integrating power oscillation suppression into the control objective and enabling the real-time optimization of the active power reference. To address the challenge of accurately acquiring grid-side parameter information, an ultra-local model is adopted. This model only relies on input–output data and constructs localized approximations around the current operating point, thereby eliminating the need for detailed system modeling [15]. Specifically, a fixed-time sliding mode (FTSM) observer is employed to estimate the system power dynamics in real time. Based on these estimations, a predictive model of future system states is constructed. Leveraging this model, the control process is optimized by jointly considering power oscillation suppression, power tracking performance, and control effort. This enables the auxiliary regulation of the active power response, thereby enhancing both dynamic response speed and system stability, while effectively suppressing synchronous oscillations.
The rest of this paper is organized as follows. Section 2 introduces the system configuration of the grid-tied GFM converter and analyzes the underlying mechanism of synchronous oscillations based on the power dynamic model. In Section 3, an ultra-local model predictive control strategy is proposed to suppress oscillations while preserving dynamic performance. Section 4 presents the simulation results to validate the effectiveness and robustness of the proposed method under various operating conditions. Finally, the conclusion is given in Section 5.
2. Interaction Analysis of Grid-Forming Converters with AC Circuits and Synchronous Oscillation Phenomena
2.1. System Description
Figure 1 illustrates the system structure of a grid-connected GFM converter. Specifically, , , , , and are, respectively, the converter-side current, the grid-side current, the GFM output voltage, the filter capacitor voltage, and the grid-side voltage. The power grid is modeled as an ideal AC voltage source . The GFM converter is connected to the grid at the point of common coupling (PCC) through an filter, where , , , , and denote the converter-side inductance and resistance, the filter capacitance, and the grid-side inductance and resistance, respectively. It is worth noting that the grid-side impedance includes both the grid line impedance and the filter-side impedance. The DC side of GFM is considered a constant DC-link voltage source In the control part, the variables , , , , , and represent the d- and q-axis components of , , , and , respectively.
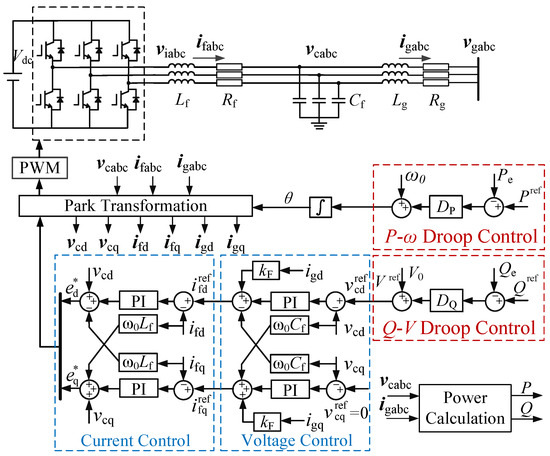
Figure 1.
Control diagram of the GFM converter.
Under grid-forming control, the converter operates as a voltage source (), with the voltage magnitude and phase angle references generated by active and reactive power control loops. The Q-V and P- droop control laws are, respectively, given by
where , , , and are, respectively, the reference of voltage magnitude, angular frequency, reactive power, and active power. and denote reactive and active power droop gain. The voltage controller is used to regulate the output voltage of the grid-forming converter and the inner current controller is used for output current regulation.
2.2. Jacobia Transfer Function Matrix of Grid-Forming Converters Considering Electromagnetic Dynamics
The grid-side dynamics of the grid-connected GFM converter are expressed as follows:
In the coordinate system aligned with the grid-side voltage vector, as shown in Figure 2, the d-axis and q-axis components of the vector are denoted by and , respectively. The corresponding components of the vector are represented by and , respectively, where represents the phase angle difference between and . By introducing a small-signal perturbation, and are derived as follows:
where denotes the perturbation of a variable, and the subscript ‘0’ refers to its corresponding steady-state value.
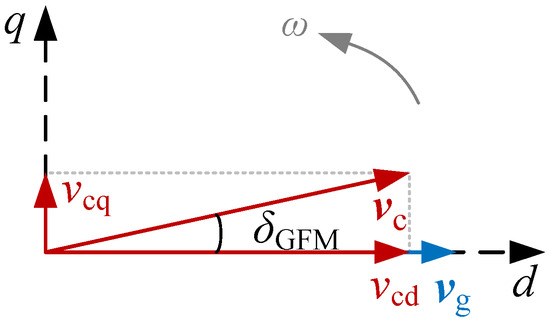
Figure 2.
Phasor diagram of the system.
Transforming into the the frame, (3) transforms into the following:
Assuming a constant grid voltage , the small-signal model of (5) can be derived through linearization as follows:
The instantaneous power output of the GFM in the frame can be expressed as follows:
Linearizing (8) at the equilibrium point, we can obtain the following:
where, based on the given phase angle and voltage magnitude, the steady-state components , , , and can be specifically expressed as follows:
Combining (6), (7), (9), and (10), the dynamic expression of the GFM converter output power can be written as follows:
where , , , and represent the Jacobian transfer functions of the active power–phase angle, active power–voltage magnitude, reactive power–phase angle, and reactive power–voltage magnitude, respectively. The detailed expressions are given as follows:
where the coefficients , , , and ( can be found in ref. [16].
2.3. Mechanism Analysis of Synchronous Oscillations
By integrating the active power controller (1) and the reactive power controller (2) of the GFM with (11), the small-signal block diagram of the system is illustrated in Figure 3. It should be noted that, in developing the power dynamic model of the GFM, the dynamic behaviors of the inner voltage and current control loops are neglected, as their control bandwidths are typically much higher than that of the outer power loop [17]. Moreover, considering that synchronization oscillations are closely related to the stability of active power control [3,12], the analysis in this subsection focuses on the dynamic characteristics of the active power control loop. To investigate the mechanism underlying the oscillation phenomenon and identify its influencing factors, the input signal of the reactive power control loop is neglected, allowing the multiple-input multiple-output (MIMO) system shown in Figure 3 to be simplified into the single-input single-output (SISO) model in Figure 4. The impact of reactive power transfer on synchronous oscillations, being relatively minor, will be briefly discussed at the end of this subsection.
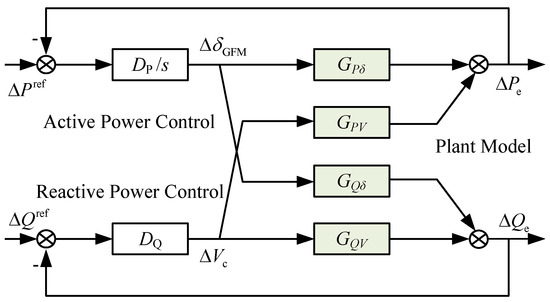
Figure 3.
Block diagram of the system’s small-signal model.
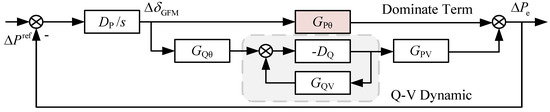
Figure 4.
Block diagram of the reconstructed SISO small-signal model.
According to (12), it can be observed that each power transfer function in the Jacobian matrix contains a pair of complex-conjugate poles . Evidently, the oscillation frequency of these poles is the synchronous frequency , and their damping (i.e., the distance from the imaginary axis) is determined by the resistance-to-inductance ratio of the grid-connected line, . Therefore, when the line resistance is relatively low, the poles tend to approach the imaginary axis, i.e., , which increases the risk of system oscillation. It is important to note that this type of synchronous oscillation originates from the intrinsic dynamics of power transfer in the physical system and is not directly related to the strength of the grid. As a result, such oscillations may occur under both strong and weak grid conditions.
To further illustrate the influence of the poles on the power control loop, the open-loop transfer function of the system shown in Figure 4 is derived as follows:
Furthermore, the closed-loop transfer function of the power control loop can be further derived as follows:
Figure 5 presents the Bode plots of the equivalent open-loop and closed-loop gains in (13) and (14), based on the system parameters listed in Table A1. It is clearly observed that the pair of complex-conjugate poles in (12) introduce a resonance peak and a sharp phase drop of -180 degree near the synchronous frequency . Under the given system parameters, and considering the cross-coupling between active and reactive power, the resulting resonance frequency is approximately 57 Hz. When the system lacks a sufficient phase margin, the resonance peak may exceed unity (0 dB), which can readily trigger synchronous oscillations. In addition, this resonance peak limits the bandwidth of the power synchronization control loop. If the bandwidth is set too high, the stability margin of the system will be further reduced, making it more prone to oscillations, especially in low-resistance networks. This, in turn, constrains both the dynamic performance and the design space for ensuring system stability. In practical applications, some grid codes will impose constraints on the bandwidth of the power control loop to mitigate potential adverse effects caused by over-rapid dynamic responses (e.g., a 5 Hz control bandwidth limit in the UK [18]).
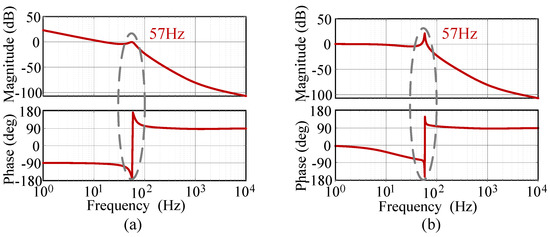
Figure 5.
Bode diagram of active power loop. (a) Open-loop transfer function. (b) Closed-loop transfer function.
In addition, Figure 6 shows the Bode plot of the closed-loop reactive power control, illustrating that the reactive power dynamics do not dominate the occurrence of synchronous oscillations. Although a resonance peak near the synchronous frequency is observed, the system maintains a relatively sufficient stability margin. This supports the conclusion that synchronous oscillations are primarily related to the stability of active power control. Therefore, analyzing the dynamic behavior of the active power loop provides a more effective means of understanding and mitigating such oscillations.
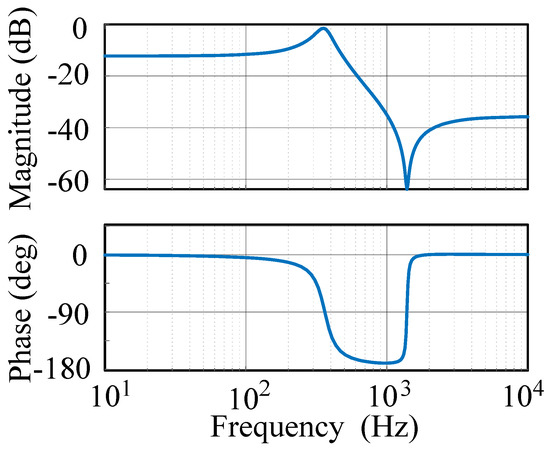
Figure 6.
Bode diagram of the reactive power closed-loop transfer function.
3. Ultra-Local Model Predictive Control Strategy for Synchronous Oscillation Suppression
To enhance the stability of GFM converters in strongly inductive grids, this section proposes a predictive control approach, in which power oscillations are incorporated into the control objective to effectively suppress synchronous oscillations. First, the limitations of conventional model-based predictive control methods, derived from physical mechanisms, are analyzed. Then, a model-free predictive control scheme that does not rely on detailed system information is proposed. Building on this, an ultra-local model predictive control strategy targeting synchronous oscillation suppression is further developed, aiming to improve both system stability and dynamic performance.
3.1. Mechanistic Model Construction
To reduce the model’s complexity, only the dynamics between the active power and phase angle () are considered, while the coupling between active and reactive power control is neglected. Under this assumption, the closed-loop transfer function of the system becomes a third-order system. Let the input variable be defined as the active power reference and the output variable as the output active power . Accordingly, the closed-loop transfer function of the system can be transformed into a state-space representation, expressed as follows:
where denotes the state variable vector, where the state variables , , and are intermediate quantities without explicit physical meaning. The corresponding system matrix parameters are given as follows:
It can be observed that the state-space model of the system includes physical parameters such as the grid-side resistance and inductance. However, from the perspective of the converter, it is difficult to accurately obtain the exact values of the grid-side impedance. Designing controllers based on inaccurate system models or mismatched parameters may not only degrade control performance but also weaken system robustness. These issues pose significant feasibility challenges for conventional model predictive control (MPC) schemes when applied to the suppression of synchronous oscillations. To address this problem, a model-free predictive control strategy that does not require detailed system information is proposed in the next subsection.
3.2. Ultra-Local Model of the Active Power Control Loop
Define the input and output variables as and , respectively. The corresponding ultra-local model is given by the following:
where is the gain of the control input, and F is the unknown offset term representing the uncertainty of system dynamics and disturbances, which will be estimated in the subsequent control design. This model uses real-time input–output data to build a local approximation, allowing online modeling. The core principle of ultra-local modeling is the real-time estimation of F based on the available measurements [15]. Given that the system under study is a physical system, it is reasonable to assume that both the offset term F and its time derivative are bounded variables, i.e., they satisfy and , where and are positive constants.
To achieve an accurate estimation of F, an observer is necessary. In this paper, a fixed-time sliding mode (FTSM) convergence method [19], characterized by fast convergence speed, strong robustness, and global stability, is employed to estimate the offset term F in the ultra-local model. This approach eliminates the dependence on an accurate mechanistic model and supports the design of the model-free predictive controller. The key idea behind the FTSM observer is to design a specific sliding surface and control law that ensure the estimation error converges to zero within a fixed time.
The sliding surface is defined as the estimation error of the output variable y, expressed as follows:
where is the estimate of y.
The time derivative of the sliding surface can be expressed as follows:
Based on the above, the FTSM observer is designed as follows:
where variables with a tilde “˜” denote the corresponding estimated values. The terms and represent the sliding mode reaching laws, which are defined as follows:
and are the gain coefficients of the observer.
Define the estimation error of the offset term as . Substituting (19) into (18) yields the fixed-time sliding mode error dynamics, expressed as follows:
According to the proof in [19], the error system reaches zero in fixed time. Therefore, the estimated output and the offset term will converge accordingly, making real-time estimation feasible.
3.3. Ultra-Local Model-Based Predictive Control
In this subsection, a predictive control strategy based on the ultra-local model is developed to suppress synchronous oscillations. The proposed method enables effective prediction of the system’s future dynamic behavior and incorporates the temporal variation of active power (i.e., the change in active power between two consecutive time steps) into the objective function of the predictive controller.
3.3.1. Predictive Model Construction
To construct a model for predicting the system’s dynamic behavior, the basic ultra-local model is extended by further considering the dynamic characteristics of the offset term F. Since F is not a constant but evolves dynamically with the system states, neglecting its variation may lead to reduced prediction accuracy and, consequently, degraded control performance. To enhance the capability of the model in describing future system dynamics, the rate of change of F is incorporated into the modeling process. The resulting predictive model is formulated as follows:
where g reflects the rate of change of the offset term F and can be estimated in real time through the observer given in (19).
Define the state variable vector of the predictive model as . The compact form of the predictive model can then be expressed as follows:
where
Then, the continuous-time formulation in (22) is converted into a discrete-time form as follows:
where is the discrete form of and k is the time step index in the discrete-time domain.
Define the control horizon as and the prediction horizon as . Based on the current state at time k, the future control trajectory , predicted state vector , and output vector are defined as follows:
where and () represent the state and output vectors at time , predicted using the state information available at time k.
Furthermore, the expression for can be derived as follows:
where
To suppress synchronous oscillations, a new variable is defined as , . The new variable represents the difference between the predicted state variables at two consecutive time steps. Accordingly, the predicted state variation matrix over the prediction horizon can be expressed as follows:
where
Using the predictive model in (23), the future dynamic behavior of the system over the prediction horizon is obtained, as shown in (25) and (26). Based on this, the influence of the control input on system performance can be further evaluated, enabling the design of a corresponding predictive control strategy to enhance overall system performance.
3.3.2. Controller Design
This study aims to ensure accurate active power tracking while mitigating the risk of synchronous oscillations. To address these, the following cost function is proposed:
where the first term is intended to suppress power oscillations, the second term ensures power tracking, and the third term constrains the amplitude of the control input to prevent excessive control actions. , , and are the weighting coefficients corresponding to each objective, respectively. is the reference output matrix composed of the reference values , i.e., .
By substituting (25) and (26) into (27) and rearranging the terms, the following expression is obtained:
When the gradient of the quadratic cost function with respect to the control input is zero (i.e., ), the optimal control trajectory that minimizes the cost function J can be obtained. The solution is given as follows:
where
Following the receding horizon control principle, the first control action from the optimized sequence is applied to the system. This approach dynamically adjusts the active power reference and effectively mitigates synchronous oscillations,
where .
In summary, the framework of the proposed ultra-local model predictive control strategy for synchronous oscillation suppression is illustrated in Figure 7. It is worth noting that, by observing (29) and (30), the resulting control law is essentially a state-feedback control law with constant gain, where the gain matrix can be obtained through offline computation. This implies that there is no need to solve the optimization problem online in real time, thereby simplifying the implementation of the model predictive control. Once the FTSM observer provides the necessary system information, the offline-designed predictive controller can directly generate the control input, effectively realizing the desired optimal control performance.
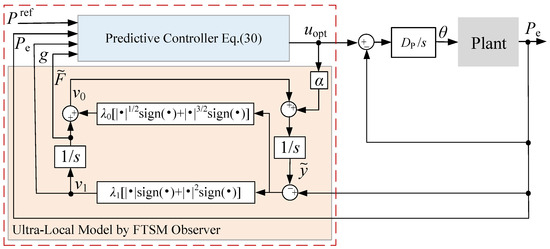
Figure 7.
Proposed ultra-local model predictive controller.
3.4. The Resultant System Dynamic Model with the Proposed Controller
The system dynamic model with the proposed controller will be derived below, which can be used to reflect its dynamic performance and stability characteristics.
Considering that the FTSM observer (19) responds much faster than the controller, it is assumed that the ultra-local model estimation in Section 3.2 is sufficiently accurate, such that the estimated value of F is approximately equal to its theoretical value. Based on the state-space model of the system given in (15), an analytical expression for the offset term F can be theoretically derived by differentiating the output y, as follows:
where . Under the assumption , the ultra-local model state variable is defined as follows:
where .
In addition, the theoretical expression for g, or the rate of change of , can be derived as follows:
where represents the control input from the previous time instant.
By substituting (32) and (33) into (30), the control law can be reformulated in terms of the reference value , the original system state vector , and the previous control input , as follows:
For the system described in (15), the proposed control strategy essentially functions as a state feedback control law. By substituting (34) back into the original state-space model (15), the closed-loop dynamic model of the system under the proposed controller can be obtained. This model enables the analysis of the system dynamic performance under the proposed control scheme. Furthermore, the corresponding closed-loop system state matrix, denoted as , can be constructed, as shown in (35). By computing the eigenvalues of , the small-signal stability characteristics of the system under the proposed control scheme can be effectively revealed.
4. Simulation Verification
To verify the effectiveness of the proposed ultra-local model-based predictive control strategy for suppressing synchronous oscillations, time-domain simulations of a GFM converter grid-connected system were conducted using MATLAB/Simulink. The main system circuit parameters and controller settings are provided in Table A1 and Table A2.
4.1. Small-Signal Stability Enhancement
This subsection aims to analyze the impact of the proposed ultra-local model-based predictive control strategy on the small-signal stability of the system. The focus is placed on examining how the strategy influences the distribution and characteristics of the system eigenvalues. By comparing the changes in eigenvalue locations, the effectiveness of the proposed control approach in suppressing synchronous oscillations and enhancing the stability of the GFM system is evaluated.
Without loss of generality, the variation of the active power droop coefficient is taken as an example to compare the eigenvalue distribution and resulting stability differences between the conventional control strategy and the proposed control strategy. Figure 8 illustrates how the closed-loop system eigenvalues change with respect to under both control schemes. As shown in Figure 8a, under the conventional PCS-based control strategy, a pair of complex-conjugate eigenvalues appear near the synchronous frequency ( rad/s), which is consistent with the analysis presented in Section 2.3. As the active power droop coefficient increases, these oscillatory eigenvalues gradually shift from the left-half plane (LHP) to the right-half plane (RHP), indicating a transition from a stable to an unstable system. In contrast, Figure 8b clearly shows that, under the proposed ultra-local model predictive control strategy designed for synchronous oscillation suppression, the eigenvalues associated with the oscillatory mode not only exhibit a shift in oscillation frequency but also move significantly away from the imaginary axis. Even under large variations in , the system remains stable, demonstrating the ability of the proposed controller to maintain system stability over a wide range of droop parameter settings. Moreover, compared to the eigenvalue distribution under the conventional strategy, the proposed method results in eigenvalues that are overall farther from the imaginary axis, indicating enhanced dynamic performance. Specifically, the reduced real parts of the eigenvalues imply a faster system response, which is beneficial for rapid restoration to steady-state operation—highlighting the advantage of the proposed approach in terms of dynamic regulation performance.
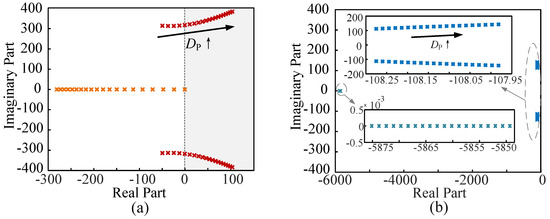
Figure 8.
Eigenvalue trajectories with droop gain from to p.u. (a) Conventional control, and (b) the proposed control.
4.2. Ultra-Local Observer Performance Validation
This subsection aims to validate the effectiveness and accuracy of the observer based on the FTSM in tracking active power and estimating the unknown dynamics. The tuning process of the observer parameters can be found in Appendix B. Figure 9 presents the dynamic response of the system’s active power under the conventional control strategy when the active power droop coefficient increases from 0.02 p.u. to 0.05 p.u. at 0.1 s, triggering synchronous oscillations. The figure also shows the real-time estimation of the output power by the observer defined in (19). The comparative analysis clearly demonstrates that the observer can accurately and rapidly track the active power, even under significant system parameter variations and pronounced power fluctuations. This indicates that the observer is capable of capturing the system output power with high accuracy, without relying on an accurate mathematical model of the system. In addition, Figure 10 compares the real-time estimation of the offset term F in the ultra-local model with its theoretical value calculated from (31). It can be observed that the estimated results closely match the theoretical values in terms of an overall trend. Although some high-frequency harmonics appear locally, they have no substantial impact on the dominant dynamic characteristics. This demonstrates that the FTSM observer can effectively identify and estimate both unknown internal dynamics and external disturbances. Therefore, the estimation results can be further utilized to design and implement a predictive control strategy based on the ultra-local model. Even in the absence of an accurate system model, this approach can effectively enhance the system stability and robustness. It is worth mentioning that the implementation of the FTSM observer involves higher computational complexity. However, the additional processing requirements can be readily managed by modern digital microcontrollers and processors.
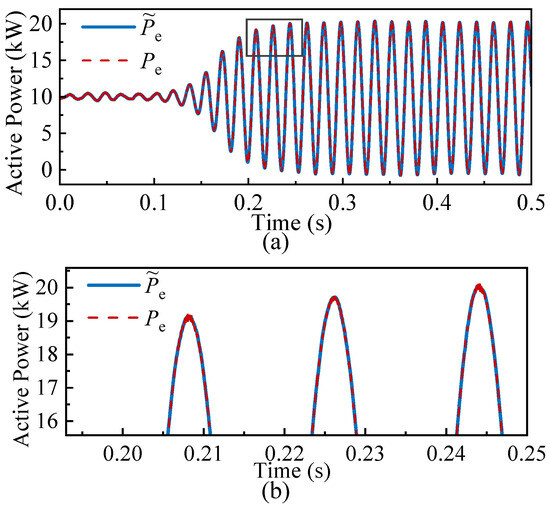
Figure 9.
Comparison between actual and estimated values of output active power: (a) Full view. (b) Zoomed-in view.
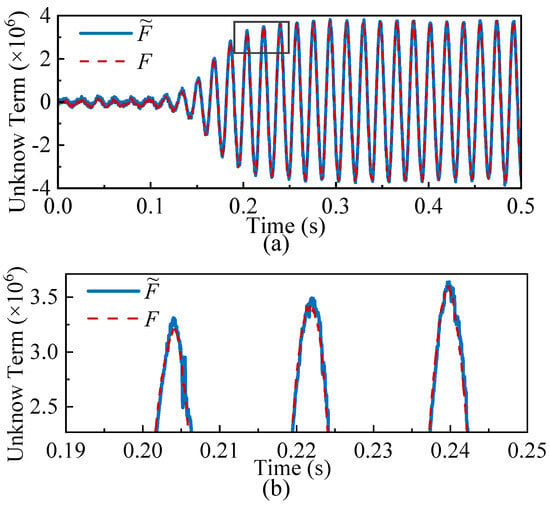
Figure 10.
Comparison between the theoretical and estimated values of the offset term: (a) Full view. (b) Zoomed-in view.
To further evaluate the robustness of the proposed FTSM observer under non-ideal conditions, simulations that consider measurement noise and input delay are conducted. The disturbance scenario remains consistent with previous tests, where the active power droop coefficient is increased from 0.02 p.u. to 0.05 p.u. at 0.1 s. Figure 11a illustrates the active power response under zero-mean Gaussian white noise with a noise power of 0.1 added to the observer input, in order to evaluate the estimation robustness under measurement disturbances. It compares the actual active power output , the noisy measurement used as the observer input , and the real-time power estimation provided by the observer . As shown, the FTSM observer maintains accurate and rapid tracking performance despite the presence of noise. Figure 11b presents the case where a 2 ms delay is introduced to the active power measurement used as the observer input. The observer closely tracks the delayed input , which results in a time shift between the estimated value and the actual active power response. The input delay results in a time lag in the estimation, which may affect control performance. However, this can be addressed by delay compensation techniques commonly used in predictive control [20].
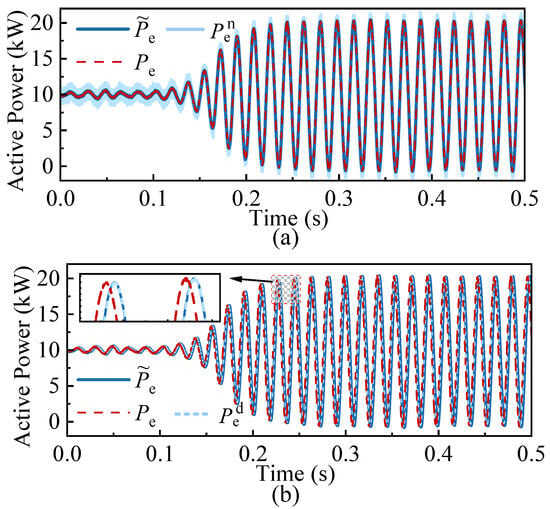
Figure 11.
Comparison of actual, non-ideal measurement, and estimated active power: (a) Measurement noise. (b) Input delay.
4.3. Synchronous Oscillation Suppression Validation
In this subsection, time-domain simulations are carried out in MATLAB/Simulink to evaluate the effectiveness of the proposed control strategy in suppressing synchronous oscillations and demonstrating its robustness against external uncertainties. The tests are conducted under various disturbance scenarios, including step changes in the power reference, grid-side voltage, and droop coefficient.
4.3.1. Power Reference Variation
Figure 12 illustrates the power step response under a sudden change in the active power reference from 1.0 p.u. to 1.5 p.u., comparing the performance of the conventional control method and the proposed control strategy. As illustrated by the red curves in Figure 12, the system exhibits oscillations under the conventional control strategy following the power step, with an oscillation amplitude reaching 0.08 p.u. The time interval between adjacent peaks is approximately 0.0175 s, corresponding to an oscillation frequency of about 57 Hz near the synchronous frequency, which aligns well with the analysis presented in Section 2.3. Although the system remains stable due to inherent damping, the prolonged oscillation duration and significant amplitude indicate limitations in both dynamic response speed and small-signal stability. In contrast, the blue curves in Figure 12 demonstrate that, under the proposed ultra-local model predictive control strategy, the system achieves fast and stable tracking of the power reference. Specifically, the system completes the tracking process within 0.05 s, with noticeably smaller fluctuations throughout the entire response. These results clearly indicate that the proposed method can effectively suppresses synchronous oscillations while achieving power tracking.
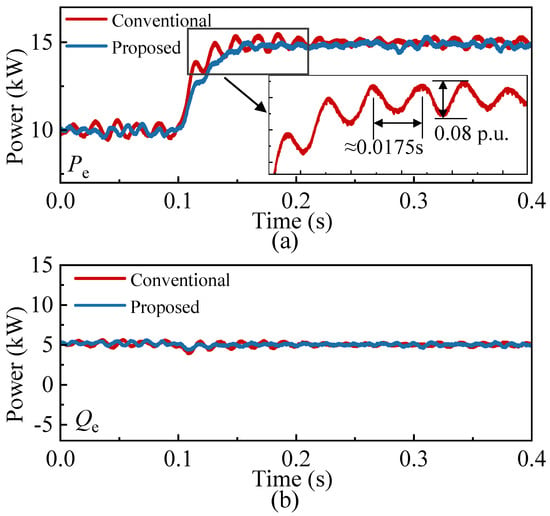
Figure 12.
Power response under active power reference variation: (a) Active power . (b) Reactive power .
4.3.2. Grid-Side Voltage Variation
Figure 13 compares the active and reactive power response of the system under a voltage disturbance, where the grid-side voltage drops from 1.0 p.u. to 0.9 p.u. at 0.1 s. The simulation results indicate that, under the conventional control strategy (the red curves in Figure 13), the system experiences sustained synchronous oscillations in response to the voltage step. The oscillation amplitude reaches up to 0.9 p.u., and the oscillations persist for a relatively long duration without converging to a steady state in a short time. This phenomenon reflects the occurrence of synchronous oscillations due to an insufficient stability margin and also reveals the dynamic coupling between active and reactive power control, which further exacerbates the instability. In contrast, the blue curves in Figure 13 illustrate the system’s response under the proposed ultra-local model predictive control strategy. Although minor oscillations still appear during the initial stage of the disturbance, the maximum oscillation amplitude is reduced to 0.65 p.u., and the system returns to a stable state within 0.1 s. This demonstrates that the proposed strategy not only enhances the dynamic response speed but also effectively suppresses synchronous oscillations triggered by disturbances. Additionally, the simulation results show that the GFM unit provides timely reactive power support during the voltage drop, contributing to the stabilization of the system voltage.
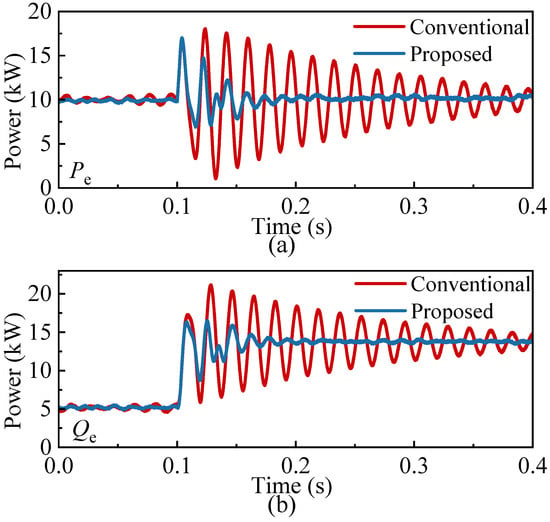
Figure 13.
Power response under voltage variation: (a) Active power . (b) Reactive power .
4.3.3. Droop Coefficient Variation
Figure 14 investigates the impact of control parameter variations on the system’s dynamic performance. In this case study, the active power droop coefficient is increased from 0.02 p.u. to 0.05 p.u. at 0.1 s. The simulation results show that, under the conventional control strategy (the red curves in Figure 14), a noticeable synchronous oscillation occurs when the droop coefficient increases. This is because an increase in the droop coefficient effectively raises the bandwidth of the power control loop, making the system more prone to resonance peaks exceeding 0 dB near the synchronous frequency in the frequency domain. As a result, the stability margin is significantly reduced, leading to oscillatory behavior. In contrast, after implementing the proposed ultra-local model predictive control strategy, the system maintains good dynamic performance and operational stability under the same control parameter changes. As shown by the blue curves in Figure 14, no oscillations are observed, and the system’s stability is significantly improved.
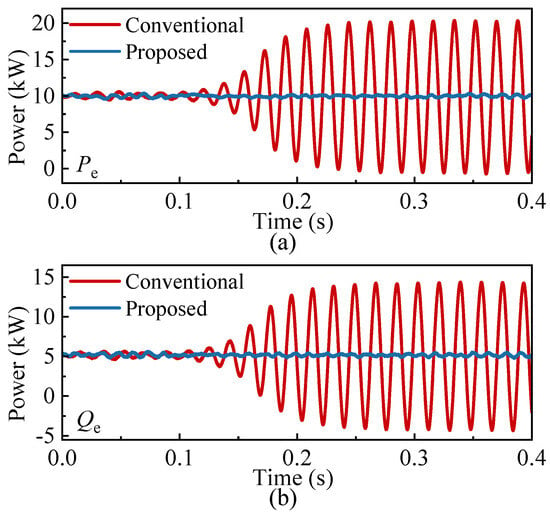
Figure 14.
Power response under droop gain variation: (a) Active power . (b) Reactive power .
We summarize the system’s responses under the three disturbance scenarios, step changes in power reference, grid-side voltage, and the droop coefficient, in Table 1. Specifically, the table compares the peak oscillation amplitude and the time needed to reach a steady state of active power under both the conventional control strategy and the proposed controller. This provides a more intuitive demonstration of the effectiveness of the proposed method in suppressing synchronous oscillations, as well as its ability to enhance system stability and disturbance rejection capability.

Table 1.
Comparison of system responses under different disturbances.
5. Conclusions
This paper investigates the issue of synchronous oscillations arising from the interaction between GFM converters and AC circuits. First, the electromagnetic dynamic characteristics of the AC lines are considered, and a power dynamic model for GFM converters is established. Based on this model, the root cause of synchronous oscillations is revealed to be the insufficient damping of resonant modes near the synchronous frequency in low-resistance lines. This phenomenon is closely related to the electromagnetic dynamics of power transfer and is reflected in the transfer function model as a pair of complex-conjugate poles located near the nominal frequency. The position of these poles relative to the imaginary axis is determined by the line ratio—when the resistance is low, the poles shift closer to the imaginary axis, thereby increasing the possibility of oscillations. To mitigate this problem, this paper introduces the concept of predictive control by incorporating power oscillation suppression into the control objective and optimizing the active power reference in real time. To overcome the difficulty of accurately identifying grid-side parameters in the model, an ultra-local model predictive control strategy that does not rely on system modeling is proposed. A fixed-time sliding mode observer is employed to estimate the system power dynamics in real time. On this basis, a predictive model of future system states is constructed, and the temporal variation of active power is integrated into the cost function of the predictive controller. This enables the auxiliary regulation of the active power response, thereby enhancing both the dynamic response speed and system stability while effectively suppressing synchronous oscillations. Finally, the effectiveness of the proposed method in improving system stability, enabling dynamic estimation, and suppressing synchronous oscillations are verified by simulations. The results demonstrate that the proposed controller accurately estimates the system states without requiring a detailed mathematical model, effectively suppresses synchronous oscillations, and significantly improves the system’s dynamic performance and robustness.
It is worth noting that the introduction of the FTSM observer inevitably increases computational complexity, although it still remains manageable with the current digital controllers. Nevertheless, exploring strategies to further reduce the computational burden represents an important direction for future work.
Author Contributions
Conceptualization, Z.W. and R.L.; methodology, R.L.; software, Z.W. and R.L.; validation, Z.W., R.L. and J.Z.; formal analysis, R.L.; investigation, J.Z.; resources, Z.W.; data curation, J.Z.; writing—original draft preparation, R.L.; writing—review and editing, Z.W. and J.Z.; visualization, R.L.; supervision, Z.W.; project administration, Z.W.; funding acquisition, Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China, grant number U2166601.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Parameters

Table A1.
System and control parameters.
Table A1.
System and control parameters.
| Description | Symbol | Value |
|---|---|---|
| Rated power | (1 p.u.) | |
| Grid voltage peak | (1 p.u.) | |
| DC-link voltage reference | ||
| Nominal angular frequency | ||
| Filter resistance | ||
| Filter inductance | ||
| Filter capacitance | ||
| Grid resistance | ||
| Grid inductance | ||
| Power droop gain | ||
| Current PI gain | / | 95/100 |
| Voltage PI gain | / | 3/8 |

Table A2.
Proposed controller parameters.
Table A2.
Proposed controller parameters.
| Description | Symbol | Value |
|---|---|---|
| Control gain in the ultra-local model | 6.67 | |
| Gain of the FTSM observer | 900 | |
| Gain of the FTSM observer | ||
| Weight factor | 1 | |
| Weight factor | 2 | |
| Weight factor | 0.01 | |
| Sampling interval | 0.001 s | |
| Control horizon | 2 | |
| Prediction horizon | 15 |
Appendix B. Tuning of the FTSM Observer
The parameters and of the FTSM observer should be chosen to ensure the fast convergence of the estimated values to the actual system states. The design of nonlinear observer parameters is often based on a trial-and-error process, guided by prior experience and insights from existing studies [21,22]. In this paper, and are tuned by observing the estimation performance under different parameter settings. Figure A1 illustrates the estimated offset term of the observer under various values of (with fixed). As observed, increasing leads to a faster convergence. However, a excessively large gain can amplify measurement noise and deteriorate robustness. Therefore, a trade-off must be made between convergence speed and noise sensitivity. Based on this analysis, is set to in our design, providing a good balance between estimation speed and robustness for the considered application. The tuning of follows a similar principle.
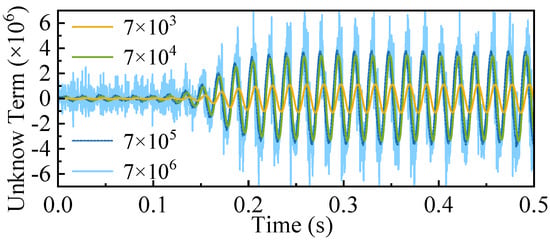
Figure A1.
Estimated offset term of the FTSM observer under various values of .
References
- Babu, V.V.; Roselyn, J.P.; Nithya, C.; Sundaravadivel, P. Development of grid-forming and grid-following inverter control in microgrid network ensuring grid stability and frequency response. Electronics 2024, 13, 1958. [Google Scholar] [CrossRef]
- Khan, S.A.; Wang, M.; Su, W.; Liu, G.; Chaturvedi, S. Grid-Forming Converters for Stability Issues in Future Power Grids. Energies 2022, 15, 4937. [Google Scholar] [CrossRef]
- Wang, X.; Taul, M.G.; Wu, H.; Liao, Y.; Blaabjerg, F.; Harnefors, L. Grid-Synchronization Stability of Converter-Based Resources-An Overview. IEEE Open J. Ind. Appl. 2020, 1, 115–134. [Google Scholar] [CrossRef]
- Xiong, X.; Zhou, Y.; Luo, B.; Cheng, P.; Blaabjerg, F. Analysis and Suppression Strategy of Synchronous Frequency Resonance for Grid-Connected Converters With Power-Synchronous Control Method. IEEE Trans. Power Electron. 2023, 38, 6945–6955. [Google Scholar] [CrossRef]
- Zhang, L.; Harnefors, L.; Nee, H.P. Power-Synchronization Control of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Syst. 2010, 25, 809–820. [Google Scholar] [CrossRef]
- Liu, R.; Wang, Z.; Wang, Y.; Shan, Y.; Wang, W.; Wu, J. Power Decoupling Control for Grid-Forming Battery Energy Storage System in Wind Farm. TechRxiv 2024. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Gu, Y.; Li, W.; He, X. Synchronous frequency resonance of virtual synchronous generators and damping control. In Proceedings of the 2015 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia), Seoul, Repulic of Korea, 1–5 June 2015; pp. 1011–1016. [Google Scholar] [CrossRef]
- Zhao, F.; Wang, X.; Zhu, T. Power dynamic decoupling control of grid-forming converter in stiff grid. IEEE Trans. Power Electron. 2022, 37, 9073–9088. [Google Scholar] [CrossRef]
- Yang, D.; Wu, H.; Wang, X.; Blaabjerg, F. Suppression of synchronous resonance for VSGs. J. Eng. 2017, 2017, 2574–2579. [Google Scholar] [CrossRef]
- Li, X.; Hu, Y.; Shao, Y.; Chen, G. Mechanism analysis and suppression strategies of power oscillation for virtual synchronous generator. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 4955–4960. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, J.; Bi, D.; Dai, Y.; Wen, Y. The Application of Microgrids Based on Droop Control With Coupling Compensation and Inertia. IEEE Trans. Sustain. Energy 2018, 9, 1157–1168. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, M.; Wang, Z. Disturbance Observer-Based Model Predictive Power Synchronization Control for Suppression of Synchronous Oscillation. In Proceedings of the IECON 2023—49th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 16–19 October 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Khalilzadeh, M.; Vaez-Zadeh, S.; Rodriguez, J.; Heydari, R. Model-free predictive control of motor drives and power converters: A review. IEEE Access 2021, 9, 105733–105747. [Google Scholar]
- Alfred, D.; Czarkowski, D.; Teng, J. Reinforcement learning-based control of a power electronic converter. Mathematics 2024, 12, 671. [Google Scholar] [CrossRef]
- Fliess, M. Model-free control and intelligent PID controllers: Towards a possible trivialization of nonlinear control? IFAC Proc. Vol. 2009, 42, 1531–1550. [Google Scholar] [CrossRef]
- Zhang, L. Modeling and Control of VSC-HVDC Links Connected to Weak AC Systems. Ph.D. Thesis, KTH, Electrical Machines and Power Electronics, Stockholm, Sweden, 2010. QC20100607. [Google Scholar]
- Liu, R.; Wang, Z.; Feng, D.; Wu, J.; Shan, Y. Decentralized Composite Control for Enhanced Power and Voltage Regulation in Grid-Forming VSC Dominated Power System. IEEE Trans. Energy Convers. 2024. early access. [Google Scholar] [CrossRef]
- NESO. GC0137: Minimum Specification Required for Provision of GB Grid Forming (GBGF) Capability (Formerly Virtual Synchronous Machine/VSM Capability). Technical Report, National Grid ESO. 2021. Available online: https://www.neso.energy/industry-information/codes/gc/modifications/gc0137-minimum-specification-required-provision-gb-grid-forming-gbgf-capability-formerly-virtual-synchronous-machinevsm-capability (accessed on 17 February 2025).
- Liu, Z.; Lin, X.; Gao, Y.; Xu, R.; Wang, J.; Wang, Y.; Liu, J. Fixed-Time Sliding Mode Control for DC/DC Buck Converters With Mismatched Uncertainties. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 472–480. [Google Scholar] [CrossRef]
- Lu, M.; Wang, X.; Loh, P.C.; Blaabjerg, F.; Dragicevic, T. Graphical Evaluation of Time-Delay Compensation Techniques for Digitally Controlled Converters. IEEE Trans. Power Electron. 2018, 33, 2601–2614. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Chen, W.H.; Chen, X. Disturbance Observer-Based Control: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).