Event-Triggered Discrete-Time ZNN Algorithm for Distributed Optimization with Time-Varying Objective Functions
Abstract
1. Introduction
- An innovative ET-CTZNN model is introduced to tackle the CTDTVO problem. The ET-CTZNN model operates within a semi-centralized framework, solving the CTDTVO problem in continuous time.
- The ET-CTZNN model is discretized using the Euler formula to develop the fully distributed ET-DTZNN algorithm. The ET-DTZNN algorithm enables agents to compute optimal solutions based on local time-varying objective functions and exchange state information with neighbors only when specific event-triggered conditions are met, significantly reducing communication consumption.
- Comprehensive theoretical analyses are conducted, establishing the convergence of both the ET-CTZNN model and the ET-DTZNN algorithm, ensuring their effectiveness in solving the DTVO problem.
2. Preliminaries and Problem Formulation for DTDTVO
2.1. Preliminaries
2.2. Problem Formulation for DTDTVO
3. Event-Triggered Continuous-Time ZNN Model
3.1. Continuous-Time ZNN Model
3.2. Event-Triggered Continuous-Time ZNN Model
4. Event-Triggered Discrete-Time ZNN Algorithm
4.1. Semi-Centralized ET-DTZNN Model
4.2. Fully Distributed ET-DTZNN Algorithm
5. Theoretical Analyses
5.1. Convergence Theorem for ET-CTZNN Model
5.2. Robustness and Zeno Behavior Analysis for ET-CTZNN Model
5.2.1. Analysis on Robustness for ET-CTZNN Model
- Case 1: If , then we obtain , which implies that tends to decrease and converges towards . That is, .
- Case 2: If , then we obtain . (i) When , we determine that is a decreasing function, which implies that is less than , and the situation turns into Case 3. (ii) When , it indicates that remains on the surface of a sphere with a radius of . That is, .
- Case 3: If , then we have . (i) When , we determine that is a decreasing function, which indicates that . (ii) When , it indicates that remains on the surface of a sphere with a radius of less than . That is, . (iii) When , we determine that is an increasing function, which indicates that the residual error tends to converge towards as time increases. That is, .
5.2.2. Analysis on Zeno Behavior for ET-CTZNN Model
5.3. Convergence Theorems of ET-DTZNN Algorithm
6. Numerical Experiments
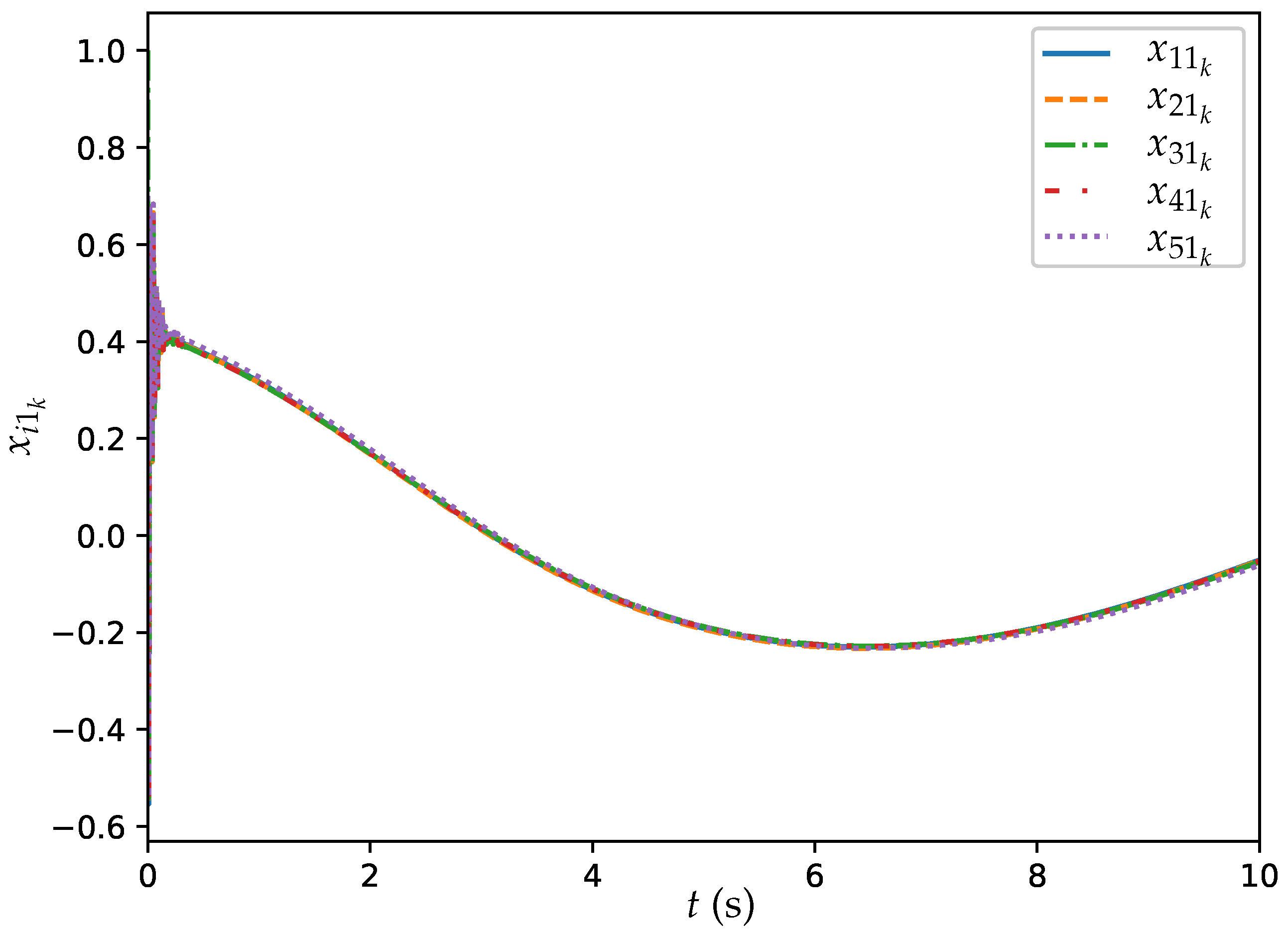
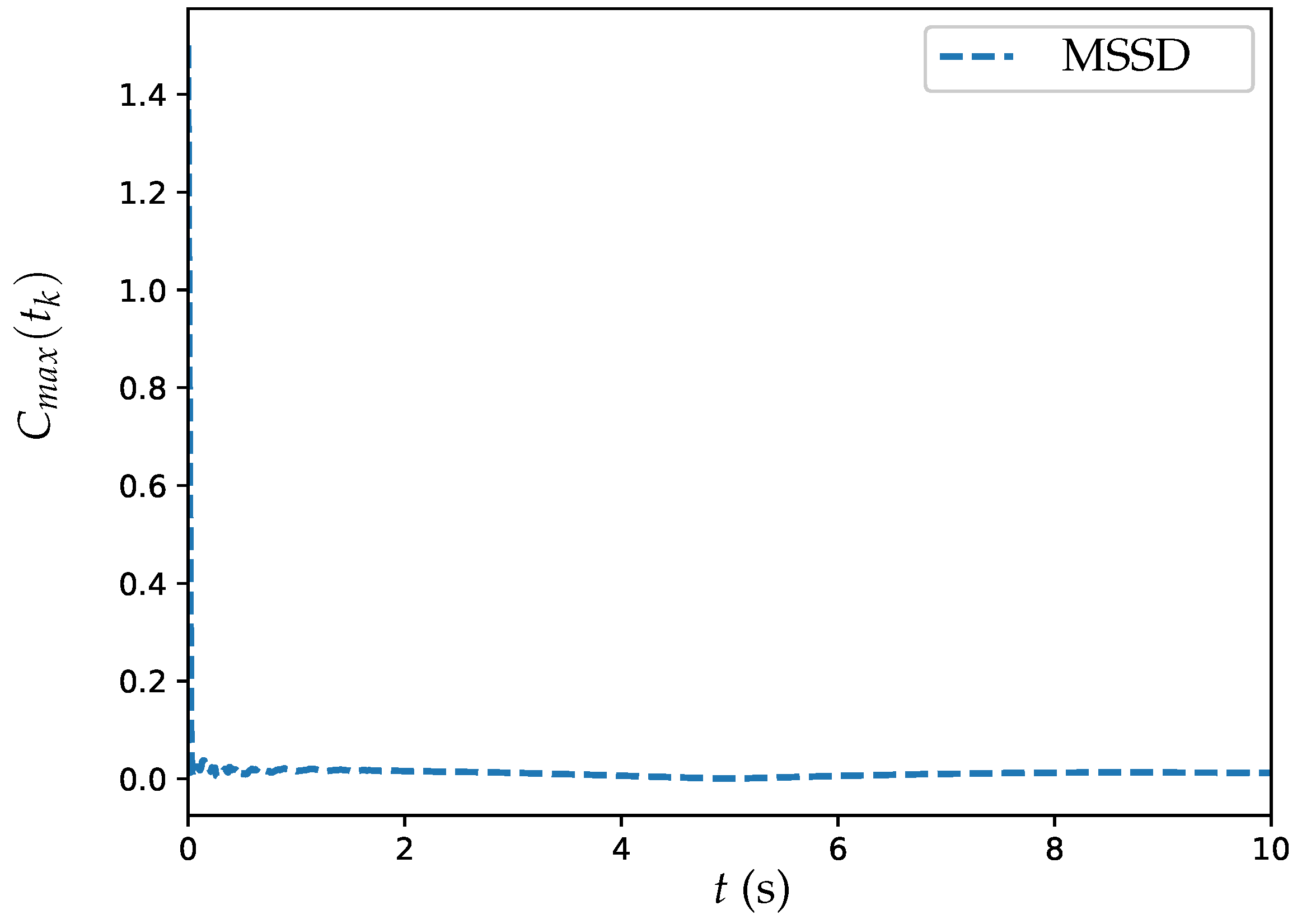
6.1. Example 1: DTDTVO Problem Solved by ET-DTZNN Algorithm
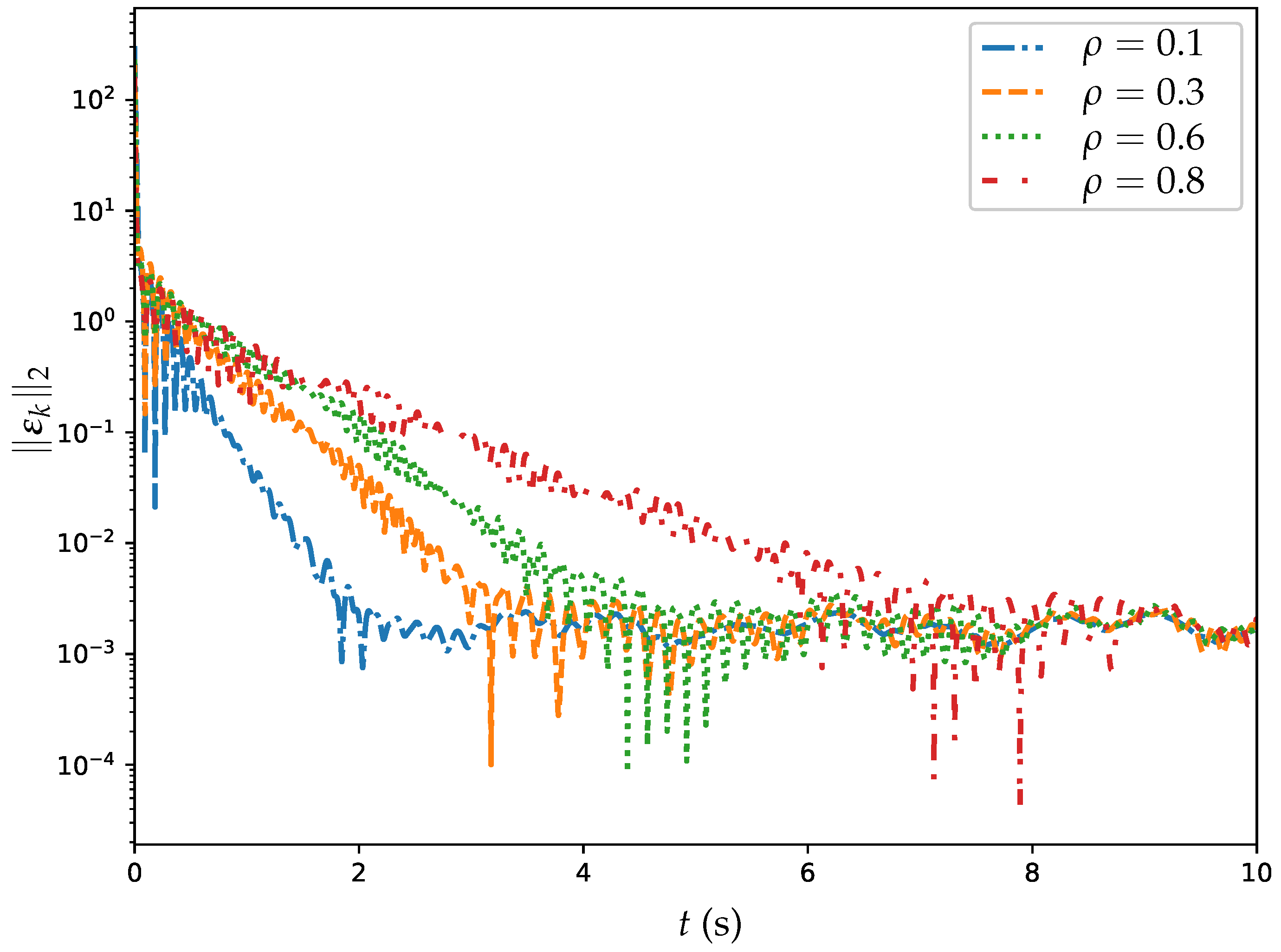
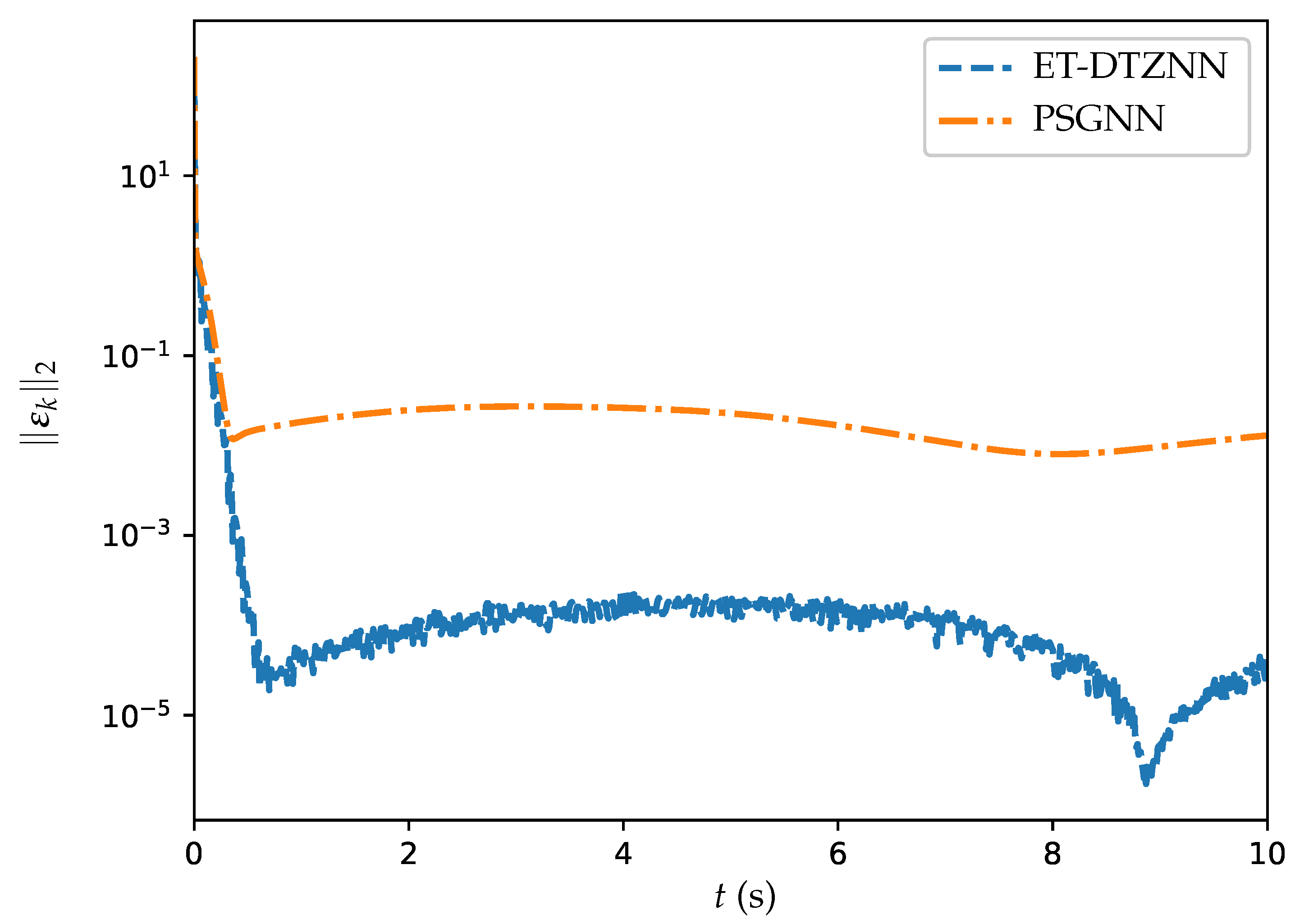
6.2. Example 2: Comparative Experiments
6.3. Example 3: DTDTVO Problem Solved by ET-DTZNN Algorithm in Large MASs
6.3.1. ET-DTZNN in Large MAS Under Static Topology
6.3.2. ET-DTZNN in Large MAS Under Dynamic Topology
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DTVO | Distributed Time-Varying Optimization |
| MASs | Multi-Agent Systems |
| ZNN | Zeroing Neural Network |
| CTDTVO | Continuous-Time Distributed Time-Varying Optimization |
| DTDTVO | Discrete-Time Distributed Time-Varying Optimization |
| CTZNN | Continuous-Time Zeroing Neural Network |
| DTZNN | Discrete-Time Zeroing Neural Network |
| ET-CTZNN | Event-Triggered Continuous-Time Zeroing Neural Network |
| ET-DTZNN | Event-Triggered Discrete-Time Zeroing Neural Network |
| MSSRE | Maximum Steady-State Residual Error |
| MSSD | Maximum Steady-State Deviation |
| GNN | Gradient Neural Network |
| PSGNN | Periodic Sampling Gradient Neural Network |
References
- Patari, N.; Venkataramanan, V.; Srivastava, A.; Molzahn, D.K.; Li, N.; Annaswamy, A. Distributed optimization in distribution systems: Use cases, limitations, and research needs. IEEE Trans. Power Syst. 2022, 37, 3469–3481. [Google Scholar]
- Cavraro, G.; Bolognani, S.; Carli, R.; Zampieri, S. On the need for communication for voltage regulation of power distribution grids. IEEE Trans. Control Netw. Syst. 2019, 6, 1111–1123. [Google Scholar]
- He, L.; Cheng, H.; Zhang, Y. Centralized and decentralized event-triggered Nash equilibrium-seeking strategies for heterogeneous multi-agent systems. Mathematics 2025, 13, 419. [Google Scholar] [CrossRef]
- Molzahn, D.K.; Dorfler, F.; Sandberg, H.; Low, S.H.; Chakrabarti, S.; Baldick, R.; Lavaei, J. A survey of distributed optimization and control algorithms for electric power systems. IEEE Trans. Smart Grid 2017, 8, 2941–2962. [Google Scholar]
- Pan, P.; Chen, G.; Shi, H.; Zha, X.; Huang, Z. Distributed robust optimization method for active distribution network with variable-speed pumped storage. Electronics 2024, 13, 3317. [Google Scholar] [CrossRef]
- Luo, S.; Peng, K.; Hu, C.; Ma, R. Consensus-based distributed optimal dispatch of integrated energy microgrid. Electronics 2023, 12, 1468. [Google Scholar] [CrossRef]
- Tariq, M.I.; Mansoor, M.; Mirza, A.F.; Khan, N.M.; Zafar, M.H.; Kouzani, A.Z.; Mahmud, M.A.P. Optimal control of centralized thermoelectric generation system under nonuniform temperature distribution using barnacles mating optimization algorithm. Electronics 2021, 10, 2839. [Google Scholar] [CrossRef]
- Yang, S.; Shen, Y.; Cao, J.; Huang, T. Distributed heavy-ball over time-varying digraphs with barzilai-borwein step sizes. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 4011–4021. [Google Scholar]
- An, W.; Ding, D.; Dong, H.; Shen, B.; Sun, L. Privacy-preserving distributed optimization for economic dispatch over balanced directed networks. IEEE Trans. Inf. Forensics Secur. 2024, 20, 1362–1373. [Google Scholar]
- Liu, M.; Li, Y.; Chen, Y.; Qi, Y.; Jin, L. A distributed competitive and collaborative coordination for multirobot systems. IEEE Trans. Mobile Comput. 2024, 23, 11436–11448. [Google Scholar]
- Huang, B.; Zou, Y.; Chen, F.; Meng, Z. Distributed time-varying economic dispatch via a prediction-correction method. IEEE Trans. Circuits Syst. I 2022, 69, 4215–4224. [Google Scholar] [CrossRef]
- He, S.; He, X.; Huang, T. A continuous-time consensus algorithm using neurodynamic system for distributed time-varying optimization with inequality constraints. J. Franklin I 2021, 358, 6741–6758. [Google Scholar] [CrossRef]
- Sun, S.; Xu, J.; Ren, W. Distributed continuous-time algorithms for time-varying constrained convex optimization. IEEE Trans. Autom. Control 2023, 68, 3931–3945. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, Q.; Wang, J. A specified-time convergent multiagent system for distributed optimization with a time-varying objective function. IEEE Trans. Autom. Control 2023, 68, 1590–1605. [Google Scholar] [CrossRef]
- Wang, B.; Sun, S.; Ren, W. Distributed time-varying quadratic optimal resource allocation subject to nonidentical time-varying hessians with application to multiquadrotor hose transportation. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 6109–6119. [Google Scholar] [CrossRef]
- Ding, Z. Distributed time-varying optimization—An output regulation approach. IEEE Trans. Cybern. 2024, 54, 1362–1373. [Google Scholar] [CrossRef]
- Rahili, S.; Ren, W. Distributed continuous-time convex optimization with time-varying cost functions. IEEE Trans. Autom. Control 2017, 62, 1590–1605. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, D.; Wang, J. A recurrent neural network for solving sylvester equation with time-varying coefficients. IEEE Trans. Neural Netw. 2002, 13, 1053–1063. [Google Scholar] [CrossRef]
- Zhang, Y.; He, L.; Hu, C.; Guo, J.; Li, J.; Shi, Y. General four-step discrete-time zeroing and derivative dynamics applied to time-varying nonlinear optimization. J. Comput. Appl. Math. 2019, 347, 314–329. [Google Scholar] [CrossRef]
- Liao, B.; Han, L.; He, Y.; Cao, X.; Li, J. Prescribed-time convergent adaptive ZNN for time-varying matrix inversion under harmonic noise. Electronics 2022, 11, 1636. [Google Scholar] [CrossRef]
- Zhou, P.; Tan, M.; Ji, J.; Jin, J. Design and analysis of anti-noise parameter-variable zeroing neural network for dynamic complex matrix inversion and manipulator trajectory tracking. Electronics 2022, 11, 824. [Google Scholar] [CrossRef]
- Xiao, L.; Luo, J.; Li, J.; Jia, L.; Li, J. Fixed-time consensus for multiagent systems under switching topology: A distributed zeroing neural network-based method. IEEE Syst. Man Cybern. Mag. 2024, 10, 44–55. [Google Scholar]
- Liao, B.; Wang, T.; Cao, X.; Hua, C.; Li, S. A novel zeroing neural dynamics for real-time management of multi-vehicle cooperation. IEEE Trans. Intell. Veh. 2024, early access, 1–16. [Google Scholar]
- Tan, N.; Yu, P.; Zhong, Z.; Zhang, Y. Data-driven control for continuum robots based on discrete zeroing neural networks. IEEE Trans. Ind. Inform. 2023, 19, 7088–7098. [Google Scholar]
- Jin, L.; Li, S.; Xiao, L.; Lu, R.; Liao, B. Cooperative motion generation in a distributed network of redundant robot manipulators with noises. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1715–1724. [Google Scholar]
- Chen, J.; Pan, Y.; Zhang, Y. ZNN continuous model and discrete algorithm for temporally variant optimization with nonlinear equation constraints via novel td formula. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 3994–4004. [Google Scholar]
- Zuo, Q.; Li, K.; Xiao, L.; Wang, Y.; Li, K. On generalized zeroing neural network under discrete and distributed time delays and its application to dynamic Lyapunov equation. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 5114–5126. [Google Scholar]
- Dai, J.; Tan, P.; Xiao, L.; Jia, L.; He, Y.; Luo, J. A fuzzy adaptive zeroing neural network model with event-triggered control for time-varying matrix inversion. IEEE Trans. Fuzzy Syst. 2023, 31, 3974–3983. [Google Scholar]
- Kong, Y.; Zeng, X.; Jiang, Y.; Sun, D. A predefined time fuzzy neural solution with event-triggered mechanism to kinematic planning of manipulator with physical constraints. IEEE Trans. Fuzzy Syst. 2024, 32, 4646–4659. [Google Scholar]
- Golub, G.; Loan, C.F. Matrix Computations, 4th ed.; John Hopkins Univesity Press: Baltimore, MD, USA, 2013; pp. 22–33. [Google Scholar]
- Diestel, R. Graph Theory, 5th ed.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 1–33. [Google Scholar]
- Bahman, G.; Jorge, C. Distributed continuous-time convex optimization on weight-balanced digraphs. IEEE Trans. Automat. Contr. 2014, 59, 781–786. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002; pp. 111–181. [Google Scholar]
- Zhang, Z.; Yang, S.; Zheng, L. A penalty strategy combined varying-parameter recurrent neural network for solving time-varying multi-type constrained quadratic programming problems. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 2993–3004. [Google Scholar]




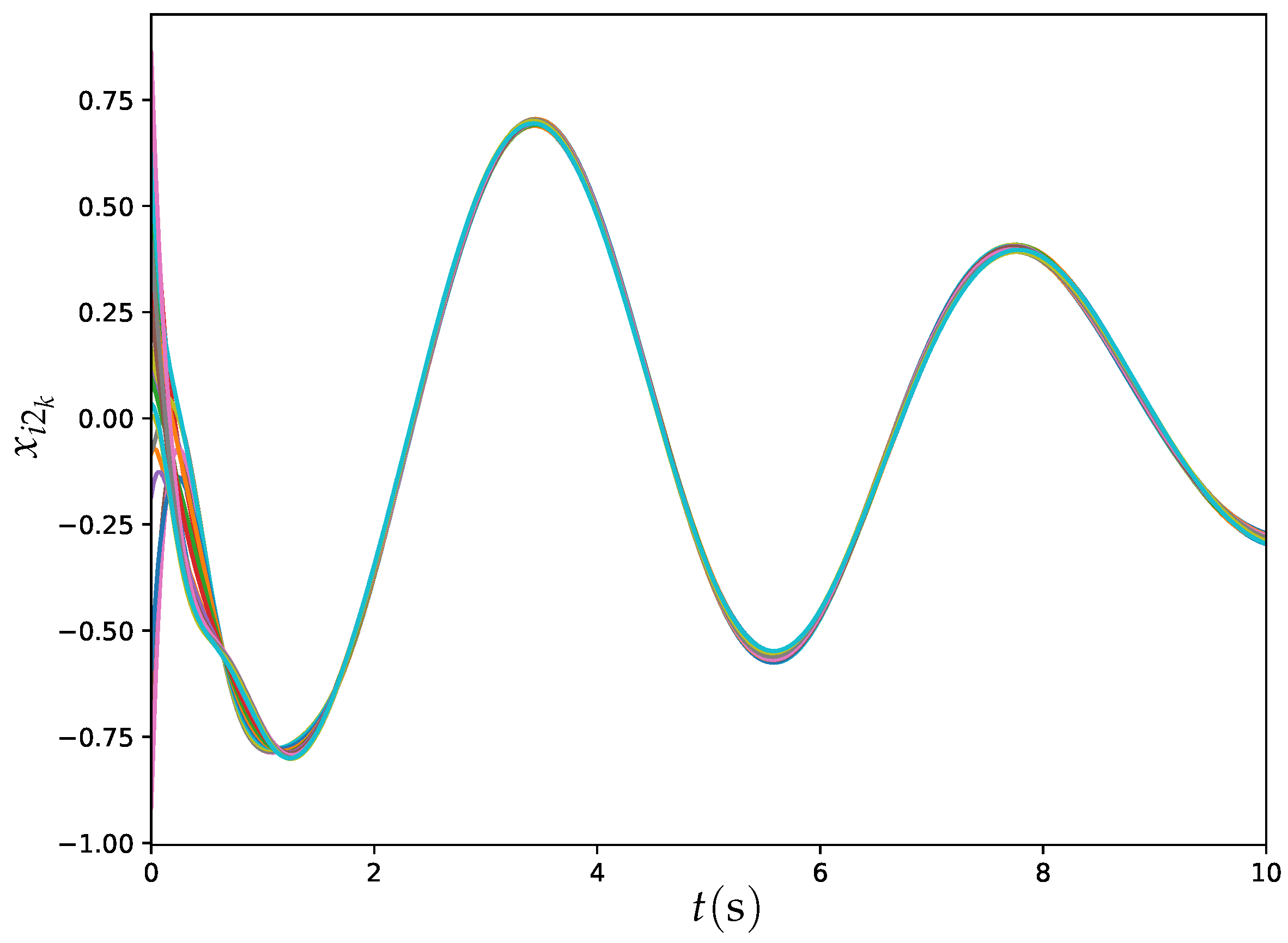
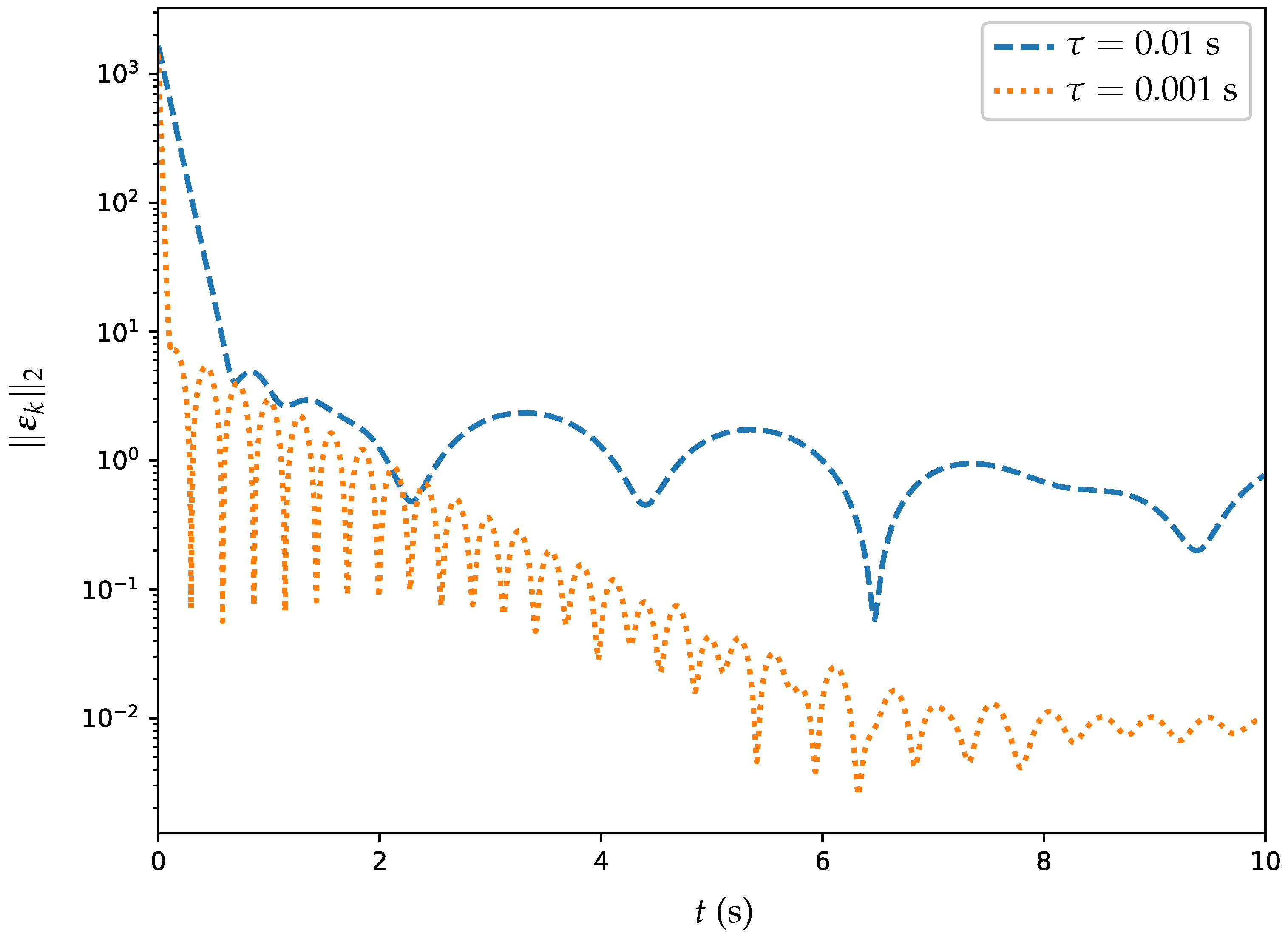
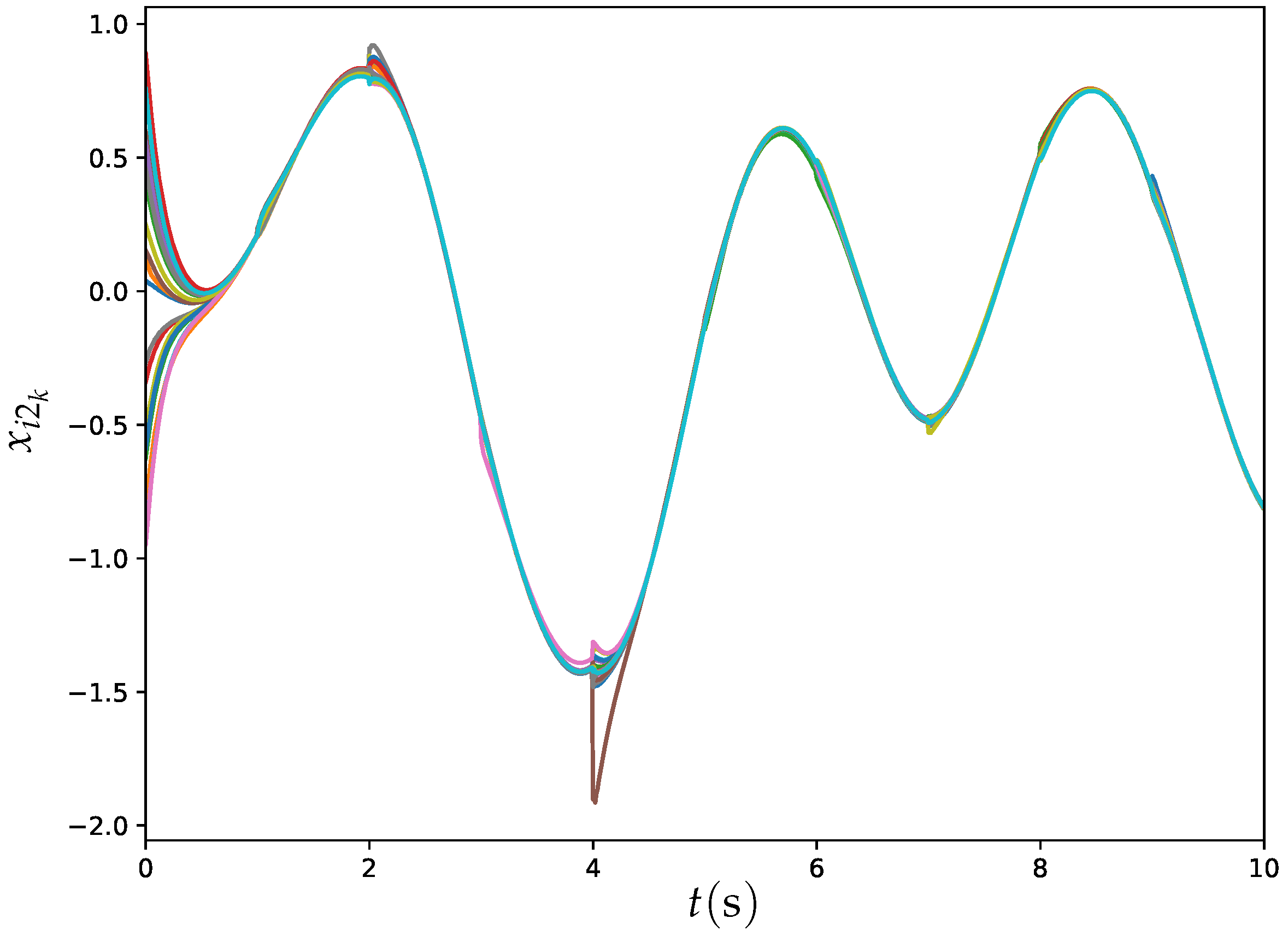
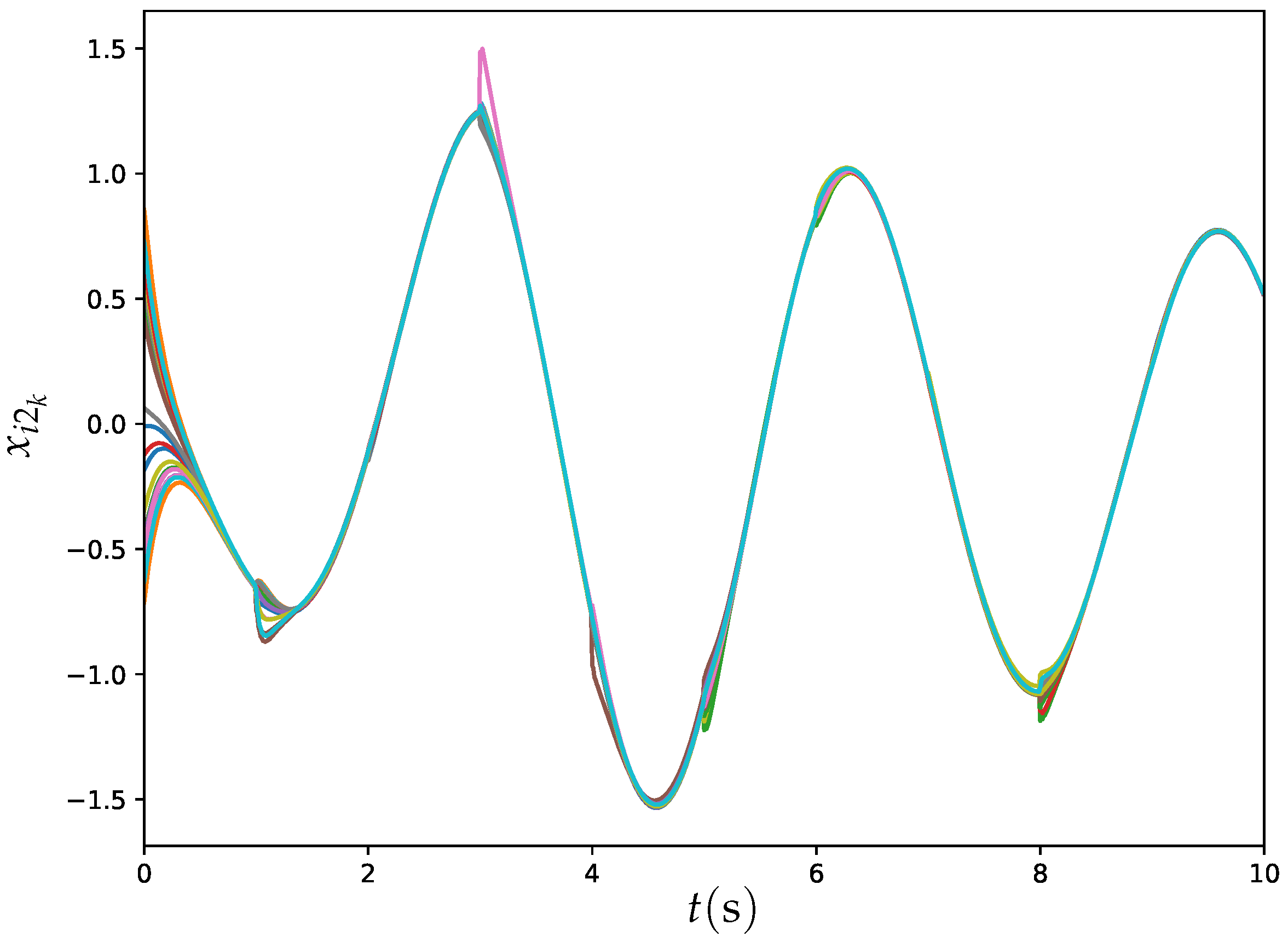

| Expression | |
|---|---|
| MSSRE | |
|---|---|
| 0.001 s | |
| 0.0005 s | |
| 0.0001 s |
| Agent | Number of Trigger Events with | Number of Trigger Events with | Number of Trigger Events with | Number of Trigger Events with |
|---|---|---|---|---|
| Agent 1 | 1915 | 1840 | 1404 | 1289 |
| Agent 2 | 5141 | 1614 | 1512 | 1444 |
| Agent 3 | 4867 | 1598 | 1439 | 1304 |
| Agent 4 | 6459 | 2417 | 2156 | 1968 |
| Agent 5 | 6161 | 2312 | 2345 | 2132 |
| MSSRE of PSGNN | MSSRE of ET-DTZNN | |
|---|---|---|
| 0.001 s | ||
| 0.0005 s | ||
| 0.0001 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, L.; Cheng, H.; Zhang, Y. Event-Triggered Discrete-Time ZNN Algorithm for Distributed Optimization with Time-Varying Objective Functions. Electronics 2025, 14, 1359. https://doi.org/10.3390/electronics14071359
He L, Cheng H, Zhang Y. Event-Triggered Discrete-Time ZNN Algorithm for Distributed Optimization with Time-Varying Objective Functions. Electronics. 2025; 14(7):1359. https://doi.org/10.3390/electronics14071359
Chicago/Turabian StyleHe, Liu, Hui Cheng, and Yunong Zhang. 2025. "Event-Triggered Discrete-Time ZNN Algorithm for Distributed Optimization with Time-Varying Objective Functions" Electronics 14, no. 7: 1359. https://doi.org/10.3390/electronics14071359
APA StyleHe, L., Cheng, H., & Zhang, Y. (2025). Event-Triggered Discrete-Time ZNN Algorithm for Distributed Optimization with Time-Varying Objective Functions. Electronics, 14(7), 1359. https://doi.org/10.3390/electronics14071359






