Logarithmic NTRU-Based Certificateless Ring Signature in E-Voting Applications

Abstract

In electronic voting systems, a large number of voters are often required to vote. It is also necessary to ensure the security of the voters and the fairness of the vote. The use of ring signatures is very suitable for e-voting systems because of their special anonymity. Among the many types of ring signatures, certificateless ring signature (CRS) stands out because it does not require certificates and avoids the need to completely trust the key generation center (KGC). In this paper, we propose a certificateless ring signature based on the special structure of the number theory research unit (NTRU) lattice, which utilizes the Merkle tree and seed tree to split commitments and integrate them again to generate signatures. At the same time, we embed the NTRU small integer solution (NTRU-SIS) problem and provide a detailed proof of security under the random oracle model (ROM). In efficiency, the Merkle tree makes the signature size logarithmically increase with the ring scale. In the era of big data explosion, this feature enables the proposed scheme to maintain a comparatively short signature size even when the number of ring members N is very large. When $N=8$, the signature size is 61.08 KB; when N increases to 512, the size is 65.02 KB. From the data, we can observe that the signature size grows slowly, by only 4 KB when N grows exponentially, which is much slower than ring signatures with linear growth.

1. Introduction

Throughout history, voting has witnessed the development of human civilization. Whether a small meeting or a large-scale election, voting is an important part of the process. In ancient times, voting was done on paper, which was convenient daily. However, as the number of people grows, or in the case of large-scale elections, paper ballots have many drawbacks. In addition to consuming a lot of manpower and resources, they have the disadvantages of being easily tampered with, and the election process may not be transparent. With the advent of the internet, e-voting has greatly improved the situation. In 1981, Chaum and David [1] proposed an electronic voting protocol. Just a few years later, Fujioka et al. [2] proposed the first large-scale use of a blind signature-based voting protocol, which allowed the use of electronic signatures to skyrocket. However, there was a risk of forgery, and even though Cong and Hu [3] later modified the protocol, it still led to the problem of voters’ identities being revealed. Over the past four decades, researchers have engaged in many efforts towards making e-voting meet basic security needs as well as enabling richer applications. At present, the underlying cryptographic techniques of anonymous e-voting protocols are divided into three types: blind signature, ring signature, and proxy signature.

A ring signature is a type of decentralized signature invented by Ron Rivest, Adi Shamir, and Yael Tauman [4] in 2001. Since then, the most commonly used ring signatures have mainly been RSA and elliptic curve ring signatures, both of which are mainly based on traditional number-theoretic problems. As early as 1994, Shor [5] proposed a prime factorization algorithm, which did not have too much impact on the traditional cryptosystems due to technical limitations. However, with the development of quantum computing, traditional cryptosystems are no longer secure. Thus, scholars have set their eyes on post-quantum cryptography solutions such as lattice-based cryptosystems. In 2018, NIST put out an open call for cryptography projects that included lattice cryptography. In recent years, lattice ring signatures have become a hot research topic among scholars, and many efficient lattice ring signature schemes have been proposed [6,7,8,9]. However, the lack of uniform standards for parameter selection in the lattice has led to a slow process of practical application. In addition to resisting quantum attacks, lattice cryptography has the advantages of worst-case to average-case reductions, good efficiency, and more. Among the many lattice-based cryptosystems, the number theory research unit (NTRU) lattice is widely used in many fields for its simplicity, fast computation speed, and small storage space. The NTRU cryptosystem was first proposed by Silverman, Hoffstein, and Pipher [10] in 1996. Its security is based on the shortest vector problem (SVP) on the lattice, meaning that it can resist attacks from the Shor algorithm and improve its performance.

Today, earlier electronic voting systems can no longer meet requirements in terms of efficiency and security. As early as 1983, Shamir [11] proposed an identity-based cryptosystem. Soon after, Zhang and Kim [12] presented the first identity-based ring signature (IBRS), which has also been adapted to e-voting. However, it requires certificate management and excessive KGC powers, meaning that it is not applicable in certain practical situations. In 2003, Al-Riyami and Paterson [13] proposed a certificateless cryptosystem that does not require certificates and can also reduce the authority of KGC. Figure 1 shows the difference between these two types of signatures when generating a user’s private key. Combining certificateless capability with ring signatures has greatly impacted certain application scenarios requiring efficient and flexible authentication. Certificateless ring signatures have good efficiency and are unforgeable, making them well-suited for e-voting systems.

However, there are many problems with existing certificateless ring signatures. Most certificateless ring signatures are not quantum-resistant and are very vulnerable to some quantum attacks. In certain practical scenarios, there is a lack of functionality expansion and inefficiency. In addition, there are problems with key storage, a widely recognized industry standard has not yet been formed, and there are few actual deployment cases. In [14,15], both schemes are based on bilinear pairs and lack resistance to quantum attacks. In [16,17], both have quantum resistance and provide corresponding application scenarios, but are less efficient. In [18], the scheme has quantum resistance, but there is no corresponding application scenario. Furthermore, it is large in terms of size, although the size is constant.

To solve the above problems, this paper proposes a certificateless ring signature scheme on an NTRU lattice (NTRU-CRS) based on an anonymous e-voting system.

1. First, the proposed scheme is based on the NTRU-SIS hard assumption, which guarantees users’ identities using the properties of the Merkle tree accumulator. By combining this with certificateless cryptography, no certificate management is required. In this way, the proposed scheme has improved efficiency while also restricting the power of the KGC.

2. In terms of security, a detailed proof of the proposed scheme’s security is provided, including its correctness, anonymity, and unforgeability. In particular, we provide a proof of security for unforgeability against two different adversaries: an external adversary and a malicious KGC.

3. In terms of effectiveness analysis, the signature size of NTRU-CRS is logarithmically related to the number of ring members N. In terms of signature time overhead, NTRU-CRS outperforms other similar schemes.

In the subsequent section, we introduce the related works on certificateless ring signatures. Section 3 provides some related preliminaries. Section 4 contains the specific parameter settings and details of our proposed scheme. In Section 5, specific security proofs are shown. Section 6 compares the performance of our scheme with other similar schemes. In Section 7, we present the application of the scheme in anonymous voting systems. The final Section 8 and Section 9 summarize the work and make suggestions for its future, respectively.

2. Related Works

Yum and Lee [19] proposed a generic construction for a certificateless signature in 2004, which they constructed using an identity- and certificate-based signature. After this, the idea of certificateless signatures began to be applied to different types of signatures. In 2007, Chow et al. [20] constructed a CRS scheme and provided a security model for it. Subsequently, Chang et al. [21] modified the security requirements of certificateless signatures in 2009 and proposed a new CRS. Most earlier types of CRS used bilinear pairings; Deng et al. [22] first proposed a CRS without pairing in 2015. Most later CRS examples [23,24,25] were constructed based on bilinear pairing, but these are generally inefficient.

With the development of the internet and quantum computing, certificateless ring signatures based on traditional hard problems have long been unsatisfactory in the face of the threat of massive data and quantum attacks. The lattice approach provides scholars with a new way of thinking due to its high efficiency and resistance to quantum attacks. In 2015, Tian et al. [26] proposed the first certificateless signature on the lattice, and encountered the problem that the scheme needs to store matrices, leading to unsatisfactory efficiency. Later scholars focused their research on improving efficiency and addressing diverse practical scenarios. In 2016, Xie et al. [27] proposed a certificateless signature scheme based on the NTRU lattice, which had improved efficiency to the one in [26]. In 2020, Deng et al. [14] proposed an elliptic curve-based linkable CRS, which effectively solves the above problem in e-voting or transactions. At the same time, Bouakkaz [15] proposed a CRS scheme based on bilinear pairs suitable for the vehicular ad hoc networks. However, neither of these schemes is quantum-resistant. In the following year, Zhang and Chen [16] proposed a CRS on the lattice with a blockchain sharing economy transaction scheme that can protect users’ privacy via the principle of bimodal Gaussian rejection sampling, which greatly reduces the sampling time in the signature phase. In 2022, Dong et al. [18] proposed a lattice-based CRS with constant-size. While this approach improves the security and efficiency of the scheme through bimodal Gaussian sampling, the signature size is too large, meaning that it lacks practical value. In 2023, Yu et al. [17] proposed an NTRU-based CRS based on the RSIS assumption, which is generated using the rejection sampling technique with the help of the polynomial ring structure of the NTRU lattice, effectively improving efficiency. This year, Zhang et al. [28] proposed a CRS on lattice for Internet of Things applications. As in [17], bimodal Gaussian sampling is used to improve the efficiency of key generation. In particular, the traceability function is supplemented for practical applications. Current related schemes focus on efficiency improvements as well as additional practical functionality. Although all of the above schemes have improved efficiency, the signature size increases significantly with N when the number of ring members is too large.

3. Preliminaries

3.1. Notation

On the ring $\mathbb{Z}\left[X\right]/(q,X^n+1)$, the norm is defined via the coefficient vector of the polynomial. Specifically, elements in ${\mathcal{R}}_q$ are uniquely represented as polynomials with coefficients confined to the following ranges: when the modulus q is even, the coefficients are integers in the interval $(-q/2,q/2)$; when the modulus q is odd, the coefficients are integers in the interval $[-(q-1)/2,(q-1)/2]$.

3.2. NTRU Lattice

Definition 1

(NTRU lattice). Let n be an integer and a power of 2; q is a prime number and $q\ge 2$. Polynomials f,$g\in {\mathcal{R}}_q$, $h=g\ast f^{-1}modq$. The matrix $\mathbf{A}=\left(\begin{array}{cc}-{\mathbf{A}}_n(H)& {\mathbf{I}}_n\\ q{\mathbf{I}}_n& 0_n\end{array}\right)$ generates a 2n dimension full-rank lattice ${\mathsf{\Lambda }}_{q,h}$ which is the NTRU lattice:

$${\mathsf{\Lambda }}_{q,h}=\{(u,v)\in {\mathcal{R}}^2|u+v\ast h=0modq\}.$$

Here, we introduce the NTRU-SIS hard problem on which the security of the proposed scheme largely depends. We take this definition from [29].

Definition 2

(NTRU-SIS). If n,m,q are all integers, a positive real $\beta \ge 0$, and the polynomial $h=g\ast f^{-1}modq\in {\mathcal{R}}_q$, then the NTRU-SIS is to find two polynomials $(u,v)\in {\mathcal{R}}_q^2$ such that $u+v\ast h=0modq$ and $\left|\right|u\left|\right|,\left|\right|q\left|\right|\le \beta$.

3.3. The Related Algorithms

The following are some of the algorithms needed for the scheme. The details of algorithms are provided in [30], and are mainly as follows:

• ${\mathbf{TrapGen}}_{\mathbf{NTRU}}(1^n)$: Let n and k be integers, where $k>3$ and $n=2^k$, and where $q=1mod2n$ is a prime number. The parameter $\beta =1.17\sqrt{q/2n}$ and $f,g,F,G\in \mathcal{R}$ satisfying $f·F-g·G=q$. A probabilistic polynomial-time (PPT) algorithm ${\mathbf{TrapGen}}_{\mathbf{NTRU}}$ outputs a polynomial $h=g\ast f^{-1}modq$ and a matrix ${\mathbf{B}}_{f,g}=\left(\begin{array}{cc}{\mathbf{A}}_n(g)& -{\mathbf{A}}_n(f)\\ {\mathbf{A}}_n(G)& -{\mathbf{A}}_n(F)\end{array}\right)\in {\mathbb{Z}}_q^{2n\times 2n}$.
• $\mathbf{SamplePre}({\mathbf{B}}_{f,g},s,t)$: This algorithm inputs a matrix ${\mathbf{B}}_{f,g}$, a Gaussian parameter $s=0.585\pi \sqrt{qln(2+2/\eta )}$ for $\eta =2^{-\lambda }/2n$, and a polynomial $t\in {\mathcal{R}}_q$. It outputs $\mathbf{z}=(z_1,z_2)$ from ${\mathbf{D}}_{h^{\perp }+\mathbf{c},s}$ such that $z_1+h\ast z_2=t$, $\parallel \mathbf{z}\parallel \le s\sqrt{2n}$.

3.4. Certificateless Ring Signature

This subsection provides the definition and security requirements for a standard certificateless ring signature.

Definition 3.

A CRS scheme mainly consists of seven PPT algorithms, which are as follows: Setup, Extract-Partial-Private-Key, Set-Secret-Value, Set-Private-Key, Set-Public-Key, CLR.Sign, and CLR.Verify:

• $\mathbf{Setup}(1^{\lambda })$: The algorithm generates the master public key $MPK$, the master secret key $MSK$, and the public parameter $PP$ through the security parameter $\lambda$.
• $\mathbf{Extract}-\mathbf{Partial}-\mathbf{Private}-\mathbf{Key}(MSK,ID)$: The KGC utilizes the algorithm that generates the user’s partial private key ${\mathbf{s}}_{ID}$ from the master secret key $MSK$ and the user’s identity $ID$.
• $\mathbf{Set}-\mathbf{Secret}-\mathbf{Value}(ID)$: Using the identity $ID$, the user randomly selects a secret value ${\mathbf{s}}_{ID}^{\prime }$.
• $\mathbf{Set}-\mathbf{Private}-\mathbf{Key}(s_{ID},{s^{\prime }}_{ID})$: The algorithm uses the partial private key ${\mathbf{s}}_{ID}$ generated by the KGC and a secret value ${\mathbf{s}}_{ID}^{\prime }$ selected by the user as input to output the full private key $SK$.
• $\mathbf{Set}-\mathbf{Public}-\mathbf{Key}(SK)$: The algorithm generates the user’s public key $PK$ using the full private key $SK$.
• $\mathbf{CLR}.\mathbf{Sign}(\mu ,R,SK)$: The algorithm inputs the message $\mu$, the ring R, and the user’s private key $SK$, then outputs the corresponding signature $\sigma$.
• $\mathbf{CLR}.\mathbf{Verify}(R,\mu ,\sigma )$: The algorithm verifies the message $\mu$, the ring R, and the signature $\sigma$, then outputs 1 if accepted and 0 if rejected.

In addition to these, there are three properties of certificateless ring signatures: correctness, anonymity, and unforgeability. Correctness means that as long as the generated signature is valid, it can be successfully verified. Anonymity means that even if the adversary knows the private keys of the ring members, they cannot know the identity of the signer in the ring. Finally, unforgeability means that an adversary cannot generate a valid signature without the user’s private key. There are two types of adversaries; type 1 is an external attacker (${\mathcal{A}}_1$), which carries out public key replacement attacks, while type 2 is the malicious KGC (${\mathcal{A}}_2$) which knows the master private key $MSK$.

3.5. Index-Hiding Merkle Tree

The index-hiding Merkle tree method [31] is an efficient way of displaying the exact position of an element, which is achieved by hashing a set of elements $A=(a_0,\cdots ,a_N)$ to construct a Merkle tree. In the following discussion, we consider a slight modification of the traditional Merkle tree construction in which we use three algorithms and a hash function $H_{Coll}={\{0,1\}}^{★}\to {\{0,1\}}^{2\lambda }$, as shown in

Table 1. Related algorithms (Merkle tree).

Algorithm	Input	Output
$\mathbf{MerkleTree}$	A	root, tree
$\mathbf{Path}$	tree, I	path
$\mathbf{RecRoot}$	a, path	root

:

• $\mathbf{MerkleTree}(A)\to (root,tree)$: This algorithm inputs some elements $A=(a_1,\cdots ,a_{2^k})$, where $k\in \mathbb{N}$. It then generates a Merkle tree using the hash function $H_{Coll}$, producing leaf and root nodes. Finally, it outputs the root node $root$ and the entire tree description $tree$.
• $\mathbf{Path}(tree,I)\to path$: This algorithm inputs $tree$ and an index $I\in \left[2^k\right]$, then outputs the path of $I,path=(p_1,\cdots ,p_k)$.
• $\mathbf{RecRoot}(a,path)\to root$: This algorithm inputs an element $a\in A$ and the path of a, $path=(p_1,\cdots ,p_k)$. It reconstructs $root$ from the element a and the hash values of its sibling and ancestor nodes. Finally, it outputs the reconstructed root node $roo{t}^{\prime }=h_k$.

As shown in Figure 2, all the elements require lexicographical ordering, where H in the figure represents $H_{Coll}$ and $H(·)$ stands for the hash on its child nodes. At the bottom is the original data block; the tree structure is generated by hashing the original data block from bottom to top. Regarding the explanation of the path, for example, the red leaf node is the target node, and its corresponding path consists of the yellow nodes.

Here we briefly state a lemma that we will use in the proof, namely, that the distribution of $a_I$ in the tree is only related to the distribution D and not to the index I. In addition, details of the relevant proofs of the properties of the Merkle tree are provided in [32].

3.6. Seed Tree

Let us first define a pseudorandom generator $\mathbf{Expand}:{\{0,1\}}^{\lambda +\lceil {log}_2(M-1)\rceil }\to {\{0,1\}}^{2\lambda }$ for any $\lambda ,M\in \mathbb{N}$ and instantiate it as a random oracle, where $\lambda ,M\in \mathbb{N}$. We build a complete binary tree with $\lambda$ bit seed values by splitting $\mathbf{Expand}(seed||d)$ into two halves, where left (right) is the left (right) child node and d is the unique identifier of its parent node. Such a binary tree is called a seed tree. It can generate many pseudorandom values; in addition, when any subset is chosen for exposure, it is guaranteed not to reveal information about the undisclosed values. Below, we provide details on the four algorithms related to the seed tree, as shown in

Table 2. Related algorithms (seed tree).

Algorithm	Input	Output
${\mathbf{Seedtree}}^{\mathcal{O}}$	$see{d}_{root},M$	$lea{f}_i$
${\mathbf{Release}}^{\mathcal{O}}$	$see{d}_{root},c$	$seed{s}_{internal}$
${\mathbf{RecLeaves}}^{\mathcal{O}}$	$see{d}_{internal},c$	${\left\{lea{f}_i\right\}}_{c_i=1}$
${\mathbf{SimulateSeeds}}^{\mathcal{O}}$	c	$seed{s}_{internal}$

.

• ${\mathbf{Seedtree}}^{\mathcal{O}}(see{d}_{root},M)\to {\left\{lea{f}_i\right\}}_{i\in \left[M\right]}$: This algorithm inputs a root seed $see{d}_{root}$ and an integer $M\in \mathbb{N}$. It generates a complete binary tree with M leaf nodes using $\mathcal{O}(\mathbf{Expand}|\left|see{d}_d\right||d)$ as outputs.
• ${\mathbf{Release}}^{\mathcal{O}}(see{d}_{root},c)\to seed{s}_{internal}$: This algorithm inputs a root seed $see{d}_{root}$ and challenge $c\in {\left\{0,1\right\}}^M$, then outputs a list $seed{s}_{internal}$, where the seeds corresponds to $c_i=1$;
• ${\mathbf{RecLeaves}}^{\mathcal{O}}(seed{s}_{internal},c)\to {\left\{lea{f}_i\right\}}_{c_i=1}$: This algorithm inputs a list $seed{s}_{internal}$ and challenge $c\in {\left\{0,1\right\}}^M$, then recovers the ${\left\{lea{f}_i\right\}}_{c_i=1}$ as outputs.
• ${\mathbf{SimulateSeeds}}^{\mathcal{O}}(c)\to seed{s}_{internal}$: The algorithm inputs challenge $c\in {\left\{0,1\right\}}^M$, which is used to identify the set of leaf nodes $c_i=1$. Then, for each of these leaf nodes, a seed is randomly selected from the set. Finally, the algorithm outputs the set of these seeds, referred to as $seed{s}_{internal}$.

In simple terms, a seed tree is a binary tree structure built from random values. On the one hand, it generates the random values required by schemes, while on the other, it enables the distribution or routing of challenge values in zero-knowledge protocols.

Here, we remain brief in our lemma stating that ${\mathbf{RecLeaves}}^{\mathcal{O}}$ and ${\mathbf{SimulateSeeds}}^{\mathcal{O}}$ produce the same leaf values. In short, ${\mathbf{SimulateSeeds}}^{\mathcal{O}}$ can prove that from the view of someone who only knows ${\mathbf{seeds}}_{internal}$ and c, all the leaves with index i that have $c_i=0$ are indistinguishable from uniformly random values. For an adversary $\mathcal{A}$ who queries the random oracle Q times, the distribution consisting of leaves and $seed{s}_{internal}$ generated by ${\mathbf{RecLeaves}}^{\mathcal{O}}$ and ${\mathbf{SimulateSeeds}}^{\mathcal{O}}$ distinguishes their advantage as only ${\displaystyle \frac{Q}{2^{\lambda }}}$. For details, see [32].

4. Constructions

4.1. Setup

The system chooses $\lambda$ and n as the system parameters, where $n=2^k$. $q=1mod2n$ is a prime number. Here, $\beta$ and s are two parameters that satisfy $\beta =1.17\sqrt{q/2n}$ and $s=0.585/\pi \sqrt{qln(2+2\eta )}$, where $\eta =2^{-\lambda }/2n$. In addition, $N,M,K$ are all integers and satisfy $M>\lambda$ as well as $\left({\displaystyle \genfrac{}{}{0pt}{}{M}{K}}\right)\ge 2^{\lambda }$. $H_0:{\{0,1\}}^{\ast }\to {\mathcal{R}}_q$ and $H_{FS}:{\{0,1\}}^{\ast }\to {\{0,1\}}^M$ randomly select a polynomial $h^{\prime }\in {\mathcal{R}}_q$. Finally, the public parameter $pp:=\{q,\beta ,s,M,K,h^{\prime },H_0,H_{FS}\}$

4.2. Key Generation

• The $\mathbf{KGC}$ utilizes the algorithm ${\mathbf{TrapGen}}_{\mathbf{NTRU}}(1^{\lambda },1^n)$ to generate a master public key $h\in {\mathcal{R}}_q$ and master secret key ${\mathbf{B}}_{f,g}\in {\mathbb{Z}}_q^{2n\times 2n}$.
• The user enters their identity ID, then the $\mathbf{KGC}$ runs $\mathbf{SamplePre}({\mathbf{B}}_{f,g},s,(H_0(ID),\mathbf{0}))$ to generate ${\mathbf{s}}_{ID}={(s_{i1},s_{i2})}^T$, where $s_{i1},s_{i2}\in {\mathcal{R}}_q$ and satisfies $H_0(ID)=s_{i1}+h{s}_{i2}$, $\parallel {\mathbf{s}}_{ID}\parallel \le s\sqrt{2n}$.
• The user randomly selects two small secrets $s_{i1}^{★},s_{i2}^{★}\in {\mathcal{R}}_q$. Let ${\mathbf{p}}_{ID}=s_{i1}^{★}+h^{\prime }{s}_{i2}^{★}$ and ${\mathbf{s}}_{ID}^{\prime }=(s_{i1}^{★},s_{i2}^{★})$.
• At this point, the user’s public key is $({\mathbf{p}}_{ID}$, $ID)$ and their private key is $SK=({\mathbf{s}}_{ID},{\mathbf{s}}_{ID}^{\prime })$.

4.3. Signing Algorithm

Let the ring R be composed of N users, where each user has an identity $I{D}_j$ with an index j (where $j\in \left[N\right]$); $I{D}_J$ is the signer and $\mu \in {\{0,1\}}^{\ast }$ is a signing message. Additionally, the scheme employs M iterations to ensure unforgeability, as shown in Algorithm 1.

• Random sampling of a $salt$ and a seed $see{d}_{root}$ from ${\{0,1\}}^{2\lambda }$ and ${\{0,1\}}^{\lambda }$, respectively.
• Call ${\mathbf{Seedtree}}^{\mathcal{O}}(see{d}_{root},salt,M)$ to compute $(see{d}_1,\cdots ,see{d}_M)$.
• Call $\mathbf{Expand}(see{d}_i)$ to obtain a set of randomness $({\mathbf{y}}_{i1},\cdots ,{\mathbf{y}}_{i4},{{\mathbf{r}}_i}_1,\cdots ,{{\mathbf{r}}_i}_N)$, where ${\mathbf{r}}_{ij}\in {\{0,1\}}^{\lambda },j\in \left[N\right]$.
• $com=(salt,roo{t}_1,\cdots ,roo{t}_M)$ are generated through the following steps:

  –

  Compute ${\mathbf{w}}_{j1}={\mathbf{y}}_{i1}+h{\mathbf{y}}_{i2}+H_0(I{D}_j)$.

  –

  Compute ${\mathbf{w}}_{j2}={\mathbf{y}}_{i3}+h^{\prime }{\mathbf{y}}_{i4}+{\mathbf{p}}_{ID}$.

  –

  Call $\mathbf{Com}({\mathbf{w}}_{j1}|\left|{\mathbf{w}}_{j2}\right||{\mathbf{r}}_{ij})$ to compute $C_j$, where $\mathbf{Com}$ is an algorithm for hiding commitment.

  –

  Call $\mathbf{Merkletree}(C_1,\cdots ,C_j,\cdots ,C_N)$ to compute $(roo{t}_i,tre{e}_i)$.

• Compute the commitments $com=(salt,roo{t}_1,\cdots ,roo{t}_M)$.
• Compute the challenge value $chall$ with $H_{FS}(\mu ,R,com)=(c_1,\cdots ,c_M)\in {\{0,1\}}^M$. There are only two types of challenges, $c_i=0$ and $c_i=1$; here, they are processed in batches. The processing steps are as follows:

  –

  For $c_i=0$, compute ${\mathbf{z}}_{i1}=({\mathbf{y}}_{i1}+s_{i1},{\mathbf{y}}_{i2}+s_{i2})$ and ${\mathbf{z}}_{i2}=({\mathbf{y}}_{i3}+s_{i1}^{★},{\mathbf{y}}_{i4}+s_{i2}^{★})$. Call $\mathbf{Path}=(tre{e}_i,I{D}_J)$ to obtain $pat{h}_i$ and let ${\mathtt{rsp}}_i=({\mathbf{z}}_{i1},{\mathbf{z}}_{i2},pat{h}_i,{\mathbf{r}}_{ij})$.

  –

  For $c_i=1$, let ${\mathtt{rsp}}_i=see{d}_i$.

• Call ${\mathbf{Release}}^{\mathcal{O}}(see{d}_{root},chall,salt)$ to compute $seed{s}_{internal}$.
• Let $rsp=(seed{s}_{internal},{rsp}_{c_i=0})$.
• The signature $\sigma =(salt,chall,rsp)$.

4.4. Verification Algorithm

After receiving the signature, the verifier needs to analyze the signature, as shown in Algortithm 2.

• Call $\mathbf{RecCom}(R,salt,chall,rsp)$ to recover $com=(salt,roo{t}_1,\cdots ,roo{t}_M)$.
• Call ${\mathbf{RecLeaves}}^{\mathcal{O}}(seed{s}_{internal},\mathbf{c})$ to recover ${rsp}_{c_i=1}$.

  –

  For $c_i=0$, use $rs{p}_i=({\mathbf{z}}_i,pat{h}_i,\mathbf{b})$ to compute ${\mathbf{w}}_{j1}^{\prime }={\mathbf{y}}_{i1}+h{\mathbf{y}}_{i2}+s_{i1}+h{s}_{i2}$, ${\mathbf{w}}_{j2}^{\prime }={\mathbf{y}}_{i3}+h^{\prime }{\mathbf{y}}_{i4}+s_{i1}^{★}+h^{\prime }{s}_{i2}^{★}$, $C_i^{\prime }=\mathbf{Com}({\mathbf{w}}_{j1}^{\prime }\left|\right|{\mathbf{w}}_{j2}^{\prime }\left|\right|{\mathbf{r}}_{ij})$, and $roo{t}^{\prime }=\mathbf{RecRoot}(C_i^{\prime },pat{h}_i)$. If $roo{t}_i^{\prime }=roo{t}_i$, then the output is “accept”; otherwise, the output is “reject”.

  –

  For $c_i=1$, compute the corresponding $roo{t}^{\prime }$ from $see{d}_i$ in $rsp$. If $roo{t}_i^{\prime }=roo{t}_i$, then return “accept”.

5. Security Analysis

A certificateless ring signature needs to fulfill the three basic properties: correctness, anonymity, and unforgeability. In particular, in the case of unforgeability, it needs to be proved against both an external adversary and an internal adversary, respectively. The difference between the two adversaries is shown in

Table 3. Comparison of different adversaries.

Type of Adversary	Type 1	Type 2
Replacement of public key	Yes	No
Knowing MSK	No	Yes
Attack target	Signature forgery through replacement attacks	Signature forgery with MSK
Simulated object	External adversary	Malicious KGC

. Finally, potential security problems that the scheme may encounter are described, mainly side-channel attacks and forward security problems.

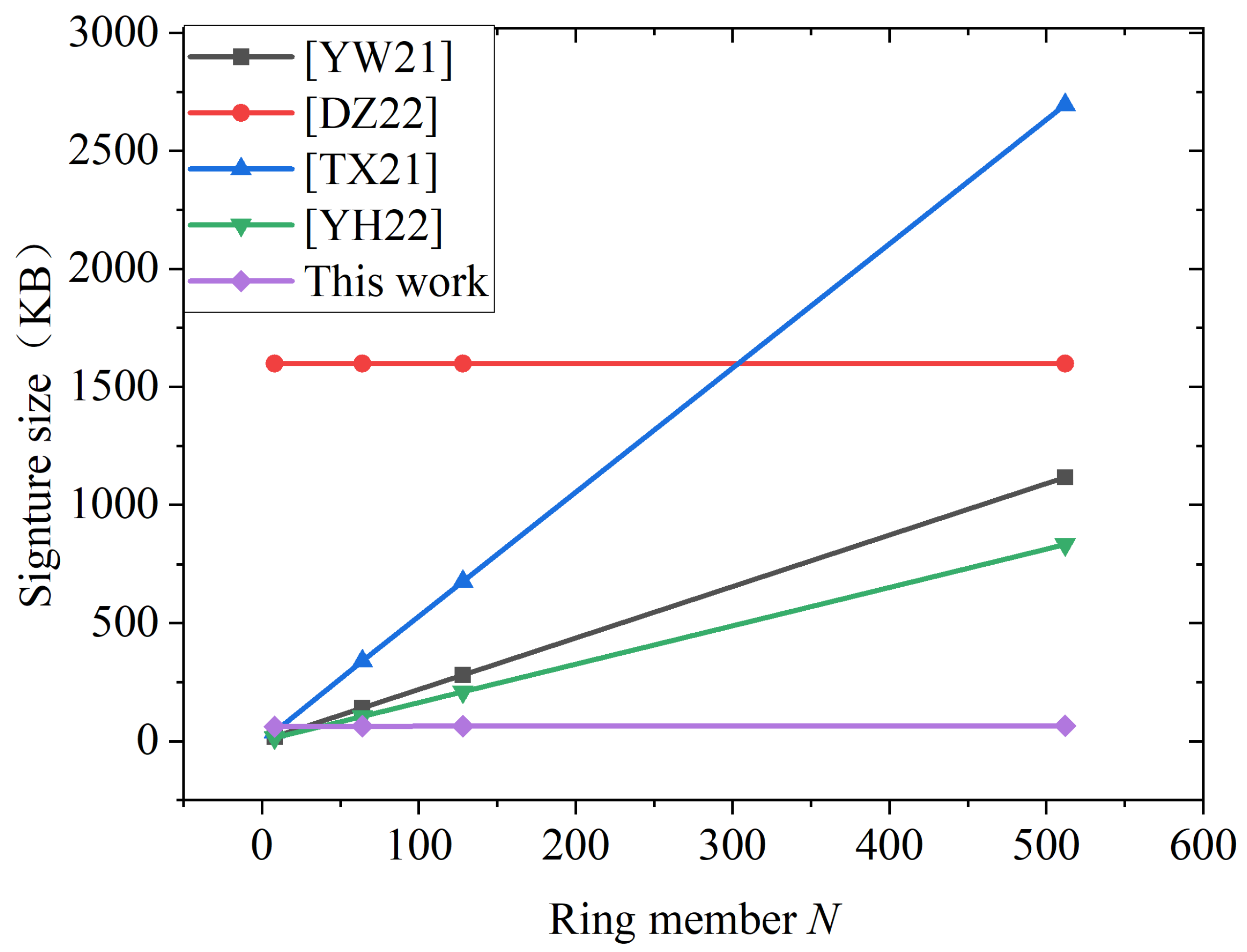
5.1. Basic Security Properties Analysis

Theorem 1.

The NTRU-CRS scheme is correct.

Proof. 

According to the signature algorithm, if the signature is valid, then

$${\mathbf{w}}_{j1}={\mathbf{y}}_{i1}+h{\mathbf{y}}_{i2}+H_0(I{D}_j)={\mathbf{y}}_{i1}+h{\mathbf{y}}_{i2}+s_{i1}+h{s}_{i2}={\mathbf{w}}_{j1}^{\prime },$$

$${\mathbf{w}}_{j2}={\mathbf{y}}_{i3}+h^{\prime }{\mathbf{y}}_{i4}+{\mathbf{p}}_{ID}={\mathbf{y}}_{i3}+h^{\prime }{\mathbf{y}}_{i4}+s_{i1}^{★}+h^{\prime }{s}_{i2}^{★}={\mathbf{w}}_{j2}^{\prime }.$$

From the above, it is clear that $C_i=C_i^{\prime }$ generated by $({\mathbf{w}}_{j1}||{\mathbf{w}}_{j2})$ and $({\mathbf{w}}_{j1}^{\prime }||{\mathbf{w}}_{j2}^{\prime })$; thus, $roo{t}_i^{\prime }=roo{t}_i$ holds. Our scheme is correct. □

Theorem 2.

Under the assumption that NTRU-SIS is hard, $H_{FS}(·)$ is collision-resistant, our scheme is anonymous in the ROM.

Proof. 

Anonymity is proved by a game between $\mathcal{A}$ and $\mathcal{C}$. The distribution of the two signatures is statistically indistinguishable for $\mathcal{A}$. Then, our scheme is anonymous.

Setup phase. The challenger $\mathcal{C}$ completes the following setup based on the inputs $\lambda$ and n along with the number of ring members N.

• Determining the ring $R=(I{D}_1,I{D}_2,\cdots ,I{D}_N)$.
• Generating the related public parameters $pp:=\{q,\beta ,s,M,K,H_0,h^{\prime }\}$ using the $\mathbf{Setup}$ algorithm, where $H_0$ is a collision-resistant hash function.
• Calling ${\mathbf{TrapGen}}_{\mathbf{NTRU}}(1^{\lambda },1^n)$ to generate the master public key MPK and secret key MSK.

The challenger $\mathcal{C}$ makes the $pp$ and MPK open, while the MSK is kept secret.

Query phase. The adversary $\mathcal{A}$ can make adaptive inquiries about the following random oracles:

• Corruption query: The adversary $\mathcal{A}$ enters the user identity $I{D}_j\in R$, then the challenger $\mathcal{C}$ computes $H_0(I{D}_j)$ and randomly chooses two small-size secrets $s_{i1}^{★},s_{i2}^{★}\in {\mathcal{R}}_q$ to compute $s_{i1}^{★}+h^{\prime }{s}_{i2}^{★}$. In addition, $\mathcal{C}$ uses $\mathbf{SamplePre}$ to compute $H_0(I{D}_j)=s_{i1}+h{s}_{i2}$, then returns $SK$ to $\mathcal{A}$ and stores $I{D}_j$ into $L_{co}$.
• $H_{FS}$ challenge oracle query: The adversary $\mathcal{A}$ first asks $\mathcal{C}$ for the challenge of $(\mu ,R,com)$, then the challenger $\mathcal{C}$ first searches the list $L_{H_{FS}}=(\mu ,R,com,chall)$ and returns it to $\mathcal{A}$ if it exists. Otherwise, $\mathcal{C}$ randomly selects a challenge value from the challenge space, returns it to $\mathcal{A}$, and stores it in $L_{H_{FS}}$.
• Signing query: The adversary $\mathcal{A}$ inquires about identity $I{D}_j$ (a message $\mu$ under ring $R\subseteq \{I{D}_1,\cdots ,I{D}_N\}$ such that $I{D}_j\in R$). If $\sigma$ exists, then the challenger $\mathcal{C}$ checks $L_{sig}=(\mu ,R,\sigma )$ to return $\sigma$; otherwise, $\mathcal{C}$ computes the corresponding private key $SK$ and calls the $H_{FS}$ challenge oracle query to generate the signature with the signing algorithm, returns $\sigma$, and stores it in $L_{sig}=(\mu ,R,\sigma )$.

Challenge phase. The adversary $\mathcal{A}$ submits a message ${\mu }^{★}$, a ring $R^{★}$, and two identities $I{D}_{j_0}^{★}$, $I{D}_{j_1}^{★}\in R^{★}$ to the challenger $\mathcal{C}$. Then, $\mathcal{C}$ randomly selects $b^{★}\in \{0,1\}$ to generate the corresponding signature ${\sigma }_{R^{\ast }}^{\ast }({\mu }^{★})=(sal{t}^{★},chal{l}^{★},rs{p}^{★})$ using the signature algorithm.

Guess phase. The adversary $\mathcal{A}$ outputs their guess of $b\in \{0,1\}$.

Analysis. For $c_i=0$, the signature is divided into three parts, where $salt$ is a random number and $chall$ is a string of 0,1 bits. Both are indistinguishable from the adversary $\mathcal{A}$ as to whether the signer is b or 1 − b. Here, ${\mathbf{r}}_{ij}$ is also a random number in $rsp$, and the remaining $\mathbf{y}$ and $\mathbf{z}$ are statistically indistinguishable under the effect of rejection sampling [33]. Finally, from $\mathbf{Lemma}\mathbf{2}.\mathbf{10}$ in [32], $path$ relies only on the distribution, and the adversary cannot obtain any information about the user’s index. For $c_i=1$, the signature is $see{d}_{internal}$ at this point, and it follows from $\mathbf{Lemma}\mathbf{2}.\mathbf{11}$ in [32] that the adversary $\mathcal{A}$ distinguishes between the $see{d}_{internal}$ generated by $\mathbf{SimulateSeeds}$ and $\mathbf{Release}$ with probability only ${\displaystyle \frac{Q}{2^{\lambda }}}$. In summary, our scheme is anonymous. □

Theorem 3.

Under the assumption that NTRU-SIS is hard, $H_0(·)$ and $H_{FS}(·)$ are CRHFs, our scheme is unforgeable in the ROM (Type 1).

Proof. 

We utilize an interactive game between ${\mathcal{A}}_1$ and $\mathcal{C}$ for the proof of unforgeability. We emphasize that unforgeability is under an adaptive chosen-message-and-identity attack (EUF-IDRS-CMIA). The adversary ${\mathcal{A}}_1$ is an external attacker who can perform a public key replacement attack. After obtaining an $NTRU-SI{S}_{q,n,2s\sqrt{2n}}$ instance related to a polynomial $h\in R_q$, the challenger $\mathcal{C}$ aims to output two non-zero small polynomials $(u,v)\in {\mathcal{R}}_q^2$ that satisfy $u+v\ast h=0modq$, $\parallel (u,v)\parallel \le 2s\sqrt{2n}$. Suppose that the adversary ${\mathcal{A}}_1$ can output a forgery with a non-negligible probability $ϵ$; then, the challenger $\mathcal{C}$ can break the NTRU-SIS problem with a non-negligible probability ${ϵ}^{\prime }$. The game is described as follows:

Setup phase. The challenger $\mathcal{C}$ first receives an instance h and runs $\mathbf{Setup}$ to generate $pp:=\{q,\beta ,s,M,K,h^{\prime }\}$, embeds h into $MPK$ as $MPK=h$, and sends $pp$ and $MPK$ to the adversary ${\mathcal{A}}_1$.

Query phase. The adversary ${\mathcal{A}}_1$ can make adaptive inquiries about the following random oracles.

• $H_0$ query: The adversary ${\mathcal{A}}_1$ inquires about identity $I{D}_j$ and the challenger $\mathcal{C}$ checks the 3-tuples list $L_{H_0}=(ID,{\mathbf{s}}_{ID},H_0(ID))$. If exists, they return $H_0(I{D}_j)$ to ${\mathcal{A}}_1$. Otherwise, $\mathcal{C}$ randomly chooses two small-size polynomials $(s_{i1},s_{i2})\in {\mathcal{R}}_q^2$ and computes $H_0(ID)=s_{i1}+h{s}_{i2}$ and $\parallel (s_{i1},s_{i2})\parallel \le s\sqrt{2n}$, returns $H_0(I{D}_j)$ to ${\mathcal{A}}_1$, and finally stores $(ID,{\mathbf{s}}_{ID},H_0(ID))$ in the list $L_{H_0}$, where ${\mathbf{s}}_{ID}=(s_{i1},s_{i2})$.
• Register query: When adversary ${\mathcal{A}}_1$ inquires about identity $I{D}_j$, the challenger $\mathcal{C}$ first checks the 3-tuples list $L_c=(ID,{\mathbf{s}}_{ID}^{\prime },{\mathbf{p}}_{ID})$. If it exists, they return $({\mathbf{p}}_{ID},ID)$; otherwise, $\mathcal{C}$ randomly chooses two small-size secret values $s_{i1}^{★},s_{i2}^{★}\in {\mathcal{R}}_q$ and computes ${\mathbf{p}}_{ID}=s_{i1}^{★}+h^{\prime }{s}_{i2}^{★}$. Finally, they store $(ID,{\mathbf{s}}_{ID}^{\prime },{\mathbf{p}}_{ID})$ and return $({\mathbf{p}}_{ID},ID)$ to the adversary ${\mathcal{A}}_1$. This query can only be made at most N times.
• Partial-Private-Key query: The adversary ${\mathcal{A}}_1$ inquires about identity $I{D}_j$ and the challenger $\mathcal{C}$ checks $L_{H_0}$ for the partial private key ${\mathbf{s}}_{ID}$. If it does not exist, they respond by calling oracle $H_0$. This query can only be made at most $q_c$ times.
• Public-Key-Replacement query: The adversary ${\mathcal{A}}_1$ provides $I{D}_j$ and a new public key ${\mathbf{p}}_{I{D}_j}^{\prime }$, then $\mathcal{C}$ searches for the public key corresponding to the $I{D}_j$ and replaces it by ${\mathbf{p}}_{I{D}_j}^{\prime }$. The challenger $\mathcal{C}$ records this replacement by adding them to $L_R=(ID,{\mathbf{p}}_{ID},{\mathbf{p}}_{ID}^{\prime })$. This query can only be made at most $N-q_c$ times.
• $H_{FS}$ query: The adversary ${\mathcal{A}}_1$ inquires about the challenge of $(\mu ,R,com)$, then $\mathcal{C}$ searches for the four-tuples list $L_{H_{FS}}=(\mu ,R,com,chall)$. If $chall$ exists, it is returned to ${\mathcal{A}}_1$. Otherwise, $\mathcal{C}$ randomly selects a challenge from the challenge space, returns it to ${\mathcal{A}}_1$, and stores it in $L_{H_{FS}}$. The query can be queried at most $q_f$ times.
• Signing query: The adversary ${\mathcal{A}}_1$ inquires about identity $I{D}_j$, a message $\mu$ under ring $R\subseteq \{I{D}_1,\cdots ,I{D}_N\}$ such that $I{D}_j\in R$. If the signature exists, then the challenger $\mathcal{C}$ checks $L_{sig}=(\mu ,R,\sigma )$ and returns it. Otherwise, $\mathcal{C}$ checks $L_c=(ID,{\mathbf{s}}_{ID}^{\prime },{\mathbf{p}}_{ID})$ and $L_{H_0}=(ID,{\mathbf{s}}_{ID},H_0(ID))$ to generate the signature with the signing algorithm, returns $\sigma$, and stores it in $L_{sig}=(\mu ,R,\sigma )$. If the corresponding private key is not found in the two lists, then the corresponding oracle is called. Note that $I{D}_j\notin L_R$.

Forgery Phase. Through a series of queries, the adversary ${\mathcal{A}}_1$ generates a valid forgery $({\mu }^{★},R^{★},{\sigma }^{★})$ about $I{D}^{★}\in R^{★}$. This forgery must be verified and must satisfy the following three conditions:

• ${\sigma }^{★}$ is a valid signature.
• The adversary ${\mathcal{A}}_1$ did not query anyone for part of the private key in $R^{★}$ and there is no public key replacement in $R^{★}$.
• The forgery ${\sigma }^{★}$ does not appear in the signing query.

Analysis. Assume that the probability that the adversary succeeds in forging a signature is $ϵ$ and that the probability of the challenger $\mathcal{C}$ solving $NTRU-SI{S}_{q,n,2s\sqrt{2n}}$ by taking advantage of adversary ${\mathcal{A}}_1$’s ability is ${ϵ}^{\prime }$.

From the forking lemma [34], it follows that two valid signatures $(\mu ,R,\sigma )$ and $({\mu }^{\prime },R^{\prime },{\sigma }^{\prime })$ are output by ${\mathcal{A}}_1$ with probability $\overline{ϵ}=ϵ·({\displaystyle \frac{ϵ}{q}}-2^{-M})$, where $R=R^{\prime },\mu ={\mu }^{\prime },com=co{m}^{\prime }$ but $chall\ne chal{l}^{\prime }$. Because ${\mathbf{y}}_i$ is a random number, we have

$${\mathbf{w}}_{j1}-{\mathbf{w}}_{j{1}^{\prime }}=s_{i1}-s_{i{1}^{\prime }}+h(s_{i2}-s_{i{2}^{\prime }})=0.$$

The case for ${\mathbf{w}}_{j2}$ and ${\mathbf{w}}_{j2}^{\prime }$ is similar. In addition, $rsp$ can be extracted only when all $chall$ are 0 with probability $(1-{(3/4)}^M)$. Because $\parallel ({\mathbf{s}}_{ID},{\mathbf{s}}_{I{D}^{\prime }})\parallel \le 2s\sqrt{2n}$, the challenger $\mathcal{C}$ solves the $NTRU-SI{S}_{q,n,2s\sqrt{2n}}$ problem with a probability of

$${ϵ}^{\prime }\ge \overline{ϵ}·(1-{(3/4)}^M)=ϵ·({\displaystyle \frac{ϵ}{q_f}}-2^{-M})·(1-{(3/4)}^M).$$

If $ϵ$ is non-negligible, then ${ϵ}^{\prime }$ is non-negligible. However, $NTRU-SI{S}_{q,n,2s\sqrt{2n}}$ is hard, which contradicts this. Thus, our scheme is unforgeable for adversary ${\mathcal{A}}_1$. □

Theorem 4.

Under the assumption that NTRU-SIS is hard, $H_0(·)$ and $H_{FS}(·)$ are CRHFs, our scheme is unforgeable in the ROM (Type 2).

Proof. 

Here, adversary ${\mathcal{A}}_2$ is an internal attacker that has the MSK and can compute a part of any user’s private key. In general, the adversary here simulates a malicious KGC. Similar to the above, the challenger $\mathcal{C}$ finds a set of polynomials $(u,v)\in {\mathcal{R}}_q^2$ that satisfies $u+v\ast h=0modq$ to break NTRU-SIS with probability ${ϵ}^{\prime }$ by utilizing an adversary ${\mathcal{A}}_2$ that can output a forgery with probability $ϵ$. The game is as follows:

Setup phase. Suppose that the challenger $\mathcal{C}$ receives an NTRU-SIS instance related to $h^{\prime }$, runs Setup and $\mathbf{TrapGen}$ to generate $pp:=\{q,\beta ,s,M,K\}$ and $(MSK,MPK)$, then sends $pp$ and $MSK$ to the adversary.

Query phase. The adversary ${\mathcal{A}}_2$ can make adaptive inquiries about the following random oracles.

• $H_0$ query: The adversary ${\mathcal{A}}_2$ inquires about identity $I{D}_j$, then the challenger $\mathcal{C}$ checks the 3-tuples list $L_{H_0}=(ID,{\mathbf{s}}_{ID},H_0(ID))$. If it exists, they return $H_0(I{D}_j)$ to ${\mathcal{A}}_2$; otherwise, $\mathcal{C}$ uses $\mathbf{SamplePre}$ to generate ${\mathbf{s}}_{ID}$, stores $(ID,{\mathbf{s}}_{ID},H_0(ID))$, and returns $H_0(ID)$.
• Register query: The adversary ${\mathcal{A}}_2$ inquires about identity $I{D}_j$ and the challenger $\mathcal{C}$ checks the 3-tuples list $L_c=(ID,{\mathbf{s}}_{ID}^{\prime },{\mathbf{p}}_{ID})$. If it exists, they return $({\mathbf{p}}_{ID},ID)$; otherwise, $\mathcal{C}$ randomly chooses two small-size secret values $s_{i1}^{★},s_{i2}^{★}\in {\mathcal{R}}_q$ and computes $s_{i1}^{★}+h^{\prime }{s}_{i2}^{★}$, then stores $(ID,{\mathbf{s}}_{ID}^{\prime },{\mathbf{p}}_{ID})$ and returns $({\mathbf{p}}_{ID},ID)$ to the adversary ${\mathcal{A}}_2$.
• Partial-Private-Key query: The adversary ${\mathcal{A}}_2$ can use the master private key to compute anyone’s partial private key.
• Public-Key-Replacement query: This is the same query as adversary ${\mathcal{A}}_1$.
• $H_{FS}$ query: The adversary ${\mathcal{A}}_2$ asks for a challenge about $(\mu ,R,com)$, then $\mathcal{C}$ searches list $L_{H_{FS}}=(\mu ,R,com,chall)$ and returns $Chall$ if it exists. Otherwise, $\mathcal{C}$ randomly selects a challenge from the challenge space and stores it in list $L_{H_{FS}}$ while returning it to ${\mathcal{A}}_2$. The query can be queried at most $q_f$ times.
• Signing query: The same query as adversary ${\mathcal{A}}_1$.

Forgery Phase. Eventually, the adversary ${\mathcal{A}}_2$ outputs a forgery $({\mu }^{★},R^{★},{\sigma }^{★})$ about $I{D}^{★}\in R^{★}$, which must satisfy the following:

• ${\sigma }^{★}$ is a valid signature.
• The adversary ${\mathcal{A}}_2$ cannot ask for anyone’s secret value in $R^{★}$.
• The adversary ${\mathcal{A}}_2$ cannot replace users’ public keys in $R^{★}$.
• The forgery ${\sigma }^{★}$ does not appear in the signing query.

Analysis. For the adversary ${\mathcal{A}}_2$, consistent with the analysis for adversary ${\mathcal{A}}_1$, the forging is still based on the forking lemma. We have

$${\mathbf{w}}_{j2}-{\mathbf{w}}_{j{2}^{\prime }}=s_{i1}^{★}-s_{i{1}^{\prime }}^{★}+h^{\prime }(s_{i2}^{★}-s_{i{2}^{\prime }}^{★})=0.$$

Meanwhile, the probability of the challenger $\mathcal{C}$ solving the NTRU-SIS problem is

$${ϵ}^{\prime }\ge \overline{ϵ}·(1-{(3/4)}^M)=ϵ·({\displaystyle \frac{1}{q_f}}-2^{-M})·(1-{(3/4)}^M).$$

If $ϵ$ is non-negligible, then ${ϵ}^{\prime }$ is non-negligible. However, $NTRU-SI{S}_{q,n,2s\sqrt{2n}}$ is hard, which contradicts this. Thus, our scheme is unforgeable for adversary ${\mathcal{A}}_2$. □

5.2. Potential Security Threats

1. Regarding side-channel attacks, the security of NTRU-CRS is based on the hardness of NTRU-SIS. If a side-channel attack could extract private keys, then this attack could then be leveraged to construct a corresponding algorithm that solves the NTRU-SIS problem. This directly contradicts the assumed hardness of NTRU-SIS, thereby demonstrating the scheme’s inherent resistance to such attacks.

• The use of temporary random numbers (e.g., $salt,see{d}_{root}$) and dynamically generated commitments (via Merkle and seed trees) during the signature process reduces the direct exposure of long-term keys. Even if some of the random numbers are captured by the side-channel, it is difficult for an adversary to reuse the leaked information to forge historical or future signatures due to the independence of the random parameters for each signature.
• When generating signature responses (e.g., ${\mathbf{z}}_{i1},{\mathbf{z}}_{i2}$), the use of rejection sampling ensures that the output distribution is indistinguishable from the random noise statistic, reducing the possibility of recovering the private key through side-channel analysis.

2. Regarding forward security, the security reduction of NTRU-SIS to the shortest vector problem (SVP) on lattices ensures that even adversaries equipped with quantum computing capabilities cannot efficiently break the forward security, as solving the SVP under quantum algorithms remains computationally infeasible. In addition to this, the tools in the scheme can also address forward security problems.

• During the signature process, independent random numbers (e.g., $salt,see{d}_{root}$) are generated each time, and these parameters are bound to the message and ring members to ensure the uniqueness of each signature. Even if the long-term private key is compromised, an adversary cannot reconstruct the random numbers required for historical signatures.
• The Merkle tree generates $com$ and $path$, which ensure that each signed commitment is independent and untamperable. Even if an attacker obtains part of the private key, it cannot forge the historical commitments.
• The random numbers generated by the seed tree ensure that the random numbers in each signature phase are independent. Even if some of the seeds are compromised, the unexposed seeds remain safe, thereby protecting historical signatures.

6. Efficiency and Comparison

We have selected five similar works for comparison. Among these five works, refs. [35,36] and use identity-based signatures, while [16,17,18] use certificateless ring signatures. For a better multidimensional comparison, we compare them in terms of private keys, signature sizes, types of signature sizes, signature cryptosystems, and hardness assumptions. As shown in

Table 4. Comparison of schemes.

Schemes	SK	Sig	Growth	Certificateless	Assumptions
[35]	$nlogq$	$(2N+1)nlogq$	linear	No	NTRU-SIS
[18]	$mklogq$	$(2+n)mlogq$	constant	Yes	SIS
[16]	$mnlogq$	$(Nm+n)logq$	linear	Yes	SIS
[36]	$4nlogq$	$(2N+1)nlogq$	linear	No	NTRU-SIS
[17]	$2nlogq$	$(2N+1)nlogq$	linear	Yes	R-SIS
This work	$2nlogq$	$M+(M+2)\lambda +K(2nlogq+2\lambda logN)$	logarithmic	Yes	NTRU-SIS

, SK and Sig are private key and signature sizes. Most of the related works are linear-size signatures, except for [18]. In terms of hardness assumptions, there are more NTRU-SIS schemes.

For a more intuitive comparison, we summarize the parameters in the different references in

Table 5. Parameters.

Scheme	n	q
[35]	256	$2^{32}$
[18]	125	7377
[36]	256	$2^{32}$
[17]	256	$2^{26}$
This work	256	≈$2^{23}$

, where we add the parameters. In [18], $m=8030$, while in our scheme $M=1749$, $K=16$, and $\lambda =168$. In order to better compare the communication overhead and time overhead of different schemes with the same security, we refer to [35] when choosing n. According to [30], the calculated root Hermite factor is less than 1.007; thus NTRU-CRS. has a security level of at least 80 bits.

In

Table 6. Comparison of storage overhead (KB).

Scheme	Signature				Signing Key	Security Level
	$\mathbf{N}=\mathbf{8}$	$\mathbf{N}=\mathbf{64}$	$\mathbf{N}=\mathbf{128}$	$\mathbf{N}=\mathbf{512}$
[35]	18.53	140.61	280.13	1117.25	2.18	80 bits
[18]	1599.63	1599.63	1599.63	1599.63	2517.21	∖
[36]	38.71	339.27	675.91	2695.75	10.52	80 bits
[17]	13.81	104.81	208.81	832.81	1.62	∖
This work	61.08	63.05	63.71	65.02	1.43	>80 bits

, we provide the signature sizes and private key sizes for different schemes under different numbers of ring members N. Some of the data are taken from references others have been estimated. Our scheme has a large size relative to other schemes for $N=8$, while with $N=64$ it becomes the shortest among all schemes. This is because our size is only $logN$ to the number of ring members N. As the number of ring members increases by a multiple of 2, the size of our scheme increases by only 1–2 KB. In terms of private key size, ours has the smallest private key size due to the chosen parameters and the NTRU lattice.

In Figure 3, it can be seen that when N is small, there is no significant size difference in the remaining schemes except for [18]. It uses a ring signature of constant size, which is advantageous only for rings of a particular size. The remaining schemes grow in size as N increases. However, the line for our scheme is almost parallel to the x-axis, which indicates that there is no significant increase in its size. When N reaches 512, it has the best size among all the schemes.

The experimental environment consisted of a Windows 10 operating system environment with a 12th Gen Intel(R) Core(TM) i5-12400F @ 2.50 GHz CPU and 8.00 GB of RAM, implemented using Python 3.6.

Table 7. Comparison of operation time $(\mu$s).

Operation	Description	Operation Time
$T_H$	hash function time	50.60
$T_P$	matrix or vector addition time	1.20
$T_M$	matrix or vector multiplication time	123.4

lists the time consumption of different operations in the signature and verification algorithms. For the seed tree-related algorithms in the scheme, most involve sorting operations, and their time overhead is considered negligible. In the Merkle tree, the algorithms are solely composed of hash functions, and their computational costs are grouped into the hash function time calculations.

Table 8. Comparison of signature time (ms).

Scheme	Signature Time
	$\mathbf{N}=\mathbf{8}$	$\mathbf{N}=\mathbf{128}$	$\mathbf{N}=\mathbf{512}$	$\mathbf{N}=\mathbf{2048}$
[35]	10.36	109.04	364.53	1367.06
[36]	2.14	75.26	261.02	1012.7
This work	3.39	45.23	180.71	722.61

compares the signing time overhead of NTRU-CRS with the schemes from [35,36]. For the small ring, the signing time of NTRU-CRS is significantly shorter than that of [35] while remaining closely comparable to [36]. When the number of ring members increases to 128, NTRU-CRS achieves nearly twice the efficiency of the best comparison scheme. The computational cost of NTRU-CRS in the signing algorithm is primarily concentrated in commitment generation and Merkle tree structure.

Table 9. Comparison of verification time (ms).

Scheme	Signature Time
	$\mathbf{N}=\mathbf{8}$	$\mathbf{N}=\mathbf{128}$	$\mathbf{N}=\mathbf{512}$	$\mathbf{N}=\mathbf{2048}$
[35]	4.63	49.81	162.53	622.34
[36]	0.74	49.92	162.72	622.56
This work	6.96	49.49	185.07	623.44

compares the verification time overhead. Because NTRU-CRS calculates two values during the signing algorithm, it requires two verification steps during the validation phase. This results in verification efficiency for NTRU-CRS that is nearly identical to the other two schemes.

Figure 4 shows a graph comparing the respective signing times and verification times. Regarding signing time overhead, NTRU-CRS does not show a significant advantage when N is small; however, as N increases, our scheme gradually demonstrates superior signing efficiency. For the verification algorithm, all three compared schemes exhibit nearly identical performance. Considering the combined advantages in terms of both time and communication overhead, NTRU-CRS maintains strong efficiency while preserving security.

7. Application

In an e-voting system, anonymity and unforgeability are critically important. To ensure the fairness of voting and prevent candidates from bribing or coercing voters, it is essential to maintain the confidentiality of voters’ identities. Unforgeability is also vital to preventing collusion between voters and candidates to fabricate ballots, which could ultimately manipulate the voting outcome.

From a system feasibility perspective, NTRU-CRS exhibits a logarithmic advantage in size, enabling it to maintain low communication overhead even when N is large. In terms of time consumption, our scheme demonstrates a significant advantage in signing time, while its verification time remains comparable to similar schemes. Therefore, the proposed electronic voting system offers distinct advantages in both time and communication overhead, striking an optimal balance between efficiency and scalability.

As shown in Figure 5, the anonymous voting system based on our certificateless ring signature consists of six parts: the Registrar, Votes, Ring, Verifier, Counters, and Bulletin Board. The workflow of the system is shown below.

First, voters submit their identities (ID or mobile phone number) to the registrar. The registrar uses the IDs to generate partial private keys. In addition, the voters generate their partial private keys. When the voters cast their votes, they request their partial private keys from the registrar and transmit them securely. After obtaining the two parts of the private keys (which are combined to form the complete private key), the voters use their complete private keys to vote on behalf of the entire ring. At this point, there is no way for the counters and verifier to know who signed, only that it is the signature of a ring member. After receiving all the ballots, the verifier verifies all the votes to ensure that all votes are valid and were cast by their voters. Finally, the counters tally the results and publish them on the bulletin board.

8. Conclusions

The certificateless ring signature scheme on the NTRU lattice proposed in this paper is well-suited for anonymous e-voting systems. We provide strict security proofs under the random oracle model based on the NTRU-SIS hardness assumption, which not only guarantees the anonymity of voters but also protects against forgery of signatures by both external and internal attackers. In terms of efficiency, there is no need to manage certificates, making it more efficient and flexible. In particular, the signature size is logarithmically related to the number of ring members. When the number of ring members is small, it will be larger than the general certificateless ring signature; however, when N is large enough, the signature size grows very little, making it ideal for large voting systems.

9. Future Work

Although innovative in its efficiency, the NTRU-CRS scheme proposed in this paper still has many shortcomings in various aspects of the current rapid iteration of lattice cryptography that are waiting to be optimized by scholars.

• Construction of a blockchain-based voting system utilizing NTRU-CRS: Compared with NTRU-CRS, blockchain technology enables distributed nodes to collectively maintain voting records, thereby eliminating centralized vote-counting authorities and preventing single-point tampering or manipulation. Each voting record is packaged into blocks as transactions, with consensus mechanisms used to ensure data consistency. Considering blockchain’s technological maturity, its implementation offers greater convenience and efficiency, enabling the practical deployment of a decentralized and high-efficiency anonymous voting system.
• Enhancing the functional capabilities of NTRU-CRS: The current scheme lacks functional extensions; potential improvements could address challenges in diverse application scenarios by incorporating features such as linkability, traceability, and others to elevate its practical utility.
• Improving resistance to side-channel attacks through RAM isolation, masking techniques, etc.