RBFAC: A Redactable Blockchain Framework with Fine-Grained Access Control Based on Flexible Policy Chameleon Hash

Abstract

While blockchain’s immutability ensures data integrity, it also poses significant challenges when dealing with illegal or erroneous data that require modification. The concept of redactable blockchain has emerged, utilizing Chameleon Hash (CH) and subsequent Policy-based Chameleon Hash (PCH) for controlled data editing. However, current redactable blockchain implementations exhibit significant limitations, particularly in their inability to separate data editing from policy modification and their insufficient support for decentralized management of diverse editing operations. To address these issues, this paper initially introduces the concept of Flexible Policy Chameleon Hash (FPCH), which integrates PCH with non-interactive zero-knowledge proofs to enable enhanced policy management flexibility. Moreover, this paper proposes a Redactable Blockchain Framework with Fine-grained Access Control (RBFAC) based on FPCH. The RBFAC framework employs a hybrid cryptographic approach to separate the right of data editing from policy modification. The framework also provides essential functionalities, including editing accountability, key tracking and revocation mechanisms, and policy privacy protection. Finally, experimental evaluations demonstrate that the RBFAC framework maintains acceptable performance overhead while delivering these advanced features. The results indicate that the proposed solution addresses the limitations of existing redactable blockchain systems, offering a more flexible and secure approach to controlled data editing in blockchain environments.

1. Introduction

Blockchain technology is fundamentally transforming the landscape of data storage and financial transaction execution. Through its innovative use of block structures and consensus mechanisms, blockchain immutably stores data across distributed networks, providing unprecedented levels of transparency, decentralization, and security [1]. These transformative characteristics have propelled blockchain’s adoption across diverse domains, including financial transactions, electronic healthcare, and cross-domain data circulation. However, the immutability that underpins blockchain’s security presents significant challenges in real-world applications. The inability to modify or delete recorded data presents critical issues, particularly in scenarios involving sensitive or inappropriate information. Notably, the General Data Protection Regulation (GDPR) [2] grants people the right to data erasure, which fundamentally contradicts traditional blockchain architecture.

These critical challenges have spurred the development of redactable blockchain solutions [3], marking a paradigm shift in blockchain technology. By incorporating chameleon hash mechanisms [4], redactable blockchain enables controlled data editing through the trapdoor while maintaining the blockchain’s structural integrity. The evolution of policy-based chameleon hash (PCH) [5] further enhances this capability by introducing sophisticated access control mechanisms, ensuring that data editing is strictly regulated and is only performed by authorized entities under predefined conditions. This advancement not only addresses regulatory compliance and security concerns but also expands blockchain’s scope to a broader range of use cases where data mutability is essential. For example, in the scenario of data storage management based on a redactable blockchain [6,7,8,9,10,11,12,13], decentralization is achieved through consensus mechanisms, thereby fully transferring data management permissions from centralized institutions to individual users.

• Our contributions: 

We propose the flexible policy chameleon hash (FPCH) to separate data editing from policy modification, which is composed of attribute-based encryption, a chameleon hash, and non-interactive zero-knowledge proofs. Unlike previous works, when users wish to modify the policies, they must submit publicly verifiable zero-knowledge proofs to demonstrate their permissions. Upon verification, the node modifies the corresponding ciphertexts. Based on the FPCH, we construct a redactable blockchain framework with fine-grained access control (RBFAC) to achieve granular data access management within the context of policy privacy protection. An RBFAC uses symmetric encryption to decouple data from readability policy and provides permission management for data readability, editability, and policy modification. According to the data owner’s three types of access policies, users are classified into three types of identities: readers, editors, and advanced editors. Readers are allowed to read the data, editors have both read and editing permissions, and advanced editors, in addition to having editor permissions, can modify the data’s readability and editability policies.

To manage editing permissions in a decentralized manner, we introduce a token committee based on a dynamic threshold signature (DTS) [14], which reviews user editing requests. Based on the user’s reputation, the committee grants editing tokens with various levels (determining whether the access policies are modified), granularities, and times, thus enabling diversified and controlled editing. Furthermore, since the members of the token committee can change dynamically based on the DTS, the decentralization of editing management is preserved. Additionally, we instantiate our solution based on TR-AP-CPABE [15], improving the ability to trace and revoke violating users while protecting privacy information of access policies.

The main contributions of this work are as follows:

(1)

We introduce the concept of flexible policy chameleon hash. Only the users whose attributes satisfy the policy of modification rule can manage the editability rights and generate valid proofs, while other users whose attributes satisfy the policy of data editability can just edit the data.

(2)

We propose a new redactable blockchain framework with fine-grained access control based on flexible policy chameleon hash, which provides essential functionalities, including editing accountability, leaked key tracing and revocation mechanisms, and policy privacy protection.

(3)

We present the security analysis and formal proofs of the RBFAC. We also provide the instantiation. Experimental evaluations demonstrate that the RBFAC framework maintains acceptable performance overhead while delivering advanced features compared to related work.

• Organization: The rest of the paper is organized as follows. Section 2 reviews related work. Section 3 introduces the necessary preliminaries. Section 4 defines FPCH and its security model. Section 5 describes the RBFAC system model in detail, with its instantiation presented in Section 6. Section 7 discusses the security analysis and proofs of RBFAC, while Section 8 evaluates its performance. Finally, Section 9 provides the conclusion.

2. Related Work

Since Ateniese et al. [3] initially proposed a redactable blockchain solution utilizing chameleon hash, significant advancements have been made in improving redactable blockchain systems. Subsequent research has focused on three primary directions: (1) developing diverse controlled editing mechanisms, (2) enhancing the flexibility of editing operations, and (3) achieving more decentralized editing management to accommodate various application scenarios.

In the domain of controlled editing mechanisms, Xu et al. [16] proposed an innovative editing protocol combining a chameleon hash with a digital signature, incorporating an editing frequency limitation and a collateral mechanism to deter malicious modifications. Chen et al. [17] addressed the challenges of varying granularities and potential editing conflicts through their diversified editing and cross-auditing solution. Shen et al. [18] advanced the field by developing an editing protocol utilizing the double trapdoor chameleon hash family supporting comprehensive editing operations. The pursuit of decentralized editing led to the development of decentralized chameleon hash schemes [19,20], enabling collaborative editing among multiple participants. Most recently, Duan et al. [21] introduced a t-times chameleon hash (t-CH) and signature (t-CS) scheme, providing both editing limitations and transparency setting.

The integration of cryptographic techniques with the chameleon hash has yielded significant progress in policy-based editing. Derler et al. [5] pioneered this direction by combining a chameleon hash with ciphertext-policy attribute-based encryption (CP-ABE) to construct a policy-based chameleon hash (PCH) and design a transaction-level editing protocol. This foundation was further developed through traceable PCH schemes [22,23], enabling authoritative institutions to monitor editing operations, and revocable PCH schemes [24,25], allowing key revocation capabilities. Ma et al. [26] enhanced decentralization through multi-authority attribute-based encryption (MA-ABE), supporting multiple authorities for trapdoor management. Zhang et al. [27] achieved significant milestones in backward-compatible readability and editability governance with linear user revocation overhead through innovative techniques like Newton interpolation-based secret sharing. The field’s latest advancement is from Tian et al. [28], who introduced an accountable blockchain with fine-grained rewriting for permissionless setting leveraging of dynamic proactive secret sharing (DPSS).

In the realm of consensus-based editing, Deuber et al. [29] introduced a novel permissionless blockchain editing protocol that relies on consensus voting. Li et al. [30] improved editing efficiency by decoupling the voting phase from the consensus layer, enabling immediate editing capabilities. The most recent development in this area is from Wang et al. [31], who introduced a decentralized trapdoor verifiable delay function (DTVDF) editing protocol, requiring threshold node consensus for block editing operations.

These collective advancements demonstrate the field’s progression from basic editing capabilities to sophisticated, policy-driven, and decentralized editing mechanisms, addressing various challenges in redactable blockchain systems. However, current redactable blockchain solutions present significant limitations in two fundamental aspects: the tight coupling between data editing and policy modification and the centralization of diversified and controlled editing.

Table 1. Detailed summary of the current related work.

	[27]	[17]	[21]	[16]	[23]	[24]	[25]	[26]	[28]
Readability Management	✓	×	×	×	×	×	×	×	×
Editability Management	✓	✓	×	✓	✓	✓	✓	✓	✓
Access Policy Editing	×	×	×	×	×	×	×	×	×
Policy Protection	✓	×	×	×	×	×	×	×	×
Diversified Editing	×	✓	×	×	×	×	×	×	×
Decentralized Editing	×	×	✓	×	×	×	×	✓	✓
Controllability	×	✓	✓	✓	×	×	×	×	×
Accountability	×	✓	✓	✓	✓	×	×	✓	✓
Traceability	×	✓	×	×	✓	×	×	×	✓
User Revocation	✓	×	×	×	×	✓	✓	×	×

Readability Management: Supports data owners in managing the readability of message. Editability Management: Supports data owners in managing the editability of message. Access Policy Editing: Supports data owners in managing the editability of access policies. Policy Protection: Protects the privacy of access policies associated with ciphertexts. Diversified Editing: Supports both block-level and transaction-level editing. Decentralized Editing: Grants editing permissions in a decentralized manner. Controllability: Limits the times that the same content can be edited. Accountability: Identifies the users responsible for specific edited transactions. Traceability: Efficiently traces the users associated with leaked keys. User Revocation: Supports the revocation of users’ attribute keys.

provides a detailed summary of the current related work.

On the one hand, they inadequately address the crucial separation between data editing and policy management during the editing process. This oversight permits users to modify the policies embedded within trapdoor ciphertexts despite practical scenarios where data editing permissions should not inherently grant policy modification rights. This becomes particularly problematic in data ownership governance frameworks that involve readability management and policy privacy protection [27,32,33], where authorized data editors must be restricted from modifying readability policy. However, when the policy privacy protection mechanism hides the readability policy within ciphertexts, existing systems are almost unable to differentiate between data editing and policy modification attempts. These limitations underscore the necessity for innovative solutions that support more flexible and fine-grained editing operations capable of addressing the diverse requirements of real-world applications.

On the other hand, existing approaches fall short of enabling simultaneously diversified and controlled editing within a decentralized framework. Transaction-level redactable blockchains face significant efficiency challenges, as editing multiple transactions requires decrypting each trapdoor ciphertext individually, resulting in substantial computational overhead. Diversified editing granularity is required to meet practical requirements. While Chen et al. [17] attempted to address granularity issues through a privileged token service, their solution compromises the fundamental principle of blockchain decentralization. Furthermore, current chameleon hash (CH)-based implementations lack essential controls over editing frequency, potentially allowing excessive modifications that could jeopardize transaction credibility. Although Duan et al. [21] introduced a t-times chameleon hash (t-CH) and signature (t-CS) scheme to limit editing frequency, their approach lacks fine-grained access control sophistication. Additionally, it cannot dynamically adjust editing permissions based on temporal or environmental factors. These limitations highlight the urgent need for a more robust and flexible framework that maintains decentralization while supporting diversified and controlled editing operations.

3. Preliminaries

In this section, we present the complexity assumptions and the fundamental components of the proposed framework.

3.1. Complexity Assumptions

Definition 1

(DL Assumption). The Discrete Logarithm (DL) assumption is defined as follows: let G be a multiplicative cyclic group of a prime order p, with g as its generator. Choose x randomly from ${\mathbb{Z}}_p$, and given $(g,g^x)$, if no polynomial-time algorithm can compute x with a non-negligible advantage, the DL assumption is satisfied.

The DL assumption will be utilized in the construction of the chameleon hash, digital signature, and non-interactive zero-knowledge proofs.

3.2. Traceable and Revocable Ciphertext Policy Attribute-Based Encryption Based on Privacy Protection

Definition 2

(TR-AP-CPABE).

Formally, the TR-AP-CPABE [15] scheme includes seven polynomial-time algorithms:

• Setup($\lambda$, $T_u$) $\to (PP,msk)$: Given a security parameter $\lambda$ and a user tree $T_u$, output the public parameters $PP$ and the master secret key $msk$.
• KeyGen($msk$, u, $\delta$) $\to s{k}_{\delta }$: Given the master secret key $msk$, user identity u, and attribute set $\delta$, output the attribute key $s{k}_{\delta }$.
• Encrypt(m, $\Lambda$, R) $\to C_m$: Given message m, policy $\Lambda$, and revocation list R, output the ciphertext $C_m$ for message m.
• Decrypt$(s{k}_{\delta },C_m)\to m$: Given the attribute key $s{k}_{\delta }$ and ciphertext $C_m$, decrypt and recover the message m.
• KeySanityCheck$(s{k}_{\delta })\to d$: Given the user’s attribute key $s{k}_{\delta }$, check if the user requires tracking and output a bit $d\in \{0,1\}$.
• Trace$(R,s{k}_{\delta })\to$$R^{\prime }$: If the attribute key $s{k}_{\delta }$ fails the $KeySanityCheck$, output the new revocation list $R^{\prime }$.
• Update$(C_m,R^{\prime },X)\to$$C_m^{\prime }$: Given the ciphertext $C_m$, revocation list $R^{\prime }$, and update parameter X, output the updated ciphertext $C_m^{\prime }$.

The security of the TR-AP-CPABE scheme relies on the q-Bilinear Diffie–Hellman Exponent (q-BDHE) assumption [34] and the ℓ-Strong Diffie–Hellman (ℓ-SDH) assumption [35] (a detailed security analysis can be found in [15]).

3.3. Chameleon Hash

In comparison to a collision-resistant hash, a chameleon hash [4] allows specific users possessing the trapdoor to efficiently compute a collision.

Definition 3

(Chameleon Hash).

• Setup($\lambda$) $\to PP$: Given a security parameter $\lambda$, output the public parameters $PP$.
• KeyGen($PP$) $\to (T,t)$: Output the trapdoor pair $(T,t)$.
• Hash(T, m) $\to (h,r)$: Given the parameter T and message m, output the hash pair $(h,r)$.
• Verify(T, m, h, r) $\to d$: Given the parameter T, message m, and hash pair $(h,r)$, output a bit $d\in \{0,1\}$.
• Adapt(t, m, $m^{\prime }$, h, r) →$r^{\prime }$: Given the trapdoor t, message m and $m^{\prime }$, and hash pair $(h,r)$, output new hash pair $(h,r^{\prime })$.

3.4. Dynamic Threshold Signature

The dynamic threshold signature [36] enables any t signers among n participants to collaboratively produce a valid signature for a given message m while it supports dynamic changes in participants.

Definition 4

(Dynamic Threshold Signature).

• Setup($\lambda$) $\to PP$: Given a security parameter $\lambda$, output the public parameters $PP$.
• KeyGen($PP$) $\to (pk,s{k}_1,\dots ,s{k}_n)$: Output the public key $pk$ and key shares $s{k}_1,\dots ,s{k}_n$.
• Sign(${s{k}_i}_{<i=1,\dots ,t>}$, m) →$\sigma$: Given the key shares $s{k}_i$ and message m, output the signature $\sigma$, where $i\in [n]$.
• Verify($pk$, m, $\sigma$) $\to d$: Given the public key $pk$, message m, and signature $\sigma$, output a bit $d\in \{0,1\}$.
• Reshare(${s{k}_i}_{<i=1,\dots ,t>}$) →$(s{k}_1^{\prime },\dots ,s{k}_n^{\prime })$: Given the key shares $s{k}_i$ for $i=1,\dots ,t$, output new key shares $s{k}_1^{\prime },\dots ,s{k}_n^{\prime }$.

4. Flexible Policy Chameleon Hash

We give the definition of the flexible policy chameleon hash (FPCH), which supports data owners in managing message editability and policy modification. Only authorized editors can edit the message, and only authorized advanced editors can generate a valid proof and modify the editability policy (when data owners need to manage message readability, advanced editors can also modify the readability policy).

4.1. Definition

The FPCH scheme is constructed from attribute-based encryption (ABE), a chameleon hash (CH), and non-interactive zero-knowledge proofs (NIZK). It includes six algorithms: $\{\mathtt{Setup},\mathtt{KeyGen},\mathtt{Hash},\mathtt{Verify},\mathtt{AdaptM},\mathtt{AdaptP}\}$:

• Setup($\lambda$) → ($PP$, $msk$): Given a security parameter $\lambda$, output the public parameters $PP$ and the system master secret key $msk$.
• KeyGen($msk$, $\delta$) →$s{k}_{\delta }$: Given the master secret key $msk$ and the attribute set $\delta \in S$, output attribute key $s{k}_{\delta }$.
• Hash($\Lambda$, m, k) → (h, r, W): Given the access policy $\Lambda$, message $m\in M$, and proof value $k\in {\mathbb{Z}}_p$, output hash pair $(h,r)$ and a proof W. The access policy $\Lambda$ includes both message editability and policy modification rules.
• Verify(m, h, r, W) → d: Given the message m, hash pair $(h,r)$, and proof W, output a bit $d\in \{0,1\}$.
• AdaptM($s{k}_{\delta }$, m, $m^{\prime }$, h, r) → $r^{\prime }$: Given the attribute key $s{k}_{\delta }$, messages m and $m^{\prime }$, and hash pair $(h,r)$, output new hash pair $(h,r^{\prime })$.
• AdaptP($s{k}_{\delta }$, $\Lambda$, h) → (${\Lambda }^{\prime }$, $W^{\prime }$): Given the attribute key $s{k}_{\delta }$, access policy $\Lambda$, and chameleon hash h, output a new access policy ${\Lambda }^{\prime }$ and a proof $W^{\prime }$.

• Correctness: The FPCH is $correct$ if for a security parameter $\lambda$ and the attribute set $\delta \in S$, for $(PP,msk)$←Setup($\lambda$), $\delta \in \Lambda$, and $s{k}_{\delta }\leftarrow$KeyGen($msk,\delta$), we have

$$\mathtt{Verify}(m,h,r,W)=\mathtt{Verify}(m^{\prime },h,r^{\prime },W^{\prime })=1.$$

(1)

where $m\in M$, $k\in {\mathbb{Z}}_p$, (h, r, W) ← Hash($\Lambda$, m, k), $m^{\prime }\in M$, $r^{\prime }$← AdaptM($s{k}_{\delta }$, m, $m^{\prime }$, h, r), and $W^{\prime }$← AdaptP($s{k}_{\delta }$, $\Lambda$, h).

4.2. Security Model

Two fundamental security properties are considered: indistinguishability and collision resistance.

Indistinguishability: An adversary cannot differentiate whether a chameleon hash comes from the Hash or the AdaptM algorithms. We present an experiment involving an adversary $\mathcal{A}$ and a challenger $\mathcal{S}$, as shown in Figure 1. During this experiment, $\mathcal{A}$ interacts with a HashOrAdaptM oracle, ensuring that the source of the chameleon hash remains indistinguishable.

We require that $\mathtt{Verify}(m^{\prime },h_0,r_0,W_0)=\mathtt{Verify}(m^{\prime },h_1,r_1,W_1)=1$, and $\mathcal{A}$’s advantage is defined as follows:

$${\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{IND}}(\lambda )=|\mathrm{Pr}[\mathcal{S}\to 1]-1/2|.$$

(2)

Definition 5.

The FPCH scheme achieves indistinguishability if for any PPT adversary $\mathcal{A}$, ${Adv}_{\mathcal{A}}^{IND}(\lambda )$ is negligible.

Collision Resistance: An adversary cannot find a collision for the chameleon hash unless they hold attribute keys that satisfy the specific policy. We present an experiment, as shown in Figure 2, and $\mathcal{A}$’s advantage is defined as follows:

$${\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{CR}}(\lambda )=\mathrm{Pr}[\mathcal{A}\to 1].$$

(3)

Definition 6.

The FPCH scheme achieves collision resistance if for any PPT adversary $\mathcal{A}$, ${Adv}_{\mathcal{A}}^{CR}(\lambda )$ is negligible.

4.3. Instantiation

The proposed FPCH consists of three components:

(1)

$\mathrm{ABE}=(\mathtt{ABE}.\mathtt{Setup},\mathtt{ABE}.\mathtt{KeyGen},\mathtt{ABE}.\mathtt{Encrypt},\mathtt{ABE}.\mathtt{Decrypt}).$

(2)

$\mathrm{CH}=(\mathtt{CH}.\mathtt{Setup},\mathtt{CH}.\mathtt{KeyGen},\mathtt{CH}.\mathtt{Hash},\mathtt{CH}.\mathtt{Verify},\mathtt{CH}.\mathtt{Adapt}).$

(3)

$\mathrm{NIZK}=(\mathtt{NIZK}.\mathtt{Setup},\mathtt{NIZK}.\mathtt{Gen},\mathtt{NIZK}.\mathtt{Verify}).$

The implementation details of the FPCH are shown below.

• Setup($\lambda$): Input a security parameter $\lambda$; output the public parameters $PP=({mpk}_{\mathrm{ABE}},P{P}_{\mathrm{CH}})$ and the master secret key ${msk}_{\mathrm{ABE}}$, where $({msk}_{\mathrm{ABE}},{mpk}_{\mathrm{ABE}})\leftarrow \mathtt{ABE}.\mathtt{Setup}(\lambda )$, and $P{P}_{\mathrm{CH}}\leftarrow \mathtt{CH}.\mathtt{Setup}(\lambda )$.
• KeyGen(${msk}_{\mathrm{ABE}}$, $\delta$): Input the master secret key ${msk}_{\mathrm{ABE}}$ and attribute set $\delta$; output the attribute key $s{k}_{\delta }$, where $s{k}_{\delta }\leftarrow \mathtt{ABE}.\mathtt{KeyGen}({msk}_{\mathrm{ABE}},\delta )$.
• Hash($\Lambda ,m,k$): Input the access policy $\Lambda$, which includes $({\Lambda }_1,{\Lambda }_2)$, message m, and proof value k; output the hash pair $(h,r)$ and a proof W, where the trapdoor $t\leftarrow \mathtt{CH}.\mathtt{KeyGen}(P{P}_{\mathrm{CH}})$, the trapdoor ciphertext $C_t\leftarrow \mathtt{ABE}.\mathtt{Encrypt}({mpk}_{\mathrm{ABE}},t,{\Lambda }_1)$, the proof value $k\leftarrow \mathtt{NIZK}.\mathtt{Setup}(PP)$, the permission proof $W\leftarrow \mathtt{NIZK}.\mathtt{Gen}(k)$, the advanced ciphertext $C_k\leftarrow \mathtt{ABE}.\mathtt{Encrypt}({mpk}_{\mathrm{ABE}},t\Vert k,{\Lambda }_2)$, and the hash pair $(h,r)\leftarrow \mathtt{CH}.\mathtt{Hash}(m)$.
• VerifyM($m,h,r,W$): If $1\leftarrow \mathtt{CH}.\mathtt{Verify}(m,h,r)$, $1\leftarrow \mathtt{NIZK}.\mathtt{Verify}(W)$, and the output is 1; otherwise, the output is 0.
• AdaptM($s{k}_{\delta },m,m^{\prime },h,r$): Input the attribute key $s{k}_{\delta }$, messages m and $m^{\prime }$, and hash pair $(h,r)$; output new hash pair $(h,r^{\prime })$, where $t\leftarrow \mathtt{ABE}.\mathtt{Decrypt}(s{k}_{\delta },C_t)$, and $r^{\prime }\leftarrow \mathtt{CH}.\mathtt{Adapt}(t,m,m^{\prime },h,r)$.
• AdaptP($s{k}_{\delta },{\Lambda }^{\prime },h$): Input the attribute key $s{k}_{\delta }$, access policy $\Lambda$, and chameleon hash h; output a new access policy ${\Lambda }^{\prime }$ and a proof $W^{\prime }$, where $(t\Vert k)\leftarrow \mathtt{ABE}.\mathtt{Decrypt}(s{k}_{\delta },C_k)$, the new access policy ${\Lambda }^{\prime }$ includes ${\Lambda }_1^{\prime }$ and ${\Lambda }_2$, the new trapdoor ciphertext $C_t^{\prime }\leftarrow \mathtt{ABE}.\mathtt{Encrypt}({mpk}_{\mathrm{ABE}},t,{\Lambda }_1^{\prime })$, and the permission proof $W^{\prime }\leftarrow \mathtt{NIZK}.\mathtt{Gen}(k)$.

5. System Model

This section outlines the construction of the redactable blockchain framework with fine-grained access control (RBFAC) based on the previously proposed FPCH. This framework enables data owners to manage data readability, editability, and policy modification effectively while also enabling diversified controlled editing and numerous other features. We detail the participants, key definitions, and mechanisms for diversified editing management in the RBFAC.

5.1. Participants

(1)

Attribute Authority (AA)

AA oversees the publication of public parameters, retains the master secret key, generates attribute keys for users, and traces or revokes malicious users. Notably, AA does not participate in editing-related events.

(2)

Data Owners

Data owners control data readability, editability, and policy modification, as well as upload data to blockchain nodes.

(3)

Users

According to the data owner’s policies, users are classified into three types of identities: readers, editors, and advanced editors. Readers are allowed to read the data, editors have both read and editing permissions, and advanced editors, in addition to having editor permissions, can modify the data’s readability and editability policies. Note that editors and advanced editors need to request a token from the token committee in order to make edits to prevent uncontrolled modifications.

(4)

Nodes

Nodes store data from data owners and respond to user access requests. If a user satisfies the specified access policy, the following actions will occur:

(i)

Nodes allow the reader to read the data;

(ii)

If the editor holds a data token, nodes allow the editor to edit the data;

(iii)

If the advanced editor holds a policy token, nodes allow the advanced editor to edit both the data and the access policies.

When user revocation occurs, nodes update ciphertexts using the update parameter sent by AA through a secure channel.

(5)

Token Committee (TC)

The token committee reviews editing requests from users, records editing activities, and grants tokens with different levels, granularities, and times based on the reputation of the user, enabling diversified and controlled editing.

The system model is presented in Figure 3. During the first epoch, users initiate the token committee election protocol [37,38], forming a token committee. Additionally, they initialize the dynamic threshold signature protocol, ensuring that each committee member holds a share. A threshold number of members can cooperate to generate tokens. In subsequent epochs, committee members can collaboratively execute the reshare process of the threshold signature, allowing for dynamic adjustments in membership.

In the permissioned blockchain, the attribute authority (AA) serves as a trusted entity, overseeing the blockchain’s operations and generating system parameters. Users, nodes, and data owners are considered semi-honest participants, meaning they execute the protocol truthfully but may attempt to infer or exploit others’ private information. Attackers may corrupt some token committee members; however, as long as there are at least t trustworthy members, valid signature generation remains secure. Even if up to $t-1$ members are malicious, they still cannot forge valid signatures.

5.2. Definition

The formal definition of the RBFAC is presented as follows:

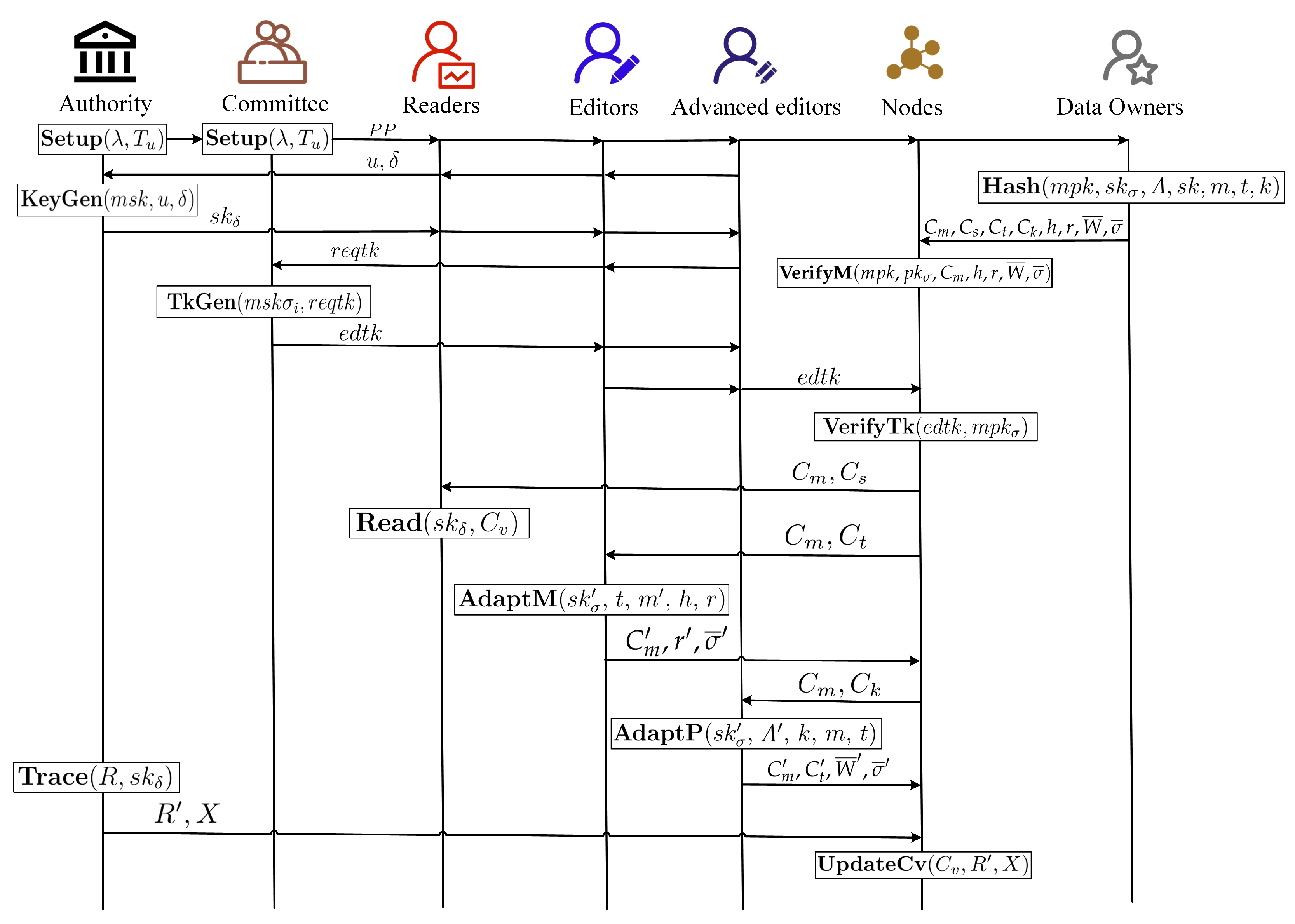
• Setup$(\lambda ,T_u)\to (msk,mpk),(ms{k}_{\sigma },mp{k}_{\sigma })$: The attribute authority (AA) and the initial token committee (TC) input a security parameter $\lambda$ and a user tree $T_u$, outputting the master key pair $(msk,mpk)$ and the signing key pair $(ms{k}_{\sigma },mp{k}_{\sigma })$. AA retains the master secret key $msk$, and TC shares $ms{k}_{\sigma }$ as key shares $ms{k}_{{\sigma }_i}$.
• KeyGen$(msk,u,\delta )\to s{k}_{\delta }$: AA inputs the master secret key $msk$, user identity u, and attribute set $\delta$, generating an attribute key $s{k}_{\delta }$, which it then sends to the user.
• Hash$(mpk,s{k}_{\sigma },\Lambda ,sk,m,t,k)\to (C_m,C_s,C_t,C_k,T,h,r,\overline{W},\overline{\sigma })$: The data owner inputs the master public key $mpk$, signing key $s{k}_{\sigma }$, access policy $\Lambda$, symmetric key $sk$, message m, trapdoor t, and proof value k, outputting message ciphertext $C_m$, readability ciphertext $C_s$, editability ciphertext $C_t$, advanced ciphertext $C_k$, chameleon hash $(T,h,r)$, proof $\overline{W}$, and signature $\overline{\sigma }$.
• VerifyM$(mpk,C_m,T,h,r,\overline{W},\overline{\sigma })\to d$: The node inputs the master public key $mpk$, message ciphertext $C_m$, chameleon hash $(T,h,r)$, proof $\overline{W}$, and signature $\overline{\sigma }$, outputting a bit $d\in \{0,1\}$.
• TkGen$(ms{k}_{{\sigma }_i},reqtk)\to edtk$: TC inputs the master signing key share $ms{k}_{{\sigma }_i}$ and a user token request $reqtk$, outputting the editing token $edtk$.
• VerifyTk$(edtk,mp{k}_{\sigma })\to d$: The node inputs the editing token $edtk$ and master signing public key $mp{k}_{\sigma }$, outputting a bit $d\in \{0,1\}$.
• Read($s{k}_{\delta },C_v$) $\to v$: The user inputs the attribute key $s{k}_{\delta }$ and ciphertext $C_v\in \{C_s,C_t,C_k\}$. If $\Lambda (\delta )=1$, it outputs the plaintext $v\subseteq \{sk,t,k\}$.
• AdaptM($s{k}_{\sigma }^{\prime }$, t, $m^{\prime }$, h, r) $\to (C_m^{\prime },r^{\prime },{\overline{\sigma }}^{\prime })$: The user inputs the signing key $s{k}_{\sigma }^{\prime }$, trapdoor t, message $m^{\prime }$, and hash pair $(h,r)$, outputting the new message ciphertext $C_m^{\prime }$, hash pair $(h,r^{\prime })$, and signature ${\overline{\sigma }}^{\prime }$.
• AdaptP($s{k}_{\sigma }^{\prime }$, ${\Lambda }^{\prime }$, k, m, t) $\to (C_m^{\prime },C_t^{\prime },{\overline{W}}^{\prime },{\overline{\sigma }}^{\prime })$: The user inputs the signing key $s{k}_{\sigma }^{\prime }$, new access policy ${\Lambda }^{\prime }$, proof value k, message m, and trapdoor t, outputting new ciphertexts $C_m^{\prime }$, $C_t^{\prime }$, proof ${\overline{W}}^{\prime }$, and signature ${\overline{\sigma }}^{\prime }$.
• Trace$(R,s{k}_{\delta })\to R^{\prime }$: AA inputs the revocation list R and attribute key $s{k}_{\delta }$, outputting new revocation list $R^{\prime }$.
• UpdateCv$(C_v,R^{\prime },X)\to C_v^{\prime }$: The node inputs ciphertext $C_v$, revocation list $R^{\prime }$, and the update parameter X, outputting the updated ciphertext $C_v^{\prime }$.

5.3. Diversified Editing Management Mechanism

(1)

Diversified Editing

As illustrated in Figure 4, the RBFAC supports the generation of both mutable transactions and mutable blocks. The mutable transaction A is generated using the FPCH function, while regular transactions (B,C,D) in Figure 4 are generated using the collision-resistant hash function H. Furthermore, the hash function used for linking blocks is also H.

(i)

Generation of Mutable Transactions: A data owner generates the chameleon hash $c{h}_{Tx}$ for transaction $T{x}_{i,1}$ by executing $\mathtt{Hash}(mpk,s{k}_{\sigma },\Lambda ,T{x}_{i,1},t,k)$ and defines an access policy $\Lambda$ to control data readability, editability, and policy modification. $T{x}_{i,1}$ typically contains the encrypted data stored by the data owner along with transaction fields, and it is used for FPCH computation. Note that elements such as nonces, ciphertexts, and signatures are stored in the non-hashed portion of the transaction.

(ii)

Tx-Level Editing: A user executes $\mathtt{AdaptM}(s{k}_{\sigma }^{\prime },t,T{x}_{i,1}^{\prime },c{h}_{Tx},r)$ to output $\langle c{h}_{Tx},{\overline{W}}^{\prime },{\overline{\sigma }}^{\prime }\rangle$. The node then verifies the editing validity by running $\mathtt{VerifyM}$.

(iii)

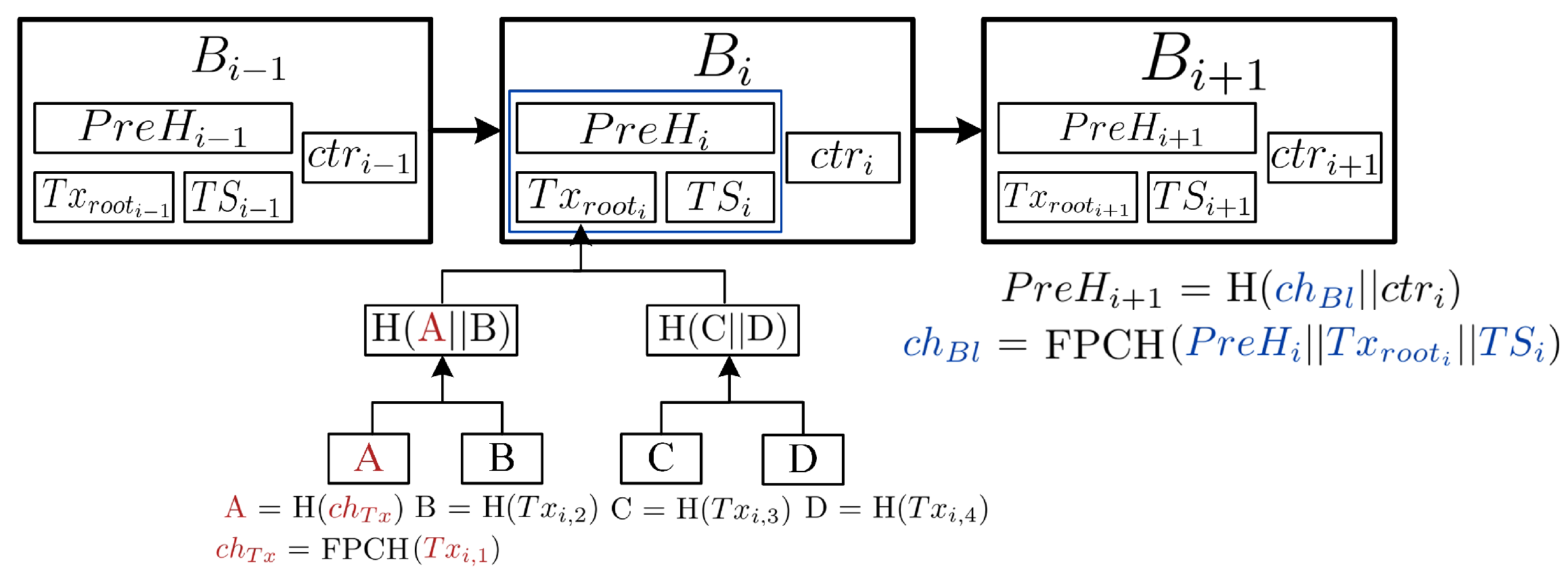
Generation of Mutable Blocks: The node first computes the Merkle root ($T{x}_{roo{t}_i}$) by applying a multi-hash algorithm to the transactions in block $B_i$, then forms $x_i=\langle Pre{H}_i,T{x}_{roo{t}_i},T{S}_i\rangle$, and finally calculates the chameleon hash $c{h}_{Bl}$ using $\mathtt{Hash}(mpk,s{k}_{\sigma },\Lambda ,x_i,t,k)$. Following the standard block-level editing protocol [3], we define the mutable parts of a block as the previous block hash $Pre{H}_i$, Merkle root $T{x}_{roo{t}_i}$, and timestamp $T{S}_i$, which are used for FPCH computation. The nonce ($ct{r}_i$) serves as the immutable component. This results in a policy-based, mutable block $B_i$. The conventional hash function H is used to compute $\mathtt{H}(c{h}_{Bl},ct{r}_i)$, serving as the $PreH$ for the next block and linking the blocks together.

(iv)

Bl-Level Editing: For Bl-level editing, a user executes $\mathtt{AdaptM}(s{k}_{\sigma }^{\prime },t,x_i^{\prime },c{h}_{Bl},r)$, which produces $\langle c{h}_{Bl},{\overline{W}}^{\prime },{\overline{\sigma }}^{\prime }\rangle$. The node verifies its validity using $\mathtt{VerifyM}$. The validity of the new block is checked using $\mathtt{ValidateBlock}(B_i^{\prime })$ by the node. Finally, to ensure the continuity of the blockchain, the condition ${PreH}_{i+1}=\mathtt{H}(c{h}_{Bl},ct{r}_i)$ must be satisfied.

(2)

Token Mechanism

We design eight types of tokens with different permission semantics to enable diversified editing management in the RBFAC system, which is categorized by editing level, granularity, and time:

(i)

Data Token (for editing data only):

• Tx-Level 1-Time/n-Times Data Token ($t1tk$/$tntk$): A user holding $t1tk$ can edit data with specific parameters only once. A user holding $tntk$ can perform up to n tx-level editings before the token expires.
• Bl-Level 1-Time/n-Times Data Token ($b1tk$/$bntk$): A user holding $b1tk$ can modify an entire block using specified parameters. A user holding $bntk$ can modify n blocks using relevant block parameters.

(ii)

Policy Token (for editing data and its access policy):

• Tx-Level 1-Time/n-Times Policy Token ($T1tk$/$Tntk$): Same as above.
• Bl-Level 1-Time/n-Times Policy Token ($B1tk$/$Bntk$): Same as above.

When a user requires editing, they send a token request $reqtk=(type|\left|u\right|\left|N\right||index)$ to the token committee (TC), where $type\in \{t1tk,tntk,b1tk,bntk,T1tk,Tntk,B1tk,Bntk\}$ represents the requested editing type, u is the user identity, n indicates the times of editing, and $index$ specifies the target indices (transactions or blocks) to be edited. The TC validates the request, assesses the user’s reputation, and it generates a signature ${\sigma }_{tc}$. It then produces the editing token $edtk=(reqtk|\left|{\sigma }_{tc}\right|\left|time\right||expire)$, where $time$ is the timestamp of token issuance, and $expire$ denotes the token’s expiration time. The editing token $edtk$ is sent to the user. The TC can automatically adjust the token validity period based on user reputation, monitor abnormal token usage in real-time, and reduce manual errors through smart contract integration. Upon detecting token leakage or potential risks, the system promptly marks the token as invalid and broadcast this status to other nodes.

5.4. Security Model

(1)

IND-CPA Security Model

The security model of RBFAC is defined as indistinguishability under a chosen-plaintext attack (IND-CPA). We present an experiment, including an adversary $\mathcal{A}$ and a challenger $\mathcal{S}$:

(i)

Init: $\mathcal{S}$ executes the Setup algorithm to generate the master key pair $(msk,mpk)$.

(ii)

Phase 1: $\mathcal{A}$ makes a series of oracle queries by selecting user u and attribute set $\delta$, requesting the corresponding attribute key $s{k}_{\delta }$ from $\mathcal{S}$. $\mathcal{S}$ executes the KeyGen algorithm to compute $s{k}_{\delta }$ and transmits it to $\mathcal{A}$.

(iii)

Challenge: $\mathcal{A}$ selects a pair of messages $M_0$ and $M_1$ for $\mathcal{S}$. $\mathcal{S}$ randomly selects $d\in \{0,1\}$, executes the Hash algorithm to compute the ciphertext $C_d$ for message $M_d$, and returns $C_d$ to $\mathcal{A}$.

(iv)

Phase 2: Phase 2 is identical to Phase 1.

(v)

Guess: $\mathcal{A}$ outputs a guess $d^{\prime }$ for d.

The advantage of $\mathcal{A}$ is defined as

$${\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{IND}\text{-}\mathrm{CPA}}(\lambda )=|\mathrm{Pr}[\mathcal{A}\to 1]-1/2|.$$

(4)

Definition 7.

The RBFAC scheme is IND-CPA-secure if for any PPT adversary $\mathcal{A}$, ${Adv}_{\mathcal{A}}^{IND\text{-}CPA}(\lambda )$ is negligible.

(2)

EUF-CMA Security Model

An adversary cannot fabricate a legitimate signature for a chameleon hash that corresponds to a specific identity. The experiment is defined in Figure 5. In this setting, we grant $\mathcal{A}$ access to the Sign oracle, enabling it to verify whether a given chameleon hash is associated with a certain identity. The set Q is utilized to store all chameleon hashes queried by $\mathcal{A}$ to the Sign oracle.

We represent an original transaction as $Tx=(h,m,r,\sigma )$ and its edited counterpart as $T{x}^{\prime }=(h,m^{\prime },r^{\prime },{\sigma }^{\prime })$, which are both linked to the chameleon hash h. Additionally, a transaction–identity association is denoted as $(T{x}^{\prime },u^{\prime })$. The advantage of $\mathcal{A}$ is defined as

$${\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{EUF}\text{-}\mathrm{CMA}}(\lambda )=Pr[\mathcal{A}\to 1].$$

(5)

Definition 8.

The RBFAC scheme is EUF-CMA-secure if for any PPT adversary $\mathcal{A}$, ${Adv}_{\mathcal{A}}^{EUF\text{-}CMA}(\lambda )$ is negligible.

6. Instantiation

In this section, we instantiate the RBFAC framework by building upon existing research. The overall system workflow is illustrated in Figure 6. First, we implement the flexible policy chameleon hash (FPCH) by combining the chameleon hash, the TR-AP-CPABE [15], and the Schnorr NIZK scheme [39]. Furthermore, we use symmetric encryption [40] to decouple data from the readability policy. This approach provides diversified access management for data owners, supports traceability and revocation of malicious users, and ensures privacy protection for access policies. Next, to establish a dynamic token committee, we adopt the SPRINT protocol [14], which provides high throughput and robustness. These properties ensure the efficient and reliable issuance of editing tokens to users. Finally, we instantiate the digital signature scheme using the Schnorr signature [41]. By leveraging its homomorphic properties concerning keys and signatures [42], we link transactions with their edited versions, enabling rapid accountability for editing operations.

Table 2. Notations table.

Notations	Descriptions
$\lambda$	security parameter
$T_u$	user tree
$(mpk,msk)$	master key pair
$ms{k}_{\sigma }=d,ms{k}_{{\sigma }_i}=d_i$	master signing secret key and shares
$mp{k}_{\sigma }=D,mp{k}_{{\sigma }_i}=D_i$	master signing public key and shares
u	user identity
$\delta$	user’s attribute set
$\Lambda$	access policies
${\Lambda }_1,{\Lambda }_2,{\Lambda }_3$	readability policy, editability policy, advanced editing policy
$sk$	data owner’s symmetric key
$s{k}_{\delta }$	user’s attribute key
m	message
$C_m$	message ciphertext
R	revocation list
$C_s,C_t,C_k$	readability ciphertext, editability ciphertext, advanced ciphertext
$(T,t)$	trapdoor pair
$(h,r)$	chameleon hash pair
$(k,Z_k)$	proof value pair
$(r_k,R_k)$	proof randomness pair
W	response
$\overline{W}=(Z_k,R_k,W)$	permission proof
$(s{k}_{\sigma },p{k}_{\sigma })$	user’s signing key pair
$(r_s,R_s)$	signature randomness pair
$(c_t,\sigma )$	message signature pair
$\overline{\sigma }=\langle p{k}_{\sigma },R_s,c_t,\sigma \rangle$	editing signature
$reqtk$	editing request
${\sigma }_{tc}$	TC’s signature
$edtk$	editing token
$C_v\in \{C_s,C_t,C_k\}$	arbitrary ciphertext
$v\subseteq \{sk,t,k\}$	plaintext set
X	ciphertext update parameter

provides an overview of the notations employed in the RBFAC.

6.1. Setup

(1)

AA Setup

The attribute authority (AA) takes a security parameter $\lambda$ and the user tree $T_u$ as input, executes TR-AP-CPABE.Setup$(\lambda ,T_u)$, and initializes the master key pair $(mpk,msk)$. Then, the AA generates attribute keys for users and revokes malicious users.

(2)

TC Setup

The members of the initial token committee (TC) collaboratively generate secret shares $\{ms{k}_{{\sigma }_i}=d_i\}$ of the master signing key $ms{k}_{\sigma }=d$. The TC then publishes the corresponding public key $mp{k}_{\sigma }=D$ ($D=g^d$) and individual public shares $\{mp{k}_{{\sigma }_i}=D_i\}$ ($D_i=g^{d_i}$). Each secret share $d_i$ corresponds to a point on a polynomial F such that $F(0)=d$. This process can be implemented using a Distributed Key Generation (DKG) protocol [43]. The TC is responsible for verifying users’ editing requests and issuing editing tokens with appropriate permissions based on the verified requests.

6.2. KeyGen

The user requests an attribute key from the AA. The AA takes as input the master secret key $msk$, the user identity u, and the attribute set $\delta$, and it executes TR-AP-CPABE.KeyGen$(msk,u,\delta )\to s{k}_{\delta }$ and sends $s{k}_{\delta }$ to the user.

6.3. Hash

The data owner formulates the data access policies $\Lambda =({\Lambda }_1,{\Lambda }_2,{\Lambda }_3)$, including the readability policy, editability policy, and advanced editing policy, and the owner executes the Hash algorithm to generate ciphertexts, signatures, and zero-knowledge proofs. The Hash algorithm consists of five steps:

(1)

Message Encryption

The data owner uses the symmetric encryption $(\mathtt{Enc},\mathtt{Dec})$ [40] to encrypt the message. Select a message m and symmetric key $sk$; then, compute ${\mathtt{Enc}}_{sk}(m)\to C_m$.

(2)

Symmetric Key Encryption

The data owner takes symmetric key $sk$, readability policy ${\Lambda }_1$, and revocation list R as input, and the owner executes TR-AP-CPABE.Encrypt$(sk,{\Lambda }_1,R)\to C_s$ to generate the ciphertext of the symmetric key $sk$. Please note that in the original encryption TR-AP-CPABE.Encrypt$(m,{\Lambda }_1,R)\to C_m$, the message m is bound to the policy ${\Lambda }_1$, and policy privacy protection prevents nodes from distinguishing between message editing and policy modification.

(3)

HashGen

The data owner randomly selects the trapdoor $t\in {\mathbb{Z}}_p$ and randomness $r\in {\mathbb{Z}}_p$; then, the owner computes

$$T=g^t,h=g^r·T^{H(C_m)},$$

(6)

and similar to Step (2), select the editability policy ${\Lambda }_2$, and encrypt the information $(sk\Vert t)$ to obtain the editability ciphertext TR-AP-CPABE.Encrypt$(sk\Vert t,{\Lambda }_2,R)\to C_t$. Only authorized editors can decrypt $C_t$ to obtain the trapdoor t. Furthermore, permissions are downward compatible, allowing authorized editors to decrypt the message ciphertext $C_m$ as well.

(4)

ProofGen

The data owner randomly selects the proof value $k\in {\mathbb{Z}}_p$ and randomness $r_k\in {\mathbb{Z}}_p$; then, the owner computes

$$Z_k=g^k,R_k=g^{r_k},W=r_k+k·H(Z_k\Vert R_k),$$

(7)

and the following proof is constructed: $\overline{W}=\langle Z_k,R_k,W\rangle$. Similar to Step (2), select the advanced editing policy ${\Lambda }_3$, and encrypt the information $(sk\Vert t\Vert k)$ to generate the advanced ciphertext TR-AP-CPABE.Encrypt$(sk\Vert t\Vert k,{\Lambda }_3,R)\to C_k$. Only authorized advanced editors can decrypt $C_k$ to obtain the proof value k. Furthermore, they can also decrypt the message ciphertext $C_m$ and edit the message.

(5)

SignatureGen

The data owner randomly selects the signing key $s{k}_{\sigma }\in {\mathbb{Z}}_p$ and randomness $r_s\in {\mathbb{Z}}_p$; then, the owner computes

$$p{k}_{\sigma }=g^{s{k}_{\sigma }},R_s=g^{r_s},\sigma =r_s+s{k}_{\sigma }·H(c_t\Vert R_s),$$

(8)

and the following signature is constructed: $\overline{\sigma }=\langle p{k}_{\sigma },R_s,c_t,\sigma \rangle$, where $c_t=g^{(s{k}_{\sigma }+t)}$ represents a message related to the trapdoor, facilitating the linking of different versions of the same transaction.

Finally, the output is as follows: $\langle C_m,C_s,C_t,C_k,T,h,r,\overline{W},\overline{\sigma }\rangle .$ The data owner uploads the ciphertexts to the node.

6.4. VerifyM

The node verifies the validity of the three tuples $\langle C_m,T,h,r\rangle$, $\langle Z_k,R_k,W\rangle$, and $\langle p{k}_{\sigma },R_s,c_t,\sigma \rangle$. If the following conditions hold as

$$h=g^r·T^{H(C_m)},g^W=R_k·Z_k^{H(Z_k\Vert R_k)},g^{\sigma }=R_s·p{k}_{\sigma }^{H(R_s\Vert c_t)},$$

(9)

the output is 1. The node stores the ciphertexts and makes consensus with other nodes.

6.5. TkGen

Users with editing needs apply for an editing token from the token committee (TC). Upon receiving a user’s editing request $reqtk=(\mathit{type}\Vert u\Vert N\Vert \mathit{index})$, the TC verifies the parameters and executes the TkGen$(d_i,reqtk)$ algorithm to generate the editing token:

$$edtk=(reqtk\Vert \mathit{expire}\Vert \mathit{time}\Vert {\sigma }_{tc}),$$

(10)

where ${\sigma }_{tc}$ is the TC’s signature, which is computed as $\mathrm{DTS}.\mathtt{Sign}(reqtk)\to {\sigma }_{tc}$. The editing token $edtk$ is subsequently sent to the user.

6.6. VerifyTk

Each node maintains a hash table $\mathcal{H}:edtk\to \langle usage\_count,state\rangle$ to record token usage states. When receiving a service request, the node performs the following validity checks and queries $\mathcal{H}$ to verify whether the specified token has been consumed. If the token is marked as used, the node immediately rejects the service request.

Given the editing token $edtk$ and the TC’s public key D, the token is considered valid if the conditions are satisfied:

(1)

$Now.time<(\mathit{time}+\mathit{expire})$.

(2)

$\mathtt{Unused}(edtk)=1$.

(3)

$u\notin R$.

(4)

$\mathrm{DTS}.\mathtt{Verify}(reqtk,D,{\sigma }_{tc})=1$.

If these conditions hold, the node processes the user’s request according to the token parameters.

Upon successfully processing a token, the node broadcasts an update message $\langle edtk,new\_state,{\sigma }_{\mathit{update}}\rangle$ to the peer-to-peer network, where ${\sigma }_{\mathit{update}}$ is a signature proving the validity of the state transition. All receiving nodes subsequently update their local hash tables $\mathcal{H}$ to maintain state consistency across the distributed system.

6.7. Read

An authorized reader applies to the node for message reading, and the node sends the ciphertexts $(C_m,C_s)$ to the reader. The reader executes TR-AP-CPABE.Decrypt$(s{k}_{\delta },C_s)\to sk$ and recovers the message ${\mathtt{Dec}}_{sk}(C_m)\to m$.

6.8. AdaptM

An authorized editor applies to the node for message editing and sends the editing token $edtk$ to the node. If $\mathtt{VerifyTk}(edtk,D)\to 1$, the node sends the ciphertexts $(C_m,C_t)$ to the editor. The editor performs the following operations:

(1)

Execute TR-AP-CPABE.Decrypt$(s{k}_{\delta },C_t)\to sk\Vert t$.

(2)

Execute ${\mathtt{Enc}}_{sk}(m^{\prime })\to C_m^{\prime }$ and compute the updated randomness $r^{\prime }=r+(H(C_m)-H(C_m^{\prime }))·t$.

(3)

Generate a new signature $R_s^{\prime }=g^{r_s^{\prime }},{\sigma }^{\prime }=r_s^{\prime }+s{k}_{\sigma }^{\prime }·H(R_s^{\prime }\Vert c_t^{\prime }),c_t^{\prime }=g^{(s{k}_{\sigma }^{\prime }+t)}$.

Output $(C_m^{\prime },r^{\prime },{\overline{\sigma }}^{\prime })$, and send it to the node. At this point, the editor has edited the message without affecting the ciphertext $C_s$ that contains the readability policy.

If $\mathtt{VerifyM}(mpk,p{k}_{\sigma }^{\prime },C_m^{\prime },h,r^{\prime },{\overline{\sigma }}^{\prime })\to 1$, the node updates the message ciphertext to $C_m^{\prime }$. Since the access policies remain unchanged, the user does not need to provide proof. Additionally, due to the homomorphic property of the Schnorr signature, the transaction and its edited version can be linked by verifying $c_t^{\prime }/c_t=p{k}_{\sigma }^{\prime }/p{k}_{\sigma }$.

6.9. AdaptP

An authorized advanced editor sends the policy token $edtk$ to the node. If $\mathtt{VerifyTk}(edtk,D)\to 1$, the node sends the ciphertexts $(C_m,C_k)$ to the advanced editor. The advanced editor performs the following operations:

(1)

Execute TR-AP-CPABE.Decrypt$(s{k}_{\delta },C_k)\to sk\Vert t\Vert k$.

(2)

Execute TR-AP-CPABE.Encrypt$(sk,{\Lambda }_1,R)\to C_s^{\prime }$ based on the new readability policy ${\Lambda }_1^{\prime }$.

(3)

Execute TR-AP-CPABE.Encrypt$(sk\Vert t,{\Lambda }_2,R)\to C_t^{\prime }$ based on the new editability policy ${\Lambda }_2^{\prime }$.

(4)

Select randomness ${r_k}^{\prime }\in {\mathbb{Z}}_p$ and compute $R_k^{\prime }=g^{{r_k}^{\prime }}$, $W^{\prime }={r_k}^{\prime }+k·H(Z_k\Vert R_k^{\prime })$; construct the new proof ${\overline{W}}^{\prime }=\langle Z_k,R_k^{\prime },W^{\prime }\rangle$.

(5)

Generate a new signature $R_s^{\prime }=g^{r_s^{\prime }},{\sigma }^{\prime }=r_s^{\prime }+s{k}_{\sigma }^{\prime }·H(R_s^{\prime }\Vert c_t^{\prime }),c_t^{\prime }=g^{(s{k}_{\sigma }^{\prime }+t)}.$

Output $(C_s^{\prime },C_t^{\prime },{\overline{W}}^{\prime },{\overline{\sigma }}^{\prime })$, and send it to the node.

If $\mathtt{VerifyM}(mpk,p{k}_{\sigma }^{\prime },{\overline{W}}^{\prime },h,r^{\prime },{\overline{\sigma }}^{\prime })\to 1$, the node updates the readability ciphertext to $C_s^{\prime }$ and the editability ciphertext to $C_t^{\prime }$. Furthermore, to mitigate potential malicious activities by revoked users who possess the symmetric key $sk$, advanced editors (with privileged permissions) can periodically update the ciphertexts by replacing $sk$ with a fresh key $s{k}^{\prime }$.

6.10. Trace

The AA takes the revocation list R and the attribute key $s{k}_{\delta }$ as input, and it executes TR-AP-CPABE.Trace$(R,s{k}_{\delta })\to R^{\prime }$.

6.11. UpdateCv

The AA transmits the update parameter X to the node. The node takes an arbitrary ciphertext $C_v$, the revocation list $R^{\prime }$, and the update parameter X as input, and it executes TR-AP-CPABE.Update$(C_v,R^{\prime },X)\to C_v^{\prime }$.

The scheme achieves indirect revocation of malicious users through the Trace algorithm and UpdateCv algorithm. The specific implementation details can be found in [15].

7. Security Proof

Theorem 1.

The FPCH achieves indistinguishability provided that the ABE scheme is semantically secure and the CH scheme is indistinguishable.

Proof. 

We introduce the following games denoted as $G_i$ for $i=0,1,\dots ,3$, and we define ${\mathrm{Adv}}_i^{\mathrm{FPCH}}$ as the adversary $\mathcal{A}$’s advantage in game $G_i$. Suppose that $\mathcal{A}$ makes no more than $n(\lambda )$ Hash queries within each game. We then define the following:

• $G_0$: This represents the initial game for indistinguishability.
• $G_1$: This game modifies $G_0$ as follows: The simulator $\mathcal{S}$ selects an index guess g from the range $[1,n(\lambda )]$ for the HashOrAdaptM query. If the adversary $\mathcal{A}$ does not issue an attack query at the g-th attempt, $\mathcal{S}$ returns a random bit and halts the game. Thus, we obtain the following:

  $${\mathrm{Adv}}_0^{\mathrm{FPCH}}\le n(\lambda )·{\mathrm{Adv}}_1^{\mathrm{FPCH}}.$$

  (11)
• $G_2$: This game modifies $G_1$ as follows: During the g-th query, $\mathcal{S}$ substitutes the trapdoor t with ⊥ in $C_t^{\ast }$. We demonstrate that, assuming the ABE scheme is semantically secure, the advantage difference between $G_1$ and $G_2$ remains negligible.
  Consider $\mathcal{S}$ targeting the semantic security of the ABE. Given the master public key $mp{k}^{\ast }$, along with access to KeyGen and Encrypt oracles, $\mathcal{S}$ attempts to differentiate the ciphertexts of $M_0$ and $M_1$ encrypted under a designated access policy $\Lambda$. The game simulation for $\mathcal{A}$ proceeds as follows:

  -

  $\mathcal{S}$ assigns $mpk=mp{k}^{\ast }$ and faithfully executes the rest of the Setup procedure.

  -

  Using the provided oracles, $\mathcal{S}$ honestly answers any KeyGen and Encrypt queries from $\mathcal{A}$. During the g-th query, $\mathcal{S}$ provides the pair of messages $(t,\perp )$ to the ABE and receives the challenge ciphertext $C_t^{\ast }$. Then, $\mathcal{S}$ returns $(C_m^{\ast },h^{\ast },r^{\ast },T^{\ast },C_t^{\ast })$ to $\mathcal{A}$, where $h^{\ast }=g^{r^{\ast }}·{T^{\ast }}^{C_m^{\ast }}$, and $T^{\ast }=g^t$. $\mathcal{S}$ can also use the trapdoor t to successfully simulate adaptM queries.

  If $C_t^{\ast }$ encrypts t, the simulation follows $G_1$; otherwise, it follows $G_2$. Thus, if there is a significant difference in the advantage of $\mathcal{A}$ between $G_1$ and $G_2$, $\mathcal{S}$ can exploit this to break the semantic security of the ABE. Thus, we obtain the following:

  $$|{\mathrm{Adv}}_1^{\mathrm{FPCH}}-{\mathrm{Adv}}_2^{\mathrm{FPCH}}|\le {\mathrm{Adv}}_{\mathcal{S}}^{\mathrm{ABE}}(\lambda ).$$

  (12)
• $G_3$: This game modifies $G_2$ as follows: During the g-th hash query, the simulator $\mathcal{S}$ hashes the ciphertext $C_m$ to obtain the chameleon hash pair $(h,r)$ instead of using AdaptM to compute $(h,r)$. We prove that if the CH scheme is indistinguishable, the advantage difference between $G_2$ and $G_3$ is negligible.
  Consider $\mathcal{S}$ targeting the indistinguishability of the CH scheme. Given the chameleon parameter $T^{\ast }$ and HashOrAdaptM oracle, $\mathcal{S}$ honestly executes the Setup process. Specifically, $\mathcal{S}$ sets the chameleon parameter for the g-th query as $T^{\ast }$. If $\mathcal{A}$ submits $(C_{m0},C_{m1},\Lambda ,\delta ,k,k^{\prime })$ during the g-th query, $\mathcal{S}$ first obtains the chameleon hash $(h_d,r_d)$ for $(C_{m0},C_{m1})$ from its HashOrAdaptM oracle. Then, $\mathcal{S}$ simulates the ciphertext $C_t$ (with the encrypted trapdoor replaced by ⊥). Finally, $\mathcal{S}$ returns $(C_m^{\ast },h_d,r_d,d,C_t)$ to $\mathcal{A}$. $\mathcal{S}$ outputs the same result as $\mathcal{A}$. If $\mathcal{A}$ correctly predicts the random bit, then $\mathcal{S}$ is able to break the indistinguishability of the CH.
  Thus, we obtain the following:

  $$|{\mathrm{Adv}}_2^{\mathrm{FPCH}}-{\mathrm{Adv}}_3^{\mathrm{FPCH}}|\le {\mathrm{Adv}}_{\mathcal{S}}^{\mathrm{CH}}(\lambda ).$$

  (13)
  Based on the results, we obtain the following:

  $${\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{FPCH}}(\lambda )\le n(\lambda )·({\mathrm{Adv}}_{\mathcal{S}}^{\mathrm{ABE}}(\lambda )+{\mathrm{Adv}}_{\mathcal{S}}^{\mathrm{CH}}(\lambda )).$$

  (14)

□

Theorem 2.

The FPCH achieves collision resistance provided that the ABE scheme is semantically secure and the CH scheme is collision-resistant.

Proof. 

We introduce the following games denoted as $G_i$ for $i=0,1,\dots ,3$ and define ${\mathrm{Adv}}_i^{\mathrm{FPCH}}$ as the adversary’s advantage in game $G_i$. Suppose the adversary $\mathcal{A}$ makes no more than $n(\lambda )$ Hash’ queries within each game. We then define the following:

• $G_0$: This represents the initial game for collision resistance.
• $G_1$: This game modifies $G_0$ as follows: $\mathcal{S}$ selects an index guess g from the range $[1,n(\lambda )]$ for the Hash’ oracle, returning the chameleon hash $(C_m^{\ast },h^{\ast },r^{\ast },T^{\ast },C_t^{\ast })$. If $\mathcal{A}$ does not issue an attack query at the g-th attempt, $\mathcal{S}$ returns a random bit and halts the game.
  Thus, we obtain the following:

  $${\mathrm{Adv}}_0^{\mathrm{FPCH}}\le n(\lambda )·{\mathrm{Adv}}_1^{\mathrm{FPCH}}.$$

  (15)
• $G_2$: This game modifies $G_1$ as follows: During the g-th query, $\mathcal{S}$ substitutes the trapdoor t with ⊥ in $C_t^{\ast }$. We follow the same procedure as in the previous game $G_2$ to prove that the advantage difference between $G_1$ and $G_2$ is negligible. Consider $\mathcal{S}$ targeting the semantic security of the ABE scheme. We obtain the following:

  $$|{\mathrm{Adv}}_1^{\mathrm{FPCH}}-{\mathrm{Adv}}_2^{\mathrm{FPCH}}|\le {\mathrm{Adv}}_{\mathcal{S}}^{\mathrm{ABE}}(\lambda ).$$

  (16)
• $G_3$: This game modifies $G_2$ as follows: During the g-th query, when $\mathcal{A}$ outputs a valid collision $(h^{\ast },C_m^{\ast },r^{\ast },C_m^{\prime \ast },r^{\prime \ast },C_t^{\ast })$ that has not been previously generated by the AdaptM’ oracle, $\mathcal{S}$ outputs a random bit. We prove that if the CH scheme achieves collision resistance, the advantage difference between $G_2$ and $G_3$ is negligible.
  Consider $\mathcal{S}$ targeting the collision resistance of the CH scheme. $\mathcal{S}$ aims to look for a collision $(C_{m0},C_{m1})$ for the given hash, and $\mathcal{S}$ uses the same simulation method as in the previous games. If $\mathcal{A}$ successfully finds a collision, $\mathcal{S}$ is able to break the collision resistance of the CH. Thus, we obtain the following:

  $$|{\mathrm{Adv}}_2^{\mathrm{FPCH}}-{\mathrm{Adv}}_3^{\mathrm{FPCH}}|\le {\mathrm{Adv}}_{\mathcal{S}}^{\mathrm{CH}}(\lambda ).$$

  (17)
  Based on the results, we obtain the following:

  $${\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{FPCH}}(\lambda )\le n(\lambda )·({\mathrm{Adv}}_{\mathcal{S}}^{\mathrm{ABE}}(\lambda )+{\mathrm{Adv}}_{\mathcal{S}}^{\mathrm{CH}}(\lambda )).$$

  (18)

□

Theorem 3.

The RBFAC is IND-CPA-secure if the ABE scheme is semantically secure.

Proof. 

Assume that an oracle ${\mathcal{O}}_{\mathrm{ABE}}$ represents the ABE scheme, where ${\mathcal{O}}_{\mathrm{ABE}}=(\mathtt{Setup}(),\mathtt{KeyGen}(),\mathtt{Encrypt}(),\mathtt{Decrypt}())$. During the $Init$ phase, $\mathcal{S}$ executes the Setup process to compute the system parameters. During Phase 1, $\mathcal{S}$ generates the attribute key based on $\mathcal{A}$’s identity u and attributes $\delta$ as follows: ${\mathcal{O}}_{\mathrm{ABE}}.\mathtt{KeyGen}(msk,u,\delta )\to s{k}_{\delta }$. During the Challenge phase, $\mathcal{A}$ sends message pair $(M_0,M_1)$ to $\mathcal{S}$ and requests the ciphertext. Upon receiving $M_0$ and $M_1$, $\mathcal{S}$ sends the messages and access policy $\Lambda$ to the oracle ${\mathcal{O}}_{\mathrm{ABE}}$ to request the ciphertext $C^{\ast }$. The oracle ${\mathcal{O}}_{\mathrm{ABE}}$ returns $C^{\ast }$ to $\mathcal{S}$.

If the probability of $\mathcal{A}$ making a correct guess is non-negligible, then $\mathcal{S}$ can break the semantic security of the ABE. In particular, if no PPT adversary has more than a negligible advantage in breaking the ABE security, then the RBFAC is IND-CPA-secure:

$${\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{RBFAC}}(\lambda )={\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{ABE}}(\lambda )+\mathrm{negl}(\lambda ).$$

(19)

□

Theorem 4.

The RBFAC guarantees that only authorized advanced editors can modify the data access policy while preventing unauthorized modifications—provided that the RBFAC is semantically secure and the NIZK scheme is sound.

Proof. 

In the RBFAC scheme, the NIZK scheme is employed to modify the access policy, with the proof value k kept confidential. Thus, ensuring the correctness of modifying the access policy relies on the security of the RBFAC and the soundness of the NIZK scheme. The response W and commitment $R_k$ are computed using the proof value k and randomness $r_k$ as follows:

$$Z_k=g^k,R_k=g^{r_k},W=r_k+k·H(Z_k\Vert R_k).$$

(20)

Without knowledge of the proof value k, the probability of $\mathcal{A}$ forging the valid proof $\overline{W}=\langle Z_k,R_k,W\rangle$ such that $g^W=R_k·Z_k^{H(Z_k\Vert R_k)}$ is negligible owing to the hardness of the DL assumption. Furthermore, as verified in Theorem 3, the RBFAC achieves IND-CPA security under the random oracle model. Therefore, the RBFAC ensures that only authorized advanced editors can modify the access policy while preventing unauthorized modifications. □

Theorem 5.

The RBFAC is EUF-CMA-secure if the DTS scheme is EUF-CMA-secure.

Proof. 

Let $\mathcal{S}$ be a forger attempting to break the EUF-CMA security of the DTS scheme, with access to the signing oracle ${\mathcal{O}}_{\mathrm{Sign}}$. $\mathcal{A}$ is assumed to make no more than $n(\lambda )$ hash queries. $\mathcal{S}$ randomly picks a chameleon hash and chooses a random index $g\in [1,n(\lambda )]$ for the forgery concerning the hash. $\mathcal{S}$ executes the Setup process honestly.

To simulate the hash for the ciphertext $C_m$, $\mathcal{S}$ first queries the oracle ${\mathcal{O}}_{\mathrm{Sign}}$ to obtain a signature $\sigma$. Then, $\mathcal{S}$ honestly generates the hash and ciphertext and returns $(C_m,h,r,C_t,c_t,\sigma )$ to $\mathcal{A}$. Owing to the homomorphic property of the DTS scheme (with respect to keys and signatures), $\mathcal{S}$ can accurately simulate the pair $(c_t,\sigma )$ for any adaptive query. $\mathcal{S}$ records all simulated hashes in the set Q.

When a forging attempt is made, $\mathcal{A}$ outputs $(C_m^{\ast },h^{\ast },r^{\ast },C_t^{\ast },c_t^{\ast },{\sigma }^{\ast })$. $\mathcal{S}$ checks the following conditions:

• The forging attempt occurs in the g-th query.
• The pair $(c_t^{\ast },{\sigma }^{\ast })$ links to the trapdoor t.
• The pair $(c_t^{\ast },{\sigma }^{\ast })\notin Q$.
• $\mathrm{DTS}.\mathtt{Verify}(c_t^{\ast },{\sigma }^{\ast })\to 1$, $\mathrm{CH}.\mathtt{Verify}(C_m^{\ast },h^{\ast },r^{\ast })\to 1$.

If all conditions hold, $\mathcal{S}$ identifies it as a successful forgery by $\mathcal{A}$. $\mathcal{S}$ obtains the result by $\mathrm{DTS}.\mathtt{Sign}(p{k}_{\sigma }^{\ast },{\sigma }^{\ast },\mathsf{\Delta }(s{k}_{\sigma }))\to \sigma$, and $\mathsf{\Delta }(s{k}_{\sigma })$ is based on $(c_t,c_t^{\ast })$. Finally, $\mathcal{S}$ outputs $\sigma$ as its forgery result. □

8. Implementation and Discussion

We implemented the proposed RBFAC framework utilizing Python 3.6.9 and the Charm framework, evaluating its performance on a PC equipped with an Intel Core i7, 16GB RAM, and a 64-bit Ubuntu 18.04 LTS. The SS-512 elliptic curve was used for bilinear pairing operations, while hash functions and pseudorandom generators were instantiated using Charm’s standard interfaces. The code is publicly available on GitHub [44].

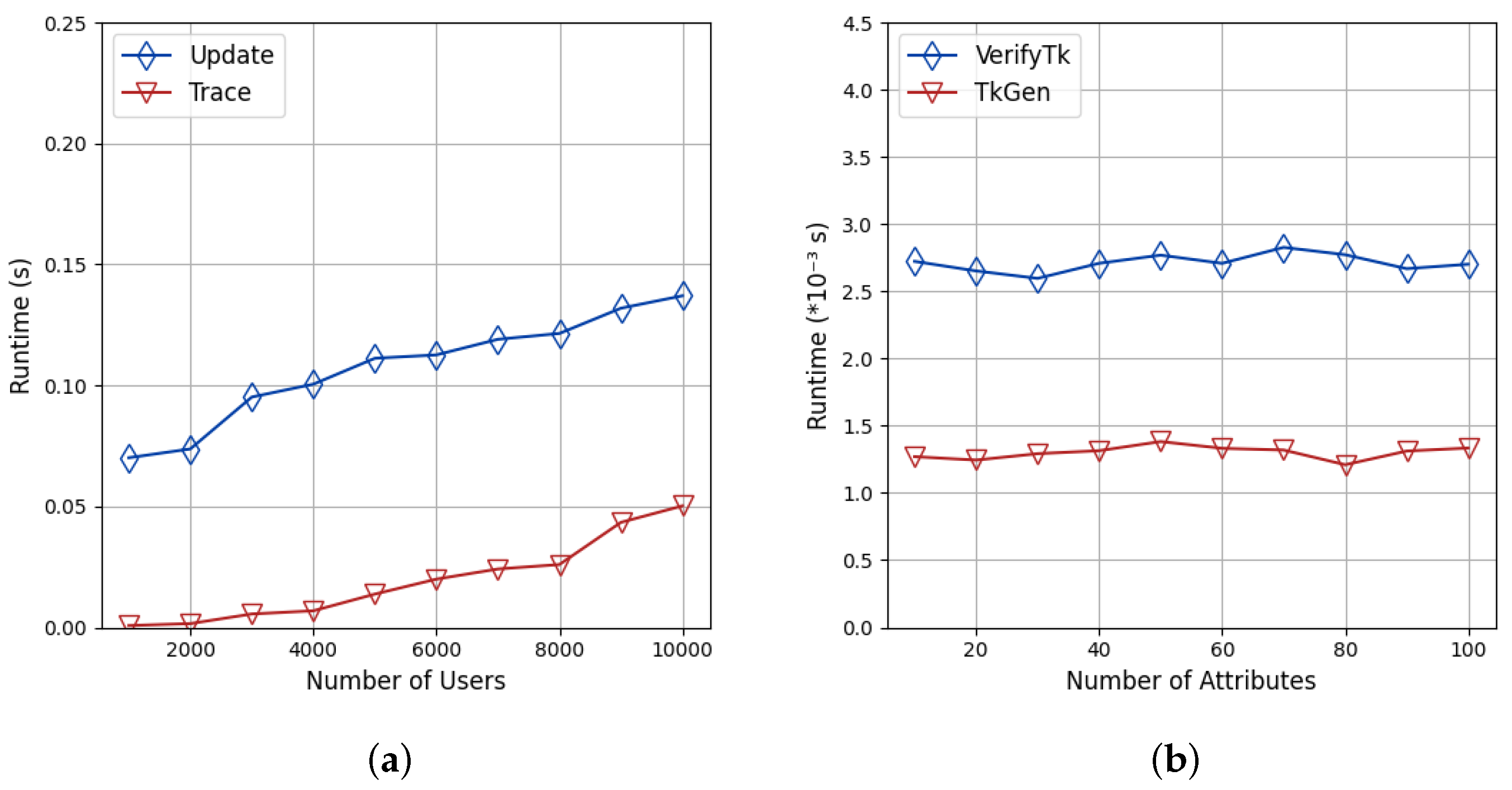
8.1. Performance Analysis

We simulated the time overhead of the system under various parameters (such as number of users, attribute set sizes, and policy complexity) and conducted 50 test runs alongside other solutions in identical environments, with the average results being recorded (all referenced schemes have provided open-source implementations).

Table 3. Runtime for setup and verify algorithms.

Scheme	Setup (ms)	Verify (ms)
CDedit [17]	212.9	6.42
PCHBA [23]	187.2	15.07
RPCH (RSA) [24]	60.9	0.75
RPCH (DL) [25]	47.4	2.32
APC2H [28]	138.3	3.57
Ours	18.8	4.02

compares the time overhead of the Setup and Verify algorithms for our scheme and existing policy-based chameleon hash schemes [17,23,24,25,28]. In the Verify algorithm, our scheme introduced additional verification steps for signatures and zero-knowledge proofs. The incurred overhead is acceptable for practical applications.

For fairness, we compared the time overhead in a non-encrypted scenario without defining advanced editing policies, where all schemes incur the overhead of a single attribute-based encryption and decryption operation. Figure 7a–c demonstrate the time overhead of KeyGen, Hash, and AdaptM across different schemes (excluding [25], which lacks policy modification capability). Note that in this case, editing permissions are managed by the token committee, while other schemes lack such permission management measures. The results indicate that the algorithm’s performance is linearly related to the number of attributes or the size of policy. Due to the use of symmetric bilinear pairings, our scheme demonstrated superior efficiency compared to existing schemes.

Figure 7d illustrates the time overhead for operations in an encrypted scenario with defined advanced editing policies, where only users with the corresponding attributes and tokens can modify the policies. Due to multiple instances of attribute-based encryption, the time overhead of the hash and policy editing algorithms was relatively high. The next step was to reduce this overhead by utilizing downward-compatible, attribute-based encryption [27]. Since the Hash and AdaptP algorithms employ multiple repeated and independent attribute-based encryption (ABE) operations, and the computational overhead of ABE accounts for over 95% of the total cost, parallel computing can significantly reduce the execution time, thereby enhancing the system’s practicality for real-world applications (implementation details are available in the source code).

Figure 8a analyzes the costs of key tracing and ciphertext updates for varying user counts. By leveraging a binary tree structure for user management, our scheme achieves $O({log}_{2}n)$ time complexity for revocation. Unlike [24,25], which require key updates for non-revoked users per epoch, our approach updates only revocation-related ciphertext components, independent of the policy size.

Figure 8b shows the time overhead of TkGen and VerifyTk, demonstrating scalability independent of attributes. In addition, the scheme SPRINT [14] provides a detailed description of how to implement large-scale Schnorr signature services on a blockchain, including sampling and generation of the committee and proactive share refreshment in each epoch. In large-scale subsampling, single-threaded implementations can generate up to 4000 signatures per minute. Thus, building our token committee based on this scheme is entirely feasible.

Our framework ensures traceability, revocability, and policy privacy protection through the underlying TR-AP-CPABE [15] while enabling efficient edit accountability via the signature scheme. It also facilitates diversified, controlled, and fully decentralized editing through the token committee. In contrast, existing solutions fail to concurrently support all of these features.

8.2. Blockchain Integration Overhead

We evaluated the framework’s impact on Bitcoin-like transaction processing as follows:

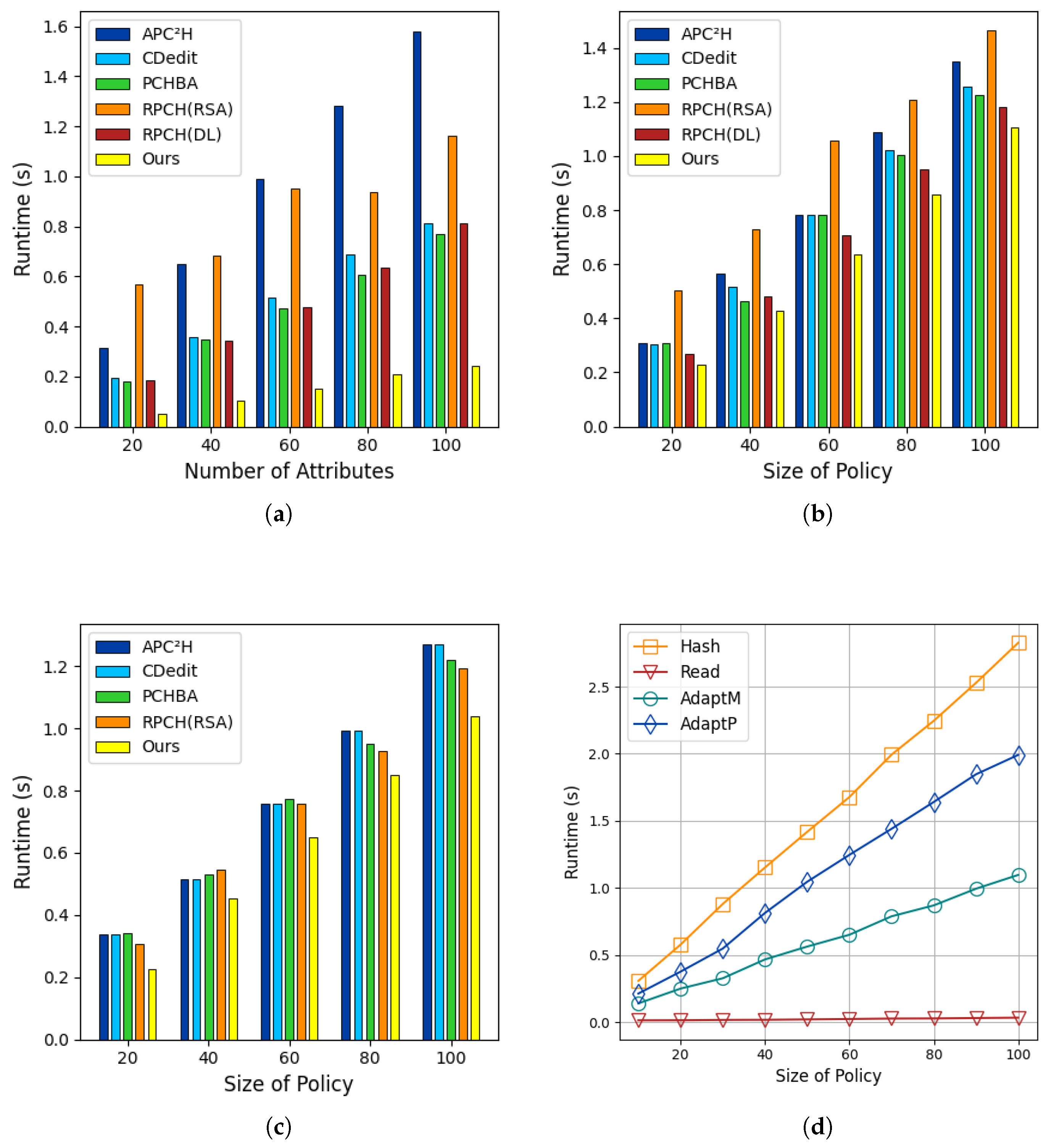
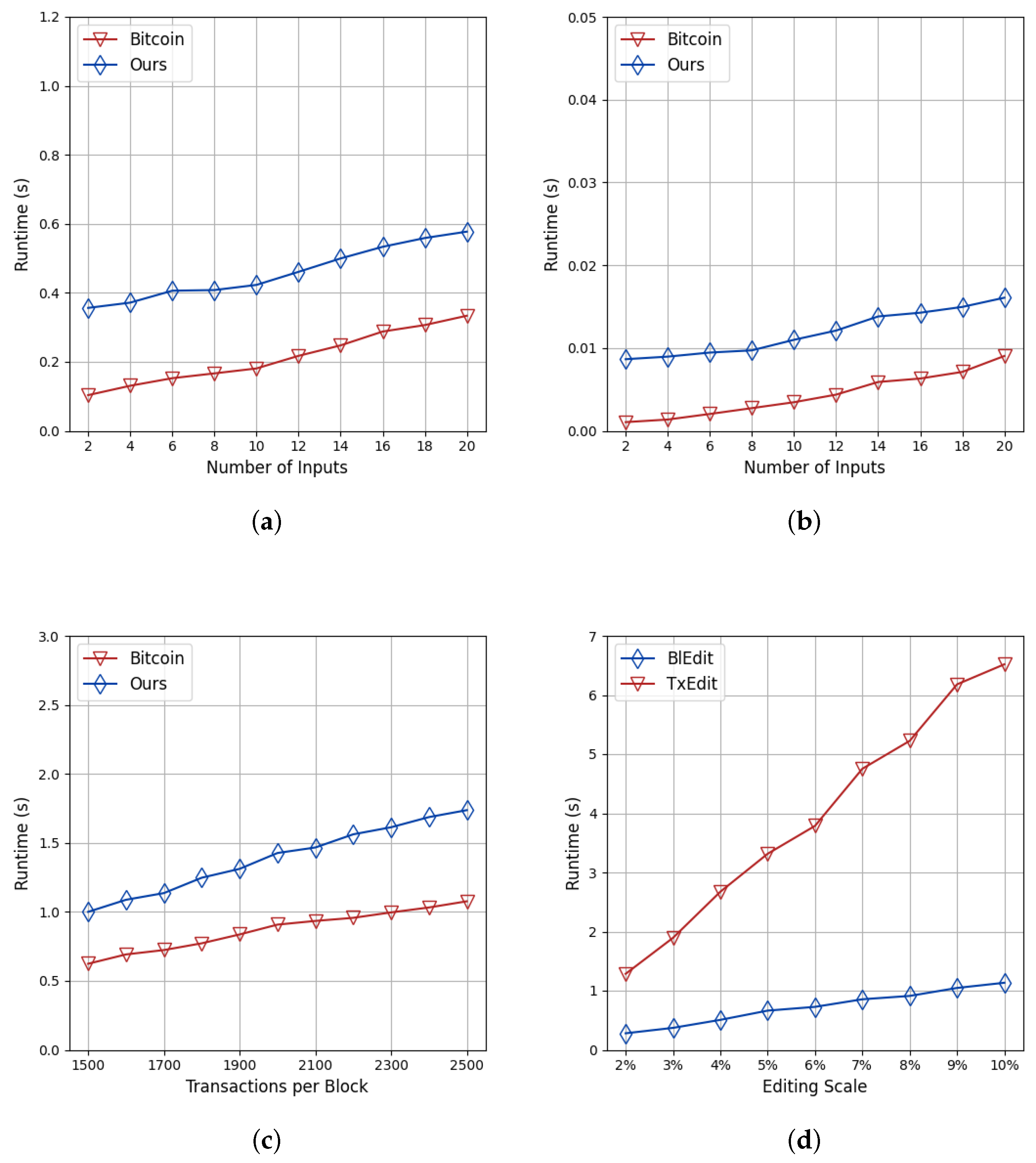
• Transaction Generation: Figure 9a shows a 0.3 s average delay compared to native Bitcoin when generating transactions with 2–20 inputs, two outputs, and a policy size of 10.
• Transaction Verification: Figure 9b reveals an additional 0.007 s overhead per transaction for validating chameleon hashes, signatures, and proofs.
• Block Generation: With 1500–2500 transactions per block and 5% mutable transactions, Figure 9c shows a 0.65 s average increase in block creation time. Since the collision-resistant hash was still used for transaction aggregation and block linking, mutable transactions or blocks introduce negligible overhead in Merkle tree generation and blockchain verification.

8.3. Overhead Comparison of Different Editing Granularities

To emphasize the necessity of editing operations at different granularities, we also compared the time overhead of transaction-level editing with block-level editing in scenarios where a large batch of transactions needs modification. Transaction-level editing entails n trapdoor decryptions, n new randomness calculations, and n signature operations. In contrast, block-level editing requires these operations only once, along with the generation of n chameleon hashes and partial updates to the Merkle tree, typically recalculating only the affected portions.

As shown in Figure 9d, assuming a block contains 2000 transactions and the ciphertext policy size is 10, we measure the runtime for editing proportions ranging from 2% to 10%. The results show that block-level editing reduces the overhead to approximately one-sixth of that required for transaction-level editing when modifying a large batch of transactions.

8.4. Other Discussion

In terms of security, Section 7 separately proves the indistinguishability and collision resistance of the FPCH, as well as the IND-CPA and EUF-CMA security of the RBFAC. Additionally, the RBFAC guarantees that only authorized advanced editors can modify the data access policy while preventing unauthorized modifications.

In terms of scalability, the RBFAC framework enables data owners to freely manage data readability, editability, and policy modification while also supporting diversified controlled editing and numerous other features. It maintains acceptable overhead under varying numbers of attributes, policy sizes, and user scales. Moreover, since it is built upon standard chameleon hash techniques, the RBFAC can freely select specific chameleon hash methods to adapt to different practical scenarios.

In terms of fault tolerance, the token committee (TC) achieves Byzantine fault tolerance through an election protocol, ensuring normal service operation as long as malicious members do not exceed one-third of the total. Furthermore, we constructed the TC based on the scheme SPRINT [14], which provides high throughput and robustness, thereby ensuring the high fault tolerance of the editing token system.

9. Conclusions

To overcome the critical challenges of editing flexibility, editing granularity, and permission control in existing redactable blockchain systems, this study introduces the flexible policy chameleon hash (FPCH) paradigm. The proposed solution combines a policy-based chameleon hash (PCH) with non-interactive zero-knowledge proofs, establishing a robust access control infrastructure. Based on this theoretical foundation, we have engineered a redactable blockchain framework with fine-grained access control (RBFAC). The RBFAC framework uses symmetric encryption to fully decouple message editing from policy modification. It also implements a decentralized, multi-granularity editing control system through a token committee mechanism utilizing a dynamic threshold signature. In addition, the RBFAC framework demonstrates comprehensive functionality, incorporating essential features such as editing accountability, key traceability, key revocation, and policy privacy protection. Extensive implementation and evaluation results confirm the framework’s adaptability across permissioned blockchain applications. Future research endeavors will concentrate on extending the framework’s applicability to trustless environments while optimizing its communication protocols and storage efficiency for enhanced performance.