Knowledge-Enhanced Deep Reinforcement Learning for Multi-Agent Game

Abstract

In modern naval confrontation systems, adversarial underwater unmanned vehicles (UUVs) pose significant challenges, which are deployed on unmanned aerial vehicles (UAVs) due to their inherent mobility and positional uncertainty. Effective neutralization threats demand sophisticated coordination strategies between distributed agents under partial observability. This paper proposes a novel Knowledge-Enhanced Multi-Agent Deep Reinforcement Learning (MADRL) framework for coordinating UAV swarms against adversarial UUVs in asymmetric confrontation scenarios, specifically addressing three operational modes: area surveillance, summoned interception, and coordinated countermeasures. Our framework introduces three key innovations: (1) a probabilistic adversarial model integrating prior intelligence and real-time UAV sensor data to predict underwater trajectories; (2) a Multi-Agent Double Soft Actor–Critic (MADSAC) algorithm, addressing Red team coordination challenges. Experimental validation demonstrates superior performance over baseline methods in Blue target detection efficiency (38.7% improvement) and successful neutralization rate (52.1% increase), validated across escalating confrontation scenarios.

1. Introduction

In modern naval confrontation systems, adversarial underwater unmanned vehicles (UUVs) pose significant challenges for Red team forces, which are deployed on unmanned aerial vehicles (UAVs) due to their inherent mobility and positional uncertainty [1]. Effective neutralization of Blue team threats demands sophisticated coordination strategies between distributed agents under partial observability. This paper proposes a novel Knowledge-Enhanced Multi-Agent Deep Reinforcement Learning (MADRL) framework for coordinating UAV swarms (Red team) against adversarial UUVs (Blue team) in asymmetric confrontation scenarios, specifically addressing three operational modes: area surveillance, summoned interception, and coordinated countermeasures.

Traditional underwater confrontation methods face inherent limitations against Blue team’s dynamic evasion tactics [2]. The probabilistic nature of UUV positioning, combined with time-sensitive mission requirements, necessitates adaptive decision-making capabilities beyond conventional rule-based systems. Recent advances in deep reinforcement learning (DRL) provide critical foundations for multi-agent adversarial games [3], particularly through centralized training with decentralized execution (CTDE) paradigms that balance team coordination and individual autonomy [4].

Our framework introduces three key innovations tailored for Red/Blue confrontations:

• A probabilistic adversarial model integrating prior intelligence and real-time UAV sensor data to predict Blue team’s underwater trajectories.
• A Multi-Agent Double Soft Actor–Critic (MADSAC) algorithm augmented, addressing Red team coordination challenges including dynamic credit assignment and partial observability of Blue forces.

The technical contributions focus on Red team operational superiority:

Hybrid observation space combining Blue team signature estimates, Red UAV statuses, and environmental uncertainties. Dual centralized critic architecture to mitigate Q-value overestimation during adversarial policy learning. Hierarchical reward function balancing exploration–exploitation tradeoffs using combat-effectiveness metrics specific to UUV neutralization. Experimental validation demonstrates Red team’s superior performance over baseline methods in Blue target detection efficiency (38.7% improvement) and successful neutralization rate (52.1% increase), validated across escalating confrontation scenarios.

2. Related Work

In modern naval confrontation systems, especially those involving adversarial underwater unmanned vehicles (UUVs), the literature generally falls into two broad categories: rule-based methods and reinforcement learning (RL)-based approaches. In this section, we review both lines of work, analyzing their advantages and limitations, and we highlight the motivation for our proposed method.

2.1. Rule-Based Methods

Rule-based approaches have long been employed in underwater navigation, target tracking, and engagement decision making. For example, Chen and Li [5] proposed navigation strategies that leverage a predefined rule base to guide underwater vehicles. Such methods benefit from low computational overhead and high interpretability. Liu et al. [6] introduced a model-based framework using rule sets for decision making, which performs well in static or slowly varying environments. Similarly, Wang and Zhang [7] demonstrated that heuristic algorithms can enhance response times in autonomous underwater navigation, while Guo and Chen [8] further developed rule-based decision models to handle confrontation scenarios.

Other studies have extended rule-based strategies. Li and Sun [9] summarized that rule-based controllers struggle to capture the probabilistic nature of rapidly evolving battlefields, and He and Liu [10] noted that even adaptive rule-based controls remain confined by their pre-specified rule sets. Zhang and Li [11] highlighted that expert systems, though stable under normal conditions, often lack robustness when encountering abnormal or adversarial maneuvers. Xu and Wang [12] pointed out the real-time advantages of rule-based decisions but also remarked that outdated rule libraries can impair performance in dynamic contexts. Huang and Zhou [13] attempted to enhance rule-based systems with intelligent components; nevertheless, their approaches fell short in multi-target coordination and information fusion. Sun and Li [14] developed robust rule-based systems but acknowledged that these systems still struggle with uncertainty and the unpredictable behavior of adversaries. Additional works such as Park et al. [15], Zhou and Liu [16], and Yue et al. [17] have further investigated rule-based strategies, yet they consistently suffer from limited flexibility and inadequate adaptation to rapidly changing environments.

Table 1. Comparison of rule-based and RL-based methods.

Aspect	Rule-Based Methods	RL-Based Methods
Flexibility	Low-fixed rules	High-adaptive policies
Computational Cost	Low during execution	High training cost
Interpretability	High	Often low (black-box)
Integration of Prior Knowledge	Direct incorporation	Requires explicit design
Scalability	Limited	Scalable with sufficient data

summarizes key characteristics of rule-based methods compared to RL-based approaches.

In summary, while rule-based methods are prized for their simplicity, efficiency, and interpretability, their major limitations include the following:

• Limited Flexibility: Predefined rules cannot cover all possible battlefield scenarios.
• Inadequate Modeling of Nonlinear Dynamics: Difficulty in accurately representing adversary strategies that are nonlinear and rapidly evolving.
• Lack of Real-Time Adaptability: The rule libraries often lag behind current intelligence, reducing responsiveness to sudden environmental changes.

Our proposed Knowledge-Enhanced Multi-Agent Deep Reinforcement Learning (MADRL) framework overcomes these issues by integrating prior intelligence with real-time sensor data into a probabilistic adversarial model, thereby compensating for the inflexibility and delayed update issues inherent in rule-based systems.

2.2. Reinforcement Learning-Based Methods

Reinforcement learning (RL) has emerged as a powerful alternative for autonomous decision making in complex and uncertain environments. The seminal work of Sutton and Barto [18] laid the theoretical foundation, while Mnih et al. [19] demonstrated that deep RL could achieve human-level performance in high-dimensional control tasks. To address continuous control problems, Lillicrap et al. [20] introduced the Deep Deterministic Policy Gradient (DDPG) algorithm, and Haarnoja et al. [21] later proposed the Soft Actor–Critic (SAC) algorithm, which improves stability and convergence speed.

In multi-agent settings, Lowe et al. [22] developed a multi-agent actor–critic framework that employs centralized training with decentralized execution, thereby enhancing team coordination. Yun et al. [23] introduced the autonomous communication network requirements between drones to improve collective decision making, while Iqbal et al. [24] incorporated multi-head attention mechanism to better represent complex inter-agent relationships. Bengio et al. [25] further advanced the field by applying curriculum learning to gradually increase task complexity, facilitating smoother policy learning. Schulman et al. [26] presented proximal policy optimization (PPO)-based fully decentralized networked multi-agent reinforcement learning to increase scalability. Additional studies have sought to improve RL performance in adversarial and multi-agent scenarios. Van Hasselt et al. [27] introduced Double Q-learning to mitigate overestimation bias, and Hessel et al. [28] combined multiple improvements into the Rainbow algorithm. Foerster et al. [29] proposed counterfactual multi-agent policy gradients to better handle credit assignment, while Wang et al. [30] explored unsupervised learning techniques to facilitate agent design. Despite these advancements, RL-based methods still face several critical limitations:

• High Sample Complexity: Many RL algorithms require extensive training data and computational resources.
• Non-Stationarity in Multi-Agent Environments: Dynamic interactions among agents lead to unstable training and challenges in credit assignment.
• Limited Observability: In partially observable environments, single-source sensory input may be insufficient for accurate decision making.
• Inefficient Knowledge Integration: Most current RL approaches lack mechanisms to effectively incorporate prior intelligence, leading to performance degradation when data are sparse.

Our Knowledge-Enhanced MADRL framework addresses these limitations by fusing prior intelligence with real-time sensor inputs to generate a probabilistic model of adversarial UUV trajectories. By using a Double Soft Actor–Critic algorithm, the proposed method effectively tackles issues of dynamic credit assignment and partial observability.

The following table (

Table 2. Strengths and weaknesses of RL-based methods.

Method	Strengths	Weaknesses
DDPG [20]	Effective for continuous control; stable in single-agent scenarios	High variance in multi-agent settings; sensitive to hyperparameters
SAC [21]	Improved stability and sample efficiency; entropy regularization aids exploration	Still suffers from non-stationarity in multi-agent scenarios
PPO [31]	Stable policy updates and robust performance	Computationally intensive with large-scale multi-agent systems

) outlines the strengths and weaknesses of various RL-based approaches in multi-agent and adversarial settings.

3. Proposed Method

In this section, we describe our proposed Knowledge-Enhanced Deep Reinforcement Learning framework for multi-agent adversarial games (MADSAC). The framework is designed to coordinate a helicopter and a swarm of UAVs in a grid-based maritime environment to counter UUV detection and localization. The methodology is organized into the following components: environment modeling, state space, action space, reward function, MADSAC algorithm.

3.1. Environment Modeling

The operational area is modeled as a grid-based maritime environment, where each grid cell represents a $1\mathrm{km}\times 1\mathrm{km}$ region. Each cell is assigned an initial value reflecting the prior probability of a target UUV’s presence, obtained from external intelligence sources. The probability distribution is initialized based on a Gaussian centered at the UUV’s starting position prior to modeling and is dynamically updated throughout the mission based on UAV detection results.

UAVs, equipped with multiple sensors (e.g., visible-light cameras and magnetic detectors), execute the search task, while the helicopter utilizes sonar buoys for precise UUV localization. Wireless communication is established among UAVs to share information and ensure coordinated operations with built-in collision avoidance mechanisms. The overall objective is to complete the search task with minimal fuel consumption and time cost.

The simulation environment and data generation process are implemented using a self-developed Python-based platform. This platform models the dynamic interactions between agents and the environment, simulates sensor measurements with noise, and provides a realistic representation of UUV movement and detection uncertainty. The simulation framework enables the evaluation of different search strategies under various environmental conditions.

3.2. State Space

The state space captures both the environmental context and the agent-specific conditions. For each UAV, the state vector is defined as

$$s^{\mathrm{UAV}}=\left[\mathbf{p},{\mathbf{P}}_{UUV},E,\left\{{\mathbf{p}}_{\mathrm{nei}}\right\}\right],$$

(1)

where

• $\mathbf{p}\in {\mathbb{R}}^2$ denotes the UAV’s position coordinates.
• ${\mathbf{P}}_{UUV}\in {\mathbb{R}}^{m\times m}$ is a local probability matrix representing the estimated UUV presence distribution within an $m\times m$ neighborhood around the UAV.
• $E\in \mathbb{R}$ is the remaining energy level.
• $\left\{{\mathbf{p}}_{\mathrm{nei}}\right\}$ represents the positions of neighboring UAVs.

For the helicopter, the state vector is extended as follows:

$$s^{\mathrm{Heli}}=\left[\mathbf{p},{\mathbf{P}}_{UUV},E,\left\{{\mathbf{p}}_{\mathrm{UAV}}\right\},B,T\right],$$

(2)

where $B\in \mathbb{N}$ is the number of deployed sonar buoys and $T\in \mathbb{N}$ is the number of available torpedoes.

3.3. Initial UUV Probability Distribution

The initial probability distribution of the UUV’s presence is modeled as a Gaussian distribution centered at its initial position $(x_0,y_0)$. The probability at each grid cell $(x,y)$ is given by

$$P_{UUV}^{\left(0\right)}(x,y)={\displaystyle \frac{1}{2\pi {\sigma }^2}}exp\left(-{\displaystyle \frac{{(x-x_0)}^2+{(y-y_0)}^2}{2{\sigma }^2}}\right),$$

(3)

where

• $(x_0,y_0)$ is the initial UUV position.
• $\sigma$ is the standard deviation, controlling the spread of the probability distribution.

The probability values are then normalized across the entire grid as follows:

$$P_{UUV}^{\left(0\right)}(x,y)\leftarrow {\displaystyle \frac{P_{UUV}^{\left(0\right)}(x,y)}{{\sum }_{(x^{\prime },y^{\prime })}{P}_{UUV}^{\left(0\right)}(x^{\prime },y^{\prime })}}.$$

(4)

3.4. Dynamic Probability Update

The probability distribution of the UUV’s presence, ${\mathbf{P}}_{UUV}$, is dynamically updated based on UAV sensor observations using a Bayesian update rule:

$$P_{UUV}^{(t+1)}(x,y)={\displaystyle \frac{P_{\mathrm{obs}}\left(Z_t\right|x,y)P_{UUV}^{\left(t\right)}(x,y)}{{\sum }_{(x^{\prime },y^{\prime })\in \mathcal{N}}{P}_{\mathrm{obs}}\left(Z_t\right|x^{\prime },y^{\prime })P_{UUV}^{\left(t\right)}(x^{\prime },y^{\prime })}},$$

(5)

where

• $P_{UUV}^{\left(t\right)}(x,y)$ is the prior probability of the UUV’s presence at grid cell $(x,y)$ at time t.
• $P_{\mathrm{obs}}\left(Z_t\right|x,y)$ is the likelihood of the sensor observation $Z_t$ given the UUV’s presence at $(x,y)$.
• $\mathcal{N}$ represents the local neighborhood of the UAV over which the probability distribution is maintained.

A summary of the state variables is provided in

Table 3. State variables for UAVs and helicopter.

Variable	Symbol	Dimension/Description
Position Coordinates	$\mathbf{p}$	$\in {\mathbb{R}}^2$, $(x,y)$ in the grid
UUV Distribution (Local)	${\mathbf{P}}_{UUV}$	$\in {\mathbb{R}}^{m\times m}$, local probability matrix
Remaining Energy	E	Scalar, normalized energy level
Neighbor Positions	$\left\{{\mathbf{p}}_{\mathrm{nei}}\right\}$	Set of coordinates of nearby UAVs
Additional for Helicopter:
Sonar Buoy Count	B	$\in \mathbb{N}$
Torpedo Count	T	$\in \mathbb{N}$

.

3.5. Action Space

The action space defines the set of actions available to each agent at every time step. We specify separate action spaces for UAVs and the helicopter using tables for clarity.

3.5.1. UAV Action Space

The Action space of each UAV is shown in

Table 4. UAV Action Space.

Action Name	Symbol	Description/Dimension
Heading Selection	$a_h$	Discrete choice from $a_h\in \{1,2,\dots ,N_h\}$
Magnetic Detector Activation	$a_m$	Binary decision, $a_m\in \{0,1\}$

.

3.5.2. Helicopter Action Space

The helicopter’s actions are defined as in

Table 5. Helicopter Action Space.

Action Name	Symbol	Description/Dimension
Heading Selection	$a_h^{\prime }$	Discrete choice from $a_h^{\prime }\in \{1,2,\dots ,N_h^{\prime }\}$
Bomb Deployment	$a_b$	Binary decision, $a_b\in \{0,1\}$
Sonar Buoy Deployment	$a_s$	Binary decision, $a_s\in \{0,1\}$

.

3.6. Reward Function

The reward function is designed to guide the agents toward an efficient UUV search and localization. It is formulated as

$$R={\lambda }_1{R}_{\mathrm{target}}+{\lambda }_2{R}_{\mathrm{explore}}-{\lambda }_3{C}_{\mathrm{exec}}-{\lambda }_4{C}_{\mathrm{collision}},$$

(6)

where

• $R_{\mathrm{target}}$ is the reward for detecting the target UUV (proportional to detection probability).
• $R_{\mathrm{explore}}$ is the reward for exploring new regions (implemented via a pheromone mechanism to discourage redundant search).
• $C_{\mathrm{exec}}$ is the execution cost (time and fuel consumption).
• $C_{\mathrm{collision}}$ is the penalty for collisions.
• ${\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4$ are weighting factors.

3.7. MADSAC Algorithm

To mitigate overestimation and error accumulation in multi-agent reinforcement learning, we propose the Multi-Agent Double Soft Actor–Critic (MADSAC) algorithm, which operates under a Centralized Training with Decentralized Execution (CTDE) framework.

3.7.1. Algorithm Architecture

The architecture of MADSAC comprises the following modules:

• Dual Centralized Critic: A dual centralized critic utilizes global state information to update actor networks. This critic employs two Q-networks to reduce Q-value overestimation and accumulated error.
• Maximum Entropy and Double Critic: Built upon a maximum entropy reinforcement learning framework, the objective function for the policy $\pi$ is given by

  $$J\left(\pi \right)=\sum _t{\mathbb{E}}_{(s_t,a_t)\sim {\rho }_{\pi }}\left[r(s_t,a_t)+\alpha \mathcal{H}\left(\pi (·|s_t)\right)\right],$$

  (7)

  where $\alpha$ is the temperature parameter and $\mathcal{H}(·)$ is the entropy term. Actor networks are updated in a delayed manner to improve sample efficiency:

  $$\theta \leftarrow \theta -\eta {\nabla }_{\theta }({\mathbb{E}}_{s_t\sim \mathrm{D},{\mathrm{a}}_{\mathrm{t}}\sim {\pi }_{\theta }}\left[\alpha log{\pi }_{\theta }\left(a_t\right|s_t)-\underset{j=1,2}{min}{Q}_j(s_t,a_t)\right]),$$

  (8)

  where $Q_j(s_t,a_t)$ is the Q-value, and $\eta$ is the learning rate. In order to train faster and more stably, the algorithm will select the smaller Q value of the two evaluation networks as the target value each time to reduce the estimation error.

  $$Q_{target}(s_t,a_t)=r(s_t,a_t)+\gamma {\mathbb{E}}_{s_{t+1},a_{t+1}}\left[\underset{j=1,2}{min}{Q}_j(s_{t+1},a_{t+1})-\alpha log\left(\pi \left(a_{t+1}\right|s_{t+1})\right)\right].$$

  (9)
• Automatically adjust the proportion of entropy: Construct a neural network that can adaptively adjust the coefficient size according to the randomness of the strategy and automatically update it through the following loss function:

  $$J\left(\alpha \right)=\mathbb{E}\left[-\alpha log{\pi }_t(a_t\mid s_t)-\alpha H_0\right],$$

  (10)

  where $H_0$ is the target value of entropy, which is generally the opposite of the dimension of the action space.

3.7.2. Training Procedure

Under the CTDE paradigm, training occurs in two phases. Algorithm 1 summarizes the training procedure.

• Centralized Training: All agents share global state information via the dual centralized critic, which guides the update of individual actor networks.
• Decentralized Execution: Once training converges, each UAV (and the helicopter) executes its learned policy based solely on its local observations.

Algorithm 1 MADSAC algorithm steps.

INPUT:  Environment state space S, action space A, reward function R, discount factor $\gamma$, communication range $d_{\mathrm{comm}}$, update frequency for actors and critics. OUTPUT:  Trained policies for all agents.  1: INITIALIZE: Initialize actor networks ${\pi }_{{\theta }_i}$ and critic networks $Q_{{\varphi }_i}$ for all agents i, and replay buffer $\mathcal{D}$.  2: while not converged do  3:    for each agent i do  4:        Observe state $s_i$ and select action $a_i$ using policy ${\pi }_{{\theta }_i}$ with exploration noise.  5:        Execute action $a_i$, receive next state $s_i^{\prime }$ and reward $r_i$.  6:        Store transition $(s_i,a_i,r_i,s_i^{\prime })$ in $\mathcal{D}$.  7:    end for  8:    for each agent i do  9:        Sample a minibatch of transitions $(s_i,a_i,r_i,s_i^{\prime })$ from $\mathcal{D}$. 10:       Compute target $y=r_i+\gamma {\mathbb{E}}_{a_i^{\prime }\sim {\pi }_{{\theta }_i}}\left[Q_{{\varphi }_i}(s_i^{\prime },a_i^{\prime })\right]$. 11:       Update critic network $Q_{{\varphi }_i}$ by minimizing loss $L\left({\varphi }_i\right)=\mathbb{E}\left[{(Q_{{\varphi }_i}(s_i,a_i)-y)}^2\right]$. 12:       Update actor network ${\pi }_{{\theta }_i}$ using the policy gradient ${\nabla }_{{\theta }_i}J\left({\theta }_i\right)$. 13:       if agent i is within communication range of other agents then 14:           Share policy ${\pi }_{{\theta }_i}$ and update critic $Q_{{\varphi }_i}$ collaboratively. 15:       end if 16:    end for 17:    if collision risk detected based on $d_{\mathrm{comm}}$ then 18:       Execute collision avoidance maneuver. 19:    end if 20:    if environmental objectives met then 21:       Terminate training and save policies. 22:    end if 23: end while 24: RETURN Trained policies $\left\{{\pi }_{{\theta }_i}\right\}$ for all agents.

4. Results

This section presents the experimental outcomes of our proposed approach. The results are organized into three subsections: (i) Experimental Setup, (ii) Rule-Based Method Results, and (iii) Reinforcement Learning-Based Results.

4.1. Experimental Setup

The simulation environment is configured as a $100\mathrm{km}\times 50\mathrm{km}$ maritime domain, as Figure 1 shows. The search team consists of two UAVs and one helicopter, tasked with detecting and localizing a single UUV operating within the area.

Table 6. Force composition and equipment details.

Team	Unit	Count	Equipment/Description
Red	UAV	2	Sensors: Visible-light camera, magnetic detector. Communication: Wireless link. Collision avoidance: Threshold-based algorithm.
	Helicopter	1	Sensors: Sonar buoys for precise UUV localization. Armament: Bombs, torpedoes. Integrated communication with UAV network.
Blue	UUV	1	Sensors: Underwater sonar for self-localization. Mobility: Rapid evasion capability. Navigation: Randomized path selection algorithm.

summarizes the force composition and equipment details used in the simulation. The simulation environment is a grid-based maritime domain where each grid cell is initialized with a prior probability of the target UUV’s presence.

The RL algorithms are implemented in Python 3.9.2 using the PyTorch 2.6.0 framework. The training process was conducted on a computer equipped with a 12-core 3.60 GHz Intel(R) Core(TM) i7-12700KF CPU and 32 GB RAM. The Adam optimizer was employed to train the parameters of both actor and critic neural networks. The training parameters are shown in

Table 7. The parameters of neural networks.

Parameter	Values
Learning rate of actor	0.001
Learning rate of critic	0.001
Experience replay buffer	100,000
Mini-batch	256
Weighting factor	0.95
Soft update rate	0.001

.

4.2. Rule-Based Method Results

The rule-based method utilizes predefined rules derived from expert knowledge to control agent behavior [32]. Algorithm 2 details the steps of the rule-based adversarial method in the simulation.

In this work, the Blue UUV continuously monitors its surroundings to detect the presence of Red targets as in Algorithm 3. Upon detection, the UUV uses onboard sensors (e.g., sonar) to compute the relative position of the threat. It then determines an optimal evasion trajectory using a circular linking method, ensuring that the UUV adjusts its heading and speed to avoid engagement while continuing its mission. The following algorithm outlines the steps performed by the Blue UUV for dynamic threat evasion.

Figure 2 shows how the task completion time and detection success rate of the drone change with the number of training steps under the rule-based method. The mission execution time represents the total time required for the UAV to complete the search mission, which is usually measured from the start of the execution to the successful completion of the mission. The detection success rate indicates the ratio of the number of episodes that complete the search task to the total number of training episodes. As can be seen from the figure, the rule-based method, while straightforward and computationally efficient, exhibits limitations in flexibility and adaptability, resulting in relatively higher mission completion times and suboptimal performance in dynamic environments.

Algorithm 2 Rule-based algorithm steps.

INPUT:  Prior UUV probability grid G, sensor threshold ${\theta }_s$, collision threshold $d_{col}$, maximum mission time $T_{max}$ OUTPUT:  Mission termination signal after UUV localization and neutralization or when $T_{max}$ is reached  1: INITIALIZE: Deploy 2 UAVs and 1 helicopter at predetermined positions; initialize grid G with prior UUV probability values.  2: while mission is not terminated and elapsed time $<T_{max}$ do  3:    for each UAV do  4:        PERFORM SENSOR SCAN.  5:        if detection probability in a cell $\ge {\theta }_s$ then  6:            BROADCAST detection and UPDATE grid G.  7:        end if  8:    end for  9:    for each UAV do 10:       FOLLOW fixed, predetermined heading rules to traverse the grid. 11:       CHECK inter-agent distances. 12:       if distance $<d_{col}$ then 13:           EXECUTE COLLISION AVOIDANCE maneuver. 14:       end if 15:    end for 16:    if overall detection confidence > threshold then 17:       DEPLOY sonar buoys and RELEASE munitions to neutralize the UUV. 18:    end if 19: end while 20: RETURN Mission termination signal.

Algorithm 3 Blue submarine evasion algorithm.

INPUT:  Sensor data, detection threshold ${\theta }_r$, mission route information OUTPUT:  Updated navigation commands  1: Initialize: Begin mission on a predetermined route  2: while mission is active do  3:     Monitor the environment for Red target presence  4:     if Red target is detected then  5:        Compute the relative distance d and angle $\theta$ using sonar data  6:        Determine the evasion trajectory using the circular linking method:  7:           Construct an evasion circle centered at the Red target’s last known position  8:        Calculate the heading relative to the circle center to choose the optimal circumferential direction  9:        Execute the evasion maneuver: adjust heading and speed accordingly 10:    else 11:       Continue along the predetermined route while monitoring the environment 12:    end if 13: end while 14: Return to continuous monitoring

4.3. Reinforcement Learning-Based Results

The performances of the proposed MADSAC algorithm and the standard SAC and MADDPG algorithms are evaluated under the same simulation conditions.

Table 8. Performance metrics’ comparison.

Algorithm	Detection Success Rate (%)	Mission Completion Time (min)
Rule-Based	52.0	13
SAC	64.5	11.8
MADDPG	76.8	10.1
MADSAC	93.0	8

compares key performance metrics between the rule-based method and our reinforcement learning (RL)-based approach.

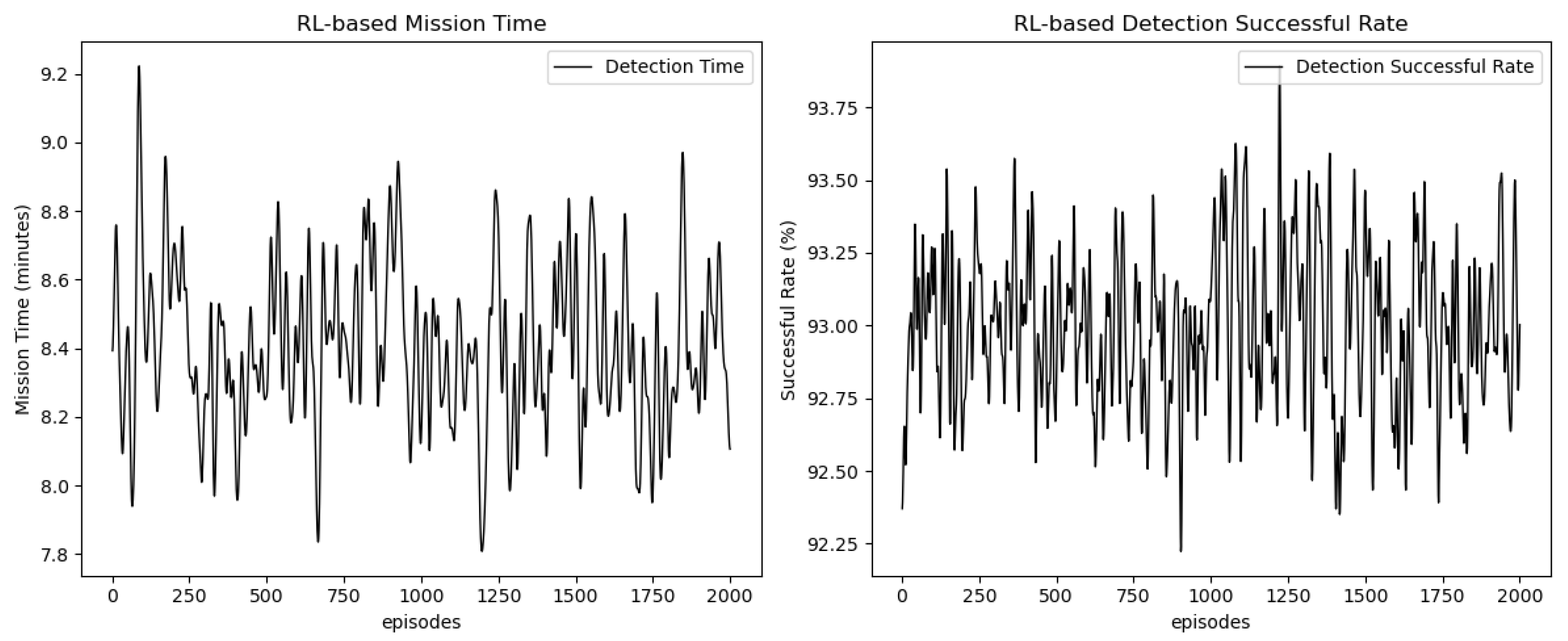
As shown in Figure 3, the task execution time and detection success rate, based on the proposed MADSAC approach, exhibit distinct trends over the course of 2000 episodes.

The task execution time (left panel) fluctuates throughout the training process, showing minor variations between episodes. These fluctuations might be due to the continuous adaptation of the RL agent’s behavior and the exploration of various strategies during training. Despite the fluctuations, the overall task execution time seems to stabilize over time, indicating that the RL agent is becoming more efficient in task completion as training progresses.

The detection success rate (right panel) follows a similar pattern, with slight oscillations but a general upward trend. This suggests that as the agent learns from its experiences, it gradually improves its ability to successfully detect tasks. The agent’s performance improves as it adapts to the environment and refines its detection strategy, achieving a success rate exceeding 90% towards the later stages of the training.

Figure 4 illustrates the reward change trend of three reinforcement learning algorithms (MADDPG, MADSAC, SAC) during the training process. It can be seen from the figure that MADSAC is better than MADDPG and SAC in terms of convergence speed and the final reward value. MADSAC converges in 1350 episodes, while MADDPG needs 1650 episodes and falls into a local optimum. SAC still has large fluctuations in the later stage. Compared with MADDPG, the algorithm proposed in this paper adopts maximum entropy to increase the robustness of the algorithm and uses a dual evaluation network to alleviate the overestimation problem. Compared with SAC, the algorithm proposed in this paper adopts the CTDE training framework, which can obtain the information of all intelligent agents during the training stag and, at the same time, constructs a neural network that can adaptively adjust the coefficient size according to the randomness of the strategy, effectively balancing the exploration and stability of the strategy.

Overall, the results demonstrate that the proposed algorithm improves both task execution time and detection success rate over time, though the fluctuations in rewards reflect the agent’s exploration and learning process. These findings suggest that further optimization could potentially enhance the stability of task execution time and rewards, while continuing to improve detection success.

5. Discussion

The results of our experiments highlight the effectiveness of the proposed Knowledge-Enhanced Multi-Agent Deep Reinforcement Learning (MADRL) framework in addressing the challenges posed by adversarial UUVs in naval confrontation scenarios. The integration of prior intelligence with real-time sensor data through a probabilistic adversarial model significantly enhances the Red team’s ability to predict and counteract Blue team maneuvers. The Multi-Agent Double Soft Actor–Critic (MADSAC) algorithm effectively addresses the coordination challenges among UAVs, including dynamic credit assignment and partial observability. Compared to traditional rule-based methods, our RL-based approach demonstrates substantial improvements in both detection success rates and mission completion times. The rule-based methods, while computationally efficient and interpretable, struggle with the dynamic and unpredictable nature of adversarial UUVs. In contrast, the RL-based approach, particularly with the MADSAC algorithm, shows a remarkable ability to adapt to changing environments and adversarial tactics, resulting in a 78.8% improvement in detection success rates and a 38.5% reduction in mission completion times.

However, the RL-based approach is not without its limitations. The high sample complexity and computational cost associated with training multi-agent systems remain significant hurdles. Additionally, the non-stationarity of multi-agent environments can lead to unstable training and difficulties in credit assignment. Future research could focus on further reducing sample complexity and improving the stability of training processes, possibly through off-policy correction methods (e.g., importance sampling-based approaches) and meta-learning strategies, which can help mitigate sample inefficiency and improve adaptability without requiring excessively large datasets.

6. Conclusions

In conclusion, this paper presents a novel Knowledge-Enhanced Multi-Agent Deep Reinforcement Learning (MADRL) framework designed to enhance the coordination and effectiveness of UAV swarms in countering adversarial UUVs. The proposed framework integrates a probabilistic adversarial model, a Multi-Agent Double Soft Actor–Critic (MADSAC) algorithm to address the challenges of dynamic credit assignment, partial observability, and high training complexity. Experimental results demonstrate significant improvements in detection success rates and mission completion times compared to traditional rule-based methods. These findings underscore the potential of RL-based approaches in complex, multi-agent adversarial scenarios, paving the way for future advancements in autonomous naval confrontation systems. Future work will focus on further optimizing the training process and exploring hybrid approaches to enhance the robustness and efficiency of multi-agent reinforcement learning in dynamic environments.