Distributed Pursuit–Evasion Game Decision-Making Based on Multi-Agent Deep Reinforcement Learning
Abstract
1. Introduction
- This paper investigates the dynamic PEG problem for multiple fixed-wing UAVs and proposes a distributed control method based on automatic subgame curriculum learning and MAPPO. In contrast to previous studies that typically assume fixed or simplistic evader strategies, our method employs a self-play mechanism to jointly train both pursuer and evader policies. This enables adaptive and dynamic encirclement of more capable and intelligent evaders.
- A reward structure tailored for encirclement missions is introduced in this paper. Unlike methods that rely solely on distance or UAV orientation to determine task success, our approach takes into account the dynamic surrounding of the evader while ensuring the safety of the pursuer, guiding the pursuer to perform effective encirclement without compromising its own security.
- To address the challenges of self-play solution difficulties and low sample efficiency, a training framework based on subgame curriculum learning and MAPPO is proposed. Compared to manually designed curricula or empirically determined subgame sequences, the proposed framework strategically plans the learning order by integrating self-guided subgame sampling. This enhances both sampling and learning efficiency while reducing reliance on human expertise and subjective bias.
2. Preliminaries
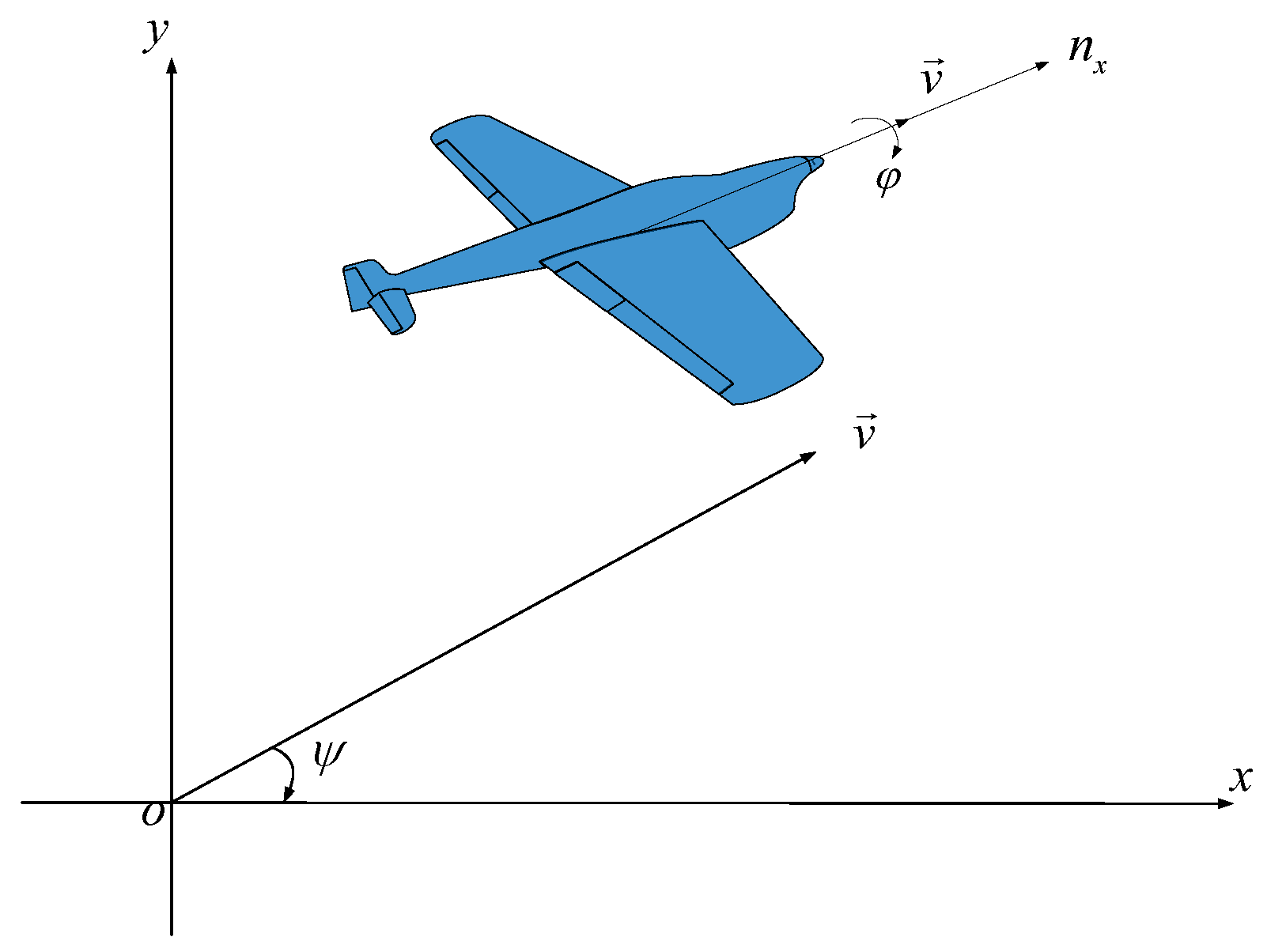
2.1. UAV Dynamics Model
2.2. Markov Game
2.3. Proximal Policy Optimization
3. Problem Formulation and Methods
3.1. Problem Statement
3.2. Pursuit–Evasion Scene
3.2.1. State Representation and Observation Model
3.2.2. Action Space
3.2.3. Reward Structure
- Relative distance-related reward. To encourage the pursuer to approach the evader and the evader to distance themselves from the pursuer, rewards and penalties are assigned based on the distance between the two parties. In addition, a stepwise reward and penalty scheme based on relative distance is designed. This metric is defined as follows.where and represent the relative distance-related reward of pursuers and evaders, respectively. and are the position vectors of pursuers i and the evader, respectively. denotes the weight coefficient of the relative distance-related reward term. When the relative distance between the pursuer and the evader is larger than the threshold , the evader is considered to have achieved victory. A significant reward is assigned to the evader, while a substantial penalty is imposed on the pursuer to encourage it to close the distance. When the relative distance falls below , the pursuer is deemed to have partially achieved its objective and is accordingly granted a reward. The thresholds and are determined by the farthest attack range and field of view of UAVs, respectively. Under this reward design, pursuers are encouraged to approach the evader while avoiding excessive proximity, thereby maintaining their own safety.
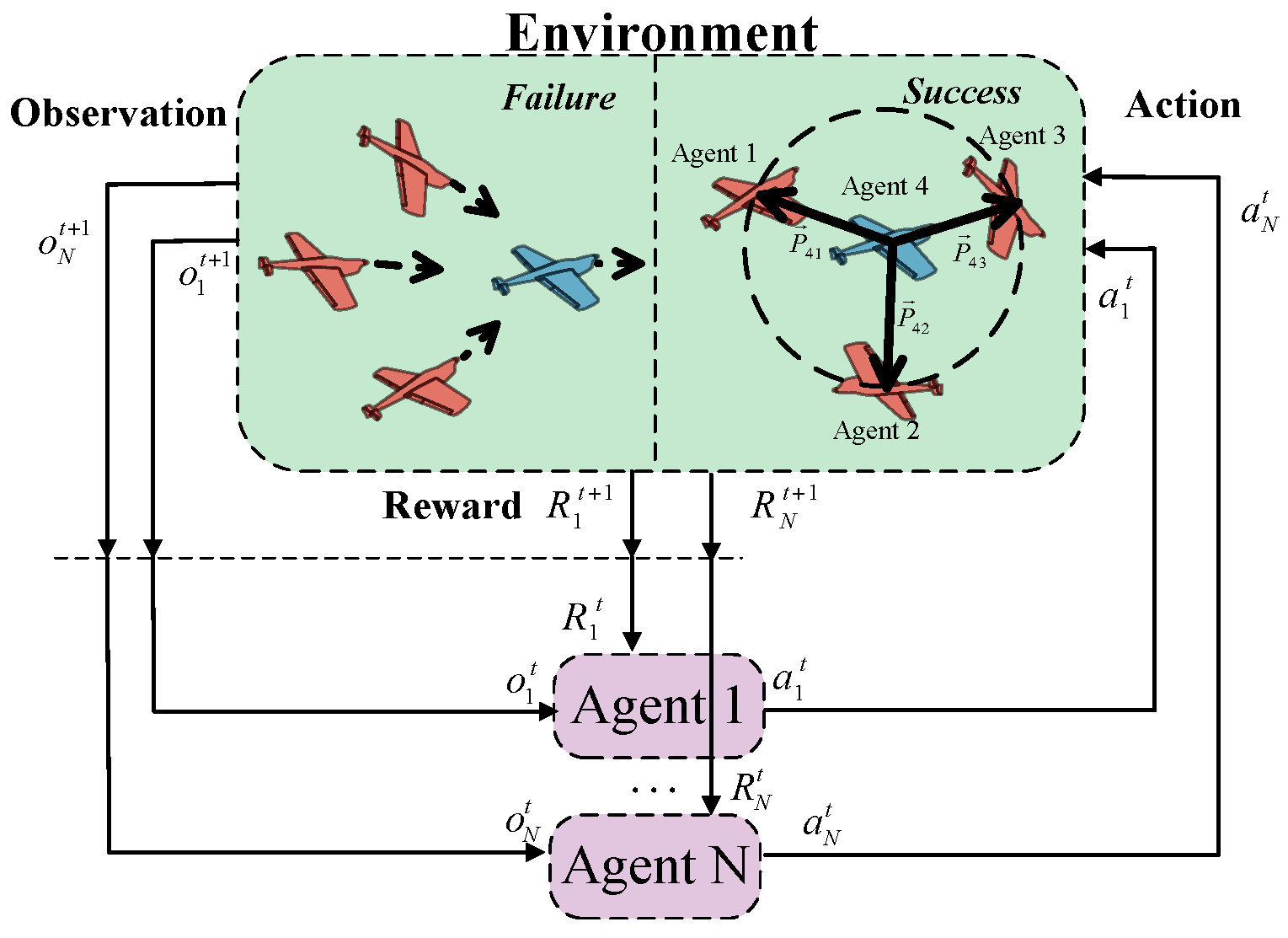
- Encirclement formation-related reward. To guide pursuers toward forming an encircling configuration around the evader, we employ a cosine-based metric to measure angular uniformity. This geometric formulation penalizes colinear configurations and encourages dispersion around the target. The reward term is defined as follows.where and represent the encirclement formation-related reward of pursuers and evaders, respectively. denotes the weight coefficient of the encirclement formation-related reward term. This formulation promotes pursuers spreading out in opposing directions around the evader, increasing the probability of successful encirclement.
- Mission success-related reward. A reward is provided for successful task completion. In this study, the pursuers succeed if they form a uniform encirclement around the evader within a certain distance; otherwise, the evader is considered successful. Therefore, task success is determined in conjunction with the encirclement-related rewards defined in (20) and (21). The specific reward for task completion is defined as follows.where and represent the mission success-related reward of pursuers and evaders, respectively. The criteria for task success include constraints on both the capture formation and the relative distances. Specifically, the task is considered successfully completed if the angles between the direction vectors from the evader to each pursuer are all obtuse, and the maximum distance between the evader and any pursuer does not exceed . With this task success reward, the pursuers are guided to form an encirclement near the farthest attack range of the evader, effectively constraining the escape space of the evader while maximizing their own safety.
3.3. Framework Design
3.4. Subgame Curriculum Learning
3.4.1. Subgame Sampling Metric
3.4.2. Subgame Sampler
| Algorithm 1 Subgame Curriculum Learning |
Require: State buffers with capacity K, probability p for sampling initial state in the state buffers, experience replay buffer , and Markov game environment .
|
3.5. Multi-Agent Reinforcement Learning
| Algorithm 2 MAPPO |
Require: Markov game environment , empty experience replay buffer , learning rate , for the actor network and critic network.
|
4. Results
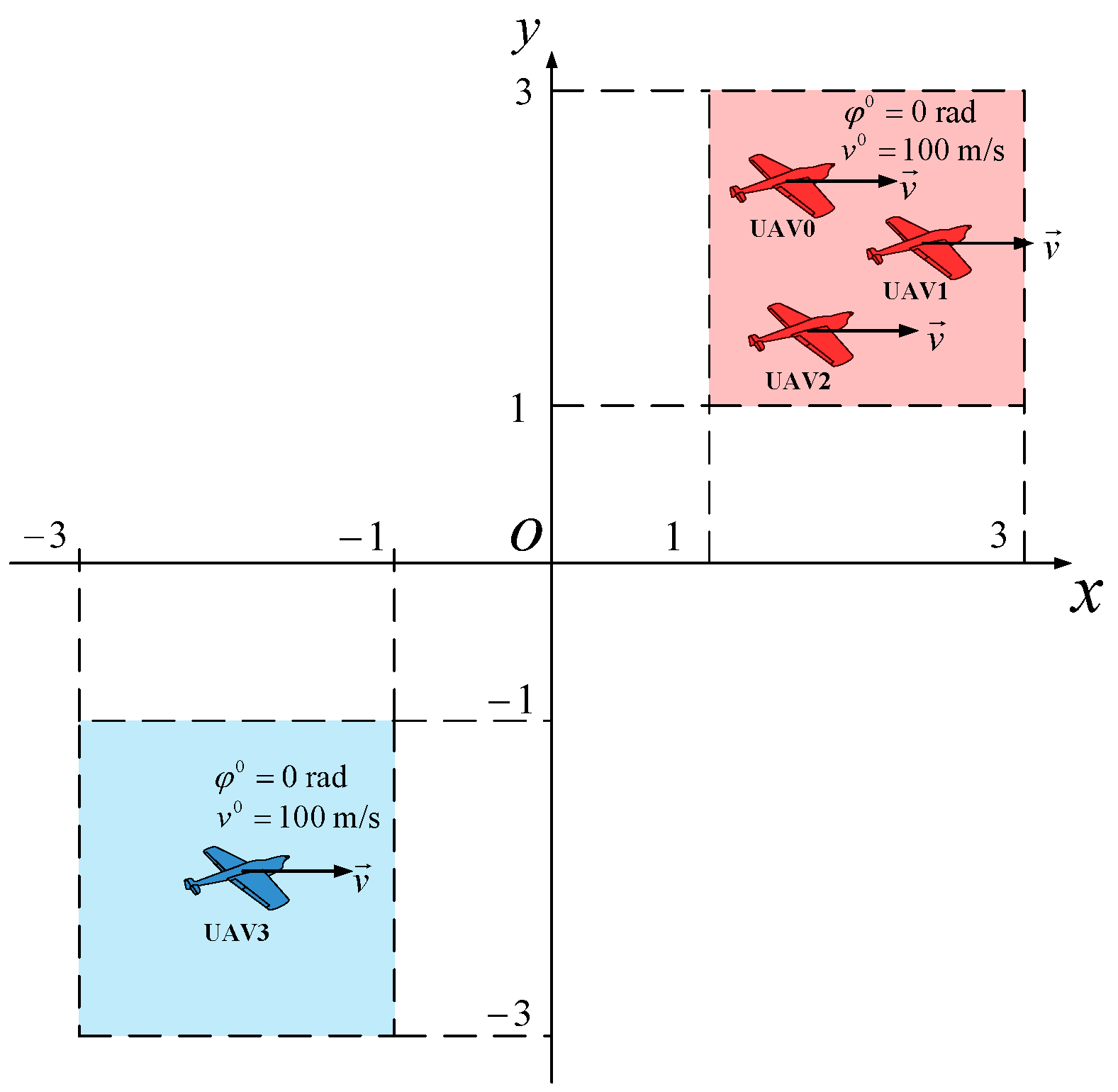
4.1. Simulation Setup
4.1.1. Environmental Parameters
4.1.2. Hyperparameters of Algorithm
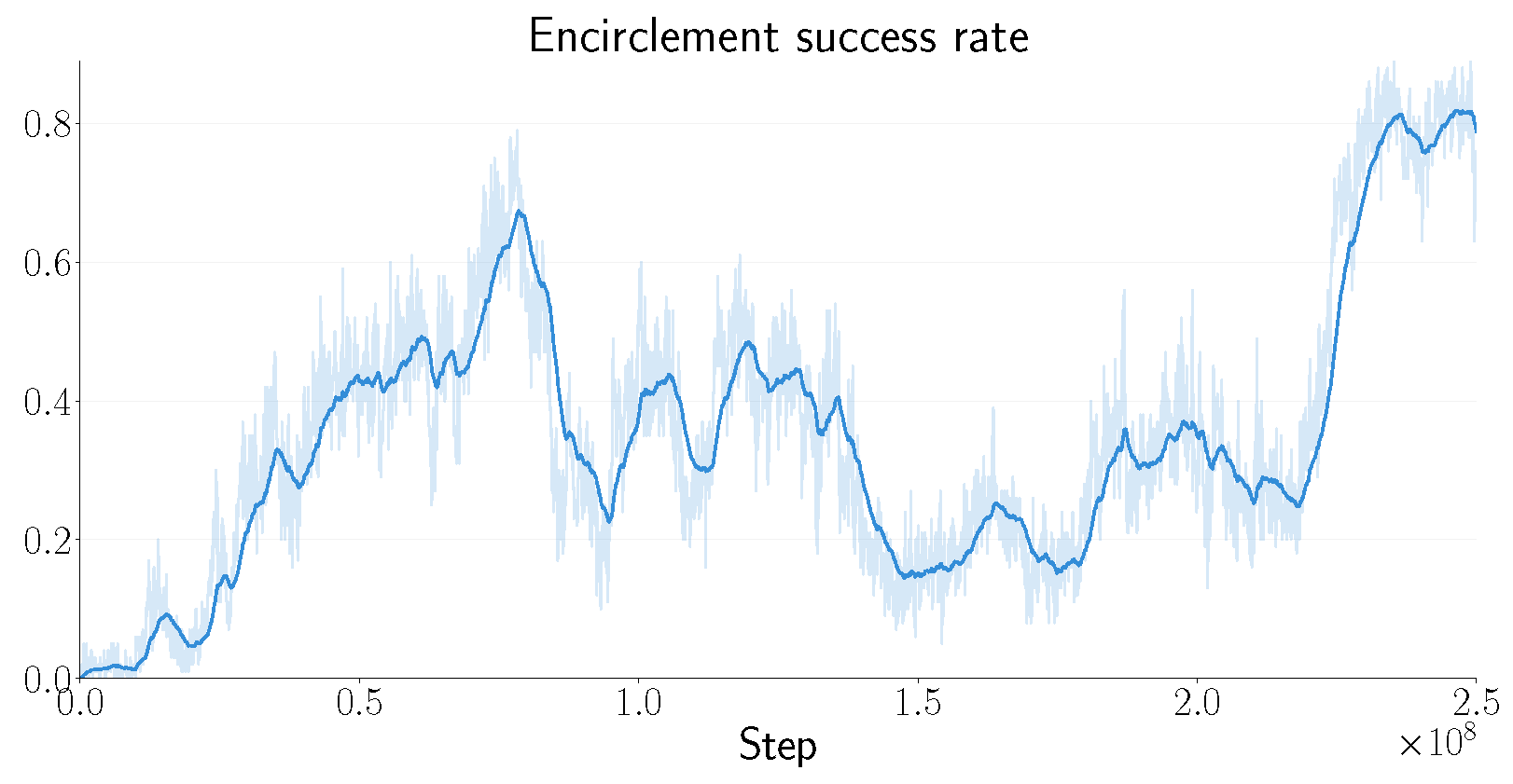
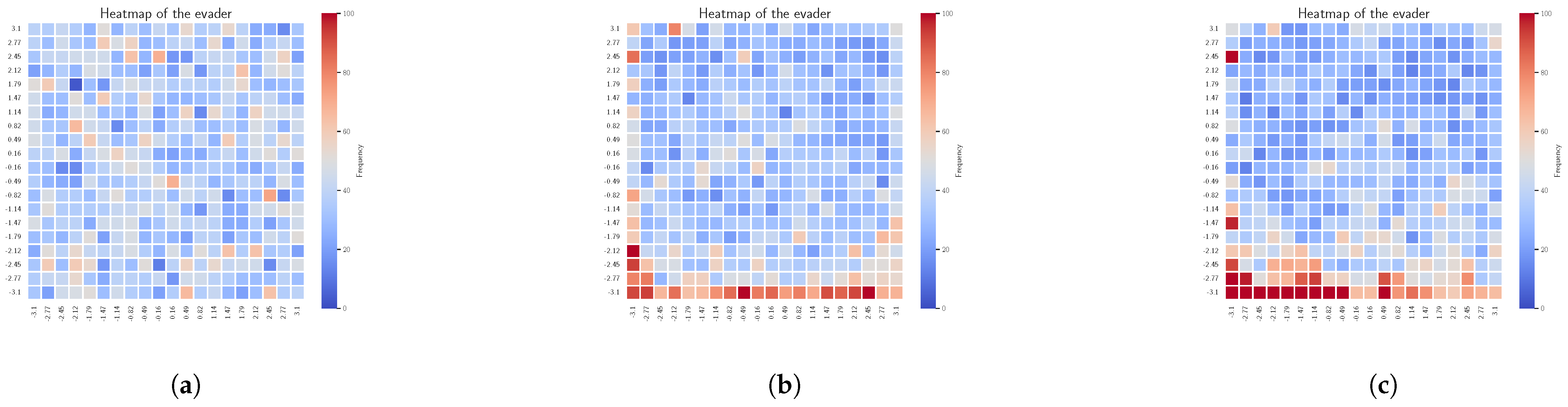
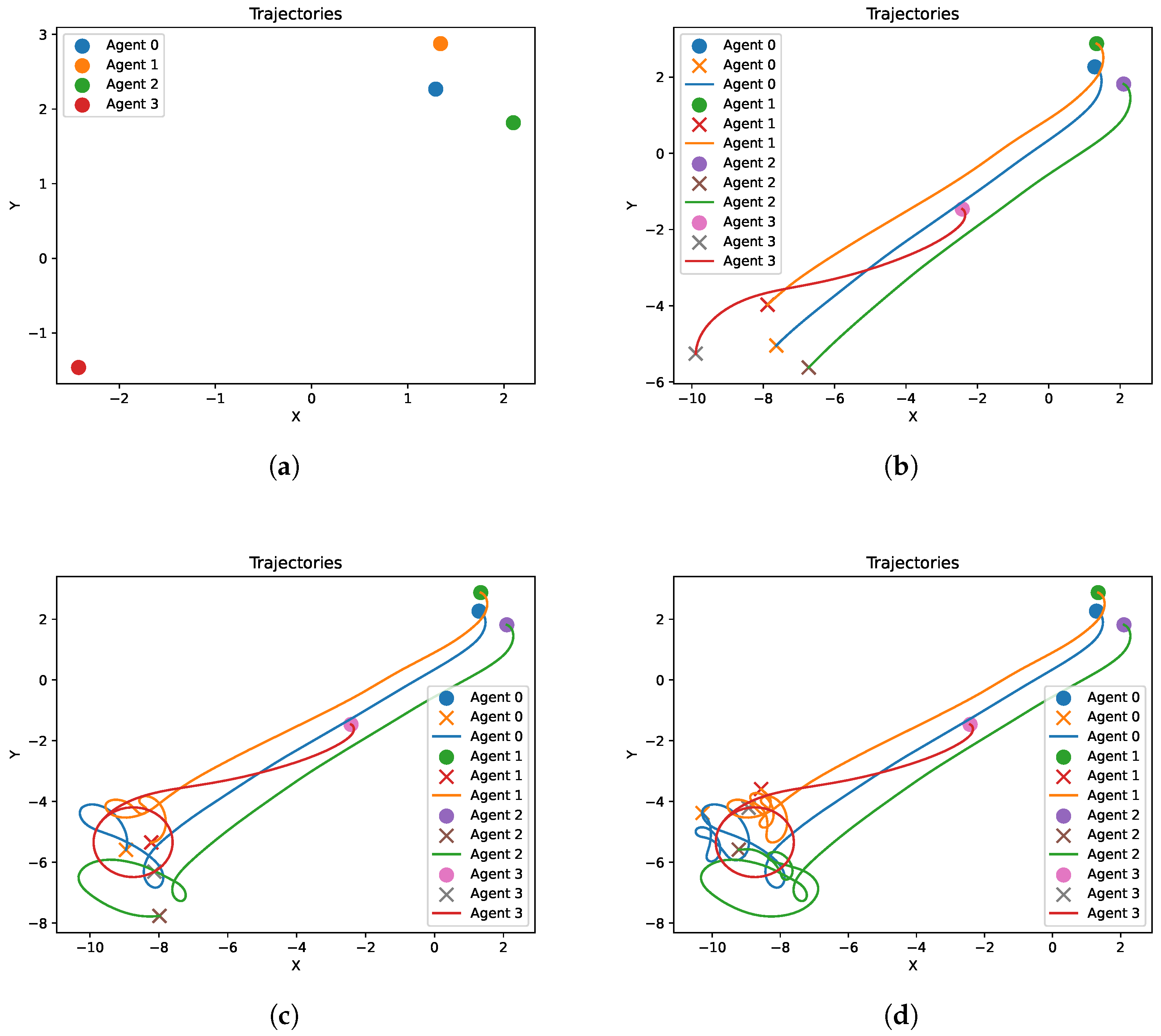
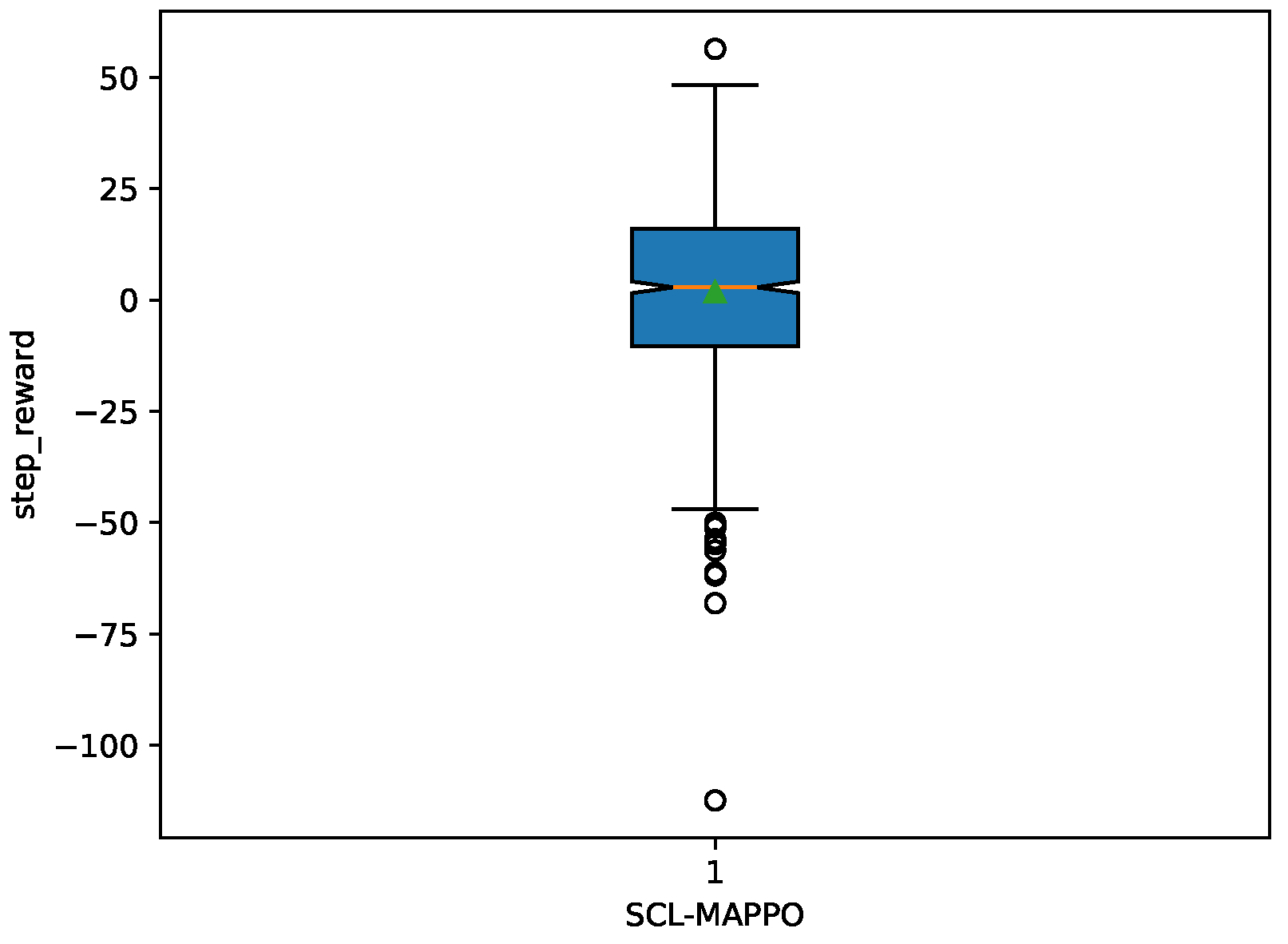
4.2. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schedl, D.C.; Kurmi, I.; Bimber, O. An autonomous drone for search and rescue in forests using airborne optical sectioning. Sci. Robot. 2021, 6, eabg1188. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Jiang, F.; Zhang, B.; Ma, R.; Hao, Q. Development of UAV-based target tracking and recognition systems. IEEE Trans. Intell. Transp. Syst. 2019, 21, 3409–3422. [Google Scholar] [CrossRef]
- Von Moll, A.; Garcia, E.; Casbeer, D.; Suresh, M.; Swar, S.C. Multiple-pursuer, single-evader border defense differential game. J. Aerosp. Inf. Syst. 2020, 17, 407–416. [Google Scholar] [CrossRef]
- Isaacs, R. Differential Games: A Mathematical Theory with Applications to Warfare and Pursuit, Control and Optimization; Courier Corporation: North Chelmsford, MA, USA, 1999. [Google Scholar]
- Li, S.; Wang, C.; Xie, G. Optimal strategies for pursuit-evasion differential games of players with damped double integrator dynamics. IEEE Trans. Autom. Control 2023, 69, 5278–5293. [Google Scholar] [CrossRef]
- Wang, C.; Chen, H.; Pan, J.; Zhang, W. Encirclement guaranteed cooperative pursuit with robust model predictive control. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 1473–1479. [Google Scholar]
- Zhang, Y.; Zhang, P.; Wang, X.; Song, F.; Li, C.; Hao, J. An open loop Stackelberg solution to optimal strategy for UAV pursuit-evasion game. Aerosp. Sci. Technol. 2022, 129, 107840. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, L.; Sun, C. Cooperative control for multi-player pursuit-evasion games with reinforcement learning. Neurocomputing 2020, 412, 101–114. [Google Scholar] [CrossRef]
- Zhang, R.; Zong, Q.; Zhang, X.; Dou, L.; Tian, B. Game of drones: Multi-UAV pursuit-evasion game with online motion planning by deep reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 7900–7909. [Google Scholar] [CrossRef]
- Kokolakis, N.M.T.; Vamvoudakis, K.G. Safety-aware pursuit-evasion games in unknown environments using gaussian processes and finite-time convergent reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 3130–3143. [Google Scholar] [CrossRef]
- Xiong, H.; Zhang, Y. Reinforcement learning-based formation-surrounding control for multiple quadrotor UAVs pursuit-evasion games. ISA Trans. 2024, 145, 205–224. [Google Scholar] [CrossRef]
- Xiao, J.; Feroskhan, M. Learning multi-pursuit evasion for safe targeted navigation of drones. IEEE Trans. Artif. Intell. 2024, 5, 2691–4581. [Google Scholar] [CrossRef]
- Chen, Y.; Shi, Y.; Dai, X.; Meng, Q.; Yu, T. Pursuit-evasion game with online planning using deep reinforcement learning. Appl. Intell. 2025, 55, 512. [Google Scholar] [CrossRef]
- Hung, S.M.; Givigi, S.N. A Q-learning approach to flocking with UAVs in a stochastic environment. IEEE Trans. Cybern. 2016, 47, 186–197. [Google Scholar] [CrossRef]
- Zhuang, X.; Li, D.; Li, H.; Wang, Y.; Zhu, J. A dynamic control decision approach for fixed-wing aircraft games via hybrid action reinforcement learning. Sci. China Inf. Sci. 2025, 68, 132201. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, J.; Shi, G.; Hu, J.; Wu, Y. Maneuver decision of UAV in short-range air combat based on deep reinforcement learning. IEEE Access 2019, 8, 363–378. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, H.; Wei, Y.; Huang, C. Autonomous maneuver decision-making method based on reinforcement learning and Monte Carlo tree search. Front. Neurorobot. 2022, 16, 996412. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, Z.; Jiang, J.; Deng, W.; Chen, X. Autonomous Air Combat Maneuver Decision-Making Based on PPO-BWDA. IEEE Access 2024, 12, 119116–119132. [Google Scholar] [CrossRef]
- Luo, D.; Fan, Z.; Yang, Z.; Xu, Y. Multi-UAV cooperative maneuver decision-making for pursuit-evasion using improved MADRL. Def. Technol. 2024, 35, 187–197. [Google Scholar] [CrossRef]
- Yan, T.; Liu, C.; Gao, M.; Jiang, Z.; Li, T. A Deep Reinforcement Learning-Based Intelligent Maneuvering Strategy for the High-Speed UAV Pursuit-Evasion Game. Drones 2024, 8, 309. [Google Scholar] [CrossRef]
- Li, L.; Zhang, X.; Qian, C.; Zhao, M.; Wang, R. Cross coordination of behavior clone and reinforcement learning for autonomous within-visual-range air combat. Neurocomputing 2024, 584, 127591. [Google Scholar] [CrossRef]
- Zhang, Y.; Ding, M.; Zhang, J.; Yang, Q.; Shi, G.; Lu, M.; Jiang, F. Multi-UAV pursuit-evasion gaming based on PSO-M3DDPG schemes. Complex Intell. Syst. 2024, 10, 6867–6883. [Google Scholar] [CrossRef]
- Wang, X.; Chen, Y.; Zhu, W. A survey on curriculum learning. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 4555–4576. [Google Scholar] [CrossRef] [PubMed]
- De Souza, C.; Newbury, R.; Cosgun, A.; Castillo, P.; Vidolov, B.; Kulić, D. Decentralized multi-agent pursuit using deep reinforcement learning. IEEE Robot. Autom. Lett. 2021, 6, 4552–4559. [Google Scholar] [CrossRef]
- Li, F.; Yin, M.; Wang, T.; Huang, T.; Yang, C.; Gui, W. Distributed Pursuit-Evasion Game of Limited Perception USV Swarm Based on Multiagent Proximal Policy Optimization. IEEE Trans. Syst. Man. Cybern. Syst. 2024, 54, 6435–6446. [Google Scholar] [CrossRef]
- Yan, C.; Wang, C.; Xiang, X.; Low, K.H.; Wang, X.; Xu, X.; Shen, L. Collision-avoiding flocking with multiple fixed-wing UAVs in obstacle-cluttered environments: A task-specific curriculum-based MADRL approach. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 10894–10908. [Google Scholar] [CrossRef]
- Wang, L.; Zheng, S.; Tai, S.; Liu, H.; Yue, T. UAV air combat autonomous trajectory planning method based on robust adversarial reinforcement learning. Aerosp. Sci. Technol. 2024, 153, 109402. [Google Scholar] [CrossRef]
- Li, B.; Wang, J.; Song, C.; Yang, Z.; Wan, K.; Zhang, Q. Multi-UAV roundup strategy method based on deep reinforcement learning CEL-MADDPG algorithm. Expert Syst. Appl. 2024, 245, 123018. [Google Scholar] [CrossRef]
- Zhao, B.; Zhao, Y.; Jia, S.; Li, Z.; Huo, M.; Qi, N. Curriculum Based Reinforcement Learning for Pursuit-Escape Game between Uavs in Unknown Environment. SSRN Prepr. 2024. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=5036940 (accessed on 21 May 2025).
- Chen, J.; Xu, Z.; Li, Y.; Yu, C.; Song, J.; Yang, H.; Fang, F.; Wang, Y.; Wu, Y. Accelerate multi-agent reinforcement learning in zero-sum games with subgame curriculum learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 11320–11328. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Timbers, F.; Bard, N.; Lockhart, E.; Lanctot, M.; Schmid, M.; Burch, N.; Schrittwieser, J.; Hubert, T.; Bowling, M. Approximate exploitability: Learning a best response in large games. arXiv 2020, arXiv:2004.09677. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Advances in Neural Information Processing Systems. Volume 30. [Google Scholar]
- Yu, C.; Velu, A.; Vinitsky, E.; Gao, J.; Wang, Y.; Bayen, A.; Wu, Y. The surprising effectiveness of ppo in cooperative multi-agent games. Adv. Neural Inf. Process. Syst. 2022, 35, 24611–24624. [Google Scholar]




| Hyperparameter | Value |
|---|---|
| Learning rate of actor network () | |
| Discount rate () | |
| GAE parameter () | |
| Gradient clipping | |
| Adam stepsize | |
| Entropy coefficient () | |
| Parallel threads | 100 |
| PPO clipping range () | |
| PPO epochs | 5 |
| Probability of subgame sampling (p) | |
| Capacity of the state buffer (K) | 10,000 |
| Weight of the value difference () |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Gao, H.; Xia, Y. Distributed Pursuit–Evasion Game Decision-Making Based on Multi-Agent Deep Reinforcement Learning. Electronics 2025, 14, 2141. https://doi.org/10.3390/electronics14112141
Lin Y, Gao H, Xia Y. Distributed Pursuit–Evasion Game Decision-Making Based on Multi-Agent Deep Reinforcement Learning. Electronics. 2025; 14(11):2141. https://doi.org/10.3390/electronics14112141
Chicago/Turabian StyleLin, Yanghui, Han Gao, and Yuanqing Xia. 2025. "Distributed Pursuit–Evasion Game Decision-Making Based on Multi-Agent Deep Reinforcement Learning" Electronics 14, no. 11: 2141. https://doi.org/10.3390/electronics14112141
APA StyleLin, Y., Gao, H., & Xia, Y. (2025). Distributed Pursuit–Evasion Game Decision-Making Based on Multi-Agent Deep Reinforcement Learning. Electronics, 14(11), 2141. https://doi.org/10.3390/electronics14112141








