Observer-Based Robust H∞ Control for Stochastic Markov Jump Delay Systems Through Dual Adaptive Sliding Mode Approach
Abstract
1. Introduction
2. Problem Statement and Preliminaries
3. Main Results
3.1. Observer Design
3.2. Sliding Surface Design
- (1)
- The closed-loop system, comprising SMDs (12) and (16), is shown to be robustly MSE stable under the condition = 0, encompassing all inaccuracies that are deemed allowable.
- (2)
- The subsequent performance criterion with index is maintained for every that belongs to the space, that is
3.3. Performance Analysis
3.4. SMC Law Synthesise
- Step 1
- Giving all the system parameters , , B, , , , , , and a prescribed performance index ;
- Step 2
- Using the MATLAB LMI Toolbox to solve the LMIs in Theorem 1 based on the parameters given in step 1 so as to obtain gain matrices and ;
- Step 3
- Parameter initialization before simulation, including step size h, , , , , , and , etc.
- Step 4
- Employing the Euler’s method to develop MATLAB code,for j = 1:N⋮end;in which denotes the mapping after discretization.
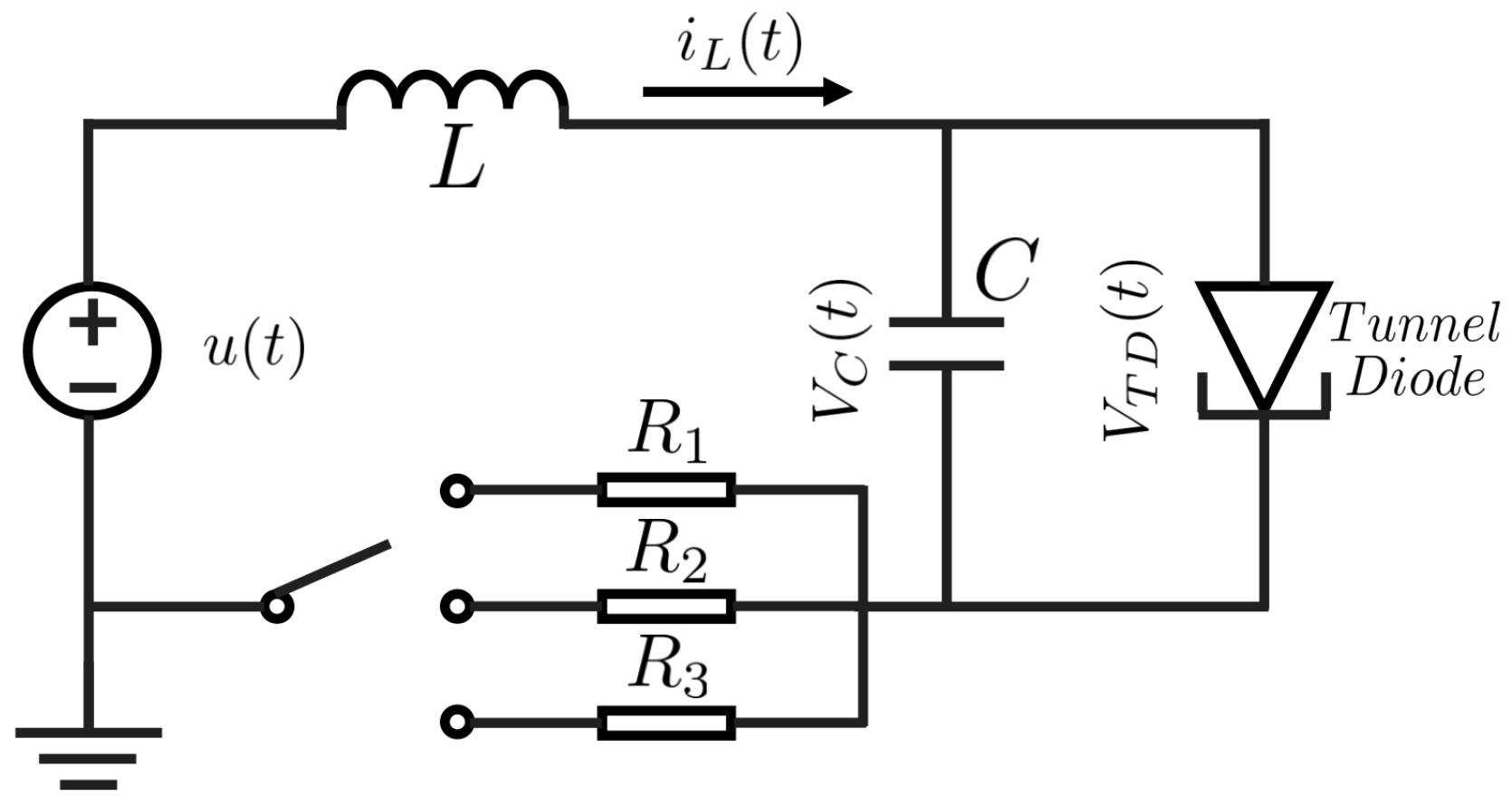
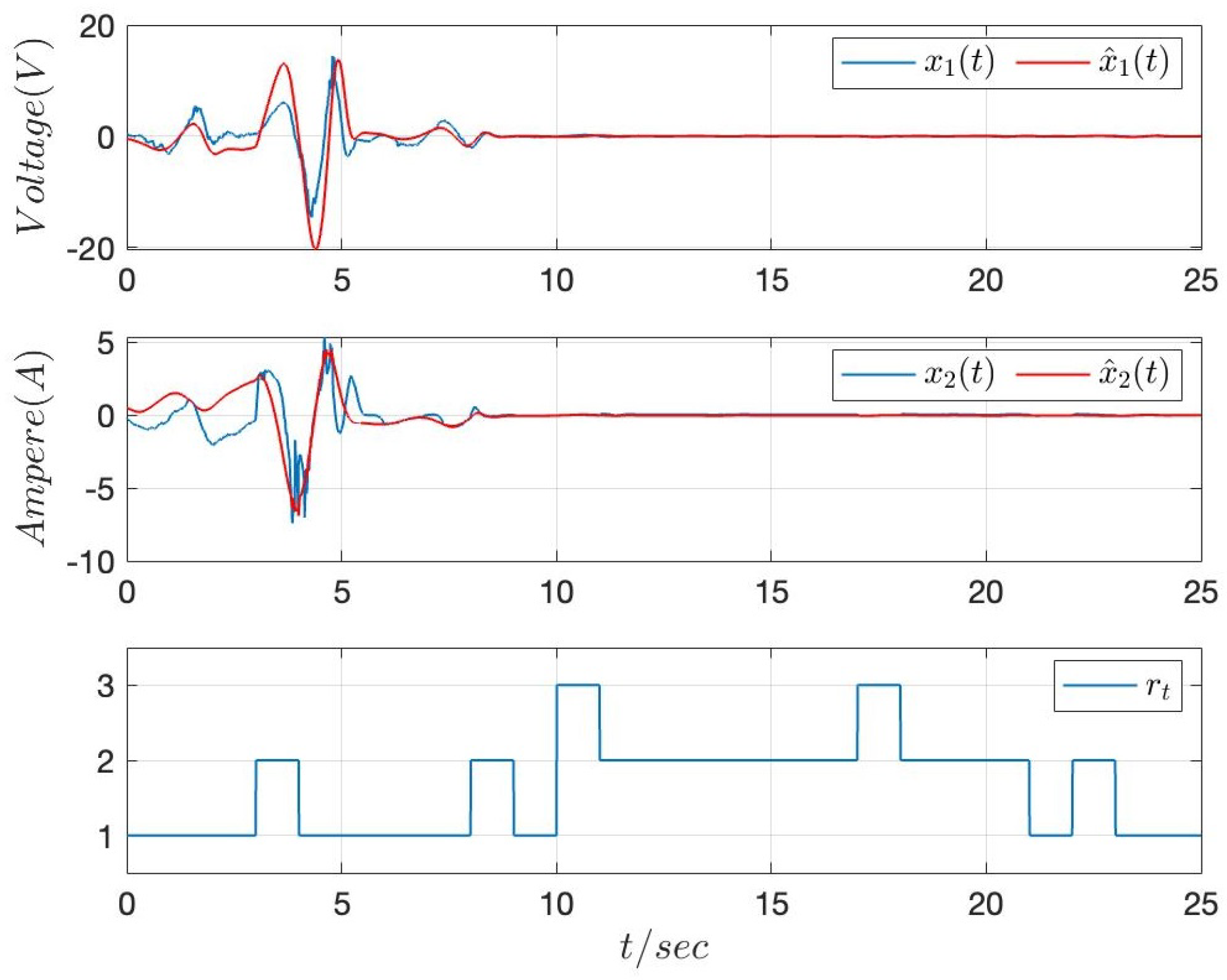
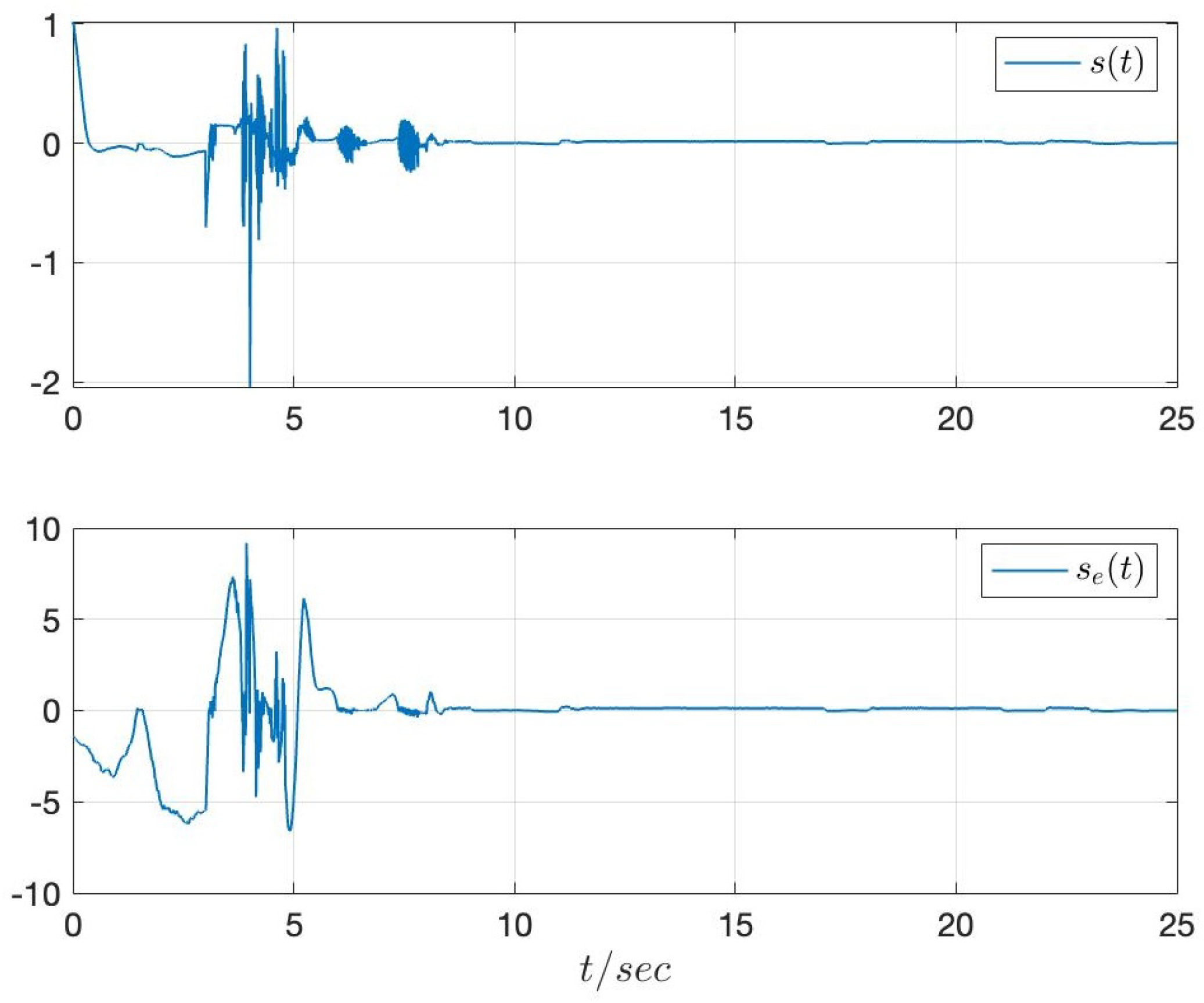
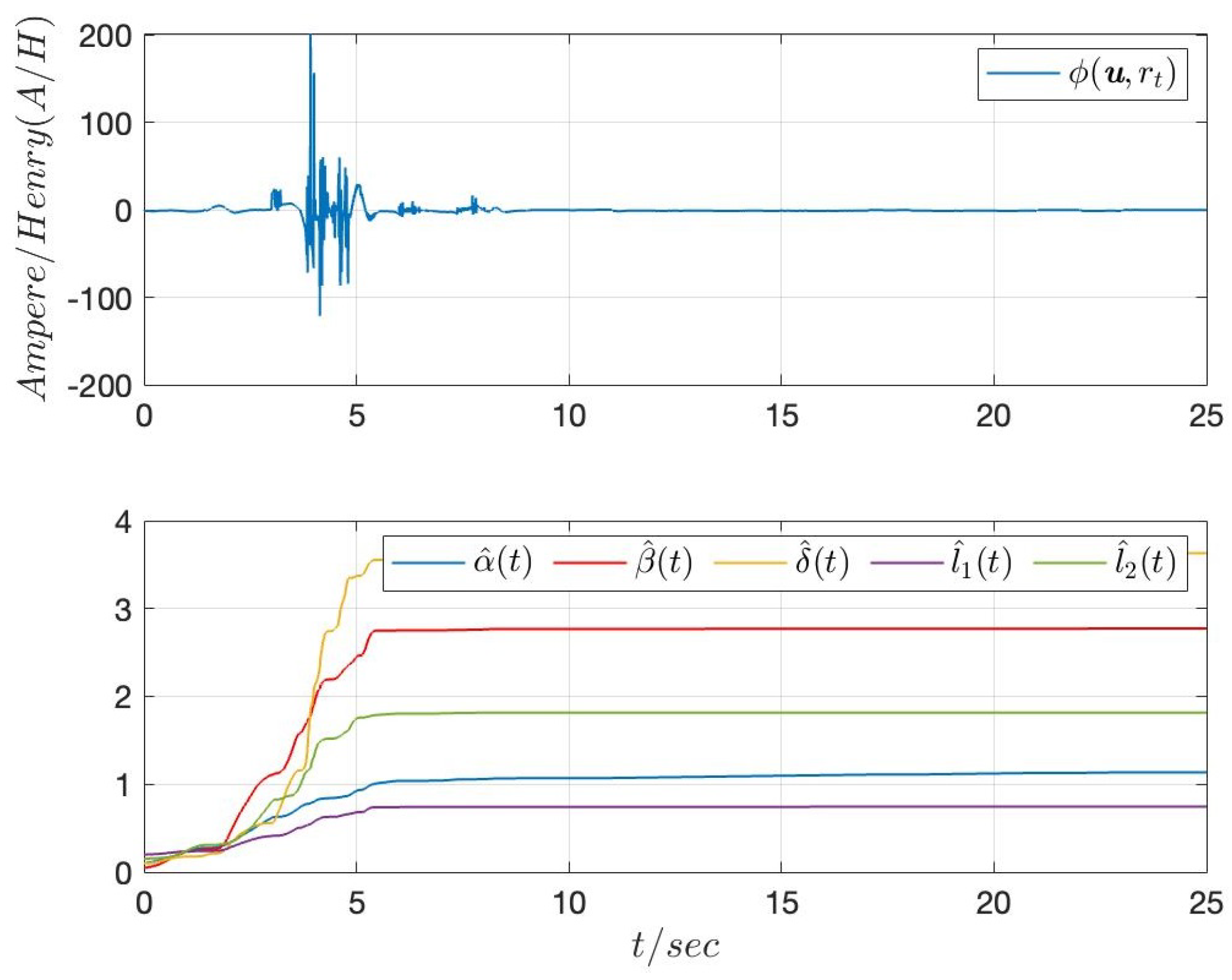
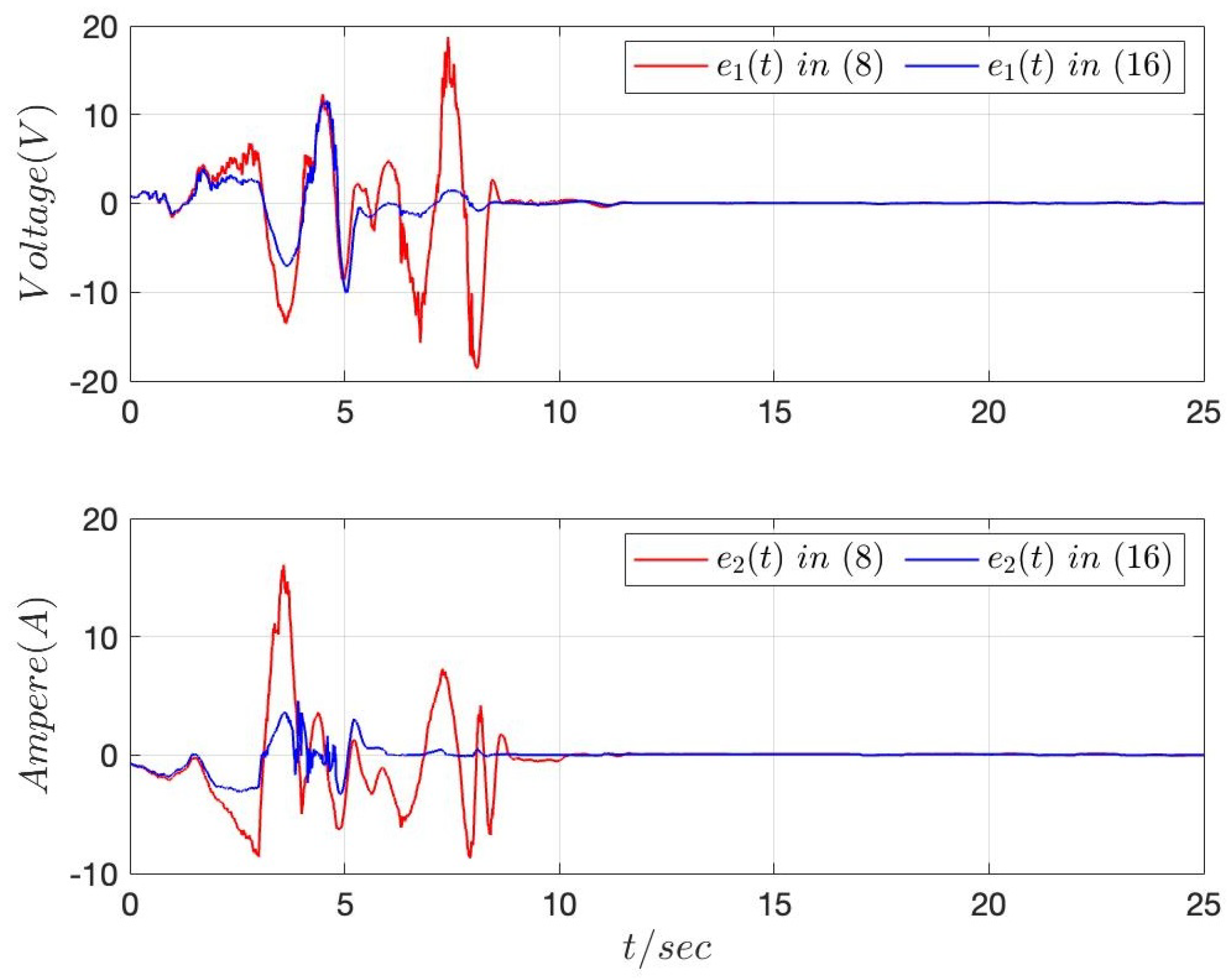
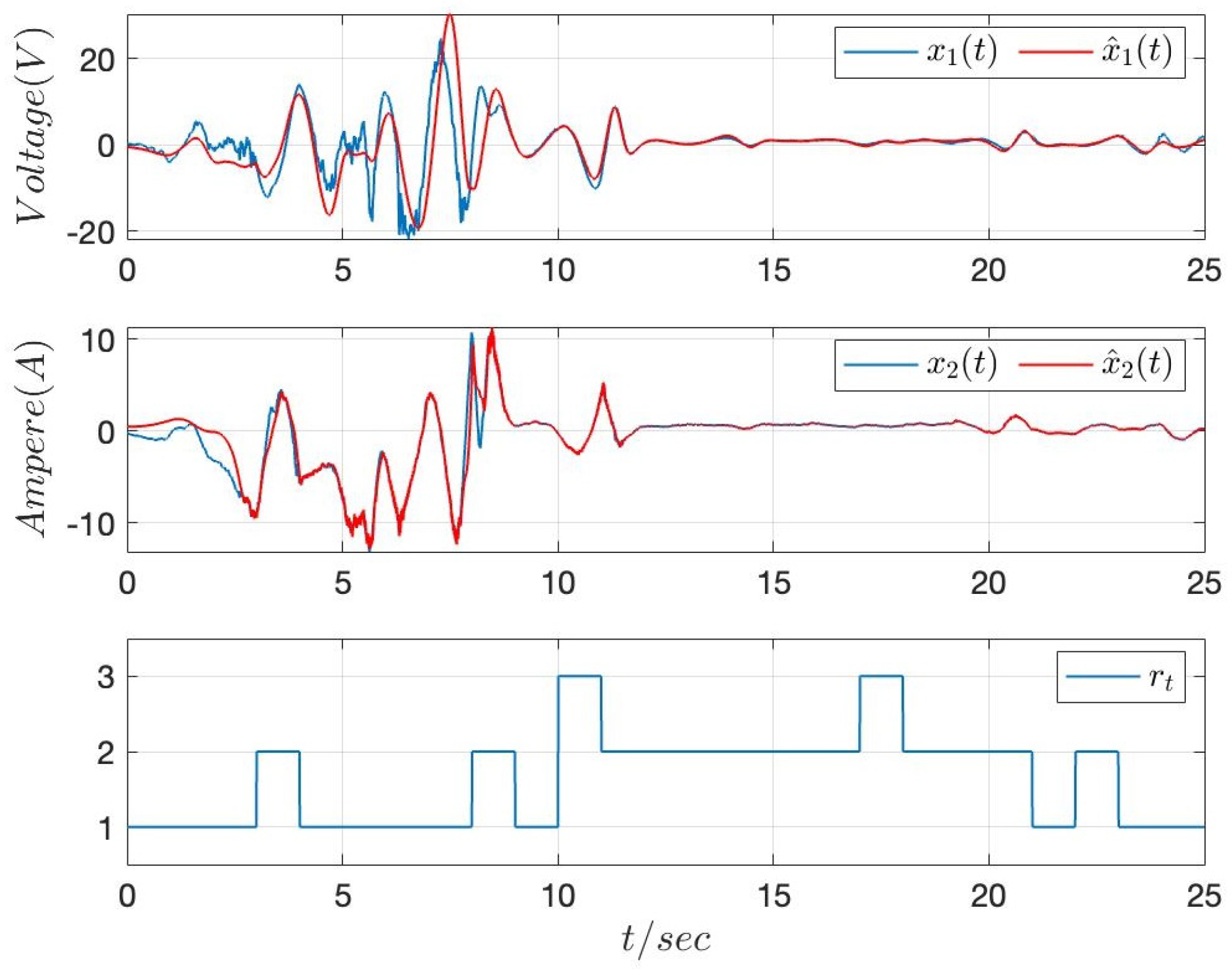
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proof for Theorem 1
Appendix B. Proof for Theorem 2
References
- Shi, P.; Li, F. A survey on Markovian jump systems: Modeling and design. Int. J. Control Autom. Syst. 2015, 13, 1–16. [Google Scholar] [CrossRef]
- Li, H.; Xu, Z.; Zhou, T.; Liu, Y. Event-based asynchronous dissipative control for nonhomogeneous Markov jump systems. Trans. Inst. Meas. Control 2024, 46, 430–441. [Google Scholar] [CrossRef]
- Zong, G.; Qi, W.; Karimi, H.R. l1 control of positive semi-Markov jump systems with state delay. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 7569–7578. [Google Scholar] [CrossRef]
- Jiang, B.; Wu, Z.; Liu, Z.; Li, B. Adaptive sliding mode security control of wheeled mobile manipulators with Markov switching joints against adversarial attacks. Control Eng. Pract. 2023, 137, 105558. [Google Scholar] [CrossRef]
- Zhai, D.; An, L.; Li, J.; Zhang, Q. Fault detection for stochastic parameter-varying Markovian jump systems with application to networked control systems. Appl. Math. Model. 2016, 40, 2368–2383. [Google Scholar] [CrossRef]
- Xu, S.; Lam, J.; Mao, X. Delay-dependent H∞ control and filtering for uncertain Markovian jump systems with time-varying delays. IEEE Trans. Circuits Syst. Regul. Pap. 2007, 54, 2070–2077. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, X.; Yu, J. Adaptive sliding mode security control for stochastic Markov jump cyber-physical nonlinear systems subject to actuator failures and randomly occurring injection attacks. IEEE Trans. Ind. Inform. 2022, 19, 3155–3165. [Google Scholar] [CrossRef]
- Jiang, B.; Kao, Y.; Gao, C.; Yao, X. Passification of uncertain singular semi-Markovian jump systems with actuator failures via sliding mode approach. IEEE Trans. Autom. Control 2017, 62, 4138–4143. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.; Liang, J.; Liu, X. Stability and synchronization of discrete-time Markovian jumping neural networks with mixed mode-dependent time delays. IEEE Trans. Neural Netw. 2009, 20, 1102–1116. [Google Scholar]
- Sakthivel, R.; Karimi, H.R.; Joby, M.; Santra, S. Resilient sampled-data control for Markovian jump systems with an adaptive fault-tolerant mechanism. IEEE Trans. Circuits Syst. II Express Briefs 2017, 64, 1312–1316. [Google Scholar] [CrossRef]
- Bolzern, P.; Colaneri, P.; De Nicolao, G. Stochastic stability of positive Markov jump linear systems. Automatica 2014, 50, 1181–1187. [Google Scholar] [CrossRef]
- Jiang, B.; Gao, C. Decentralized adaptive sliding mode control of large-scale semi-Markovian jump interconnected systems with dead-zone input. IEEE Trans. Autom. Control 2022, 67, 1521–1528. [Google Scholar] [CrossRef]
- Utkin, V.I.; Vadim, I. Sliding mode control. In Variable Structure Systems: From Principles to Implementation; Institution of Engineering and Technology: London, UK, 2004; Volume 66, p. 1. [Google Scholar]
- Islam, S.; Liu, X.P. Robust sliding mode control for robot manipulators. IEEE Trans. Ind. Electron. 2010, 58, 2444–2453. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, M.; Xu, J. Robust adaptive sliding mode control of underactuated autonomous underwater vehicles with uncertain dynamics. Ocean. Eng. 2019, 173, 802–809. [Google Scholar] [CrossRef]
- Balaji, B.; Ganesan, S.; Pugazhendiran, P.; Subramanian, S. Sliding mode controlled DC microgrid system with enhanced response. J. Control Decis. 2024, 11, 331–344. [Google Scholar] [CrossRef]
- Gao, H.; Wang, J.; Liu, X.; Xia, Y. Fuzzy fixed-time event-triggered consensus control for uncertain nonlinear multi-agent systems with memory based learning. IEEE Trans. Fuzzy Syst. 2024, 32, 3682–3692. [Google Scholar] [CrossRef]
- Gao, X.; Han, Y. Event-triggered sliding mode control for singular discrete-time fuzzy Markov jump networked systems. Trans. Inst. Meas. Control 2024, 46, 01423312241232377. [Google Scholar] [CrossRef]
- Li, F.; Wu, L.; Shi, P.; Lim, C.C. State estimation and sliding mode control for semi-Markovian jump systems with mismatched uncertainties. Automatica 2015, 51, 385–393. [Google Scholar] [CrossRef]
- Zhang, P.; Kao, Y.; Hu, J.; Niu, B. Robust observer-based sliding mode H∞ control for stochastic Markovian jump systems subject to packet losses. Automatica 2021, 130, 109665. [Google Scholar] [CrossRef]
- Ren, J.; He, G.; Fu, J. Robust H∞ sliding mode control for nonlinear stochastic TS fuzzy singular Markovian jump systems with time-varying delays. Inf. Sci. 2020, 535, 42–63. [Google Scholar] [CrossRef]
- Wang, Z.; Lam, J.; Liu, X. Exponential filtering for uncertain Markovian jump time-delay systems with nonlinear disturbances. IEEE Trans. Circuits Syst. II Express Briefs 2004, 51, 262–268. [Google Scholar] [CrossRef]
- Qin, Y.; Liang, Y.; Yang, Y.; Pan, Q.; Yang, F. Minimum upper-bound filter of Markovian jump linear systems with generalized unknown disturbances. Automatica 2016, 73, 56–63. [Google Scholar] [CrossRef]
- Wang, Z.; Qiao, H.; Burnham, K.J. On stabilization of bilinear uncertain time-delay stochastic systems with Markovian juming parameters. IEEE Trans. Autom. Control 2002, 47, 640–646. [Google Scholar] [CrossRef]
- Su, X.; Wang, C.; Chang, H.; Yang, Y.; Assawinchaichote, W. Event-triggered sliding mode control of networked control systems with Markovian jump parameters. Automatica 2021, 125, 109405. [Google Scholar] [CrossRef]
- Shi, P.; Liu, M.; Zhang, L. Fault-tolerant sliding-mode-observer synthesis of Markovian jump systems using quantized measurements. IEEE Trans. Ind. Electron. 2015, 62, 5910–5918. [Google Scholar] [CrossRef]
- Yan, H.; Meng, M.Q.; Zhang, H. Robust H∞ filtering for uncertain stochastic Markovian jump systems with mode-dependent time delays and nonlinear disturbances. In Proceedings of the 2009 Chinese Control and Decision Conference, Guilin, China, 17–19 June 2009; pp. 2104–2109. [Google Scholar]
- Xu, C.; Tong, D.; Chen, Q.; Zhou, W.; Shi, P. Exponential stability of Markovian juming systems via adaptive sliding mode control. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 954–964. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, J.; Wang, Y. Sliding-mode control for singular Markovian jump systems with Brownian motion based on stochastic sliding mode surface. IEEE Trans. Syst. Man Cybern. Syst. 2017, 49, 494–505. [Google Scholar] [CrossRef]
- Jiang, B.; Kao, Y.; Gao, C. Integrator-based robust sliding mode control of uncertain stochastic Markovian jump delay systems with non-linear perturbations. IET Control Theory Appl. 2017, 11, 1124–1133. [Google Scholar] [CrossRef]
- Shi, P.; Xia, Y.; Liu, G.P.; Rees, D. On designing of sliding-mode control for stochastic jump systems. IEEE Trans. Autom. Control 2006, 51, 97–103. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, J.; Meng, X.; Jiang, B. Observer-Based Robust H∞ Control for Stochastic Markov Jump Delay Systems Through Dual Adaptive Sliding Mode Approach. Electronics 2025, 14, 132. https://doi.org/10.3390/electronics14010132
Deng J, Meng X, Jiang B. Observer-Based Robust H∞ Control for Stochastic Markov Jump Delay Systems Through Dual Adaptive Sliding Mode Approach. Electronics. 2025; 14(1):132. https://doi.org/10.3390/electronics14010132
Chicago/Turabian StyleDeng, Jianping, Xin Meng, and Baoping Jiang. 2025. "Observer-Based Robust H∞ Control for Stochastic Markov Jump Delay Systems Through Dual Adaptive Sliding Mode Approach" Electronics 14, no. 1: 132. https://doi.org/10.3390/electronics14010132
APA StyleDeng, J., Meng, X., & Jiang, B. (2025). Observer-Based Robust H∞ Control for Stochastic Markov Jump Delay Systems Through Dual Adaptive Sliding Mode Approach. Electronics, 14(1), 132. https://doi.org/10.3390/electronics14010132




