Advancing Mapping Strategies and Circuit Optimization for Signed Operations in Compute-in-Memory Architecture
Abstract
1. Introduction
- We enhanced the existing ISP and IOSP mapping strategies to accommodate both signed/unsigned weights and signed/unsigned inputs in both DCIM and analog CIM.
- We modified the wiring of the adder tree and shift adders in DCIM architecture to enable the macro to support signed operation in SBIPW, ISP, and IOSP mapping strategies with minimal cost.
- We conducted performance validation of the improved array using the latest NeuroSim V1.4 [16], which facilitates the simulation of DCIM architectures. The results demonstrate that our enhancements to ISP and IOSP achieve a 4× and 3.59× improvement in energy efficiency for single-layer networks, respectively. The combined use of the three strategies in testing on Yolov3-tiny also achieved a 68.4% boost in energy efficiency and a 56.2% increase in speed.
2. The Proposed Bit-Level Mapping Strategy Optimization and Circuit Design for Signed Operations
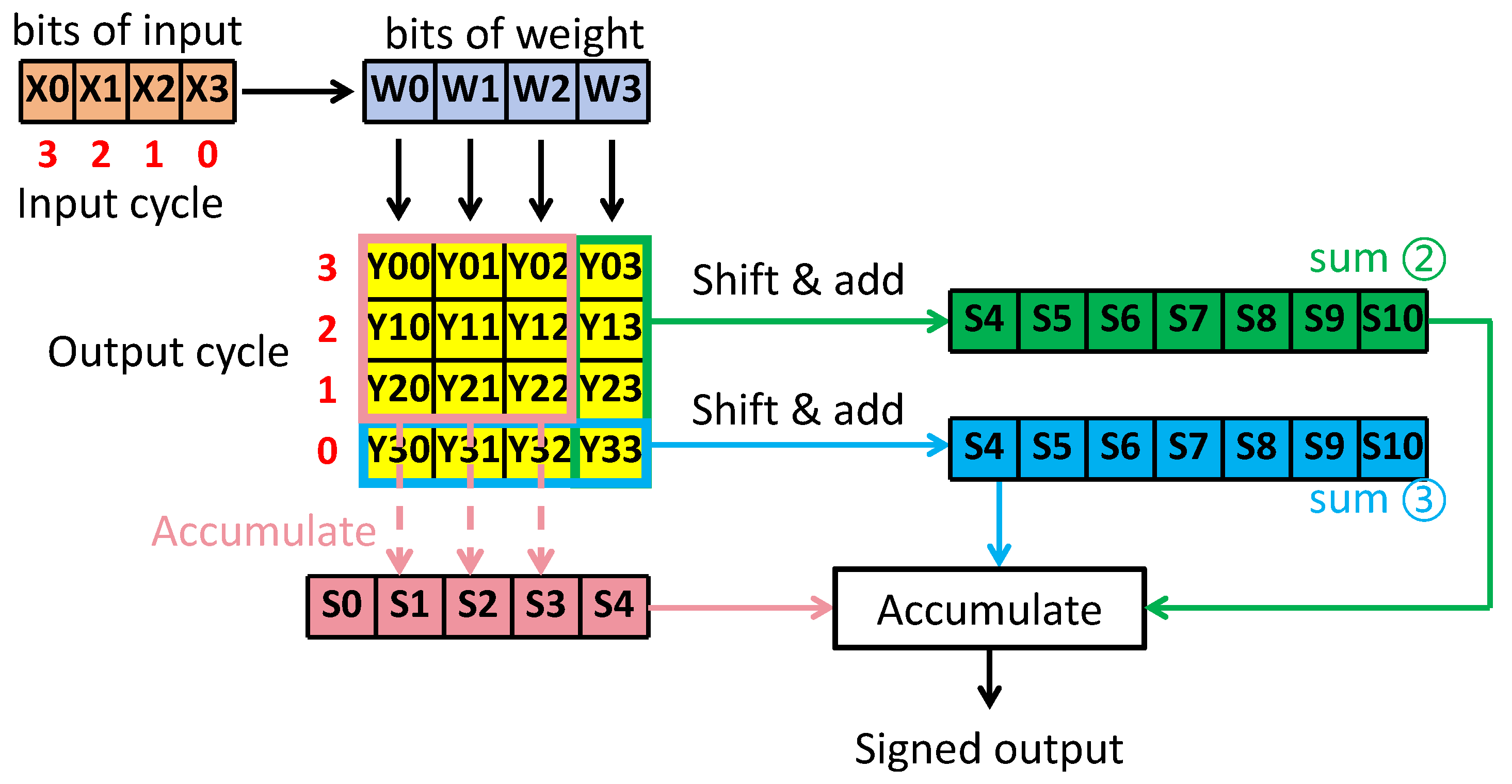
2.1. Improved Input-Side Parallel Mapping Strategy
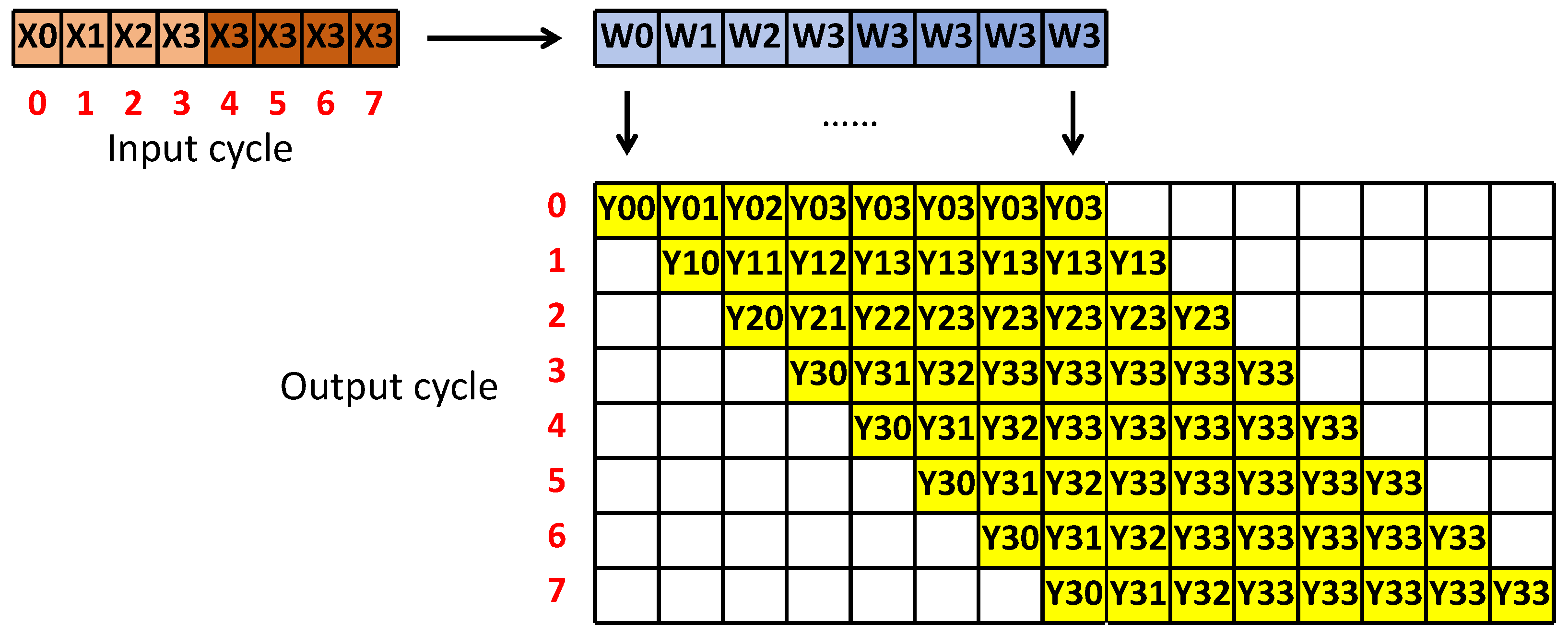
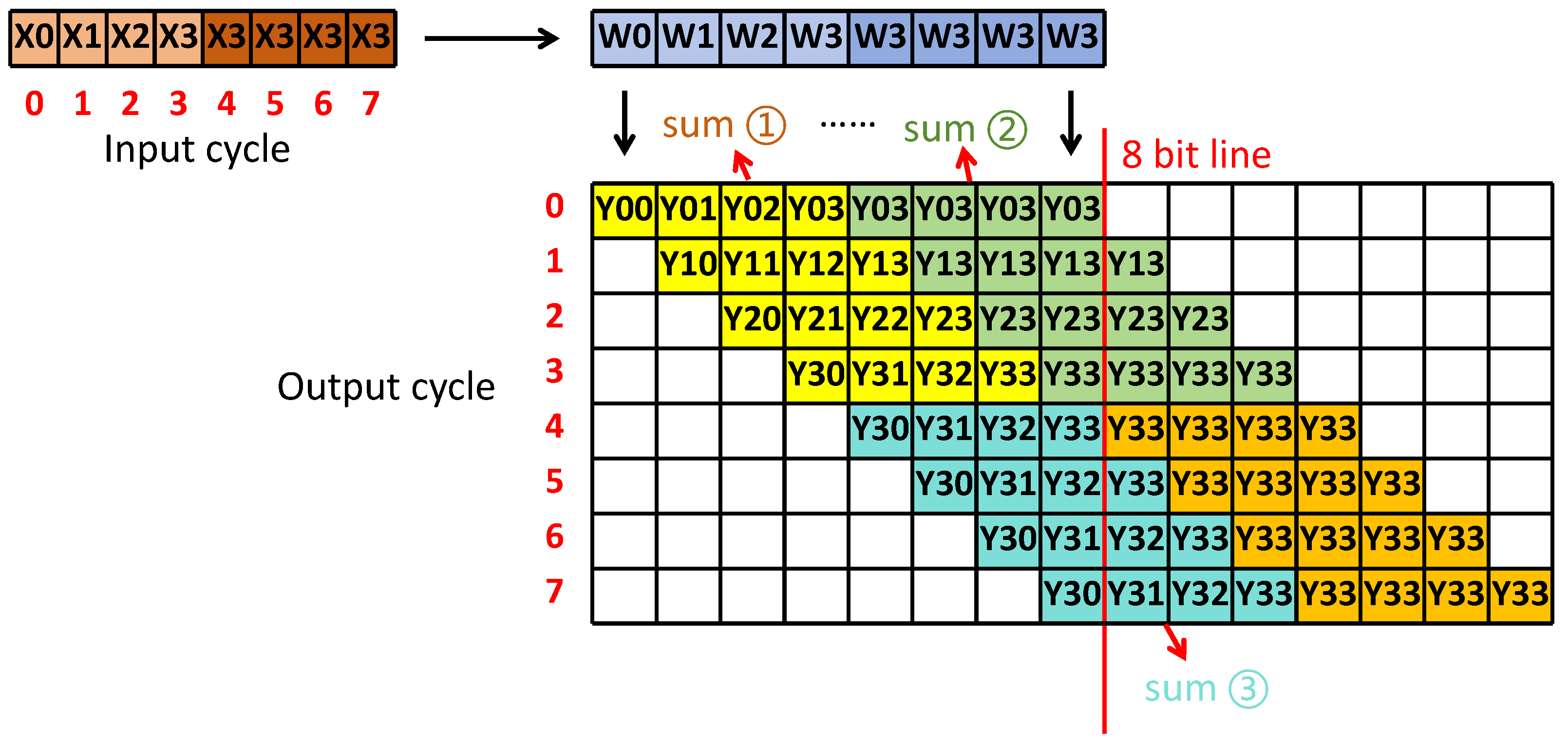
2.2. Improved Input- and Output-Side Parallel Mapping Strategy
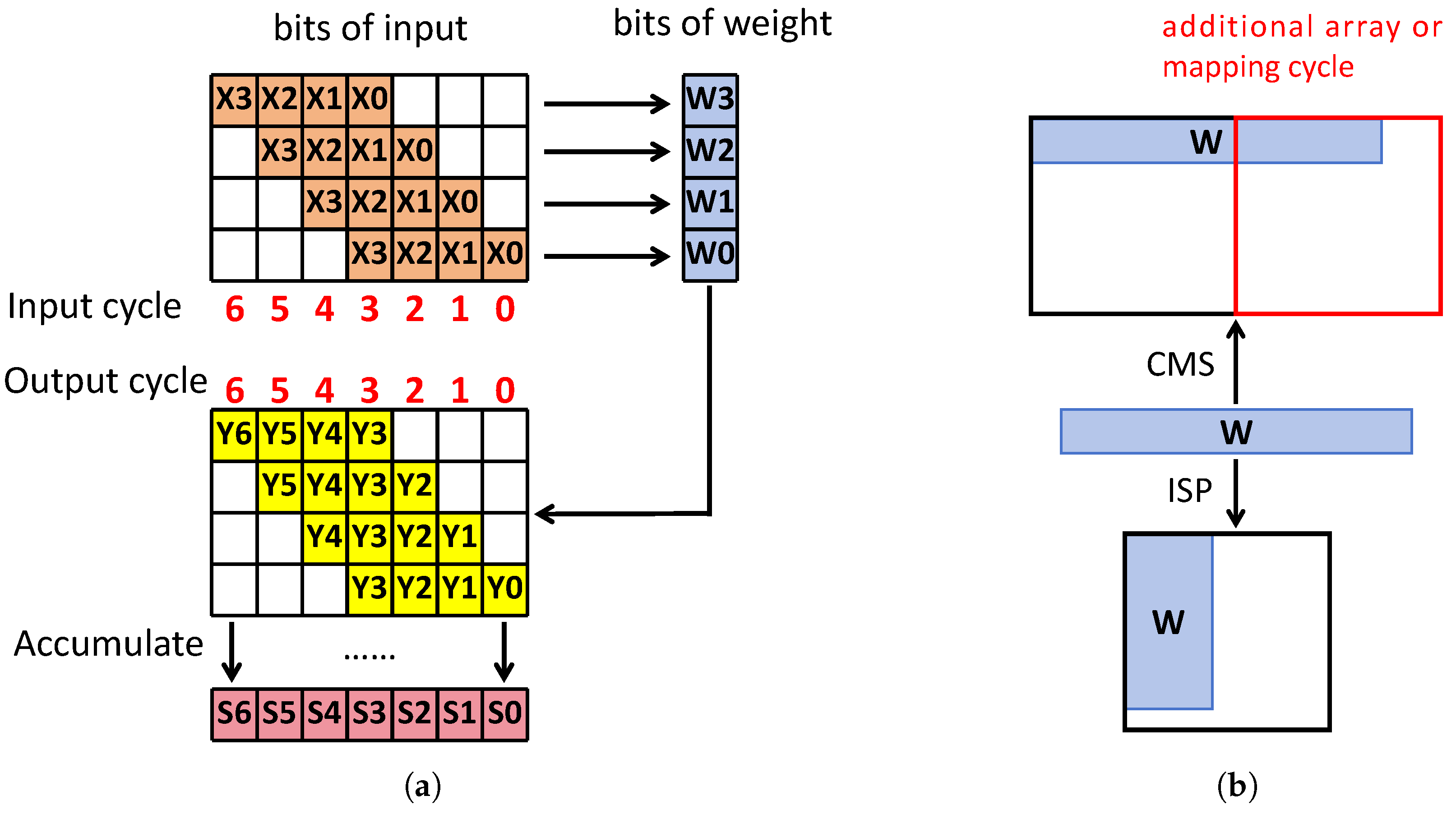
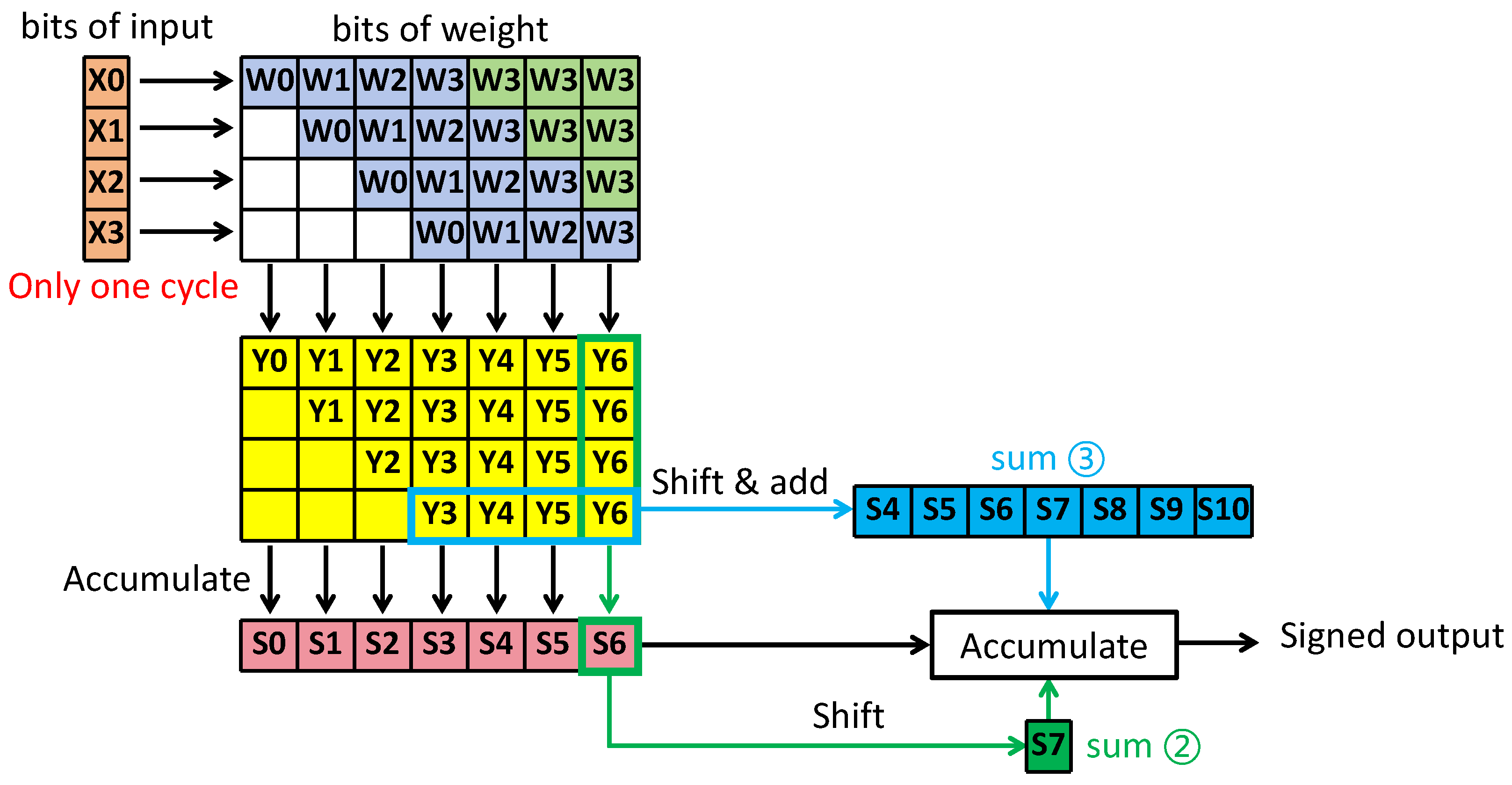
2.3. Improved Serial Bit Input Parallel Weight Mapping Strategy
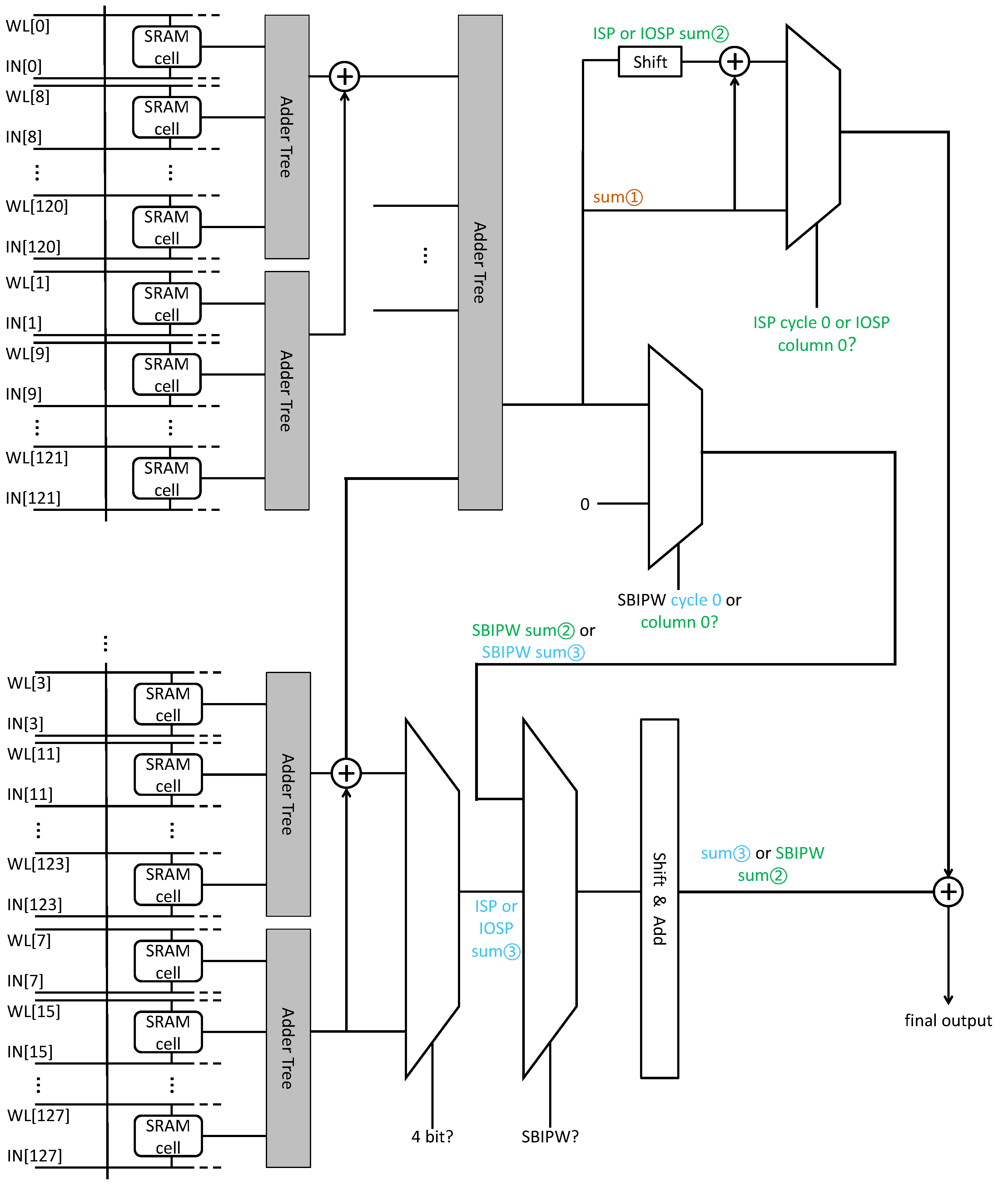
2.4. Improved Peripheral Circuits for Supporting Three Mapping Strategy
3. Evaluation and Results
3.1. NeuroSim Introduction
3.2. Evaluation Configuration
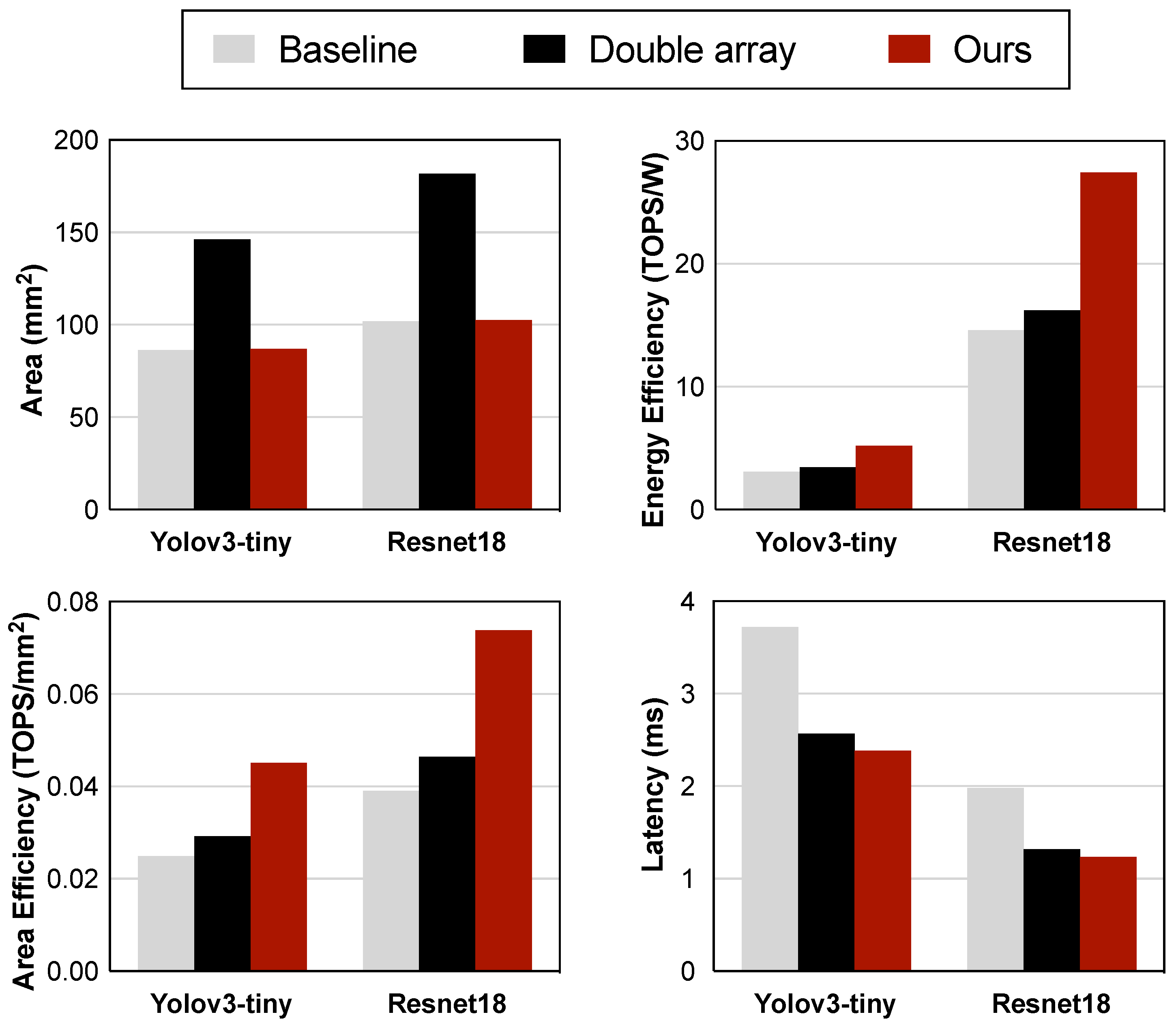
3.3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CIM | Compute-In-Memory |
| DCIM | Digital Compute-In-Memory |
| CMS | Conventional Mapping Strategy |
| SBIPW | Serial Bit Input Parallel Weight Mapping Strategy |
| ISP | Input-Side Parallel Mapping Strategy |
| IOSP | Input- and Output-Side Parallel Mapping Strategy |
| MAC | Multiply–Accumulate |
| ADC | Analog-to-Digital Converter |
| RAM | Random Access Memory |
References
- Shafiee, A.; Nag, A.; Muralimanohar, N.; Balasubramonian, R.; Strachan, J.P.; Hu, M.; Williams, R.S.; Srikumar, V. ISAAC: A Convolutional Neural Network Accelerator with In-Situ Analog Arithmetic in Crossbars. In Proceedings of the 2016 ACM/IEEE 43rd Annual International Symposium on Computer Architecture (ISCA), Seoul, Republic of Korea, 18–22 June 2016; pp. 14–26. [Google Scholar] [CrossRef]
- Zhu, Z.; Lin, J.; Cheng, M.; Xia, L.; Sun, H.; Chen, X.; Wang, Y.; Yang, H. Mixed Size Crossbar based RRAM CNN Accelerator with Overlapped Mapping Method. In Proceedings of the 2018 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Diego, CA, USA, 5–8 November 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Zhang, Y.; He, G.; Wang, G.; Li, Y. Efficient and Robust RRAM-Based Convolutional Weight Mapping with Shifted and Duplicated Kernel. IEEE Trans.-Comput.-Aided Des. Integr. Circuits Syst. 2021, 40, 287–300. [Google Scholar] [CrossRef]
- Rhe, J.; Moon, S.; Ko, J.H. VW-SDK: Efficient Convolutional Weight Mapping Using Variable Windows for Processing-In-Memory Architectures. In Proceedings of the 2022 Design, Automation and Test in Europe Conference and Exhibition (DATE), Antwerp, Belgium, 14–23 March 2022; pp. 214–219. [Google Scholar] [CrossRef]
- Peng, X.; Liu, R.; Yu, S. Optimizing Weight Mapping and Data Flow for Convolutional Neural Networks on Processing-in-Memory Architectures. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 1333–1343. [Google Scholar] [CrossRef]
- Qiao, X.; Cao, X.; Yang, H.; Song, L.; Li, H. AtomLayer: A Universal ReRAM-Based CNN Accelerator with Atomic Layer Computation. In Proceedings of the 2018 55th ACM/ESDA/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 24–28 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, S.; Liang, F.; Cao, Q.; Wang, Y.; Li, H.; Liang, J. A Weight Mapping Strategy for More Fully Exploiting Data in CIM-Based CNN Accelerator. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 2324–2328. [Google Scholar] [CrossRef]
- Bai, Y.; Li, Y.; Zhang, H.; Jiang, A.; Du, Y.; Du, L. A Compilation Framework for SRAM Computing-in-Memory Systems with Optimized Weight Mapping and Error Correction. IEEE Trans.-Comput.-Aided Des. Integr. Circuits Syst. 2024, 43, 2379–2392. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, Z.; Jin, Q.; He, Y.; Wang, J.; Lin, S.; Li, D.; Wang, Y.; Yang, K. CAP-RAM: A Charge-Domain In-Memory Computing 6T-SRAM for Accurate and Precision-Programmable CNN Inference. IEEE J.-Solid-State Circuits 2021, 56, 1924–1935. [Google Scholar] [CrossRef]
- He, Y.; Wang, Y.; Zhao, X.; Li, H.; Li, X. Towards State-Aware Computation in ReRAM Neural Networks. In Proceedings of the 2020 57th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 20–24 July 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Jiang, H.; Huang, S.; Peng, X.; Su, J.W.; Chou, Y.C.; Huang, W.H.; Liu, T.W.; Liu, R.; Chang, M.F.; Yu, S. A Two-way SRAM Array based Accelerator for Deep Neural Network On-chip Training. In Proceedings of the 2020 57th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 20–24 July 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Lu, L.; Tuan, D.A. A 47 TOPS/W 10T SRAM-Based Multi-Bit Signed CIM with Self-Adaptive Bias Voltage Generator for Edge Computing Applications. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 3599–3603. [Google Scholar] [CrossRef]
- Choi, I.; Choi, E.J.; Yi, D.; Jung, Y.; Seong, H.; Jeon, H.; Kweon, S.J.; Chang, I.J.; Ha, S.; Je, M. An SRAM-Based Hybrid Computation-in-Memory Macro Using Current-Reused Differential CCO. IEEE J. Emerg. Sel. Top. Circuits Syst. 2022, 12, 536–546. [Google Scholar] [CrossRef]
- Jain, S.; Lin, L.; Alioto, M. ±CIM SRAM for Signed In-Memory Broad-Purpose Computing From DSP to Neural Processing. IEEE J.-Solid-State Circuits 2021, 56, 2981–2992. [Google Scholar] [CrossRef]
- You, H.; Li, W.; Shang, D.; Zhou, Y.; Qiao, S. A 1–8b Reconfigurable Digital SRAM Compute-in-Memory Macro for Processing Neural Networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 1602–1614. [Google Scholar] [CrossRef]
- Lee, J.; Lu, A.; Li, W.; Yu, S. NeuroSim V1.4: Extending Technology Support for Digital Compute-in-Memory Toward 1 nm Node. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 1733–1744. [Google Scholar] [CrossRef]
- Peng, X.; Huang, S.; Luo, Y.; Sun, X.; Yu, S. DNN+NeuroSim: An End-to-End Benchmarking Framework for Compute-in-Memory Accelerators with Versatile Device Technologies. In Proceedings of the 2019 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 7–11 December 2019; pp. 32.5.1–32.5.4. [Google Scholar] [CrossRef]




| Mapping Strategy | Area (mm2) | Latency (us) | TOPS/W | |
|---|---|---|---|---|
| Baseline [8] | SBIPW | 2.637 | 56.40 | 2.047 |
| ISP | 3.285 | 106.40 | 1.211 | |
| IOSP | 6.144 | 47.00 | 1.110 | |
| Ours | SBIPW | 1.830 | 42.00 | 4.027 |
| ISP | 1.698 | 39.80 | 4.871 | |
| IOSP | 3.399 | 45.60 | 4.643 | |
| Mapping Strategy | Area (mm2) | Latency (us) | TOPS/W | |
|---|---|---|---|---|
| Baseline [8] | SBIPW | 1.335 | 56.40 | 2.047 |
| ISP | 3.285 | 66.20 | 0.177 | |
| IOSP | 0.780 | 15.64 | 1.177 | |
| Ours | SBIPW | 0.915 | 42.00 | 4.027 |
| ISP | 1.698 | 34.20 | 0.436 | |
| IOSP | 0.780 | 10.42 | 4.225 | |
| Technology Node | 22 nm | 10 nm | 7 nm | |||
|---|---|---|---|---|---|---|
| Baseline | Ours | Baseline | Ours | Baseline | Ours | |
| Area (mm2) | 156.78 | 157.43 | 43.91 | 44.46 | 21.77 | 22.08 |
| Latency (ms) | 168.44 | 103.06 | 98.21 | 60.962 | 80.01 | 50.81 |
| Energy Efficiency (TOPS/W) | 26.69 | 51.24 | 50.56 | 96.24 | 72.12 | 137.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Ma, B.; Liang, F.; Cao, Q.; Wang, Y.; Chen, H.; Lu, B.; Wang, S. Advancing Mapping Strategies and Circuit Optimization for Signed Operations in Compute-in-Memory Architecture. Electronics 2025, 14, 1340. https://doi.org/10.3390/electronics14071340
Chen Z, Ma B, Liang F, Cao Q, Wang Y, Chen H, Lu B, Wang S. Advancing Mapping Strategies and Circuit Optimization for Signed Operations in Compute-in-Memory Architecture. Electronics. 2025; 14(7):1340. https://doi.org/10.3390/electronics14071340
Chicago/Turabian StyleChen, Zhenjiao, Binghe Ma, Feng Liang, Qi Cao, Yongqiang Wang, Hang Chen, Bin Lu, and Shang Wang. 2025. "Advancing Mapping Strategies and Circuit Optimization for Signed Operations in Compute-in-Memory Architecture" Electronics 14, no. 7: 1340. https://doi.org/10.3390/electronics14071340
APA StyleChen, Z., Ma, B., Liang, F., Cao, Q., Wang, Y., Chen, H., Lu, B., & Wang, S. (2025). Advancing Mapping Strategies and Circuit Optimization for Signed Operations in Compute-in-Memory Architecture. Electronics, 14(7), 1340. https://doi.org/10.3390/electronics14071340






