Hybrid CNN-BiGRU-AM Model with Anomaly Detection for Nonlinear Stock Price Prediction
Abstract
1. Introduction
2. Methodology
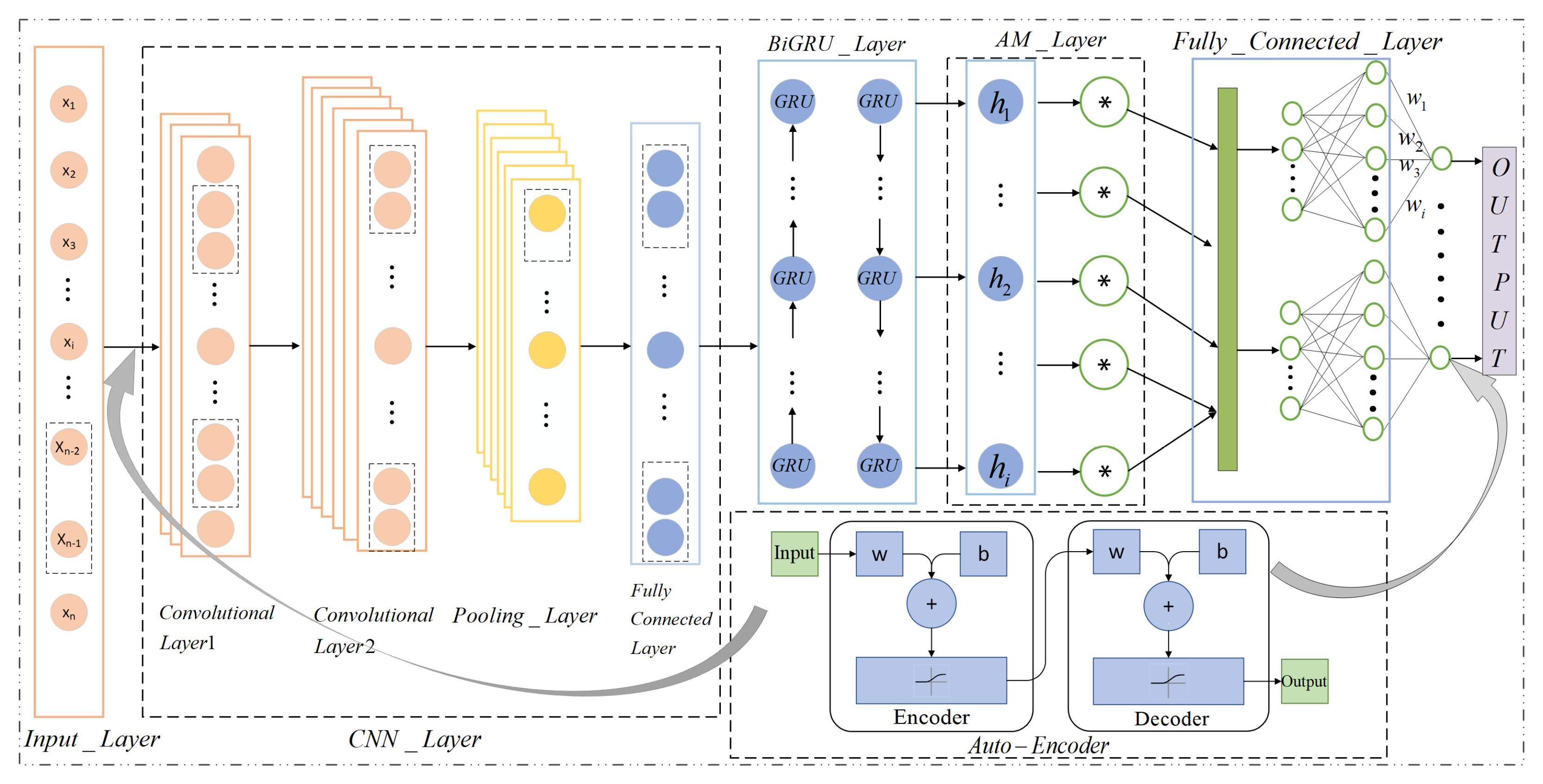
2.1. Overview of the Forecasting Framework
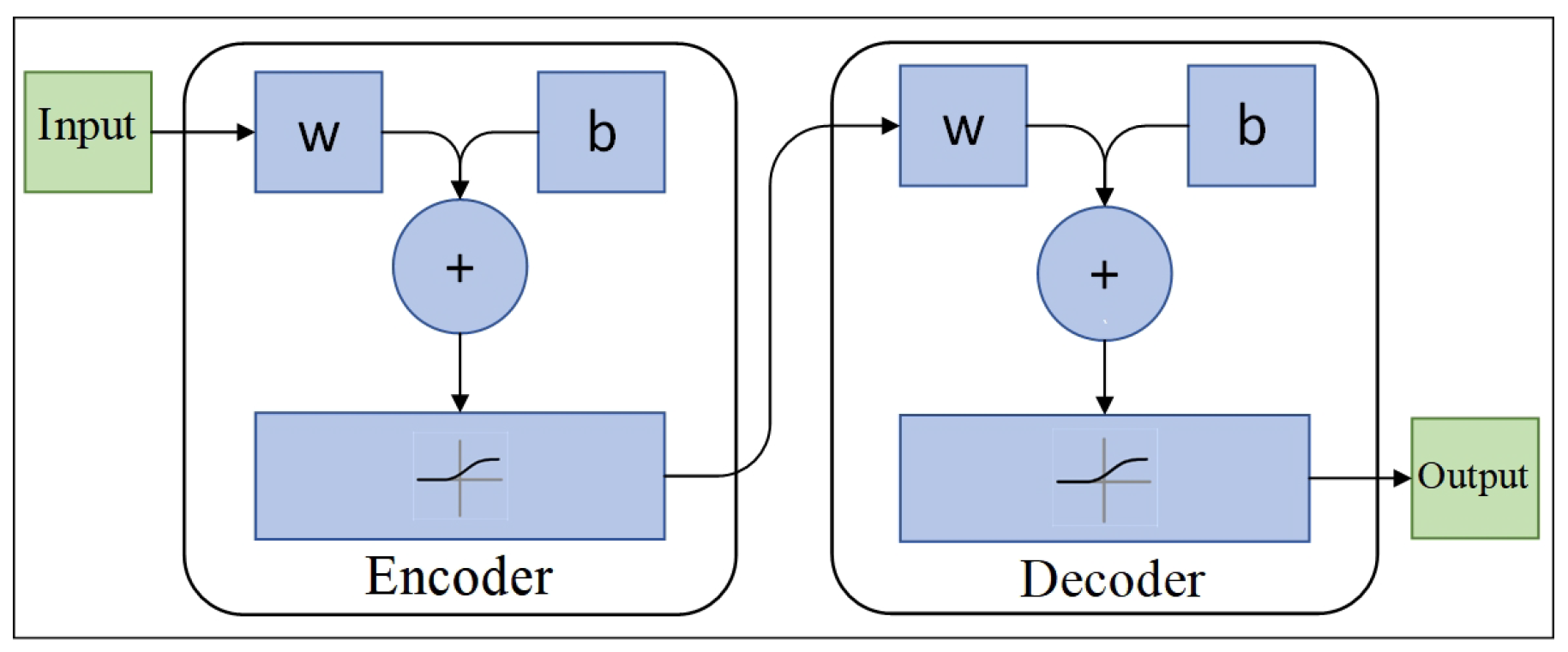
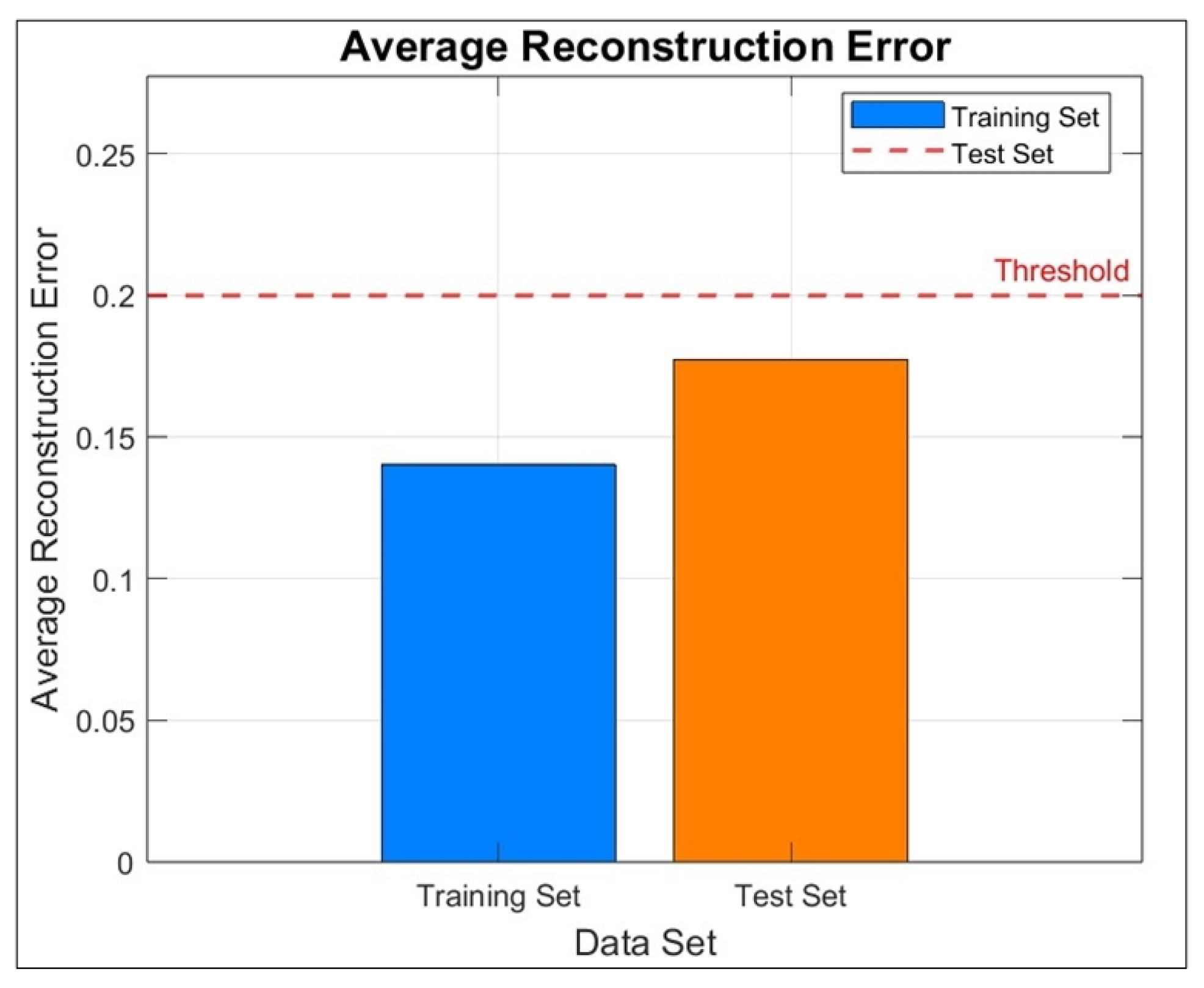
2.2. Auto-Encoder in Anomaly Detection
2.3. Convolutional Neural Network
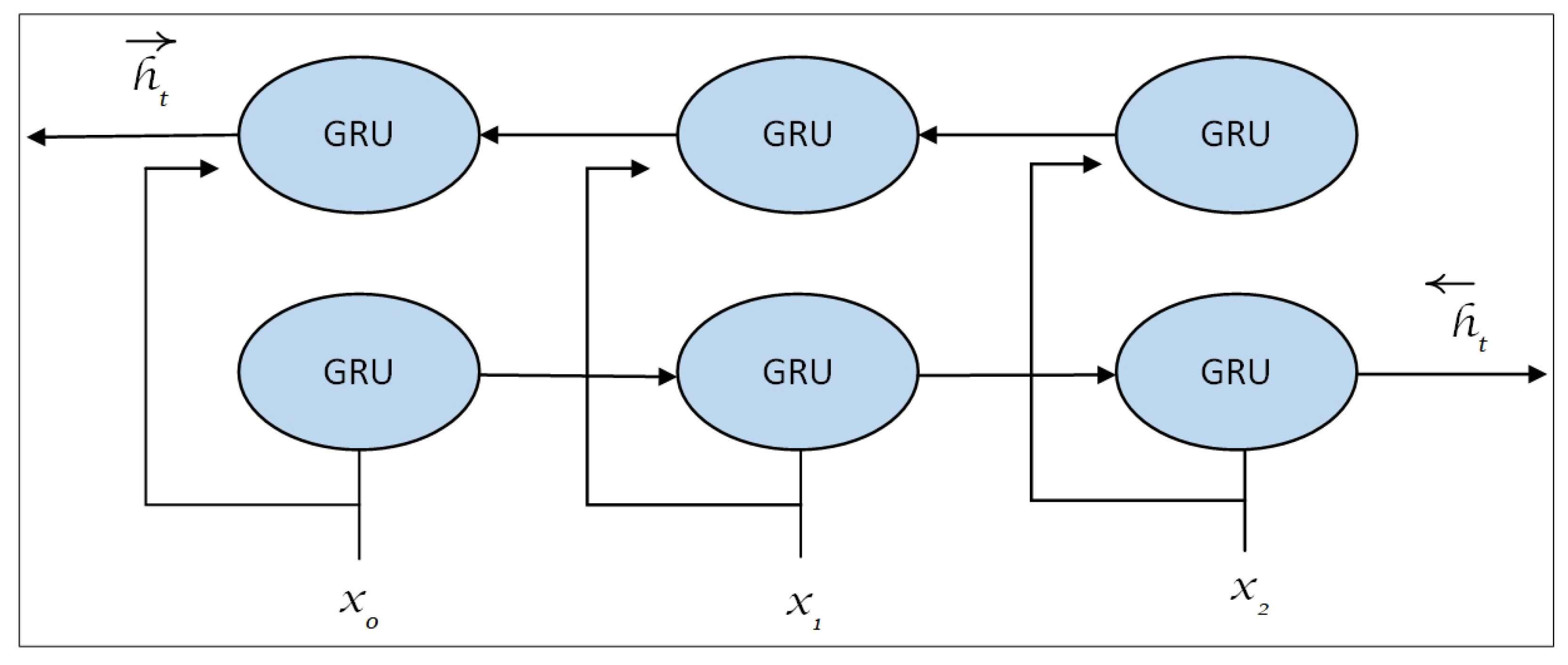
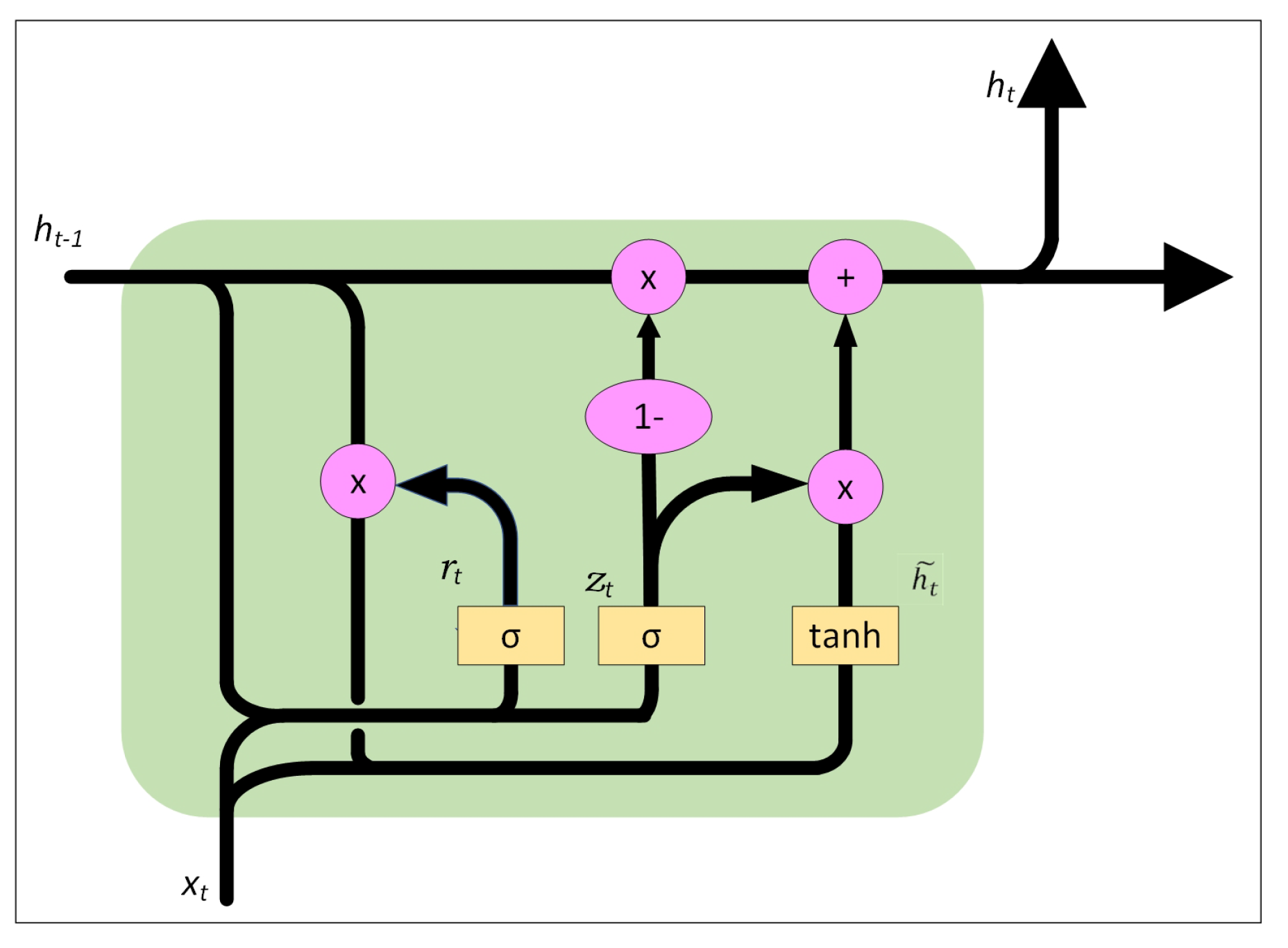
2.4. BiGRU Model
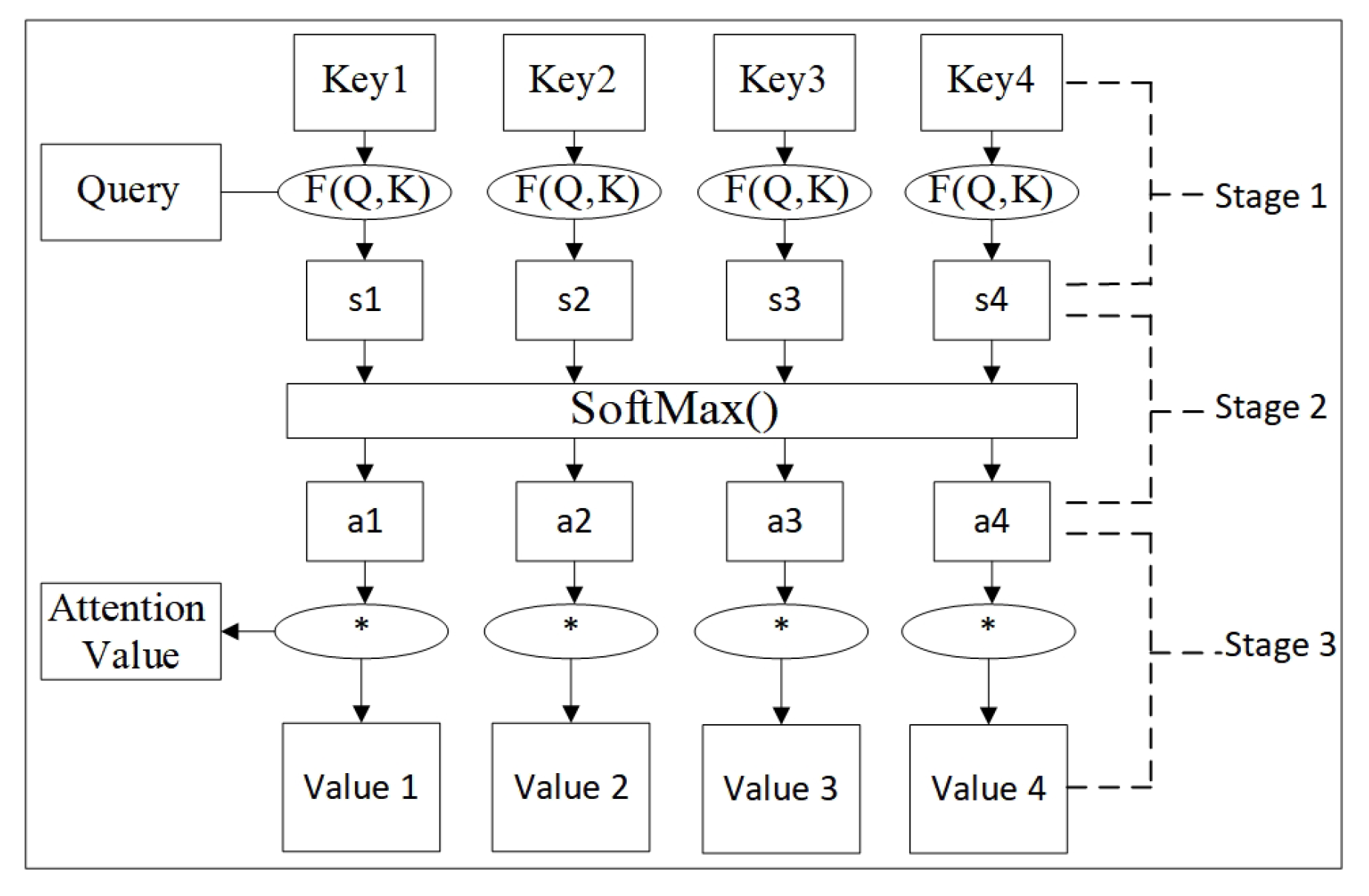
2.5. Attention Mechanism
3. Experimental Results and Discussion
3.1. Data Selection
3.2. Data Processing
3.3. Evaluation Index
3.4. Model Hyper-Parameters Setting
3.5. Experimental Analyses
3.6. Comparative Experimental Analyses
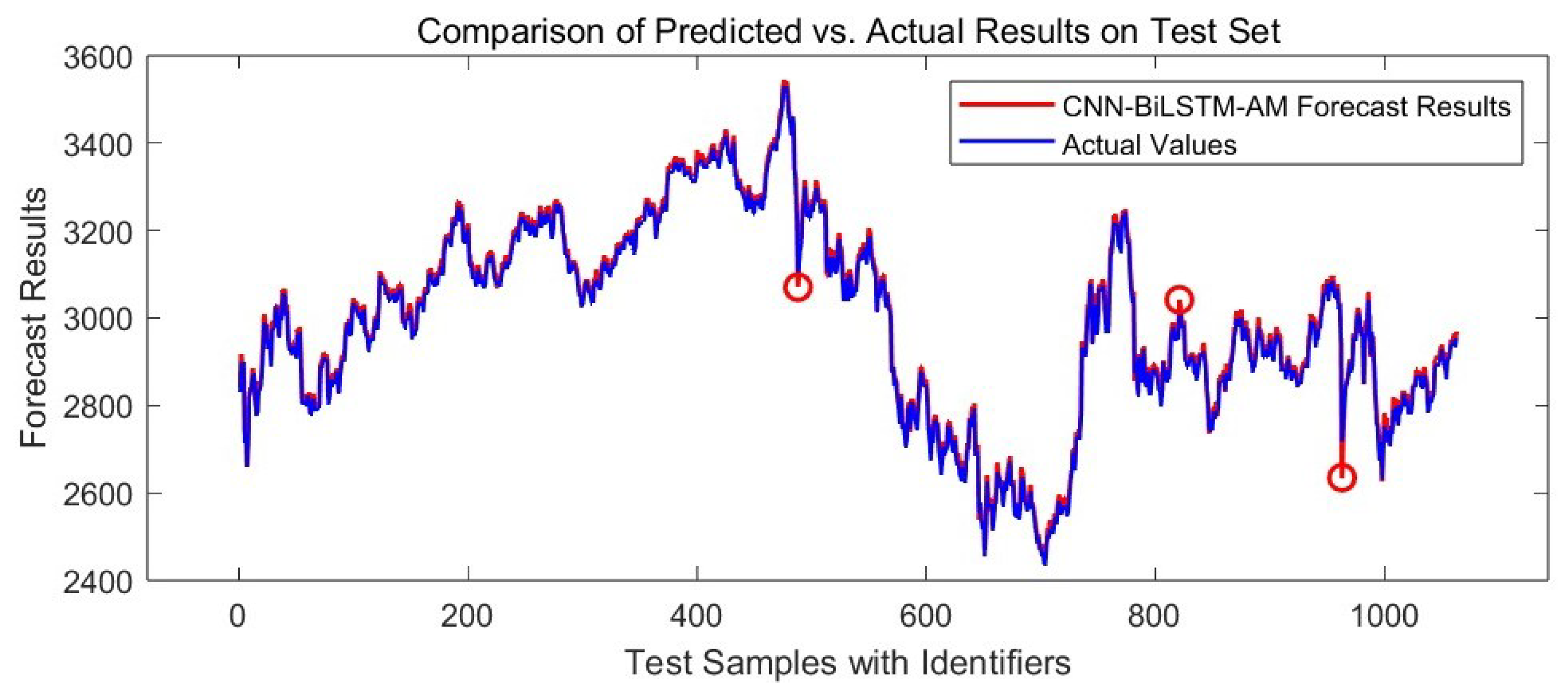
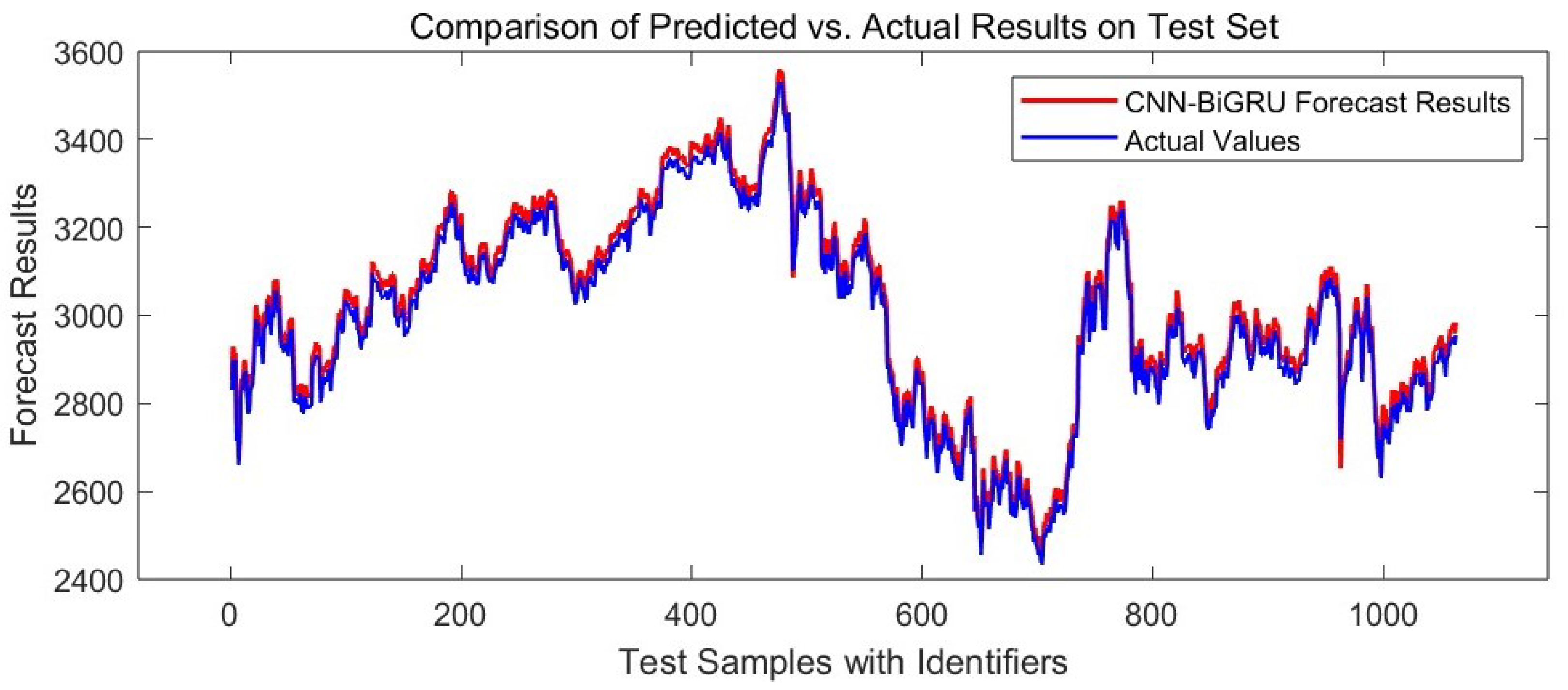
3.6.1. Line Chart Analysis
3.6.2. Analysis of Evaluation Indices
3.7. Discussion
4. Conclusions
- Multimodal Collaborative Optimization Mechanism: This mechanism enables the seamless integration of CNN-based local mutation feature extraction, BiGRU-based bidirectional time series modeling, and AM-AE-based dynamic feature purification, overcoming the limitations of traditional hybrid models that simply stack components. Experiments demonstrate that this architecture achieves an of 0.9903 for Shanghai Composite Index prediction, which is 0.08% higher than the best-performing baseline model, CNN-BiLSTM-AM ( = 0.9895), and 1% higher than the ablation comparison model, CNN-BiGRU ( = 0.9801), thereby validating the significant improvement in prediction accuracy through feature collaborative optimization.
- Anomaly Immunity Prediction Paradigm: A three-stage anomaly handling framework, comprising “pre-detection, mid-filtering, and post-correction”, is proposed to overcome the limitations of isolated anomaly analysis in traditional approaches. By deeply integrating anomaly detection into the feature learning process, this paradigm enables adaptive feature optimization, mitigating the impact of anomalies while preserving the model’s ability to capture normal price mechanisms. This approach fosters an endogenous synergy between anomaly immunity and prediction optimization.
- Risk-Return Balance Ability: Risk exposure is dynamically adjusted through the attention mechanism, resulting in a model Sharpe ratio of 0.65, which is 22.6% higher than that of GRU-AM (0.53) and 16.1% higher than BiGRU (0.56).
- Market Dynamics Analysis: The model feature weights reveal the underlying driving mechanisms of price fluctuations and offer a quantitative reference for understanding the multi-scale coupling effects within the market, such as the nonlinear interactions between macro policies and micro trading behaviors.
- Investment Decision Optimization: The risk-return dynamic balance mechanism offers an adaptive regulatory framework for portfolio management, facilitating the transition from traditional experience-based strategies to a data-driven, intelligence-enhanced paradigm.
- Fusion of Multi-Source Heterogeneous Data: Incorporating unstructured information, such as news sentiment analysis (BERT), institutional holdings data (13F Filings), and public opinion factors, to construct a cross-modal prediction system is anticipated to enhance prediction accuracy.
- Real-Time Decision Support: Explore lightweight deployment solutions to address the low-latency prediction requirements in high-frequency trading scenarios.
- Enhanced Interpretability: SHAP values are employed to analyze the model’s decision logic, with a focus on uncovering the impact of nonlinear feature interactions on prediction outcomes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CNNs | Convolutional Neural Networks |
| BiGRU | Bidirectional Gated Recurrent Unit |
| AM | Attention Mechanism |
| GRU | Gated Recurrent Unit |
| RNNs | Recurrent Neural Networks |
| LSTM | Long Short-Term Memory Network |
| 13Filings | SEC Form 13F |
References
- Badea, L.; Ionescu, V.; Guzun, A.A. What is the causal relationship between stoxx europe 600 sectors? but between large firms and small firms? Econ. Comput. Econ. Cybern. Stud. Res. 2019, 53, 5–20. [Google Scholar] [CrossRef]
- Mandal, R.C.; Kler, R.; Tiwari, A.; Keshta, I.; Abonazel, M.R.; Tageldin, E.M.; Umaralievich, M.S. Enhancing Stock Price Prediction with Deep Cross-Modal Information Fusion Network. Fluct. Noise Lett. 2024, 23, 2440017. [Google Scholar] [CrossRef]
- Wahlen, J.M.; Wieland, M.M. Can financial statement analysis beat consensus analysts’ recommendations? Rev. Account. Stud. 2011, 16, 89–115. [Google Scholar] [CrossRef]
- Barberis, N.; Mukherjee, A.; Wang, B. Prospect Theory and Stock Returns: An Empirical Test. Rev. Financ. Stud. 2016, 29, 3068–3107. [Google Scholar] [CrossRef]
- Temur, G.; Birogul, S.; Kose, U. Comparison of Stock “Trading” Decision Support Systems Based on Object Recognition Algorithms on Candlestick Charts. IEEE Access 2024, 12, 83551–83562. [Google Scholar] [CrossRef]
- Beniwal, M.; Singh, A.; Kumar, N. A comparative study of static and iterative models of ARIMA and SVR to predict stock indices prices in developed and emerging economies. Int. J. Appl. Manag. Sci. 2023, 15, 352–371. [Google Scholar] [CrossRef]
- Jarrah, M.; Derbali, M. Predicting Saudi Stock Market Index by Using Multivariate Time Series Based on Deep Learning. Appl. Sci. 2023, 13, 8356. [Google Scholar] [CrossRef]
- Houssein, E.H.; Dirar, M.; Abualigah, L.; Mohamed, W.M. An efficient equilibrium optimizer with support vector regression for stock market prediction. Neural Comput. Appl. 2022, 34, 3165–3200. [Google Scholar]
- Akhtar, M.M.; Zamani, A.S.; Khan, S.; Shatat, A.S.A.; Dilshad, S.; Samdani, F. Stock market prediction based on statistical data using machine learning algorithms. J. King Saud Univ.-Sci. 2022, 34, 101940. [Google Scholar]
- Zakhidov, G. Economic indicators: Tools for analyzing market trends and predicting future performance. Int. Multidiscip. J. Univ. Sci. Prospect. 2024, 2, 23–29. [Google Scholar]
- Billah, M.M.; Sultana, A.; Bhuiyan, F.; Kaosar, M.G. Stock price prediction: Comparison of different moving average techniques using deep learning model. Neural Comput. Appl. 2024, 36, 5861–5871. [Google Scholar] [CrossRef]
- Kaya, D.; Reichmann, D.; Reichmann, M. Out-of-sample predictability of firm-specific stock price crashes: A machine learning approach. J. Bus. Financ. Account. 2024. early view. [Google Scholar] [CrossRef]
- Xu, X.; Ye, T.; Gao, J.; Chu, D. The effect of green, supply chain factors in predicting China’s stock price crash risk: Evidence from random forest model. Environ. Dev. Sustain. 2024. [Google Scholar] [CrossRef]
- Sulastri, H.; Intani, S.M.; Rianto, R. Application of bagging and particle swarm optimisation techniques to predict technology sector stock prices in the era of the COVID-19 pandemic using the support vector regression method. Int. J. Comput. Sci. Eng. 2023, 26, 255–267. [Google Scholar] [CrossRef]
- Liu, J.X.; Leu, J.S.; Holst, S. Stock price movement prediction based on Stocktwits investor sentiment using FinBERT and ensemble SVM. PeerJ Comput. Sci. 2023, 9, e1403. [Google Scholar] [CrossRef] [PubMed]
- Vuong, P.H.; Phu, L.H.; Nguyen, T.H.V.; Duy, L.N.; Bao, P.T.; Trinh, T.D. A bibliometric literature review of stock price forecasting: From statistical model to deep learning approach. Sci. Prog. 2024, 107, 00368504241236557. [Google Scholar] [CrossRef]
- Chang, V.; Xu, Q.A.; Chidozie, A.; Wang, H. Predicting Economic Trends and Stock Market Prices with Deep Learning and Advanced Machine Learning Techniques. Electronics 2024, 13, 3396. [Google Scholar] [CrossRef]
- Carosia, A.E.d.O.; da Silva, A.E.A.; Coelho, G.P. Predicting the Brazilian Stock Market with Sentiment Analysis, Technical Indicators and Stock Prices: A Deep Learning Approach. Comput. Econ. 2024. [Google Scholar] [CrossRef]
- Das, N.; Sadhukhan, B.; Bhakta, S.S.; Chakrabarti, S. Integrating EEMD and ensemble CNN with X (Twitter) sentiment for enhanced stock price predictions. Soc. Netw. Anal. Min. 2024, 14, 29. [Google Scholar] [CrossRef]
- Rath, S.; Das, N.R.; Pattanayak, B.K. Stacked BI-LSTM and E-Optimized CNN-A Hybrid Deep Learning Model for Stock Price Prediction. Opt. Memory Neural Netw. 2024, 33, 102–120. [Google Scholar] [CrossRef]
- Tian, B.; Yan, T.; Yin, H. Forecasting the Volatility of CSI 300 Index with a Hybrid Model of LSTM and Multiple GARCH Models. Comput. Econ. 2024. [Google Scholar] [CrossRef]
- Tu, S.; Huang, J.; Mu, H.; Lu, J.; Li, Y. Combining Autoregressive Integrated Moving Average Model and Gaussian Process Regression to Improve Stock Price Forecast. Mathematics 2024, 12, 1187. [Google Scholar] [CrossRef]
- Huo, Y.; Jin, M.; You, S. A study of hybrid deep learning model for stock asset management. PeerJ Comput. Sci. 2024, 10, e2493. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.; Hong, Y.; Song, Y. On Stock Volatility Forecasting under Mixed-Frequency Data Based on Hybrid RR-MIDAS and CNN-LSTM Models. Mathematics 2024, 12, 1538. [Google Scholar] [CrossRef]
- Mu, S.; Liu, B.; Gu, J.; Lien, C.; Nadia, N. Research on Stock Index Prediction Based on the Spatiotemporal Attention BiLSTM Model. Mathematics 2024, 12, 2812. [Google Scholar] [CrossRef]
- Duan, G.; Yan, S.; Zhang, M. A Hybrid Neural Network Model for Sentiment Analysis of Financial Texts Using Topic Extraction, Pre-Trained Model, and Enhanced Attention Mechanism Methods. IEEE Access 2024, 12, 98207–98224. [Google Scholar] [CrossRef]
- Jayanth, T.; Manimaran, A.; Siva, G. Enhancing Stock Price Forecasting With a Hybrid SES-DA-BiLSTM-BO Model: Superior Accuracy in High-Frequency Financial Data Analysis. IEEE Access 2024, 12, 173618–173637. [Google Scholar] [CrossRef]
- Thi, H.L.; Nguyen, T. Variational Quantum Algorithms in Anomaly Detection, Fraud Indicator Identification, Credit Scoring, and Stock Price Prediction. In Proceedings of Ninth International Congress on Information and Communication Technology, ICICT 2024; Yang, X., Sherratt, S., Dey, N., Joshi, A., Eds.; Lecture Notes in Networks and Systems; Springer: Singapore, 2024; Volume 1003, pp. 483–492. [Google Scholar] [CrossRef]
- Wu, K.; Karmakar, S.; Gupta, R.; Pierdzioch, C. Climate Risks and Stock Market Volatility over a Century in an Emerging Market Economy: The Case of South Africa. Climate 2024, 12, 68. [Google Scholar] [CrossRef]
- Liu, H.; Dahal, B.; Lai, R.; Liao, W. Generalization error guaranteed auto-encoder-based nonlinear model reduction for operator learning. Appl. Comput. Harmon. Anal. 2025, 74, 101717. [Google Scholar] [CrossRef]
- Biswas, D.; Gil, J.M. Design and Implementation for Research Paper Classification Based on CNN and RNN Models. J. Internet Technol. 2024, 25, 637–645. [Google Scholar] [CrossRef]
- Weerasena, H.; Mishra, P. Revealing CNN Architectures via Side-Channel Analysis in Dataflow-based Inference Accelerators. ACM Trans. Embed. Comput. Syst. 2024, 23, 1–25. [Google Scholar] [CrossRef]
- Tharun, S.B.; Jagatheswari, S. A U-shaped CNN with type-2 fuzzy pooling layer and dynamical feature extraction for colorectal polyp applications. Eur. Phys. J.-Spec. Top. 2024. [Google Scholar] [CrossRef]
- Luo, H.; Chen, J.; Sun, Z.; Zhang, Y.; Zhang, L. Improved Marine Predators Algorithm Optimized BiGRU for Strip Exit Thickness Prediction. IEEE Access 2024, 12, 56719–56729. [Google Scholar] [CrossRef]
- Li, D.; Li, W.; Zhao, Y.; Liu, X. The Analysis of Deep Learning Recurrent Neural Network in English Grading Under the Internet of Things. IEEE Access 2024, 12, 44640–44647. [Google Scholar] [CrossRef]
- Sun, W.; Chen, J.; Hu, C.; Lin, Y.; Wang, M.; Zhao, H.; Zhao, R.; Fu, G.; Zhao, T. Clock bias prediction of navigation satellite based on BWO-CNN-BiGRU-attention model. GPS Solut. 2025, 29, 46. [Google Scholar] [CrossRef]
- Fan, J.; Yang, H.; Li, X.; Jiang, Y.; Wu, Z. Prediction of FeO content in sintered ore based on ICEEMDAN and CNN-BiLSTM-AM. Ironmak. Steelmak. 2025. [Google Scholar] [CrossRef]


| Hyperparameter | Applicable Scope | Value | Remarks |
|---|---|---|---|
| MaxEpochs | CNN-BiGRU-AM | 200 | Maximum number of training epochs for the entire model. |
| Initial Learning Rate | CNN-BiGRU-AM | 0.001 | The initial learning rate of the entire model. |
| BatchSize | CNN-BiGRU-AM | 64 | The batch size during each training iteration. |
| L2 Regularization Factor | CNN-BiGRU-AM | 1 × 10−5 | The parameter that prevents overfitting. |
| Learning Rate Decay Factor | CNN-BiGRU-AM | 0.5 | Factor for controlling the decay of the learning rate. |
| Learning Rate Decay Period | CNN-BiGRU-AM | 150 | Period for controlling learning rate decay. |
| Number of Filters in Convolutional Layer | CNN Layer | 16/32 | 16 is the number of filters in the first convolutional layer, and 32 in the second. |
| Kernel Size | CNN Layer | [1, 1] | The size of the convolutional kernels in the convolutional layer is 1 × 1. |
| Activation Function | CNN Layer | ReLU | The activation function |
| GRU Units | BiGRU Layer | 50 | Number of units in a single GRU layer to process the sequential data. |
| Activation Function | BiGRU Layer | ReLU | The activation function |
| Number of Neurons in Fully Connected Layer | AM Layer | 8/32 | The first layer(8) compresses features, and the second(32) generates more detailed features for attention weight calculation. |
| Activation Function | AM Layer | Sigmoid | This function is used to generate attention weights. |
| Activation Function | AM Layer | ReLU | The activation function |
| Model | RMSE | MAE | R2 | Sharpe Ratio |
|---|---|---|---|---|
| CNN-BiGRU-AM | 22.027 | 19.043 | 0.9903 | 0.65 |
| CNN-BiLSTM-AM | 21.357 | 20.252 | 0.9895 | 0.63 |
| CNN-BiGRU | 23.727 | 21.851 | 0.9801 | 0.66 |
| BiGRU | 29.671 | 24.231 | 0.9725 | 0.56 |
| LSTM | 29.331 | 24.361 | 0.9770 | 0.45 |
| GRU-AM | 27.391 | 24.991 | 0.9712 | 0.53 |
| CNN | 30.254 | 25.621 | 0.9682 | 0.48 |
| GRU | 33.642 | 26.081 | 0.9699 | 0.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, J.; Cao, Y.; Xie, K.; Wen, C.; Ruan, Y.; Ji, J.; He, J.; Zhang, W. Hybrid CNN-BiGRU-AM Model with Anomaly Detection for Nonlinear Stock Price Prediction. Electronics 2025, 14, 1275. https://doi.org/10.3390/electronics14071275
Luo J, Cao Y, Xie K, Wen C, Ruan Y, Ji J, He J, Zhang W. Hybrid CNN-BiGRU-AM Model with Anomaly Detection for Nonlinear Stock Price Prediction. Electronics. 2025; 14(7):1275. https://doi.org/10.3390/electronics14071275
Chicago/Turabian StyleLuo, Jiacheng, Yun Cao, Kai Xie, Chang Wen, Yunzhe Ruan, Jinpeng Ji, Jianbiao He, and Wei Zhang. 2025. "Hybrid CNN-BiGRU-AM Model with Anomaly Detection for Nonlinear Stock Price Prediction" Electronics 14, no. 7: 1275. https://doi.org/10.3390/electronics14071275
APA StyleLuo, J., Cao, Y., Xie, K., Wen, C., Ruan, Y., Ji, J., He, J., & Zhang, W. (2025). Hybrid CNN-BiGRU-AM Model with Anomaly Detection for Nonlinear Stock Price Prediction. Electronics, 14(7), 1275. https://doi.org/10.3390/electronics14071275






