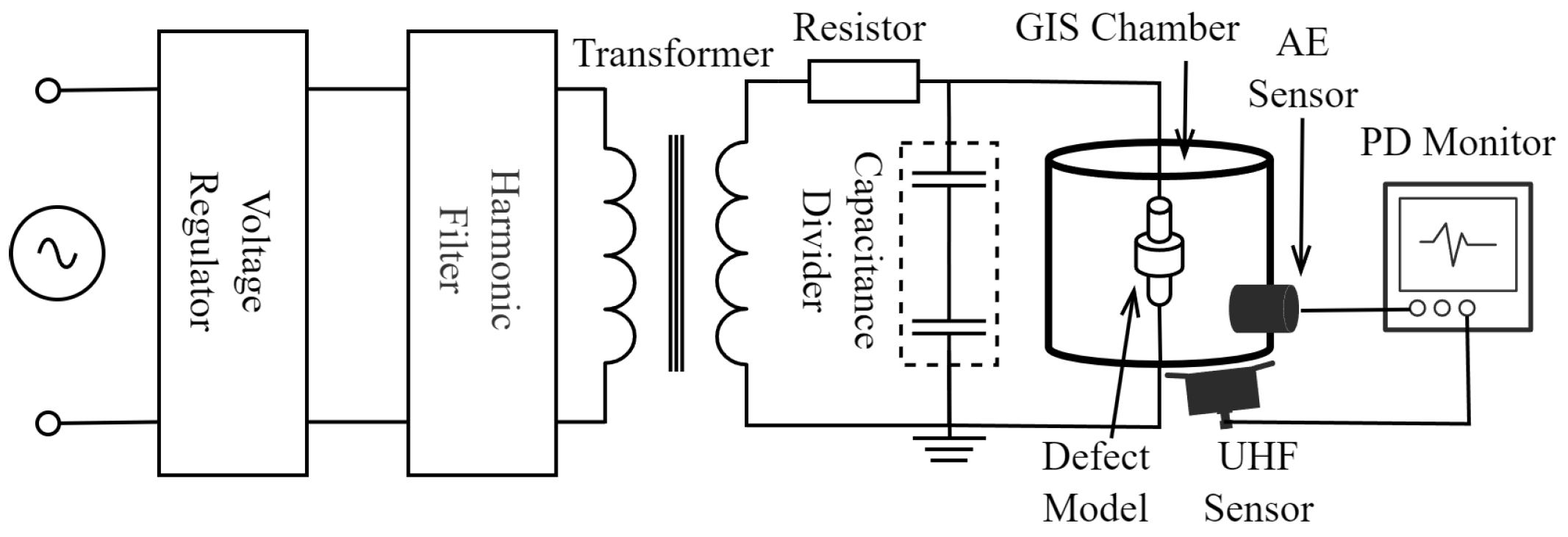
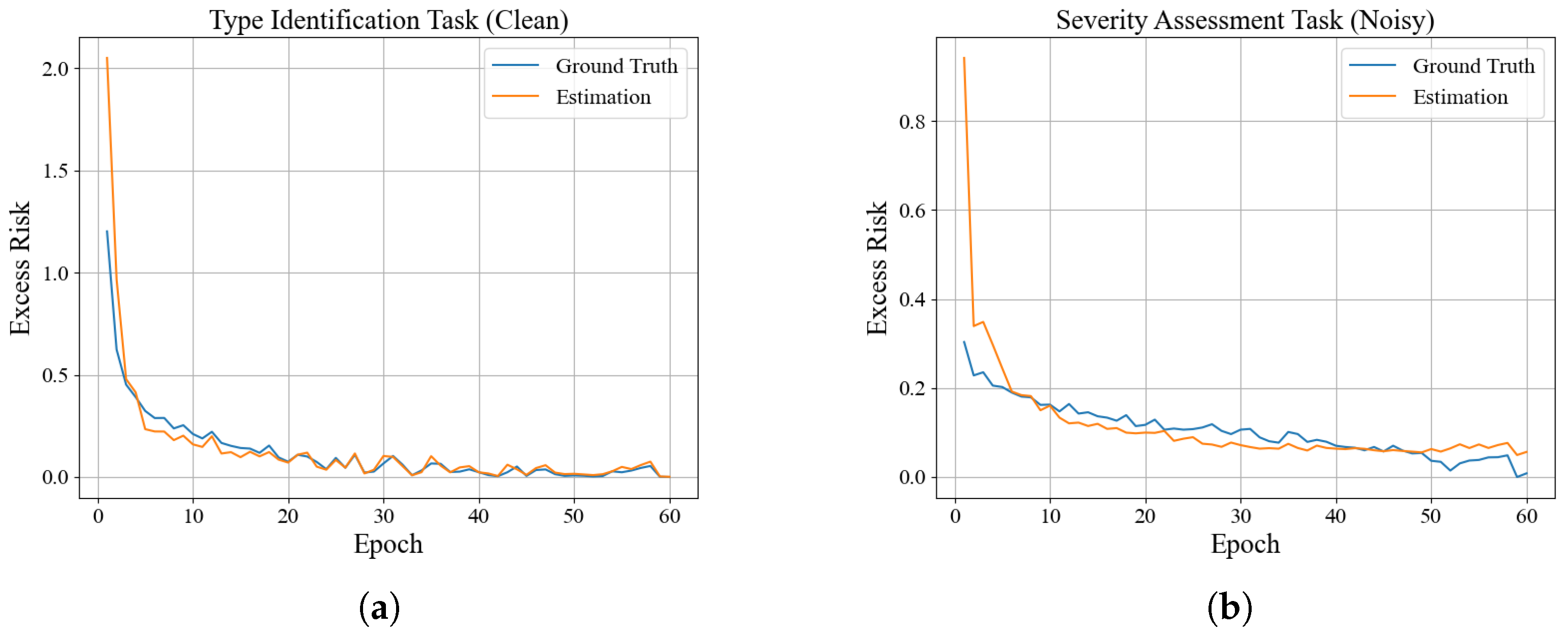
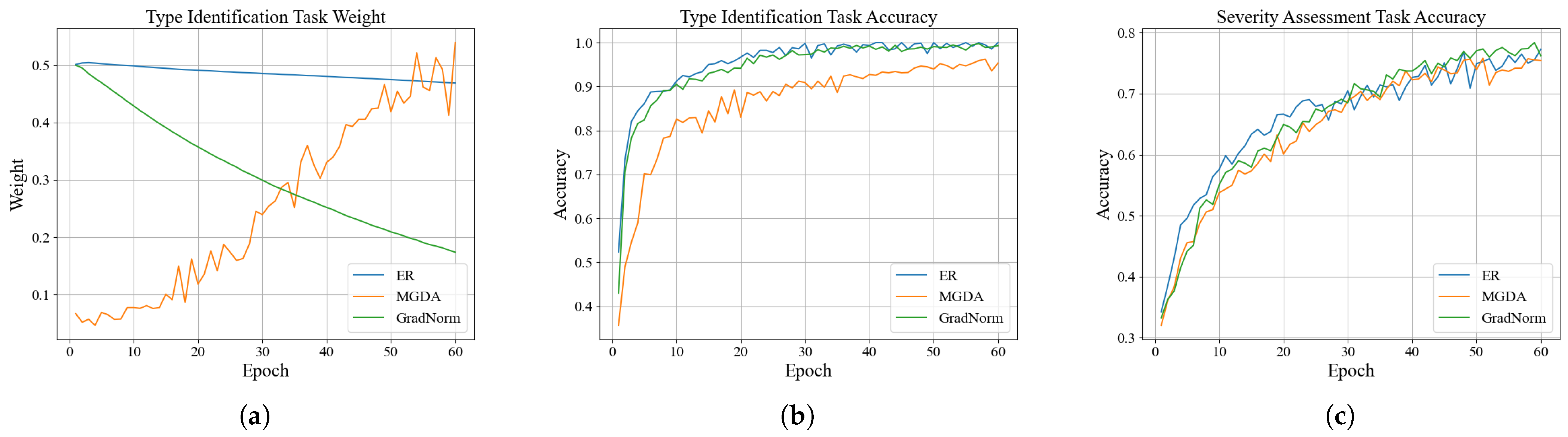
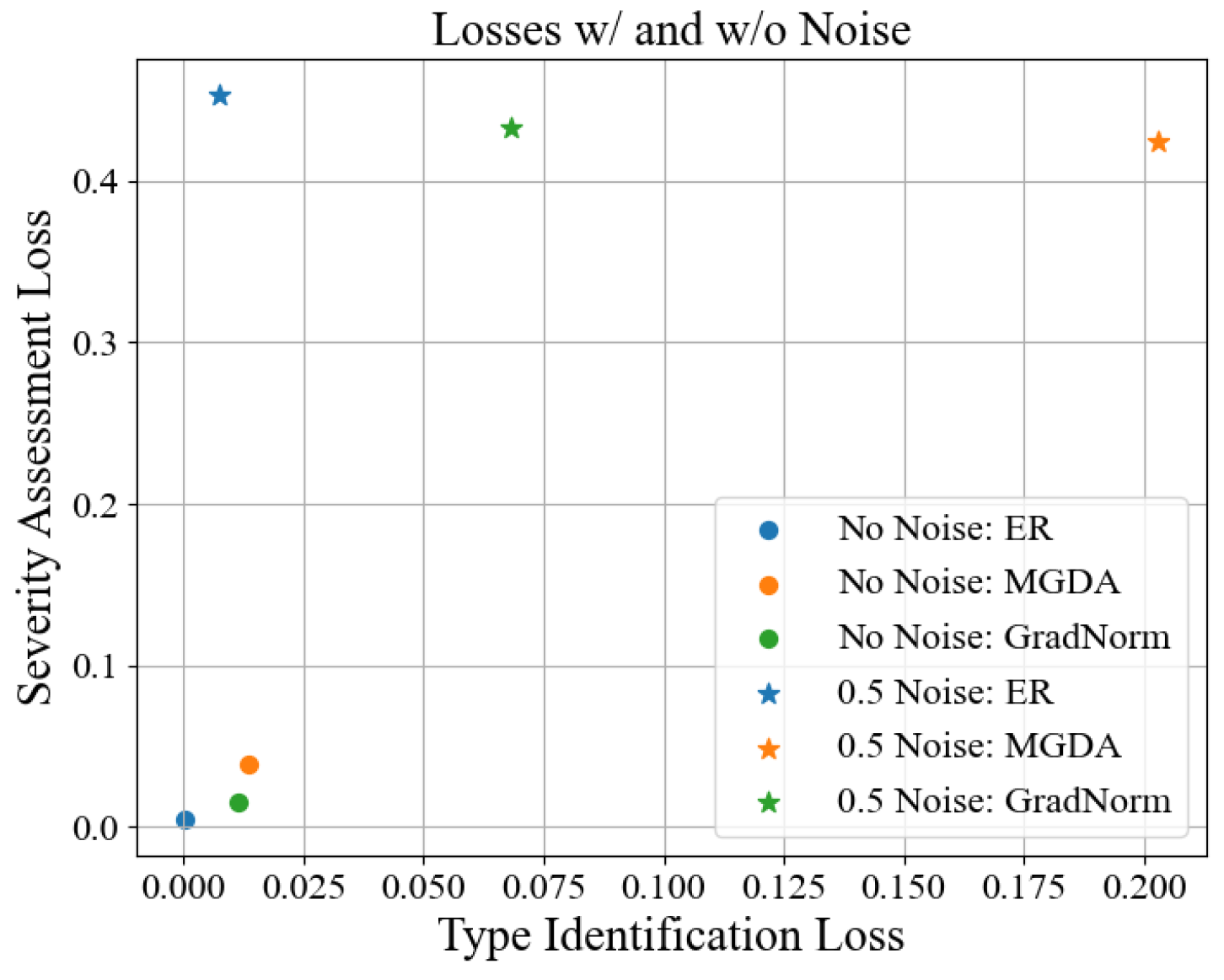
1. Introduction
Gas-Insulated Switchgear (GIS) is widely utilized in modern power systems due to its high reliability and compact structure [
1]. However, partial discharge (PD) phenomena within GIS often indicate potential insulation defects [
2], and, if not promptly detected and diagnosed, can lead to severe equipment failures [
3]. Therefore, accurate GIS PD diagnosis is of paramount importance for ensuring the safe and stable operation of power grids.
Currently, data-driven GIS PD diagnostic methods have become a prominent research focus. In the field of GIS PD diagnosis, type identification is one of the most fundamental and critical tasks. To accurately identify different types of PD signals, researchers have extensively explored deep learning techniques and proposed various innovative approaches. For instance, early studies attempted to classify PD patterns using Deep Belief Networks (DBNs) [
4]. With the continuous advancement of deep learning technology, researchers have introduced more advanced network architectures, such as Residual Networks (ResNets) [
5,
6] and DenseNet models [
7], combined with techniques like transfer learning [
8,
9] and knowledge graphs [
5], to enhance the generalization ability of models in small-sample and complex environments. Furthermore, novel deep learning models, such as Generative Adversarial Networks (GANs) [
6,
8] and capsule networks [
9], have also been applied to PD-type identification, aiming for superior performance in feature extraction and pattern classification. These research efforts have significantly improved the accuracy and robustness of GIS PD-type identification, laying a foundation for equipment condition assessment.
Severity assessment is another crucial aspect of GIS PD diagnosis and directly impacts the effectiveness of equipment maintenance decisions. To more precisely assess the severity of PD, researchers have begun to explore more diverse methodologies. For example, some studies have attempted to utilize semantic analysis techniques [
10], integrating structured and unstructured text information to comprehensively evaluate PD ultra-high-frequency signals. Deep learning models, such as Stacked Sparse Autoencoders (SSAEs) [
11], have also been applied to PD severity assessment, aiming to automatically extract effective features from complex data. In addition, feature selection algorithms [
12] and methods combining Long Short-Term Memory (LSTM) networks with ensemble learning [
13] have been proposed to overcome the limitations of traditional methods in feature engineering and time-series data processing and achieve more reliable severity assessment.
However, the aforementioned studies largely treat type identification and severity assessment as independent tasks, overlooking the potential intrinsic connections between them and the performance gains that joint analysis could offer. The rise of multi-task learning methods [
14] provides a new perspective for addressing this issue. Multi-task learning can simultaneously train models for multiple related tasks, improving learning efficiency and generalization ability through shared representations and knowledge transfer, thereby achieving superior diagnostic performance under limited data conditions. Recent applications in GIS PD diagnosis have explored MTL networks integrated with cutting-edge technologies such as edge computing [
15], subdomain adaptation [
16], and digital twins [
17] to develop intelligent and efficient condition assessment frameworks. Nevertheless, existing research utilizing multi-task learning for GIS PD diagnosis has paid insufficient attention to the ordinal regression nature of the severity assessment task.
Ordinal regression [
18] refers to multi-classification tasks where there is a natural order among the categories. Multi-task ordinal regression methods closely related to this research have demonstrated unique advantages and potential in other fields. For instance, Gao et al. [
19] viewed multi-location spatial event scale prediction as a multi-task ordinal regression problem, imposing similar event scale patterns on spatially closer tasks. Wang et al. [
20] modeled multiple ordinal regression tasks through structured regularization terms and learned a series of thresholds to partition ordered categories. Zhao et al. [
21] applied ordinal multi-task learning to image analysis tasks, improving segmentation performance by explicitly modeling the hierarchical relationships among object parts. Xiao et al. [
22] focused on adaptively learning weights for different ordinal regression tasks to enhance accuracy while better understanding the relationships between tasks. These studies demonstrate that multi-task ordinal regression methods offer significant advantages in handling tasks with inherent hierarchical relationships.
Despite the progress made in multi-task ordinal regression problems, two key challenges remain in developing effective frameworks for GIS PD diagnosis. First, severity assessment is essentially an ordinal regression problem that typically contains more label noise due to subjective annotation and the absence of well-defined quantitative boundaries between adjacent severity levels. Existing MTL methods that dynamically adjust task weights often rely on loss magnitude to measure task difficulty. However, this approach is susceptible to high label noise, as noisy tasks tend to have higher losses, leading to over-allocation of weights and reduced overall performance. Second, maintaining ranking consistency in severity prediction results is crucial. This implies that when decomposing the ordinal regression task into binary classification sub-tasks, the output probabilities from adjacent classifiers must exhibit monotonicity, reflecting the intrinsic order of the categories. Traditional regression or classification methods often fail to preserve these ranking relationships, leading to inconsistent prediction rankings and consequently affecting diagnostic accuracy.
As an example, GIS PD can originate from different types of insulation defects, such as metallic protrusions, floating electrodes, free metallic particles, and insulator gaps. To reflect the degree of insulation deterioration, PD is classified into three severity levels: initial, developing, and severe. Using multi-task learning for GIS PD diagnosis enables simultaneous type identification and severity assessment through shared representations. Considering that severity assessment is an ordinal regression task, it is crucial to overcome the impact of its label noise on multi-task weight allocation and maintain ranking consistency in its predictions.
To address these challenges, this paper proposes a novel multi-task learning framework—Ordinal Regression Multi-Task Learning (OR-MTL)—which integrates ranking consistency into severity assessment while dynamically adjusting task weights based on the excess risk of each task to enhance robustness against label noise. Our approach reconstructs the severity prediction task using a structured probability model with enforced monotonicity constraints to ensure ranking consistency. Additionally, we introduce a noise-robust task-weighting strategy based on excess risk estimation, which determines task priorities based on relative convergence progress rather than raw loss values. Through joint optimization of these components, OR-MTL achieves higher accuracy and stability in GIS PD diagnosis. The main contributions of this paper are summarized as follows:
A novel multi-task learning framework, known as OR-MTL, is proposed for simultaneous discharge-type identification and severity assessment in GIS PD diagnosis, explicitly incorporating the ordinal regression nature inherent to the severity assessment task;
A dynamic task-weighting strategy based on excess risk estimation is developed to mitigate the negative impact of label noise on other tasks within multi-task learning;
Ranking consistency is incorporated into severity assessment, ensuring that the severity predictions conform to objective physical principles and enhancing the reliability of the assessment results;
Extensive experiments on a GIS PD dataset demonstrate that OR-MTL outperforms existing methods in both type identification and severity assessment tasks, especially under noisy conditions.
The remainder of this paper is organized as follows.
Section 2 details the excess risk-based dynamic task-weighting strategy.
Section 3 formalizes the conditional probability-based ordinal regression loss.
Section 4 presents the experimental configurations, dataset characteristics, and comparative results analysis.
Section 5 concludes with future research directions.
2. Excess Risk-Based Task Weighting for GIS PD Diagnosis
In multi-task learning (MTL), balancing the optimization of multiple tasks is crucial for improving overall performance. Traditional methods often employ static or loss-based weighting strategies, which may assign higher weights to tasks with larger losses. However, this approach can be problematic when some tasks have high label noise, as these tasks typically exhibit larger losses and are consequently assigned excessively high weights, ultimately impacting overall model performance negatively.
Ordinal regression tasks, such as severity assessment, are particularly prone to substantial label noise due to the lack of clear quantitative boundaries between adjacent levels and the subjectivity inherent in the labeling process. Existing research on label noise [
23,
24] has successfully mitigated its impact on the noisy task itself to some extent, whereas this paper focuses on reducing the influence of label noise on other tasks within multi-task learning. To address this issue, this paper introduces a dynamic task-weighting strategy based on excess risk estimation [
25], as outlined in Algorithm 1. This strategy prioritizes tasks based on their learnability rather than raw loss values. Excess risk quantifies the discrepancy between the current task performance and its optimal achievable performance, rendering it a robust metric for adjusting task weights in noisy environments.
| Algorithm 1 Dynamic task weighting based on excess risk |
Require: Model parameter learning rate , task weight learning rate Initialize , , and for to epoch do for do Calculate task losses Calculate gradients Estimate Hessian matrix using Equation ( 10) Estimate excess risk using Equation ( 9) Update task-specific parameters end for Update task weights using Equation ( 13) Calculate weighted total loss Update shared parameters end for
|
2.1. Multi-Task Learning
The GIS PD multi-task diagnosis investigated in this paper includes two tasks: discharge-type identification (
) and severity assessment (
). The given dataset is defined as
, containing
N training samples, where
represents the input signal of the
n-th sample (only single-input scenarios are considered in this study, i.e., all tasks share the same input).
and
represent the labels of the
n-th sample for the two tasks, respectively. Each task has a loss function, denoted as
and
. The objective of multi-task learning is to minimize the total loss function
, which is the weighted sum of the loss functions for each task, expressed as
where
represents the weight of the loss function for task
, typically determined by the importance or difficulty of the task;
represents the parameters shared among tasks in the multi-task model; and
represents the task-specific model parameters for the
k-th task.
2.2. Excess Risk
Consider input data
and its label
from distribution
, with loss function
L. The expected loss (risk) of a prediction model
is defined as [
26]
Let
be the optimal model within the hypothesis space
, and let
be the optimal solution among all possible models, i.e., the Bayes optimal model. The expected loss of
can be further decomposed into
where
is the estimation error;
is the approximation error; and
is the Bayes error.
When the hypothesis space is sufficiently expressive, the approximation error asymptotically approaches zero. In contrast, the Bayes error is irreducible, stemming from the inherent randomness in data generation processes (e.g., label noise). This property, intrinsic to the dataset, leads to an increase in under high label noise. Traditional risk metrics (e.g., ) conflate reducible and irreducible errors, rendering them unreliable for performance evaluation in noisy settings.
To address this limitation, excess risk emerges as a more principled metric. It quantifies the discrepancy between the model’s current risk and the theoretically achievable minimum within
, thereby isolating reducible errors from
. In this study, where the GIS PD diagnosis model structure fixes
to reside in
, excess risk
is defined as
Excess risk measures the distance between the model’s risk and the optimal achievable risk within , effectively filtering out label noise effects. Since dataset quality (and thus ) is often uncontrollable, serves as a robust performance metric, particularly under label noise. By focusing exclusively on improvable risk components, it serves as a reliable indicator of model efficacy. However, direct computation of is generally infeasible due to the inaccessibility of , necessitating specialized estimation methods.
2.3. Excess Risk Estimation Based on Taylor Approximation
For notational simplicity, we denote
as the combined parameters
in subsequent derivations. Since directly computing the risk of the optimal attainable model (
) is infeasible, this work employs a local optimality approximation via a second-order Taylor expansion. For task-specific risk
, assuming continuous second-order derivatives, the risk at parameter
is expanded as
where
is the gradient of
at
;
is the Hessian matrix of
at
; and
is the Peano remainder term of the Taylor expansion. Substituting the locally optimal parameters
into Equation (
5) and neglecting the remainder term, the excess risk can be estimated as
To resolve the parameter difference
, we perform a first-order Taylor expansion of the gradient
at
:
Substituting
into Equation (
7) and leveraging the local optimality condition
(with remainder terms neglected), we obtain
Substituting Equation (
8) into Equation (
6) yields the simplified excess risk estimator:
For computational efficiency, the constant coefficient
may be omitted. In the derivation from Equations (6)–(9), the Taylor expansion approximation was employed. When the parameters approach the local optimum, higher-order terms of the loss function can be reasonably neglected. The validity of this approximation naturally improves as training proceeds and parameters approach their local optimal values. Additionally, the experiments in
Section 4.3.1 empirically demonstrate that this approximation remains accurate and effective.
To further reduce computational overhead, we adopt a diagonal approximation of the empirical Fisher information matrix [
27] for Hessian estimation. This approach constructs a diagonal matrix by accumulating outer products of historical gradients. Specifically, let
denote the gradient of task
at training step
. The Hessian approximation at step
t is given by
where
extracts the main diagonal elements to form a diagonal matrix. This approximation achieves
computational complexity (with
d being parameter dimensionality), ensuring practical feasibility for large-scale models. Although the diagonal approximation of the Hessian matrix may introduce a certain degree of accuracy loss, it significantly improves computational efficiency. Considering that our primary goal is to allocate task weights based on relative excess risk rather than obtaining precise Hessian estimations, the potential accuracy trade-off involved in this approximation is practically acceptable.
2.4. Exponential Gradient-Based Weight Update
Following the estimation of excess risk, the task weights must be systematically updated. To establish an optimal task-weighting strategy, the multi-task learning framework for GIS PD diagnosis is formulated as a minimax optimization problem:
where
w denotes the task weight vector and
represents the 1-dimensional probability simplex, enforcing non-negative weights that sum to unity.
While the one-hot solution for
w in Equation (
11) maximizes the weighted excess risk, it exhibits instability due to its exclusion of gradient information from auxiliary tasks, which potentially compromises training efficiency. To address this limitation, online mirror descent (OMD) [
28] is implemented with KL divergence regularization to design the weight update rule. Following the iterative OMD framework, the weight vector is updated by solving
where
is the learning rate for weights,
denotes the gradient of the weighted excess risk with respect to
w,
is the inner product operator, and
defines the KL divergence. Solving this using Lagrange multipliers yields the closed-form update:
where the denominator acts as a normalization factor to preserve the
simplex constraint. This exponential weighting mechanism dynamically prioritizes tasks with elevated excess risks, thereby mitigating the adverse impact of label noise on weight allocation.
3. Severity Assessment Loss Function Based on Conditional Probability Ordinal Regression
In GIS PD diagnosis, severity assessment is an ordinal regression problem, where severity levels possess a natural order (e.g., normal, initial, developing, and severe). Unlike traditional classification methods, ordinal regression requires maintaining ranking consistency in prediction results (described in detail in
Section 3.1) to ensure the reasonableness of predictions. Failure to maintain this ordering affects the reliability of prediction results and may lead to reduced prediction accuracy. Recent solutions for ensuring ranking consistency [
29,
30] typically require modifications to neural network structures. In contrast, this paper explores a loss function that inherently ensures ranking consistency and can be directly applied to any neural network architecture. Therefore, this paper adopts ordinal regression based on conditional probability [
31] to ensure ranking consistency in severity assessment predictions, as shown in Algorithm 2.
| Algorithm 2 Conditional probability-based ordinal regression loss function |
Require: Batch sample probability predictions , batch sample labels Initialize loss , sample count for to 3 do Select relevant samples for current binary classification if then Convert binary labels Select relevant predictions for current binary classification Calculate current binary classification loss function end if end for return
|
3.1. Ranking Consistency in Severity Assessment
The severity levels of GIS PD are categorized into four distinct classes: “normal” (), “initial” (), “developing” (), and “severe” (), formally represented as . Unlike conventional multi-class classification, severity assessment constitutes an ordinal regression problem, where explicit partial ordering relations exist between classes: , reflecting the progressive escalation of discharge severity.
Traditional multi-class classification approaches fail to capture these ordinal relationships and assign uniform misclassification costs across all errors (e.g., penalizing misclassification of
as
equivalently to
), which contradicts practical diagnostic requirements. The mainstream approach to handling ordinal regression problems is based on the extended binary classification framework [
32], which decomposes an
I-class ordinal regression problem (
in our case) into
binary classification sub-tasks. Specifically, the ordinal labels are reformulated into binary labels
for
. The predicted severity level
(where
) is determined by
where
denotes the probabilistic output of the
j-th binary classifier, indicating the likelihood that the sample’s severity exceeds
, and
represents the indicator function. Critically, this formulation inherently lacks ranking consistency guarantees—there exists no enforced monotonicity constraint ensuring that
.
As illustrated in
Figure 1, consider a PD sample with severity label
(“developing”). Both consistent and inconsistent probability profiles may yield identical final predictions (
) through Equation (
14). However, the inconsistent case (violating monotonicity) achieves correct classification merely by coincidence rather than reliable ordinal reasoning. This underscores the necessity of enforcing ranking consistency to ensure physically plausible and interpretable severity predictions, aligned with GIS insulation degradation patterns.
3.2. Conditional Probability Modeling
For the severity assessment task, given the dataset , the ordinal severity labels are extended into binary labels , indicating whether the severity exceeds threshold (). While the OR-MTL framework similarly configures three outputs in its severity assessment branch to address these binary sub-tasks, conventional implementations fail to guarantee ranking consistency in predictions. To address this limitation, a structured conditional probability modeling approach is adopted to enforce ordinal constraints explicitly.
Specifically, the severity assessment branch estimates a sequence of conditional probabilities through a constrained training paradigm (detailed in
Section 3.3, where the output of the
j-th binary task
corresponds to
The conditional relationship
inherently reflects the physical reality that surpassing a higher severity threshold
necessitates prior exceedance of its predecessor
. By applying the probabilistic chain rule, these conditional probabilities are transformed into joint probabilities:
Given
for all
j, the following monotonicity property is analytically guaranteed:
This formulation ensures that the probability of exceeding higher severity thresholds decreases monotonically, thereby intrinsically preserving ranking consistency across all binary sub-tasks. The resulting predictions align with the ordinal structure of severity progression while enhancing model interpretability and diagnostic reliability.
3.3. Conditional Subset-Based Training and Prediction
The severity assessment branch of OR-MTL aims to estimate the base probability and conditional probabilities and . Estimating constitutes a standard binary classification task under the extended binary framework, utilizing binary labels . To estimate conditional probabilities such as , the model focuses exclusively on the subset of training data where . Consequently, when minimizing the binary cross-entropy loss over these conditional subsets, the output probabilities for each binary task inherently preserve their conditional probability interpretations.
To model the conditional probabilities defined in Equation (
15), conditional training subsets are constructed to compute loss functions minimized via backpropagation. These subsets are derived from the original training set as follows:
where
and
denotes the cardinality of subset
. Each subset
(for
) contains only samples with severity levels exceeding
, ensuring the model learns sequential relationships between severity grades.
For training via backpropagation, the binary cross-entropy loss is adopted for each probability prediction unit
:
The total loss
for the severity assessment task is formulated as a weighted sum:
Here, the sample size-driven adaptive weights
mitigate distribution imbalance caused by hierarchical subset construction through sample count normalization.
To predict the severity level
for the
n-th sample, the rank index
is computed by thresholding the product of conditional probabilities and summing binary indicators:
Thus, the severity prediction for the
n-th training sample is
.
5. Conclusions
This paper proposes an Ordinal Regression Multi-Task Learning (OR-MTL) framework to address the ordinal regression nature of the severity assessment task in GIS PD multi-task diagnosis, which addresses two key issues introduced by ordinal regression tasks in multi-task learning.
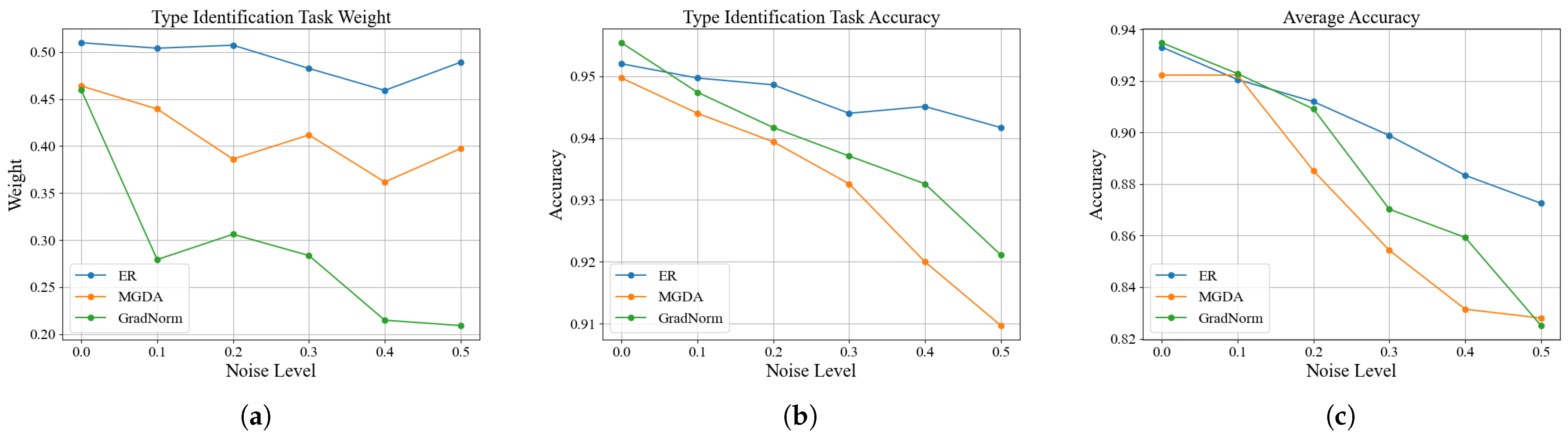
First, by addressing the impact of label noise in ordinal regression tasks on task weight allocation, this paper proposes a dynamic task-weighting strategy based on excess risk. This strategy adjusts the weights by estimating task excess risk rather than the original loss, effectively mitigating the impact of label noise in the severity assessment task on the discharge-type identification task. Experimental results show that under different noise levels, this strategy consistently maintains high weights and accuracy for clean tasks, demonstrating greater robustness than traditional methods.
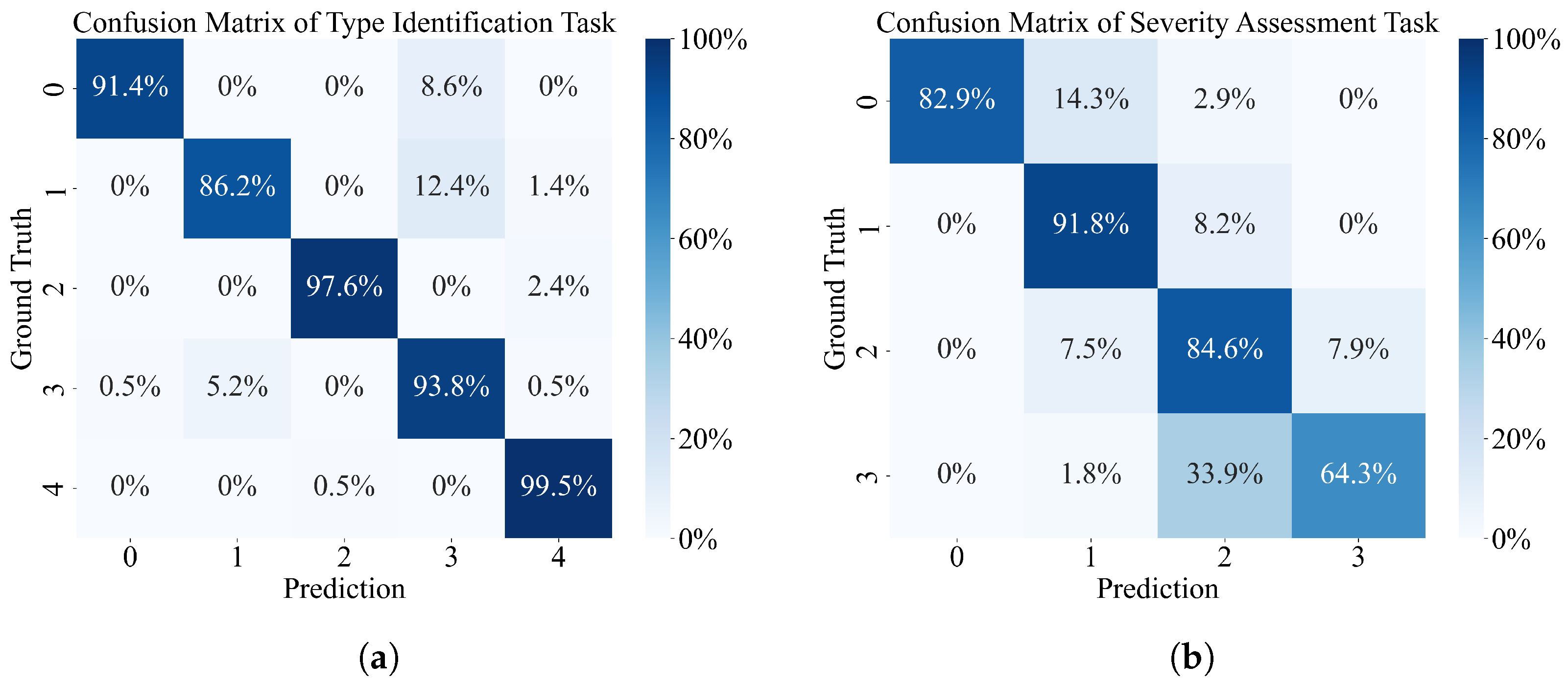
Second, by addressing the ranking inconsistency problem in ordinal regression predictions, this paper introduces a conditional probability-based ordinal regression loss function, which ensures ranking consistency in severity predictions through a conditional probability sequence. Experiments demonstrate that this loss function outperforms the traditional cross-entropy and ordinary ordinal regression loss functions in terms of severity assessment accuracy, mean absolute error, and root mean squared error. Ablation experiments further confirm that the complete OR-MTL framework achieves optimal performance in both the discharge-type identification and severity assessment tasks.
Due to the lack of publicly available GIS PD datasets and the practical challenges in obtaining defect samples from actual operating environments, the validation in this study was conducted solely on a laboratory-generated dataset. In future work, we plan to cooperate closely with power utilities to collect additional real-world GIS PD data, aiming to further verify and enhance the generalizability of our proposed method. This research not only provides more effective technical support for the intelligent operation and maintenance of GIS equipment but also offers new insights into multi-task learning involving ordinal regression tasks.