Structural, Vibrational, and Dielectric Properties of BiFeO3/LaFeO3 Superlattices Grown on (001)-SrTiO3
Abstract
1. Introduction
2. Experimental Details
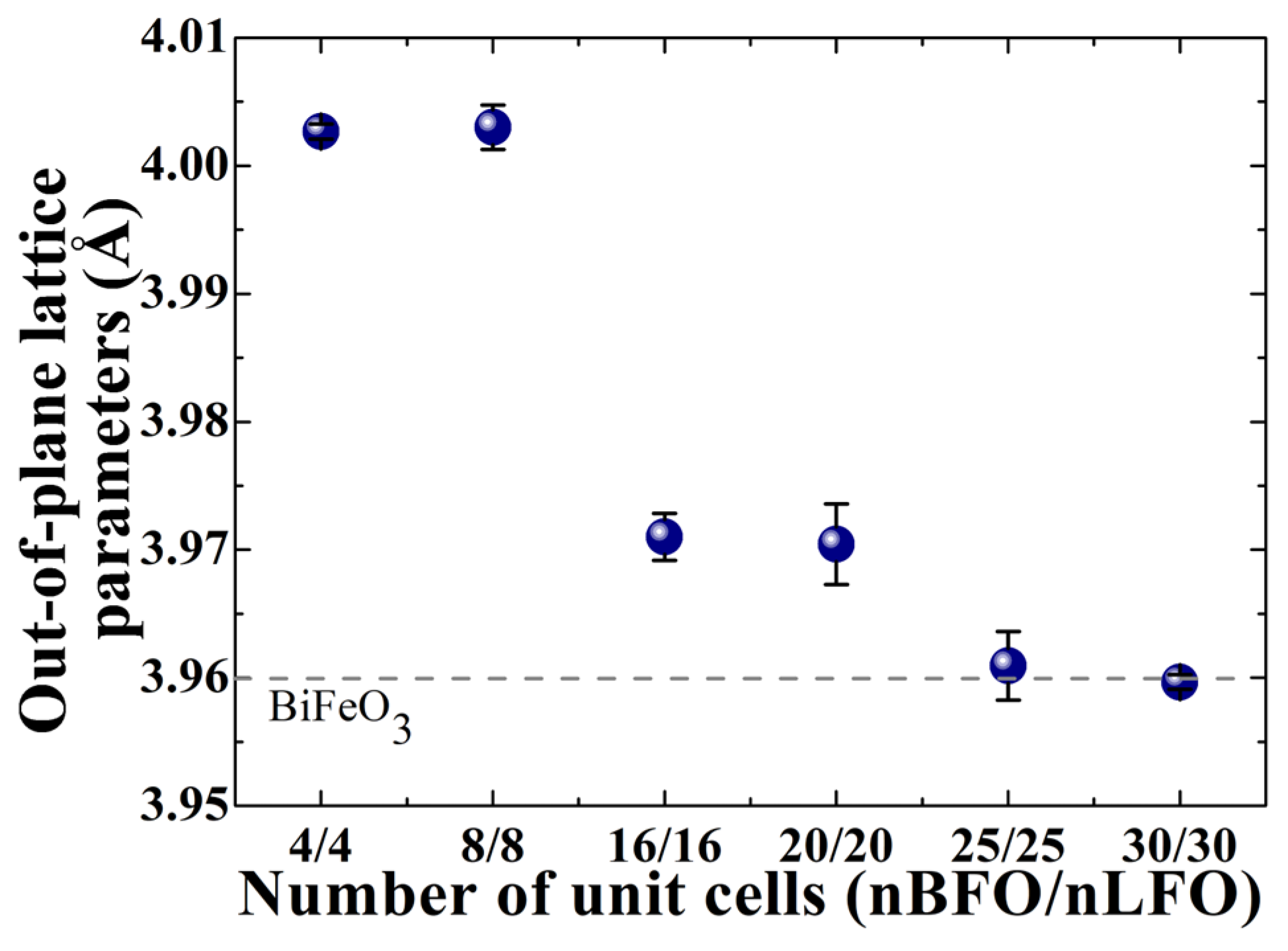
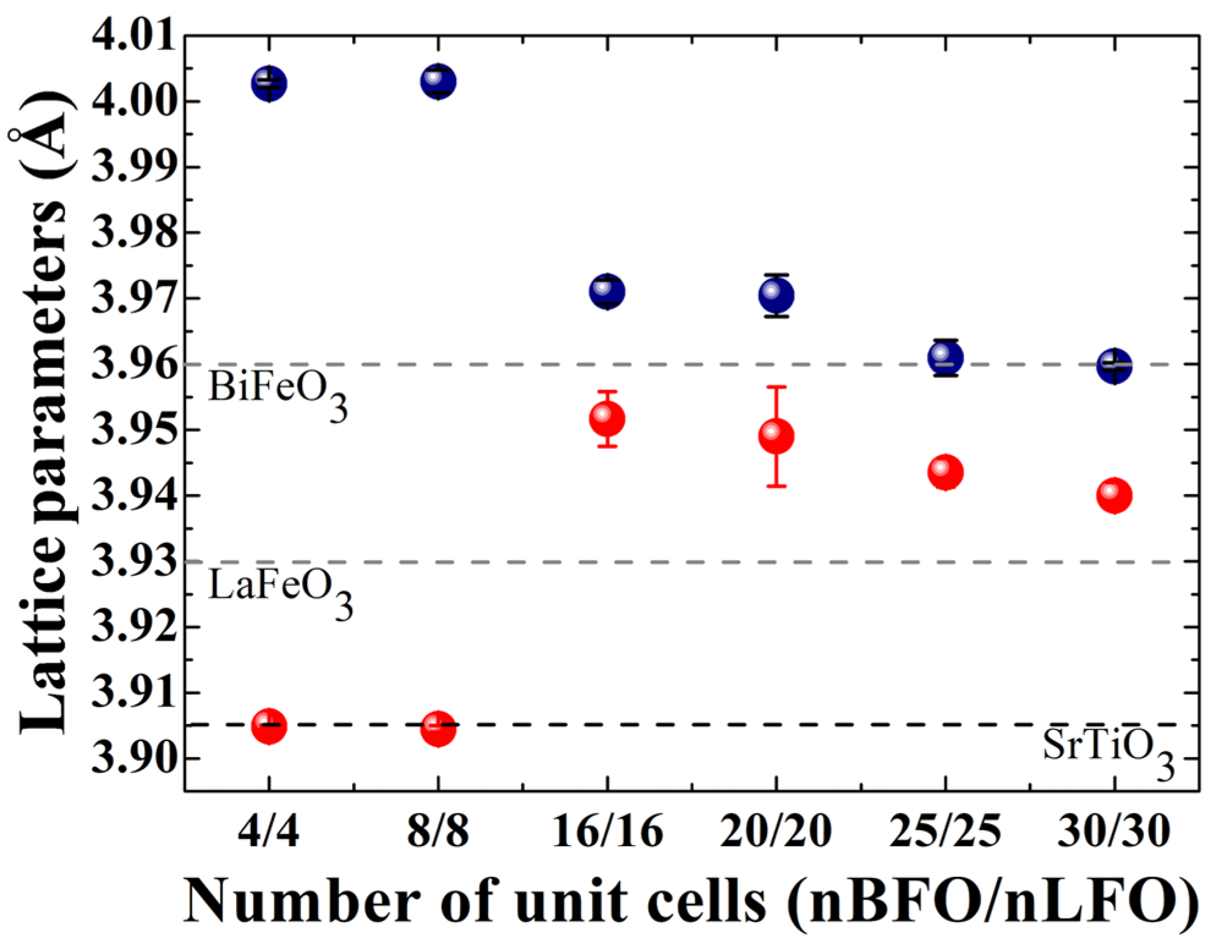
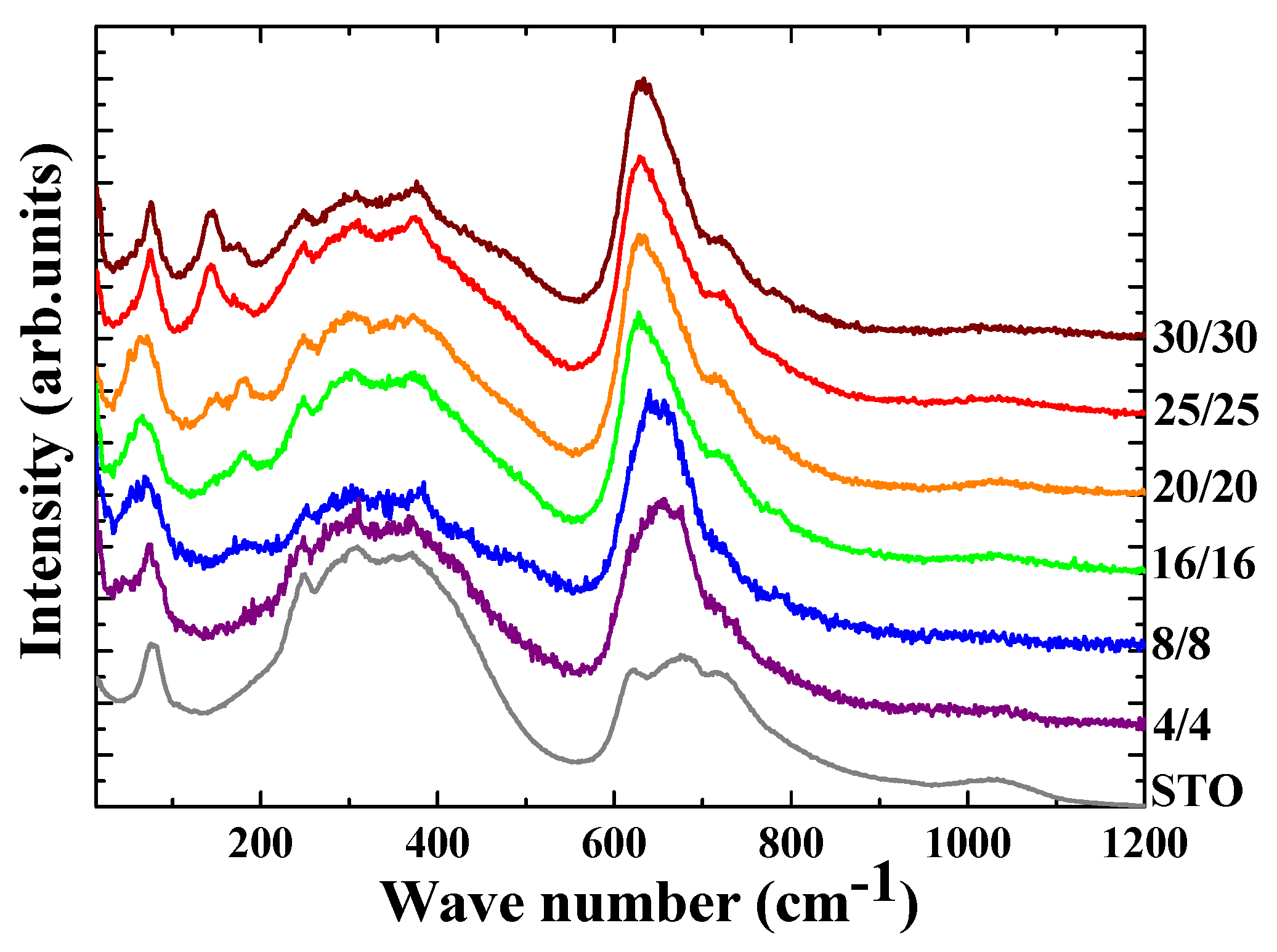
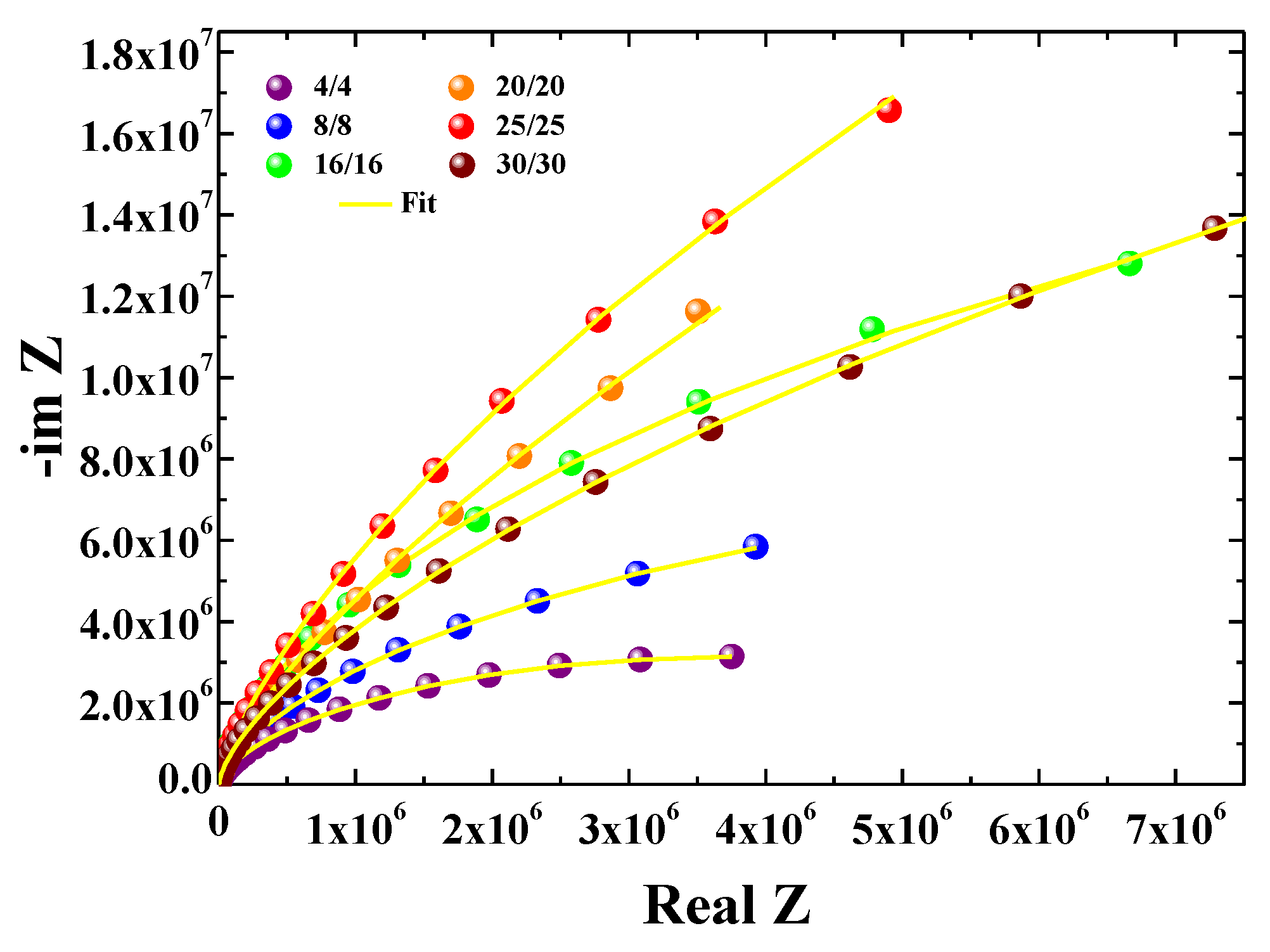
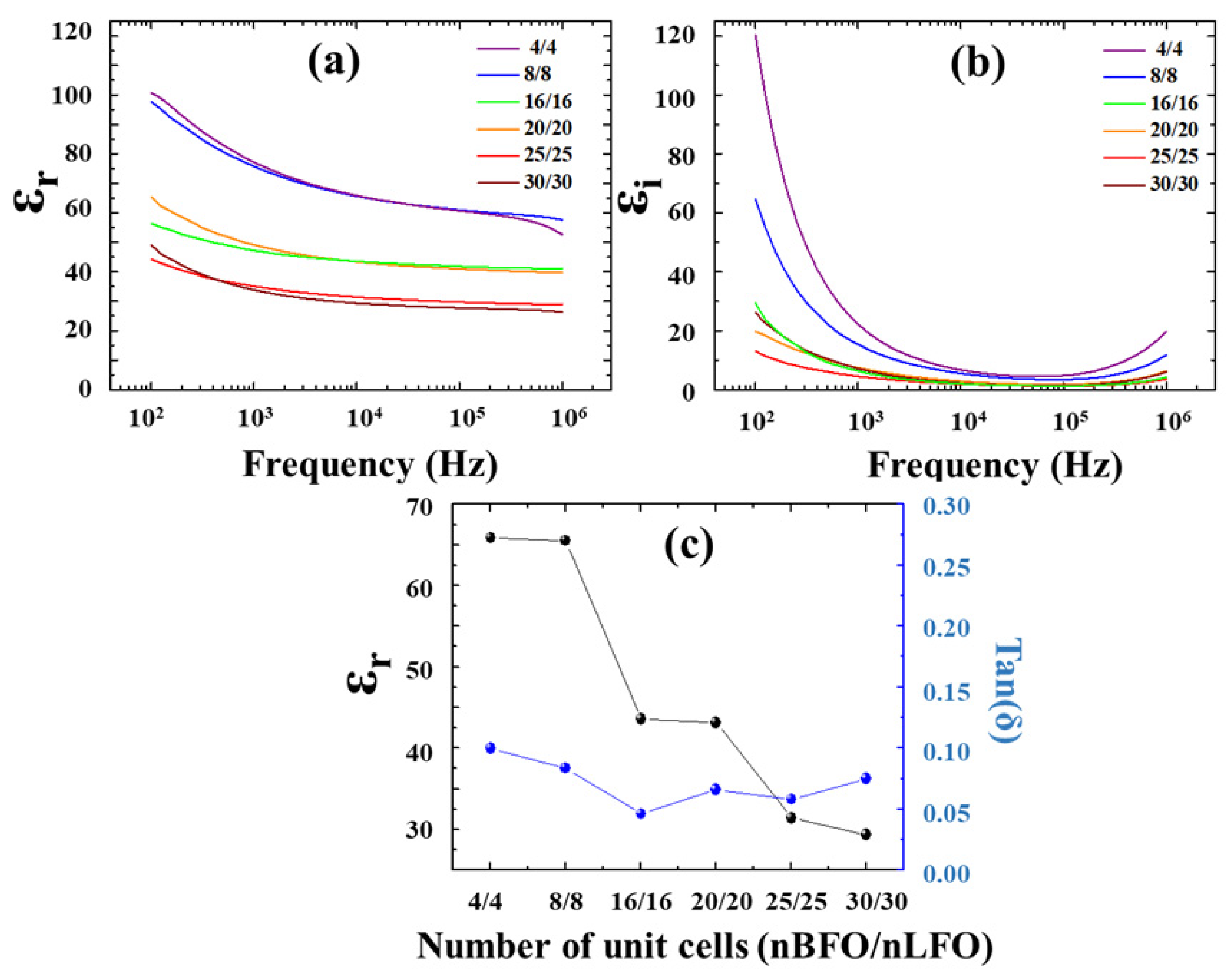
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Catalan, G.; Scott, J.F. Physics and Applications of Bismuth Ferrite. Adv. Mater. 2009, 21, 2463–2485. [Google Scholar] [CrossRef]
- Yakout, S.M. Spintronics and Innovative Memory Devices: A Review on Advances in Magnetoelectric BiFeO3. J. Supercond. Nov. Magn. 2021, 34, 317–338. [Google Scholar] [CrossRef]
- Tablero, C. Photovoltaic application of the multiferroic Bi2FeCrO6 double perovskite. Sol. Energy 2016, 137, 173–178. [Google Scholar] [CrossRef]
- Haruna, A.; Abdulkadir, I.; Idris, S.O. Photocatalytic activity and doping effects of BiFeO3 nanoparticles in model organic dyes. Heliyon 2020, 6, e03237. [Google Scholar] [CrossRef] [PubMed]
- Kashif, M.; Quader, A.; Khan, M.A.; Ramay, S.M.; Atiq, S. Effectively coupled BiFeO3-MnFe2O4-Cr2O3 tri-phase multiferroic composites for efficient energy storage and fast switching. J. Alloys Compd. 2022, 929, 167274. [Google Scholar] [CrossRef]
- Scarisoreanu, N.D.; Craciun, F.; Birjega, R.; Ion, V.; Teodorescu, V.S.; Ghica, C.; Negrea, R.; Dinescu, M. Joining Chemical Pressure and Epitaxial Strain to Yield Y-doped BiFeO3 Thin Films with High Dielectric Response. Sci. Rep. 2016, 6, 25535. [Google Scholar] [CrossRef]
- Wang, N.; Luo, X.; Han, L.; Zhang, Z.; Zhang, R.; Olin, H.; Yang, Y. Structure, Performance, and Application of BiFeO3 Nanomaterials. Nano-Micro Lett. 2020, 12, 81. [Google Scholar] [CrossRef]
- Martin, L.W.; Rappe, A.M. Thin-film ferroelectric materials and their applications. Nat. Rev. Mater. 2016, 2, 16087. [Google Scholar] [CrossRef]
- Khan, A.I.; Yu, P.; Trassin, M.; Lee, M.J.; You, L.; Salahuddin, S. The effects of strain relaxation on the dielectric properties of epitaxial ferroelectric Pb(Zr0.2Ti0.8)TiO3 thin films. Appl. Phys. Lett. 2014, 105, 022903. [Google Scholar] [CrossRef]
- Ma, H.; Levy, J.; Biegalski, M.D.; Trolier-McKinstry, S.; Schlom, D.G. Room-temperature electro-optic properties of strained SrTiO3 films grown on DyScO3. J. Appl. Phys. 2009, 105, 014102. [Google Scholar] [CrossRef]
- Nagarajan, V.; Roytburd, A.; Stanishevsky, A.; Prasertchoung, S.; Zhao, T.; Chen, L.; Melngailis, J.; Auciello, O.; Ramesh, R. Dynamics of ferroelastic domains in ferroelectric thin films. Nat. Mater. 2003, 2, 43–47. [Google Scholar] [CrossRef]
- Shilnikov, A.V.; Burkhanov, A.I.; Kudashev, A.S.; Sigov, A.S.; Vorotilov, K.A. Electric Non-Linearity in Ferroelectric Films of the BaxSr1−xTiO3 Type. Ferroelectrics 2004, 307, 167–170. [Google Scholar] [CrossRef]
- Das, S.; Hong, Z.; McCarter, M.; Shafer, P.; Shao, Y.-T.; Muller, D.A.; Martin, L.W.; Ramesh, R. A new era in ferroelectrics. APL Mater. 2020, 8, 120902. [Google Scholar] [CrossRef]
- Singh, P.; Park, Y.; Sung, K.; Hur, N.; Jung, J.; Noh, W.-S.; Kim, J.-Y.; Yoon, J.; Jo, Y. Magnetic and ferroelectric properties of epitaxial Sr-doped BiFeO3 thin films. Solid State Commun. 2010, 150, 431–434. [Google Scholar] [CrossRef]
- Wang, H.; Khatkhatay, F.; Jian, J.; Huang, J.; Fan, M.; Wang, H. Strain tuning of ferroelectric and optical properties of rhombohedral-like BiFeO3 thin films on SrRuO3-buffered substrates. Mater. Res. Bull. 2019, 110, 120–125. [Google Scholar] [CrossRef]
- Fan, Z.; Wang, J.; Sullivan, M.B.; Huan, A.; Singh, D.J.; Ong, K.P. Structural Instability of Epitaxial (001) BiFeO3 Thin Films under Tensile Strain. Sci. Rep. 2014, 4, 4631. [Google Scholar] [CrossRef]
- Akbashev, A.R.; Plokhikh, A.V.; Barbash, D.; Lofland, S.E.; Spanier, J.E. Crystallization engineering as a route to epitaxial strain control. APL Mater. 2015, 3, 106102. [Google Scholar] [CrossRef]
- Rabe, K.M. Theoretical investigations of epitaxial strain effects in ferroelectric oxide thin films and superlattices. Curr. Opin. Solid State Mater. Sci. 2005, 9, 122–127. [Google Scholar] [CrossRef]
- Blok, J.L.; Blank, D.H.A.; Rijnders, G.; Rabe, K.M.; Vanderbilt, D. Interplay of epitaxial strain and rotations in PbTiO3/PbZrO3 superlattices from first principles. Phys. Rev. B 2011, 84, 205413. [Google Scholar] [CrossRef]
- Yousfi, S.; El Marssi, M.; Bouyanfif, H. Structural behaviour of BiFeO3/SrRuO3 superlattices: An X-ray diffraction and Raman spectroscopy investigation. Superlattices Microstruct. 2021, 156, 106983. [Google Scholar] [CrossRef]
- Govinden, V.; Tong, P.; Guo, X.; Zhang, Q.; Mantri, S.; Seyfouri, M.M.; Prokhorenko, S.; Nahas, Y.; Wu, Y.; Bellaiche, L.; et al. Ferroelectric solitons crafted in epitaxial bismuth ferrite superlattices. Nat. Commun. 2023, 14, 4178. [Google Scholar] [CrossRef]
- Carcan, B.; Bouyanfif, H.; El Marssi, M.; Le Marrec, F.; Dupont, L.; Davoisne, C.; Wolfman, J.; Arnold, D.C. Interlayer strain effects on the structural behavior of BiFeO3/LaFeO3 superlattices. J. Appl. Phys. 2018, 124, 044105. [Google Scholar] [CrossRef]
- Carcan, B.; Bouyanfif, H.; El Marssi, M.; Le Marrec, F.; Dupont, L.; Davoisne, C.; Wolfman, J.; Arnold, D.C. Phase Diagram of BiFeO3/LaFeO3 Superlattices: Antiferroelectric-Like State Stability Arising from Strain Effects and Symmetry Mismatch at Heterointerfaces. Adv. Mater. Interfaces 2017, 4, 1601036. [Google Scholar] [CrossRef]
- Lee, H.J.; Lee, S.S.; Kwak, J.H.; Kim, Y.-M.; Jeong, H.Y.; Borisevich, A.Y.; Lee, S.Y.; Noh, D.Y.; Kwon, O.; Kim, Y.; et al. Depth resolved lattice-charge coupling in epitaxial BiFeO3 thin film. Sci. Rep. 2016, 6, 38724. [Google Scholar] [CrossRef] [PubMed]
- Sando, D.; Xu, B.; Bellaiche, L.; Nagarajan, V. A multiferroic on the brink: Uncovering the nuances of strain-induced transitions in BiFeO3. Appl. Phys. Rev. 2016, 3, 011106. [Google Scholar] [CrossRef]
- Bielecki, J.; Svedlindh, P.; Tibebu, D.T.; Cai, S.; Eriksson, S.-G.; Börjesson, L.; Knee, C.S. Structural and magnetic properties of isovalently substituted multiferroic BiFeO3: Insights from Raman spectroscopy. Phys. Rev. B 2012, 86, 184422. [Google Scholar] [CrossRef]
- Mundy, J.A.; Heikes, C.A.; Grosso, B.F.; Segedin, D.F.; Wang, Z.; Goodge, B.H.; Meier, Q.N.; Nelson, C.T.; Prasad, B.; Kourkoutis, L.F.; et al. A high-energy density antiferroelectric made by interfacial electrostatic engineering. arXiv 2018, arXiv:1812.09615. [Google Scholar] [CrossRef]
- Yuan, G.; Or, S.; Wang, Y.; Liu, Z.; Liu, J. Preparation and multi-properties of insulated single-phase BiFeO3 ceramics. Solid State Commun. 2006, 138, 76–81. [Google Scholar] [CrossRef]
- Béa, H.; Dupé, B.; Fusil, S.; Mattana, R.; Jacquet, E.; Warot-Fonrose, B.; Wilhelm, F.; Rogalev, A.; Petit, S.; Cros, V.; et al. Evidence for Room-Temperature Multiferroicity in a Compound with a Giant Axial Ratio. Phys. Rev. Lett. 2009, 102, 217603. [Google Scholar] [CrossRef]
- Rusakov, D.A.; Abakumov, A.M.; Yamaura, K.; Belik, A.A.; Van Tendeloo, G.; Takayama-Muromachi, E. Structural Evolution of the BiFeO3−LaFeO3 System. Chem. Mater. 2011, 23, 285–292. [Google Scholar] [CrossRef]
- Infante, I.C.; Lisenkov, S.; Dupé, B.; Bibes, M.; Fusil, S.; Jacquet, E.; Geneste, G.; Petit, S.; Courtial, A.; Juraszek, J.; et al. Bridging Multiferroic Phase Transitions by Epitaxial Strain in BiFeO3. Phys. Rev. Lett. 2010, 105, 057601. [Google Scholar] [CrossRef] [PubMed]
- Hadjimichael, M.; Li, Y.; Yedra, L.; Dkhil, B.; Zubko, P. Domain structure and dielectric properties of metal-ferroelectric superlattices with asymmetric interfaces. Phys. Rev. Mater. 2020, 4, 094415. [Google Scholar] [CrossRef]
- O’neill, D.; Bowman, R.M.; Gregg, J.M. Dielectric enhancement and Maxwell–Wagner effects in ferroelectric superlattice structures. Appl. Phys. Lett. 2000, 77, 1520–1522. [Google Scholar] [CrossRef]
- Kubel, F.; Schmid, H. Structure of a ferroelectric and ferroelastic monodomain crystal of the perovskite BiFeO3. Acta Crystallogr. Sect. B Struct. Sci. 1990, 46, 698–702. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, S.; Jiang, W.; Cao, W. Losses in ferroelectric materials. Mater. Sci. Eng. R Rep. 2015, 89, 1–48. [Google Scholar] [CrossRef]




| SRO Layer | SLs (BFO and LFO) | |
|---|---|---|
| Target | SRO | BFO and LFO |
| Fluence (J·cm−2) | 2 | 0.8 |
| Repetition rate (Hz) | 6 | 4 |
| Oxygen pressure (mbar) | 10−1 | 5 × 10−2 |
| Temperature (°C) | 700 | 740 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khiari, M.; Burcea, R.; Condurache, O.; Vallet, M.; Cantaluppi, A.; Melhem, A.; Dkhil, B.; Bouyanfif, H. Structural, Vibrational, and Dielectric Properties of BiFeO3/LaFeO3 Superlattices Grown on (001)-SrTiO3. Electronics 2025, 14, 1117. https://doi.org/10.3390/electronics14061117
Khiari M, Burcea R, Condurache O, Vallet M, Cantaluppi A, Melhem A, Dkhil B, Bouyanfif H. Structural, Vibrational, and Dielectric Properties of BiFeO3/LaFeO3 Superlattices Grown on (001)-SrTiO3. Electronics. 2025; 14(6):1117. https://doi.org/10.3390/electronics14061117
Chicago/Turabian StyleKhiari, Mouna, Razvan Burcea, Oana Condurache, Maxime Vallet, Anna Cantaluppi, Amani Melhem, Brahim Dkhil, and Houssny Bouyanfif. 2025. "Structural, Vibrational, and Dielectric Properties of BiFeO3/LaFeO3 Superlattices Grown on (001)-SrTiO3" Electronics 14, no. 6: 1117. https://doi.org/10.3390/electronics14061117
APA StyleKhiari, M., Burcea, R., Condurache, O., Vallet, M., Cantaluppi, A., Melhem, A., Dkhil, B., & Bouyanfif, H. (2025). Structural, Vibrational, and Dielectric Properties of BiFeO3/LaFeO3 Superlattices Grown on (001)-SrTiO3. Electronics, 14(6), 1117. https://doi.org/10.3390/electronics14061117






