Communication Efficient Secure Three-Party Computation Using Lookup Tables for RNN Inference

Abstract

Many leading technology companies currently offer Machine Learning as a Service Platform, enabling developers and organizations to access the inference capabilities of pre-trained models via API calls. However, due to concerns over user data privacy, inter-enterprise competition, and legal and regulatory constraints, directly utilizing pre-trained models in the cloud for inference faces security challenges. In this paper, we propose communication-efficient secure three-party protocols for recurrent neural network (RNN) inference. First, we design novel three-party secret-sharing protocols for digit decomposition, B2A conversion, enabling efficient transformation of secret shares between Boolean and arithmetic rings. Then, we propose the lookup table-based secure three-party protocol. Unlike the intuitive way of directly looking up tables to obtain results, we compute the results by utilizing the inherent mathematical properties of binary lookup tables, and the communication complexity of the lookup table protocol is only related to the output bit width. We also design secure three-party protocols for key functions in the RNN, including matrix multiplication, sigmoid function, and Tanh function. Our protocol divides the computation into online and offline phase, and places most of the computations locally. The theoretical analysis shows that the communication round of our work was reduced from four rounds to one round. The experiment results show that compared with the current SOTA-SIRNN, the online communication overhead of sigmoid and tanh functions decreased by 80.39% and 79.94%, respectively.

1. Introduction

In recent years, many leading technology companies have introduced “Machine Learning as a Service” (MLaaS) platforms, such as Amazon SageMaker, Microsoft Azure Machine Learning, Google Cloud AI Platform, Alibaba Cloud Platform of Artificial Intelligence, and Tencent Cloud TI Platform. These platforms provide users with easy access to pre-trained neural network models through simple API calls, without requiring a deep understanding of the underlying technical details. As a result, users can quickly perform inference tasks using their own data. This approach has significantly lowered the barrier to using neural network technologies, making it possible for more businesses and individuals to benefit from the advantages of neural network models.

However, behind the convenience of these services lies a significant risk of privacy leakage and challenges that cannot be ignored. On one hand, when users’ data are uploaded to cloud servers for processing, there exists the risk of these private data being leaked or misused. For example, in 2023, the short-video platform TikTok faced widespread privacy concerns globally due to its data-collection and -processing practices. Governments and regulatory authorities in multiple countries have investigated its data-handling methods, fearing that user private data might be employed for improper purposes. On the other hand, when users employ machine learning models provided by service providers for inference tasks, there is a risk of leakage of model parameters and training data. Malicious users can potentially reverse-engineer model parameters and even deduce parts of the training dataset content through repeated access to the model. This poses a significant threat to enterprises that rely on highly confidential data to train their models. Therefore, ensuring the privacy of both users’ input data and neural network models during the model inference phase has become one of the current research hotspots.

Secure Multi-Party Computation (MPC) allows multiple data owners to perform arbitrary computational tasks without revealing their private data. This technology provides an effective method for addressing the challenges. Current research on privacy-preserving deep neural network inference using MPC primarily focuses on convolutional neural networks (CNNs) that handle spatially distributed data [1,2,3,4,5,6,7,8,9,10,11,12]; these efforts have advanced secure inference for image and grid-structured tasks. With the rapid development of large language models in recent years, models that can handle sequence problems have become a focus of research. Recurrent Neural Networks (RNNs) is an architecture specifically designed for time series such as speech signals, physiological time series, and financial transaction flows, while there are relatively limited works on RNNs [13,14,15]. RNNs are more complex in structure compared to CNNs, particularly due to the inclusion of complex nonlinear activation functions (e.g., sigmoid/Tanh function). On one hand, existing work for RNNs only supports secure inference between two parties, without considering the high communication overhead associated with involving multiple parties. On the other hand, existing methods often use piecewise linear functions for approximate computations, which can result in lower accuracy. To address these issues, we propose a communication-efficient secure three-party RNN inference method. In summary, we made the following contributions:

(1)

We construct novel three-party secret-sharing-based digit decomposition, B2A conversion protocols.These protocols complement the existing three-party secret-sharing scheme, effectively reducing the communication overhead in the online phase.

(2)

We propose the lookup table-based secure three-party protocol by utilizing the inherent mathematical properties of binary lookup tables, and the communication complexity of the LUT protocol is only related to the output bit width.

(3)

We propose the lookup table-based secure three-party protocols for RNN inference, including key functions in RNNs, such as matrix multiplication, sigmoid and Tanh function, and achieving lower online communication overhead compared to current SOTA-SIRNN.

The rest of this paper is organized as follows: Section 2 describes work related to this work. Section 3 introduces the preliminaries of the secret sharing scheme and lookup table. Section 4 provides the protocol constructions, including the system model, conversions of secret sharing, and the lookup table-based 3PC protocol. Section 5 gives the basic building blocks of RNN based on the secure protocols of Section 4. Section 6 provide the security analysis. Section 7 provides performance analysis from theoretical and experimental perspectives, and Section 8 summarizes the conclusions.

2. Related Work

In recent years, privacy preservation has become a crucial concern across various domains, reflecting the growing need to protect sensitive data in increasingly interconnected environments. In cloud computing, significant advancements have been made in enabling secure and verifiable machine learning model training [16], as well as in developing efficient frameworks for privacy-preserving neural network training and inference [17]. In the realm of path planning, researchers have introduced techniques to manage complex multi-task assignments while maintaining data privacy [18]. Additionally, the blockchain sector has progressed in privacy governance by ensuring data integrity and controlling access within decentralized databases [19]. Despite these diverse applications, there remains a critical need to specifically address the security issues of sensitive data and privacy models in neural network computation.

There are already many works aimed at CNNs in the privacy-preserving machine learning field, designing secure computing protocols for specific structures in CNNs. For works only focusing on two parties involving secure neural network computations, many of them use different techniques to evaluate secure inference [1,2,3,4,5,6,7,8,9]. Some work ignores nonlinear mathematical functions [1,6,10,11], since whether a monotonic mathematical function is used or not does not affect the inference result in some cases. In 2PC settings, some works use higher-degree polynomials to approximate nonlinear mathematical functions [12] to ensure accuracy. Some previous works use ad hoc approximations to approximate nonlinear functions, but this may cause a loss in model accuracy while achieving higher computational efficiency [3,9]. Rathee et al. [13] utilized a lookup table for some complex nonlinear math functions and the model accuracy was improved to a certain extent. Flute et al. [20] utilized a lookup table for some complex nonlinear math functions, and the model accuracy of nonlinear math functions was improved under 2PC settings.

In order to improve the performance of two-party secure neural network computations, many works introduce a third party to provide randomness during the offline phase to assist computation or involve computations. Similar to the previous work under 2PC settings, 3PC works still use polynomial approximation to compute nonlinear math functions [21,22,23,24]. Chameleon et al. [21] utilized a semi-honest third-party server to assist in generating correlated random numbers during the offline phase and Yao’s Garbled Circuits for nonlinear functions. To reduce the expensive computing operations caused by garbled circuits, some work (e.g., [25]) used ad hoc approximations instead of GC to calculate nonlinear functions, such as maxpool, ReLU, and so on. Moreover, ref. [26] proposed improved replication secret sharing that improved the online communication efficiency. In addition, some multi-party works focus on application scenarios where malicious adversaries exist, thus requiring more communication and computation overhead [27,28,29,30].

However, in many practical scenarios, such as those involving sequential data, Recurrent Neural Networks (RNNs) are essential for effective computation. Early efforts in secure inference of RNNs include ref. [13] addressing SIRNN, which used lookup tables to calculate commonly used nonlinear activation functions like sigmoid and tanh in RNNs. This approach enabled high accuracy with a two-server setup, making it a significant step forward in secure RNN inference, particularly for speech and time series sensor data. Building on this, Zheng et al. [14] introduced a three-party secure computation protocol to handle nonlinear activation functions and their derivatives in RNNs, leveraging Fourier series approximations to balance precision and computation efficiency.

RNNs still face significant challenges in secure computation, particularly in real-world applications. One major issue is the high communication overhead associated with secure RNN inference, which is caused by the complexity of nonlinear activation functions and the recurrent structure of RNNs. Our work focuses on designing secure computation protocols for complex nonlinear functions in RNNs to reduce online communication.

3. Preliminaries

This section provides the fundamental theory required by our method. We introduce the related 3PC secret sharing scheme for the whole framework of our works, and the lookup table technology for nonlinear layers. The notations used in this work are listed in

Table 1. Notation table.

Notation	Description
$\left[·\right]$	3-out-of-3 sharing
$〈·〉$	2-out-of-3 replicated secret sharing
$[[·]]$	3PC secret sharing in this work
$\delta$-to-$\sigma$ T	LUT T with $\sigma$ inputs and $\delta$ outputs
$2^{\mathcal{I}}$	Powerset of set $\mathcal{I}$
${\{{\overrightarrow{\mathcal{E}}}^u\}}_{u\in [\delta ]}$	Input encoding of LUT T with bit size $2^{\delta }$
${\{{\overrightarrow{\xi }}^w\}}_{w\in [\sigma ]}$	Output encoding of LUT T with bit size $2^{\sigma }$
$\overline{v}$	Complement of bit $v\in \{0,1\}$, $\overline{v}=1\oplus v$

.

3.1. Secret Sharing

In this paper, we utilize the optimized 3PC secret sharing scheme provided in Meteor [26] to calculate the linear layer of the RNN, which can accelerate fixed-point multiplication of two inputs and integer multiplication of N inputs, and this scheme can be easily extended to more party settings. The scheme is executed with three parties ${\{P_i\}}_{i\in [0,2]}$ over a Boolean ring ${\mathbb{Z}}_2$ (or arithmetic ring ${\mathbb{Z}}_{2^l}$, where l is the bit width). Given two private bits $\{x,y\}$, Boolean sharing refers to the secret sharing scheme of bit size $l=1$ and with logical AND, XOR, NOT operations, denoting $\wedge ,\oplus ,\overline{x}$, respectively.

3.1.1. $\left[·\right]$-Sharing

• For $\left[·\right]$-sharing over Boolean ring ${\mathbb{Z}}_2$, any Boolean value $v\in \{0,1\}$ is secret shared by three random values $v_0$, $v_1$, $v_2\in {\mathbb{Z}}_2$, and $P_i$ holds its share ${[v]}_i=v_i$, such that $v={[v]}_0\oplus {[v]}_1\oplus {[v]}_2$.
• For $\left[·\right]$-sharing over arithmetic ring ${\mathbb{Z}}_{2^l}$, any arithmetic value $v\in {\mathbb{Z}}_{2^l}$ is secret shared by three random values $v_0$, $v_1$, $v_2\in {\mathbb{Z}}_{2^l}$, and $P_i$ holds its share ${[v]}_i=v_i$, such that $v=v_0+v_1+v_2(mod{2}^l)$.

3.1.2. $〈·〉$-Sharing

$〈·〉$-Sharing is similar to $\left[·\right]$-sharing, but it is the three-party 2-out-of-3 replicated secret sharing scheme.

For $〈·〉$-sharing over Boolean ring ${\mathbb{Z}}_2$, any Boolean value $v\in \{0,1\}$ is secret shared by three random values $v_0$, $v_1$, $v_2\in {\mathbb{Z}}_2$, where $v={[v]}_0\oplus {[v]}_1\oplus {[v]}_2$. $P_i$ holds ${〈v〉}_i=(v_i,v_{i+1})$, such that any two parties can construct the secret value v.

For $〈·〉$-sharing over arithmetic ring ${\mathbb{Z}}_{2^l}$, any arithmetic value $v\in {\mathbb{Z}}_{2^l}$ is secret shared by three random values $v_0$, $v_1$, $v_2\in {\mathbb{Z}}_{2^l}$, where $v=v_0+v_1+v_2(mod{2}^l)$. Also, $P_i$ holds ${〈v〉}_i=(v_i,v_{i+1})$, such that any two parties can construct the secret value v.

• Linear Operation: For secret shared Boolean values $〈x〉$ and $〈y〉$, three parties ${\{P_i\}}_{i\in [3]}$ can compute value $〈z〉=c_1〈x〉\oplus c_2〈y〉\oplus c_3$, where $c_1,c_2,c_3$ are public constant bits. In the Boolean ring ${\mathbb{Z}}_2$, each party $P_i$ can locally compute its secret shares ${〈z〉}_i$, such that any two parities of ${\{P_i\}}_{i\in [3]}$ can recover the secret value z. It is similar for arithmetic rings ${\mathbb{Z}}_{2^l}$, by replacing the XOR operation ⊕ with the ADD operation +, and taking the modulus of $2^l$ for the result.
• AND Operation: For secret shared Boolean values $〈x〉$ and $〈y〉$, three parties ${\{P_i\}}_{i\in [3]}$ can compute the secret shared value $〈z〉=〈x〉\wedge 〈y〉$ as follows: (a) each party $P_i$ locally computes $z_i=x_i{y}_i\oplus x_{i+1}{y}_i\oplus x_i{y}_{i+1}$; (b) each party $P_i$ locally computes $z_i^{\prime }=z_i\oplus {\alpha }_i$, where ${\alpha }_0\oplus {\alpha }_1\oplus {\alpha }_2=0$ (for random number generation, please refer to Appendix A); (c) all three parties together perform re-sharing to obtain the sharing of $z_i^{\prime }$ by sending $z_i^{\prime }$ to $P_{i-1}$ so that each $P_i$ holds ${〈z〉}_i=(z_i^{\prime },z_{i+1}^{\prime })$.
• Multiplication: For secret shared arithmetic values $〈x〉$ and $〈y〉$, three parties ${\{P_i\}}_{i\in [3]}$ can compute the secret shared value $〈z〉=〈x〉\times 〈y〉$ as follows: (a) each party $P_i$ locally computes $z_i=x_i{y}_i+x_{i+1}{y}_i+x_i{y}_{i+1}$; (b) each party $P_i$ computes $z_i^{\prime }=z_i+{\alpha }_i$, where ${\alpha }_0+{\alpha }_1+{\alpha }_2=0$ (for generation of ${\alpha }_0,{\alpha }_1,{\alpha }_2$, please refer to Appendix A); (c) all three parties together perform re-sharing so that each party $P_i$ holds its own secret share ${〈z〉}_i=(z_i^{\prime },z_{i+1}^{\prime })$.

3.2. Secret Sharing Semantics of This Work

In order to improve the computational efficiency of the $\left[·\right]$-sharing and $〈·〉$-sharing, we provide the novel and efficient three-party secret sharing scheme denoted as $[[·]]$-sharing inspired by the scheme in [9,26]. With the aid of using $[[·]]$-sharing, we further divide the computation into online and offline phases.

For $[[·]]$-sharing over Boolean ring ${\mathbb{Z}}_2$, any Boolean value $v\in \{0,1\}$ is secret shared with a mask value $m_v\in {\mathbb{Z}}_2$ and the $〈·〉$-sharing of a random value ${\lambda }_v\in {\mathbb{Z}}_2$, $P_i$ holds ${[[v]]}_i=(m_v,{〈{\lambda }_v〉}_i)$, where $m_v=v\oplus {\lambda }_v$ is known to all three parties, $i\in \{0,1,2\}$.

For $[[·]]$-sharing over arithmetic ring ${\mathbb{Z}}_{2^l}$, any arithmetic value $v\in {\mathbb{Z}}_{2^l}$ is secret shared with a mask value $m_v\in {\mathbb{Z}}_{2^l}$ and the $〈·〉$-sharing of a random value ${\lambda }_v\in {\mathbb{Z}}_{2^l}$, $P_i$ holds ${[[v]]}_i=(m_v,{〈{\lambda }_v〉}_i)$, where $m_v=v+{\lambda }_v(mod{2}^l)$ is known to all three parties, $i\in \{0,1,2\}$. In addition, the complement of v can be computed as $[[\overline{v}]]=[[1\oplus v]]$ by setting $m_{\overline{v}}=\overline{m_v}$.

• Linear operation: This pattern is linear for both Boolean and arithmetic rings. For example, for Boolean sharing, assume $c_1,c_2,c_3$ are public constant bits, $[[x]],[[y]]$ are two secret-shared values, and $z=c_{1}x\oplus c_{2}y\oplus c_3$, then each party $P_i$ can compute its share ${[[z]]}_i=(m_z,{〈{\lambda }_z〉}_i)$ locally by setting $m_z=c_0{m}_x\oplus c_1{m}_y\oplus c_2$ and ${〈{\lambda }_z〉}_i=c_0{〈{\lambda }_x〉}_i\oplus c_1{〈{\lambda }_y〉}_i$, for $i\in \{0,1,2\}$.
• Secret share operation: Secret share operation enables a privacy data owner (assume $P_i$ is the data owner) to generate $[[·]]$-sharing of its private input x. In the offline phase, all parties jointly invoke ${\mathcal{F}}_{Rand}^{〈·〉}$ in Appendix A to sample random values $〈{\lambda }_x〉$, where privacy data owner $P_i$ knows ${\lambda }_x$ clearly. In the online phase, $P_i$ computes and reveals $m_x=x\oplus {\lambda }_x$ in a Boolean ring and $m_x=x-{\lambda }_x(mod{2}^l)$ in an arithmetic ring. The above process can be carried out using ${\mathcal{F}}_{Share}^{[[·]]}$ function.
• Reconstruct operation: ${\mathcal{F}}_{Rec}^{[[·]]}$ can reconstruct x by invoking ${\mathcal{F}}_{Rec}^{〈·〉}$ first to obtain ${\lambda }_x$, and then parties can locally compute $x=m_x\oplus {\lambda }_x$ in a Boolean ring and $x=m_x+{\lambda }_x(mod{2}^l)$ in an arithmetic ring.
• AND operation: With the functionality ${\mathcal{F}}_{2-AND}^{[[·]]}$ AND two Boolean secret value $[[x]],[[y]]$, and output $[[z]]$, where $z=x\wedge y$, we have:

  $$\begin{array}{cc}\hfill m_z& =x\wedge y\oplus {\lambda }_z=(m_x\oplus {\lambda }_x)(m_y\oplus {\lambda }_y)\oplus {\lambda }_z\hfill \\ \hfill & =m_x{m}_y\oplus {\lambda }_x{m}_y\oplus {\lambda }_y{m}_x\oplus {\lambda }_x{\lambda }_y\oplus {\lambda }_z\hfill \end{array}$$

  (1)

  As shown in Equation (1), all terms except for ${\lambda }_x{\lambda }_y$ can be computed locally since $m_x,m_y$ is known to all parties. Therefore, the main difficulty becomes calculating $〈{\lambda }_x{\lambda }_y〉$ given $〈{\lambda }_x〉$ and $〈{\lambda }_y〉$. Since ${\lambda }_x$ and ${\lambda }_y$ is input-independent, $〈{\lambda }_x{\lambda }_y〉$ can be computed in the offline phase using ${\mathcal{F}}_{2-AND}^{〈·〉}$. In the offline phase, parties interactively generate the randomness $〈{\lambda }_z〉$ using the method in Appendix A, and in the online phase, each party $P_i$ computes $〈m_z〉=z\oplus {\lambda }_z$. The protocols of function ${\mathcal{F}}_{2-AND}^{[[·]]}$ are shown in Algorithm 1.

  Algorithm 1 ${\mathcal{F}}_{2-AND}^{[[·]]}$: two-input AND in boolean ring

  Input: $[[·]]$-shares of x and y. Output: $[[·]]$-shares of z.  Offline Phase:  1. $P_i$ sample random values $〈{\lambda }_z〉$ where $i\in \{0,1,2\}$.  2. Parties mutually generate $〈{\lambda }_x{\lambda }_y〉$ using ${\mathcal{F}}_{2-AND}^{〈·〉}$.  Online Phase:  1. Parties locally set ${〈m_{\Delta }〉}_i=m_y{〈{\lambda }_x〉}_i\oplus m_x{〈{\lambda }_y〉}_i\oplus {〈{\lambda }_x{\lambda }_y〉}_i\oplus {〈{\lambda }_z〉}_i$, where $i\in \{0,1,2\}$.  2. Parties reveal $m_{\Delta }$ and set $m_z=m_{\Delta }\oplus m_x{m}_y$.  3. $P_i$ hold ${[[z]]}_i=(m_z,{〈{\lambda }_z〉}_i)$.

• Multi-input AND operation: For multi-input AND gates, ${\mathcal{F}}_{N-AND}^{[[·]]}$ takes the N Boolean value $(x_1,x_2,\cdots ,x_N)$ as input, and output $z={\bigwedge }_{i=0}^N{x}_i$, then we have:

  $$\begin{array}{cc}\hfill m_z& =\underset{i=0}{\overset{N}{\bigwedge }}{x}_i\oplus {\lambda }_z=\underset{i=0}{\overset{N}{\bigwedge }}(m_{x_i}\oplus {\lambda }_{x_i})\oplus {\lambda }_z\hfill \\ \hfill & =\underset{\mathcal{I}\subseteq \{1,\cdots ,N\}}{⨁}(\underset{j\notin \mathcal{I}}{\bigwedge }{m}_{x_j}·\underset{k\in \mathcal{I}}{\bigwedge }{\lambda }_{x_k})\oplus {\lambda }_z\hfill \end{array}$$

  (2)

  So as the procedure of the two-input AND gate, parties compute the input-independent $〈·〉$-sharing of ${{\bigwedge }_{k\in \mathcal{I}}{\lambda }_{x_k}}_{\mathcal{I}\subseteq \{1,\cdots ,N\}}$ by invoking ${\mathcal{F}}_{2-AND}^{〈·〉}$ in a tree-like combinatorial manner in the offline phase.
• Two-input multiplication: the multiplication of two numbers in an arithmetic ring ${\mathcal{F}}_{2-Mult}^{[[·]]}$ is similar to that in Boolean sharing, simply replacing the OR operation in Boolean sharing with addition and the AND operation with multiplication. The multiplication of two numbers under arithmetic sharing is depicted in Equation (3):

  $$\begin{array}{cc}\hfill m_z& =x\times y-{\lambda }_z=(m_x+{\lambda }_x)(m_y+{\lambda }_y)-{\lambda }_z\hfill \\ \hfill & =m_x{m}_y+{\lambda }_x{m}_y+{\lambda }_y{m}_x+{\lambda }_x{\lambda }_y-{\lambda }_z\hfill \end{array}$$

  (3)

  Similarly, the shares of $〈{\lambda }_x{\lambda }_y〉$ can be calculated using ${\mathcal{F}}_{2-Mult}^{〈·〉}$ in Section 3.1.2. As introduced in Section 3.3, the calculation of secure inference uses fixed-point representation in ${\mathbb{Z}}_{2^l}$; after precise multiplication, the decimal part of the result will double its original size, i.e., $x·2^d\times y·2^d=xy·2^{2d}$. Therefore, we should truncate the last d bits of the product to obtain an approximate result. In a secret sharing scheme, truncation takes into account two types of probability errors: a small error caused by carry bit error and a large error caused by overflow during multiplication calculation. And the shares of output that make $z^{\prime }=z/2^d$ hold a probability of 1 are called faithful truncation. We use faithful truncation methods from [9,26]: In the offline phase, parties mutually generate the $〈·〉$-sharing of ${\lambda }_z$ and ${{\lambda }_z}^{\prime }$ where ${\lambda }_z={{\lambda }_z}^{\prime }/2^d$. During the online phase, all parties $P_i$ locally compute $〈{m_z}^{\prime }〉=x\times y-〈{{\lambda }_z}^{\prime }〉$ and reveal ${m_z}^{\prime }$, and then parties set $m_z={m_z}^{\prime }/2^d$. The protocols of ${\mathcal{F}}_{2-Mult}^{[[·]]}$ are shown in the Algorithm 2.

  Algorithm 2 ${\mathcal{F}}_{2-Mult}^{[[·]]}$: two-input multiplication in arithmetic ring

  Input: $[[·]]$-shares of x and y. Output: $[[·]]$-shares of z.  Offline Phase:  1. $P_i$ sample random values $〈{\lambda }_z〉$ and set $〈{{\lambda }_z}^{\prime }〉$ where $i\in \{0,1,2\}$.  2. Parties mutually generate $〈{\lambda }_x{\lambda }_y〉$ using ${\mathcal{F}}_{2-Mult}^{〈·〉}$.  Online Phase:  1. Parties locally set ${〈m_{\Delta }〉}_i=m_y{〈{\lambda }_x〉}_i+m_x{〈{\lambda }_y〉}_i+{〈{\lambda }_x{\lambda }_y〉}_i-{〈{{\lambda }_z}^{\prime }〉}_i$, where $i\in \{0,1,2\}$.  2. Parties reveal $m_{\Delta }$ and set ${m_z}^{\prime }=m_{\Delta }+m_x{m}_y$.  3. $P_i$ hold ${[[z]]}_i=({m_z}^{\prime }/2^d,{〈{\lambda }_z〉}_i)$.

• Multi-input multiplication: Similar to the multi-input AND operation under Boolean sharing, multiplication of multiple numbers under arithmetic sharing is shown in Equation (4):

  $$\begin{array}{cc}\hfill m_z& =\sum _{i=1}^N{x}_i-{\lambda }_z=\prod _{i=1}^N(m_{x_i}+{\lambda }_{x_i})-{\lambda }_z\hfill \\ \hfill & =\sum _{\mathcal{I}\subseteq \{1,\cdots ,N\}}(\prod _{j\notin \mathcal{I}}{m}_{x_j}·\prod _{k\in \mathcal{I}}{\lambda }_{x_k})-{\lambda }_z\hfill \end{array}$$

  (4)

3.3. Fixed-Point Representation

Practical applications such as machine learning and mathematical statistics usually require the floating-point numbers for calculations. While in MPC, it is generally calculated in finite rings or fields, so it is necessary to encode floating-point numbers as fixed-point numbers [3,11,21,24,31]. The conversion relationship between floating-point numbers and fixed-point numbers is as follows: given a floating-point number $x\in \mathbb{R}$, its corresponding fixed-point number $x^{\prime }=\lfloor x·2^d\rfloor (mod{2}^l)$, where l is bit width and d is precision. We use $[0,2^{l-1})$ and $[2^{l-1},2^l)$ to represent positive and negative numbers, respectively.

3.4. Lookup Table

The lookup table (LUT) structure is used to pre-compute and store the inputs and corresponding results of the function. The corresponding results can be found by looking up the input in the table, without the need to calculate again.

The lookup table of a function in this paper refers to the set of all inputs and their corresponding outputs within a certain range, i.e., $f:{\{0,1\}}^{\delta }\to {\{0,1\}}^{\sigma }$ [32], where $\sigma$ and $\delta$ are bit width of input and output, respectively. Using this representation, any function can construct its corresponding lookup table within a certain range, and the computational complexity of the lookup table is related to its size. Therefore, logically complex lookup tables are theoretically more suitable to computing using lookup tables.

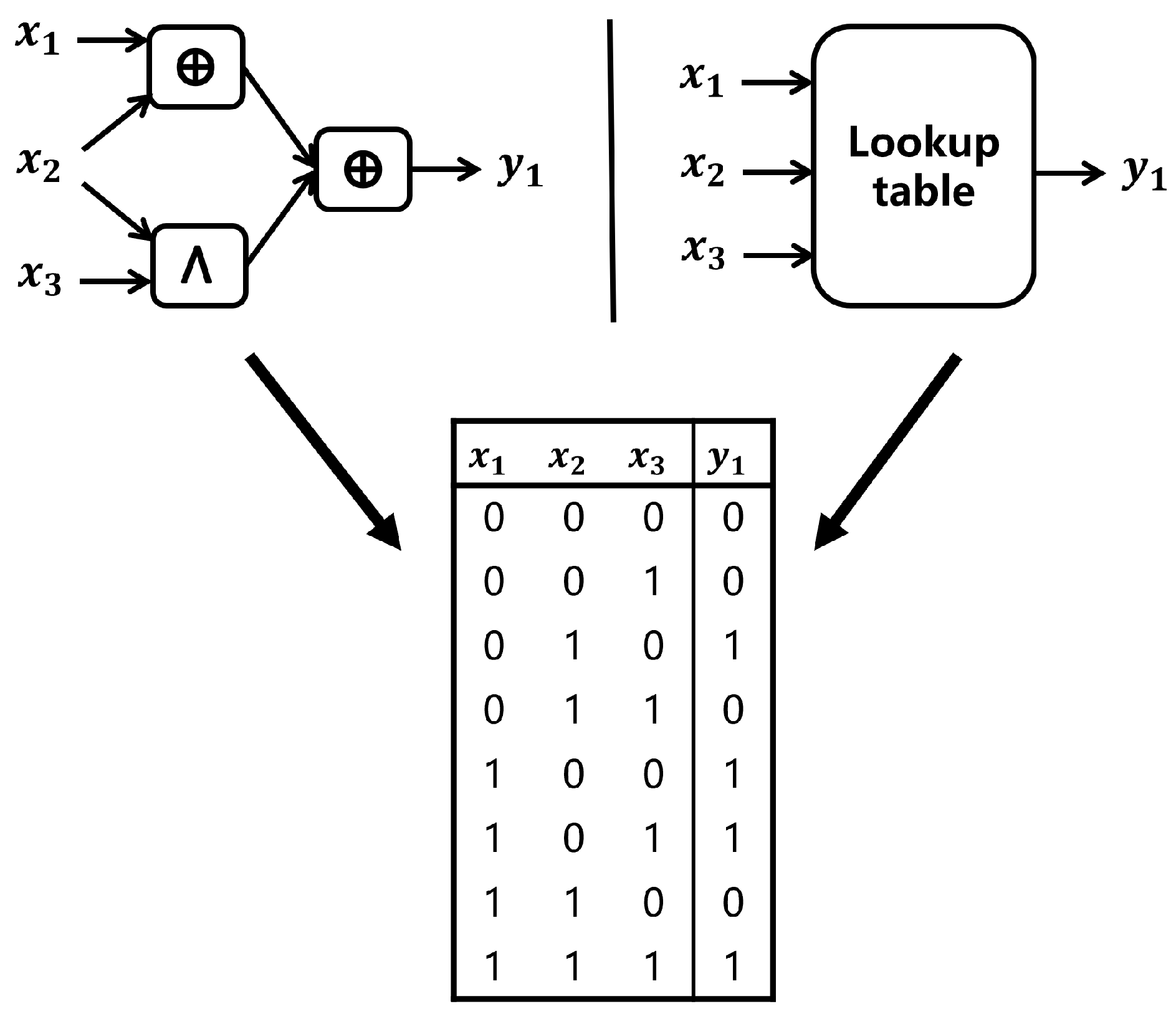
An instance of an LUT is demonstrated in Figure 1. In this work, ${\{{\overrightarrow{\mathcal{E}}}^u\}}_{u\in [\delta ]}$ is the input column of the table and ${\{{\overrightarrow{\xi }}^w\}}_{w\in [\sigma ]}$ is the output column, where each length is $2^{\delta }$, for example, ${\overrightarrow{\mathcal{E}}}^2$ is 00110011 and ${\overrightarrow{\xi }}^1$ is 00101101. In practical scenarios, the bit width design of lookup tables (LUTs) requires a balance between computational efficiency and numerical accuracy requirements. Our lookup table (LUT) selects 12 bit input/12 bit output precision, achieving a balance between the actual deployability of RNNs and model accuracy. In latency-critical scenarios like real-time ECG anomaly detection (sampling rates ≤ 250 Hz), 12-bit input limits LUT size to 4 KB. For applications such as speech recognition that are not sensitive to real-time efficiency, 12-bit can also ensure good accuracy. However, if users want to use a look-up table for models with large numbers or high accuracy requirements, they need to optimize the look-up table structure by using an automation toolchain to reduce the level of look-up table circuits and achieve higher performance.

4. Protocol Constructions

In this section, to provide a clearer exposition of the protocol we have constructed, we first present the system model in this paper. Then, we provide the digit decomposition, B2A and Bit2A conversion protocols based on the $[[·]]$-sharing. Finally, we proposed a lookup table-based secure three-party protocol.

4.1. System Model

Consider a computing scenario with three servers that are independent of each other. We execute a secure computing protocol under a semi-honest model, As shown in Figure 2, there are three roles in a system model: model owner, data owner, and computation participants.

(1)

Model owner: This is the model’s architecture and parameters, typically having a machine learning model that has been trained or needs to be trained. In the initial stage of computation, the model owner must send the model parameters to the computation participants in the form of secret shares, but does not receive the computation results.

(2)

Data owner: This has real data and aims to conduct joint inference without exposing data privacy. The data owner sends the secret shares of private data to the computation participants at the beginning of the calculation, and receives the result shares sent by the computation participants after the secure computation is completed.

(3)

Computation participants: These act as the actual “computing executors” within the secure computation protocol, typically serving as third-party platforms, service providers, or distributed nodes with multi-party secure computation capabilities. In the context of this paper, the computation participant servers are three servers that initially receive the model shares from the model owner and the data shares from the data owner. After executing the secure computation protocol, three servers send their result shares back to the data owner, respectively.

To demonstrate this system model’s practical applicability, we take the healthcare field as an example. Some medical institutions utilize speech-recognition technology to develop electronic medical record (EMR)-management platforms, which enables physicians to complete clinical documentation through voice dictation, significantly reducing documentation burdens and improving workflow efficiency. Concurrently, the technology assists clinicians in rapidly retrieving patients’ historical medical records, thereby providing robust support for accurate diagnosis. However, as patient medical information involves sensitive personal privacy, the system model in this work can be used. For this case, the model owner as in Figure 2 is the medical institution, it can train the model locally or via other methods using relevant datasets, and then the model parameters are distributed to three servers through secret sharing. The data owner is a physician (or patient); they can split their private personal data into secret shares and transmit them to the same three servers. Following secure computation protocols, the servers return the result shares to the physician. This process effectively prevents leakage of both the medical institution’s model parameters and the patient’s private information.

4.2. Conversions of Sharing

In the lookup table protocol, the inputs are ${[[·]]}^2$-shares of every $\delta$ bit. Therefore, a secure digit decomposition function ${\mathcal{F}}_{DigDec}^{[[·]]}$ under a 3PC $[[·]]$-sharing scheme is required before each invoking of a lookup table protocol. In this protocol, the wrap function and the 3PC private-compare function (the same as the protocol in [31]) under the $\langle ·\rangle$-sharing scheme will be invoked. The following describes the protocol in detail.

4.2.1. Wrap Function

The wrap function $Wra{p}_3$ calculates the carry bit when the secret shares held by three parties are added together, and the output may be 0, 1 or 2, i.e., assume three secret shares are $a_0,a_1,a_2\in {\mathbb{Z}}_{2^l}$, and  $Wra{p}_3(a_0,a_1,a_2)$ is:

$$Wra{p}_3(a_0,a_1,a_2)=\left\{\begin{array}{cc}\hfill 0& ,if{a}_0+a_1+a_2<2^l\hfill \\ \hfill 1& ,if{2}_l\le a_0+a_1+a_2<2·2^l\hfill \\ \hfill 2& ,if2·2_l\le a_0+a_1+a_2<3·2^l\hfill \end{array}\right.$$

But since the operands in the lookup table protocol are all bits, the wrap function defined here is modulo 2 on the original result, i.e., ${\mathcal{F}}_{Wra{p}_3}^{\langle ·\rangle }=Wra{p}_{3}mod2$. The details of the secure wrap protocol can refer to [31].

4.2.2. Private Compare

In the digit decomposition protocol, the operation should obtain the bit shares of comparison results of secret value x and a public number r. The 3PC private compare function ${\mathcal{F}}_{PC}^{\langle ·\rangle }$ can be realized in [31].

4.2.3. Digit Decomposition

${\mathcal{F}}_{DigDec}^{[[·]]}$ converts secret shares in arithmetic ring ${\mathbb{Z}}_{2^l}$ into shares in Boolean ring ${\mathbb{Z}}_2$. Given private input ${[[x]]}_i=(m_x,{\langle {\lambda }_x\rangle }_i),x\in {\mathbb{Z}}_{2^l},i\in \{0,1,2\}$, output ${[[x_j]]}_i=(m_{x_j},{\langle {\lambda }_{x_j}\rangle }_i),j\in [l]$, where $x_j$ is the jth bit of x (i.e., $x={\sum }_{j=0}^{l-1}{x}_j·2^j$). For ease of calculation, each party locally decomposes value $m_x$, then obtains public bits ${\{m_{x_j}\}}_{j\in [l]}$, where $m_x={\sum }_{j=0}^{l-1}{m}_{x_j}·2^j$. Next, each party interactively converts the $\langle ·\rangle$-shares into Boolean shares.

The challenge of the three-party decomposition protocol under $[[·]]$-sharing lies in how to construct a specific $\langle {\lambda }_{x_j}\rangle \in {\mathbb{Z}}_{2^l}$ on the basis of an existing arithmetic ring $\langle {\lambda }_x\rangle \in {\mathbb{Z}}_{2^l}$. Based on the mathematical observation, we propose a three-party decomposition protocol under $[[·]]$-sharing, enabling most calculations to be completed offline for decomposition. Below, we describe the mathematical observation and the corresponding protocol in detail. Given the secret sharing ${[[x]]}_i=(m_x,{\langle {\lambda }_x\rangle }_i)$, where $m_x,{\lambda }_x\in {\mathbb{Z}}_{2^l},i\in \{0,1,2\}$, suppose $g_{i,j}={\lambda }_{i,j}\parallel {\lambda }_{i,j-1}\parallel \cdots \parallel {\lambda }_{i,0},j<l$, then the $\langle ·\rangle$-sharing follows Formula (5):

$$\begin{array}{c}\hfill {\lambda }_{x_j}={\lambda }_{0,j}+{\lambda }_{1,j}+{\lambda }_{2,j}+c_j(mod2)\end{array}$$

(5)

where $c_j$ is the carry bit of $g_{0,j-i},g_{1,j-i},g_{2,j-i}$, i.e., $c_j={\mathcal{F}}_{Wrap3}^{\langle ·\rangle }(g_{0,j-i},g_{1,j-i},g_{2,j-i},2^j)$.

Similarly, suppose there is $Y_j={\lambda }_j\parallel {\lambda }_{j-1}\parallel \cdots \parallel {\lambda }_0$, $B_j=m_{x_j}\parallel m_{x_{j-1}}\parallel \cdots \parallel m_{x_0}$, $j<l$. The secret sharing $[[x]]$ satisfies:

$$\begin{array}{cc}\hfill x_j& ={\lambda }_{x_j}+m_{x_j}+c_j^{\prime }(mod2)\hfill \\ \hfill & ={\lambda }_{0,j}+{\lambda }_{1,j}+{\lambda }_{2,j}+c_j+m_{x_j}+c_j^{\prime }(mod2)\hfill \end{array}$$

(6)

where $c_j^{\prime }$ is the carry bit of $Y_{j-1}+B_{j-1}$, i.e., $c_j^{\prime }=Wra{p}_2(Y_{j-1},B_{j-1},2^j)$. However, in actual computation, $Y_{j-1}$ is encrypted, so $c_j^{\prime }$ cannot be directly computed. By observation, we can deduce $c_j^{\prime }=Wra{p}_2(Y_{j-1},B_{j-1},2^j)=Y_{j-1}+B_{j-1}<2^j?0:1=(g_{0,j-1}+g_{1,j-1}+g_{2,j-1}(mod{2}^j))<2^j-B_{j-1}?0:1$

Since $B_{j-1}$ is a public value, this term can be moved to the right side of the inequality, i.e., $c_j^{\prime }=g_{0,j-1}+g_{1,j-1}+g_{2,j-1}(mod{2}^j)<2^j-B_{j-1}?0:1={\mathcal{F}}_{PC}^{\langle ·\rangle }(g_{0,j-1},g_{1,j-1},g_{2,j-1},2^j-B_{j-1})$. Since $Wra{p}_2$ can be computed locally, there is no online communication. The protocols of the ${\mathcal{F}}_{DigDec}^{[[·]]}$ are described in Algorithm 3.

Algorithm 3 ${\mathcal{F}}_{DigDec}^{[[·]]}$: 3PC digit decomposition

Input: $[[·]]$-shares of x, where $x\in {\mathbb{Z}}_{2^l}$. Output: $[[·]]$-shares of $x_j$, where $x_j\in {\mathbb{Z}}_2,j\in [l]$.  Offline Phase:  1. Each party locally converts the shares ${\lambda }_x$ into bits $\{{\lambda }_{b,j}\}$ and computes $g_{b,j-1}$ locally, where $b\in \{0,1,2\},j\in \{0,\dots ,l-1\}$;  2. Each party invokes the function ${\mathcal{F}}_{Wrap3}^{\langle ·\rangle }(g_{0,j-1},g_{1,j-1},g_{2,j-1},2^j)$ to obtain $\langle c_j\rangle$;  3. Each party locally computes $u_{b,j}={\lambda }_{b,j}+c_{b,j}$.  Online Phase:  1. Each party locally converts the shares $m_x$ into bits $m_{x_j},B_{j-1}$;  2. Each party invokes the function ${\mathcal{F}}_{PC}^{\langle ·\rangle }(g_{0,j-1},g_{1,j-1},g_{2,j-1},2^j-B_{j-1})$ to obtain $\langle c_j^{\prime }\rangle$;  3. Each party locally computes ${\psi }_{b,j}=u_{b,j}+c_{b,j}^{\prime }$. The final share after bit conversion is $[[x_j]]=(m_{x_j},\langle {\psi }_{b,j}\rangle )$.

4.2.4. B2A Conversion

Boolean to arithmetic function ${\mathcal{F}}_{B2A}^{[[·]]}$ is the inverse operation of digit decomposition. It converts the bit shares $(x_0,x_1,\cdots ,x_{l-1})\in {\mathbb{Z}}_2$ to value $x\in {\mathbb{Z}}_{2^l}$, such that $x={\sum }_{j=0}^{l-1}{x}_j·2^j,x\in {\mathbb{Z}}_{2^l}$. We can first convert $x_i$ to the arithmetic ring, and then use the linear property of $[[·]]$-sharing to calculate. Then, for secret $x\in {\mathbb{Z}}_2$ in $[[·]]$-sharing that $x=m_x\oplus {\lambda }_x$, we can derive the following mathematical properties: $x^A=m_x^A+{\lambda }_x^A-2m_x^A{\lambda }_x^A$; so we have:

$$\begin{array}{cc}\hfill x^A& =m_x^A+{\lambda }_x^A-2m_x^A{\lambda }_x^A\hfill \\ \hfill & =m_x^A+(1-2m_x^A){\lambda }_x^A\hfill \\ \hfill & =m_x^A+(1-2m_x^A)({\lambda }_0\oplus {\lambda }_1\oplus {\lambda }_2)\hfill \\ \hfill & =m_x^A+(1-2m_x^A)({\lambda }_0^A+{\lambda }_1^A+{\lambda }_2^A-2{\lambda }_0^A{\lambda }_1^A-2{\lambda }_1^A{\lambda }_2^A-2{\lambda }_0^A{\lambda }_2^A+4{\lambda }_0^A{\lambda }_1^A{\lambda }_2^A)\hfill \end{array}$$

(7)

We have $x=m_x\oplus {\lambda }_x=m_x\oplus {\lambda }_0\oplus {\lambda }_1\oplus {\lambda }_2$, and assume that the arithmetic value in ${\mathbb{Z}}_{2^l}$ is $x^A,m_x^A,{\lambda }_x^A$, respectively. Therefore, we can derive the mathematical equation in Equation (7) in the same way. All items except for ${\lambda }_0^A{\lambda }_1^A{\lambda }_2^A$ can be computed locally, but we can have one of the participants $P_i,i\in \{0,1,2\}$ locally compute ${\lambda }_i{\lambda }_{i+1}$, and then securely compute ${\lambda }_0^A{\lambda }_1^A{\lambda }_2^A$ using the Du-Atallah protocol [21].

4.3. Lookup Table-Based 3PC Protocol

We assume that the function to be evaluated is represented as a lookup table, and the LUT is public that all parties can know the input encoding ${\{{\overrightarrow{\mathcal{E}}}^u\}}_{u\in [\delta ]}$ and output encoding ${\{{\overrightarrow{\xi }}^w\}}_{w\in [\sigma ]}$, and the parties have Boolean secret sharing of the private input. In secure two-party computation, there are several approaches to compute a lookup table. The most widely applied are One Time True Table (OTTT) [33], Online-LUT (OP-LUT) [32], and Setup-LUT (SP-LUT) [32]. But in the 3PC scenario, there are no efficient computation schemes. In order to increase the efficiency of the online phase, we proposed a 3PC lookup table protocol, expanding the application scenarios of Flute [20] from 2PC to 3PC settings.

This approach converts the lookup process of the lookup table into a computing function that is related to the private input representing the inner product. The previous lookup table method enumerated all inputs [32,33] or all outputs [32] and then obtained the final lookup table output by utilizing the obvious transfer (OT). This is regular but the complexity of computation and communication are too high because the whole table will be sent to the other party. Therefore, we only require part of the lookup table to be evaluated rather than an entire table. There are four steps involved in this conversion, and the specific steps are shown below.

(1) The first step: compute the fully disjunctive normal form of the input. When evaluating a Boolean $\delta$-to-$\sigma$ lookup table, we only need to focus on the rows where the result is 1, then the output of LUT can be represented as the full disjunctive normal form (DNF) of the corresponding input for those rows. Taking a lookup table with output 1 as an example in Figure 1, assuming there are $\alpha$ rows whose results are 1, then for each $j\in [\alpha ]$, we compute all terms ${\bigwedge }_{i=1}^{\delta }{\overrightarrow{\mathcal{L}}}_j^i$, where ${\overrightarrow{\mathcal{L}}}_j^i=x_i$ if $x_i=1$ in the LUT and ${\overrightarrow{\mathcal{L}}}_j^i=\overline{x_i}$ if $x_i=0$ for all $i\in [\delta ]$, and then connect all terms using the OR operation, output $LUT(x_1,x_2,x_3)={\bigvee }_{j=1}^{\alpha }{\bigwedge }_{i=1}^{\delta }{\overrightarrow{\mathcal{L}}}_j^i$.

Using the lookup table depicted in Figure 1 as an illustration, the output of the third, fifth, sixth rows is 1, i.e., $\alpha =4$, and assuming the input is $(x_1,x_2,x_3)=(0,1,1)$, the output of LUT is 0. And then we calculate the formula; then, we can exactly obtain the output result $LUT(x_1,x_2,x_3)=(\overline{x_1}\wedge x_2\wedge \overline{x_3})\bigvee (x_1\wedge \overline{x_2}\wedge \overline{x_3})\bigvee (x_1\wedge \overline{x_2}\wedge x_3)\bigvee (x_1\wedge x_2\wedge x_3)=0$.

(2) The second step: replace the OR operation with the XOR operation. Evaluating the above DNF expression requires $\delta ·\alpha -1$ AND and OR operations, which costs high online communication. However, We remove OR operations with the following significant properties: Given the input $(x_1,\cdots ,x_{\delta })$, in the above DNF equation ${\bigwedge }_{i=1}^{\delta }{\overrightarrow{\mathcal{L}}}_j^i$, at most one term can result in 1 [20], which means that it is impossible for any two different terms to each result in 1. Based on this property, we can obtain the following Equation (8):

$$\begin{array}{c}\hfill \underset{j=1}{\overset{\alpha }{\bigvee }}\underset{i=1}{\overset{\delta }{\bigwedge }}{\overrightarrow{\mathcal{L}}}_j^i=\underset{j=1}{\overset{\alpha }{⨁}}\underset{i=1}{\overset{\delta }{\bigwedge }}{\overrightarrow{\mathcal{L}}}_j^i\end{array}$$

(8)

Still taking the lookup table in Figure 1 as an example, $\alpha =4$, and assuming the input is $(x_1,x_2,x_3)=(0,1,1)$, the output of LUT is 0. Then, compute the improved formula to obtain $LUT(x_1,x_2,x_3)=(\overline{x_1}\wedge x_2\wedge \overline{x_3})⨁(x_1\wedge \overline{x_2}\wedge \overline{x_3})⨁(x_1\wedge \overline{x_2}\wedge x_3)⨁(x_1\wedge x_2\wedge x_3)=0$.

(3) The third step: replace the previous formula with an equivalent inner product computation. The purpose of this step is to transform the equation from the previous step into a more easily computable and efficient form. When $\alpha =1$, the equation is ${\bigwedge }_{i=1}^{\delta }{\overrightarrow{\mathcal{L}}}_j^i$, which can be seen as multi-input AND gate in Section 3.2. When $\delta =2$, the transformed equation is ${⨁}_{j=1}^{\alpha }{\overrightarrow{\mathcal{L}}}_j^1\wedge {\overrightarrow{\mathcal{L}}}_j^2$, which is equivalent to the vector inner product operation over a Boolean ring. Therefore, we use the aforementioned protocols to calculate the inner product and the multi-input AND gate, inspired by [9,20]. Finally, the equation is as follows in Equation (9)

$$\begin{array}{cc}\hfill LUT(x_1,x_2,x_3)& =\underset{j=1}{\overset{\alpha }{\bigvee }}\underset{i=1}{\overset{\delta }{\bigwedge }}{\overrightarrow{\mathcal{L}}}_j^i\hfill \\ \hfill & =\underset{j=1}{\overset{\alpha }{⨁}}\underset{i=1}{\overset{\delta }{\bigwedge }}{\overrightarrow{\mathcal{L}}}_j^i\hfill \\ \hfill & =\underset{i=1}{\overset{\delta }{⨀}}{\overrightarrow{\mathcal{L}}}^i\hfill \end{array}$$

(9)

where ⨀ denotes an inner product operation like the form in vector. Assume $\alpha =3$, and the input is $(x_1,x_2,x_3)=(0,1,1)$; the output of LUT is 0. Then, compute the improved formula to obtain $LUT(x_1,x_2,x_3)=\left(\begin{array}{c}\overline{x_1}\\ x_1\\ x_1\\ x_1\end{array}\right)·\left(\begin{array}{c}{x}_2\\ \overline{x_2}\\ \overline{x_2}\\ x_2\end{array}\right)·\left(\begin{array}{c}\overline{x_3}\\ \overline{x_3}\\ x_3\\ x_3\end{array}\right)=0$, and we can see that the result is correct.

4.3.1. Mathematical Expression of Multi-Input LUT

Consider a $\delta$ input vector $\mathcal{I}=({\overrightarrow{x}}^1,{\overrightarrow{x}}^2,\cdots ,{\overrightarrow{x}}^{\delta })$ and 1-bit output, the dimension of each component ${\overrightarrow{x}}^i$ is represented as d where $i\in \{1,2,\cdots ,\delta \}$. Based on the above conclusion, we need to calculate $output={\overrightarrow{x}}^1\odot {\overrightarrow{x}}^2\odot \cdots \odot {\overrightarrow{x}}^{\delta }$. Let ${\mathcal{I}}_j=({\overrightarrow{x}}_j^1,{\overrightarrow{x}}_j^2,\cdots ,{\overrightarrow{x}}_j^{\delta })$ be a set of the jth element of each ${\overrightarrow{x}}^i\in \mathcal{I}$. As we mentioned in Section 3.2, the secret value x is $[[·]]$-sharing in this work, so we have:

$$\begin{array}{cc}\hfill y& ={\overrightarrow{x}}^1\odot {\overrightarrow{x}}^2\odot \cdots \odot {\overrightarrow{x}}^{\delta }\hfill \\ \hfill & =\underset{j=1}{\overset{d}{⨁}}\underset{i=1}{\overset{\delta }{\bigwedge }}{\overrightarrow{x}}_j^i\hfill \\ \hfill & =\underset{j=1}{\overset{d}{⨁}}\underset{i=1}{\overset{\delta }{\bigwedge }}\left(m_{{\overrightarrow{x}}_j^i}\oplus {\lambda }_{{\overrightarrow{x}}_j^i}\right)\hfill \\ \hfill & =\underset{j=1}{\overset{d}{⨁}}\left(\underset{{\mathcal{S}}_j\in 2^{{\mathcal{I}}_j}}{⨁}\left(m_{{\mathcal{S}}_j}\wedge {\lambda }_{{\mathcal{I}}_j\setminus {\mathcal{S}}_j}\right)\right)\hfill \end{array}$$

(10)

In Equation  (10), it is easy to derive the equations for the first three lines from Section 4, while in the fourth step, ${⨁}_{{\mathcal{S}}_j\in 2^{{\mathcal{I}}_j}}(m_{{\mathcal{S}}_j}\wedge {\lambda }_{{\mathcal{I}}_j\setminus {\mathcal{S}}_j})$ is the expansion of ${\bigwedge }_{i=1}^{\delta }(m_{{\overrightarrow{x}}_j^i}\oplus {\lambda }_{{\overrightarrow{x}}_j^i})$, which follows the distribution law, and its expension has $2^{\sigma }$ items in total, power set $2^{{\mathcal{I}}_j}$ means all the expanded items, and ${\mathcal{S}}_j$ is one of a subset in $2^{{\mathcal{I}}_j}$, and ${\mathcal{I}}_j\setminus {\mathcal{S}}_j$ means difference set, where $j\in \{1,\cdots ,d\}$, i.e., ${\mathcal{I}}_j\setminus {\mathcal{S}}_j={\mathcal{I}}_j-{\mathcal{S}}_j$. Although the expression contains $d·(2^{\delta }-\delta -1)$ AND gates, these AND gates can be locally calculated to obtain the shares of each term leading to low online communication since ${\lambda }_{{\mathcal{I}}_j\setminus {\mathcal{S}}_j}$ can be computed by ${\mathcal{F}}_{N-AND}^{〈·〉}$ locally and $m_{{\mathcal{S}}_j}$ is clear to all parties.

4.3.2. Lookup Table Protocol

Given a $\delta$-to-$\sigma$ LUT T, we calculate the lookup table results bit by bit, so the goal is to compute $LUT(x_1,\cdots ,x_{\delta })=(y_1,\cdots ,y_{\sigma }),y_{t\in [\sigma ]}={⨀}_{i=1}^{\delta }{\overrightarrow{\mathcal{L}}}^i={⨁}_{j=1}^{\alpha }\left({⨁}_{{\mathcal{S}}_j\in 2^{{\mathcal{I}}_j}}\left(m_{{\mathcal{S}}_j}\wedge {\lambda }_{{\mathcal{I}}_j\setminus {\mathcal{S}}_j}\right)\right)$ as mentioned in Equation (10), where $\alpha$ is the number of rows that output 1. To filter out rows with output 1, we can multiply this expression by the output encoding of LUT ${\{{\overrightarrow{\xi }}^w\}}_{w\in [\sigma ]}$, so the rows with output 0 will be deleted. Since the lookup table is public, the output encoding is also public, so no additional communication is required to obtain all rows with output 1 as in Equation (11).

$$\begin{array}{cc}\hfill y_{t\in \sigma }& =\underset{j\in 2^{\sigma },{\overrightarrow{\xi }}_j^t=1}{⨁}\underset{i=1}{\overset{\delta }{\bigwedge }}{\overrightarrow{\mathcal{L}}}_j^i\hfill \\ \hfill & ={\overrightarrow{\mathcal{L}}}^1\odot \cdots \odot {\overrightarrow{\mathcal{L}}}^{\delta }\odot {\overrightarrow{\xi }}^t\hfill \end{array}$$

(11)

In Equation (11), we also need to handle the mapping relationship between the input vector $(x_1,\cdots ,x_{\delta })$ and vector ${\overrightarrow{\mathcal{L}}}^i$ for $i\in [\delta ]$. We can see from Section 4.3 that ${\overrightarrow{\mathcal{L}}}_j^i=x_i$ if $x_i=1$ and ${\overrightarrow{\mathcal{L}}}_j^i=\overline{x_i}$ if $x_i=0$ for all $i\in [\delta ]$. Since the lookup table is public, we can also obtain the input encoding ${\{{\overrightarrow{\mathcal{E}}}^u\}}_{u\in [\delta ]}$, so we can obtain ${\overrightarrow{\mathcal{L}}}^i$ as Equation (12):

$$\begin{array}{cc}\hfill {\overrightarrow{\mathcal{L}}}_j^i& =x_i\oplus (1\oplus {\overrightarrow{\mathcal{E}}}_j^i)\hfill \\ \hfill & =(m_{x_i}\oplus {\lambda }_{x_i})\oplus (1\oplus {\overrightarrow{\mathcal{E}}}_j^i)\hfill \\ \hfill & =(m_{x_i}\oplus 1\oplus {\overrightarrow{\mathcal{E}}}_j^i)\oplus {\lambda }_{x_i}\hfill \end{array}$$

(12)

where $i\in [\delta ]$, $j\in 2^{\delta }$. Because the input encoding ${\overrightarrow{\mathcal{E}}}^i$ is public and the secret sharing scheme we used in Section 3.2 is linear, no additional communication is required for this step of processing.

Furthermore, in our secret sharing scheme, calculating the complement $\overline{x_i}$ only needs to compute the complement of $m_{x_i}$z, but ${\lambda }_{x_i}$ remains unchanged, such that $[[\overline{x_i}]]=[[\overline{m_{x_i}}\oplus {\lambda }_{x_i}]]$. Thus, we can observe that the term ${\lambda }_{{\mathcal{I}}_j\setminus {\mathcal{S}}_j}$ for all $j\in [2^{\delta }]$ in Equation (13) is the same for each row with input vector $\mathcal{I}=\{x_1,\cdots ,x_{\delta }\}$, so the same random number ${\lambda }_{\mathcal{I}\setminus \mathcal{S}}$ can be used. Therefore, we can obtain the following derivation formula as Equation (13):    

$$\begin{array}{cc}\hfill y_w& ={\overrightarrow{\mathcal{L}}}^1\odot \cdots \odot {\overrightarrow{\mathcal{L}}}^{\delta }\odot {\overrightarrow{\xi }}^w=\left(\underset{j=1}{\overset{2^{\delta }}{⨁}}\underset{i=1}{\overset{\delta }{\bigwedge }}{\overrightarrow{\mathcal{L}}}_j^i\right)\wedge {\overrightarrow{\xi }}^w\hfill \\ \hfill & =\underset{j=1}{\overset{2^{\delta }}{⨁}}\left(\left(\underset{i=1}{\overset{\delta }{\bigwedge }}{\overrightarrow{\mathcal{L}}}_j^i\right)\wedge {\overrightarrow{\xi }}_j^w\right)\hfill \\ \hfill & =\underset{j=1}{\overset{2^{\delta }}{⨁}}\left(\left(\underset{i=1}{\overset{\delta }{\bigwedge }}\left(m_{{\overrightarrow{\mathcal{L}}}_j^i}\oplus {\lambda }_{{\overrightarrow{\mathcal{L}}}_j^i}\right)\right)\wedge {\overrightarrow{\xi }}_j^w\right)\hfill \\ \hfill & =\underset{j=1}{\overset{2^{\delta }}{⨁}}\left(\underset{{\mathcal{S}}_j\in 2^{{\mathcal{I}}_j}}{⨁}\left(m_{{\mathcal{S}}_j}\wedge {\lambda }_{{\mathcal{I}}_j\setminus {\mathcal{S}}_j}\wedge {\overrightarrow{\xi }}_j^w\right)\right)\hfill \\ & =\underset{\mathcal{S}\in 2^{\mathcal{I}}}{⨁}\left(\left(\underset{j=1}{\overset{2^{\delta }}{⨁}}\left(m_{{\mathcal{S}}_j}\wedge {\overrightarrow{\xi }}_j^w\right)\right)\wedge {\lambda }_{\mathcal{I}\setminus \mathcal{S}}\right)\hfill \\ \hfill & =\underset{\mathcal{S}\in 2^{\mathcal{I}}}{⨁}\left(\left({\overrightarrow{m}}_{\mathcal{S}}\odot {\overrightarrow{\xi }}^w\right)\wedge {\lambda }_{\mathcal{I}\setminus \mathcal{S}}\right)\hfill \end{array}$$

(13)

where ${\overrightarrow{\xi }}^w$ denotes the output encoding of LUT for all $w\in [\sigma ]$, ${\mathcal{S}}_j$ denotes a set replacing each $x_i$ with ${\overrightarrow{\mathcal{L}}}_j^i$, $m_{{\overrightarrow{\mathcal{L}}}_j^i}$ and ${\lambda }_{{\overrightarrow{\mathcal{L}}}_j^i}$ is the secret shares of ${\overrightarrow{\mathcal{L}}}_j^i$ for $i\in [\delta ],j\in [2^{\delta }]$, and $m_{{\mathcal{S}}_j},{\lambda }_{{\mathcal{I}}_j\setminus {\mathcal{S}}_j}$ is the shares of each ${\mathcal{S}}_j$ where $m_{{\mathcal{S}}_j}$ is replaced with $m_{{\overrightarrow{\mathcal{L}}}_j^i}$, and ${\lambda }_{{\mathcal{I}}_j\setminus {\mathcal{S}}_j}$ stays the same. The third to fourth lines follow the law of distribution, and since it is observed that $m_{{\mathcal{S}}_j}$ and ${\overrightarrow{\xi }}_j^w$ are public parameters, these two items are combined for computation. And then according to Equation (9), the final equation, Equation (13), can be obtained.

Because ${\lambda }_{{\mathcal{I}}_j\setminus {\mathcal{S}}_j}$ are reused, in the offline phase, we just need to invoke the ${\mathcal{F}}_{2-AND}^{〈·〉}$$2^{\delta }-\delta -1$ times.

The protocol details are shown in Protocol 4. In the second step of the online phase in Algorithm 4, to prevent parties repeat calculating the ${\overrightarrow{m}}_{\mathcal{I}}$, we move this term in the fourth step for calculation.

Algorithm 4 ${\mathcal{F}}_{LUT}^{[[·]]}$: protocol of LUT

Input: a public $\delta$-to-$\sigma$ LUT T with input encoding ${\{{\overrightarrow{\mathcal{E}}}^u\}}_{u\in [\delta ]}\in {\{0,1\}}^{2^{\delta }}$ and output encoding ${\{{\overrightarrow{\xi }}^w\}}_{w\in [\sigma ]}\in {\{0,1\}}^{2^{\delta }}$, and $[[·]]$-shares of input vector $([[x_1]],\cdots ,[[x_{\delta }]])$. Output: $[[\overrightarrow{y}]]$, where $\overrightarrow{y}=(y_1,\cdots ,y_{\sigma })=LUT(x_1,\cdots ,x_{\delta })$.  Offline Phase:  1. Each party ${\{P_t\}}_{t\in [0,2]}$ sample random values ${\lambda }_{y_j}^t\in \{0,1\}$ using ${\mathcal{F}}_{Rand}^{〈·〉}$ for $t\in \{0,1,2\}$, $j\in [\sigma ]$.  2. Each party ${\{P_t\}}_{t\in [0,2]}$ interactively generates $〈{\lambda }_{\mathcal{S}}〉$ for $\mathcal{S}\in 2^{\mathcal{I}}$ by invoking ${\mathcal{F}}_{2-AND}^{\langle ·\rangle }$.  Online Phase:  1. All parties locally set ${\overrightarrow{\mathcal{L}}}_j^i=x_i\oplus (1\oplus {\overrightarrow{\mathcal{E}}}_j^i)$ in Equation (12) for $i\in [\delta ],j\in [2^{\delta }]$.  2. Each Party ${\{P_t\}}_{t\in [0,2]}$ locally computes: $$v_w^t=\underset{\mathcal{S}\in 2^{\mathcal{I}},\mathcal{S}\ne \mathcal{I}}{⨁}\left(\left({\overrightarrow{m}}_{\mathcal{S}}\odot {\overrightarrow{\xi }}^w\right)\wedge {\lambda }_{\mathcal{I}\setminus \mathcal{S}}\right)\oplus {\lambda }_{y_j}^t$$  3. All parties renconstruct $v_w$ by exchanging $v_w^t$ and computing $v_w=v_w^0\oplus v_w^1\oplus v_w^2$.  4. All parties locally compute $m_{y_j}=v_w\oplus ({\overrightarrow{m}}_{\mathcal{I}}\odot {\overrightarrow{\xi }}^w)$.

5. The 3PC Protocols of Secure RNNs Operators

In this section, we will introduce secure matrix multiplication and secure activation functions of nonlinear layers commonly used in RNNs, such as sigmoid, and tanh as shown in

Table 2. RNN model and corresponding activation function.

Model	Activation Function
vanilla RNN	Sigmoid, Softmax
LSTM	Sigmoid, Tanh
GRU	Sigmoid, Tanh
FastGRNN	Sigmoid, Tanh

. In computers, only finite numbers can be represented; complex mathematical functions cannot be accurately represented. Therefore, floating-point numbers are usually used to approximate infinite numbers [34].

5.1. Matrix Multiplication

The linear part of the model is usually matrix computation. The protocol for matrix multiplication is similar to ${\mathcal{F}}_{2-Mult}^{[[·]]}$. An $m\times o$ matrix ${[[X]]}_i=(m_X,{\langle {\lambda }_X\rangle }_i)$ is multiplied by an $o\times n$ matrix ${[[Y]]}_i=(m_Y,{\langle {\lambda }_Y\rangle }_i)$, then we obtain matrix $m\times n$ and matrix ${[[Z]]}_i=(m_Z,{\langle {\lambda }_Z\rangle }_i)$. In the offline phase, all parties $P_i$ mutually generate $\langle {\lambda }_{XY}\rangle$ by invoking ${\mathcal{F}}_{Mult}^{\langle ·\rangle }$, and then in the online phase, all parties $P_i$ reveal $m_X,m_Y$ and compute $m_Z$ locally. The details are shown in Algorithm 5.

Algorithm 5 Matrix multiplication ${\mathcal{F}}_{MatMul}([[x]])$

Input: $[[·]]$-shares of matrix X and Y. Output: $[[·]]$-shares of Z where $Z=X·Y$.  Offline Phase:  1. $P_i$ sample random values $〈{\lambda }_Z〉$ and set $〈{{\lambda }_Z}^{\prime }〉$ where $i\in \{0,1,2\}$.  2. Parties mutually generate $〈{\lambda }_X{\lambda }_Y〉$ using ${\mathcal{F}}_{2-Mult}^{〈·〉}$.  Online Phase:  1. $P_i$ locally sets ${〈m_{\Delta }〉}_i=m_Y{〈{\lambda }_X〉}_i+m_X{〈{\lambda }_Y〉}_i+{〈{\lambda }_X{\lambda }_Y〉}_i-{〈{{\lambda }_Z}^{\prime }〉}_i$, where $i\in \{0,1,2\}$.  2. Parties reveal $m_{\Delta }$ and set ${m_Z}^{\prime }=m_{\Delta }+m_X{m}_Y$.  3. $P_i$ hold ${[[Z]]}_i=({m_Z}^{\prime }/2^d,{〈{\lambda }_Z〉}_i)$.

5.2. Exponential

Consider the following exponential function: $rEx{p}^l(x)=e^{-x},x\in {\mathbb{R}}^{+}$. Due to the properties of exponential functions, this can be equivalent to $rExp(x)=e^{-x}=rExp(2^{d(k-1)}{x}_{k-1})·\cdots ·rExp(2^d{x}_1)·rExp(2x_0)$, where x of length l is divided into k parts, each with a length of d [13], where this can be easily computed by invoking ${\mathcal{F}}_{DigDec}^{[[·]]}$ in Section 3 first, and then invoking the lookup table protocols separately in Algorithm 4. To reduce communication and computing costs as well as memory usage, the private inputs from the larger arithmetic ring are decomposed into smaller one ${\mathbb{Z}}_{2^8}$. The details are in Algorithm 6.

Algorithm 6 Functionality of exponential ${\mathcal{F}}_{rExp}([[x]])$

Input: $[[·]]$-shares of x. Output: $[[·]]$-shares of $y\approx e^{-x}=rExp(x)$.  offline phase:  1. Each party $P_i$ invokes the offline phase of ${\mathcal{F}}_{DigDec}^{[[·]]}$ with input $[[x_i]]\in {\mathbb{Z}}_l$ to obtain $u_j^b$ where $i,b\in \{0,1,2\},j\in \{0,\cdots ,l-1\}$, l is the bit width of x.  2. After obtaining the $[[x_{ij}]]\in {\mathbb{Z}}_2$ (it can be obtained in the first step of the offline phase and the first step of the online phase in ${\mathcal{F}}_{rExp}([[x]])$), each party $P_i$ invokes the offline phase of ${\mathcal{F}}_{LUT}^{[[·]]}$ with input $[[x_{ij}]]\in {\mathbb{Z}}_2$ and the input encoding and output encoding corresponding to the exponential function, then one obtains randomness ${\lambda }_{y_j}^t$ and $\langle {\lambda }_{\mathcal{S}}\rangle$ where $t\in \{0,1,2\},j\in \{0,\cdots ,l-1\}$, l is the bit width of x.  Online Phase:  1. Each party $P_i$ invokes the online phase in ${\mathcal{F}}_{DigDec}^{[[·]]}$ to obtain output $[[x_{ij}]]\in {\mathbb{Z}}_2$ where $i\in \{0,1,2\},j\in [l]$.  2. Each party $P_i$ invoke the online phase of ${\mathcal{F}}_{LUT}^{[[·]]}$ that for each $t\in k$, compute and obtain $[[y_j]]={\mathcal{F}}_{LUT}^{[[·]]}([[x_j^t]])$ after building a lookup table with $\delta =d,\sigma =d$, where $j\in [l]$, $x_j^t$ means the input for jth bit of output.  3. Each party $P_i$ convert bit shares to $[[z]]$ in arithmetic shares by using ${\mathcal{F}}_{B2A}^{[[·]]}$ respectively.

5.3. Sigmoid

The sigmoid function can be simply assumed to be composed of an exponential function $e^{-x}$ and a reciprocal ${\displaystyle \frac{1}{x}}$. Therefore, we sequentially calculate the exponential function and the reciprocal to obtain the result of the sigmoid function. For exponential function $e^{-x}$, we can use ${\mathcal{F}}_{rExp}([[x]])$ and obtain the accurate approximate results (the accuracy depends on the size of the lookup table). Then, for reciprocal ${\displaystyle \frac{1}{x}}$, we use the Goldschmidt iteration method (similar to the method in [13]); this method’s accuracy largely depends on the initial iteration value. In order to obtain a closer initial value, we construct a lookup table to obtain a more reliable approximation of the reciprocal function, and then continuously iterate on this basis to improve accuracy. The details are in Algorithm 7.

Algorithm 7 Functionality of exponential ${\mathcal{F}}_{\mathrm{sigmoid}}([[x]])$

Input: $[[·]]$-shares of x. Output: $[[·]]$-shares of $y\approx {\displaystyle \frac{1}{1+e^{-x}}}=\mathrm{sigmoid}(x)$.   offline phase:  1. Each party $P_i$ invokes the offline phase of ${\mathcal{F}}_{DigDec}^{[[·]]}$ with input $[[x_i]]\in {\mathbb{Z}}_l$ to obtain $u_j^b$ where $i,b\in \{0,1,2\},j\in \{0,\cdots ,l-1\}$, l is the bit width of x.  2. Each party $P_i$ invokes the second step of the offline phase in ${\mathcal{F}}_{rExp}^{[[·]]}$ to obtain randomness ${\lambda }_{y_j}^t$ and $\langle {\lambda }_{\mathcal{S}}\rangle$ where $t\in \{0,1,2\},j\in \{0,\cdots ,l-1\}$, l is the bit width of x.   Online Phase:  1. Each party $P_i$ invokes the online phase of ${\mathcal{F}}_{DigDec}^{[[·]]}$ to obtain output $[[x_{ij}]]\in {\mathbb{Z}}_2$ where $i\in \{0,1,2\},j\in [l]$.  2. Each party $P_i$ invokes the online phase of ${\mathcal{F}}_{rExp}^{[[·]]}$ to obtain $[[z]]$ where $i\in \{0,1,2\}$, and then obtain output by executing Goldschmidt iteration.

5.4. Tanh

The hyperbolic tangent (tanh) has many application scenarios in neural networks, mainly as activation functions for hidden layers. It is a variant of the sigmoid function. The tanh function maps the input value to a continuous value in the range of −1 to 1. According to the definition, the following equation holds: tanh $=2$ sigmoid$(2x)-1$; thus, it can be computed by invoking the sigmoid function.

6. Security Analysis

We prove security protocols under both real world execution and ideal world simulation paradigms, and consider the security in the semi-honest model with all three parties following the protocol exactly.

Proof: assume $\mathcal{A}$ is a semi-honest adversary in the real world that cannot corrupt more than one party at the same time, and $\mathcal{S}$ is a simulator of the ideal world. In the real world, all parties involved execute the protocol in the presence of adversary $\mathcal{A}$; in an ideal world, all parties send their inputs to the simulator $\mathcal{S}$ and have $\mathcal{S}$ execute the protocol honestly. Any knowledge that adversary $\mathcal{A}$ can obtain in the real world can also be obtained by simulator $\mathcal{S}$ in the ideal world, so the real world and the ideal world are indistinguishable.

Security for ${\mathcal{F}}_{Share}^{\langle ·\rangle }$, ${\mathcal{F}}_{Rec}^{\langle ·\rangle }$, ${\mathcal{F}}_{AND}^{\langle ·\rangle }$, ${\mathcal{F}}_{Mult}^{\langle ·\rangle }$,, ${\mathcal{F}}_{Wrap3}^{\langle ·\rangle }$, ${\mathcal{F}}_{PC}^{\langle ·\rangle }$, ${\mathcal{F}}_{Share}^{[[·]]}$, ${\mathcal{F}}_{Rec}^{[[·]]}$, ${\mathcal{F}}_{AND}^{[[·]]}$, ${\mathcal{F}}_{Mult}^{[[·]]}$. Since we use the 3PC protocol of [26] as our secret sharing primitiveness, the security of these protocols in this paper are inherited from [26].

Security for ${\mathcal{F}}_{LUT}^{[[·]]}$: let $\mathcal{A}$ corrupt $S_0$ during the protocol ${\mathcal{F}}_{LUT}^{[[·]]}$, and it is symmetric to $S_1,S_2$. In the offline phase, each party invokes ${\mathcal{F}}_{Rand}^{〈·〉}$ to generate correlation randomness and invokes ${\mathcal{F}}_{2-AND}^{\langle ·\rangle }$ to obtain the multi-input dot inner product, so security is guaranteed by these two functions. In both real and ideal protocols, the only key information obtained by the corrupt party $S_0$ from the honest party is a bit $v_m^0$. Whether in real or ideal execution, this bit is masked by a random number ${\lambda }_{y_j}^2$ selected by the honest party, which is invisible for $S_0$, making it a random bit that follows a uniform distribution in $S_0$ view. Since this is the only mask message that $S_0$ can observe, from its perspective, the execution of the real world and the simulation of the ideal world are indistinguishable.

Security for ${\mathcal{F}}_{DigDec}^{[[·]]}$: let $\mathcal{A}$ corrupt $S_0$ during the protocol ${\mathcal{F}}_{DigDec}^{[[·]]}$, and let it be symmetric to $S_1,S_2$. The interaction between the parties only occurs when invoking protocol ${\mathcal{F}}_{Wraps}^{\langle ·\rangle }$ and ${\mathcal{F}}_{PC}^{\langle ·\rangle }$, and all other calculations are completed locally. Therefore, this protocol’s security is guaranteed by the security of ${\mathcal{F}}_{Wraps}^{\langle ·\rangle }$ and ${\mathcal{F}}_{PC}^{\langle ·\rangle }$.

7. Evaluation

This chapter provides experimental results and corresponding experimental settings for the proposed protocol.

Experiment setting: The experiment was run on an Intel(R) Xeon(R) Platinum 8176 M CPU @ 2.10 GHz and 48 GB RAM and was conducted on a single threaded LAN and WAN, and we created three docker containers representing three servers in Ubuntu 20.04. The bandwidth in the LAN was approximately 1 GB/s and round-trip time (RTT) was 1ms, while the bandwidth in the WAN was 40 MB/s and RTT was 70 ms. The code implementation written in C++ programming language.

For our work’s benchmark, we compared the state-of-the-art SIRNN [13] in current RNN secure inference. In theoretical analysis, we compared the complexity of online communication and online communication rounds. Then, we compared the running time respectively under LAN and WAN, and communication volume of key building blocks. Finally, we applied our sigmoid and tanh protocols to end-to-end RNN secure inference and compared it with SIRNN [13] under the same setting. We simulated the fastGRNN [35] model on the Speech Command dataset [36], which identified keywords in short speech (such as digits, simple command, or directions). Its primary goal is to provide a way to build and test models that detect when a single word is spoken, from a set of ten target words, and the datasize size is 8.17 GiB. The FastGRNN model contains 99 sigmoid and 99 tanh layers; each layers has 100 instances.

7.1. Comparison of Theoretical Communication Cost on Building Blocks

As shown in

Table 3. Online communication rounds.

Operator	Rounds
	SIRNN	ABY3	SecureNN	Ours
2-Mult	4	1	2	1
DigDec	$l+1$	-	-	$l+logl+1$
B2A	-	$1+logl$	-	1
LUT	$d+1$	-	-	1

Note: In the table, l is bit width, and assume there is a $\delta$-to-$\sigma$ lookup table divided into several sub-blocks based on the input length $\delta$, then the length of each sub block is d; “-” means that the baseline does not implement this function.

and

Table 4. Online communication complexity.

Operator	Comm (MB)
	SIRNN	ABY3	SecureNN	Ours
2-Mult	$\lambda (l+3)+1.5l^2+2.5l+2$	$11l$	$5l$	l
DigDec	$l+logl+1$	-	-	$2l$
B2A	-	$l+llogl$	-	$l^2$
LUT	$2\lambda +Nl$	-	-	$\sigma$

Note: In the table, $\lambda$ is the computational security parameter, l is bit width, and assume there is a $\delta$-to-$\sigma$ lookup table divided into several sub-blocks based on the input length $\delta$, then the length of each sub block is d; “-” means that baseline does not implement this function.

, we compared the online communication complexity and communication rounds of basic building blocks of our 3PC work with the previous current optimal RNN work [13]. Note that the sigmoid and tanh functions of SIRNN is in 2PC setting. Moreover, we also compared with the typical three-party computation (3PC) framework ABY3 [24] and SecureNN [25], which are not specifically designed for RNNs, to obtain more comprehensive comparison results. For ${\mathcal{F}}_{2-Mult}^{[[·]]}$, compared to SIRNN with a communication complexity of $\lambda (l+3)+1.5l^2+2.5l+2$, our method reduces the communication complexity by an order of magnitude to l, and the communication rounds are reduced from 4 to 1. Our work reduces the online communication complexity by 10 times and 4 times compared to ABY3 and SecureNN, respectively, while also decreasing the number of communication rounds by one round compared to SecureNN, maintaining the same number of communication rounds as ABY3. For ${\mathcal{F}}_{DigDec}^{[[·]]}$, the online communication complexity and communication rounds of basic building blocks of our work are not much different from ref. [13]. For ${\mathcal{F}}_{B2A}^{[[·]]}$, SIRNN and SecureNN do not implement ${\mathcal{F}}_{B2A}^{[[·]]}$. Although the communication complexity of our work is slightly lower than that of ABY3, the communication rounds are reduced from $1+logl$ to 1. For ${\mathcal{F}}_{LUT}^{[[·]]}$, the communication complexity of our work was reduced so that it was only related to the output bit width $\sigma$, and the communication round was reduced to only one round.

7.2. Online Cost of RNN Building Blocks and End-to-End Inference

We tested the basic building blocks of RNN, including matrix multiplication, sigmoid, and tanh. It should be noted that our work focused on reducing online communication overhead, so the communication cost and runtime we provide are obtained during the online phase. Similarly, we also evaluated the online communication overhead and runtime for SIRNN. However, since SIRNN does not strictly divide the calculation into online/offline phases, all computations are related to the privacy input. Therefore, we took the total communication cost and runtime of SIRNN as online communication cost and online runtime. Compared with SIRNN [13], the online communication of RNN key building blocks matrix multiplication, sigmoid, and tanh in our research work was reduced by 27.56%, 80.39%, and 79.94%, respectively, as shown in

Table 5. Online communication of RNN operators.

Building Block	Size	Comm (MB)
		SIRNN	Ours
MatMul	$(128,500,100)$	0.156	0.109
sigmoid	$(128,128)$	0.933	0.183
tanh	$(128,128)$	0.947	0.190

Note: The data with better performance in the table is displayed in bold.

. The results of online runtime for RNN’s building blocks under LAN and WAN are shown in

Table 6. Online runtime of RNN operators under LAN and WAN.

Building Block	LAN (ms)		WAN (s)
	SIRNN	Ours	SIRNN	Ours
sigmoid	302	296	6.15	5.65
tanh	322	297	6.03	5.81

. In the LAN setting, for the sigmoid and tanh functions, the online runtime of our work is similar to that of SIRNN. However, in the WAN setting, for the sigmoid function, our work is 8% faster than SIRNN in terms of online runtime, and for the tanh function, our scheme is 3% faster than SIRNN. Also, we conducted end-to-end RNN secure inference using the Google-30 dataset [36] on fastGRNN [35]. As shown in

Table 7. Online cost of end-to-end RNN inference with FastGRNN on speech command dataset.

Work	Comm (MB)	LAN (s)	WAN (s)
SIRNN	102.80	10.29	522.07
ours	62.25	10.31	598.10

, although our work is slightly slower than SIRNN in terms of online communication time (LAN: SIRNN 10.29s vs. Ours 10.31s; WAN: SIRNN 522.07 s vs. Ours 598.10 s), our online communication overhead is reduced by 39.45% compared to SIRNN.

8. Conclusions

In this work, we introduce an innovative protocol to improve the efficiency of three-party secret sharing and secure inference in recurrent neural networks (RNNs). The experimental results show that compared with SIRNN, the online communication of the core building blocks of the RNN model is significantly reduced (matmul, 27.56%; sigmoid, 80.39%; tanh, 79.94%), making our protocol available for delay-sensitive applications, such as real-time healthcare diagnosis, motion detection, financial risk control detection, and smart voice assistants.

However, it is important to acknowledge potential limitations. When our protocol is applied to RNN models with more layers or more complex structures, it may lead to a linear increase in the total/online communication overhead. In addition, although our lookup table protocol requires only one round of online communication, the performance of our method in a distributed environment may be affected by network latency, which may affect the communication time of the online phase in real deployment.

In summary, this research presents significant advancements in reducing communication costs for secure three-party computations in RNNs, but it also highlights areas for further improvement. Future work will focus on integrating these protocols into real-world model inference tasks, addressing scalability and latency challenges, and enhancing the privacy and security of lookup tables. Considering the balance of communication efficiency and security, our work only supports semi-honest security. We plan to improve the work further to support malicious security in the future. In addition, multi-valued logic (MVL) may work in reducing the communication overhead of the lookup table in theory, so future research will consider improvements with MVL. By exploring these methods, we aim to broaden the utility and robustness of secure computation protocols in practical applications.