Optimal Control Model of Electromagnetic Interference and Filter Design in Motor Drive System
Abstract
1. Introduction
2. Motor Drive System Conducted EMI Prediction Mode
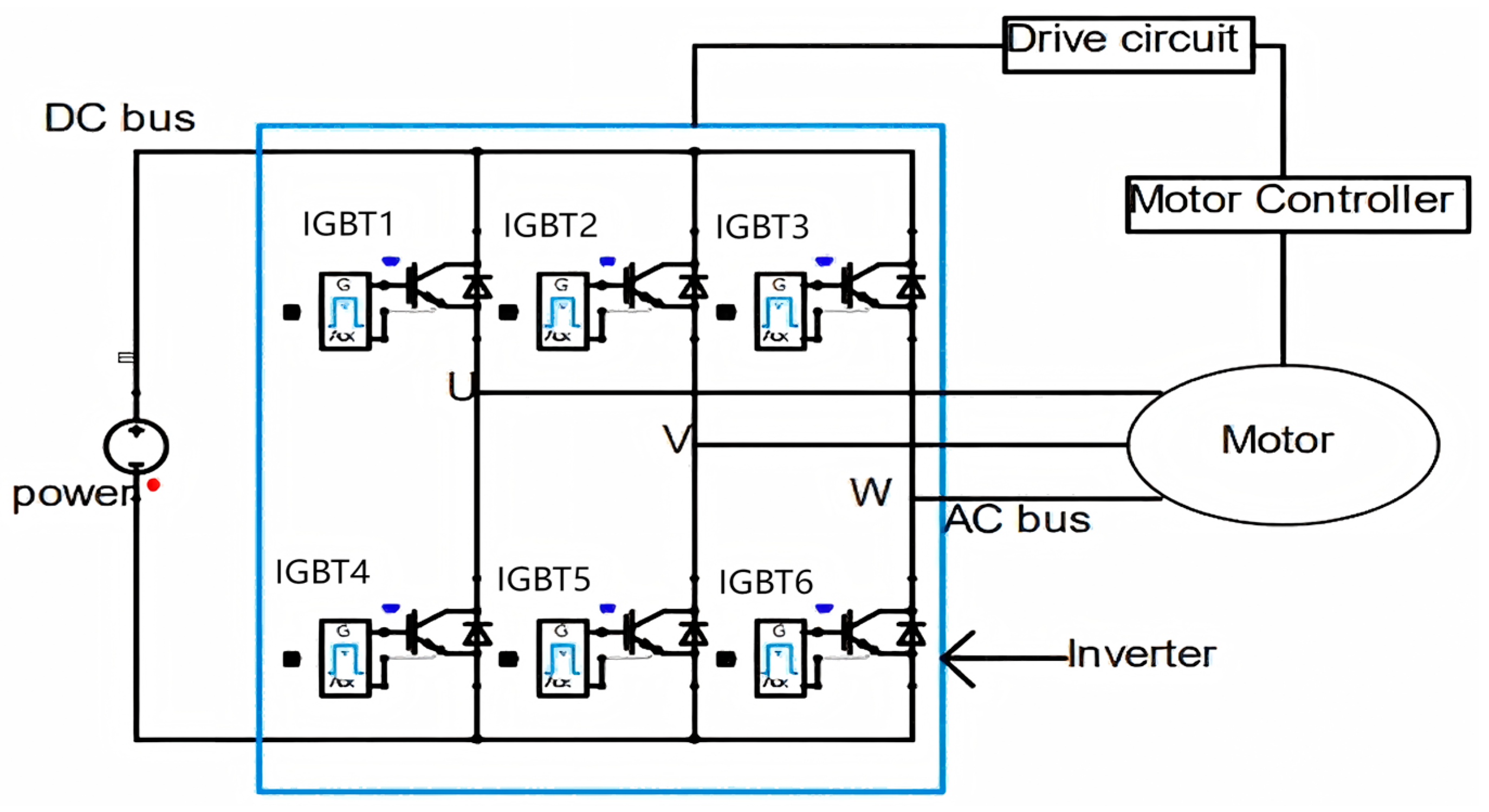
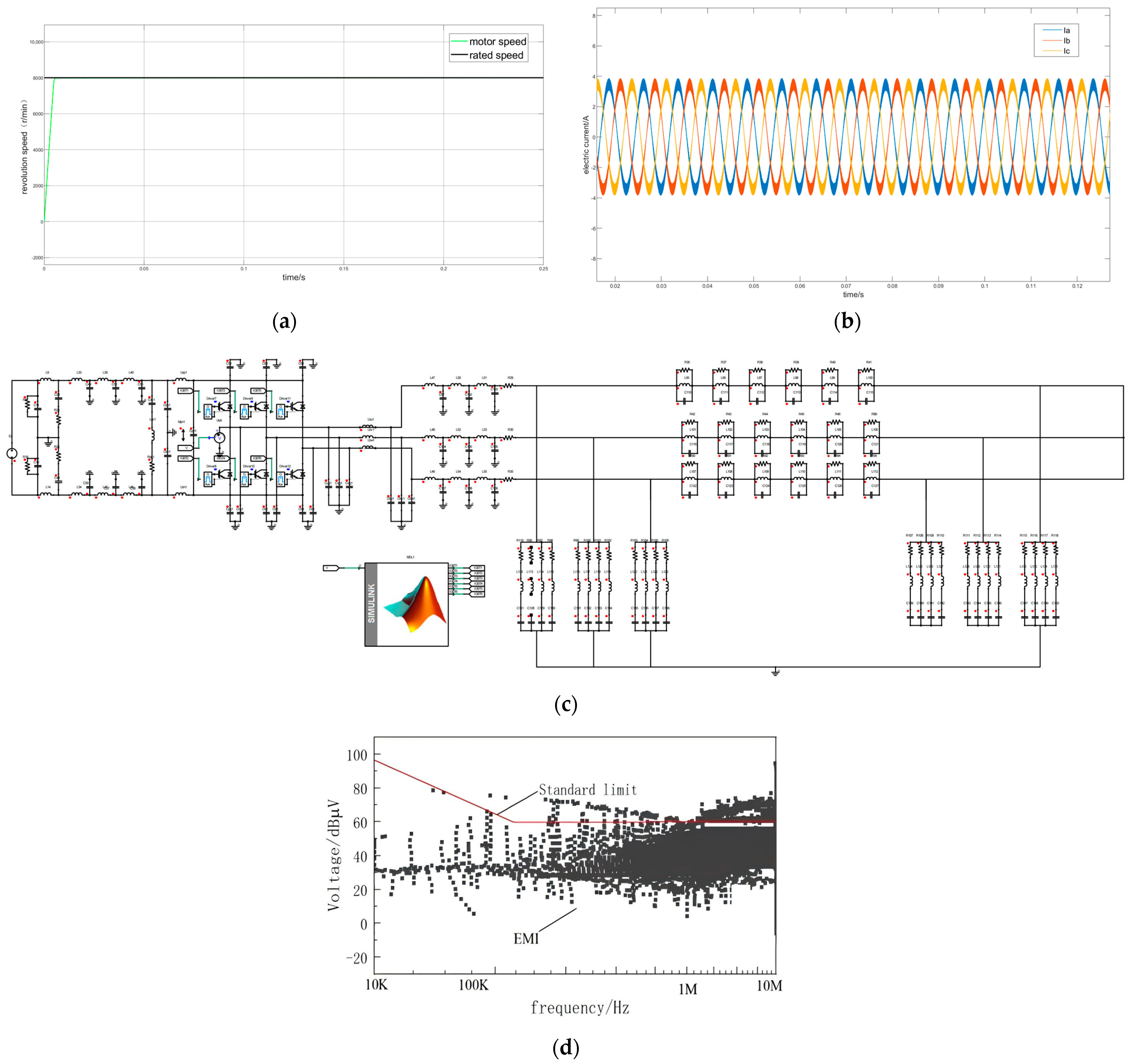
2.1. Composition and Working Principle of the Motor Drive System
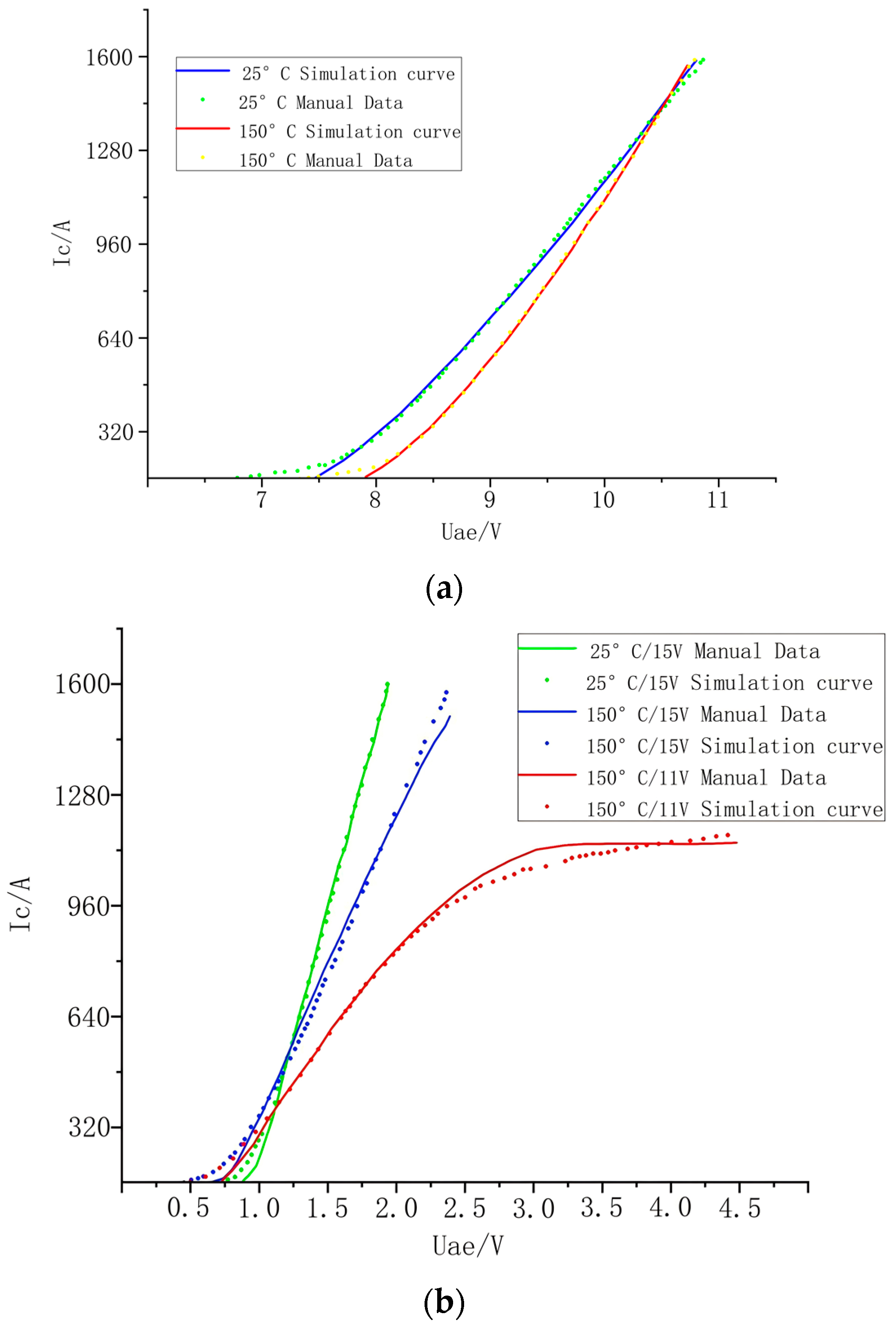
2.2. IGBT Model
2.3. Motor Model
2.4. Cable Model
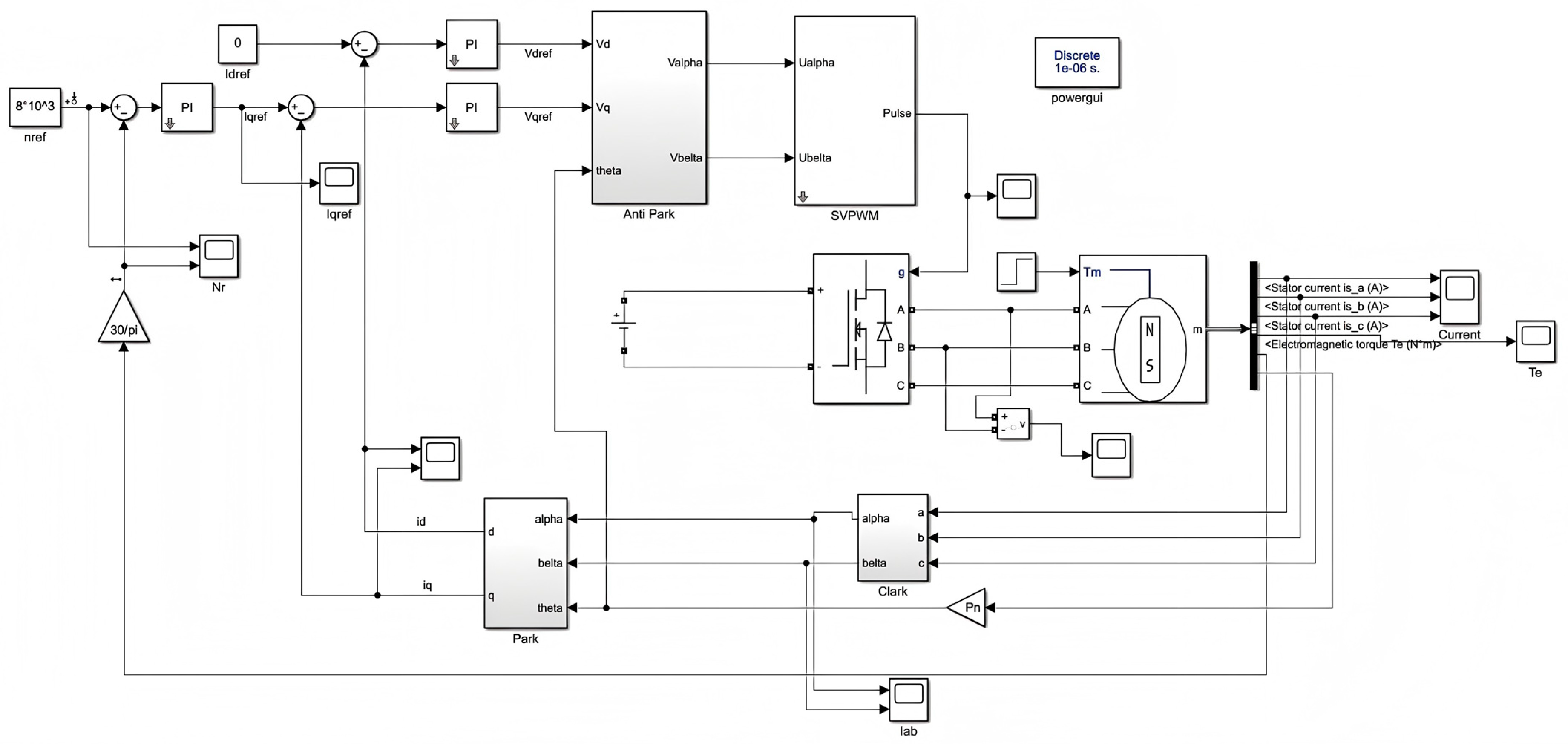
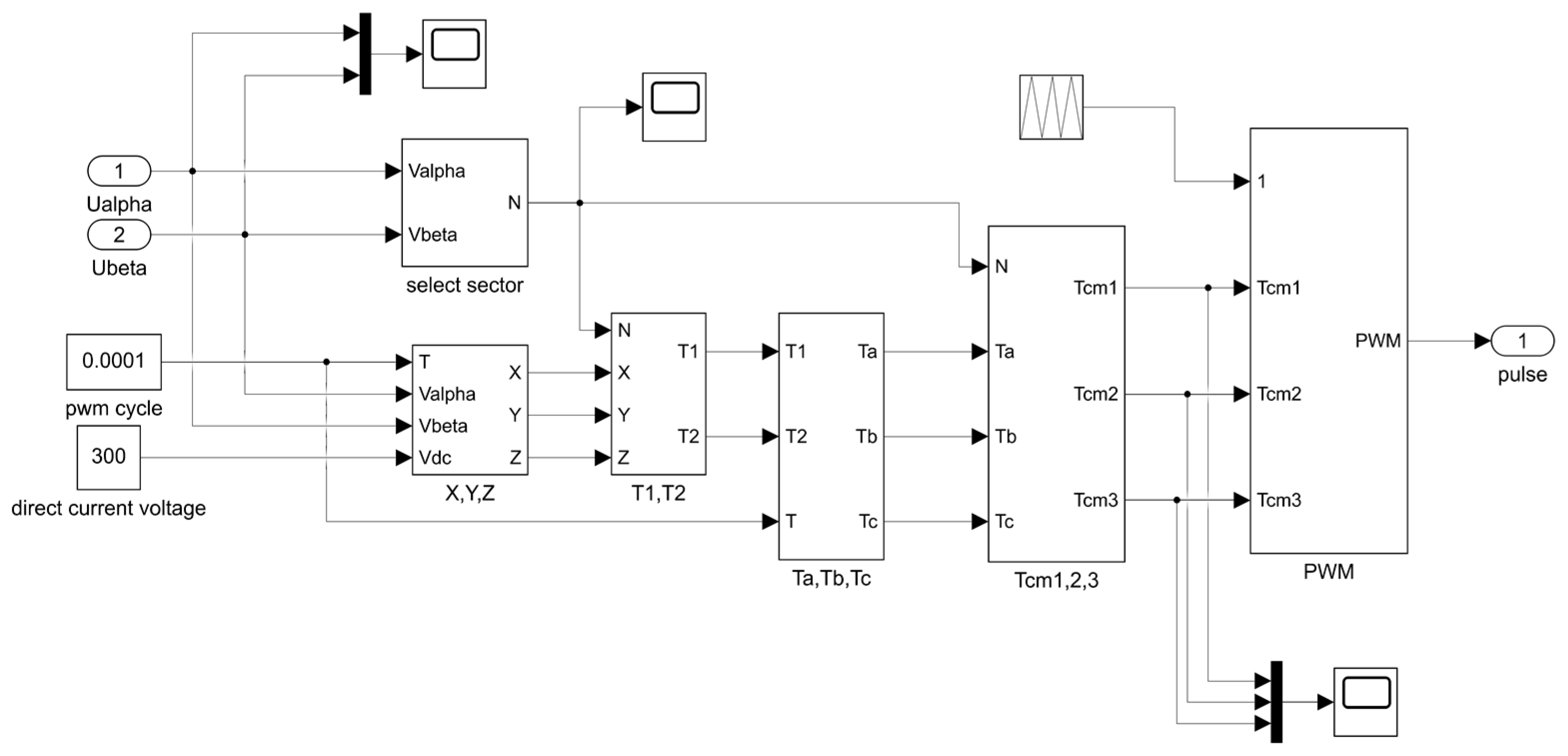
2.5. Control Model
- Optimize the dead-time: by dynamically adjusting the dead-time compensation, the voltage overshoot during the switching of the switch tube is reduced [24].
- Current loop dynamic compensation: by adjusting the d-q axis current error in real time, the torque response time is shortened to 2 ms (the traditional model is 5 ms).
- Integrated EMI modeling: The conducted EMI sub-module is embedded in Simulink to monitor PWM harmonic distribution in real time.
- Dead-time optimization algorithm: an adaptive dead-time compensation strategy is used to reduce the overshoot voltage of the switch tube by 18%.
2.6. Co-Simulation
3. Filter Design
3.1. Differential and Common-Mode Separation
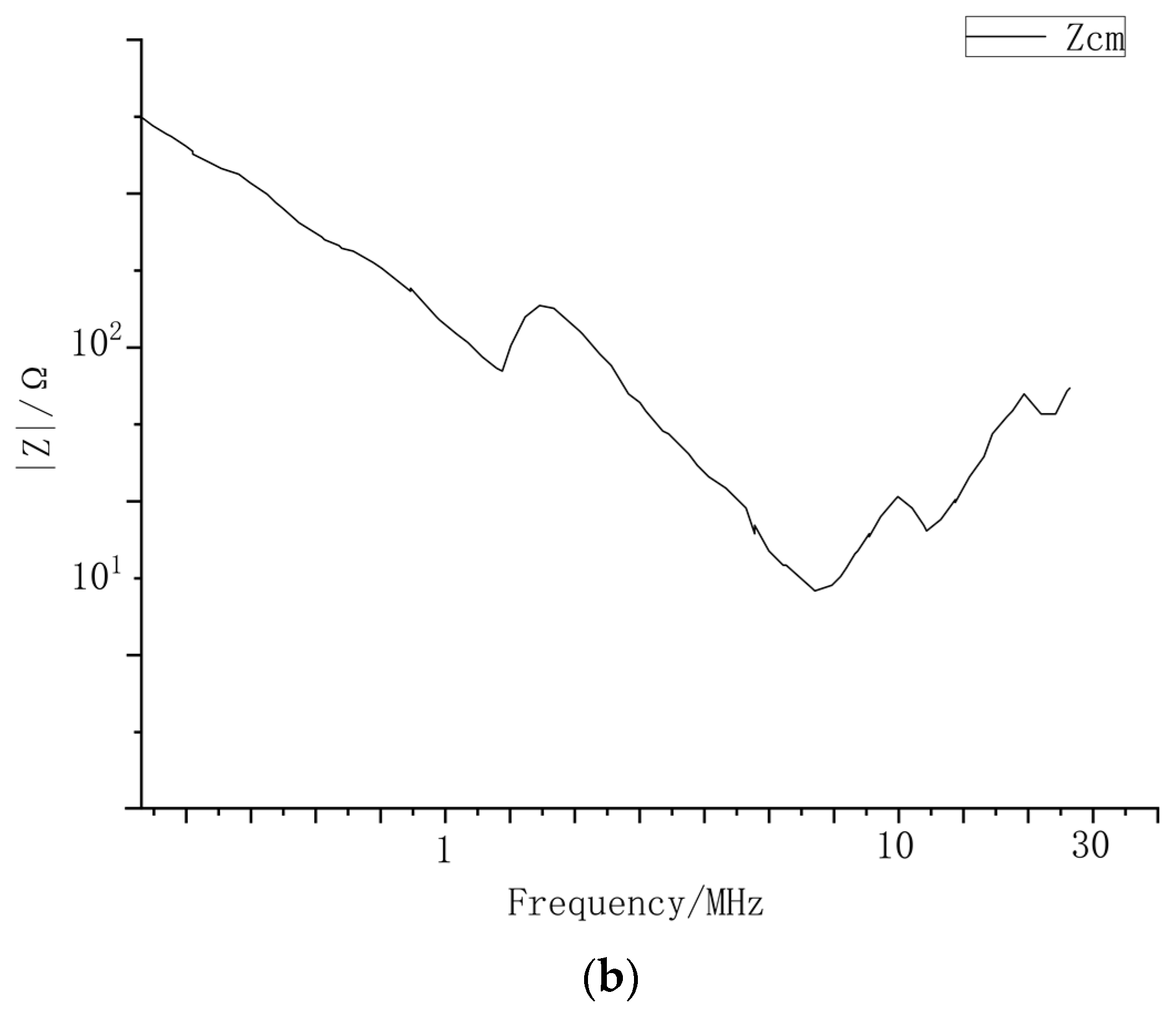
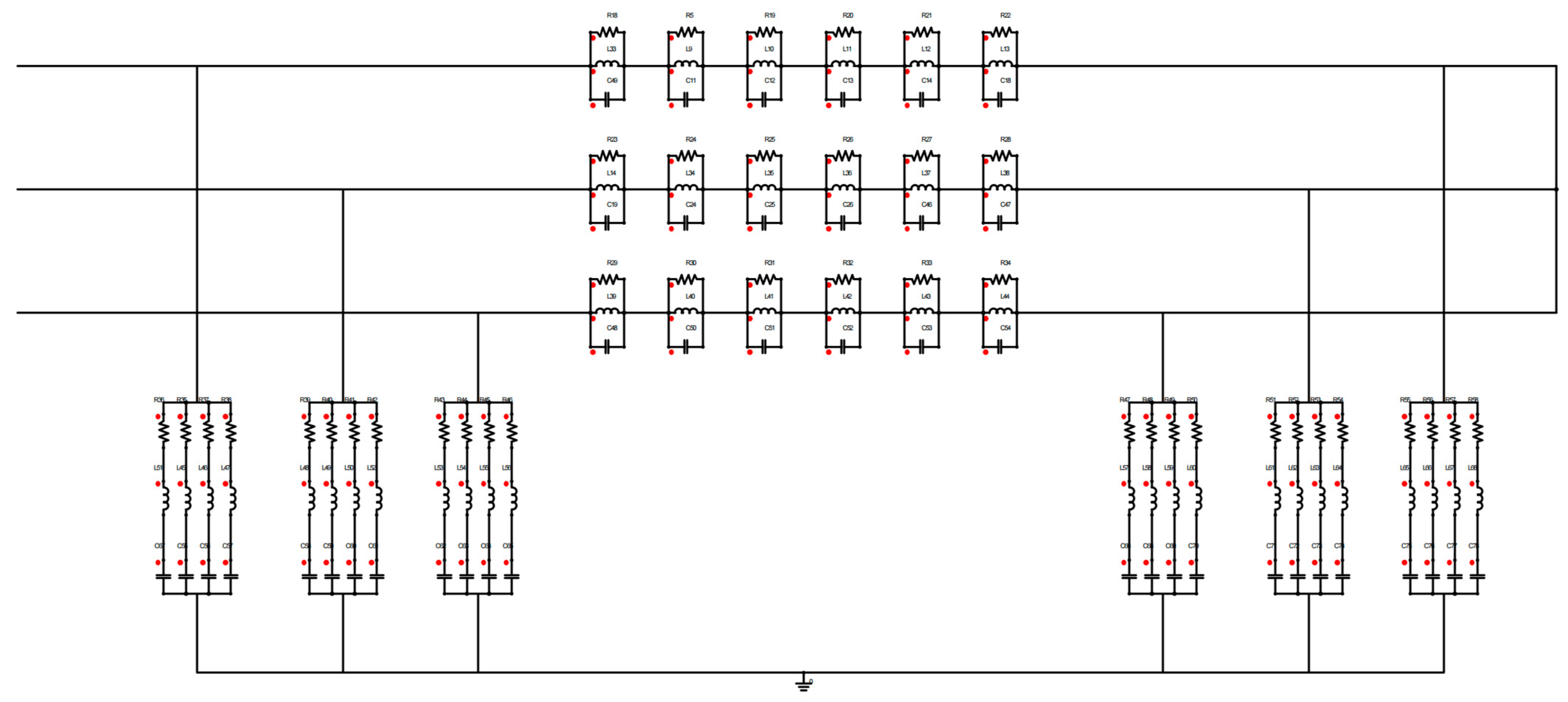
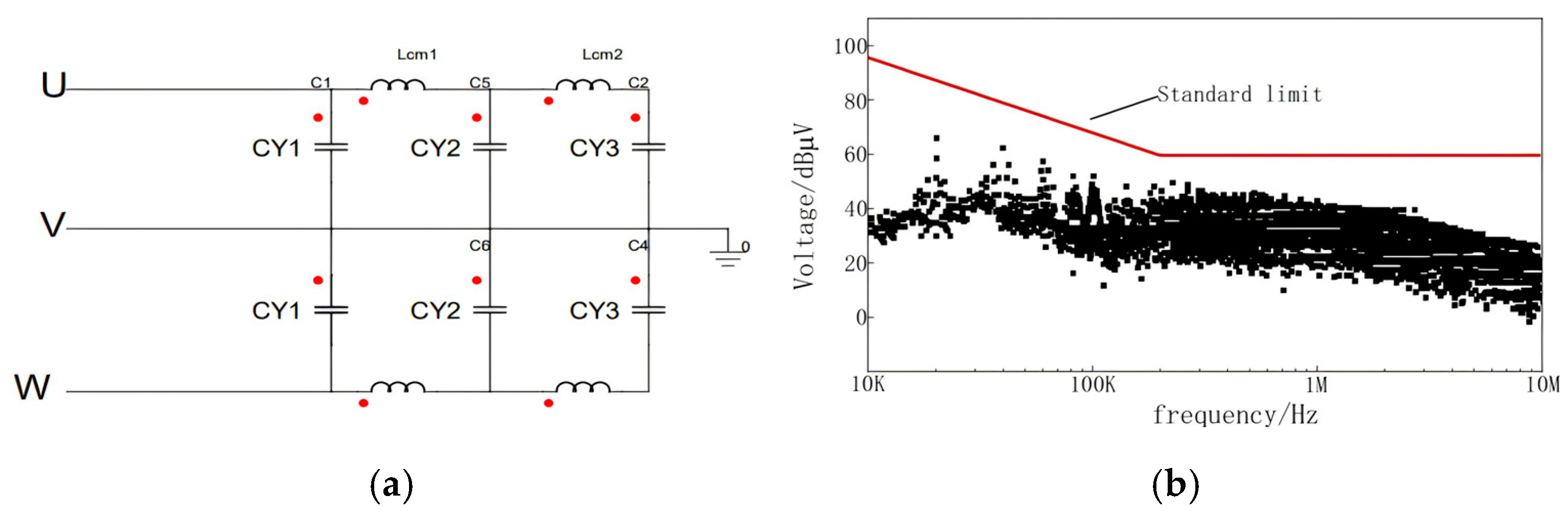
3.2. Common-Mode Filter Design
3.3. Differential-Mode Filter Design
4. Experimental Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shuo, Z.; Xuerong, L.; Xing, C.; Yang, W.; Chengning, Z. Parameter disturbance suppression method of PMSM. Trans. Beijing Inst. Technol. 2022, 42, 184–191. (In Chinese) [Google Scholar]
- Jiang, X. A Brief Analysis of the Differences and Connections between Electromagnetic Interference in Pure Electric Vehicles and Fuel Vehicles. Automot. Electr. Appl. 2018, 8, 11–12. [Google Scholar]
- Xu, X.; Chen, W.; Liu, C.; Chen, N.; Wang, F.; Wang, Y.; Zhang, K.; Ma, Y.; Zhang, S.; Zhou, Q.; et al. A Novel IGBT with Self-Regulated Potential for Extreme Low EMI Noise. IEEE Electron Device Lett. 2018, 40, 71–74. [Google Scholar] [CrossRef]
- Sun, R.; Deng, X.; Li, X.; Li, X.; Wu, H.; Wen, Y.; Zhang, B. A Novel SiC Trench MOSFET Embedding Auto-Adjust Source-Potential Region with Switching Oscillation Suppression. IEEE Electron Device Lett. 2023, 40, 1817–1820. [Google Scholar] [CrossRef]
- Fan, G. A brief discussion on the generation mechanism of electromagnetic interference in the motor drive of new energy vehicles. Times Automob. 2023, 112–114. [Google Scholar]
- Li, H.; Tang, S.; Wang, J. Electromagnetic compatibility design of in-cabin fan for space station. Micro Spec. Mot. 2024, 52, 22–25. [Google Scholar]
- Alamsyah, M.S.; Vieira, F.L.; Garbe, H.; Koj, S. The Effect of Stray Capacitance to the Common Mode Current on Three-Phase System. In Proceedings of the 2021 IEEE International Joint EMC/SI/PI and EMC Europe Symposium, Raleigh, NC, USA, 26 July–13 August 2021; pp. 430–433. [Google Scholar]
- Middelstaedt, L.; Wang, J.; Stark, B.H.; Lindemann, A. Direct Approach of Simultaneously Eliminating EMI-Critical Oscillations and Decreasing Switching Losses for Wide Bandgap Power Semiconductors. IEEE Trans. Power Electron. 2019, 34, 10376–10380. [Google Scholar] [CrossRef]
- GB/T 33012.1-2016; Road Vehicles—Electromagnetic Compatibility of Vehicles—Part 1: Terminology and Definitions. China Standard Press: Beijing, China, 2016.
- Li, X.; Wang, L.; He, J. Research of the electromagnetic compatibility design technology of battery management system on electric vehicle. Int. J. Electr. Hybrid Veh. 2013, 5, 69–78. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, S.; Kang, X. Conducted electromagnetic interference modeling method for booster circuit of electronic safety system. J. Detect. Control 2024, 46, 63–69. [Google Scholar]
- Guo, Y.; Wang, L.; Liao, C. Systematic Analysis of Conducted Electromagnetic Interferences for the Electric Drive System in Electric Vehicles. Prog. Electromagn. Res. 2013, 134, 359–378. [Google Scholar] [CrossRef]
- Yang, Y.M.; Peng, H.M.; Wang, Q.D. Common Model EMI Prediction in Motor Drive System for Electric Vehicle Application. J. Electr. Eng. Technol. 2015, 10, 205–215. [Google Scholar] [CrossRef]
- Duan, Z.; Wen, X. A new analytical conducted EMI prediction method for SiC motor drive systems. eTransportation 2020, 3, 100047. [Google Scholar] [CrossRef]
- Yang, M.; Lyu, Z.; Xu, D.; Long, J.; Shang, S.; Wang, P.; Xu, D. Resonance Suppression and EMI Reduction of GaN-Based Motor Drive with Sine Wave Filter. IEEE Trans. Ind. Appl. 2020, 56, 2741–2751. [Google Scholar] [CrossRef]
- Li, Z.; Shuangjie, Y.; Guixing, H.; Shuliang, W. Modeling of Conducted Electromagnetic Interference in Electric Vehicle Motor Drive System. J. Beijing Inst. Technol. 2022, 42, 824–833. [Google Scholar]
- Kim, H.; Fan, J.; Lee, S.; Hong, S.; Sim, B.; Kim, J. Analytical Expressions of Differential-mode Harmonics in Loosely-coupled Series-resonant Wireless Power Transfer System. In Proceedings of the 2019 IEEE International Symposium on Electromagnetic Compatibility, Signal & Power Integrity (EMC+SIPI), New Orleans, LA, USA, 22–26 July 2019; 2019; pp. 648–653. [Google Scholar]
- Zhuo, Y.; Donghai, L.; Liu, Y.; Rongxun, J.; Wei, S. Research on EMC simulation technology of electric vehicle drive system based on ANSYS. China Automot. 2020, 9, 53–57. [Google Scholar]
- Chen, P.; Chen, W.; Li, B. EMI model of permanent magnet synchronous motor based on vector fitting method. J. Power Supply 2021, 19, 126–133. [Google Scholar]
- Kumar, S.M.; Rani, J.A. Reduction of conductedelectromagnetic interference by using filters. Comput. Electr. Eng. 2018, 72, 169–178. [Google Scholar] [CrossRef]
- Li, W.; He, Y. Parameterization and Performance of Permanent Magnet Synchronous Motor for Vehicle Based on Motor-CAD and OptiSLang. Wirel. Commun. Mob. Comput. 2022, 2022, 8217386. [Google Scholar] [CrossRef]
- Holtz, J. Pulsewidth Modulation for Electronic Power Conversion. IEEE Trans. Ind. Electron. 1992, 39, 410–420. [Google Scholar] [CrossRef]
- Bose, B.K. Power Electronics and Motor Drives: Advances and Trends; Academic Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Li, R.; Xu, D. Dead-Time Compensation for SVPWM-Based Motor Drives. IEEE Trans. Power Electron. 2015, 30, 3457–3465. [Google Scholar]
- Zhang, Y. EMI Reduction in SiC Motor Drives via Optimized SVPWM. IEEE Trans. Electromagn. Compat. 2020, 62, 812–820. [Google Scholar]
- Xu, H.; Luo, S.; Bi, C.; Sun, W.; Zhao, H.; Liu, J. Design of broadband hybrid EMI filter based on SiCMOSFET synchronous BuckDC-DC converter. Trans. China Electrotech. Soc. 2024, 39, 3060. [Google Scholar]





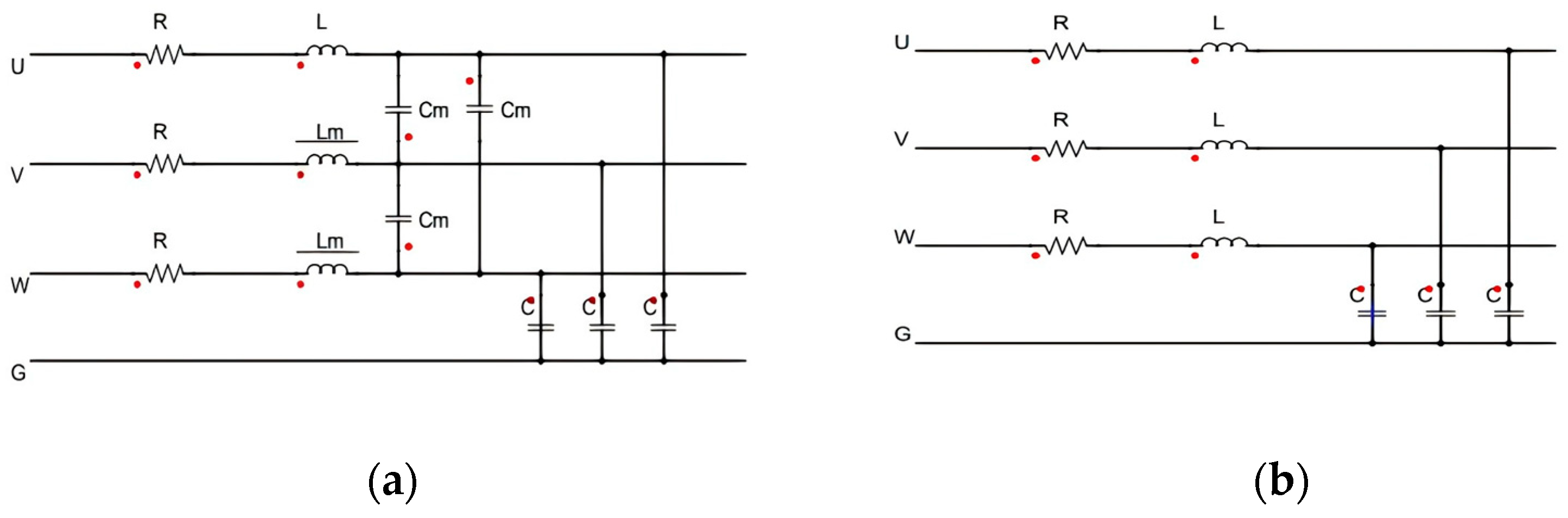

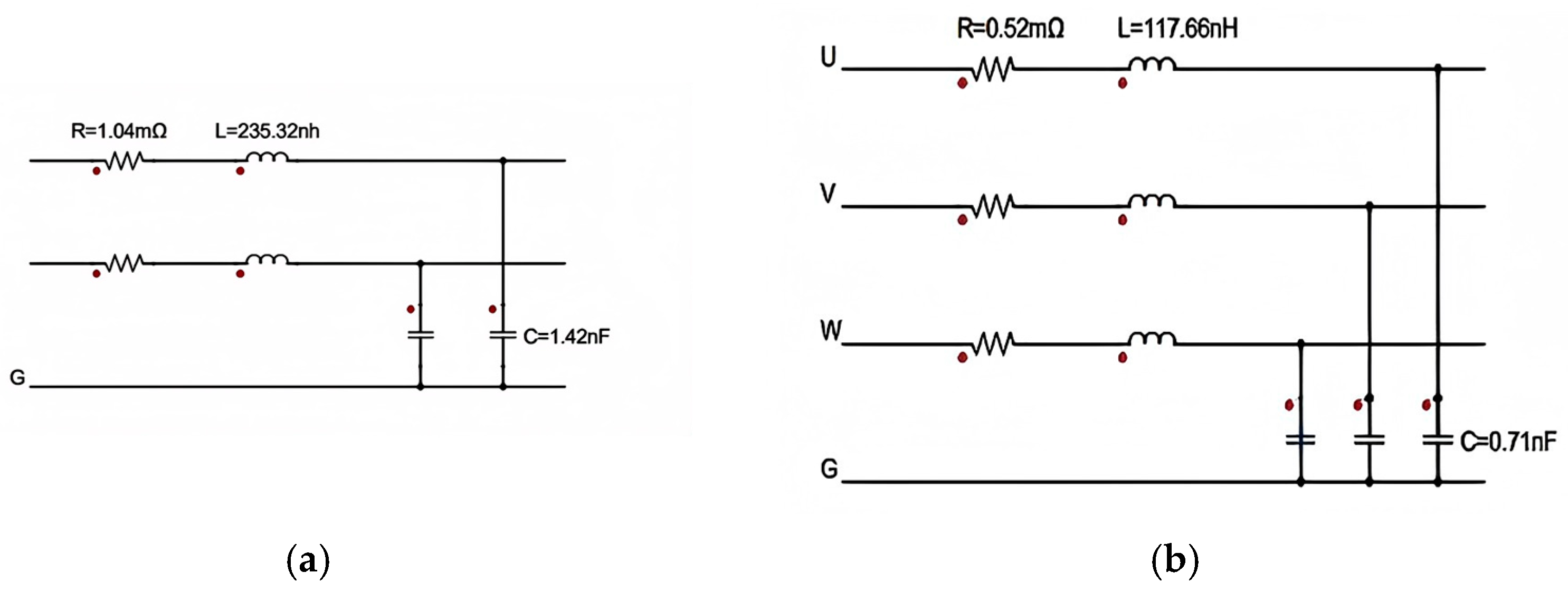




| Category | Parameter | Value | Unit | Category | Parameter | Value | Unit |
|---|---|---|---|---|---|---|---|
| Basic Electrical | Collector–Emitter Voltage () | 400 | V | Capacitance | Input Capacitance () | 80 | nF |
| Collector Current () | 450 | A | Miller Capacitance () | 0.3 | nF | ||
| Reference Temperature | 150 | °C | Resistance | Gate Resistance () | 0.7 | Ω | |
| Gate Drive | Gate-On Voltage () | 15 | V | Collector–Emitter Resistance () | 35 | mΩ | |
| Gate-Off Voltage () | 8 | V | External Gate-On Resistance () | 2.4 | Ω | ||
| Breakdown Characteristics | Breakdown Voltage () | 750 | V | External Gate-Off Resistance () | 5.1 | Ω | |
| Breakdown Current () | 1650 | A | Inductance | Collector–Emitter Stray Inductance () | 4 | nH | |
| Breakdown Temperature | 175 | °C | Cascaded Modules’ Stray Inductance () | 20 | nH |
| Per Unit Length Resistance R | Capacitance C | Inductance L |
|---|---|---|
| 0.52 mΩ | 0.71 nF | 117.66 nH |
| 1 nF | 0.3 nF | 0.5 nF | 6 mH |
| 3.5 µF | 3 µF | 5.8 µH |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zhao, W.; Zong, X.; Zhang, W. Optimal Control Model of Electromagnetic Interference and Filter Design in Motor Drive System. Electronics 2025, 14, 980. https://doi.org/10.3390/electronics14050980
Wang S, Zhao W, Zong X, Zhang W. Optimal Control Model of Electromagnetic Interference and Filter Design in Motor Drive System. Electronics. 2025; 14(5):980. https://doi.org/10.3390/electronics14050980
Chicago/Turabian StyleWang, Shufen, Wei Zhao, Xianming Zong, and Wenzhuo Zhang. 2025. "Optimal Control Model of Electromagnetic Interference and Filter Design in Motor Drive System" Electronics 14, no. 5: 980. https://doi.org/10.3390/electronics14050980
APA StyleWang, S., Zhao, W., Zong, X., & Zhang, W. (2025). Optimal Control Model of Electromagnetic Interference and Filter Design in Motor Drive System. Electronics, 14(5), 980. https://doi.org/10.3390/electronics14050980





