Optimal Grid-Forming Strategy for a Remote Hydrogen Production System Supplied by Wind and Solar Power Through MMC-HVDC Link

Abstract

Large-scale renewable power supply system design for remote hydrogen production is a challenging task due to the 100% power electronics sending-end subsystem. The proper grid-forming strategy for a sending-end system to achieve large-scale remote hydrogen production still remains a research gap. This study first designs two grid-forming strategies for the concerned renewable power supply system, with one being based on virtual synchronous generator (VSG) and another one being based on V/f control. Then, the impedance analysis is carried out for ensuring the small-signal stable operation of the sending-end system including wind power plant and PV plant. Numerical simulation results implemented on PSCAD verify that the VSG-based grid-forming strategy configured on the sending-end modular multilevel converter (MMC) station of the MMC-based high-voltage direct-current (HVDC) link has a larger transient stability margin. Hence, the MMC-HVDC-based grid-forming strategy is a better choice for the power supply of large-scale remote hydrogen production. The enhanced stability margin ensures more robust operation under disturbances, which is critical for maintaining continuous power supply to large-scale electrolyzers.

1. Introduction

Producing hydrogen using green power has both high economical and environmental benefits [1]. With the rapid increase of wind and solar power generation capacity, flexible utilization of the green power will reduce the consumption burden of the power grid and the controllable hydrogen production load can be used to improve the power angle and frequency stability of the power grid [2]. However, the grid structure and control system design of the renewable power supply system for the hydrogen production load is a challenging task. First, the grid structure should be able to support the black start of the system, and the maximum number of operation strategies should be allowed [3]. Second, the sending-end renewable energy base is normally a 100% power electronics system, and the grid-forming control of such a system is quite difficult and there is no consensus on how to control such a system [4].

With respect to the grid structure of a remote hydrogen production system, there are several plans for hydrogen production using green power. Firstly, the integration of offshore wind power with onshore hydrogen production is investigated in [5]. During the full scale output period of the offshore wind power plant, the hydrogen production load is main supplied by wind power. Nevertheless, the full scale output period is normally three or four hours per day, and the hydrogen production is supplied by the external power grid during the remaining time. In this system configuration, there is little instability risk due to the strong support from the external power grid. Secondly, a PV directly coupled hydrogen production load through AC transmission is designed in [6]. This kind of standalone system is a good choice for a small-scale hydrogen production system, in which intermittent hydrogen production is allowed. However, if the distance between the PV plant and the hydrogen production load is significant, then the AC transmission system may encounter risks of frequency and voltage oscillations.

To overcome the frequency and voltage instability in AC grid integration of a renewable power and hydrogen production system, DC grid integration has been designed in [7]. Since the hydrogen electrolyzer is supplied by DC power, it can be directly connected with the DC side of PV cells or wind power generators without frequency oscillation. Nevertheless, the external power grid must be connected to the DC grid through an AC/DC converter such that power balance can be satisfied when the renewable power is in shortage. The stable operation of AC and DC microgrids with hydrogen production load highly rely on the control system. Various control techniques have been developed for stability control of the hydrogen production microgrids [8].

An adaptive power sharing control strategy is designed for microgrids integrated with hydrogen production, PV station, and the external AC power grid in [9]. Since the microgrid is established with the support of distribution grids, grids following controllers are employed for PV cells and battery energy storage devices. A hierarchical self-regulation control framework is proposed in [10], in which the hydrogen production loads are connected on both AC and DC subsystems. The entire hybrid microgrid operates in standalone mode, and the PV and wind power sources are the power suppliers. The virtual synchronous generator is employed for the control of wind power generators for grid-forming in the AC subsystem. The system is able to operate in steady-state, but the hydrogen production scale is kW level and its operation relies on the availability of the solar and wind resources, which does not match the large-scale power generation demand.

According to the review of the existing studies, hybrid hydrogen production operating and being supplied by an AC system will encounter the risks of frequency and voltage instability, which will impede the long-distance power transmission of renewable power. Additionally, hydrogen production in a DC microgrid system eliminates the problem of frequency oscillation, but the production scale is limited compared with that in the AC system. Hence, the design of power grids with large capacity remote hydrogen production load has a research gap; the remote hydrogen production load refers to a plant that is more than 200 km away from the renewable power source. This scenario is especially important and represents typical cases of northern China and Europe [11,12]. The potential challenges that exist in traditional AC transmission are not economic for remote power transmission, and using an HVDC link will introduce extra difficulties into the stability control of the system [13]. The sending-end system may be a 100% power electronics system, and a grid-forming control technique that ensures stable frequency and voltage must be employed. Various grid-forming techniques have been invented, such as VSG [14], V/f control, droop control, and match control [15], but which one is the best for this scenario is unknown.

Catering to the above research gaps, this study designs a remote power supplied topology for large capacity hydrogen production loads. Two kinds of grid-forming strategies are compared and the superior one is suggested through numerical studies. The main contributions of the work can be summarized as follows:

• A remote power supply system is designed for large-scale hydrogen production. A renewable power base consisting of wind power, solar power, and battery energy storage is connected to a remote hydrogen production load through a MMC-HVDC link. Compared with the traditional hydrogen production in an AC system and DC microgrid, the proposed schemes can achieve stable operation at a total scale of 400 MW through a 200 km DC transmission line. The topology is suitable for various industrial production scenarios in practice.
• Two grid-forming strategies are designed for the hydrogen production system. The first one is a battery energy storage-based grid-forming strategy, in which V/f control is employed for the battery energy storage station. The second one is a MMC-HVDC-based grid-forming strategy, in which the sending-end MMC station is control by VSG. Different from the conventional grid-following converter relying on the external power grid, the proposed two grid-forming schemes can achieve the support of voltage and frequency for the sending-end station. At the same time, the problem of frequency oscillation is overcome in long-distance transmission by equipping the system with MMC-HVDC.
• Impedance analysis is carried out for controller parameter optimization of renewable power sources and battery energy storage devices. Numerical simulations are undertaken to compare the performance of the two grid-forming strategies in the cases of both sending-end and receiving-end AC grid faults.

Compared to the existing studies, the MMC-HVDC-based grid-forming strategy proposed in this paper has integrated renewable power generation with hydrogen electrolyzer load, and impedance-based parameter tuning is employed for various distributed controllers in the system. Overall, this paper is organized as follows. The power supply system for hydrogen production is designed in Section 2, and the grid-forming strategies are introduced. Section 3 shows the parameter optimization of various distributed controllers based on impedance analysis. Simulation results are shown in Section 4, based on which discusses are undertaken in Section 5. Conclusions are drawn in Section 6.

2. Design of System Structure and Grid-Forming Strategies

2.1. System Structure Design

The concerned remote hydrogen production system is as configured in Figure 1, where a 300 MW hydrogen production load is the main load of the system. The MMC-HVDC transmission lines are used for power transmission from a renewable energy base that is 200 km away from the hydrogen production load. The renewable energy base consists of a 250 MW wind power plant, a 250 MW PV power plant, and a 200 MW battery energy storage station. The rated RMS phase-to-phase voltage of the collector bus of the wind, solar, and battery energy storage plants is 33 kV, and the rated voltage of the DC transmission lines of the MMC-HVDC link is 500 kV. The receiving-end of the MMC-HVDC link is also connected to the main grid through a 5 km AC transmission line, and the main grid will guarantee the stable operation of the hydrogen production load under various conditions.

2.2. Grid-Forming Strategies

Two grid-forming strategies are designed for the sending-end renewable energy base. The first one is the battery energy storage-based grid-forming strategy, in which the V/f grid-forming control is used for the battery energy storage and other grid elements are controlled by grid-following controllers. The second one is the sending-end MMC-based grid-forming strategy, in which the VSG is employed for the sending-end MMC station and other grid components are regulated by grid-following controllers. Maximum power point tracking is set as the control objective in the control systems of wind power and solar power plants. The hydrogen production load is controlled in grid-following mode as well, and the operational characteristics of electrolyzers are modeled. The detailed modeling and control framework of the above grid components are introduced as follows.

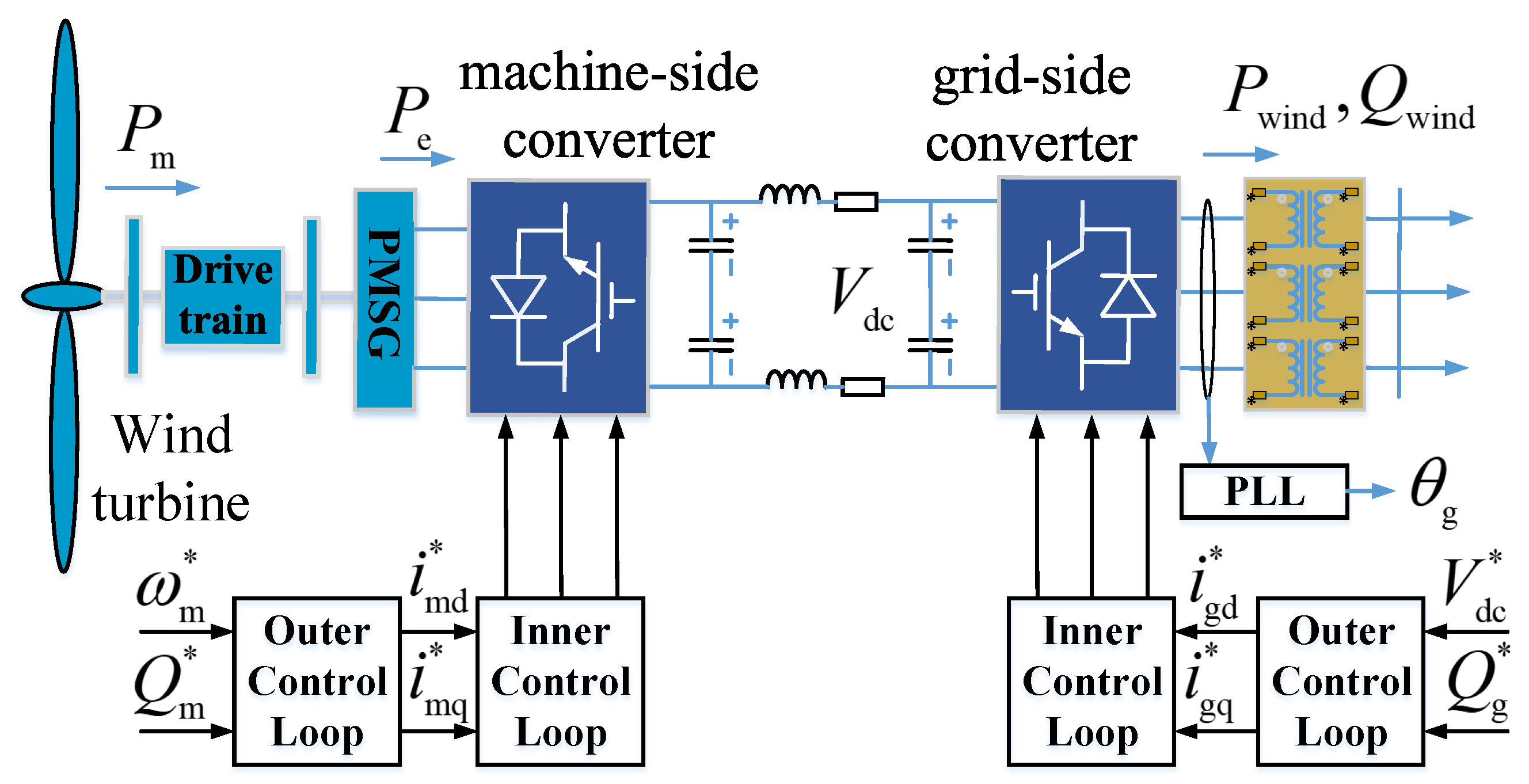
2.3. Control Scheme for Wind Power Plant

The wind power plant is modeled by amplifying the current output of a single type 4 wind power generator, and the full-scale direct-drive wind turbine is employed. The control schemes used for the machine-side converter and the grid-side converter are configured as follows. Firstly, the machine-side converter is controlled to realize the maximum power tracking of turbine blades, and the reactive power reference is set to zero. Secondly, the grid-side converter is regulated to control the DC link voltage and the reactive power output of the converter. The grid-side converter is synchronized with the external power grid through the phase-locked loop (PLL). The overall configuration of the type 4 wind turbine is as shown in Figure 2, where $P_{\mathrm{m}}$ is the mechanical power extracted from the wind by the turbine blades, $P_{\mathrm{e}}$ denotes the electromagnetic power output of the permanent magnetic synchronous generator (PMSG), $V_{\mathrm{dc}}$ is the DC link voltage, $P_{\mathrm{wind}}$ denotes the active power output of the grid-side converter, $Q_{\mathrm{wind}}$ represents the reactive power output of the grid-side converter, ${\omega }_{\mathrm{m}}^{\ast }$ is the reference for rotor speed, $Q_{\mathrm{m}}^{\ast }$ is the reference for the reactive power output of the PMSG, $V_{\mathrm{dc}}^{\ast }$ is the reference for $V_{\mathrm{dc}}$, $Q_{\mathrm{g}}^{\ast }$ is the reference for $Q_{\mathrm{wind}}$, $i_{\mathrm{md}}^{\ast }$ and $i_{\mathrm{mq}}^{\ast }$ are d-axis and q-axis reference currents for the machine-side converter, and $i_{\mathrm{gd}}^{\ast }$ and $i_{\mathrm{gq}}^{\ast }$ are d-axis and q-axis reference currents for the grid-side converter.

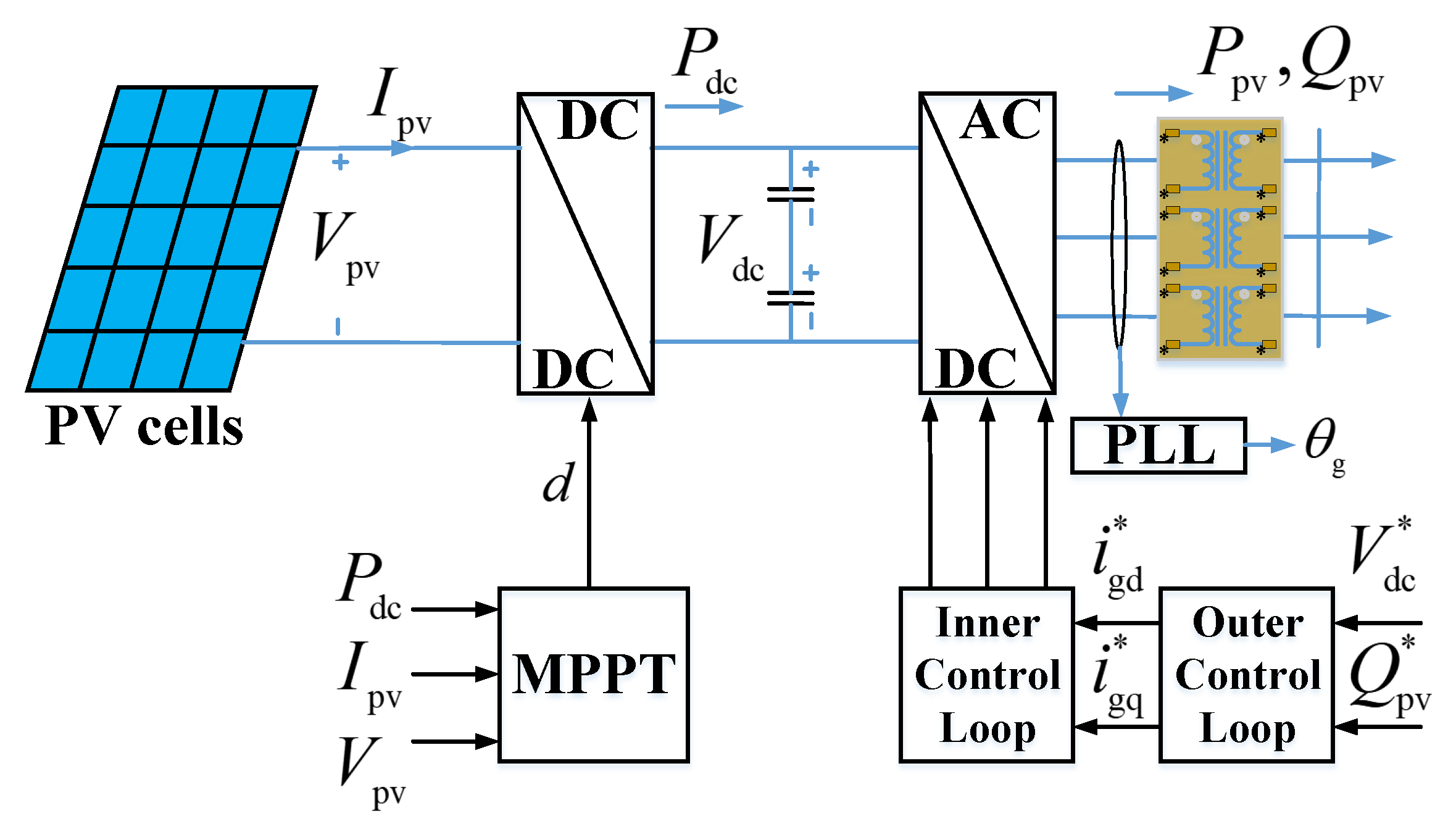
2.4. Control Scheme for PV Power Plant

The PV power plant is modeled by amplifying the current output of an integrated PV panel. The PV panel is composed of PV cells, a DC/DC converter, a DC/AC converter, and their control systems, as illustrated in Figure 3. The controller of the DC/DC converter is designed to achieve the maximum power point tracking, where $P_{\mathrm{dc}}$ denotes the power transferred to the DC link, $P_{\mathrm{pv}}$ denotes the active power output of the PV grid-side converter, $I_{\mathrm{pv}}$ is the current output of the PV cells, and $V_{\mathrm{pv}}$ is the voltage output of the PV cells. The duty cycle signal is generated by the controller and fed into the DC/DC converter. The controller of the DC/AC converter is designed to control the DC link voltage $V_{\mathrm{dc}}$ and the reactive power output $Q_{\mathrm{pv}}$ of the converter. Conventional grid-following control architecture is employed for the DC/AC converter, and the PLL is used to track the phase angle ${\theta }_{\mathrm{g}}$ of the AC terminal voltage. As shown in Figure 3, the outer control loop of the controller is used to track the DC link voltage reference $V_{\mathrm{dc}}^{\ast }$ and the reactive power output reference $Q_{\mathrm{pv}}^{\ast }$. The inner control loop is used to track the reference values of the d-axis and q-axis output currents of the converter, i.e., $i_{\mathrm{gd}}^{\ast }$ and $i_{\mathrm{gq}}^{\ast }$.

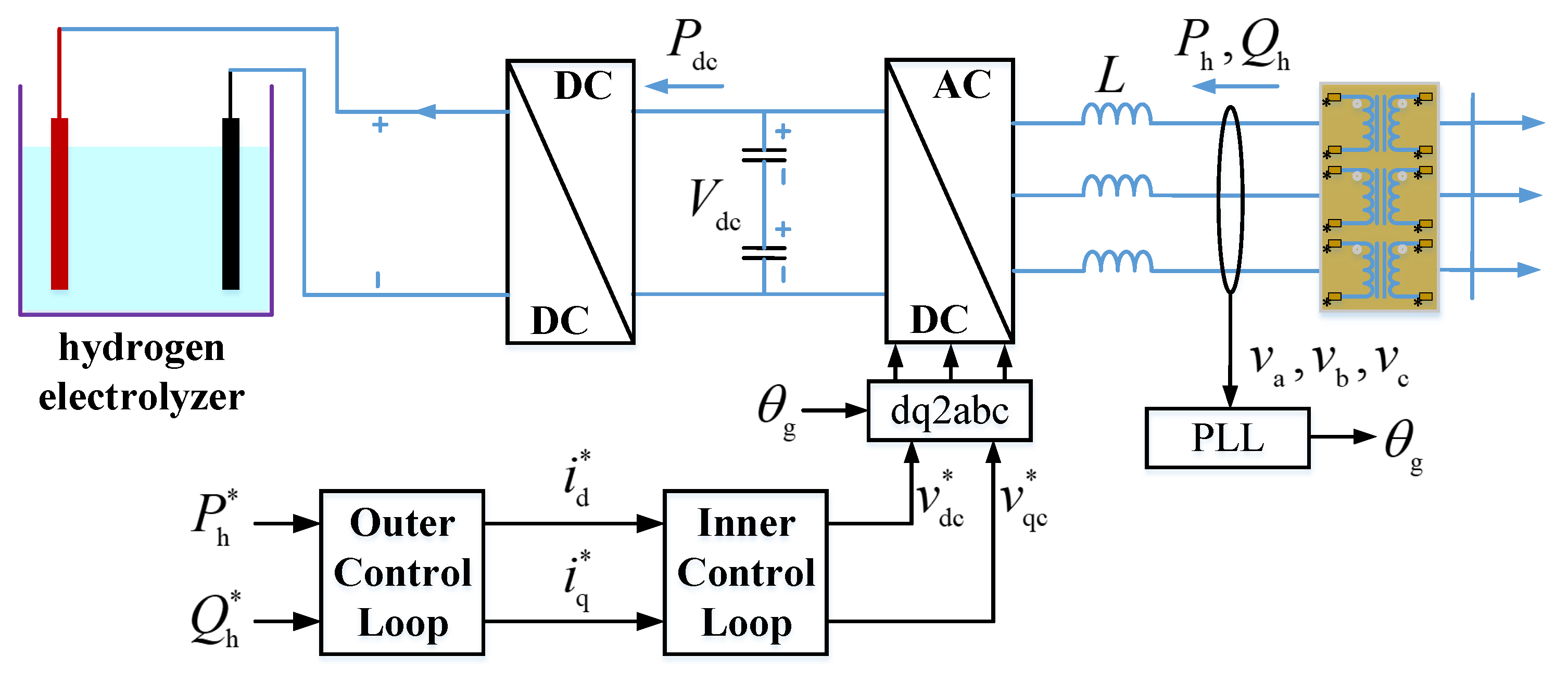
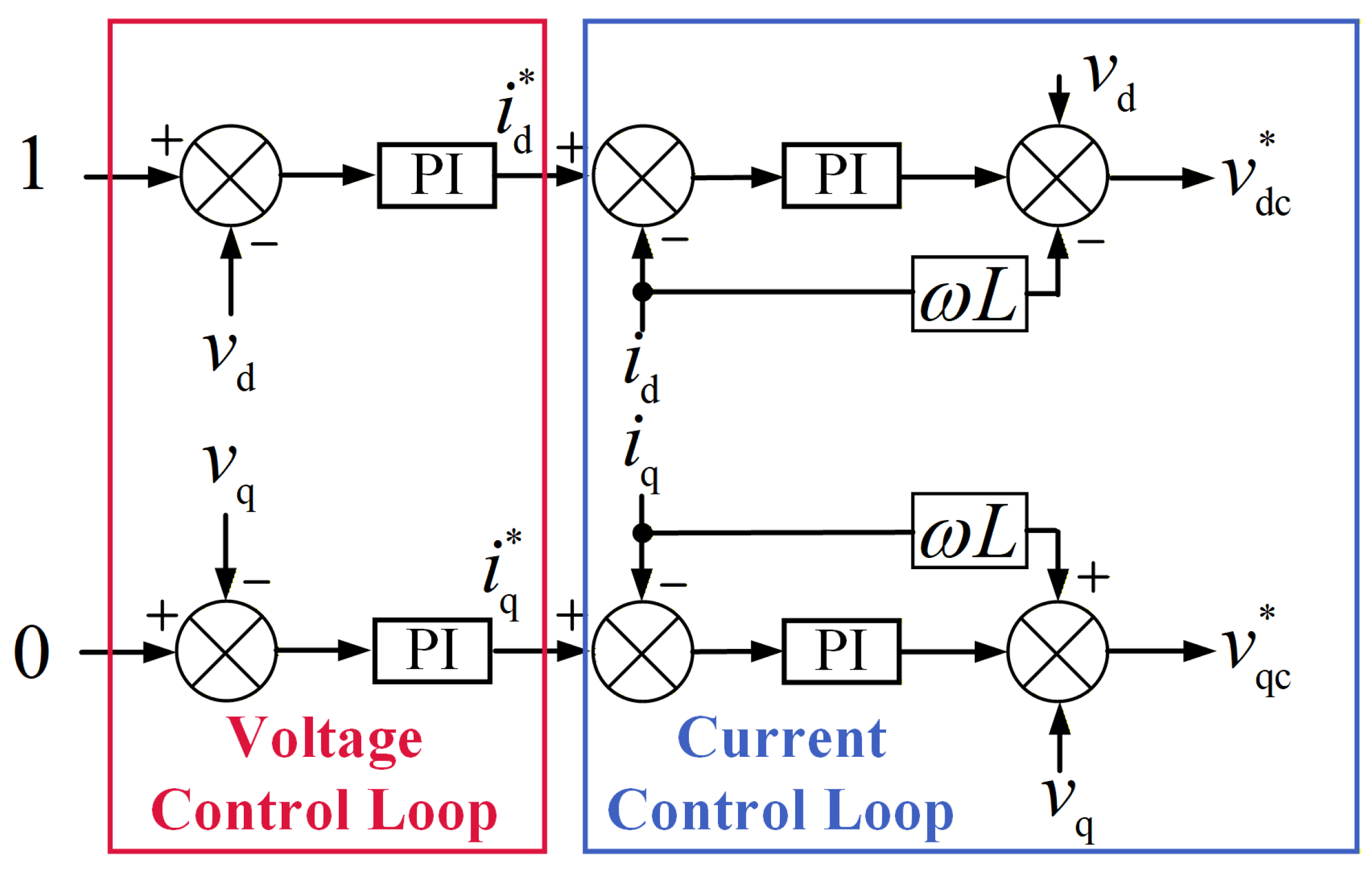
2.5. Hydrogen Production Load and Its Control System

While the solid oxide electrolyzer works at a high temperature, the stability of the electrolytic cell materials is relatively poor. Proton exchange membrane (PEM) hydrogen production has the advantages of high purity and flexibility and efficiency, but its cost and service life are unsatisfactory. Compared with the solid oxide electrolyzer and PEM methods, the alkaline electrolyzer is widely implemented due to its mature technology, long service life, and high hydrogen production capacity [16]. Thus, this paper adopts an alkaline electrolyzer for modeling. The hydrogen electrolyzer is the key component of the hydrogen production load. The V-I characteristics of the hydrogen electrolyzer is described by

$$V_{\mathrm{el}}=E_0+{\displaystyle \frac{R{T}_{\mathrm{el}}}{2F}}\ln {\displaystyle \frac{P_{H_2}{P}_{0.5O_2}}{a_{H_{2}O}}}+i{R}_{\mathrm{elohm}}+{\displaystyle \frac{R{T}_{\mathrm{el}}}{2\alpha F}}\ln {\displaystyle \frac{i}{i_0}}$$

(1)

where $V_{\mathrm{el}}$ denotes the open-circuit voltage of the hydrogen electrolyzer, $T_{\mathrm{el}}$ represents the temperature of the electrolyzer, R is the air constant, $a_{H_{2}O}$ denotes the water activity between the anode and the electrolyte, $E_0$ is the standard electromotive force, i.e., $E_0=\mathsf{\Delta }{G}_{\mathrm{f}}/\left(2F\right)$, where $\mathsf{\Delta }{G}_{\mathrm{f}}$ is the independent energy change constant in chemical reaction, F denotes Faraday constant, $\alpha$ denotes the exchange coefficient of the electrolytic membrane, $P_{H_2}$ and $P_{0.5O_2}$ denote the active power of $H_2$ and $O_2$, i denotes the current density, $i_0$ is the exchange current density, and $R_{\mathrm{elohm}}$ represents the equivalent resistance of the electrolytic membrane.

In practice [17,18], (1) is approximated by the following equation:

$$U_{\mathrm{el}}=U_{\mathrm{r}}+{\displaystyle \frac{r_1+r_2{T}_{\mathrm{el}}}{A}}{I}_{\mathrm{el}}+K_{\mathrm{el}}\ln \left({\displaystyle \frac{K_{\mathrm{t}1}+K_{\mathrm{t}2}/T_{\mathrm{el}}+K_{\mathrm{t}3}/T_{\mathrm{el}}^2}{A}}{I}_{\mathrm{el}}+1\right)$$

(2)

where $U_{\mathrm{el}}$ is the output voltage of the hydrogen electrolyzer, $U_{\mathrm{r}}$ denotes the reversible voltage of the electrolyzer, $I_{\mathrm{el}}$ is the current supplied to the electrolyzer, $T_{\mathrm{el}}$ is the temperature of the electrolyzer, $r_1$ and $r_2$ are equivalent resistances, $K_{\mathrm{el}}$, $K_{\mathrm{t}1}$, $K_{\mathrm{t}2}$ and $K_{\mathrm{t}3}$ are over-voltage coefficients of the electrolyzer, A is the area of the electrode of the electrolyzer, and $U_{\mathrm{r}}$ denotes the reversible voltage of the electrolyzer, which can be expressed as

$$U_{\mathrm{r}}=U_{\mathrm{r}0}-K_{\mathrm{r}}(T_{\mathrm{el}}-298.15)$$

(3)

where $K_{\mathrm{r}}$ is the empirical temperature coefficient of the reversible voltage, and $U_{\mathrm{r}0}$ denotes the reversible voltage under normal operation conditions. The hydrogen production rate can be described by

$$q_{H_2}={\displaystyle \frac{{\eta }_{\mathrm{F}}{n}_{\mathrm{c}}{I}_{\mathrm{el}}}{2F}}$$

(4)

where ${\eta }_{\mathrm{F}}$ is the current efficiency of the electrolyzer and can be denoted as

$${\eta }_{\mathrm{F}}={\displaystyle \frac{{(I_{\mathrm{el}}/A)}^2}{K_{\mathrm{f}1}+{(I_{\mathrm{el}}/A)}^2}}{K}_{\mathrm{f}2}$$

(5)

All the symbols used in (1)–(5) are briefly summarized in

Table 1. Symbols used in the model of the alkaline electrolyzer.

Symbol	Description
$V_{\mathrm{el}}$	the open-circuit voltage of the hydrogen electrolyzer
$T_{\mathrm{el}}$	the temperature of the electrolyzer
R	air constant
$a_{H_{2}O}$	the water activity between the anode and the electrolyte
$E_0$	the standard electromotive force
$\mathsf{\Delta }{G}_{\mathrm{f}}$	the independent energy change constant in chemical reaction
F	Faraday constant
$\alpha$	the exchange coefficient of the electrolytic membrane
$P_{H_2}$	the active power of $H_2$
$P_{0.5O_2}$	the active power of $O_2$
i	the current density
$i_0$	the exchange current density
$R_{\mathrm{elohm}}$	the equivalent resistance of the electrolytic membrane
$U_{\mathrm{el}}$	output voltage of the hydrogen electrolyzer
$U_{\mathrm{r}}$	the reversible voltage of electrolyzer
$I_{\mathrm{el}}$	the current supplied to the electrolyzer
$T_{\mathrm{el}}$	the temperature of the electrolyzer
$r_1$	equivalent resistance
$r_2$	equivalent resistance
$K_{\mathrm{el}}$	over-voltage coefficient of the electrolyzer
$K_{\mathrm{t}1}$	over-voltage coefficient of the electrolyzer
$K_{\mathrm{t}2}$	over-voltage coefficient of the electrolyzer
$K_{\mathrm{t}3}$	over-voltage coefficient of the electrolyzer
A	the area of the electrode of the electrolyzer
$K_{\mathrm{r}}$	the empirical temperature coefficient of the reversible voltage
$U_{\mathrm{r}0}$	the reversible voltage under normal operation conditions
${\eta }_{\mathrm{F}}$	the current efficiency of the electrolyzer

. The value of parameters used in (2) are shown in

Table 2. Parameters of alkaline electrolyzer.

Parameter	Value	Parameter	Value	Parameter	Value
$U_{\mathrm{r}0}$ (V)	1.23	A (m2)	0.1	$K_{\mathrm{r}}$ (V/K)	1.93 × ${10}^{-3}$
$r_1$ ($\mathsf{\omega }$ · m2)	8.232$\times {10}^{-5}$	$r_2$ ($\mathsf{\omega }$ · m2)	−4.51 × ${10}^{-7}$	$K_{\mathrm{el}}$ (V)	0.185
$K_{\mathrm{t}1}$ (m2/A)	2.54 × ${10}^{-2}$	$K_{\mathrm{t}2}$ (m2 · K2/A)	−0.158	$K_{\mathrm{t}3}$ (m2· K2/A)	1.212 × ${10}^3$
$n_{\mathrm{c}}$	1	$K_{\mathrm{f}1}$	2.54 × ${10}^4$	$K_{\mathrm{f}2}$	0.96

.

The control system of the hydrogen electrolyzer is as depicted in Figure 4, and a grid-following control scheme is employed. In Figure 4, ${\theta }_{\mathrm{g}}$ is the phase angle of the PCC voltage vector measured by PLL, and it is used for dq to abc and abc to dq transformation in the controller. A two loop control structure is utilized for the decoupled control of the active power $P_{\mathrm{h}}$ and the reactive power $Q_{\mathrm{h}}$. $P_{\mathrm{h}}^{\ast }$ and $Q_{\mathrm{h}}^{\ast }$ are the reference active power and reference reactive power of the hydrogen generation. The outer loop controller generates the references for d-axis output currents $i_{\mathrm{d}}^{\ast }$ and q-axis output currents $i_{\mathrm{q}}^{\ast }$, and the inner loop controller generates the references for d-axis output voltages $v_{\mathrm{dc}}^{\ast }$ and q-axis output voltages $v_{\mathrm{qc}}^{\ast }$ of the DC/AC converter. With the above control system, the active and reactive power consumed by the hydrogen electrolyzer is controlled flexibly.

2.6. Battery Energy Storage Station

The battery energy storage station is modeled by electric battery cells, DC/DC converter, DC/AC converter, and their control systems, as shown in Figure 5. The DC/DC converter is used for the charging and discharging control of the battery cells to maintain the stability of the DC link voltage, i.e., $V_{\mathrm{dc}}$. It can be operated in step-down mode for discharging and step-up mode for charging. In the MMC-HVDC-based grid-forming strategy, the battery energy storage is controlled in a grid-following scheme. The DC/AC converter regulates the DC link voltage and reactive power output with a controller, which has the same structure of the grid-side converter of the type 4 wind turbine and the PV converter. The DC/DC converter is used for active power control to obtain a desired SOC or to satisfy the power command from the control center.

In the battery energy storage-based grid-forming strategy, the V/f control scheme is employed for the control of the DC/AC converter, and the battery energy storage station functions as a grid-forming power source. The DC/DC converter is regulated to maintain a stable DC link voltage. In Figure 5, $i_{\mathrm{a}}$, $i_{\mathrm{b}}$, and $i_{\mathrm{c}}$ are three-phase currents measured at the point of common coupling (PCC), and $v_{\mathrm{a}}$, $v_{\mathrm{b}}$, and $v_{\mathrm{c}}$ are three-phase voltages at the PCC. L indicates the filter inductance. $f_{\mathrm{n}}$ is the nominal frequency of the system in Hz, ${\theta }_{\mathrm{g}}$ is the phase angle generated for the output voltage vector of the converter, and ${\theta }_{\mathrm{g}0}$ is its initial value. ${\theta }_{\mathrm{g}}$ is used to describe the angle from the a-axis to d-axis of the rotational reference frame, and the PCC voltage is assumed to be aligned with the d-axis. ${\theta }_{\mathrm{g}}$ is utilized in abc to dq and dq to abc transformation. In the V/f controller, the reference for $v_{\mathrm{d}}$ is 1, and the reference for $v_{\mathrm{q}}$ is 0. The control scheme of the inner control loop is shown in Figure 6, which contains the voltage control loop and current control loop. The voltage control loops are used to generates reference dq-axis current $i_{\mathrm{d}}^{\ast }$ and $i_{\mathrm{q}}^{\ast }$. The current control loop controllers are used to generate the references for d-axis and q-axis output currents of the converter, and the inner loop controllers are used to generate the references for the d-axis and q-axis output voltages of the converter, i.e., $v_{\mathrm{dc}}^{\ast }$ and $v_{\mathrm{qc}}^{\ast }$.

The dynamic voltage characteristics of the battery cells are modeled as well, and the following equation is used to describe the terminal voltage $V_{\mathrm{b}}$ of the battery cells.

$$V_{\mathrm{b}}=V_{\mathrm{b}0}-K{\displaystyle \frac{1}{SOC}}+A{\mathrm{e}}^{-BQ(1-SOC)}$$

(6)

where $V_{\mathrm{b}0}$ denotes the no-load voltage, K represents the polarization voltage, Q is the capacity of the battery cells, $SOC$ denotes the state-of-charge, and A and B are the property parameters of the battery cells.

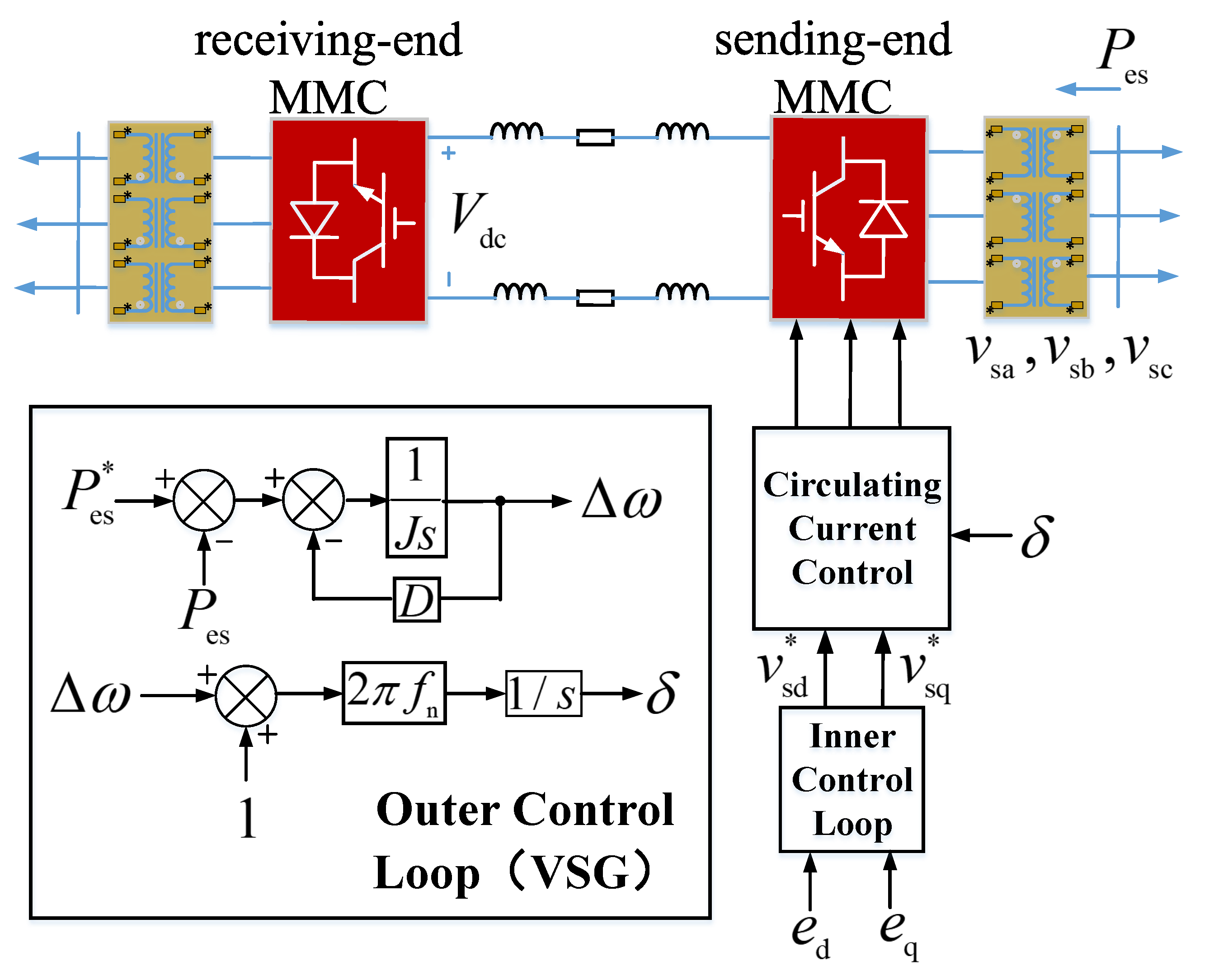
2.7. MMC-HVDC Link and Its Control System

In the battery energy storage-based grid-forming strategy, the sending-end and receiving-end MMCs are controlled in the grid-following mode. The schematic of the grid-following control system is as depicted in Figure 7, where $v_{\mathrm{sa}}$, $v_{\mathrm{sb}}$, and $v_{\mathrm{sc}}$ are three-phase voltages of the sending-end AC bus, and $v_{\mathrm{ra}}$, $v_{\mathrm{rb}}$, and $v_{\mathrm{rc}}$ are three-phase voltages of the receiving-end AC bus of the MMC-HVDC link. ${\theta }_{\mathrm{s}}$ and ${\theta }_{\mathrm{r}}$ are the phase angles measured by the PLL on the sending-end and receiving-end AC buses, respectively. $P_{\mathrm{es}}$ is the active power input into the sending-end MMC station, and $P_{\mathrm{es}}^{\ast }$ is the reference value. $V_{\mathrm{s}}^{\ast }$ denotes the RMS magnitude of $v_{\mathrm{sa}}$, $v_{\mathrm{sb}}$, and $v_{\mathrm{sc}}$. $V_{\mathrm{r}}^{\ast }$ denotes the RMS magnitude of $v_{\mathrm{ra}}$, $v_{\mathrm{rb}}$, and $v_{\mathrm{rc}}$. $V_{\mathrm{dc}}$ represents the DC voltage of the receiving-end MMC, and $V_{\mathrm{dc}}^{\ast }$ denotes the reference value for $V_{\mathrm{dc}}$.

In the MMC-HVDC-based grid-forming strategy, the sending-end MMC is controlled by the grid-forming controller based on VSG, and the schematic of the controller is as illustrated in Figure 8. $v_{\mathrm{sd}}$ and $v_{\mathrm{sq}}$ are the d-axis and q-axis components of $v_{\mathrm{sa}}$, $v_{\mathrm{sb}}$, and $v_{\mathrm{sc}}$, and the phase angle $\delta$ generated by VSG is used for Park transformation. $e_{\mathrm{d}}$ and $e_{\mathrm{q}}$ are the reference values for $v_{\mathrm{sd}}$ and $v_{\mathrm{sq}}$. $P_{\mathrm{es}}^{\ast }$ is the reference for $P_{\mathrm{es}}$; J denotes the virtual inertia coefficient, where a higher value of J will slow down the movement of the virtual power angle and enables the converter to output more active power when the external phase angle decelerates and output less active power when the external phase angle accelerates, which will reduce the rate of change of frequency of the AC power system; D denotes the virtual damping coefficient, where a high value of D will increase the energy dissipation of the equivalent rotor and reduce the deviation of virtual rotor speed when external disturbances occur; $\mathsf{\Delta }\omega$ is the virtual rotor speed deviation; and $\delta$ is the virtual rotor angle of the VSG. The control scheme of the inner control loop is the same as the scheme presented in Figure 6. The above two kinds of grid-forming strategies will be discussed and compared in the later part of this paper. Due to the start-up requirements of the MMC-HVDC-based grid-forming strategy, the receiving-end MMC should be connected to an AC power grid such that the initial power supply can be provided by the AC power grid for a black start of the system.

3. Controller Parameter Optimization for Renewable Energy Base

3.1. Theory of Impedance Stability Analysis

The impedance stability analysis is employed for controller parameter optimization of various controllers in the renewable energy base. By dividing the whole system into two subsystems, i.e., the inverter subsystem and the power grid subsystem, the Nyquist Criterion is employed for stability judgment and stability margin calculation of the whole system. For the grid-following converter with current source characteristics, the transfer function of the output voltage ina complex domain can be written as [19]

$$V\left(s\right)=I_{\mathrm{s}}\left(s\right)Z_{\mathrm{g}}\left(s\right){\displaystyle \frac{1}{1+Z_{\mathrm{g}}\left(s\right)/Z_{\mathrm{s}}\left(s\right)}}$$

(7)

where $I_{\mathrm{s}}\left(s\right)$ is the output current of the converter, $Z_{\mathrm{g}}\left(s\right)$ denotes the equivalent load impedance, $Z_{\mathrm{s}}\left(s\right)$ represents the equivalent converter impedance, and $V\left(s\right)$ is the PCC voltage of the converter. Normally, it is acknowledged that the output current and load impedance are stable, namely, $I_{\mathrm{s}}\left(s\right)Z_{\mathrm{g}}\left(s\right)$ is stable and has no poles on the right-half complex plane. Hence, the small-signal stability of $V\left(s\right)$ is determined by the second part of the transfer function. The bode diagrams of $Z_{\mathrm{g}}\left(s\right)$ and $Z_{\mathrm{s}}\left(s\right)$ can be obtained by impedance scanning. In bode diagrams, the real axis of the frequency magnitude diagram corresponds to the unit circle in the Nyquist diagram, and the −180° line of the frequency phase diagram corresponds to the negative real axis in the Nyquist diagram. Correspondingly, the requirement that the Nyquist curve of $Z_{\mathrm{g}}\left(s\right)/Z_{\mathrm{s}}\left(s\right)$ does not encircle the (−1, j0) point in the clockwise direction is equivalent to that of the phase frequency curve of $Z_{\mathrm{g}}\left(s\right)/Z_{\mathrm{s}}\left(s\right)$ going down through the −180° line after its magnitude frequency curve goes down through the real axis.

If we use the frequency scanning method to obtain the bode diagrams of $Z_{\mathrm{g}}\left(s\right)$ and $Z_{\mathrm{s}}\left(s\right)$, respectively, then the above stability criterion is equivalent to that of $arg\left(Z_{\mathrm{g}}\left(s\right)\right)-arg\left(Z_{\mathrm{s}}\left(s\right)\right)>-180°$ at the frequency $|Z_{\mathrm{g}}\left(s\right)/Z_{\mathrm{s}}\left(s\right)|=1$. The phase margin of the system can be written as $PM=arg\left(Z_{\mathrm{g}}\left(s\right)\right)-arg\left(Z_{\mathrm{s}}\left(s\right)\right)+180°$. According to the above stability criterion, the optimal network as well as controller parameters are chosen for all controllable devices in the following subsection.

3.2. Description of Impedance Measurement Method in PSCAD

To measure the impedance at different disturbance frequencies in PSCAD, the Matlab platform is necessary, as shown in Figure 9. Firstly, the three-phase voltage source is connected between the grid-side and converter-side in the electromagnetic transient model in PSCAD. Then, the disturbance frequency from 1 Hz to 1000 Hz is injected into the system through the voltage source. Thereafter, the A-phase voltage $v_{\mathrm{a}}\left(t\right)$ and A-phase current $i_{\mathrm{a}}\left(t\right)$ are collected by oscilloscope and then exported to the Matlab platform. Through Fast Fourier Transform (FFT) in Matlab, we can obtain the value of voltage and current in different disturbance frequencies $f_{dis}$. In Figure 9, ${\mathbf{f}}_{dis}$ is the disturbance frequency matrix, $\mathbf{V}\left(f_{dis}\right)$ is the voltage matrix in regard to different disturbance frequency, and $\mathbf{I}\left(f_{dis}\right)$ is the current matrix in regard to different disturbance frequencies. Finally, the impedance value in different disturbance frequencies can be obtained by dividing $V\left(f_{dis}\right)$ by $I\left(f_{dis}\right)$ in the corresponding disturbance frequency. And then the impedance results are obtained by drawing in the Matlab.

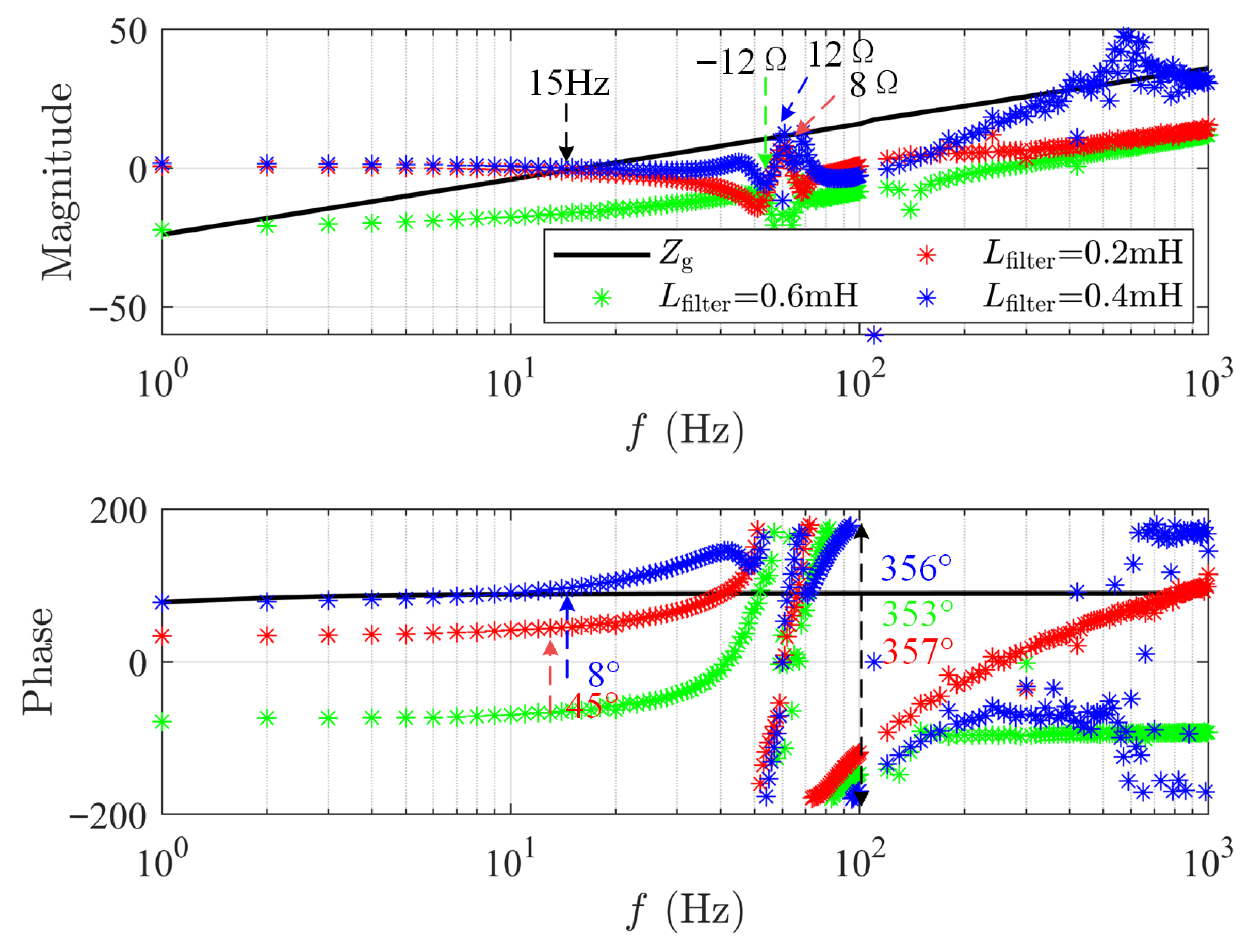
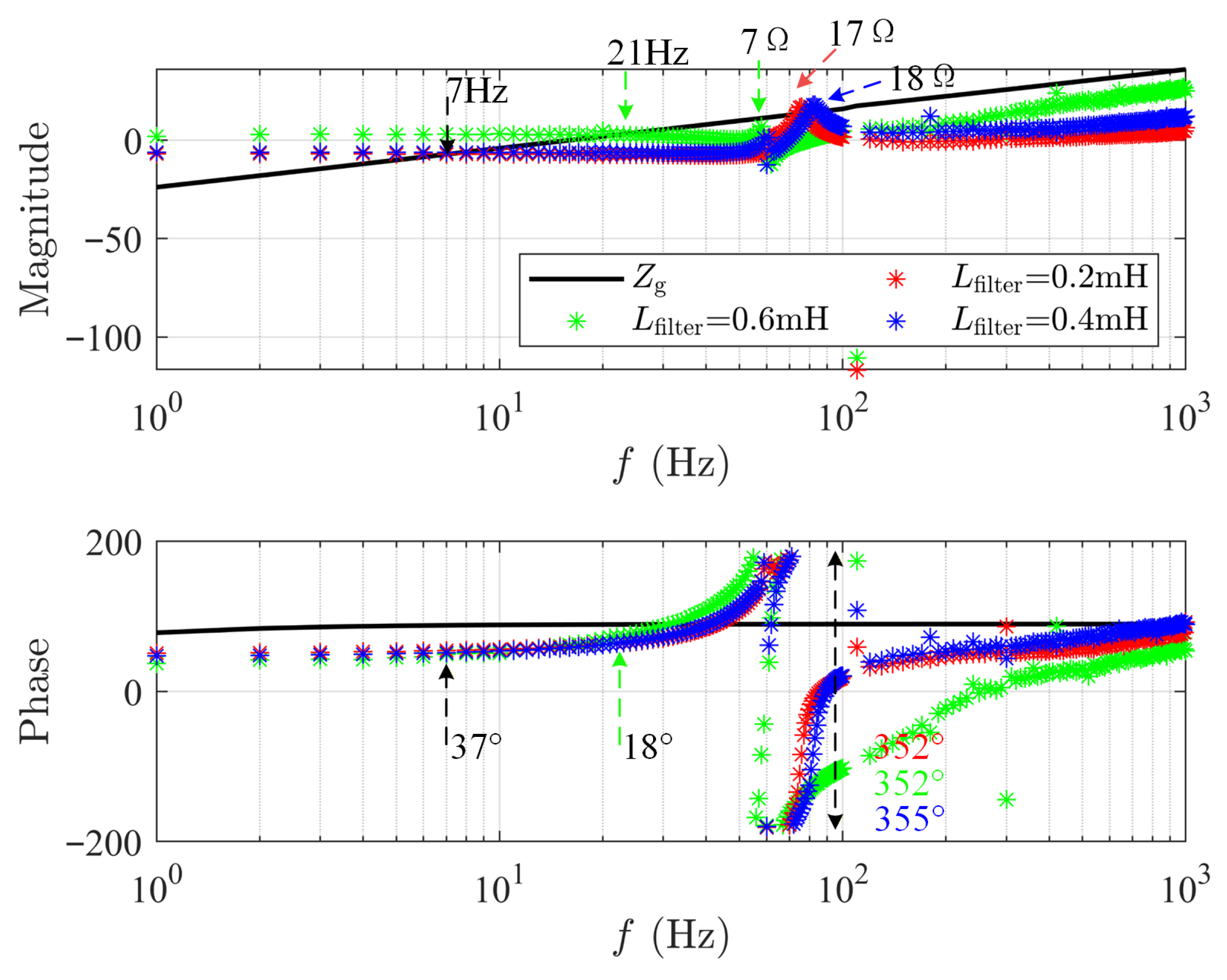
3.3. Parameter Optimization for Wind Power Generators

By frequency scanning, the bode diagrams of the impedance of the wind power generator and the external power grid are obtained as shown in Figure 10 and Figure 11. In Figure 10, the proportional coefficient $K_{\mathrm{pEDC}}$ of the PI controller of the DC link voltage control loop is changed, and different sets of bode diagrams are obtained for $Z_{\mathrm{s}}\left(s\right)$. According to the results, the crossover frequency is 16 Hz, $|Z_{\mathrm{s}}\left(s\right)|$ intersects with $|Z_{\mathrm{g}}\left(s\right)|$ and the phase difference of the case that $K_{\mathrm{pEDC}}=1$ is 12°, which is smaller that the other two cases. The phase margin is the largest in $K_{\mathrm{pEDC}}=1$. At 60 Hz, the magnitude frequency curve shows amplitude gain of the case in which $K_{\mathrm{pEDC}}=1$ is the smallest, which indicates that the oscillation shoot is the smallest when $K_{\mathrm{pEDC}}=1$. Therefore, the proportional coefficient of the DC link voltage control loop should be chosen as $K_{\mathrm{pEDC}}=1$.

In Figure 11, the variations of magnitude and phase frequency characteristics with respect to different filter inductances are illustrated. According to the results, the crossover frequency is 15 Hz for the case when $L_{\mathrm{filter}}=0.2$ mH and $L_{\mathrm{filter}}=0.4$ mH, and the phase difference are 45° and 8°, respectively. However, in the low frequency range, there is no crossover frequency between $|Z_{\mathrm{s}}\left(s\right)|$ and $|Z_{\mathrm{g}}\left(s\right)|$ when $L_{\mathrm{filter}}=0.6$ mH, which indicates that there is no oscillation risk in the low frequency range and the phase margin is the largest when $L_{\mathrm{filter}}=0.6$ mH. Additionally, the amplitude gain is the smallest at the resonant frequency (60 Hz) when $L_{\mathrm{filter}}$ is $0.6$ mH. As for the phase shift at the resonant frequency, the phase shift value is also the smallest when $L_{\mathrm{filter}}$ is $0.6$ mH. According to the above, $L_{\mathrm{filter}}=0.6$ mH is selected for the wind power generators.

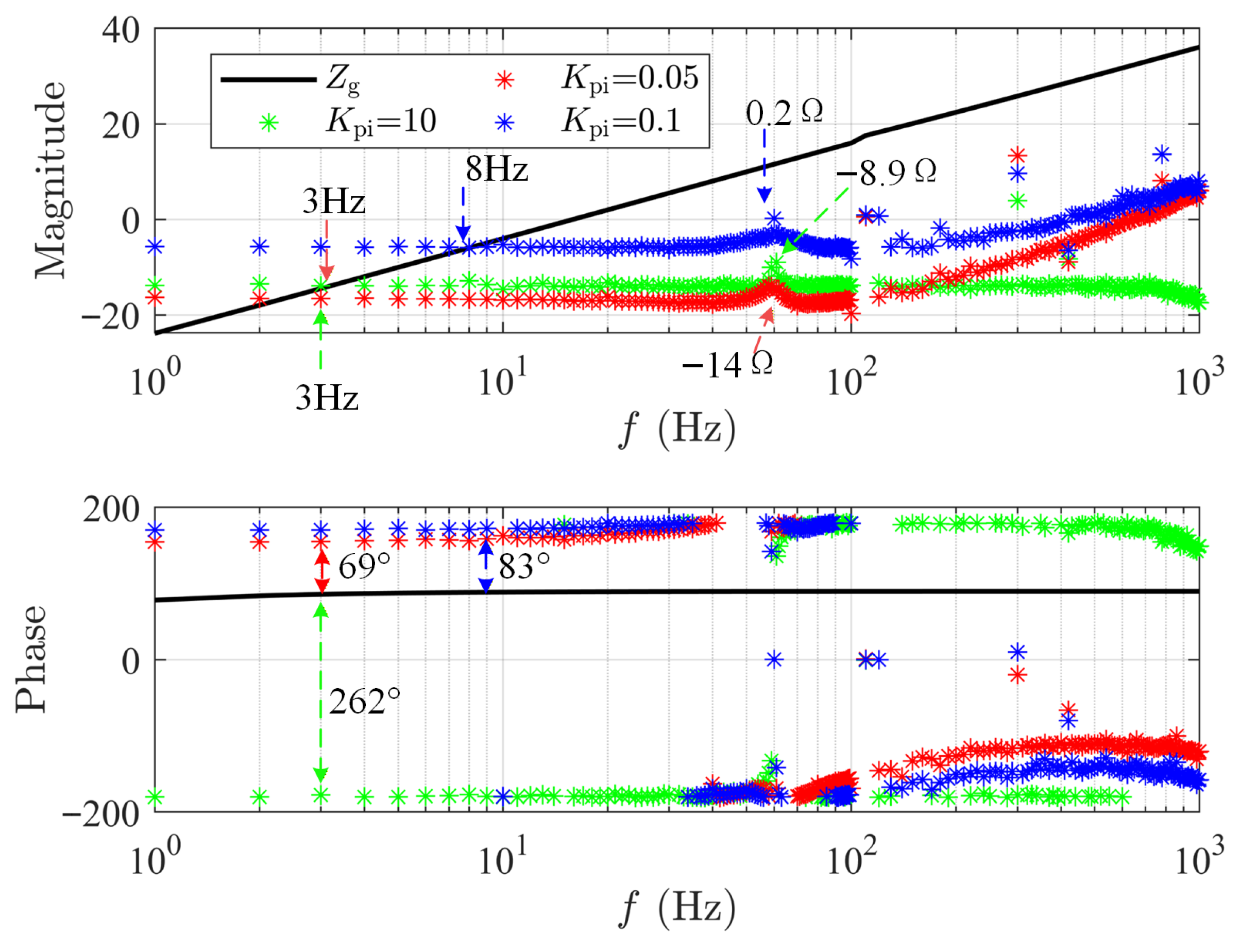
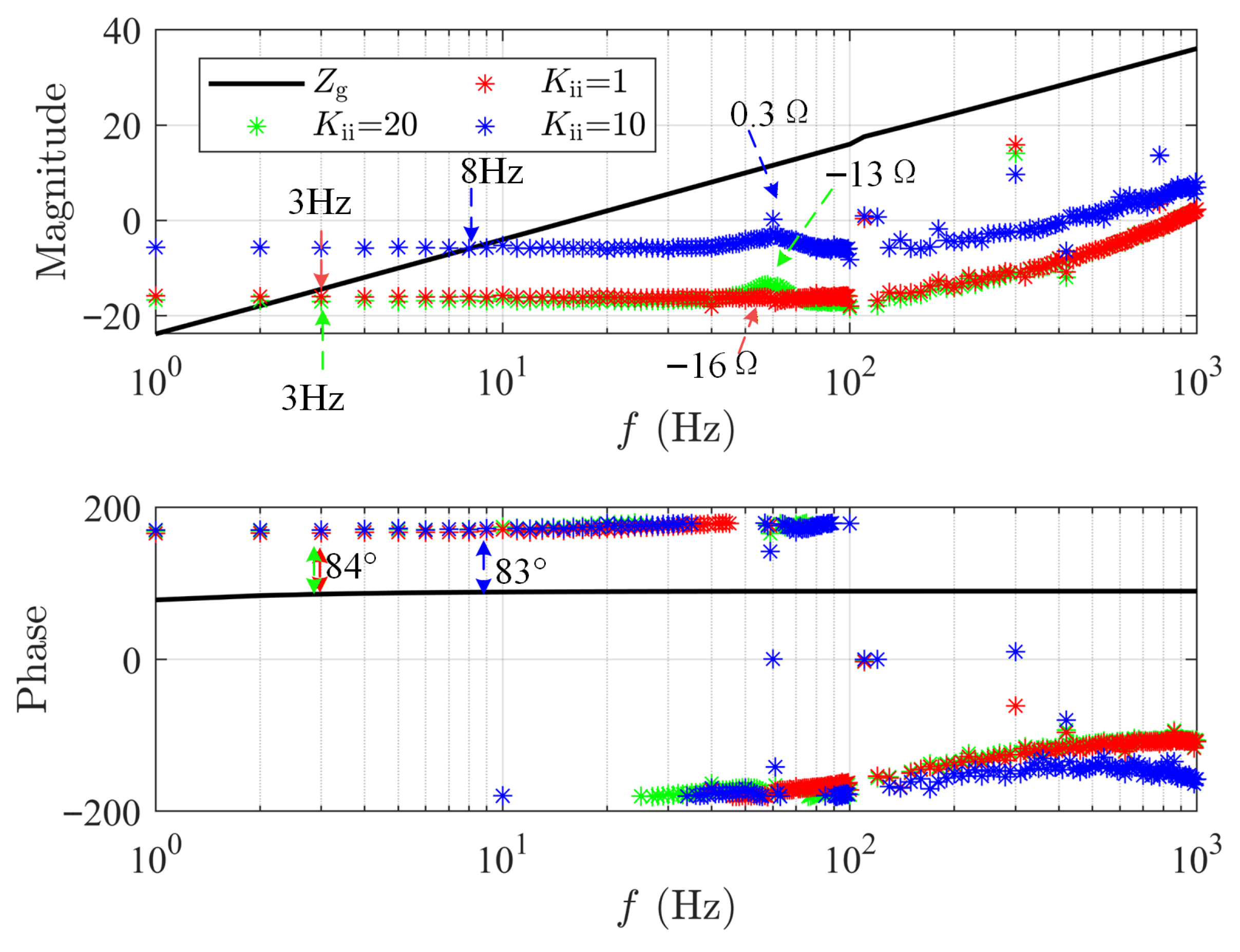
3.4. Parameter Optimization for Hydrogen Production Loads

The bode diagrams of $Z_{\mathrm{g}}\left(s\right)$ and $Z_{\mathrm{s}}\left(s\right)$ of the hydrogen production load when the proportional coefficient of the active power control loop changed are obtained by frequency scanning, as shown in Figure 12. The first crossover frequency between $Z_{\mathrm{g}}\left(s\right)$ and $Z_{\mathrm{s}}\left(g\right)$ of the hydrogen generation system is 8 Hz in the three cases concerned. At the crossover frequency, the phase differences are 34°, 29° and 41° when $K_{\mathrm{pP}}$ = 1, 0.5, 2, respectively. Meanwhile, the amplitude gains are almost the same. However, the phase shift value at the resonant frequency is 140° when $K_{\mathrm{pP}}=2$, which is significantly smaller than the other two cases. It indicates that the phase margin is the biggest when $K_{\mathrm{pP}}=2$. Therefore, the proportional coefficient of the active power control loop should be selected as $K_{\mathrm{pP}}=2$.

As shown in Figure 13, when the integral coefficient of the active power control loop of the converter of the hydrogen production load is changed, the bode diagrams of $Z_{\mathrm{g}}\left(s\right)$ and $Z_{\mathrm{s}}\left(s\right)$ are nearly identical when $K_{\mathrm{iP}}$ is chosen as 1, 20, and 30. The crossover frequency is 8 Hz, and the phase differences are all 35°. As for the amplitude gain at the resonant frequency, the values are 14, 14, and 18 when $K_{\mathrm{iP}}$ is chosen as a different value. Additionally, the phase shift values are the same at the resonant frequency. Hence, we know that the integral coefficient is not sensitive and can be chosen according to the large-disturbance performance of the system, which needs to be carried out by electromagnetic transient simulations. The integral gain $K_{\mathrm{iP}}$ in the outer active power control loop exhibits limited sensitivity primarily due to its deliberate low-bandwidth design and the cascaded control structure. The power loop’s dynamics are heavily constrained by the much faster inner current loop, which dominates the overall system response. As a result, while $K_{\mathrm{iP}}$ is essential for eliminating steady-state error, its tuning has a minimal impact on key dynamic performance and stability metrics compared to other parameters like the inner loop gains or the outer loop’s proportional gain.

The impact of filter inductance of the DC/AC converter of the hydrogen production load is shown by Figure 14. The crossover frequency is 7 Hz when $L_{\mathrm{filter}}$ are 0.2 mH and 0.4 mH, and the phase differences are the same 37° at this frequency. However, the crossover frequency is 21 Hz when $L_{\mathrm{filter}}=0.6$ mH, and the phase difference is 18°, which indicates that the system has the higher phase margin in this case. At the same time, the amplitude gain is the smallest at the resonant frequency, which indicates that the system has the bigger gain margin in this case. The phase shift values are closely the same. Thus, the system has higher phase margin and gain margin when $L_{\mathrm{filter}}=0.6$ mH. Hence, for the purpose of damping of resonances, this choice of filter inductance would offer strong damping for low-frequency and sub-synchronous oscillations. In comparison, the case where $L_{\mathrm{filter}}=0.6$ mH is selected and thus has the best small-signal stability property.

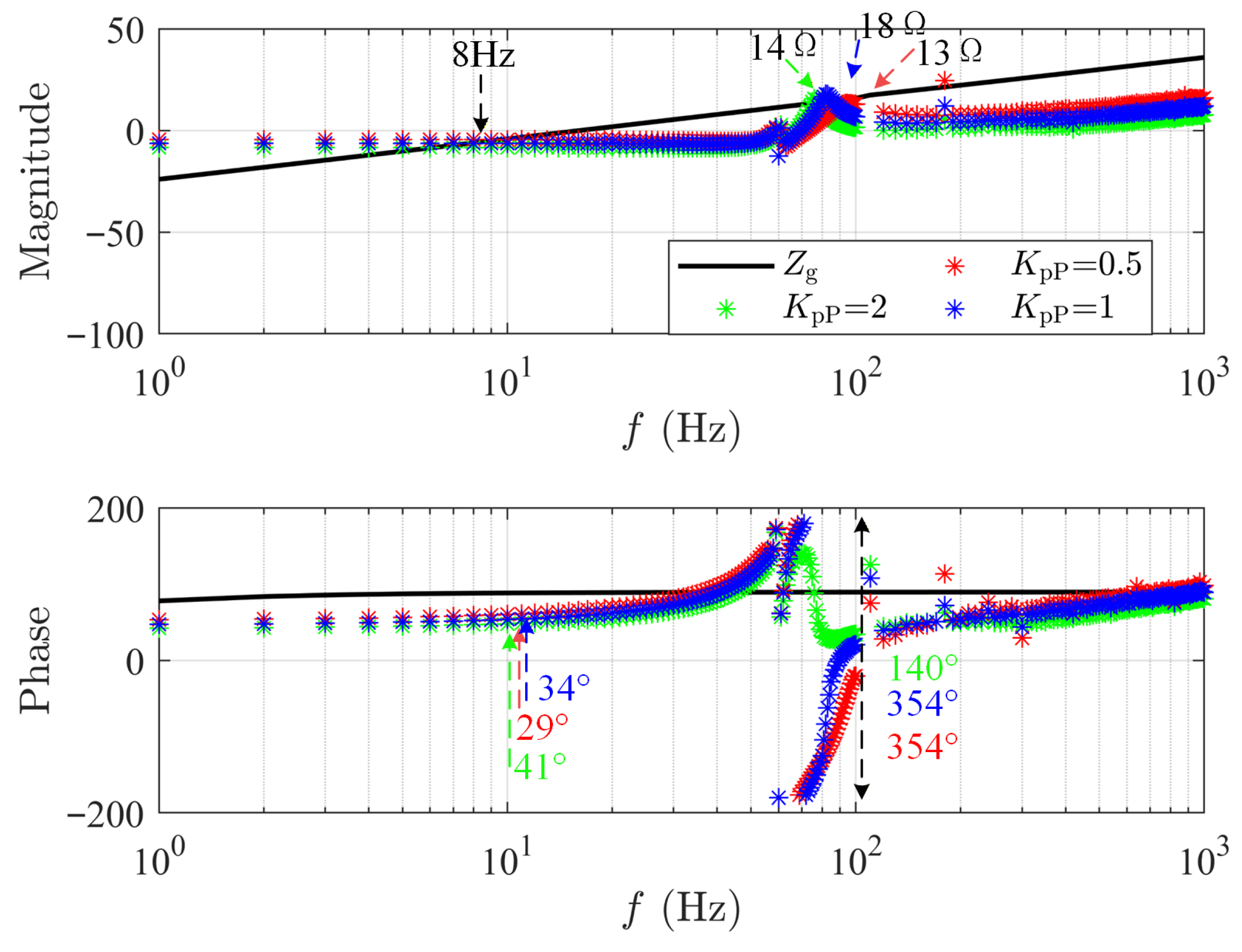
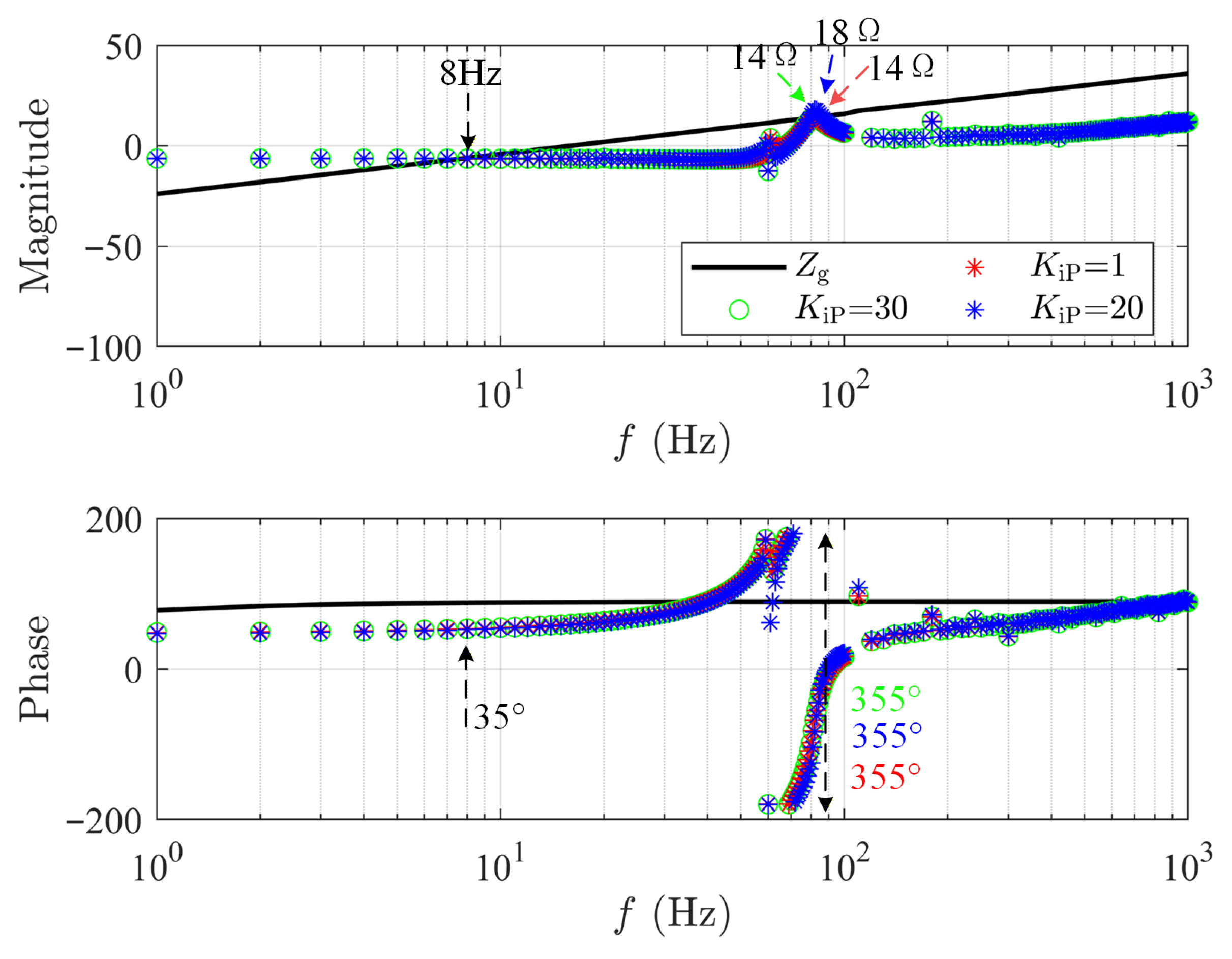
3.5. Parameter Optimization for Battery Energy Storage Stations

In the battery energy storage-based grid-forming strategy, the battery energy storage employs the V/f control scheme. In Figure 15, the bode diagrams of $Z_{\mathrm{g}}\left(s\right)$ and $Z_{\mathrm{s}}\left(s\right)$ with respect to the changes of the proportional coefficient $K_{\mathrm{pV}}$ of the voltage control loop are given. According to the results, the crossover frequencies are 11 Hz and 8 Hz when $K_{\mathrm{pV}}$ is 0.05 and 0.5. At the crossover frequency, the phase differences are 84° and 83°, which indicates that the energy system has the same phase margin in these two cases. However, there is no crossover frequency when $K_{\mathrm{pV}}$ is 5. At the same time, the gain amplitude is desired to be smaller and thus $K_{\mathrm{pV}}=5$ is chosen.

With respect to the proportional coefficient $K_{\mathrm{pi}}$ of the current control loop, the bode diagrams of $Z_{\mathrm{g}}\left(s\right)$ and $Z_{\mathrm{s}}\left(s\right)$ are given in Figure 16. It can be observed that the crossover frequencies are 3 Hz, 8 Hz, and 3 Hz when the $K_{\mathrm{pi}}$ is 0.05, 0.1, and 10, respectively. Thus, the phase differences are 69°, 83°, and 262°, which indicates that the system has the larger phase margin in the case of $K_{\mathrm{pi}}=0.05$. Simultaneously, the amplitude gain values at the resonant frequency are −14, −8.9, and 0.2. Thus, the system with $K_{\mathrm{pi}}=0.05$ has the larger gain margin. Therefore, $K_{\mathrm{pi}}=0.05$ is selected and the system has the largest small-signal stability margin.

The bode diagrams of $Z_{\mathrm{g}}\left(s\right)$ and $Z_{\mathrm{s}}\left(s\right)$ considering the variations of the integral gain $K_{\mathrm{ii}}$ of the PI controller of the current control loop are as presented in Figure 17. As can be seen, the crossover frequencies are 3 Hz, 8 Hz, and 3 Hz when the $K_{\mathrm{ii}}$ is 1, 10, and 20, respectively. Accordingly, the phase differences are 84°, 83°, and 84°, which shows that the systems in these three cases have the same phase margin. At the resonant frequency 60 Hz, the amplitude gain values are −16, 0.3, and −13; thus, the system has smaller amplitude shoot at the resonant frequency when $K_{\mathrm{ii}}$ is 1. Hence, $K_{\mathrm{ii}}=1$ is chosen.

Optimal controller parameters are also designed for other grid components of the system studied based on impedance analysis. The results will not be given here since the methodology used is similar. Moreover, the impedance stability analysis method is suitable for small-signal analysis using guiding parameter design and suppressing harmonics, and large disturbances require electromagnetic transient simulation. In the following, the performance of the two kinds of grid-forming strategies will be investigated under various operating conditions through electromagnetic transient simulations.

4. Results

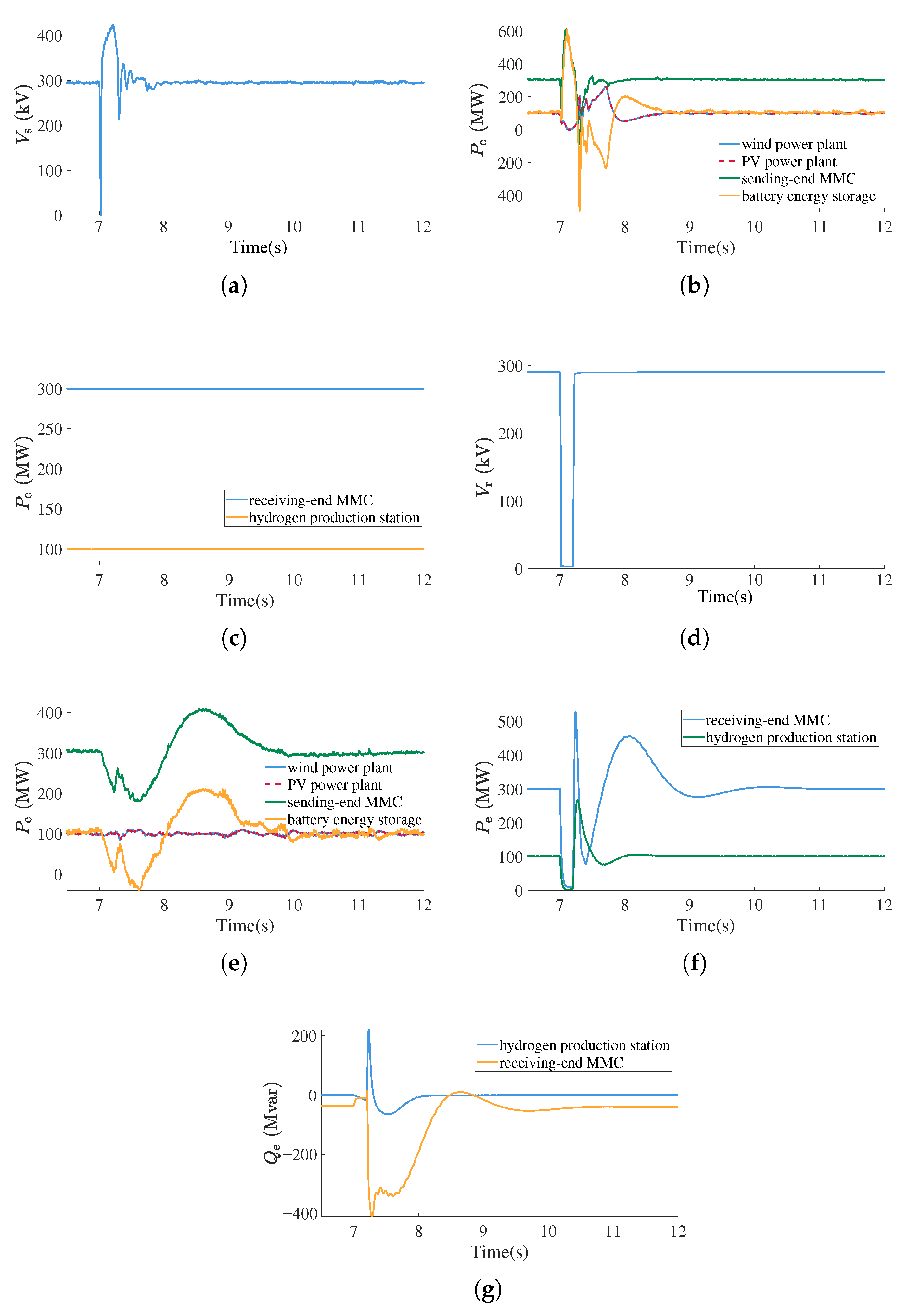
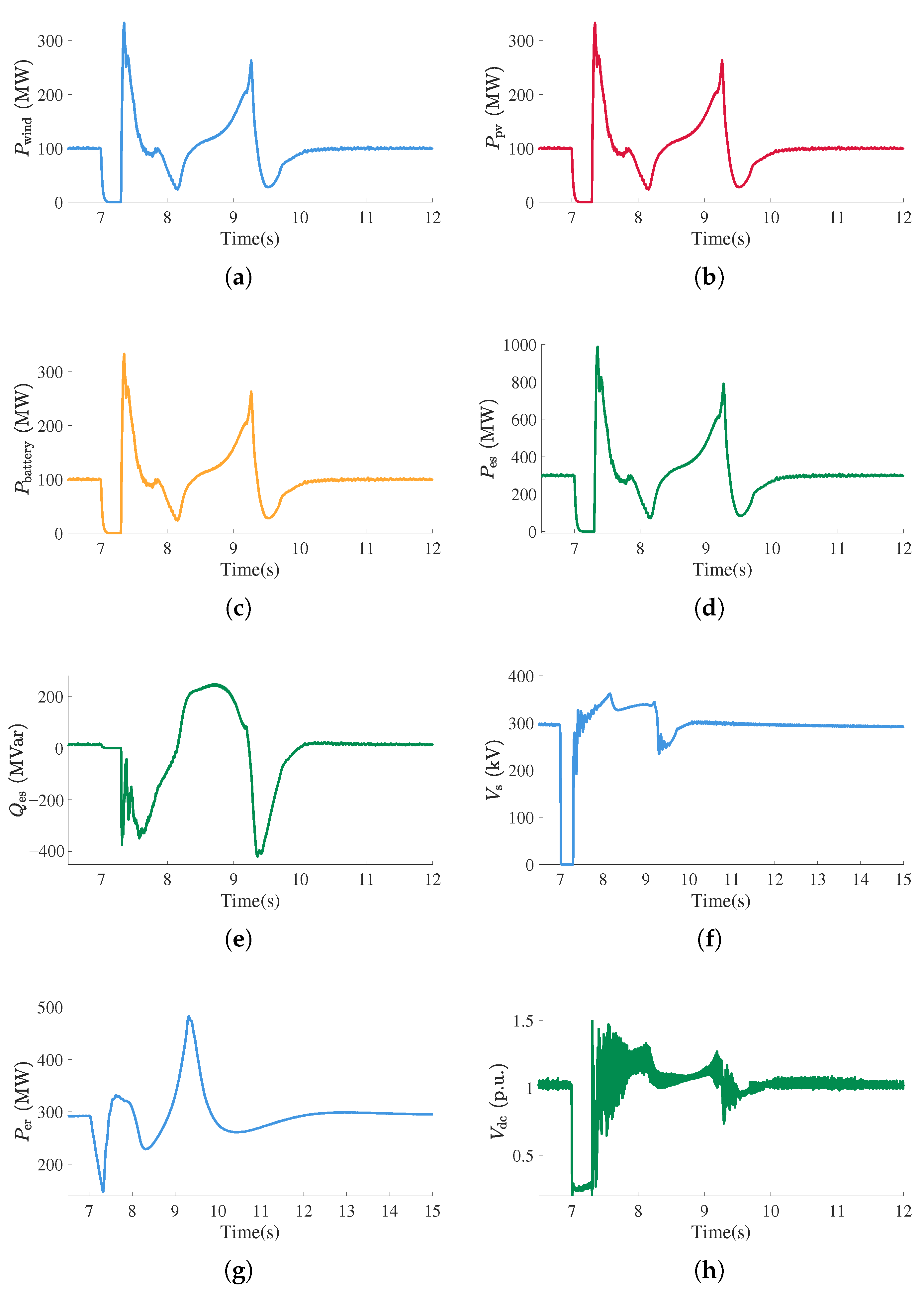
4.1. Transient Dynamics of Battery Energy Storage-Based Grid-Forming Strategy

The system shown in Figure 1 is configured with the battery energy storage-based grid-forming strategy in this subsection. In steady-state, the wind power plant, PV power plant, and the battery energy storage station generate 100 MW active power, respectively. The MMC-HVDC link transfers 300 MW to the load center. The hydrogen production load consumes 100 MW active power, and the AC power grid absorbs 200 MW. The simulation stepsize is set as 20 µs, and the GFortran 4.6.2 solver is selected. The detailed MMC submodule model is chosen, in which the number of submodules is 144 per phase. The control delay is set as 0.05 s. The frequency-dependent cable model is adopted. The transformer model in PSCAD is based on the classical modeling approach. The parameters of the main circuit are given in

Table 3. Parameters of the main circuit.

Parameter	Value	Parameter	Value	Parameter	Value
resistance/km	0.18 $\Omega$	inductance/km	8$\times {10}^{-7}$ H	capacitance/km	10 $\times {10}^{-6}$ F
$S_{\mathrm{wind}}$	400 MVA	$S_{\mathrm{pv}}$	400 MVA	$S_{\mathrm{battery}}$	400 MVA

. The parameters of the MMC-HVDC link as set as given in

Table 4. Parameters of the MMC-HVDC link with the sending-end and the receiving-end MMCs controlled in grid-following mode.

Parameter	Value	Parameter	Value	Parameter	Value
base MVA	1000 MVA	arm resistance	0.3 $\Omega$	arm inductance	0.24 H
filter resistance	0.46 $\Omega$	filter inductance	0.064 H	submodule number	264
rated frequency	60 Hz	rated AC voltage	290 kV	rated DC voltage	500 kV
PI outer loop	2, 1	PI inner loop	0.9, 0.05

.

In the first case, a 0.02 s three-phase-to-ground fault is applied on the 290 kV bus of the sending-end system. The fault duration of 0.02 s represents the response time of common instantaneous protection. The results obtained using PSCAD is as shown in Figure 18a–c. Due the short AC grid fault, the voltage of the sending-end 290 kV bus drops and presents an overshot as soon as it is cleared, as presented in Figure 18a. Consequently, the active power output of the wind power plant, PV power plant, battery energy storage station, and that absorbed by the sending-end MMC station present a drop first and an overshot thereafter. Moreover, the active power present negative surge after the overshot is recovered as shown in Figure 18b, and it is caused by the oscillation of the AC bus voltage. However, the receiving-end MMC station and the hydrogen production load are not affected by the sending-end fault, as can be observed from the active power given in Figure 18c. The system can recover to the stable state in 0.02 s fault, but becomes instable when the fault clearing time larger than 0.02 s.

In the second case, a 0.2 s three-phase-to-ground fault is applied on the 33 kV AC bus of the receiving-end system. The fault duration of 0.2 s denotes response time of the backup protection. The RMS value of the fault bus voltage is as shown in Figure 18d, and the voltage drops to zero during the fault. The active power output of the receiving-end MMC station and the active power consumed by the hydrogen production load drop to zero accordingly, as presented by Figure 18f. In order to compensate the AC voltage drop, the reactive power output of the receiving-end MMC station boosts as shown in Figure 18g. The active power of power sources and the sending-end MMC station is given in Figure 18e, and it can be seen that only the battery energy storage station controlled in V/f mode is impacted and a 2 s’ fluctuation is observed.

4.2. Transient Dynamics of MMC-HVDC-Based Grid-Forming Strategy

The system shown in Figure 1 is configured with the MMC-HVDC-based grid-forming strategy in this subsection. The steady-state power flow of the system is as follows. The wind power plant, PV power plant, and the battery energy storage station output 100 MW active power, respectively. The MMC-HVDC link transfers 300 MW active power to the load center, and the hydrogen production load consumes 100 MW power and the other 200 MW is transferred to the external AC power grid. The parameters of the MMC-HVDC link are given in

Table 5. Parameters of the MMC-HVDC link with the sending-end MMC controlled by VSG and the receiving-end MMC controlled in grid-following mode.

Parameter	Value	Parameter	Value	Parameter	Value
base MVA	1000 MVA	arm resistance	0.3 $\Omega$	arm inductance	0.24 H
filter resistance	0.46 $\Omega$	filter inductance	0.064 H	submodule number	264
rated frequency	60 Hz	rated AC voltage	290 kV	rated DC voltage	500 kV
PI outer loop	2, 1	PI inner loop	0.9, 0.05	D	0.5
virtual inertia	2 s	$P_{\mathrm{es}}^{\ast }$	−0.3 p.u.

.

A 0.06 s three-phase-to-ground fault is applied on the 290 kV bus of the sending-end system. The fault duration of 0.06 s denotes the typical primary protection clearing time. Due to the fault, the RMS value of the fault bus drops to zero, as shown in Figure 19f. Correspondingly, the active power output of the wind power plant, PV power plant, and battery energy storage station drops to zero as well since they share the same high voltage bus, as illustrated in Figure 19a–c. It also agrees with the active power output formula of an AC transmission line, i.e., $P_{\mathrm{e}}=V_1{V}_{2}sin\left(\delta \right)/X$.

During the fault process, the power angle $\mathsf{\Delta }\delta$ generated by the VSG of the sending-end MMC increases continuously due to the imbalance between $P_{\mathrm{es}}$ and $P_{\mathrm{es}}^{\ast }$, and a larger value of $\mathsf{\Delta }\delta$ is reached when the fault is cleared. This further leads to the active power absorbed by the sending-end MMC surging to about 1000 MW, and an over 200 MW active power increase is generated by the wind power plant, PV power plant, and battery energy storage station, respectively. Oscillations of the virtual power angle of the VSG result in the oscillations of the active power transferred by the MMC-HVDC link, as can be seen from the waveforms of the active power.

The significant active power overshoot observed immediately after fault clearance in Figure 19 is a direct consequence of the interaction between the energy dynamics of the MMC submodule capacitors and the inertial angle swing of the VSG control. In the first place, the converter’s AC-side voltage collapses, drastically reducing the power transfer capability during the grid fault. The energy stored in the MMC’s submodule capacitors is partially discharged to support the internal arm currents and any residual power flow. This creates a capacitor energy deficit relative to the pre-fault operating point. Concurrently, the VSG control’s virtual rotor equation integrates the imbalance between the mechanical power reference (set by the power loop) and the drastically reduced electrical output power during the fault. This integration causes the VSG power angle to advance or “swing forward” significantly, storing kinetic energy in the virtual rotor. Upon fault clearance, the grid voltage is restored. The advanced VSG power angle now represents a large angular difference with the grid, creating a potent driving force for power transfer. The converter immediately begins to inject a large current to restore the submodule capacitor energy to its nominal level and deliver the “pent-up” power corresponding to the advanced VSG angle, as the virtual rotor begins to decelerate back toward a steady-state angle.

The reactive power absorbed by the sending-end MMC is shown in Figure 19e. As can be observed, the VSG generates reactive power to the renewable energy base to boost the AC bus voltage. Overshot of the reactive power has led to the overshot of the AC bus voltage as well during the period from 7.5 s to 9.5 s. In spite of the large disturbance on the sending-end system, the DC bus voltage and the receiving-end power of the MMC-HVDC link remain stable, as presented in Figure 19g,h. Hence, the MMC-HVDC-based grid-forming strategy shows a great stability margin and is able to endure more severe external faults and disturbances.

5. Discussion

According to the simulation results, the comparison of the dynamic responses of the two system is presented in

Table 6. Comparison of the dynamic responses of the two systems.

Dynamic Response	Battery Energy Storage-Based Grid-Forming Strategy	MMC-HVDC-Based Grid-Forming Strategy
Critical clearing time in sending-end station	0.02 s	0.3 s
Damping and inertia support	no	yes
Recovery time from fault and fault duration	0.02 s/2 s	0.3 s/4.7 s

. Faults on the AC subsystems have significant impact on the active power generation of power sources as well as the power transmission of MMC-HVDC links. Over voltage and fluctuations of voltage will occur when the fault is cleared, which is caused by the reactive power control loops in various controllers. Due to the external AC power source, the receiving-end subsystem is not impacted by the fault on the sending-end system. Most importantly, it has been found that the critical clearing time of the sending-end AC subsystem is 0.3 s when the MMC-HVDC-based grid-forming strategy is employed. The critical clearing time of the sending-end AC subsystem is 0.02 s when the battery energy storage-based grid-forming strategy is utilized. The critical clearing time reflects the transient stability margin of the system, and is mainly determined by the capacity of the grid-forming converter source as well as the location of the grid-forming power source. Compared with the V/f grid-forming strategy, the MMC-HVDC-based grid-forming strategy employed enables the system to have enough damping to recover to stable operation from longer fault duration. Furthermore, enhancing the inertia and damping ratio by multi-objective optimization algorithms is also a practical and feasible solution to enhance the stability margin [13].

The post-fault voltage overshoot is a direct consequence of the reactive power control dynamics. During the fault, the voltage dip triggers the reactive power controllers to inject maximum reactive current to support the grid. However, due to the amplitude limitation of the controllers and current limitation strategy of MMC, there is a lag in reducing the reactive current injection once the fault is cleared and the voltage recovers. This temporary oversupply of reactive power causes the voltage to rise above its nominal value. The magnitude of this overshoot is influenced by the controller gains and the available reactive current headroom, which is constrained by the MMC current limiting value.

Furthermore, as shown in Figure 19g,h, during the system recovery process, the dynamic response of the MMC DC link voltage is synchronized with the receiving-end active power. Thus, the robust DC link voltage of the MMC, maintained by the energy in its submodule capacitors, ensures that the active power balance is managed effectively during this transient, preventing DC link voltage collapse that could otherwise destabilize the system.

For future research, the grid-forming capability of MMC-HVDC under weak grid conditions is worth investigating, focusing on its synchronization stability, adaptive virtual impedance control, and black-start capability in networks with high impedance and low short-circuit ratio. Second, research on the impact of large-scale hydrogen electrolyzer loads on system stability is also a main part of future work. The core of this research lies in the synergistic analysis of the two elements above: developing integrated models to study how the fast, controllable power consumption of hydrogen loads can be strategically coordinated with MMC-HVDC’s grid-forming control.

6. Conclusions

This study proposed two grid-forming strategies for the remote hydrogen production station supplied by a wind–solar renewable energy base through an MMC-HVDC link. Both of the grid-forming strategies are able to realize the stable operation of the system, but they have different transient stability margins. It was verified that the MMC-HVDC-based grid-forming strategy is able to provide longer critical clearing time for the system, which indicates the stronger transient stability of the system. The optimal controller and circuit design based on impedance analysis was also verified to be effective for the reliable start and steady-state operation of the system. In future studies, the fault current characteristics and the impact of grid strength can be a topic of research.