Investigations of Anomalies in Ship Movement During a Voyage

Abstract

This study proposes a method for identifying anomalous ship behavior using AIS data and prediction-error analysis based on a Long Short-Term Memory (LSTM) neural network. The approach compares predicted and observed positions, courses, and speeds to detect significant deviations indicative of abnormal maneuvers, route changes, or intentional AIS manipulation. A trajectory prediction model was trained on historical AIS streams and evaluated using independent test vessels. Quantitative criteria and threshold values for anomaly detection were derived from navigational standards, AIS accuracy characteristics, and empirical sensitivity analysis. The method was validated on voyages between the North Sea and the Baltic Sea, demonstrating its capability to highlight potentially unsafe or suspicious vessel behavior. The results show that combining machine-learning-based prediction and multi-parameter deviation analysis can improve automated maritime surveillance and support operational decision-making.

1. Introduction

In recent years, two phenomena have been observed in maritime economic activity: the further development of shipping and the ongoing industrialization of the seas. There has been a dynamic development of the offshore industry, particularly in the exploration and exploitation of mineral and energy resources, as well as in the implementation of large-scale renewable energy projects such as offshore wind farms. These activities are accompanied by the expansion of essential operational infrastructure, power supply lines and stations, transmission lines, and monitoring means and infrastructure required for their operation. The infrastructure necessary for the long-distance transmission and transport of raw materials, energy, and information is located both on the sea surface and on the seabed. At the same time, shipping activity—involving the transport of goods, passengers, and other services by the commercial fleet—has remained high and continues to grow.

The freedom to choose a sea route for a vessel is becoming increasingly restricted due to the presence or proximity of offshore infrastructure. In areas with high traffic density, traffic separation schemes and recommended shipping routes are established to ensure safety and navigational efficiency. The possibility of free anchoring is also becoming more limited. This situation is particularly evident in the Baltic Sea, which is entirely classified as a sensitive area. The likelihood of ship–infrastructure collisions is increasing, and incidents of both unintentional and intentional damage have already been reported.

In most collision-related cases, vessels exhibit abnormal behavior compared to other ships in the area—for example, they alter course inexplicably (deviating from recommended routes), change speed without apparent navigational reasons (such as anticollision action), or come to a stop in unjustified locations and circumstances. Such behavior may also result from deliberate actions intended to damage hydrotechnical or communication structures like underwater cables, pipelines, etc., for example, by using ship anchors. Anchors can reach objects located hundreds of meters below the sea surface, posing a serious risk to underwater infrastructure. Therefore, it appears justified to identify and analyze vessel behaviors that deviate from standard operational patterns. Such deviations are defined by authors as anomalies.

In this study, a ship movement anomaly is defined as a measurable deviation between the predicted and observed ship motion parameters—position, course over ground (COG), and speed over ground (SOG)—that exceeds predefined operational thresholds and cannot be explained by typical maneuvering behavior or AIS noise. It can be identified based on the analysis of vessel movement, specifically through:

(1)

changes in speed, e.g., significant reduction or unexpected stopping;

(2)

changes in course;

(3)

deviations from recommended routes.

Variations in navigational parameters may result from the characteristics of the voyage or from operational causes. The operational reasons for such behaviors may include:

(1)

speed reduction for purposes such as:

• embarking or disembarking a pilot;
• executing a collision-avoidance action;
• maintaining a reduced speed under restricted visibility conditions;

(2)

deviation from the recommended route in order to:

• take on fuel (bunkering), receive supplies, or exchange crew;
• execute an anti-collision maneuver;
• intended action;
• due to propulsion failure;

(3)

deviation combined with speed reduction as a result of:

• equipment or engine failure;
• waiting for a pilot or port entry clearance.

The vessel traffic monitoring systems implemented in the Baltic Sea region and other maritime areas enable real-time or post-voyage analysis of ship movements. These analyses are based primarily on data recorded by the Automatic Identification System (AIS). In this system, ships continuously transmit dynamic voyage data such as geographic position, speed, and course, as well as static data describing the vessel’s characteristics. The installation and operation of AIS are regulated by international conventions and local national requirements.

Given the large number of ship voyages and the vast volume of transmitted and recorded data, there is a growing need for automated methods to identify non-standard vessel behaviors—both offline (post factum) and online (in real time, during the voyage).

1.1. Related Work—State of the Art

In recent years, the problem of monitoring vessel traffic has gained increasing importance. This is due both to the necessity of such monitoring and to the expanding capabilities for recording and subsequently analyzing vessel behavior based on historical data. At the same time, real-time vessel tracking technologies continue to advance rapidly. Research on vessel behavior analysis, anomaly detection, and trajectory prediction using AIS data has grown rapidly in recent years. Existing studies can be grouped into two main areas: detection of anomalous or suspicious movement patterns, and prediction of vessel trajectories using machine-learning or deep-learning models.

A method for predicting ship movements based on recurrent neural networks was presented by Copabianco et al. [1]. Other deep learning approaches for trajectory prediction and their applications were discussed in [2,3]. The use of various versions of the YOLO algorithm was described in [4,5,6]. A “cascade vector” tracking method was introduced by Liu et al. [7], while Zhang et al. proposed “A reliable unmanned aerial vehicle multi-ship tracking method” [8]. Innovative approaches to autonomous ship tracking were presented, respectively, by Shao et al., Damas et al., and Li et al. in [9,10,11]. Chen et al. [12] presented an adaptive FairMOT tracking method applicable to marine targets, and adaptive dynamic programming (ADP)-based control of course tracking was described in [13].

Coastal ship tracking techniques were proposed, among others, in An Enhanced SiamMask Network for Coastal Ship Tracking [14] and Coastal Ship Tracking with Memory-Guided Perceptual Network [15]. The modern architecture of satellite-based global ship tracking systems, networks, and devices (GST) was described by Ilcev [16]. Wu et al. [17] presented ESPO-Based Course-Tracking Control of Ships with Input Delay. Other ship tracking and detection methods were reported in [18,19,20,21].

The problem of ship trajectory extraction using interpolation was addressed by Setiawan et al. in the paper “Ship Trajectory Extraction Using Python Vessel Tracking Interpolation Method” [22]. Shao et al. [23] presented an approach for tracking moving ships using distributed acoustic sensing data. An early detection system for suspicious ship activities based on AIS data and official databases, employing a multi-criteria method, was proposed by Wielgosz and Małyszko [24].

Additionally, recent studies have begun to incorporate semantic information into prediction frameworks. Rakhmanov & Wiseman present a method for compressing GNSS data to accelerate communication with autonomous vehicles, improving the efficiency of navigation data transfer in real-time applications [25]. Zhang Y. et al. introduce a deep-learning trajectory prediction model that incorporates prior knowledge of collision risk, enhancing the accuracy and safety relevance of vessel movement forecasting in maritime IoT environments [26].

Zhang J. et al. propose an improved LSTM-based ship trajectory prediction model that enhances accuracy by optimizing temporal feature extraction from AIS data [27]. Raj & Kumar provide a comprehensive review of vessel trajectory prediction methods, summarizing traditional and deep-learning approaches and outlining current challenges and development trends [28].

Seong et al. developed a graph-based detection framework that captures structural relationships within AIS trajectories, demonstrating its effectiveness in identifying abnormal movements in dense maritime environments [29].

Alternative approaches focus on modeling behavior in confined ports and coastal waters. Li et al. proposed a method combining kernel density estimation and text-similarity-based movement description, enabling detection of deviations from expected local traffic patterns [30]. A broader overview of anomaly detection methodologies is provided by Wolsing et al., who compared clustering-based, density-based, and other unsupervised techniques applied to AIS streams [31].

More recently, Wen et al. introduced a hybrid data- and knowledge-driven framework for behavior analysis, including detection of sudden accelerations, decelerations, or maneuvers inconsistent with navigational norms [32]. In fishing-vessel monitoring, Rodríguez et al. demonstrated that trajectory-based anomaly indicators are transferable to other vessel classes and traffic regimes [33]. These studies highlight that atypical behavior may manifest through changes in speed profiles, heading variations, route deviations, or temporal inconsistencies in AIS messages.

Despite the progress in anomaly detection techniques, many existing solutions rely on pre-segmented trajectories, expert-defined behavioral rules, or unsupervised clustering, which may limit interpretability or operational deployment. Furthermore, the integration of predictive models for detecting deviations from expected movement patterns is still underexplored.

Trajectory-prediction models constitute the second major research direction. Hybrid graph-attentional and recurrent neural networks have been shown to improve the prediction accuracy by incorporating spatial relationships between vessels, as demonstrated by Li et al. [34]. Deep-learning approaches, including LSTM, GRU, and bidirectional variants, have been systematically evaluated by Evmides et al., highlighting the importance of sequence length and temporal dependencies in long-term prediction [35].

Zaman et al. compared CNN-, DNN-, LSTM-, and GRU-based architectures using large-scale AIS datasets, showing that recurrent models remain competitive for multi-step prediction in dynamic maritime environments [36]. Earlier foundational work by Tang et al. demonstrated the suitability of LSTM networks for vessel-trajectory forecasting and established a widely used modeling baseline [37].

Qiao et al. present an approach to anomaly detection and trajectory prediction using advanced spatio-temporal analysis techniques. In the context of our work, it serves as an important reference, as it demonstrates the significance of integrating vessel movement data with behavioral analysis [38]. Guo et al. apply a Sparse Bayesian Learning (SBL) approach for the simultaneous detection and reconstruction of moving objects in an acoustic environment. Although the context relates to sonar systems, the methodology of sparse learning and signal/interference separation can inspire analogous analyses of vessel trajectories and the detection of atypical movement [39].

1.2. Research Gap

Although numerous methods for trajectory prediction and anomaly detection exist, few studies combine both components into a unified, interpretable framework. Current predictive models rarely quantify deviations between predicted and actual motion in a way that can support operational anomaly assessment. Similarly, anomaly detection models seldom integrate multi-parameter (position, speed, course) prediction errors as quantitative indicators.

These gaps motivate the present work. To address these gaps, this study proposes a coherent anomaly identification approach based on differences between predicted and observed vessel states, supported by evaluation on real AIS trajectories for representative voyages.

Due to the increasing occurrence of non-standard vessel behaviors, the problem of their identification remains highly relevant. Existing identification methods are being improved, and new approaches are continuously sought. The authors propose a method for anomaly detection based on the analysis of differences between the actual and predicted ship speeds, courses, and positions. The predicted parameters are determined from previous values of these variables using artificial neural networks (ANNs).

In the following sections of the paper, Section 2 describes the data used in the analysis of ship movement processes, recorded via the AIS. The application of ANNs for predicting vessel motion parameters is proposed, along with the procedures for preparing training data and conducting the learning process. The scope of the research is also detailed.

Section 3 presents the anomaly identification process for a selected vessel voyage according to the proposed method, including the applied criteria and identification procedures.

Section 4 provides a case study illustrating the detection of different types of anomalies with their detailed analysis. A discussion of the results obtained is included, along with a comparison to other proposed anomaly identification methods and a summary of conclusions.

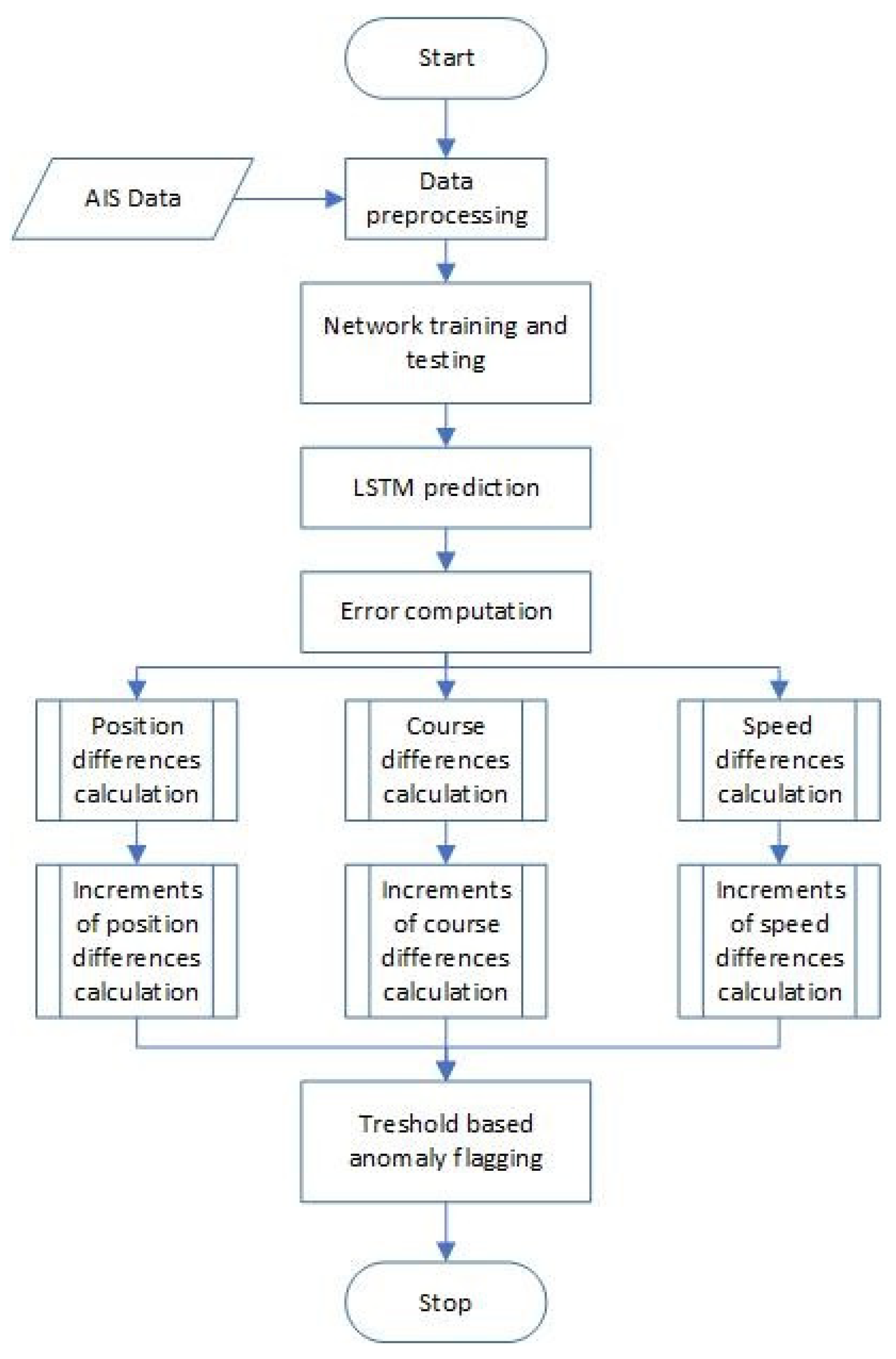
2. Materials and Methods

The following anomaly identification methodology, presented in Figure 1, was adopted.

The anomaly detection method consists of four stages:

(1)

AIS data preprocessing and temporal alignment;

(2)

Network training and testing;

(3)

LSTM-based trajectory prediction for the next timesteps;

(4)

Computation of prediction errors for position, COG, and SOG;

(5)

Threshold-based classification of anomalies.

2.1. AIS Data

The analysis was based on AIS (Automatic Identification System) data recorded and provided by the Danish Maritime Authority (DMA). The AIS is an automatic and autonomous radio communication system used in maritime navigation for the real-time exchange of vessel-related data in a standardized format. Since its mandatory implementation on ships under the SOLAS Convention, AIS has become a fundamental component of maritime safety and surveillance systems. It also plays a crucial role in maintaining situational awareness at sea.

In AIS, vessels regularly transmit both static data, which include ship information (e.g., vessel name, IMO number) and voyage details (e.g., destination port), as well as dynamic data, such as current position, draft, course, and speed. Based on AIS messages, it is possible to remotely identify ships, determine their current and historical movement trajectories, monitor vessel passages, predict future trajectories, and detect potential anomalies in vessel behavior. Such anomalies may be understood as deviations from planned routes or inconsistencies with the behavior of other vessels of the same type operating in the same area, as well as discrepancies between transmitted and actual data.

In this study, the analysis utilized AIS-transmitted data on ship size, position, course, and speed for the selected vessels.

2.2. LSTM-Based Trajectory Prediction Model

This subsection describes the recurrent neural network architecture used to generate short-term trajectory predictions from AIS-derived motion parameters. The model is based on a unidirectional LSTM with optimized hyperparameters obtained through validation experiments. Predicting the trajectories of maritime vessels is a critical aspect of navigation safety, logistics, and collision avoidance. The Automatic Identification System (AIS) provides a valuable source of sequential data, broadcasting vessel positions, speeds, and courses at regular time intervals. These spatiotemporal patterns make AIS data an ideal foundation for data-driven modeling approaches, particularly those grounded in time series analysis.

To address the temporal dependencies and sequential nature of AIS data, this study employs a Long Short-Term Memory (LSTM) neural network. LSTM is a type of recurrent neural network (RNN) that effectively mitigates the vanishing gradient problem, enabling the learning of long-term temporal dependencies [40,41]. Its architecture incorporates memory cells and gating mechanisms that capture nonlinear temporal relationships, making it particularly suitable for trajectory forecasting tasks, where past vessel behavior strongly informs future movement [1,42].

2.2.1. Data Preparation and Feature Construction

The dataset used in this study consists of records collected from six maritime scenarios stored in mat files. Each entry contains timestamped information, including latitude, longitude, speed over ground (SOG), course over ground (COG), and vessel identifiers (MMSI). During preprocessing, all records with missing or incomplete entries were removed. The data were then grouped by unique vessel ID to construct complete trajectory sequences.

To ensure temporal consistency, each trajectory was uniformly resampled at four different intervals: 5, 10, 15, and 20 min. This was achieved by down-sampling the data arrays at fixed index steps (e.g., every 25th or 50th record), reflecting realistic reporting frequencies under various operational conditions. Each geographical trajectory was projected onto a local Cartesian coordinate system using a first-order approximation of the Earth’s curvature, enabling the calculation of Euclidean displacements between consecutive points.

The next step involved constructing input–output pairs suitable for supervised learning. For each vessel trajectory, a sliding window of fixed length (typically four time steps) was moved along the data to generate a set of training sequences. Each sequence consisted of displacement vectors and trigonometric encodings of the course and vessel speed. The corresponding prediction target was defined as the next-step displacement and change in course and speed. Consequently, the resulting dataset encapsulated dynamic motion trends and directional information in a format suitable for temporal modeling. Separate test vessels were excluded from training and used exclusively for evaluation, ensuring that model generalization was assessed on previously unseen trajectories.

2.2.2. LSTM Model Architecture and Training

The predictive model employed in this study was a unidirectional LSTM network implemented using MATLAB’s Deep Learning Toolbox (Matlab 2024b). The architecture consisted of three primary layers: a sequence input layer receiving five-dimensional feature vectors, an LSTM hidden layer with 64 units, and a fully connected output layer mapping the LSTM state to a five-dimensional regression output. The network concluded with a standard regression layer minimizing the mean squared error (MSE) between predictions and true values.

Training was performed using the Adam optimizer over 100 epochs with a mini-batch size of 64 samples. The data were shuffled at each epoch to prevent overfitting temporal patterns within individual trajectories. The network was trained on all sequences derived from the training vessels and validated through inference on the test vessel trajectories. The five predicted outputs from the network corresponded to the displacement vector (Δx, Δy), COG described with directional components cos(COG) and sin(COG), and the change in speed over ground. These outputs were subsequently decoded into geographic coordinates, courses, and speed values during the post-processing stage.

To investigate the impact of temporal resolution on model structure and learning dynamics, the LSTM network was implemented in four variants, differing only in input sampling frequency: every 5, 10, 15, or 20 min. These sampling intervals directly influenced the data volume and temporal granularity, which in turn affected the network’s learning potential and representational capacity. Despite identical architectures, the input data distributions varied considerably across variants. At higher sampling frequencies, vessel trajectories exhibited finer temporal resolution, resulting in smoother motion vectors and denser training sequences. Conversely, at lower frequencies, the sequences were shorter and captured coarser motion trends. This difference directly translates into variations in the number of training samples.

The network’s sliding window mechanism remained fixed across all variants, typically using a window of four consecutive time steps to forecast the subsequent step. However, as the real-time duration represented by each time step increased with lower sampling frequencies, the effective prediction horizon also extended. For instance, the 5 min model predicted vessel dynamics 5 min ahead, whereas the 20 min model projected movements 20 min into the future. This extended horizon introduced greater uncertainty and nonlinearity, placing higher demands on the LSTM’s memory and generalization capabilities. The feature set also exhibited different statistical characteristics across sampling frequencies: at shorter intervals, displacement vectors (Δx, Δy) and speed changes tended to be smaller and more stable, while at longer intervals, greater variance and abrupt changes were observed. Despite these differences, the same model architecture was retained to ensure comparability across all experiments.

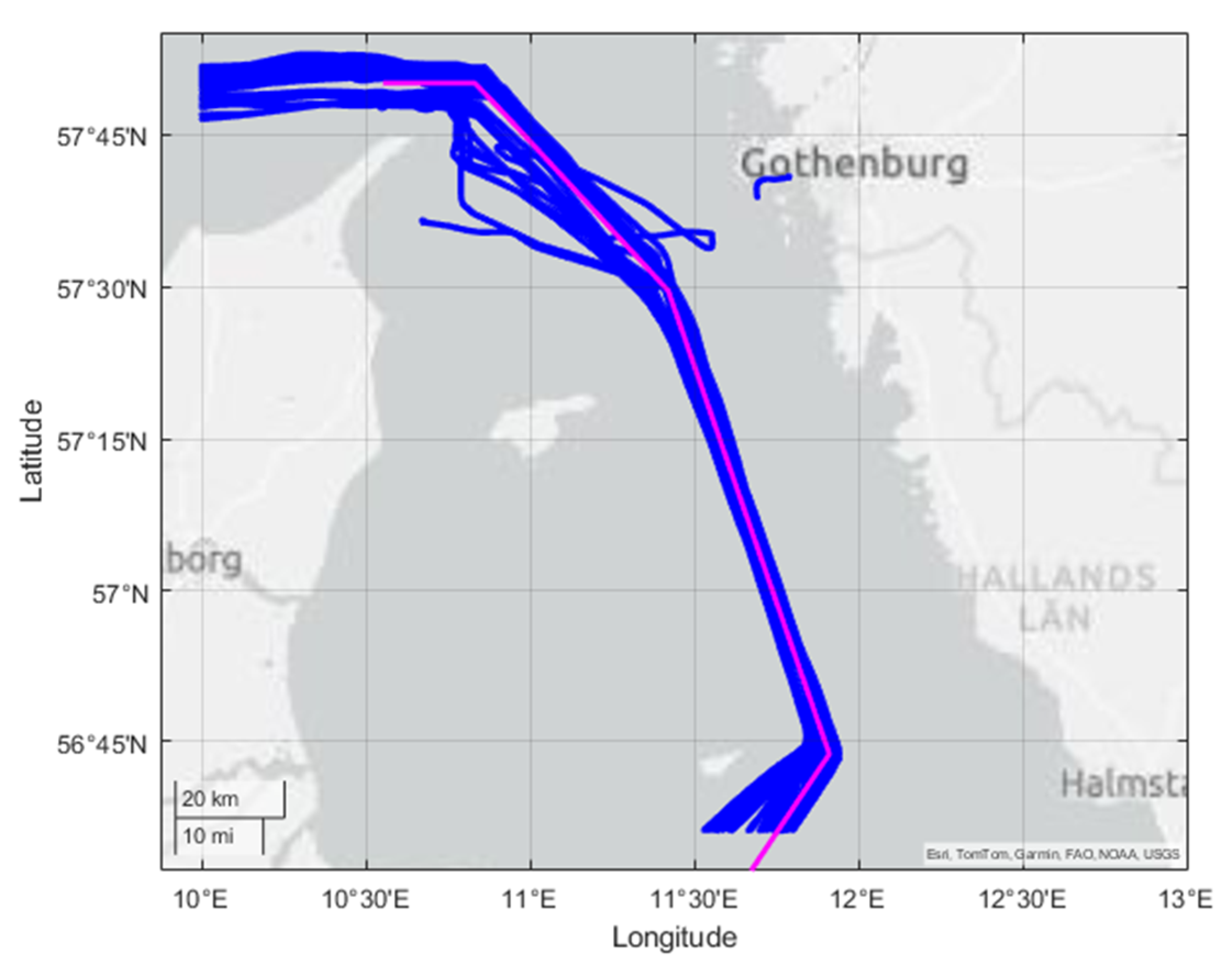
2.3. Area of Research

The study was conducted in the Danish Straits, including the Kattegat, Skagerrak, Great Belt, Langeland Belt, and the Sound (Øresund), as well as the adjacent waters (Figure 2).

2.4. Data Preparation and Selection

The analysis included vessels in transit navigating along designated and recommended routes, as obtained from AIS:

• Route T and DW (Deep Water Route) via the Kattegat, Skagerrak, Great Belt, and Langeland Belt, with a minimum draft of 12 m (maximum approximately 15 m);
• Route H, with a draft of up to 10 m;
• Route S, with a draft of up to 7.7 m.

The dataset used for the analysis consisted of AIS records collected over seven consecutive days in November 2024.

Figure 3 presents the AIS-recorded vessel tracks (blue points) of ships of all sizes within the selected study area for this article study area (Section Belt 1), with the recommended deep-water Route T marked in magenta.

Table 1. Stage I of pre-processing-decoded messages.

Time	MMSI	Latitude	Longitude	Status	SOG [kn]	COG [deg]	Type	Length [m]	Draught [m]
02:26:20	372713xxx	55.54523	5.392	0	8.9	12.5	70	290	10.7
02:26:30	372713xxx	55.54487	5.392	0	8.8	13	70	290	10.7
02:32:00	372713xxx	55.55922	5.39235	0	8.9	12	70	290	10.7
02:32:10	372713xxx	55.55962	5.392333	0	8.9	12	70	290	10.7
02:32:20	372713xxx	55.56045	5.392317	0	8.9	12.5	70	290	10.7

where MMSI—Marine Mobile Service Identity, Status—current ship navigational status—here: 0 = underway using engine, SOG—speed over ground, COG—course over ground, Type—ship type, here: 70 = cargo ship.

presents the decoded and filtered AIS data of a representative vessel used for the analysis (the MMSI number is partially concealed).

3. Research

The following research procedure was adopted:

(1)

selection of the study area and the group of analyzed vessels;

(2)

acquisition and preliminary processing of AIS data (preprocessing);

(3)

development of an artificial neural network architecture for ship movement prediction and execution of the network training process;

(4)

definition and calculation of indicators for ship movement anomaly identification;

(5)

identification of anomalies in vessel movement based on the proposed indicators using the artificial neural network.

The underlying assumptions were established, and the anomaly identification process was demonstrated using the example of a selected vessel voyage. A preliminary validation of the proposed anomaly identification method was conducted, and the verification results are presented.

3.1. Assumptions

For the study, a section of the recommended deep-water Route T in the Skagerrak Strait area was selected. The analysis focused on large vessels of the Panamax class, with lengths ranging from 222 to 295 m, breadths from 32 to 45 m, and loaded drafts between 13.0 and 15.0 m. This group was chosen because such vessels must follow the only navigable route available for passage to and from the Baltic Sea.

Figure 4 presents the selected tracks of these vessels (in blue) together with the analyzed segment of Route T (in magenta).

3.2. Anomaly Identification Process

One of the vessel passages (Vessel A) along the above-mentioned route was analyzed. This ship is of the Panamax type, with a length of 223 m, beam of 32 m, and draft of 13.3 m. Figure 5a presents its trajectory (blue points and line) based on AIS data, with time markers indicated in minutes. The green arrow shows the general direction of movement. Time stamps in minutes are clearly visible.

A detailed analysis of the vessel’s passage revealed non-standard behavior. During the voyage, a circulation maneuver was identified, which is not typical for vessel movement within a restricted area (Figure 5b).

A detailed analysis of the vessel’s speed and course profiles revealed significant variations in these parameters (Figure 6), corresponding to the circulation maneuver. A reduction in vessel speed was observed during turning phases, followed by a return to the initial speed once the course was stabilized (Figure 6a). Such behavior is typical during pronounced maneuvers.

At the beginning of the voyage, Vessel A maintained a course of approximately 90°, after which it turned to starboard, increasing its heading through 360°, and then—starting again from 0°—returned to its original course of about 90°. Thus, the vessel completed full circulation, accompanied by a temporary decrease in speed (Figure 6b).

This demonstrates that by monitoring changes in course and speed, it is possible to identify potential anomalies in vessel behavior.

Figure 5 and Figure 6 clearly confirm the execution of a circulation maneuver, which was unexpected at this location. The above analysis was conducted manually. This raises the question of how to automate the process of detecting anomalies based on AIS data. The complexity of this task arises from the diversity of routes taken by different vessels when traversing the same water areas.

The authors proposed an approach for anomaly identification based on the analysis of differences between the actual and predicted ship positions, courses, and speeds. These parameters are determined from the real motion characteristics of the vessel obtained from the AIS. They are described by the ship state vector ${\mathit{V}}_{R,i}^j$.

$${\mathit{V}}_{R,i}^j=\left[\begin{array}{c}\begin{array}{c}{x}_{R,i}^j\\ y_{R,i}^j\end{array}\\ {COG}_{R,i}^j\\ {SOG}_{R,i}^j\end{array}\right]$$

(1)

where

• $n$—the number of AIS messages recorded for the vessel,
• $x_{R,i}^j$—the x-coordinate of the position of ship j at time i, $i=0,1,\dots ,n$,
• $y_{R,i}^j$—the y-coordinate of the position of ship j at time i, $i=0,1,\dots ,n$,
• ${COG}_{R,i}^j$—the course over ground of ship j at time i, $i=0,1,\dots ,n$,
• ${SOG}_{R,i}^j$—the speed over ground of ship j at time i, $i=0,1,\dots ,n$.

The predicted positions, courses, and speeds of ship j are determined based on the m previous values of these parameters, using a Long Short-Term Memory (LSTM) artificial neural network to predict the increments of these parameter values:

$${\mathbf{∆}\mathit{V}}_{P,i}^j=f\left({\mathit{V}}_{R,i-1}^j,{\dots ,\mathit{V}}_{R,i-m}^j\right)$$

(2)

$${∆\mathit{V}}_{P,i}^j=\left[\begin{array}{c}\begin{array}{c}∆x_{P,i}^j\\ ∆y_{P,i}^j\end{array}\\ {∆COG}_{P,i}^j\\ ∆{SOG}_{P,i}^j\end{array}\right]$$

(3)

$${\mathit{V}}_{P,i}^j={\mathit{V}}_{R,i-1}^j+{\mathbf{∆}\mathit{V}}_{P,i}^j$$

(4)

$${\mathit{V}}_{P,i}^j=\left[\begin{array}{c}\begin{array}{c}{x}_{P,i}^j\\ y_{P,i}^j\end{array}\\ {COG}_{P,i}^j\\ {SOG}_{P,i}^j\end{array}\right]=\left[\begin{array}{c}\begin{array}{c}{x}_{R,i}^j+\mathbf{∆}{x}_{P,i}^j\\ y_{R,i}^j+\mathbf{∆}{y}_{P,i}^j\\ {{COG}_{R,i}^j+\mathbf{∆}COG}_{P,i}^j\end{array}\\ {SOG}_{R,i}^j+\mathbf{∆}{SOG}_{P,i}^j\end{array}\right]$$

(5)

where

• ${\mathit{V}}_{P,i}^j$—the predicted state vector of ship j at time i,
• $\mathit{\Delta }{\mathit{V}}_{P,i}^j$—the increments of the state vector of ship j at time i,
• $f$—the prediction function for the increments of the ship’s state vector,
• $m$—the length of the input data vector of the artificial neural network,
• $\mathit{\Delta }{x}_{P,i}^j$—the predicted increment of the x-coordinate of ship j at time i, $i=m,\dots ,n$,
• $\mathit{\Delta }{y}_{P,i}^j$—the predicted increment of the y-coordinate of ship j at time i, $i=m,m+1,\dots ,n$,
• $\mathit{\Delta }{COG}_{P,i}^j$—the predicted change in the course over ground of ship j at time i, $i=m,m+1,\dots ,n$,
• $\mathit{\Delta }{SOG}_{P,i}^j$—the predicted change in the speed over ground of ship j at time i, $i=m,m+1,\dots ,n$,
• $x_{P,i}^j$—the predicted x-coordinate of the position of ship j at time i, $i=m,m+1,\dots ,n$,
• $y_{P,i}^j$—the predicted y-coordinate of the position of ship j at time i, $i=m,m+1,\dots ,n$,
• ${COG}_{P,i}^j$—the predicted course over ground of ship j at time i, $i=m,m+1,\dots ,n$,
• ${SOG}_{P,i}^j$—the predicted speed over ground of ship j at time i, $i=m,m+1,\dots ,n$,
• ${POSx}_{P,i}^j$—the predicted position x of ship j at time i, $i=0,1,\dots ,n$,
• ${POSy}_{P,i}^j$—the predicted position y of ship j at time i, $i=0,1,\dots ,n$.

In the presented formulas, four parameters of the ship’s state vector are considered.

For the purposes of trajectory prediction using the neural network, the course parameter is represented by its components cos(COG) and sin(COG) (see Section 2.2). Therefore, the input vector becomes five-dimensional.

The inverse operation is performed on the LSTM output vector, which is transformed back into a four-element state vector. Based on the predicted course components cos(COG) and sin(COG), the predicted course COG is obtained using the following relationship:

$${COG}_{P,i}^j=mod(atan2d\left(cos{(COG}_{P,i}^j),sin{(COG}_{P,i}^j)\right),360)$$

(6)

where

• atan2d—four quadrant inverse tangent,
• $cos{(COG}_{P,i}^j$), $sin{(COG}_{P,i}^j$),—predicted vertical and horizontal components of ${COG}_{P,i}^j$

The predicted change in the course over ground $\mathit{\Delta }{COG}_{P,i}^j$ was determined based on the following relationship:

$${\mathbf{∆}COG}_{P,i}^j={{COG}_{P,i}^j-COG}_{R,i}^j$$

(7)

In the subsequent analysis, the distances between the actual and predicted positions at a given time i were considered instead of the x and y coordinates.

$$\mathbf{∆}{POS}_{P,i}^j=\sqrt{{\left(x_{R,i}^j-x_{p,i}^j\right)}^2+{\left(y_{R,i}^j-y_{p,i}^j\right)}^2}$$

(8)

The differences between the actual and predicted positions, courses, and speeds of ship j at time i are then represented by a three-dimensional vector.

$${\mathit{d}\mathit{i}\mathit{f}\mathit{f}}_{\mathit{i}}^{\mathit{j}}=\left[\begin{array}{c}\mathbf{∆}{POS}_{P,i}^j\\ \left|\mathbf{∆}{COG}_{P,i}^j\right|\\ \left|\mathbf{∆}{SOG}_{P,i}^j\right|\end{array}\right]$$

(9)

The increments of these differences, representing the trends in the changes in the above-mentioned parameters, are then determined using the following relationship:

$${∆diff}_{POS,k}^j=\mathbf{∆}{POS}_{P,k}^j-{\mathbf{∆}POS}_{P,k-1}^j;k=m+2,\dots ,n$$

(10)

$${∆diff}_{COG,k}^j=\mathbf{∆}{COG}_{P,k}^j-{\mathbf{∆}COG}_{P,k-1}^j;k=m+2,\dots ,n$$

(11)

$${∆diff}_{SOG,k}^j=\mathbf{∆}{SOG}_{P,k}^j-{\mathbf{∆}SOG}_{P,k-1}^j;k=m+2,\dots ,n$$

(12)

where k denotes the time instant for which the increments of the differences in the respective parameters were determined.

This relationship can be expressed in vector form.

$${\mathbf{∆}\mathit{d}\mathit{i}\mathit{f}\mathit{f}}_{\mathit{i}}^{\mathit{j}}=\left[\begin{array}{c}{∆diff}_{POS,k}^j\\ {∆diff}_{COG,k}^j\\ {∆diff}_{SOG,k}^j\end{array}\right]$$

(13)

In the study, the increments of the parameter values were predicted based on the m = 4 previous values of the ship’s state vector, using different time intervals. This approach stems from the fact that each of the analyzed ship motion parameters has its own specific dynamics and possible variability over time. It appears reasonable to analyze parameters with higher variability (e.g., course) at shorter time intervals, and those with lower variability (e.g., speed, relative distance, or traveled path) at longer intervals. Therefore, time intervals of 5, 10, 15, and 20 min were selected empirically to evaluate the effectiveness of anomaly identification.

For preliminary verification of the proposed method, the voyage of the ship excluded from the LSTM training dataset (ship A, see Figure 4) was analyzed. The differences and increments of differences in relative distances, courses, and speeds were examined for the actual and predicted trajectories.

Figure 7 presents the actual and predicted trajectories (Figure 7a) and a fragment of these trajectories for ship A with a 5 min time step, showing the difference in relative distance between corresponding points (Figure 7b, black arrow). The numbers 0, 200, 400, and 600, as well as the small circles, indicate the time instant in minutes.

Figure 8 presents the plots of differences and increments of differences for the analyzed parameters (blue solid lines). It was observed that using increments of differences instead of direct differences allows for a significant reduction in short-term fluctuations, such as inaccuracies in position readings, course oscillations (yawing), or speed variations. This effect is illustrated by the example plots for a 5 min interval shown in Figure 8. The dashed magenta lines indicate the limits of the analyzed parameters.

Based on this observation, in the subsequent part of the study, the motion processes were analyzed using the increments of differences in the described parameters as indicators for anomaly identification. With reference to the definition of anomaly in Section 1, an anomaly is flagged when one or more of the following conditions are met:

• position error > 0.5 L, where L—ship length;
• speed deviation > 0.2 kn;
• course deviation > 30°.

These thresholds represent limits above which the deviation is considered operationally significant.

The acceptable range of the increments of distance differences was assumed to be equal to one-half of the ship’s length (Figure 8b), indicated by a magenta line. For the increments of speed differences, the acceptable limits were set to ±0.2 knots (Figure 8d), also marked with a magenta line. Similarly, for the increments of course differences, the limits were set to ±30° (Figure 8f) and marked with a magenta dashed line.

The time instants at which the indicator values exceeded the established limits were subjected to detailed analysis for potential anomaly detection. An example is the exceedance of indicator values beyond the acceptable ranges between the 30th and 45th minute, during which a ship circulation maneuver was identified. A similar situation occurred around the 580th minute, when the vessel executed a significant turn. In this case, however, exceeding the defined limits was not associated with an anomaly but resulted from the possibility of selecting alternative route variants in that area.

Different time steps were analyzed to assess the effectiveness of anomaly identification based on each of the considered indicators. The variations in the increments of differences corresponding to the maneuvers described are presented in Figure 9, Figure 10 and Figure 11.

Figure 9 shows the increments of distance differences for time steps of 5, 10, 15, and 20 min. As before, the limits of the acceptable range for the increments of distance differences were set to one-half of the ship’s length (here, ½ L = 110 m) and marked with a magenta line. Values above +110 m and below −110 m were considered anomalies. According to expert navigators’ analysis, these anomalies corresponded to the circulation maneuver and the course change performed before the branching of the recommended routes.

The limits were exceeded for the 5- and 10 min time steps. Figure 10 presents the increments of speed differences for time steps of 5, 10, 15, and 20 min. For the increments of speed differences, the acceptable limits were set to ±0.2 knots and marked with a magenta line. Values above +0.2 knots and below −0.2 knots were considered anomalies. According to the expert navigator’s analysis, these anomalies correspond, as in the previous case, to the circulation maneuver and the course change performed before the branching of the recommended routes.

The limits were exceeded during the circulation maneuver for the 5-, 10-, 15-, and 20 min time steps. For the course change maneuver around the 560th minute, the limits were exceeded for the 5- and 20 min time steps.

Figure 11 presents the increments of course differences for time steps of 5, 10, 15, and 20 min. The acceptable limits were set to ±30° and marked with a magenta line (see Figure 8f). Values above +30° or below −30° were considered anomalies. According to the expert navigator’s analysis, these anomalies corresponded, as in the previous cases, to the circulation maneuver and the course change performed before the branching of the recommended routes.

Based on this analysis, an anomaly was identified during the initial and final minutes of the recorded ship passage. The limits were exceeded during the circulation maneuver for the 5-, 10-, 15-, and 20 min time steps. Similarly, around the 560th min, the limits were exceeded for the 5- and 15 min time steps, which was associated with the course change maneuver.

4. Results

The method described was applied to identify anomalies in the voyage of another ship—ship B. This vessel is a tanker with a length of 250 m and a draft of 13.5 m. An analysis of the ship’s motion parameters was performed, revealing a significant number of behaviors deviating from the standard patterns observed in the analyzed water area.

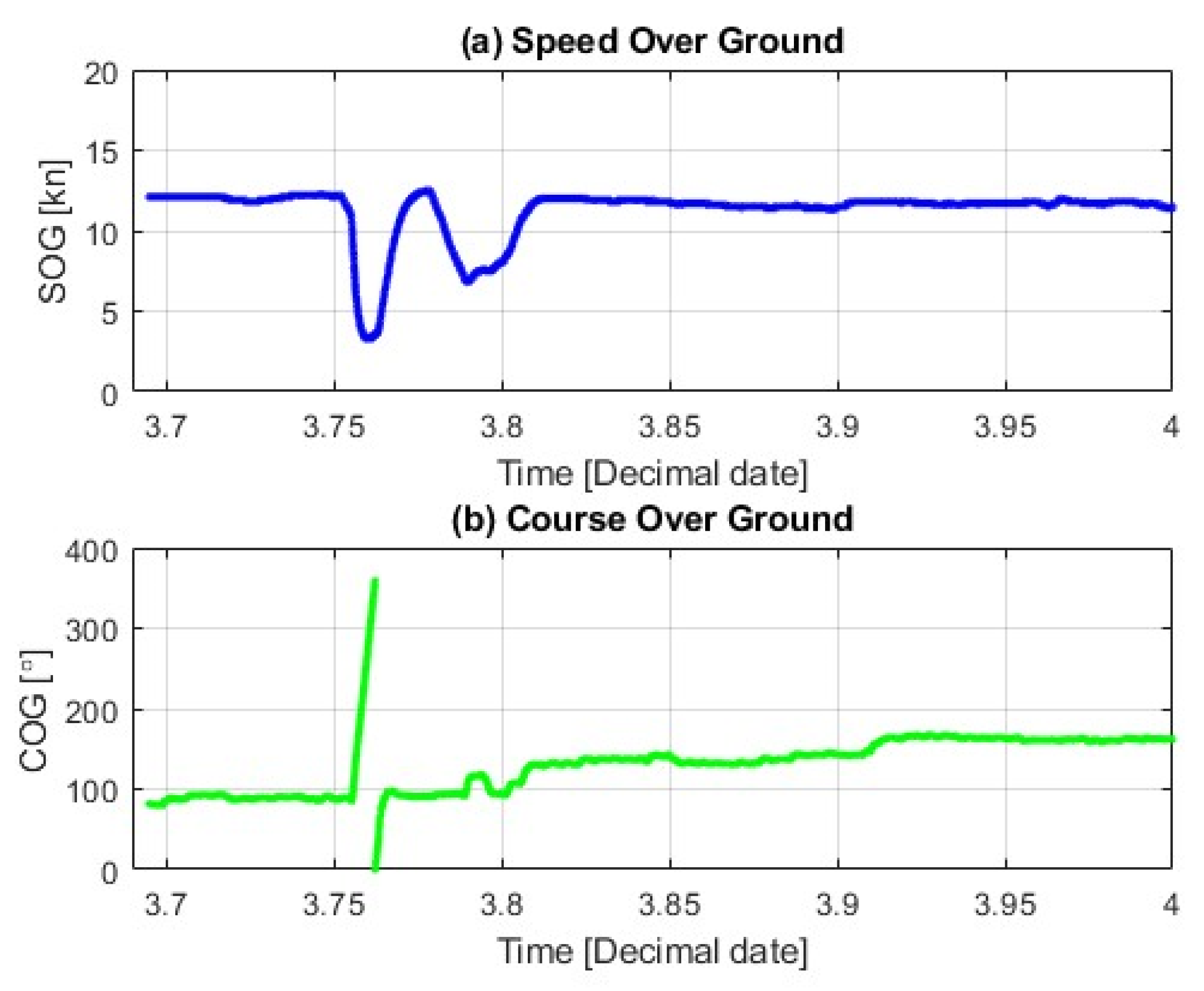
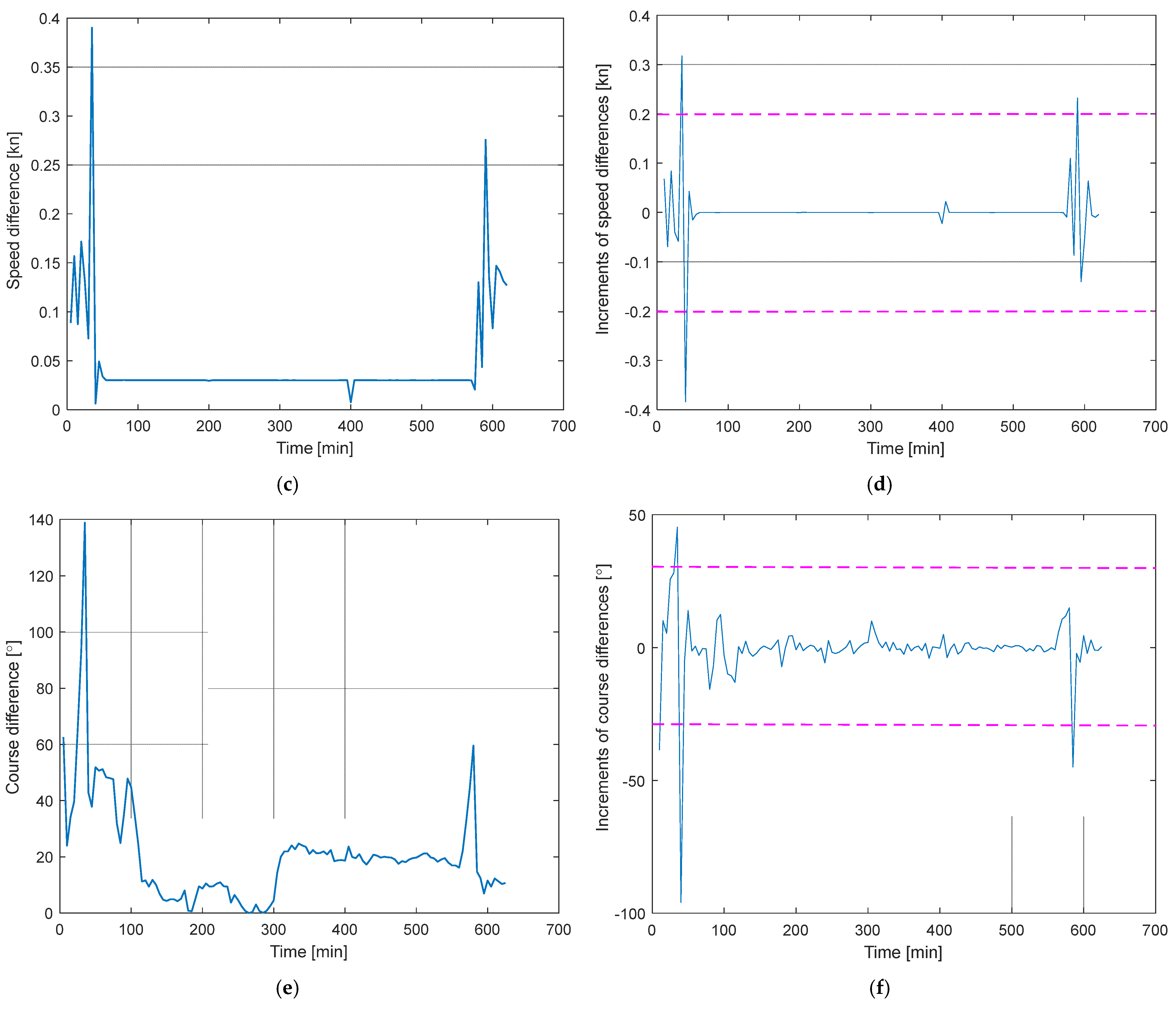
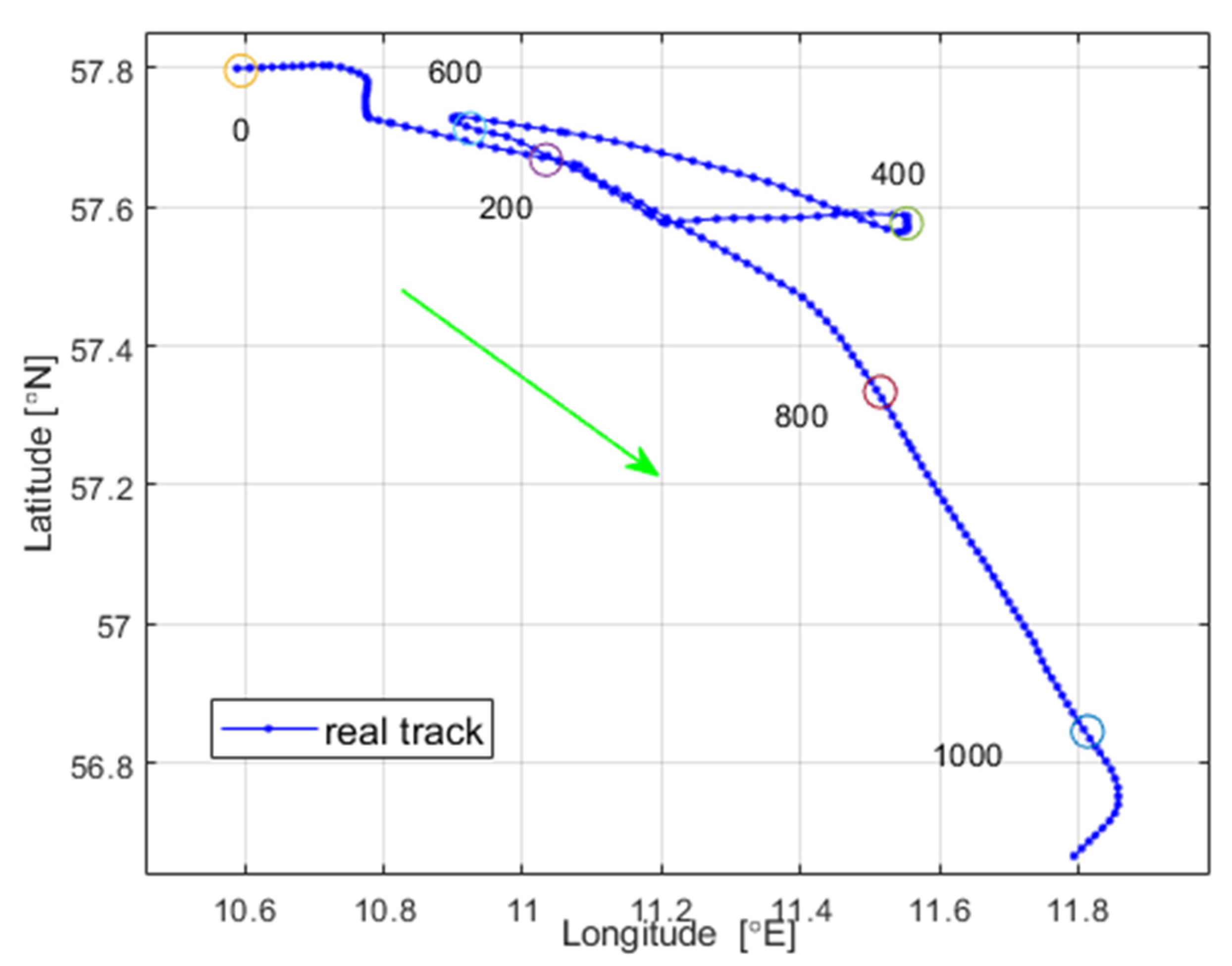
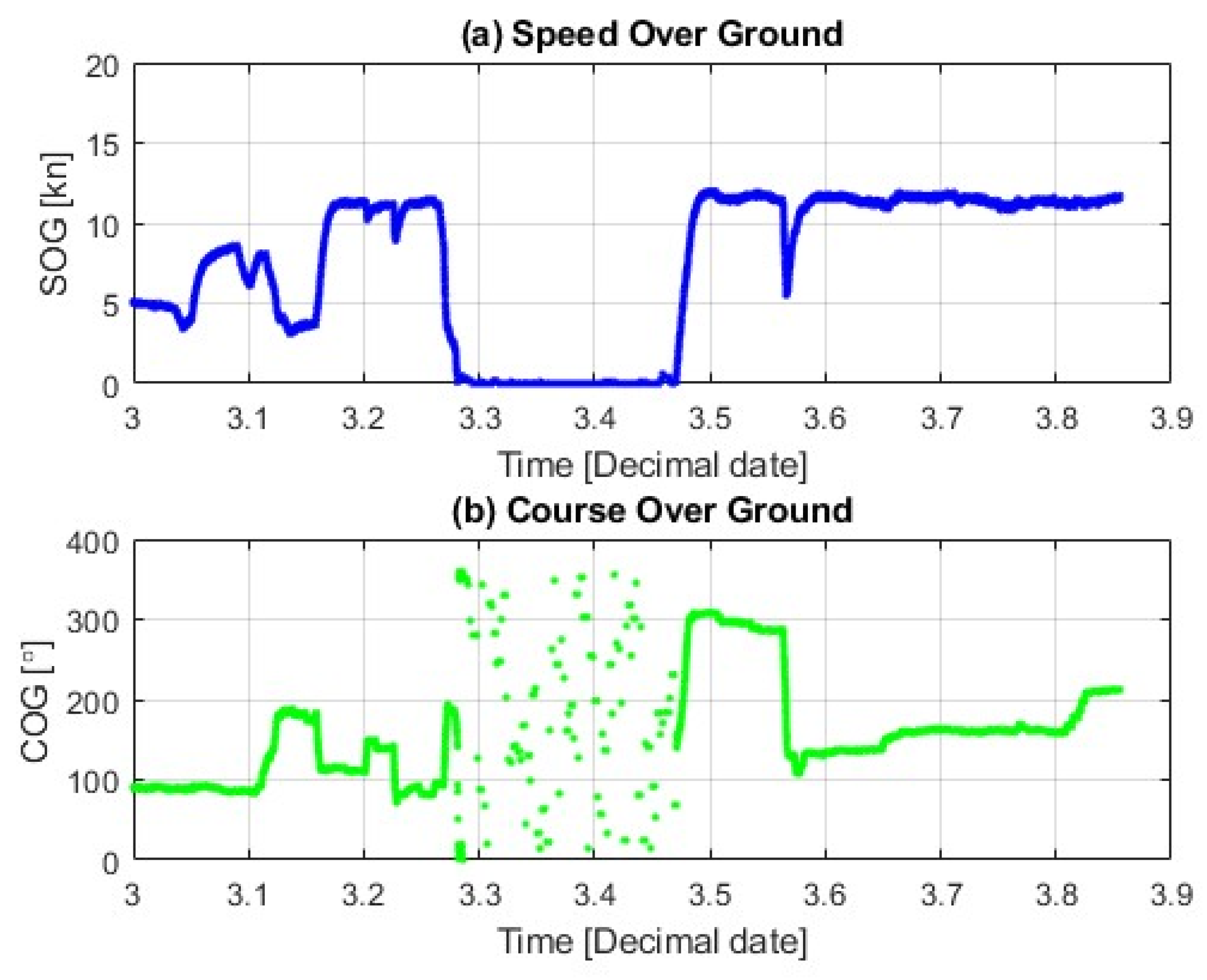
4.1. Case Study

Figure 12 presents the ship’s trajectory (blue points and line) determined based on AIS data. The green arrow indicates the general direction of movement.

Additionally, time markers were added for the 0th, 200th, 400th, 600th, 800th, and 1000th minutes of the analyzed voyage segment. The trajectory deviates significantly from the recommended route.

Figure 13 presents the reconstructed speed and course values of this vessel, which indicate atypical ship behavior. Frequent and considerable changes in both speed and course can be observed in what is typically a transit area. In theory, the ship should have followed the recommended IMO T-route from the North Sea through the Danish Straits toward the Baltic Sea (see Figure 1). However, the vessel deviated from this route, performed turns, and remained adrift for certain periods. Eventually, after several hours, it returned to the route and continued its passage.

Based on the analysis of the ship’s motion parameters and trajectory, at least four situations were identified as anomalies: a course change relative to the recommended (reference) route, deviation from the reference trajectory, a drop in speed (drifting or lack of progression), and a return to the trajectory (change in intention—anomaly termination).

Four representative cases, selected by expert navigators, were analyzed in detail.

Figure 13 shows the variations in ship B speed over the analyzed period (Figure 13a) and its course (Figure 13b).

Significant and unexpected changes in movement parameters observed in the analyzed water area are presented in Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 and are subjected to detailed navigational analysis below. Figure 14 shows a segment of the route of Ship B, with marked significant and unexpected changes in course and speed, numbered 1, 2, 3, and 4, which were identified by expert navigators as anomalies.

The marked sections of the trajectory in the figure correspond to:

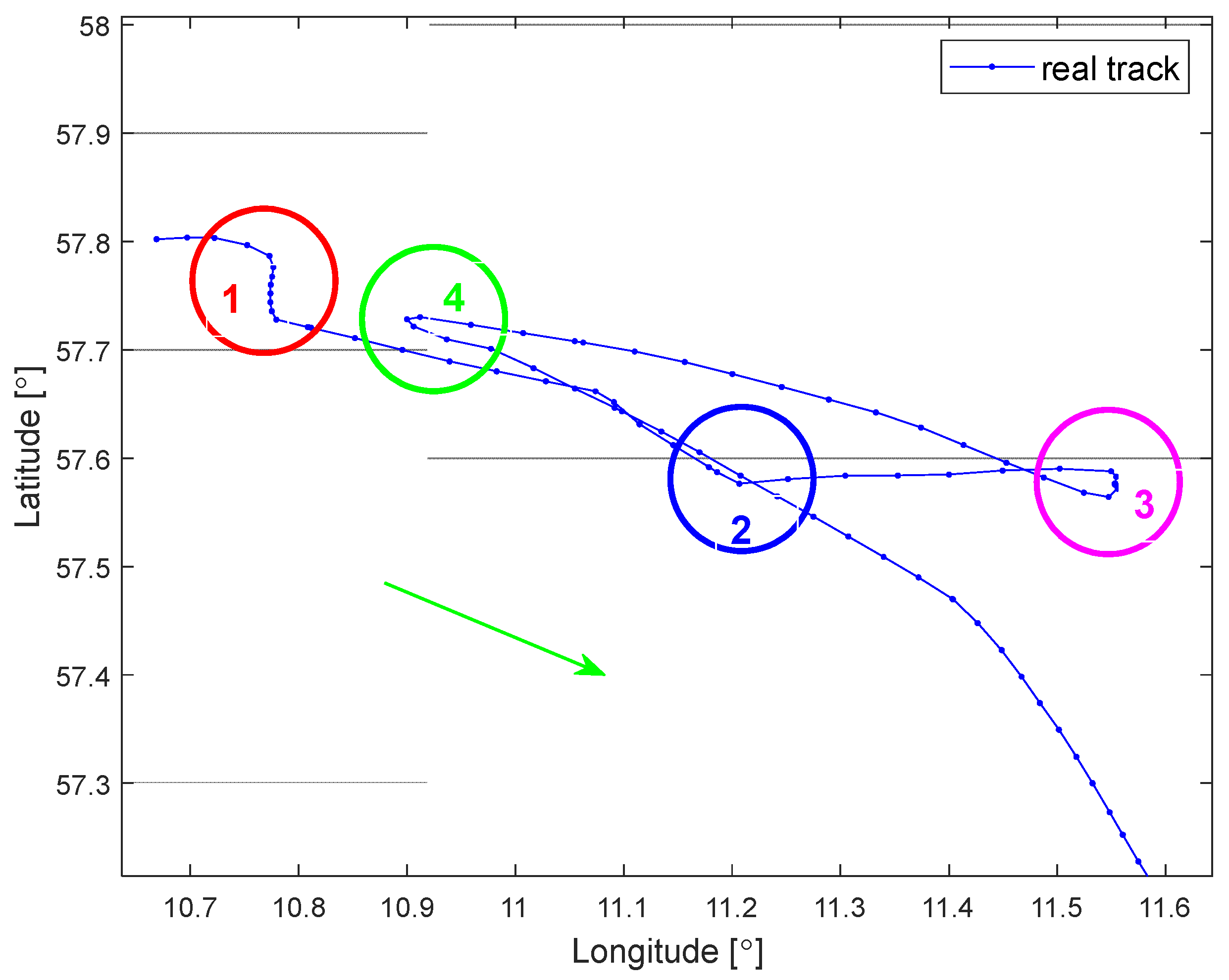
(1)

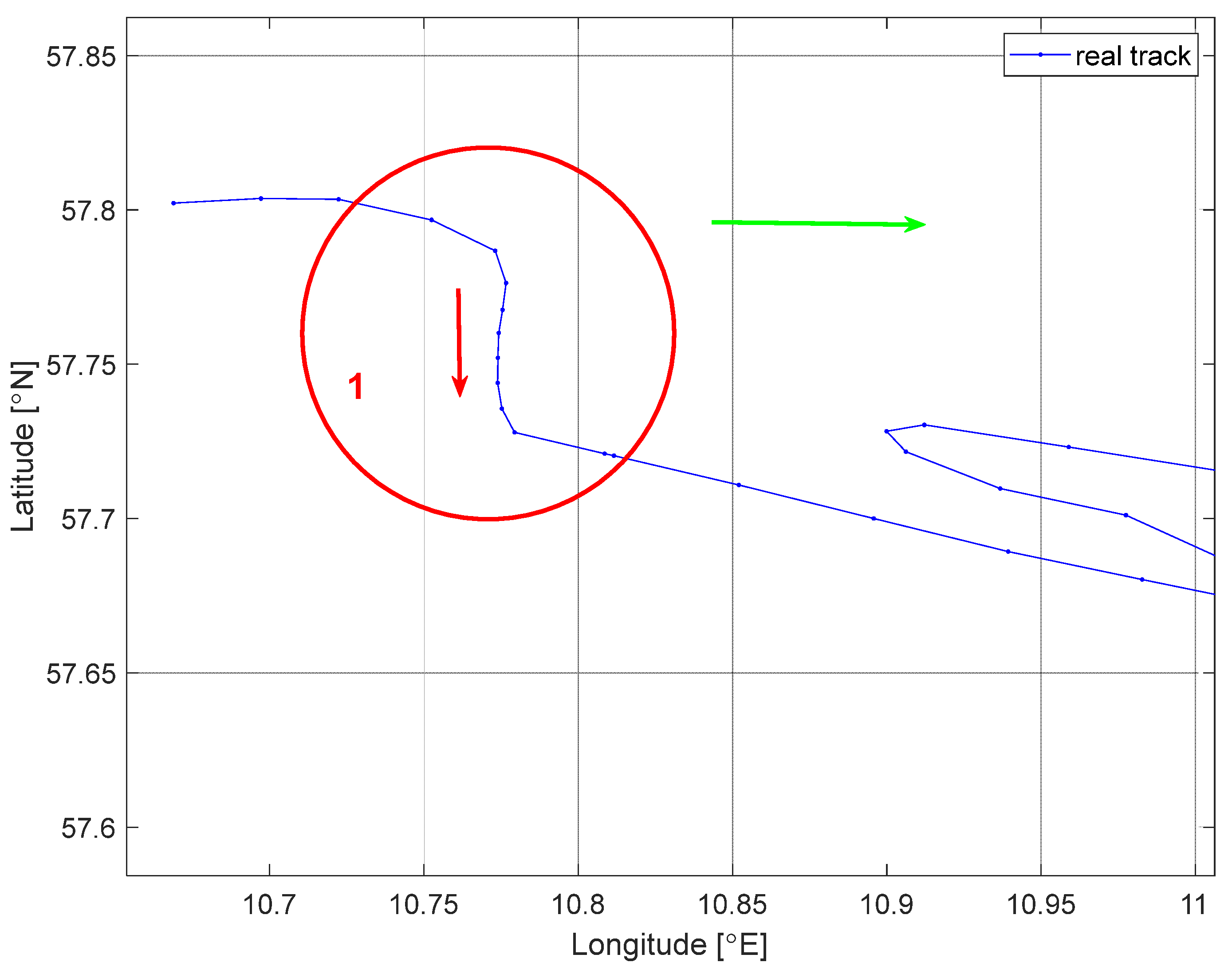
a course alteration—anomaly #1;

(2)

a course alteration and deviation from the recommended route—anomaly #2;

(3)

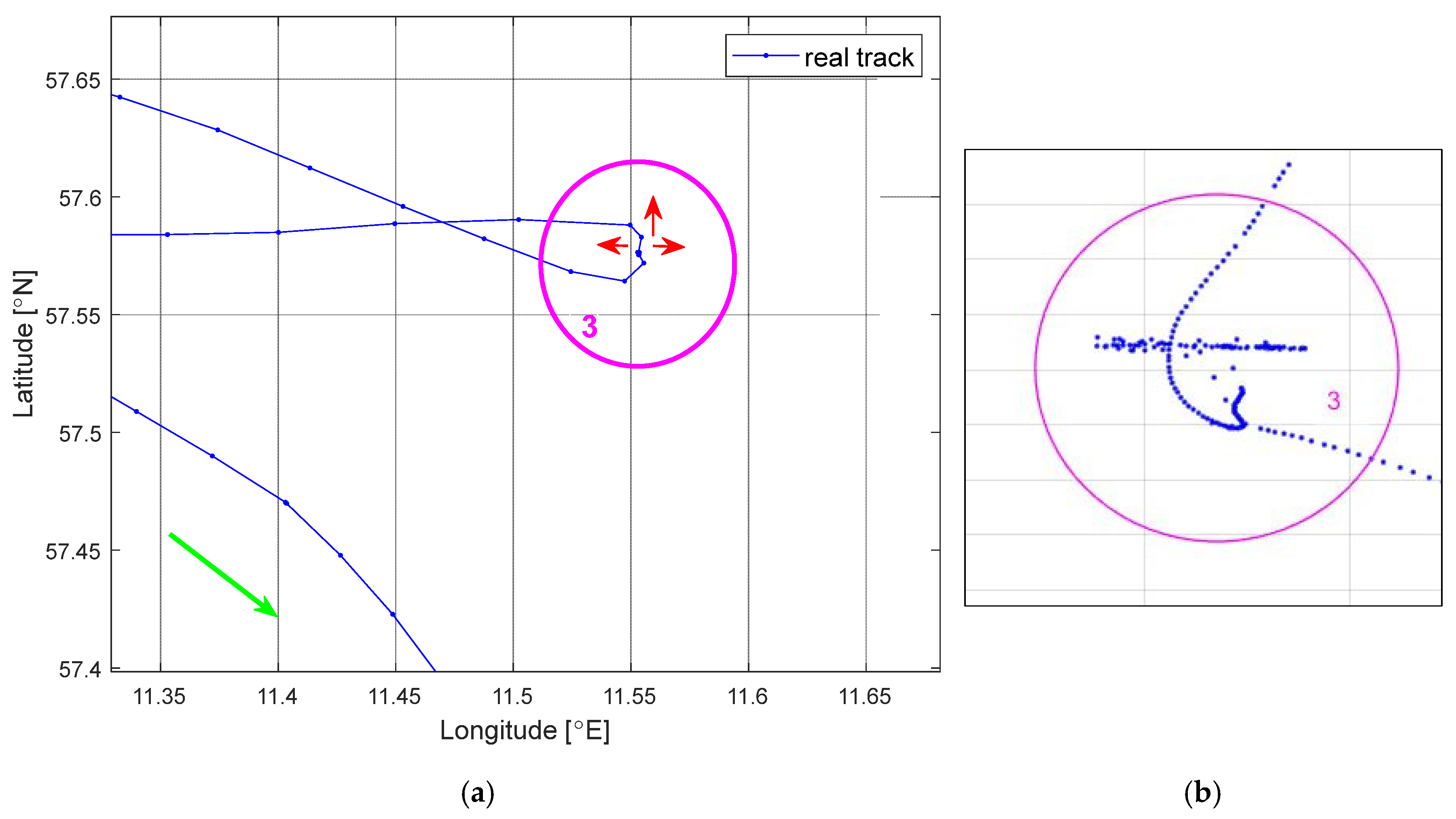
a decrease in speed and drifting stop—anomaly #3;

(4)

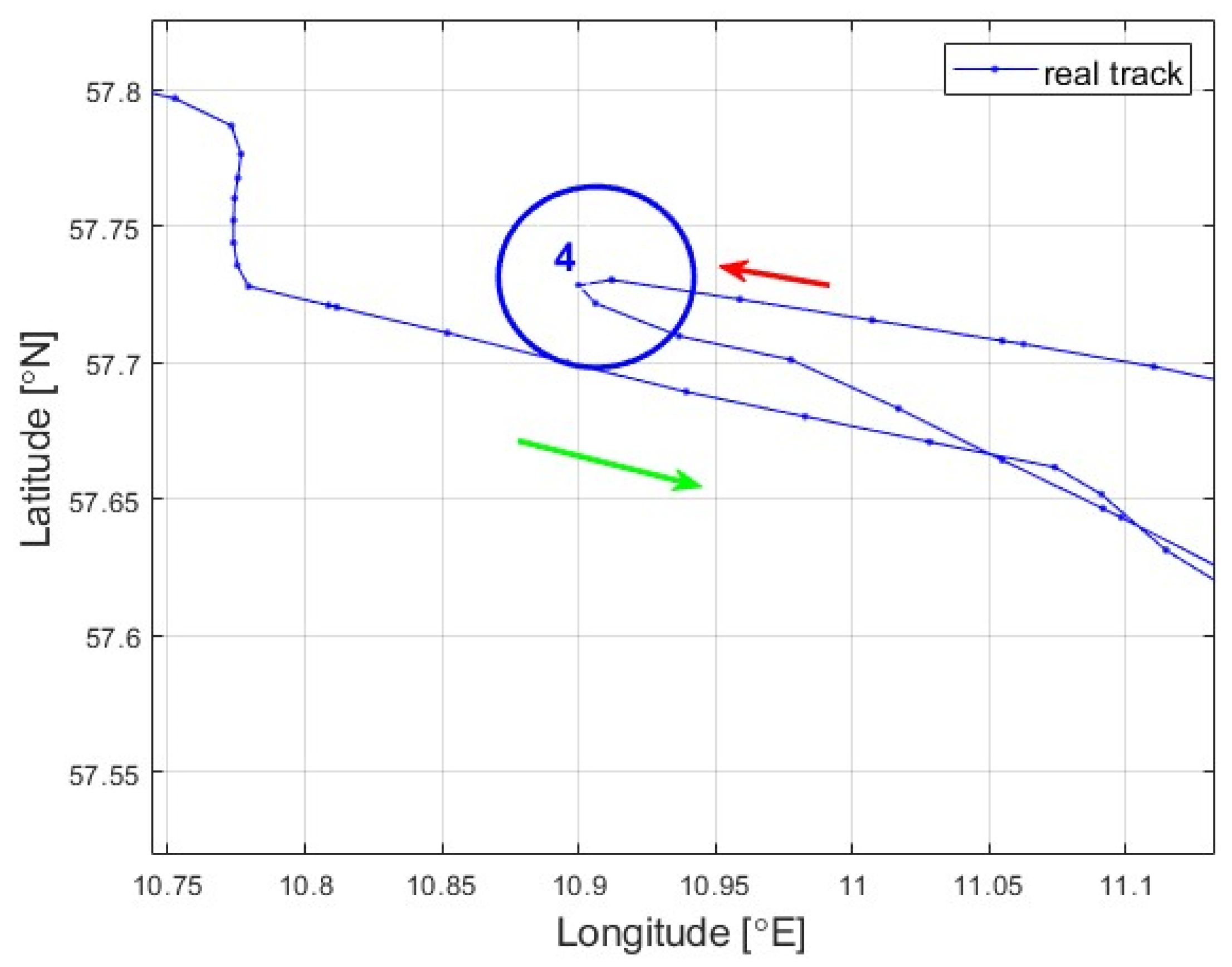
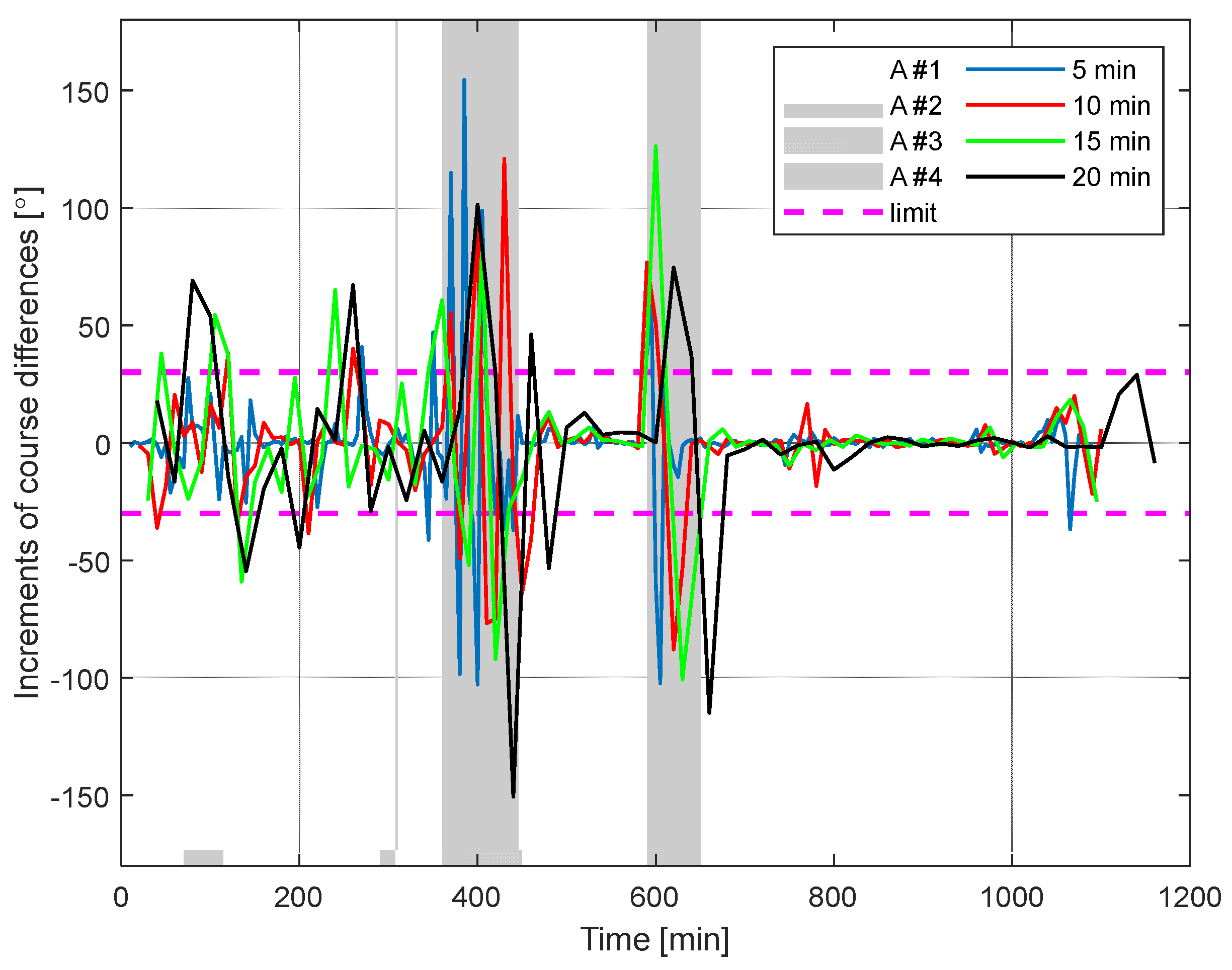
a sudden 180° course change to return to the original trajectory—anomaly #4.

Based on the analysis of the real trajectory (Figure 12 and Figure 14), the time intervals during which these anomalies occurred were determined as follows:

• anomaly #1: 70–150 min;
• anomaly #2: 290–310 min;
• anomaly #3: 360–450 min;
• anomaly #4: 590–650 min.

• Anomaly 1—Course alteration

Figure 15 presents the first observed anomaly. The ship, moving on a course of approximately 090°, suddenly makes a right turn of about 90° instead of continuing on its maintained course, while simultaneously reducing its speed. The green arrow indicates the general direction of movement, whereas the red arrow shows the new, altered course.

The analyzed ship, initially proceeding on a course of approximately 090°, changed its course (a right turn) to about 180°, while the recommended trajectory required a turn to 130°. The vessel remained on this course for about 40 min before making a left turn to return to the recommended route (see Figure 3).

• Anomaly 2—Course alteration and deviation from the recommended route

Anomaly no. 2, shown in Figure 16, also involved an unexpected course alteration and deviation from the recommended trajectory. The ship was sailing on a course of approximately 135°, after which it changed its course (a left turn) to about 80°. The green arrow indicates the general direction of movement, while the red arrow shows the new, altered course.

• Anomaly no. 3—decrease in speed and drifting stop

Anomaly no. 3 (Figure 17) involves a significant reduction in speed, stopping of the vessel, and remaining adrift outside the recommended route. The green arrow indicates the general direction of movement, while the red arrows show the varying directions of the drifting ship’s movement (Figure 17). Figure 17b shows a close-up of the ship’s track and positions during the drifting period (blue dots).

• Anomaly no. 4—sudden 180° course change

The fourth analyzed anomaly (Figure 18) is a sudden course change made to return to the recommended trajectory. It represents an abrupt 180° course alteration. The green arrow indicates the general direction of movement, while the red arrow shows the varying direction of the ship’s movement.

The analyzed ship, sailing on a course of approximately 280°, changed its course (a left turn) to about 110° and gradually returned to the recommended route while increasing its speed.

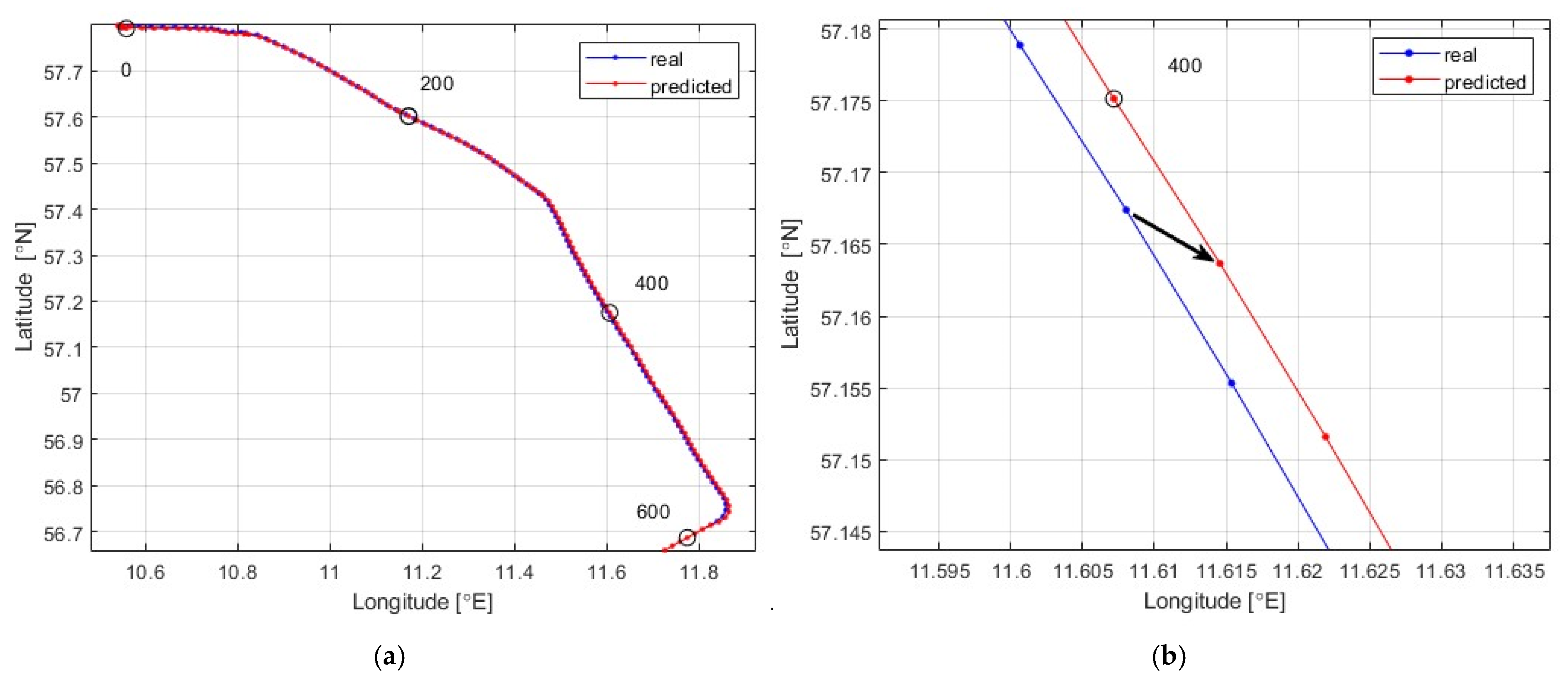
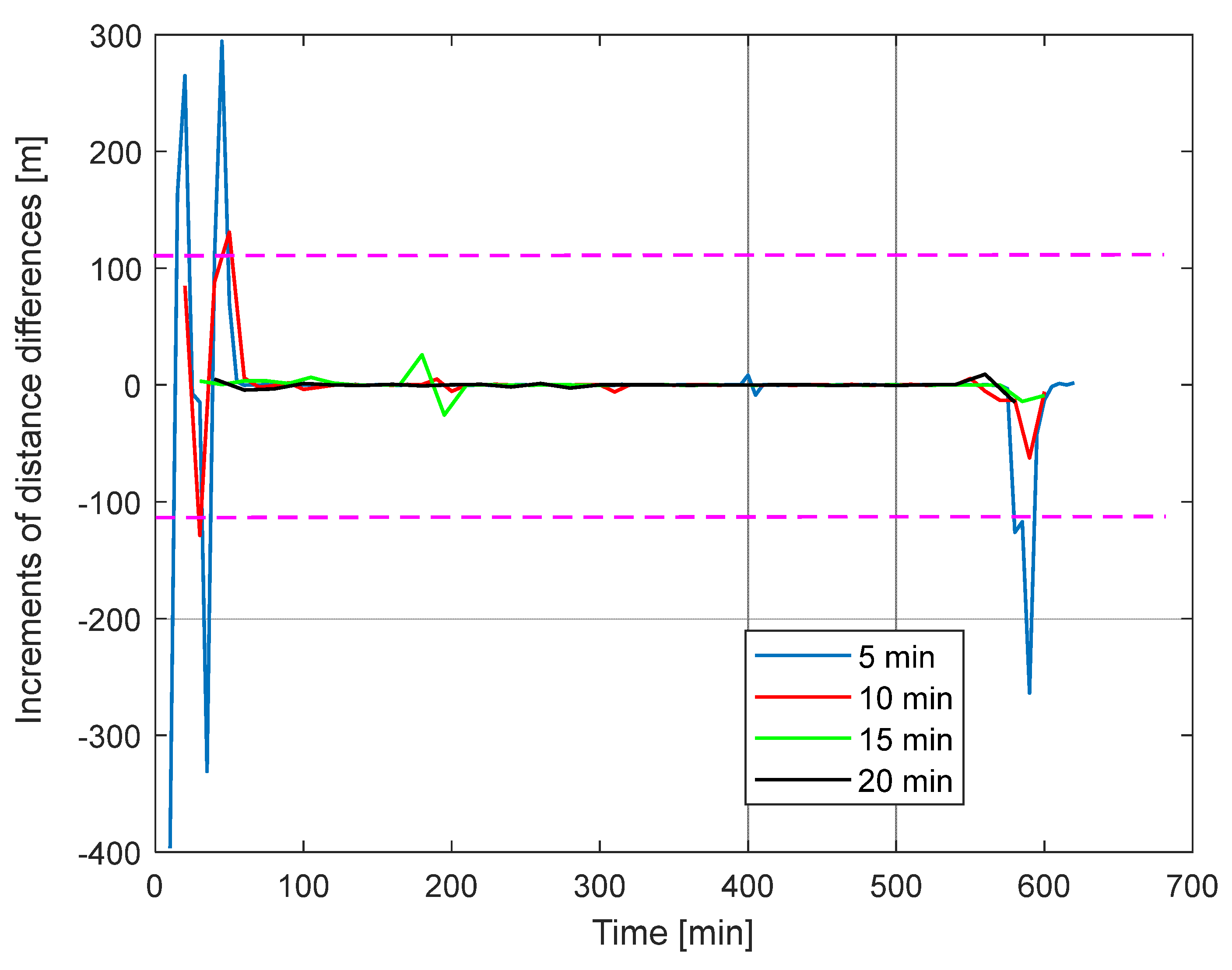
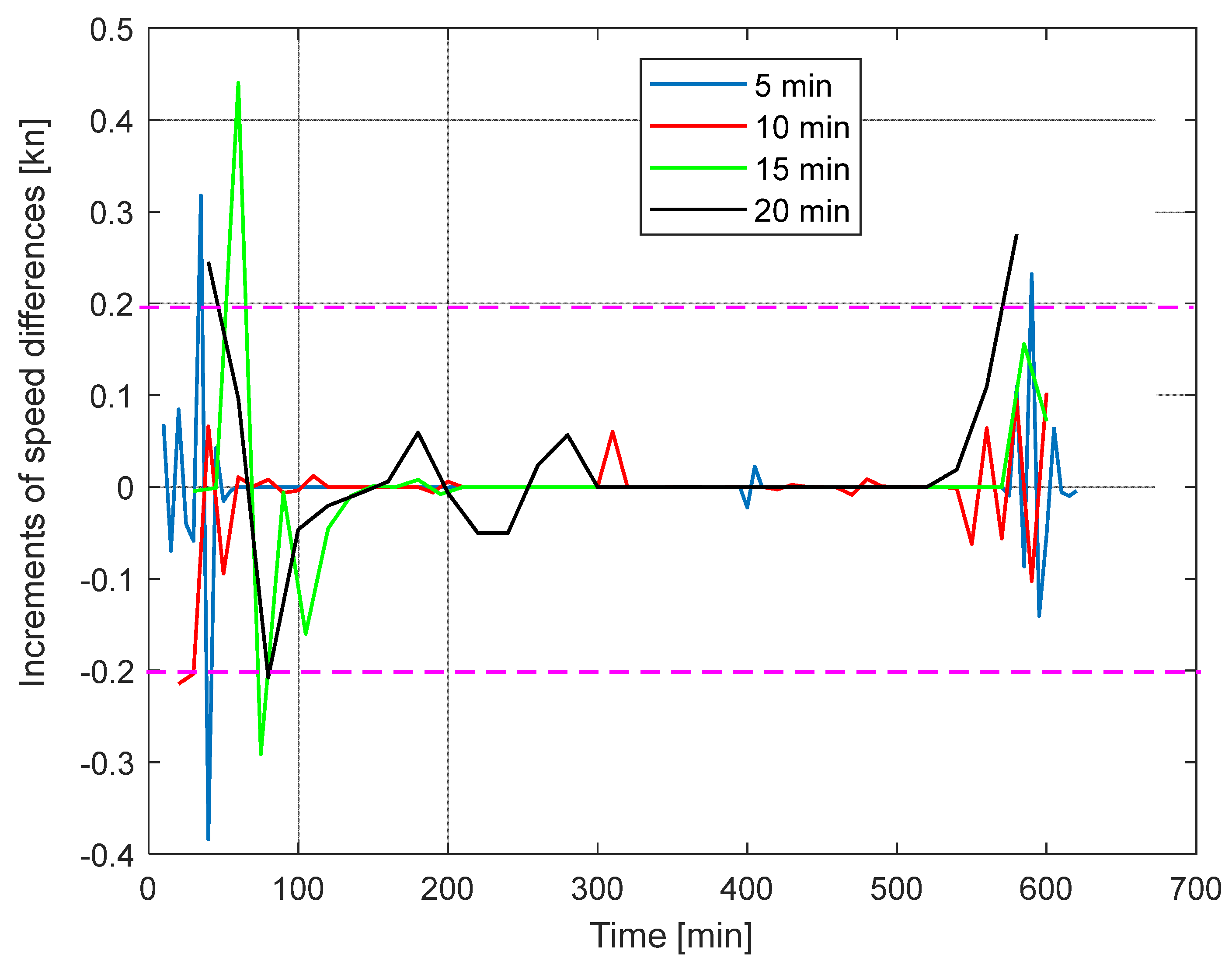
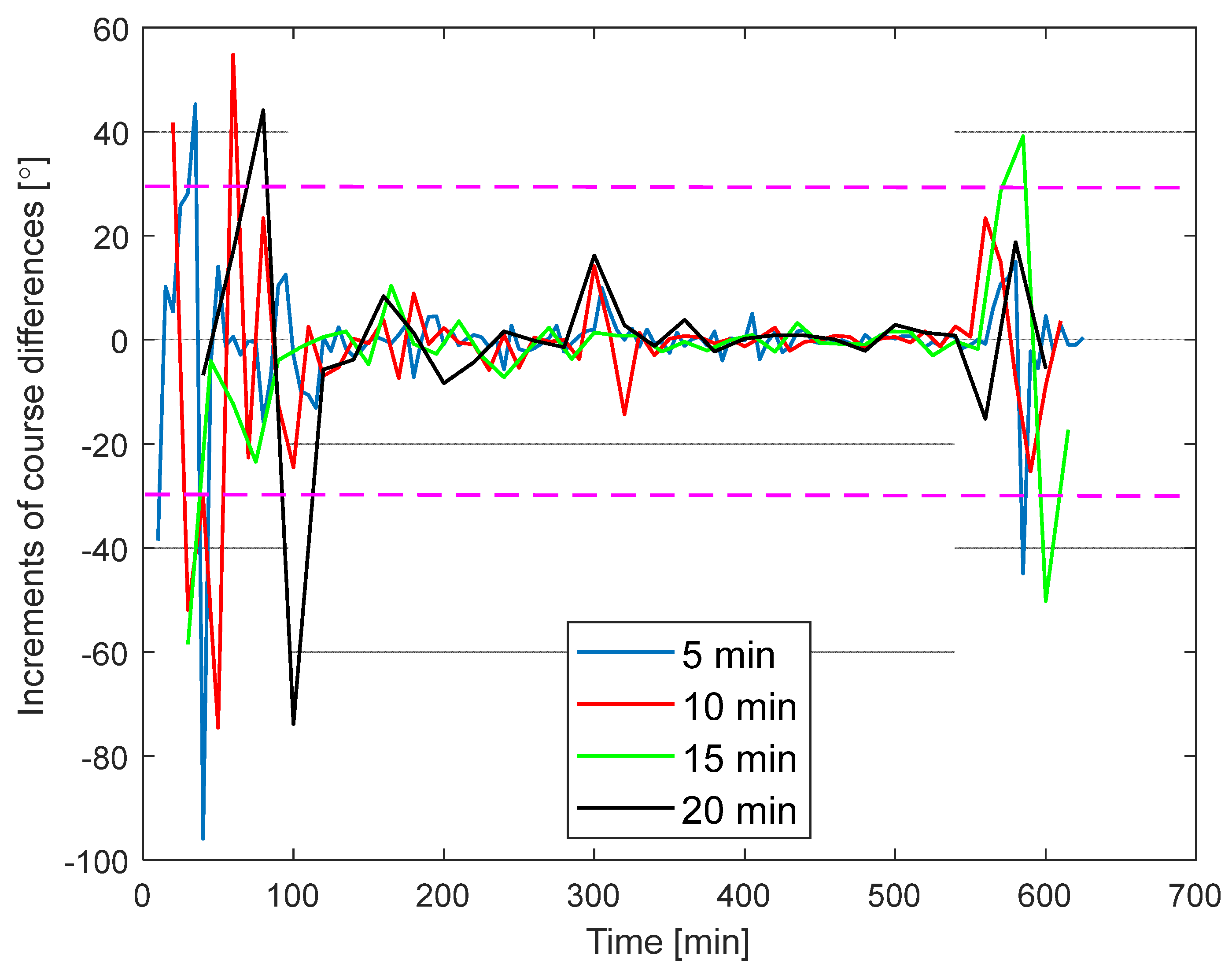
4.2. Analysis of Movement Processes

Analogously to Ship A, analyses of the differences and increments of differences in distance, speed, and course between the actual and predicted movement trajectories were performed to identify anomalies 1 through 4 (see Figure 14).

Figure 19 presents the increments of distance differences for time steps of 5, 10, 15, and 20 min. As the limits (boundaries) of the acceptable range of distance difference increments, one-half of the ship’s length (here ½ L = 125 m) was adopted and marked with a magenta line. Values above 125 m and below −125 m are considered anomalies. The time intervals of anomaly occurrence are highlighted in the background with different shades of gray.

Based on the increments of distance differences, anomalies #1 and #2 were not identified. The limits were exceeded for anomaly #3 at time steps of 5, 10, and 15 min, and for anomaly #4 at time steps of 5, 10, and 20 min.

Figure 20 presents the increments of speed differences for time steps of 5, 10, 15, and 20 min. In the case of speed difference increments, the limits (boundaries) were set at ±0.2 knots and are marked with a purple line. Values above 0.2 knots and below −0.2 knots were considered anomalies. The time intervals of anomaly occurrence are highlighted in the background with different shades of gray.

The limits were exceeded in all four cases analyzed:

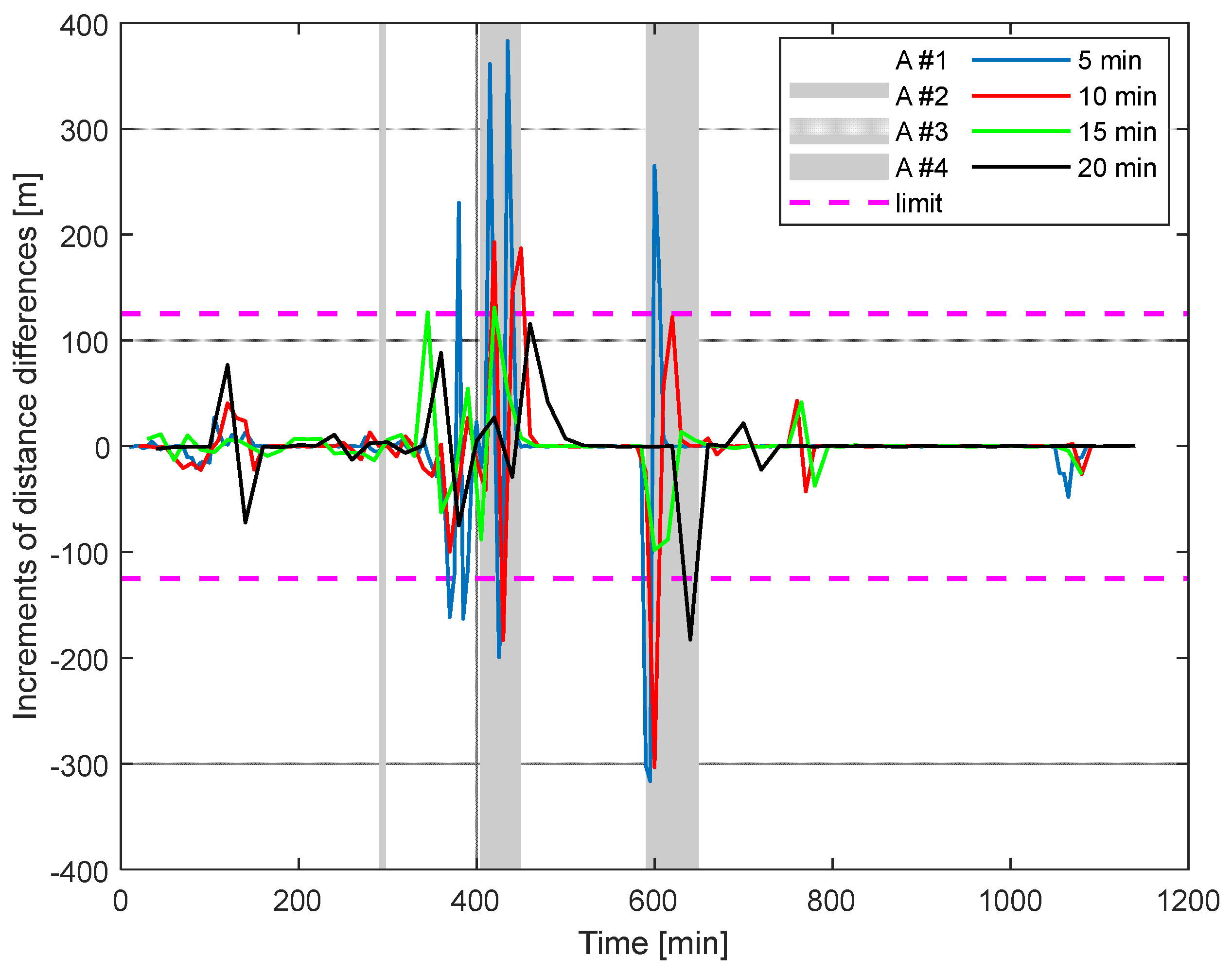
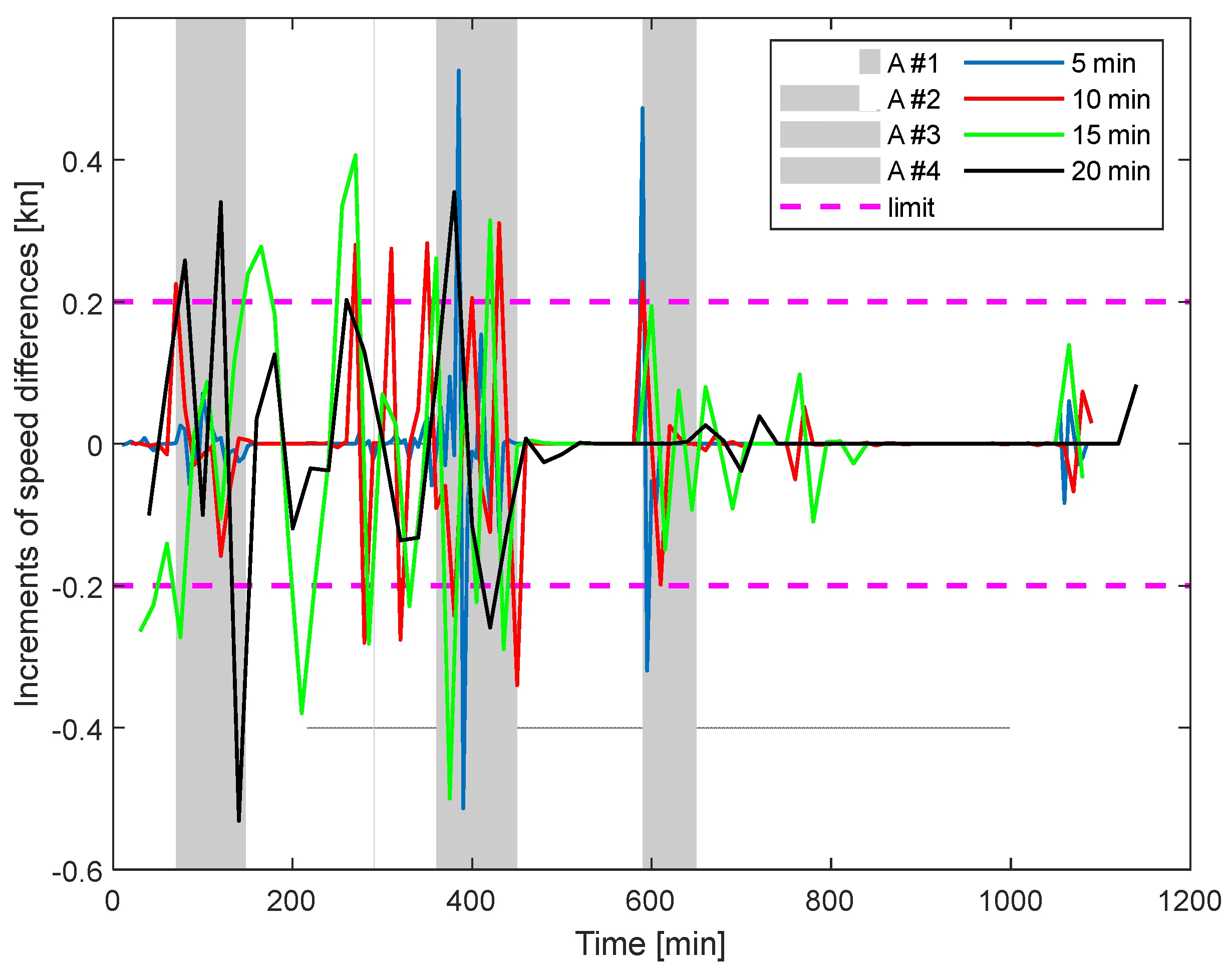
• anomaly #1 (70–150 min) for time steps of 10, 15, and 20 min;
• anomaly #2 (290–310 min) for time steps of 10 and 15 min;
• anomaly #3 (360–450 min) for all time steps;
• anomaly #4 (590–650 min) for time steps of 10 and 15 min.

Figure 21 presents the increments of course differences for time steps of 5, 10, 15, and 20 min. The limits (boundaries) were set at ±30°, marked with a magenta line. Values above +30° and below −30° were considered anomalies. The time intervals of anomaly occurrence are highlighted in the background with different shades of gray.

The limits were exceeded in all four cases analyzed:

• anomaly #1 (70–150 min) for time steps of 10, 15, and 20 min;
• anomaly #2 (290–310 min)—no anomalies detected;
• anomaly #3 (360–450 min) for all time steps;
• anomaly #4 (590–650 min) for all time steps.

The results of anomaly identification are summarized in

Table 2. Identification of anomalies based on increments of distance, speed, and course differences for various time steps.

Anomalies	Increments of Differences	Time Step
		5 min	10 min	15 min	20 min
A #1	Dist.	-	-	-	-
	SOG	-	x	x	x
	COG	-	x	x	x
A #2	Dist.	-	-	-	-
	SOG	-	x	x	-
	COG	-	-	-	-
A #3	Dist.	x	x	x	-
	SOG	x	x	x	x
	COG	x	x	x	x
A #4	Dist.	x	x	-	x
	SOG	x	x	x	-
	COG	x	x	x	x

, where x indicates the occurrence of an anomaly.

Exceedances were also observed at other time intervals (beyond the identified anomalies).

The exceedances of the adopted limits for the increments of parameter differences, as shown in Figure 19, Figure 20 and Figure 21, correspond to the situations manually assessed by the operator as anomalies.

5. Discussion

The detection of anomalies in a vessel’s movement, such as a sudden change in speed or a significant deviation from the course along the analyzed segment, does not necessarily indicate illegal activity. Therefore, it is advisable that the detected behaviors be subjected to an individual expert assessment to exclude routine operational maneuvers or emergency actions.

Different time steps were considered in the anomaly identification process due to the specific characteristics of the route and variations in speed and course. Under normal operational conditions, a ship follows a planned route from the starting point to the destination at a constant speed. Both deviations from the planned route (which require an amendment to the voyage plan approved by the master) and changes in speed are not standard behaviors. Except in cases of unexpected failures or other operational circumstances, such deviations should not occur.

Changes in speed may result from adjustments to the ship’s propulsion settings or may be a consequence of rapid and substantial course alterations. A situation may also arise in which both speed and course remain nearly constant, but maintaining such a condition leads to a gradual deviation from the planned trajectory and, consequently, the occurrence of an anomaly.

Course variations associated with collision-avoidance maneuvers, turning circles, and other navigational maneuvers require the use of a shorter prediction horizon. It can be expected that course changes will be the first indicator of an anomaly, followed by speed, and subsequently by distance.

The results of the conducted study confirm that anomalies in ship movement can be effectively identified based on the increments of differences between actual and predicted values of distance, speed, and course parameters—serving as indicators for anomaly detection. These indicators (increments of parameter differences) proved to be sensitive to irregularities suggesting non-standard vessel behavior, including unexpected course alterations and speed reductions leading to trajectory changes.

Previous research conducted by other authors has primarily focused on methods for tracking vessel trajectories using statistical tools and machine learning techniques. These studies have mainly addressed estimation tasks (elimination of erroneous messages, interpolation of missing data) and prediction of vessel movement parameters (forecasted movement characteristics). However, no prior studies have proposed the identification of anomalies based on the analysis of differences and increments of differences in these parameters.

The results obtained for passages between the North Sea and the Baltic Sea demonstrate the potential of the proposed method for early detection of suspicious behaviors. Sudden drops in speed were often associated with operational constraints or environmental conditions, while course deviations could indicate deliberate actions or technical failures. The combined use of distance-, speed-, and course-based indicators can improve and automate the anomaly identification process, thereby reducing the number of misinterpretations of performed maneuvers.

It was proposed that an anomaly should be defined as a situation in which at least two indicators exceed their threshold values, each for at least three analyzed time steps. According to these criteria, all anomalies in the movement of Ship A were correctly identified. In the case of Ship B (see Table 1), three out of four analyzed anomalies (#1, #3, and #4) were detected, with threshold exceedances observed for all indicators.

Difficulties occurred in identifying anomaly #2—a single course-change maneuver. Only the speed difference increment indicator suggested the presence of an anomaly. The reason for this may lie in the short duration of the maneuver, which might have gone unnoticed within the analyzed time steps.

Despite the promising results obtained, this study has certain limitations associated with the adopted simplifications. The analysis was conducted for a specific maritime area, a defined dataset, particular regional conditions, and a selected group of vessels. Therefore, generalizing the results on a global scale requires further adaptation of the proposed method to the specific characteristics of other maritime regions. Moreover, AIS data are inherently susceptible to errors, manipulation, and interruptions in transmission, which may affect the accuracy of anomaly detection. A potential improvement could involve the application of data estimation methods and tools proposed by other researchers. Furthermore, the integration of additional data sources, such as radar and satellite observations, could enhance the robustness and reliability of the proposed approach.

6. Conclusions

This study addressed the problem of anomaly identification in ship movements, focusing on the detection of irregularities that may indicate safety threats or non-compliant behavior. The proposed method introduces an innovative quantitative analysis of deviations in ship motion parameters from reference passages to identify anomalies in vessel trajectories.

The method is based on the analysis of differences and difference increments between the predicted and actual values of key navigational parameters—ship position, speed, and course—derived from AIS data. This approach enables a quantitative assessment of vessel behavior and provides interpretable indicators supporting maritime traffic monitoring.

Such a solution is valuable for authorities responsible for navigation safety, as it facilitates the automation of anomaly identification and decision-making processes. The results demonstrated that the proposed indicators effectively reveal deviations from typical navigational patterns, such as sudden speed changes or route deviations. The analysis of selected ship passages confirmed the applicability of the method for detecting anomalies arising from both operational and potentially intentional causes.

Compared with approaches presented in the literature, the proposed deterministic method is characterized by consistent anomaly identification criteria. At the same time, it supports expert evaluation of vessel behavior, which is of significant importance for practical applications in maritime safety monitoring systems. This method can be employed in both processing and post-processing stages.

In the proposed method, artificial intelligence tools in the form of artificial neural networks were employed. The application of Long Short-Term Memory (LSTM) networks for ship trajectory prediction based on AIS data demonstrated high potential. The model effectively captured spatiotemporal dependencies across different sampling frequencies and transformed motion history into accurate short-term forecasts of position, course, and speed.

This study further shows that although a single network architecture can be applied to multiple sampling schemes, the temporal resolution of the input data significantly affects the structure and volume of the training dataset, model performance, and forecast stability. Future work may include dynamic architecture tuning, the incorporation of external variables (e.g., weather conditions), or multi-step forecasting to enhance the robustness and practical applicability of the model.

Artificial intelligence tools, specifically artificial neural networks, were applied in the proposed method. The use of Long Short-Term Memory (LSTM) neural networks for vessel trajectory prediction based on AIS data demonstrated considerable potential. The model effectively captured spatiotemporal dependencies across various sampling frequencies and translated motion history into accurate short-term forecasts of position, course, and speed.

The obtained results provide a foundation for developing early warning mechanisms within vessel traffic monitoring systems. Future research should include the analysis of other shipping routes and the integration of additional information sources, such as radar and satellite observations, to enhance the robustness of the method. This may, in the future, enable adaptive risk assessment in a dynamic maritime environment and contribute to improving navigation safety, environmental protection, and the monitoring of critical maritime routes.

While the proposed method demonstrates strong performance in identifying anomalies across selected voyages, several limitations remain. First, AIS data are subject to temporal irregularities, reception gaps, and sensor noise. Second, the method currently relies on a threshold-based interpretation of prediction errors, which may require calibration across different vessel types or regions. Third, the approach does not yet incorporate additional sensor sources such as radar or satellite imagery. Future work will address these limitations by integrating multi-sensor fusion, extending the method to diverse geographic regions, and exploring hybrid models that incorporate collision risk and environmental context.