Author Contributions
Conceptualization, N.Z., S.P. and A.S.; Methodology, N.Z., S.P., A.S. and T.C.H.; Software, N.Z. and S.P.; Validation, N.Z., S.P., A.S., T.C.H. and P.C.E.; Formal analysis, N.Z., S.P. and A.S.; Resources, S.P. and P.C.E.; Writing—original draft, N.Z.; Writing—review & editing, N.Z., S.P., A.S., T.C.H. and P.C.E.; Visualization, N.Z. and S.P.; Supervision, S.P.; Funding acquisition, T.C.H., P.C.E., S.P. and A.S. All authors have read and agreed to the published version of the manuscript.
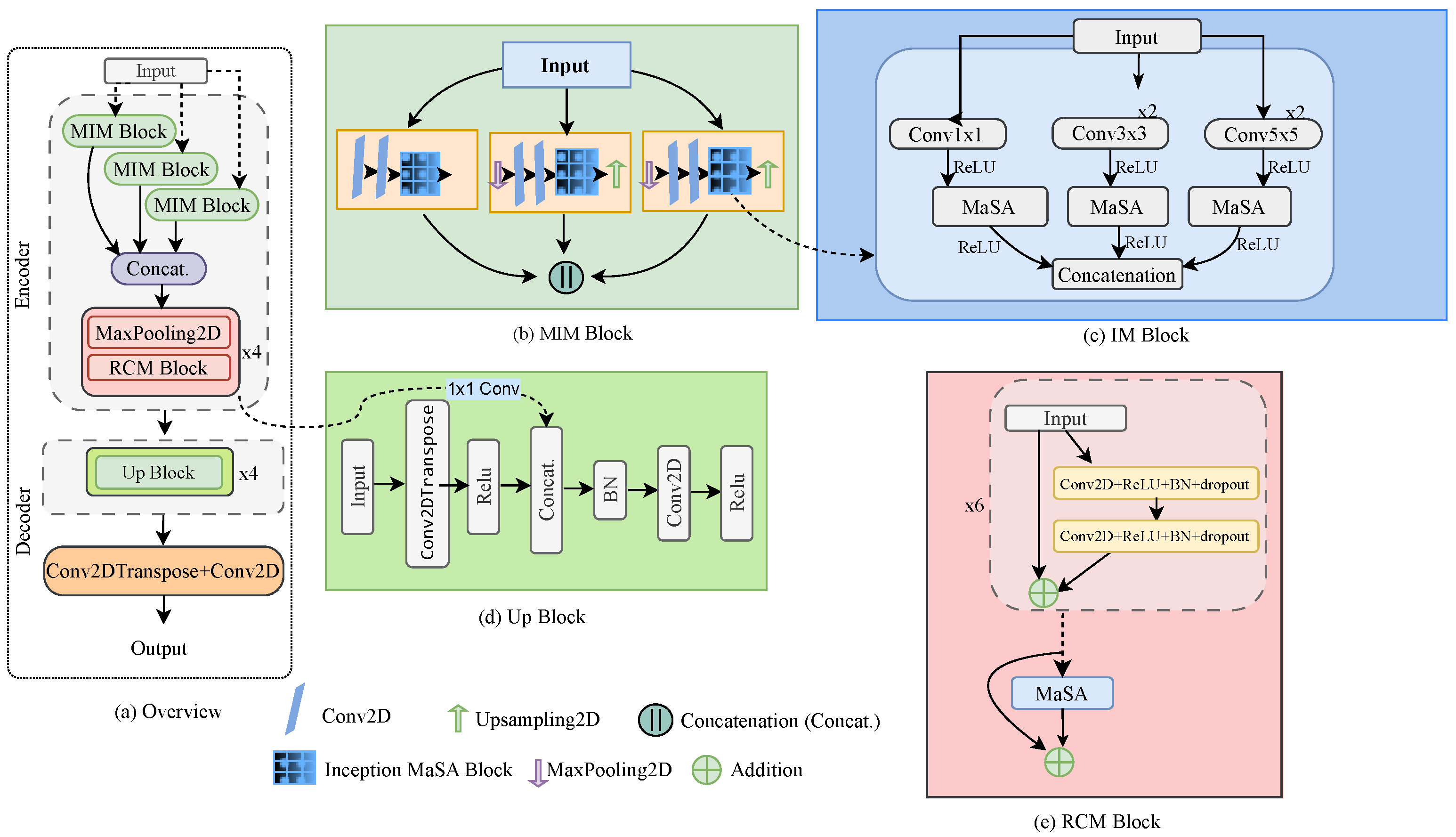
Figure 1.
Overview of the proposed MIMAR-Net architecture for underwater image SR: (a) overall architecture of the proposed deep network, (b) multiscale inception MaSA (MIM) block, (c) inception MaSA (IM) block, (d) upsampling block (Up block), and (e) residual convolutional MaSA (RCM) block.
Figure 1.
Overview of the proposed MIMAR-Net architecture for underwater image SR: (a) overall architecture of the proposed deep network, (b) multiscale inception MaSA (MIM) block, (c) inception MaSA (IM) block, (d) upsampling block (Up block), and (e) residual convolutional MaSA (RCM) block.
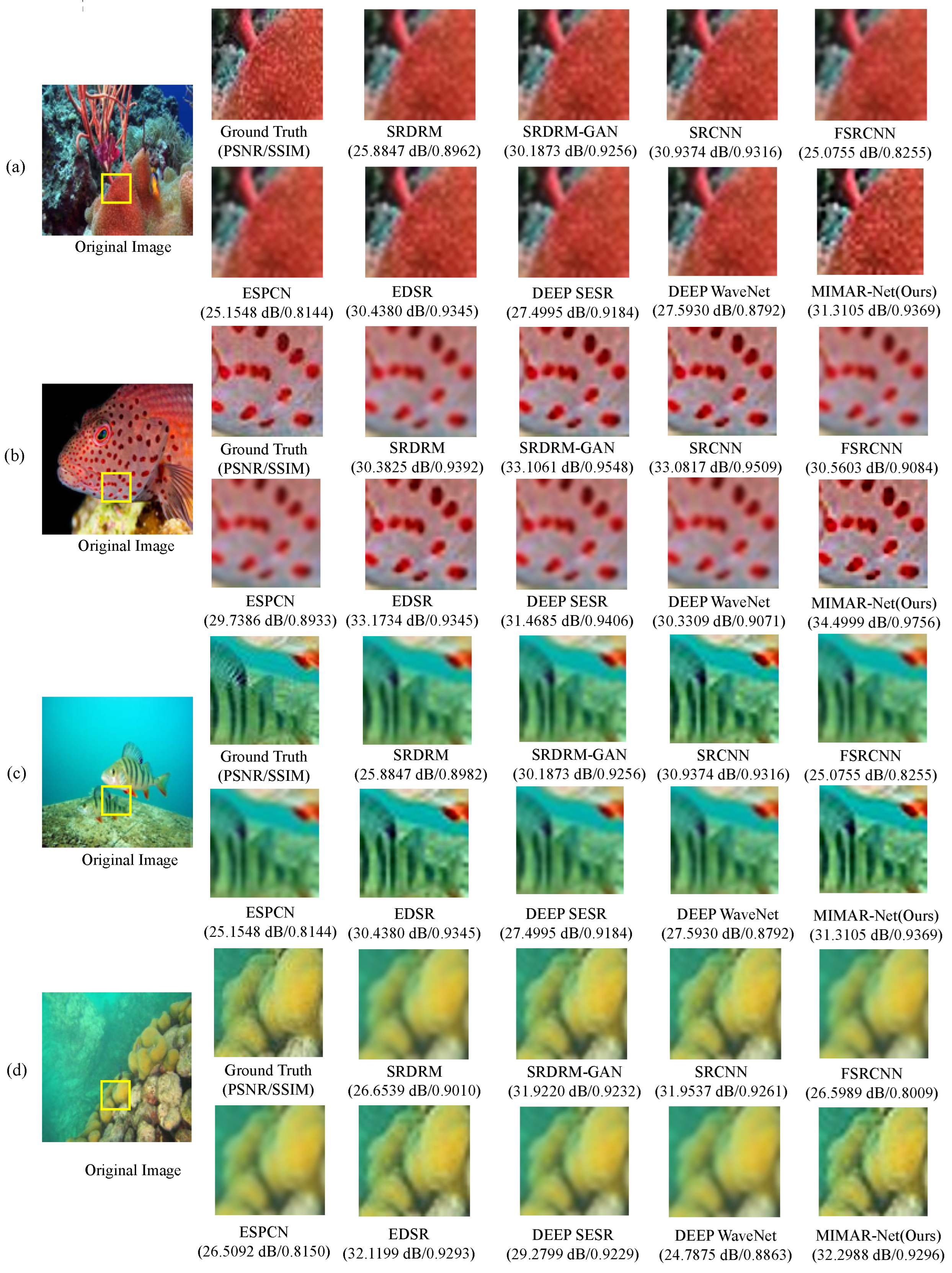
Figure 2.
Visual comparisons for upsampling on underwater image sampled from UFO-120 dataset. Images (a–d) are different sample images from this dataset.
Figure 2.
Visual comparisons for upsampling on underwater image sampled from UFO-120 dataset. Images (a–d) are different sample images from this dataset.
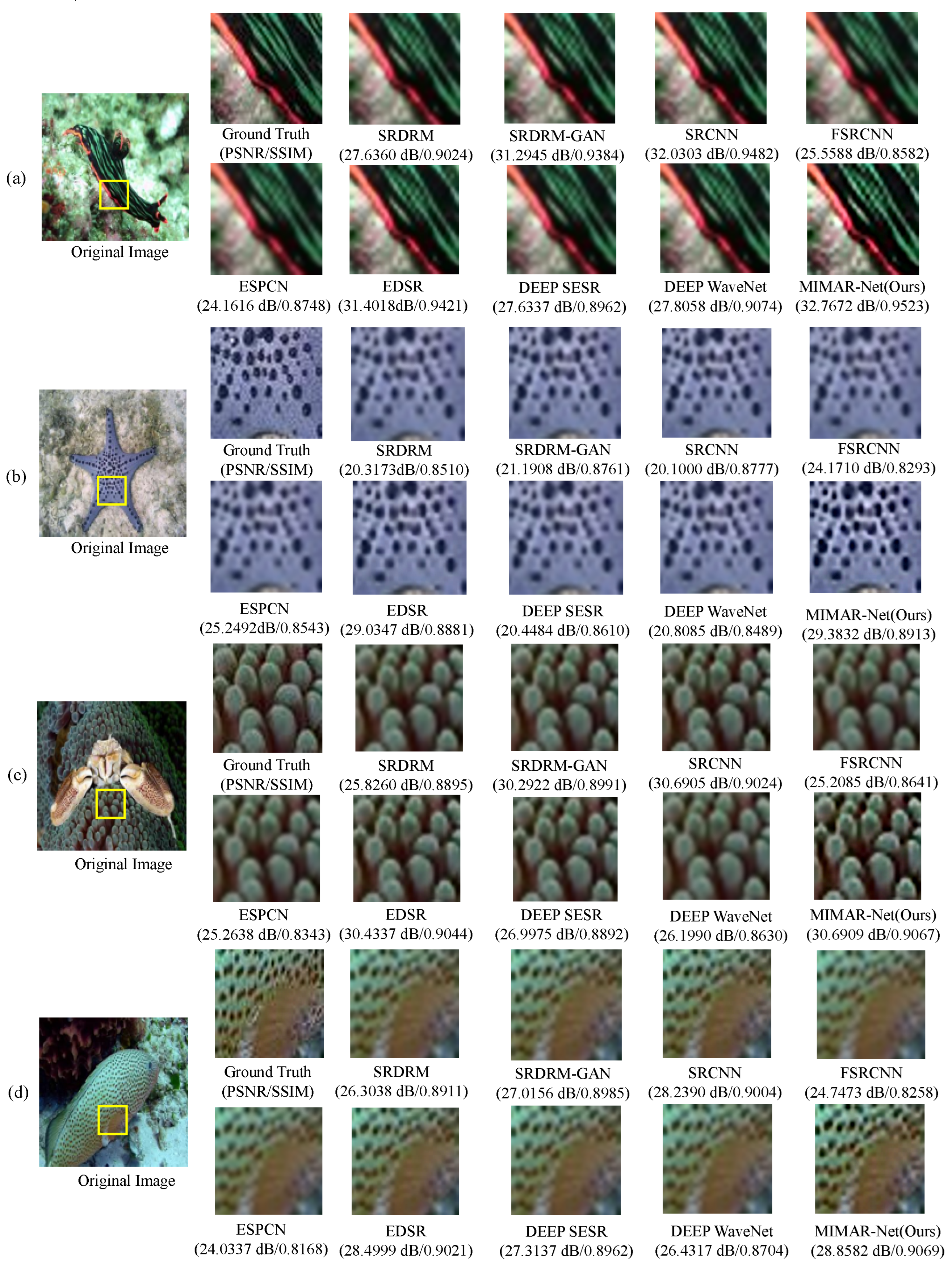
Figure 3.
Visual comparisons for upsampling on underwater image sampled from USR-248 dataset. Images (a–d) are different samples images from this dataset.
Figure 3.
Visual comparisons for upsampling on underwater image sampled from USR-248 dataset. Images (a–d) are different samples images from this dataset.
Figure 4.
Visual comparisons for upsampling on an underwater image sampled from the EUVP dataset. Images (a–d) are different samples images from this dataset.
Figure 4.
Visual comparisons for upsampling on an underwater image sampled from the EUVP dataset. Images (a–d) are different samples images from this dataset.
Table 1.
Quantitative evaluation of SISR models on the UFO-120 dataset at upscaling. We report mean ± SD for PSNR, SSIM, UIQM, LPIPS, and FID. Best results are in bold. The ↑ indicates that higher values represent better performance and the ↓ indicates that lower values represent better performance.
Table 1.
Quantitative evaluation of SISR models on the UFO-120 dataset at upscaling. We report mean ± SD for PSNR, SSIM, UIQM, LPIPS, and FID. Best results are in bold. The ↑ indicates that higher values represent better performance and the ↓ indicates that lower values represent better performance.
| Model | PSNR (dB) ↑ | SSIM ↑ | UIQM ↑ | LPIPS ↓ | FID ↓ |
|---|
| SRDRM [16] | 26.46 ± 1.89 | 0.8412 ± 0.06 | 2.5811 ± 0.012 | 0.0018 | 2.66 |
| SRDRM-GAN [16] | 27.93 ± 2.10 | 0.8710 ± 0.05 | 2.5981 ± 0.011 | 0.0016 | 2.62 |
| SRCNN [14] | 28.25 ± 3.18 | 0.8780 ± 0.05 | 2.5982 ± 0.010 | 0.0017 | 2.51 |
| FSRCNN [15] | 28.01 ± 3.17 | 0.8720 ± 0.05 | 2.6002 ± 0.010 | 0.0022 | 2.76 |
| ESPCN [23] | 29.02 ± 3.23 | 0.8419 ± 0.05 | 2.6018 ± 0.011 | 0.0025 | 2.80 |
| EDSR [24] | 29.00 ± 3.10 | 0.8710 ± 0.05 | 2.5701 ± 0.010 | 0.0015 | 2.46 |
| Deep SESR [17] | 28.58 ± 2.21 | 0.8603 ± 0.05 | 2.5907 ± 0.010 | 0.0018 | 2.72 |
| Deep WaveNet [25] | 26.91 ± 2.72 | 0.8359 ± 0.12 | 2.5910 ± 0.009 | 0.0022 | 2.67 |
| MIMAR-Net (Ours) | 29.18 ± 3.40 | 0.8831 ± 0.05 | 2.6788 ± 0.008 | 0.0012 | 2.49 |
Table 2.
Quantitative evaluation of SISR models on the UFO-120 dataset at upscaling. We report mean ± SD for PSNR, SSIM, UIQM, LPIPS, and FID. Best results are in bold. The ↑ indicates that higher values represent better performance and the ↓ indicates that lower values represent better performance.
Table 2.
Quantitative evaluation of SISR models on the UFO-120 dataset at upscaling. We report mean ± SD for PSNR, SSIM, UIQM, LPIPS, and FID. Best results are in bold. The ↑ indicates that higher values represent better performance and the ↓ indicates that lower values represent better performance.
| Model | PSNR (dB) ↑ | SSIM ↑ | UIQM ↑ | LPIPS ↓ | FID ↓ |
|---|
| SRDRM [16] | 25.77 ± 2.71 | 0.7345 ± 0.10 | 2.5805 ± 0.010 | 0.0024 | 2.72 |
| SRDRM-GAN [16] | 25.94 ± 2.75 | 0.7353 ± 0.09 | 2.5859 ± 0.009 | 0.0020 | 2.67 |
| SRCNN [14] | 26.34 ± 3.39 | 0.7432 ± 0.11 | 2.5836 ± 0.007 | 0.0021 | 2.57 |
| FSRCNN [15] | 26.54 ± 3.04 | 0.7472 ± 0.10 | 2.5844 ± 0.008 | 0.0026 | 2.80 |
| ESPCN [23] | 26.54 ± 3.20 | 0.7485 ± 0.10 | 2.5852 ± 0.008 | 0.0031 | 2.83 |
| EDSR [24] | 26.59 ± 3.27 | 0.7490 ± 0.10 | 2.5648 ± 0.008 | 0.0019 | 2.51 |
| Deep SESR [17] | 25.89 ± 2.71 | 0.7318 ± 0.10 | 2.5859 ± 0.010 | 0.0025 | 2.78 |
| Deep WaveNet [25] | 25.97 ± 2.71 | 0.7381 ± 0.12 | 2.5842 ± 0.008 | 0.0028 | 2.75 |
| MIMAR-Net (Ours) | 26.79 ± 3.16 | 0.7517 ± 0.10 | 2.6528 ± 0.008 | 0.0018 | 2.55 |
Table 3.
Quantitative evaluation of SISR models on the USR-248 dataset at upscaling. We report mean ± SD for PSNR, SSIM, UIQM, LPIPS, and FID. Best results are in bold. The ↑ indicates that higher values represent better performance and the ↓ indicates that lower values represent better performance.
Table 3.
Quantitative evaluation of SISR models on the USR-248 dataset at upscaling. We report mean ± SD for PSNR, SSIM, UIQM, LPIPS, and FID. Best results are in bold. The ↑ indicates that higher values represent better performance and the ↓ indicates that lower values represent better performance.
| Model | PSNR (dB) ↑ | SSIM ↑ | UIQM ↑ | LPIPS ↓ | FID ↓ |
|---|
| SRDRM [16] | 26.74 ± 1.91 | 0.8551 ± 0.05 | 2.9280 ± 0.009 | 0.0021 | 2.63 |
| SRDRM-GAN [16] | 27.91 ± 2.05 | 0.8678 ± 0.05 | 2.9087 ± 0.008 | 0.0019 | 2.57 |
| SRCNN [14] | 28.05 ± 3.39 | 0.8764 ± 0.05 | 2.8289 ± 0.010 | 0.0018 | 2.48 |
| FSRCNN [15] | 27.63 ± 3.01 | 0.8696 ± 0.05 | 2.8009 ± 0.010 | 0.0021 | 2.75 |
| ESPCN [23] | 28.08 ± 3.18 | 0.8615 ± 0.06 | 2.8011 ± 0.009 | 0.0024 | 2.77 |
| EDSR [24] | 29.01 ± 3.26 | 0.8612 ± 0.05 | 2.8020 ± 0.010 | 0.0017 | 2.49 |
| Deep SESR [17] | 27.61 ± 2.15 | 0.8703 ± 0.05 | 2.7216 ± 0.011 | 0.0020 | 2.66 |
| Deep WaveNet [25] | 25.98 ± 2.68 | 0.8244 ± 0.13 | 2.7091 ± 0.010 | 0.0023 | 2.71 |
| MIMAR-Net (Ours) | 29.10 ± 2.87 | 0.8827 ± 0.06 | 2.9035 ± 0.007 | 0.0013 | 2.44 |
Table 4.
Quantitative evaluation of SISR models on the USR-248 dataset at upscaling. We report mean ± SD for PSNR, SSIM, UIQM, LPIPS, and FID. Best results are in bold. The ↑ indicates that higher values represent better performance and the ↓ indicates that lower values represent better performance.
Table 4.
Quantitative evaluation of SISR models on the USR-248 dataset at upscaling. We report mean ± SD for PSNR, SSIM, UIQM, LPIPS, and FID. Best results are in bold. The ↑ indicates that higher values represent better performance and the ↓ indicates that lower values represent better performance.
| Model | PSNR (dB) ↑ | SSIM ↑ | UIQM ↑ | LPIPS ↓ | FID ↓ |
|---|
| SRDRM [16] | 22.67 ± 2.67 | 0.7108 ± 0.08 | 2.9029 ± 0.010 | 0.0024 | 2.70 |
| SRDRM-GAN [16] | 25.41 ± 2.71 | 0.7044 ± 0.09 | 2.8871 ± 0.007 | 0.0021 | 2.65 |
| SRCNN [14] | 26.27 ± 3.29 | 0.7411 ± 0.10 | 2.8039 ± 0.009 | 0.0020 | 2.56 |
| FSRCNN [15] | 25.72 ± 3.07 | 0.7387 ± 0.09 | 2.7847 ± 0.009 | 0.0024 | 2.79 |
| ESPCN [23] | 26.28 ± 3.12 | 0.7454 ± 0.10 | 2.7959 ± 0.008 | 0.0028 | 2.81 |
| EDSR [24] | 26.33 ± 3.21 | 0.7421 ± 0.10 | 2.7851 ± 0.009 | 0.0017 | 2.50 |
| Deep SESR [17] | 24.62 ± 2.88 | 0.7391 ± 0.11 | 2.6755 ± 0.010 | 0.0023 | 2.74 |
| Deep WaveNet [25] | 23.83 ± 2.84 | 0.6849 ± 0.12 | 2.6860 ± 0.009 | 0.0025 | 2.72 |
| MIMAR-Net (Ours) | 26.65 ± 3.11 | 0.7496 ± 0.09 | 2.8889 ± 0.008 | 0.0015 | 2.52 |
Table 5.
Quantitative evaluation of SISR models on the EUVP dataset at upscaling. We report mean ± SD for PSNR, SSIM, UIQM, LPIPS, and FID. Best results are in bold. The ↑ indicates that higher values represent better performance and the ↓ indicates that lower values represent better performance.
Table 5.
Quantitative evaluation of SISR models on the EUVP dataset at upscaling. We report mean ± SD for PSNR, SSIM, UIQM, LPIPS, and FID. Best results are in bold. The ↑ indicates that higher values represent better performance and the ↓ indicates that lower values represent better performance.
| Model | PSNR (dB) ↑ | SSIM ↑ | UIQM ↑ | LPIPS ↓ | FID ↓ |
|---|
| SRDRM | 30.42 ± 1.98 | 0.9033 ± 0.03 | 4.0480 ± 0.012 | 0.0019 | 2.41 |
| SRDRM-GAN | 37.17 ± 2.25 | 0.9707 ± 0.02 | 4.1671 ± 0.010 | 0.0014 | 2.37 |
| SRCNN | 37.42 ± 2.38 | 0.9701 ± 0.02 | 4.1208 ± 0.011 | 0.0013 | 2.28 |
| FSRCNN | 36.92 ± 2.52 | 0.9658 ± 0.02 | 4.1049 ± 0.010 | 0.0016 | 2.32 |
| ESPCN | 36.90 ± 2.40 | 0.9662 ± 0.02 | 4.1110 ± 0.009 | 0.0018 | 2.25 |
| EDSR | 37.68 ± 2.30 | 0.9660 ± 0.02 | 4.1185 ± 0.009 | 0.0012 | 2.22 |
| Deep SESR | 30.60 ± 1.85 | 0.9383 ± 0.03 | 4.2405 ± 0.009 | 0.0017 | 2.48 |
| Deep WaveNet | 31.16 ± 2.00 | 0.9063 ± 0.04 | 4.0106 ± 0.010 | 0.0020 | 2.51 |
| MIMAR-Net (Ours) | 38.96 ± 2.43 | 0.9720 ± 0.02 | 4.1989 ± 0.010 | 0.0011 | 2.18 |
Table 6.
Quantitative evaluation of SISR models on the EUVP dataset at upscaling. We report mean ± SD for PSNR, SSIM, UIQM, LPIPS, and FID. Best results are in bold. The ↑ indicates that higher values represent better performance and the ↓ indicates that lower values represent better performance.
Table 6.
Quantitative evaluation of SISR models on the EUVP dataset at upscaling. We report mean ± SD for PSNR, SSIM, UIQM, LPIPS, and FID. Best results are in bold. The ↑ indicates that higher values represent better performance and the ↓ indicates that lower values represent better performance.
| Model | PSNR (dB) ↑ | SSIM ↑ | UIQM ↑ | LPIPS ↓ | FID ↓ |
|---|
| SRDRM | 29.93 ± 2.04 | 0.8949 ± 0.03 | 3.5821 ± 0.010 | 0.0021 | 2.49 |
| SRDRM-GAN | 37.32 ± 2.40 | 0.9505 ± 0.02 | 3.6878 ± 0.011 | 0.0016 | 2.41 |
| SRCNN | 37.13 ± 2.36 | 0.9499 ± 0.02 | 3.5231 ± 0.009 | 0.0015 | 2.31 |
| FSRCNN | 36.01 ± 2.48 | 0.9498 ± 0.02 | 3.6045 ± 0.010 | 0.0019 | 2.30 |
| ESPCN | 36.11 ± 2.47 | 0.9402 ± 0.02 | 3.6104 ± 0.010 | 0.0022 | 2.35 |
| EDSR | 37.43 ± 2.51 | 0.9516 ± 0.02 | 3.6060 ± 0.009 | 0.0014 | 2.26 |
| Deep SESR | 30.21 ± 1.96 | 0.9281 ± 0.03 | 3.5181 ± 0.008 | 0.0020 | 2.54 |
| Deep WaveNet | 31.09 ± 2.10 | 0.8951 ± 0.03 | 3.7936 ± 0.008 | 0.0021 | 2.59 |
| MIMAR-Net (Ours) | 38.39 ± 2.61 | 0.9549 ± 0.02 | 3.6278 ± 0.009 | 0.0013 | 2.22 |
Table 7.
Quantitative evaluation of SISR models on the BSD100 dataset at upscaling, using PSNR and SSIM. Best results are in bold. The ↑ indicates that higher values represent better performance.
Table 7.
Quantitative evaluation of SISR models on the BSD100 dataset at upscaling, using PSNR and SSIM. Best results are in bold. The ↑ indicates that higher values represent better performance.
| Model | Year | PSNR (dB) ↑ | SSIM ↑ |
|---|
| SRGAN [43] | 2017 | 25.17 | 0.6408 |
| SRResNet [43] | 2017 | 26.32 | 0.6940 |
| MS-LapSRN [44] | 2017 | 27.41 | 0.7306 |
| HGFormer [45] | 2025 | 27.88 | 0.7480 |
| EARFA [46] | 2024 | 27.75 | 0.7431 |
| MIMAR-Net (Ours) | N/A | 26.16 | 0.7395 |
Table 8.
GFLOPs and parameter counts for each model (evaluated on 128 × 128 inputs). All models were tested on an NVIDIA RTX 6000 GPU.
Table 8.
GFLOPs and parameter counts for each model (evaluated on 128 × 128 inputs). All models were tested on an NVIDIA RTX 6000 GPU.
| Model | Params (M) | GFLOPs |
|---|
| SRDRM | 1.78 | 58.226 |
| SRDRM-GAN | 6.99 | 217.871 |
| SRCNN | 0.057 | 1.894 |
| FSRCNN | 0.012 | 0.404 |
| ESPCN | 0.020 | 0.701 |
| EDSR | 43.00 | 1419.852 |
| Deep SESR | 2.07 | 127.028 |
| Deep WaveNet | 10.22 | 351.149 |
| Lightweight MIMAR-Net (Ours) | 9.72 | 106.89 |
| MIMAR-Net (Ours) | 22.78 | 368.744 |
Table 9.
Ablation study of loss functions for and upscaling on the UFO-120 dataset. The best scores are marked in bold. The ↑ indicates that higher values represent better performance. The ✓ indicates the inclusion of that loss component.
Table 9.
Ablation study of loss functions for and upscaling on the UFO-120 dataset. The best scores are marked in bold. The ↑ indicates that higher values represent better performance. The ✓ indicates the inclusion of that loss component.
| Loss Functions | | |
|---|
| | | PSNR (dB) ↑ | SSIM ↑ | UIQM ↑ | PSNR (dB) ↑ | SSIM ↑ | UIQM ↑ |
| ✓ | | | 26.1737 | 0.8795 | 2.6012 | 23.1827 | 0.7205 | 2.5866 |
| ✓ | ✓ | | 27.4347 | 0.8762 | 2.5919 | 24.2086 | 0.7246 | 2.5861 |
| ✓ | ✓ | ✓ | 29.1830 | 0.8831 | 2.6788 | 26.7902 | 0.7517 | 2.6528 |
Table 10.
Ablation study of loss functions on the and upscaling dataset on the USR-248 dataset. The best scores are marked in bold. The ↑ indicates that higher values represent better performance. The ✓ indicates the inclusion of that loss component.
Table 10.
Ablation study of loss functions on the and upscaling dataset on the USR-248 dataset. The best scores are marked in bold. The ↑ indicates that higher values represent better performance. The ✓ indicates the inclusion of that loss component.
| Loss Functions | | |
|---|
| | | PSNR (dB) ↑ | SSIM ↑ | UIQM ↑ | PSNR (dB) ↑ | SSIM ↑ | UIQM ↑ |
| ✓ | | | 28.1015 | 0.8799 | 2.8022 | 26.0128 | 0.7464 | 2.8873 |
| ✓ | ✓ | | 28.5140 | 0.8801 | 2.8020 | 25.9603 | 0.7440 | 2.8867 |
| ✓ | ✓ | ✓ | 29.1049 | 0.8827 | 2.9035 | 26.6512 | 0.7496 | 2.8889 |
Table 11.
Ablation study of loss functions on the and upscaling dataset on the EUVP dataset. The best scores are marked in bold. The ↑ indicates that higher values represent better performance. The ✓ indicates the inclusion of that loss component.
Table 11.
Ablation study of loss functions on the and upscaling dataset on the EUVP dataset. The best scores are marked in bold. The ↑ indicates that higher values represent better performance. The ✓ indicates the inclusion of that loss component.
| Loss Functions | | |
|---|
| | | PSNR (dB) ↑ | SSIM ↑ | UIQM ↑ | PSNR (dB) ↑ | SSIM ↑ | UIQM ↑ |
| ✓ | | | 35.7727 | 0.9714 | 4.1626 | 36.2289 | 0.9515 | 3.5805 |
| ✓ | ✓ | | 35.8370 | 0.9671 | 4.1337 | 33.2465 | 0.9359 | 3.5796 |
| ✓ | ✓ | ✓ | 38.9560 | 0.9720 | 4.1989 | 38.3866 | 0.9549 | 3.6278 |
Table 12.
Ablation study of different SSIM, MSE, and MAE loss weight combinations for the ×4 upscaling task on the UFO-120 dataset. The best scores are marked in bold. The ↑ indicates that higher values represent better performance.
Table 12.
Ablation study of different SSIM, MSE, and MAE loss weight combinations for the ×4 upscaling task on the UFO-120 dataset. The best scores are marked in bold. The ↑ indicates that higher values represent better performance.
| | | PSNR (dB) ↑ | SSIM ↑ | UIQM ↑ |
|---|
| 1.0 | 1.0 | 1.0 | 26.7502 | 0.7511 | 2.6508 |
| 0.3 | 0.5 | 0.2 | 24.0863 | 0.7325 | 2.5993 |
| 0.6 | 0.2 | 0.2 | 26.7902 | 0.7517 | 2.6528 |
| 0.5 | 0.3 | 0.2 | 24.8060 | 0.7384 | 2.6063 |
| 0.4 | 0.3 | 0.3 | 26.5500 | 0.7510 | 2.6063 |
Table 13.
Ablation study of different MIMAR-Net blocks on the upscaling for the UFO-120 dataset. The best scores are marked in bold. The ↑ indicates that higher values represent better performance. The ✓ indicates the inclusion of that block.
Table 13.
Ablation study of different MIMAR-Net blocks on the upscaling for the UFO-120 dataset. The best scores are marked in bold. The ↑ indicates that higher values represent better performance. The ✓ indicates the inclusion of that block.
| Multiscale Block | IM Block | RCM Block | PSNR (dB) ↑ | SSIM ↑ | UIQM ↑ |
|---|
| ✓ | ✓ | | 26.6814 | 0.7503 | 2.6459 |
| | ✓ | ✓ | 26.0669 | 0.7468 | 2.6460 |
| ✓ | | ✓ | 26.6463 | 0.7504 | 2.6455 |
| ✓ | ✓ | ✓ | 26.7902 | 0.7517 | 2.6528 |
Table 14.
Ablation study of different MIMAR-Net blocks on the upscaling for the USR-248 dataset. The best scores are marked in bold. The ↑ indicates that higher values represent better performance. The ✓ indicates the inclusion of that block.
Table 14.
Ablation study of different MIMAR-Net blocks on the upscaling for the USR-248 dataset. The best scores are marked in bold. The ↑ indicates that higher values represent better performance. The ✓ indicates the inclusion of that block.
| Multiscale Block | IM Block | RCM Block | PSNR (dB) ↑ | SSIM ↑ | UIQM ↑ |
|---|
| ✓ | ✓ | | 26.4418 | 0.7458 | 2.8868 |
| | ✓ | ✓ | 26.5429 | 0.7469 | 2.8859 |
| ✓ | | ✓ | 26.3201 | 0.7451 | 2.8853 |
| ✓ | ✓ | ✓ | 26.6512 | 0.7496 | 2.8889 |
Table 15.
Ablation study of different MIMAR-Net blocks on the upscaling for the EUVP dataset. The best scores are marked in bold. The ↑ indicates that higher values represent better performance. The ✓ indicates the inclusion of that block.
Table 15.
Ablation study of different MIMAR-Net blocks on the upscaling for the EUVP dataset. The best scores are marked in bold. The ↑ indicates that higher values represent better performance. The ✓ indicates the inclusion of that block.
| Multiscale Block | IM Block | RCM Block | PSNR (dB) ↑ | SSIM ↑ | UIQM ↑ |
|---|
| ✓ | ✓ | | 36.9680 | 0.9547 | 3.5803 |
| | ✓ | ✓ | 36.4013 | 0.9535 | 3.5523 |
| ✓ | | ✓ | 37.7093 | 0.9525 | 3.5321 |
| ✓ | ✓ | ✓ | 38.3866 | 0.9549 | 3.6278 |
Table 16.
Ablation study comparing MIMAR-Net with alternative attention modules (CBAM and SENet) instead of MaSA across the UFO-120 dataset with upscaling. The best scores are marked in bold. The ↑ indicates that higher values represent better performance. The ✓ indicates the inclusion of that block.
Table 16.
Ablation study comparing MIMAR-Net with alternative attention modules (CBAM and SENet) instead of MaSA across the UFO-120 dataset with upscaling. The best scores are marked in bold. The ↑ indicates that higher values represent better performance. The ✓ indicates the inclusion of that block.
| CBAM | SENet | MaSA | PSNR (dB) ↑ | SSIM ↑ | UIQM ↑ |
|---|
| ✓ | | | 27.8152 | 0.8774 | 2.2215 |
| | ✓ | | 28.5035 | 0.8807 | 2.2343 |
| | | ✓ | 29.1830 | 0.8831 | 2.6788 |
Table 17.
Ablation study comparing MIMAR-Net with alternative attention modules (CBAM and SENet) instead of MaSA across the USR-248 dataset with upscaling. The best scores are marked in bold. The ↑ indicates that higher values represent better performance. The ✓ indicates the inclusion of that block.
Table 17.
Ablation study comparing MIMAR-Net with alternative attention modules (CBAM and SENet) instead of MaSA across the USR-248 dataset with upscaling. The best scores are marked in bold. The ↑ indicates that higher values represent better performance. The ✓ indicates the inclusion of that block.
| CBAM | SENet | MaSA | PSNR (dB) ↑ | SSIM ↑ | UIQM ↑ |
|---|
| ✓ | | | 28.2767 | 0.8795 | 2.4362 |
| | ✓ | | 28.5813 | 0.8811 | 2.4082 |
| | | ✓ | 29.1049 | 0.8827 | 2.9035 |
Table 18.
Ablation study comparing MIMAR-Net with alternative attention modules (CBAM and SENet) instead of MaSA across the EUVP dataset with upscaling. The best scores are marked in bold. The ↑ indicates that higher values represent better performance. The ✓ indicates the inclusion of that block.
Table 18.
Ablation study comparing MIMAR-Net with alternative attention modules (CBAM and SENet) instead of MaSA across the EUVP dataset with upscaling. The best scores are marked in bold. The ↑ indicates that higher values represent better performance. The ✓ indicates the inclusion of that block.
| CBAM | SENet | MaSA | PSNR (dB) ↑ | SSIM ↑ | UIQM ↑ |
|---|
| ✓ | | | 36.7816 | 0.9541 | 4.3901 |
| | ✓ | | 34.6770 | 0.9630 | 4.1092 |
| | | ✓ | 38.9560 | 0.9720 | 4.1989 |