Range Extension for Underwater Communication via Magnetic Induction Using Parametric Analysis of MI Coils in IoUT Networks

Abstract

This paper discusses the method for extending the range of Magnetic Induction (MI) and its application in underwater networks for the Internet of Underwater Things (IoUT). In underwater communication, this technology would provide a wider frequency band than acoustic systems, shorter propagation delay, and increased conductivity, with the added benefit of underwater wireless power transfer. As a use case, we consider a system that allows energy to be transferred from one circuit to another without cables, as in an aerial environment. In this work, transmit and receive coils for underwater environments are designed and analyzed using ANSYS Maxwell v16.0 software. The results show an improvement in terms of underwater magnetic field propagation. We have conducted underwater experiments by applying a frequency range up to 100 kHz and 12 Volts with varied current, achieving a distance up to 80% greater than in air, as determined by parametric analysis. With an improved bit error rate, a delay of less than 2 microseconds, a packet delivery ratio near 100%, and a packet loss ratio less than 10%, the results show an improvement in magnetic field propagation underwater. This demonstrates that it is possible to conduct future research into other underwater applications by implementing MI for underwater communication.

1. Introduction

IoUT is a sub-category of the Internet of Things (IoT) that provides internet connectivity to the devices that operate underwater. Some of the typical applications for IoUT are environmental surveillance (including water quality, pollution monitoring, oil and gas pipeline monitoring), submarine exploration (shipwrecks, biomass stock, fauna and benthic biology, and other natural resources discovery), disaster preparedness (flood and earthquake detection), military applications (submarine and mine detection), and in analysis of sports and navigational aids [1,2].

The Underwater Wireless Sensor Networks (UWSNs) are used to propagate data through these IoUT devices. However, underwater communication has five major challenges: latency, reliability, bandwidth, energy consumption, and mobility. Latency is a challenge because the propagation of underwater signals is as low as 1500 m/s and is vulnerable to environmental factors such as pressure, salinity, temperature, and transceiver depth. Reliability is another challenge that depends on error-free data delivery. In acoustic communication, the data rate is very low, but by using MI, high data rates can be achieved that may enable underwater IoT connectivity [3]. Bandwidth magnitude, using low energy for underwater communication, is another challenge. Replacing batteries or charging the sensor node is another challenge. Water currents are in motion, so there is a chance a node will drift away [4].

Wireless power transfer (WPT) is emerging as a new approach for powering underwater equipment. This technology offers significant advantages over traditional methods, as it improves the safety, reliability, and convenience of charging. Specifically, underwater wireless power transfer (UWPT) can automate power supply for underwater equipment, potentially eliminating the need for manual charging operations. Magnetic Induction, which is also a common basis for underwater wireless power transfer, can also be used for data communication. It is relatively stable and less influenced by changes in the underwater environment.

A WPT module consists of two coils, with or without a core, used as a transmitter and receiver. When current passes through a conductive coil, an electromagnetic field is produced, which is transmitted between the coils by means of their mutual inductance. The magnetic flux produced in the primary coil must be received in the secondary coil with minimal leakage inductance. The design parameters to be considered for both coils are the number of turns, wire gauge, coil material, and coil size. To avoid leakage inductance, LC circuits are used with resonance frequencies such that maximum flux is achieved in the receiving coil, and maximum power transfer occurs [5].

This work has the following structure: Section 2 presents the most recent work related to MI technology applied to networks and possible architectures for the WPT module. Section 3 provides a discussion of the results obtained from the parametric analysis conducted with the ANSYS Maxwell solver and the real-time laboratory experimentation. Section 4 concludes the comprehensive work with future recommendations.

Preliminaries

Radio frequency is absorbed by water; hence, RF cannot be used for communication purposes underwater.

Underwater acoustic signals are affected by various environmental factors like salinity, temperature, pressure, and the depth of the transmitting and receiving devices. Additional challenges include absorption and transmission losses, as well as scattering and the Doppler effect caused by the movement of the devices or changes in the environment [6,7].

Optical signals are susceptible to scattering and require a line of sight. They are affected by absorption losses and turbulence.

Table 1. Permeability and conductivity comparison.

	Magnetic Permeability µ (H/m)	Electrical Conductivity σ (S/m)
Water	1.256627 × 10−6	4.8
Air	1.256637 × 10−6	10−15 to 10−9

shows the comparison of magnetic permeability and electrical conductivity in air and water, the two most common media when considering MI.

Table 2. Underwater communication techniques [3].

Communication Type	Data Rate	Range	Constraints
MI	Mb/s	10 m to 100 m	Conductivity
EM	Mb/s	<10 m	Conductivity
Optical	Mb/s	10 m to 100 m	Light scattering, line of sight communication, and ambient light noise
Acoustic	Kb/s	<100 km	Doppler, temperature, pressure, salinity, environmental sound noise

shows the competitive advantage of MI in terms of data rate over alternative communication technologies.

Table 3. Advantages and disadvantages of using MI.

Advantages

Disadvantages

(MI) is not affected by scattering and reflection. It can penetrate through ice, water, rock, and soil [8]. Propagation delay (underwater) is very low [9]: (MI): 3.33 × 10−7 s/m (Acoustic): 0.6 × 10−3 s/m Electrical conductivity in water is greater than in air [3]: water: 4.8 σ (S/m) air: 10−15…10−9 σ (S/m) Wireless power transfer (WPT) is possible in MI [3] High data rates are achievable in MI Stealth communication is possible in MI

Range lower than acoustic (<100 m) [3] Magnetic field varying in time; affects info exchange Tx-Rx

shows the advantages and disadvantages of using MI.

In order to improve the range between coils, the values for the design parameters discussed in this work have been adjusted to achieve the most effective results while maintaining acceptable cost, power consumption, and size of coil. In [10], the author discusses the energy efficiency research gaps in the IoUT.

In Refs. [3,11] the importance of MI is discussed for the IoUT. It provides a platform to overcome challenges faced in underwater wireless communication. By achieving a high data rate in underwater environments, countless wireless applications can be used to enable the IoUT. Figure 1 explains the parameters and constraints for a WPT system.

In a WPT system, performance varies with changes in the number of coil turns or in the input supply, including power, voltage, and current. Environmental temperatures, like in the air or the sea, not only may affect the magnetic field but also the coils. For this reason, they should be made of such a material that can withstand harsh environments like rusting conditions in seawater. Another consideration is that sea currents are always moving, so applications like floating buoys should be tied together so that the sensor nodes are not lost. For a better performance, increasing all parameters like the number of turns, the area of cross-section, and the high input current would lead to higher cost, heavy sensor nodes, and they might end up occupying more space [12] So, to reach a compromise is necessary. We may also use an array of coil topologies to increase the coverage area, as mentioned in [13,14]

The process involved in WPT is based on mutual induction, just like in a transformer, where a magnetic field is used to transfer voltage between two coils. The primary coil is excited at a suitable frequency by an AC power source (called the transmitter) while the secondary coil is used as the destination of the transferred power (called the receiver). So, a traditional WPT system consists of three parts: transmitter, inductive coupler, and receiver, as shown in Figure 2 [15].

A basic classification for WPT systems concerns the distance between transmitter and receiver. A WPT system is static when this distance is fixed, and dynamic in the case of a varying distance [12]. Recent research has covered various factors, like multiple transmitters and multiple receivers in a dynamic WPT environment [16], which have the potential to provide greater scope for powering very low-power devices. For high-power applications, energy efficiency is limited by leakage inductance. This problem can be avoided by adding to the coils a compensation circuit with a variety of possible configurations [6], as shown in Figure 3 below, along with a proper study of the resonance frequency.

A further classification of WPT systems [3] is presented in Figure 4, which shows that only MI can be used for underwater communication in close MPT applications.

In UWSN, several nodes communicate with each other and use MI coils for WPT to transfer data. This architecture, already used in smart cities [1], can be adapted for marine exploration. Another application of MI is the Underground Wireless Communication Networks (UGWN) [17,18]. In these systems, the medium through which propagation occurs is the ground, rather than the air. UGWN helps in monitoring and predicting landslides and earthquake forecasting [19]. Other applications of MI in the sea are discussed in [20,21].

Complex applications that need moderate/high data rates, like the IoUT, require low interference between transceivers. The UWSN architecture, as explained in [11], has the potential to be used in IoUT deployment.

2. Related Work

The progress in work related to the underwater MI communications is highlighted in [22] and is as follows:

2.1. Reliability Guarantee

In the context of underwater Magnetic Induction (MI) communication, the main challenge is guaranteeing reliable data transmission due to the high sensitivity of path loss (signal attenuation) to the relative orientation of the transmitter and receiver coils. When the coils are not perfectly aligned (coaxial), the path loss surges to an undesirable level, making communication unreliable. Unfortunately, in real-world underwater applications, transceivers are constantly moved by ocean waves, which causes their relative orientations to frequently and uncontrollably change. The combination of this orientation-sensitive path loss and the dynamic, uncontrollable nature of coil positioning poses significant challenges to maintaining a stable MI link.

2.2. Range Extension

The effective transmission range of underwater Magnetic Induction (MI) communication is severely limited by rapid path loss (signal attenuation) that increases significantly with distance. This constraint is primarily due to two factors: first, the magnetic field strength attenuates rapidly—at the sixth power of the distance—meaning the signal drops off very quickly as the separation between the transmitter and receiver increases. Second, the eddy current losses (energy dissipation in the conductive seawater) are high in undersea environments and increase with the transmission range. The combined effect of these two high-loss factors directly leads to a dramatic increase in total path loss, constraining the effective range over which reliable data transmission can be guaranteed.

2.3. Capacity Enhancement

Although Magnetic Induction (MI) communication is theoretically capable of achieving high data rates (up to the order of Mbps), the actual performance in underwater environments is practically limited to much lower values, typically an effective bandwidth within 100 kHz and a channel capacity within 100 kbps. This restriction is due to two primary factors: first, the system’s effective bandwidth is significantly narrowed because even minor deviations from the coil’s optimal operating frequency can cause considerable power reflections. Second, and more importantly, MI communication systems are forced to operate at low frequencies to effectively mitigate the high attenuation caused by eddy currents in highly conductive seawater, which inherently restricts the achievable bandwidth and, consequently, the maximum data rate.

2.4. Channel Modeling

Channel modeling for Magnetic Induction (MI) communication is a complex task because the propagation medium is highly dynamic seawater. The MI channel itself consists of active and passive coils used to transmit data, but the propagation characteristics are significantly influenced by environmental factors such as salinity, tides, and various sources of noise, all of which must be accurately accounted for to understand and predict reliable data transmission through this challenging medium.

3. Results and Discussion

3.1. Excitation Circuit Requirements and Resonance Circuits

A WPT system needs to be excited at a suitable operating frequency. For low-powered devices, non-resonant circuits can be used, but in order to deliver maximum power for high-power transfer, a resonance frequency needs to be applied at the source. This is because leakage flux causes some power to be lost during transfer, and in the case of resonance circuits, this effect of inductive reactance is canceled out, and maximum power is transferred.

As previously said, there are four topologies to make resonant excitation circuits for WPT (see Figure 3): Series–series, series–parallel, parallel–parallel, and parallel–series [15]. The first word is used for the LC configuration on the transmitter side, and the second word represents the LC configuration on the receiver side of the coil.

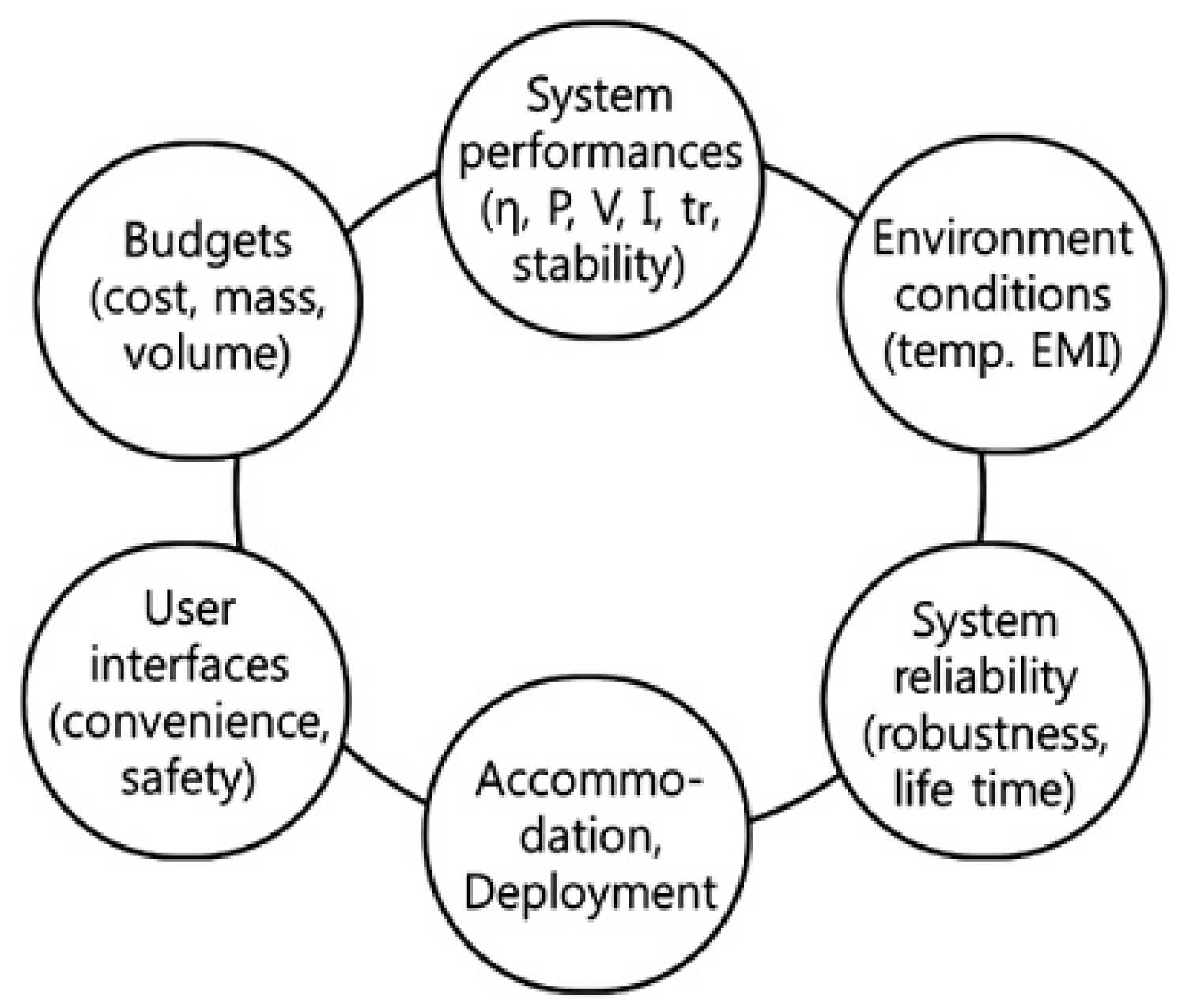
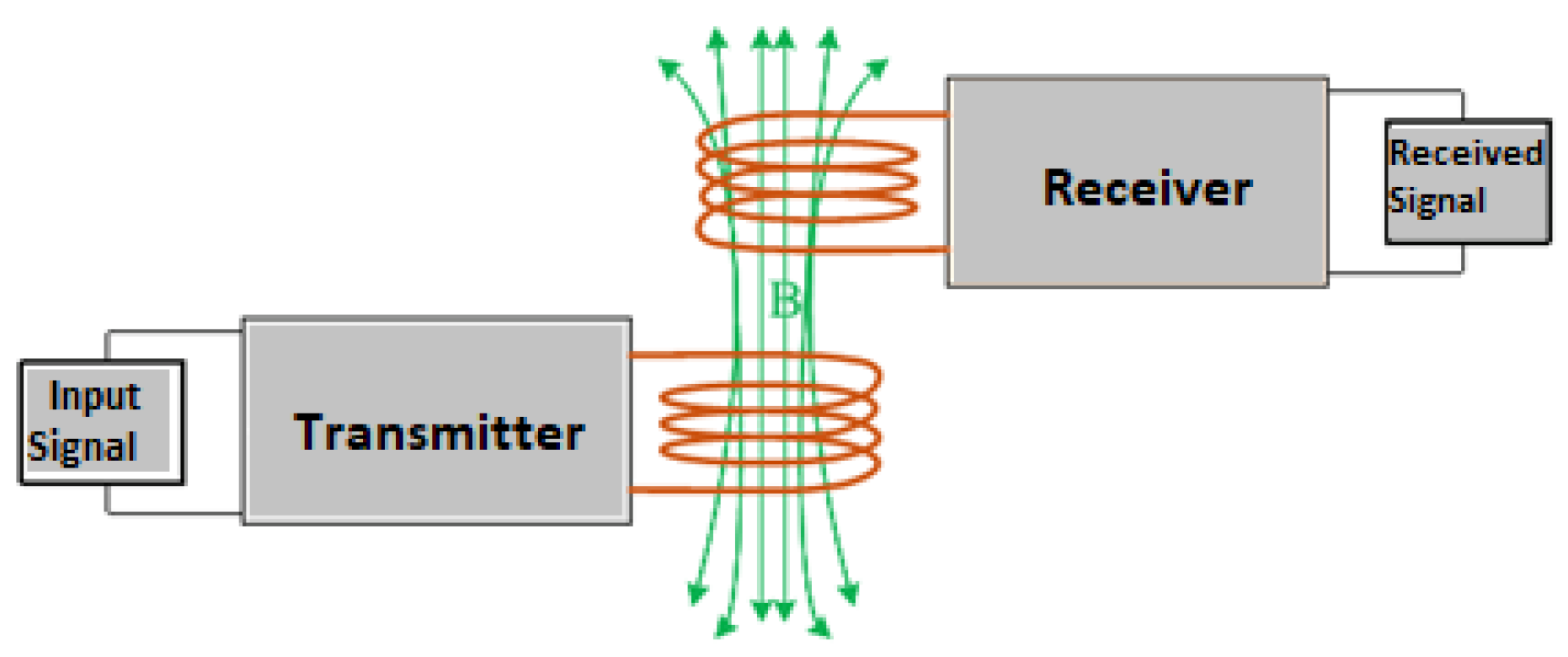
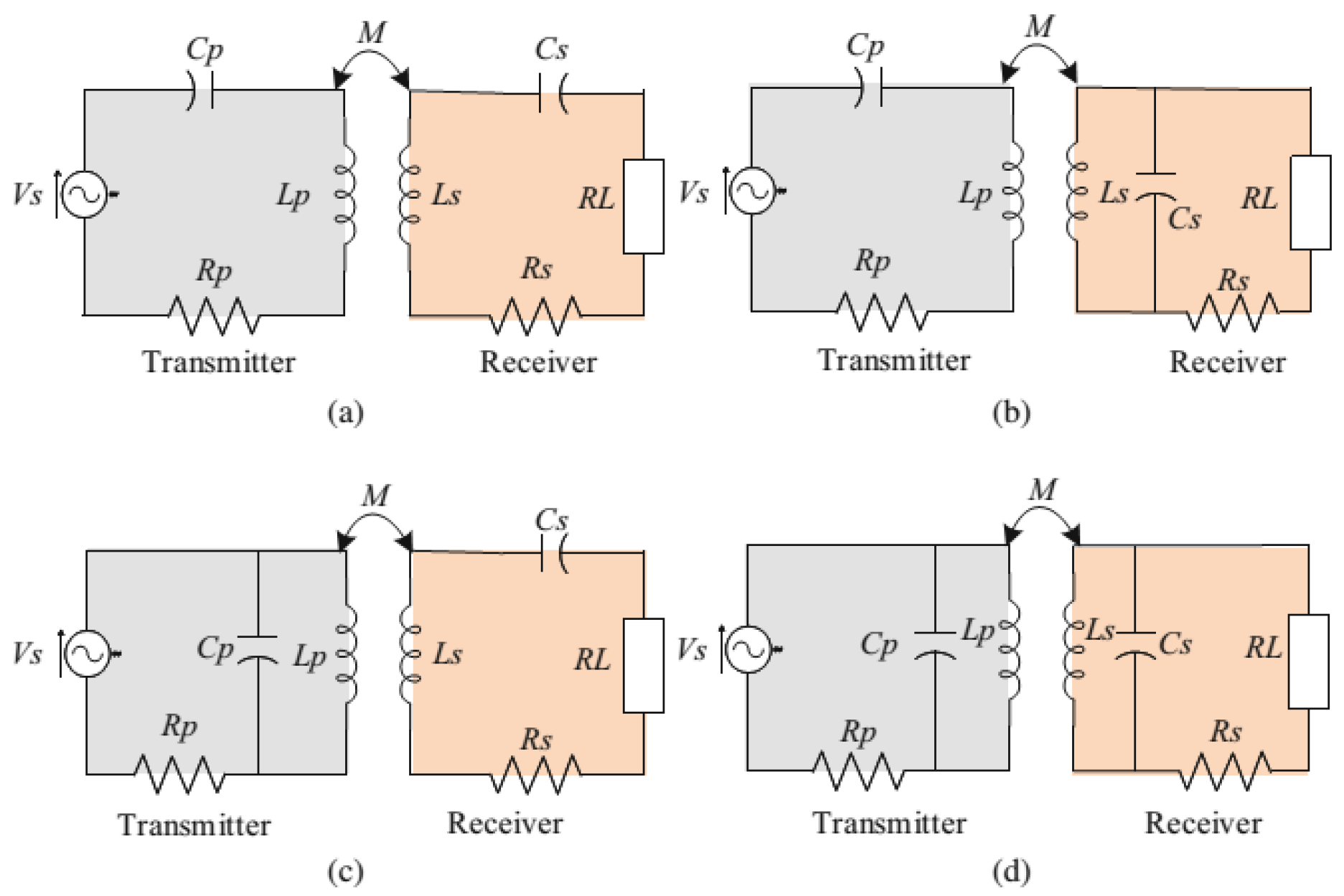
3.2. Computation for S11

For an antenna, the loss constant $tg\delta$ can be found by the following equation:

$$tg\delta ={\displaystyle \frac{\omega {\epsilon }^{″}+\sigma }{\omega {\epsilon }^{\prime }}}$$

(1)

where ${\epsilon }^{″}$ = 0, ${{\epsilon }^{\prime }=\epsilon }_r\times {\epsilon }_0$ (${\epsilon }_r=81$ in seawater), ${\epsilon }_0$ = 8.85 × 10⁻¹² F/m, and is the angular frequency.

The phase constant β can be found by the following equation:

$$\beta =\sqrt{{\displaystyle \frac{1}{2}}{\omega }^2\mu {\epsilon }^{\prime }\left(1+\left(\sqrt{1+{tg\delta }^2}\right)\right)}\mathrm{rad}/\mathrm{m}$$

(2)

where $\mu {=\mu }_0{·\mu }_r$ (${\mu }_0=4\pi \times {10}^{-7}$ H/m and ${\mu }_r=1$ in water). The wavelength is given by the following:

$$\lambda ={\displaystyle \frac{2\pi }{\beta }} \mathrm{m}$$

(3)

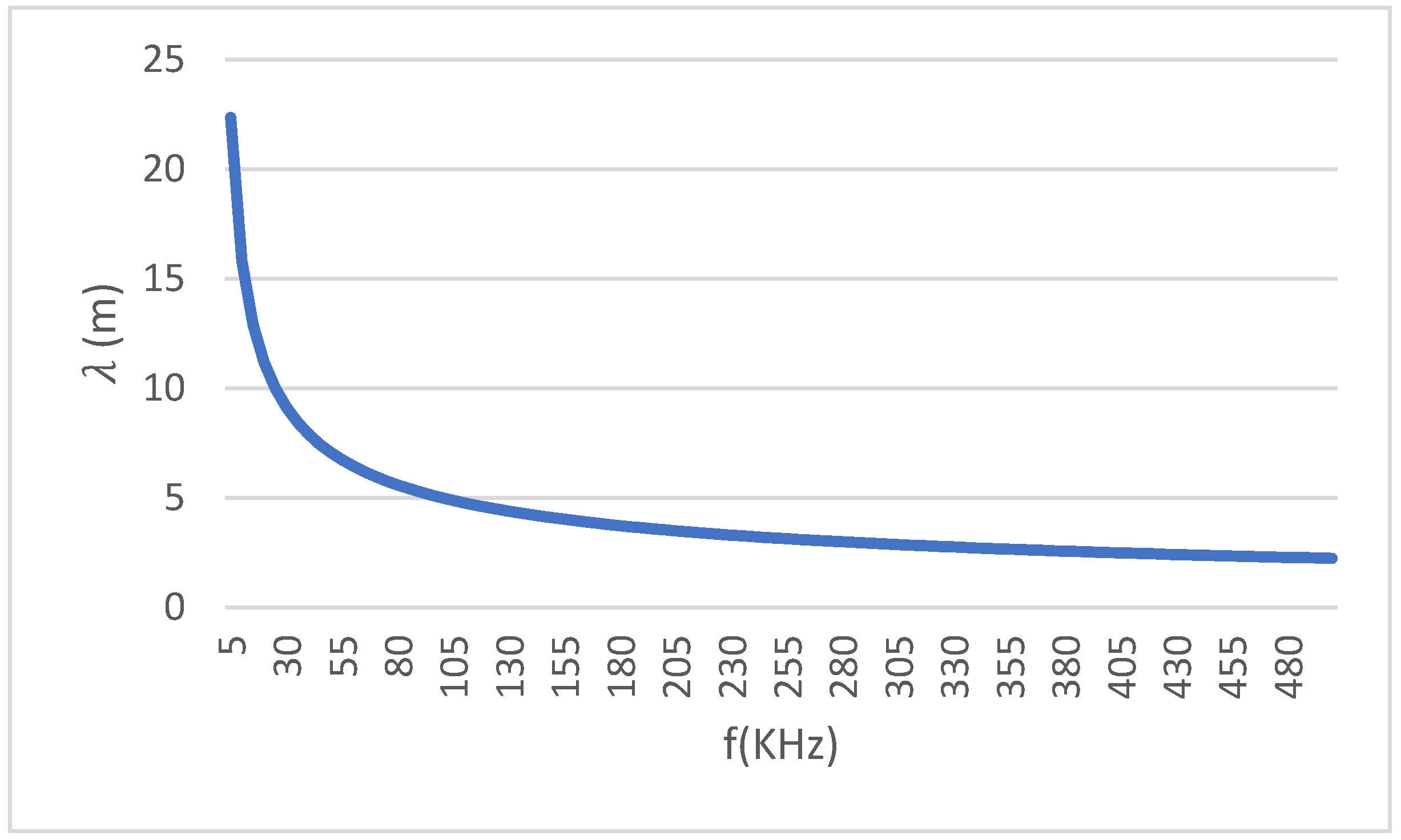
Using the above parameters in Equation (3) and by varying frequency from 0 to 5 kHz, we get the plot in Figure 5.

The attenuation constant α is given by the following:

$$\alpha =\sqrt{{\displaystyle \frac{1}{2}}{\omega }^2\mu {\epsilon }^{\prime }\left(-1+\left(\sqrt{1+{tg\delta }^2}\right)\right)} \mathrm{N}\mathrm{p}/\mathrm{m}$$

(4)

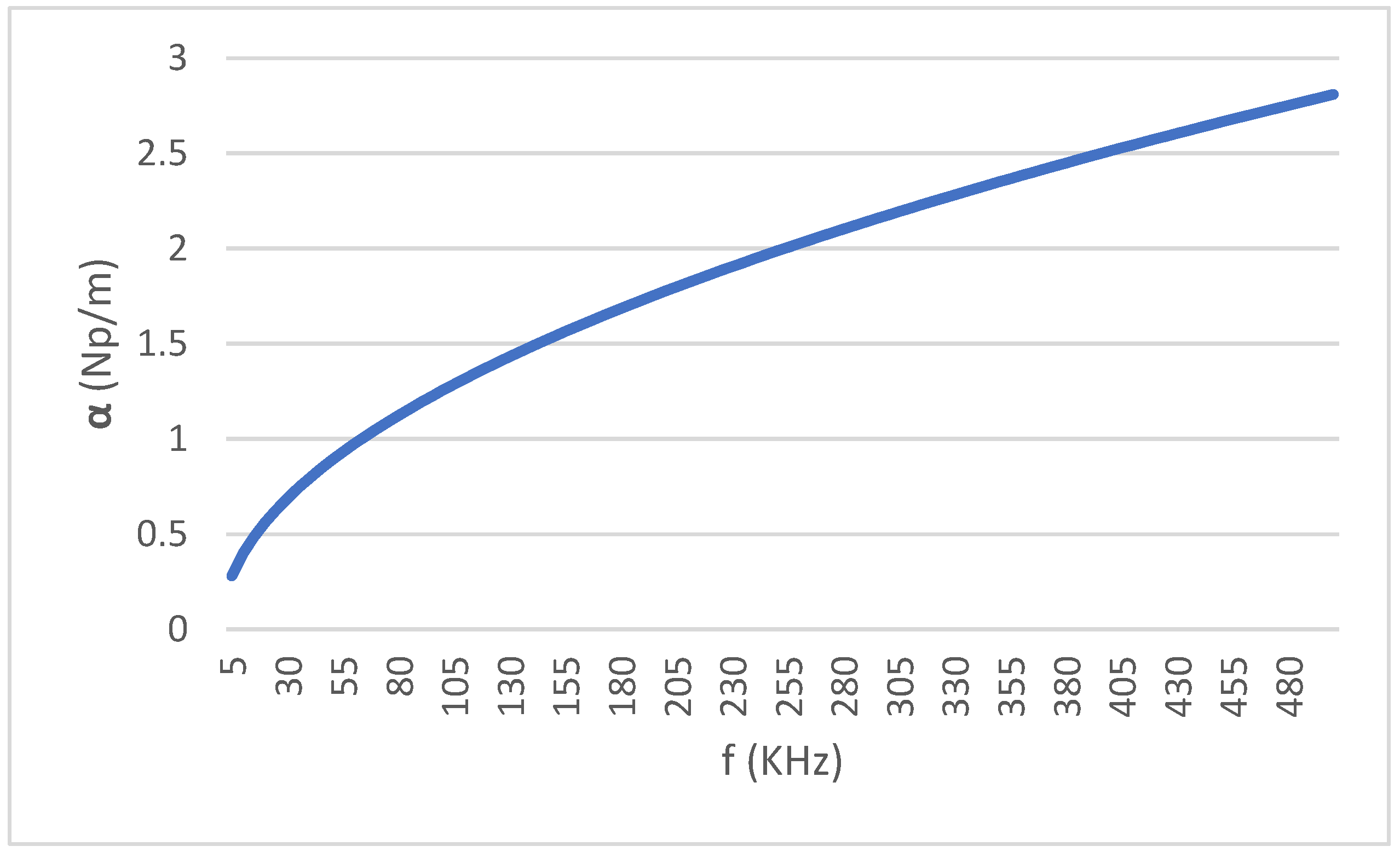
Using (4), we get the attenuation vs. frequency presented in Figure 6.

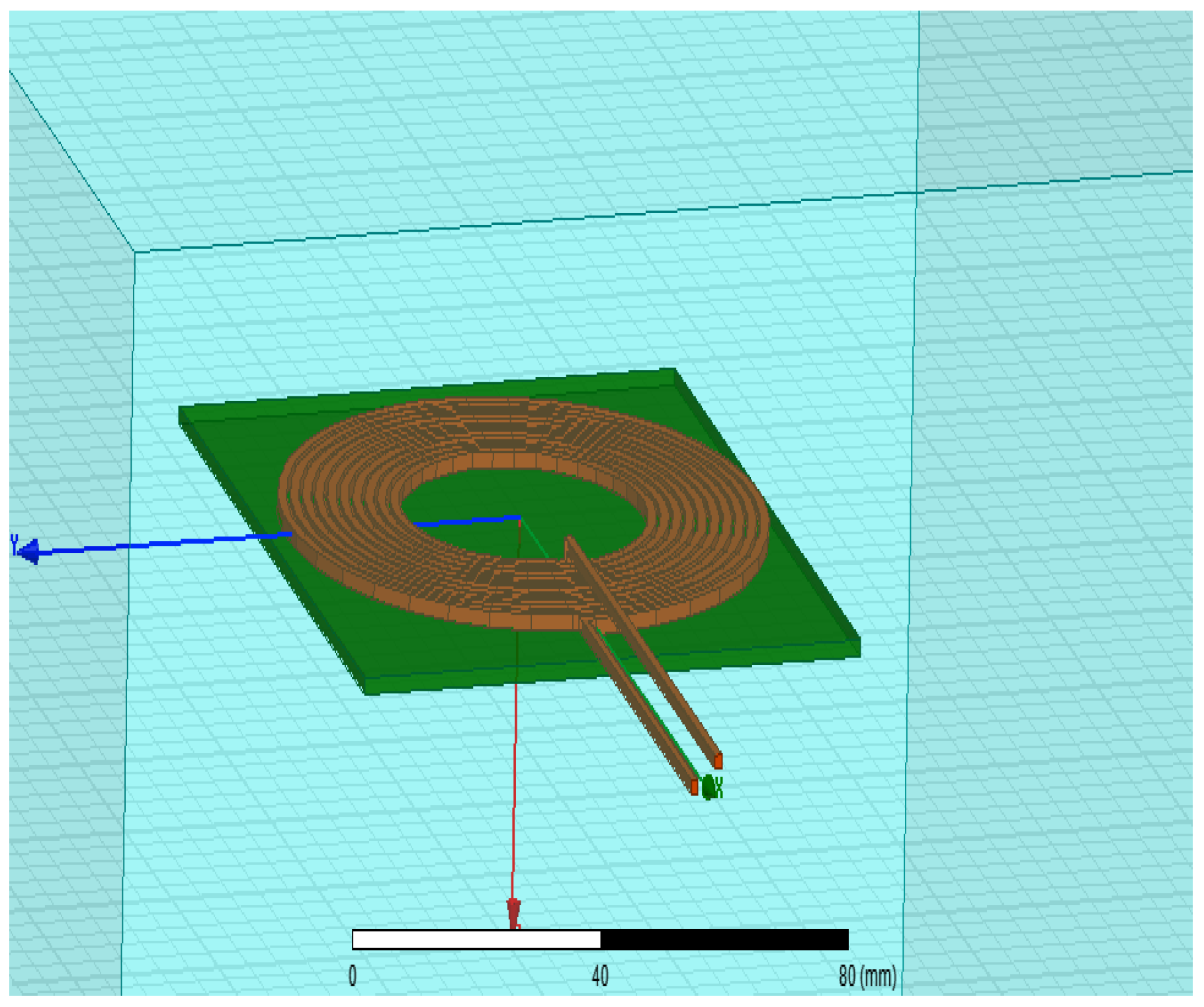
In the next step, we used the following coil that has a radius of 1 mm, ten turns, and an inductive reactance of 6.92 µH, attached to an FR4 plate of 1.5 mm thickness for simulation purposes in ANSYS Maxwell v16.

The reflection coefficient Γ can be found by the following:

$$\Gamma = {\displaystyle \frac{Z_{coil}-Z_0}{Z_{coil}+Z_0}}$$

(5)

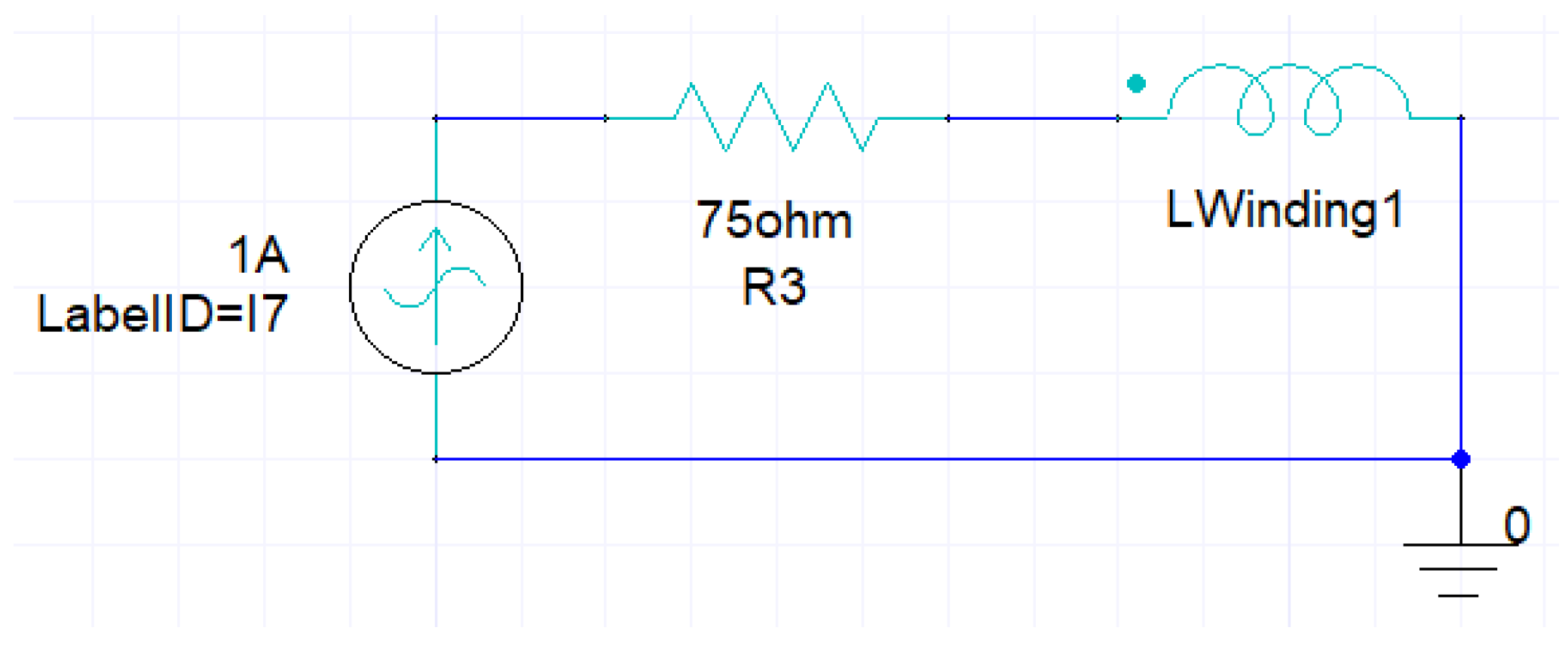
Let $Z_0$, the system impedance, to be 50 ohms. We are using an RL circuit to excite the coil which includes resistance Ra of 75 ohms, and Xa can be varied at different frequencies. Therefore, the final impedance will be the following:

$$Z_{coil}=75+X_a\left(f\right)$$

(6)

This circuit is a series configuration at the input for the transmitter. We have used the same series confirmation for the receiver coil as the one shown in Figure 3a.

As per output characteristics amongst the four mentioned basic WPT topologies, the series-series topology is the simplest configuration, it provides constant current, easily flexible to parametric change in the coil and achieves resonance

The reflection coefficient S₁₁ in dB can be found by the following:

$$S_{11}\left(f\right)=20.{Log}_{10}\left(\left|\Gamma \left(f\right)\right|\right)\mathrm{dB}$$

(7)

For a system using the S-S compensation topology, a simplified model based on Kirchhoff’s laws can be derived. The relationship between the currents and voltages in the primary and secondary circuits can be expressed as follows:

$$\left(\begin{array}{c}\dot{U_1}\dot{U_2}\end{array}\right)=\left(\begin{array}{cc}j\mathsf{\omega }{L}_1+{\displaystyle \frac{1}{j\mathsf{\omega }{C}_p}}+R_1& j\mathsf{\omega }M\\ j\mathsf{\omega }M& j\mathsf{\omega }{L}_2+{\displaystyle \frac{1}{j\mathsf{\omega }{C}_s}}+R_2\end{array}\right)\left(\begin{array}{c}\dot{i_1}\dot{i_2}\end{array}\right)$$

(8)

where

• $\dot{U_1}\dot{U_2}$ are the voltages of the primary and secondary coils.
• $\dot{i_1}\dot{i_2}$ are the currents of the primary and secondary coils.
• $L_1$, $L_2$ are the self-inductances of the primary and secondary coils.
• $C_p$, $C_s$ are the compensation capacitances.
• $R_1$, $R_2$ are the resistances of the coils.
• M is the mutual inductance.
• ω is the angular frequency.

To calculate the basic efficiency of two magnetically coupled (MI) coils, you will need to consider several key parameters that govern their interaction and energy transfer.

$$\mathsf{\eta }={\displaystyle \frac{{\mathrm{k}}^2{\mathrm{Q}}_1{\mathrm{Q}}_2}{\left(1+\frac{{\mathrm{R}}_1}{{\mathrm{R}}_{\mathrm{S}}}\right)+{\mathrm{k}}^2{\mathrm{Q}}_1{\mathrm{Q}}_2+\frac{{\mathrm{R}}_{\mathrm{L}}}{{\mathrm{R}}_2}\left(1+{\mathrm{k}}^2{\mathrm{Q}}_1{\mathrm{Q}}_2\right)}}$$

(9)

A more simper form is calculated as follows:

$${\mathsf{\eta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}={\displaystyle \frac{{\mathrm{k}}^2{\mathrm{Q}}_1{\mathrm{Q}}_2}{{\left(1+\sqrt{1+{\mathrm{k}}^2{\mathrm{Q}}_1{\mathrm{Q}}_2}\right)}^2}}$$

(10)

where

• k is the coupling coefficient.
• Q₁ is the quality factor of the transmitting coil.
• Q₂ is the quality factor of the receiving coil.

$$\mathrm{and} \mathrm{Q}={\displaystyle \frac{2\mathsf{\pi }\mathrm{f}\mathrm{L}}{\mathrm{R}}}={\displaystyle \frac{\mathsf{\omega }\mathrm{L}}{\mathrm{R}}}$$

(11)

From the above, we get to know that if we increase the coefficient of coupling or the quality factor, we get more efficiency. It would decrease with higher resistance.

3.3. ANSYS Maxwell Simulation

In the next step of analysis, the coil, along with its excitation circuit shown in Figure 7 and Figure 8, is analyzed with Ansys Maxwell software. This circuit is a circular copper coil submerged underwater with 10 turns and a radius of 1 mm. It is powered by a 1 A current.

Table 4. Magnetic field (H) and magnetic flux density (B) vs. frequency.

Frequency (Hz)	H (A/m)	B (T)
5	9.3839 × 10−8	1.7952 × 10−13
10	1.8768 × 10−7	2.3584 × 10−13
15	2.8152 × 10−7	3.5376 × 10−13
20	3.7536 × 10−7	4.7168 × 10−13
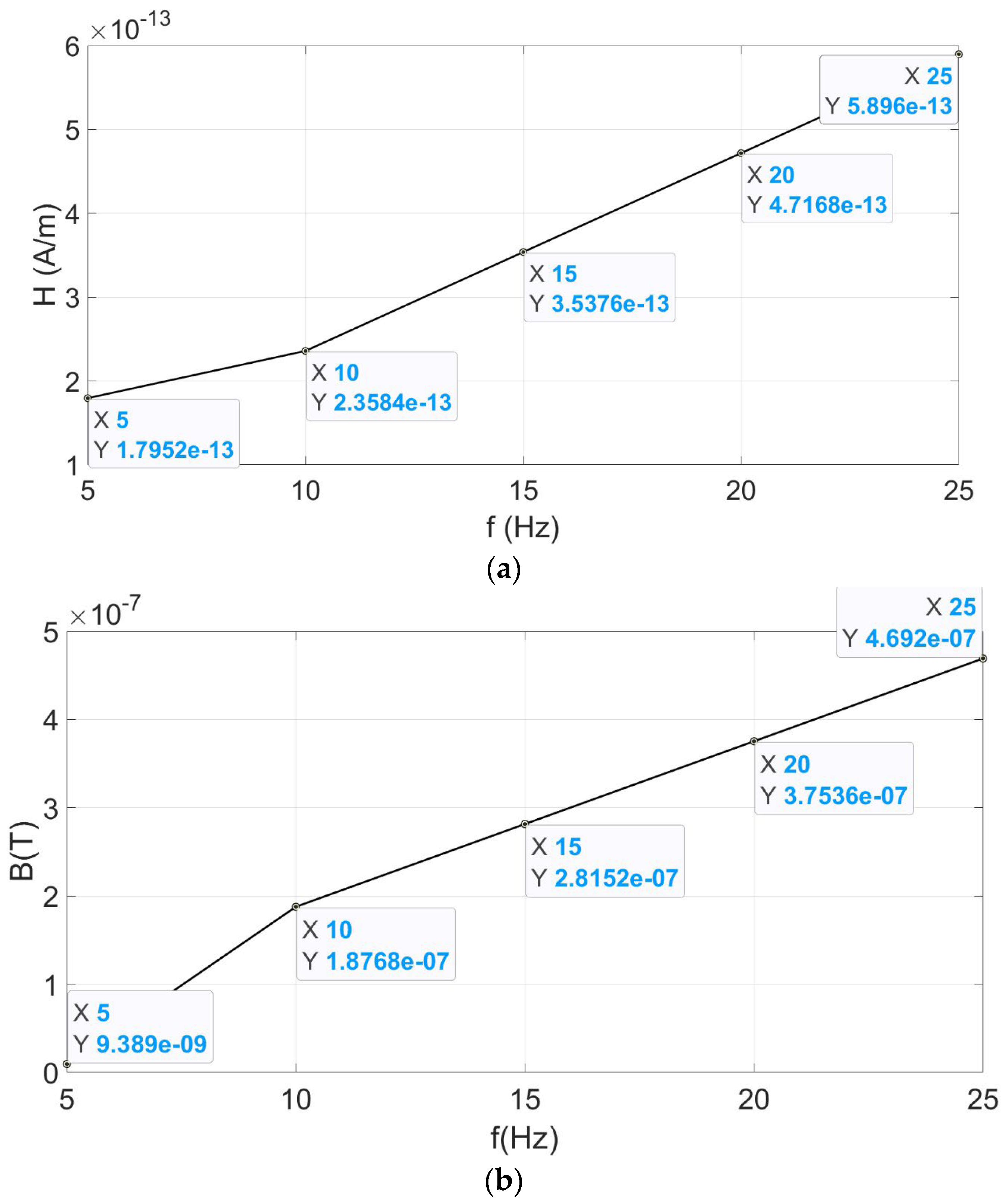
25	4.692 × 10−7	5.896 × 10−13

shows the obtained absolute value for magnetic flux density (B, in Tesla units, T) and

Table 5. Magnetic flux density (B) vs. coil thickness.

Coil Thickness (mm)	B (T)
0.2	1.1232 × 10−12
0.4	7.375 × 10−13
0.6	6.0253 × 10−13
0.8	5.1039 × 10−13
1	4.6525 × 10−13

for magnetic field intensity (H, in Ampere/meter units) when frequency excitation in the coil varies from 5 to 25 Hz.

From Figure 9a,b, it can be seen that H shows a linear relationship with frequency, whereas B does not. The relation between magnetic field intensity (H) and magnetic flux density (B) is the magnetic permeability µ (µ = B/H). In the case of ferromagnetic materials (iron, copper, etc.), the magnetic permeability can exhibit nonlinear behavior with frequency, for example, hysteresis phenomena.

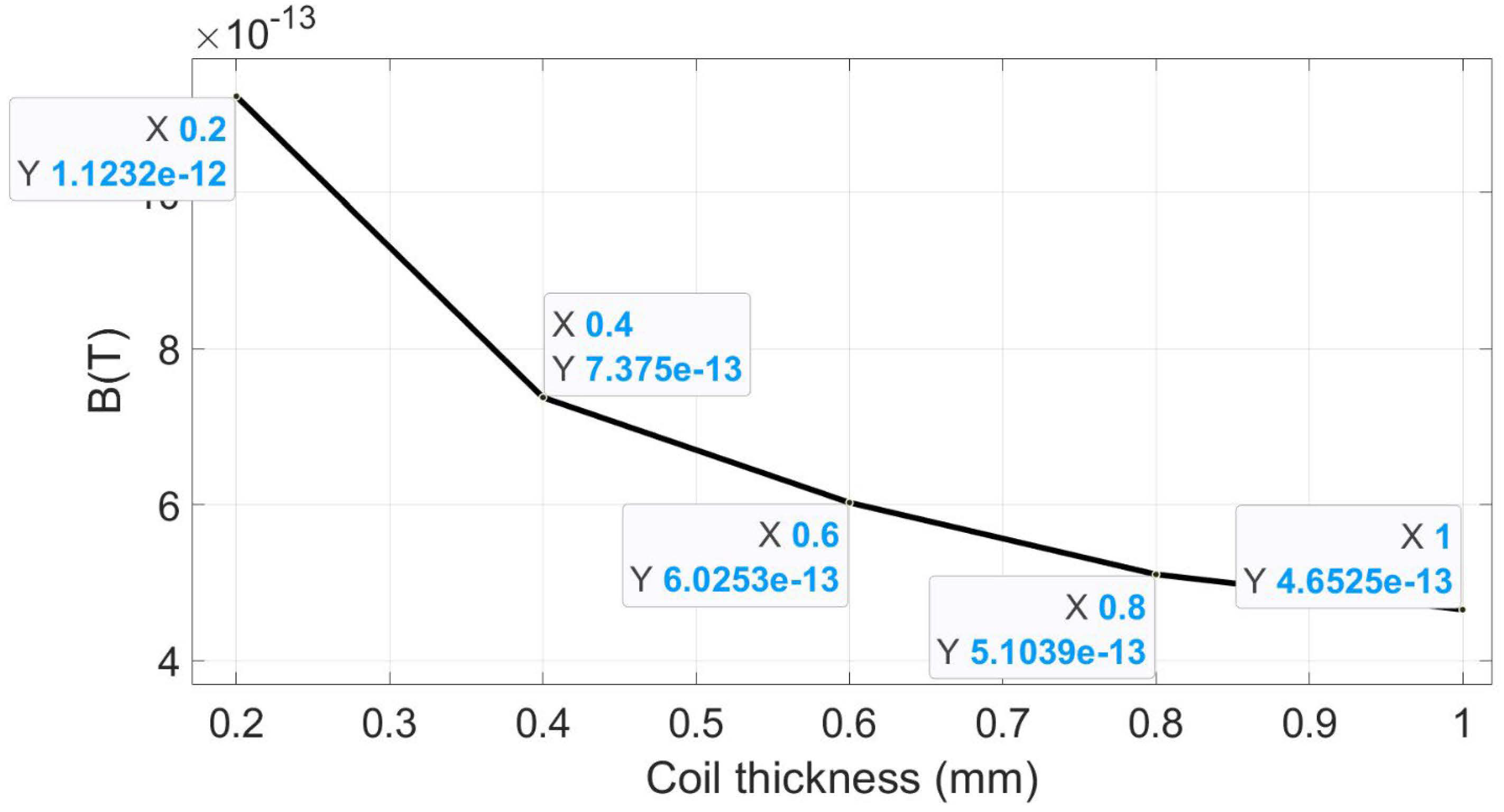
Let us fix the input frequency to 20 Hz and vary the coil thickness or coil radius in the same circuit from 0.2 to 1 mm (spacing between turns is fixed at 2.05 mm). The results obtained are presented in Figure 10 and Table 5.

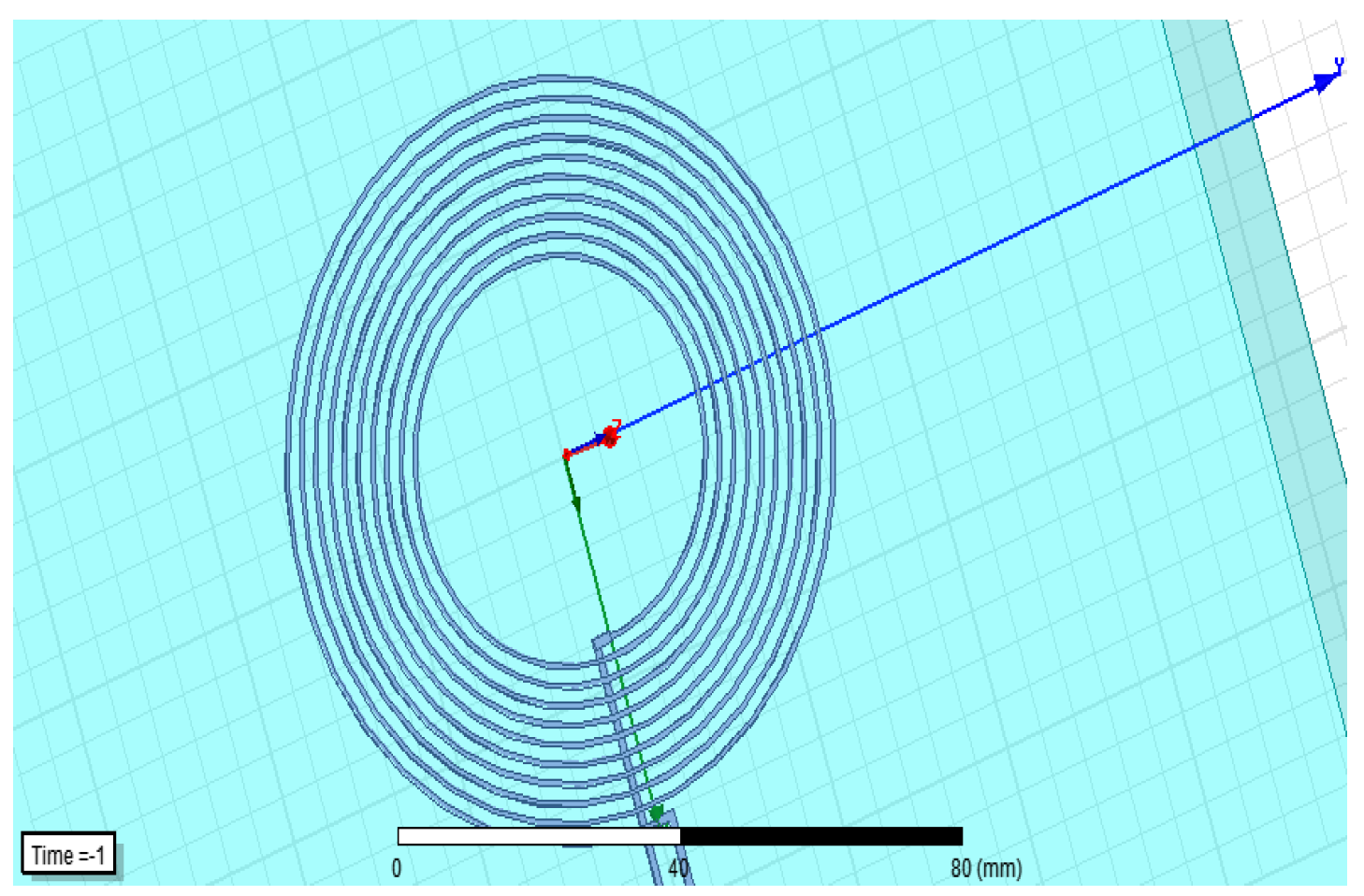
In Figure 11, a set of different coils is shown in order to be used with the underwater setup of the WPT system.

As shown in Table 5 and Figure 12, the flux density decreases as the coil thickness is increased. This means that coil thickness can be adjusted to achieve the optimum magnetic field while selecting the right wire gauge. Increasing the current will also improve the results (a higher MI value). Further, the number of turns and weight can be balanced. A higher number of turns would also improve the MI, while increasing the coil’s weight.

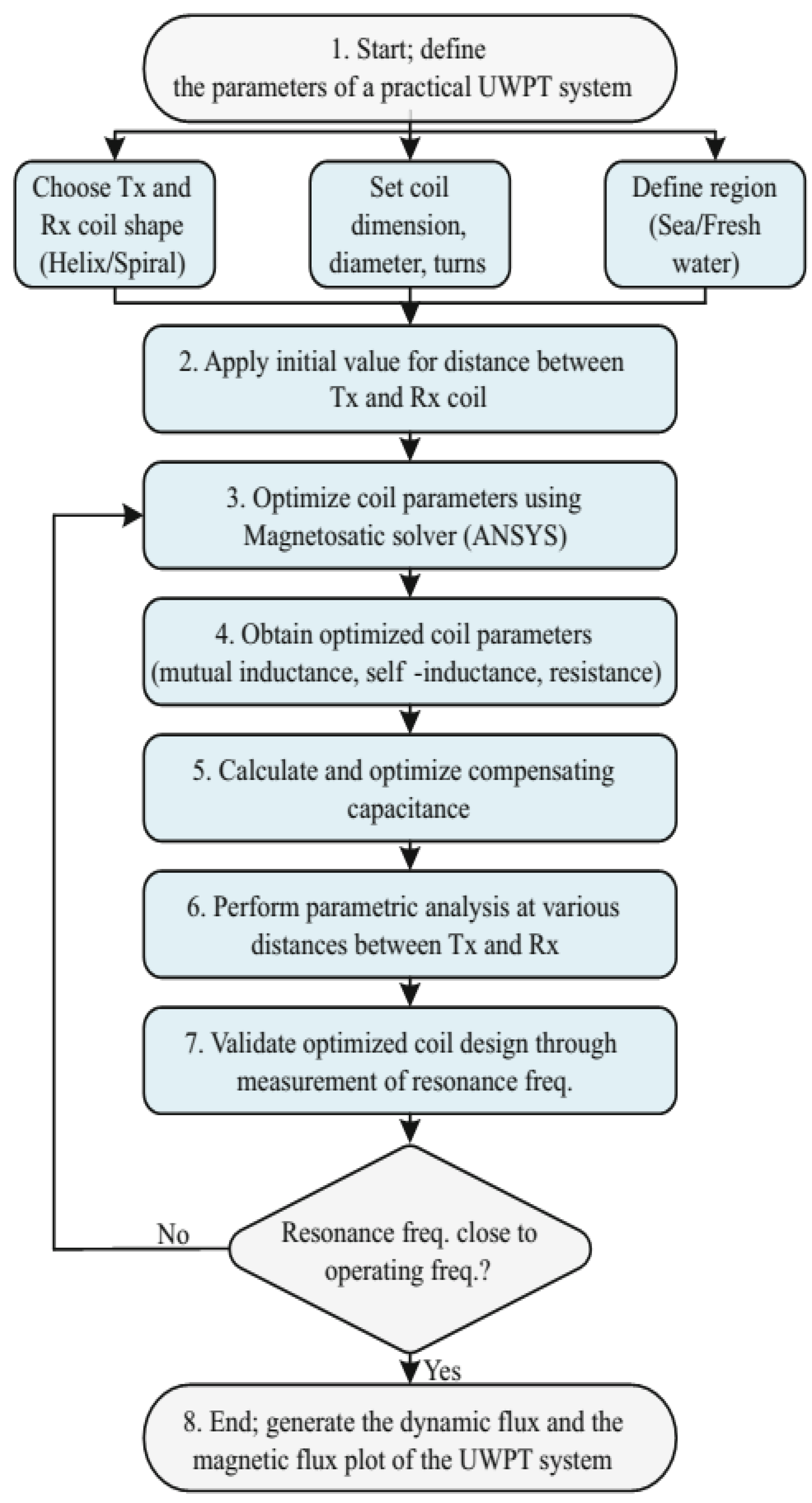
The following flow chart in Figure 13 explains the steps that may be taken to experiment with various coil shapes, their parameters, underwater environment, excitation, and receiver circuit combinations in a magnetic solver in order to configure an optimized transmitter receiver setup that may provide more distance between them.

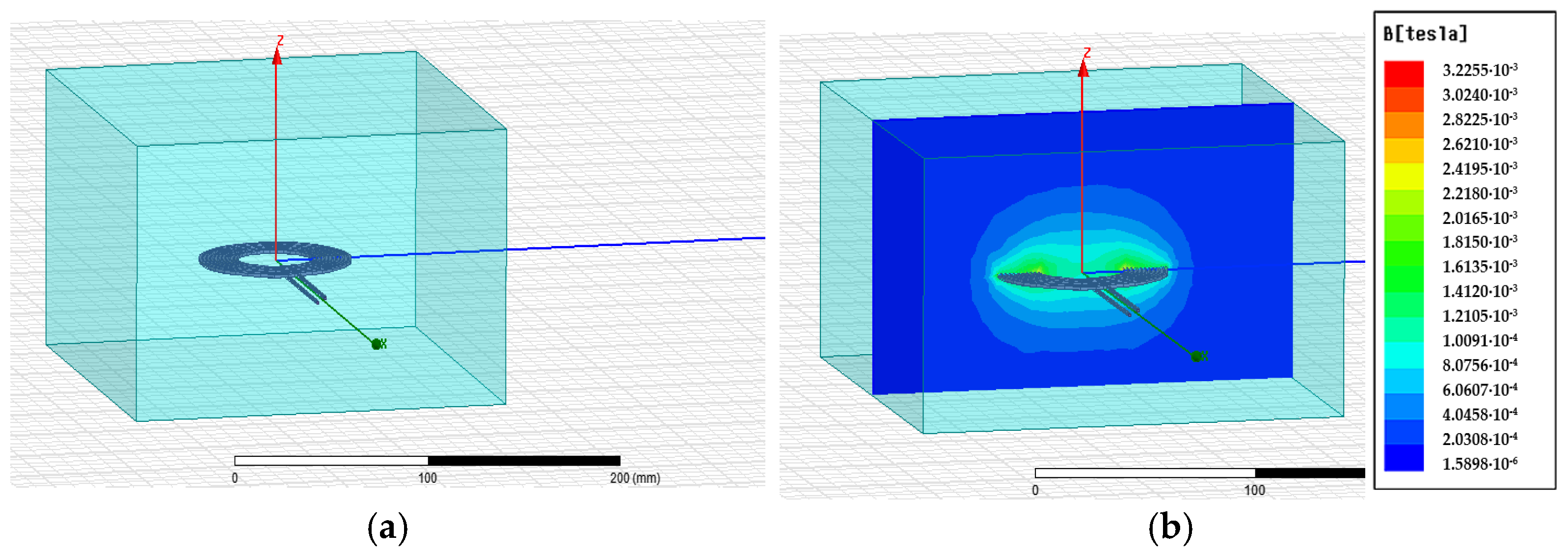
In order to follow the process shown in Figure 13, the next step for simulation will be to place the previous copper coil (circular shape, 10 turns, and radius 1 mm) in seawater, as is presented in Figure 14a, with its corresponding simulated magnetic flux density (Figure 14b).

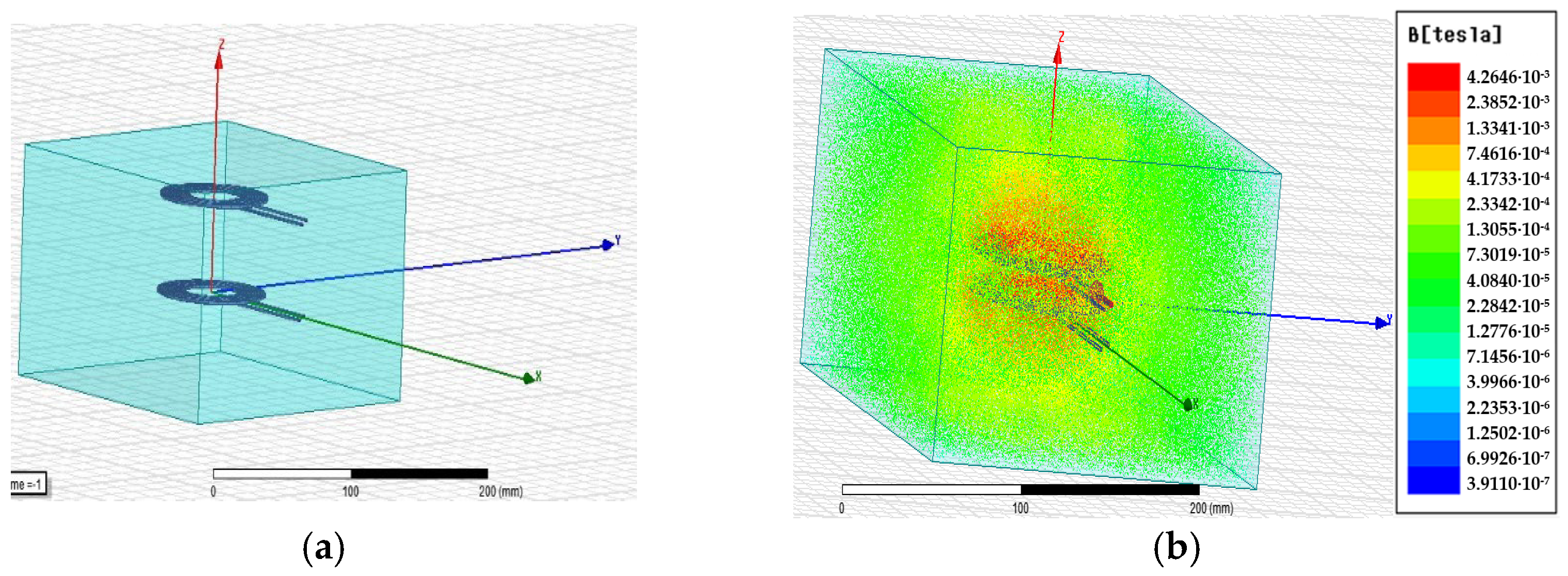
In the next step, we now set up two coils equal to those in Figure 14a but with an exciting current of 5A. The setup is presented in Figure 15a and its corresponding B flux in Figure 15b.

An important parameter which measures the coupling between the coils is the mutual inductance M, defined by the following:

$$M=k \sqrt{L_{11}\times L_{22}} \mathrm{H}$$

(12)

where K is the coupling magnetic coefficient, and $L_{11}$, $L_{22}$ the self-inductance of coils 1 and 2, respectively. In this new experiment, we keep the current constant at 5A and only the distance between the coils is varied.

Table 6. Parameters K, M for varying distance. Data: current 5A, circular shape, 10 turns, radius 1 mm (identical coils).

Distance (mm)	K	M (μH)	L11, L22 (μH)
5	0.7695	5.5731	7.25
10	0.523	3.7923
15	0.3914	2.8352
20	0.3075	2.2264
25	0.2236	1.6176
30	0.1745	1.2587

shows the change in $M$ between the coils, and their self-inductance is isolated.

From Table 6, it can also be seen how the mutual inductance ($M$) and coefficient of coupling ($K$) increase when both coils are closer, but they decrease when they are kept far apart.

3.4. Experimentation in the Laboratory

In order to verify WPT operation, a simple aerial prototype is made in the laboratory using handmade coils. The setup is shown in Figure 16 and can be seen as the energy transmitter (right circuit connected to the power supply), feeding the receiver circuit (on the left), which lights the LED array. The setup parameters and results obtained are presented in

Table 7. WPT prototype results. Data: Transmitter coil: 8 turns, 0.6 mm thickness, 75 mm diameter. Supply: 9 V, 1 A. Receiver coil: 12 turns, 0.6 mm thickness, 75 mm diameter.

	Output Voltage (V) in Receiver Coil
Distance (cm)	Air	Water
1	9	9
2	5	6
3	1.5	2.5
4	0.5	1.5

.

An important feature of a WPT system is the range between the two circuits, the transmitter and the receiver. To estimate this, the supply current varied from 1 A to 4 A in the same prototype. The results obtained for both the aerial and submarine configurations are shown in

Table 8. Range for WPT prototypes: aerial and underwater.

Input Current (A)	Aerial Range (cm)	Underwater Range (cm)
1	3	4
2	3.5	4.3
3	4.5	5.4
4	5.6	6.3

.

From the information in Table 8, we observe that the voltage received decreases less when the range is increased underwater. From Table 8, we observe that when power is transmitted underwater, the range is comparatively greater when the current increases.

To enhance the range available between transmitter and receiver, we can increase the quality coil Q, defined by the following expression:

$$Q={\displaystyle \frac{2\pi f\mu r{N}^2\pi r^2}{LR}}$$

(13)

where f is the signal frequency; r is the spiral radius; $\mu$ the magnetic permeability; N is the number of turns; R is the resistance of coil; and L is the length of the coil. Another figure of merit related to the quality of the coil is the loss factor, given by the following expression:

$$Loss factor\propto {\displaystyle \frac{1}{k\times Q}}$$

(14)

The loss factor decreases when the coupling factor $k$ or coil $Q$ quality increases. From (9), it can be observed that an increase in the number of turns and radius of the coil results in a higher quality factor. At the same time, this increase would come at the cost of a longer coil and, consequently, higher resistance. Another way is to set the frequency very high, but it is limited to the point where attenuation is at a minimum, as shown in Figure 6.

The loss factor includes both the skin effect and the proximity effect. Skin effect is when current tends to flow on the outer surface only, rather than being uniformly distributed across the cross-section, and proximity effects [23]. Due to this effect, eddy currents may flow into nearby coils, thereby producing the proximity effect by crowding the current in the nearby conductor.

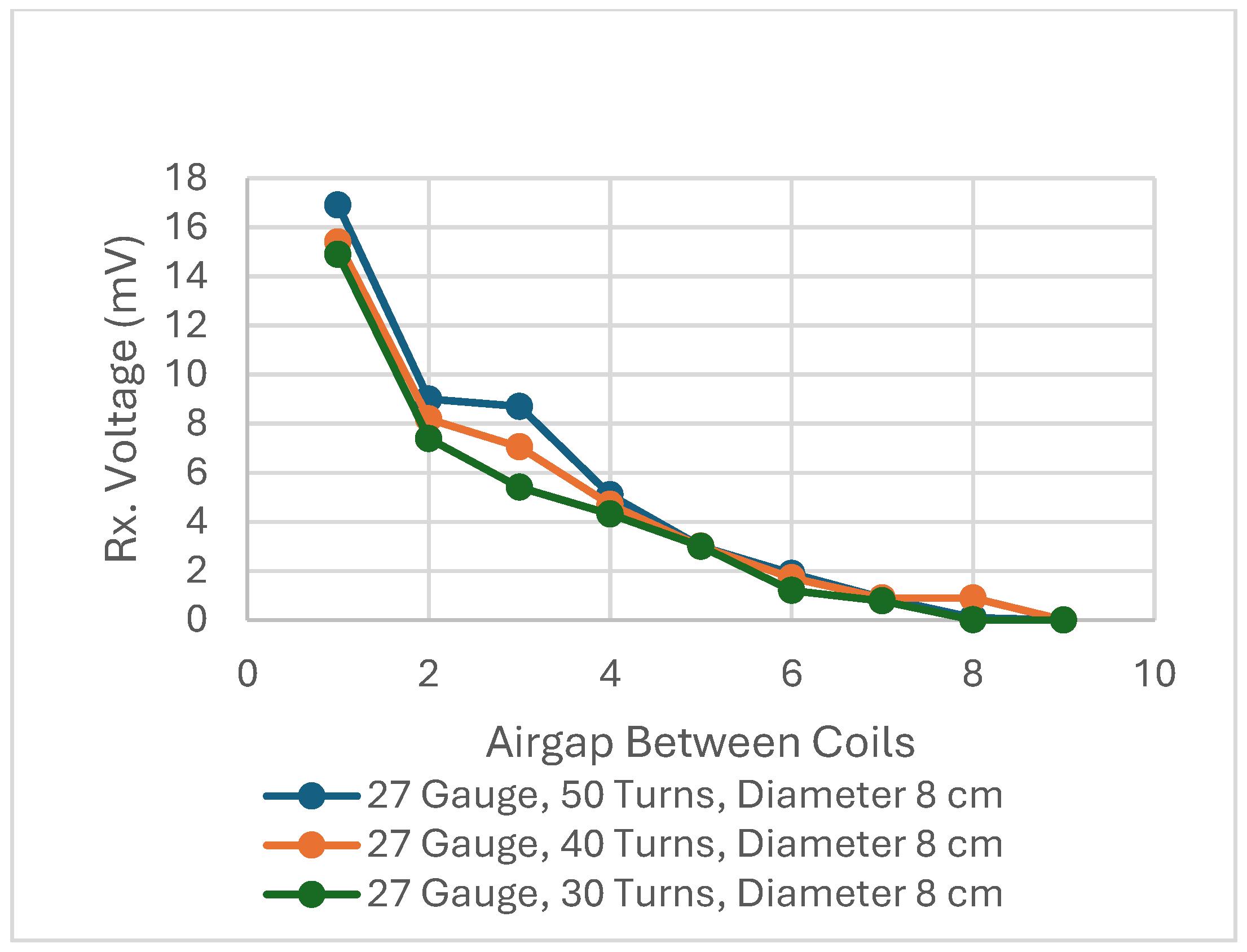
In the next step, we prepare a setup to conduct the experiment on the coils using basic transistor-based ASK modulation as shown in Figure 17, which is an amplitude shift keying method, to propagate signals between the coils while keeping air as the medium. At first, we change the number of turns of both coils, whereas other parameters are kept the same.

The above results in

Table 9. Voltage received in Rx when the number of turns is changed for 27-gauge coils having a diameter of 8 cm.

Distance (cm)	50 Turns	40 Turns	30 Turns
1	16.9	15.4	14.9
2	9	8.19	7.39
3	8.7	7.051	5.41
4	5.1	4.71	4.32
5	3.01	3.005	3.0012
6	1.9	1.72	1.2
7	0.9	0.89	0.78
8	0.1	0.9	0.01
9	0	0	0

and Figure 18 show that the coil having a higher number of turns achieves more mutual voltage and is able to operate at a further distance as compared to others.

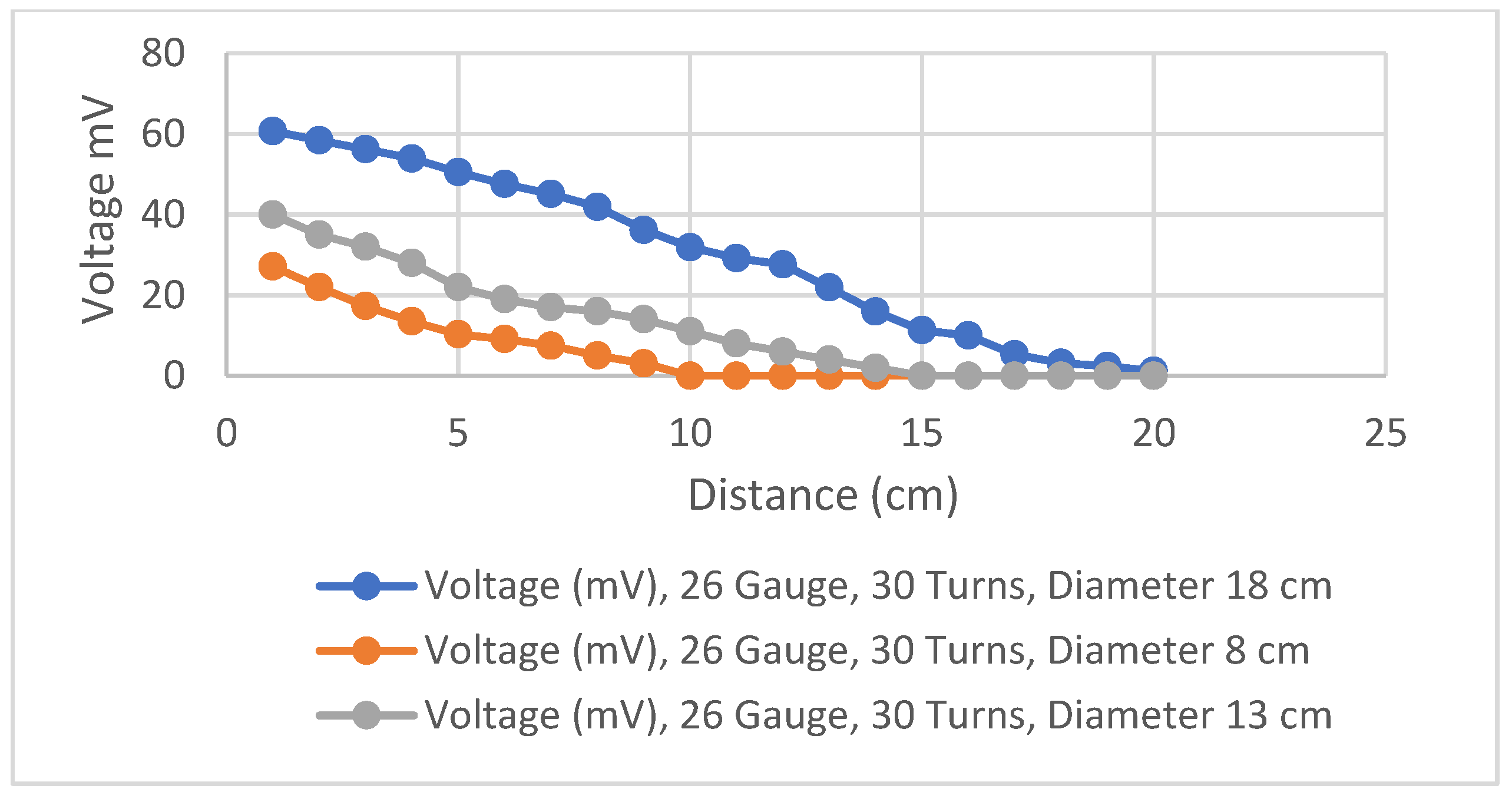
In the next step, we change the diameter to see the results: 8 cm, 13 cm, and 18 cm with the same gauge and number of turns.

The results in

Table 10. Voltage received in Rx when the diameter of the coil is changed.

Distance cm	Diameter 18 cm	Diameter 13 cm	Diameter 8 cm
1	60.7	40	27.1
2	58.4	35	22
3	56.2	32	17.3
4	53.9	28	13.5
5	50.5	22	10.3
6	47.6	19	9.12
7	45.1	17	7.45
8	41.9	16	5.01
9	36.2	14	3.07
10	31.9	11	0
11	29.2	8	0
12	27.6	6	0
13	21.9	4	0
14	15.9	2	0
15	11.3	0	0
16	9.98	0	0
17	5.3	0	0
18	3.2	0	0
19	2.4	0	0
20	1.2	0	0

and Figure 19 show that the coil with a larger diameter has a higher mutual voltage and can operate at a greater distance than the others.

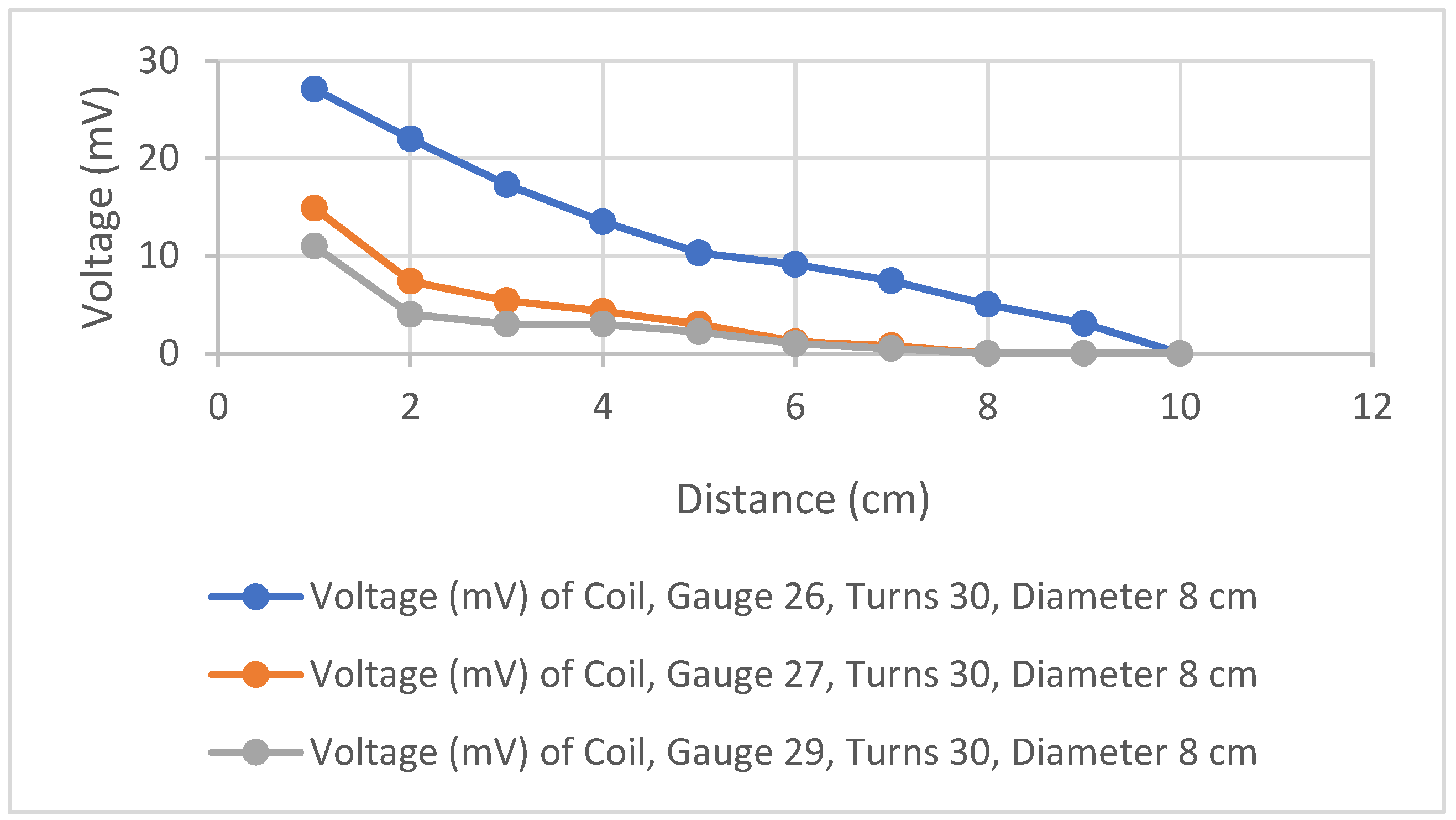
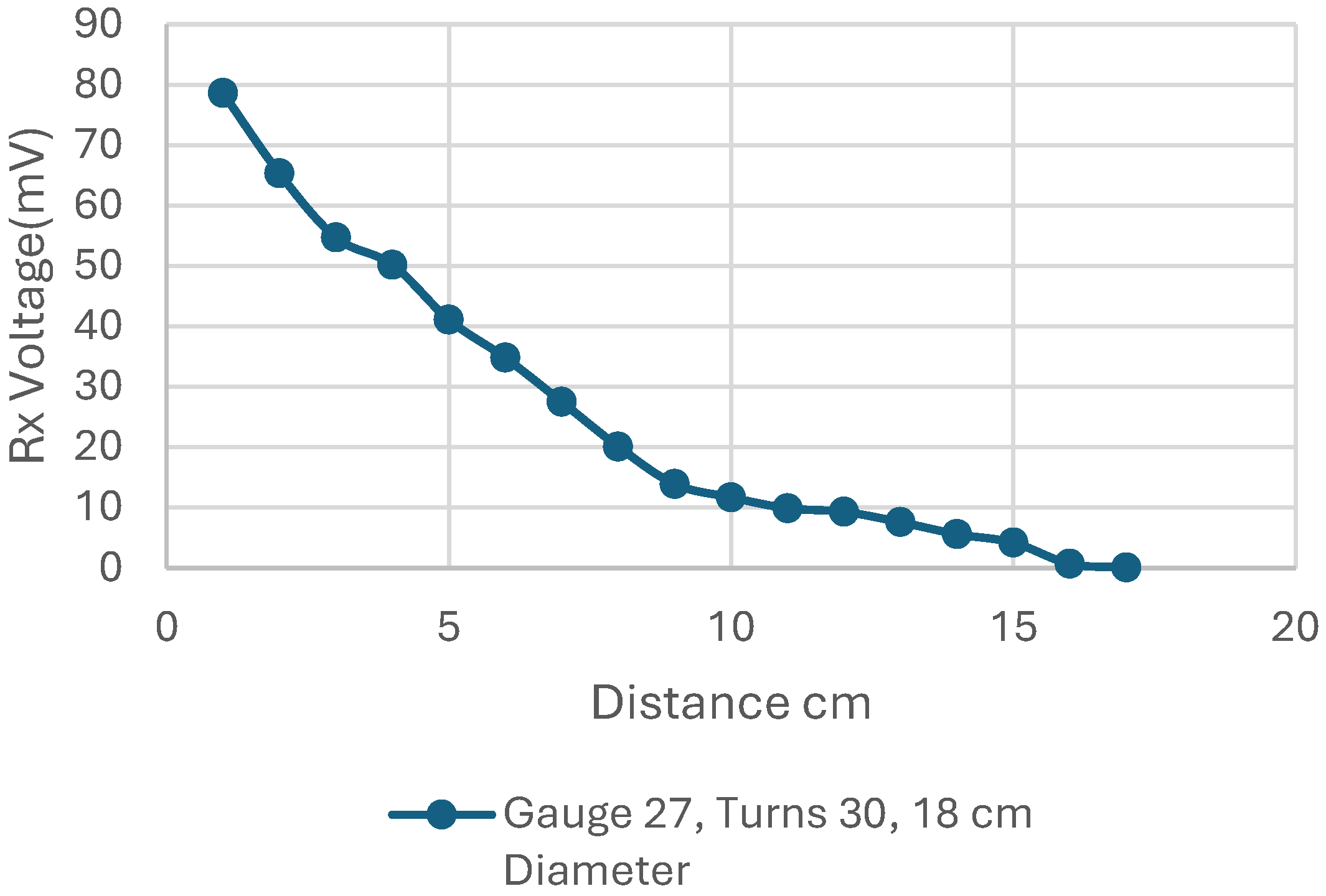
In the next step, we change the cable gauge, which varies in thickness as the two are inversely proportional to each other. We keep the rest of the parameters the same, i.e., 30 turns and an 8 cm diameter.

The results in

Table 11. Voltage received in Rx when AWG is changed.

Distance (cm)	26 AWG	27 AWG	29 AWG
1	27.1	14.9	11
2	22	7.39	4
3	17.3	5.41	3
4	13.5	4.32	3
5	10.3	3.0012	2.2
6	9.12	1.2	1
7	7.45	0.78	0.5
8	5.01	0.01	0
9	3.07	0	0
10	0	0	0

and Figure 20 show that the coil with greater thickness, that is, a lower wire gauge, produces higher mutual voltage and can operate at a greater distance than others. In the next step, we change the input current of the transmitting coil and keep other parameters unchanged.

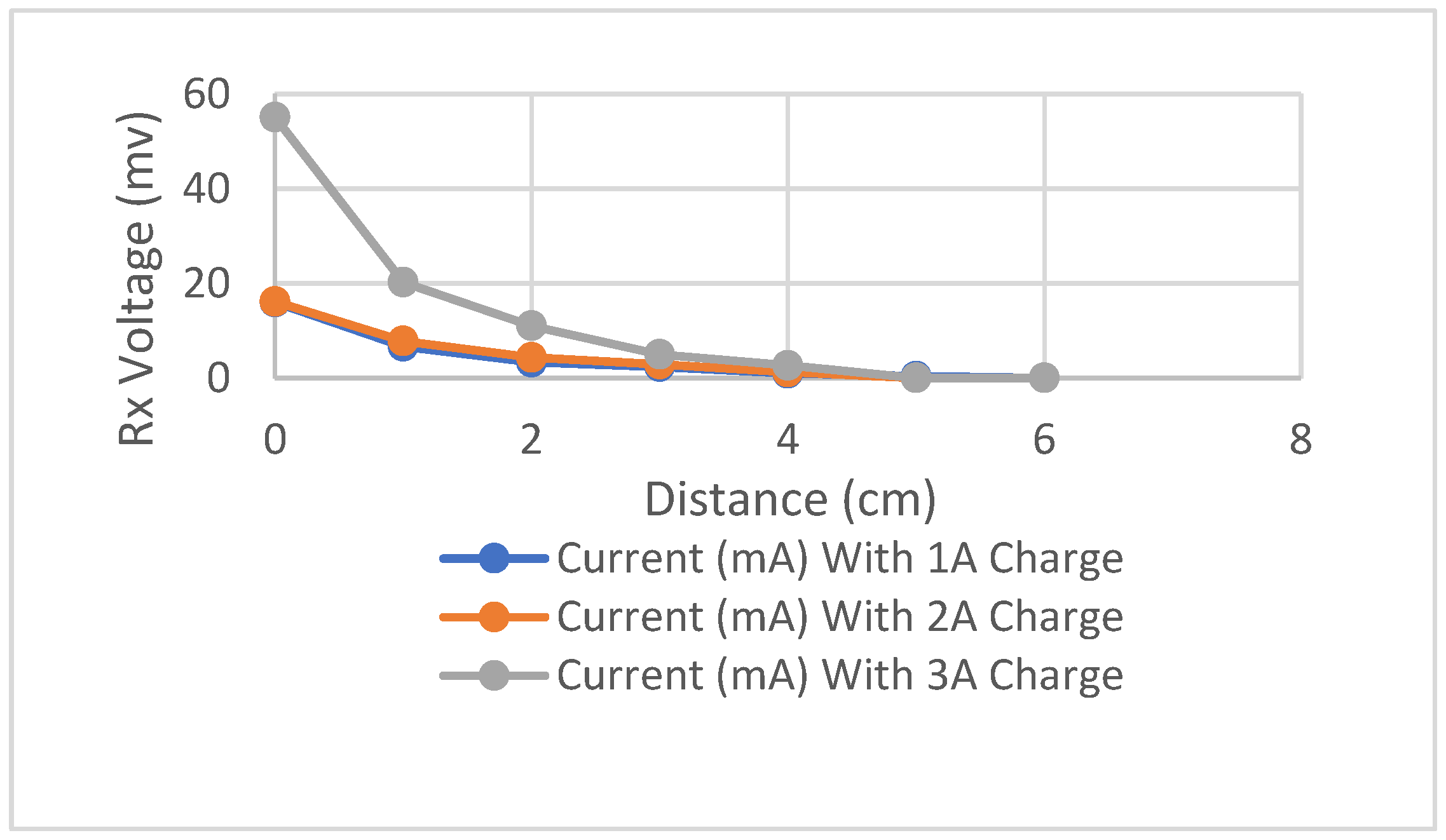
The above results in

Table 12. Voltage received in Rx when input current is changed.

Distance (cm)	Input Current 1 A	Input Current 2 A	Input Current 3 A
0	16.01	16.16	55.1
1	6.67	7.81	20.23
2	3.33	4.35	11.02
3	2.37	2.9	4.99
4	0.99	1.25	2.68
5	0.4	0.01	0.01
6	0.001	0	0

and Figure 21 show that the coil that has more input current tends to cover a greater distance. In order to avoid the melting of copper wire, the input current should not exceed the maximum current supported by the wire’s thickness. A thicker wire means that is having less gauge is able to carry more current. Hence the input current can be increased if a lesser gauge wire is used as per its rated value.

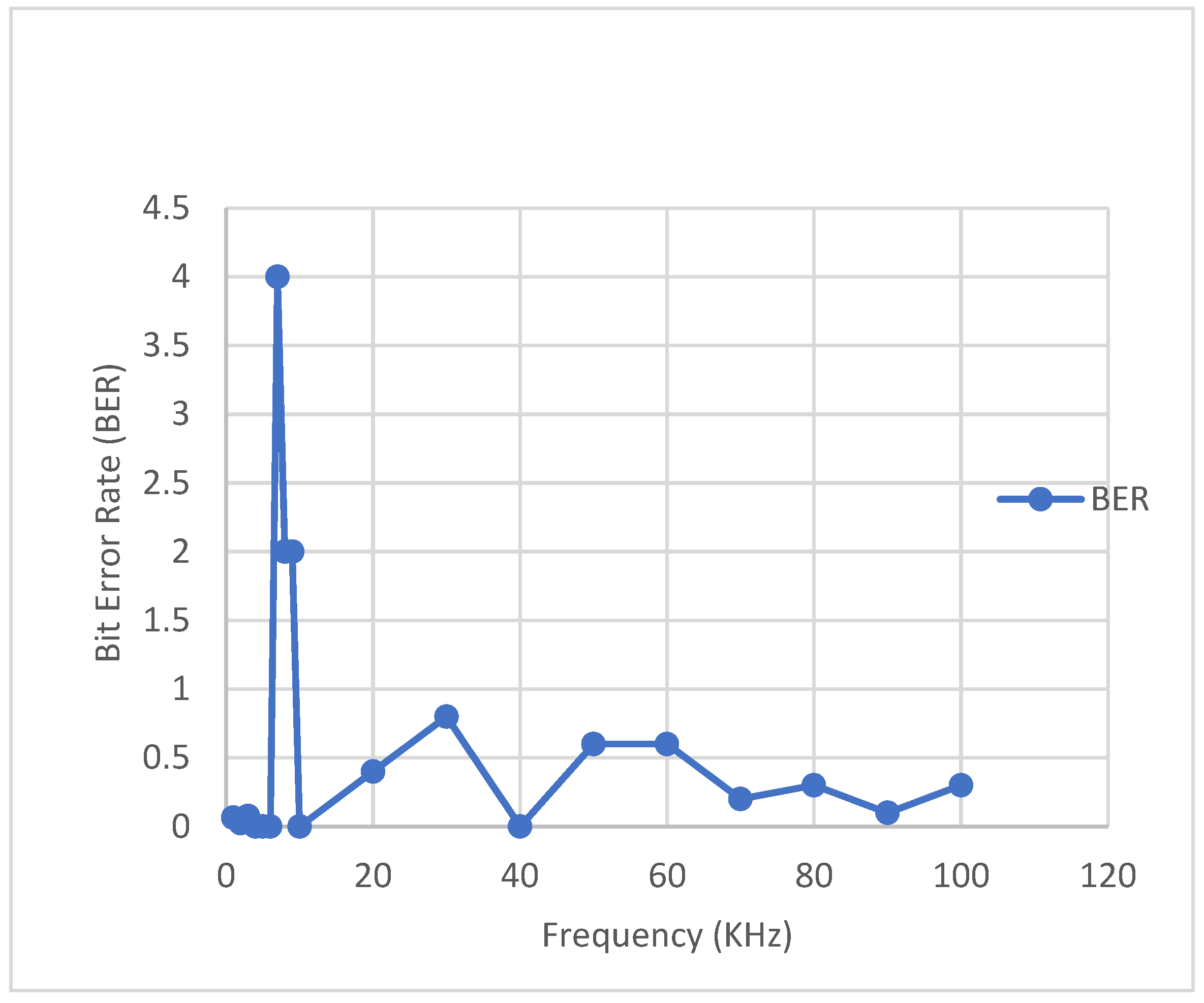
In the next step, we tend to find the bit error when the frequency is varied for the same set of coil parameters. The results are shown in

Table 13. Bit error rate experiment in the air.

Freq (kHz)	Receive Time Trx (μs)	Transmit Time Ttx (μs)	Throughput at Tx (kbps)	Throughput at Rx (kbps)	BER	Delay (μs)	Packet Delivery Ratio (%)	Packet Loss Ratio (%)
1	452	516	2.21	1.93	0.064	64	87	3
2	240	264	4.16	3.81	0.024	24	92	8
3	104	180	9.61	5.55	0.076	76	58	42
4	126	124	7.93	8.06	0	2	100	0
5	104	100	9.61	10	0	4	100	0
6	80	84	12.5	11.9	0	4	95	5
7	70	70	14.2	14.2	4	0	100	0
8	58	60	17.2	16.6	2	2	97	3
9	52	54	19.2	18.5	2	2	96	4
10	48	48	20.8	20.8	0	0	100	0
20	24	24.4	41.6	40.9	0.4	0.4	98	2
30	16.8	16	59.5	62.5	0.8	0.8	100	0
40	12.4	12.8	78.1	78.1	0	0.4	100	0
50	9	10	111	100	0.6	1	90	10
60	7.6	8.2	131	121	0.6	0.6	92	8
70	7	6.8	142	147	0.2	0.2	100	0
80	5.9	6.2	169	161	0.3	0.3	95	5
90	5.5	5.4	181	185	0.1	0.1	100	0
100	5.4	5.1	185	196	0.3	0.3	100	0

and Figure 22.

In the next step, we prepare a setup by using a water tank as per the dimensions used in Figure 15 for simulations conducted underwater with equidistant dimensions for both coils.

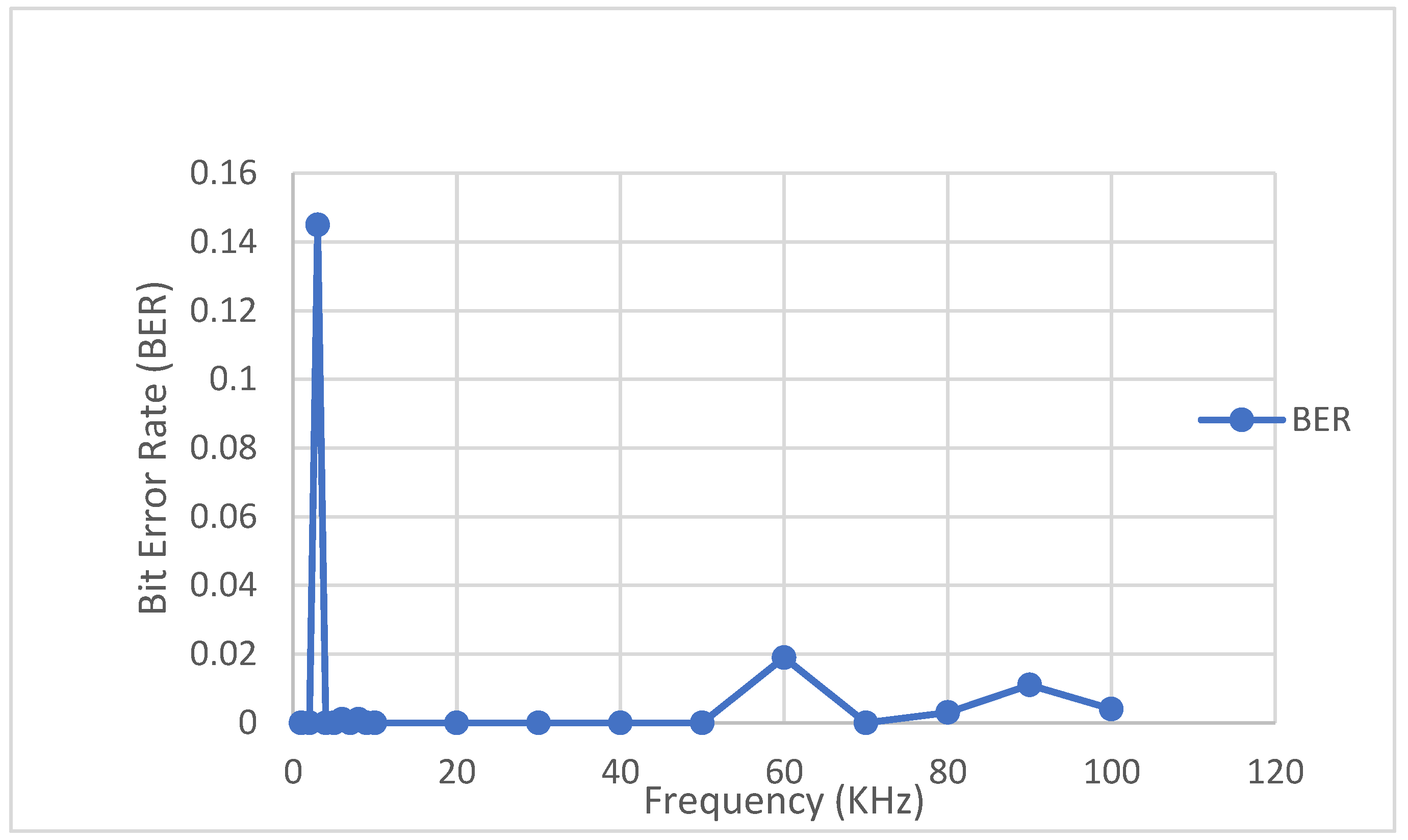
The results in

Table 14. Bit error rate experiment in water.

Freq (kHz)	Receive Time Trx (μs)	Transmit Time Ttx (μs)	Throughput at Tx (kbps)	Throughput at Rx (kbps)	BER	Delay (μs)	Packet Delivery Ratio %	Packet Loss Ratio (%)
1	490	490	2.04	2.04	0	0	100	0
2	244	244	4.09	4.09	0	0	100	0
3	164	168	6.09	5.95	0.145	4	98	2
4	124	122	8.06	8.19	0	2	100	0
5	96	96	10.4	10.4	0	0	100	0
6	80	86	12.5	11.6	0.001	6	93	7
7	74	72	13.5	13.8	0	2	100	0
8	60	64	16.6	15.6	0.001	4	94	6
9	58	56	17.2	17.8	0	2	100	0
10	50	50	20	20	0	0	100	0
20	24.4	24.4	40.9	40.9	0	0	100	0
30	16.4	16.8	60.9	59.5	0	0.4	98	2
40	12.4	12.4	80.6	80.6	0	0	100	0
50	10	10	100	100	0	0	100	0
60	7.2	8.4	138	119	0.019	1.2	86	4
70	6.8	6.8	147	147	0	0	100	0
80	6.1	6	163	166	0.003	0.1	100	0
90	5.5	5.2	181	192	0.011	0.3	100	0
100	4.9	5	204	200	0.004	0.1	98	2

and Figure 23 show that the bit error rate is zero more often at separate frequencies in water than in air. We have measured the transmit time of the signal from a digital oscilloscope and similarly the receive time. We found out in the result that by varying the frequency, the difference in both time intervals was negligible in water at many frequencies as compared to air.

The following Figure 24 shows the setup used to conduct the experiment in water.

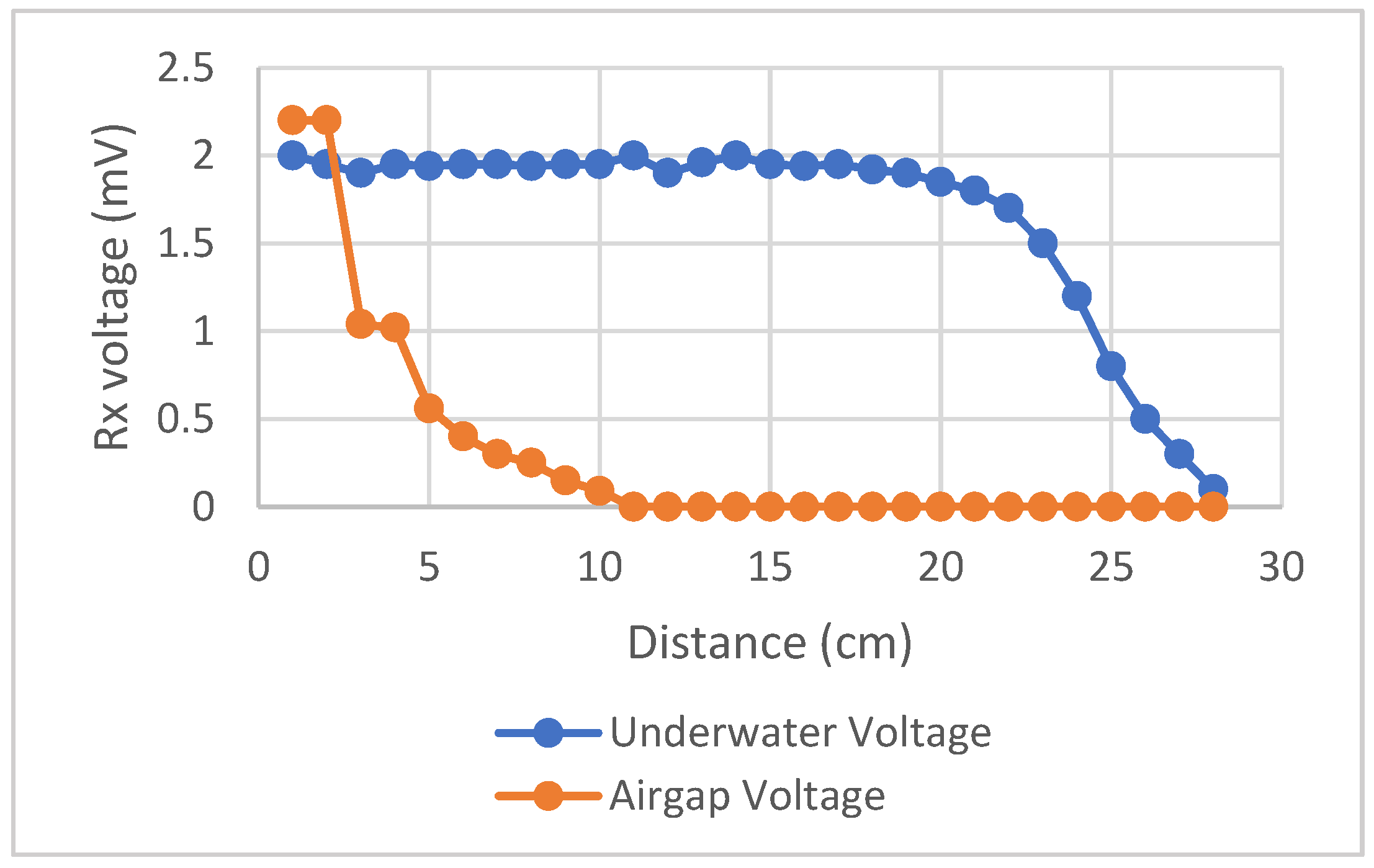
In the next step, we measure the distance covered by applying a 220 kHz signal to the transmitting coil. Both coils have 30 turns of 29 AWG, and a diameter of 8 cm in water and in air.

The results in Figure 25 and

Table 15. Underwater vs. airgap voltage.

Distance (cm)	Underwater Voltage (mV)	Air Gap Voltage (mV)
1	2	2.2
2	1.95	2.2
3	1.9	1.04
4	1.95	1.02
5	1.94	0.56
6	1.95	0.4
7	1.95	0.3
8	1.94	0.25
9	1.95	0.15
10	1.95	0.09
11	2	0
12	1.9	0
13	1.96	0
14	2	0
15	1.95	0
16	1.94	0
17	1.95	0
18	1.92	0
19	1.9	0
20	1.85	0
21	1.8	0
22	1.7	0
23	1.5	0
24	1.2	0
25	0.8	0
26	0.5	0
27	0.3	0
28	0.1	0

show that conductivity is higher in water than in air between both coils.

In the next step, we increased the temperature of the water and tried to get the results on the receiving coil. The results are shown in

Table 16. Effect of temperature on MI coils of 8 cm diameter with 30 turns of 27 AWG.

Distance (cm)	Rx Voltage at 16 °C	Rx Voltage at 65 °C
1	14.6	16.7
2	10	11.3
3	7.5	8
4	4.7	5.7
5	3.5	3.9
6	3.3	3.1
7	3.1	2.8
8	3	2.6
9	2.7	2.5
10	2.3	2.4
11	2.2	2.3
12	2.1	2.2
13	2	2
14	1.9	1.9
15	1.9	1.8
16	1.8	1.7
17	1.8	1.7
18	1.7	2.8
19	1.6	3.8
20	1.5	3.4
21	1.4	2.6
22	1.3	3.1
23	1.2	3.1
24	1.1	3.2
25	1	3

and Figure 26.

At room temperature, the temperature of water is 16 degrees centigrade. We then used a heating rod to raise the temperature of the water to 65 degrees centigrade and then checked the results.

The above result shows a better range achieved for a higher temperature of water

In the next experiment, in order to change the pH of water, we used saline water whose pH is known to be 8.5, and normal water has 7; hence, the pH of water was increased from 7 to 8.5, and an experiment was conducted to check the results. The results are shown in

Table 17. Rx voltage vs. distance at pH 7.0 and pH 8.5 (30 Turns 27 AWG, 8 cm coil).

Distance (cm)	Rx Voltage, pH 7.0	Rx Voltage, pH 8.5
1	13.5	14.6
2	12.1	10
3	10.9	7.5
4	9.3	4.7
5	7.8	3.5
6	5.4	3.3
7	4.1	3.1
8	3.1	3
9	2.8	2.7
10	1.9	1.3
11	1.5	1.2
12	1.1	1
13	1	0.8
14	0.8	0.6
15	0.5	0

and Figure 27.

The above result shows an improved result at a lower pH of water, but the difference in covered distance is negligible.

In the next experiment as shown in Figure 28, a relay method that uses three coils of similar configuration is conducted. The results are shown in Figure 29.

The above results show the accumulated range achieved by using the relay method of MI coils.

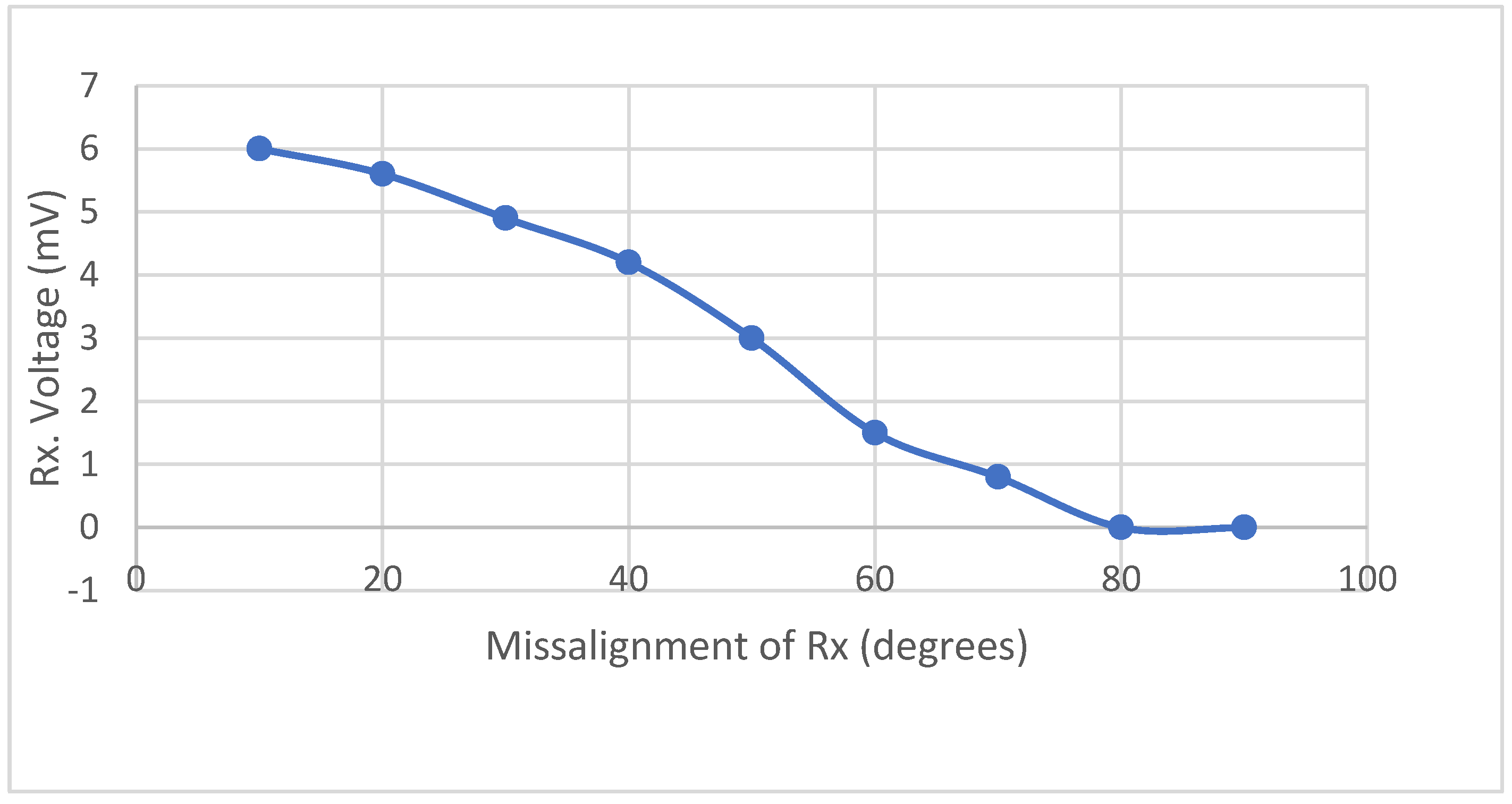
In the next step, we used the two coils (30 turns, 27 AWG, 8 cm coil) and checked the effect of misalignment on the receiver side per 10-degree change. The results are shown in

Table 18. Rx voltage vs. degrees of misalignment (30 Turns 27 AWG, 8 cm coil).

Misalignment (Degrees)	Rx Voltage (mv)
10	6
20	5.6
30	4.9
40	4.2
50	3
60	1.5
70	0.8
80	0
90	0

and Figure 30.

The above result shows the effect of misalignment between the receiving coils on their output signal, which decreases when they are not aligned in parallel.

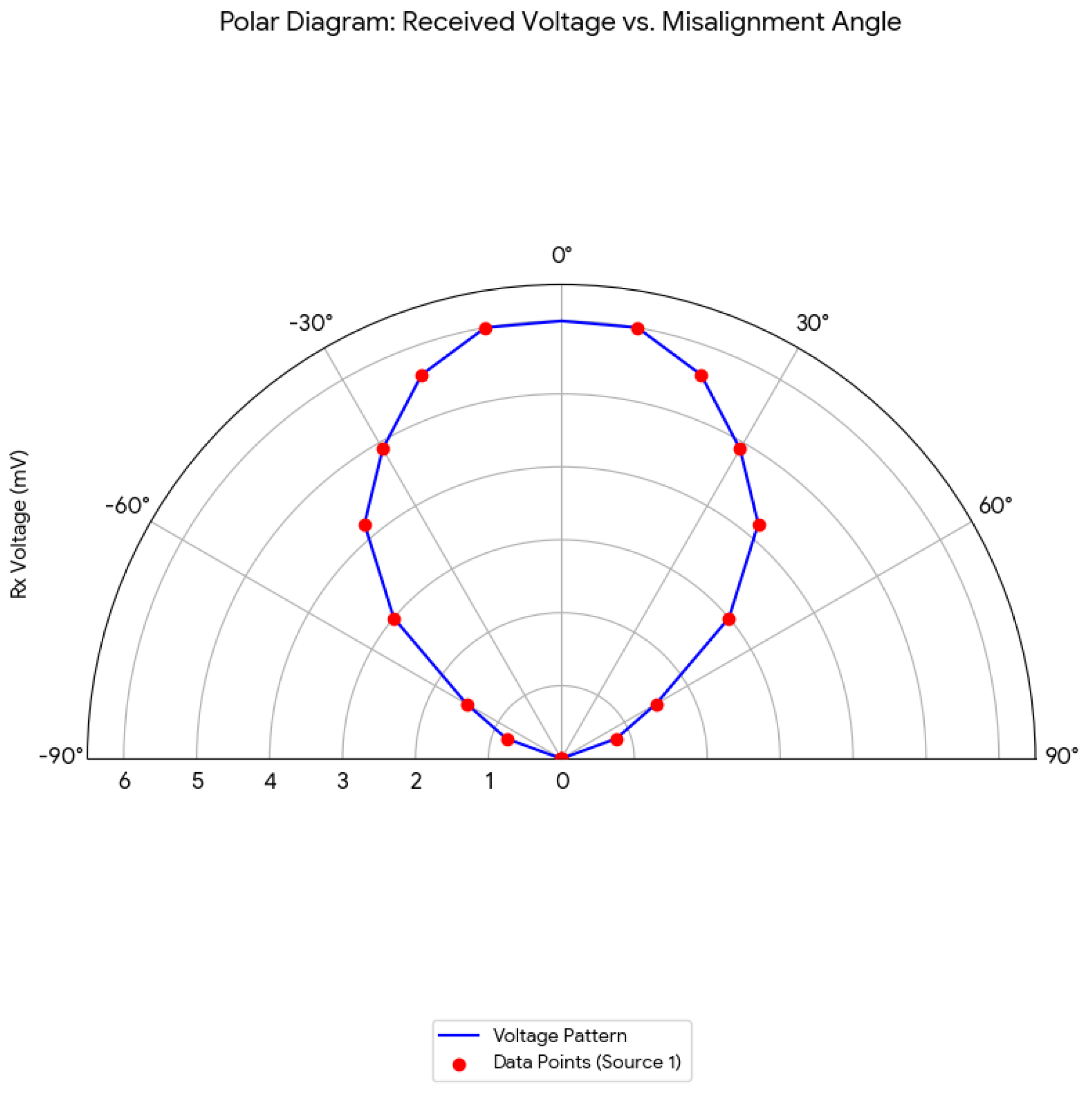
The following Figure 31 shows the polar form of the above result.

4. Future Directions

The process for optimization can be enhanced to achieve better results and applied to various applications; for example, in [24], the authors have used MI coils to send wakeup calls to passive coils that send wakeup signals only on acquiring data on a certain parameter, like gas pipeline leakage underwater. In [25], the authors have used two sets of coils, one for charging and the other for only data acquisition. This application may be used where batteries are not feasible due to high-temperature considerations, and coils may just acquire data and send it to the nodes that charge those coils remotely. The work performed above may be useful for designing coils based on the application and ensuring they operate as required. In [26], the authors built a prototype that considers misalignment tolerance, lightweight construction, and the system’s thermal safety.

5. Conclusions

The results suggest that we can achieve a greater range in water than in air if we consider the right input frequency at which the Bit Error is zero and configure coils with a greater number of turns, a larger diameter, a smaller gauge, and a reasonable amount of input current. After applying a frequency range of up to 100 kHz and 12 Volts with varying current, we have achieved a distance up to 80% greater than in air, as determined by parametric analysis, up to 25 cm. With improved bit error rate, less delay under 2 microseconds, increased packet delivery ratio near 100% and less packet loss ratio that is less than 10%. This demonstrates that it is possible to conduct future research into other underwater applications by implementing MI for underwater communication.

The results obtained from the methodologies used to assess changes in WPT parameters can be applied to different applications, where different trade-offs can be considered.