Abstract
This paper presents a novel approach to address the problem of intercepting non-cooperative targets with multiple satellites in Earth orbit. The multi-satellite interception problem is formulated as a multi-player pursuit–evasion game that explicitly accounts for stochastic disturbances and control constraints. By combining differential game theory with stochastic optimization techniques, the paper derives optimal interception trajectories that ensure safety and performance under modeling uncertainties. A linear exponential quadratic cost functional is established, and corresponding Nash equilibrium strategies are obtained to determine the optimal control laws. Numerical simulations validate the effectiveness and robustness of the proposed approach in achieving reliable interception performance.
1. Introduction
For traditional non-cooperative rendezvous problems, they mainly focus on scenarios where the target does not possess maneuvering capabilities, such as the clearing of malfunctioning satellites or space debris [1]. However, when the target exhibits maneuvering behavior, the solution requires the adoption of either unilaterally optimal robust control methods [2] or bilaterally optimal control methods based on differential games [3,4]. In unilaterally optimal control methods, the minor thrust exerted by the target spacecraft is treated as disturbances to the interception control system, for which a robust controller is devised to enhance the system’s tolerance towards these disturbances. As a representative example, Gao et al. successfully tackled the challenges of applying synchronous control algorithms to complex spacecraft systems, and they utilized this controller along with relevant theories to design a robust control algorithm for close-range relative spacecraft motion [5]. From the evader’s perspective, when the target is threatened by the pursuer, it adopts maneuvering strategies advantageous to itself to evade interception [6]. Building on this line of research, ref. [7] provided the first rigorous investigation of pursuit–evasion games in three-dimensional space with three-degree-of-freedom pursuer dynamics, where the equilibrium strategies are derived via the Hamilton–Jacobi–Bellman–Isaacs framework and further analyzed in terms of capture conditions and escape thresholds. These studies [8] collectively highlight that in the presence of maneuvering targets, bilaterally optimal control methods grounded in differential game theory are indispensable.
With the demand for space game-theoretic adversarial technologies, an increasing number of scholars and institutions have begun to focus on the pursuit–evasion game of spacecraft and have produced a series of research achievements [9,10]. In parallel with the development of pursuit–evasion game theory, advances in distributed filtering have significantly enhanced the foundation for collaborative estimation and control in multi-agent systems. In particular, Sayed et al. [11] have revised the stability and convergence paradigm of distributed filtering, demonstrating that distributed filters can achieve stability under the same conditions as centralized ones. Conway et al. have published several significant papers in the field of spacecraft pursuit–evasion games, in which they propose a class of semi-direct methods to solve the three-dimensional orbital pursuit–evasion differential game of spacecraft [12]. Subsequently, Prince applied this method to a series of practical spacecraft games, such as interception, rendezvous, energy matching, and other scenarios [8]. In parallel, Sun et al. transformed the game problem into two optimal control problems and proved that solving these optimal control problems sequentially is equivalent to solving the original pursuit–evasion differential game [13]. Gong et al. confirmed the existence of a Nash equilibrium through the minimax principle and, by integrating adaptive dynamic programming with a linear quadratic cost function, designed a real-time control law for a two-player pursuit–evasion game [14]. Ye et al. utilized heuristic search and Newton’s method to solve the satellite proximity pursuit–evasion game problem and discussed the algorithm efficiency for different initial states considering thruster layout [15]. Under the assumption that there is an unknown maneuvering target with colored noise, the game control laws for the pursuer under different line-of-sight observation conditions were derived based on linear quadratic differential game theory in [16]. Extending beyond spacecraft scenarios, recent work [17] has introduced a reinforcement learning-based formation-surrounding control framework for multi-quadrotor UAV pursuit–evasion games, which ensures stability under external disturbances and achieves Nash equilibrium with proven surrounding properties. The research on satellite pursuit–evasion games has paved the way for further investigations into multi-satellite interception.
In the context of multi-satellite interception, each satellite plays a distinct role as a participant, giving rise to a dynamic interplay of cooperation and competition among them. The exploration of methodologies for multi-satellite interception encompasses a diverse range of interdisciplinary fields and technical approaches, including game theory, optimization algorithms, and machine learning methods [18,19]. Shirazi introduced an innovative high-thrust orbital transfer optimization method, employing a hybrid algorithm that combines simulated annealing and genetic algorithms. This approach effectively optimizes orbital maneuvers during the interception of multiple satellites [20]. In [21], Liu addressed the problem of optimization of intercept trajectories involving an attacker, a target, and an interceptor. The relative motion kinematic equation and differential game model are formulated, and the robust tripartite optimal strategy is successfully obtained by transforming the interception countermeasure problem into the problem of finding the Nash equilibrium point. However, it is essential to acknowledge that the investigations on multi-satellite interception tasks mentioned above have not fully accounted for significant uncertainties, which may play a crucial role in real-world scenarios.
According to the unique characteristics of non-cooperative targets, such as information communication constraints, uncoordinated maneuvering behavior, and incomplete prior knowledge, it becomes imperative to incorporate uncertainties into the design of trajectory control methods for interception spacecraft. Repperger et al. made noteworthy contributions by developing a stochastic model to construct a two-satellite optimal terminal rendezvous game model. They effectively employed the Kalman filter to manage noisy output measurements, ensuring optimal estimation of the rendezvous state [22]. Based on the preceding analysis, most existing design methods focus on enhancing the robustness of controllers to overcome non-cooperative target maneuvering and external disturbances. Bai et al. analyzed many-to-many interception strategies using a Mean Field Game framework, but did not incorporate explicit control input constraints, limiting its applicability to practical interception problems [23]. In addition, Zhang et al. proposed a fixed-time adaptive dynamic programming framework for multi-satellite pursuit–evasion zero-sum games, deriving Nash equilibrium strategies and capture conditions with improved computational efficiency [24]. However, the uncertainty regarding the upper bound of non-cooperative target maneuvering often leads to conservative controller designs, which consequently hinder fuel optimization and interception accuracy improvements.
With the rapid expansion of space activities, the number of autonomous spacecraft operating in orbit has dramatically increased, leading to more complex interactions among cooperative and non-cooperative targets. In practical mission scenarios, such as space security operations, debris removal, and on-orbit servicing, the interception of non-cooperative or even adversarial targets has become a critical capability for ensuring the safety and sustainability of the orbital environment. However, existing interception strategies are often developed under idealized assumptions, neglecting uncertainties caused by stochastic perturbations, control saturation, and limited inter-satellite communication. These factors significantly affect interception success rates and may compromise system stability and resource efficiency in realistic missions. Therefore, it is of both theoretical significance and engineering importance to develop a multi-satellite cooperative interception framework that explicitly incorporates stochastic disturbances and control constraints while ensuring safety and performance guarantees. Inspired by the traditional non-cooperative rendezvous problems, this paper investigates the multi-satellite interception problem considering stochastic uncertainty based on differential games. The main contributions of this study can be summarized as follows:
(a) A stochastic differential game framework is established for the multi-satellite interception problem involving a maneuvering non-cooperative target. By explicitly modeling stochastic perturbations, the proposed formulation captures the uncertainty inherent in real orbital environments.
(b) An analytical Nash equilibrium solution is derived for the linear-quadratic multi-satellite stochastic game, providing a tractable closed-form strategy representation that facilitates real-time implementation.
(c) To address actuator saturation and safety constraints, a segmented control scheme is developed to ensure bounded inputs, safe interception trajectories, and efficient resource utilization throughout the interception process.
2. Preliminaries
2.1. Scenario Description
This article focuses on the orbital control problem of non-cooperative target interception, considers the interception task of multiple micro-satellites against a target spacecraft, and attempts to propose an optimal control method for pursuit–evasion game based on exponential quadratic cost functional for linear stochastic systems. In the satellite interception task, there are multiple tracking satellites as the pursuers and one target spacecraft as the evader. The pursuer attempts to intercept the target spacecraft by selecting an appropriate strategy that minimizes energy consumption, while the evader tries to escape with minimum energy consumption. Since the thrust force provided by the propulsion system of the satellite is not infinitely large, we consider that both the pursuing and target satellites have energy constraints. In addition, to ensure the implementation of the interception mission, the upper energy limit of the pursuer needs to be higher than that of the target.
To achieve the above mission objectives, we will establish a relative motion model based on the reference satellite orbit coordinate system, and transform the non-cooperative target intercept task into a pursuit–evasion game task considering stochastic perturbations. By solving the pursuit–evasion game strategy, the Nash equilibrium strategy, which enables the tracking spacecraft to achieve non-cooperative target interception with minimum energy consumption, is obtained.
2.2. Construction of Satellite Interception Model
Multiple satellites orbit the earth together with the reference satellite. It is assumed that the reference satellite moves in a near circular orbit and the relative distance between the active satellites and the reference satellite is much smaller than the distance between the earth and the reference satellite. The dynamics of active satellite in the local-vertical local-horizontal (LVLH) frame can be simplified into the following Clohessy–Wiltshire (CW) equation
where X, Y and Z represent the three-dimensional coordinates of the active satellites relative to the reference satellite in LVLH frame, , and represent the three-axis thrust of the active satellites, and represents the orbital angular velocity of the reference satellite. The linearized CW equations in (1), which govern the relative motion dynamics of this study, are derived from the full nonlinear relative motion model. This derivation relies on the two key assumptions stated above: a near-circular reference orbit and a small relative separation compared to the orbital radius. For a complete derivation, see [25].
The relative position of the reference satellite and active satellites are depicted in Figure 1 where and r are the inertial position vectors of the reference satellite and active satellites, respectively, and is the position vector of active satellite i relative to the reference satellite.
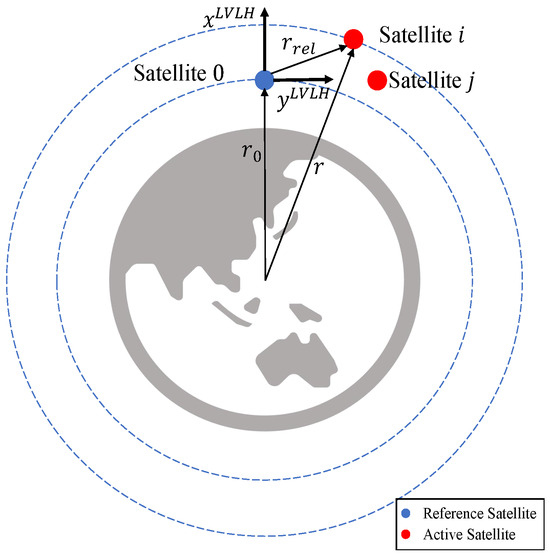
Figure 1.
Relative geometry and LVLH coordinate frame of satellites.
Define the state variable and control variable , the above dynamic can be written in the form of state space equation as follows
where , , is the null matrix, is the identity matrix, is the angular velocity of the active satellites, is the distance from the active spacecraft to the center of the earth, is the gravitational constant.
The state-space equation for tracking satellites in the reference spacecraft orbital coordinate system can be expressed as follows:
where and are the state variable and control variable respectively, for the tracking satellite, is the control matrix with constant .
Similarly, the state space equations for the target satellite in the reference spacecraft orbital coordinate system can be expressed as:
where and are respectively the state and control variables for the target satellite, and the control matrix with constant .
It should be noted that this paper assumes the use of a single thruster on each satellite, capable of adjusting its direction to control translational movement. Similar to [26], the thrusts are subject to constraints on their magnitude.
In order to ensure successful interception, it is assumed that the pursuer possesses greater maneuverability than the target, specifically .
2.3. Communication Topology
The information exchange among the intercepting satellites is represented by a directed graph , where denotes the set of intercepting satellites and represents the set of directed communication links. If , it implies that satellite i can receive information from satellite j.
The adjacency matrix of is denoted by , where if and otherwise. The in-degree of node i is , and the corresponding Laplacian matrix is with .
In this study, the communication network is assumed to be a directed graph containing at least one directed spanning tree. Such a structure ensures that information from the root node can be transmitted to all other nodes through directed paths, maintaining effective coordination among satellites. The communication channels are considered ideal, that is, free of time delays and transmission errors, and all links are assumed to be reliable during the interception process. Since only a single target satellite is considered in this work, its state information is assumed to be available to all intercepting satellites through the directed communication topology, enabling cooperative interception.
2.4. Relative Motion Dynamics with Disturbances
The above state space equation represents the dynamic of active satellite relative to reference satellite. Based on the aforementioned dynamic equations, the relative state variable between the tracking satellite and a corresponding non-cooperative target are defined.
Therefore, the modeling of the relative motion dynamics in the reference satellite orbit coordinate system is as follows:
The above relative motion dynamics represents the ideal relative dynamic between the pursuit satellite and target satellite under the reference spacecraft orbital coordinate system. However, it is only deterministic dynamic. Due to the influence of randomness in the real world (including sensor and actuator hardware), it is important to consider stochastic in system dynamics. The deterministic dynamics (7) will be replaced by an It stochastic system driven by noise of random processes representing real world variations.
where is an matrix that maps process noise into the relative state vectors, is a real-valued Brownian process defined on the complete probability space , where is the sample space, is the event space and is the probability measure. The following lemma holds for the aforementioned It stochastic system.
Lemma 1
([27]). It is assumed that there is a twice continuously differentiable function . is the stochastic differential process, i.e.,
where is the drift coefficient, reflecting the movement caused by deterministic factors, is the disturbance intensity. is the Brownian process.
Then, is also the stochastic differential process, and satisfies
where is the infinitesimal generator of the stochastic process for , given by:
3. Formulation of the Multi-Satellite Interception
The implementation of multi-satellite interception tasks consists of three components: the game participants , the admissible strategy sets , for each participant , and the objective functions of the participants. To meet the requirements of the interception task, the following objective function is designed:
where is the weighted sum of all strategies obtained by pursuer i. , and are given symmetric positive definite matrices, is a symmetric non-negative matrix and is a fixed real number. Besides, is a weighted term of relative state variables used to constrain the relative position between the tracking satellite and the targeted spacecraft. and represent the energy consumption of the tracking satellite and the targeted spacecraft, respectively, which are used to enforce constraints on control energy.
Remark 1.
It is worth noting that the exponential-quadratic form of the cost function in (12) is inspired by the risk-sensitive stochastic optimal control theory. This design enables the pursuer to take into account not only the expected performance but also the sensitivity of the interception process to random perturbations. In this context, the weighting matrices , , and balance the trade-off between interception precision, control effort, and robustness against uncertainty. The terminal weighting matrix ensures that the relative distance between the pursuer and the target asymptotically converges to a safe capture region at the terminal time. Therefore, the proposed cost function captures both the physical requirements of orbital interception and the stochastic characteristics of the orbital dynamics, providing a realistic and implementable optimization criterion for multi-satellite cooperative interception tasks.
As all of the N tracking satellites will participate in the game process and affect the decision-making of the targeted spacecraft, the global payment functional of the tracking party is represented by the weighted sum of individual tracking satellite payment functions as follows:
Analogously, define the payoff functional of the target as
where M represents the number of elements in the set , and denotes the set of neighboring intercepting satellites from which the target spacecraft can acquire information.
The assumptions about in (12) can be stated to guarantee the uniqueness and positive symmetry of the solution of the Riccati equation.
(A1) is constrained so that the inequality is satisfied.
To solve the multi-satellite interception, one gives the following definitions.
Definition 1.
If the following inequalities
hold for all agents in the multi-satellite interception. Then, the strategies and form a Nash equilibrium.
Definition 2.
Suppose that if all intercepting satellites satisfy the condition . Then, the system will achieve successful interception. is the capture radius. is the relative distance between satellite i and the target.
4. Solution of the Multi-Satellite Interception
The following theorem combines the completion of squares and the Radon-Nikodym derivative methods to provide the optimal Nash equilibrium strategies for the multi-satellite interception systems.
Theorem 1.
Consider the multi-satellite interception systems given by pursuer (3), evader (4), the cost functional (12)–(15). The admissible strategies and is given by
where is the relative state variable of tracking satellite i and the target for . is the unique positive symmetric solution of the following Riccati equation
Then, the MPE stochastic differential games are in Nash equilibrium.
Proof.
The solution of Nash equilibrium strategies in multi-satellite interception missions is inspired by the study of two-player stochastic differential game strategies. By taking the derivative of equation and integrating it afterwards, and combining the stochastic process with It formula in Lemma 1, one can obtain
To simplify the expression, the cost functional for individual tracking satellite is represented as
where . By combining the above equation with , one obtains
Furthermore, the cost function for individual pursuit satellite can be obtained as
Letting the expressions of and be equivalent to the optimal policies and , and substituting (18) and (19) into the above equation, we obtain
where is the expectation of measure probability expressed by
According to the result of likelihood function in [28], is a Brownian motion with the incremental covariance. Thus, the random integral term and the increasing process in (26) constitute the Radon-Nikodym derivative. In addition, by the properties of the Radon-Nikodym derivative, the expectation is 1.
Next, we will demonstrate that the optimal strategies (18) and (19) are Nash equilibrium strategies, assuming there is a deviation between the actual input strategy and the optimal strategy, expressed by the following equations:
where and are measurable and bounded errors. Substituting (27) and (28) into (24), one obtains the analogue of (24) as
By comparing the payoff functions (25) and (29) under the optimal strategy pairs and the assumed actual strategy pairs , we can see that the multi-satellite interception system can achieve Nash equilibrium under the effects of the Nash equilibrium policies and . Therefore, and .
Since the individual pursuer’s payoff function is the optimal cost function under the optimal strategy, the global payoff function consisting of the N individual payoff functions is also optimal, expressed as:
Analogously, the optimal payoff functional of the target is
The above discussion leads to the following inequalities:
Since the above inequality is satisfied, according to the definition of Nash equilibrium, it can be concluded that the multi-satellite non-cooperative target approach control system, consisting of N tracking satellites and one target spacecraft, can achieve Nash equilibrium under the control of optimal strategies and . □
Remark 2.
The combination of the Radon–Nikodym derivative and the completion of squares technique serves both theoretical and physical purposes. The Radon–Nikodym derivative is used to transform the probability measure under stochastic disturbances, effectively converting the stochastic dynamics into an equivalent deterministic form for optimization. This transformation allows the controller to account for random perturbations in the orbital environment through a probabilistic weighting of trajectories. Meanwhile, the completion of squares method provides an analytical way to minimize the quadratic cost function by balancing control effort and tracking accuracy. In physical terms, it ensures that the interceptor satellites achieve an optimal trade-off between energy consumption and interception precision under uncertainty, thereby realizing a stable Nash equilibrium in the stochastic game framework.
The limitation in the satellite’s maneuverability, which leads to a restriction in the thruster output, indicates that the control law derivation and design mentioned earlier cannot be implemented directly in engineering. The control strategy consists of two components: amplitude and unit directional vector d, namely:
Based on the formula for thrust constraint (5) and the optimal control strategies (18) and (19), the control strategy for multi-satellite interception in practical engineering applications can be expressed as:
where , denotes the maximum amplitude of the control strategy for the pursuer satellite and the target spacecraft.
where , is the sum of all relative states, and denotes the maximum amplitude of the control strategy for the pursuer satellite and the target spacecraft. To ensure the successful capture of the target, it is required that . The thrust saturation in Equation (35) may slightly slow convergence when the desired control exceeds the thrust limit. Nevertheless, as long as the pursuers’ maximum thrust satisfies , convergence inside the capture radius is preserved.
Remark 3.
The control strategy for the target involves the Riccati matrix and the relative state variable , originating from the intercepting satellite closest to the target. In other words, if the nearest intercepting satellite switches, the strategy for the target will also undergo the corresponding transition. Besides, the Nash equilibrium obtained from the coupled Riccati equations is unique under the standard LQ game assumptions of positive-definite cost weights and stabilizable system pairs. In more general nonlinear or nonconvex settings, the equilibrium may not be unique; in such cases, convergence can still be achieved if the iterative mapping between players’ control policies is contractive.
Remark 4.
In this study, the cooperative interception problem is investigated under the assumption of reliable, delay-free communication among pursuing satellites, which are connected through a directed topology with a spanning tree. Each pursuer can obtain the target’s state information through this communication network. It should be noted that the proposed stochastic differential game-based control scheme does not explicitly address communication interruptions, false data injection (FDI) attacks [29], or network-induced delays. Therefore, its effectiveness is guaranteed only under normal communication conditions. Extending the framework to include fault-tolerant or resilient control mechanisms under stochastic FDI attacks and partial communication loss will be an important direction for future research.
5. Numerical Simulations
To demonstrate the effectiveness of above control strategies, this section presents simulation examples conducted in the context of Earth orbit satellite interception scenarios. In cases involving malfunctioning satellites within the space environment, achieving resource reuse requires not only interception but also attitude takeover control. Consequently, in three-dimensional space, a minimum of three interceptors is necessary to achieve target state control. Thus, the focus is on the end-stage process of three intercepting satellites converging on a single target satellite. As per Definition 2, successful interception is indicated when the relative positions between all intercepting satellites and the target satellite satisfy . The intercepting radius of the attacker is set as , the sampling time is , the terminal time is , and the parameters , , and are utilized. The standard Brownian processes . Each intercepting satellite and target spacecraft possess distinct relative state vectors, and the initial states of the players are presented as: , , and .
The distance from the reference spacecraft to the Earth’s center is , with the Earth’s gravitational constant being . The chosen matrixes are as follows: , , , , , , , .
5.1. Without Input Saturation Constraints
This condition is relatively ideal and serves as a means to assess the feasibility of the proposed control strategies (1) and (2). Figure 2 illustrates the trajectory of the tracking satellite when intercepting the target spacecraft, Figure 3 depicts the relative positions between the tracking satellite and the target and Figure 4 illustrates the signal variations of the designed control strategy.
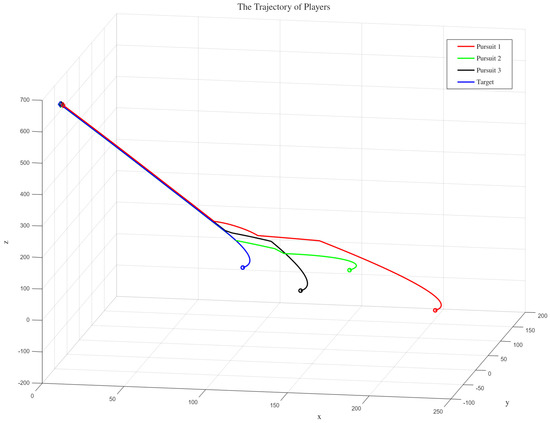
Figure 2.
The trajectory of agents without input saturation constraints.
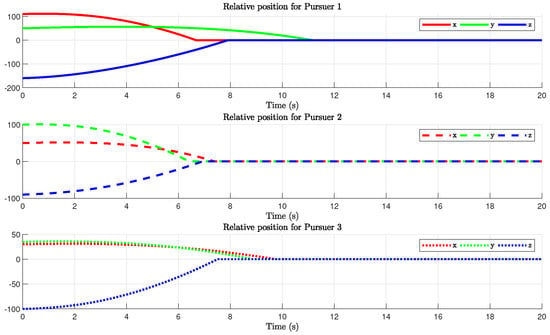
Figure 3.
The relative positions without input saturation constraints.
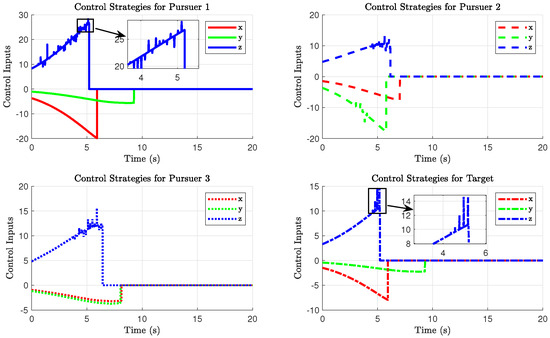
Figure 4.
The strategy of agents without input saturation constraints.
Based on the analysis of Figure 2, it is evident that the control strategy designed in this study has successfully achieved the interception of the non-cooperative target. Furthermore, as observed in Figure 3, the Pursuer 2 successfully caught up with the non-cooperative target at , followed by Pursuer 3 accomplishing the interception at . Subsequently, both spacecraft maintained a relative stationary position with respect to the target after interception. Finally, at , Pursuer 1 also successfully intercepted the non-cooperative target. Hence, it can be concluded that the multi-tracker system has effectively intercepted the non-cooperative target. Observing the control input trajectory depicted in Figure 4, it becomes evident that when the control inputs are relatively large, oscillations appear in the strategy trajectory. Excessive oscillations can potentially lead to overloading of system components or actuators. In the absence of upper bounds, control signals may surpass the hardware’s tolerable limits, resulting in equipment damage or performance degradation. Therefore, in the following cases, we consider the inclusion of input bounds and constraints.
5.2. With Input Saturation Constraints
In this scenario, to prevent the system’s input signals from exceeding the system’s capacity, we assume both the pursuer satellite and the target satellite have control upper bounds. The motion trajectories of the satellites, the relative positions of the tracking satellite and the target, as well as the curves depicting the time-varying control accelerations of the satellites, are shown in the following figure:
By observing Figure 5, it can be seen that, when considering control constraints, the designed control strategy enables the pursuer to intercept the non-cooperative target. Figure 6 illustrates that Pursuer 2 achieves tracking of the target earliest, followed by Pursuer 3, and finally Pursuer 1 intercepts the target at . It can be observed that, when taking control constraints into account, the time taken by the pursuers to intercept the target is significantly reduced. By examining Figure 7, it is noticeable that during the entire approach of the non-cooperative target, the initial relative distance in the z-axis direction for tracking spacecraft 1 was comparatively large, requiring a substantial control force to approach the non-cooperative target. However, due to the constraints of the control upper bound, control strategies exceeding the boundary values would employ the upper bound value as the control input. This observation indicates that, under the influence of the control strategy, the system has successfully achieved the interception of the non-cooperative target while avoiding control saturation scenarios.
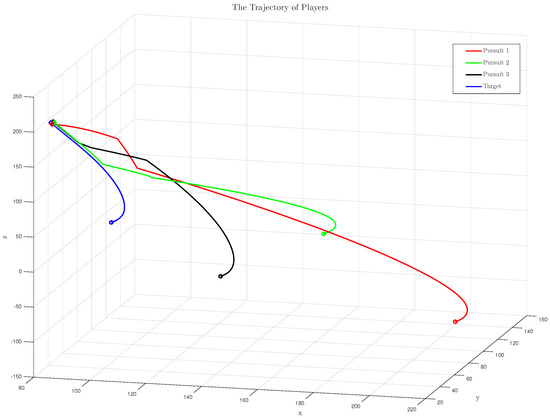
Figure 5.
The trajectory of agents with input saturation constraints.
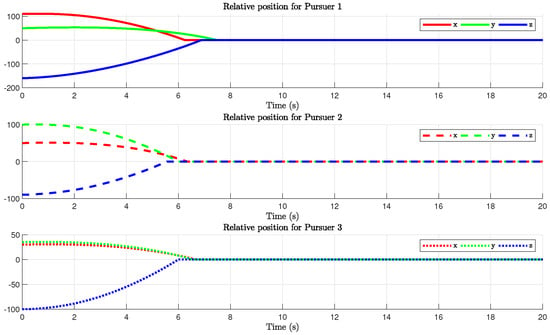
Figure 6.
The relative positions with input saturation constraints.
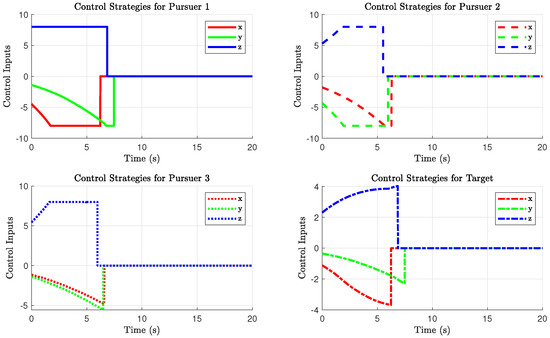
Figure 7.
The strategy of agents with input saturation constraints.
5.3. Sensitivity Analysis and Energy Consumption
To further evaluate the robustness and adaptability of the proposed stochastic pursuit-control strategy, a set of Monte Carlo simulations was conducted under random disturbances, control saturation, and varying initial conditions. In each trial, Gaussian white noise was added to the pursuers’ position and velocity channels to emulate sensor and actuator uncertainties. The noise amplitude was selected as for position and for velocity components, which is representative of realistic onboard sensor noise levels in small-satellite systems. All other system parameters were kept consistent with the baseline case to isolate the effect of disturbances.
Figure 8 and Figure 9 show the three-dimensional trajectories of Pursuer 1 under ten independent realizations of stochastic noise. Despite the stochastic perturbations, all trajectories converge to the target within a narrow region around the nominal interception point. The right-hand inset in Figure 8 provides a magnified view of the terminal phase, where it can be seen that the deviation among different trials remains within a small bounded region, indicating that the proposed control law exhibits strong robustness to random process disturbances. This result verifies the stochastic stability property derived in the theoretical analysis section.
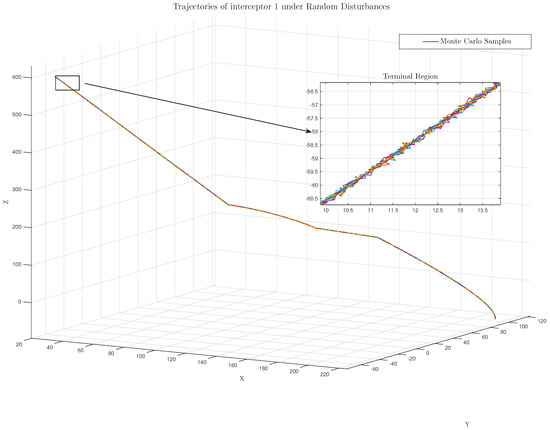
Figure 8.
Trajectories of interceptor 1 under Stochastic Disturbances (Input-Saturation-Free).
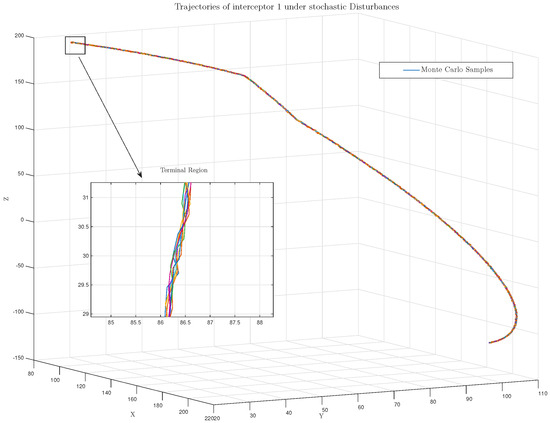
Figure 9.
Trajectories of interceptor 1 under Stochastic Disturbances and input saturation.
The dynamic control energy consumption of each agent is shown in Figure 10 and Figure 11. The cumulative energy curves reveal that the three pursuers exhibit similar energy profiles, with smooth control responses and no excessive oscillations. The cumulative energy comparison further demonstrates that the cooperative control strategy achieves successful interception with balanced and efficient control effort. Overall, the above results demonstrate that the proposed control law is robust, energy-efficient, and tolerant to both stochastic disturbances and actuator saturation. The inclusion of the magnified trajectory view and time-varying energy curves provides strong quantitative and visual evidence supporting the controller’s reliability and practical feasibility.
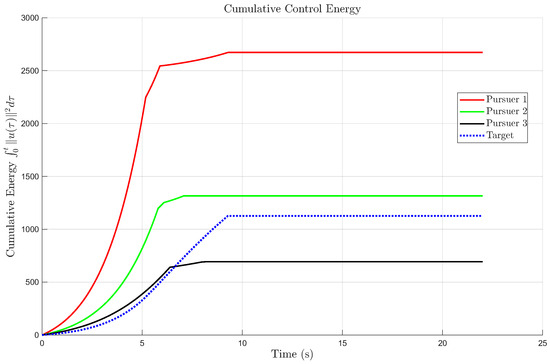
Figure 10.
Cumulative control energy without input saturation.
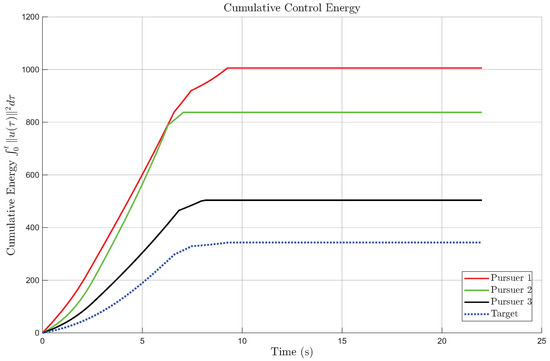
Figure 11.
Cumulative control energy under input saturation.
6. Related Work
Research on multi-satellite interception has gained increasing attention with the rapid growth of autonomous on-orbit operations. Existing studies mainly employ game-theoretic and optimization-based approaches to coordinate multiple pursuers in intercepting a maneuvering target. For example, Wu et al. [30] designed optimal interception trajectories under continuous amplitude-limited thrust, while Liu et al. [21] formulated a tripartite differential game to derive Nash equilibrium strategies for coordinated interception. Shirazi [20] further applied a hybrid simulated annealing–genetic algorithm for optimizing multi-satellite orbital transfers. Bai et al. [23] extended these frameworks to multi-agent cooperative interception scenarios based on fixed-time and mean-field games, respectively. However, most of these works assume deterministic system dynamics, which limit their adaptability to stochastic perturbations or uncertain maneuvers frequently encountered in real orbital environments.
In contrast, stochastic differential games explicitly account for random disturbances and model uncertainties, providing a rigorous mathematical framework for analyzing optimal strategies under uncertainty. Classical studies, such as Repperger et al. [22], introduced stochastic terminal rendezvous games using Kalman filtering for noisy state estimation, while Wang et al. [31] proposed a reinforcement learning–based adaptive controller to handle uncertain target behaviors. More recent advances have explored stochastic game formulations for aerospace systems with uncertain dynamics and incomplete information [32]. These studies demonstrate strong robustness and theoretical completeness but often focus on two-player engagements or simplified control models, limiting their applicability to high-dimensional multi-satellite interception scenarios.
Moreover, control restriction problems, such as actuator saturation, thrust magnitude limits, and safety constraints, are crucial for realistic spacecraft interception missions. Representative works, including Jiang et al. [33] and Sun et al. [13], incorporated fixed-time fault-tolerant and sequential optimal control strategies, respectively, to improve robustness under bounded control inputs. Recent studies have further addressed control constraints within multi-agent systems through constrained optimal control and safety-guaranteed learning frameworks [34,35]. Although these methods enhance practical feasibility and ensure safety, they typically lack explicit integration with stochastic game formulations, resulting in conservative or suboptimal performance when balancing control limitations and uncertainty propagation.
7. Conclusions
This paper addresses the complex challenge of multi-satellite interception in Earth’s orbit. By amalgamating differential game theory with stochastic optimization techniques, we successfully devise optimal relative spacecraft interception trajectories that adhere to safety constraints and exhibit outstanding performance, even when factoring in controller constraints and dynamic modeling errors. Numerical results further confirm the feasibility and robustness of the proposed Nash equilibrium strategies under stochastic disturbances. Compared with conventional deterministic interception methods, the proposed framework provides improved adaptability to model uncertainties and operational constraints. Future research will extend the stochastic game formulation to nonlinear orbital dynamics and distributed real-time architectures, and will further embed fault-tolerant, resilient control mechanisms that sustain performance in the presence of stochastic FDI attacks and partial communication loss.
Author Contributions
Conceptualization, G.L. and X.W.; Data curation, W.L.; Formal analysis, G.L.; Funding acquisition, G.L.; Investigation, X.W. and M.W.; Methodology, G.L.; Project administration, G.L.; Resources, H.G.; Software, H.G.; Supervision, G.L.; Validation, G.L. and X.W.; Visualization, H.G.; Writing—original draft, G.L.; Writing—review and editing, X.W., M.W. and WL. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China under Grant No. 62503433, by the Ningbo Public Welfare Science and Technology Project under Grant No. 2025S020, and by the Key R&D Program of Ningbo City, Zhejiang Province under Grant No. 2024Z299.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The initial draft of this work was completed during Li Guilu’s tenure at Beijing Institute of Technology. Subsequent improvements were carried out after Li Guilu’s employment at Zhejiang Wanli University, with the support of the university’s facilities and funding.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LVLH | Local-Vertical Local-Horizontal |
| CW | Clohessy–Wiltshire |
References
- Liou, J.C.; Johnson, N.L.; Hill, N. Controlling the growth of future LEO debris populations with active debris removal. Acta Astronaut. 2010, 66, 648–653. [Google Scholar] [CrossRef]
- Hu, Q.; Chen, W.; Guo, L. Fixed-time maneuver control of spacecraft autonomous rendezvous with a free-tumbling target. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 562–577. [Google Scholar] [CrossRef]
- Shima, T.; Shinar, J. Time-varying linear pursuit-evasion game models with bounded controls. J. Guid. Control. Dyn. 2002, 25, 425–432. [Google Scholar] [CrossRef]
- Li, S.; Wang, C.; Xie, G. Optimal strategies for pursuit-evasion differential games of players with damped double integrator dynamics. IEEE Trans. Autom. Control 2023, 69, 5278–5293. [Google Scholar] [CrossRef]
- Gao, Y.; Li, D.; Ge, S.S. Time-synchronized tracking control for 6-dof spacecraft in rendezvous and docking. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 1676–1691. [Google Scholar] [CrossRef]
- Chi, S.; Li, S.; Wang, C.; Guangming, X. A review of research on pursuit-evasion games. Acta Autom. Sin. 2025, 51, 705–726. [Google Scholar]
- Chen, N.; Li, L.; Mao, W. Equilibrium strategy of the pursuit-evasion game in three-dimensional space. IEEE/CAA J. Autom. Sin. 2024, 11, 446–458. [Google Scholar] [CrossRef]
- Prince, E.R.; Hess, J.A.; Cobb, R.G.; Carr, R.W. Elliptical orbit proximity operations differential games. J. Guid. Control. Dyn. 2019, 42, 1458–1472. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhang, P.; Yuan, J. Nonzero-Sum Pursuit-Evasion Game Control for Spacecraft Systems: A Q-Learning Method. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3971–3981. [Google Scholar] [CrossRef]
- Wang, M.; Wu, H.N. Autonomous Game Control for Spacecraft Rendezvous via Adaptive Perception and Interaction. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3188–3200. [Google Scholar] [CrossRef]
- Talebi, S.P.; Werner, S.; Gupta, V.; Huang, Y.F. On stability and convergence of distributed filters. IEEE Signal Process. Lett. 2021, 28, 494–498. [Google Scholar] [CrossRef]
- Pontani, M.; Conway, B.A. Numerical solution of the three-dimensional orbital pursuit-evasion game. J. Guid. Control. Dyn. 2009, 32, 474–487. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, Q.; Loxton, R.; Li, B. Numerical solution of a pursuit-evasion differential game involving two spacecraft in low earth orbit. J. Ind. Manag. Optim. (JIMO) 2015, 11, 1127–1147. [Google Scholar] [CrossRef]
- Gong, Z.; He, B.; Liu, G.; Zhang, X. Solution for pursuit-evasion game of agents by adaptive dynamic programming. Electronics 2023, 12, 2595. [Google Scholar] [CrossRef]
- Ye, D.; Shi, M.; Sun, Z. Satellite proximate pursuit-evasion game with different thrust configurations. Aerosp. Sci. Technol. 2020, 99, 105715. [Google Scholar] [CrossRef]
- Wang, Z.; Gong, B.; Yuan, Y.; Ding, X. Incomplete Information Pursuit-Evasion Game Control for a Space Non-Cooperative Target. Aerospace 2021, 8, 211. [Google Scholar] [CrossRef]
- Xiong, H.; Zhang, Y. Reinforcement learning-based formation-surrounding control for multiple quadrotor UAVs pursuit-evasion games. ISA Trans. 2024, 145, 205–224. [Google Scholar] [CrossRef]
- Chai, Y.; Luo, J.; Han, N.; Xie, J. Linear quadratic differential game approach for attitude takeover control of failed spacecraft. Acta Astronaut. 2020, 175, 142–154. [Google Scholar] [CrossRef]
- Luo, Y.; Li, Z.; Zhu, H. Survey on spacecraft orbital pursuit-evasion differential games. Sci. Sin. Technol. 2020, 50, 1533–1545. [Google Scholar] [CrossRef]
- Shirazi, A. Analysis of a hybrid genetic simulated annealing strategy applied in multi-objective optimization of orbital maneuvers. IEEE Aerosp. Electron. Syst. Mag. 2017, 32, 6–22. [Google Scholar] [CrossRef]
- Liu, S. Mission Planning and Orbit Optimization for Multi-Satellite Interception. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2018. [Google Scholar]
- Repperger, D.; Koivo, A. Optimal terminal rendezvous as a stochastic differential game problem. IEEE Trans. Aerosp. Electron. Syst. 1972, 3, 319–326. [Google Scholar] [CrossRef]
- Bai, Y.; Zhou, D.; He, Z. Optimal Pursuit Strategies in Missile Interception: Mean Field Game Approach. Aerospace 2025, 12, 302. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, K.; Xie, X.; Sun, J. Fixed-time zero-sum Pursuit–Evasion game control of multisatellite via adaptive dynamic programming. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 2224–2235. [Google Scholar] [CrossRef]
- Stastny, N.B. Optimal Relative Path Planning for Constrained Stochastic Space Systems. Ph.D. Thesis, Utah State University, Logan, UT, USA, 2022. [Google Scholar]
- Dong, Y.; Mingming, S.; Zhaowei, S. Satellite proximate interception vector guidance based on differential games. Chin. J. Aeronaut. 2018, 31, 1352–1361. [Google Scholar] [CrossRef]
- Krstic, M.; Deng, H. Stabilization of Nonlinear Uncertain Systems; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Duncan, T.E. Evaluation of likelihood functions. Inf. Control 1968, 13, 62–74. [Google Scholar] [CrossRef]
- Liu, G.; Sun, Q.; Su, H.; Wang, M. Adaptive Cooperative Fault-Tolerant Control for Output-Constrained Nonlinear Multi-Agent Systems Under Stochastic FDI Attacks. IEEE Trans. Circuits Syst. I Regul. Pap. 2025, 72, 6025–6036. [Google Scholar] [CrossRef]
- Wu, W.; Chen, J.; Liu, J. A hybrid optimisation method for intercepting satellite trajectory based on differential game. Aeronaut. J. 2023, 127, 900–922. [Google Scholar] [CrossRef]
- Wang, X.; Shi, P.; Wen, C.; Zhao, Y. Design of parameter-self-tuning controller based on reinforcement learning for tracking noncooperative targets in space. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4192–4208. [Google Scholar] [CrossRef]
- Tang, X.; Ye, D.; Luo, S.; Low, K.S.; Sun, Z. A Hybrid Game Strategy for the Pursuit of Out-of-Control Spacecraft under Incomplete-Information. Aerospace 2022, 9, 455. [Google Scholar] [CrossRef]
- Jiang, B.; Hu, Q.; Friswell, M.I. Fixed-time rendezvous control of spacecraft with a tumbling target under loss of actuator effectiveness. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1576–1586. [Google Scholar] [CrossRef]
- Dai, C.; Qiang, H.; Zhang, D.; Hu, S.; Gong, B. Relative orbit determination algorithm of space targets with passive observation. J. Syst. Eng. Electron. 2024, 35, 793–804. [Google Scholar] [CrossRef]
- Chihabi, Y.; Ulrich, S. New angle-only observability criteria for spaceborne optimal evasive maneuvers under perturbations. J. Guid. Control. Dyn. 2024, 47, 1437–1446. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).