High-Efficiency Soft-Switching Technique for a Cascaded Buck–Boost Converter Based on Model Predictive Control Using GaN Devices
Abstract
1. Introduction
- A segmented control strategy is proposed, which can be effectively combined with soft-switching operation, providing a theoretical foundation for MPC implementation.
- A model-based duty-ratio generation scheme is developed, allowing faster voltage reference tracking and improved current transient response compared with conventional PI control.
- The high-speed switching capability of GaN FETs is fully utilized in conjunction with the MPC strategy to further enhance the converter performance.
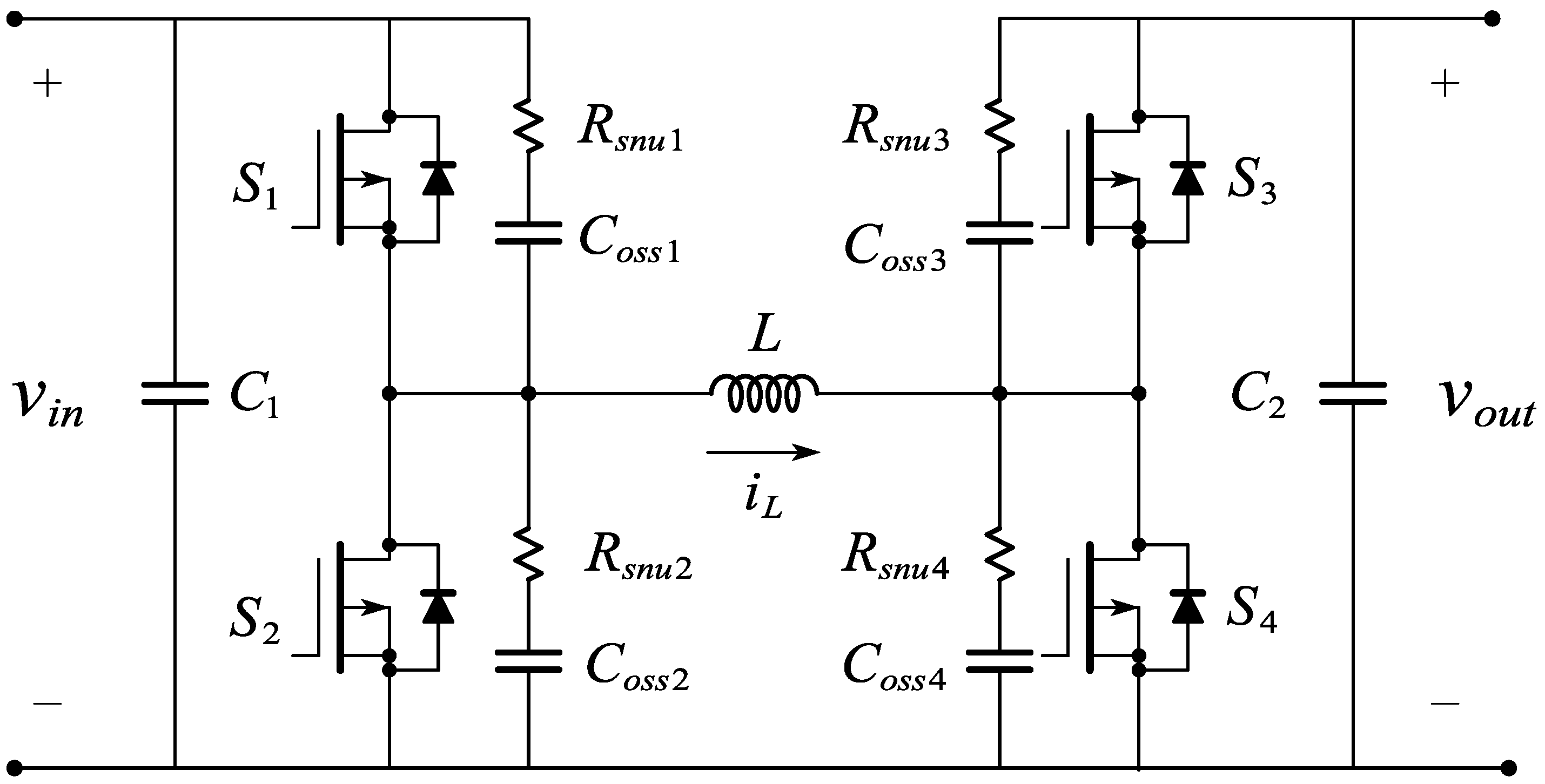
2. Circuit Configuration and Operating Mechanism
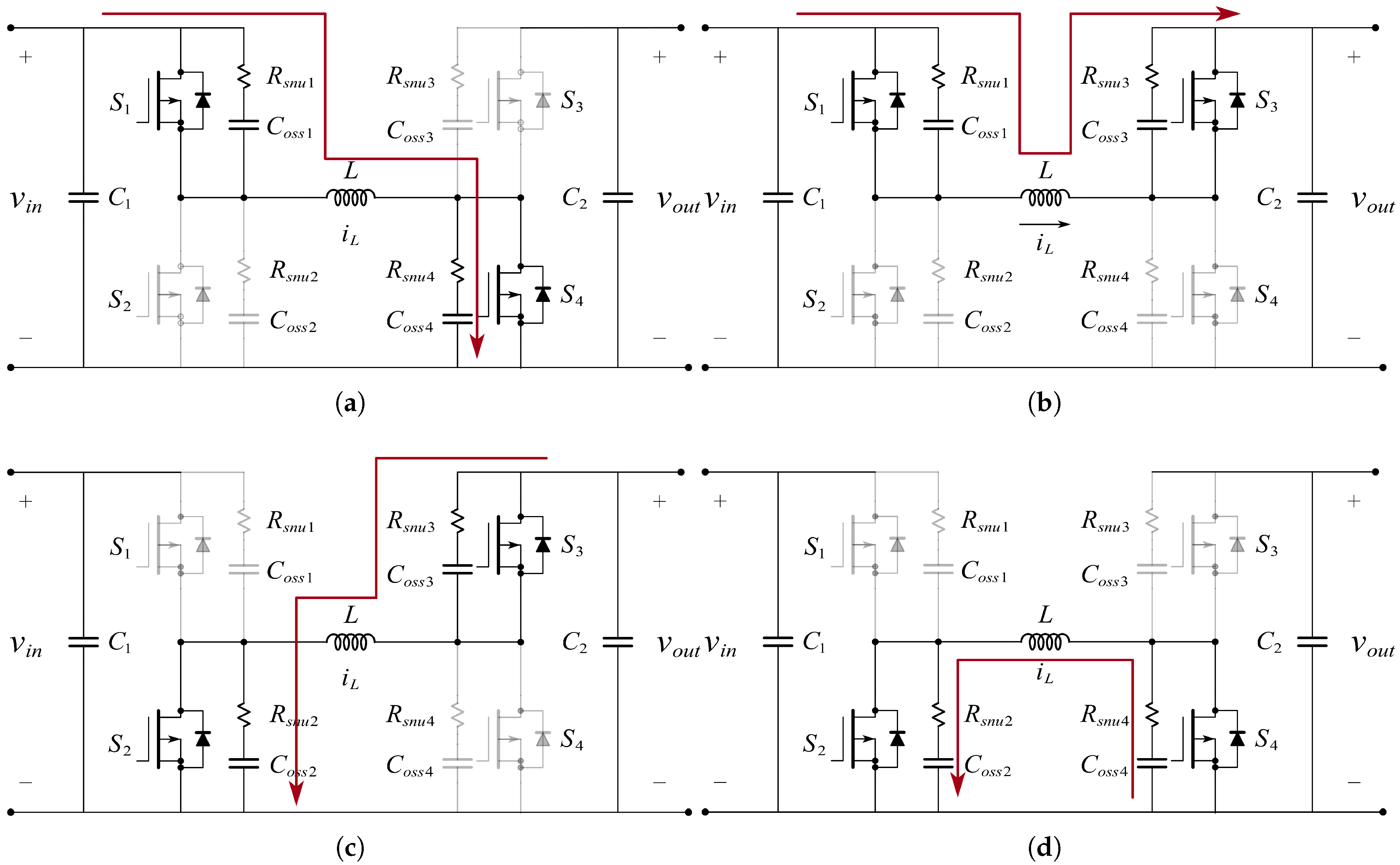
2.1. Topology and Its Segmented Model
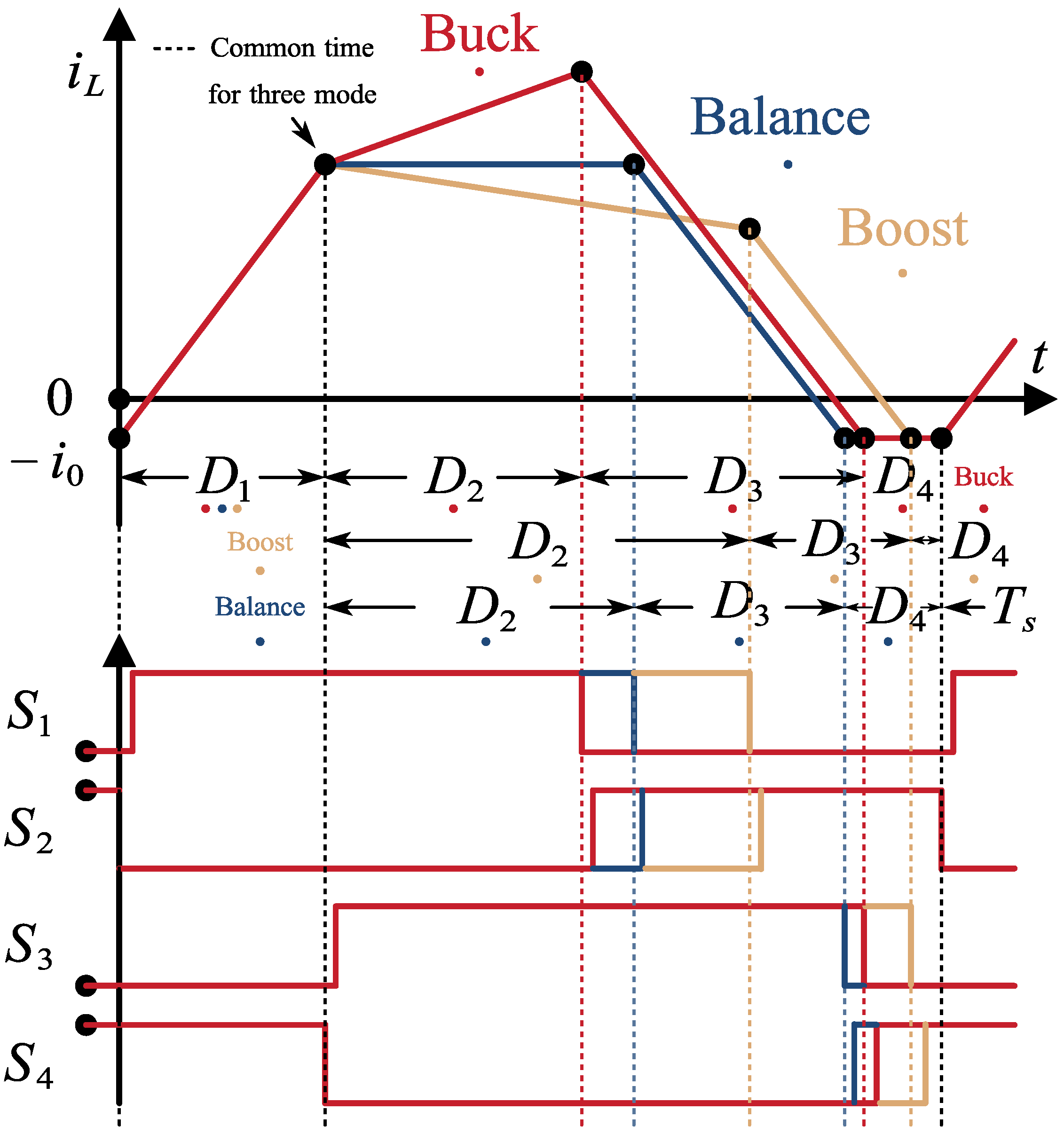
2.2. Discontinuous Conduction Mode
2.3. Principle of Soft Switching
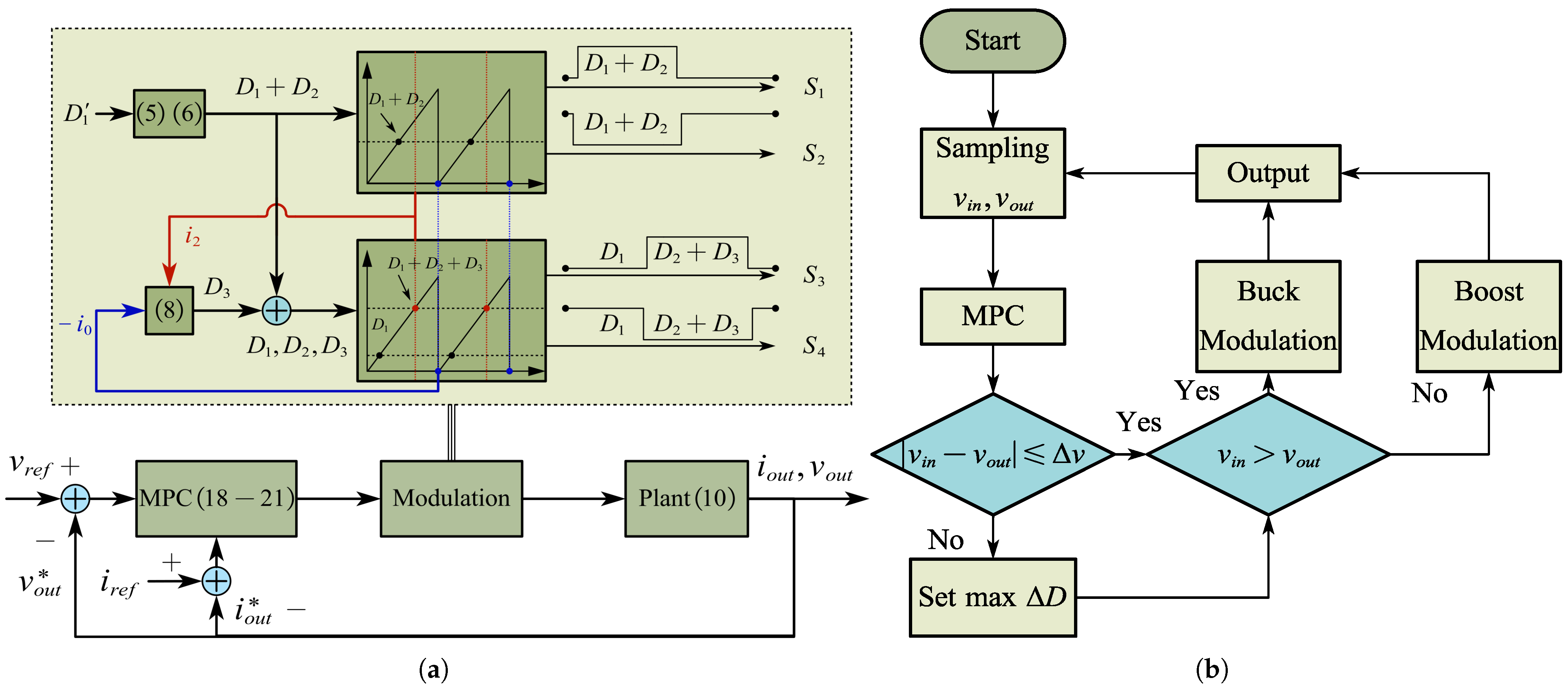
3. Formulation of Model Predictive Control
3.1. Model Construction for MPC
3.2. Formulation of the Cost Function
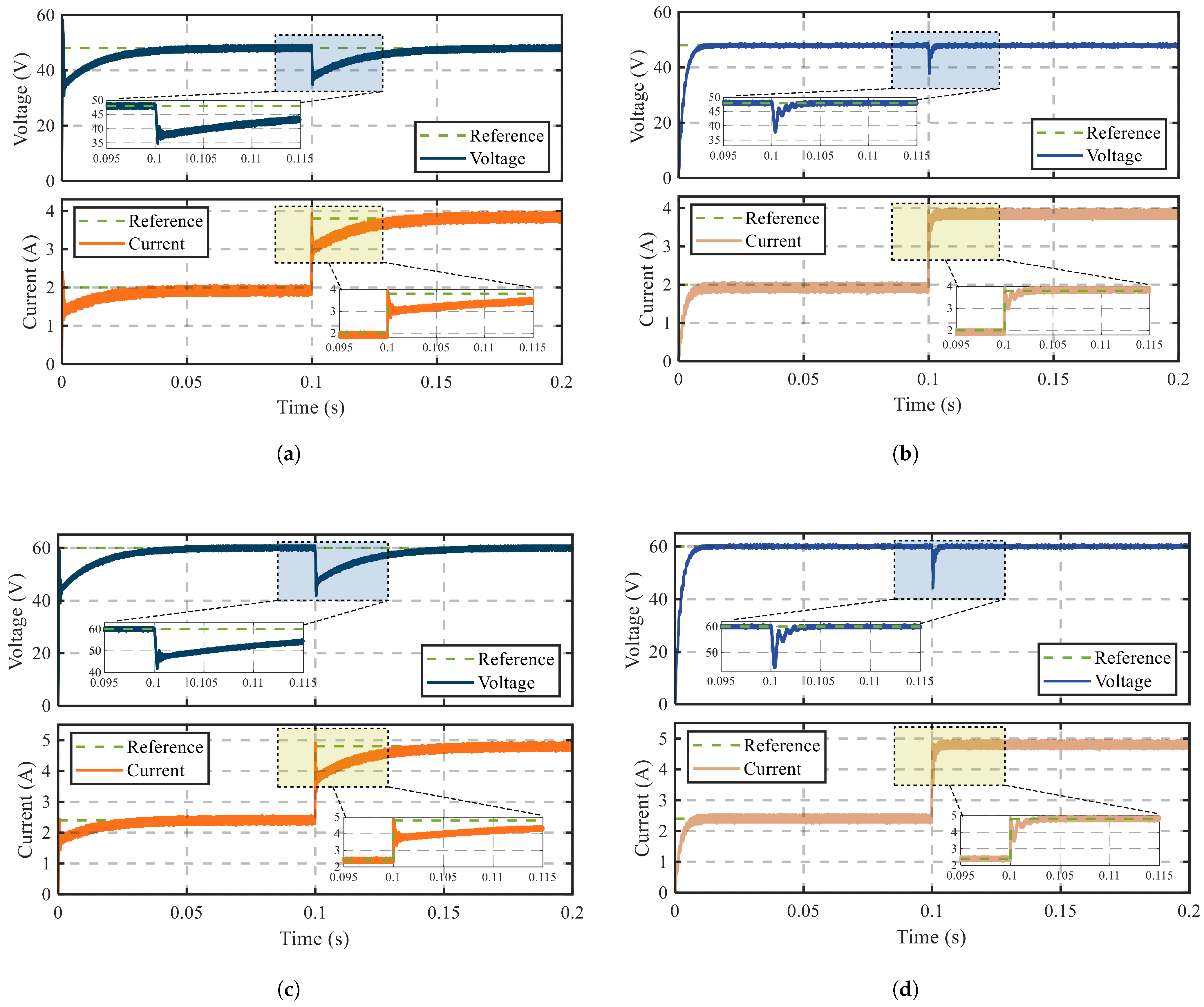
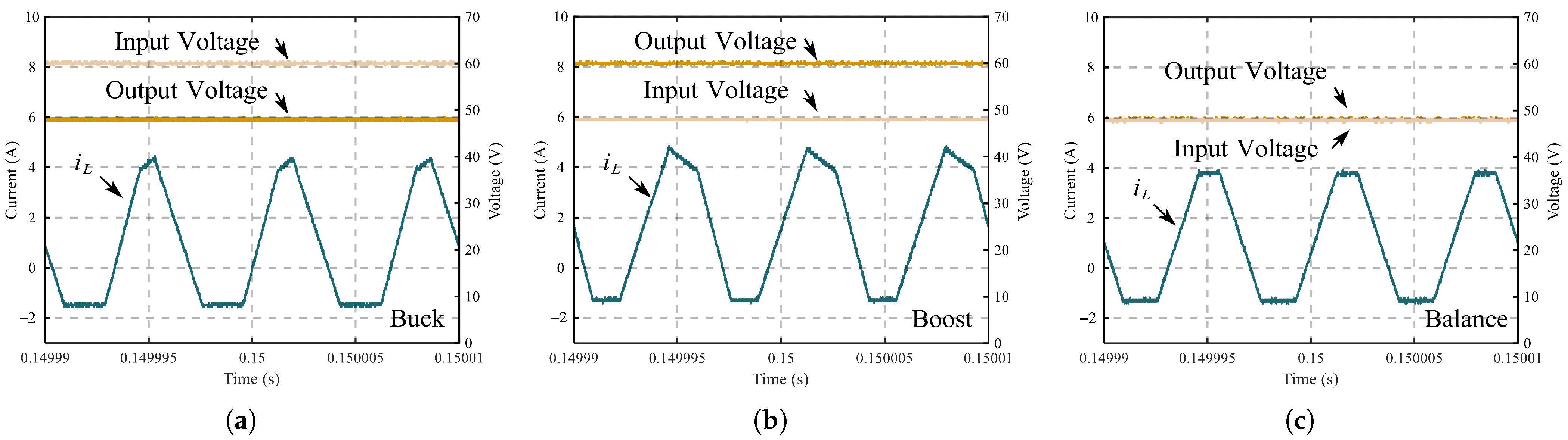
4. Experiment
4.1. Dynamic and Steady-State Response Results
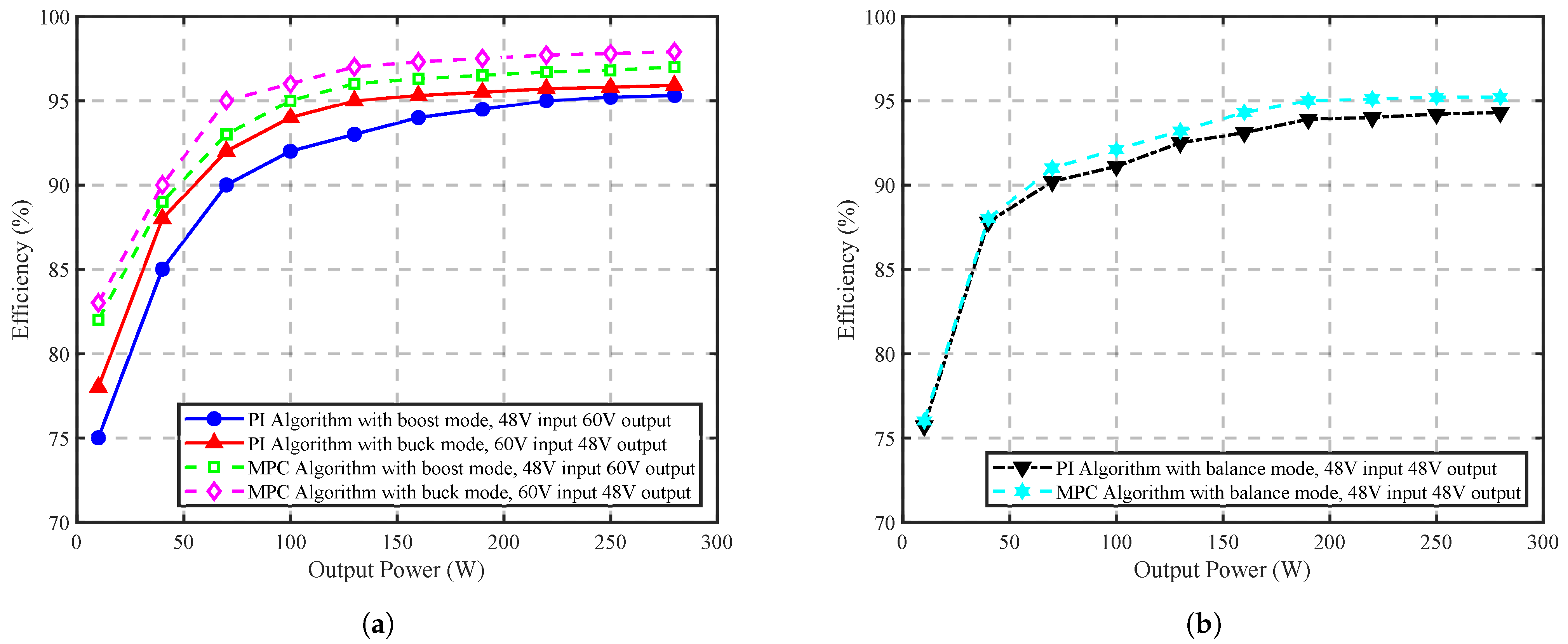
4.2. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bull, S.R. Renewable energy today and tomorrow. Proc. IEEE 2001, 89, 1216–1226. [Google Scholar] [CrossRef]
- Dincer, I. Renewable energy and sustainable development: A crucial review. Renew. Sustain. Energy Rev. 2000, 4, 157–175. [Google Scholar] [CrossRef]
- Umuhoza, J.; Zhang, Y.; Zhao, S.; Mantooth, H.A. An adaptive control strategy for power balance and the intermittency mitigation in battery-PV energy system at residential DC microgrid level. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 1341–1345. [Google Scholar]
- Kim, D.; Lee, B.; Hur, J. Light-load efficiency improving algorithm in cascaded buck-boost converter. In Proceedings of the 2015 18th International Conference on Electrical Machines and Systems (ICEMS), Pattaya, Thailand, 25–28 October 2015; pp. 448–451. [Google Scholar]
- Chen, Z. PI and sliding mode control of a Cuk converter. IEEE Trans. Power Electron. 2012, 27, 3695–3703. [Google Scholar] [CrossRef]
- Hwu, K.I.; Peng, T.J. A novel buck–boost converter combining KY and buck converters. IEEE Trans. Power Electron. 2011, 27, 2236–2241. [Google Scholar] [CrossRef]
- Banaei, M.R.; Bonab, H.A.F. A high efficiency nonisolated buck–boost converter based on ZETA converter. IEEE Trans. Ind. Electron. 2019, 67, 1991–1998. [Google Scholar] [CrossRef]
- Gholizadeh, H.; Sharifi, S.R.; Hashemi, M.R.; Afjei, E.; Saman, A.G. Design and implementation a single-switch step-up DC-DC converter based on cascaded boost and luo converters. Energies 2021, 14, 3584. [Google Scholar] [CrossRef]
- Chen, X.; Pise, A.A.; Batarseh, I. Magnetics-based efficiency optimization for low power cascaded-buck-boost converter. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 5611–5623. [Google Scholar] [CrossRef]
- Cheng, Z.; Li, Z.; Li, S.; Gao, J.; Si, J.; Das, H.S.; Dong, W. A novel cascaded control to improve stability and inertia of parallel buck-boost converters in DC microgrid. Int. J. Electr. Power Energy Syst. 2020, 119, 105950. [Google Scholar] [CrossRef]
- Tian, L.; Liu, H.; Zhang, Y.; Wu, X. A Reduced-Order Small-Signal Model for Four-Switch Buck–Boost Under Soft-Switching Current Shaping Control Strategy. Electronics 2025, 14, 2564. [Google Scholar] [CrossRef]
- Waffler, S.; Kolar, J.W. A novel low-loss modulation strategy for high-power bidirectional buck + boost converters. IEEE Trans. Power Electron. 2009, 24, 1589–1599. [Google Scholar] [CrossRef]
- Jones, E.A.; Wang, F.F.; Costinett, D. Review of commercial GaN power devices and GaN-based converter design challenges. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 707–719. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, R.; Yang, Q.; Song, Q.; Litchford, E.; Walker, A.J.; Pidaparthi, S.; Drowley, C.; Dong, D.; Li, Q.; et al. Evaluation and MHz Converter Application of 1.2-kV Vertical GaN JFET. IEEE Trans. Power Electron. 2024, 39, 15720–15731. [Google Scholar] [CrossRef]
- Huang, X.; Liu, Z.; Li, Q.; Lee, F.C. Evaluation and Application of 600 V GaN HEMT in Cascode Structure. IEEE Trans. Power Electron. 2013, 29, 2453–2461. [Google Scholar] [CrossRef]
- Bang, T.; Park, J.W. Development of a ZVT-PWM buck cascaded buck–boost PFC converter of 2 kW with the widest range of input voltage. IEEE Trans. Ind. Electron. 2017, 65, 2090–2099. [Google Scholar] [CrossRef]
- Yu, J.; Liu, M.; Song, D.; Su, M. A soft-switching control for cascaded buck-boost converters without zero-crossing detection. IEEE Access 2019, 7, 32522–32536. [Google Scholar] [CrossRef]
- Chen, X.; Pise, A.A.; Elmes, J.; Batarseh, I. Ultra-highly efficient low-power bidirectional cascaded buck-boost converter for portable PV-battery-devices applications. IEEE Trans. Ind. Appl. 2019, 55, 3989–4000. [Google Scholar] [CrossRef]
- Lee, I.O.; Moon, G.W. Half-bridge integrated ZVS full-bridge converter with reduced conduction loss for electric vehicle battery chargers. IEEE Trans. Ind. Electron. 2013, 61, 3978–3988. [Google Scholar] [CrossRef]
- Roschatt, P.M.; Pickering, S.; McMahon, R.A. Bootstrap voltage and dead time behavior in GaN DC–DC buck converter with a negative gate voltage. IEEE Trans. Power Electron. 2015, 31, 7161–7170. [Google Scholar] [CrossRef]
- Callegaro, L.; Ciobotaru, M.; Fletcher, J.E.; Rios, P.A.; Pagano, D.J. Design of cascaded control loop for solar power optimizer based on a buck-boost converter. In Proceedings of the 2016 IEEE 2nd Annual Southern Power Electronics Conference (SPEC), Auckland, New Zealand, 5–8 December 2016; pp. 1–6. [Google Scholar]
- Guler, N.; Komurcugil, H.; Bayhan, S.; Abu-Rub, H. Simplified single-stage buck-boost rectifier with proportional-integral and cascaded proportional-resonant control method. IEEE Trans. Ind. Electron. 2023, 71, 348–359. [Google Scholar] [CrossRef]
- Dey, S.; Mallik, A. An Online-Optimized ZVS-Current Tracked Soft-Switching Modulation for Triple Active Bridge Converter. IEEE Trans. Power Electron. 2024, 39, 14708–14728. [Google Scholar] [CrossRef]
- Tian, G.; Chen, S.; Ding, X.; Peng, J.; Kou, Z. Isolated High Step-up Soft-switching quasi-Zsource DC-DC Converter. IEEE Access 2024, 12, 49927–49936. [Google Scholar] [CrossRef]
- Kim, J.; Park, S.; Lee, J.; Cho, J.; Cho, G.; Kim, H. A Floating Voltage Source-Based Turn-Off Snubber for a Nonisolated Multilevel SiC DC-DC Converter. IEEE Trans. Ind. Electron. 2025, 72, 390–400. [Google Scholar] [CrossRef]
- Alajmi, B.N.; Marei, M.I.; Abdelsalam, I.; Ahmed, N.A. Multiphase Interleaved Converter Based on Cascaded Non-Inverting Buck-Boost Converter. IEEE Access 2022, 10, 42497–42506. [Google Scholar] [CrossRef]
- Wu, C.C.; Liu, C.Y.; Wang, G.B.; Shieh, Y.T.; Chieng, W.H.; Chang, E.Y. A new GaN-based device, P-cascode GaN HEMT, and its synchronous buck converter circuit realization. Energies 2021, 14, 3477. [Google Scholar] [CrossRef]



| Parameters | Description | Values |
|---|---|---|
| Rated Output Power | 300 W | |
| Input Voltage | 20–60 V | |
| Output Voltage | 20–60 V | |
| Switching frequency | 100 kHz | |
| Boost/Buck switch (GS61008T) | GaN, 100 V/90 A @25 °C | |
| L | Inductor (7443643300) | 0.33 mH, 250 V/30 A @20° C |
| Input Capacitor | 190 F, 100 V @25 °C | |
| Output Capacitor | 470 F, 100 V @25 °C | |
| Snubber Resistance | 50 , 150 V/0.5 W @20 °C | |
| Snubber Capacitor | 4.7 pF, 100 V @25 °C |
| Operation Mode | Buck Mode | Boost Mode | Balance Mode |
|---|---|---|---|
| PI Method | 95.9% | 95.3% | 94.3% |
| MPC Method | 97.9% | 96.9% | 95.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Dai, J.; Lee, J.; Kang, S.; Jin, C. High-Efficiency Soft-Switching Technique for a Cascaded Buck–Boost Converter Based on Model Predictive Control Using GaN Devices. Electronics 2025, 14, 4499. https://doi.org/10.3390/electronics14224499
Liu L, Dai J, Lee J, Kang S, Jin C. High-Efficiency Soft-Switching Technique for a Cascaded Buck–Boost Converter Based on Model Predictive Control Using GaN Devices. Electronics. 2025; 14(22):4499. https://doi.org/10.3390/electronics14224499
Chicago/Turabian StyleLiu, Li, Jialiang Dai, Ju Lee, Seonheui Kang, and Changsung Jin. 2025. "High-Efficiency Soft-Switching Technique for a Cascaded Buck–Boost Converter Based on Model Predictive Control Using GaN Devices" Electronics 14, no. 22: 4499. https://doi.org/10.3390/electronics14224499
APA StyleLiu, L., Dai, J., Lee, J., Kang, S., & Jin, C. (2025). High-Efficiency Soft-Switching Technique for a Cascaded Buck–Boost Converter Based on Model Predictive Control Using GaN Devices. Electronics, 14(22), 4499. https://doi.org/10.3390/electronics14224499







