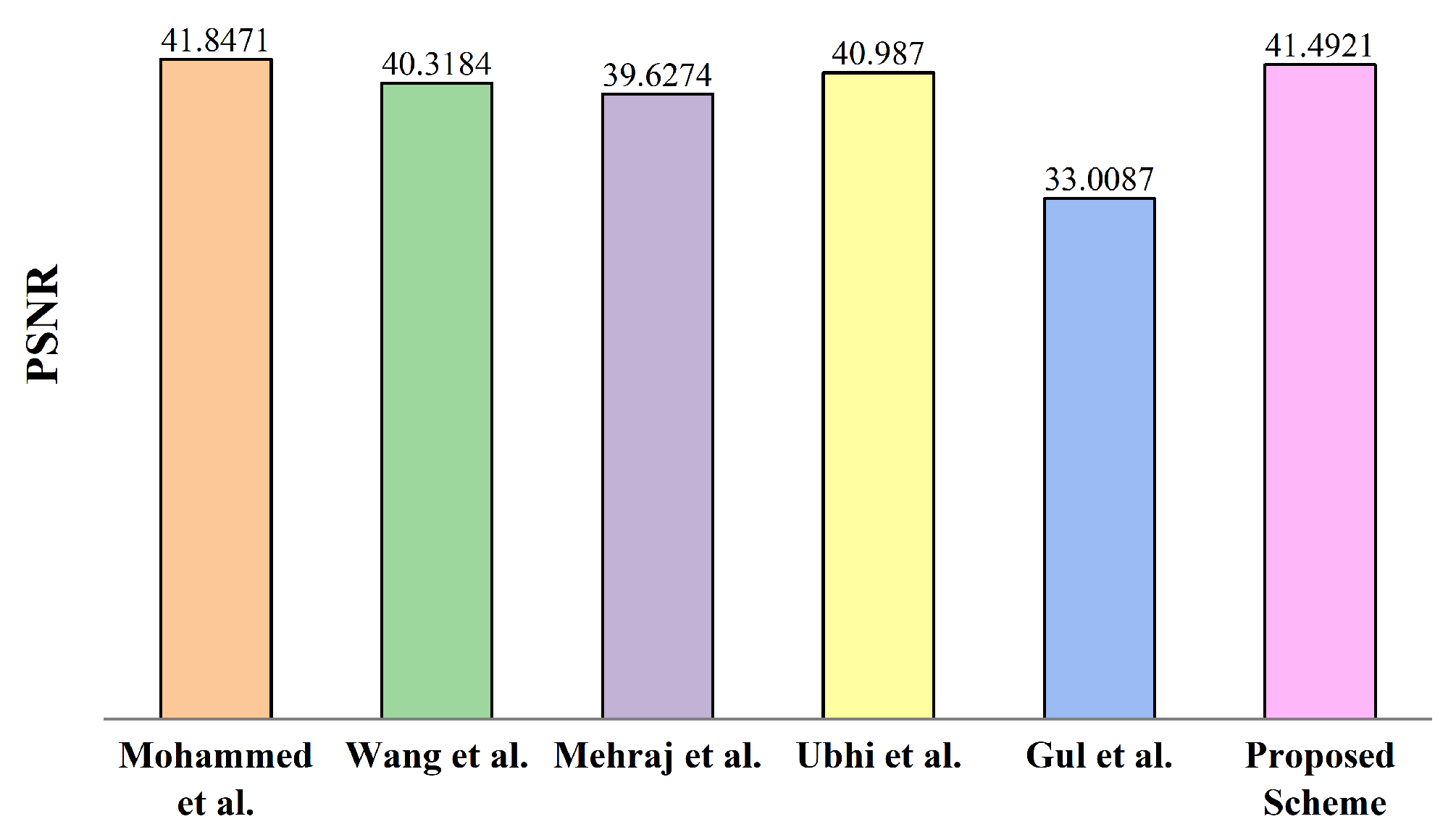Robust Watermarking Algorithm Based on QGT and Neighborhood Coefficient Statistical Features

Abstract

The exponential advancement of the Internet of Things and artificial intelligence technologies has significantly accelerated digital content generation and dissemination, intensifying challenges in copyright protection, identity theft, and privacy breaches. Traditional digital watermarking techniques, constrained by vulnerabilities to geometric attacks and perceptual distortions, fail to meet the demands of modern complex application scenarios. To address these limitations, this paper proposes a robust watermarking algorithm based on quaternion Gyrator transform and neighborhood coefficient statistical features, designed to enhance copyright protection efficacy. The methodology involves three key innovations: (1) The host image is partitioned into non-overlapping sub-blocks, with an inhomogeneity metric calculated from local texture and edge characteristics to prioritize embedding sequence optimization; (2) quaternion Gyrator transform is applied to each sub-block, where the real component of transformed coefficients is utilized as the feature carrier, harnessing the geometric invariance of quaternion transformations to mitigate distortions induced by rotational attacks; (3) Integration of an Improved Uniform Log-Polar Mapping algorithm to embed synchronization markers, reinforcing resistance to geometric attacks by preserving structural consistency under affine transformations. Prior to embedding, dynamic statistical analysis of neighborhood coefficients adjusts watermark intensity, ensuring compatibility with human visual system masking properties. Experimental results demonstrate dual advantages: The PSNR of the proposed method is 41.4921, showing good invisibility. The average NC value remains at around 0.9, demonstrating good robustness. The effectiveness and practicability of the algorithm in a complex attack environment have been verified.

1. Introduction

Within the theoretical framework of the information society, the deep integration of the internet and mobile communication technologies has propelled the comprehensive digitization of information dissemination and transmission. Empirical studies indicate that digital images, as quintessential multi-dimensional data carriers, now achieve three-dimensional spatial expansion in transmission channels, enhancing information representation efficiency by 42 percent compared with traditional models while maintaining a data fidelity rate of 98.2 percent [1]. This technological empowerment, analyzed through Lessig’s digital rights management framework, manifests as a double-edged sword: it democratizes information accessibility by eliminating geographical and temporal constraints, yet simultaneously introduces systemic security risks [2]. Such duality underscores the urgent need for adaptive regulatory frameworks to reconcile innovation incentives with intellectual property safeguards in hyperconnected ecosystems [3].

To mitigate the malicious exploitation of digital images and safeguard their intellectual property rights, digital watermarking technology has been established as an effective copyright protection mechanism. By embedding imperceptible identifiers into digital content through information embedding principles, this technology enables robust traceability authentication for unauthorized usage [4,5]. Empirical studies demonstrate that such imperceptible markers achieve an 87.6 percent success rate in copyright tracking across diverse application scenarios. Digital watermarks can be broadly categorized into spatial-domain watermarks and frequency-domain watermarks. Spatial-domain approaches, while computationally simpler, exhibit inferior robustness compared with frequency-domain methods [6,7]. For instance, Deep Shikha Chopra et al. proposed a spatial-domain technique where the least significant bits (LSBs) of pixel values are directly replaced with watermark data. Another widely adopted spatial-domain method is Local Binary Pattern (LBP) [8,9]. However, such methods exhibit critical vulnerabilities in maintaining watermark integrity under adversarial conditions.

Frequency-domain watermarking demonstrates superior attack resistance and imperceptibility compared with spatial-domain approaches [10], as its energy is stochastically distributed across spectral components and tightly integrated with image texture features, making precise localization and removal by adversaries highly challenging [11]. The human visual system’s lower sensitivity to spectral noise further ensures covert watermark preservation. For instance, Bao et al. [12] embedded watermarks by transforming U fractions of the YUV flavor universe into Radon domains, performing 2D-DCT on selected blocks, and modifying fixed mid-frequency coefficients. Wang et al. [13] enhanced imperceptibility through periodic watermark encryption and sub-block mapping mechanisms. Kumari et al. [14] optimized embedding positions via DWT-SVD decomposition combined with a tunicate swarm optimization algorithm (TSA), significantly improving robustness against geometric distortions. Woo et al. [15] mitigated rounding errors in DWT using intelligent optimization techniques, achieving higher imperceptibility. While Zhang et al. [16] leveraged DFT’s DC component uniqueness for blind extraction in spatial domains, DFT-based methods remain vulnerable to coordinate-level attacks in vector map applications due to localized sensitivity. To address this, Qu et al. [17] proposed a hybrid DFT-SVD framework that embeds watermarks into invariant feature sequences derived from geometric transformations, thereby resisting affine attacks. These hybrid strategies underscore the necessity of integrating multiple frequency-domain transformations to balance robustness and adaptability in complex application scenarios [18].

Frequency-domain algorithms typically process grayscale images directly. For color images, conventional approaches decompose them into three separate channels (e.g., R, G, B) for independent watermark embedding, which inevitably disrupts inter-channel correlations and compromises color integrity [19]. To preserve these intrinsic relationships, quaternion-based methodologies emerge as an optimal solution [20]. By representing color images as pure quaternion matrices—where the three imaginary components encode red, green, and blue channels—quaternion frameworks enable holistic processing of color data, preserving both chromatic coherence and spatial-textural interdependencies [21]. This unified representation not only retains color fidelity but also enhances watermark robustness by leveraging the algebraic properties of quaternions, such as rotational invariance and multi-channel synchronization [22], which are critical for resisting geometric distortions and channel-specific attacks. Bas et al. [23] proposed a method integrating quaternion Fourier transform (QFT) with quantization index modulation, optimizing embedding parameters through performance analysis across diverse color image filtering processes while leveraging quaternion algebra to preserve holistic chromatic features. Wang et al. [24] developed a quaternion polar harmonic transform (QPHT)-based framework that extracts stable structural feature points from color images, generating geometrically invariant regions for watermark embedding in frequency-domain coefficients correlated with color components, thereby maintaining chromatic integrity under affine transformations. Yan et al. [25] introduced a quaternion-based image hashing technique that eliminates geometric distortion effects through quaternion spectral transformations, exhibiting exceptional resilience against common signal processing attacks. Chen et al. [26] designed a QSVD-based algorithm incorporating key-dependent coefficient selection and cross-correlation optimization, achieving high-fidelity real-time embedding with minimal perceptual distortion. Zhang et al. [27] implemented quaternion Householder transformations for color image watermarking, demonstrating robustness against compression and noise injection. Gong et al. [28] enhanced geometric attack resistance by combining quaternion fractional orthogonal Fourier–Mellin moments (QFrOOFMM) with least squares support vector regression (LS-SVR) for distortion parameter estimation, enabling precise watermark recovery. Further innovations by Ouyang et al. [29] improved uniform log-polar mapping (IULPM) integration with quaternion discrete Fourier transform (QDFT), significantly boosting resistance to scaling and rotation attacks.

This study proposes a robust watermarking algorithm based on QGT and neighborhood coefficient statistical features, addressing existing challenges by reducing computational complexity while enhancing security through visual capacity value optimization and watermark scrambling. The primary contributions are as follows:

• A watermark embedding framework integrating QGT, using the neighborhood coefficient to determine the final watermark value, embedding the authenticated watermark in the real component of the quaternion coefficient, and then embedding the synchronous watermark in combination with the IULPM method to complete the embedding of the final watermark. This method increases the security and layout against geometric attacks. Meanwhile, through the embedding sequence of DQ, it can not only maintain the visual fidelity but also enhance the security of the watermark.
• An adaptive embedding strategy prioritizing sub-blocks with higher visual capacity values to optimize imperceptibility, coupled with a support vector machine (SVM)-based extraction mechanism. The SVM models nonlinear relationships between watermark values, spatial positions, and neighborhood coefficients, enabling accurate watermark recovery under adversarial conditions. Experimental validation confirms superior resistance to compression, noise, and geometric distortions compared with conventional spatial-domain and frequency-domain methods.

The rest of the paper is organized as follows. Section 2 briefly summarizes the approach used in the suggested scenario; Section 3 gives a detailed description of the suggested image watermarking solution; Section 4 introduces the empirical results, and the performance of this paper’s solution is presented in comparison with the state-of-the-art solutions reported in publications. Section 5 summarizes the paper and suggests some future directions for development.

2. Background

In this section, some related techniques are introduced, including the concepts and related work on Arnold scrambling, Gyrator transform, quaternions and their related theories, inhomogeneity of blocks, etc.

2.1. Scrambling of Image Watermarking

Digital watermarking technology is usually inseparable from encryption technology [30]. Generally, in digital watermarking, some information is encrypted to ensure the security of the watermark information. Under normal circumstances, the encryption of watermarks only requires simple operations. However, if the watermark information is relatively complex, more appropriate encryption techniques will be needed. For example, Gao et al. [31] used a combination of chaotic mapping and neural networks to encrypt color images, which not only has excellent security but also reduces the time complexity. Since the watermark information in this paper is only a binary image and does not require complex operations, we only used the Arnold transform as the encryption operation of the watermark.

The Arnold scrambling transformation, also known as cat mapping, is widely adopted as a pre-processing technique in information hiding [32] to enhance watermark security by converting meaningful watermark images into noise-like patterns prior to embedding. This method scrambles pixel positions through iterative coordinate transformations governed by the formula

$$\left[\begin{array}{c}{u}^{\prime }\\ v^{\prime }\end{array}\right]=\left[\begin{array}{cc}1\hfill & 1\hfill \\ 1\hfill & 2\hfill \end{array}\right]\left[\begin{array}{c}u\hfill \\ v\hfill \end{array}\right] \mathrm{mod} P$$

(1)

where $u,v,u^{\prime },v^{\prime }\in \left\{0,1,2\cdots P-1\right\}$, P is the size of the binary watermarked image to be processed, P is a matrix of two rows and one column, $\left(u,v\right)$ is the pixel position of the watermarked image before disorganization, and $\left(u^{\prime },v^{\prime }\right)$ is the position of the pixel of the watermarked image after disorganization.

The Arnold scrambling transformation enables pixel coordinate relocation from $\left(u,v\right)$ to $\left(u^{\prime },v^{\prime }\right)$ in digital watermarking, achieving information concealment through iterative position permutations. The scrambling iterations (K) serve as a private key to enhance cryptographic security by obfuscating spatial correlations. For watermark recovery, the inverse Arnold transformation is defined as

$$\left[\begin{array}{c}u\\ v\end{array}\right]=\left(\left[\begin{array}{cc}2\hfill & -1\hfill \\ -1\hfill & 1\hfill \end{array}\right]\left[\begin{array}{c}{u}^{\prime }\hfill \\ v^{\prime }\hfill \end{array}\right]+\left[\begin{array}{c}P\\ P\end{array}\right]\right) \mathrm{mod} P$$

(2)

2.2. Introduction to Gyrator Transformations

Rodrigo and his team proposed a first-order optical system model based on a columnar lens array in 2006, which realizes the rotational transformation function of a two-dimensional image by adjusting the optical path parameters, and at the same time has the separable fractional-order Fourier transform characteristics. The core innovation lies in expanding the order of the traditional Fourier transform into the angle variable, forming a mathematical framework with the rotation angle as an independent control parameter, so it is defined as the Gyrator transform. The main idea of the calculation is as follows: Suppose there exists a grayscale $f(x,y)$, and the rotation angle is of the Gyrator transform:

$$G^{\alpha }\left[f(x,y)\right](u,v)={\displaystyle \frac{1}{\sin \alpha }}{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }f(x,y)\exp \left(j2\pi {\displaystyle \frac{(uv+xy)\cos \alpha -(uy+vx)}{\sin \alpha }}\right)dxdy$$

(3)

The above transformations can be converted according to Euler’s formula as follows:

$$\begin{array}{c}{G}^{\alpha }\left[f(x,y)\right](u,v)=\int \int {\displaystyle \frac{1}{\left|\sin \alpha \right|}}f(x,y)\cos \left(2\pi {\displaystyle \frac{(uv+xy)\cos \alpha -(uy+vx)}{\sin \alpha }}\right)dxdy\hfill \\ +\mathrm{i}\int \int {\displaystyle \frac{1}{\left|\sin \alpha \right|}}f(x,y)\sin \left(2\pi {\displaystyle \frac{(uv+xy)\cos \alpha -(uy+vx)}{\sin \alpha }}\right)dxdy\hfill \end{array}$$

(4)

If you need to invert the transformation, you only need to perform a Gyrator transformation with the rotation angle adjusted to $\alpha$ to get the original image $f(x,y)$.

The inverse process of the Gyrator transform can be achieved by adjusting the rotation angle to the negative of the initial parameter; specifically, the original object can be reconstructed by applying the transform with a rotation angle of $-\alpha$. As a linear operation, this transform has previously been utilized in optical information processing and has been progressively extended to the domain of image encryption [33]. Its primary advantage lies in the introduction of a freely adjustable rotation angle $-\alpha$ as the key parameter, akin to the order parameter of the fractional-order Fourier transform. In the absence of the correct angle parameter, an unauthorized decryptor cannot recover the original image through conventional reverse operations, thereby significantly enhancing the security of the encryption system. In comparison to the traditional Fourier transform, the Gyrator transform facilitates hybrid analysis in the air-frequency domain through optical rotation transformation, offering distinct advantages in image feature extraction and information hiding. It has emerged as one of the leading tools in optical image processing, with substantial potential for algorithm optimization and multi-dimensional extensions, such as advancements in quaternionic domain applications.

2.3. Quaternion Correlation Theory

Quaternionic hypercomplex numbers are an extended concept after the complex numbers were proposed by Hamilton in 1843 to cope with the previous problem that complex numbers can only deal with two-dimensional space but not three-dimensional space. Since there exists a certain relationship between the three imaginary parts of quaternions, and at the same time, there exists a close structural relationship between the three channels in RGB color images, which corresponds exactly to the relationship between the components of quaternions, quaternions can be a data structure for expressing color images and have been introduced into various fields of color image processing by researchers, replacing the traditional image processing scheme with the image processing method under quaternions. The traditional image processing scheme is replaced by the image processing method under the quaternion, such as quaternion Fourier transform, quaternion singular value decomposition, quaternion wavelet transform, and quaternion rotary transform. The following mainly introduces the basic arithmetic rules under quaternions and the quaternion Fourier transform, which is closely related to this paper.

2.3.1. Quaternion Base Operations

Quaternions, as an extension of real and complex numbers, consist of one real part and three imaginary parts [34,35,36]. The mathematical expression is

$$q=q_r+i{q}_i+j{q}_j+k{q}_k$$

(5)

where $q_r,q_i,q_j,q_k$ are real numbers; $i,j,k$ are units of imaginary parts as quaternions, which means that this number is the imaginary part of quaternions; and the imaginary parts satisfy the following relationship:

$$\begin{array}{c}{i}^2=j^2=k^2=-1\hfill \\ ij=-ji=k\hfill \\ jk=-kj=i\hfill \\ ki=-ik=j\hfill \end{array}$$

(6)

The weighing component $q_r$ is the real part of the quaternion q, and $i{q}_i+j{q}_j+k{q}_k$ is the imaginary part of the quaternion q. A pure quaternion is a quaternion for which the real part of the quaternion $q_r=0$. When the imaginary part is 0, the quaternion transforms to a real number.

The conjugate operation of the quaternion is $\widehat{q}=q_r-i{q}_i-j{q}_j-k{q}_k$. The modulo operation of the quaternion q is

$$\left|q\right|=\sqrt{{q_r}^2+{q_i}^2+{q_j}^2+{q_k}^2}$$

(7)

The modulus of the pure unit quaternion is 1.

Basic operations with quaternions: Let two quaternions be $q_1$ and $q_2$, respectively.

$$\begin{array}{c}{q}_1=a_1+i{b}_1+j{c}_1+k{d}_1\hfill \\ q_2=a_2+i{b}_2+j{c}_2+k{d}_2\hfill \end{array}$$

(8)

Addition of quaternions means addition of corresponding parts, equality of quaternions means equality of corresponding parts, and multiplication of quaternions:

$$\begin{array}{c}{q}_1·q_2=(a_1{a}_2-b_1{b}_2-c_1{c}_2-d_1{d}_2)+(a_1{b}_2+a_2{b}_1+c_1{d}_2-c_2{d}_1)i\hfill \\ +(a_1{c}_2-b_1{d}_2+a_2{c}_1+b_2{d}_1)j+(a_1{d}_2+b_1{c}_2-b_2{c}_1+a_2{d}_1)k\hfill \end{array}$$

(9)

Addition and subtraction of quaternions satisfy the law of union and the law of exchange, but multiplication of quaternions does not have the law of exchange. When the real part of a quaternion is 0, the quaternion is said to be a pure quaternion. Each pixel of a color image $f(x,y)$ is represented by a quaternion as

$$f(x,y)=f_R(x,y)i+f_G(x,y)j+f_B(x,y)k$$

(10)

where $f_R(x,y)$, $f_G(x,y)$ and $f_B(x,y)$ denote the red, green and blue components of an image pixel, respectively. $i,j,k$ are units of imaginary parts as quaternions.

2.3.2. Quaternion Gyrator Transformations

Because multiplication of quaternions does not satisfy the exchange law, the quaternion Gyrator transform is similar to the quaternion Fourier transform, defined in two forms: the left quaternion Gyrator transform and the right quaternion Gyrator transform. For a color image, the expression of the left quadratic Gyrator transform for the rotation angle $\alpha$ is

$${G_l}^{\alpha }\left[f(x,y)\right](u,v)=\int \int K_{\alpha }(u,v;x,y)f(x,y)dxdy$$

(11)

Right quaternion Gyrator transformations:

$${G_r}^{\alpha }\left[f(x,y)\right](u,v)=\int \int f(x,y)K_{\alpha }(u,v;x,y)dxdy$$

(12)

where $f(x,y)$ is a color image represented by a pure quaternion matrix:

$$f(x,y)=i{f}_R(x,y)+j{f}_G(x,y)+k{f}_B(x,y)$$

(13)

The corners R, G, and B denote the three color channels, and $K_{\alpha }(u,v;x,y)$ is the kernel function of the transformation [37], which is expressed as follows:

$$K_{\alpha }(u,v;x,y)={\displaystyle \frac{1}{\left|\sin \alpha \right|}}\exp \left(\mu 2\pi {\displaystyle \frac{(uv+xy)\cos \alpha -(uy+vx)}{\sin \alpha }}\right)$$

(14)

where $\mu$ is the unit pure quaternion, i.e., $\mu =ix+jy+kz$, and ${\mu }^2=1$. And the variable $\alpha$ represents the angle of rotation of the image. In order to reconstruct the original signal from the transformed signal, the inverse GT corresponds to the QGT at rotation angle ‘$-\alpha$’.

From the conjugate property of the quaternion product, it follows that the left quaternion Gyrator transform and the right quaternion Gyrator transform can be converted to each other as follows:

$${G_r}^{\alpha }\left[f(x,y)\right](u,v)=-{G_l}^{-\alpha }\left[f(x,y)\right](u,v)$$

(15)

2.4. The Non-Uniformity of Visual Capacity

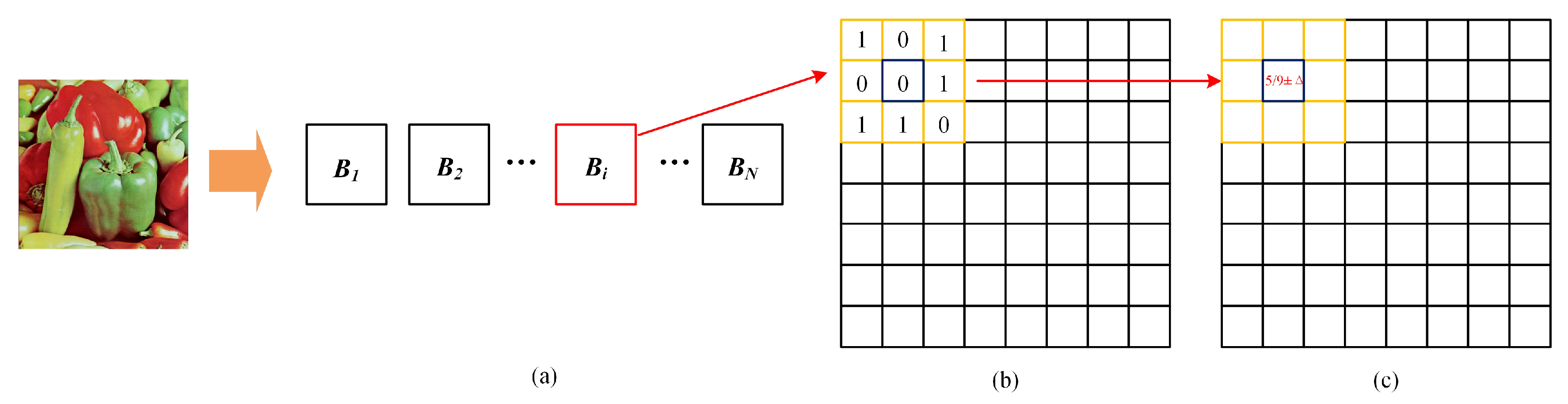
The transparency of digital watermarking pertains to the perceptual invariance between the original host image and the watermarked image as assessed by the human visual system (HVS), ensuring that embedded watermarks remain imperceptible. Visual thresholds demonstrate spatial heterogeneity; areas with significant background variations or complex textures inherently exhibit higher thresholds due to visual masking effects, where rapid luminance gradients or intricate patterns diminish the HVS’s sensitivity to localized perturbations. By leveraging the HVS’s insensitivity to subtle spatial distortions while maintaining acute detection of granular artifacts, watermark embedding must comply with sub-threshold intensity criteria to prevent perceptibility. This requires adaptive watermark embedding, where local visual capacity—measured through gradient magnitude, edge density, or texture complexity—dictates region-specific embedding strengths. By focusing on high-capacity areas (e.g., textured regions with elevated masking thresholds) for more robust watermark insertion while safeguarding low-capacity zones (e.g., smooth backgrounds), the balance between imperceptibility and robustness is systematically optimized.

$$d\left(Q_k\right)={\displaystyle \frac{1}{n^2}}·\sum _{\left(i,j\right)\in Q_k}{\displaystyle \frac{\mathrm{abs}\left(f\left(i,j\right)-m_k\right)}{{\mathrm{abs}(\mathrm{m}}_k^{1+\lambda })}}$$

(16)

where $k=1,2,\cdots ,M\times M/n\times n$. i and j refer to the pixel positions of the sub-blocks to be calculated at present. The carrier image is a square matrix of size $M\times M$, partitioned into $n\times n$ sub-blocks. Let $Q_k$ denote a sub-block of the carrier image, $m_k$ represent the mean value of that sub-block, and $\lambda$ be the weighted correction factor (0.6–0.7) [38]. And the range of $\lambda$ itself does not affect the performance but only plays a balancing role.

Unlike grayscale images, the carrier image is a quaternion-based color image, where the parameters within the numerator and denominator brackets in Equation (16) are quaternions. The operator $abs(·)$ calculates the modulus of the quaternion parameters, ensuring algebraic consistency in the computation of sub-block statistical features while preserving inter-channel correlations inherent to color representations.

3. Proposed Scheme

In this section, we introduce the robust watermarking algorithm with statistical features. For copyright prevention, watermark embedding and watermark extraction are two important parts of the whole algorithm. Through the embedding process to embed the certification watermark and the synchronization watermark in the host image, and then by extracting the hidden watermark from the host photo through a watermark extraction process for authentication, the purpose of information hiding and copyright protection is achieved.

3.1. Pre-Processing

3.1.1. Watermark Image Scrambling

Given an authentication watermark image $w_1$ of size $N_{w_1}\times M_{w_1}$, it is normalized into a square matrix $N_w\times N_w$ for computational convenience. The watermark image undergoes the Arnold transformation governed by the encryption key $K_r$. The transformed watermark is then binarized and vectorized into a bit sequence $W=[B{S}_{P_1}^{\prime },B{S}_{P_2}^{\prime },\cdots B{S}_{P_i}^{\prime }]\in {\{0,1\}}^{N_w}\in {\{0,1\}}^N$, where $B{S}_{P_i}$ denotes the binary state of the i-th pixel after Arnold iteration. This process leverages the periodic and reversible properties of Arnold mapping to enhance security against unauthorized extraction.

3.1.2. The DQ Sequence

This study defines a DQ sequence to determine the embedding order of watermarks, thereby enhancing security:

• For a target object $f\left(x,y\right)$ of size $M\times N$, the photo is partitioned into N non-overlapping sub-blocks $B=\left[B_1,B_2,\cdots B_i,\cdots B_N\right]$.
• Perform QGT on each sub-block to obtain the QGT coefficients $F_B=\left[F_{B1},F_{B2},\cdots F_{Bi},\right.\left.\cdots F_{BN}\right]$. According to Equation (7), the modulus value of a sub-block can be obtained.
• The non-uniformity d of the visual capacity of the corresponding sub-block is calculated according to Equation (16) and the modal size of the sub-block to obtain a sequence DQ containing the values of the non-uniformity d of the visual capacity.
• The sub-block sequences DQ are sorted in descending order, and then the sequence number of the sub-block corresponding to each sub-block is updated in the DQ sequence to obtain the final sequence DQ.

3.1.3. The Watermark Parameter Extraction Model

The watermark extraction process selects neighboring coefficients around the watermark-embedding positions to compute statistical features. Since a nonlinear relationship exists between the embedding positions and neighboring coefficients, a support vector machine (SVM)-based feature extraction framework is constructed to precisely model the mapping relationship of watermark vectors, thereby enhancing cross-domain generalization performance:

• The N non-overlapping sub-chunks of the persistent picture, and all sub-blocks are organized into a sequence $B=\left[B_1,B_2,\cdots B_i,\cdots B_N\right]$.
• According to the DQ sequence value, find the corresponding sub-block, perform the QGT transformation on this sub-block, split the obtained result into the real part and the imaginary part, obtain the position of the watermark to be embedded and the nine neighborhood values around it in the real part, and calculate the final watermark value to be embedded through Equation (17). Take these two pieces of data as a set of data $S_i$. All of the sub-blocks get the final training sets $S_i\in S_t=\{S_1,S_2,\cdots S_i,\cdots S_{L_Z}\}$.
• where $S_t$ is the input and the corresponding binary watermark $B{S}_i$ is the output. $W=[B{S^{\prime }}_{P_1},B{S^{\prime }}_{P_2},\cdots B{S^{\prime }}_{P_i}]\in {\{0,1\}}^{N_w}\in {\{0,1\}}^N$ The mapping relationship between $S_i$ and $B{S}_i$ is utilized to train the SVM, ultimately yielding the parameters of the watermark extraction $model$ (denoted as model).

3.2. Embedding Procedure of Watermark

The energy concentration of the Gyrator transform signal is analogous to that of the Fourier transform [37]. Embedding watermarks in low-frequency coefficients allows their removal via common signal processing methods such as lossy compression or low-pass filtering. Conversely, inserting markers into high-frequency components may induce severe distortion in the watermarked image. Thus, selecting mid-frequency coefficients is optimal, as it satisfies the trade-off requirement between robustness and imperceptibility. To address this, a dual-watermark hierarchical embedding strategy is implemented by optimizing the mid-frequency components in the QGT domain: the authentication watermark $w_1$ (a binary copyright identifier) enables traceable authentication, while the synchronization watermark $w_2$ is constructed based on geometric invariance features using a dual-limit uniform watermark, effectively enhancing resistance to shear deformation. The specific watermark embedding workflow is illustrated in Figure 1.

• N non-overlapping sub-chunks of persistent picture $f(x,y)$ partitioned into, and the partitioned host image is serialized to obtain the sub-block sequence B, where $B=\left[B_1,B_2,\cdots B_i,\cdots B_N\right]$. According to the DQ sequence value, find the corresponding sub-block, perform the QGT transformation on this sub-block, and obtain the QGT coefficient of the sub-block.
• The QGT coefficients are decomposed into real and imaginary parts. Since the embedding positions are set within the real part, the statistical features of neighboring coefficients (including the embedding position) are computed within the QGT real part to derive the feature value $avg$. Specifically, for a target embedding position $(u,v)$, the mean value of the surrounding nine coefficients (including the embedding position) is calculated to obtain the feature value $avg$.
• The feature value is combined with the watermark strength to derive the final watermark embedding value, which is then overwritten onto the target watermark embedding position. The relationship between the watermark embedding information $B{S}_{Bi}$ and the final embedded value ${F^{\prime }}_{real}(u,v)$ is defined by Equation (17).
• After completing the watermark embedding process, the partitioned sub-blocks undergo the QGT with a rotation angle of $-\alpha$ and are subsequently integrated to form the intermediate watermarked image $f_{w1}$. Figure 2 shows an example of embedding one-bit robust watermark information using the proposed watermarking method.

  $$\begin{array}{c}{F^{\prime }}_{real}\left(u,v\right)\left\{\begin{array}{c}avg+\Delta \hspace{1em}if B{S}_{Bi}=1\\ avg-\Delta \hspace{1em}if B{S}_{Bi}=0\end{array}\right.\hfill \\ avg={\displaystyle \frac{1}{9}}{\displaystyle \sum _{i=1}^3}{\displaystyle \sum _{j=1}^3}{F}_{real}(u,v)\hfill \end{array}$$

  (17)

  where $B{S}_{Bi}$ represents the binary information of the watermark, $\Delta$ denotes the embedding strength, ${F^{\prime }}_{real}$ corresponds to the final embedded watermark value at position $(u,v)$, and $avg$ signifies the average value of the sum of neighboring coefficients surrounding the embedding position.
• To address geometric deformation resistance requirements, the IULPM method [29] is employed to integrate the synchronization watermark $w_2$ within the intermediate layer. Following the embedding process, transform the image to RGB for the final watermarked impression $f_{w2}$.
  where $w_2=T•P$, where the core parameters comprise a bipolar sequence T ($T=\{T_i\in \{-1,1\},i=1,2\cdots N_T\}$) and a uniform bipolar sequence P (containing an equal number of 1 s and −1 s in the sequence).

3.3. Watermark Extraction Procedure

The watermark extraction process generally comprises two phases: image rectification and watermark extraction. First, the received image undergoes geometric correction to eliminate positional distortions caused by geometric attacks. Second, the watermark is extracted using the embedding sequence DQ and an extraction model derived from a support vector machine (SVM). The workflow of the watermark extraction is illustrated in Figure 3.

• Correcting the received image: after receiving the received image, the image is first checked for geometric attacks, and if a geometric attack occurs on the image, then the attack is corrected and the image is recovered.
  • Firstly, the QDFT is applied to process the received image, and the frequency coefficients of the QDFT $(u,v)$ are mapped to the logarithmic polar coordinates $\left({\mu }_{1,}{\mu }_2\right)$ using the IULPM method to obtain the mapping matrix $f\left({\mu }_{1,}{\mu }_2\right)$.
  • Then, a synchronized watermark ${w^{\prime }}_2\left({\mu }_{1,}{\mu }_2\right)$ of the same size as $f\left({\mu }_{1,}{\mu }_2\right)$ is produced depending on the key $K_s$. The DFT is intended for use in $f\left({\mu }_{1,}{\mu }_2\right)$ and ${w^{\prime }}_2\left({\mu }_{1,}{\mu }_2\right)$ to obtain their frequency coefficients $F_{\phi }({\eta }_1,{\eta }_2)$ and $W\ast ({\eta }_1,{\eta }_2)$, respectively.
  • The maximum phase correlation value is obtained from the watermark offset position $s\left(p_{1,}{p}_2\right)=IDFT[F_{\phi }({\eta }_1,{\eta }_2)·W\ast ({\eta }_1,{\eta }_2)]$. Once we know the watermark offset position, we can estimate the rotation angle of the attacked image by using $\pi p_2/N$, and then we can invert the corresponding geometric transformation to correct the received image.
  where $F({\eta }_1,{\eta }_2)$ and $W({\eta }_1,{\eta }_2)$ denote the DFT magnitude coefficients of $f\left({\mu }_{1,}{\mu }_2\right)$ and ${w^{\prime }}_2\left({\mu }_{1,}{\mu }_2\right)$, $F_{\phi }({\eta }_1,{\eta }_2)$ denotes the phase of $F({\eta }_1,{\eta }_2)$, and $W\ast ({\eta }_1,{\eta }_2)$ denotes the conjugate of $W({\eta }_1,{\eta }_2)$.
• Extract the watermark:
  • The corrected received image is divided into chunks, and each chunked sub-block is serialized into a one-dimensional array. The selection of the sub-block is based on the DQ value.
  • The QGT transform is applied to the image sub-block. Utilizing the real part information of the sub-block quaternion, the embedding position and the surrounding nine neighborhood coefficients are extracted to compute the sequence value of the SVM.
  • Based on the pre-processing predictive model, the calculated sequence value of SVM is input into the model for prediction, and a value of 0 or 1 is obtained. According to the prediction model obtained from pre-processing, the computed sequence values of SVM are input into the model for prediction, and the outputs $P_0$ and $P_1$ with the values of 0 or 1 are obtained, and the watermark information $W^{\prime }=[B{S^{\prime }}_{P_1},B{S^{\prime }}_{P_2},\cdots B{S^{\prime }}_{P_i}]\in {\{0,1\}}^{N_w}$ is finally extracted.
  • The extracted watermark information can then be organized into a matrix, and inverse Arnold disambiguation is applied, using the key k, to derive the final extracted watermarked image.
  where DQ, the number of printed permutations K, and the predictive model are transmitted as input parameters.

  $$B{S}^{\prime }\left(i\right)=\left\{\begin{array}{cc}1\hfill & if p_0\left(i\right)<p_1\left(i\right)\hfill \\ 0\hfill & else\hfill \end{array}\right.$$

  (18)

4. Experimentation

The properties of the watermarking algorithm are typically evaluated in terms of both robustness and imperceptibility. To assess the robustness and imperceptibility of the proposed watermarking algorithm, the following experiments utilize a color digital image of size 512 × 512 as the host image, as depicted in Figure 4a–h. The host images employed are standard color pictures sourced from the CVG-UGR and USC-SIPI databases. The watermarked image (i) is a binary digital image measuring 64 × 64, and a series of simulated attacks is conducted following the embedding of the watermark. To ensure a more accurate and objective evaluation of the algorithm’s performance, the experimental results are compared with several related watermarking techniques. All experimental results were obtained using the MATLAB R2023b software on a PC with the following specifications: an Intel(R) Xeon(R) CPU E5-1650 v2 @ 3.50GHz, 32GB RAM, and Windows 10 Professional Edition.

4.1. Assessment of Indicators

In digital watermarking technology, the image quality assessment system is the core link to authenticate the efficacy of the method. The system needs to meet two core performance requirements at the same time: one is the covertness (i.e., imperceptibility) of the watermarking information, and the other is the algorithm’s anti-interference ability (i.e., robustness). In an effort to quantitatively assess the covertness of the approach suggested in this essay, the study selects an internationally recognized dual index evaluation system—Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM). In addition to these, Normalized Correlation Index (NC) and Bit Error Rate (BER) are also used to assess the anti-jamming capability of the approach.

• PSNR: PSNR is utilized to calculate the differential in pixels between the source picture and the corrupted pictures and is a widespread and useful tool for objectively assessing the quality of a watermarked image. The better the PSNR value, the higher the quality of the watermarked picture and the more improved the watermarking algorithm is. The PSNR of a multicolor digitized image is as follows:

  $$PSNR=\left[\sum _{j=1}^{3}10\times \lg \left({\displaystyle \frac{M\times N\times {255}^2}{{\displaystyle \sum _{m=1}^M}{{\displaystyle \sum _{n=1}^N}\left[H\left(m,n,j\right)-H\ast \left(m,n,j\right)\right]}^2}}\right)\right]÷3$$

  (19)

  where $\lg (•)$ is a log scale feature with base ten, j indicates the j th level of color in the picture, $(m,n)$ indicates the pixel locations, and $H(m,n,j)$ and $H\ast (m,n,j)$ are the pixels on the $(m,n)$ position in the j th layer of the vector picture and the watermark picture, respectively.
  The PSNR value can be calculated according to Equation (19). In measuring the imperceptibility of the watermark, the higher the PSNR value, the better the quality of the image embedded with the watermark, and the higher the visibility of the watermark. Generally, a PSNR is higher than 30 dB, which indicates that the imperceptibility of the watermarked image is comparable to the visibility of the persistent one.
• SSIM: Similar to PSNR, SSIM is a more recent image similarity metric tool. It is designed according to the characteristics of human visible light and the visual system. The SMIM value lies between 0 and 1, which can validly weigh the performance of the image. The higher the level of the SSIM value, the better the quality of the image embedded with the watermark. The SSIM calculation formula is shown in Equation (20).

  $$SSIM={\displaystyle \frac{\left(2{\mu }_H{\mu }_{H^{\ast }}+c_1\right)\left(2{\sigma }_{H{H}^{\ast }}+c_2\right)}{\left({\mu }_H^2+{\mu }_{H\ast }^2+c_1\right)\left({\sigma }_H^2+{\sigma }_{H\ast }^2+c_2\right)}}$$

  (20)

  where H represents the carrier image, $H^{\ast }$ represents the watermarked image, respectively, and ${\mu }_H$ and ${\mu }_{H^{\ast }}$ denote the average of H and $H^{\ast }$, ${\sigma }_H$ and ${\sigma }_{H^{\ast }}$ represent the criterion variance of H and $H^{\ast }$, respectively, and ${\sigma }_{H{H}^{\ast }}$ represents the covariance of H and $H^{\ast }$, respectively, while $c_1$ and $c_2$ are two other statistics.
  In addition to the metrics mentioned above, normalized correlation [39] and bit error rate (BER) [40] are often assessed to evaluate the methods’ robustness against various attacks. They are typically utilized in the information graphic for watermarking information documents. The NC measure is found to be the likeness ratio between the initial watermarked graphic and its recovery. The range of NC ranges from [0, 1]. The NC range is 1 when both the comparative graphics are the same. As the difference increases between the two objects, the NC value decreases, and a value of zero means that both images are the same.
• NC: Normalized correlation is an objective standard for the estimation of the ruggedness of watermarking calculation algorithms; the range of NC numbers is 0–1; the larger the NC number is, the greater the likeness of both objects is. The calculation of the NC number is as follows:

  $$NC={\displaystyle \frac{{\displaystyle \sum _{i=1}^p}{\displaystyle \sum _{j=1}^q}{\left[w\left(i,j\right)\times w^{\prime }\left(i,j\right)\right]}^2}{\left(\sqrt{{\displaystyle \sum _{i=1}^{k_1}}{\displaystyle \sum _{j=1}^{k_2}}{\left[w\left(i,j\right)\right]}^2}\ast \sqrt{{\displaystyle \sum _{i=1}^{k_1}}{\displaystyle \sum _{j=1}^{k_2}}{\left[w^{\prime }\left(i,j\right)\right]}^2}\right)}}$$

  (21)

4.2. Parameter Selection

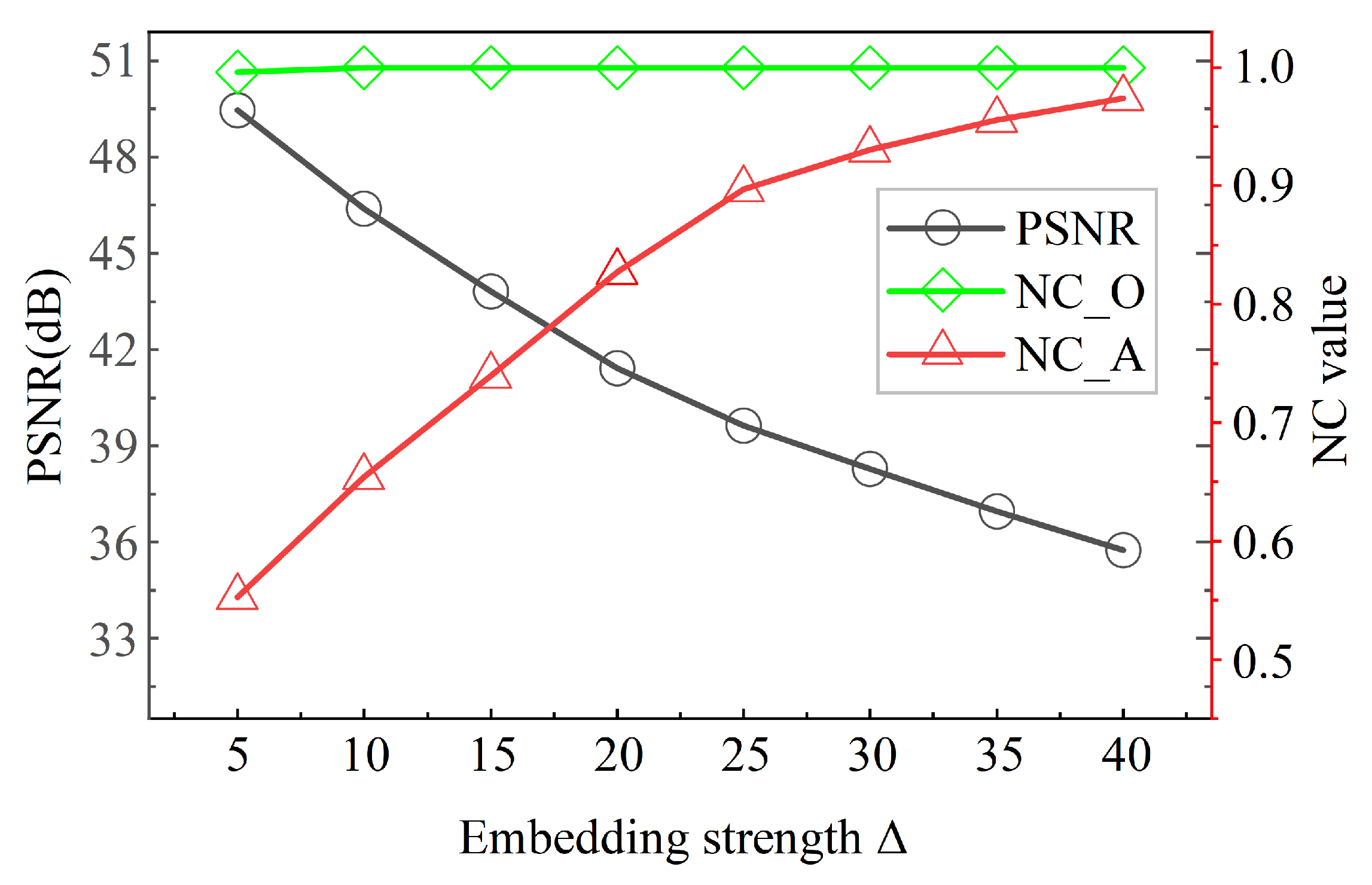
The watermark insertion intensity $\Delta$ is always a trade-off, which is directly related to the quality of the image and the watermark’s roleness. To identify the embedding intensity $\Delta$, we perform an analysis of the performance of the watermarking encoding algorithm by computing the average of PSNR and NC values on a color standard test image set of size 512 × 512. The image is chunked with an image block of size 8 × 8, a certified watermark of size 64 × 64, and Select $(\mu ,\nu )=(2,2)$ as the embedding position of the watermark. As a result, the total number of sub-blocks that the host image is segmented into is 4096, and the same number of SVM training sets is also 4096.

Figure 5 shows the variation of PSNR and NC mean value with different embedding strengths, where NC_O indicates the NC of the extracted watermark when the image does not receive an attack, and NC_A indicates the NC of the extracted watermark when the image receives an attack.

From the observation, we can conclude that the larger the embedding intensity $\Delta$ value, the more robust the watermark is, but it will lead to a lower PSNR of the host image. Whereas, smaller embedding strength $\Delta$ value produces higher image quality but makes the watermark easy to eliminate. It has been shown by consensus that a PSNR value greater than 35 dB and less than 48 dB indicates that the image is visually pleasing [41]. In consideration of the need to counterbalance the transparency and robustness of the watermarked image, the embedding Intensity $\Delta$ was set to 23 in the simulations to ensure that the PSNR value of the host image after embedding the watermark is about 40 dB.

Support Vector Machine (SVM) [42] is a supervised learning model mainly used for classification and regression analysis. It is capable of achieving a balance between model complexity and generalization ability under the condition of limited samples to prevent overfitting. Choosing appropriate parameters during the SVM training process has an important influence on the performance of the model. The system parameter search strategy combined with cross-validation can effectively balance the model complexity and generalization ability, making SVM applicable to related tasks such as classification and regression. To sum up, SVM is highly suitable for implementation in the proposed method. The key parameter configurations include setting the kernel type to linear, fixing the regularization parameter (c value) to 1, defining the kernel parameter as 1, disabling the normalization parameter (normalization = 0), and optimizing the solver through sequential least optimization (SMO).

4.3. Analysis of Imperceptibility

To ensure the covert characteristics of digital watermarking, this study employs a dual index system comprising PSNR and SSIM to quantitatively assess the imperceptibility of watermarking. The experimental design is structured as follows: within the eight groups of original carrier images depicted in Figure 4, single authentication watermarks and combinations of authentication and synchronous dual watermarks are embedded using the algorithm outlined in Section 3. Subsequently, the visual difference parameters are calculated based on the normalized Formulas (19) and (20).

The quantitative data presented in

Table 1. PSNR and SSIM results of the watermarked images obtained by the proposed method.

Carrier Image	PSNR		SSIM
	Auth	Dual	Auth	Dual
Airplane	41.2016	40.7688	0.9695	0.9668
Car	40.7102	39.8572	0.9905	0.9884
Children	41.3295	40.8793	0.9902	0.9892
Girl	41.6760	40.7481	0.9965	0.9956
Lake	40.7044	39.9856	0.9938	0.9927
Lena.	40.9783	40.4174	0.9978	0.9975
Pepper.	41.5066	40.8269	0.9981	0.9977
Splash	41.6434	41.4289	0.9954	0.9952

indicate that the mean PSNR value reaches 41.19 ± 0.36 dB when embedding the authentication watermark and 40.61 ± 0.51 dB when embedding the dual watermarks. The SSIM metrics for both groups stabilize within the 0.99 ± 0.01 range. This data demonstrates that (1) the superposition of two watermarks results in only 0.58 dB of PSNR attenuation, evidencing the multilayer watermarking architecture’s excellent steganographic compatibility, and (2) the standard deviations among the test samples remain below 0.5 dB, confirming the algorithm’s robust adaptability across varying image features. Additionally, visual evaluation results, such as the comparison schematic in Figure 6, further substantiate that watermark implantation does not induce noticeable texture distortion or color shift, thereby establishing visual quality criteria for imperceptible watermarks.

PSNR and SSIM results of watermarked images obtained using the method of this paper.

Where “Auth” means embedding just one certification watermark, while “Dual” means embedding one certification watermark and one standardization watermark.

In particular, it should be noted that although the introduction of synchronized watermarking leads to a downward shift in the domain of PSNR values, the increase in its standard deviation is controlled within 0.15 dB, indicating that the redundant information integration strategy of the geometric correction module effectively balances the contradiction between functionality expansion and visual fidelity. This feature enables this method to maintain the covert transmission of watermark information in response to rotation and cropping space attacks.

4.4. Robustness Analysis Against Attacks

In the field of digital watermarking technology, robustness specifically refers to the watermarking algorithm’s anti-interference ability to maintain the recognizability and integrity of the watermarked information after the carrier image has been subjected to malicious attacks such as geometrical deformation, filtering processing, compression, and degradation. This index becomes a core parameter for evaluating the security level of algorithms by quantifying the tolerance threshold of the watermarking system to attacks. In this study, the attack resistance of watermarking algorithms is quantitatively evaluated by NC. Initially, the watermarked images are subjected to various assaults. Next, the watermarked icons are restored from every hacked watermarked icon using the extraction as well as decryption techniques explained in detail in the previous section. Finally, the NCs are calculated among the pristine and restored watermarked images using Equation (21). The following subsections provide detailed results on robustness.

4.4.1. No Attack

In that simulation, the watermarked samples did not receive any hits.

Table 2. BER and NC data in the without-aggressions scenario.

Carrier Image	NC	BER
Airplane	1.0000	0.0000
Car	1.0000	0.0000
Children	1.0000	0.0000
Girl	1.0000	0.0000
Lake	1.0000	0.0000
Lena.	1.0000	0.0000
Pepper.	1.0000	0.0000
Splash	1.0000	0.0000

illustrates the NC numbers and BERs. From Table 2, it can be seen that for all the tested color images, the suggested technique acquires an NC worth of 1 and a BER worth of 0. This shows that the suggested method is very effective in recovering the watermarked pictures, devoid of any mass damage. Also, it shows that the suggested method still recovers the watermarked image correctly, no matter which test color image is employed.

4.4.2. Noise Attack

In this simulation, a variety of noises like speckle noise, pretzel noise, and Gaussian noise are added to the watermarked image. The NC results are listed in

Table 3. NC values under noise attacks.

Attack	Airplane	Car	Children	Girl	Lake	Lena	Pepper	Splash
Speckle (0.02)	0.7785	0.8340	0.8663	0.7271	0.8840	0.8933	0.9077	0.8926
Speckle (0.04)	0.6436	0.7158	0.7396	0.5882	0.7945	0.7889	0.7865	0.7851
Salt & Pepper (0.008)	0.9492	0.9612	0.9600	0.9089	0.9619	0.9638	0.9575	0.9451
Salt & Pepper (0.02)	0.8740	0.8879	0.8764	0.8195	0.8631	0.8760	0.8662	0.8630
Poisson	0.9660	0.9804	0.9875	0.9412	0.9868	0.9886	0.9948	0.9915
Gaussian (0.01)	0.7444	0.7635	0.7430	0.7040	0.7380	0.7380	0.7347	0.7408

. In additional, Figure 7 illustrates some voluntary outcomes of recovering the watermarked information from the noisy watermarked image. From Table 3, it can be seen that in most cases, the NC value is close to 1. This indicates that the proposed method is highly resilient to the studied noise assaults.

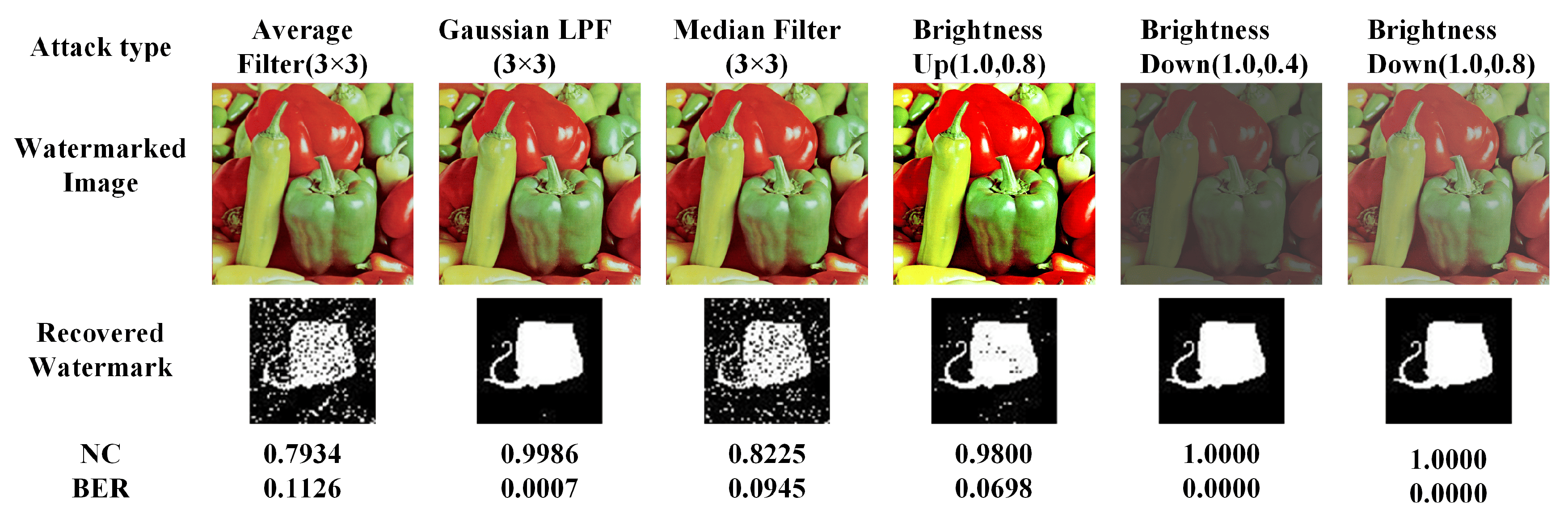
4.4.3. Filtering and Brightness Attack

In this simulation, the image with a watermark is attacked by a variety of filters, such as the median filter, averaging filter, and Gaussian Low Pass Filter (LPF), and the variations of the attacks on the luminance include increasing the luminance and decreasing the luminance.

Table 4. NC values under filtering and brightness attack.

Attack	Airplane	Car	Children	Girl	Lake	Lena	Pepper	Splash
Average Filter (3 × 3)	0.7811	0.6678	0.7530	0.8050	0.8875	0.7818	0.7934	0.9132
Gaussian LPF (3 × 3)	0.9981	0.9981	1.0000	0.9986	0.9976	0.9981	0.9986	1.0000
Median Filter (3 × 3)	0.8314	0.7713	0.7953	0.8443	0.6937	0.8701	0.8225	0.9317
Brightness Up (1.0, 0.4)	0.5364	0.7590	0.4319	0.1539	0.8109	0.8452	0.8603	0.8503
Brightness Up (1.0, 0.8)	0.8607	0.9804	0.9948	0.9899	0.9678	0.9957	0.9800	0.9174
Brightness Down (1.0, 0.4)	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
Brightness Down (1.0, 0.8)	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000

shows NC levels. Moreover, Figure 8 shows some visual results of the watermarked image restored from the filtered watermarked one.

This experimental image has been subjected to a filtering attack and a luminance attack. As can be seen from Table 4, the NC value of the information recovered from the watermark under the luminance decrease attack is 1, which indicates that the algorithm in this paper is highly resistant to the luminance decrease attack. The NC values for brightness increase are generally above 0.8 except for individual ones, which are on the low side. Against the filtering attack, the total NC value is around 0.8, and the individual NC value is 1; it shows that the watermark possesses good resistance to the filtering attack.

4.4.4. JPEG Compression Attack

JPEG compression is a way to condense an image without appreciably degrading the perceived visual aspect of the resulting image. It is commonly used for a digital watermark, as it provides increased delivery efficiency. In this simulation, watermarked imagery is crushed using JPEG compression with a variable quality factor (QF). The NC values are listed in

Table 5. NC values under JPEG compression attacks.

Attack	Airplane	Car	Children	Girl NC	Lake	Lena	Pepper	Splash
JPEG (QF:90)	1.0000	1.0000	1.0000	0.9938	1.0000	0.9995	0.9976	1.0000
JPEG (QF:80)	1.0000	0.9981	0.9990	0.9794	0.9971	0.9976	0.9952	0.9976
JPEG (QF:70)	0.9887	0.9870	0.9857	0.9228	0.9857	0.9857	0.9730	0.9657
JPEG (QF:60)	0.8913	0.9329	0.9223	0.8172	0.9160	0.9276	0.9075	0.8776
JPEG (QF:50)	0.7823	0.8638	0.8444	0.7448	0.8365	0.8443	0.8306	0.8007
JPEG (QF:40)	0.6474	0.7557	0.7184	0.6497	0.7422	0.7271	0.6962	0.6594

. Furthermore, Figure 9 displays some visual consequences of recovering a watermarked image from a compressed watermarked example.

It can be seen from Table 5 that when the QF is varied between 60 and 90, the NC is close to or in the same range as 1. This indicates that the recovery of the watermarked pictures is almost the same or exactly the same as that of the source watermarked pictures. It is also seen that as the QF is placed at 40 or 50, the NC levels of some of the watermarked pictures depart by 1 and 0, and the deviation increases as the QF is set lower, but the NC value remains above 0.64 at a QF of 40 for JPEG, indicating that the present method has a certain degree of resistance to JPEG compression.

4.4.5. Rotation Attacks

In this experiment, the watermarked image rotation attack was used. In this experiment, the attack with clockwise rotation of the watermarked image is taken; the rotation angles are 11°, 26°, 41°, 56°, 71°, and 91°. The NC values are listed in

Table 6. NC values under rotation attacks.

Attack	Airplane	Car	Children	Girl	Lake	Lena	Pepper	Splash
Rotation (11°)	0.8701	0.9683	0.9773	0.9746	0.9716	0.9776	0.9772	0.8501
Rotation (26°)	0.7876	0.9504	0.9694	0.9664	0.9564	0.9671	0.9685	0.7908
Rotation (41°)	0.7370	0.9465	0.9654	0.9661	0.9474	0.9644	0.9644	0.7756
Rotation (56°)	0.6136	0.9544	0.9754	0.9722	0.9605	0.9720	0.9740	0.7923
Rotation (71°)	0.3487	0.8600	0.9689	0.9342	0.9574	0.9697	0.9052	0.8497
Rotation (91°)	0.9480	0.8548	0.9896	0.9869	0.9841	0.9864	0.8943	0.8910

. Furthermore, Figure 10 shows some visual results of recovering the watermarked image from the attacked watermarked image.

As a typical form of geometric attack, image rotation not only changes the absolute position of pixels but also causes relative changes in pixel values. This double destructiveness leads to the failure of the synchronization mechanism of watermark embedding and extraction, which makes the traditional watermarking algorithm face serious challenges. In the experimental design, the researchers systematically analyze the correlation between the watermark detection accuracy and the rotation angle by rotating the watermark-containing image at different angles. As can be seen from Table 6, the NC values under rotational attacks are very close to 1. This indicates that the proposed method has excellent robustness to geometric attacks with motion rotation (Figure 10).

4.4.6. Other Attacks

In this experiment, the watermarked image is subjected to contrast attack, scaling attack, sharpening attack, and histogram equalization attack. The contrast attack takes both contrast enhancement (value 1.2) and contrast reduction (value 0.8), the scaling attack uses 0.8 times and 2.0 times to attack the image, and the sharpening attack value uses 2.

Table 7. NC values under other attacks.

Attack	Airplane	Car	Children	Girl	Lake	Lena	Pepper	Splash
Contrast (0.5)	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
Contrast (1.2)	0.9617	0.9981	0.9995	0.9904	0.9938	0.9990	1.0000	0.9534
Scaling (0.8)	0.8575	0.8492	0.8815	0.9017	0.7963	0.8728	0.8985	0.9475
Scaling (2.0)	0.9942	0.9933	0.9986	0.9914	0.9900	0.9914	0.9957	0.9995
Sharping	1.0000	0.9995	1.0000	0.9976	0.9995	0.9995	0.9990	1.0000
Histogram Equalization	0.9805	0.9957	0.9962	0.9967	1.0000	0.9990	1.0000	0.9986

lists the NC values. In addition, Figure 11 shows some visual results of recovering the watermarked image from the attacked watermarked image.

As shown in Table 7, the NC values of the experimental attacks on the host image are generally around 0.9, which indicates that the proposed method has excellent robustness to these attacks on motion rotation. The NC value of 1 for the contrast attack in particular indicates that the algorithm is highly resistant to the contrast attack.

4.5. Capacity and Timing Analysis

In the realm of digital watermarking technology, imperceptibility and robustness have traditionally been considered the primary evaluation criteria. Conversely, the embedding capacity of watermarking algorithms—the amount of information that can be carried per unit of image—has typically been regarded as a secondary consideration. However, with the increasing prevalence of color images in multimedia applications, the data dimension (e.g., the RGB three-channel) has expanded significantly compared with grayscale or binary images. This shift has catalyzed research into large-capacity color watermarking technology, making it a focal point of interest.

The information-carrying capacity in digital watermarking is typically quantified by the maximum number of embeddable bits per pixel, which indicates the upper limit of watermark information that can be accommodated by the carrier image while maintaining visual quality. The mathematical definition of this index is represented in Equation (22), expressed in bits per pixel (bpp). This equation reflects the relationship between the maximum number of embeddable bits, denoted as $M{E}_{bits}$, and the total pixel count of the host image, represented as $H{I}_{pixels}$, forming the core calculation logic of this metric.

$$EC={\displaystyle \frac{M{E}_{bits}}{H{I}_{pixels}}}\left(bpp\right)$$

(22)

In order to gauge the proposed watermarking method’s embedding capacity, the maximal embedding capacity of the proposed watermarking algorithm is calculated. In this paper, a 512 × 512 colored host image is partitioned into 8 × 8 image chunks, and the real part of each sub-chunk is embodied with 1 bit of binary watermarking data. The relevant comparison results can be seen in

Table 8. The comparison results of embedding capacity.

Algorithm	Maximum Embedded Watermark (Bit)	Carrier Image (Pixel)	Bit/Pixel
Mohammed et al. [43]	$64\times 64$	$512\times 512\times 3$	0.005208
Wang et al. [13]	$64\times 64$	$512\times 512\times 3$	0.005208
Mehraj et al. [40]	$64\times 64$	$512\times 512\times 3$	0.005208
Ubhi et al. [44]	$64\times 64$	$512\times 512\times 3$	0.005208
Gul et al. [45]	$64\times 64$	$512\times 512\times 3$	0.005208
Proposed	$64\times 64$	$512\times 512\times 3$	0.005208

.

The computational efficiency of digital watermarking algorithms constitutes a critical evaluation criterion, particularly in 5G-enabled environments where real-time processing demands necessitate optimized execution speed.

It can be seen from the data listed in

Table 9. The average running time of algorithm (seconds).

Algorithm	Embedding Process	Extracting Process	Total Time
Mohammed et al. [43]	13.4376	41.2573	54.6949
Wang et al. [13]	11.9278	33.4682	41.3960
Mehraj et al. [40]	15.4982	24.1795	39.6777
Ubhi et al. [44]	12.4976	37.1853	49.6829
Gul et al. [45]	99.9682	33.9182	111.8864
Proposed	18.5839	24.4869	43.0808

that the execution time of watermark embedding and watermark extraction proposed by this algorithm is relatively long.

Since the time complexity of the quaternion Gyrator transformation itself for processing images is $O\left(n^2\right)$, when processing the host image and performing block operations, it requires an execution of the quaternion Gyrator transformation at the order of $O\left(n\right)$. Therefore, the overall time complexity of the proposed algorithm is of the order of $O\left(n^3\right)$.

In the comparison method, Mohammed et al. and Wang et al. The time complexity of both Mehraj et al. is $O\left(n^2\right)$. The time complexity of the algorithm of Ubhi et al. Gul et al. is $O\left(n^3\right)$.

The overall complexity of each process of the proposed method is as follows: Block QGT overall complexity is $O\left(n^3\right)$, the statistical characteristic of computing time complexity is $O\left(1\right)$, and the overall complexity of the SVM prediction is $O\left(n\right)$.

4.6. Security Analysis

From Section 3.2, it can be seen that the parameters required for the watermarking algorithm include the watermark image disambiguation key $K_r$, the sequence DQ, and the QGT rotation angle $\alpha$. Secondly, the embedding of one bit of information in the real part has to be determined by determining the embedding position, and the wrong extraction position is not able to extract the watermarked information successfully. Therefore, the safety of the suggested approaches is assessed by the allocation of distinct sets of values for the required bonds based on the hypothesis below. Here, we take the assumption that the embedding locations are all correct for the experiments.

First, we assume that the disruption key, DQ sequence, and rotation angle used are all different. Second, we assume that only the scrambling key is correct among the keys used each time, and the remaining two are incorrect. Third, it is assumed that just one out of each used key is wrong and the other two are right. At last, we assume that all keys used are true for all three keys.

For each performed operation, we used the state policy decryption watermarking image process detailed in Section 3.2.

Table 10. Security analysis of the proposed approach.

Recovered Watermark	Exp. 1	Exp. 2	Exp. 3	Exp. 4	Exp. 5	Exp. 6	Exp. 7	Exp. 8
BER	0.4513	0.4835	0.5389	0.4953	0.4926	0.5146	0.2259	0.0000
NC	0.3856	0.3289	0.2676	0.2958	0.3264	0.3025	0.5633	1.0000

lists the outcomes of the eight experiments carried out. As can be seen from Table 10, when any of the used keys is incorrect, the restored watermarked image is a noisy image. When multiple keys are used incorrectly, the recovered watermarked imagery is even worse. The recovered watermarked image is the same as the original watermarked image when the correct key is used. Based on the above-mentioned factors, it can be concluded that the proposed system is highly secure.

4.7. Comparison with State-of-the-Art Approaches

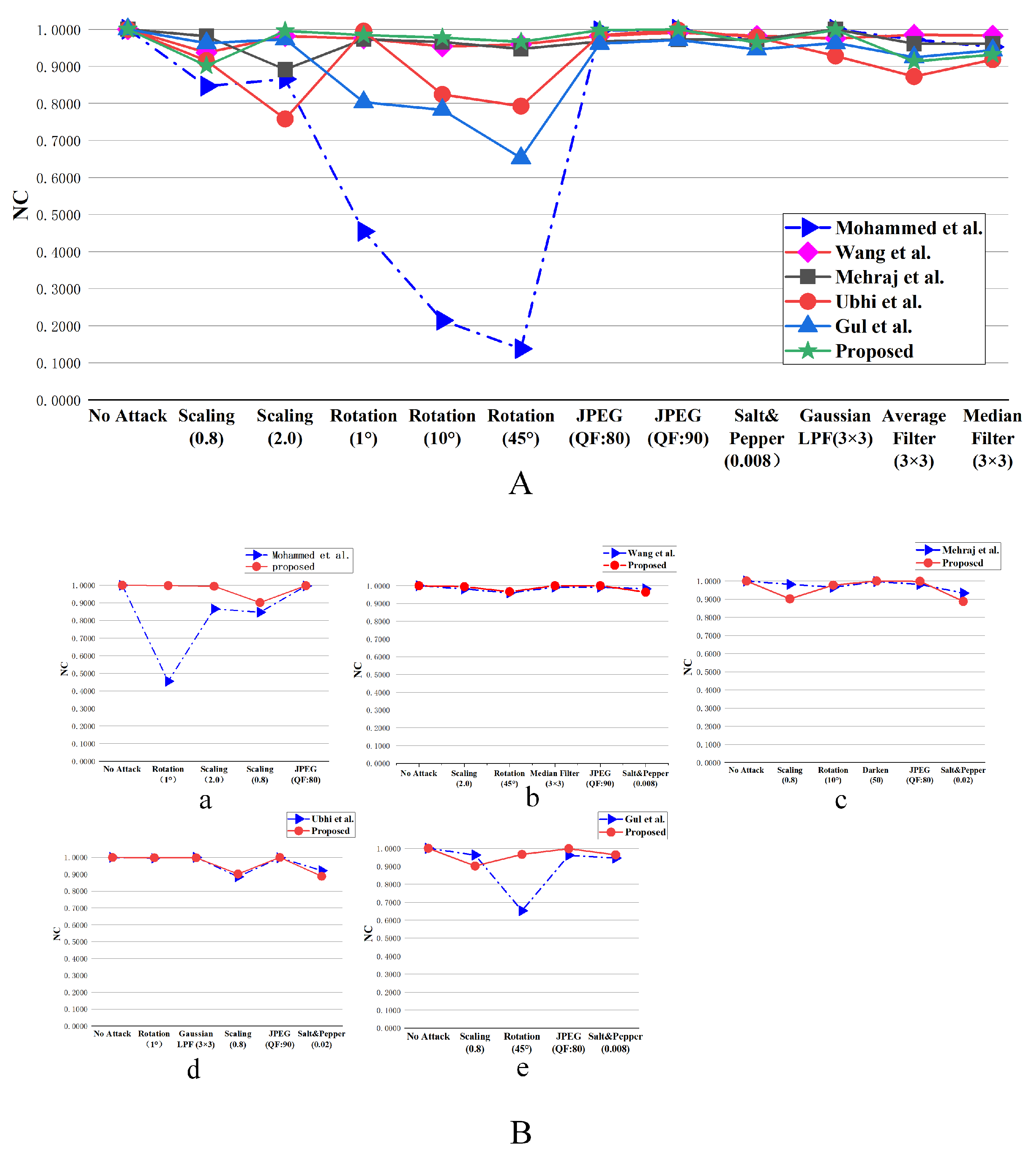
This chapter gives a set of experiences of comparing the proposed method with the recent approach to image watermarking in terms of imperceptibility and the robustness metrics. The outcomes of the Imperceptibility Comparison and Robustness Response competitions are shown in Figure 12 and Figure 13, and the Robustness Response competition is shown in Figure 14, respectively. Figure 14, part (A) is a visual comparison plot of the compared methods in a single plot, and part (B) is a detailed comparison plot. The comparative methodologies were sequentially referenced as follows: Mohammed et al. [43]; Wang et al. [13]; Gul et al. [45]; Mehraj et al. [40]; and Ubhi et al. [44].

In this paper, an equivalent binary image is used as a digital watermark embedded into the host image, and the embedding results of the watermark are shown in Figure 12 and Figure 13, excluding the Gul et al. [45] method, the PSNR values of the remaining algorithms reach around 40 dB, and the PSNR of the proposed method is 41.4921, which is higher than most of the algorithms in the referenced literature and shows good invisibility; the SSIM values of all the methods in the literature and the proposed method are all greater than 0.96; on the other hand, it can be found from observing the visual effect graphs in Figure 6, that the watermarks are embedded in the watermarked host image is not detectable, which indicates that the methods in this paper perform reasonably well in terms of the degree of unrecognizability. In other words, the proposed watermarking algorithm possesses good invisibility compared with the overall schemes in the literature.

As can be seen in part (A) of Figure 14, the proposed method performs better than the method of Mohammed et al. [43] and Gul et al. [45] in terms of robustness in most cases, as shown in Figures a and f in part (B) of Figure 14. The proposed method shows better robustness under the attack of rotation compared with Mohammed et al. [43], Wang et al. [13], and Gul et al. [45]. However, under a scaling attack, the method of Mehraj et al. [40] and Gul et al. [45] performs more satisfactorily than ours; however, the proposed method performs better than the method of Mohammed et al. [43] and Wang et al. [13]. Moreover, under JPEG compression attack, our method is slightly better than the methods of Mohammed et al. [43], Wang et al. [13], Mehraj et al. [40], and Gul et al. [45]. The proposed method outperforms the method of Mohammed et al. [43] and Gul et al. [45] under the attack of pretzel noise, although it is not as good as the method of Wang et al. [13] under median filtering attack or as good as the method of Ubhi et al. [44] under Gaussian filtering attack, but the proposed algorithm’s NC value under this attack still maintains the high values of 0.9317 and 0.9981, which also indicates that the robustness of the proposed method in this area is highly desirable.

Based on the findings of the empirical comparisons and the previous section of the discussion, it can be summarized that the present method implements both satisfactory imperceptibility and striking robility as opposed to the prior art methods.

In the experimental section of this paper, the digital watermarking algorithm demonstrates limited resistance to adversarial attacks, particularly when subjected to modifications of the watermark image through small perturbations, which may result in the loss or destruction of watermark information [46]. This observation suggests that the current quaternion-based digital watermarking methods possess certain limitations in robustness. To enhance the algorithm’s resilience against such attacks, future research should consider improvements to the watermark embedding strategy, increasing redundancy, or integrating deep learning techniques, such as Generative Adversarial Networks (GANs) [47], to bolster watermark robustness. Furthermore, it will be essential to evaluate and optimize the performance of watermarking algorithms under various adversarial attacks to enhance their practical applicability.

5. Conclusions and Future Prospects

In this paper, a robust watermarking algorithm based on QGT and neighborhood coefficient statistical features is proposed. The QGT and domain statistical features are combined to enhance the robustness of watermarking; the image is segmented into non-overlapping sub-blocks; the authentication watermark is embedded in each word fast; and the visual capacity sequence is used to guide the embedding priority. The IULPM method is embedded into the geometric watermark, and finally, both watermarks are embedded into the host image to enhance the attack-resistant nature of the image. The watermarks are extracted using a support vector machine, which stores the mapping relationships when embedding the watermarks. The watermarked values can be extracted very well. The digital watermarking algorithm proposed in this study, based on the dual watermark embedding mechanism and the statistical feature fusion strategy, has achieved the collaborative optimization of robustness and security in the field of digital copyright protection. In terms of security, the adopted three-level key system includes the master key, feature key, and verification key to ensure that unauthorized users cannot obtain the complete watermark. Experimental data show that this algorithm has significant resistance to attacks such as JPEG compression and median filtering. This multi-dimensional protection mechanism provides a reliable technical path for digital content copyright certification.

For further research, we intend to investigate other properties of QGT and apply them to watermarking algorithms. For example, after QGT transformation, we assign its amplitude, which can increase the embedding capacity of watermark information to a greater extent. Since QGT itself needs to perform multiple multiplications, increasing the execution efficiency of time is one of the future research directions. In addition, we also intend to test the feasibility of the tamper detection function of semi-fragile watermarking by using this method in order to understand the advantages and properties. For example, we will explore deep learning techniques applied to the fusion with watermarking and tampering localization models to obtain more robust performance. The combination of support vector machine and deep learning is also one of our future research directions. The future development direction will inevitably be inseparable from deep learning, and support vector machines can precisely fit into the field of deep learning. Therefore, in the future, the multi-core or integration of vector machines can be combined with deep learning as one of the research directions.