Bilateral Trading Strategy for the Wind–Thermal Storage System Considering Peak Shaving

Abstract

To alleviate the peak-shaving pressure caused by large-scale renewable energy integration, this paper proposes a bilateral trading strategy for wind–thermal energy storage (TES) systems. Based on the classification of TES electricity-receiving and heat-receiving pathways, the distinct electrical and thermal flexibilities of TES are quantified, and a Stackelberg game is formulated in which TES enterprises bid quantities, whereas wind farms bid prices. By doing so, the complex coupling between TES and thermal power units is clearly decoupled, significantly enhancing the market participation of both TES enterprises and wind farms. Finally, simulations using operational data from a real wind farm with 1665 MWh of curtailed wind demonstrate that the proposed method accommodates 61.26% of the curtailed energy and raises the net-load valley by 131.6 MW, confirming its effectiveness and practical feasibility of the proposed strategy.

1. Introduction

Under a high penetration of variable renewable energy, power systems face growing peak shaving requirements. During the heating season, wind power accommodation is limited by the “electricity determined by heat” mode of combined heat and power (CHP) units, which results in substantial wind curtailment [1,2]. To address this issue, extensive flexibility retrofits have been implemented in coal-fired units, including low-load boiler operation, integration of TES, and low-pressure cylinder cut-off compensation [3,4,5,6]. However, conventional measures remain insufficient to accommodate the high variability of renewables [7].

The prosumer concept, originating from distributed energy systems, highlights the dual role of entities in both energy production and consumption. Prosumers feature rapid adjustability and operational flexibility, making them outstanding market participants. In this study, wind farms are regarded as variable-output producers, while stand-alone TES units are modeled as consumers capable of storing and releasing heat. As the wind–thermal storage system, they form a prosumer coalition that coordinates peak shaving and enables more efficient resource allocation through bidirectional interactions. Market-based trading models for prosumers have been examined in extensive research. A prosumer market-clearing model and revenue-sharing scheme based on generalized Nash bargaining are proposed for aggregations of varied distributed resources in Reference [8], balancing system security with equitable benefit allocation. Benefit allocation within prosumer coalitions is addressed via a cooperative game under centralized scheduling in Reference [9], which achieves maximal joint welfare. Privacy in large-scale centralized prosumer dispatch is further considered in References [10,11] by formulating a two-stage model and solving it with distributed algorithms that preserve participant confidentiality during scheduling. Contract theory is employed to aggregate small prosumers, and a bilevel trading model for regulation services is established in Reference [12], which focuses on the frequency-regulation market. Despite advances in energy and ancillary service markets, applications of TES in peak-shaving markets remain scarce. This gap is largely due to real-time strategic competition and information asymmetry, which hinder effective management of wind power variability and reduce the investment returns of TES systems [13,14].

On the other hand, interactions among resource types in current peak shaving ancillary service markets have been observed to be weak in [15], which leads to poor allocative efficiency and inflated price signals. High variability of renewable output and low returns on investment for TES enterprises are shown to reduce participation further in Reference [16]. Under single-sided bidding schemes, renewable units can only passively accept ancillary service prices; they lack bargaining power, and they cannot reveal their true preferences and costs, which distorts resource allocation and price signals [17]. Therefore, a more flexible, market-oriented bilateral trading mechanism should be introduced to address these issues. Under this mechanism, prosumers negotiate both quantities and prices, utilize their dual roles in production and consumption, improving the allocation of peak shaving resources, and achieve a dynamic balance of interests among participants. However, the introduction of this mechanism brings a key challenge: how to effectively determine traded quantities and clearing prices within bilateral transactions.

Game-theoretic methods provide a natural framework for capturing cooperation and competition among prosumers. Within this framework, wind farms and TES enterprises jointly participate in peak-shaving operations. These actors act as independent market entities with varied objectives and strategies; reliance on centralized dispatch alone cannot ensure fair benefit allocation or efficient resource utilization. Therefore, the Stackelberg (leader–follower) game, as a non-cooperative framework, is particularly suited to competitive bilateral trading environments, as it effectively accommodates information asymmetry and uncertainty to enhance transaction efficiency. The Stackelberg game has been widely used in electricity markets [18,19]. Reference [20] proposes a low-carbon scheduling model for integrated energy systems that integrates bilateral demand response with a two-level Stackelberg game involving integrated energy systems operators, load aggregators, and users; this approach dynamically determines and integrates bilateral demand response subsidy prices to ensure equitable interest allocation. Similarly, Reference [21] formulates a Stackelberg model between an electric boiler equipped with thermal storage and a wind power producer to optimize trading decisions while promoting fair profit distribution. Extending this concept, the present study employs a Stackelberg formulation for bilateral trading between wind power and thermal storage, incorporating multi-round negotiations to address dynamic competition, establish traded quantities and prices, and achieve efficient resource allocation with balanced payoffs.

In summary, this study proposes a novel bilateral trading mechanism for wind power–TES integrated systems, in which wind farms act as price setters while TES enterprises determine the traded quantities. The mechanism fully leverages the regulation capability of independent TES units, enhances coordination between producers and consumers, and promotes active engagement from both TES and wind power stakeholders. The main contributions of this paper are summarized as follows:

• Pathways for TES participation in peak shaving are delineated from a prosumer perspective. Devices are classified as independent or coupled based on voltage level, point of interconnection, and installed capacity.
• A bilateral-trading peak shaving model is established for wind power and an independent TES. The Stackelberg (leader–follower) framework is employed to maximize the economic benefits for both parties. A multi-round process, consisting of quantity bids by TES and price offers by wind farms, is used to determine the final accommodated wind energy and the equilibrium trading price. This approach reflects cooperative intent and improves resource allocation.
• Case studies using operational data from a real wind farm demonstrate the effectiveness and practicality of the proposed framework. Results show that it increases wind energy accommodation, enhances the system’s down-regulation capability, and improves the economic outcomes for market participants.

The remainder of this paper is organized as follows. Section 2 analyzes the electricity- and heat-receiving pathways of TES. Section 3 presents the design of a novel bilateral trading mechanism between independent TES enterprises and wind farms, including the trading process, model formulation, and solution approach. Section 4 presents the simulation analysis. Section 5 concludes the paper and provides an outlook.

2. Analysis of Electrical Supply and Thermal Pathways of Thermal Energy Storage Units

This section establishes a novel framework for classifying TES units and elucidates the superior peak-shaving capability of independent units, thereby providing a theoretical foundation for the bilateral trading model proposed in this study.

Unlike the common taxonomy that classifies TES by storage mechanism [22], this study distinguishes independent and coupled TES units based on interconnection voltage level, point of connection, and installed capacity. These attributes are reflected in the electro-thermal supply pathways and shape each unit’s prosumer potential: an independent TES (As shown by the dotted line in Figure 1) connects on the load side with a relatively loose pathway, enabling flexible absorption of curtailed wind energy and the production of heat (and, where applicable, electricity), thus forming a prosumer coalition with wind power; a coupled TES connects on the supply side with a tightly bound pathway constrained by CHP operations, exhibiting weaker prosumer attributes and lower flexibility.

The electrical-supply pathway reflects differences in the point of interconnection and voltage level. These differences directly determine the degree of coupling. As illustrated in Figure 1, a coupled TES connects to the thermal power unit via low-voltage plant auxiliary power at node A and is constrained by plant dispatch. This path is tightly integrated with the CHP system; prosumer attributes are weak, and the coupled TES primarily supports internal balancing. By contrast, an independent TES (e.g., a storage electric boiler or an electric-molten salt TES system) connects to the grid on the high-voltage side of the public network at node B. This pathway is relatively independent, provides load-side self-regulation capability, and entails wheeling (network use-of-system) charges, but enhances the device’s potential to participate in prosumer-oriented markets.

The thermal energy pathway further accentuates the classification by revealing conversion capability. In the coupled TES units, the pathway is subject to CHP-induced time-lag constraints [23]; it typically supports electricity-to-heat conversion for plant heat supply. Although certain coupled designs permit limited electricity–heat–electricity cycling, overall flexibility remains bounded by system constraints. By contrast, the independent pathway supports bidirectional electricity–heat–electricity conversion, enabling the load side to respond effectively to wind variability, absorb otherwise curtailed output, and release heat on demand.

In summary, the electro-thermal pathway analysis motivates the classification into independent and coupled TES. From the perspective of production-oriented consumers, the advantages of the former lie in high autonomy and conversion flexibility. These advantages attribute position-independent TES as a key enabler of peak shaving in wind–TES joint systems and provide the theoretical foundation for the bilateral trading model developed in the next section.

3. Bilateral Trading Model for Independent Thermal Energy Storage in Grid Peak Shaving

This section presents the coordinated peak-shaving participation mechanism, the design of the bilateral trading schemes, the operational procedures, and the bilateral trading model between independent TES enterprises and wind farms, developed within a Stackelberg game framework. This model analyzes solely from a market perspective, ignoring the internal physical properties of wind farms and TES. The complex internal physical characteristics of thermal storage are approximated by the thermoelectric conversion efficiency. The decision variables are the “TES-quantity’’ and “wind-price’’.

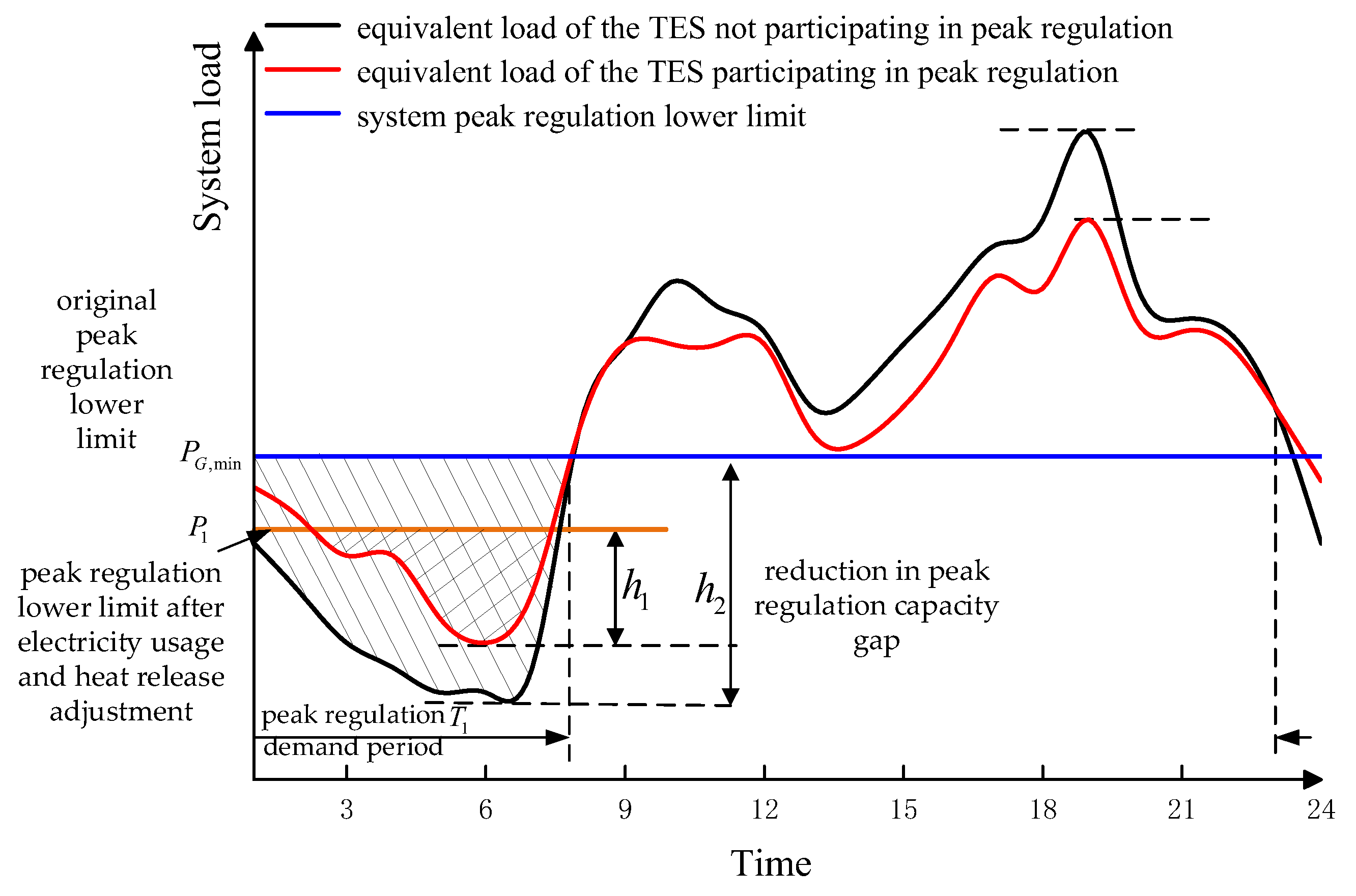
3.1. Mechanism of Joint Peak-Shaving Participation by Independent TES and Wind Power

The stochastic volatility and counter-peaking effect of wind generation increase the peak–valley spread of the system’s net load (actual demand minus wind output) once large-scale integration occurs, thereby increasing peak-shaving requirements, as indicated by the highlighted region in Figure 2. TES has expanded rapidly in recent years; during the winter heating season, a single enterprise can exhibit peak demand exceeding 200 MW. With its dual characteristics of energy storage and controllability, TES can be coordinated with wind power to reshape and flatten the load profile, effectively mitigating peak-shaving pressure on the system [24].

During curtailment periods, TES charges using surplus wind power, raising electricity consumption and effectively lifting the “valley” of the net-load profile. In parallel, shifting a portion of heat demand into curtailment hours allows TES to supply heat that would otherwise be provided by CHP units, thereby lowering the CHP minimum electrical output and partially relaxing the heat-led constraint. As a result, electricity use in non-curtailment hours declines, the peak–valley requirements of the net load are reduced (from $h_1$ to $h_2$), wind absorption increases, and system peak-shaving pressure is alleviated.

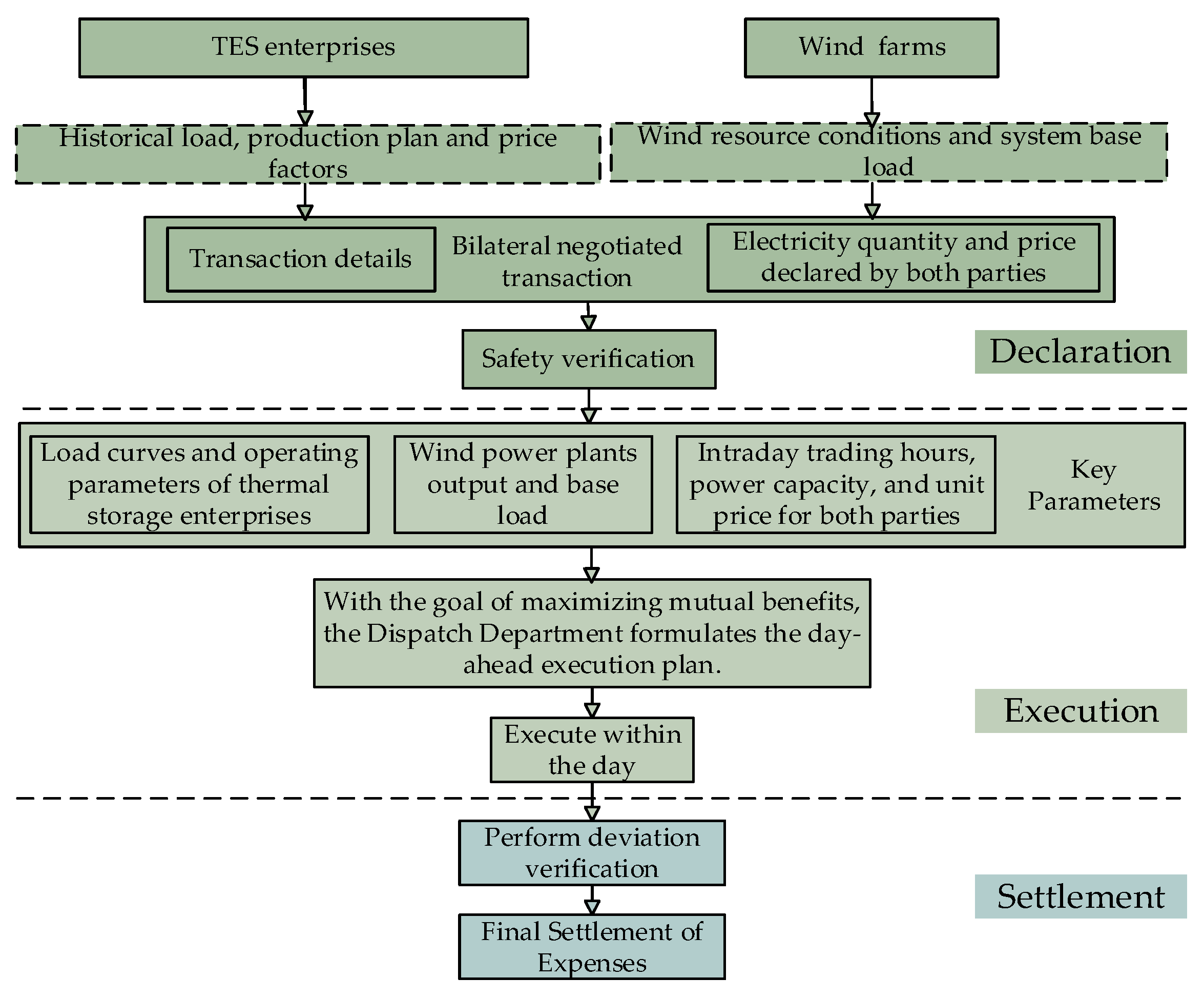
3.2. Design of the Bilateral Trading Mechanism for Wind Power and TES in Peak Shaving

In bilateral trading between wind farms and TES enterprises, three schemes are commonly considered: (i) TES submits quantity bids while wind submits price offers; (ii) wind submits quantity bids while TES submits price offers; and (iii) both parties bid quantities and prices [25]. Compared with the alternatives, the “TES-quantity, wind-price” design emphasizes TES as the leading party: it leverages demand-side flexibility to set a transactional baseline, while the wind farm responds with price offers. This scheme streamlines clearing, enables rapid response, and suits small- to medium-scale regional trades. By contrast, the “wind-quantity, TES-price” design may fail when the wind offer exceeds TES absorption capability. Under this scheme, the “both-quantity-and-price” design requires a more complex platform and entails higher transaction costs.

Accordingly, this study adopts the TES enterprise-quantity–wind-price scheme as the bilateral trading design. First, the scheme incentivizes proactive TES enterprises’ participation. As the leader in peak shaving, a TES enterprise’s storage capability and heat demand directly determine its potential to absorb otherwise curtailed wind output. By submitting quantity first, TES can adjust its participation to operating conditions, while the wind farms, acting as the follower, post price offers in response, enabling precise supply–demand matching and avoiding resource waste. Second, the scheme alleviates information asymmetry: TES enterprises have better knowledge of available storage capacity and heat demand, whereas the wind farms observe the volume of constrained wind energy. The sequential order of declarations reduces informational frictions. In grid operations, this mechanism increases wind accommodation, compresses the net-load peak–valley spread, and lowers peak-shaving costs.

Based on the above advantages, this study designs the bilateral trading workflow between wind farms and TES enterprises as shown in Figure 3. Specifically, the wind farms forecast next-day output and intended injections using historical meteorological and load data, and submit these to the dispatch center. The TES enterprises determine the next-day load according to production planning and likewise submit it to the dispatch center. Subject to system security and the satisfaction of internal load supply, the dispatch authority sets the trading window and power level for the peak-shaving capacity between the wind farms and the TES enterprises. Using the maximization of the profits of TES enterprises and the wind farms as the scheduling objective, the operator formulates and executes the dispatch plan, yielding mutually beneficial outcomes for both parties.

This process can ensure stable accommodation of wind energy and a competitively priced electricity supply. The wind farms and the TES enterprises may negotiate directly according to their respective requirements and conclude a bilateral contract [26].

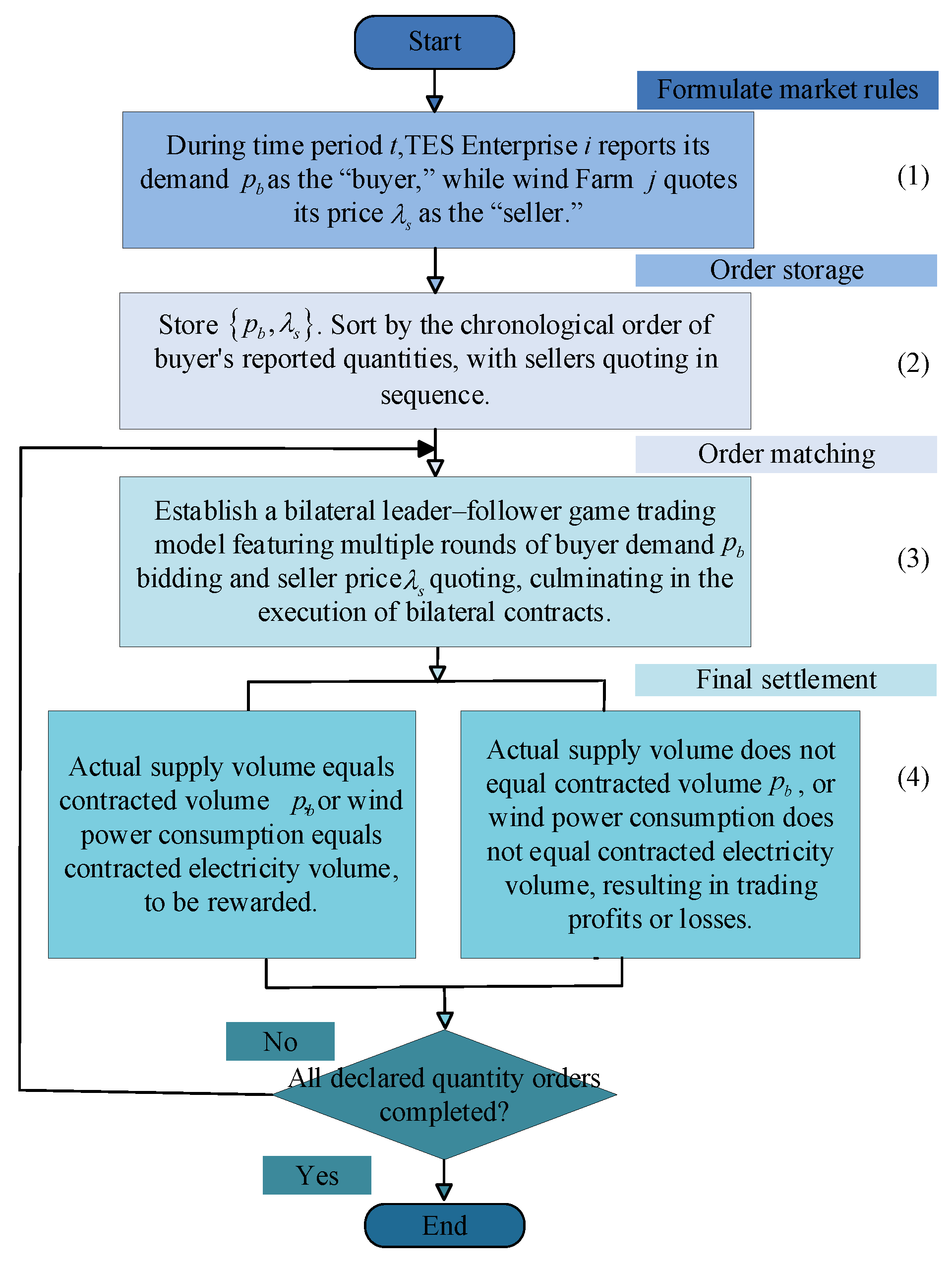
3.3. Execution Workflow for Bilateral Trading Between Wind Power and TES in Peak Shaving

A bilateral contract between the TES enterprises and the wind farms enables coordinated absorption of otherwise curtailed wind while simultaneously providing peak-shaving services to the grid. Market rules permit the TES enterprises to adjust their electricity purchases dynamically in response to wind output, thereby preserving their flexibility as a prosumer. The detailed execution workflow of the bilateral trade is shown in Figure 4. The steps are as follows:

(1)

Rule setting. Counterparties are chosen autonomously. The TES enterprise i acts as the buyer and, according to its operational needs, first submits the intended purchase of constrained wind energy $p_b$ (MWh). The wind farm j, as the seller, submits the offer price ${\lambda }_s$(CNY/MWh) based on its declared constrained energy.

(2)

Order-booking. A trusted trading center serves as the third party and records all TES quantity submissions for that time in an order book to ensure transparency. Submissions are time-stamped and sorted by arrival time; matching then proceeds sequentially in that order.

(3)

Matching rule. A quantity-based pricing bilateral model is employed. Using the first-round quantity declarations from both sides, the buyer submits a second-round price bid; the seller then adjusts its quantity offer accordingly. This bargaining iterates over multiple rounds until the equilibrium price and traded quantity are determined. The matching process continues in the order book until all executable orders are cleared.

(4)

Clearing and settlement. After security verification by the dispatch center, the TES enterprises and the wind farms settle the transaction [27]. Operational deviations may create energy imbalances; therefore, a deviation-settlement scheme is applied. Parties whose actual transacted energy equals the contracted quantity receive an additional incentive via a bonus mechanism. When discrepancies arise between actual and contracted quantities, the surplus or shortfall is bought from or sold to the third party at the on-grid tariff.

3.4. Stackelberg Game-Based Decision Method for Bilateral Trading

Building on the bilateral trading framework in Section 3.3 for TES participation in peak shaving, TES enterprises are modeled as the leader that first declares its purchase quantity, while the wind farms act as the follower that adjusts its offer price in response. This Stackelberg formulation captures the cooperative and competitive interactions between prosumers in the bilateral trade.

3.4.1. Payoff Model for the Wind Plants

When formulating the supplier-side pricing model, the wind farm’s revenue derives from electricity sales, while costs consist of generation and O&M expenses, a curtailment penalty, and a contracted-quantity deviation penalty. The deviation term captures volatility in wind output. The set of curtailment hours $T^B$ is defined as

$$T^B=\left\{t|\right.\left.P_{load}^t-P_G^{\min }<0\right\}$$

(1)

where $P_{load}^t$ denotes the system load and $P_G^{\min }$ is the minimum stable output of the thermal unit.

During curtailment periods, the wind farms maximize their own profit, which is written as

$$I_w=R_w^{T^B}-C_w^{T^B}-C_{abd}^{T^B}-C_{dev}^{T^B}$$

(2)

where $R_w^{T^B}$ is the total revenue from bilateral trades, $C_w^{T^B}$ is the generation and O&M cost, $C_{abd}^{T^B}$ is the curtailment penalty, and $C_d^{T^B}$ is the penalty for deviations from the contracted quantity.

The bilateral-trading revenue and the generation cost are given by

$$R_w^{T^B}={\displaystyle \sum _{t=1}^{T^B}{P}_{w,sell}^t}{\lambda }_w^t$$

(3)

$$C_w^{T^B}=E_{w,sell}^{T^B}({\lambda }_{w0}+{\lambda }_{wp})$$

(4)

where $P_{w,sell}^t$ is the electricity sold by the wind farms at time t in the bilateral trade, ${\lambda }_w^t$ is the agreed bilateral price at time t, and $E_{w,sell}^{T^B}$ is the total traded energy over curtailment hours. Parameters ${\lambda }_{w0}$ and ${\lambda }_{wp}$ denote the unit generation cost and the unit O&M cost, respectively.

Curtailment and deviation penalties are written as

$$C_{abd}^{T^B}={\lambda }_{abd}(E_w^{T^B}-E_{w,sell}^{T^B})={\lambda }_{abd}{\displaystyle \sum _{t=1}^{T^B}(P_w^t-P_{w,sell}^t)}$$

(5)

$$C_{dev}^{T^B}={\lambda }_{dev}{\eta }_w{E}_{w,sell}^{T^B}$$

(6)

where ${\lambda }_{abd}$ is the unit curtailment-penalty rate; $E_w^{T^B}$ is the cumulative energy sold through the bilateral trade; $P_w^t$ is the wind power output at time t; ${\lambda }_{dev}$ is the unit penalty for deviations from the contracted quantity; and ${\eta }_w$ is the ratio of volatility-related energy to the forecast energy.

Contract and physical feasibility constraints include price bounds and the available curtailed energy:

$${\lambda }_{w0}\le {\lambda }_w^t\le {\lambda }_p^t$$

(7)

$$0\le P_{w,sell}^t\le P_w^t$$

(8)

where ${\lambda }_p^t$ denotes the wind farm’s planned on-grid electricity price (CNY/MWh).

3.4.2. Payoff Model for the TES Enterprises

During curtailment hours, the TES enterprises modulate their charging power to absorb curtailed wind energy and purchase this energy from the wind farms to meet their own electricity demand. The enterprise’s revenue consists of heating-service income and emissions reduction benefits, while costs include electricity procurement, network use-of-system (wheeling) charges, and regulation/adjustment costs. Accordingly, during curtailment periods, the TES enterprise’s bilateral-trading profit is formulated as

$$I_H=R_H^{T^B}+R_{H,c}^{T^B}-C_{H,b}^{T^B}-C_{H,t}^{T^B}-C_{H,r}^{T^B}$$

(9)

Heating revenue and emissions reduction revenue are given by

$$R_H^{T^B}={\lambda }_{eq}^t{E}_{H,buy}^{T^B}={\lambda }_{eq}^t{\displaystyle \sum _{t=1}^{T^B}{P}_{H,buy}^t}$$

(10)

$$R_{H,c}^{T^B}={\lambda }_c\mu E_{H,buy}^{T^B}={\lambda }_c\Delta \mu {\displaystyle \sum _{t=1}^{T^B}{P}_{H,buy}^t}$$

(11)

where ${\lambda }_{eq}^t$ is the heating-equivalent electricity price (determined by the heat tariff, building heat load, and heating-season duration), ${\lambda }_c$ is the carbon price, and $\Delta \mu$ is the difference in emission factors between the reference supply and wind-based electrified heat. Neglecting losses, the wind energy sold equals the TES energy purchased, i.e., $E_{H,buy}^{T^B}=E_{w,sell}^{T^B}$.

The electricity-purchase cost, wheeling charge, and regulation cost are

$$C_{H,b}^{T^B}={\lambda }_w^t{E}_{H,buy}^{T^B}={\displaystyle \sum _{t=1}^{T^B}{\lambda }_w^t{P}_{H,buy}^t}$$

(12)

$$C_{H,t}^{T^B}={\lambda }_g{\displaystyle \sum _{t=1}^{T^B}{P}_{w,sell}^t}$$

(13)

$$C_{H,r}^{T^B}=a{(E_{H,buy}^{T^B})}^2+b{E}_{H,buy}^{T^B}+c$$

(14)

where ${\lambda }_g$ is the standard transmission–distribution (wheeling) tariff, and a, b, c are regulation coefficients.

The constraints comprise the following: (i) the TES enterprise’s ability to absorb curtailed wind energy, (ii) bounds on the end-use electricity price (the sum of the curtailed-wind on-grid price and the fixed wheeling charge), and (iii) upper–lower bounds on the TES level:

$$0\le P_{w,sell}^t\le P_{w,\max }^t$$

(15)

$${\lambda }_{L,\min }\le ({\lambda }_w^t+{\lambda }_g)\le {\lambda }_{L,\max }$$

(16)

$$Q_{H,\min }\le Q_{H,0}+{\omega }_H{\displaystyle \sum _{t=1}^{T^B}{P}_{H,buy}^t}\le Q_{H,\max }$$

(17)

where $P_{w,\max }^t=\min \left\{\left.P_{w,e},P_{L,\max }^t\right\}\right.$ is the maximum amount of curtailed wind available for sale at time t. $Q_{H,\min }$ and $Q_{H,\max }$ are the minimum and maximum heat-storage requirements, and $Q_{H,0}$ is the initial stored heat.

3.4.3. Solution of the Stackelberg Game Model

The Stackelberg game for bilateral bidding is specified by four elements—players, strategy sets, payoff functions, and the Stackelberg–Nash equilibrium—which are defined as follows:

(1)

Players:

$$C=\left\{\left.N_w,N_H\right\}\right.$$

(18)

where $N_H$ is the leader (TES enterprises) and $N_w$ is the follower (wind farms).

(2)

Strategy sets:

$$S=\left\{\left.{\lambda }_w^t,P_{w,sell}^t\right\}\right.$$

(19)

where the TES enterprises choose the quantity $P_{w,sell}^t$ (bid power for the bilateral trade), and the wind farms choose the price ${\lambda }_w^t$ in response to that quantity.

(3)

Payoff functions:

$$\begin{array}{l}I=\left\{\left.I_H,I_w\right\}\right.\\ \left\{\begin{array}{l}{I}_H=I_H({\lambda }_w^t,P_{w,sell}^t)\\ I_w=I_w({\lambda }_w^t,P_{w,sell}^t)\end{array}\right.\end{array}$$

(20)

with $I_H$ and $I_w$ defined in Section 3.4.2 and Section 3.4.1, respectively.

(4)

Stackelberg–Nash equilibrium:

The follower’s best response to a given quantity is

$$\left\{\begin{array}{l}{E_{w,sell}^{T^B}}^{*}=\underset{{\lambda }_{w(k)}^t}{\arg \max }{I}_{H(k)}^t({\lambda }_{w(k)}^t,P_{w,sell(k)}^t)\\ {{\lambda }_w^t}^{*}=\underset{E_{w,sell(k)}^{T^B}}{\arg \max }{I}_{w(k)}^t({\lambda }_{w(k)}^t,P_{w,sell(k)}^t)\end{array}\right.$$

(21)

The equilibrium pair $({\lambda }_{w(k)}^t,P_{w,sell(k)}^t)$ is obtained for each curtailed interval $t\in T^B$ via multi-round leader–follower negotiation over quantity and price, yielding the optimal price–quantity schedule and enabling mutually beneficial trade.

Compared with the KKT-based methods, the metaheuristic algorithm can operate directly on the proposed two-layer structure and avoid the numerical difficulties associated with complementary relaxation [28].

The above leader–follower model is solved with the Coati Optimization Algorithm (COA) as follows:

(1)

Initialization: Prepare basic data for the wind farms and the TES enterprises participating in the game, and set the COA parameters.

(2)

Candidate generation: For each curtailed interval $t\in T^B$, the TES enterprises use COA to generate a set of candidate absorption quantities $P_{w,sell(k)}^t$. For each candidate $P_{w,sell(k)}^t$, the wind farms compute the profit-maximizing price offer ${\lambda }_{w(k)}^t$ from their payoff function.

(3)

Fitness evaluation: Given ${\lambda }_{w(k)}^t$, the TES enterprises evaluate the profit (fitness) associated with each candidate $P_{w,sell(k)}^t$. The feasible traded quantity is

$$P_{w,sell(k)}^t=\min \left\{\left.E_{w,0}^{\max }{\displaystyle \frac{{\lambda }_{w(k)}^t-{\lambda }_{w0}}{{\lambda }_p^t-{\lambda }_{w0}}},P_{w,\max }^t\right\}\right.$$

(22)

where $E_{w,0}^{\max }$ is the maximum available curtailed energy.

(4)

COA update: Apply COA’s update mechanism to produce a new round of candidates $P_{w,sell(k)}^t$; repeat Steps (2)–(4) until the best price offer ${\lambda }_{w(k)}^t$ is obtained.

(5)

Payoff calculation: Substitute ${\lambda }_{w(k)}^t$ and $P_{w,sell(k)}^t$ into (2) and (9) to compute the wind farm’s and the TES enterprise’s profits, respectively.

(6)

Equilibrium check: Compare the current round’s profits with those of the previous round. If the changes for both parties remain below a preset threshold over several consecutive iterations, an approximate Stackelberg–Nash equilibrium is deemed reached. Otherwise, adjust the COA parameters and return to Step (2); if satisfied, proceed to Step (7).

(7)

Next interval: Set $T^B=T^B+1$ and repeat Steps (1)–(6) to obtain the equilibrium for the next trading interval.

(8)

Output: Return the final trading price and traded quantity for all curtailed intervals, yielding the optimal decision schedule.

4. Case Study

4.1. Simulation Setup

Simulations were conducted using a representative day dataset from a real-world power system, which comprised a wind farm and an independent TES enterprise. The curtailed wind power for the representative day is presented in Figure 5.

Figure 5 shows that wind curtailment is primarily concentrated during the overnight and early morning hours (approximately 23:00–06:00). The total curtailed energy amounts to 1665 MWh. To enhance wind energy accommodation during these periods, such incentives are necessary. Consequently, a bilateral Stackelberg trading scheme was employed to negotiate the transaction price and quantity, thereby facilitating curtailment relief. The TES unit has a rated electrical charging capacity of 150 MW, requires 800 MWh of energy to achieve full charge, and exhibits an electric-to-heat conversion efficiency of 90%. The remaining parameter Settings in the experiment are shown in

Table 1. Example parameter Settings.

Parameter (Unit)	Value	Parameter (Unit)	Value
${\lambda }_{w0}$/(CNY·MWh−1)	90	${\lambda }_{w0}$/(CNY·MWh−1)	150
${\lambda }_p^t$/(CNY·MWh−1)	308	a	0.1
${\lambda }_g$/(CNY·MWh−1)	119	b	10
${\lambda }_{wp}$/(CNY·MWh−1)	11	c	0.2
${\lambda }_{abd}$/(CNY·MWh−1)	15	$\Delta \mu$ (g CO2·MWh−1)	800
${\lambda }_{dev}$/(CNY·MWh−1)	90

below.

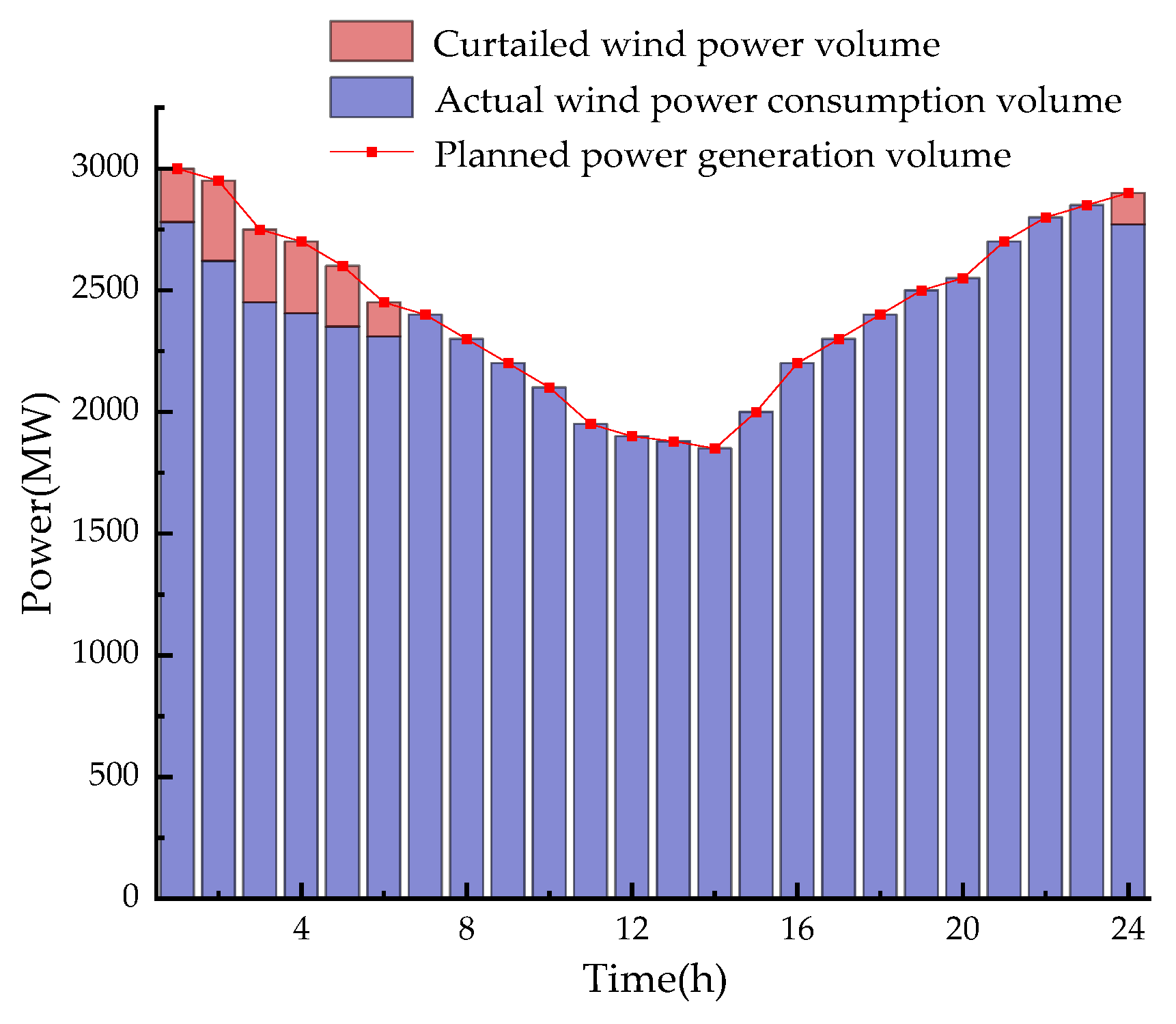
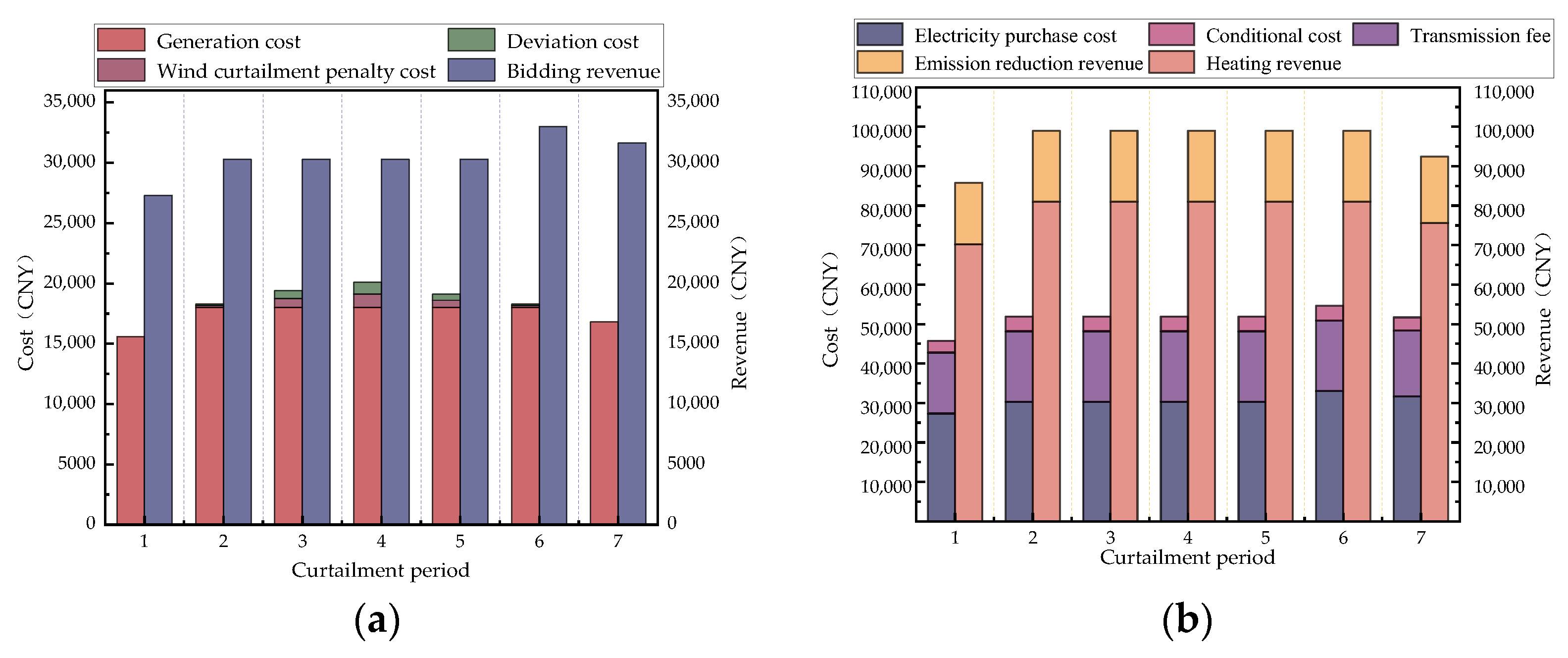
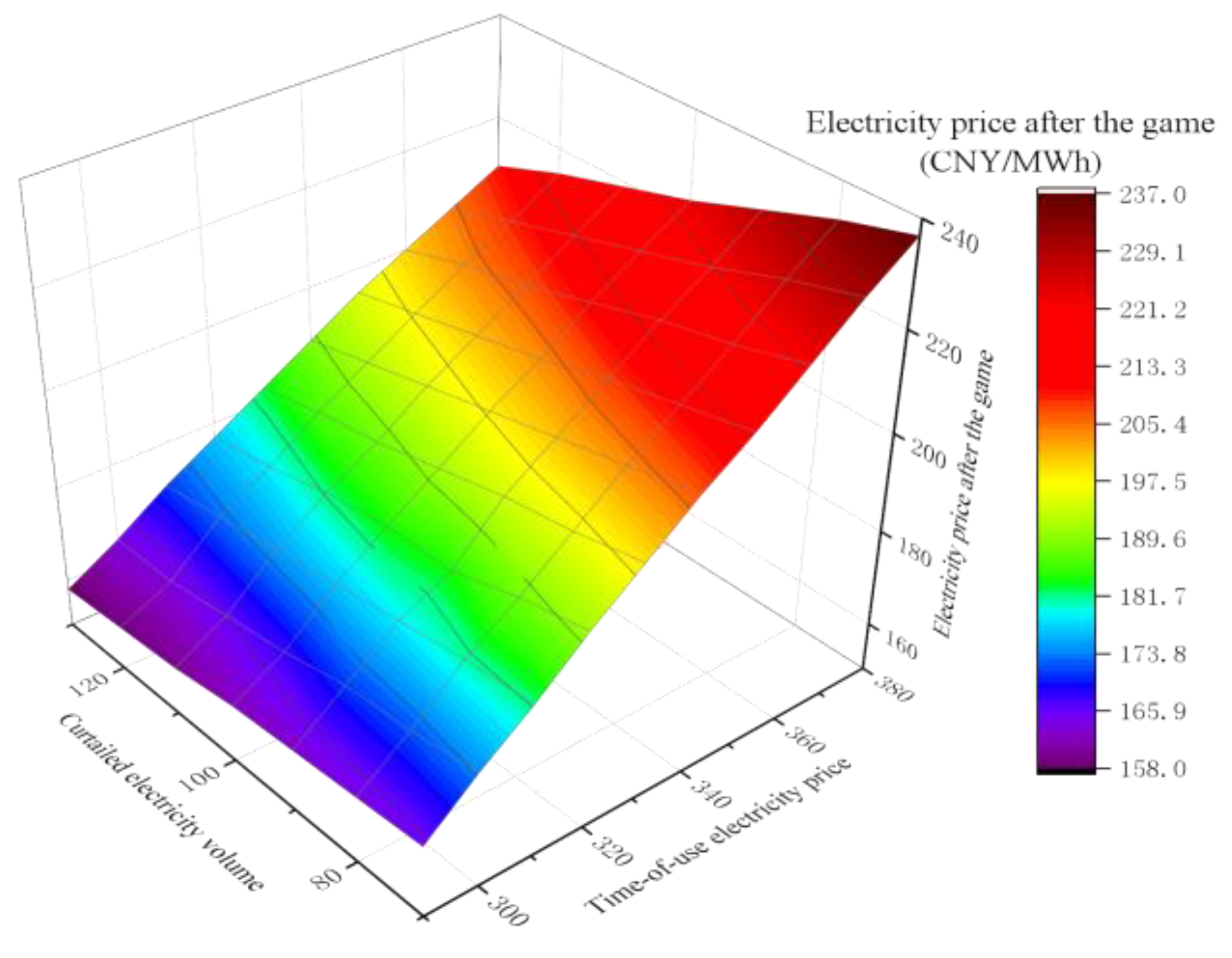
4.2. Simulation Results and Analysis

For the 04:00–05:00 trading interval, as an example, the game converged at iteration k = 14, at which point the payoffs of both parties stabilized, signifying a bilateral equilibrium. The results are presented in Figure 6.

The trading price and traded quantity yielded by the solution to the bilateral Stackelberg game are presented in Figure 7. As shown, during non-curtailment periods, electricity is acquired by the TES enterprise at the time-of-use (TOU) tariff, and peak-shaving services are not provided. During nighttime curtailment periods, negotiations were conducted between the parties through the Stackelberg game. The resulting game-clearing price was lower than the TOU tariff, thereby incentivizing the TES enterprise to proactively adjust its output and absorb the curtailed wind energy.

As illustrated in Figure 7a, if the TES enterprise does not participate in the bilateral Stackelberg game during curtailment periods and instead acquires electricity under the conventional TOU tariff, wind curtailment cannot be effectively accommodated, which results in elevated procurement costs for the TES enterprise. Such an outcome proves detrimental to production.

As illustrated in Figure 7b, a clear incentive is offered by the game-clearing price: thermal demand is increased in curtailment periods through the shifting of a portion of electricity consumption from non-curtailment periods to those intervals, thereby enabling greater absorption of curtailed wind. In terms of the net-load profile, this approach is equivalent to elevating the valley by 131.6 MW, thereby narrowing the peak–valley spread and enhancing the system’s down-regulation capability.

Based on these findings, the game decisions for all curtailment periods are presented in

Table 2. Game decision results during blocked periods.

Time Interval	Game-Clearing Price (CNY/MWh)	Curtailed Wind Power (MWh)	Traded Energy (MWh)	Incremental Revenue—Wind Farms (104 CNY)	Incremental Revenue—TES Enterprises (104 CNY)
23:00–0:00	210	130	130	2.925	1.924
0:00–1:00	202	160	150	3.242	2.310
1:00–2:00	202	200	150	3.189	2.310
2:00–3:00	202	225	150	3.158	2.310
3:00–4:00	202	190	150	3.203	2.310
4:00–5:00	220	160	150	3.512	4.440
5:00–6:00	226	140	140	3.374	4.074

.

During the curtailment period (23:00–06:00), the clearing outcomes were influenced by price fluctuations in the game and the TES capacity limitations. Consequently, lower transaction prices resulted in greater absorption of curtailed wind and a more pronounced improvement in down-regulation capability. The minimum clearing price was 202 CNY/MWh.

Integration of Table 2 and Figure 8 shows that, for the wind farms, generation costs are the dominant component of costs, while revenue gains arise from the additional accommodation of curtailed wind through bilateral trades, which markedly enhances sales. For the TES enterprise, electricity procurement and wheeling charges constitute the primary costs. On the revenue side, beyond heating income, the acquisition of renewable electricity for storage reduces purchases from the upstream grid, thereby indirectly reducing emissions and consequently enhancing carbon-reduction revenue. During the 05:00–06:00 interval, when the TOU tariff transitions from the nighttime valley to the flat period, the TES incremental revenue exceeds that observed in most bilateral periods. This occurs because, under the planned schedule, the cost of acquiring electricity from the upstream grid would have been substantially higher, whereas fulfilling the load via wind purchases reduced that expenditure and resulted in a larger incremental gain.

Using the first curtailment period (23:00) as an example, an examination was conducted on how changes in the TOU tariff and curtailed energy affect the game-clearing price (Figure 9). From the wind farms’ perspective, curtailed wind is regarded as available supply: a larger supply suppresses the price, whereas a smaller supply elevates it, consistent with supply–demand fundamentals. From the TES enterprise’s perspective, the valley tariff serves as the reference cost and guides the procurement decision. Figure 9 illustrates that price adjustments are influenced by supply–demand conditions and cost substitution: when curtailed energy decreases, the transaction price increases because a tighter supply strengthens the wind farms’ bargaining position; when the valley tariff rises, the transaction price also increases because the TES enterprise’s alternative cost is higher, and it is willing to pay more. These responses reflect the balance between market dynamics and bilateral negotiation, facilitate effective joint participation of wind and TES in peak shaving, and enhance the system’s down-regulation capability.

5. Conclusions

In this study, the electrical and thermal pathways of the TES enterprise were first clarified, and subsequently, a Stackelberg game-based bilateral trading decision method was developed that enables wind–TES joint participation in peak shaving from a prosumer perspective. The approach enhances the system’s down-regulation capability and provides mutually beneficial economic outcomes for both the load and generation sides. The main conclusions are as follows:

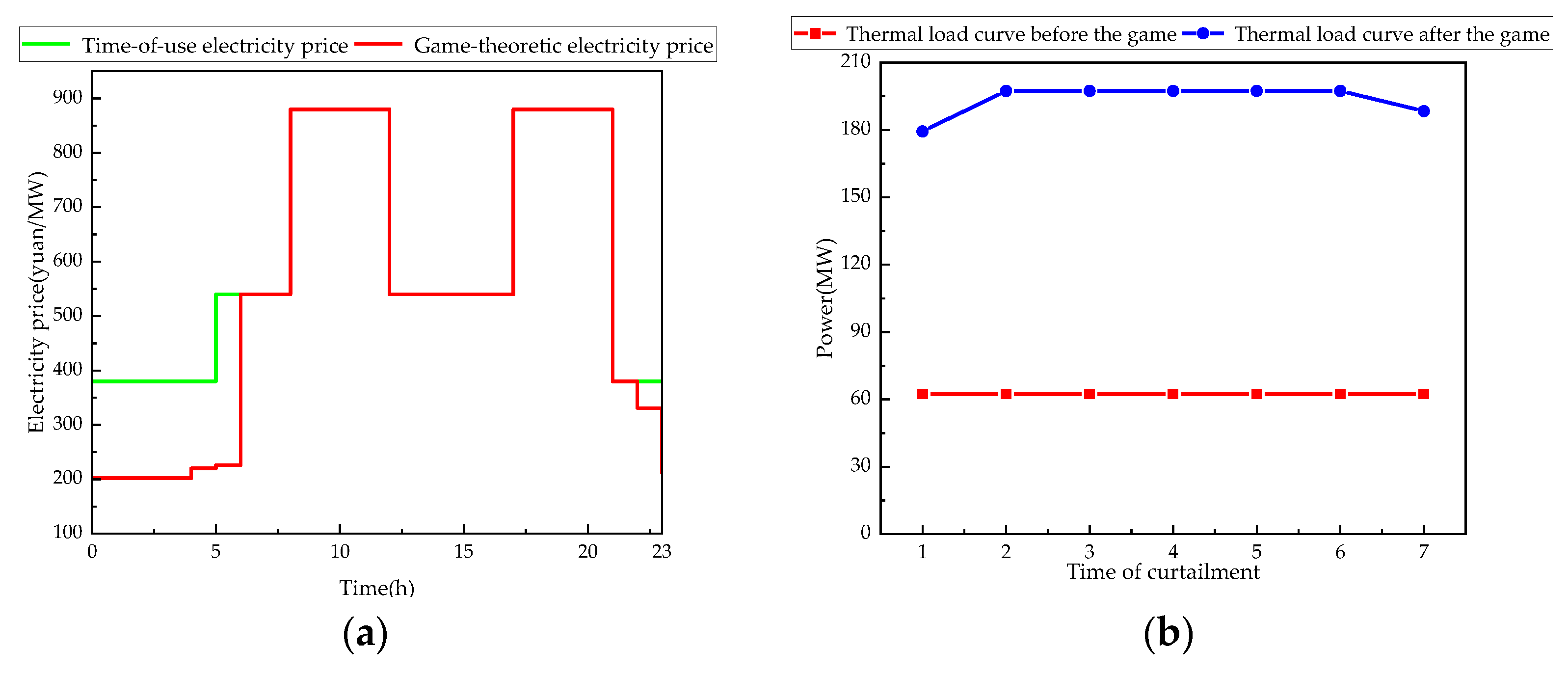
• In this study, the thermal and electrical pathways of TES were delineated, and a role classification was proposed based on the point of interconnection, voltage level, and installed capacity. From a prosumer perspective, independent TES enterprises coordinated with wind farms act as a flexible consumer. Furthermore, by reducing wind curtailment, the proposed model enhances the ability of independent TES enterprises to participate in peak shaving and increases the power load capacity by 131.6 MW during off-peak hours.
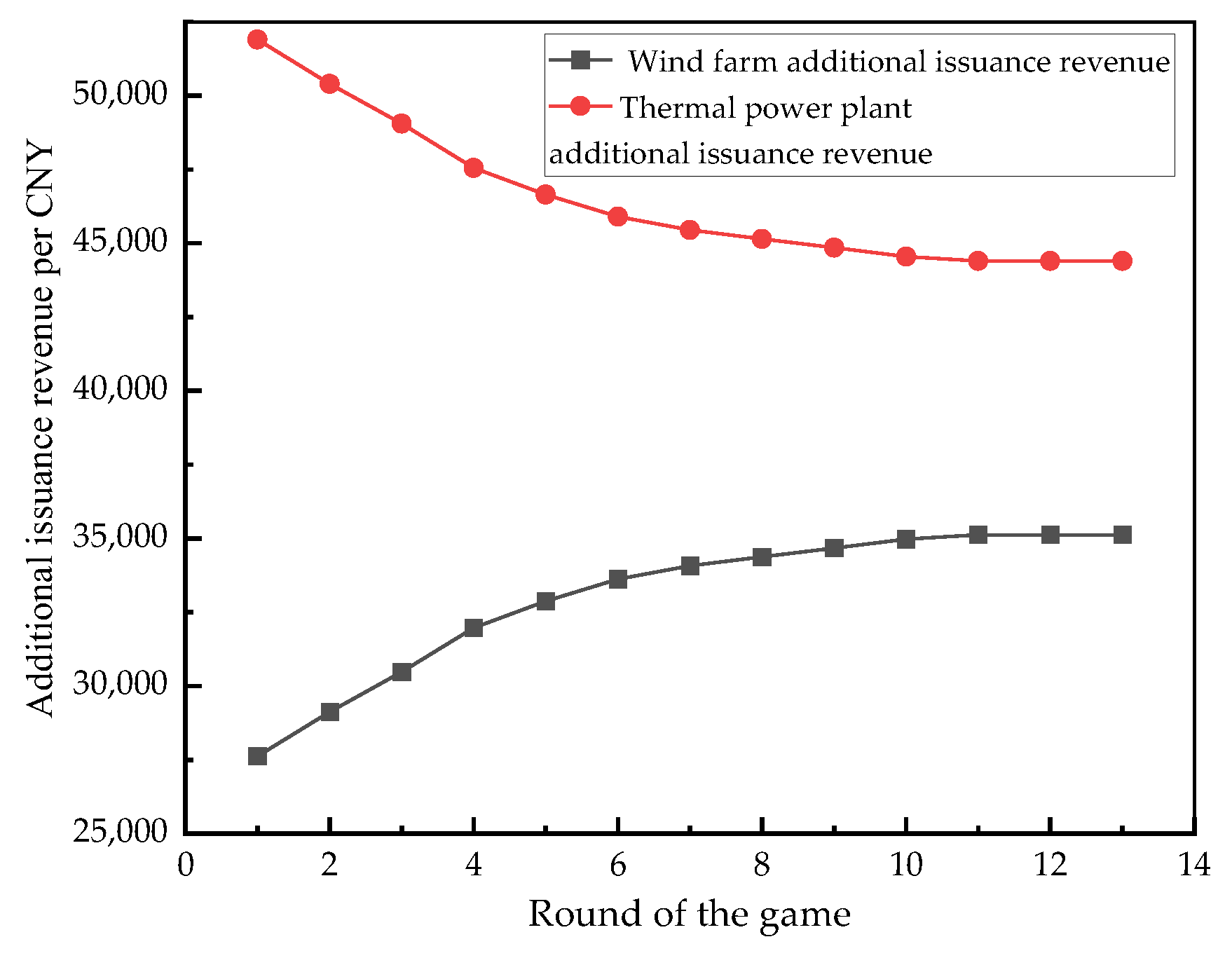
• A Stackelberg leader–follower framework with TES-quantity bids and wind-price offers was established, which mitigates ambiguity in benefit allocation across multiple stakeholders. By leveraging the TES enterprise’s load-shifting capability, the scheme enhances nighttime wind power absorption. Under typical daily conditions where obstructed wind power reaches 1665 MWh, the proposed method can achieve an additional absorption rate of 61.26% for obstructed wind power.
• A bilateral trading mechanism for peak shaving between the wind farms and the TES enterprise was proposed, which effectively promotes participation on both sides. These results indicate that the prosumer framework enhances wind–TES coordination, mitigates information asymmetry, significantly reduces the profit margin gap between TES and wind farms from an initial 24,275.4 to 9275.4 CNY, and leverages market signals to incentivize peak-shaving behaviors.

In summary, the proposed bilateral Stackelberg trading mechanism effectively incentivizes joint peak-shaving participation between wind farms and TES enterprises, enhances wind energy accommodation, and provides practical value for the dispatch and operation of power systems with high renewable penetration. Although the article explores the feasibility of a bilateral trading mechanism for independent TES to participate in wind power integration, in practice, limitations in TES conversion efficiency may significantly impact its economic benefits, thereby constraining the actual effectiveness of this mechanism, which will be considered in future work.