Quantum-Inspired Cross-Attention Alignment for Turkish Scientific Abstractive Summarization

Abstract

This paper presents a quantum-inspired cross-attention alignment approach for abstractive summarization. The motivation is that current neural summarizers often lose key content and produce summaries that are weakly grounded in the source, especially for long and information-dense scientific articles in low-resource languages. The method itself is model-agnostic and aims to strengthen token-level alignment without introducing additional trainable parameters or inference overhead, by exploiting a Born-rule-based similarity between encoder and decoder states. This general idea is instantiated and tested on the task of summarizing Turkish scientific articles in Mathematics Education, which provides a challenging low-resource test bed with long and dense source texts. Six different fine-tuning variants built upon the mBART-50 model are examined, including SFT, LoRA baselines, and two novel quantum-augmented decoders: the parameter-free SFT + QDA + QKernel and SFT + QDA + QBorn (Born-rule-inspired, learnable classical mapping). Models are trained with five random seeds and evaluated using beam search and sampling schemes. Statistical significance is assessed via bootstrap confidence intervals, Benjamini–Hochberg FDR correction, and Cliff’s δ effect size. Beam search consistently outperforms sampling across all architectures. Our best configuration, SFT + QDA + QKernel, achieves strong results (ROUGE-L: 0.2966, BERTScore-F1: 0.8890) and yields statistically significant, large-effect gains over all baselines. These findings indicate that the proposed parameter-free quantum kernel provides a practical way to improve abstraction quality and faithfulness, particularly in low-resource summarization settings.

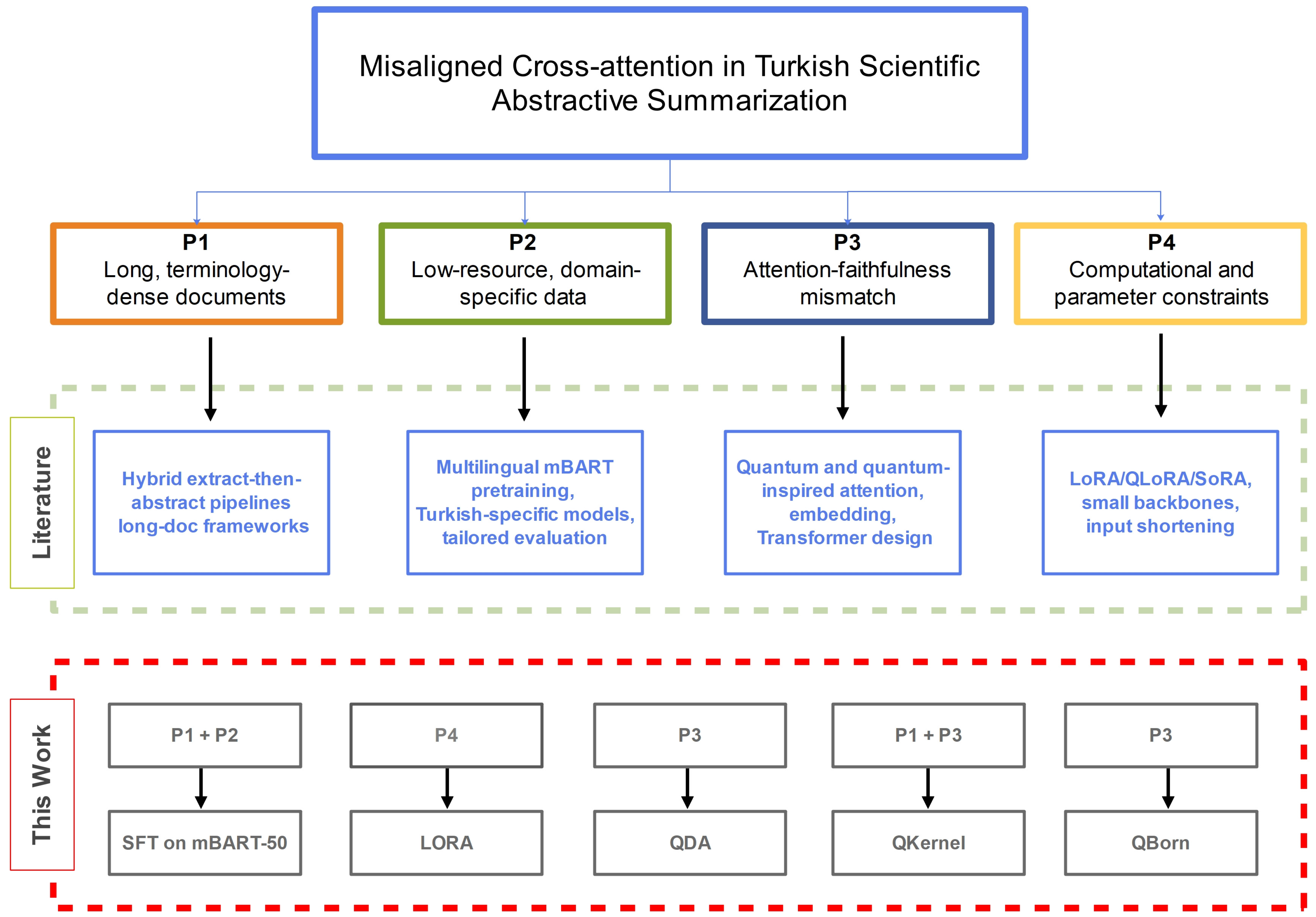
1. Introduction

Text summarization is formally defined as the process of producing a shorter yet informative representation of content derived from one or more sources by selecting their most important and relevant components [1]. The primary goal is to maximize information density while preserving semantic coherence and context as comprehensively as possible. In recent years, the exponential growth of digital text—across channels such as scientific publications, news streams, social media, and corporate reports—has rendered the manual creation of summaries economically and temporally unsustainable. This development, in turn, has cemented the role of automatic summarization as an essential intermediate step in modern workflows, including search, business analytics, and report generation [2,3,4].

Automatic approaches to summarization fall into two main categories: extractive methods, which select sentences based on pre-defined importance scores, and abstractive methods, which require the system to understand the source content and subsequently rephrase it in entirely new sentences [5,6,7]. Although abstractive techniques can yield outputs that are closer to human writing—often being more coherent and flexible—they are also inherently more prone to factual inaccuracies due to the complexities of natural language generation [8,9]. Initially, these challenges were partially mitigated by early systems that combined Recurrent Neural Networks (RNNs) and Long Short-Term Memory (LSTM) architectures with attention mechanisms within encoder–decoder frameworks [10]. However, the decisive breakthrough was achieved with the advent of the Transformer architecture. Transformer-based large language models—such as BERT, GPT, BART, and T5—leverage self-attention to capture long-range semantic dependencies more effectively, thereby establishing a new state-of-the-art for both extractive and abstractive summarization tasks [11,12,13].

Modern abstractive summarizers are often observed to yield source–output mismatches when the attention and inference mechanisms fail to sufficiently “lock onto” the most relevant source passages for each target unit. In the context of long and dense documents, attention weights may be spread over irrelevant regions rather than semantic cores. Furthermore, objectives that prioritize fluency may down-weight accuracy and faithfulness, and factors such as length bias, exposure bias, and domain shift can further exacerbate this mismatch [14,15,16,17]. Consequently, summaries can be grammatically well-formed yet may also be incomplete, weakly supported, or partially contradictory with respect to the source content. Existing work has attempted to mitigate these issues through several families of methods. Coverage and pointer mechanisms explicitly track which source tokens have been attended to, reducing omissions but still struggling with long-range discourse structure [18,19]. Faithfulness-oriented losses encourage the model to penalize hallucinated content, yet they often trade accuracy for fluency and can be sensitive to noisy automatic labels [20,21]. More recent approaches modify the attention architecture or sparsify attention weights, which improves focus on salient spans but typically requires non-trivial changes to the base model and may be tightly coupled to specific hardware or implementations [22,23].

A growing body of work has explored quantum-inspired ideas for natural language processing, encompassing quantum probability models, quantum kernels, and quantum circuit-based encoders. These approaches suggest that Hilbert-space embeddings and Born-rule-based similarity measures can capture richer relational structure than purely classical representations. However, this literature remains largely confined to short-text classification or toy sequence tasks in high-resource languages, and typically treats quantum-inspired components as standalone classifiers or similarity modules. Consequently, lightweight and hardware-agnostic distribution-alignment methods that directly regularize the attention/inference distribution in sequence-to-sequence models—especially for token-level alignment in long, low-resource scientific summarization—remain substantially underexplored [24,25,26,27].

Although much of this progress has been concentrated on resource-rich languages such as English, summarization for Turkish, an agglutinative and morphologically rich language, presents distinct challenges. The inherent structural complexity of Turkish and the relative scarcity of dedicated datasets have necessitated significant efforts in both resource creation and model adaptation. For example, a Turkish news summarization dataset was compiled by Ertam and Aydın [28] from multiple agencies, and Turkish headline generation was targeted by Karaca and Aydın [29] using encoder–decoder models. Furthermore, it has been demonstrated by Baykara and Güngör [30] that monolingual BERT models trained solely on Turkish generally outperform multilingual counterparts on large-scale datasets such as TR-News and MLSum. More recently, a 2000-document Turkish legal summarization dataset was introduced by Albayati and Fındık [31], who also proposed a hybrid approach. Collectively, these critical advances in the news and legal domains underscore the pressing need to adapt existing methods to the unique characteristics of long, term-dense academic texts.

Motivated by these limitations, the present work is focused on directly shaping the attention and inference distributions rather than altering the underlying architecture. The aim is to provide a lightweight, hardware-agnostic mechanism that can be attached to existing encoder–decoder models without the introduction of additional trainable parameters or inference overhead. To this end, a quantum-inspired view of attention is adopted: encoder and decoder states are treated as amplitude vectors in a Hilbert space, and a kernel derived from Born-rule probabilities is used to construct a target distribution that emphasizes evidence-bearing spans. During training, this target is used to softly guide the cross-attention and token-level inference distributions, while the base mBART-50 architecture is deliberately kept unchanged to preserve compatibility with standard toolchains and parameter-efficient variants such as LoRA.

The process of evaluating summary quality remains contentious. Given that ROUGE relies solely on lexical overlap, semantic correctness, coherence, and readability may not be fully reflected, especially in agglutinative languages such as Turkish [32,33]. Consequently, both ROUGE and BERTScore are reported in this work, complemented by several key diagnostics to obtain a comprehensive view of quality. Specifically, the degree of abstraction is quantified using Novel-n, Coverage, and Density metrics, while diversity is assessed using Distinct-n and Self-BLEU [34,35,36,37]. Furthermore, robust evaluation protocols are adopted, including reporting uncertainty across multiple seeds, applying Benjamini–Hochberg False Discovery Rate control (BH-FDR), and utilizing effect size measures such as Cliff’s δ [38,39,40,41,42,43]. Nevertheless, despite this established evaluation literature, lightweight and hardware-agnostic distribution-alignment methods that directly regularize the attention/inference distribution to improve faithfulness remain substantially underexplored, leaving seq2seq token-level alignment in long, low-resource scientific summarization largely open [44,45,46,47,48,49]. To address this gap, a lightweight, hardware-agnostic Quantum Distribution Alignment (QDA) framework is introduced for reducing source–output mismatch in Turkish academic texts.

The primary objective of this work is to strengthen token-level source–summary alignment in the Turkish scientific abstractive summarization by pulling mBART-50 cross-attention distributions toward more evidence-focused patterns via Born-rule-inspired similarity signals, without modifying the underlying architecture.

Four core contributions are made by this work: (i) Quantum-Inspired Distribution Alignment (QDA) is formulated as a lightweight, hardware-agnostic regularization scheme for sequence-to-sequence (seq2seq) models. This scheme is designed to softly nudge the attention/inference distribution toward a kernel-derived target without adding trainable parameters or altering the base architecture. (ii) QDA is instantiated with two complementary quantum-inspired designs, QKernel (parameter-free circuit) and QBorn (Born-rule-inspired, learnable classical mapping). Through this instantiation, the trade-off between zero-overhead alignment signals and learnable circuit capacity is clarified. (iii) To the best of our knowledge, the first systematic study of token-level alignment regularization for long, term-dense Turkish academic texts is offered, and practical pathways for improving faithfulness in low-resource settings without incurring inference overhead are highlighted. (iv) A comprehensive evaluation protocol—combining ROUGE, BERTScore, abstraction and diversity diagnostics, multi-seed uncertainty estimates, Benjamini–Hochberg False Discovery Rate control, and effect sizes—is provided and proposed as a template for future work on low-resource abstractive summarization.

The remainder of this paper is organized as follows. Section 2 reviews the background on abstractive summarization, Turkish-language resources, and quantum-inspired alignment methods. Section 3 describes the proposed approach in detail, including dataset construction, preprocessing, mBART-50-based model configurations (SFT, SFT + LoRA, SFT + LoRA + QDA, SFT + QDA, SFT + QDA + QKernel, SFT + QDA + QBorn), training settings, and the evaluation protocol. Section 4 presents the experimental setup and results, combining quantitative metrics with qualitative case studies on Turkish scientific articles. Section 5 discusses the main findings and limitations, and concludes with potential directions for future work.

2. Background

The rapid growth in text volume across fields such as news, scientific publications, legal documents, and clinical reports has rendered automatic summarization an unavoidable necessity, particularly for long and information-dense documents. Within this context, different trajectories have emerged for abstractive summarization. One line of research is composed of hybrid models that initially select important sentences or keywords before generating an abstractive summary. For instance, a two-stage extractive + pointer-generator architecture was employed by [50], while the Key-Information-Guided Neural (KIGN) model was guided by key information [51]. Similarly, extractive filtering followed by BART/T5-based or attention-mechanism-equipped abstractive models have been utilized for multi-document or news summarization by Ghadimi and Beigy [52] and Muniraj et al. [53].

Conversely, the methodological foundation for modern Transformer-based abstractive summarizers was established by [10] using a neural sequence-to-sequence (seq2seq) architecture with input-conditioned attention mechanisms. In a parallel development, it has been demonstrated by Liu et al. [54] that the multilingual pre-trained mBART architecture provides strong transfer capabilities for seq2seq tasks, such as translation and summarization, in low-resource languages like Turkish. Nevertheless, recent surveys emphasize that issues concerning factual consistency, hallucination, and scalability persist for long and domain-specific texts. Consequently, the need for new abstractive summarization approaches in both architectural design and training strategies is strongly highlighted [55,56,57,58].

The mBART-50 architecture, which is the multilingual variant of BART’s denoising autoencoder-based encoder–decoder Transformer, is adopted as the summarization model in this study. This architecture employs a 12-layer encoder–decoder framework with a shared subword (BPE) vocabulary. Through self-supervision of over 50 languages on large monolingual corpora, cross-lingual shared representations are learned via noise-to-denoise pretraining objectives, allowing for end-to-end fine-tuning for downstream seq2seq tasks like summarization and translation.

mBART-50 is positioned as an established backbone in multilingual seq2seq research, encompassing both generation and evaluation. In the GEM’24 Multilingual Summarization Report, two-stage pipelines utilizing mBART-50 or similarly sized T5-small models were reported to offer a balanced quality-to-cost profile in low-resource languages, and mBART-50 is recommended as a strong multilingual baseline [59]. Similarly, the mBART family’s use as a reference seq2seq backbone in the multilingual summarization evaluation ecosystem is demonstrated, with the multilingual version of BARTScore being built upon mBART-large-50 [60].

However, while monolingual BART-derived models trained solely on Turkish have been reported to outperform their multilingual counterparts in some tasks, this approach is emphasized as carrying high data and computational costs and thus is not considered practical for every scenario [61]. Conversely, the mBART family’s effectiveness has been demonstrated as a multilingual backbone that offers a strong starting point, is quickly adaptable with limited data and benefits from transfer learning in studies focusing on long, domain-specific texts (e.g., legal documents) in low-resource languages like Turkish [62]. Furthermore, mBART-50 has been reported to outperform Transformers trained from scratch on low-resource translation pairs, yielding notable BLEU gains upon fine-tuning [46].

Accordingly, the choice of mBART-50 is motivated by three primary factors: (i) Strong Cross-lingual Transfer: The pretraining across 50 languages enables robust transfer and zero/few-shot generalization in low-resource/multilingual conditions. (ii) Architectural Suitability: The encoder–decoder design is naturally suited for sequence-to-sequence generation tasks, which require encoding long contexts and producing fluent outputs. (iii) Empirical Efficiency: Empirical evidence supports the high efficiency attained by domain-adaptive fine-tuning from limited labeled data in scenarios such as legal summarization and low-resource translation [63,64].

Low-Rank Adaptation (LoRA) is defined as a parameter-efficient fine-tuning method that adapts large Transformer models via a low-rank update instead of full weight updates. The update to a weight matrix $\left(\Delta \mathrm{W}\in {\mathrm{R}}^{\mathrm{d}\times \mathrm{k}}\right)$ is factorized as $\Delta$W = BA with rank r. This permits training only 0.1–1% of the total parameters while achieving performance comparable to full fine-tuning [65]. The LoRA family has become the de facto standard fine-tuning approach for large models due to its low computational cost and ability to operate under hardware constraints. This popularity is driven by three main factors: (i) memory and computation are substantially reduced; (ii) the method enables lightweight, modular adapters for rapid domain adaptation; and (iii) in small-to-medium data regimes, the constrained search space can be leveraged to mitigate overfitting [66,67,68,69]. Given the requirement within this study to systematically compare multiple model variants in a low-resource language like Turkish and with a limited computational budget, the adoption of a LoRA-based, parameter-efficient fine-tuning approach is justified on both practical and methodological grounds. Accordingly, LoRA is used in our setting to achieve strong reproducibility and to reduce overfitting while preserving the favorable quality-to-cost trade-off.

The quantum-inspired literature provides a principled basis for the kernel-based and Born-rule-based components of the proposed QDA framework. Quantum kernels map inputs into a Hilbert space via quantum feature maps and were introduced to make high-dimensional inner products and complex similarity structures tractable [70,71]. Subsequent work has shown how task-adapted quantum kernels can be discovered automatically and how properties such as circuit depth, connectivity, and data distribution govern generalization [72,73]. In parallel, quantum circuit Born machines and their conditional variants demonstrate that quantum circuits can reproduce target distributions, generalize from limited data, and support condition-aware sampling [74,75]. Quantum-like NLG, quantum-inspired embedding/cross-attention, and quantum-enhanced Transformers indicate that Hilbert-space representations, entanglement, and interference can help capture long-range dependencies and alignment, albeit typically with extra parametric circuits and inference cost [76,77,78,79]. Modern derivations of the Born Rule further argue that amplitude-squared probabilities arise from the internal logic of superposition-based probability theories and measurement models rather than from an ad hoc physical postulate, reinforcing the mathematical soundness of Born-type distributions [80,81,82,83].

Transformer-based encoder–decoders are the dominant architecture for abstractive summarization, where cross-attention yields softmax-normalized weights often interpreted as a probability distribution over source positions. However, maximum-likelihood training and long-document dynamics do not guarantee faithfulness: attention mass can diffuse away from semantic cores, fluency-oriented losses may favor grammatically well-formed but weakly supported content, and factors such as exposure bias and domain shift can worsen misalignment. As a result, the learned attention distribution does not always reflect the true evidence structure, motivating additional supervision to steer attention and inference toward relevant source spans.

Building on these observations, the overall problem space in this study is decomposed into four interacting dimensions: P1 (long, terminology-dense documents), P2 (low-resource, domain-specific data), P3 (attention–faithfulness mismatch), and P4 (computational and parameter constraints). Prior work offers partial remedies for each: hybrid extract-then-abstract pipelines and long-document frameworks for P1, multilingual mBART pretraining and Turkish-specific models for P2, (quantum-inspired) attention and Transformer designs for P3, and LoRA-style parameter-efficient tuning for P4. Our approach, summarized in Figure 1, builds directly on this landscape: mBART-50 and SFT address P1–P2 and LoRA targets P4, while the proposed QDA, QKernel, and QBorn components are explicitly designed to improve cross-attention alignment (P3) on long Turkish scientific articles, under realistic low-resource and computational budgets.

3. Materials and Methods

In this section, the proposed approach built on mBART-50 is described in detail. The model family comprises six configurations: (i) SFT (Supervised Fine-Tuning); (ii) SFT + LoRA (Low-Rank Adaptation); (iii) SFT + QDA (Quantum Distribution Alignment); (iv) SFT + LoRA + QDA, and two quantum-inspired comparison variants; (v) SFT + QDA + QKernel (parameter-free) and (vi) SFT + QDA + QBorn (Born-rule-inspired, learnable classical mapping). To reveal the impact of the proposed Born-inspired alignment approach on model behaviour and its interaction with different fine-tuning regimes, the model variants are structured as a controlled ablation study. The SFT baseline represents full supervised fine-tuning of mBART-50 without any additional alignment mechanism and serves as the reference for all extensions. The SFT + QDA variant isolates the pure alignment effect of the proposed Quantum Distribution Alignment (QDA) regularizer on cross-attention, while keeping the underlying architecture and optimization protocol identical to SFT. In parallel, SFT + LoRA is included as a parameter-efficient baseline, motivated primarily by the need to reduce computational and memory cost, as commonly suggested in the literature. Building on this, SFT + LoRA + QDA is designed to test whether QDA-based alignment still improves the model when the backbone is adapted via low-rank updates rather than full fine-tuning.

On the quantum-inspired side, the SFT + QDA + QKernel and SFT + QDA + QBorn variants are constructed to examine whether an additional Hilbert-space similarity structure (parameter-free QKernel) or a Born-rule-inspired, learnable classical mapping (QBorn) can further refine cross-attention alignment beyond classical QDA. These quantum variants are defined on top of the full SFT backbone rather than LoRA, because preliminary experiments on Turkish summarization showed that SFT + LoRA and SFT + LoRA + QDA underperform SFT + QDA and SFT + QDA + QKernel; combining QKernel/QBorn with LoRA could therefore risk confounding the alignment effects with limitations arising from a weaker backbone. Overall, this design enables the alignment-focused contributions of SFT, LoRA, QDA, QKernel, and QBorn to be disentangled in a controlled and interpretable way.

These six models are trained under a common experimental protocol and are systematically compared in terms of summarization quality, diversity, and abstraction. For all configurations, performance is reported together with statistical significance procedures, including bootstrap confidence intervals, Benjamini–Hochberg False Discovery Rate (FDR) control, and Cliff’s δ effect sizes.

3.1. Dataset Construction

3.1.1. Corpus Compilation and Preprocessing

The corpus was compiled from articles published after 2014 in Turkish mathematics education journals indexed in ESCI, SCI-EXPANDED, and TR. Initially, 765 articles were downloaded. All articles were publicly available and accessed in compliance with the publishers’/indexes’ terms. Processing was limited to text for research; no redistribution of PDFs or supplementary materials was performed. After duplicates and full English texts were removed, 642 records remained. Compliance with the “Abstract-Introduction–Method–Findings–Conclusion” schema was taken as the primary criterion for classification as a research article. The separation into “research” versus “other” was performed independently by five experts with domain experience. The reliability of this coding was confirmed by finding Fleiss’s κ, Gwet’s AC1, and Krippendorff’s α coefficients within the substantial agreement band. Following this process, 430 research articles were selected. Only the text content of the selected articles was processed. Sections were separated using standard in-line tags (Abstract–Introduction–Method–Findings–Conclusion), and the Turkish abstract section was used as the gold standard target output while being entirely removed from the source side to prevent data leakage.

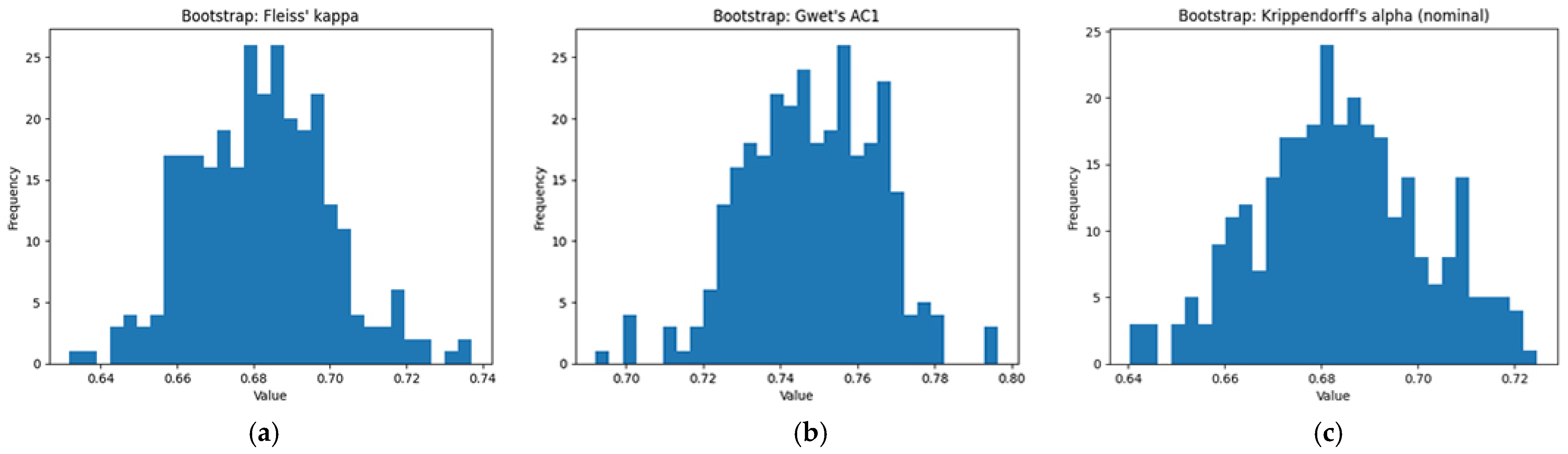
3.1.2. Reliability Metrics and Rationale

Fleiss’s κ coefficient is the classic measure of inter-rater agreement, balancing the observed agreement against the agreement expected by chance [84]. Gwet’s AC1 coefficient is recommended as a more stable alternative that mitigates the “prevalence bias” to which κ is susceptible, especially when some categories are very common or very rare [85,86]. Krippendorff’s α coefficient is used as a measure of reliability generalizable to different scale types (nominal, ordinal, etc.) that naturally handles missing votes and variability in the number of raters [87]. In the interpretation of all coefficients in this study, the commonly used intervals defined by Landis and Koch [88] were adopted: 0.00–0.20 is considered “slight,” 0.21–0.40 “fair,” 0.41–0.60 “moderate,” 0.61–0.80 “substantial,” and 0.81–1.00 “almost perfect” agreement. The κ, AC1, and α values obtained were all located within the substantial band (κ = 0,682 (95% CI: 0.648–0.718), AC1 = 0.749 (95% CI: 0.713–0.779) and α = 0.682 (95% CI: 0.651–0.717)), and their narrow, unimodal distributions estimated by bootstrap are shown in Figure 2. The rationale for selecting only research articles that strictly conform to the “Introduction-Method-Findings-Discussion-Conclusion” schema is based on ensuring that the abstracts are structurally uniform and comparable, derived from empirical findings. This process is intended to prevent the summarization model from being challenged by unnecessary genre noise and differing discourse objectives seen in types such as review articles, method notes, or case reports.

3.2. Text Preprocessing and Structuring

The preprocessing pipeline was designed to be sensitive to Turkish language specificities and was executed using PyMuPDF for PDF text extraction in Python 3, augmented by regex-based rule sets. Noise originating from PDF sources-such as page numbers, headers/footers, footnotes, bibliography titles, and reference lists-was cleaned using regular expressions. Texts were passed through Unicode normalization to ensure the lossless preservation of Turkish-specific characters (İ, ı, ğ, ş, ç, ö, ü). Typographical variations (e.g., in quotation marks, hyphens, ellipses, spacing) were converted to standard characters to ensure consistent tokenization, and all letters were converted to lowercase form. Furthermore, blocks of keywords, links, email addresses, DOI numbers, journal names, volume/issue/page information, publication years, and captions/cross-references related to figures, tables, and graphs were also removed from the text. English abstracts and keywords present in some journals were entirely removed from the source text to ensure that the model focuses exclusively on Turkish content.

Subsequently, documents were structurally segmented by means of regular expression-based matching of section headers and were marked under a standard schema using inline tags: <ozet|abstract> … </ozet|abstract> > <giris|introduction> … </giris|/introduction> <yontem|method> … </yontem|/method> <bulgular|findings> … </bulgular|/findings> <sonuc|conclusion> … </sonuc|/conclusion>. The Turkish abstract section was utilized as the gold-standard target output (author summary) in the modelling process and was completely removed from the source side to prevent data leakage. Turkish sentence boundaries were then determined, punctuation and spacing usage were standardized, and the official SentencePiece subword tokenizer was applied for compatibility with mBART-50. Source and target sequences were clipped (truncated) if they exceeded the predefined maximum length limits. Situations that could disrupt structural consistency (e.g., empty or unusually short/long sections, missing tags) were detected through semi-automatic checks, and records that could not be remedied were excluded from the dataset. The final data splits were created once using a single random split seed, and the same training/validation/test partitions were used across all experiments; thus, the model was trained to generate the corresponding author abstract from source texts enriched with section tags and purified of data leakage.

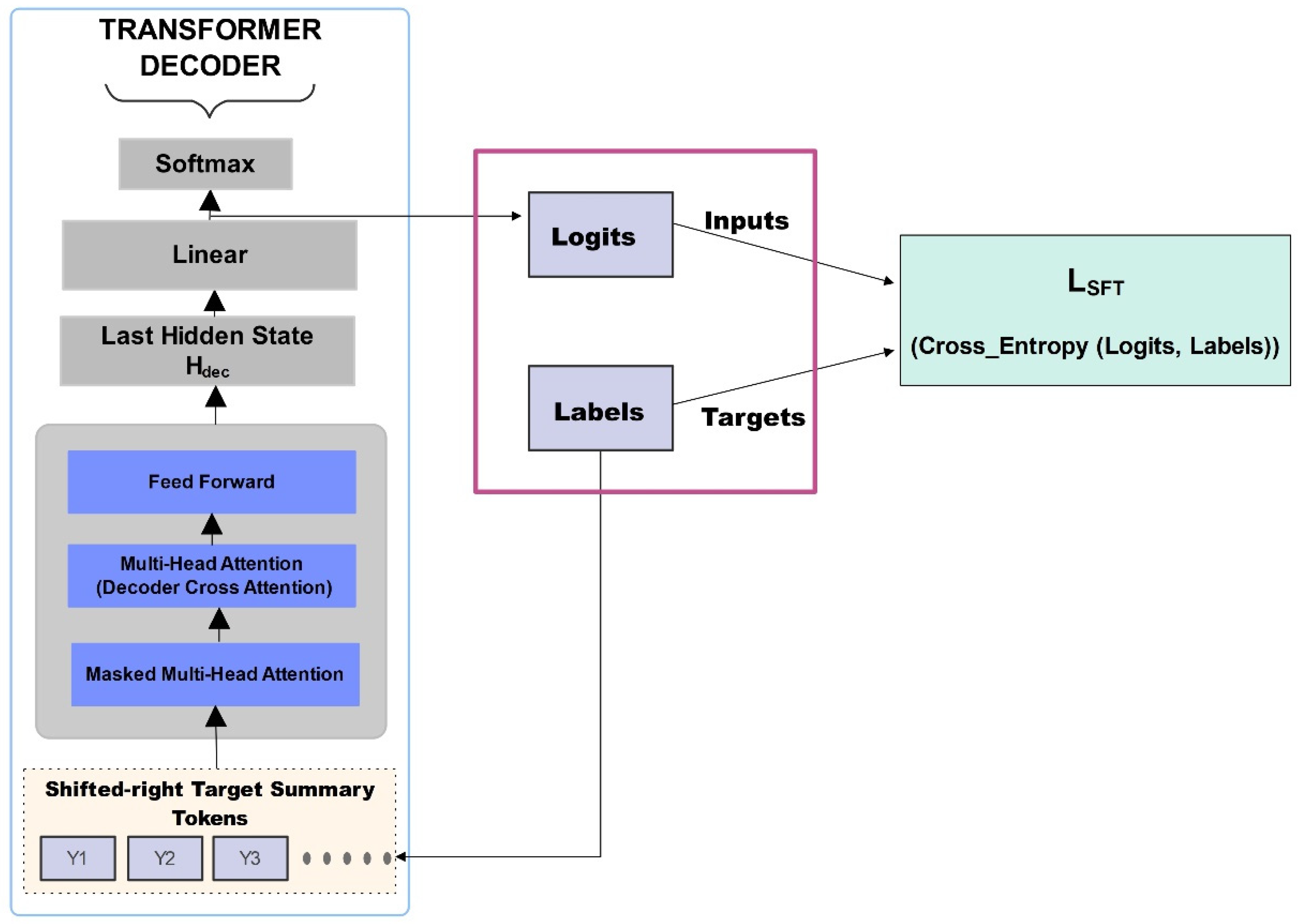
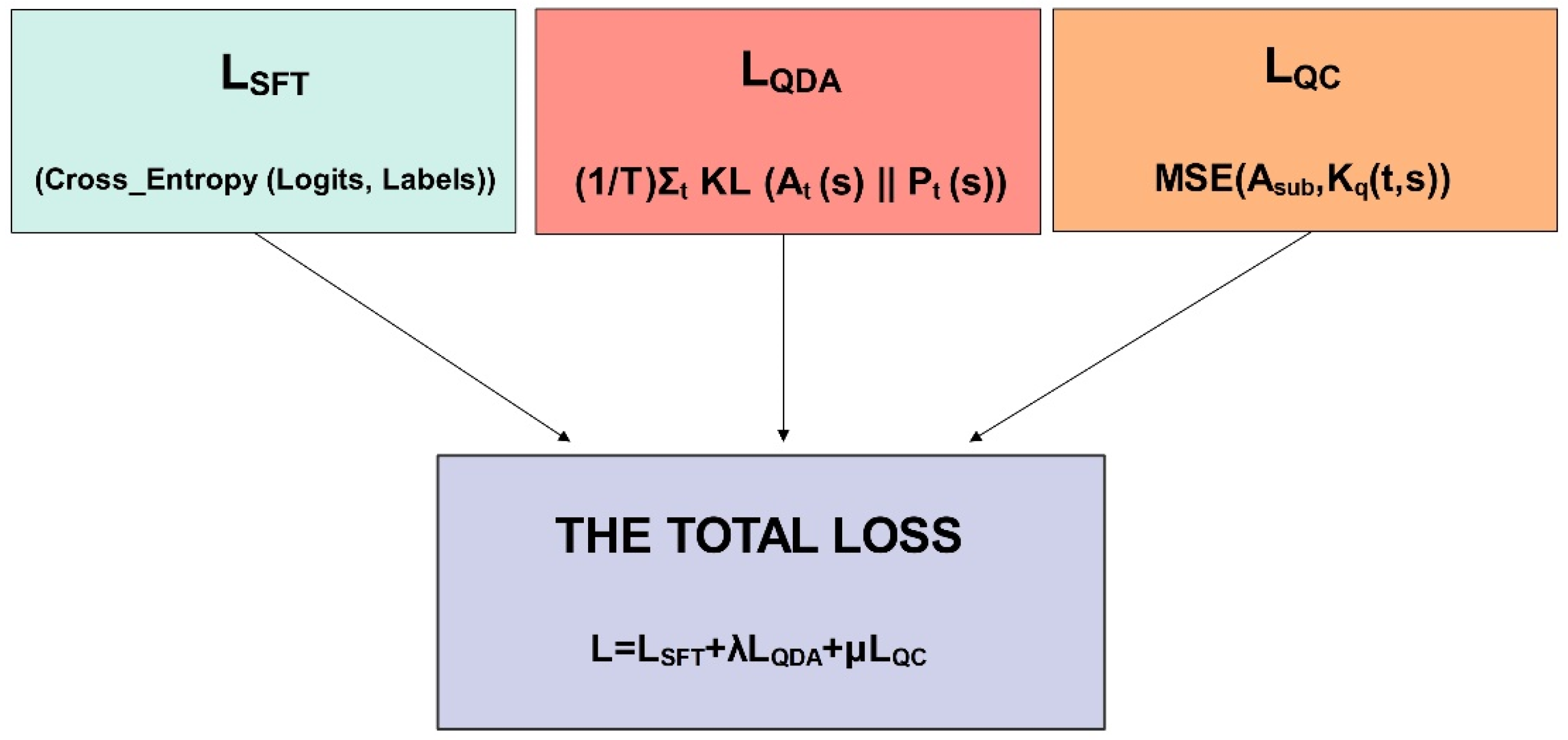
3.3. Base Model (SFT) and Parameter-Efficient Fine-Tuning (LORA)

In supervised fine-tuning (SFT), the pre-trained mBART-50 encoder–decoder model is adapted to the Turkish summarization task by maximizing the conditional likelihood p_θ(y|x) of target summaries given source documents [89,90]. Specifically, we minimize the standard sequence-level cross-entropy loss

$$\mathcal{L}\mathrm{sft}\left(\mathrm{\theta }\right)=-\sum _{\mathrm{i}=1}^{\mathrm{N}}\sum _{\mathrm{t}=1}^{\mathrm{T}}\log {\mathrm{p}}_{\mathrm{\theta }}\left({\mathrm{y}}_{\mathrm{i},\mathrm{t}}∣{\mathrm{y}}_{\mathrm{i}<\mathrm{t}},\hspace{0.17em}{\mathrm{x}}_{\mathrm{i}}\right)$$

(1)

where θ denotes model parameters, N the minibatch size, T_i the length of the i-th target sequence, y_i,t the gold token at time step t, and y_i<t the preceding gold tokens. Training is performed with teacher forcing [91], i.e., the right-shifted target sequence is fed to the decoder as input and the model is asked to predict the next token at each step. To handle variable-length sequences, target texts are padded to a fixed length using a special PAD token, and PAD positions are masked in the loss via the ignore_index = −100 setting so that they do not contribute to the optimization. We further apply label smoothing with a smoothing factor of 0.03 [92,93], which replaces the one-hot target distribution with a softened version to improve generalization and reduce overconfidence. The cross-entropy loss implementation (with label smoothing and ignore_index) already combines log-softmax and the loss computation for numerical stability and efficiency, so the output scores (logits) do not need to be passed through an additional softmax during training; softmax is only applied at inference time to obtain normalized probabilities for decoding (greedy, beam search, or sampling). Early stopping on the validation loss is employed to prevent overfitting [94]. This SFT configuration serves as the full fine-tuning baseline for all subsequent variants. The overall SFT pipeline-including teacher forcing, padding with masked cross-entropy, label smoothing (0.03), and early stopping-is summarized in Figure 3.

Building on this full fine-tuning baseline, we next consider a parameter-efficient variant based on Low-Rank Adaptation (LoRA). LoRA is adopted as a parameter-efficient fine-tuning strategy on top of mBART-50. In the SFT + LoRA configuration, all original mBART-50 weights are frozen, and trainable low-rank adapters are injected into the projection matrices of the multi-head attention modules (W_q, W_k, W_v, W_o) and the feed-forward layers (fc1, fc2). Each adapter factorizes the update ΔW ∈ R^d×k as ΔW = BA with rank r ≪ min(d, k) [65], where d and k denote the input and output dimensions of the weight matrix, respectivel; B ∈ R^d×r and A ∈ R^r×k are the trainable low-rank matrices; and r is a small rank hyperparameter controlling the capacity and parameter count of the adapter. In our experiments, we set the LoRA rank to r = 32, the scaling factor to α = 64 (α/r = 2), and the LoRA dropout rate to 0.10, following common practice in the literature and preliminary tuning under our computational constraints. This setup allows only a small fraction of the total parameters to be trained, while providing a fair and transparent comparison between the full SFT baseline and its parameter-efficient counterparts [65,67].

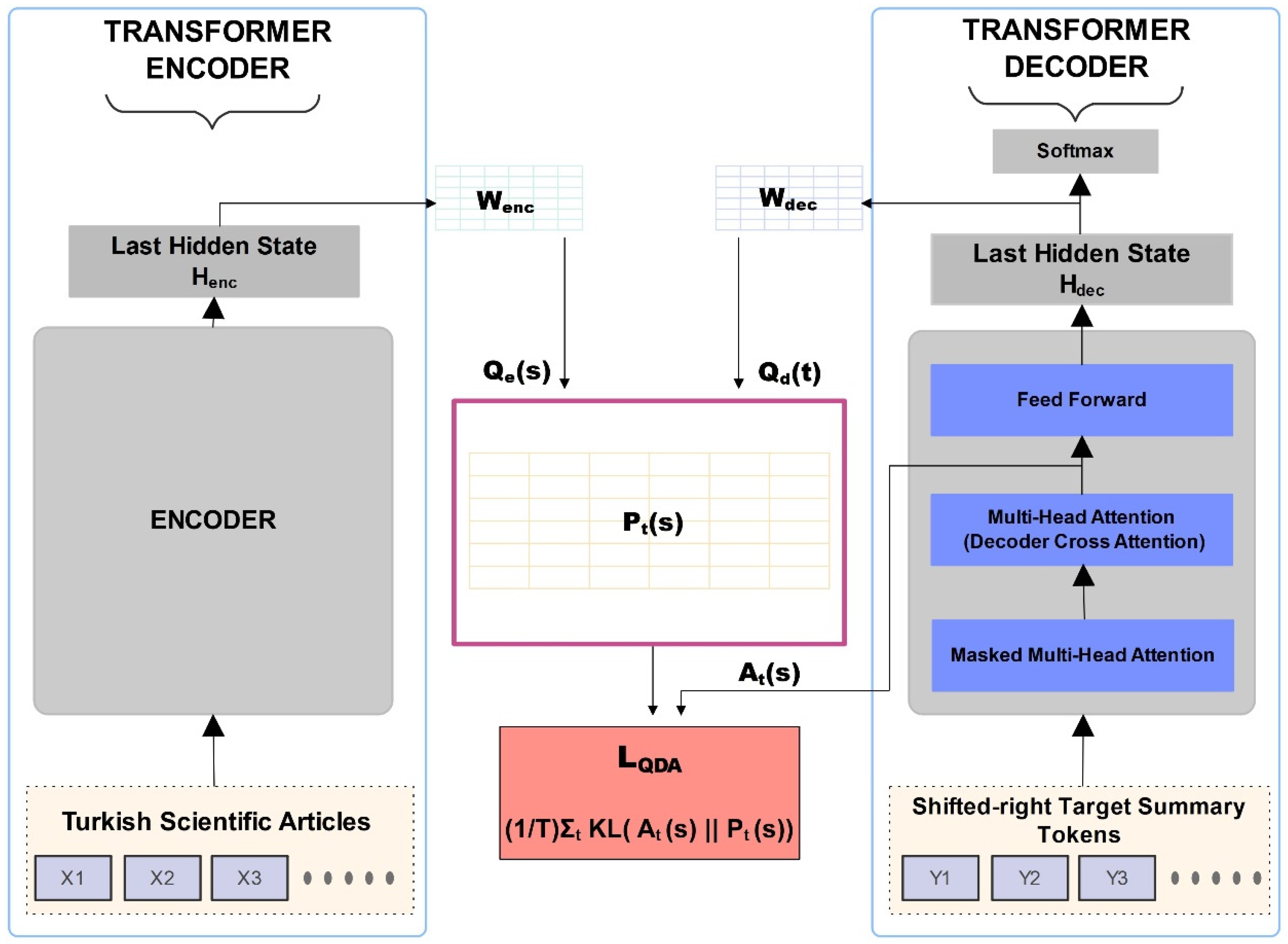
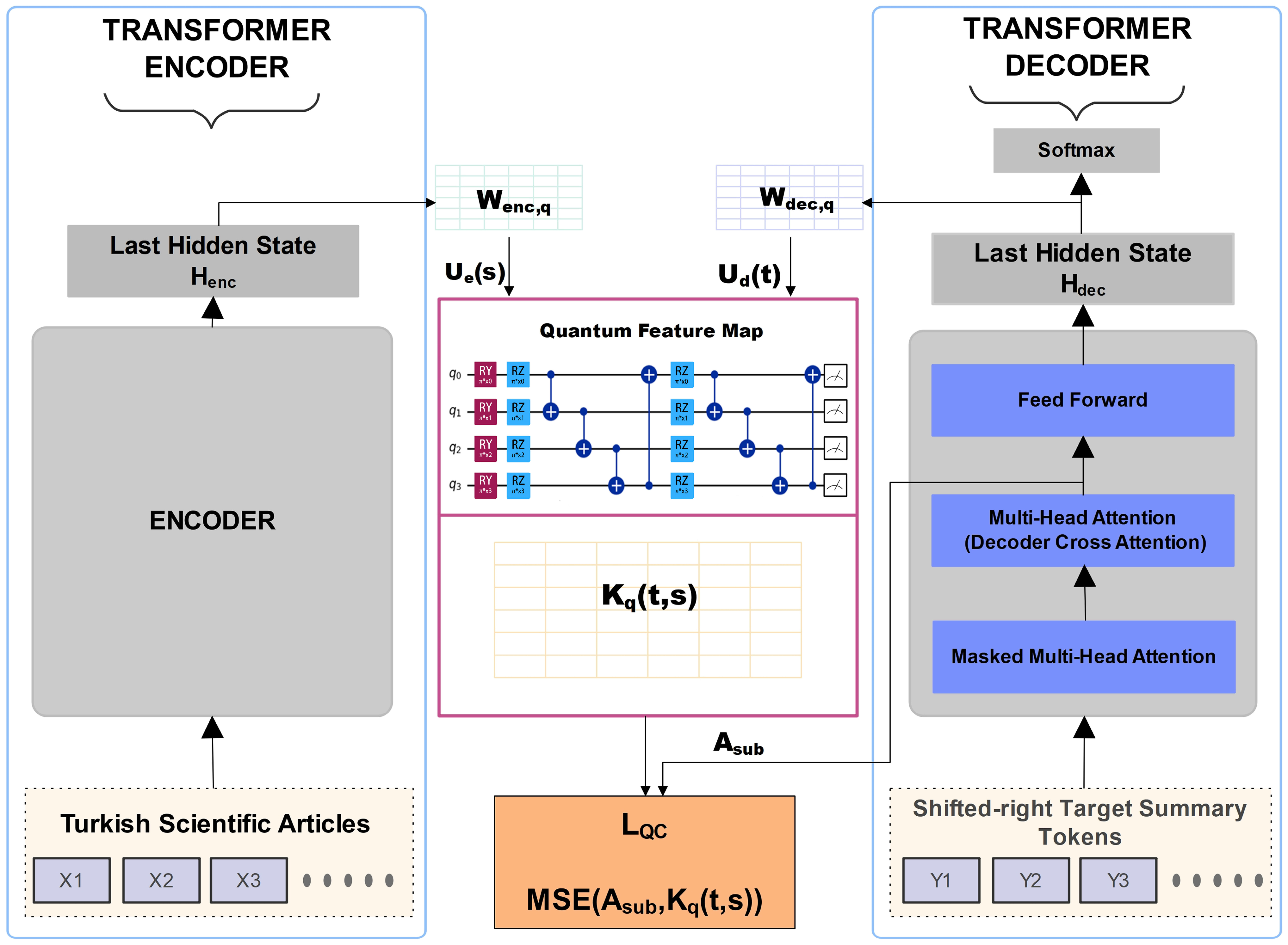
3.4. QDA (Quantum Distribution Alignment)

To directly regularize attention and inference without modifying the underlying architecture, a Quantum Distribution Alignment (QDA) term is introduced on top of mBART-50 (with or without LoRA). The idea is to softly steer the cross-attention distribution toward a kernel-based, Born-rule-inspired target that emphasizes evidence-bearing source spans.

For a decoder time step t, the standard cross-attention distribution over source positions s is given by [95]

$${\mathrm{A}}_{\mathrm{t}}\left(\mathrm{s}\right)={\mathrm{softmax}}_{\mathrm{s}}\left( {\displaystyle \frac{{\mathrm{q}}_{\mathrm{t}}^{\mathrm{\top }}{\mathrm{k}}_{\mathrm{s}}}{\sqrt{\mathrm{d}}}}\right),\hspace{1em}{\mathrm{q}}_{\mathrm{t}}={\mathrm{W}}_{\mathrm{q}} {\mathrm{h}}_{\mathrm{t}}^{\mathrm{dec}},\hspace{1em}{\mathrm{k}}_{\mathrm{s}}={\mathrm{W}}_{\mathrm{k}} {\mathrm{h}}_{\mathrm{s}}^{\mathrm{enc}}$$

(2)

where q_t is the query vector for decoder token t, k_s is the key vector for source token s, and d is the attention key dimension.

To construct a QDA target distribution, the encoder and decoder hidden states are first projected into a shared feature space and L2-normalized:

$${\mathrm{Q}}_{\mathrm{e}}\left(\mathrm{s}\right)=\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\left({\mathrm{W}}_{\mathrm{e}\mathrm{n}\mathrm{c}}{\mathrm{h}}_{\mathrm{s}}^{\mathrm{enc}}\right), {\mathrm{Q}}_{\mathrm{d}}\left(\mathrm{t}\right)=\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\left({\mathrm{W}}_{\mathrm{d}\mathrm{e}\mathrm{c}}{\mathrm{h}}_{\mathrm{t}}^{\mathrm{dec}}\right),$$

(3)

where ${\mathrm{h}}_{\mathrm{t}}^{\mathrm{dec}}, {\mathrm{h}}_{\mathrm{s}}^{\mathrm{enc}}\in {\mathrm{R}}^{\mathrm{d}}$ denote the encoder and decoder hidden states, respectively, W_q, W_k ∈ R^d×d are learned projection matrices, and norm (⋅) applies L2 normalization. A Born-rule-inspired similarity is then defined as.

$${\mathcal{l}}_{\mathrm{t},\mathrm{s}}=({{{{\mathrm{Q}}_{\mathrm{d}}\left(\mathrm{t}\right)}^{\mathrm{T}}\mathrm{Q}}_{\mathrm{e}}\left(\mathrm{s}\right))}^2\ge 0$$

(4)

and converted into a probability distribution by a temperature-controlled softmax:

P_t = softmaxs(βℓ_t,s)

(5)

where β > 0 is a temperature hyperparameter controlling the sharpness of the target distribution. The QDA loss is formulated as the Kullback–Leibler (KL)divergence between the target $A_t$ and the model attention P_t:

$${\mathcal{L}}_{\mathrm{QDA}}={\displaystyle \frac{1}{\mathrm{T}}}\sum _{\mathrm{t}=1}^{\mathrm{T}}\mathrm{KL}\left({\mathrm{A}}_{\mathrm{t}} \left|\right| {\mathrm{P}}_{\mathrm{t}}\right)$$

(6)

The overall training objective is given by

$$\mathcal{L}={\mathcal{L}}_{\mathrm{T}\mathrm{a}\mathrm{s}\mathrm{k}}+\mathrm{\lambda }{\mathcal{L}}_{\mathrm{QDA}},\hspace{1em}\mathrm{\lambda }>0.$$

(7)

This formulation allows attention/inference patterns to be nudged toward kernel-based similarity structures without changing the base mBART-50 architecture or incurring inference-time overhead.

Importantly, the underlying mBART-50 encoder–decoder architecture was deliberately kept unchanged for all QDA variants. QDA is implemented purely as a loss-level regularization term on top of the existing cross-attention and hidden states, without inserting additional layers or modifying the forward computation graph. This design choice serves three purposes: (i) it isolates the effect of distribution-level alignment from architectural changes, enabling fair comparisons against SFT and SFT + LoRA baselines; (ii) it preserves full compatibility with off-the-shelf mBART-50 checkpoints and parameter-efficient adapters such as LoRA/QLoRA, making the approach hardware-agnostic and easily reusable; and (iii) it avoids any inference-time overhead, since only the training objective is augmented while the deployed model remains architecturally identical to the base mBART-50 summarizer.

In our Turkish summarization setup (Figure 4), QDA is applied to the cross-attention distributions of the top decoder layer. This alignment is performed while attending to all encoder tokens derived from the: <ozet|abstract> … </ozet|abstract> > <giris|introduction> … </giris|/introduction> <yontem|method> … </yontem|/method> <bulgular|findings> … </bulgular|/findings> <sonuc|conclusion> … </sonuc|/conclusion> of the source document. This design explicitly targets long, term-dense academic documents, where evidence-bearing spans are often distributed across multiple sections. The projection matrices W_enc and W_dec are implemented as shallow linear layers with dimensionality d′ (d′ < d), so that the QDA module remains lightweight relative to the base mBART-50 model. The temperature β and the regularization weight λ are selected on the validation set of the Turkish mathematics education corpus by grid search, balancing gains in ROUGE-L and BERTScore against potential degradation in fluency; in practice, we keep λ small so that QDA acts as a gentle alignment prior rather than dominating the task loss. QDA is only active during training, and no additional computation is incurred at inference time.

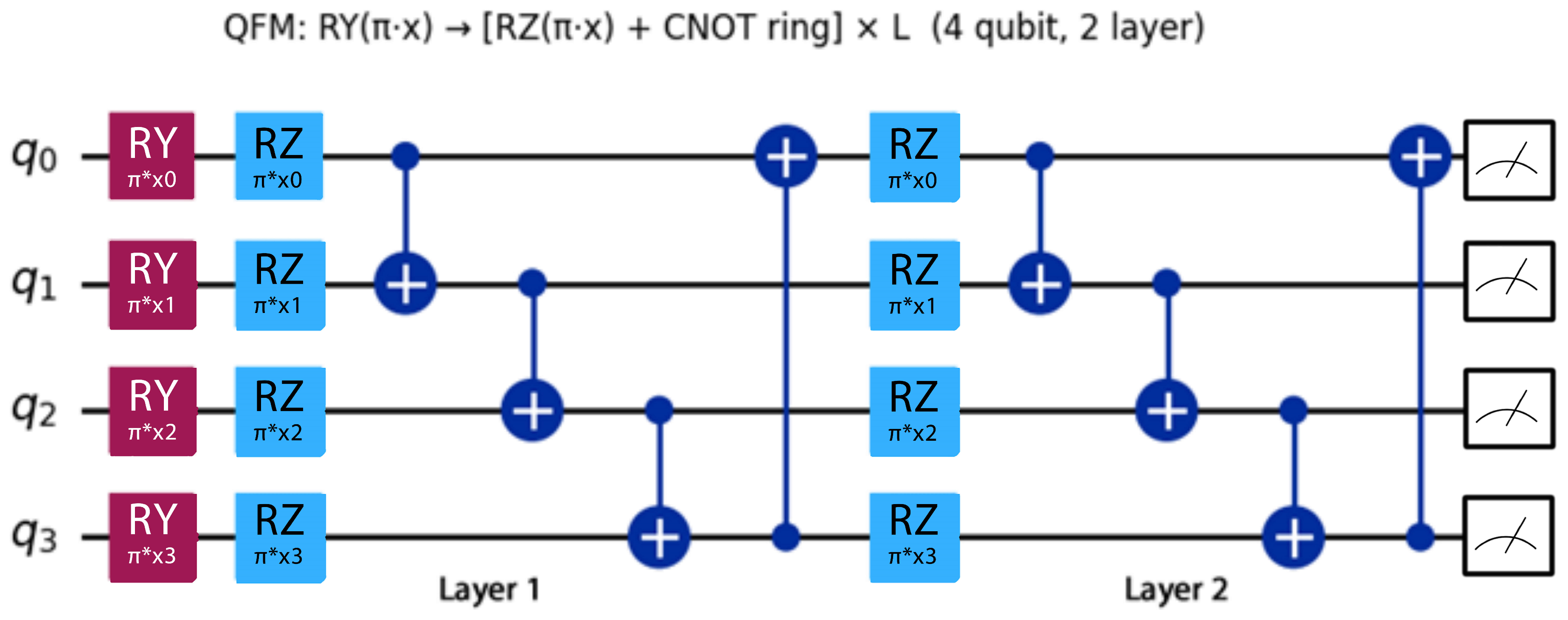
3.5. QKernel and QBorn Instantiations

In this work, the quantum-related components are not trained as full variational quantum circuits. Instead, the QKernel feature map is kept parameter-free, and only the surrounding classical projection layers are optimized; the QBorn branch, in turn, adopts a Born-rule-inspired classical mapping rather than a parametrized quantum circuit. This training strategy is motivated by three considerations. First, in long-sequence seq2seq summarization, back-propagating through deep or highly expressive quantum circuits would risk unstable gradients and substantial slow-downs, whereas using a fixed circuit as a kernel allows QDA to be integrated as a smooth regularizer on top of a well-behaved SFT baseline. Second, keeping the QKernel circuit parameter-free and detaching gradients at the q-node output yields a clean separation between linguistic learning and alignment regularization, ensuring that improvements over SFT/SFT + LoRA can be attributed to distribution alignment rather than to hidden quantum capacity. Third, GPU-based simulation of variational circuits at the Turkish scientific article scale would incur prohibitive computational cost, while the primary goal in this study is to assess the usefulness of quantum-inspired alignment signals under realistic low-resource constraints, not to optimize quantum hardware performance. For these reasons, QKernel is trained only via an MSE loss on a quantum-inspired similarity matrix, and QBorn is implemented as a lightweight Born-like classical mapping, jointly providing stable alignment guidance without altering the base mBART-50 architecture or increasing inference-time complexity.

3.5.1. Parameter-Free Kernel (QKernel)

Within the QKernel instantiation, training operates on two complementary levels. A_t the first level, the Supervised Fine-Tuning (SFT) arm preserves the model’s fundamental linguistic competence by using teacher forcing and minimizing the standard cross-entropy loss ${\mathcal{L}}_{\mathrm{S}\mathrm{F}\mathrm{T}}$. A_t the second level, two regularization signals are introduced to discipline the model’s cross-attention distributions: (i) a Born-like classical alignment component, QDA, and (ii) a parameter-free quantum kernel component, QKernel. QDA nudges the model’s attention distribution A_t toward a classical target distribution P_t derived from normalized squared inner products between encoder and decoder projections, while QKernel provides an additional quantum-inspired similarity signal that softly supports this target alignment via an MSE loss between a subsampled reference alignment and the quantum kernel similarity. In this way, the linguistic adequacy governed by ${\mathcal{L}}_{\mathrm{S}\mathrm{F}\mathrm{T}}$ is preserved, and token-level alignment is refined by two complementary, lightweight signals.

In the QKernel component, encoder and decoder hidden states ${\mathrm{h}}_{\mathrm{t}}^{\mathrm{dec}}, {\mathrm{h}}_{\mathrm{s}}^{\mathrm{enc}}$∈R^d are first projected into low-dimensional linear subspaces and L2 normalized:

$${\mathrm{U}}_{\mathrm{e}}\left(\mathrm{s}\right)=\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\left({\mathrm{W}}_{\mathrm{e}\mathrm{n}\mathrm{c},\mathrm{q}}{\mathrm{h}}_{\mathrm{s}}^{\mathrm{enc}}\right),\hspace{1em}{\mathrm{U}}_{\mathrm{d}}\left(\mathrm{t}\right)=\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\left({\mathrm{W}}_{\mathrm{d}\mathrm{e}\mathrm{c},\mathrm{q}}{\mathrm{h}}_{\mathrm{t}}^{\mathrm{dec}}\right)$$

(8)

where W_enc,q, W_dec,q ∈ R^d′×d are small, task-specific projection matrices. Each projected vector is then embedded into a parameter-free, hardware-efficient Quantum Feature Map (QFM) circuit (Figure 5):

∣ψ(x)⟩:  RY(πx)  →  [RZ(πx) + CNOT_ring] × ^L

(9)

The QFM is fixed as a shallow circuit with Q = 4 qubits and L = 2 layers. Rotation gates (RY/RZ) provide a non-linear encoding of classical components in Hilbert space, while CNOT-ring connectivity creates entanglement between qubits to represent more holistic contextual relationships. In this way, a rich non-linear embedding is obtained on top of the classical latent representations without introducing additional trainable quantum parameters.

At the circuit output, probability distributions are obtained via the Born rule for each source and target position:

$${\mathrm{P}}_{\mathrm{e}}\left(\mathrm{s}\right)=\left({\left|⟨\mathrm{z}∣\mathrm{\psi }\left({\mathrm{U}}_{\mathrm{e}}\left(\mathrm{s}\right)\right)⟩\right|}^2\right),\hspace{1em}{\mathrm{P}}_{\mathrm{d}}\left(\mathrm{t}\right)=\left({\left|⟨\mathrm{z}∣\mathrm{\psi }\left({\mathrm{U}}_{\mathrm{d}}\left(\mathrm{t}\right)\right)⟩\right|}^2\right),\hspace{1em}\mathrm{z}\in {\{0, 1\}}^{\mathrm{Q}}$$

(10)

where z ∈ {0, 1}^Q denotes computational-basis measurement outcomes. A quantum-inspired similarity matrix between target step t and source position s is then defined as

$${\mathrm{K}}_{\mathrm{q}}\left(\mathrm{t},\mathrm{s}\right)=\mathrm{row\_norm}\left({{\mathrm{P}}_{\mathrm{d}}\left(\mathrm{t}\right)}^{\mathrm{T}}{\mathrm{P}}_{\mathrm{e}}\left(s\right)\right)$$

(11)

where row_norm(⋅) normalizes each row to sum to one so that each K_q(t,s) can be interpreted as an attention-like distribution over source tokens.

The reference alignment A_sub is constructed from the model’s own cross-attention maps by averaging all heads in the last K layers, row-normalizing, masking PAD positions (label = −100), and optionally subsampling timesteps and restricting to a top-k_src subset of source positions. The QKernel loss is defined as the mean-squared error (MSE) between this reference alignment and the quantum-inspired similarity:

$${\mathcal{L}}_{\mathrm{QC}}=\mathrm{MSE}({\mathrm{A}}_{\mathrm{sub}},{\mathrm{K}}_{\mathrm{q}}(\mathrm{t},\mathrm{s}\left)\right)$$

(12)

Because the quantum circuit is parameter-free, gradients are stopped at the q-node outputs, and ${\mathcal{L}}_{\mathrm{QC}}$ back-propagates only through the small projection layers W_enc,q, W_dec,q ∈ R^d′×d. The term acts as a gentle regularizer added to the total loss with a fixed coefficient μ, softly pulling the reference alignment toward the quantum-inspired similarity. The entire process is summarized in Figure 6.

The three components—SFT, QDA, and QKernel—are combined into a single training objective (Figure 7):

$$\mathcal{L}={\mathcal{L}}_{\mathrm{SFT}}+\mathrm{\lambda }{\mathcal{L}}_{\mathrm{QDA}}+\mathrm{\mu }{\mathcal{L}}_{\mathrm{QC}}$$

(13)

Here, λ is linearly warmed up across epochs so that the SFT signal dominates the early stages of training and the QDA signal is introduced gradually. In contrast, μ is kept constant to ensure a stable influence from the quantum regularizer. The overall design goal is to enable the model to learn, at each target step, where to look in the source in a more consistent and evidence-driven manner, while preserving the linguistic competence governed by ${\mathcal{L}}_{\mathrm{SFT}}$.

The generalization behaviour of kernels induced by quantum feature maps can be analyzed via the effective dimension d_eff. Very deep or large-qubit circuits increase representational power but may worsen the conditioning of Gram matrices and raise sample complexity [96,97]. The fixed 4-qubit/2-layer circuit used here is deliberately shallow to limit overlap concentration and d_eff inflation, while still providing a useful non-linear Hilbert-space embedding. Distinctively, QKernel is employed not as a classifier but as a regularization signal for token-level alignment in a seq2seq/attention setting.

From a computational standpoint, QKernel is active only during training, adding a modest forward-pass cost for computing QFM probabilities and the matrix K_q(t,s). Because MSE matching is performed on A_sub, which is row-normalized and restricted to a top-k_src source subset, the additional complexity is O(Tk_srcd), on the same order as the classical QDA similarity. Crucially, no extra latency or memory overhead is incurred at inference time, since the quantum pipeline is completely disabled during generation.

In the context of Turkish scientific article summarization, these design choices are motivated by both data and resource constraints. The shallow QFM offers a non-linear Hilbert-space embedding that can highlight subtle term relationships in long, terminology-dense texts, while avoiding over-parameterization and excessive sample complexity. The warm-up schedule for λ prevents the Born-based alignment signal from destabilizing training in the early epochs, whereas a fixed, moderate μ ensures that QKernel provides a steady, global regularization effect. Together, these elements are intended to improve token-level alignment on long Turkish source documents—where evidence is sparse and dispersed—without incurring additional inference cost or overfitting the limited labelled corpus.

3.5.2. QBorn (Born-Rule-Based Alignment)

In the QBorn variant, the alignment target is constructed via a Born-rule-based similarity defined over the quantum feature–map outputs, rather than directly in the classical embedding space.

Building directly on the QKernel pipeline (Section 3.5.1), QBorn reuses the same projected encoder/decoder representations ${\mathrm{U}}_{\mathrm{e}}\left(\mathrm{s}\right),{\mathrm{U}}_{\mathrm{d}}\left(\mathrm{t}\right)$ and the fixed Quantum Feature Map (QFM) circuit defined in Equations (8) and (9). As described there, these are mapped into the Hilbert space and measured to obtain the encoder and decoder Born probability vectors ${\mathrm{P}}_{\mathrm{s}}^{\mathrm{e}\mathrm{n}\mathrm{c}}$ and ${\mathrm{P}}_{\mathrm{t}}^{\mathrm{d}\mathrm{e}\mathrm{c}}$ for each source position $s$ and target step $\mathrm{t}$.

A classical similarity score ${\mathcal{l}}_{\mathrm{t},\mathrm{s}}$ between decoder step $\mathrm{t}$ and source position $s$ is then defined as the inner product of these probability vectors:

$$\begin{array}{cccc}& {\mathcal{l}}_{\mathrm{t},\mathrm{s}}=⟨{\mathrm{P}}_{\mathrm{t}}^{\mathrm{d}\mathrm{e}\mathrm{c}},{\mathrm{P}}_{\mathrm{s}}^{\mathrm{e}\mathrm{n}\mathrm{c}}⟩={\displaystyle \sum _{\mathrm{z}}}{\mathrm{P}}_{\mathrm{t}}^{\mathrm{d}\mathrm{e}\mathrm{c}}(\mathrm{z}) {\mathrm{P}}_{\mathrm{s}}^{\mathrm{e}\mathrm{n}\mathrm{c}}(\mathrm{z}),\hspace{1em}{\mathrm{P}}_{\mathrm{t}}(\mathrm{s})={\displaystyle \frac{\mathrm{e}\mathrm{x}\mathrm{p}(\mathrm{\beta } {\mathcal{l}}_{\mathrm{t},\mathrm{s}})}{\sum _{\mathrm{u}}\mathrm{e}\mathrm{x}\mathrm{p}(\mathrm{\beta } {\mathcal{l}}_{\mathrm{t},\mathrm{u}})}}& & \end{array}$$

(14)

where ${\mathrm{P}}_{\mathrm{t}}\left(\mathrm{s}\right)$ is the Born-like alignment target for time step $\mathrm{t}$ and $\mathrm{\beta }$ is a similarity temperature (set to $\mathrm{\beta }=1$ in our experiments). The QDA loss then softly regularizes the model’s cross-attention ${\mathrm{A}}_{\mathrm{t}}$ toward this Born-inspired target via a KL divergence defined in Equation (6).

Although the QFM circuit itself is fixed and introduces no inference-time overhead, computing $\mathrm{K}\mathrm{L}({\mathrm{A}}_{\mathrm{t}} \parallel {\mathrm{P}}_{\mathrm{t}})$ on long documents can still be costly during training. To keep QBorn tractable for long Turkish scientific articles, two practical optimizations are applied:

Top-$\mathrm{k}$ source restriction (${\mathrm{k}}_{\mathrm{s}\mathrm{r}\mathrm{c}}$); for each decoder step $\mathrm{t}$, QDA is computed only on the top-${\mathrm{k}}_{\mathrm{s}\mathrm{r}\mathrm{c}}$ source positions instead of all Stokens, effectively reducing the alignment cost from $\mathrm{O}\left(\mathrm{T}\mathrm{S}\mathrm{d}\right)$ to $\mathrm{O}\left(\mathrm{T}{\mathrm{k}}_{\mathrm{s}\mathrm{r}\mathrm{c}}\mathrm{d}\right)$ while focusing the Born-based supervision on the most salient spans.

Target subsampling (${\mathrm{\mu }}_{\mathrm{t}}$); the QDA loss is evaluated on a subsampled subset of target positions with rate ${\mathrm{\mu }}_{\mathrm{t}}\in (0, 1]$, preserving sufficient alignment signal while lowering total computation.

Crucially, this additional cost appears only during training: the QBorn branch is completely disabled at inference, so generation speed and memory footprint remain identical to the classical SFT + QDA baseline. The temperature $\mathrm{\beta }$ is fixed to 1 and sweeps over ${\mathrm{k}}_{\mathrm{s}\mathrm{r}\mathrm{c}}$ and ${\mathrm{\mu }}_{\mathrm{t}}$ within reasonable ranges lead to only minor score variations without altering the ranking or relative performance of the model variants.

In the context of Turkish scientific article summarization, QBorn thus provides a Born-rule-based, quantum-inspired alignment target that sharpens evidence focus on long, terminology-dense documents, while respecting realistic computational and data constraints.

3.6. Training Configuration

To ensure robustness and reproducibility, all experiments were conducted with five independent random seeds, SEEDS = {11, 22, 33, 42, 55}. Random seeds affect the initialization of model weights, minibatch ordering, and dropout masks; relying on a single run can therefore yield misleading conclusions [98,99,100]. Using five seeds strikes a compromise between statistical stability and computational cost, and allows us to report mean performance together with uncertainty estimates.

A single, stable training protocol is used across all configurations. Optimization is performed with AdamW [101], which decouples weight decay from the Adam update and thus provides more stable regularization for large Transformer models than standard Adam. The initial learning rate is set to $5\times {10}^{-5}$, a moderate value commonly used in seq2seq fine-tuning that avoids divergence while still allowing sufficiently fast convergence. A warm-up phase is applied over the first 10% of training steps, during which the learning rate is linearly increased from zero to its peak value, followed by cosine decay over the remaining steps [95]. This schedule is chosen to stabilize early training on long Turkish inputs and to let the model settle gradually into a good local optimum, rather than abruptly reducing the learning rate.

Due to GPU memory constraints with long inputs (up to 1024 subword tokens) and the mBART-50 architecture, the per-step batch size is limited to 2 documents. To obtain a more informative gradient signal without exceeding memory limits, gradient accumulation is employed: gradients from 16 successive minibatches are accumulated before performing a parameter update, yielding an effective batch size of 32 documents [102]. This configuration was selected as the largest stable effective batch size under our VRAM budget, balancing gradient quality and runtime.

Label smoothing with a factor of 0.03 is applied to mitigate overconfidence and improve generalization [92,93]. The value 0.03 was chosen as a mild smoothing level that regularizes the model in the low-resource Turkish setting without over-flattening the target distribution. Gradient norms are clipped at 1.0 (L2-norm) to prevent exploding gradients and stabilize training, which is particularly important when combining long sequences with additional regularization terms [103]. Models are trained for up to 5 epochs with early stopping on validation loss; this relatively short schedule reflects the fact that large pre-trained seq2seq models typically converge quickly and tend to overfit if trained for many epochs on medium-sized datasets [89,90,104].

All experiments were conducted in Google Colaboratory (Colab) on NVIDIA A100 GPUs (Ampere architecture, NVIDIA Corporation, Santa Clara, CA, USA). Mixed-precision training is enabled to balance numerical stability and computational efficiency: model weights are maintained in FP32, while most forward and backward computations use BF16 activations and gradients, leveraging hardware support on Ampere GPUs [105]. TensorFloat-32 (TF32) tensor cores are activated for matrix multiplications, accelerating FP32 workloads while maintaining accuracy close to full precision. This configuration was chosen to maximize the effective batch size and training speed under strict VRAM constraints imposed by long Turkish documents and the hidden dimensionality of mBART-50.

Decoding is evaluated under two regimes to capture both quality-focused and diversity-oriented behavior. In the beam search regime, we use num_beams = 4 with early stopping enabled. This medium beam size provides a good quality-cost trade-off, avoiding both degenerate greedy decoding and prohibitively expensive large beams. A length penalty of 0.9 is applied to counteract the inherent bias of log-probability sums toward very short outputs while still discouraging excessively long summaries [106,107,108]. The value 0.9 was chosen to lightly dampen length bias without encouraging verbose outputs. To reduce repetitive patterns, we set no_repeat_ngram_size = 3, which prevents the model from generating any trigram more than once in a summary; this value empirically suppresses looping behavior while preserving natural Turkish discourse markers.

In the sampling regime, num_beams = 1 and early stopping is disabled; generation is performed with temperature $\mathrm{T}=0.9$ and nucleus sampling with top_p = 0.95. This configuration is chosen to introduce controlled stochasticity: a temperature slightly below 1.0 reduces extremely risky low-probability choices, while top_p = 0.95 restricts sampling to a high-probability nucleus, increasing lexical and structural diversity without sacrificing coherence. Reporting both beam search and sampling results provides a more complete picture of how each model behaves under a conservative decoding regime (quality-oriented) and a more exploratory regime (diversity-oriented).

Overall, these hyperparameter choices are driven by three practical constraints of Turkish scientific summarization in this setting: (i) limited labeled data, which motivates strong but careful regularization (label smoothing, gradient clipping, early stopping, multi-seed runs); (ii) long, term-dense inputs and a large multilingual backbone, which require memory-aware optimization (gradient accumulation, mixed precision); and (iii) the need to fairly compare multiple model variants under a consistent and computationally feasible training and decoding protocol.

3.7. Evaluation Protocol

Model outputs are evaluated along three complementary axes: lexical/semantic faithfulness, abstraction vs. copying behavior, and diversity/fluency. All metrics are computed on the held-out test set and macro-averaged over documents.

The primary faithfulness metrics are ROUGE-1, ROUGE-2, ROUGE-L, and ROUGE-Lsum, which quantify unigram, bigram, and longest-common-subsequence overlaps between system summaries and the gold author abstracts [32]. These scores capture surface-level n-gram matches and shallow word-order agreement. To complement ROUGE’s lexical focus—especially important for morphologically rich Turkish—BERTScore-F1 is reported using multilingual contextual embeddings (e.g., XLM-R) to approximate semantic similarity between tokens via cosine similarity [109]. This combination allows both surface overlap and deeper meaning preservation to be assessed.

To characterize how models use the source text, the NEWSROOM-style Coverage, Density, and Compression metrics are computed [35]. Coverage measures the proportion of the summary that can be explained by contiguous spans copied from the source; Density measures the average length of such copied spans, where higher values indicate more extractive behavior; Compression is defined as the ratio of source length to summary length, with extreme values suggesting over-compression (information loss) or under-summarization.

To analyze the trade-off between copying, abstraction, and fluency, several diversity-related metrics are reported. Novel-n (n = 1, 2, 3, 4) measures the proportion of generated n-grams that do not appear in the source, with very low values indicating excessive copying and very high values suggesting topic drift or hallucination. The repetition rate of 3-g (rep-3) quantifies intra-summary repetition; higher values typically correlate with disfluencies and degenerate loops [20,21]. Distinct-2 measures the global diversity of bigrams across all summaries, serving as an indicator of lexical and structural richness [36]. Finally, Self-BLEU is used to estimate how similar summaries generated by the same model are to one another; low Self-BLEU scores indicate higher inter-sample diversity [37]. Together, these diagnostics provide a more fine-grained view of whether improvements in ROUGE/BERTScore are achieved via safe copying or genuinely more abstractive, yet still coherent, generation.

Model comparisons are conducted in a paired setting: for each test document, summaries from model A and model B are compared on the same item, and score differences Δ are formed (e.g., Δ = ROUGE-L(A) − ROUGE-L(B)). To quantify uncertainty due to finite test size and random initialization, paired bootstrap resampling is applied to these per-item differences, yielding 95% percentile-based confidence intervals [38,39]. When the confidence interval does not cross zero, the superiority of one model over the other is considered statistically consistent.

Because multiple pairwise comparisons are performed across systems and metrics, p-values are adjusted using the Benjamini–Hochberg procedure to control the False Discovery Rate (FDR) and reduce the chance of spurious findings [40,110,111]. In addition to significance, Cliff’s δ is reported as a non-parametric effect size, capturing the probability that a randomly chosen test item favors model A over model B minus the probability of the reverse [41]. Following common thresholds, |δ| ≈ 0.11, 0.28, and 0.43 are interpreted as small, medium, and large effects, respectively [42,43]. This combination of paired bootstrap CIs, FDR control, and effect-size reporting is adopted to ensure that observed performance differences reflect robust and practically meaningful improvements rather than random variation.

This evaluation design is particularly important for Turkish scientific abstracts, which are typically short, information-dense, and morphologically rich. In such settings, n-gram overlap alone can over-penalize valid paraphrases or morphological variants, while ignoring hallucinations and omitted evidence; combining ROUGE with BERTScore, abstraction/copying diagnostics, and diversity metrics provides a more faithful picture of how well the models capture the factual content and discourse structure of long Turkish source documents.

3.8. Software Infrastructure and Libraries

All experiments are conducted in a Google Colaboratory environment equipped with NVIDIA A100 GPUs (Ampere architecture), which enables efficient mixed-precision training (BF16/TF32) for large Transformer models. The implementation is based on Python (version: 3.12.12) and the standard scientific computing stack.

PDF text extraction for Turkish academic articles is performed using PyMuPDF (fitz), which provides reliable access to layout-aware text from publisher PDFs. Regular-expression handling (Python re) is used for Unicode normalization, typographical normalization, and rule-based filtering of non-content elements (headers/footers, references, metadata). Section-wise splitting and tagging of <ozet|abstract>, <giris|introduction>, <yontem|method>, <bulgular|findings>, and <sonuc|conclusion> is also driven by regex-based header matching. Intermediate statistics and experiment summaries are stored and exchanged via pandas DataFrames and exported with openpyxl to Excel format when needed.

All neural models are implemented in PyTorch (version: 2.8.0+cu126) [112]. The mBART-50 backbone, tokenization (SentencePiece), and training utilities are provided via the Hugging Face Transformers ecosystem, with PEFT used to implement parameter-efficient LoRA adapters for the SFT + LoRA variants. Optimization is carried out with AdamW and custom learning-rate schedulers (warm-up + cosine decay) built on PyTorch’s optimizer and scheduler APIs.

The quantum-inspired modules (QKernel and QBorn) are implemented using PennyLane and PennyLane-Lightning, which provide differentiable quantum circuit simulation and Born-rule probability interfaces [113,114]. Parameter-free quantum feature maps and shallow 4-qubit/2-layer circuits are executed on GPU-backed simulators (lightning.gpu), and their probability outputs are integrated into the PyTorch training loop as regularization signals. The design deliberately restricts quantum computations to the training phase so that no additional overhead is incurred during inference.

Lexical overlap metrics such as ROUGE are computed using standard Python implementations; abstraction and copying diagnostics (coverage, density, compression) and diversity metrics (Novel-n, rep-3, Distinct-2) are implemented with NumPy for vectorized operations [115]. NLTK is used for sentence segmentation, tokenization, and BLEU-based computations underlying Self-BLEU diversity estimates [116,117]. Semantic similarity evaluation (BERTScore) and auxiliary embedding-based analyses rely on the sentence-transformers library with a multilingual encoder such as paraphrase-xlm-r-multilingual-v1 [118].

For statistical analysis, SciPy is employed to compute bootstrap confidence intervals, basic descriptive statistics, and to support the estimation of effect sizes and significance measures [119]. NumPy and pandas are used together to aggregate results over seeds and splits, compute summary tables, and prepare the final metrics for reporting and visualization.

Overall, this software and library stack was chosen to (i) support reproducible large-scale seq2seq training under realistic GPU memory constraints, (ii) integrate quantum-inspired regularizers into a standard PyTorch workflow with minimal friction, and (iii) provide a rich but well-established toolkit for evaluation and statistical analysis in the context of long, low-resource Turkish scientific summarization.

4. Results

This section briefly summarizes the evaluation protocol for experiments conducted with five different seeds. We report ROUGE-1/2/L/Lsum and BERTScore-F1 as the primary accuracy metrics, and we analyze the copy–abstraction balance using diversity and coverage diagnostics (novel-1/2/3/4, coverage, density, compression, rep-3, distinct-2, self-BLEU). For statistical validity, we compute 95% confidence intervals via paired bootstrap resampling, control the false discovery rate across multiple model/decoding comparisons using the Benjamini–Hochberg procedure, and report Cliff’s δ to numerically summarize the direction and magnitude of effects. The complete set of detailed metric tables is provided in the Appendix A, to which readers are referred for full numerical results.

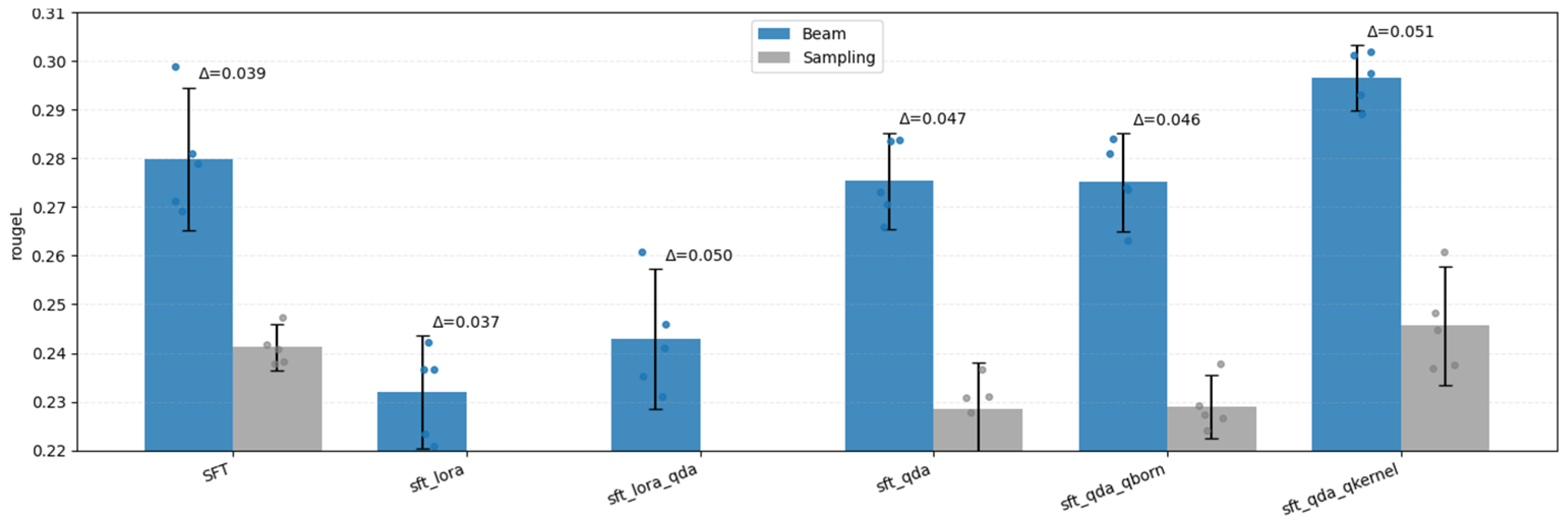
4.1. Decoding Mode Comparison: Beam vs. Sampling

Beam search decoding outperforms sampling across all architectures on ROUGE-L/Lsum and BERTScore-F1. This advantage is observed consistently across all five seeds.

Figure 8 shows that, for all models, beam decoding attains higher mean ROUGE-L scores than sampling. Bars (means), error bars (95% CIs), and seed markers are displayed in the same style as Figure 8; the Δ values in the titles indicate the magnitude of the Beam–Sampling difference. The systematic increase in ROUGE-L suggests that, with length normalization and no-repeat n-gram constraints, beam better preserves sequence-level alignment. The fact that, for most models, the CIs do not cover 0 and the differences are consistently positive strengthens the case for adopting beam as the default decoding mode for formal overlap-oriented summarization.

Figure 9 shows that, across all architectures, beam decoding outperforms sampling in terms of BERTScore-F1. Bars denote the mean over five seeds, error bars indicate the 95% confidence interval (CI), and point markers show per-seed scores. The Δ label atop each model title gives the mean Beam–Sampling difference (Δ > 0 ⇒ in favor of beam). Although the magnitude varies by architecture, the differences are consistently positive; the non-overlapping CIs and the tight clustering of seed points indicate that beam improves semantic adequacy (contextual similarity) and that results are stable with respect to seed choice.

4.2. Architectural Comparison

Table 1. Pairwise ROUGE-L comparisons under beam decoding.

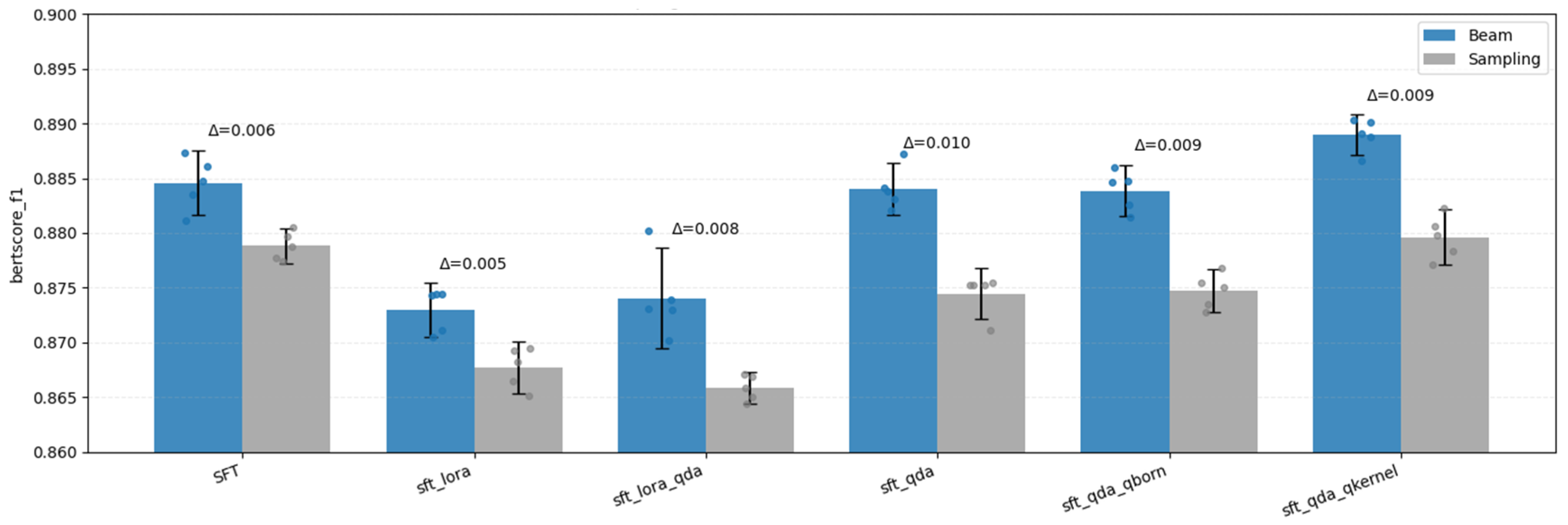
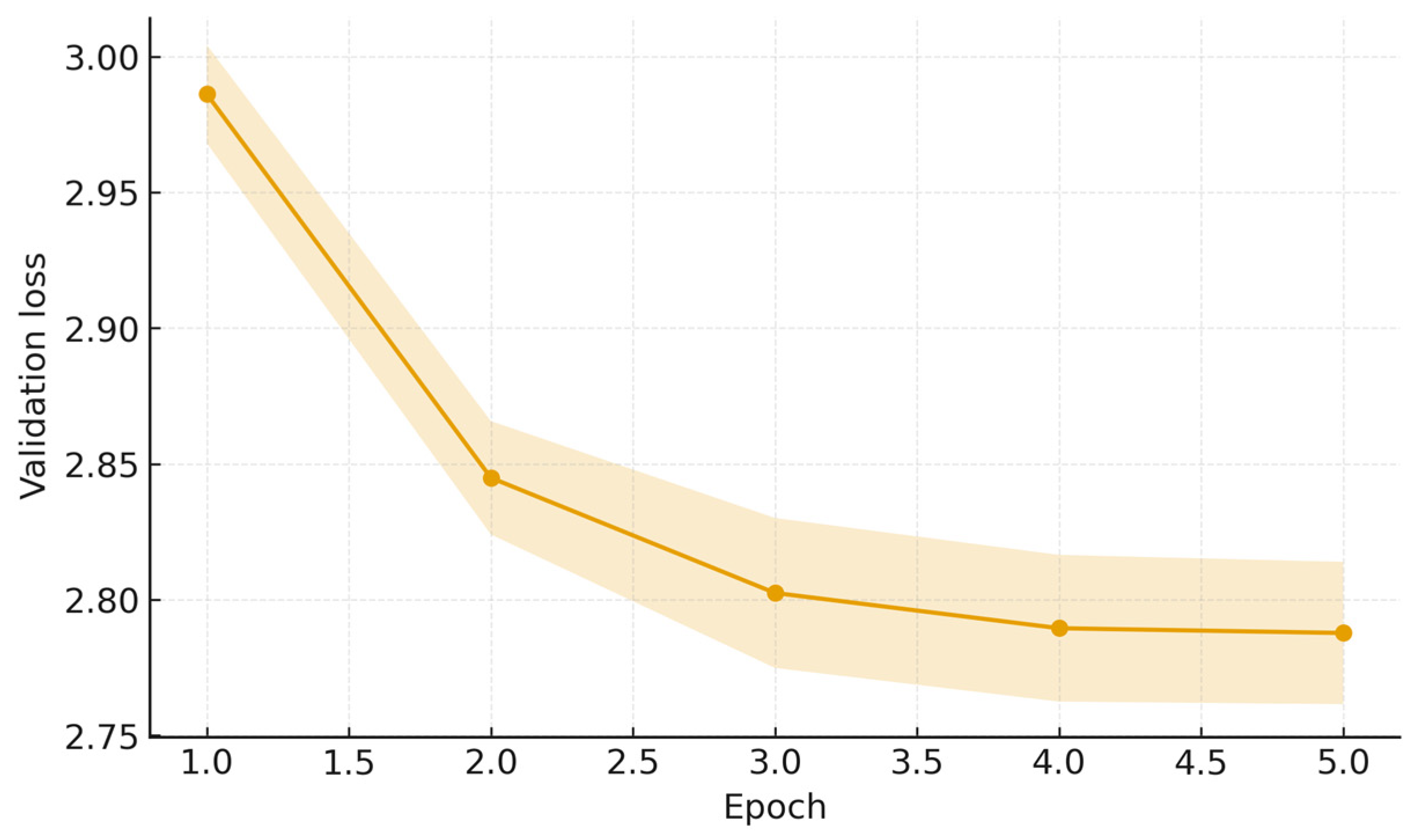
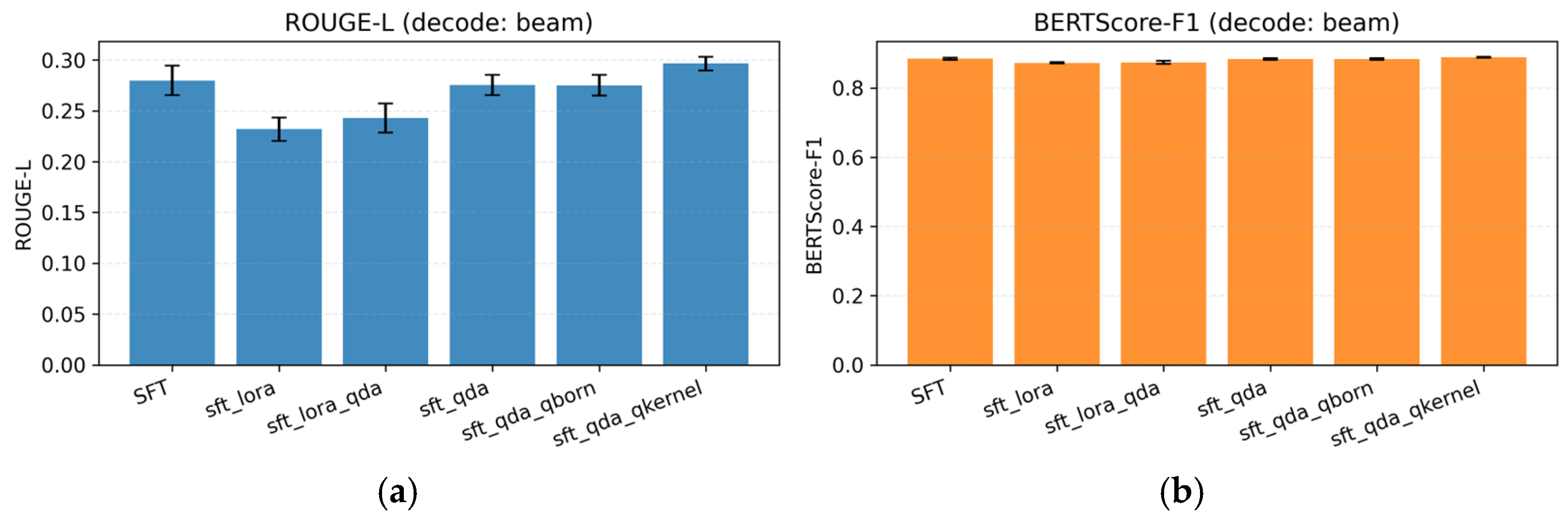
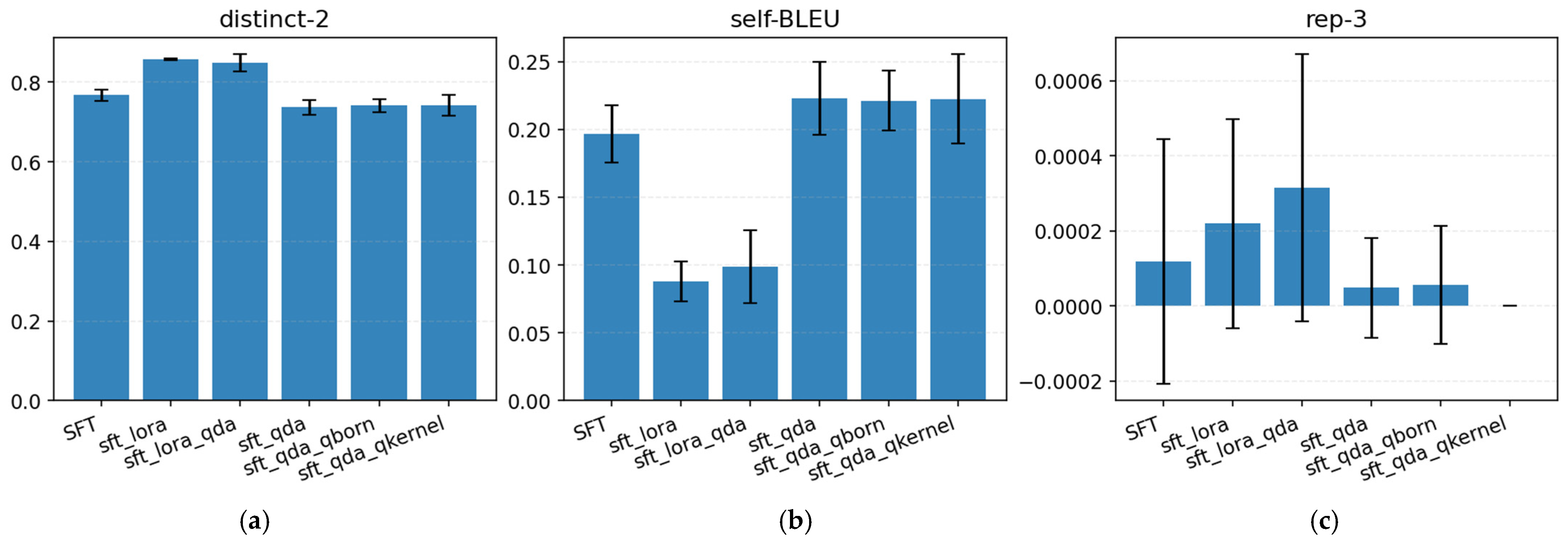
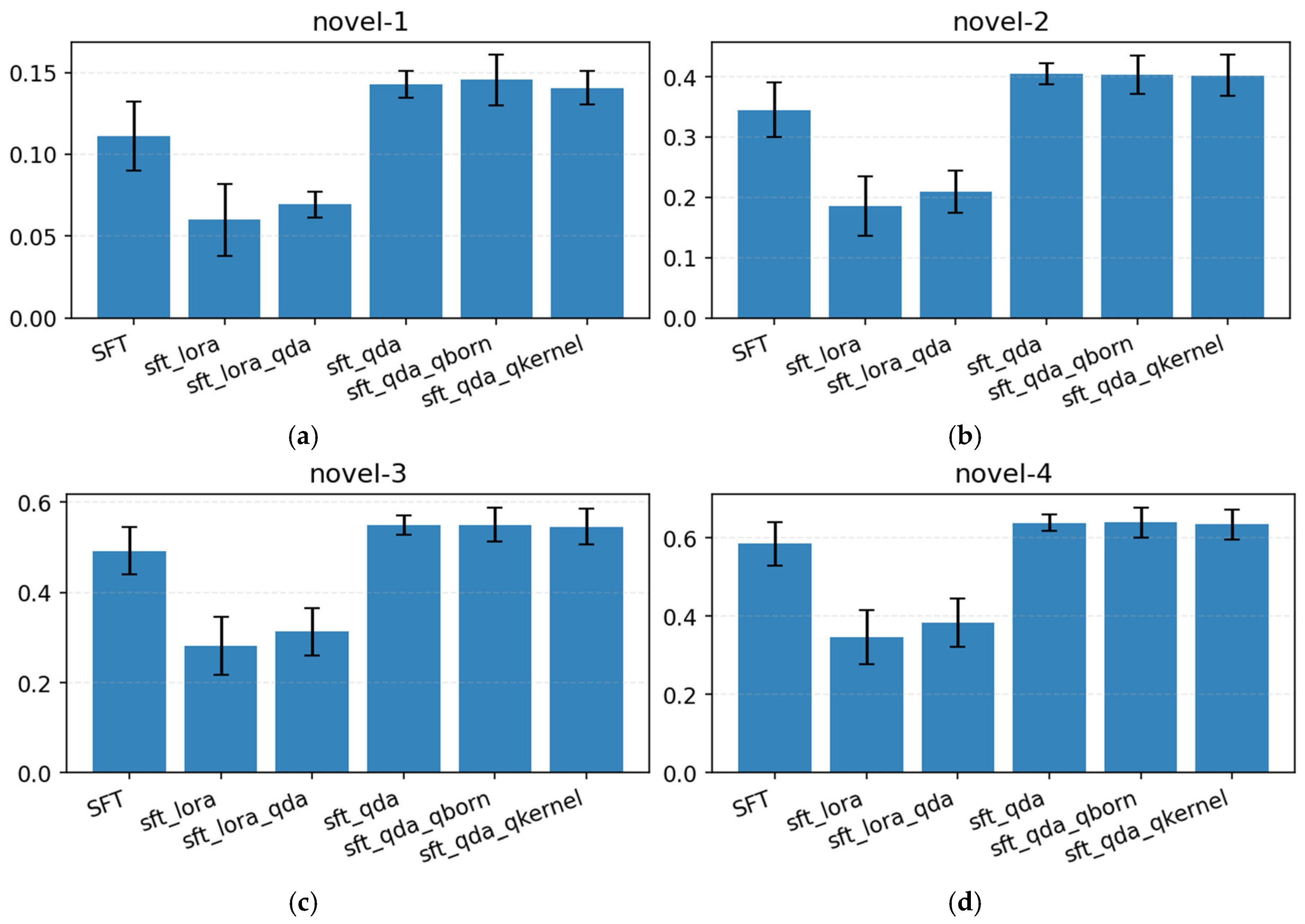
Model (A)	Karşılaştırılan (B)	Δ = A − B	95% CI	Cliff’s δ	q_dir (FDR)
sft_qda_qkernel	sft_lora	0.0646	[0.0543, 0.0750]	1.0 (large)	0.000007
sft_qda_qkernel	sft_lora_qda	0.0537	[0.0470, 0.0597]	1.0 (large)	0.000007
sft_qda_qkernel	sft_qda_qborn	0.0214	[0.0189, 0.0242]	1.0 (large)	0.000007
sft_qda_qkernel	sft_qda	0.0211	[0.0167, 0.0251]	1.0 (large)	0.000007
sft_qda_qkernel	SFT	0.0167	[0.0021, 0.0277]	0.6 (large)	0.013957

reports pairwise ROUGE-L differences under beam decoding with SFT_QDA_QKernel taken as the reference model, where Δ = ROUGE-L(A) − ROUGE-L(B) and positive values favor the reference. Across five seeds, percentile bootstrap 95% confidence intervals do not include zero for any comparison, and Benjamini–Hochberg-adjusted one-sided p-values are below the significance threshold (q_dir ≈ 7 × 10⁻⁶ against SFT + LORA, SFT + LORA + QDA, SFT + QDA, and SFT + QDA + QBorn; q_dir ≈ 1.4 × 10⁻² against SFT). Effect sizes measured by Cliff’s δ are large in every case, with δ ≈ 1.0 versus SFT + LORA, SFT + LORA + QDA, SFT + QDA, and SFT + QDA + QBorn, and δ ≈ 0.6 versus SFT. Numerically, the gains range from Δ ≈ 0.0167 to 0.0646, with the largest margins observed against SFT + LORA (Δ ≈ 0.0646 [0.0543, 0.0750]) and SFT + LORA + QDA (Δ ≈ 0.0537 [0.0470, 0.0597]). These results indicate that the reference model exhibits a consistent and statistically robust advantage over all competing architectures.

Figure 10 shows the evolution of validation loss (val_loss) across epochs for the SFT + QDA + QKernel pipeline, reported as the mean over five seeds with bootstrap-based 95% confidence intervals. The curve indicates rapid initial improvement with a pronounced drop from epoch 1 to 2, followed by diminishing gains and a tendency to plateau from epoch 3 onward. The narrow confidence band suggests low-to-moderate across-seed variability and stability with respect to seed choice. As no U-shaped increase in validation loss is observed over the five epochs, there is no evidence of overfitting; this supports model selection via the lowest validation loss checkpoint (without applying early stopping patience).

Figure 11 compares architectures under beam decoding using ROUGE-L (a) and BERTScore-F1 (b), reporting five-seed means with 95% confidence intervals. Along ROUGE-L, the SFT baseline yields the lowest scores; SFT + LORA performs noticeably worse than SFT, whereas adding QDA (SFT + QDA) produces a clear improvement over both LoRA and SFT. The Born variant of QDA (SFT + QDA + QBorn) remains in a similar band, while SFT + QDA + QKernel achieves the highest ROUGE-L among all architectures. The largely non-overlapping confidence bands (±95% CI) indicate that this superiority is stable under seed variability. On BERTScore-F1, all models cluster around 0.88, but the QKernel and QDA variants show small yet consistent gains; the LoRA add-on alone does not yield a notable improvement in semantic similarity and even trails SFT slightly. Taken together, the findings suggest that LoRA by itself is insufficient for this task and that alignment-oriented QDA—especially when coupled with a parameter-free quantum kernel (QKernel)—improves both surface-form overlap (ROUGE-L) and semantic alignment (BERTScore), with SFT + QDA + QKernel emerging as the best-performing architecture.

4.3. Diversity and Copying Dynamics

Figure 12 shows that, under beam decoding, all architectures achieve high coverage (≈0.88–0.97), indicating that a large fraction of each summary is composed of n-gram fragments copied from the source. Density (the average length of copied fragments), however, differentiates the models: LoRA-based variants (especially SFT + LORA and SFT + LORA + QDA) exhibit markedly higher density (longer copied blocks), whereas SFT + QDA and SFT + QDA + QKernel operate at more moderate densities with shorter/medium segments. This pattern suggests that the LoRA line tends toward a more “extractive” strategy, while QDA and QKernel constrain fragment lengths and encourage more segmented rephrasing. In terms of compression (source-to-summary length ratio), SFT yields the highest compression (shorter summaries), LoRA-based models produce relatively lower compression (longer summaries), and QKernel maintains a reasonable mid-range, preserving the coverage-brevity trade-off.

Figure 13 illustrates that SFT + LORA and SFT + LORA + QDA achieve the highest word-level lexical diversity (distinct-2), whereas SFT, QDA, and QKernel produce more balanced but slightly more template-driven outputs relative to LoRA. The self-BLEU metric, which captures within-model similarity, tells the reverse story: self-BLEU is higher for SFT + QDA, SFT + QDA + QBorn, and SFT + QDA + QKernel (summaries are more similar to one another), and lowest for SFT + LORA + QDA (more varied outputs). Taken together, these indicators suggest that QKernel preserves content coverage while slightly increasing pattern conformity, whereas the LoRA line boosts diversity (high distinct-2, low self-BLEU) but tends to copy longer blocks. Overall, the SFT + QDA + QKernel architectures appear to strike a more consistent quality-diversity trade-off and yield edit-friendly summaries.

Figure 14 presents abstractiveness indicators, showing that, under beam decoding, the LoRA line (especially SFT + LORA and SFT + LORA + QDA) behaves more extractively, with lower novel-1/2/3/4 rates, whereas SFT + QDA and the quantum-kernel variant SFT + QDA + QKernel produce clearly higher proportions of new n-grams across all n values. The SFT baseline sits in the mid-range, while QDA-based variants yield significant gains on novel-1/2 and reach the highest levels on novel-3/4, indicating stronger paraphrasing capacity. The narrow and, in many cases, non-overlapping 95% confidence bands suggest this pattern is stable across the five seeds. Because excessive abstractiveness can raise hallucination risk, these results should be read alongside the copying/coverage analysis: despite higher novel-n, the QDA(+QKernel) family keeps coverage and fragment density within a reasonable range.

4.4. Qualitative Analysis (Case Studies)

Brief qualitative remarks are provided for three representative examples below. The original gold abstracts and system outputs are written in Turkish, and the English versions shown in

Table 2. Case Studies on Turkish Scientific Abstracts (Gold vs. Best Model).

Paper ID	Gold Summary	Best Model − sft + qda + qkernel (Beam = 4, no_repeat_ngram_size = 3, length_penalty = 0,9, Seed = 22)	Evaluation
635	bu çalışma ilköğretim matematik öğretmenliği programı öğrencilerinin koordinat düzleminde birim çemberi kullanarak tanjant ve kotanjant fonksiyonları nın grafiklerinin çiziminde sayı doğrusu kullanımlarını araştıran betimsel bir çalış madır. çalışmada nicel veri toplama yöntemlerinin yanında gözlem ve görüşme gibi nitel veri toplama yöntemleri de kullanılabilen tarama modeli kullanılmıştır. çalışma türkiye nin doğu anadolu bölgesinin nüfusça orta ölçekli bir ilinde yapılmış tır. çalışma grubunu ilköğretim matematik öğretmenliği programına kayıtlı 56 birinci sınıf öğrencisi oluşturmaktadır. çalışmaya katılan öğrencilere on bir adet beşli likert tipi ve altı adet açık uçlu soru sorulmuş ve veriler analiz edilerek elde edilen bulgular sunulmuştur. (This study is a descriptive investigation exploring the use of the number line by prospective primary school mathematics teachers in drawing the graphs of tangent and cotangent functions using the unit circle on a coordinate plane. The study employed a survey research design, utilizing both quantitative data collection methods and qualitative methods such as observation and interviews. The research was conducted in a medium-sized province in the Eastern Anatolia region of Turkey. The study group consisted of 56 first-year students enrolled in the primary school mathematics teaching program. The students participating in the study were administered a questionnaire comprising eleven 5-point Likert-type scale questions and six open-ended questions. The findings obtained from the analysis of the collected data are presented.)	bu çalışmanın amacı ilköğretim matematik öğretmenliği programında yer alan tanjant ve kotanjant fonksiyonlarının grafik çizimi ve doğru sayı doğrusu uygulamaları ile ilgili öğrencilerin algılarını ortaya çıkarmaktır. araştırmada nitel veri toplama yöntemlerinden gözlem ve görüşme yöntemleri kullanılmıştır. araştırmanın çalışma grubunu 2010–2011 eğitim öğretim yılı bahar yarıyılında doğu anadolu bölgesinin orta ölçekli bir ilinde yer alan bir eğitim fakültesinde öğrenim görmekte olan altı birinci sınıf öğrencisi oluşturmaktadır. verilerin toplanmasında bilgi algılama ölçeği ve bilgi testi kullanılmış olup verilerin analizinde betimsel analiz yöntemi kullanılmıştır. (The primary objective of this study is to reveal the students’ perceptions regarding the graphing of tangent and cotangent functions and the correct number line applications, which are part of the primary school mathematics teaching program curriculum. Observation and interview methods, which are qualitative data collection techniques, were employed in the research. The study group consisted of 6 first-year students who were enrolled in a Faculty of Education in a medium-sized province in the Eastern Anatolia region during the Spring semester of the 2010–2011 academic year. A Knowledge Perception Scale and a knowledge test were used for data collection, and the descriptive analysis method was utilized for the analysis of the data.)	The model output correctly captures the study type (“descriptive/survey”), the context (a faculty of education in Eastern Anatolia), and the data-collection instruments, establishing strong topical alignment. However, it diverges from the gold summary by reporting the sample size as 56 instead of 6 and introduces numerical specifics (e.g., “11 Likert + 6 open-ended items”) that create factual inconsistencies. Overall: high coverage/fluency, but a numeric error and unnecessary detail.
485	bu araştırmada sınıf öğretmeni adaylarına uygulanan stem proje tabanlı öğrenme etkinlikleri sonunda öğretmen adaylarının ürettikleri matematik projeleri incelenmiştir. gerçekleştirilen çalışmada sınıf eğitimi birinci sınıf programında yer alan temel matematik ii dersi kapsamında katı cisimlerin alan ve hacimleri trigonometri ve koordinat sistemi konularını içeren 4 farklı stem etkinliği yürütülmüştür. stem etkinlikleri bina modelleme teodolit tasarımı simülasyon tasarımı ve oyun tasarımı şeklinde olup bu etkinliklerin her birinin sonunda sınıf öğretmeni adaylarına bir proje olmak üzere toplam 4 proje ödevi verilmiştir. araştırmaya sınıf eğitimi birinci sınıfta öğrenim gören 23 öğretmen adayı katılmıştır (This research examined the mathematics projects produced by prospective primary school teachers following the implementation of STEM project-based learning activities. The study involved conducting four distinct STEM activities within the scope of the Basic Mathematics II course, a component of the first-year primary education curriculum. These activities covered the topics of area and volume of solids, trigonometry, and the coordinate system. The STEM activities were designed as building modeling, theodolite design, simulation design, and game design. Following each of these activities, prospective primary school teachers were assigned a total of four project assignments, one project after each activity. Twenty-three prospective teachers enrolled in the first year of the primary education program participated in the research.)	bu çalışmada sınıf eğitimi birinci sınıfta yer alan temel matematik ii dersinde dört stem etkinliği yapılmış ve etkinlikler sonunda öğretmen adaylarına proje ödevleri verilmiştir. bu etkinliklerin incelenmesinde öğretmen adaylarının stem projesi hazırlama beceri düzeyleri betimsel istatistiklerle değerlendirilmiştir. araştırma 2016–2017 eğitim öğretim yılı bahar döneminde orta karadeniz bölgesindeki bir üniversitenin eğitim fakültesinde gerçekleştirilmiştir. araştırmanın veri toplama aracı olarak çalışma grubunu oluşturan 23 öğretmen adayı oluşturmuştur. (In this study, four STEM activities were conducted within the scope of the Basic Mathematics II course, which is taught in the first year of the primary education program, and project assignments were given to prospective teachers upon the completion of these activities. To evaluate these activities, the prospective teachers’ skill levels in preparing STEM projects were assessed using descriptive statistics. The research was carried out at a Faculty of Education at a university located in the Central Black Sea region during the Spring semester of the 2016–2017 academic year. The study group, consisting of 23 prospective teachers, also constituted the data collection instrument for the research.)	The model correctly conveys the four STEM activities, the assignment of project tasks, and the sample of 23 preservice teachers; by explicitly naming the thematic topics (solid geometry/volumes, trigonometry, coordinate system), it enhances content coverage and maintains high fidelity to the gold summary. Overall: good fluency and rich content, with no substantive errors beyond minor verbosity.
142	bu araştırma öğrencilerin matematik korkusunun nedenlerini belirlemeye yönelik bir ölçek geliştirmek amacıyla yapılmıştır. çalışmanın örneklemini 2018–2019 öğretim yılında uşak il genelinde ilkokul ortaokul ve lise kademesinde öğrenim gören 2580 öğrenci oluşturmuştur. ölçek geliştirme aşamaları kapsamında alan yazın taranmıştır. ölçekle ilgili madde havuzunun oluşturulmasından sonra uzman görüşüne başvurulmuştur. pilot çalışma yapı geçerliliği ve güvenirliğinin tespiti çalışmaları yapılmıştır. açımlayıcı faktör analizi sonucunda her biri beş sorudan oluşan öğretmenden kaynaklı matematik korkusu çevreden kaynaklı matematik korkusu matematiğin yapısından kaynaklı matematik korkusu öğrencinin kendi kişisel özelliklerinden kaynaklı matematik korkusu boyutları oluşmuştur (This research was conducted with the aim of developing a scale to determine the causes of students’ mathematics anxiety. The study’s sample comprised 2580 students attending primary, middle, and high schools throughout the province of Uşak during the 2018–2019 academic year. Within the scope of the scale development process, an extensive literature review was performed. Following the creation of the initial item pool for the scale, expert opinion was sought. Subsequently, pilot studies and examinations for construct validity and reliability were conducted. The results of the Exploratory Factor Analysis (EFA) yielded four dimensions, each consisting of five items: Mathematics Anxiety Caused by the Teacher, Mathematics Anxiety Caused by the Environment, Mathematics Anxiety Caused by the Nature of Mathematics, and Mathematics Anxiety Caused by Student’s Own Personal Characteristics.)	bu çalışmanın amacı ortaokul öğrencilerinin matematik korkusunun nedenlerini belirlemek için bir ölçeğin geliştirilmesidir. araştırmada betimsel tarama modeli kullanılmıştır. araştırmanın örneklemini 2018–2019 öğretim yılında uşak il genelinde ilkokul ve liselerde öğrenim gören 300 öğrenci oluşturmuştur. araştırmaya katılan öğrencilerden matematik korkusu nedenlerini ortaya koymak amacıyla bir ölçek geliştirilmeye çalışılmıştır. madde havuzu oluşturmak için ilgili alanyazın taranması ve uzman görüşleri alınmıştır. çalışmada veri toplama aracı olarak matematikten kaynaklı korku ölçeği ve matematik dersine yönelik akıl yürütme araçlarından biri olan matematiğe yönelik tutum ölçekleri kullanılmıştır (The purpose of this study is the development of a scale to determine the causes of mathematics anxiety of middle school students. A descriptive survey model was used in the research. The sample of the research was constituted by 300 students who were studying in primary schools and high schools across the province of Uşak in the 2018–2019 academic year. An effort was made to develop a scale from the students who participated in the research in order to reveal the causes of mathematics anxiety. The related literature review and expert opinions were taken for creating the item pool. In the study, the Fear Caused by Mathematics Scale and attitude scales towards mathematics, which is one of the reasoning tools related to the mathematics course, were used as data collection instruments.)	The model correctly states the objective of “developing a mathematics anxiety scale” and concisely summarizes the methodological steps (literature review, expert judgment, pilot study, EFA), even recovering the four-factor structure. However, it diverges from the gold summary by inflating the sample size to 2580 (gold: 300 students) and broadening the grade levels. Overall: high content coverage but weakened fidelity due to numeric and population-scope errors. In general, while coverage and fluency are strong, the numerical specifics call for cautious normalization.

are manually translated and included solely for readability. All training and automatic evaluation were conducted on the original Turkish texts.

5. Discussion and Conclusions

The primary goal of this study was to improve token-level alignment between source documents and generated summaries for long, terminology-dense Turkish scientific articles, without modifying the underlying encoder–decoder architecture or incurring inference-time overhead. To this end, a Born-inspired Quantum Distribution Alignment (QDA) regularizer was introduced and instantiated in several variants on top of mBART-50, together with parameter-efficient fine-tuning (LoRA) and quantum-inspired kernel components (QKernel, QBorn). The experimental results indicate that this alignment-centred design is effective: across six configurations, models equipped with QDA consistently outperform purely classical baselines under beam decoding, particularly on ROUGE-L/Lsum and BERTScore-F1, while preserving the original architecture and decoding pipeline.

From a quantitative standpoint, the SFT baseline provides a strong reference for full fine-tuning on Turkish scientific summarization, and SFT + LoRA offers a competitive parameter-efficient alternative under tight computational budgets. However, adding the QDA regularizer on top of full SFT (SFT + QDA) yields clear improvements in content selection and semantic similarity, showing that explicit cross-attention alignment can compensate for the well-known tendency of abstractive models to “drift” away from the source in long documents. Extending QDA with the parameter-free QKernel component (SFT + QDA + QKernel) further strengthens this effect and emerges as the best overall configuration, achieving ROUGE-L ≈ 0.30 and BERTScore-F1 ≈ 0.89 on the test set. In contrast, SFT + LoRA and SFT + LoRA + QDA remain weaker than their full-SFT counterparts in this setting, suggesting that, for the present corpus, the representational capacity of the full mBART-50 backbone is more critical than the reduction in trainable parameters. The QBorn variant, which replaces the parameter-free kernel with a Born-rule-inspired learnable mapping, provides an additional alignment signal but at substantially higher training cost: under the shared training protocol, SFT + QDA + QBorn requires roughly 26,238.9 s (≈7.29 h), about 6.34× longer than SFT + QDA + QKernel (≈4136.2 s, ≈1.15 h), while not overturning the ranking established by QKernel.

Beyond headline metrics, the abstraction and diversity diagnostics provide further insight into how the proposed alignment mechanisms affect model behaviour. QDA-based variants, particularly SFT + QDA + QKernel, tend to move away from purely extractive behaviour: NEWSROOM-style coverage/density/compression profiles indicate less reliance on long verbatim spans, while Novel-n statistics show an increase in novel n-grams relative to the source, signalling more genuine rephrasing rather than simple copying. At the same time, repetition-focused measures such as rep-3 and Self-BLEU remain within acceptable ranges, and Distinct-2 scores indicate that lexical variety is improved rather than degraded. Taken together, these patterns suggest that QDA(+QKernel) helps the model to generate summaries that are both more abstractive and more semantically faithful, rather than trading one dimension off against the other.

These empirical gains can be interpreted in light of the alignment objective. In standard SFT, cross-attention weights are optimized only indirectly through the likelihood of the next token, and nothing guarantees that the resulting attention distributions reflect the true evidential structure of the source-an issue that becomes especially acute in long, dense Turkish scientific texts. The proposed QDA framework explicitly regularizes cross-attention toward a Born-like target distribution constructed from encoder–decoder projections, thereby encouraging the model to “look” at source spans that are geometrically consistent with the emerging target representation. QKernel augments this process with a fixed quantum-inspired feature map that embeds these projections into a Hilbert-space-like probability simplex and constructs a similarity matrix acting as a parameter-free regularizer. For Turkish mathematics education articles, where critical terminology can be sparsely and unevenly distributed across long sections, this combination provides a lightweight mechanism for sharpening evidence focus without adding new trainable modules or changing the mBART-50 architecture.

The quantum-inspired design also has practical implications. QKernel offers a favourable trade-off between expressivity and efficiency: it introduces no additional trainable parameters, is applied only during training, and adds a modest computational overhead that remains manageable even for long documents. QBorn explores the other end of the spectrum by using a Born-rule-inspired learnable mapping, yielding a somewhat richer alignment signal but at a significantly higher training-time cost. Given their relative performance and efficiency, SFT + QDA + QKernel can be recommended as the default configuration for practitioners who aim to improve faithfulness and abstraction quality in low-resource summarization scenarios similar to those studied here, while SFT and SFT + LoRA remain useful as baselines under stricter resource limits.

Several limitations of the present work should be acknowledged. First, all evaluations are based on automatic metrics; although a broad suite of measures was employed (ROUGE, BERTScore, abstraction/copying profiles, diversity and repetition diagnostics) and robust statistical procedures were applied across five random seeds, human judgements of fluency, faithfulness, and usefulness were not collected. Second, the experiments are restricted to a single domain (Turkish mathematics education articles) and a single backbone (mBART-50); it remains an open question how well the proposed alignment mechanisms transfer to other scientific fields, genres, or stronger monolingual Turkish models. Third, the quantum-inspired components are implemented via classical simulation on GPUs, and no claims are made about quantum hardware advantages; the focus is strictly on the algorithmic value of quantum-style kernels and Born-like targets under realistic low-resource constraints.

These limitations point to several directions for future research. Human evaluation and QA-based factuality metrics could be incorporated to validate and refine the automatic findings, especially in cases where different metrics disagree. Broader ablation and sensitivity studies could be conducted to further disentangle the contributions of QDA and QKernel, explore alternative similarity functions and temperature schedules, and test more aggressive or adaptive subsampling schemes for alignment. Applying the same protocol to other low-resource languages, domains (e.g., law, clinical text), and backbones (including strong monolingual Turkish models) would clarify the external validity of the approach. Finally, as quantum hardware and hybrid toolchains mature, it may become feasible to replace the simulated feature maps with real devices or more expressive variational circuits, thereby extending the present framework toward genuinely quantum-accelerated alignment.

In conclusion, this study shows that a Born-inspired alignment regularizer, combined with a parameter-free quantum-style kernel, can meaningfully improve abstractive summarization quality and faithfulness for long, low-resource Turkish scientific texts, while leaving the base encoder–decoder architecture untouched and incurring no inference-time overhead. The proposed QDA(+QKernel) framework, together with the multi-seed evaluation protocol and decoding recommendations, thus provides a practical and portable recipe that can be adopted or extended in future work on alignment-aware summarization.