Abstract
This paper introduces a novel theoretical framework that reformulates optimal control as a quantum search problem using Grover’s algorithm, leveraging its quadratic speedup. Specifically, the method encodes all possible control inputs into a quantum superposition state and uses a reference value interpreted as a candidate minimum to evaluate which inputs yield a lower control cost. To guide the search, we integrate a quantum comparator circuit to identify the inputs below this reference, and quantum counting to estimate their number. The reference is iteratively updated using a sigmoid-based rule until only one input satisfies the condition, thereby ensuring convergence to the global minimum within the discretized control space. Although full quantum implementation is currently infeasible due to oracle complexity and hardware limitations, we simulate the process using a classical controller as a pseudo-oracle to illustrate the algorithmic structure. This work does not aim to demonstrate performance gains but rather to establish a foundational method for embedding control synthesis within Grover-based quantum circuits. The framework paves the way for scalable quantum control systems once hardware resources permit full realization.
1. Introduction
The emergence of quantum computing and its ability to outperform classical computing in some tasks has made it an active field for researchers wishing to improve classical algorithms in terms of time complexity. One of the most notable quantum algorithms is Grover’s algorithm [1], designed for unstructured search tasks. It offers a quadratic speedup O(√N) over its classical counterparts and has been extended to find an element within an unknown-sized set of labeled elements [2]. In robotics, especially for manipulator robots, finding the optimal control law is crucial when high accuracy is required. Importantly, the optimal control law can be viewed as an optimization problem, specifically, a combinatorial optimization [3]. For quantum combinatorial optimization, there are two main approaches [4]: the quantum approximate optimization algorithm (QAOA) [5] and the use of Grover’s algorithm for global optimization. Durr and Hoyer (1999) [6] proposed a quantum algorithm to find the minimum in an unsorted list of N elements based on Grover’s search algorithm. Baritompa et al. (2005) [7] suggested another method called BBW for global optimization in Grover adaptive search (GAS), proving that Durr and Hoyer’s method was optimal for repeated objective function values but less efficient than their method for distinct objective function values. Based on this, Liu et al. [8] (2010) presented two methods that improved on the BBW method, BBW2 and BBW2D. Subsequently Liu et al. (2012) [9] introduced a hybrid quantum global optimization method that combined the generalized Grover operator and BBW2D, highlighting its outperformance in various optimization scenarios. Wang Yan (2014) [10] proposed an improved BBW method by incorporating continuous time quantum walks, showing improved performance and indicating that BBW-QW is more efficient than simulated annealing and genetic algorithms. Gilliam et al. (2021) [11] discussed the suitability of the Grover adaptive search (GAS) algorithm for constrained polynomial time optimization (CPBO) problems, demonstrating the potential for practical applications of quantum computing in optimization tasks. Baykov et al. (2022) [12] introduced an improved method called Grover binary search (GBS) to improve the efficiency of GAS for discrete optimization problems by incorporating binary search and quantum counting; they showed better results. However, this approach involves more quantum gates. Giuffrida et al. (2022) [13] proposed new parameter management strategies in the GAS algorithm, which aimed to solve unconstrained quadratic binary optimization (QUBO) problems more efficiently. The results indicate that the proposed mechanism significantly reduces Grover rotations. For more practical applications, Oliveira et al. (2007) [14] presented a quantum bit string comparator that compares two strings of n qubits each, showing that their design is more resource-efficient and highlighting its potential as an oracle for the GAS algorithm. Federer et al. (2023) [15] explored the application of the GAS algorithm to optimizing the bidirectional charging schedule of electric vehicles (EVs). The results highlight the need for further optimization of quantum circuits. Bogatyrev et al. (2023) [16] demonstrated that Grover’s algorithm can significantly improve route optimization in route planning, traffic management, and congestion forecasting. However, despite the theoretical potentials, they pointed out the lack of practical implementation due to the limitations of quantum hardware. Krol et al. (2024) [17] designed and implemented a quantum algorithm for the industrial shift planning problem using GAS. The results were validated by numerical simulation showing significant speedup. Shukla et al. (2018) [18] presented a framework for trajectory optimization formulated as a discrete space search problem. Comparing the classical and quantum search algorithms (Grover’s algorithm) in the brachistochrone problem, isoperimetric problem, and moon landing problem, the results demonstrate significant outperformance of quantum algorithms. Chella et al. (2023) [19] developed a path planning algorithm based on Grover’s search algorithm for a swarm of robots. Their results highlight the superiority of their method, with fast convergence to the target. Falk Matthew (2013) [20] explored the application of Grover’s algorithm to a quantum robot walking along a two-dimensional grid, showing that his algorithm works efficiently on a 2D grid.
Other research has addressed the topic of solving robot manipulator problems using quantum computing. Litvintseva et al. (2020) [21] performed robustness tests on a quantum PID (QPID) controller against traditional PID controllers in complex, nonlinear, and unpredictable environments. They found that QPID was more robust in controlling a carriage pole system and 3-DOF robot manipulators. Zioui et al. (2021) [22] introduced a model using a single qubit to describe the position of robotic arms, proving its equivalence to the quaternion model. Fazilat et al. (2022) [23] validated this model by simulation and introduced a new quantum formulation for the homogeneous Denavit–Hartenberg matrix. Ulyanov et al. (2023) [24] designed intelligent control systems based on quantum and soft computing technologies for industrial robots in hazardous environments. The quantum fuzzy inference (QFI) circuit outperformed classical methods throughout simulations and benchmark tests performed on balancing robots and 3-DOF manipulators. Khoshnoud et al. (2020) [25] described the use of quantum entanglement and cryptography for automation and control of dynamic systems while providing a theoretical framework that combines system dynamics with quantum states for feedback control, providing only an experimental setup. S. Dereli and R. Köker (2020) [26] proposed a quantum behavior-based particle swarm optimization (PSO) algorithm to solve the inverse kinematics problem of a seven-degree-of-freedom serial manipulator, proving the efficiency and accuracy of QPSO through the provided results in terms of solution time and position error compared to other algorithms. Abdulridha et al. (2017) [27] solved an inverse kinematics problem using a quantum neural network (QNN) and designed a QNN-PID controller, showing that the system responses were better when using the QNN-PID controller than a classical PID controller. Cheng et al. (2018) [28] performed the trajectory planning and simulation of a six-degree of freedom (6-DOF) robotic manipulator by adopting the quantum ant colony algorithm. Their results showed that the adopted strategy was superior to other algorithms. Cao et al. (2021) [29] solved the inverse kinematics problem for a 7-DOF robot using improved quantum particle swarm optimization, showing faster and more accurate convergence than PSO and QPSO algorithms. Chen et al. (2021) [30] implemented the QPSO quantum particle swarm optimization algorithm for 5-DOF robots to solve the inverse kinematics problem for a generated optimal path, achieving high accuracy, which is considered suitable for industrial applications. Cao et al. (2021) [31] combined dual quantum particle swarm optimization (DQPSO) with an extended Kalman filter (EKF) to improve the position accuracy of the robot manipulator, achieving a 99% reduction in the average error of the robot position compared with previous methods. Luo et al. (2023) [32] used the improved quantum particle swarm optimization (IQPSO) algorithm for optimal trajectory planning in joint space, proving that IQPSO achieves optimal solutions more efficiently than standard QPSO. Guo et al. (2010) [33] applied quantum particle swarm optimization (QPSO) algorithms to generate point-to-point trajectories for planar redundant manipulators, showing accurate and fast computation using QPSO compared to genetic algorithms (GA). Ayyıldız and Çetinkaya (2016) [34] compared the quantum particle swarm optimization (QPSO) algorithm with the gravitational search algorithm (GSA), the particle swarm optimization algorithm, and the genetic algorithm (GA) in trajectory planning for 4-DOF manipulators. The authors found that QPSO was the most efficient method. Similarly, Zhang et al. (2022) [35] proposed an improved QPSO to find optimal trajectories and minimize the basic perturbations in the redundant space robot. The authors demonstrated by simulation that IQPSO was superior to QPSO, PSO, and SAPSO in finding the optimal solution and convergence time. More recently, Fazilat et al. (2025) [36] tackled the development of a quantum-inspired sliding-mode control (QSMC) strategy to enhance the classic SMC’s robustness, precision, and computational efficiency with an application to a six-jointed articulated robotic arm. The results confirmed that the quantum method outperformed the classic counterpart by reducing the chattering, improving tracking accuracy, and decreasing the energy consumption. The methods found in the literature are mostly based on quantum-inspired methods or quantum methods improved for existing classical approaches. Grover’s search algorithm seems never to have been used as a potential optimization method to solve optimization problems in robotics.
In this work, we propose a new theoretical framework that reformulates the optimal control problem as a quantum search task. The control input space is encoded into quantum superposition, allowing all candidate inputs to be processed simultaneously. At each iteration, a reference value is used to represent a candidate minimum of the cost function. A quantum comparator circuit identifies the inputs whose costs are lower than this reference, and quantum counting is used to estimate how many such candidates exist. The reference is then iteratively updated through a sigmoid-based rule until only one candidate remains, thereby guaranteeing convergence to the global minimum within a discretized resolution. Although a full simulation of the proposed method is currently infeasible due to hardware limitations, in the results section, we simplify the task by using pseudo-oracle to demonstrate the theoretical flow of the algorithm and validate the feasibility of the proposed quantum control architecture through classical simulation.
This work reflects the broader context of current research in quantum technologies and contributes to the ongoing transition toward practical quantum computing [37,38].
The remainder of this paper is organized as follows. Section 2 presents the background and foundational tools, including quantum computing principles, the robotic manipulator model, and supporting quantum components. Section 3 introduces the proposed optimization methodology, which reformulates the control synthesis task as a quantum search problem guided by quantum counting. Section 4 reports the simulation results obtained using a pseudo-oracle to illustrate the theoretical framework. Finally, Section 5 concludes the paper by summarizing the contributions and outlining future research directions.
2. Background and Preliminaries
2.1. Quantum Computing
2.1.1. Qubit State
The quantum bit, or qubit, is the unit of information of quantum computing. Its state can exist in two eigenstates: or in a linear combination of both. This linear combination is referred to as a superposition state. Mathematically, this can be expressed as follows:
where and are the amplitudes of in the directions of the eigenstates and , respectively.
and are complex numbers that satisfy the normalization condition . This condition ensures that the probability of obtaining is and the probability of obtaining is as the sum of both gives 1.
According to Dirac notation, the superposition expressed in (1) can be represented with the following column vector:
Subsequently, the vectors representing the eigenstates and are as follows:
Hence, the qubit state can be described geometrically using the Bloch sphere as illustrated in Figure 1. For simplicity, the figure illustrates the geometrical representation considering real numbers for and [39].
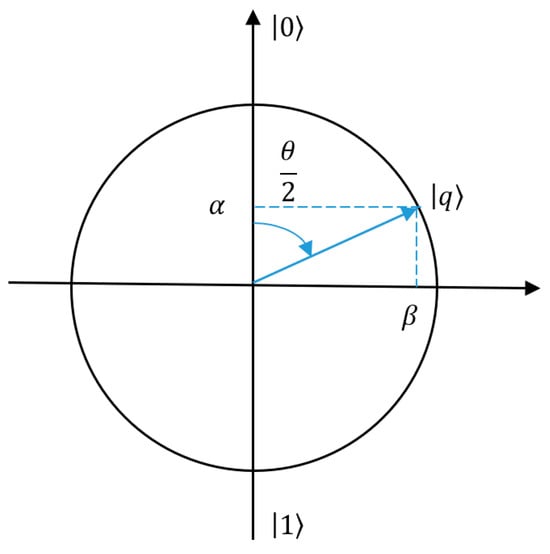
Figure 1.
Geometrical representation of a qubit state on the Bloch sphere (image adapted from [39]).
2.1.2. Quantum Gates
Quantum gates operate on the qubit state by changing its phase, meaning they act as a linear unitary transformation represented by matrices . From a geometric point of view, these unitary transformations are rotations in the Bloch sphere. This means that they are reversible (their conjugate is equal to their inverse: ). The most common quantum gates that operate with a single qubit state are the following:
The X Gate:
This is the quantum equivalent of the classical NOT gate. It flips the current state and is expressed as follows:
The Z Gate:
This gate changes the relative phase between the eigenstates and without changing the state basis. Thus, it can be defined as follows:
The Y Gate:
This gate is a combination of the X and Z gates. It is referred to as a bit phase flip. It maps to and to . This can be formulated as the following:
The Hadamard gate:
The Hadamard gate is one of the most important gates in quantum computing. It takes the eigenstate or and produces an equal superposition of both states. It is represented as follows:
The CNOT Gate:
The controlled NOT (CNOT) gate is a multi-qubits gate. It involves a control qubit and a target qubit. It performs an X gate on the target qubit if the control qubit is in the state . If the control qubit is , the target qubit remains unchanged. This can be expressed as in Equation (8).
The Toffoli Gate:
The Toffoli gate consists of two control qubits and one target qubit. The operation performs an X gate on the target qubit only when both control qubits are in the state .
The matrix representations and functionalities of the gates described above follow the definitions presented in [Nielsen and Chuang, 2010] [40].
2.2. Robotic Manipulator Model
2.2.1. Forward Kinematics
Robotic manipulators are composed of rigid bodies called links connected to each other by joints. The joints can have degrees of freedom as prismatic or revolute joints. At the end, the robotic arm has an end effector to interact with the environment and perform tasks.
The forward kinematic model describes the position and orientation of the end effector in the Cartesian space for given joint positions of the robot. Denavit–Hartenberg is a conventional method to obtain the transformation matrix that can describe the end effector. The D–H formulation requires only four parameters to define each subsequent transformation matrix. Based on the D–H method, each joint is assigned a coordinate frame. For revolute joints, the rotation axis is selected as the axis, and for prismatic joints, the Z axis is selected coincident with the prismatic joint and parallel to the sliding direction. The axis of the joint should be perpendicular to the and axes. Then, the homogeneous transformation is represented as a product of four basic transformations, as per the following:
where is a rotation matrix and is a translation matrix.
Hence, Equation (10) stands.
are parameters associated with joint and link , called the joint angle, link offset, link length, and link twist, respectively, and defined as
: The angle of rotation about the to let and parallel.
: The offset along the axis to align the origins of the coordinate frames.
: The distance along the axis between the origins of the coordinate frames.
: The angle of rotation about the axis to align with axis [41].
2.2.2. Dynamics
To derive the dynamics of a system, we can use the Lagrange formulation, which is based on the system’s kinetic and potential energy. The Lagrangian is given by the following:
where is the total kinetic energy and is the total potential energy of the system, represents the generalized joints’ variable vector, and is the joint’s velocity vector.
The kinetic energy can be expressed as follows:
where and are the linear and angular velocities. is the inertia tensor relative to the center of mass of link i when expressed in the base frame, and is the rotation matrix from link frame to the base frame.
The potential energy is calculated as follows:
where is the gravity acceleration homogeneous vector in the base frame, e.g., if is the vertical axis, and is the center of mass position of link in the world frame.
The Lagrange equation is formulated as follows:
where is the torque applied to each joint .
Finally, the equation of motion is derived in the following form:
where , , and are mass matrix, Coriolis, centrifugal, and Gravitational terms, respectively [42].
2.2.3. The Control Method
The control approach adopted incorporates Grover’s algorithm as an optimization method combined with feedback linearization to construct the optimal control for the proposed model.
The feedback linearization control law is formulated as follows:
By substituting the expression of into Equation (15), we obtain the following:
The above differential Equation (17) can be discretized by defining and as in Equation (18).
where is the sampling period.
After discretization, we describe the resulting difference equation as a quantum circuit using only arithmetic circuits. Then, we set in a superposition state and map it to angle solutions with the given resolution which is the number of qubits used. We then compare the desired angles with the mapped output to obtain the error . This error is squared, and the elements with values less than the chosen threshold are marked. Finally, we estimate the number of these elements using Quantum Phase Estimation along with Grover’s Algorithm. We repeat the process until the specified number of elements is achieved.
2.2.4. Grover’s Algorithm
Grover’s algorithm is a quantum search algorithm for unstructured search. It offers quadratic speedup compared to its classical counterparts, since for the same problem we can solve it using a classical computer with time complexity .
The goal in Grover’s algorithm is to find an element in a database, where . The algorithm is divided into three steps, as follows:
State preparation: qubits are initialized. Then, a Hadamard gate is applied to set them all to a uniform superposition state, where all states have equal probability amplitudes, as described in Equation (19).
Grover’s Oracle: We mark the element we are looking for by inversing its phase. Suppose that we have a function that maps inputs and to a single bit output . Therefore, we can formulate the oracle as follows:
The construction of the oracle for real-world problems could be challenging, which makes Grover’s algorithm less efficient.
Diffusion operator: After marking , we apply the diffusion operator to increase the marked state amplitude and reduce the unmarked ones.
We repeat the last two steps times to enhance the probability of measuring the marked state.
Searching items within an unstructured database requires iterations using Grover’s algorithm [43].
2.2.5. Quantum Phase Estimation
Quantum Phase Estimation (QPE) is a quantum algorithm that estimates the eigenvalue (or phase) of an eigenvector of a unitary operator .
One of the main elements of QPE is the quantum Fourier transform, which is defined by the following equation and depicted in Figure 2.
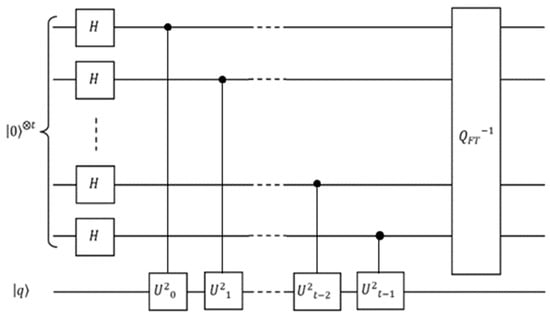
Figure 2.
Quantum Phase Estimation (QPE) circuit diagram utilizing controlled unitary operations and inverse Quantum Fourier Transform. (Image adapted from [44]).
Before applying the inverse QFT block, we have the following state:
After applying the inverse quantum Fourier transform, we obtain
Thus, the measurement of the ancillary qubits gives an integer j that is within of . This estimate can be improved by increasing the value of [44].
2.2.6. Quantum Counting
Quantum counting applies Quantum Phase Estimation (QPE) to the Grover search algorithm to determine the number of marked solutions for the given search problem. Specifically, it estimates the number of marked elements in a search space [44].
The key steps are as follows:
Initialization: We start by preparing a uniform superposition of all states in the database.
Grover Operator: We apply Grover operator , where is the diffusion operator and is the oracle that marks the items.
Quantum Phase Estimation: We apply QPE to the Grover operator to estimate the phase , as defined in Equation (26).
where is the decimal obtained value and is the number of ancillas used in QPE.
The obtained phase from QPE has a relation to the number of marked items. After measuring the phase register, we can calculate the number of marked items as follows:
2.2.7. Quantum Bit Comparator Circuit
The quantum bit string comparator (QBSC) compares two quantum states representing bit strings and identifies which of them is the largest or lowest, or if they are equal. Given two quantum states and , the QBSC is a unitary transformation that works as follows:
The ancilla has qubits, since the first ancilla bit does not carry important information and the last two indicate the comparison results. For instance:
If then and .
If then and .
If then and y .
Figure 3 illustrates the quantum circuit of the comparator between two strings of three qubits.
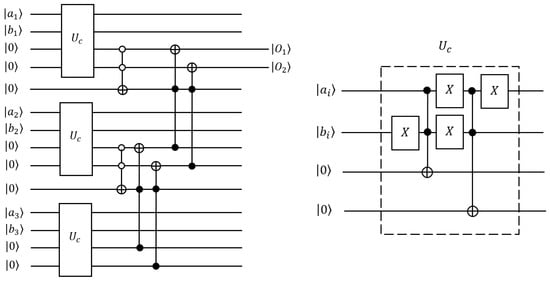
Figure 3.
Quantum comparator circuit diagram for comparing two three-qubit strings bitwise (image adapted from [14]).
The circuit compares the quantum bit string bit to bit from the left to the right, where the most significant bit is on the left.
and are the dominant bits. If then and . Therefore, . Subsequently, if , then the output will be the result of the next bit comparison and so on [14].
C1 is a Toffoli gate activated at zero.
2.2.8. Path Planning
Path planning is the description of a robot’s end effector movement in the Cartesian 3D frame. To generate the path, we implemented a fifth-order polynomial, which is considered a conventional method to design a trajectory in both Cartesian and joints’ schemes.
To determine the coefficients, we must consider the following initial conditions:
where is the final time.
are the starting and end points, respectively.
We obtain
The trajectory depends on time, but in the paper’s implementation, we considered only spatial point profiles, for simplification [45].
3. Proposed Methodology
The idea of using Grover for optimization purposes could be highly robust, as finding the minimum is almost guaranteed theoretically. Initially, we initialize qubits in a superposition state forming strings of qubits. We then apply a unitary operation that ensures the mapping as depicted in Figure 4. In an optimization context, is the objective function of which the minima need to be determined.
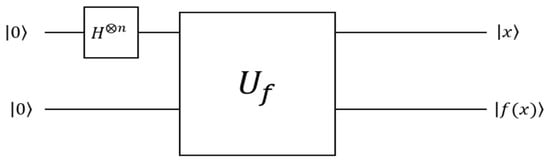
Figure 4.
Unitary operation circuit for mapping to .
This approach permits the exploration of the entire search space at once, leveraging the superposition. Next, a comparator circuit is applied as an oracle to mark all elements below the chosen arbitrary reference value by cutting the search space. Quantum counting then provides the number of marked elements by iteratively updating the reference value according to the marked elements. The algorithm narrows the set of the potential candidates: if the number of marked elements is less than the reference value, the repeated circuit execution is stopped; otherwise, we continue to update the reference value. Eventually, we consider the last updated reference value as the optimal minima.
The update of reference value is a crucial part of the algorithm time complexity. We propose in this paper to use a modified sigmoid function that maps to , such as
where .
The parameter is adjusted according to how fast it goes from 0 to 1.
is the first number of marked elements.
is the number of current marked elements.
The reference value is updated as follows:
where is a chosen incrementing or decrementing constant.
If , then the algorithm is out of search space scope.
Figure 5, Figure 6 and Figure 7 illustrate the optimization procedure according to the proposed methodology for different thresholds. Minimizing the reference value means seeking the minimum value within the search space.
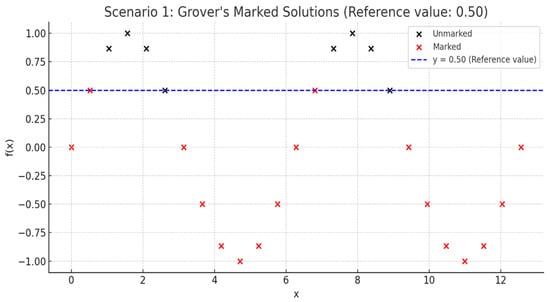
Figure 5.
Optimization scenario illustrating iterative refinement using Grover’s algorithm and quantum counting for threshold updates.
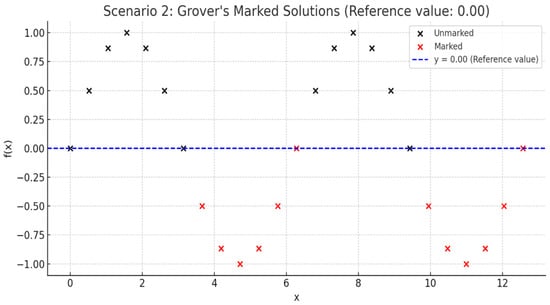
Figure 6.
Second optimization scenario demonstrating progressive narrowing of marked candidate solutions via iterative quantum counting.
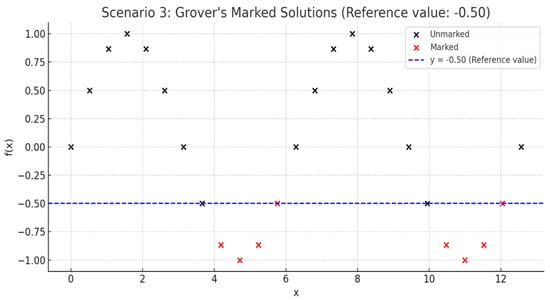
Figure 7.
Third optimization scenario showing the iterative convergence process toward the global minimum using quantum counting and comparator circuits.
In practical applications, estimation of the number of marked elements using quantum counting is sensitive to the accuracy of phase estimation. The phase θ obtained via the Quantum Phase Estimation (QPE) subroutine depends on the number of ancilla qubits used and is susceptible to noise and discretization error. An imprecise estimate of θ can result in incorrect calculation of the number of marked items M, affecting the reference update and convergence behavior of the optimization algorithm. This sensitivity can be mitigated by increasing the number of ancilla qubits, which improves the resolution of the phase estimation. Alternatively, iterative or adaptive QPE schemes may be employed to enhance precision without significantly increasing circuit depth. However, for robust implementation on near-term quantum hardware, quantum error correction mechanisms would be required to handle decoherence and gate noise, which remain a limitation for current devices. In our simulation, these effects are ignored in our noise-free classical emulation, but must be addressed in future hardware-based implementations.
Figure 8 illustrates a flowchart describing the proposed quantum-based optimization methodology. The algorithm initializes quantum states in a superposition, maps control inputs to their respective costs, and employs a quantum comparator circuit to mark inputs with costs lower than a dynamically updated reference value. Quantum counting estimates marked elements, and the algorithm iteratively updates this reference until the marked elements fall below a threshold, thus converging on an optimal solution. This clearly illustrates the step-by-step logic and feedback loops integral to the proposed Grover-based optimal control strategy.
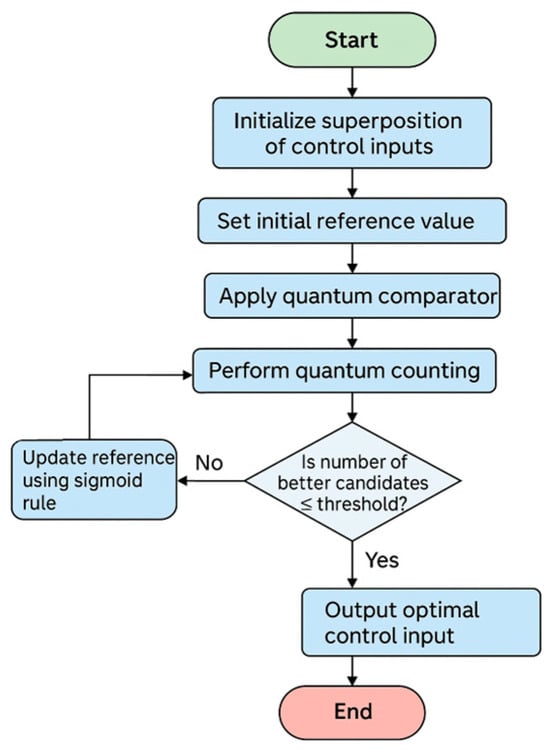
Figure 8.
Flowchart of the proposed Grover-based quantum optimization methodology, outlining key algorithmic steps.
4. Results
All the simulations were performed on MATLAB R2023a using an Intel(R) computer, Core (TM) i7-8700 CPU and 8 GB of RAM, running on Windows 10.
The objective of this experiment was to explore the use of Grover’s algorithm to optimize the control inputs for a second-order system that models the actuators of the robotic arm. By applying Grover’s algorithm, we aim to leverage quantum computing’s potential to identify optimal control inputs efficiently.
The considered robotic arm model in this study is a six-axis robotic arm with parameters and joint constraints as in Table 1 and Table 2, respectively. The robot’s frames and parameters are illustrated in Figure 9.

Table 1.
The robot’s parameters according to the D–H formalism [23,36].

Table 2.
Mechanical characteristics of the robot [23,36].
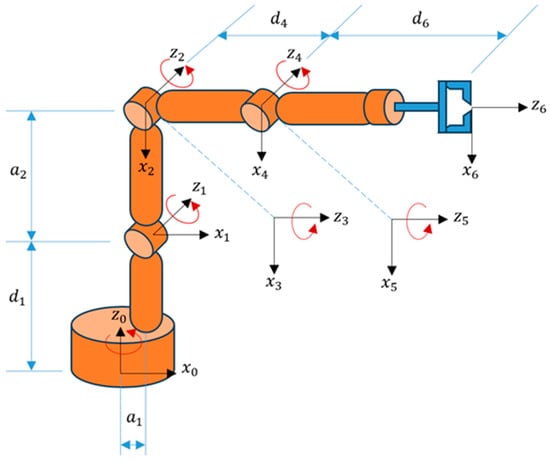
Figure 9.
Frames and parameters of the robot according to the D–H formalism [23,36].
The objective is to make each joint follow a desired trajectory (sine wave, ramp, and circle). The control objective is to determine the optimal control input , which corresponds to the angular acceleration required to follow the desired trajectory.
The desired trajectory for each joint’s motion is modeled as over a time interval from 0 to 10 s with a sampling interval of 0.1 s. The first derivative of the desired trajectory, , represents the desired angular velocity. The second derivative of the desired trajectory is the angular acceleration, which is equal to the control input .
The optimal control law was first calculated using the backstepping methodology after performing feedback linearization. We obtained a second-order differential equation as follows:
The control law is computed as in the following:
Encoding control inputs into quantum states using Grover’s algorithm requires mapping the calculated optimal control values in binary to find the optimal element encoded into quantum states. The control inputs were scaled in a range of [−10, 10] and then further scaled to fit within a resolution of 10 bits (ranging from 0 to 1024) using Equation (36). This allowed us to encode the optimal control inputs into quantum states that could be manipulated by Grover’s algorithm.
where is the number of the qubits.
Grover’s algorithm was then used to amplify the quantum states that correspond to the optimal control inputs. To this end, we started by creating a qubit string that represents the control input and initialized it in a superposition using Hadamard gates, followed by Grover iterations designed to amplify the desired states. Although we have omitted the oracle design to reduce the complexity of the problem, the calculated control serves as a pseudo-oracle marking the control values that align with the desired trajectory. Ultimately, we aim to highlight the potential of Grover’s algorithm in optimization contexts; in real applications where a string represents the optimal control in a superposition state and the oracle is a quantum circuit that marks the optimal control, we would apply the Grover diffusion operator circuit to measure the optimal control in each resolution.
After we make a measurement on the quantum system, the results need to be decoded back from binary into the range of control inputs. The optimal control is then applied to the system to simulate its response. The equation below shows how to decode the optimal control value within the range of the control input and resolution.
The system’s response, , was computed by integrating the optimal control inputs over time to determine the resulting angular velocities and positions.
Figure 10 and Figure 11 illustrate the comparison between the desired trajectory () and the system’s response using the optimal control inputs derived through Grover’s algorithm ().
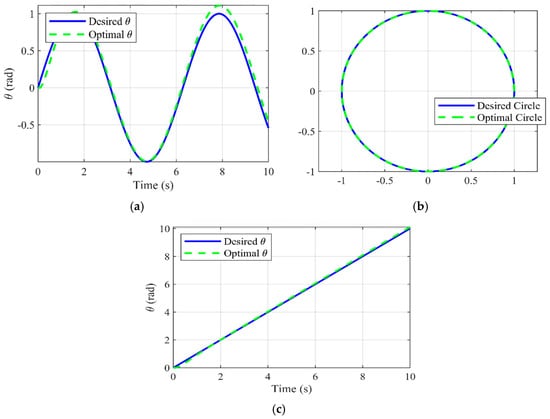
Figure 10.
System response using Grover’s search algorithm-based optimal control using 12 qubits: (a) sine wave, (b) circle, and (c) straight line.
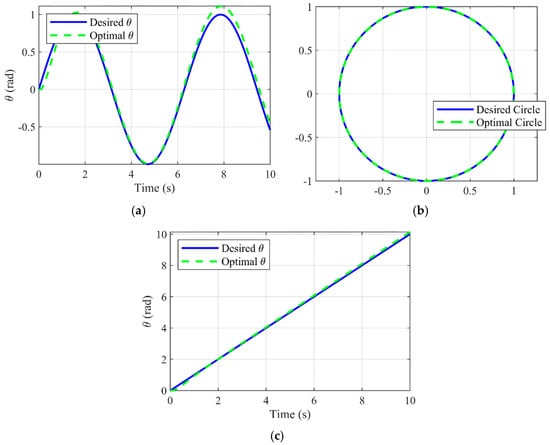
Figure 11.
System response using Grover’s search algorithm-based optimal control using 10 qubits: (a) sine wave, (b) circle, and (c) straight line.
In this case, we used 12 qubits for trajectory tracking considering three different trajectories: sine wave, circle, and straight line.
The results meet the expectation and show that the optimal control perfectly tracks the desired trajectory, demonstrating the effectiveness of Grover’s algorithm in amplifying the correct control inputs. The small deviation suggests parameter tuning of the controller. However, such adjustment would be unnecessary in real-case scenarios because it only reflects oracle oversimplification.
Moreover, the results suggest that the number of qubits only reflects the resolution, indicating that the required qubit number depends on problem formulation and desired resolution. This relationship allows us to reduce the complexity of the quantum system, since, in our case, we achieved similar performance using fewer qubit states.
Figure 12 shows the relationship between the RMSE and the number of qubits used for the three trajectories. As the resolution increases, the error generally decreases. However, we notice that, beyond 8 qubits, the error plateaus, suggesting that for the given problem, 8 qubits could be sufficient. Increasing the resolution further could increase the complexity of the quantum system without any significant improvement in accuracy.
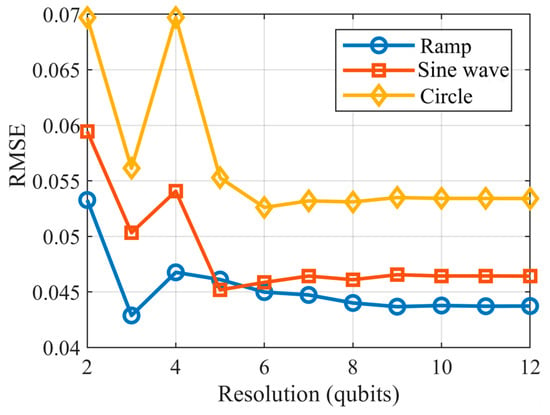
Figure 12.
RMSE vs. resolution for different trajectory types.
The use of quantum state amplification provides a novel approach to optimizing control inputs, reducing reliance on exhaustive classical computations.
This experiment successfully demonstrated the application of Grover’s algorithm to optimize control inputs for a second-order system representing a robotic arm. By encoding the control problem into quantum states and using Grover’s iterations to amplify the desired states, the algorithm efficiently identified the optimal control inputs. The approach showcases the potential of quantum computing in control optimization tasks, providing a pathway for further research in real-time, high-dimensional control systems using quantum algorithms. While the proposed method is not evaluated through direct numerical comparison with existing quantum-inspired control techniques (e.g., QPSO, GA), it offers distinct theoretical advantages. Most of the existing methods operate as heuristic solvers and cannot guarantee convergence to the global minimum. In contrast, our method—based on quantum counting and Grover’s operator—ensures convergence to the minimum within the discretized control space. Furthermore, unlike methods such as QPSO that require iterative fitness evaluations and parameter tuning, our method operates as a structured quantum search guided by an oracle and counting mechanism, offering quadratic efficiency over exhaustive search.
However, it should be noted that, due to the available resource limitations, full oracle circuit implementation was not feasible. Instead, we opted to replace the oracle part with a classical calculation. More specifically, we used a backstepping controller as a pseudo-oracle. Practically, these results can be understood by imagining the backstepping controller as an oracle that knows and marks what the optimal control is at each time step. This simplifies implementation while leveraging classical control theory as a black box quantum oracle to achieve oracle-like behavior. Additionally, this strategy highlights Grover’s algorithm as a potential optimization technique where there are enough resources to fully implement it.
5. Conclusions
The application of Grover’s algorithm as an optimization technique and control strategy for a six-jointed robotic arm demonstrates its potential to offer a new paradigm in control theory, where the task of computing the control law is reformulated as a search problem. By encoding all candidate control inputs in a superposition state and iteratively refining a reference using quantum counting, the proposed method guarantees convergence to the global minimum within a discretized space. This framework shows high theoretical efficiency in applications requiring both speed and accuracy, benefiting from the parallel evaluation enabled by quantum superposition.
The simulation results, using a classical pseudo-oracle, confirm the feasibility of the approach: trajectory tracking was achieved accurately across various reference trajectories, including sine wave, circle, and straight line. Moreover, we observed that increasing the resolution beyond 8 qubits yields diminishing returns in accuracy, as illustrated by the RMSE trends in Figure 12. This finding reflects an important trade-off between precision and quantum resource requirements, which holds practical relevance for future hardware-limited implementations.
One of the main advantages of the proposed method is that it eliminates the need to explore the entire control space exhaustively, as in metaheuristic methods. Instead, it relies on structured quantum logic to converge on optimal inputs, reducing computational effort significantly. While this work does not implement a full quantum oracle due to hardware limitations, the substitution of a classical feedback controller demonstrates the method’s conceptual validity and supports its potential for future implementation.
The study also highlights the inherent resolution problem in quantum encoding, where precision depends on the number of qubits used. Addressing this challenge either by improving encoding strategies or enhancing quantum hardware is critical for extending the practical applicability of this framework.
While this framework presents a promising approach to quantum control synthesis, it is important to acknowledge its current limitations. First, the quantum oracle was not implemented and instead replaced with a classical pseudo-oracle, which limits the demonstration to a conceptual simulation rather than a true quantum implementation. Second, quantum counting is sensitive to noise and phase estimation accuracy, which can affect convergence when deployed on real quantum hardware. Finally, the feasibility of this method in practical settings is constrained by current limitations in quantum hardware, particularly the lack of fault-tolerant qubit systems and high-fidelity quantum gates. These factors must be addressed in future work to realize the full potential of Grover-based control optimization.
Author Contributions
Conceptualization, M.S.D.; Methodology, M.S.D. and N.Z.; Validation, N.Z.; Formal analysis, M.S.D.; Investigation, M.S.D.; Resources, N.Z.; Data curation, M.S.D. and N.Z.; Writing—original draft, M.S.D. and N.Z.; Writing—review & editing, N.Z.; Visualization, M.S.D. and N.Z.; Supervision, N.Z.; Project administration, N.Z.; Funding acquisition, N.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by NSERC Canada.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar]
- Boyer, M.; Brassard, G.; Høyer, P.; Tapp, A. Tight Bounds on Quantum Searching. Fortschritte Der Physik 1998, 46, 493–505. [Google Scholar] [CrossRef]
- Du, D.-Z.; Pardalos, P.; Hu, X.; Wu, W. (Eds.) Introduction to Combinatorial Optimization; Springer International Publishing: Cham, Switzerland, 2022; pp. 1–11. [Google Scholar]
- Sano, Y.; Mitarai, K.; Yamamoto, N.; Ishikawa, N. Accelerating Grover Adaptive Search: Qubit and Gate Count Reduction Strategies With Higher Order Formulations. IEEE Trans. Quantum Eng. 2024, 5, 3101712. [Google Scholar] [CrossRef]
- Farhi, E.; Goldstone, J.; Gutmann, S. A quantum approximate optimization algorithm. arXiv 2014, arXiv:1411.4028. [Google Scholar]
- Durr, C.; Høyer, P.; A Quantum Algorithm for Finding the Minimum. January 1999. Available online: https://arxiv.org/abs/quant-ph/9607014 (accessed on 25 May 2024).
- Baritompa, W.P.; Bulger, D.W.; Wood, G.R. Grover’s Quantum Algorithm Applied to Global Optimization. SIAM J. Optim. 2005, 15, 1170–1184. [Google Scholar] [CrossRef]
- Liu, Y.; Koehler, G.J. Using modifications to Grover’s Search algorithm for quantum global optimization. Eur. J. Oper. Res. 2010, 207, 620–632. [Google Scholar] [CrossRef]
- Liu, Y.; Koehler, G.J. A hybrid method for quantum global optimization. J. Glob. Optim. 2012, 52, 607–626. [Google Scholar] [CrossRef]
- Wang, Y. Global Optimization with Quantum Walk Enhanced Grover Search. In Proceedings of the Design Automation Conference, Buffalo, NY, USA, 17–20 August 2014. [Google Scholar]
- Gilliam, A.; Woerner, S.; Gonciulea, C. Grover Adaptive Search for Constrained Polynomial Binary Optimization. Quantum 2021, 5, 428. [Google Scholar] [CrossRef]
- Baykov, A.; Protasov, S. Grover Binary Search for Discrete Quantum Optimization. In Proceedings of the Nonlinearity, Information and Robotics, Innopolis, Russia, 4 July 2022. [Google Scholar]
- Giuffrida, L.; Volpe, D.; Cirillo, G.A.; Zamboni, M.; Turvani, G. Engineering Grover Adaptive Search: Exploring the Degrees of Freedom for Efficient QUBO Solving. IEEE J. Emerg. Sel. Top. Circuits Syst. 2022, 12, 614–623. [Google Scholar] [CrossRef]
- Oliveira, D.; Ramos, R. Quantum bit string comparator: Circuits and applications. Quantum Comput. Comput. 2017, 7, 17–26. [Google Scholar]
- Federer, M.; Lenk, S.; Müssig, D.; Wappler, M.; Lässig, J. Constrained Grover Adaptive Search for Optimization of the Bidirectional EV Charging Problem; GI Quantum Computing Workshop: Berlin, Germany, 2023. [Google Scholar]
- Bogatyrev, V.A.; Moskvin, V.S. Application of Grover’s Algorithm in Route Optimization. In Proceedings of the 2023 Intelligent Technologies and Electronic Devices in Vehicle and Road Transport Complex (TIRVED), Moscow, Russian, 15–17 November 2023; pp. 1–5. [Google Scholar]
- Krol, A.M.; Erdmann, M.; Mishra, R.; Singkanipa, P.; Munro, E.; Ziolkowski, M.; Luckow, A.; Al-Ars, Z. QISS: Quantum Industrial Shift Scheduling Algorithm. arXiv 2024, arXiv:2401.07763. [Google Scholar]
- Shukla, A.; Vedula, P. Trajectory optimization using quantum computing. J. Glob. Optim. 2019, 75, 199–225. [Google Scholar] [CrossRef]
- Chella, A.; Gaglio, S.; Mannone, M.; Pilato, G.; Seidita, V.; Vella, F.; Zammuto, S. Quantum planning for swarm robotics. Robot. Auton. Syst. 2023, 161, 104362. [Google Scholar] [CrossRef]
- Falk, M. Quantum Search on the Spatial Grid. arXiv 2013, arXiv:1303.4127. [Google Scholar]
- Litvintseva, L.V.; Nikolaeva, A.V.; Ulyanov, S.V. Quantum Software Engineering Supremacy PT 2. Application of Quantum Computing Optimizer. Int. J. Educ. (IJE) 2020, 5. [Google Scholar] [CrossRef]
- Zioui, N.; Mahmoudi, Y.; Mahmoudi, A.; Tadjine, M.; Bentouba, S. A novel quantum-computing-based quaternions model for a robotic arm position. Int. J. Comput. Intell. Control 2021, 13, 71–77. [Google Scholar]
- Fazilat, M.; Zioui, N.; St-Arnaud, J. A novel quantum model of forward kinematics based on quaternion/Pauli gate equivalence: Application to a six-jointed industrial robotic arm. Results Eng. 2022, 14, 100402. [Google Scholar] [CrossRef]
- Ulyanov, S.; Reshetnikov, A.; Zrelova, D. Industrial robotic intelligent robust control system: Applying quantum soft computing technologies and quantum software engineering in unpredicted control situations. Softw. Syst. 2023, 36, 26–45. [Google Scholar]
- Khoshnoud, F.; Esat, I.I.; Javaherian, S.; Bahr, B. Quantum Entanglement and Cryptography for Automation and Control of Dynamic Systems. arXiv 2020, arXiv:2007.08567. [Google Scholar]
- Dereli, S.; Köker, R. A meta-heuristic proposal for inverse kinematics solution of 7-DOF serial robotic manipulator: Quantum behaved particle swarm algorithm. Artif. Intell. Rev. 2020, 53, 949–964. [Google Scholar] [CrossRef]
- Abdulridha, H.M.; Hassoun, Z.A. Control Design of Robotic Manipulator Based on Quantum Neural Network. J. Dyn. Syst. Meas. Control 2017, 140, 061002. [Google Scholar] [CrossRef]
- Cheng, X.; Zhao, M. Analysis on the Trajectory Planning and Simulation of Six Degrees of Freedom Manipulator. In Proceedings of the 2018 3rd International Conference on Mechanical, Control and Computer Engineering (ICMCCE), Huhhot, China, 14–16 September 2018. [Google Scholar]
- Cao, Y.; Wang, W.; Ma, L.; Wang, X. Inverse Kinematics Solution of Redundant Degree of Freedom Robot Based on Improved Quantum Particle Swarm Optimization. In Proceedings of the 2021 IEEE 7th International Conference on Control Science and Systems Engineering (ICCSSE), Qingdao, China, 30 July–1 August 2021. [Google Scholar]
- Chen, Y.-T.; Chen, W.-J. Optimizing the obstacle avoidance trajectory and positioning error of robotic manipulators using multigroup ant colony and quantum-behaved particle swarm optimization algorithms. Int. J. Innov. 2021, 17, 595–611. [Google Scholar]
- Cao, H.Q.; Nguyen, H.X.; Nguyen, T.T.; Nguyen, V.Q.; Jeon, J.W. Robot Calibration Method Based on Extended Kalman Filter–Dual Quantum Behaved Particle Swarm Optimization and Adaptive Neuro-Fuzzy Inference System. IEEE Access 2021, 9, 132558–132568. [Google Scholar] [CrossRef]
- Luo, L.; Guo, T.; Cui, K.; Zhang, Q. Trajectory Planning in Robot Joint Space Based on Improved Quantum Particle Swarm Optimization Algorithm. Appl. Sci. 2023, 13, 7031. [Google Scholar] [CrossRef]
- Guo, J.; Wang, X.; Zheng, X. Trajectory planning of redundant robot manipulators using QPSO algorithm. In Proceedings of the 2010 8th World Congress on Intelligent Control and Automation, Jinan, China, 7–9 July 2010. [Google Scholar]
- Ayyıldız, M.; Çetinkaya, K. Comparison of four different heuristic optimization algorithms for the inverse kinematics solution of a real 4-DOF serial robot manipulator. Neural Comput. Appl. 2015, 27, 825–836. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, F.; Nie, G.; Zhang, J. Optimal Trajectory Planning for Minimizing Base Disturbance of a Redundant Space Robot with IQPSO. J. Electr. Comput. Eng. 2022, 2022, 3398810. [Google Scholar] [CrossRef]
- Fazilat, M.; Zioui, N. Quantum-Inspired Sliding-Mode Control to Enhance the Precision and Energy Efficiency of an Articulated Industrial Robotic Arm. Robotics 2025, 14, 14. [Google Scholar] [CrossRef]
- Illiano, J.; Caleffi, M.; Manzalini, A.; Cacciapuoti, A.S. Quantum Internet protocol stack: A comprehensive survey. Comput. Netw. 2022, 213, 109092. [Google Scholar] [CrossRef]
- Rozenman, G.G.; Kundu, N.K.; Liu, R.; Zhang, L.; Maslennikov, A.; Reches, Y.; Youm, H.Y. The quantum internet: A synergy of quantum information technologies and 6G networks. IET Quantum Commun. 2023, 4, 147–166. [Google Scholar] [CrossRef]
- Lahoz-Beltra, R. Quantum Genetic Algorithms for Computer Scientists. Computers 2016, 5, 24. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Spong, M.W.; Hutchinson, S.; Vidyasagar, M. Forward Kinematics: The Denavit-Hartenberg Conventio. In Robot Modeling and Control; John Wiley & Sons, Inc.: New York, NY, USA; Chichester, UK; Weinheim, Germany; Brisbane, Australia; Singapore; Toronto, ON, Canada, 1989; pp. 65–69. [Google Scholar]
- Shuman, A.M. Modeling and Control of 6-Axis Robot Arm; Division of Automatic Control Department of Electrical Engineering Linköping University: Linköping, Sweden, 2020. [Google Scholar]
- Liu, Y.-C.; Liu, M.-F. Implementation of Grover’s Algorithm & Bernstein-Vazirani Algorithm with IBM Qiskit. J. Inform. Web Eng. 2024, 3, 76–95. [Google Scholar]
- Chung, N.; Nepomechie, R.I. Quantum counting, and a relevant sign. arXiv 2023, arXiv:2310.07428v1. [Google Scholar]
- Parikh, P.A.; Trivedi, R.R.; Joshi, K.D. Trajectory planning of a 5 DOF feeding serial manipulator using 6th order polynomial method. J. Phys. Conf. Ser. 2021, 1921, 12088. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).