SPaRLoRA: Spectral-Phase Residual Initialization for LoRA in Low-Resource ASR

Abstract

Parameter-efficient fine-tuning (PEFT) methods like Low-Rank Adaptation (LoRA) are widely used to adapt large pre-trained models under limited resources, yet they often underperform full fine-tuning in low-resource automatic speech recognition (ASR). This gap stems partly from initialization strategies that ignore speech signals’ inherent spectral-phase structure. Unlike SVD/QR-based approaches (PiSSA, OLoRA) that construct mathematically optimal but signal-agnostic subspaces, we propose SPaRLoRA (Spectral-Phase Residual LoRA), which leverages Discrete Fourier Transform (DFT) bases to create speech-aware low-rank adapters. SPaRLoRA explicitly incorporates both magnitude and phase information by concatenating real and imaginary parts of DFT basis vectors, and applies residual correction to focus learning exclusively on components unexplained by the spectral subspace. Evaluated on a 200-h Sichuan dialect ASR benchmark, SPaRLoRA achieves a 2.1% relative character error rate reduction over standard LoRA, outperforming variants including DoRA, PiSSA, and OLoRA. Ablation studies confirm the individual and complementary benefits of spectral basis, phase awareness, and residual correction. Our work demonstrates that signal-structure-aware initialization significantly enhances parameter-efficient fine-tuning for low-resource ASR without architectural changes or added inference cost.

1. Introduction

Language is the most fundamental and efficient tool for human communication and an essential vehicle for cultural transmission [1]. Both Mandarin Chinese and ethnic minority languages are treasured components of Chinese civilization and serve as vital symbols of their respective ethnic identities.

However, in the context of globalization and increasing cultural integration among ethnic groups, the preservation and transmission of minority language heritage has become increasingly urgent.

Sichuanese, as a representative branch of Southwestern Mandarin within the Chinese dialect continuum, not only embodies the millennia-old historical memory and regional culture of the Bashu area but also plays an irreplaceable role in daily communication, local performing arts (such as Sichuan opera), folk literature, and intangible cultural heritage.

Yet, with the widespread promotion of Standard Mandarin, accelerated urbanization, and shifting linguistic habits among younger generations, the frequency of Sichuanese usage and its intergenerational transmission are experiencing significant decline [2]. Certain dialectal features are even weakening or disappearing altogether.

Large-scale pre-trained models have achieved remarkable success in natural language processing [3,4], computer vision [5,6,7], and automatic speech recognition (ASR) [8,9]. These models are typically pre-trained on massive general-domain data, exhibiting strong generalization, and are subsequently adapted to downstream tasks via full fine-tuning (FT). However, as the number of parameters and the scale of data continue to grow, the computational, storage, and energy costs of FT increase dramatically, making it prohibitive on edge devices or in low-resource scenarios.

To alleviate this issue, parameter-efficient fine-tuning (PEFT) methods have been proposed. The core idea of PEFT is to update only a small fraction of the model parameters (often <1%) while freezing the majority of the pre-trained weights, thereby significantly reducing training costs while preserving model performance. Representative approaches include Adapter modules [10], Prefix-Tuning [11], Prompt Tuning, and Low-Rank Adaptation (LoRA) [12].

Among them, LoRA has become one of the most widely adopted PEFT techniques due to its architectural neutrality, zero inference latency, simplicity of implementation, and strong empirical performance. LoRA constrains weight updates to low-rank matrix decompositions, drastically reducing the number of trainable parameters while maintaining the inference efficiency of the original model. Kalajdzievski et al. [13] demonstrated that increasing the rank, combined with an appropriate scaling factor, can significantly boost performance, albeit at the cost of exponentially increasing the number of trainable parameters. Moreover, LoRA has shown promising potential in low-resource speech recognition [14,15].

Despite its practical success, a non-negligible performance gap still exists between LoRA and full fine-tuning in low-resource ASR tasks, often attributed to limited trainable parameters or sub-optimal initialization [16]. We argue that this gap is not merely due to parameter scarcity, but more fundamentally because standard initializations (e.g., Kaiming) fail to exploit the inherent time-frequency structure of speech signals. Since speech is intrinsically a time-frequency signal, the corresponding model weights often encode rich spectral magnitude and phase patterns. Choi et al. [17] demonstrated that phase awareness improves ASR performance, while Zeng et al. [18] successfully leveraged spectral-phase information in multimodal algorithms, converting model weights from the spectral domain to the time domain to achieve better low-resource performance. Therefore, designing a low-rank subspace that aligns with spectral-phase priors could fundamentally improve initialization quality, accelerate convergence, and enhance final performance. Motivated by this, we propose a novel LoRA initialization strategy that leverages natural spectral bases and phase information from signal processing to guide the low-rank subspace, enabling faster convergence and greater robustness under low-resource conditions.

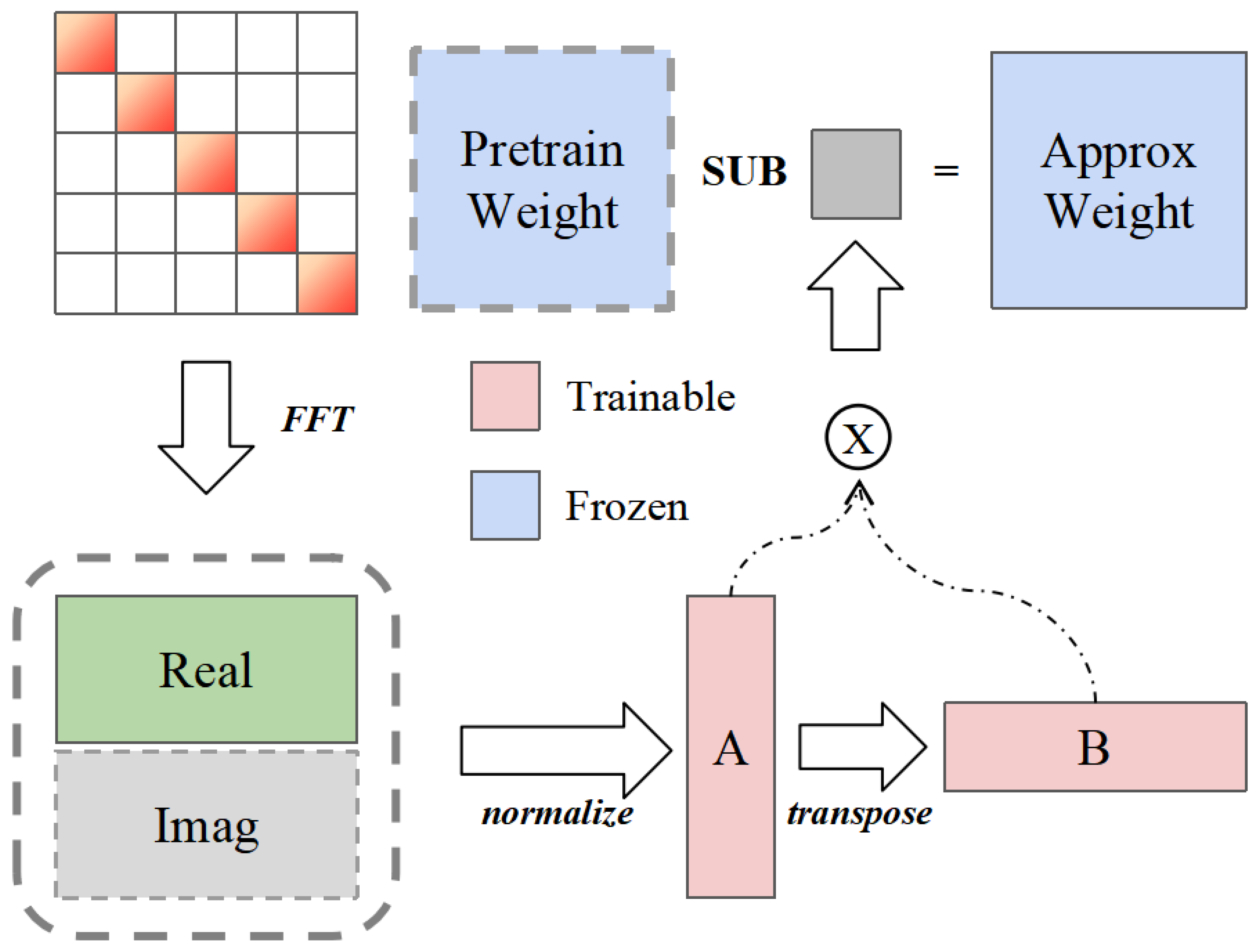
Specifically, we propose Spectral-Phase Residual LoRA Initialization (SPaRLoRA): the method first constructs discrete Fourier transform (DFT) bases and uses the columns of the DFT matrix as the low-rank initial bases for LoRA; when necessary, both real and imaginary parts are retained. Additionally, we introduce an optional residual correction strategy: a low-rank approximation constructed from the initial bases is first used to explain the explainable component of the frozen weights, and this approximation is then subtracted from the main weights, yielding residualized base weights. Consequently, the subsequent LoRA training focuses exclusively on compensating for the component not covered by the low-rank basis.

To realize the above design, we devise an intuitive initialization pipeline, illustrated in Figure 1: first, an fast fourier transform (FFT) is applied to the pre-trained weights to extract their frequency-domain representation; second, the real and imaginary parts are concatenated and normalized to form the initial matrix A, and matrix B is obtained by transposition; finally, the low-rank approximation produced by A and B is used to perform residual correction on the original weights, ensuring that the inference result remains unchanged after LoRA insertion. This pipeline guarantees that the entire initialization process is both structured and efficient.

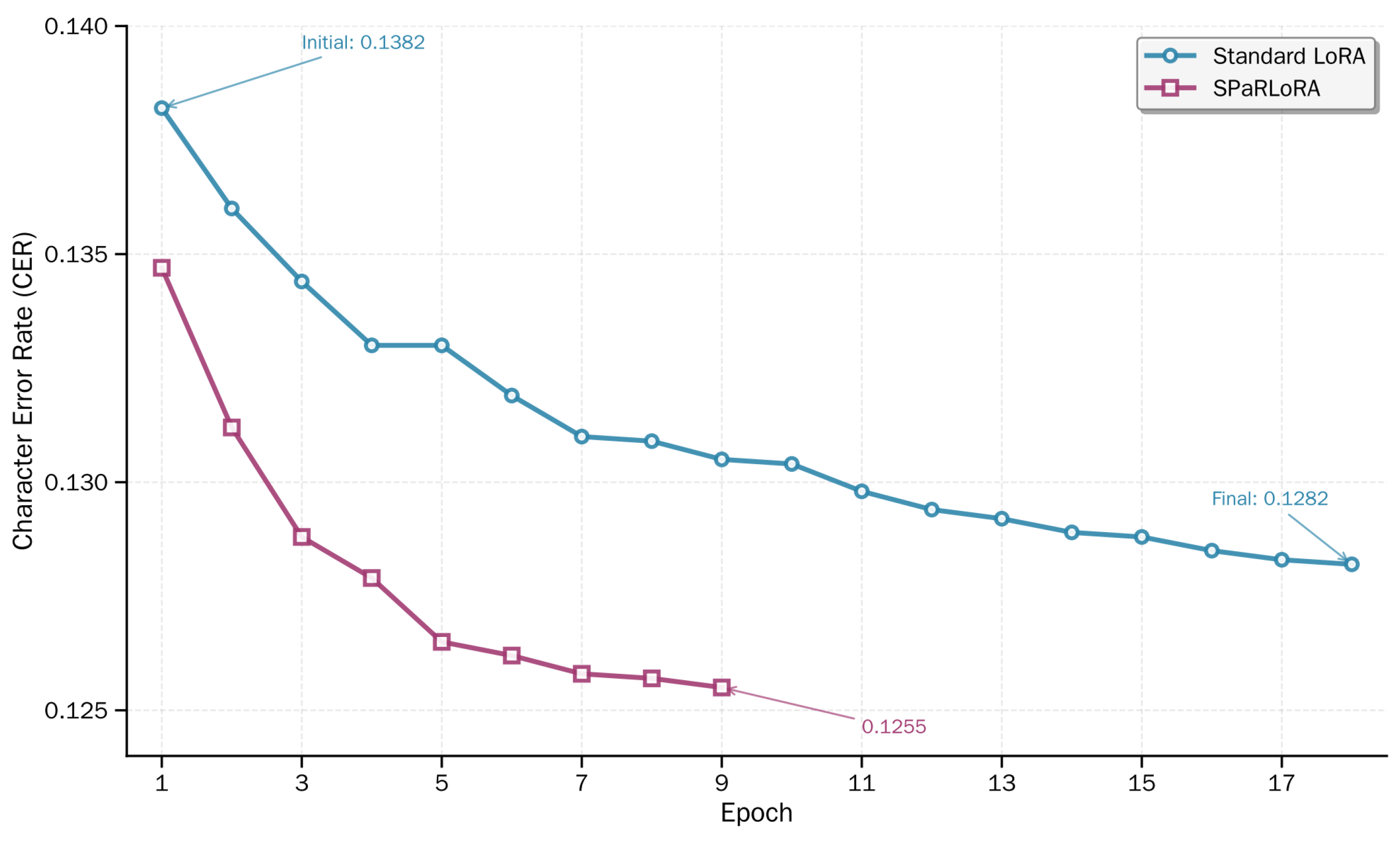
Figure 2 highlights the key advantage of SPaRLoRA: faster convergence and superior final performance in terms of character error rate (CER). By plotting CER over training epochs on a representative low-resource speech recognition benchmark, we observe that SPaRLoRA consistently achieves lower error rates than standard LoRA from early epochs onward, and continues to improve more effectively throughout training. Across multiple low-resource speech recognition benchmarks, SPaRLoRA consistently outperforms standard LoRA and several of its variants—without compromising inference efficiency—by accelerating convergence and significantly reducing CER under data-scarce conditions.

Systematic ablation studies verify the contributions of the three design components—the DFT spectral basis, phase information, and residual correction—where both phase and residual terms provide independent and complementary gains.

Our main contributions are summarized as follows:

• We provide an in-depth analysis of LoRA initialization strategies, reveal the limitations of common initializations in representing speech spectral structures, and introduce spectral priors from signal processing into low-rank initialization.
• We propose SPaRLoRA: a LoRA initialization method based on DFT spectral bases that explicitly retains phase information and optionally incorporates residual correction. By embedding signal-processing priors into initialization and combining them with a residual correction mechanism, SPaRLoRA improves both performance and training stability in low-resource speech recognition fine-tuning.
• We conduct comparative experiments and ablation analyses on low-resource speech recognition tasks; results show that SPaRLoRA outperforms LoRA and its variants under various data scales and noise conditions, and verify the effectiveness of each constituent.

The remainder of the paper is organized as follows. We first review related work in Section 2, then detail the construction and algorithmic implementation of SPaRLoRA in Section 3, and finally present experimental setups, results, and ablation analyses in Section 4.

2. Related Work

2.1. Parameter-Efficient Fine-Tuning

Parameter-efficient fine-tuning (PEFT) aims to match the performance of full fine-tuning while updating only a small subset of model parameters, enabling feasible adaptation when compute and storage are limited. Existing PEFT methods can be broadly divided into three categories.

The first family is adapter-based approaches: small trainable modules are inserted between the frozen layers of a pre-trained model, so that only a few task-specific parameters need to be stored. Representative work such as the original Adapter [10] demonstrates significant parameter savings on NLP tasks.

The second family is prompt-based methods, which prepend trainable continuous vectors (soft prompts) to the input, e.g., P-Tuning [19]. These methods usually require minimal architectural changes, but they modify the input-processing pipeline. Both adapter and prompt approaches may introduce inference latency or require specialized handling of inputs/structures.

The third family is architecture-free low-rank/projection methods. LoRA (Low-Rank Adaptation) is the most prominent example: it keeps the original network intact during inference, while reparameterizing the weight update as the product of two skinny matrices, drastically reducing trainable parameters without sacrificing accuracy [12]. Owing to its simplicity and efficiency, LoRA has become the de facto choice for fine-tuning large models in both industry and academia.

2.2. LoRA and Its Variants

Since the introduction of LoRA, numerous extensions have emerged to enhance its expressiveness, improve parameter allocation, and stabilize training. On one hand, dynamic rank allocation methods such as AdaLoRA assign variable low-rank budgets to different weight matrices according to their importance, boosting both performance and parameter utilization [20]. On the other hand, decomposition-based methods re-design the update rule: DoRA disentangles the weight update into magnitude and direction, applying low-rank adaptation only to the direction term, which better mimics full fine-tuning and improves stability [21]. These studies reveal that architectural changes alone are insufficient to close the gap between LoRA and full fine-tuning; the initialization and allocation of the low-rank parameters play a critical role.

Although many LoRA variants focus on structure or training strategy, a recent line of work directly targets the initialization of the low-rank matrices, because the choice of the initial subspace significantly affects convergence speed and final accuracy. Representative methods include PiSSA, which initializes A and B with the leading singular vectors and keeps the remaining singular values as a frozen residual [22], and OLoRA, which constructs an orthogonal basis via QR decomposition to improve conditioning at initialization [23]. CorDA further incorporates task-related contextual information by decomposing activation covariance or a small set of examples to obtain a “task-aware” adapter [24]. Across diverse tasks and model scales, these approaches demonstrate the benefits of starting from a more informative subspace. Although LoRA and its variants have achieved certain success in speech recognition tasks, the potential of LoRA in the frequency domain has not yet been fully exploited.

Our research aims to fill this gap by investigating the application of spectral and phase information within the LoRA framework, with a focus on optimizing early-stage adaptation signals during LoRA fine-tuning to improve convergence and generalization in low-resource scenarios.

3. Method

This section embeds a spectral-phase prior into the initialization of LoRA. We start from the observation that speech is a typical time-frequency signal; hence, the weight matrices of acoustic models implicitly contain spectral and phase patterns that can be exploited as a structural prior for selecting the low-rank subspace. To this end, we propose SPaRLoRA—an initialization strategy that builds low-rank adapters from the Discrete Fourier Transform (DFT) basis and optionally corrects the frozen weights by their own low-rank approximation (Algorithm 1). Unlike PiSSA, OLoRA or other SVD/QR-based schemes, SPaRLoRA explicitly encodes magnitude and phase information from a signal-processing perspective, and “residualizes” the base weights so that the adapter only needs to compensate for the remaining, structurally less trivial component. This design is particularly appealing for low-resource speech recognition, where gradient noise is high and every informative prior matters.

We first revisit the standard LoRA formulation and its common initialization strategies, revealing potential limitations in gradient dynamics and information content (Section 3.1). We then justify, from both signal-processing and matrix-approximation viewpoints, why the DFT basis is a natural choice for the initial subspace, why phase must be retained, and why residual correction is beneficial (Section 3.2).

Algorithm 1 SPaRLoRA Initialization.
Require: base weight $W\in {\mathbb{R}}^{d_{\mathrm{out}}\times d_{\mathrm{in}}}$, rank r (even), scale_mode $\in \{\mathrm{unit},\mathrm{xavier}\}$, LoRA alpha $\gamma$
Ensure: initial factors $A\in {\mathbb{R}}^{r\times d_{\mathrm{in}}}$, $B\in {\mathbb{R}}^{d_{\mathrm{out}}\times r}$, residualized weight $W_{\mathrm{res}}$
1: $n\leftarrow d_{\mathrm{in}}$
2: $F_{\mathrm{in}}\leftarrow \mathrm{FFT}\left(I_n\right)$	▹$(n\times n)$ DFT matrix, column j is the j-th basis
3: $C\leftarrow F_{\mathrm{in}}[:,0:r/2]$	▹ select first $r/2$ complex bases
4: $A_{\mathrm{raw}}\leftarrow {\left[\Re \left(C\right);\Im \left(C\right)\right]}^{\top }\in {\mathbb{R}}^{r\times n}$	▹ concatenate real and imaginary parts
5: Normalize each column of $A_{\mathrm{raw}}$ to unit ${\mathsf{\ell }}_2$ norm $\to \tilde{A}$
6: if $d_{\mathrm{out}}==d_{\mathrm{in}}$ then
7:     $\tilde{B}\leftarrow {\tilde{A}}^{\top }$
8: else
9:     Construct $F_{\mathrm{out}}$ analogously from $I_{d_{\mathrm{out}}}$ and form $\tilde{B}\in {\mathbb{R}}^{d_{\mathrm{out}}\times r}$
10: end if
11: $\widehat{W}\leftarrow \gamma \tilde{B}\tilde{A}$	▹ initial low-rank approximation
12: $W_{\mathrm{res}}\leftarrow W-\widehat{W}$	▹ residualize base weight
13: return $A=\tilde{A}$, $B=\tilde{B}$, $W_{\mathrm{res}}$

3.1. Revisiting LoRA and Its Initialization

Consider a linear layer with frozen weight matrix $W\in {\mathbb{R}}^{d_{\mathrm{out}}\times d_{\mathrm{in}}}$. LoRA reparameterizes the fine-tuning update as

$$W^{\prime }=W+\Delta W,\Delta W=\gamma BA,$$

(1)

where $A\in {\mathbb{R}}^{r\times d_{\mathrm{in}}}$, $B\in {\mathbb{R}}^{d_{\mathrm{out}}\times r}$, rank $r\ll \min (d_{\mathrm{in}},d_{\mathrm{out}})$, and scalar $\gamma$ (usually set to $\alpha /r$). Only A and B are updated during training; W remains frozen, yielding parameter-efficient adaptation.

In the original implementation A is initialized with a small random distribution (e.g., Kaiming) and B with zeros. Below we show that zero-initializing B can be sub-optimal from the perspectives of both gradient flow and Fisher information, especially when data are scarce.

3.1.1. Gradient Flow

Let $L\left(W^{\prime }\right)$ denote the training loss. The gradients w.r.t. B and A are

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathsf{\partial }L}{\mathsf{\partial }B}}& =\gamma {\displaystyle \frac{\mathsf{\partial }L}{\mathsf{\partial }{W}^{\prime }}}{A}^{\top },\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathsf{\partial }L}{\mathsf{\partial }A}}& =\gamma B^{\top }{\displaystyle \frac{\mathsf{\partial }L}{\mathsf{\partial }{W}^{\prime }}}.\hfill \end{array}$$

(3)

If B is initialized to zero, $\mathsf{\partial }L/\mathsf{\partial }A=0$ at the first step, blocking any immediate update of A. All learning signals must therefore reach A indirectly through updates of B (Equation (2)).

Conversely, if A is initialized with “informative” bases—e.g., DFT vectors whose span is likely to overlap with speech-related structures—the operator norm ${\parallel A\parallel }_2$ and the alignment between the column space of A and $\mathsf{\partial }L/\mathsf{\partial }{W}^{\prime }$ can be larger, amplifying the effective gradient component for B and indirectly accelerating the subsequent update of A.

3.1.2. Information Content

Initialization also determines how much “information” the newly introduced parameters can contribute at $t=0$. For a data pair $(x,y)$, the Fisher information matrix of LoRA parameters $\theta =\left(\mathrm{vec}\right(A),\mathrm{vec}(B\left)\right)$ is

$$\mathcal{I}\left(\theta \right)\approx \mathbb{E}\left[\left({\nabla }_{\theta }\log p_{\theta }(y\mid x)\right){\left({\nabla }_{\theta }\log p_{\theta }(y\mid x)\right)}^{\top }\right].$$

(4)

With $B_0=\mathbf{0}$, Equation (3) implies that the gradient w.r.t. A is initially zero; hence, the top-left block of $\mathcal{I}\left(\theta \right)$ corresponding to A is near zero, i.e., the new parameters carry almost no Fisher information (low entropy, low identifiability). Optimizers therefore cannot effectively explore this subspace in the early stage, a severe drawback when labeled data are limited.

Together, the above arguments motivate the introduction of spectral–phase priors: by initializing A and B with speech-informed spectral bases, the low-rank adapter starts from a subspace that captures domain-specific structure, which can lead to stronger initial gradients and more effective learning under data scarcity.

3.2. Residual Frequency-Domain Analysis

We explain, from both signal processing and matrix approximation perspectives, why incorporating frequency-domain priors and phase information into LoRA initialization is beneficial, and why decoupling the low-rank approximation from the base weights during initialization improves performance in low-resource automatic speech recognition (ASR). Figure 3 illustrates the core concept of residualization: how the original weight matrix $\mathbf{W}$ is decomposed into a low-rank DFT approximation $\widehat{\mathbf{W}}$ and a residual ${\mathbf{W}}_{\mathrm{res}}$.

3.2.1. Low-Rank Priors in Speech Spectra

Speech signals are inherently non-stationary but exhibit strong time-frequency structure. Their local stationarity allows many linear transformations commonly used in speech processing—such as filtering, convolution, or key-value projections in attention mechanisms—to be locally approximated as stationary linear systems. Under ideal circular boundary conditions, the weight matrices (or sub-blocks) corresponding to such systems can be modeled as circulant matrices C. Circulant matrices possess a crucial spectral property: they are diagonalized by the discrete Fourier transform (DFT) matrix F, i.e.,

$$C=F^{\mathsf{H}}\Lambda F,$$

(5)

where $F\in {\mathbb{C}}^{n\times n}$ is the unitary DFT matrix ($F^{\mathsf{H}}F=I$), and $\Lambda =\mathrm{diag}({\lambda }_1,\dots ,{\lambda }_n)$ represents the frequency response (i.e., the filter’s spectral response). This implies that any circulant operation reduces in the frequency domain to independent scaling of each frequency component. In speech, energy is typically concentrated in a few dominant frequencies—such as the fundamental frequency and its harmonics—particularly within formant regions.

Although weight matrices W in practical neural networks are not strictly circulant, extensive empirical evidence shows that trained ASR models (e.g., Conformer, Transformer feed-forward or attention projection layers) often exhibit approximate shift-invariance or localized band-selectivity. Consequently, their weights demonstrate energy concentration in the DFT basis: most of the Frobenius norm can be captured by a linear combination of only the top $r\ll n$ DFT basis vectors. For instance, low-frequency DFT bases correspond to slowly varying global patterns (e.g., intonation contours), while mid- to high-frequency bases capture local spectral details such as formants and fricatives.

Therefore, initializing the LoRA low-rank factor A with the first r columns of the DFT matrix (or an energy-ranked subset thereof) naturally aligns its row space with the most informative spectral subspace of speech signals. This not only reduces reliance on the optimizer to “discover” spectral structure from scratch but also ensures that low-rank updates directly modulate the frequency bands most critical for ASR. In contrast, random initializations (e.g., Kaiming) yield subspaces that are spectrally diffuse and struggle to capture such structured priors efficiently—especially under data scarcity, where they are prone to sub-optimal convergence.

Moreover, modern ASR systems like Paraformer typically operate on frequency-domain features (e.g., log-Mel filterbanks), which are already compressed representations of spectral magnitude. However, magnitude alone is insufficient to fully characterize the temporal structure of speech: phase determines the time alignment of frequency components and is crucial for intelligibility and perceptual quality.

Thus, by explicitly preserving the complex structure of DFT bases during initialization (e.g., concatenating real and imaginary parts), the LoRA subspace gains the capacity to jointly modulate both magnitude and phase, enabling a more complete modeling of speech operators in the frequency domain.

3.2.2. The Modeling Value of Phase Information

DFT basis vectors are inherently complex: their real parts correspond to cosine components and imaginary parts to sine components, jointly encoding both magnitude and phase at each frequency. Traditional speech processing often emphasizes magnitude spectra (e.g., Mel spectrograms), assuming phase has limited perceptual impact. However, recent studies have clearly demonstrated that phase information is vital for improving intelligibility and model robustness—especially in challenging scenarios such as low-resource, noisy, or dialectal ASR.

From a signal reconstruction perspective, magnitude spectra alone cannot uniquely determine the original time-domain signal; phase governs the relative temporal alignment of frequency components. For example, distinguishing a voiceless fricative from a vowel depends not only on spectral energy distribution but also on instantaneous phase changes in high-frequency regions. Similarly, dialect-specific phenomena—such as tonal shifts or speaking rate variations—often manifest as systematic deviations in the phase structure of the fundamental frequency and its harmonics. Choi et al. [17] have shown that explicitly modeling phase or complex spectral features in end-to-end ASR significantly boost accuracy under low-resource conditions.

In the context of LoRA initialization, using only the real part of the DFT basis (i.e., cosine functions) to construct the initial matrix A effectively constrains all frequency components to initial phases of 0 or $\pi$, thereby eliminating the ability to model arbitrary phase offsets. This severely limits the expressive capacity of the low-rank subspace: even with identical rank r, the function space spanned by real-only bases is far smaller than that achievable with both real and imaginary components. Specifically, concatenating real and imaginary parts is equivalent to introducing orthogonal basis pairs $\left\{\cos \right(2\pi kn/N),\sin (2\pi kn/N\left)\right\}$ in the real domain, enabling LoRA to independently adjust both magnitude and phase for each frequency component—thus achieving finer spectral modulation.

Importantly, this phase modeling introduces no additional parameters: since LoRA operates in the real domain, we simply concatenate the real and imaginary parts of the complex DFT basis as independent row vectors in A (e.g., for each frequency k, include both $\Re \left(f_k\right)$ and $\Im \left(f_k\right)$). This doubles the effective spectral degrees of freedom without increasing the rank. Experimental results confirm this benefit: under a fixed rank $r=32$, incorporating phase information (via real-imaginary concatenation) further reduces the character error rate (CER) from 12.64% to 12.60%, demonstrating its distinct and irreplaceable contribution in low-resource ASR.

Hence, explicitly preserving phase information is not only physically faithful to the nature of speech signals but also a key design choice for enhancing the expressive efficiency of LoRA initialization. It endows the low-rank adapter, from the very beginning of training, with sensitivity to critical time-frequency cues such as temporal alignment and harmonic relationships, thereby accelerating convergence and improving final performance.

3.2.3. Optimization Benefits of Residualization

Let the constructed initialization matrices $\tilde{A}$ (from DFT bases) and $\tilde{B}$ (its dual) yield an initial low-rank approximation $\widehat{W}=\gamma \tilde{B}\tilde{A}$, where $\gamma$ is a scaling factor. From a least-squares perspective, for fixed $\tilde{A}$, the optimal $B^{★}$ satisfies (see Proposition):

$$B^{★}=W{\tilde{A}}^{\top }{\left(\tilde{A}{\tilde{A}}^{\top }\right)}^{-1},$$

(6)

and $B^{★}\tilde{A}=W{P}_{\tilde{A}}$, where $P_{\tilde{A}}$ is the projection matrix onto the row space of $\tilde{A}$. By residualizing,

$$W_{\mathrm{res}}=W-\widehat{W}\approx W(I-P_{\tilde{A}}--p),$$

(7)

we first remove the component of W explainable by spectral bases, allowing subsequent training to focus exclusively on the orthogonal complement (i.e., the residual). Theoretically, this offers two key advantages:

• Smaller and more informative search space: If most of W’s energy is captured by the spectral basis, the Frobenius norm of the residual $W_{\mathrm{res}}$ is significantly smaller than that of W. Parameter updates then only need to fit a lower-norm target, leading to more stable optimization and reduced overfitting under data scarcity.
• More focused gradient signals: As seen in Equations (2) and (3), the efficacy of training signals depends on the alignment between the error and the parameter subspace. Residualization suppresses interference from explainable components, directing gradients more precisely toward the part of W that cannot be captured by the prior subspace—thereby improving convergence efficiency.

In low-resource scenarios, where the number of reliable gradient updates is limited, SPaRLoRA prevents the optimizer from wasting samples on re-learning structures that are already captured by the spectral prior, and concentrates modeling capacity on the remaining, task-specific residual.

3.2.4. Computational Complexity Analysis

The initialization computational cost varies significantly across different LoRA variants. Standard LoRA with random initialization has $O\left(nr\right)$ time complexity (where n is the matrix dimension and r is the rank), making it the fastest but least informative initialization. In contrast, PiSSA requires singular value decomposition with $O\left(\min (m{n}^2,m^{2}n)\right)$ complexity for an $m\times n$ matrix, which is substantially more expensive.

SPaRLoRA’s fast fourier transform based initialization has $O\left(n^2\log n\right)$ time complexity per matrix. While this is higher than random initialization, it is significantly more efficient than SVD-based methods. For a typical transformer layer with $d_{\mathrm{in}}=d_{\mathrm{out}}=512$ and rank $r=32$, empirical measurements show that SPaRLoRA initialization takes approximately 2–3× longer than LoRA but is 10–20× faster than PiSSA. Given that initialization is a one-time cost and the benefits in terms of better final performance (12.55% vs 12.82% CER), this computational trade-off is highly favorable.

4. Experiment

We conducted comprehensive experiments comparing SPaRLoRA against baseline methods and current mainstream LoRA variants on speech recognition tasks.

For the speech recognition task, Paraformer is a single-pass non-autoregressive model known for its high accuracy and computational efficiency. It is pre-trained on large-scale annotated Mandarin speech data. Since Sichuanese is a dialect of Mandarin, we adopt Paraformer [9] as our base model and use full-parameter fine-tuning as the qualitative baseline.

All experiments were conducted under identical conditions unless otherwise specified.

Table 1. Train environment.

Name	Description
OS	Ubuntu 22.04
framework	Pytorch 2.7
CPU	Intel Gold 6148
Memory	128 GB
GPU	NVIDIA RTX A6000

summarizes our experimental environment. To ensure fair comparison, we set AdaLoRA with initial rank 64 and target rank 32, whereas all other methods (LoRA, DoRA, PiSSA, OLoRA, and SPaRLoRA) use rank 32. Other hyperparameters are listed in

Table 2. Train params.

Name	Description
Epochs	20
Batch Size	32
learning rate	2 × 10−4
alpha	64
bias	N/A

. During training, we employed the AdamW optimizer with a learning rate warm-up over the first 3000 steps, followed by cosine decay scheduling to dynamically adjust the learning rate:

$${\eta }_t={\eta }_{\min }+{\displaystyle \frac{1}{2}}({\eta }_{\max }-{\eta }_{\min })\left(1+\cos \left({\displaystyle \frac{t}{T}}\pi \right)\right)$$

(8)

where t denotes the current training step, T is the total number of training steps, and ${\eta }_{\min }$ and ${\eta }_{\max }$ represent the minimum and maximum learning rates, respectively.

To determine the optimal LoRA rank for SPaRLoRA, we systematically evaluated rank values 8, 16, 32, 64 on a 200 h Sichuan dialect ASR dataset. The rank-32 configuration achieved 12.55% character error rate (CER), demonstrating statistically significant improvement over rank-16 (p < 0.05) while exhibiting negligible performance difference from rank-64 (12.54%). Computational analysis revealed that rank-32 required only 0.066 h additional training time compared to rank-16, while multi-dimensional efficiency evaluation positioned the rank-32 configuration in the optimal efficiency quadrant. Ablation studies confirmed 2.1% performance improvement over standard LoRA implementation. Consequently, rank-32 was selected for all subsequent SPaRLoRA experiments as it provides the optimal balance between recognition performance and computational efficiency. Figure 4 illustrates the detailed rank selection analysis, showing the performance, efficiency, and statistical significance across different rank values.

4.1. Dataset

Our dataset contains 200 h of spontaneous two-speaker conversations recorded under three conditions: preset phrases, preset scenarios, and free dialogue. Each utterance is annotated with start/end times, simplified Chinese transcription, and anonymized speaker IDs. In total, 160 h were used for training and 40 h for validation.

Prior to training, the speech data underwent preprocessing to standardize the input format. Each full audio recording was segmented according to punctuation marks, followed by a series of text normalization steps, including Unicode normalization, full-width/half-width character unification, conversion between traditional and simplified Chinese characters, case normalization, removal of padding/control characters and invisible characters, punctuation stripping, normalization of numeric expressions into Arabic numerals, and collapsing of spaces and multiple consecutive whitespace characters.

4.2. Evaluation Metrics

We adopt character error rate (CER) as the primary metric. CER is computed with the Levenshtein distance to align the recognized hypothesis with the reference, counting substitutions (S), deletions (D), and insertions (I):

$$\mathrm{CER}={\displaystyle \frac{S+D+I}{N}}$$

(9)

where N is the number of characters in the reference.

4.3. Results

The ablation study in

Table 3. Ablation experiment about SPaRLoRA.

Name	Spectral	Phase	Residual	CER
A	-	-	-	12.82%
B	✓	-	-	12.64%
C	✓	✓	-	12.60%
D	✓	-	✓	12.57%
E	✓	✓	✓	12.55%

“-” indicates the component is not used, and “✓” indicates the component is used. Bold indicates the best result.

demonstrates that each component of SPaRLoRA—spectral basis, phase awareness, and residual correction—contributes positively to final performance. While the absolute gains may appear modest, their impact stems from aligning the low-rank adaptation subspace with fundamental properties of speech signals.

Specifically, the inclusion of phase information (real and imaginary parts of DFT bases) enables the adapter to model not only spectral magnitude but also temporal alignment of frequency components. Since tonal distinctions and consonantal transitions in Sichuanese heavily rely on fine-grained phase relationships [17], this explains why even a small rank suffices to capture linguistically critical variations that random or magnitude-only initializations miss.

The residual correction step further enhances this effect by ensuring that the LoRA module focuses exclusively on the part of the weight update orthogonal to the DFT subspace—i.e., deviations that cannot be explained by stationary spectral priors. In low-resource settings, where gradient signals are noisy and data scarce, this prevents the adapter from redundantly relearning what is already well-approximated by the frozen backbone, thereby directing optimization toward truly task-specific adjustments.

Thus, the improvements are not merely empirical but rooted in signal-theoretic principles: spectral-phase initialization injects domain-aware inductive bias, while residualization sharpens the learning objective. Together, they make more efficient use of limited labeled data.

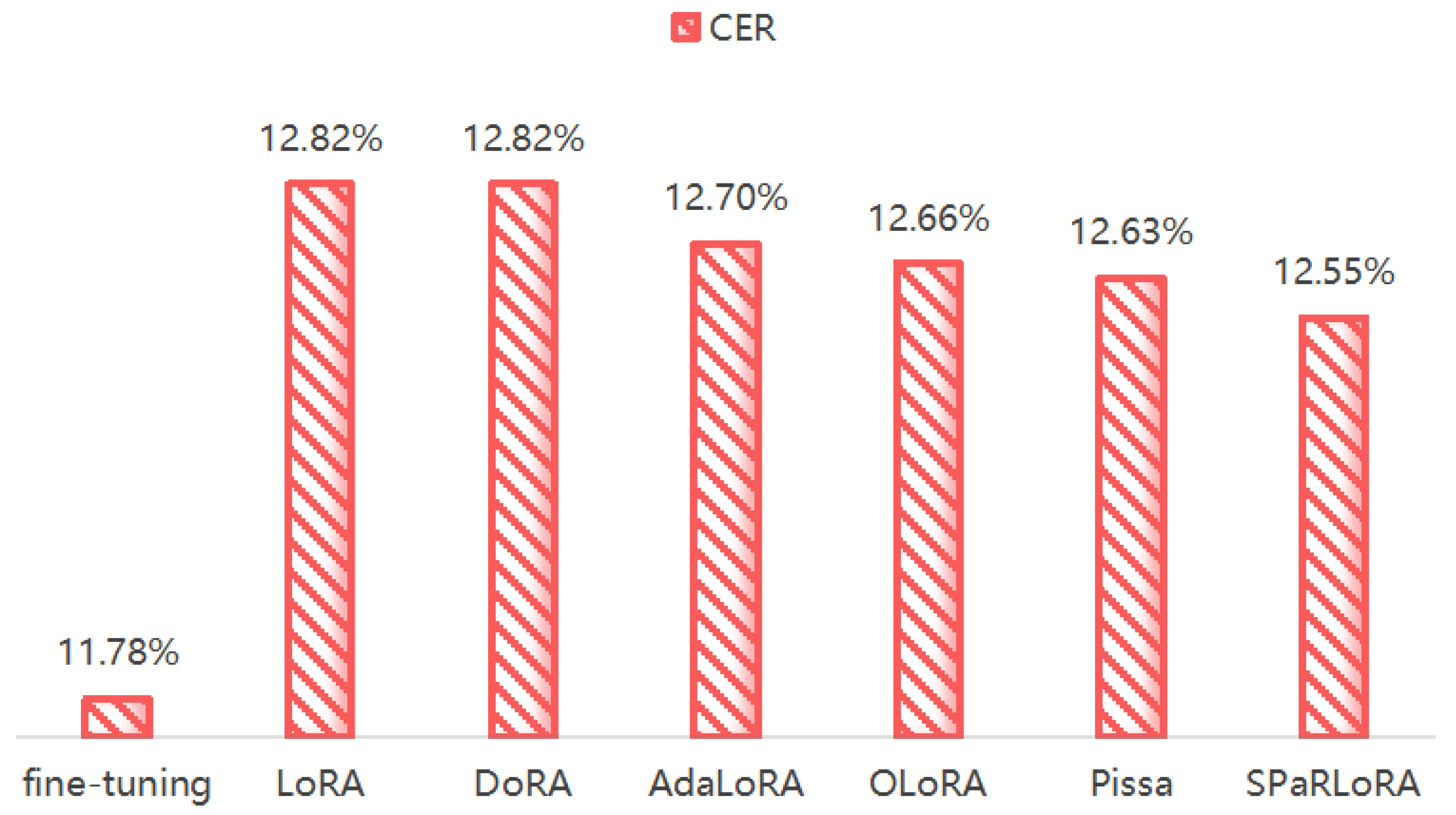
Figure 5 summarizes the performance of SPaRLoRA against baseline methods on the Sichuan dialect test set. SPaRLoRA achieves 12.55% CER, outperforming standard LoRA (12.82%) by a relative 2.1% and converging approximately 30% faster. It also surpasses DoRA, AdaLoRA, and PiSSA while introducing zero additional latency at inference.

5. Conclusions and Future Work

This paper identifies a previously overlooked limitation of standard LoRA in low-resource speech recognition: its default initialization fails to exploit the spectral-phase structure inherent in acoustic weight matrices. To address this gap, we introduce SPaRLoRA, a drop-in replacement that only modifies the initial low-rank factors and optionally residualizes the frozen weights. The method requires no architectural changes, adds zero inference cost, and can be fused back into the pre-trained weights after training.

On a 200 h Sichuan dialect Mandarin ASR benchmark, SPaRLoRA reduces CER from 12.82% (LoRA) to 12.55%—a 2.1% relative improvement—while accelerating convergence by roughly 30%. Ablation studies confirm that the DFT spectral basis, explicit phase encoding, and residual correction each contribute independently and synergistically.

Future research will explore several promising extensions. One compelling direction is to enrich SPaRLoRA with semantic- or context-aware signals, inspired by recent advances in cross-modal transfer learning. For instance, prior work in multi-visual activity recognition has demonstrated that leveraging contextual dependencies across modalities significantly improves generalization under data scarcity [25]. Adapting similar principles to low-resource ASR—by integrating linguistic priors, prosodic cues, or even visual speech information into the initialization or training dynamics of SPaRLoRA—could further enhance its adaptability and robustness. Additionally, we plan to investigate adaptive, task-specific spectral bases learned from data, extend the framework to non-linear layers via locally linear approximations, and develop automated strategies for basis selection to facilitate large-scale deployment.