Reconstruction of Impedance Criteria and Stability Enhancement Strategies for Grid-Connected Inverters
Abstract
1. Introduction
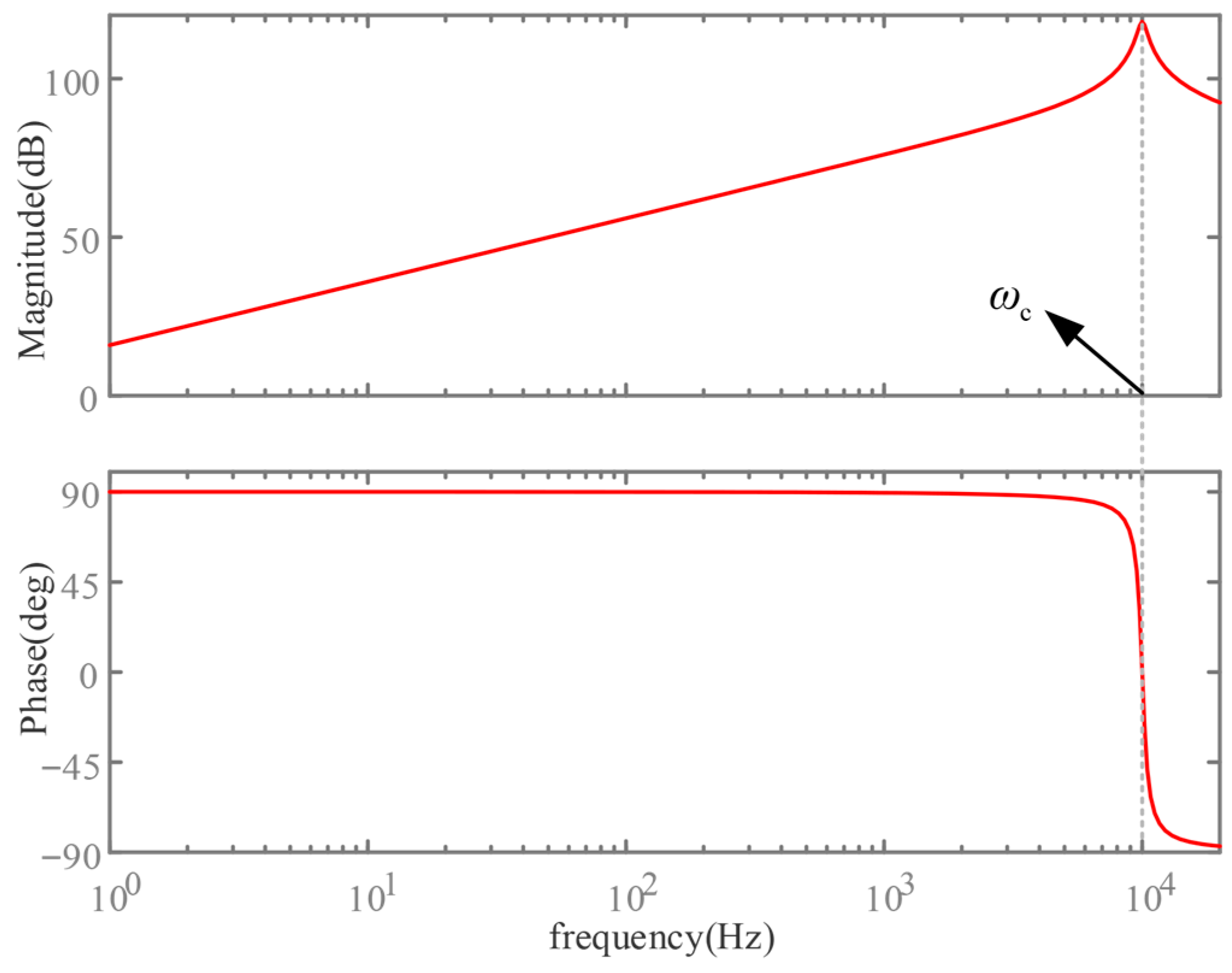
2. VSG Control Principle and Performance Analysis
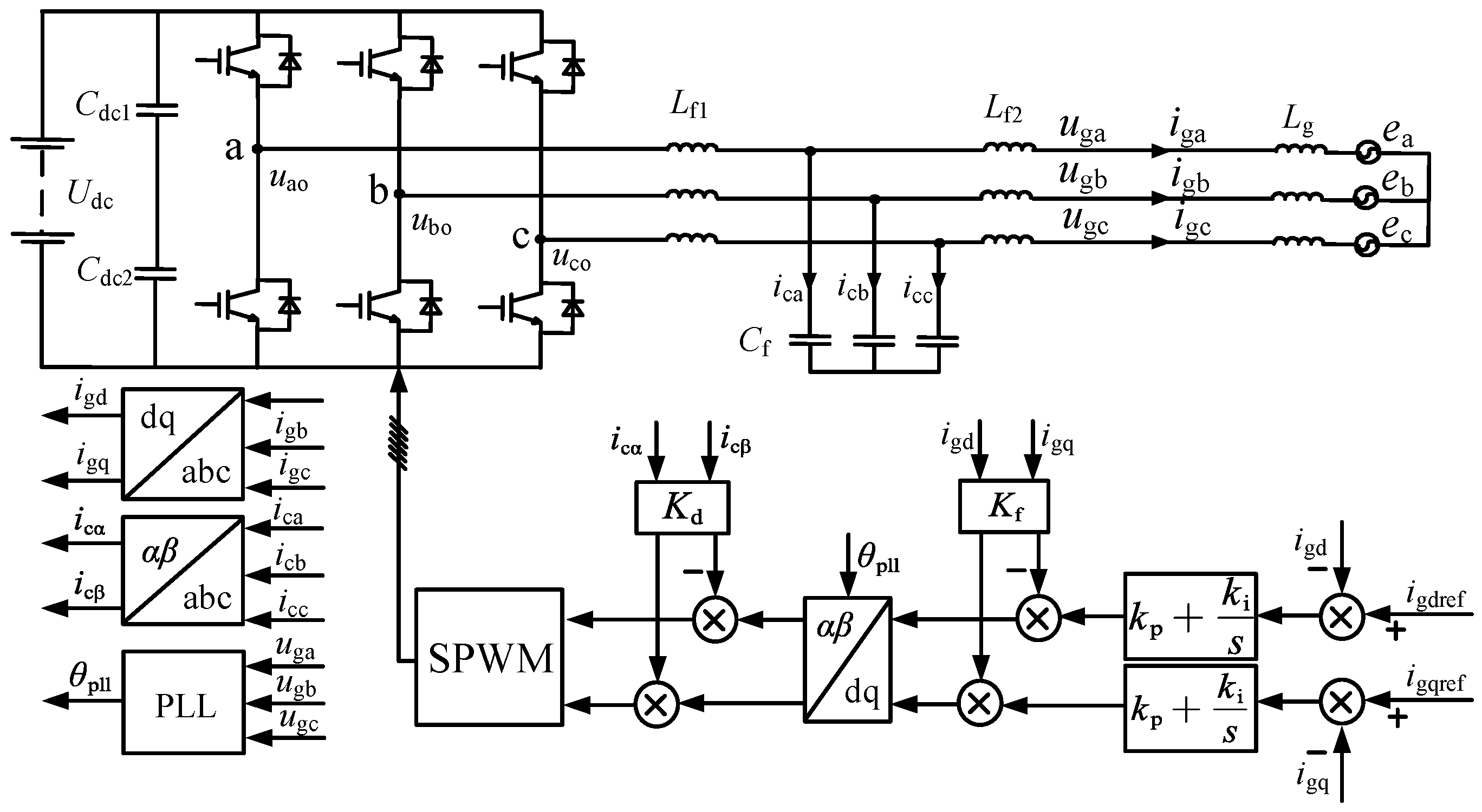
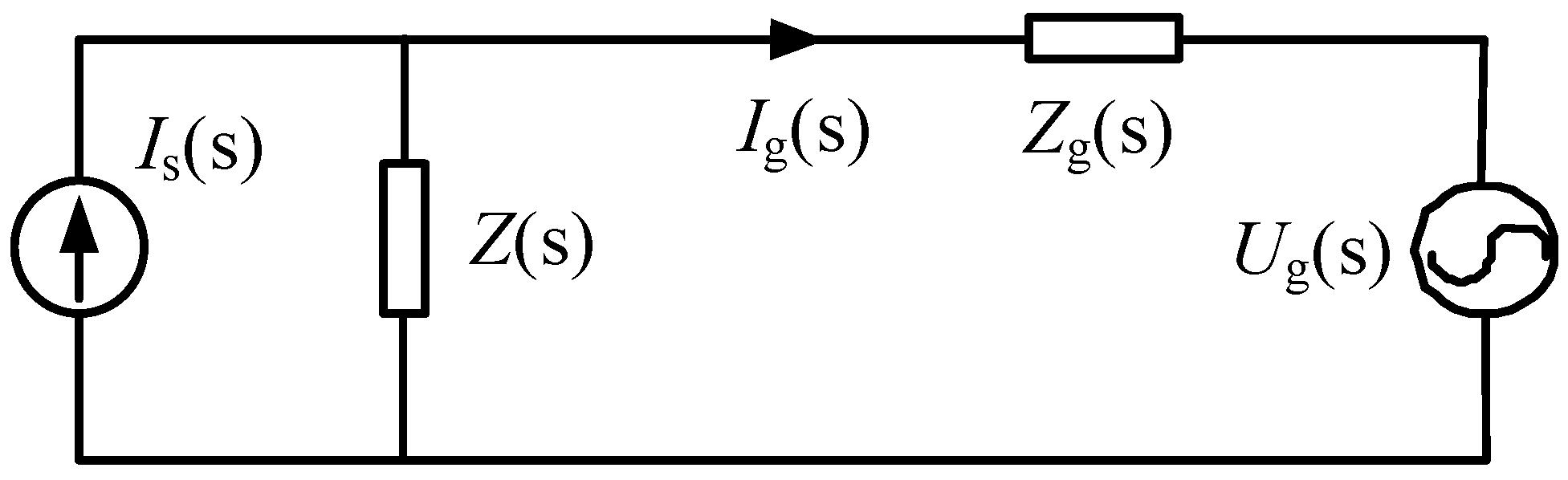
3. Reshaped Impedance Criterion of Grid-Connected Inverters
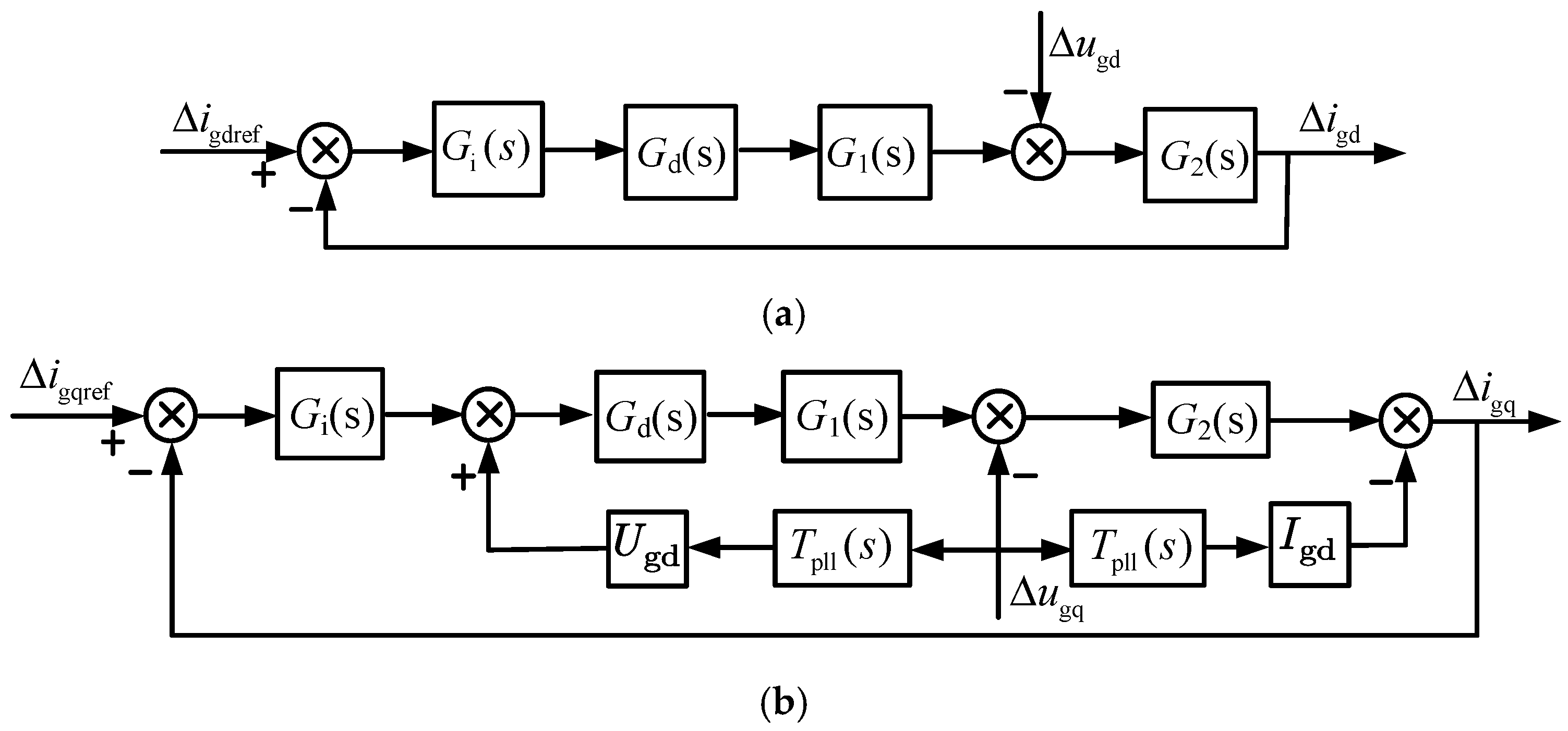
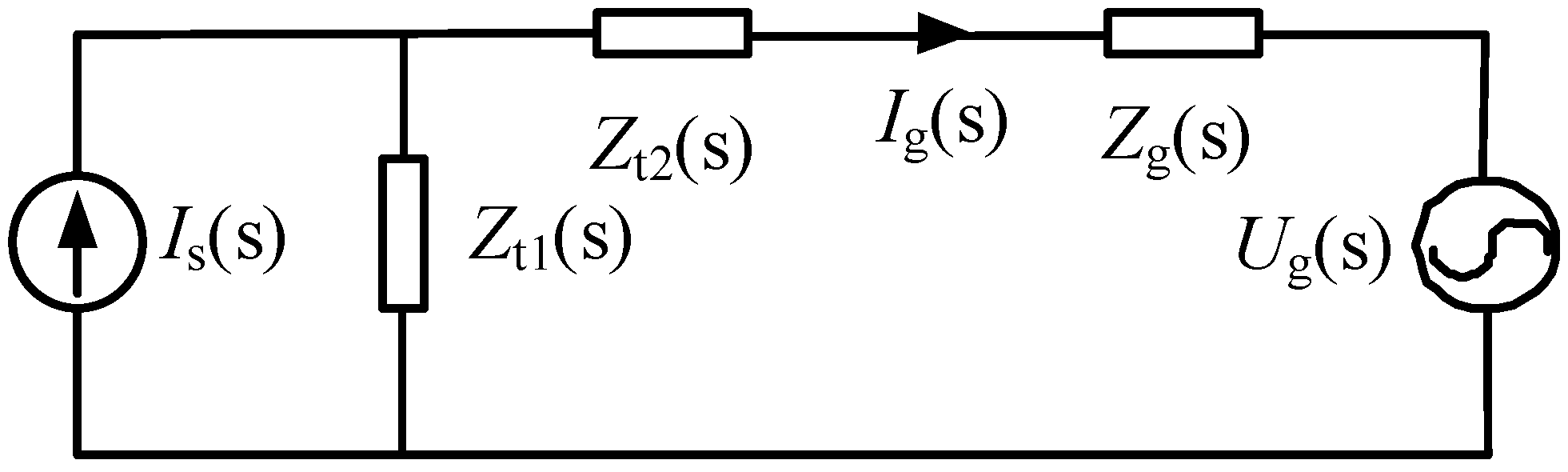
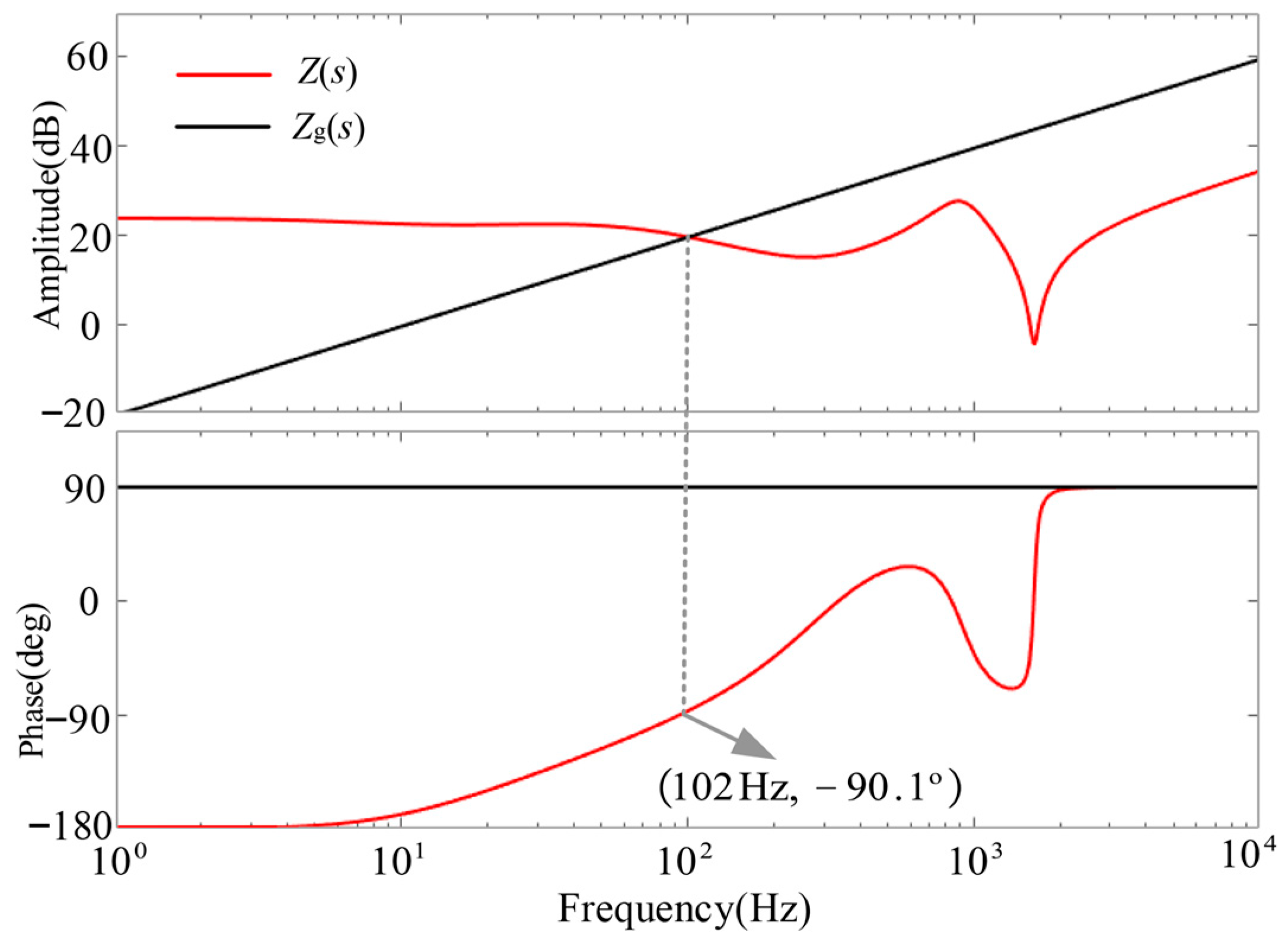
3.1. Reshaped Impedance Criterion
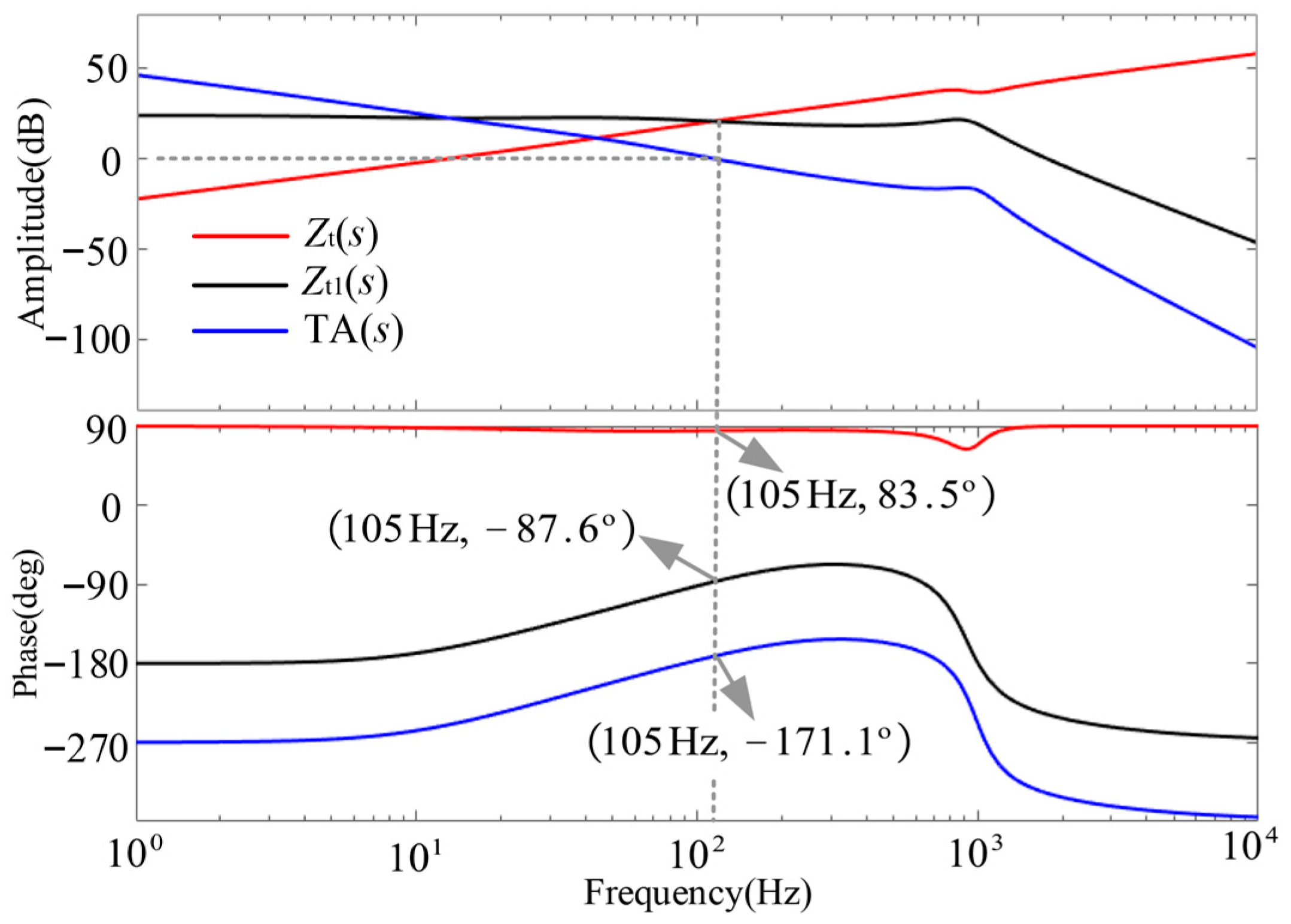
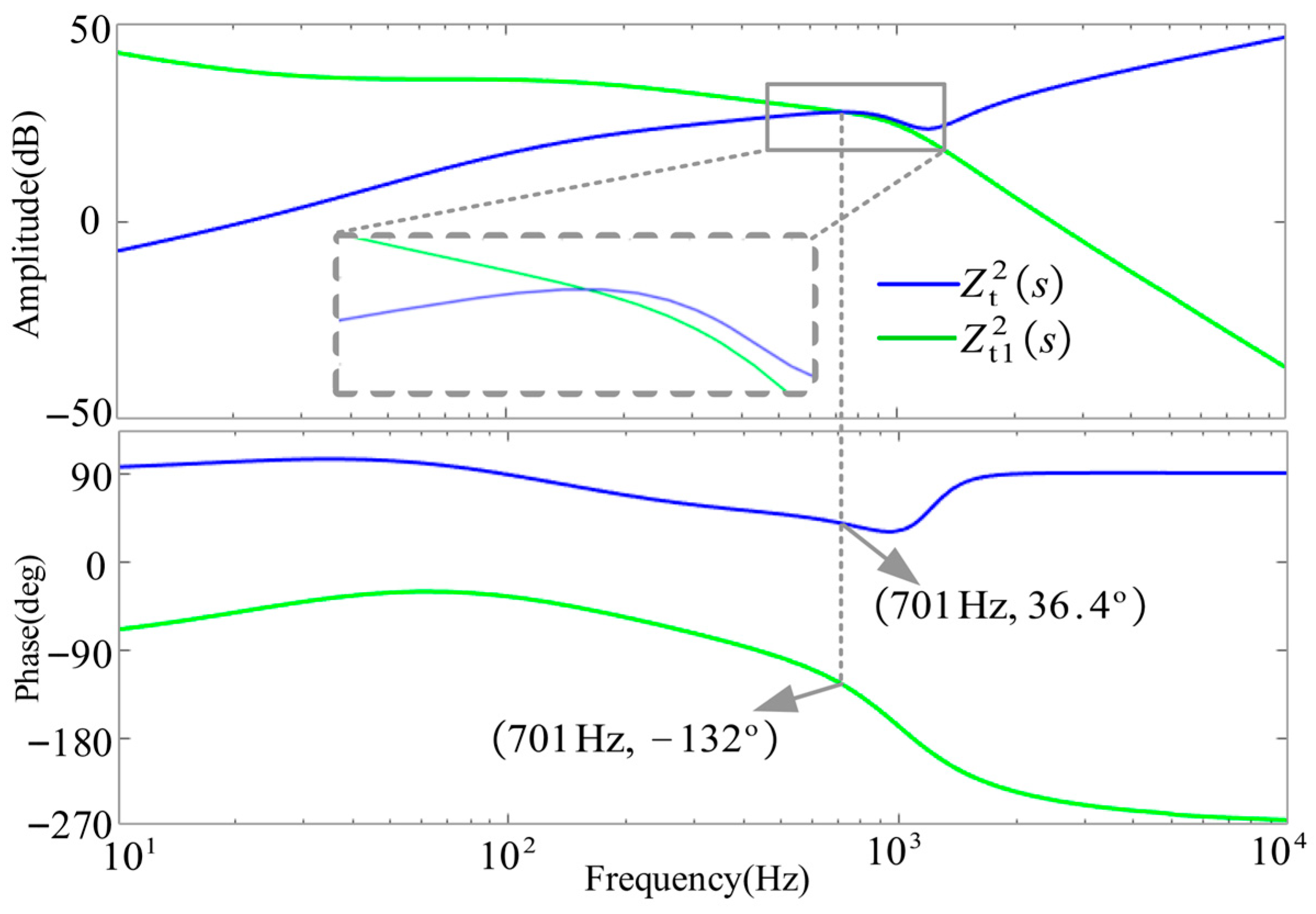
3.2. Comparison Between the Reshaped Impedance Criterion and the Traditional Criterion
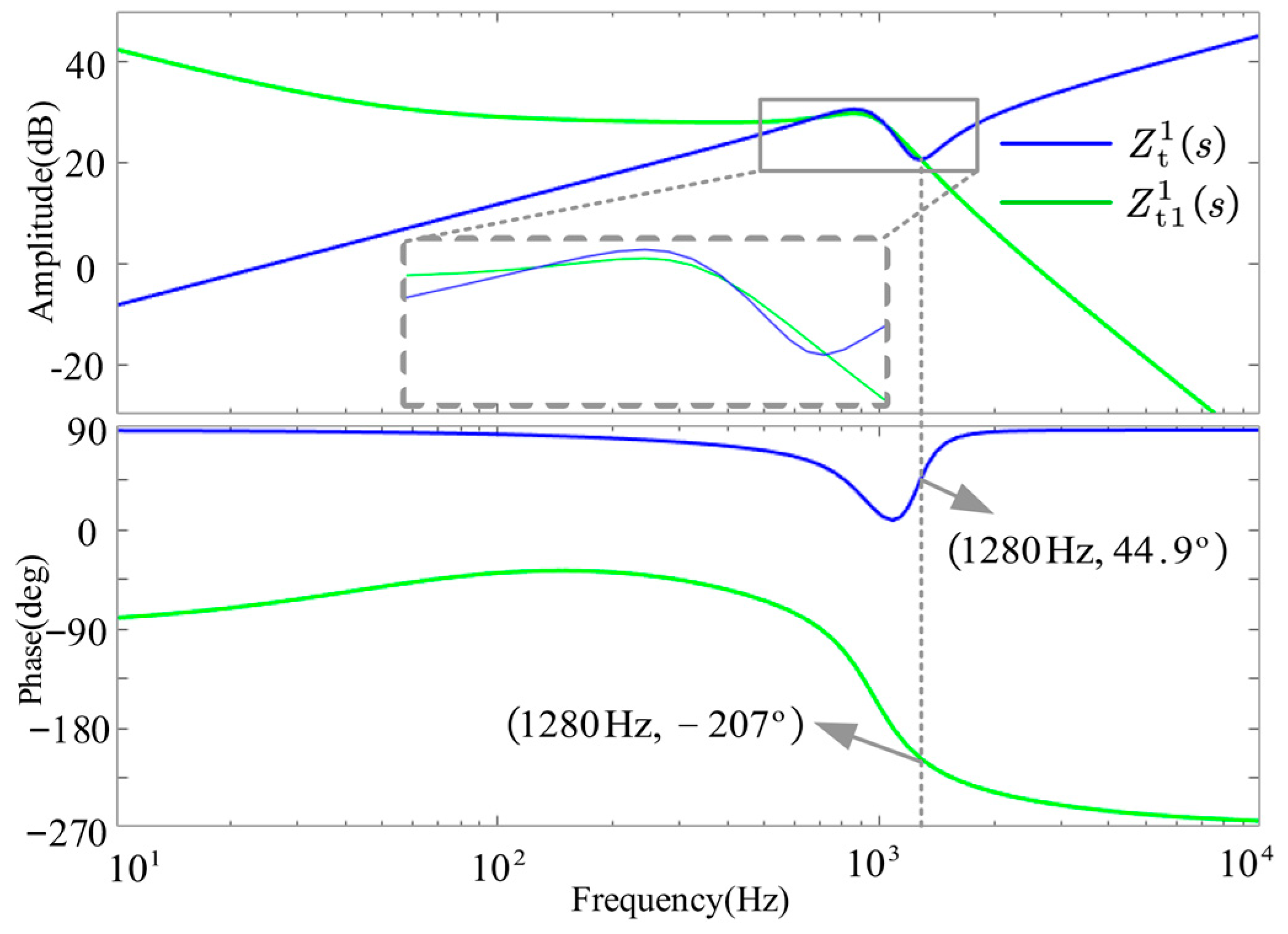
3.3. q-Axis Control Compensation Strategy
3.4. Improved q-Axis Control Compensation Strategy
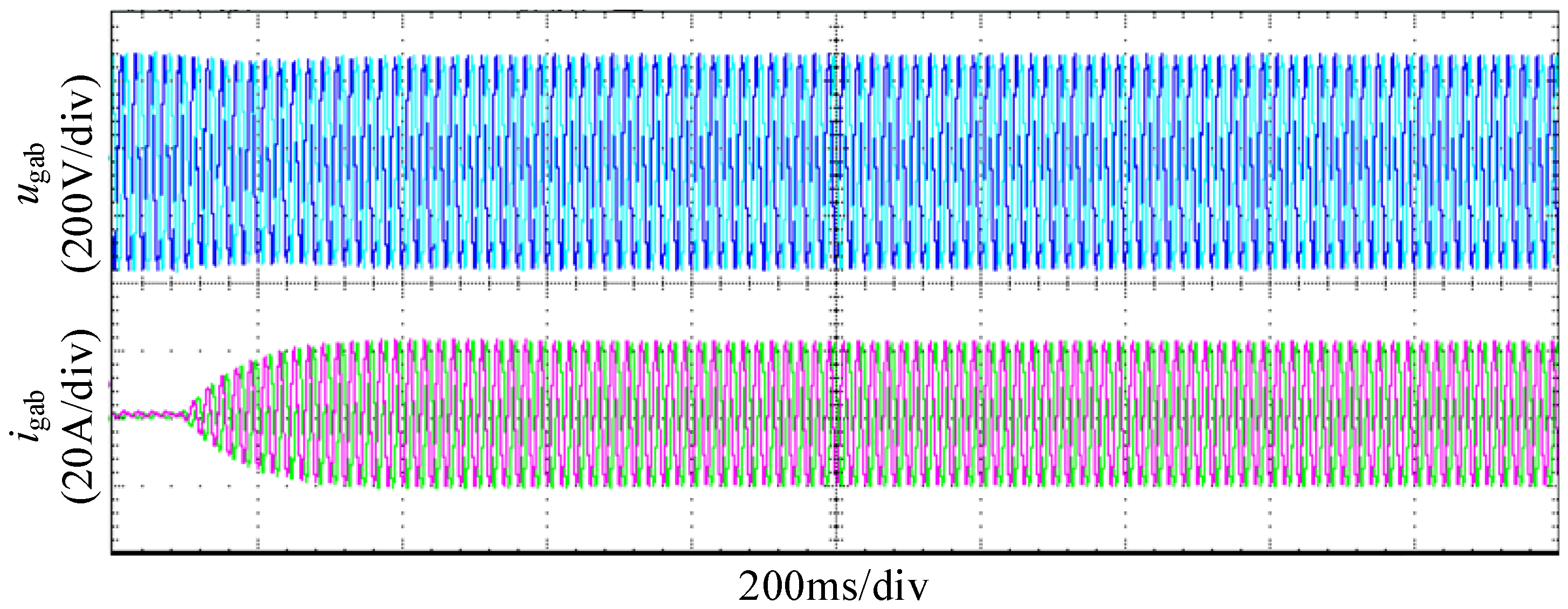
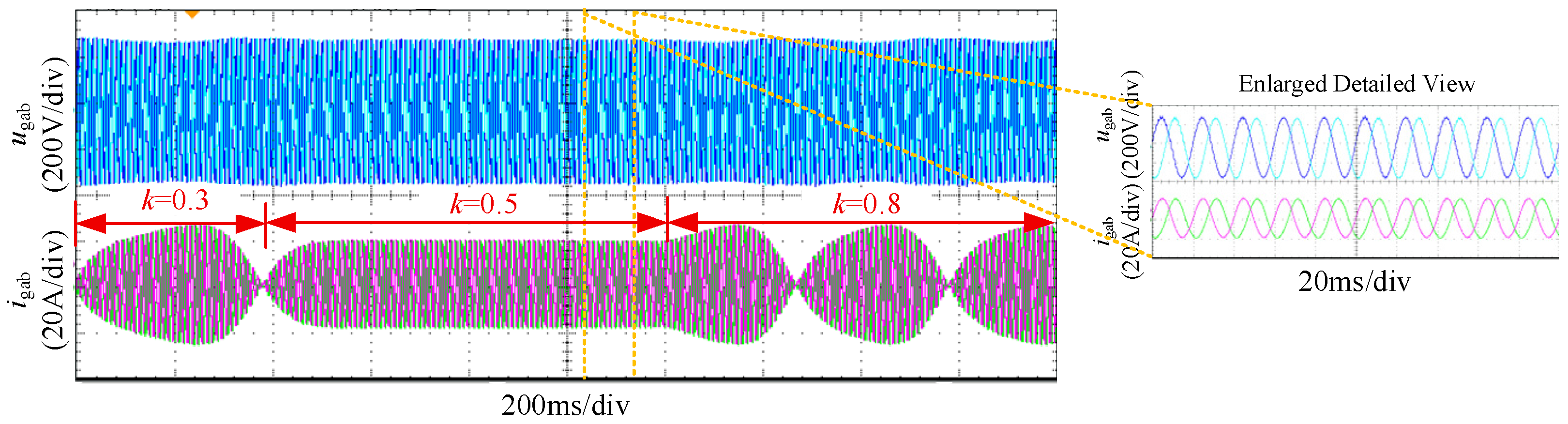
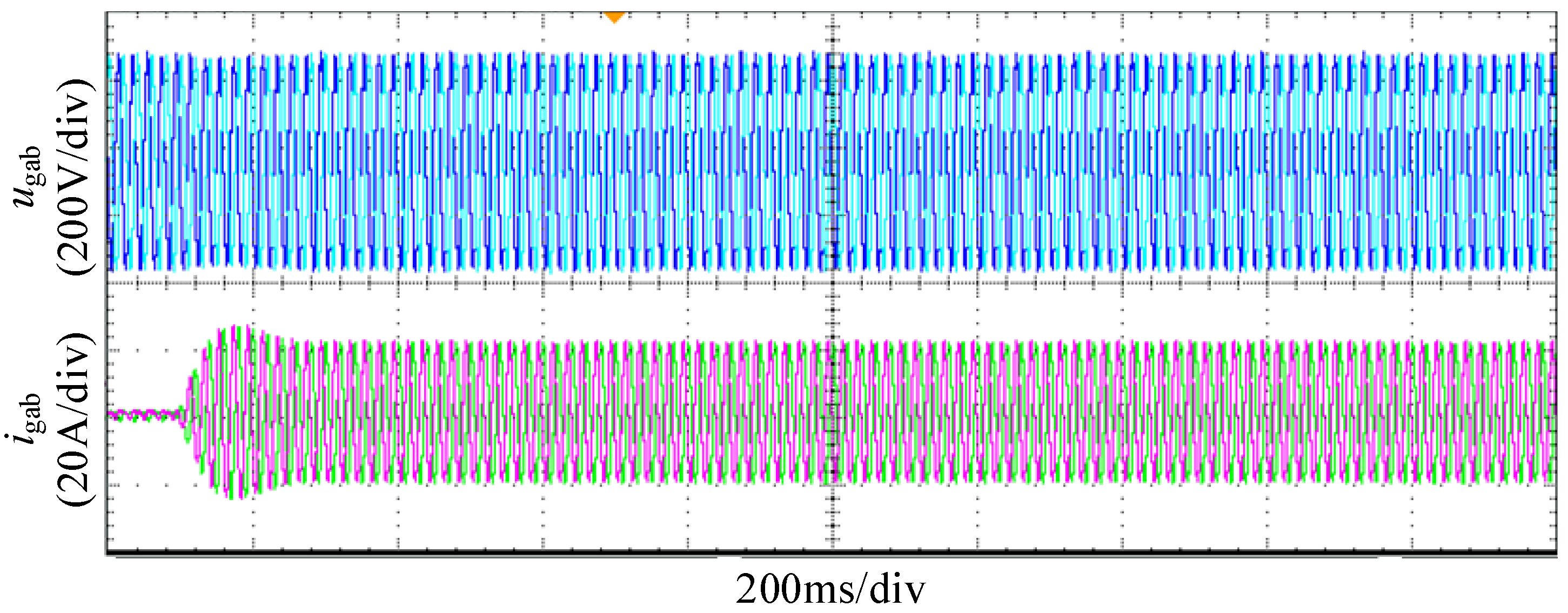
4. Experimental Validation
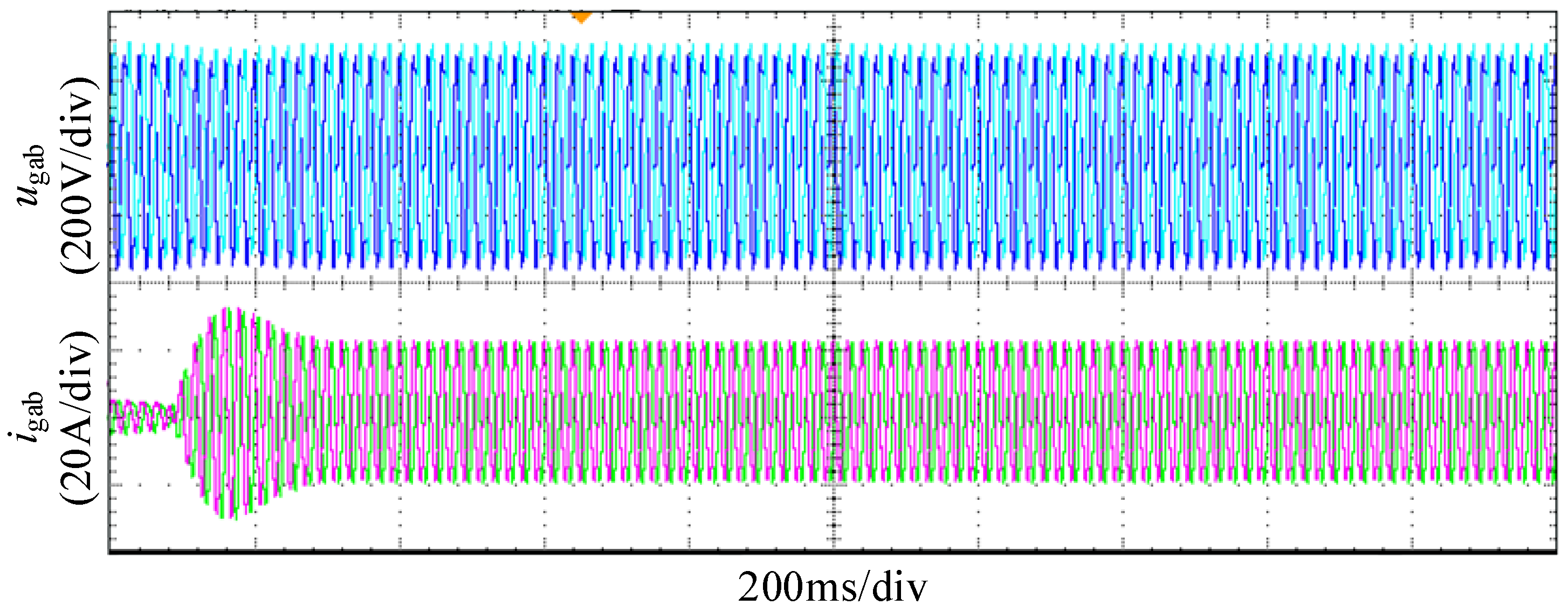
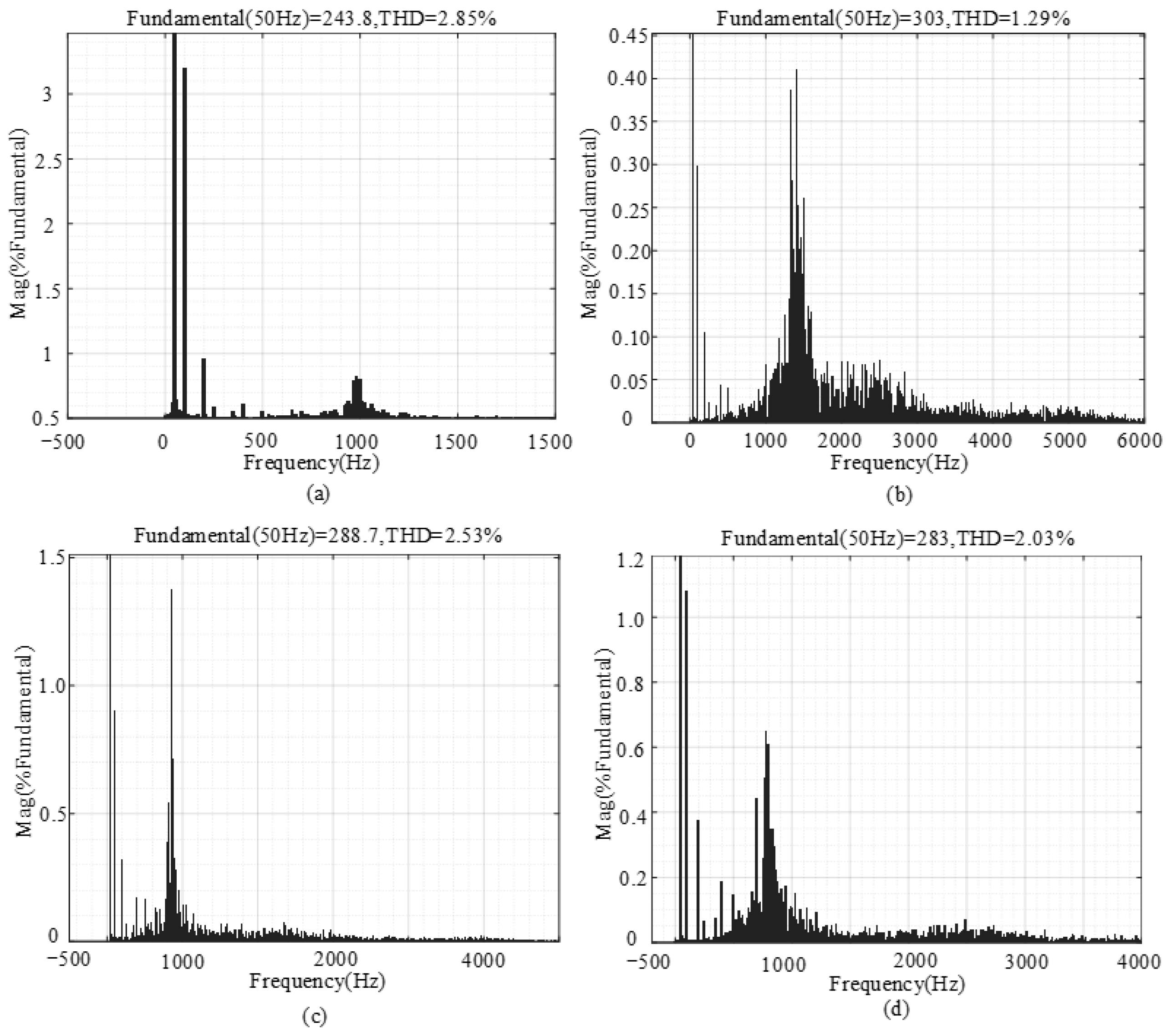
4.1. Experimental Comparison Before and After Impedance Criterion Reshaping
4.2. Experimental Analysis of q-Axis Control Compensation Introduction
4.3. Experimental Analysis of the Improved q-Axis Control Compensation
5. Conclusions
- (1)
- The reshaped impedance criterion method can accurately characterize the actual phase margin of the control system, effectively resolving the phase error inherent in traditional impedance criteria, and provides a more precise tool for stability analysis in practical applications. This method significantly enhances the accuracy of system stability assessments, especially in areas where grid impedance varies significantly.
- (2)
- The proposed improved q-axis compensation control not only enhances the adaptability of the inverter under high-line-impedance conditions but also addresses the instability problem under low-line-impedance conditions, thereby significantly expanding the adaptability range of the grid impedance. In addition, the impedance model established based on the reshaped impedance criterion can accurately reflect the actual phase margin of the system, completely avoiding the characterization errors of traditional methods.
- (3)
- The method proposed in this study has great potential for practical engineering applications. By improving the inverter control strategy, it can effectively enhance stability under various grid conditions and provide strong support for the optimization of renewable energy grid integration systems. It also offers technical guarantees for the construction of smart grids and future power systems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wilk-Jakubowski, J.L.; Pawlik, L.; Wilk-Jakubowski, G.; Harabin, R. State-of-the-Art in the Use of Renewable Energy Sources on the Example of Wind, Wave Energy, Tidal Energy, and Energy Harvesting: A Review from 2015 to 2024. Energies 2025, 18, 1356. [Google Scholar] [CrossRef]
- Azam, M.A.; Khan, M.R.; Saeed, A. A Review of Sustainable Energy Sources Using Machine Learning. Energies 2023, 16, 6236. [Google Scholar]
- Mimouni, A.; Laribi, S.; Bizhani, H.; Iwanski, G. Switch Fault Diagnosis of Grid-Connected Inverter Using Symmetrical Components. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 5258–5272. [Google Scholar] [CrossRef]
- Pang, Y.; Li, Y.; Zhang, J.; Yang, H.; Ji, Y.; Zhang, X.; Zhu, Y.; Li, G.; Xiang, Z.; Gong, C.; et al. A Multiple Energy Conversion Channels Fusion Grid-Connected Inverter for Large-Scale PV Active Power Injection Preventing Power Loss Caused by Insufficient MPP PV Voltage. IEEE Trans. Power Electron. 2025, 40, 13415–13433. [Google Scholar] [CrossRef]
- Malkhandi, A.; Senroy, N.; Mishra, S. A Dynamic Model of Impedance for Online Thevenin’s Equivalent Estimation. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 194–198. [Google Scholar] [CrossRef]
- Jin, Z.; Wang, X. A DQ-Frame Asymmetrical Virtual Impedance Control for Enhancing Transient Stability of Grid-Forming Inverters. IEEE Trans. Power Electron. 2022, 37, 4535–4544. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Blaabjerg, F.; Chen, Z. Harmonic Instability Assessment Using State-Space Modeling and Participation Analysis in Inverter-Fed Power Systems. IEEE Trans. Ind. Electron. 2017, 64, 806–816. [Google Scholar] [CrossRef]
- Cai, Y.; He, Y.; Zhang, H.; Zhou, H.; Liu, J. Research on Harmonic State-Space Modeling and Calculation Analysis of Low-Switching-Frequency Grid-Connected Inverter Considering the Impact of Digitization. IEEE Trans. Power Electron. 2023, 38, 1003–1021. [Google Scholar] [CrossRef]
- Li, Z.; Li, H.; Sun, S. Virtual Model Predictive Control for Inverters to Achieve Flexible Output Impedance Shaping in Harmonic Interactions With Weak Grids. IEEE Trans. Power Electron. 2024, 39, 10754–10767. [Google Scholar] [CrossRef]
- Qian, Q.; Xie, S.; Xu, J.; Xu, K.; Bian, S.; Zhong, N. Output Impedance Modeling of Single-Phase Grid-Tied Inverters With Capturing the Frequency-Coupling Effect of PLL. IEEE Trans. Power Electron. 2020, 35, 5479–5495. [Google Scholar] [CrossRef]
- Gao, J.Y.; Zhao, J.B.; Chen, X.B.; Qu, K. Reshaped Impedance-Based Stability Criterion Under Weak Grid Conditions. Power Syst. Technol. 2017, 41, 2762–2768. (In Chinese) [Google Scholar]
- Zhu, D.H.; Zhou, S.Y.; Zou, X.D.; Kang, Y. Improved Design of PLL Controller for LCL-Type Grid-Connected Converter in Weak Grid. IEEE Trans. Power Electron. 2020, 35, 4715–4727. [Google Scholar] [CrossRef]
- Gao, J.Y.; Xiao, F.; Jiang, F.; Guo, Q.; Lu, B.H. Grid-Connected Inverter Impedance Phase Reshaping Control With Novel PLL Structure in Weak Grid. Proc. CSEE 2020, 40, 6682–6694. (In Chinese) [Google Scholar]
- Karimi-Ghartemani, M.; Karimi, H.; Khajehoddin, S.A.; Hoseinizadeh, S.M. Efficient Modeling and Systematic Design of Enhanced Phase-Locked Loop Structures. IEEE Trans. Power Electron. 2022, 37, 9061–9072. [Google Scholar] [CrossRef]
- Yang, D.; Ruan, X.; Wu, H. A Virtual Impedance Method to Improve the Performance of LCL-Type Grid-Connected Inverters Under Weak Grid Conditions. Proc. CSEE 2014, 34, 2327–2335. (In Chinese) [Google Scholar]
- Lin, X.; Liang, Z.; Zheng, Y.; Lin, Y.; Kang, Y. A Current Limiting Strategy with Parallel Virtual Impedance for Three-Phase Three-Leg Inverter Under Asymmetrical Short-Circuit Fault to Improve the Controllable Capability of Fault Currents. IEEE Trans. Power Electron. 2019, 34, 8138–8149. [Google Scholar] [CrossRef]
- Zhu, D.H.; Zhou, S.Y.; Zou, X.D.; Kang, Y.; Zou, K. Small-Signal Disturbance Compensation Control for LCL-Type Grid-Connected Converter in Weak Grid. IEEE Trans. Ind. Appl. 2020, 56, 2852–2861. [Google Scholar] [CrossRef]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Analysis of D-Q Small-Signal Impedance of Grid-Tied Inverters. IEEE Trans. Power Electron. 2016, 31, 675–687. [Google Scholar] [CrossRef]
- Tu, C.M.; Gao, J.Y.; Xiao, F.; Guo, Q.; Jiang, F. Stability Analysis of the Grid-Connected Inverter Considering the Asymmetric Positive Feedback Loops Introduced by the PLL in Weak Grids. IEEE Trans. Ind. Electron. 2022, 69, 5793–5802. [Google Scholar] [CrossRef]
- Zhou, S.; Zou, X.; Zhu, D.; Tong, L.; Zhao, Y.; Kang, Y.; Yuan, X. An Improved Design of Current Controller for LCL-Type Grid-Connected Converter to Reduce Negative Effect of PLL in Weak Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 648–663. [Google Scholar] [CrossRef]
- Yu, H.; Su, J.; Zheng, L.; Zhang, T.; Zhang, D.; Shi, Y. Mechanism Analysis and Suppression Method of Sub-Synchronous Resonance for Energy Storage Inverter Connected to Grid. Autom. Electr. Power Syst. 2020, 44, 99–108. (In Chinese) [Google Scholar]
- Xin, Z.; Loh, P.C.; Wang, X.; Blaabjerg, F.; Tang, Y. Highly Accurate Derivatives for LCL-Filtered Grid Converter with Capacitor Voltage Active Damping. IEEE Trans. Power Electron. 2016, 31, 3612–3625. [Google Scholar] [CrossRef]




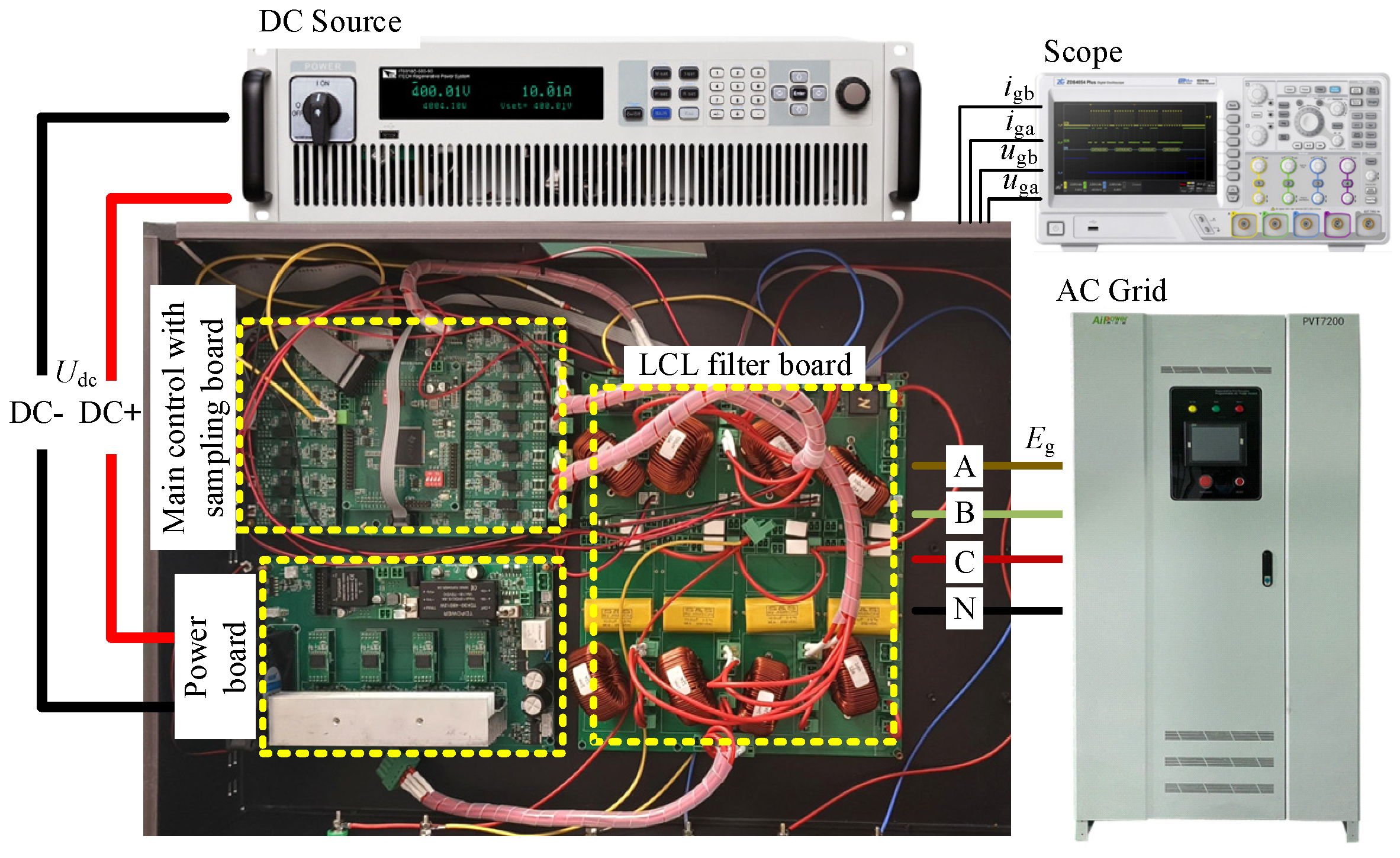

| Parameter | Symbol | Value |
|---|---|---|
| DC Voltage | Udc | 700 V |
| Grid Voltage | Eg | 311 V |
| Rated Capacity | Sn | 10 kVA |
| Filter Inductance1 | Lf1 | 3 mH |
| Filter Inductor2 | Lf2 | 0.8 mH |
| Filter Capacitor | Cf | 15 uF |
| Switching Frequency | fs | 10 kHz |
| Active Damping Coefficient | Kd | 13 |
| Proportional Coefficient of the Current Loop | kp | 2 |
| Integral Coefficient of the Current Loop | ki | 350 |
| Proportional Coefficient of PLL | kppll | 0.8 |
| Integral Coefficient of PLL | kipll | 32 |
| Proportional Coefficient | k | 0.5 |
| Cutoff Angular Frequency | 5000 rad/s | |
| Maximum Gain Angular Frequency | 104π rad/s |
| Control Method | Stable Operating Range for Lg |
|---|---|
| Traditional compensation control | 3–15 mH |
| Improved compensation control | 0–15 mH |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, H.; Yang, X. Reconstruction of Impedance Criteria and Stability Enhancement Strategies for Grid-Connected Inverters. Electronics 2025, 14, 4402. https://doi.org/10.3390/electronics14224402
Mao H, Yang X. Reconstruction of Impedance Criteria and Stability Enhancement Strategies for Grid-Connected Inverters. Electronics. 2025; 14(22):4402. https://doi.org/10.3390/electronics14224402
Chicago/Turabian StyleMao, Haoyu, and Xiaohui Yang. 2025. "Reconstruction of Impedance Criteria and Stability Enhancement Strategies for Grid-Connected Inverters" Electronics 14, no. 22: 4402. https://doi.org/10.3390/electronics14224402
APA StyleMao, H., & Yang, X. (2025). Reconstruction of Impedance Criteria and Stability Enhancement Strategies for Grid-Connected Inverters. Electronics, 14(22), 4402. https://doi.org/10.3390/electronics14224402






