Learning Path Recommendation Enhanced by Knowledge Tracing and Large Language Model

Abstract

With the development of large language model (LLM) technology, AI-assisted education systems are gradually being widely used. Learning Path Recommendation (LPR) is an important task in personalized instructional scenarios. AI-assisted LPR is gaining traction for its ability to generate learning content based on a student’s personalized needs. However, the native-LLM has the problem of hallucination, which may lead to the inability to generate learning content; in addition, the evaluation results of the LLM on students’ knowledge status are usually conservative and have a large margin of error. To address these issues, this work proposes a novel approach for LPR enhanced by knowledge tracing (KT) and LLM. Our method operates in a “generate-and-retrieve” manner: the LLM acts as a pedagogical planner that generates contextual reference exercises based on the student’s needs. Subsequently, a retrieval mechanism constructs the concrete learning path by retrieving the top-N most semantically similar exercises from an established exercise bank, ensuring the recommendations are both pedagogically sound and practically available. The KT plays the role of an evaluator in the iterative process. Rather than generating semantic instructions directly, it provides a quantitative and structured performance metric. Specifically, given a candidate learning path generated by the LLM, the KT model simulates the student’s knowledge state after completing the path and computes a knowledge promotion score. This score quantitatively measures the effectiveness of the proposed path for the current student, thereby guiding the refinement of subsequent recommendations. This iterative interaction between the KT and the LLM continuously refines the candidate learning items until an optimal learning path is generated. Experimental validations on public datasets demonstrate that our model surpasses baseline methods.

1. Introduction

Learning Path Recommendation (LPR) systems leverage real-time analysis of students’ knowledge acquisition to construct personalized learning trajectories tailored to their specific needs [1]. By dynamically adapting instructional content and methodologies, these systems not only enhance learning efficiency but also foster deeper engagement and intrinsic motivation, thereby significantly augmenting overall educational outcomes. As AI applications become increasingly pervasive in education, the interpretability and fairness of recommendation systems have also received growing attention [2,3,4]. An ideal LPR system should not only be effective but also transparent, trustworthy, and fair. In recent years, research in the field of LPR has exhibited a noticeable upward trend. Some researchers have applied knowledge tracing (KT) to LPR. The KT model has the ability to predict students’ knowledge status, so as to enhance the ability of the LPR system to dynamically evaluate students’ knowledge status and adjust the path based on this [5,6]. However, the existing KT model only has the ability of single-step prediction, that is, it can only predict the knowledge state of students at time $t+1$, which is difficult to meet the requirements of LPR for multi-step prediction of students’ knowledge status.

Recent advances in large language models (LLMs) have opened up new possibilities for LPR. LLMs can understand educational materials in textual format, generate textual content that can be used for teaching purposes, or provide answers to questions in learning [7,8]. These methods make use of the text comprehension and reasoning capabilities of LLMs. Based on the semantic understanding of the description text of the interaction of students’ learning behavior by LLM, the current knowledge state of students is inferred. However, it is also difficult to correctly reason about the knowledge state of the student’s future multi-step in this way. In addition, the LLM assessment results of students’ knowledge status are always concentrated on a certain average, for example, if it is asked to rank the student’s knowledge state from 1 to 5 according to the student’s learning record, the result given is always around 3 points. This is because LLMs have a tendency to be greedy too early, that is, they tend to choose safe answers that occur frequently in the training data to avoid extreme judgments [9]. LLM prematurely locks in the local optimal solution in decision-making, resulting in a decrease in action coverage instead of comprehensively exploring the optimal strategy. Therefore, in the ranking task, the area around the comfort zone of the model is because of the lowest risk.

To address these challenges, we propose a novel Learning Path Recommendation Enhanced by Knowledge Tracing and Large Language Model, referred to as LPReKL. Primarily, to enhance KT’s capability for multi-step prediction of students’ knowledge status, we probabilistically replace a portion of students’ responses with masked tokens during training. In addition, we have introduced information on the difficulty of the exercises in the KT model. Through this process, KT can accurately infer the student’s level of mastery of a particular knowledge concept at $t+n$ steps. Subsequently, leveraging feedback from KT and predefined prompt templates, the LLM is designed to generate the new reference exercise text. Finally, exercises with high similarity to these reference exercise text are retrieved from an exercise bank as the candidate item of the learning path. This content undergoes validation by the KT—if deemed appropriate, it is presented to students; otherwise, the LLM refines its generated content based on KT-driven feedback through the continuous interaction and optimization between KT and LLM. The contributions of this work can be summarized as follows:

• This work proposes a novel learning path recommendation method that fuses KT models and LLMs. It introduces a feedback mechanism that guides LLMs to automatically adjust what they generate based on KT’s predictions.
• We reconstruct the students’ historical interaction data by incorporating mask markers, enabling KT’s training to predict the students’ state of knowledge at the next $t+n$ time step.
• A series of experimental results on multiple public datasets show that the proposed model is effective and has advantages over existing methods.

Traditional sequential or graph-based recommendation methods [10,11] rely on static, historical associations to recommend items [12]. In contrast, our approach performs dynamic simulation: before recommending a top-N exercise path, it forecasts the student’s knowledge state after completing the entire sequence, enabling evaluation of long-term effectiveness and selection of paths with optimal cumulative gains rather than immediate benefits. Moreover, the masking mechanism—by randomly hiding historical responses during training—forces the model to reason under incomplete information, improving its robustness and generalization for multi-step prediction. This allows reliable simulation of entirely new, unseen learning paths.

The remainder of this paper is organized as follows. Section 2 reviews related work on learning path recommendation. Section 3 formalizes the problem definition. Section 4 elaborates on the proposed methodology in detail. Experimental results and analyses are presented in Section 5. Finally, Section 6 concludes this paper and outlines future research directions.

2. Related Work

2.1. Learning Path Recommendation

Learning path recommendation systems can provide customized learning content and teaching strategies based on individual student characteristics, effectively meeting the demands of personalized education [13]. Existing LPR methods mainly fall into two categories. The first category relies on manually defined rules, including constructing learning resource dependency models based on prerequisite relationships [14,15] and modeling knowledge concept correlations using knowledge graphs [16]. Although these methods offer certain interpretability, they exhibit notable limitations in practical applications: first, the systems lack flexibility to adapt to dynamically changing learning needs; second, they incur high maintenance costs. For instance, knowledge graphs require continuous updates to maintain timeliness, otherwise their performance may degrade when handling new knowledge-related exercises. The second category formulates LPR as a sequential recommendation problem [17,18]. These methods generate complete learning paths by analyzing students’ historical behavior data. For example, Zhang et al. [1] employ a recursive propagation approach to process learner–course interaction data, utilizing graph convolutional networks to generate predicted course ratings, which are subsequently integrated with learning style similarity scores to achieve personalized course recommendations. Liu et al. construct learning networks by analyzing learning records and propose a combinatorial recommendation algorithm [19].

While achieving certain results, these methods fail to effectively capture real-time changes in students’ knowledge states, resulting in recommendations that lack personalization and adaptability. The introduction of KT effectively addresses these limitations. Unlike previous recommendation methods that rely on static rules, KT models can dynamically adjust and optimize recommendation paths by continuously analyzing students’ real-time learning performance, thereby significantly enhancing the adaptability and personalization of recommendation systems.

2.2. Knowledge Tracing for LPR

By analyzing student interactions with learning materials, KT predicts students’ mastery of specific knowledge concepts [20,21]. Bayesian Knowledge Tracing is one of the classic approaches, using Bayesian inference to estimate students’ knowledge states [22]. In 2015, Piech et al. use recurrent neural networks for KT [23], leveraging LSTMs to capture students’ knowledge states and temporal dependencies, leading to improved prediction accuracy. The advent of deep KT has significantly advanced the development of learning path recommendation systems [5,24]. By employing data-driven dynamic modeling approaches, this technology transforms traditional one-size-fits-all learning paths into personalized adaptive recommendations, thereby effectively enhancing learning efficiency and outcomes. Specifically, Zhang et al. [5] utilized knowledge tracing to annotate students’ knowledge states in historical learning logs, incorporating these state features as model inputs to generate personalized learning paths that capture both sequential relationships and selection logic among learning resources. Chen et al. [24] proposed an auxiliary prediction module based on knowledge tracing, which continuously evaluates students’ mastery levels at each node of the learning path and optimizes model parameters through cross-entropy loss functions, significantly improving recommendation stability. Notably, the application of multimodal data provides online learning systems with more comprehensive and multi-dimensional representations of student behaviors, creating opportunities for building more accurate personalized learning experiences [25,26].

However, current KT models exhibit two critical limitations: they cannot effectively predict exercises for the next $t+n$ step and typically require large amounts of high-quality training data. These constraints significantly challenge their applicability in LPR, where sparse data and continuously emerging new exercises are common. Additionally, Wang et al. [27] argue that existing methods often fail to adequately capture complex behavioral patterns unless they effectively leverage rich world knowledge for deeper reasoning about learning materials. This limitation has prompted researchers to explore novel applications of LLMs in this field.

2.3. LLM-Assisted Recommendation

Recent advancements in deep learning have ushered in transformative breakthroughs, particularly within the domain of natural language processing. Cutting-edge LLMs, including DeepSeek and the Qwen series, exhibit unparalleled proficiency in natural language comprehension [28,29], providing robust technical support for LPR. The integration of LLMs into the educational field presents a salient advantage. LLMs possess contextual understanding and reasoning capabilities. When students struggle with overwhelming learning materials, LLMs generate personalized content based on their learning progress and knowledge states, ensuring access to the most relevant educational resources [8,30,31]. Wang et al. [31] propose a ChatGPT-based personalized English reading comprehension support system, which enhances learning by predicting students’ reading skills, generating tailored questions, and automatically evaluating responses. Cui et al. [32] employ KT techniques to estimate students’ mastery of knowledge concepts based on their learning history and subsequently generated exercise recommendations using a pre-trained language model. Li et al. [15] integrate LLM with knowledge graphs to recommend appropriate learning materials tailored to students’ knowledge states and the human knowledge system. However, current LLM-assisted recommendations suffer from two notable shortcomings: first, they directly adopt model-generated content while overlooking potential logical fallacies or factual inaccuracies; second, they lack effective interactive feedback mechanisms—once the model provides recommendations to students, it cannot collect meaningful learning feedback, thereby hindering dynamic optimization of the recommended content.

The distinctions between LPReKL and prior approaches lie in two aspects:

• Conceptually: Previous methods used LLM and KT in a one-way pipeline, lacking bidirectional interaction [33,34]. LPReKL introduces an iterative feedback loop where KT not only diagnoses the initial knowledge state but also evaluates the quality of the LLM-generated learning path and provides feedback for dynamic refinement, forming a closed-loop optimization system.
• Practically: We propose a masked tokens strategy that enables KT to predict performance on unknown exercises, whereas traditional KT only supports prediction for known exercises. We employ a retrieval mechanism to match LLM-generated reference exercises with real items from the exercise bank, ensuring that recommended content is pedagogically sound and practically available, rather than relying directly on potentially hallucinated LLM outputs.

3. Problem Formulation

In this section, we review the definition of LPR and explain some key terms within this work. We have listed some frequently used symbols in

Table 1. Key notations.

Notation	Description
Q = {$q_1,q_2,\cdots$}	All exercises in the exercise bank
U = {$u_1,u_2,\cdots$}	All involved students
C = {$c_1,c_2,\cdots$}	All relevant knowledge concepts
$u^i$ = {$\left(q_1,a_1\right),\left(q_2,a_2\right),\cdots$}	A specific student’s learning records
$a_i$	Exercise answer, $a_i\in$ [0, 1]
$E_{sup}$	Full score of the examination
$E_s$	Beginning score of the examination
$E_e$	Ending score of the examination
$E_{\phi }$	A student’s promotion in specific knowledge concepts
$KC\left(q\right)$	A set of knowledge concepts contained in q
$Diff\left(q_i\right)$	Exercise difficulty of $q_i$
d	Expected difficulty
$l{p}_c$	Candidate exercises
$s^i$	A specific knowledge state of the student i

and provide a detailed explanation of their roles in this context.

Learning Path Recommendation. The learning path is illustrated in Figure 1. In the Learning Path Recommendation task, the student is first assessed and receives an initial score of $E_s$ at the beginning. The recommendation system then proposes a candidate learning path $l{p}_c=\left\{q_1,q_2,\cdots ,q_K\right\}$, where the student engages in the recommended exercises and generates new learning records $u_t=\{(q_1,a_1),(q_2,a_2),\cdots ,(q_K,a_K)\}$, along with a final score $E_e$. The student’s learning records and knowledge states are updated accordingly, such that $u_t=u_t\cup u_{t-1}$. The effectiveness of the learning path, denoted as $E_{\phi }$ [14,24,35], can be calculated using the following formula:

$$E_{\phi }={\displaystyle \frac{E_e-E_s}{E_{sup}-E_s}},$$

(1)

where $E_{sup}$ is the maximum score for the path, $E_s$ is the student’s initial score, and $E_e$ is the score after completing the target path. A higher $E_{\phi }$ indicates a more effective learning path that better matches the needs of student.

In this work, we define a learning path as a carefully curated sequence of learning items designed to achieve a specific learning goal. The internal logic of the path lies in its targeted addressing of the student’s weak knowledge concepts and its overall effectiveness, concretely represented as an ordered list of exercises $l{p}_c=\left\{q_1,q_2,\cdots ,q_K\right\}$.

Knowledge State. Given a set of $\left|U\right|$ students, $\left|C\right|$ knowledge concepts, and $\left|Q\right|$ exercises, each student’s historical learning process is represented as a sequence:

$$LP\left(u^i\right)=\{(q_1,a_1),(q_2,a_2),\cdots ,(q_t,a_t),\cdots ,(q_L,a_L)\},$$

(2)

where $u^i\in U$, $q_t\in Q$ denotes the exercise answered by the student at time step t, and $a_t\in \left\{0,1\right\}$ indicates the correctness of the response (1 for correct, 0 for incorrect). Each exercise $q_t$ is associated with one or more knowledge concepts $c_t$. By analyzing students’ historical data, we can pinpoint their weaknesses and determine the knowledge concepts that require further reinforcement, as described below:

$$\mathbb{P}\left(u_{t+1}^i\right)=\mathrm{\Omega }\left(\{(q_1,a_1,c_1),(q_2,a_2,c_2),\cdots ,(q_t,a_t,c_t)\}\right),$$

(3)

where $\mathrm{\Omega }$ corresponds to a trainable algorithm or model, and $u^i$ represents the ith student. This formulation aims to predict the next learning step $u_{t+1}^i$ for each student, enabling the system to dynamically adapt to their evolving knowledge states and optimize their learning trajectories.

Exercise Difficulty. The difficulty of an exercise significantly affects student learning. Exercises that are too easy or too difficult can demotivate students [36], while appropriately challenging ones enhance understanding and stimulate interest [37]. We define the difficulty of an exercise $q_i$ as the average error rate of its associated knowledge concepts from students’ learning histories:

$$\mathrm{Diff}\left(q_i\right)={\displaystyle \frac{1}{N}}\sum _{K=1}^{N}error(q_i,\left\{c^k\right|c^k\in \mathrm{KC}\left[q_i\right]\}),$$

(4)

where N is the number of knowledge concepts in the set $KC\left[q_i\right]$, $error\left(q_i\right)$ is the error rate of concept $c^k$. Zhang et al. suggest that an error rate around 30% optimally engages students [37].

4. Methodology

This section first introduces the framework and workflow of LPReKL, followed by a detailed discussion of each component.

4.1. Framework Overview

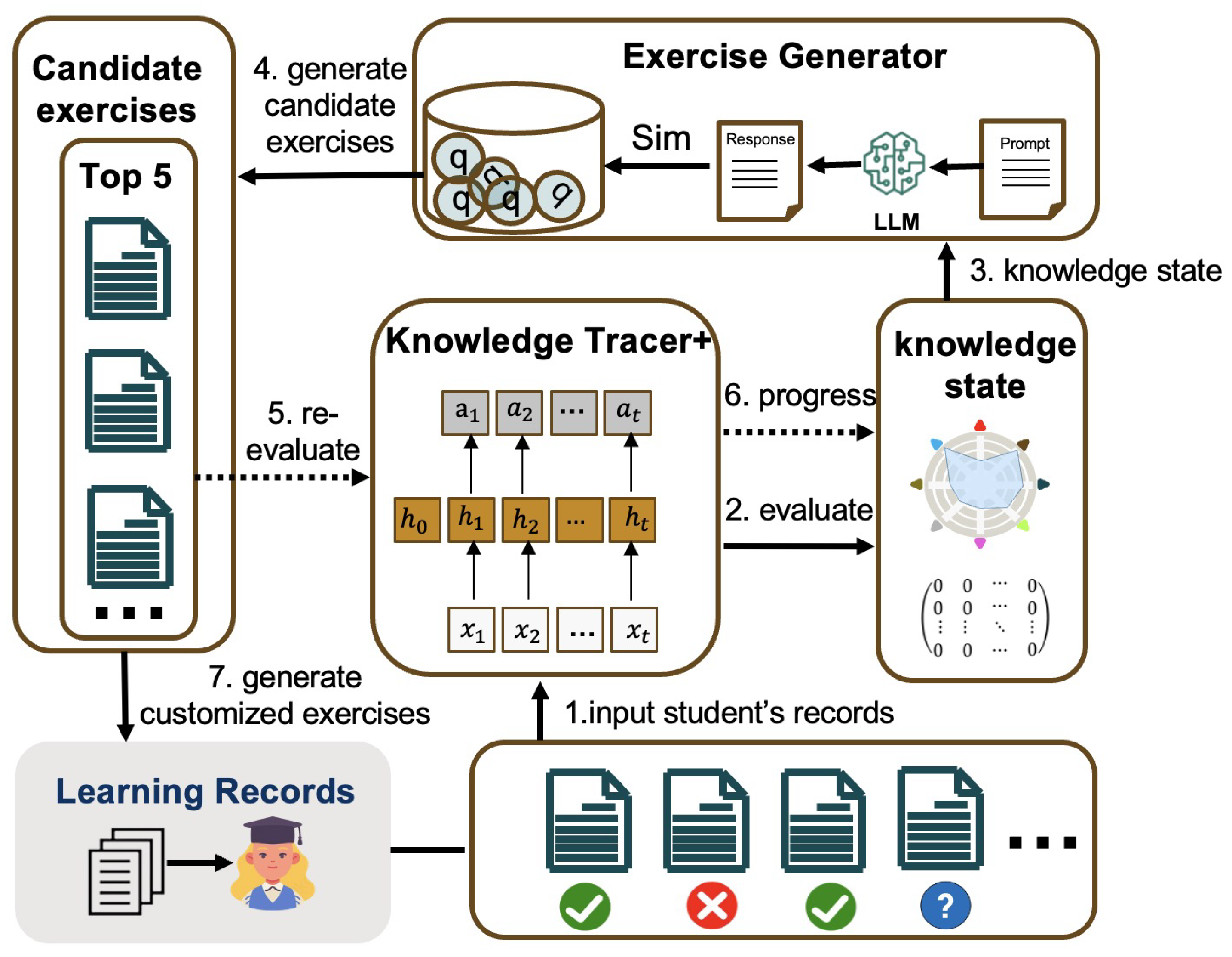
Figure 2 presents the overall architecture of LPReKL. First, a KT with the ability to predict students’ multi-step knowledge states is used to detect students’ initial knowledge states. These students’ initial knowledge states are then fused into prompt templates and transferred to the LLM, which generates a learning project for reference. These items are used as references to retrieve the most similar exercises from the practice library to construct an initial learning path. This learning path is then fed into the KT model again to evaluate the improvement value of the student’s knowledge status after using the learning path. Finally, based on the feedback of the improved value, the prompt template is adjusted and fed back to the LLM to continue or stop generating new learning items. If the LLM continues to generate new learning items, the subsequent operations will be repeated until the optimization goal is achieved.

The details of the procedures for LPR based on LPReKL are as shown in Algorithm 1.

Algorithm 1: LPReKL framework

Input:  learning records $u^i$, masked rate $\tau$, Exercise bank Q. Output:  recommendation learning path $l{p}_c$ 1: $KT\leftarrow Pretraining(u^i,\tau )$ 2: for each u in U do 3:     $s_{t-1}^i\leftarrow KT\left(u_{t-1}^i\right)$ 4:     $prompt\_template\leftarrow PreparePrompt(u_{t-1}^i,\left[KC\right],\left[q_i\right],d)$ 5:     $List\left[q_j^{\prime }\right]\leftarrow LLM(prompt\_template)$                                                 ▹ Equation (10) 6:     $l{p}_c\leftarrow MatchExercises(List\left[q_j^{\prime }\right],Q)$                                                   ▹ Equation (12) 7:     $s_t^i\leftarrow KT\left(l{p}_c\right)$ 8:     while not $IsSatisfied(s_{t-1}^i,s_t^i)$ do 9:           $prompt\_template\leftarrow PreparePrompt(u_t^i,\left[KC\right],\left[q_i\right],d)$ 10:         $List\left[q_j^{\prime }\right]\leftarrow LLM(prompt\_template)$                                            ▹ Equation (10) 11:         $l{p}_c\leftarrow MatchExercises(List\left[q_j^{\prime }\right],ExerciseBank)$                             ▹ Equation (12) 12:     end while 13:     Return $l{p}_c$ 14: end for

4.2. Knowledge Tracing for Multi-Step Predictions

We introduce a novel masked mechanism during the training of the KT model to enable multi-step knowledge state prediction. The intuition is to simulate the uncertainty in future student responses when planning a multi-step learning path. For each training sequence, we randomly mask a proportion of the historical records by setting their mask indicator $(m_i=0)$. This forces the model to rely on a broader context rather than just the most recent interactions, thereby improving its ability to forecast knowledge states several steps ahead.

The robust capabilities of DKT have been well established [24], prompting us to adopt the original DKT architecture [23] as the foundational simulator [5]. However, we introduce a novel mechanism: the use of masked tokens to reconstruct students’ historical interaction data, thereby enabling the model for multi-step knowledge states prediction. Given the historical response sequence of the student j as $u_{<t}^j=\{(q_1,a_1),(q_2,a_2),\cdots ,(q_{t-1},a_{t-1})\}$, where $q_i$ and $a_i$ denote the exercise index and the corresponding response. Furthermore, we maintain a mask value $m_i$ for each record, indicating whether the answer should remain visible $(m_i=1)$ or be masked $(m_i=0)$. The reconstructed data is expressed as:

$${\tilde{u}}_{<t}^j=\{(q_1,m_1,a_1),(q_2,m_2,a_2),\cdots ,(q_{t-1},m_{t-1},a_{t-1})\}.$$

(5)

During training, for masked records $(m_i=0)$, the response is replaced with a special token to indicate missing data. The input to the KT model is formulated as:

$$\begin{array}{cc}\hfill & q_{t-1}=W_q{e}_{t-1}^q,\hfill \\ \hfill & m_{t-1}=W_m{e}_{t-1}^m,\hfill \\ \hfill & a_{t-1}=W_a{e}_{t-1}^a,\hfill \\ \hfill & x_{<t}^j=q_{t-1}\oplus m_{t-1}\oplus a_{t-1},\hfill \end{array}$$

(6)

where $e_{t-1}^q$, $e_{t-1}^m$, and $e_{t-1}^a$ are one-hot vector representations of the respective symbols, and $W_{\ast }$ indicates weight matrices. The model then predicts the student’s knowledge states as follows:

$$\begin{array}{cc}\hfill & i_t=\mathrm{sigmoid}(W_{xi}{x}_{<t}^j+W_{hi}{h}_{t-1}+b_i),\hfill \\ \hfill & f_t=\mathrm{sigmoid}(W_{xf}{x}_{<t}^j+W_{hf}{h}_{t-1}+b_f),\hfill \\ \hfill & o_t=\mathrm{sigmoid}(W_{xo}{x}_{<t}^j+W_{ho}{h}_{t-1}+b_o),\hfill \\ \hfill & c_t=f_t{c}_{t-1}+i_{t}tanh(W_{xc}{x}_{<t}^j+W_{hc}{h}_{t-1}+b_c),\hfill \\ \hfill & h_t=o_{t}tanh\left(c_t\right),\hfill \\ \hfill & s_t=\mathrm{sigmoid}(W_{os}{o}_t+b_0).\hfill \end{array}$$

(7)

Here, $i_{\ast }$, $f_{\ast }$, $o_{\ast }$, $c_{\ast }$ correspond to the input gate, forget gate, output gate, and memory cell, respectively. Both $tanh(\ast )$ and $sigmoid(\ast )$ denote activation functions, while $W_{\ast }$ and $b_{\ast }$ are trainable parameters. The output vector $s_t$ has a dimension equal to the number of knowledge concepts, with each entry indicating the student’s mastery of a specific knowledge concept. Our model not only predicts students’ knowledge states but also balances the impact of exercise difficulty on performance. The binary cross-entropy loss for n iterations and exercise difficulty regulation are defined as:

$$\begin{array}{cc}\hfill & {\ell }_{bce}=\sum _{k=1}^{n}BCE(a_k,r_k),\hfill \\ \hfill & {\ell }_{diff}={\displaystyle \frac{1}{n}}\sum _{i=1}^n|\mathrm{d}-Diff\left(q_i\right)|,\hfill \end{array}$$

(8)

where $\mathrm{d}$ is a predefined difficulty level tailored to student needs. The final optimization objective is:

$$\ell =\alpha {\ell }_{bce}+\beta {\ell }_{diff},$$

(9)

where $\alpha$ and $\beta$ are weighting parameters.

4.3. Prompt Template of LLM

LLMs refer to ultra-large-scale neural networks trained via deep learning techniques, capable of comprehending and generating human language with remarkable fluency. These models are typically pre-trained on extensive textual corpora, allowing them to capture nuanced linguistic patterns and contextual dependencies. Owing to their transformative impact across a wide range of natural language processing tasks—such as text generation and machine translation—LLMs have garnered increasing attention in the domain of recommendation systems [38,39]. Prompt templates serve as an effective mechanism to enhance the interpretability and reasoning capabilities of LLMs; when carefully crafted, they can guide the model to produce responses that are not only coherent but also closely aligned with task-specific objectives [40]. Qwen (version 2.0; Alibaba Cloud, Hangzhou, China) is a language model introduced by Alibaba Cloud, and we have deployed this model on our servers with a parameter size of 32 billion. As illustrated in Figure 3, the prompt template is carefully designed to guide the LLM in its role as an intelligent exercise generation assistant. The blue section highlights that the LLM should focus on students’ evolving understanding of specific knowledge concepts and the desired exercise difficulty. Newly generated reference exercises should adhere to the format provided in the examples. For each student with multiple weak knowledge concepts, the LLM aims to generate exercises covering as many of these knowledge concepts as possible to optimize knowledge improvement. To ensure content quality, the reference exercises are matched against the exercise bank, with the top five most similar exercises selected for recommendation. The yellow section corresponds to each student’s learning situation, which is updated before each recommendation. The green section represents the response of LLM. The process is outlined below:

$$\mathrm{LP}=\mathrm{LLM}(s_t^i;\left[\mathrm{KC}\right];[q_i,q_j];\mathrm{d}),$$

(10)

where $s^i$ denotes the student’s knowledge states, $\left[KC\right]$ is the set of relevant knowledge concepts, $\left[q_i\right]$ provides example exercises, and $\mathrm{d}$ represents the expected difficulty level.

The LLM used in this work is the Qwen2-32B pre-trained model. We did not fine-tune this model; instead, we fully leveraged its in-context learning capability through carefully designed prompt templates. The temperature in the text generation process was set to 0.5.

4.4. Exercise Retrieval

We employ a pre-trained BERT model to obtain textual embeddings for the exercises. For each exercise, we input its text into the BERT model and use the corresponding output vector as its semantic embedding, which is then used for subsequent similarity computation.

To ensure the effectiveness and accuracy of the recommended content, we match the candidate exercises generated by the LLM with existing items in the exercise bank and select the top-N most similar ones for recommendation.

Given a reference exercise $q=\{w_1,w_2,\cdots ,w_n\}$ and a candidate exercise $q^{\prime }=\{w_1^{\prime },w_2^{\prime },\cdots ,w_m^{\prime }\}$, where $w_i$ and $w_i^{\prime }$ represent words in the exercise and n and m are the number of words in each exercise text, we utilize a pre-trained BERT model to obtain contextualized vector embeddings for each token:

$$\mathbb{E}\left(q_i\right),\mathbb{E}\left(q_j^{\prime }\right)\in {\mathbb{R}}^d,$$

(11)

where $\mathbb{E}\left(q_i\right)$ and $\mathbb{E}\left(q_j^{\prime }\right)$ are the d-dimensional embeddings produced by BERT [41]. The semantic similarity between a reference and a candidate exercise is computed using cosine similarity:

$$\mathrm{sim}(q_i,q_j^{\prime })={\displaystyle \frac{\mathbb{E}\left(q_i\right)\odot \mathbb{E}\left(q_j^{\prime }\right)}{\left|\right|\mathbb{E}\left(q_i\right)\left|\right|\left|\right|\mathbb{E}\left(q_j^{\prime }\right)\left|\right|}}.$$

(12)

Here, ⊙ denotes the dot product and $\left|\right|\ast \left|\right|$ is the Euclidean norm. Ultimately, the top $N=5$ candidate exercises with the highest similarity scores are selected:

$${\mathrm{lp}}_{\mathrm{c}}={\mathrm{Rank}}_5=\{q_1,q_2,\cdots ,q_5\}.$$

(13)

Before generating a learning path, the student’s knowledge state—provided by the KT model—is transformed into explicit, structured pedagogical objectives, namely the “set of knowledge concepts requiring reinforcement” and the “target difficulty level.” These objectives are clearly communicated to the LLM through carefully designed prompt templates, thereby guiding the generation process in a controlled and purposeful manner. Based on the entire exercise bank, we compute the semantic similarity between the LLM-generated reference item and all candidate exercises using a pre-trained BERT model and select the top-N most similar exercises. Through this design, the LLM functions more like a “pedagogical assistant” that operates within a well-defined instructional framework, generating contextually appropriate and semantically rich reference content. Meanwhile, the retrieval mechanism ensures that the final recommended exercises are drawn from the authentic, curated exercise bank. This separation of responsibilities effectively aligns the creative capacity of the LLM with educational fidelity, thereby preserving consistency with the intended pedagogical goals.

The detailed process of exercise retrieval is documented in Algorithm 2.

Algorithm 2: MatchExercises

Input: $List\left[q_j^{\prime }\right]$ generated by LLM, Exercise bank Q,     Number of exercises to retrieve n Output: $top\_n\_exercises$     $all\_candidates\leftarrow \left[\right]$     for each $ref$ in $List\left[q_j^{\prime }\right]$ do         $re{f}_{rec}\leftarrow BER{T}_{E}mbed\left(ref\right)$         for each $candidate$ in Q do             $candidat{e}_{rec}\leftarrow BER{T}_{E}mbed\left(candidate\right)$             $sim\leftarrow CosineSimilarity(re{c}_{ref},candidat{e}_{rec})$             $Append(candidate,sim)toall\_candidates$         end for     end for     $sorted\_candidates\leftarrow Sort(al{l}_{c}andidates,by=sim,descending=True)$     $top\_n\_exercises\leftarrow GetTopN(sorted\_candidates,n)$

5. Experiment

In order to understand the model more clearly, we conducted experiments that addressed the following research questions:

RQ1: In the task of assessing students’ knowledge status, do the results generated by direct use of LLM tend to be conservative and lack discrimination?

RQ2: Is LPReKL more effective than the existing LPR?

RQ3: What impact do the individual core components of LPReKL have on the model’s overall performance?

RQ4: How do hyperparameters in the model contribute to overall performance?

5.1. Dataset and Simulator

5.1.1. Dataset

To evaluate the performance of the proposed LPReKL, we conduct experiments on three publicly available datasets. MOOCCubeX (https://github.com/THU-KEG/MOOCCubeX?tab=readme-ov-file, accessed on 1 March 2025) is one of the largest and most comprehensive MOOC datasets, containing a wealth of exercises, knowledge concepts, and student interaction records. We extract students’ activity logs related to physics subjects for our experiments. MOOPer (http://data.openkg.cn/dataset/mooper, accessed on 1 March 2025) is derived from interaction data collected between 2018 and 2019 on the EduCoder platform, where students participated in practical programming exercises. XES3G5M (https://github.com/ai4ed/xes3g5m, accessed on 1 March 2025) is collected from a real-world online mathematics learning platform and contains third-grade students’ historical interaction records on math exercises. The processed dataset details are summarized in

Table 2. Dataset statistics.

Dataset	Students	Exercise	KCs	Interations
MOOCCubeX	13,091	156	71	1,206,646
MOOPer	26,603	1756	1360	2,007,572
XES3G5M	16,378	6006	828	4,803,902

.

5.1.2. Simulator

To evaluate the effectiveness of different methods in LPR, we follow prior work [14,24,35] and utilize our proposed KT to assess the quality of the generated learning paths. The KT model is trained on large-scale real-world data with the objective of accurately predicting students’ responses to exercises. Therefore, it can serve as a reliable simulator for students’ knowledge state evolution, enabling a fair comparison of the expected effectiveness of learning paths generated by different recommendation methods.

5.2. Implementation Details

We discard student records with fewer than ten interactions and retain only the associated knowledge concepts. The remaining data is split into training, validation, and test sets with a ratio of 8:1:1. The hidden dimension of the KT is set to 200, and the output layer size matches the number of knowledge concepts in the dataset. Dropout with a rate of 0.6 is applied to mitigate overfitting. We use the Adam optimizer with a momentum of 0.9, a gradient clipping threshold of 3.0, an initial learning rate of 0.01, and a decay rate of 0.75. The input sequence length is fixed to 200, and shorter sequences are padded with null values. All experiments are conducted on a Tesla V100 GPU with Python 3.10, PyTorch 2.1.2, and CUDA 11.8.

5.3. Baselines and Evaluation Metric

5.3.1. Baselines

We compare LPReKL with several state-of-the-art methods:

• FISM [42]: Generates recommendations based on a similarity matrix.
• CluLSTM [43]: Clusters students into groups and uses LSTM to predict learning paths.
• DQN [44]: Applies Q-learning and deep neural networks for decision-making.
• GRU4Rec [45]: Utilizes gated recurrent units to process students’ historical interactions and generate learning paths.
• LightGCN [46]: Employs multi-layer graph convolution to extract deep features among entities for recommendation.
• GEHRL [35]: Tracks students’ knowledge states with KT and adopts hierarchical reinforcement learning for goal planning and recommendation.
• SKarRec [15]: Leverages LLMs to construct textual descriptions of learning items and combines KT with graph neural networks for recommendation.
• KGNN-KT [33]: Utilize LLMs to construct a knowledge graph from unordered knowledge concepts, and then model student behavior using GNNs.

5.3.2. Evaluation Metric

We adopt $E_{\phi }$ (Equation (1)) to measure the effectiveness of learning paths [14,24,35] and compare all methods based on their performance using this metric. Traditional recommendation metrics (e.g., NDCG, Precision) aim to measure item “relevance” or “ranking quality.” However, in education, the ultimate goal is not merely the alignment between students and resources but the actual improvement in students’ knowledge state. A highly “relevant” exercise may fail to promote learning if it is too easy or too difficult. Optimizing for relevance alone risks recommending items that appear suitable but yield little educational benefit. In contrast, our evaluation metric, $E_{\phi }$, directly quantifies the gain in a student’s knowledge state after completing the recommended path—i.e., the learning gain. This ensures that our model optimization is aligned with the fundamental objective of education: meaningful and measurable knowledge advancement.

5.4. Exploring the Predictive Capabilities of LLM (RQ1)

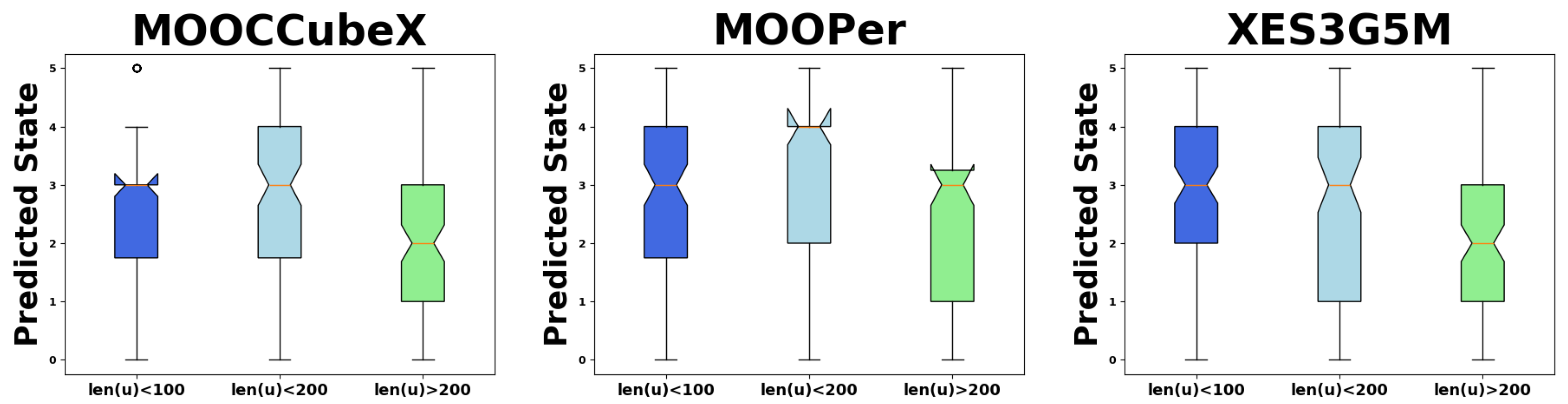
In this experiment, we use KT instead of LLM to directly predict the knowledge state of the students, primarily because LLMs exhibit a pronounced central tendency in their assessments of knowledge states. To validate this phenomenon, we randomly sample students with varying record lengths from three datasets, input their response histories into the LLM, and obtain predictions of their knowledge states. Specifically, we categorize students’ historical learning records into three groups based on length (fewer than 100 entries, fewer than 200 entries, and more than 200 entries), randomly select 100 students from each group, and visualize the LLM’s predictions using box plots (Figure 4).

For all three datasets, when the record length is fewer than 200, the median predicted state is relatively high and the data distribution is more dispersed. In contrast, when the record length exceeds 200, the median predicted state is comparatively lower and the distribution is more concentrated. With longer input sequences, the LLM can better capture the input information, leading to more stable predictions. In summary, the LLM tends to produce moderate predictions in scoring tasks, remaining in a comfort zone to avoid extreme judgments. In comparison, KT does not suffer from this limitation and can more accurately predict students’ knowledge states. Therefore, we opt for the KT to evaluate students’ learning capabilities.

5.5. Overall Performance Comparison (RQ2)

To thoroughly evaluate the capabilities of various models, we configure three settings for selecting candidate exercises: 1 $\rho =1$: randomly sample n exercises. 2 $\rho =2$: divide all exercises into $\left({\displaystyle \frac{N}{n+1}}\right)$ groups, each of size n, and randomly select one group as the candidate set. 3 $\rho =3$: use all available exercises. N denotes the total number of exercises. For the MOOCCubeX, MOOPer, and XES3G5M datasets, n is set to 100, 500, and 500, respectively. The three settings are referred to as $\rho =$ 1, 2, and 3 in the following experiments.

5.5.1. Promotion Comparison

As shown in

Table 3. Comparison of different methods in terms of promotion. Bold indicates the best result and underlining indicates the second best. * indicates significant improvement over baselines (p < 0.01).

		FISM	CluLSTM	DQN	GRU4Rec	LightGCN	GEHRL	SKarRec	KGNN-KT	LPReKL
	$\rho =1$	0.1009	0.1590	0.2067	0.1802	0.1643	0.2179	0.2011	0.2032	${0.2433}^{\ast }$
MOOCCubeX	$\rho =2$	0.1519	0.2188	0.1923	0.2105	0.2294	0.2577	0.2371	0.2291	0.2574
	$\rho =3$	0.2428	0.3422	0.3114	0.2956	0.2861	0.3446	0.3593	0.3015	${0.3885}^{\ast }$
	$\rho =1$	0.1417	0.2499	0.2044	0.2208	0.1629	0.2391	0.2371	0.2205	${0.2607}^{\ast }$
MOOPer	$\rho =2$	0.1858	0.2355	0.2168	0.1977	0.2126	0.3065	0.3109	0.2817	${0.3356}^{\ast }$
	$\rho =3$	0.2407	0.3696	0.3235	0.3316	0.3576	0.4973	0.4641	0.3762	0.4852
	$\rho =1$	0.0196	0.0774	0.1642	0.1355	0.1178	0.1469	0.2028	0.1847	0.1952
XES3G5M	$\rho =2$	0.0888	0.0417	0.1916	0.1755	0.1040	0.2021	0.2415	0.2163	${0.2587}^{\ast }$
	$\rho =3$	0.0165	0.2474	0.2168	0.2178	0.2062	0.2318	0.2671	0.2492	${0.3002}^{\ast }$

, LPReKL achieves superior performance in most experimental settings, being outperformed by other models only in a few cases. When the number of candidate exercises is limited ($\rho =1$ and $\rho =2$), the performance of all models declines significantly. This is mainly because the randomly selected exercises in these scenarios often fail to cover the specific knowledge deficiencies of students, resulting in limited improvement. In contrast, when $\rho =3$, i.e., when the entire exercise bank is available, all models demonstrate notable performance gains, with LPReKL achieving particularly remarkable improvement. This highlights the model’s ability to accurately identify and address students’ weaknesses when provided with sufficient and diverse learning resources. However, LPReKL performs slightly less effectively on the XES3G5M dataset compared to the other two datasets. A possible explanation is the large number of knowledge concepts in XES3G5M, which makes it difficult for a fixed set of five recommended exercises to meet students’ diverse learning needs. Additionally, the strong semantic understanding capabilities of the LLM embedded in LPReKL are better leveraged in datasets with rich textual information, such as MOOCCubeX and MOOPer. Notably, SKarRec—which also employs an LLM—demonstrates strong competitiveness on these two datasets, further confirming the potential of LLMs in the context of LPR. For other models, FISM and CluLSTM heavily rely on co-occurrence similarity between items, and their recommendation quality deteriorates significantly when candidate exercises are randomly generated. DQN, as a classic reinforcement learning algorithm, can dynamically adjust its strategy based on the environment state, thereby demonstrating relatively stable performance. GRU4Rec and LightGCN critically depend on sufficient historical interaction data to capture student behavior patterns; as such, their representational capacity is limited in cases of data sparsity or short interaction sequences. GEHRL achieves competitive performance by decoupling the recommendation process into two stages—goal planning and exercise recommendation—and by incorporating awareness of students’ evolving knowledge states. However, its architecture lacks a closed-loop mechanism that enables real-time optimization of the recommendation strategy based on student feedback. SkarRec and KGNN-KT attempt to leverage LLMs to uncover semantic relationships among learning items. Nevertheless, in real-world educational scenarios, knowledge systems are large-scale and dynamically evolving, making it impractical to exhaustively encode and input all conceptual relationships into the LLM. This limitation hinders their generalization ability and practical applicability.

Specifically, we performed paired t-tests to compare LPReKL against the two strongest baseline models, GEHRL and SkarRec. The performance improvement of LPReKL over the best baseline is statistically significant (p < 0.05) on MOOCCubeX ($\rho =1$, $\rho =3$), MOOPer ($\rho =1$, $\rho =2$), and XES3G5M ($\rho =2$, $\rho =3$). In the remaining cases, the performance differences did not reach conventional significance levels. Nevertheless, our method consistently demonstrates a favorable numerical advantage across all settings, indicating its robustness and effectiveness.

5.5.2. Difficulty Comparison

An appropriate level of exercise difficulty can significantly enhance students’ learning motivation, whereas exercises that are too simple or too difficult may hinder their long-term engagement. As shown in

Table 4. Comparison of different methods in terms of difficulty. Values closer to 0.3 indicate better performance. Bold indicates the best result and underlining indicates the second best.

		FISM	CluLSTM	DQN	GRU4Rec	LightGCN	GEHRL	SKarRec	LPReKL
	$\rho =1$	0.4909	0.3559	0.3795	0.3822	0.3648	0.2194	0.4011	0.3321
MOOCCubeX	$\rho =2$	0.2147	0.2311	0.4346	0.2394	0.2417	0.3734	0.3505	0.2849
	$\rho =3$	0.4416	0.3655	0.3420	0.2324	0.3614	0.3981	0.2573	0.2790
	$\rho =1$	0.4636	0.3448	0.3826	0.4227	0.4116	0.2264	0.2391	0.3784
MOOPer	$\rho =2$	0.4026	0.4058	0.2005	0.2152	0.2157	0.4463	0.3744	0.2374
	$\rho =3$	0.3617	0.3540	0.3675	0.3874	0.2391	0.3746	0.2256	0.2851
	$\rho =1$	0.4314	0.2258	0.2499	0.4375	0.2088	0.3914	0.4021	0.3480
XES3G5M	$\rho =2$	0.4121	0.3608	0.3750	0.2356	0.2165	0.2210	0.2572	0.3505
	$\rho =3$	0.2444	0.3734	0.2338	0.3571	0.3753	0.4107	0.3847	0.2871

, LPReKL consistently achieves favorable results under all three settings. This is primarily because our framework integrates both the LLM and KT components to explicitly account for difficulty when generating learning paths, ensuring that the recommended exercises align well with the predefined difficulty expectations. In contrast, other methods do not incorporate difficulty as a consideration during the recommendation process, resulting in learning paths of inconsistent quality, which may negatively impact students’ learning experience. These findings suggest that incorporating external factors—such as exercise difficulty—is crucial for delivering personalized learning services, as it helps efficiently target students’ weaknesses and accelerates progress toward their learning goals.

5.6. Ablation Study (RQ3)

We design the following variants to investigate the contribution of each component in LPReKL:

• LPReKL-F: Removes the feedback mechanism. Candidate exercises retrieved from the exercise bank are directly recommended without iterative adjustment.
• LPReKL-K: Reverts to the original DKT by omitting the masking mechanism when reconstructing historical interaction data.
• LPReKL-L: Excludes the LLM. Instead, exercises relevant to students’ weak knowledge concepts, as identified by KT, are retrieved from the exercise bank for recommendation.

As shown in

Table 5. Ablation study. Bold indicates the best result.

		LPReKL-F	LPReKL-K	LPReKL-L	LPReKL
	$\rho =1$	0.1899	0.2647	0.1037	0.2643
MOOCCubeX	$\rho =2$	0.2681	0.2501	0.1676	0.2507
	$\rho =3$	0.3589	0.3829	0.2036	0.3885
	$\rho =1$	0.1046	0.2591	0.1398	0.2607
MOOPer	$\rho =2$	0.0948	0.3359	0.1666	0.3356
	$\rho =3$	0.2127	0.4812	0.3198	0.4852
	$\rho =1$	0.0414	0.1894	0.0857	0.1952
XES3G5M	$\rho =2$	0.1745	0.2609	0.1659	0.2587
	$\rho =3$	0.2141	0.2973	0.2184	0.3002

, the performance of LPReKL-K is on par with LPReKL, indicating that traditional KT still performs excellently in predicting student knowledge states. However, it typically requires more structured training data and cannot be generalized to multi-step prediction tasks. LPReKL-F and LPReKL-L yield the weakest performance, highlighting the critical roles of both the feedback mechanism and the LLM. The LLM’s semantic understanding and reasoning capabilities allow it to infer students’ weaknesses from contextual information and generate personalized learning items accordingly. The feedback mechanism guides the LLM to iteratively adjust its instructional strategies. Unlike prior studies, which largely overlook student feedback and rely solely on historical data for one-way recommendations, our framework introduces a dynamic, student-aware loop. This enables the model to better align with students’ evolving needs and individual learning profiles.

5.7. Parameter Analysis (RQ4)

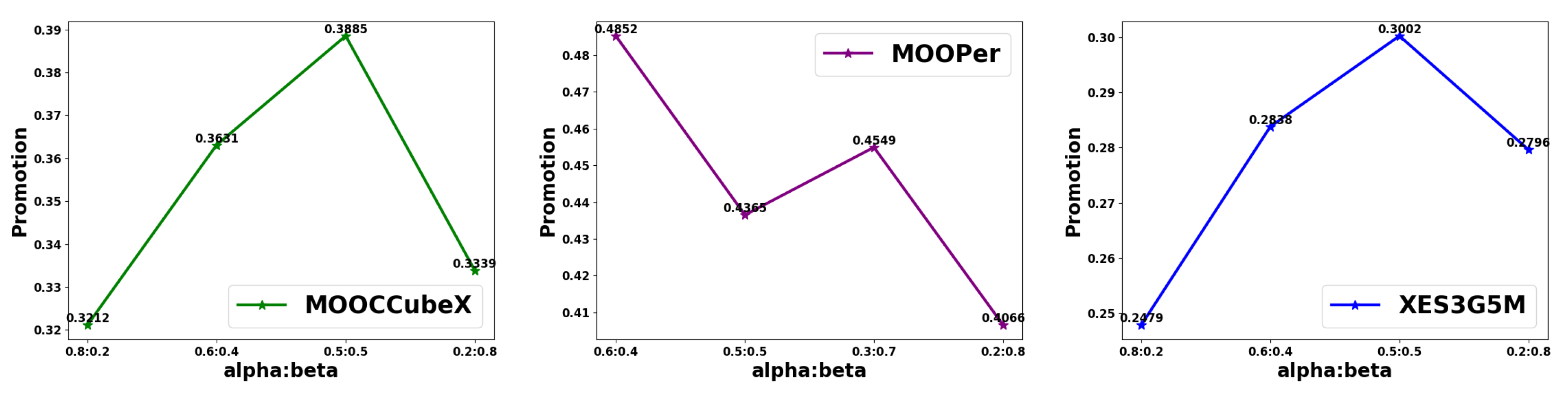
5.7.1. Weight Coefficients of Knowledge Tracing+

The KT in our framework involves two key hyperparameters, $\alpha$ and $\beta$ (as defined in Equation (9)). We vary these parameters to examine their influence on model performance. The results are presented in Figure 5. When $\alpha$ and $\beta$ are set to 0.5:0.5, the model achieves the best performance on the MOOCCubeX and XES3G5M datasets. However, increasing either $\alpha$ or $\beta$ disproportionately leads to a significant drop in performance. The MOOPer dataset presents a more complex pattern. The model performs best when $\alpha$ and $\beta$ are set to 0.6:0.4, while further adjustments cause noticeable fluctuations in performance. We attribute this to the larger number of knowledge components in MOOPer, which requires a more balanced consideration of prediction accuracy and item difficulty—an aspect that aligns more closely with real-world educational settings. These observations highlight the importance of dataset-specific parameter tuning, as appropriate values of $\alpha$ and $\beta$ are crucial for optimizing model performance.

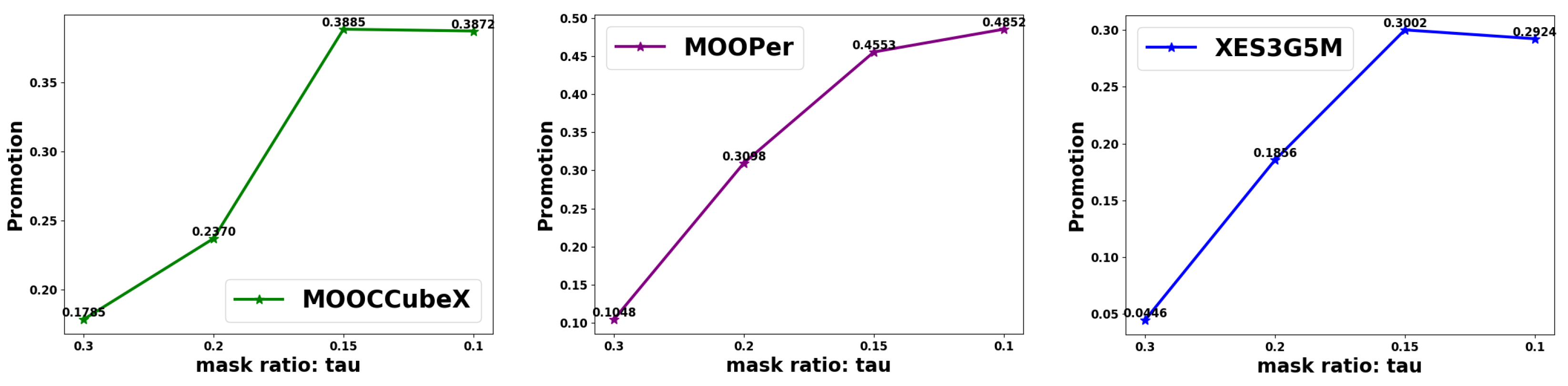
5.7.2. Mask Ratio of Knowledge Tracing+

In real-world educational scenarios, the problem of a large exercise bank arises. To enable the KT to predict students’ knowledge states for the next multi-step, we reconstruct students’ historical records during training by randomly masking their responses with a certain probability. Figure 6 shows the impact of different masking rates on model performance. The results indicate that excessively high masking rates significantly degrade model performance. This is because with too many missing student records, the model struggles to accurately assess students’ knowledge states, hindering the generation of personalized learning paths. For the MOOPer dataset, which contains the most knowledge concepts, reducing the masking rate allows for more comprehensive training, leading to more precise decisions. For the other two datasets, optimal performance is achieved at a masking rate of 0.15, with further reductions yielding minimal improvements. We attribute this to the moderate number of knowledge concepts in these datasets, where a masking rate of 0.15 is sufficient for the model to make reasonably accurate predictions based on the available data.

6. Discussion

Traditional rule-based methods lack flexibility, while early sequential recommendation models struggle to capture the dynamics of knowledge acquisition. Although KT models and LLMs have individually shown promise in addressing these challenges, the former are often limited to single-step prediction, while the latter suffer from hallucination and a conservative bias in evaluation. The proposed LPReKL framework is designed to synergize the strengths of both KT and LLM to overcome these limitations. Experimental results demonstrate that LPReKL performs well across multiple datasets and settings, primarily due to two key design principles. First, the iterative feedback loop between KT and LLM enables dynamic adaptation. Unlike conventional “one-shot” recommendation approaches, our system continuously refines the learning path: the KT model evaluates the expected effectiveness of candidate paths and feeds this information back to the LLM, which then adjusts its generation strategy accordingly. This closed-loop interaction allows for personalized and context-aware path refinement. Second, the paradigm of “LLM-generated reference items + semantic retrieval from a question bank” effectively balances creativity with reliability. The LLM interprets complex pedagogical intentions and concretizes them into reference exercises, while the retrieval mechanism ensures that the final recommended items are drawn from a curated, high-quality item bank. This division of labor not only mitigates the hallucination issues commonly associated with LLMs but also enhances the system’s scalability—new, high-quality exercises can be seamlessly integrated into the bank and become immediately available for recommendation. Nevertheless, a limitation of this work lies in using the same KT model both as a component within the framework and as the primary evaluator. While this practice is common in the field and the KT model itself is robust and well validated on large-scale data, it may introduce potential evaluation bias. To further strengthen the validity of our findings, we acknowledge the importance of future online A/B testing in real educational platforms. Such studies would allow us to assess the long-term impact of LPReKL in authentic teaching and learning environments, beyond simulated offline evaluations.

7. Conclusions

In this paper, we proposed LPReKL, a novel learning path recommendation framework that synergizes Knowledge Tracing (KT) with a Large Language Model (LLM) to address the limitations of traditional educational approaches. By dynamically tracking students’ knowledge states through an enhanced KT model and leveraging the generative capabilities of LLMs, our system provides highly personalized and adaptive learning recommendations. The integration of a feedback mechanism ensures continuous optimization of the recommended content, aligning it with students’ evolving needs and balancing exercise difficulty to enhance engagement. Experimental results on multiple public datasets demonstrated that LPReKL outperforms existing baselines in terms of recommendation effectiveness and adaptability, particularly in scenarios with abundant learning resources. Ablation studies further validated the critical roles of the feedback mechanism, LLM-generated content, and the masked training strategy for KT in improving performance. Future work will explore incorporating additional personalized factors (e.g., learning styles, engagement metrics) and refining the model architecture to better handle complex real-world educational environments. This research contributes to the advancement of AI-driven educational technologies, offering a scalable solution to deliver tailored learning experiences and improve educational outcomes. Additionally, the LLM adjusts its strategy by processing feedback through natural language prompts, rather than via gradient updates. While this design offers advantages in computational efficiency and safety, and has proven effective in practice, the adjustment granularity is indeed relatively coarse. Future work may explore finer-grained optimization techniques, such as reinforcement learning from human or synthetic feedback, to refine the LLM’s decision-making process and potentially achieve further performance gains.