An Adaptive Observer-Based Voltage Parameter Estimation Method for Single-Phase Grid with DC Offset
Abstract
1. Introduction
- A novel adaptive observer is proposed that achieves a rapid dynamic response.
- The method enables accurate voltage parameter estimation in the presence of DC offsets, thereby eliminating steady-state errors commonly encountered in conventional techniques.
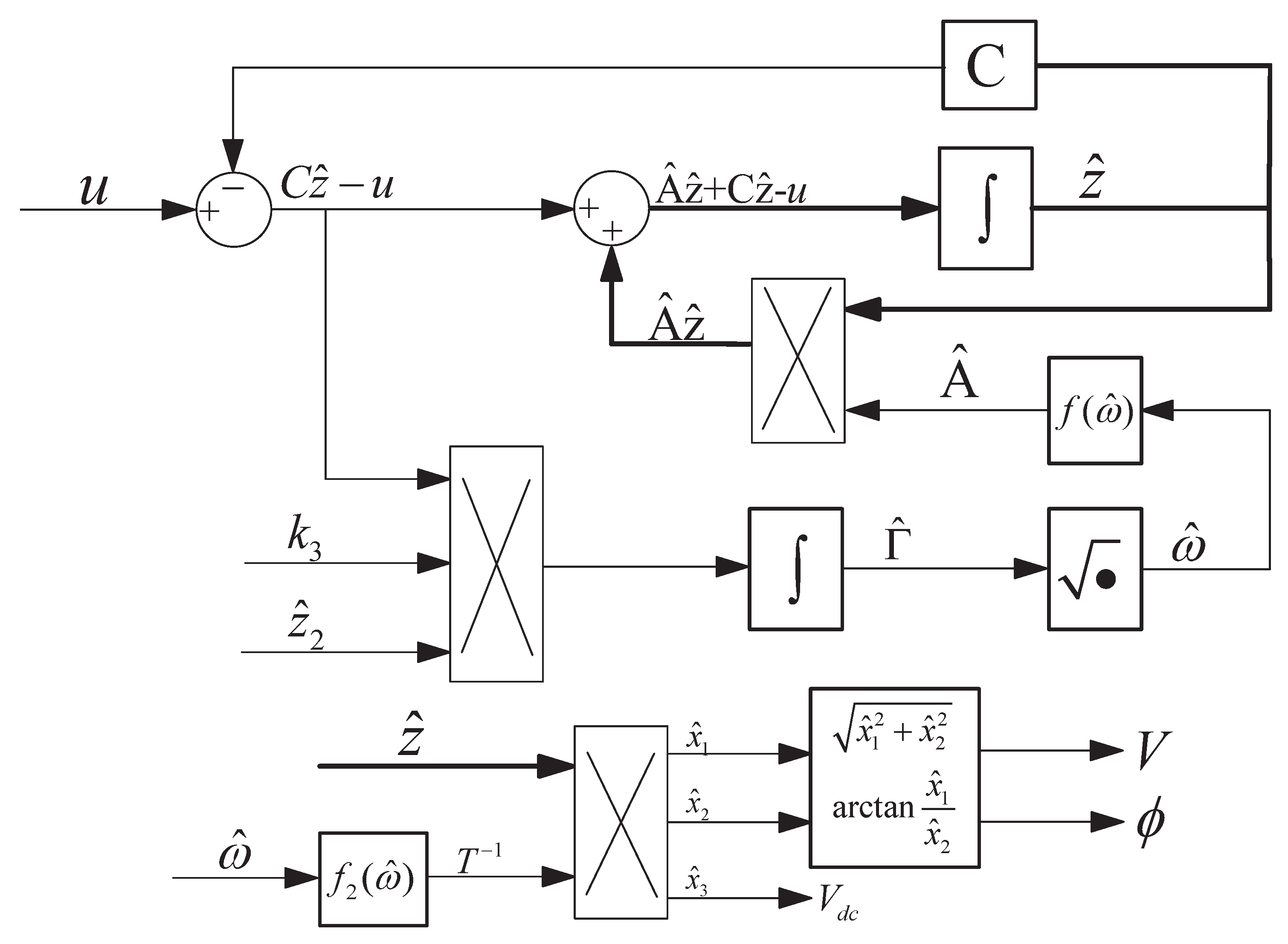
2. Proposed Adaptive Observer
2.1. Proposed Adaptive Observer Design
2.2. Stability Analysis
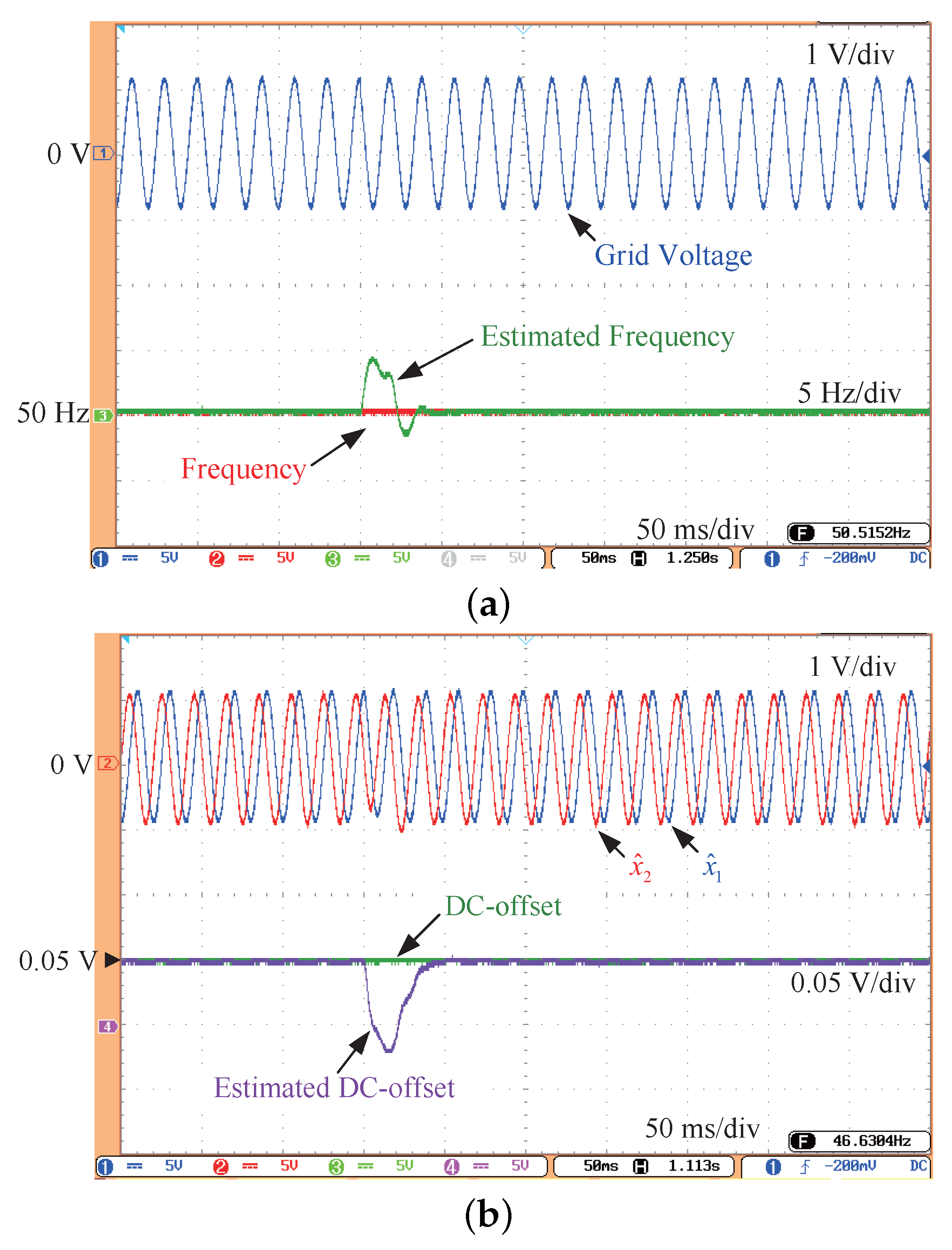
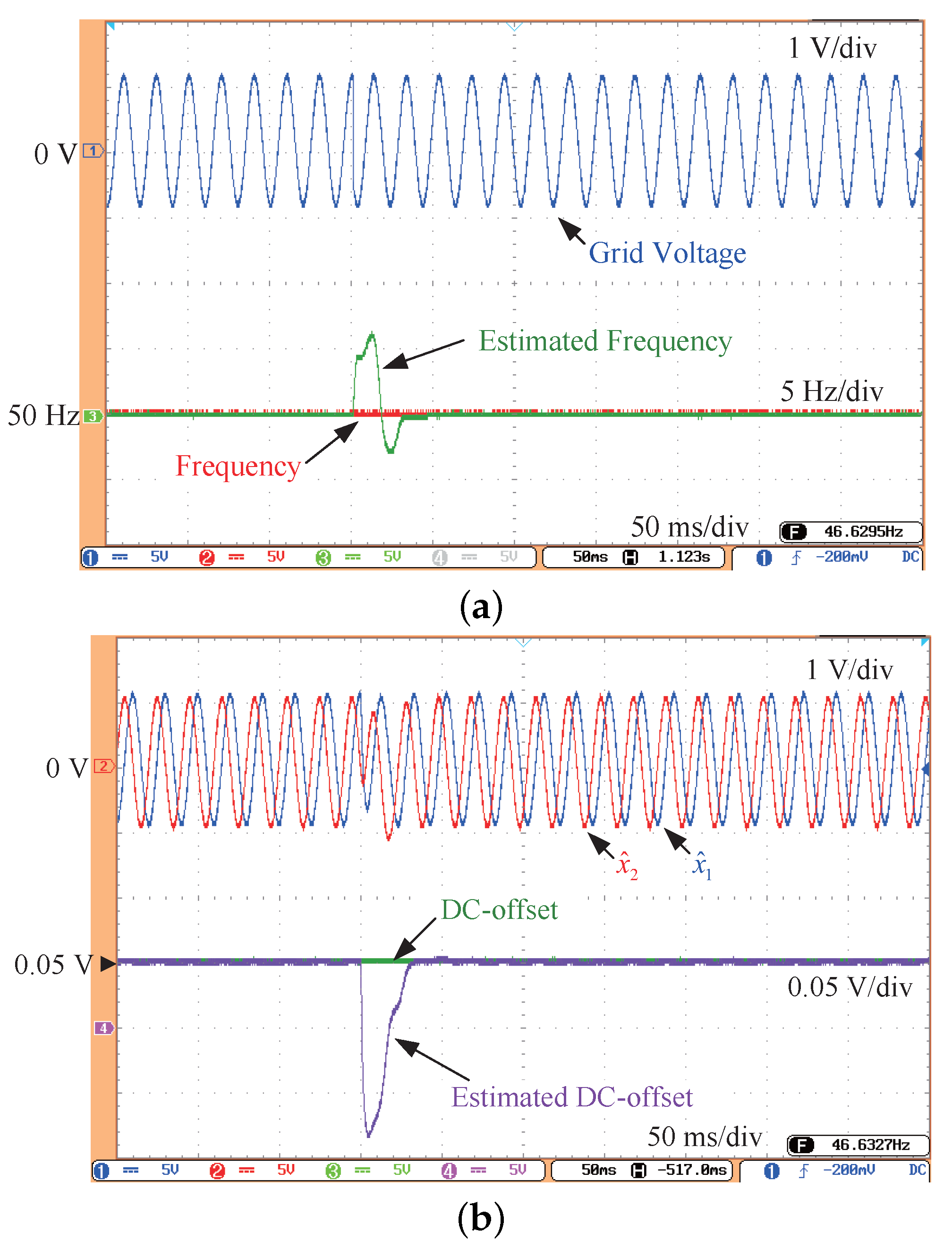
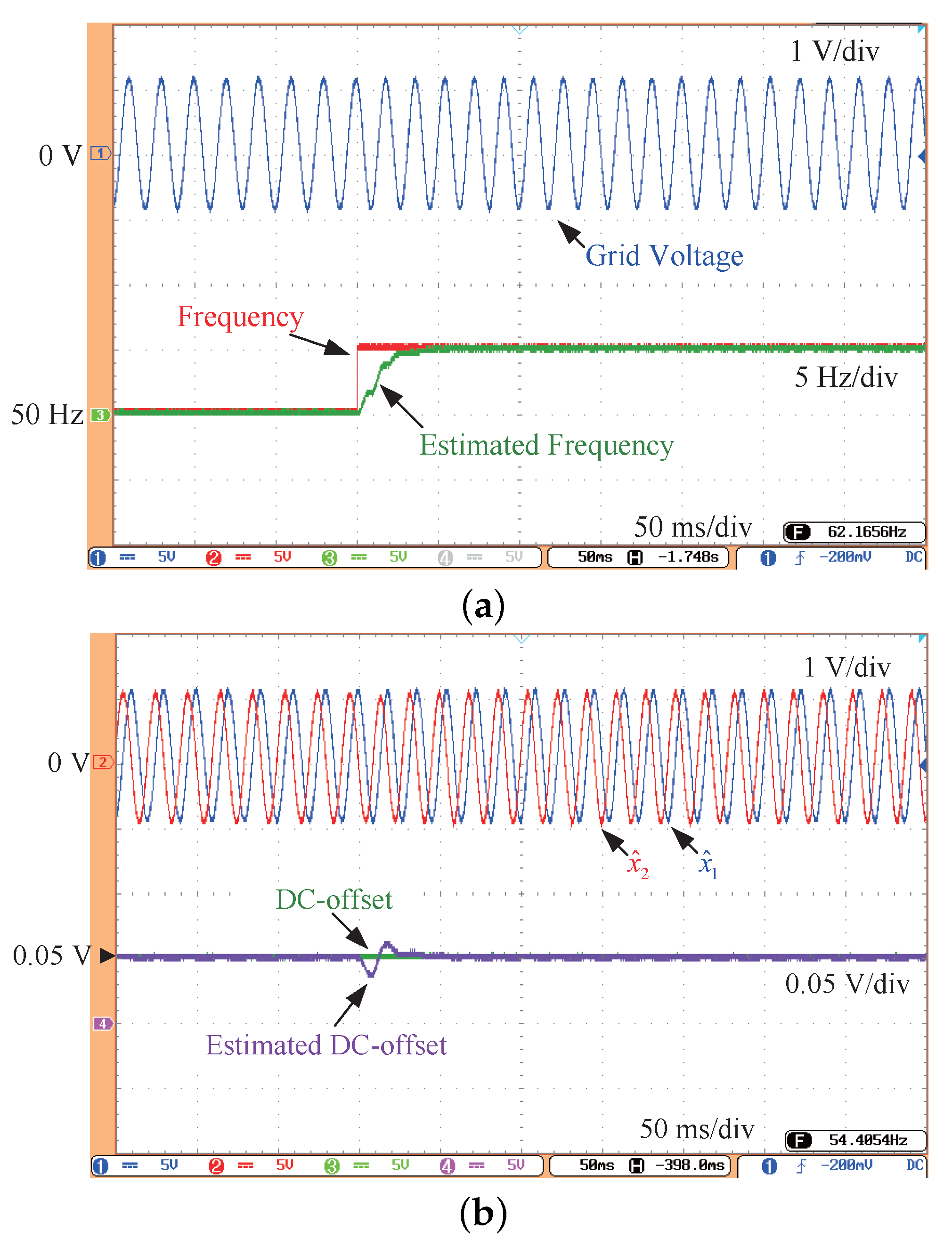
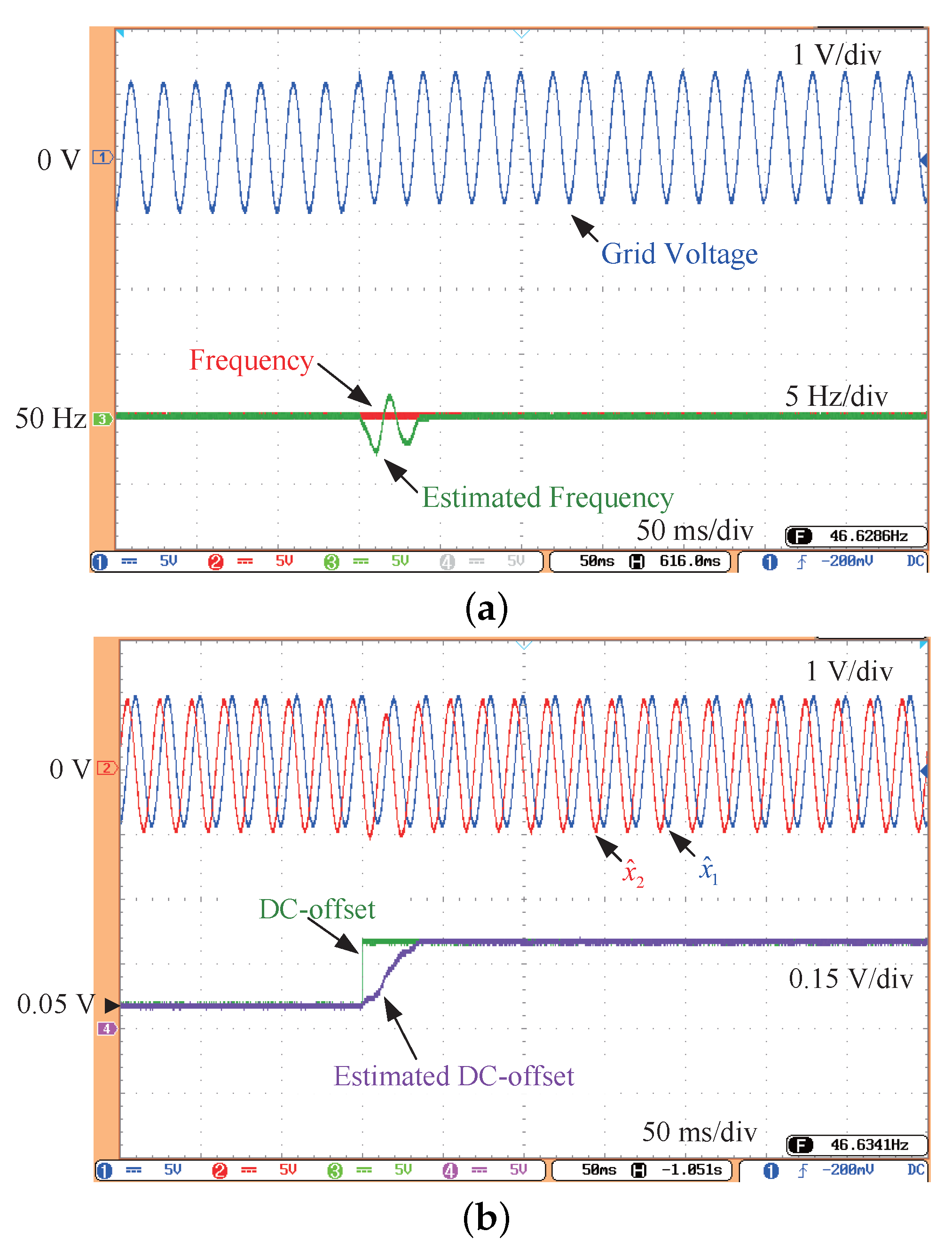
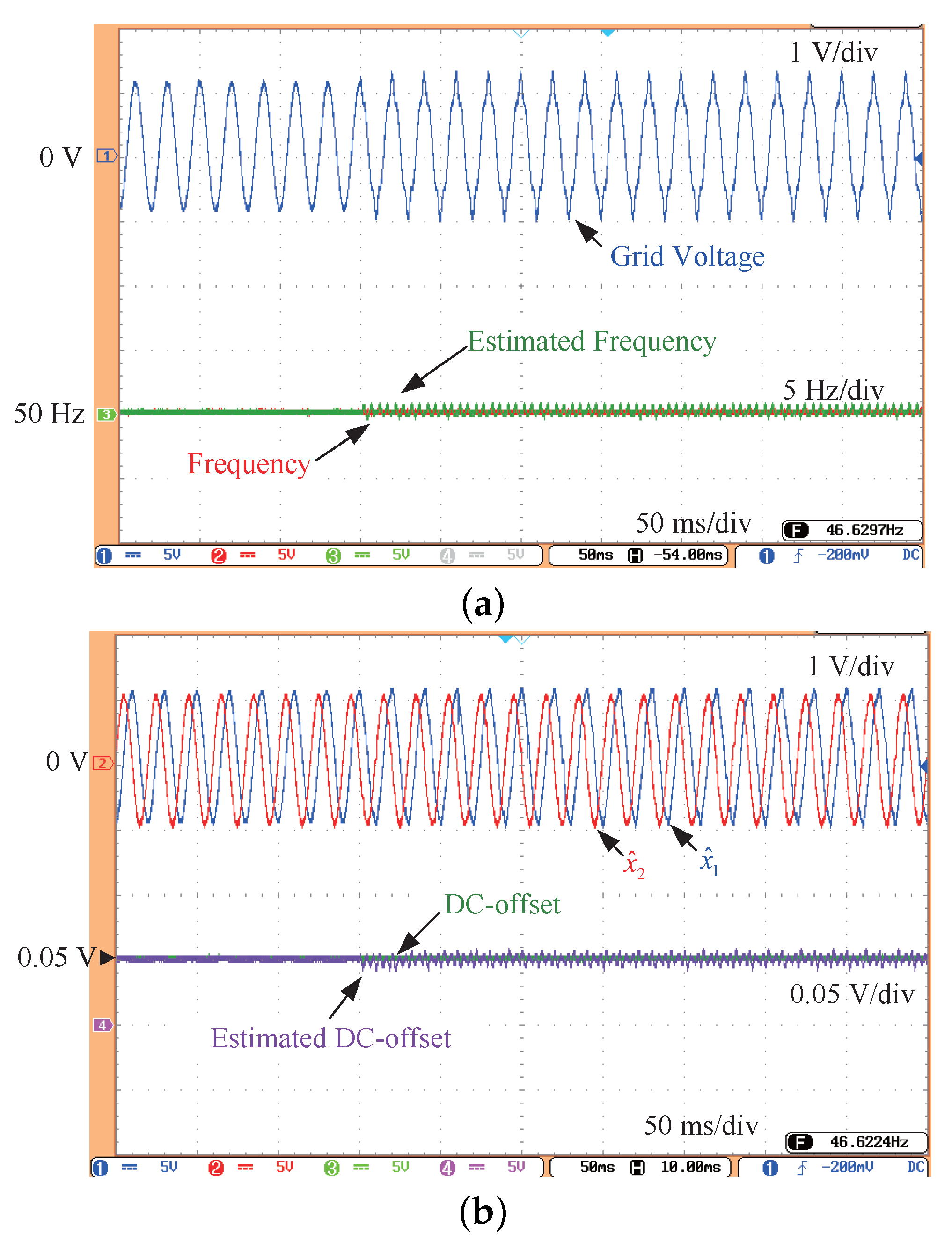
3. Experimental Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DC | Direct current |
| AC | Alternating current |
| GCDG | Grid-connected distributed generation |
| FFT | Fast Fourier Transform |
| DFT | Discrete Fourier Transform |
| OSG | Orthogonal Signal Generator |
| PLL | phase locked loop |
| SOGI | second-order generalized integrator |
| CCF-PLL | complex-coefficient filter PLL |
| DOEC-PLL | DC offset error compensation PLL |
| VTD-PLL | variable time-delay PLL |
References
- Pahlevani, M.; Eren, S.; Guerrero, J.M.; Jain, P. A Hybrid Estimator for Active/Reactive Power Control of Single-Phase Distributed Generation Systems with Energy Storage. IEEE Trans. Power Electron. 2016, 31, 2919–2936. [Google Scholar] [CrossRef]
- Strasser, T.; Andren, F.; Kathan, J.; Cecati, C.; Buccella, C.; Siano, P.; Leitão, P.; Zhabelova, G.; Vyatkin, V.; Mařík, V.; et al. A Review of Architectures and Concepts for Intelligence in Future Electric Energy Systems. IEEE Trans. Ind. Electron. 2015, 62, 2424–2438. [Google Scholar] [CrossRef]
- Jia, K.; Yang, Z.; Fang, Y.; Bi, T.; Sumner, M. Influence of Inverter-Interfaced Renewable Energy Generators on Directional Relay and an Improved Scheme. IEEE Trans. Power Electron. 2019, 34, 11843–11855. [Google Scholar] [CrossRef]
- Prakash, S.; Singh, J.K.; Behera, R.K.; Mondal, A. A Type-3 Modified SOGI-PLL with Grid Disturbance Rejection Capability for Single-Phase Grid-Tied Converters. IEEE Trans. Ind. Appl. 2021, 57, 4242–4252. [Google Scholar] [CrossRef]
- Trinh, Q.N.; Wang, P.; Tang, Y.; Koh, L.H.; Choo, F.H. Compensation of DC Offset and Scaling Errors in Voltage and Current Measurements of Three-Phase AC/DC Converters. IEEE Trans. Power Electron. 2018, 33, 5401–5414. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, C. An Improved Accuracy Harmonic Extraction Method for Microcontrollers. IEEE Trans. Ind. Electron. 2025, 72, 5344–5352. [Google Scholar] [CrossRef]
- Liu, H.; Hu, H.; Chen, H.; Zhang, L.; Xing, Y. Fast and Flexible Selective Harmonic Extraction Methods Based on the Generalized Discrete Fourier Transform. IEEE Trans. Power Electron. 2018, 33, 3484–3496. [Google Scholar] [CrossRef]
- Borkowski, J.; Kania, D.; Mroczka, J. Interpolated-DFT-Based Fast and Accurate Frequency Estimation for the Control of Power. IEEE Trans. Ind. Electron. 2014, 61, 7026–7034. [Google Scholar] [CrossRef]
- Kuwałek, P.; Bracale, A.; Sikorski, T.; Rezmer, J. Synchronized Approach Based on Empirical Fourier Decomposition for Accurate Assessment of Harmonics and Specific Supraharmonics. IEEE Trans. Ind. Electron. 2025, 72, 992–1002. [Google Scholar] [CrossRef]
- Derviškadić, A.; Romano, P.; Paolone, M. Iterative-Interpolated DFT for Synchrophasor Estimation: A Single Algorithm for P- and M-Class Compliant PMUs. IEEE Trans. Instrum. Meas. 2018, 67, 547–558. [Google Scholar] [CrossRef]
- Song, J.; Mingotti, A.; Zhang, J.; Peretto, L.; Wen, H. Fast Iterative-Interpolated DFT Phasor Estimator Considering Out-of-Band Interference. IEEE Trans. Instrum. Meas. 2022, 71, 9005814. [Google Scholar] [CrossRef]
- Li, M.; Nian, H.; Li, H.; Hu, B.; Liao, Y.; Li, H.; Liu, Y.; Wang, Y. HW-DFT-Based Measurement Method of Frequency-Coupling Characteristics Considering Fundamental Frequency Deviation for Stability Analysis. IEEE Trans. Power Electron. 2023, 38, 6613–6626. [Google Scholar] [CrossRef]
- Lin, H.C. Power Harmonics and Interharmonics Measurement Using Recursive Group-Harmonic Power Minimizing Algorithm. IEEE Trans. Ind. Electron. 2012, 59, 1184–1193. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, M.; Lu, Y.; Hu, X.; Xu, X.; Wu, C.; Ma, R.; Yang, Y. An Adaptive Enhanced Complex-Coefficient Filter-Based PLL in Variable Frequency Grid. IEEE Trans. Power Electron. 2024, 39, 3950–3955. [Google Scholar] [CrossRef]
- Dai, Z.; Li, G.; Fan, M.; Huang, J.; Yang, Y.; Hang, W. Global Stability Analysis for Synchronous Reference Frame Phase-Locked Loops. IEEE Trans. Ind. Electron. 2022, 69, 10182–10191. [Google Scholar] [CrossRef]
- Han, Y.; Luo, M.; Zhao, X.; Guerrero, J.M.; Xu, L. Comparative Performance Evaluation of Orthogonal-Signal-Generators-Based Single-Phase PLL Algorithms—A Survey. IEEE Trans. Power Electron. 2016, 31, 3932–3944. [Google Scholar] [CrossRef]
- Xiao, F.; Dong, L.; Li, L.; Liao, X. A Frequency-Fixed SOGI-Based PLL for Single-Phase Grid-Connected Converters. IEEE Trans. Power Electron. 2017, 32, 1713–1719. [Google Scholar] [CrossRef]
- Golestan, S.; Monfared, M.; Freijedo, F.D. Design-Oriented Study of Advanced Synchronous Reference Frame Phase-Locked Loops. IEEE Trans. Power Electron. 2013, 28, 765–778. [Google Scholar] [CrossRef]
- Hwang, S.-H.; Liu, L.; Li, H.; Kim, J.-M. DC Offset Error Compensation for Synchronous Reference Frame PLL in Single-Phase Grid-Connected Converters. IEEE Trans. Power Electron. 2012, 27, 3467–3471. [Google Scholar] [CrossRef]
- Ozdemir, A.; Yazici, I. Fast and robust software-based digital phase locked loop for power electronics applications. IET Gener. Transmiss. Distrib. 2013, 7, 1435–1441. [Google Scholar] [CrossRef]
| Attribute | Fourier-Based | PLL-Based |
|---|---|---|
| Advantage | High detection accuracy; direct amplitude and phase measurement. | Fast real-time phase and frequency tracking; low computational load. |
| Disadvantage | Sensitive to frequency drift and spectral leakage; poor transient response. | Dependence on output-side filters/OSG; degrades with DC offset and strong harmonics. |
| Applicable scene | Steady-state analysis; harmonic computation. | Real-time synchronization and grid-following control in moderately distorted grids. |
| Cases | Experiment Conditions |
|---|---|
| Case A | 0.05 p.u. DC-offset and Phase jump |
| Case B | 0.05 p.u. DC-offset and Phase jump |
| Case C | 0.05 p.u. DC-offset and 5 Hz Frequency jump |
| Case D | DC-offset jump from 0.05 p.u. to 0.2 p.u. |
| Case E | 0.05 p.u. DC-offset and 0.1 p.u. 5th−, 0.05 p.u. 7th− |
| order harmonic injection |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, J.; Zhang, J.; Tan, S.; Dai, Z.; Wang, X. An Adaptive Observer-Based Voltage Parameter Estimation Method for Single-Phase Grid with DC Offset. Electronics 2025, 14, 4383. https://doi.org/10.3390/electronics14224383
Xiao J, Zhang J, Tan S, Dai Z, Wang X. An Adaptive Observer-Based Voltage Parameter Estimation Method for Single-Phase Grid with DC Offset. Electronics. 2025; 14(22):4383. https://doi.org/10.3390/electronics14224383
Chicago/Turabian StyleXiao, Ji, Jiaming Zhang, Shishun Tan, Zhiyong Dai, and Xuetong Wang. 2025. "An Adaptive Observer-Based Voltage Parameter Estimation Method for Single-Phase Grid with DC Offset" Electronics 14, no. 22: 4383. https://doi.org/10.3390/electronics14224383
APA StyleXiao, J., Zhang, J., Tan, S., Dai, Z., & Wang, X. (2025). An Adaptive Observer-Based Voltage Parameter Estimation Method for Single-Phase Grid with DC Offset. Electronics, 14(22), 4383. https://doi.org/10.3390/electronics14224383






