An Intelligent Suppression Method for Interference Pulses in Partial Discharge Detection of Transformers Based on Waveform Feature Recognition
Abstract
1. Introduction
2. Adaptive Suppression Algorithm for Periodic Pulsation Interference
2.1. Construction of the Pulse Array
2.1.1. Instantaneous Zero-Crossing Density of the Time-Series
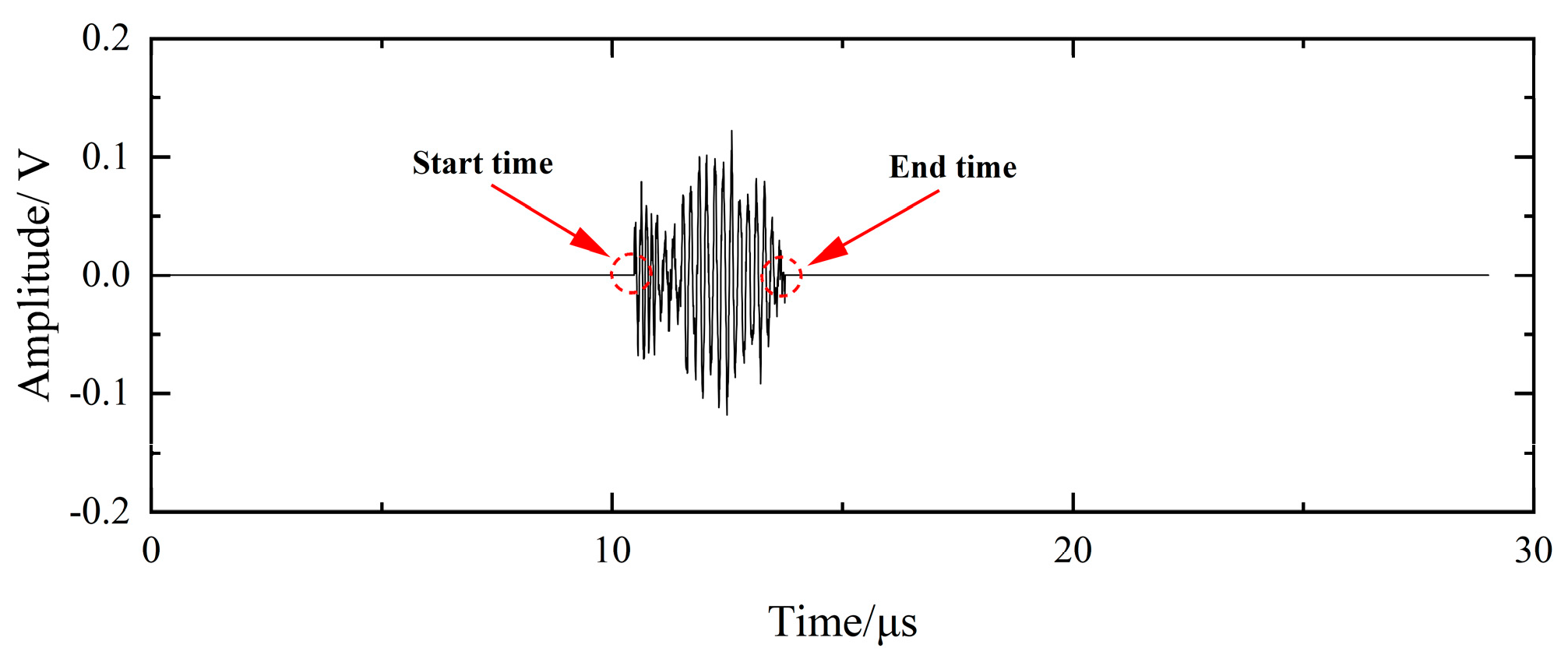
2.1.2. Extraction of Pulse Waveforms
2.2. Identification of PD Pulses
2.2.1. Extraction of Waveform Features
- (1)
- Waveform Polarity Deviation Ratio (WPDR).
- (2)
- Peak Time Ratio (PTR)
- (3)
- Peak Interval Ratio (PIR)
2.2.2. Waveform Feature Identification
- (1)
- Traverse Features. For each feature fi (i = 1, 2, …, 5), traverse all possible split points t.
- (2)
- Calculate Gini Index. For each split point t, divide the dataset into a left subset (fi ≤ t) and a right subset (fi > t), and calculate the weighted Gini index [17]:
- (3)
- Select Optimal Threshold. Choose the split point t* that minimizes the Gini index as the global discrimination threshold for feature fi:
3. Suppression of On-Site Noise Interference in PD Signals
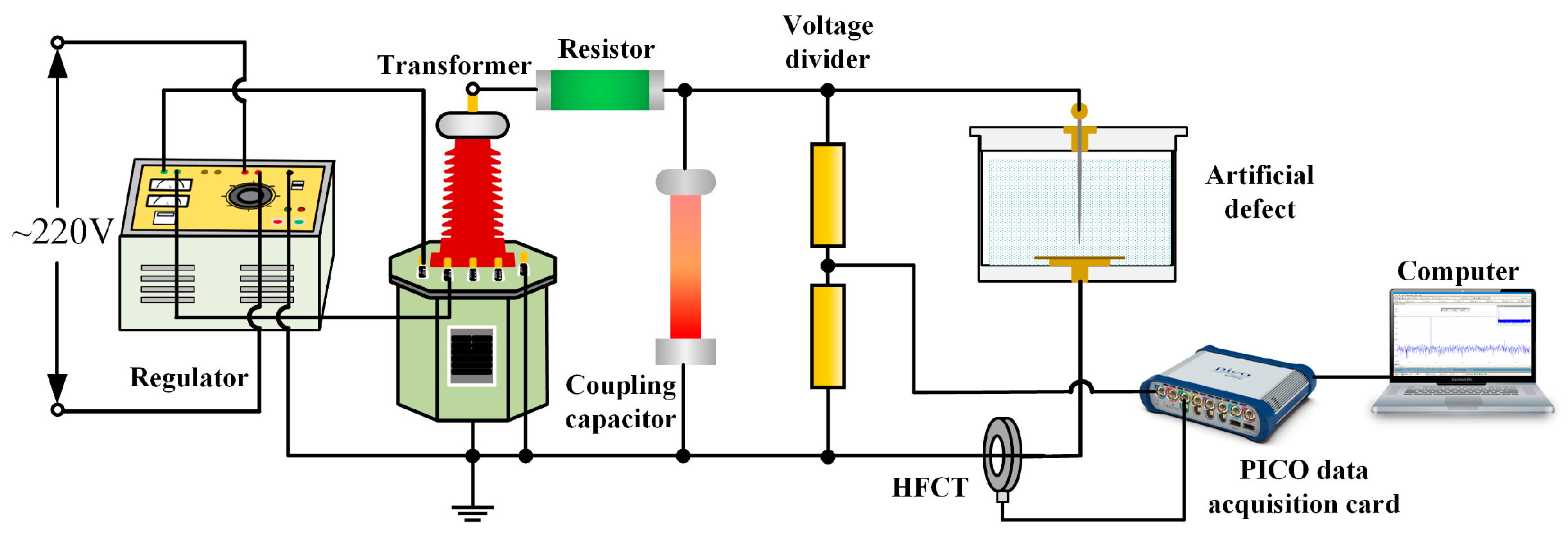
3.1. Acquisition of PD Signals
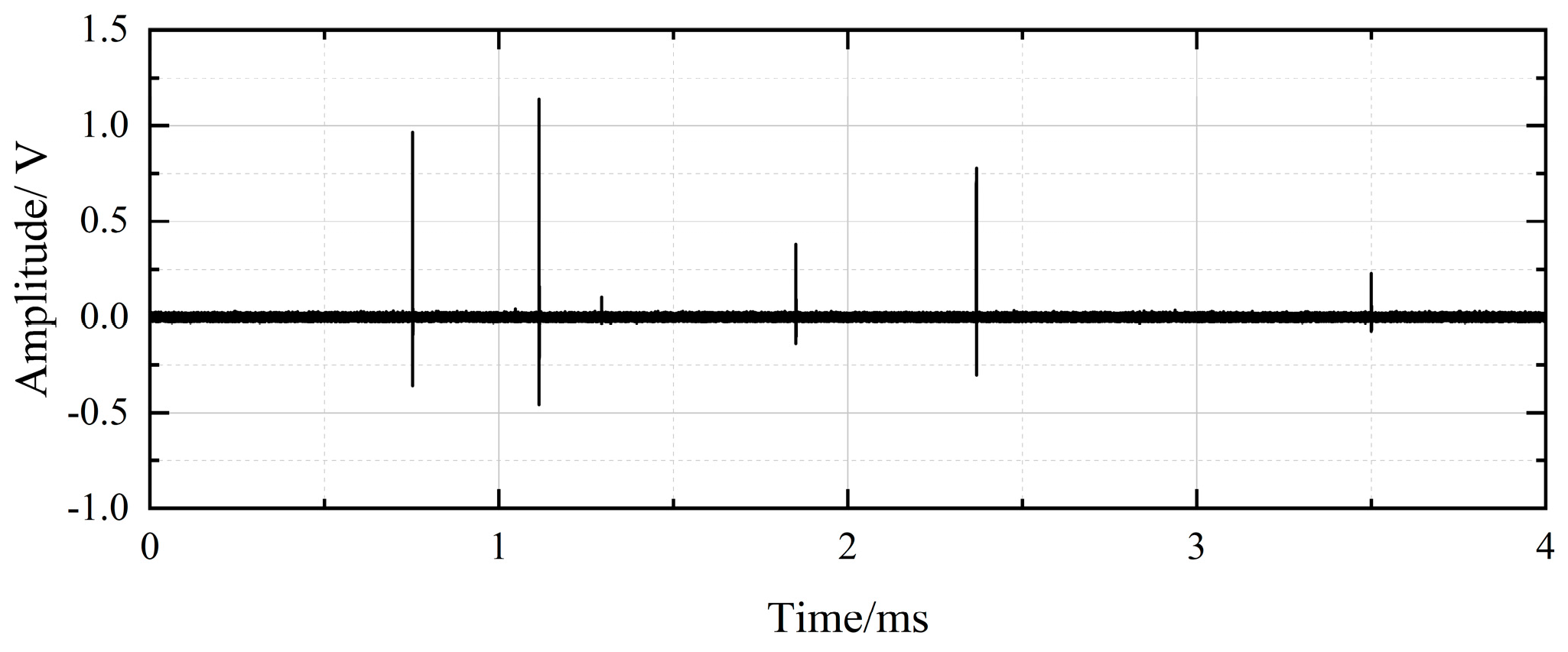
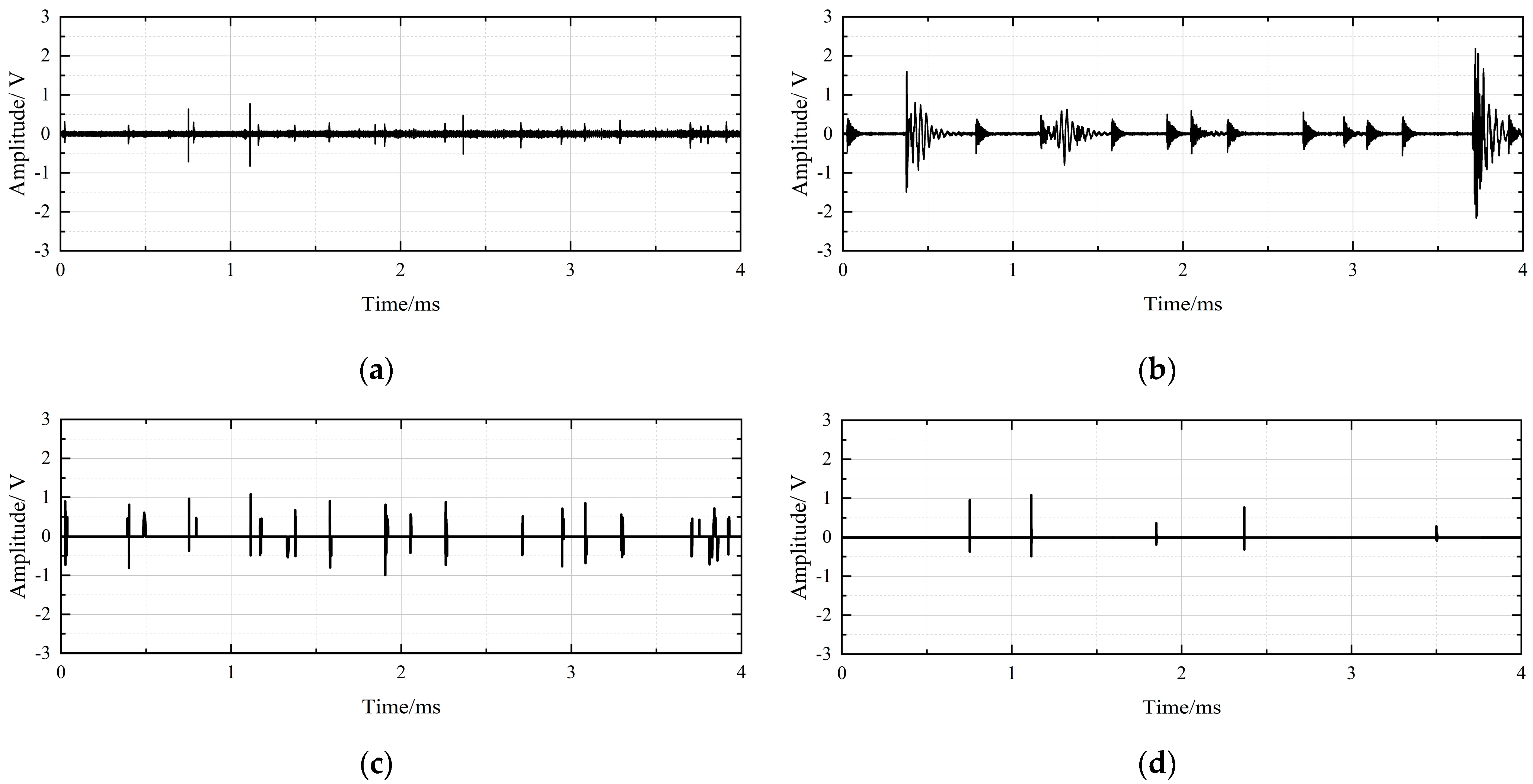
3.2. The Denoising Results of On-Site Noise Interference
4. Denoising of Field-Measured Signals
5. Conclusions
- (1)
- The instantaneous zero-crossing density of white noise is greater than that of pulse waveforms. However, the presence of periodic narrowband interference can significantly reduce the instantaneous zero-crossing density of the noise signal. By using a 10 MHz high-pass filter, the impact of periodic narrowband interference on the instantaneous zero-crossing density of non-pulse noise signals can be effectively eliminated.
- (2)
- The Waveform Polarity Deviation Ratio, Peak Time Ratio, and Peak Interval Ratio effectively distinguish PD signals from interference pulses while capturing the common characteristics of different PD signals. Adaptive calculation of discrimination thresholds for individual features using univariate analysis enables rapid and accurate identification of PD pulses.
- (3)
- The proposed algorithm effectively suppresses noise interference while significantly reducing the attenuation of PD signals. It adaptively calculates threshold parameters and intelligently identifies PD signals, making it suitable for the rapid suppression of complex noise interference in on-site PD detection at substations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mahmud, S.; Chen, G.; Golosnoy, I.O.; Chen, G.; Wilson, G.; Jarman, P. Bridging phenomenon in contaminated transformer oil. In Proceedings of the 2012 IEEE International Conference on Condition Monitoring and Diagnosis, Bali, Indonesia, 23–27 September 2012; pp. 180–183. [Google Scholar]
- Li, Q.; Li, S.; Si, W. Analysis of the key problem about insulation condition assessment of oil-paper in power transformers based on partial discharge. High Volt. Eng. 2017, 43, 2558–2565. Available online: http://dianda.cqvip.com/Qikan/Article/Detail?id=672917476&from=Qikan_Search_Index (accessed on 1 November 2025).
- Duan, L.; Hu, J.; Zhao, G.; Chen, K.; He, J.; Wang, S.X. Identification of partial discharge defects based on deep learning method. IEEE Trans. Power Deliv. 2019, 34, 1557–1568. [Google Scholar] [CrossRef]
- Liao, R.; Yang, L.; Li, J.; Grzybowski, S. Aging condition assessment of transformer oil-paper insulation model based on partial discharge analysis. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 303–311. [Google Scholar] [CrossRef]
- Hussein, R.; BashirShaban, K.; El-Hag, A.H. Denoising of acoustic partial discharge signals corrupted with random noise. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 1453–1459. [Google Scholar] [CrossRef]
- Hussain, M.R.; Refaat, S.S.; Abu-Rub, H. Overview and partial discharge analysis of power transformers: A literature review. IEEE Access 2021, 9, 64587–64605. [Google Scholar] [CrossRef]
- Zhong, J.; Bi, X.; Shu, Q.; Zhang, D.; Li, X. An improved wavelet spectrum segmentation algorithm based on spectral kurtogram for denoising partial discharge signals. IEEE Trans. Instrum. Meas. 2021, 70, 3514408. [Google Scholar] [CrossRef]
- Luo, X.; Niu, H.; Hu, R.; Liu, F.; Wu, J. A modified method of suppressing narrow-band interference using fast fourier transform power spectrum. Proc. CSEE 2013, 33, 167–175. Available online: http://dianda.cqvip.com/Qikan/Article/Detail?id=45614426&from=Qikan_Article_Detail (accessed on 1 November 2025).
- Zhong, J.; Bi, X.; Shu, Q.; Chen, M.; Zhou, D.; Zhang, D. Partial discharge signal denoising based on singular value decomposition and empirical wavelet transform. IEEE Trans. Instrum. Meas. 2020, 69, 8866–8873. [Google Scholar] [CrossRef]
- Chan, J.; Ma, H.; Saha, T.; Ekanayake, C. Self-adaptive partial discharge signal de-noising based on ensemble empirical mode decomposition and automatic morphological thresholding. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 294–303. [Google Scholar] [CrossRef]
- Ashtiani, M.; Shahrtash, S. Partial discharge de-noising employing adaptive singular value decomposition. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 775–782. [Google Scholar] [CrossRef]
- Fan, G.; Liu, S.; Liu, W.; Wang, L. Suppression of the periodic narrow-band noise in discharge signal by FFT spectrum minimum entropy deconvolution filtering. High Volt. Eng. 2017, 43, 1378–1385. Available online: http://dianda.cqvip.com/Qikan/Article/Detail?id=671862401&from=Qikan_Search_Index (accessed on 1 November 2025).
- Lei, Z.; Wang, F.; Li, C. A denoising method of partial discharge signal based on improved SVD-VMD. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 2107–2116. [Google Scholar] [CrossRef]
- Hua, X.; Mu, H.; Jin, L.; Ji, Y.; Zhan, J.; Shao, X.; Zhang, G. A novel adaptive parameter optimization method for denoising partial discharge ultrasonic signals. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 2734–2743. [Google Scholar] [CrossRef]
- Maresch, K.; Freitas-Gutierres, L.; Oliveira, A.; Borin, A.; Cardoso, G.; Damiani, J.; Morais, A.; Correa, C.; Martins, E. Advanced diagnostic approach for high-voltage insulators: Analyzing partial discharges through zero-crossing rate and fundamental frequency estimation of Acoustic Raw Data. Energies 2023, 16, 6033. [Google Scholar] [CrossRef]
- Sahoo, N.; Salama, M.; Bartnikas, R. Trends in partial discharge pattern classification: A survey. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 248–264. [Google Scholar] [CrossRef]
- Yao, R.; Li, J.; Hui, M.; Bai, L.; Wu, Q. Feature selection based on random forest for partial discharges characteristic set. IEEE Access 2020, 8, 159151–159161. [Google Scholar] [CrossRef]
- Imburgia, A.; Di Fatta, A.; Romano, P.; Rizzo, G.; Li Vigni, V.; Ala, G. A study on partial discharges pattern recognition under DC voltage through clustering algorithms and cross-correlation filter. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 2543–2550. [Google Scholar] [CrossRef]
- Ardilla-Rey, J.; Rivera-Caballero, O.; Boya-Lara, C. Sample Entropy as a Performance Indicator of UHF Real Signal Denoising from Partial Discharges. IEEE Trans. Dielectr. Electr. Insul. 2025, 32, 1333–1342. [Google Scholar] [CrossRef]




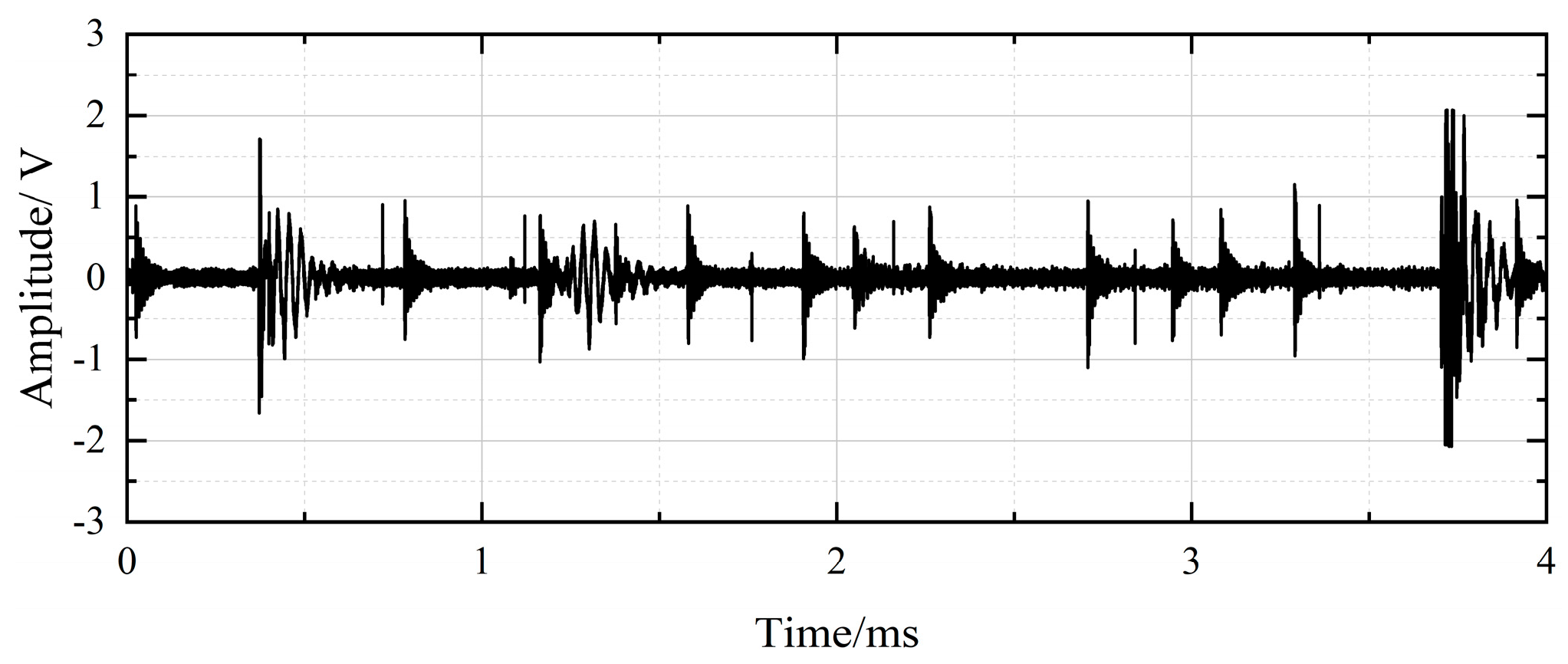
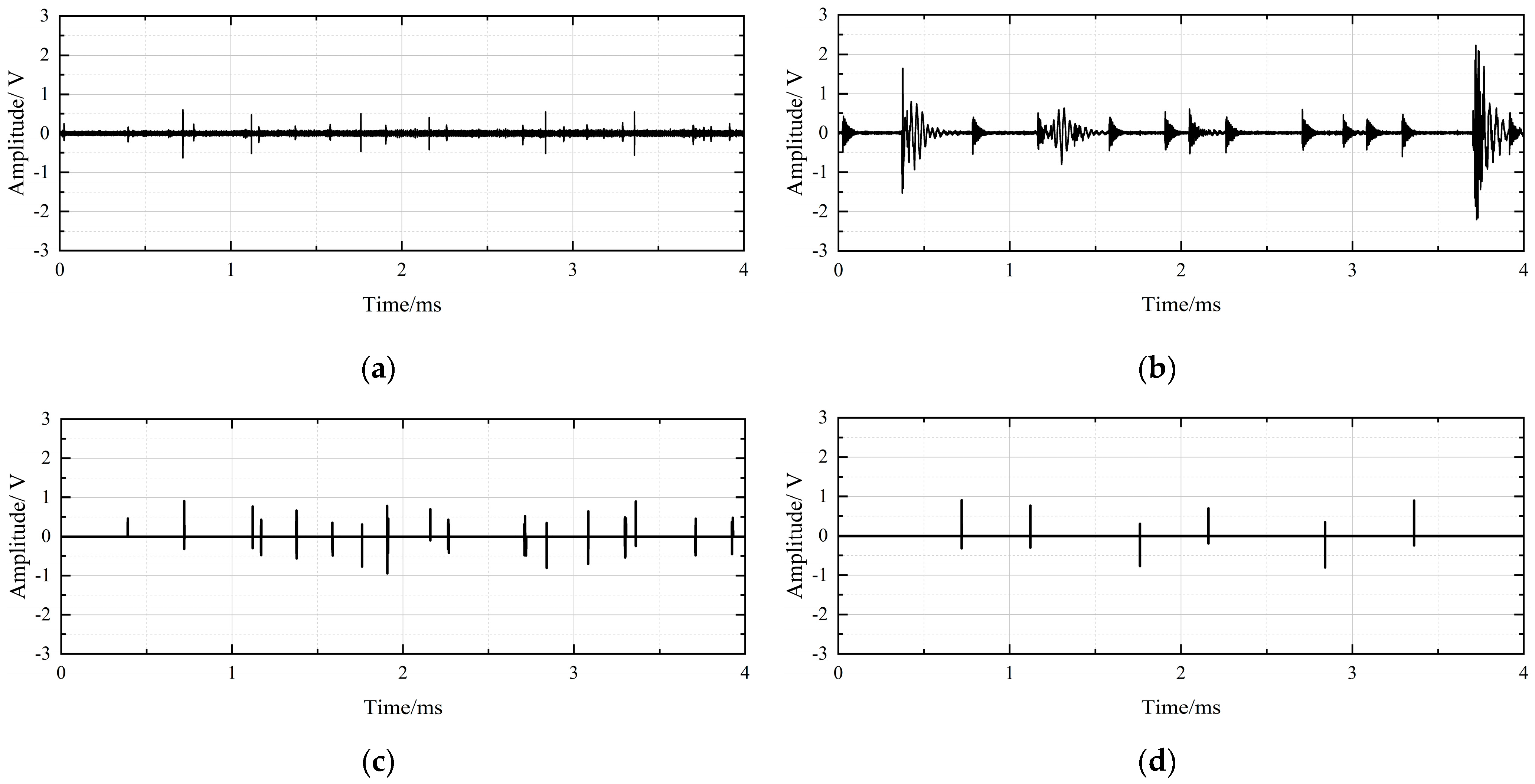
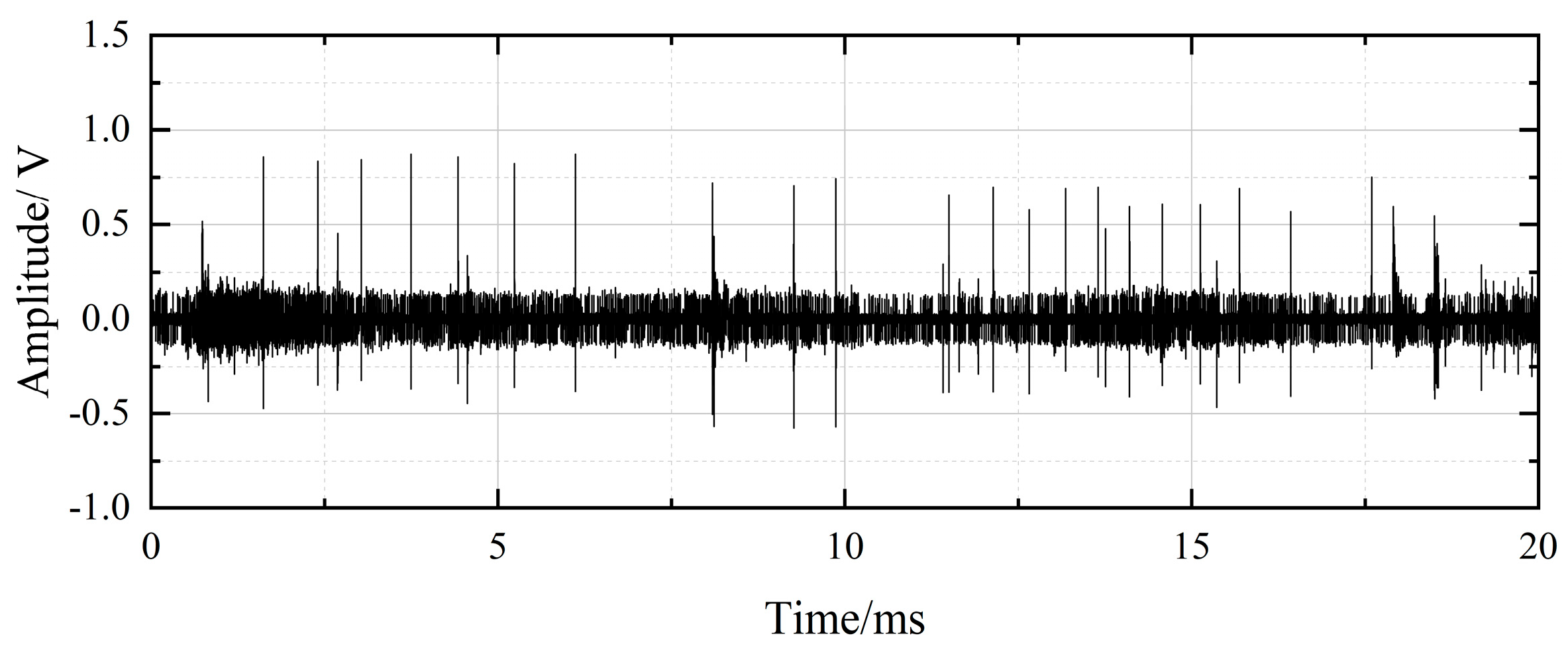

| Waveform Feature | PD Signals | Interference Pulses |
|---|---|---|
| WPDR | 0.60 | 0.30 |
| PTR | 0.19 | 0.42 |
| PIR1 | 0.08 | 0.18 |
| PIR2 | 0.10 | 0.17 |
| PIR3 | 0.06 | 0.15 |
| Method | RMSE | NCC | SNR/dB | NRR |
|---|---|---|---|---|
| 10 MHz high-pass filter | 0.0240 | 0.2432 | −8.011 | 18.45 |
| VMD-LB-PSO-WTD | 0.1905 | 0.0002 | −26.01 | 0.6138 |
| T-F map | 0.0616 | 0.0359 | −16.21 | 10.46 |
| The proposed algorithm | 0.0079 | 0.8769 | 1.644 | 30.21 |
| Method | SE |
|---|---|
| 10 MHz high-pass filter | 5.4065 |
| VMD-LB-PSO-WTD | 0.4511 |
| T-F map | 0.0031 |
| The proposed algorithm | 0.0001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Xu, Z.; Lai, Z.; Wang, Z.; Wang, H.; Wu, X.; Yao, R.; Xie, W.; Mu, H. An Intelligent Suppression Method for Interference Pulses in Partial Discharge Detection of Transformers Based on Waveform Feature Recognition. Electronics 2025, 14, 4380. https://doi.org/10.3390/electronics14224380
Chen S, Xu Z, Lai Z, Wang Z, Wang H, Wu X, Yao R, Xie W, Mu H. An Intelligent Suppression Method for Interference Pulses in Partial Discharge Detection of Transformers Based on Waveform Feature Recognition. Electronics. 2025; 14(22):4380. https://doi.org/10.3390/electronics14224380
Chicago/Turabian StyleChen, Shaoyu, Ziyue Xu, Zekai Lai, Zhulu Wang, Hongli Wang, Xinjian Wu, Ran Yao, Weidong Xie, and Haibao Mu. 2025. "An Intelligent Suppression Method for Interference Pulses in Partial Discharge Detection of Transformers Based on Waveform Feature Recognition" Electronics 14, no. 22: 4380. https://doi.org/10.3390/electronics14224380
APA StyleChen, S., Xu, Z., Lai, Z., Wang, Z., Wang, H., Wu, X., Yao, R., Xie, W., & Mu, H. (2025). An Intelligent Suppression Method for Interference Pulses in Partial Discharge Detection of Transformers Based on Waveform Feature Recognition. Electronics, 14(22), 4380. https://doi.org/10.3390/electronics14224380







