A 5.3 to 6.2-GHz Fractional-N Frequency Synthesizer with Variable Gain Automatic Frequency Calibration Using Cycle Slips in 65 nm CMOS

Abstract

The paper presents an automatic frequency calibration (AFC) technique for a charge pump-based phase-locked loop (CPPLL) with 5–6 μsec correction time. The architecture detects frequency offset in real time while keeping the loop active and performs a variable gain calibration that increases the correction gain at large frequency offsets to accelerate lock acquisition and gradually reduce the gain near locking frequency to suppress residual oscillation and overshoot. The implemented synthesizer rapidly re-acquires the lock within several adjacent coarse-tuning codes after frequency drift and maintains continuous operation without interruption. It demonstrates that the designed AFC achieves seamless frequency recovery in dynamically varying environments. Fabricated in a 65 nm CMOS process, the prototype fractional-N synthesizer occupies an active area of 0.603 mm² and operates over a 5.3–6.2 GHz tuning range. At 5.8 GHz, the design achieves a phase noise of −107 dBc/Hz at 1 MHz offset and consumes 21.5 mW from a 1.2 V supply.

1. Introduction

As the performance of data communication systems continues to improve, the demand for low phase noise and fast clock generation has become increasingly important. A frequency synthesizer is widely used to generate precise clock frequency by synchronizing an on-chip voltage-controlled oscillator (VCO) to a stable reference. To maintain low phase noise and spur levels, recent synthesizers are designed with reduced VCO gain (K_VCO), which improves noise performance but narrows down the frequency tuning range. To compensate for the limited range, designers typically increase the number of coarse-tuning bits (code) by employing a coarse capacitor bank [1]. As a result, the VCO’s total tuning range can be extended while maintaining low K_VCO. However, as the number of coarse-tuning codes increases, often reaching about 2⁵–2⁷ discrete coarse-tuning codes [2,3,4], the calibration time required to locate the correct code also increases, making a fast and efficient automatic frequency calibration (AFC) indispensable. The AFC schemes digitally search the coarse-tuning code that contains the target frequency (f_target) before phase locking.

Along with the industry trend toward multi-band transceiver implementation with wide tuning range [5], VCO frequency (f_VCO) drift, due to operating environment changes such as voltage and temperature (VT) variation, has become an issue [6]. In the event of frequency drift where the initially selected coarse code no longer covers the target frequency, the loop should quickly find a new valid code within several adjacent coarse-tuning codes by using calibration algorithms. The designed cycle slip-based closed-loop AFC detects frequency offset in real time while keeping the loop active. In addition, it employs a variable gain calibration algorithm that increases the correction gain for large frequency offset conditions to increase convergence speed and decrease the gain near locking frequency for stable settling of the coarse code, achieving a convergence speed comparable to previous AFC techniques and enabling smooth, continuous lock operation even under frequency drift conditions. Operating in the 5.3–6.2 GHz frequency band, the synthesizer is well suited for Wi-Fi 6/6E and 5 GHz ISM-band wireless transceivers, which often require fast and reliable frequency switching during channel hopping. It is also suitable for high-performance clock-generation circuits used in SoC, industrial, and automotive environments, where temperature drift and mechanical vibration can influence frequency stability.

The paper is organized as follows. Section 2 presents the designed AFC algorithm that corrects the synthesizer coarse code efficiently and discusses the motivation behind the implemented calibration scheme. Section 3 explains its operation principle, and Section 4 shows the implemented circuits of the synthesizer with the AFC. Section 5 includes the measurement results, and conclusions are drawn in Section 6.

2. Motive of Designed AFC System

2.1. Conventional Open-Loop and Closed-Loop AFC Technique

Figure 1a shows a V_ctrl monitoring-based AFC scheme in which the analog V_ctrl voltage is continuously compared with threshold V_ctrl,high and V_ctrl,low, and it decides whether to increase or decrease the coarse code of VCO [7,8]. The schemes presented in [7,8] usually set the coarse transition step as one code and the calibration time grows exponentially for the increased number of coarse bits. However, for several adjacent coarse-tuning codes of frequency drift, the coarse code transfers to a new valid frequency band smoothly with a short period of calibration time.

Figure 1b presents an open-loop binary-searching AFC circuit that utilizes a counter-based frequency-to-digital converter (FDC) for monitoring frequency offset [2,3,4]. During the coarse band searching, the output of the loop filter (LF) is disconnected, and V_ctrl is connected to a VDD/2 voltage source. A binary-searching algorithm completes the calibration in n-sequential rounds for n-bit coarse codes. Although the counter should wait for the VCO to oscillate properly in every temporary coarse round, the number of rounds of binary searching is guaranteed to finish fast in n-sequential rounds for all target code ranges. But the n-round searching has to happen even for several adjacent coarse code corrections that normally arise from a frequency drift by other operation environment changes such as temperature variation.

2.2. Designed Cycle Slip-Based Closed-Loop AFC

To overcome the limitations of conventional calibration techniques, we present a new closed-loop AFC that can operate efficiently for several adjacent coarse code frequency drifts while concurrently reducing calibration time with variable gain calibration modes. Figure 2 shows the overall architecture of the frequency synthesizer with the designed AFC. The AFC continuously detects cycle slips caused by the frequency deviation on the phase–frequency detector (PFD) input clocks, CLK_REF and CLK_DIV. The frequency error is fed to the integrator to adjust the 5-bit coarse code of the VCO, and its calibration speed is dynamically controlled by a variable gain calibration algorithm, considering both frequency drift and calibration time after monitoring VCO frequency by the counter continuously. The conventional open-loop AFC systems should perform n-round binary searches even when only several neighboring coarse code drifts occur, and the frequency over-/undershoot to recover the correct code, as illustrated in Figure 3a, which can cause interference between adjacent channels and deterioration of system stability. In contrast, the designed scheme can quickly and smoothly recover the lock by searching within several adjacent coarse-tuning codes when the synthesizer loses the lock. The approach achieves both the moderate convergence speed of open-loop calibration methods and the stable lock retention characteristic of closed-loop operation concurrently.

Table 1. Summary of the key characteristics of various AFC techniques.

	Open-Loop AFC	Closed-Loop AFC	Designed AFC
Loop state	Open	Closed	Closed
Searching algorithm	Binary	Linear	Variable gain
Detection scheme	Counter	Vctrl monitoring	Cycle slip detector and counter
Calibration speed	Fast	Slow	Moderate
Behavior under frequency drift	Not smooth	Smooth	Smooth

summarizes the key characteristics and operating features of each AFC technique. The detailed operation principle of the designed AFC algorithm will be presented in the next section.

3. Operation Principle of Designed AFC Algorithm

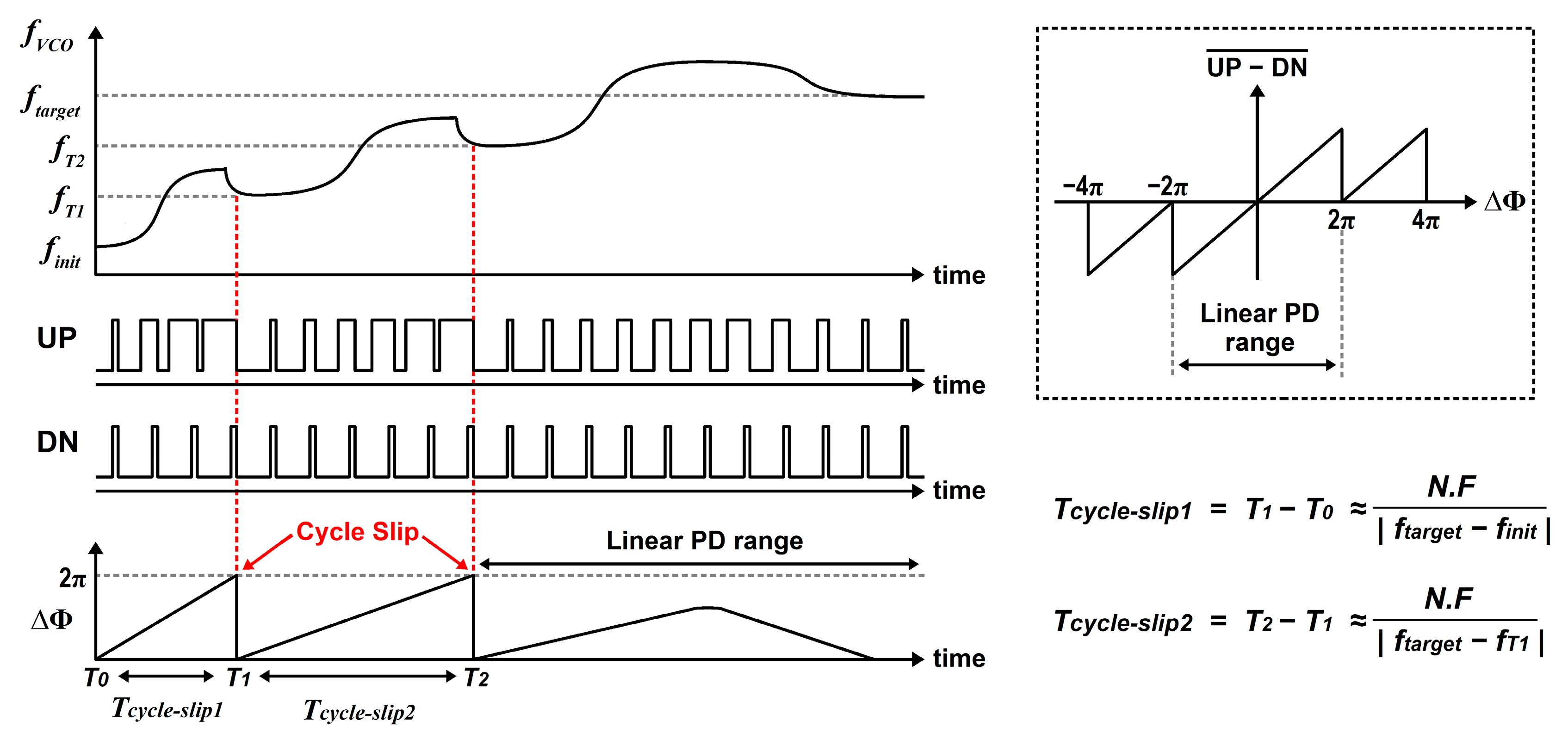
Figure 4 illustrates the UP/DN waveforms of PFD for the cases that the initial VCO frequency (f_init) is far from the f_target during PLL lock. If the frequencies of the two PFD input clocks are far apart, either UP or DN pulse’s duty accumulates rapidly and another round of accumulation cycle restarts because the detection range of PFD is limited to 2π in a phase domain. The accumulation period can be expressed roughly as N.F/| f_target − f_Tn | where N.F is a division ratio and f_Tn is the VCO frequency at the start of a new accumulation cycle. The period gradually becomes longer as the f_Tn approaches f_target, and finally the PLL enters into the linear PD range in which the PFD operates as a phase detector only and its operation range does not surpass beyond the 2π limit. Based on the occurrence of such cycle slips, the frequency information can be extracted within the closed loop. The AFC detects every “cycle slip” logically before the loop falls into the linear PD range and uses it as indicators of frequency error existence and the polarity of two input clock’s frequency offset.

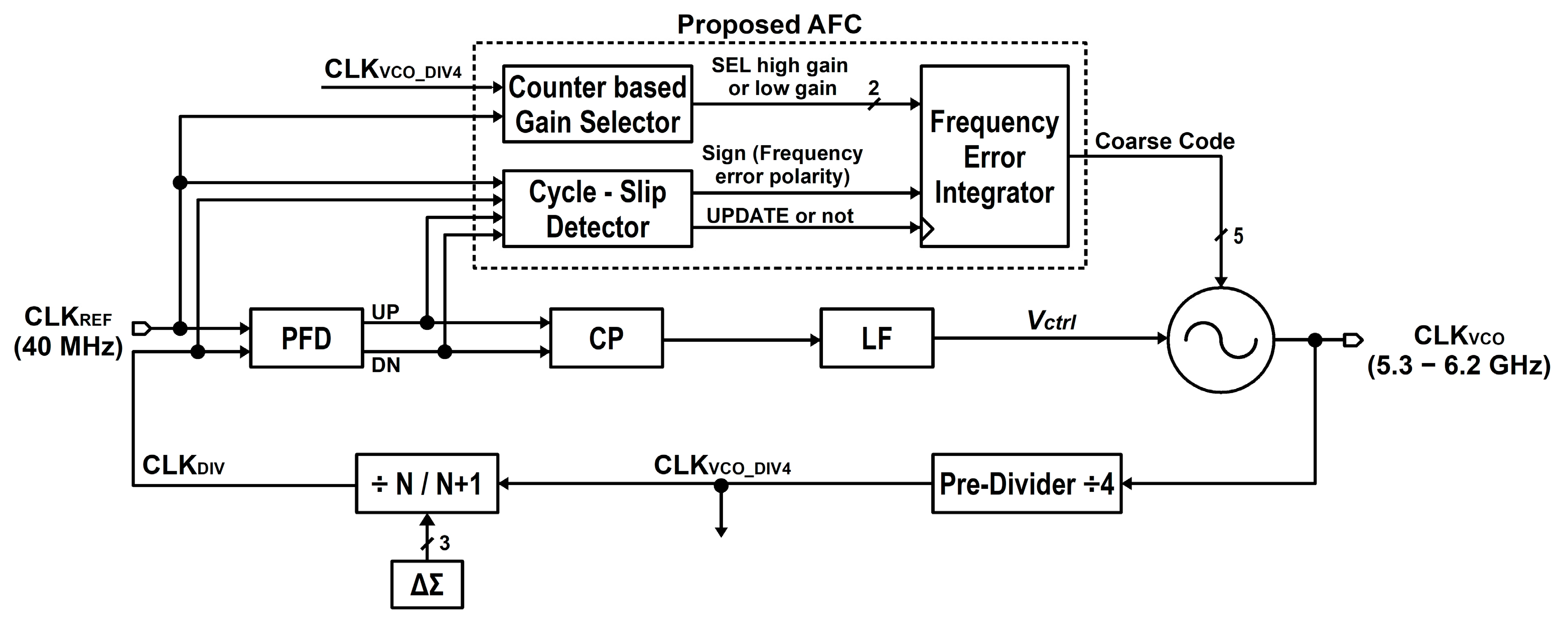
Figure 5a shows the designed cycle slip detector that monitors if there is a frequency error between CLK_REF and CLK_DIV. The UPDATE pulse is generated at the cycle slip timing by NANDing UP_A ⊕ UP_B and DN_A ⊕ DN_B, and it is used to trigger the entire AFC state machine. If the frequency locks, the UPDATE pulse is no longer produced with the AFC turned off, and power can be saved afterward. However, the “frequency error detection logic” keeps monitoring the frequency offset with low power and is ready to restart the AFC to correct the coarse code of VCO whenever the frequency drift occurs. Figure 5b presents the timing diagram of each node in the detection logic for a case of f_REF > f_DIV. The sign is produced by sampling the DN signal by the UP signal. The sign becomes 0 if CLK_REF leads CLK_DIV, and vice versa.

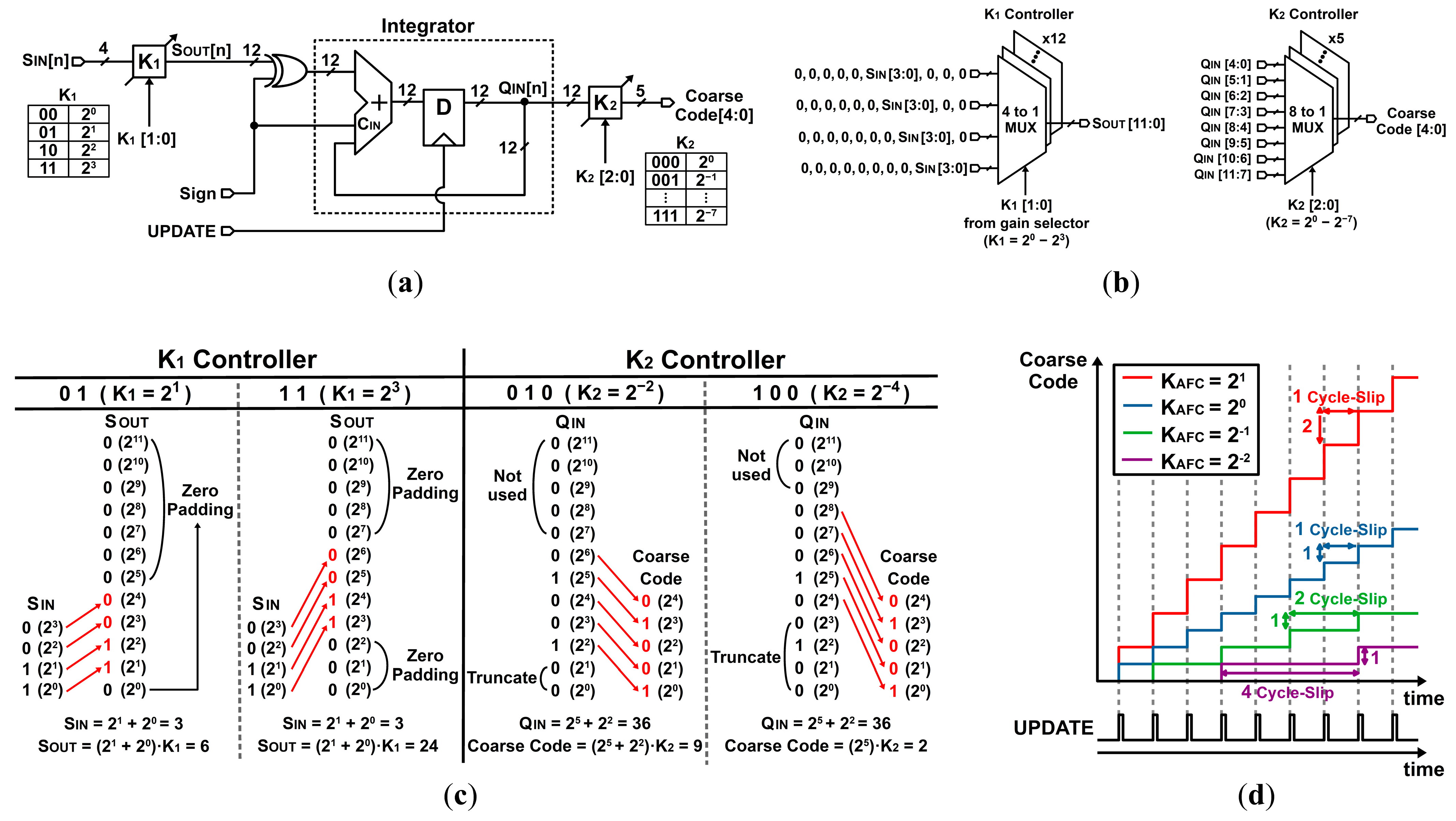
Figure 6a presents a circuit diagram of frequency error integrator in the designed AFC with a wide range of calibration gain control. The sign and input integrator gain K₁ (2⁰–2³) determines the polarity and magnitude of frequency error, and it is integrated afterward. Output integrator gain K₂ provides another degree of freedom to adjust the calibration gain with a range of 2⁰–2⁻⁷. Both K₁ and K₂ are implemented with binary-shifting multiplexers (MUXs), as shown in Figure 6b. Figure 6c illustrates the MUX connection mapping rules of K₁ and K₂ for gain control. K₁ controls the gain based on binary shift in S_IN [3:0], and the remaining bits of the output are padded with 0. In the event of toggling Q_IN LSB at the vicinity of frequency lock, which is undesirable for stable code convergence, lowering K₂ by truncation can prevent the toggling Q_IN LSB from being reflected on the coarse code directly. The total AFC gain (K_AFC) with K₁ and K₂ is defined as

$$K_{AFC}=S_{IN}·K_1·K_2={\displaystyle \frac{amount of coarse code increase}{number of cycle slip}}$$

(1)

Figure 6d illustrates behavior of the frequency error integration for K_AFC = 2¹, 2⁰, 2⁻¹, and 2⁻² if the input S_IN value is set as +1. The whole AFC block is triggered by the UPDATE pulse generated from the preceding PFD only when the cycle slip occurs. Once the PLL enters into the linear PD range, the whole AFC stops operating and the coarse code is fixed for a condition of f_REF ≈ f_DIV with a high stability.

A low AFC gain (K_AFC,Low) would achieve a good calibration stability but degrade the calibration speed. In contrast, a high AFC gain (K_AFC,High) expedites the convergence speed while the stability is traded off, especially on the verge of completing the calibration. The variable gain calibration algorithm has two pre-defined gains, and the high or low gain mode is chosen depending on amount of frequency offset between f_VCO and f_target. 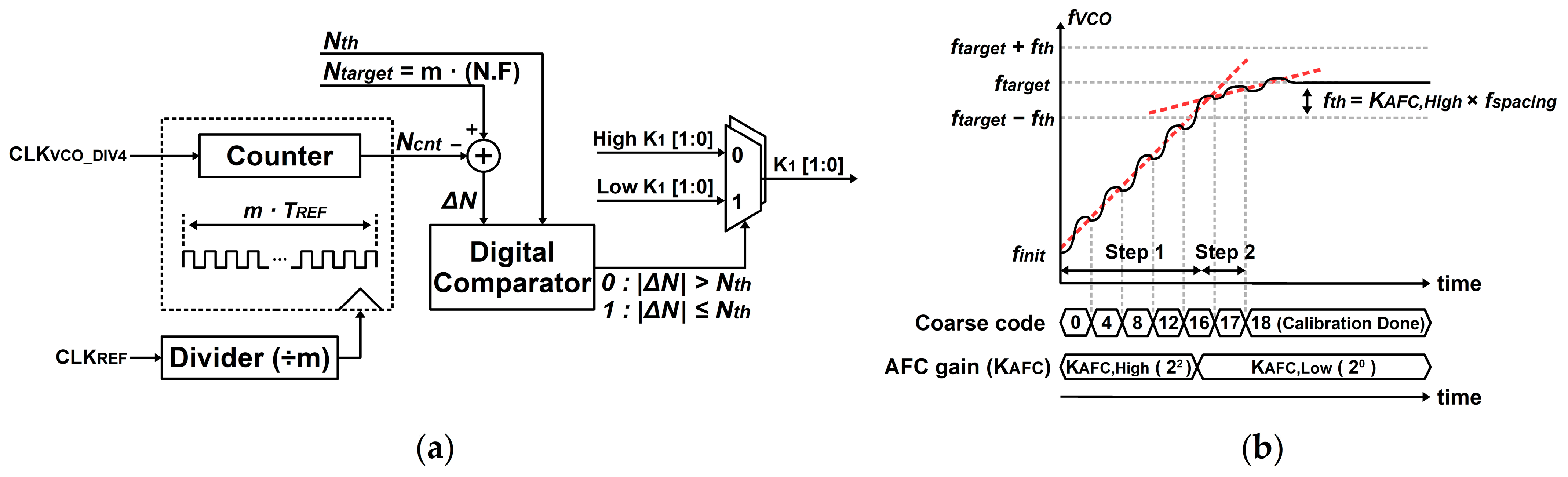As shown in Figure 7a, the gain selector continuously monitors the frequency offset (ΔN) using a counter. It then compares ΔN with a pre-set threshold (Nth) to choose the gain mode. The variable gain control ensures stable calibration for small frequency offsets while reducing the calibration time for large frequency offsets. Figure 7b illustrates an AFC operation with the variable gain transition. Initially, the adaptation begins with a calibration speed of K_AFC,High for fast convergence. As the VCO approaches the target frequency, the gain is switched to K_AFC,Low within the threshold frequency (fth) offset to accomplish a good stability while trading off the calibration speed. Even in the event of frequency drift, the lock recovers within several adjacent coarse code values with K_AFC,Low smoothly. If the fth is too wide, calibration time increases because the AFC would operate with K_AFC,Low for a longer time. If it is too narrow, the coarse code update may become unstable, and it can lead to the failure of frequency lock.

The designed AFC shown in Figure 8 performs both digital coarse calibration (digital coarse path) and analog fine calibration (analog V_ctrl path) concurrently in the closed loops; so, the convergence speeds of the two paths should be carefully designed. Unless the convergence speeds of the two paths are appropriately managed, the PLL may end up with an unstable or a low-speed calibration. Therefore, it is necessary to analyze the variation rate of V_ctrl determined by the loop dynamics. Figure 9 illustrates the increase in V_ctrl with respect to the various frequency offset conditions or constant phase offset ΔΦ = π at the PFD input, where V_ctrl (t) = ΔΦ · I_CP · t/(2π · C_P) [9]. With a frequency offset, ΔΦ gradually increases from 0 to 2π over one cycle slip period and its average phase offset can be regarded as π (ΔΦ = π, Δf = 0 case) in the long time regardless of various frequency offset values (Δf = 0.2, 0.4, 0.8 MHz case). The full-scale transition time of the analog V_ctrl path is roughly 4.8 μs (≈ 2π · 200 pF · 1.2 V/(π · 100 μA)) in our IP.

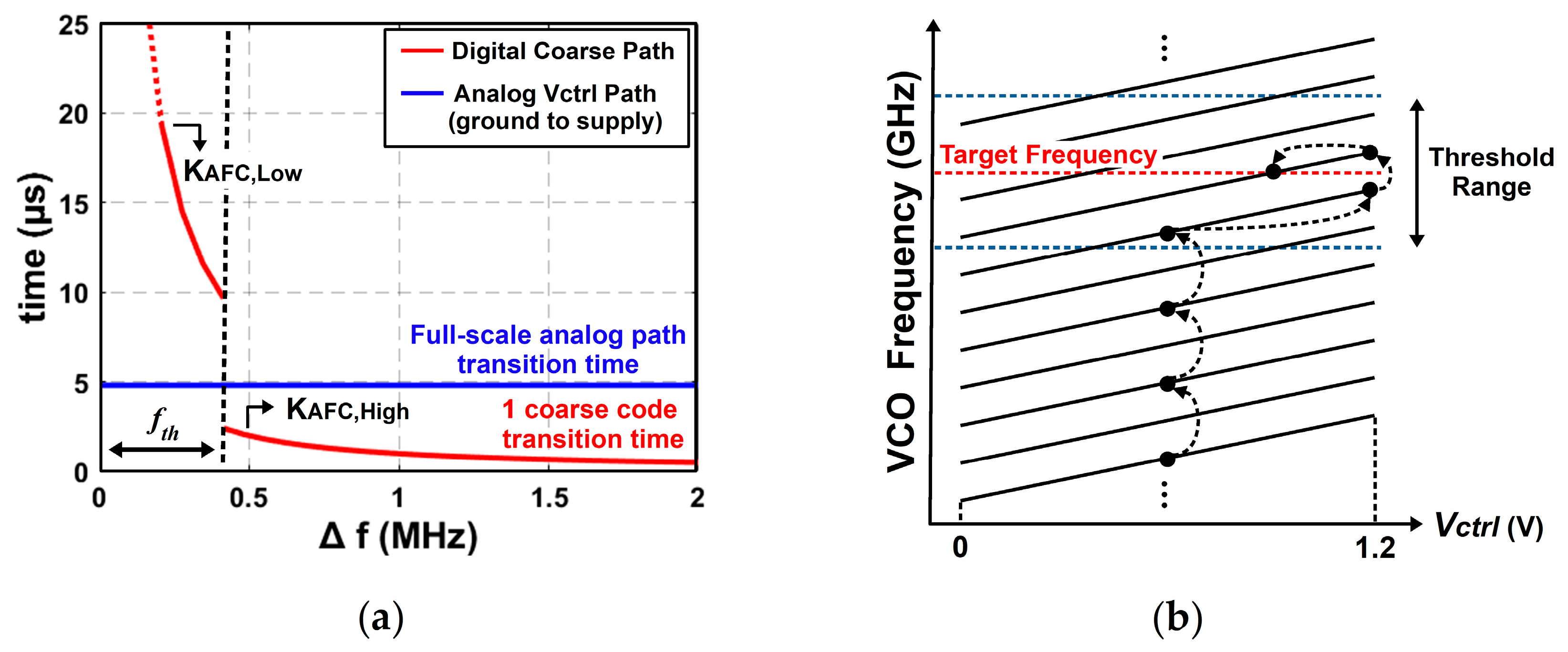
The single coarse code transition time of the cycle slip-based digital coarse path is given by 1/(K_AFC × Δf). The coarse code step size (K_AFC) per cycle slip can be digitally controlled and it allows the transition time of the digital coarse path to be independently tuned. The graph of Figure 10a compares the frequency transition time of the analog V_ctrl from GND to VDD and one coarse code transition time at various frequency offset positions. If the frequency offset is larger than fth, the frequency transition speed of the digital coarse path is faster than the analog V_ctrl path. On the other hand, inside the threshold fth range, the AFC gain is intentionally reduced so that the analog V_ctrl path moves quickly, which makes the analog path complete the convergence stably. Figure 10b illustrates the AFC operation on the VCO profile, considering the speeds of two paths. Outside the threshold range, the coarse code transitions rapidly, while the analog V_ctrl almost remains at a certain voltage due to its lower speed. However, inside the threshold, the V_ctrl moves faster and reaches either VDD or VSS before the coarse code changes. After the coarse code converges, the PLL operates in the loop dynamics and begins linear phase lock without coarse code transitions. V_ctrl moves from VDD or VSS to the target analog voltage. Through the convergence speed management, the AFC achieves a stable lock without code toggling and reduced overall calibration time.

The calibration time in the variable gain calibration algorithm is more accurately calculated as the cumulative sum of each cycle slip period, and it consists of T_AFC,step1 and T_AFC,step2. With each coarse code change, the frequency offset decreases by K_AFC,High × f_spacing in step 1 (high gain mode) and K_AFC,Low × f_spacing in step 2 (low gain mode) as f_VCO approaches f_target. Assuming a constant f_spacing, the convergence time in each step can be expressed as

$$T_{AFC,step1}(D_{codi})=\sum _{a=0}^{A-1}{\displaystyle \frac{N.F}{\left(D_{codi}-a·K_{AFC,High}\right)·f_{spacing}}}$$

(2)

$$T_{AFC,step2}(D_{codi})=\sum _{b=0}^{B-1}{\displaystyle \frac{N.F}{\left(\left(D_{codi}-b\right)·f_{spacing}-A·K_{AFC,High}\right)·K_{AFC,Low}}}$$

(3)

where D_codi is the decimal value of the code distance between the target coarse code and the initial starting coarse code, and A and B are the quotient and the remainder of D_codi/K_AFC,High, respectively. The AFC updates the coarse VCO code with “A” sequential rounds in step 1 and with “B” sequential rounds in step 2. The total calibration time is given by T_AFC = T_AFC,step1 + T_AFC,step2.

The calibration time depends on the D_codi. To compute the calibration time generally, the average calibration time over all D_codi values is defined as

$$T_{AFC,step1,avg}={\displaystyle \frac{1}{2^n-K_{AFC,High}}}\sum _{D_{codi}=K_{AFC,High}}^{2^n-1}{T}_{AFC,step1}\left(D_{codi}\right)$$

(4)

$$T_{AFC,step2,avg}={\displaystyle \frac{1}{K_{AFC,High}}}\sum _{D_{codi}=0}^{K_{AFC,High}-1}{T}_{AFC,step2}\left(D_{codi}\right)$$

(5)

where n is the number of bits in the coarse VCO code, and T_AFC,avg = T_{AFC,step1,avg} + T_{AFC,step2,avg}. T_{AFC,step1,avg} and T_{AFC,step2,avg} denote the arithmetic means over K_AFC,High ≤ D_codi < 2ⁿ (outside threshold) and 0 ≤ D_codi < K_AFC,High (inside threshold), respectively. Figure 11 shows the calculated T_AFC,avg under various K_AFC settings. If K_AFC,High = K_AFC,Low = 2⁰, it indicates that the AFC operates without gain selector (1-step calibration). Notice that using the gain selector by setting K_AFC,High = 2¹ and K_AFC,Low = 2⁰ reduces the average calibration time by approximately half when it is used. If K_AFC,High is set too high, the threshold range should be set as a high value for stability as well, which can increase the time spent in step 2. By properly setting K_AFC,Low, K_AFC,Low, and Nth (fth), the calibration can be completed within an average of 5–6 μs in our IP parameters. Unlike the designed AFC, conventional AFC using an open-loop binary search algorithm requires a total calibration time defined as n × (T_idle + T_meas), which results in approximately 8 μs for a 7-bit coarse VCO code [10], where T_idle is the intentionally inserted idle time allowing VCO clock to settle and T_meas is the frequency counting time. If scaled down to 5-bit, the calibration time becomes approximately 5.71 μs, which is comparable to the designed AFC set to K_AFC,High = 2², K_AFC,Low = 2⁰.

Figure 12 shows the measured VCO output frequency and f_spacing at V_ctrl = 0.6 V. Unlike the constant f_spacing assumption, the measured f_spacing varies from 21 to 38 MHz and is non-uniform. Based on the measured data, a manual calculation that considers f_spacing variation under K_AFC,High = 2² and K_AFC,Low = 2⁰ shows that T_AFC,avg increases from 6.45 μs to 6.82 μs (+5.8%). The increase mainly comes from smaller f_spacing in low coarse code region, and overall, the deviation is modest.

4. Circuit Design

Figure 13a shows the implemented LC-VCO structure that has a tuning range of 5.3–6.2 GHz. The VCO is designed to achieve a low K_VCO using a 5-bit coarse metal–insulator–metal (MIM) capacitor bank. The Widler feedback tail structure fixes the V_X node to a constant voltage level and the drain voltages of M₁ and M₂ are biased to VDD, and a variable poly resistor R₁ controls the tail current and, thus, output swing. M₁ and M₂ operate in either the cut-off or saturation region and it reduces the variation in parasitic capacitance, enabling low phase noise performance [11,12,13]. Figure 13c presents the simulated tail current of the VCO under VT variation, showing that the current remains nearly constant due to the inherent temperature robustness of the Widlar tail current configuration. The structure effectively stabilizes the VCO bias point against thermal variation. To achieve high output swing and low flicker noise, an NMOS-only g_m-cell structure is used. But since the topology applies a VDD-level output bias, the linear range of the varactor is limited. Adding a ground bias in the varactor bank cancels nonlinearities from both branches in opposite directions and enhances the overall V-to-C linearity of the varactor bank [12,13,14]. Figure 13b shows the measured VCO frequency characteristics with a tuning range of 5.3–6.2 GHz and a K_VCO of 65–100 MHz/V across the entire sub-band tuning curve.

Figure 14 presents a detailed circuit diagram of the implemented charge pump. A 3-bit binary-weighted switching structure controls MOSFET M₁–M₃ to generate variable output charge pump currents from 50 to 220 μA. To improve current mismatch and to increase output impedance, an opamp-based feedback structure is employed [15]. Additionally, using dummy MOSFETs (M₄–M₁₀) preserves the symmetry of UP/DN branches for reduced mismatch and reference spur. The transconductance simulation results presented in Figure 15 show that the charge pump operates linearly from approximately 0.1–1.1 V at an output current of 50 µA (CP gain code 000) and 0.2–1.0 V at 220 µA (CP gain code 111). The current mismatch percentage, calculated as 2 × |I_UP − I_DN|/(I_UP + I_DN) × 100 (%), remains within ±0.5% across the V_ctrl linear range. At CP_out = 0.6 V, the simulation results under VT variation show that, although a slight difference appears due to changes in the operating region with supply voltage variation, the charge pump maintains a wide linear range of approximately 1 V and low current mismatch percentage. The charge pump was optimized at room temperature and, a slight increase in current mismatch is observed under temperature variation due to the imbalance in the driving capability between the NMOS and PMOS switches. Because the charge pump maintains linear operation over a wide control voltage range, The operating V_ctrl point variation for various frequencies tuning has a limited impact on the noise performance variation, and similar noise levels are measured across various coarse code and V_ctrl operating conditions. Figure 16 shows the die photograph of the frequency synthesizer with the implemented AFC. The chip is designed and fabricated in a 65 nm CMOS process, and all synthesizer components including the loop filter are implemented on-chip. The active area is 0.603 mm², in which the AFC occupies 0.018 mm².

5. Measurement Results

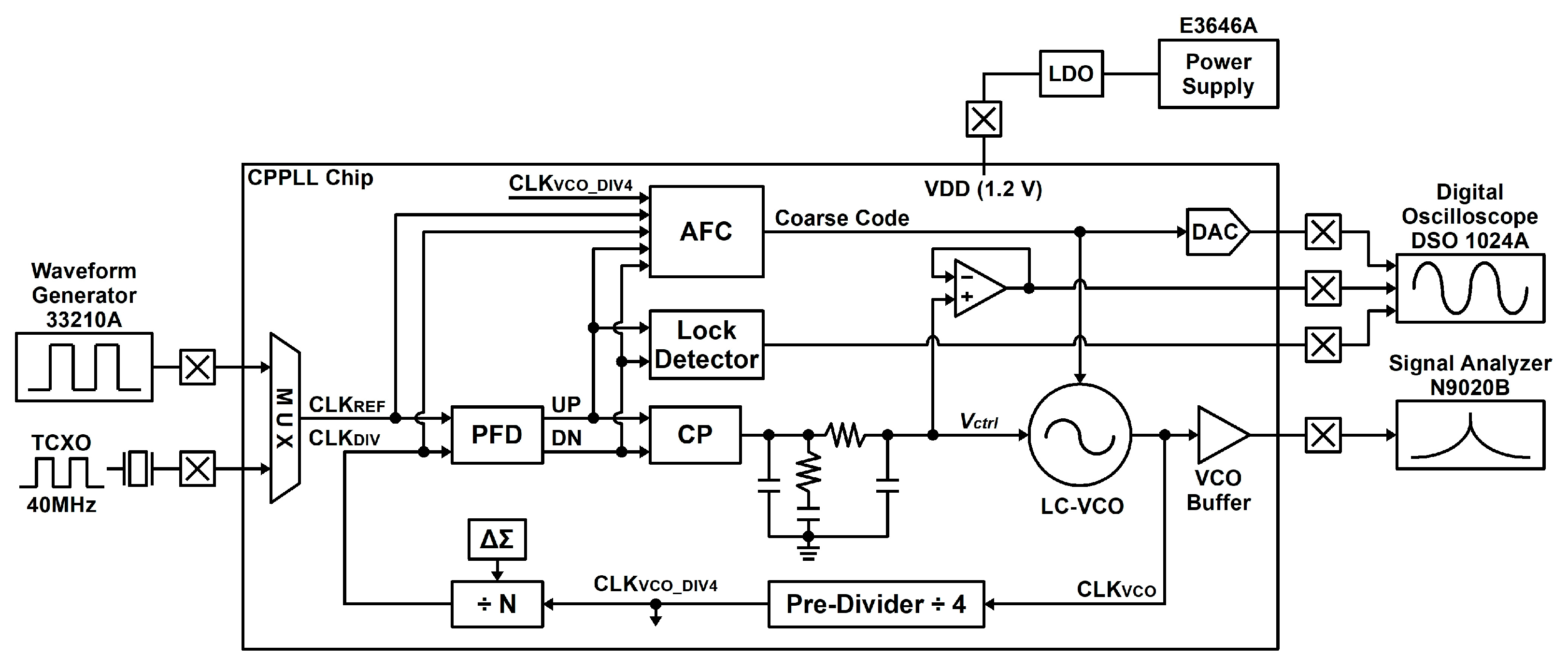
Figure 17 describes the measurement environment settings for the implemented frequency synthesizer. An E3646A power supply supplies 1.2 V VDD. The 40 MHz TCXO provides the reference clock, but a 33210A waveform generator is used when various reference frequencies are required. The digital-to-analog converter (DAC) converts the 5-bit coarse code into an analog voltage in real time. A 1024A digital oscilloscope monitors the coarse code (DAC output), the lock detector (LD) output, and the V_ctrl node to observe the PLL lock process and the AFC operation. An N9020B signal analyzer measures phase noise and spurs for the buffered VCO output (CLK_VCO).

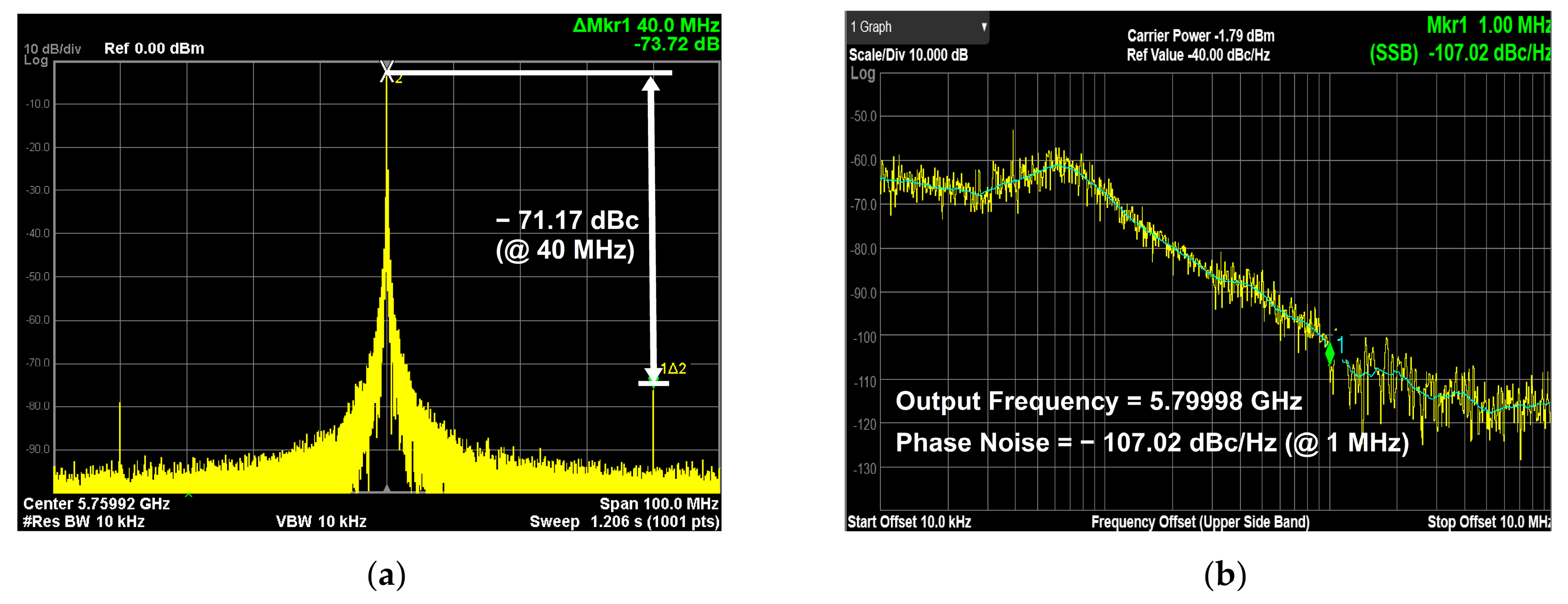
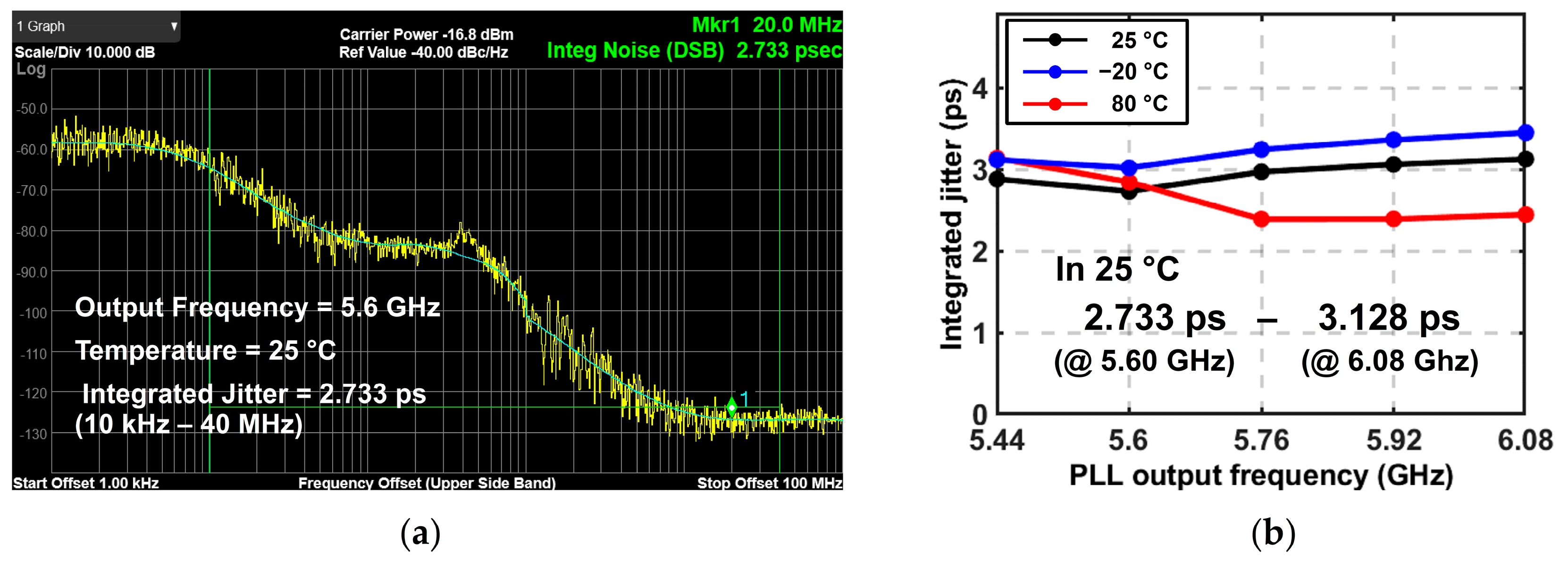
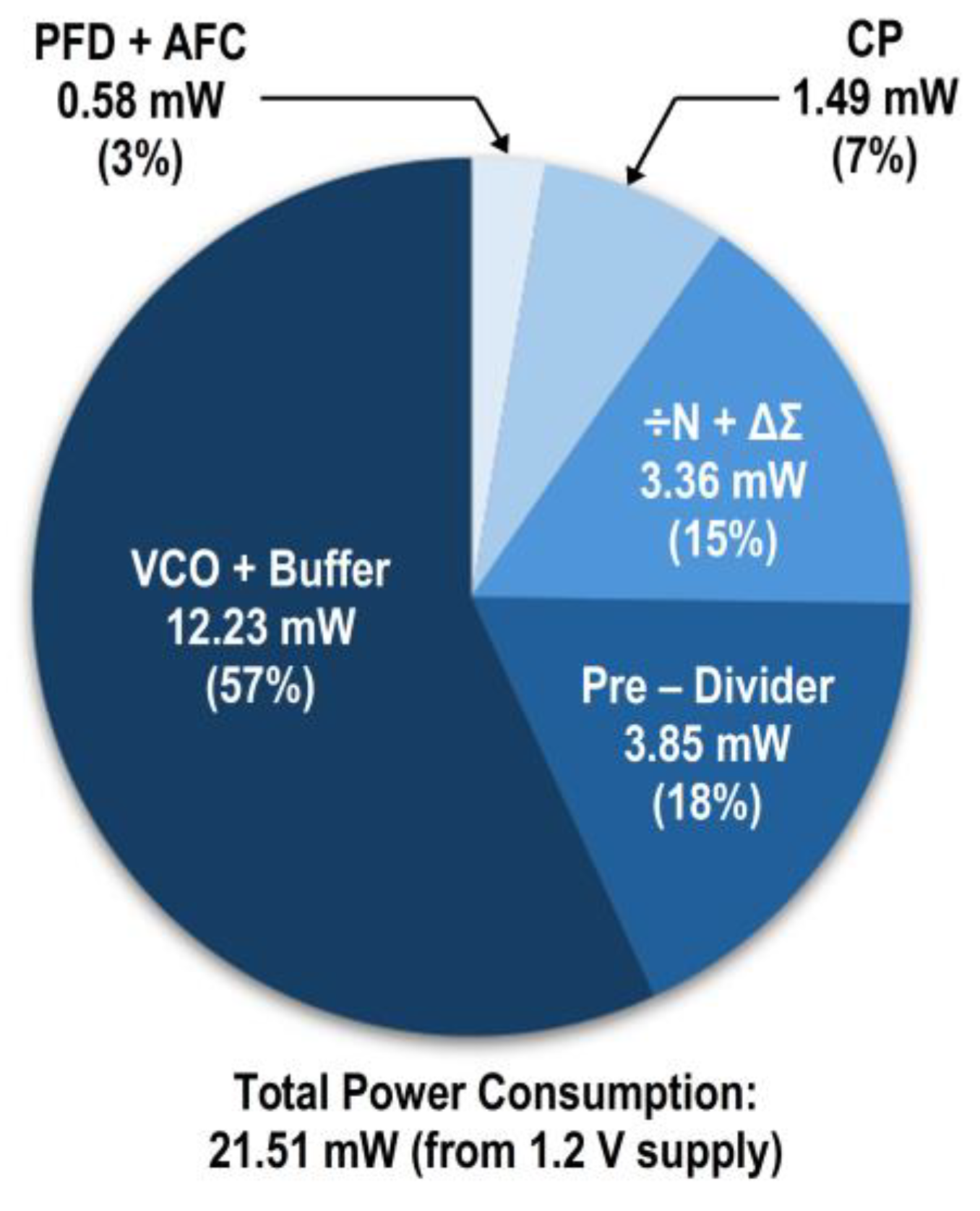
Figure 18a shows the measured reference spur of −71.17 dBc, resulting from improved current matching in the charge pump. The measured phase noise profile at a carrier frequency of 5.8 GHz is shown in Figure 18b, which presents −107.02 dBc/Hz at 1 MHz offset. As shown in Figure 19a, the measured integrated jitter, over a 10 kHz–40 MHz offset range, is 2.733 ps at 5.60 GHz. Figure 19b presents the integrated jitter results across the PLL output frequency range and under temperature variation, showing measured values of 2.733 ps at 5.60 GHz and 3.128 ps at 6.08 GHz in 25 °C. The overall jitter slightly increases at low temperature due to the temperature dependence of the loop dynamics, where the relative contributions of VCO noise and in-band noise vary with temperature, resulting in subtle changes in the effective loop bandwidth and noise-filtering characteristics. The synthesizer consumes 21.51 mW from a 1.2 V supply at the operation frequency of 5.8 GHz, and the power breakdown is shown in Figure 20. Excluding the VCO output buffer, the power consumption is measured as 17.95 mW. The AFC consumes 0.54 mW, which can be powered down after the calibration. The total power varies within ± 5% over the output frequency range of 5.3 to 6.2 GHz.

Figure 21a shows the measured V_ctrl node voltage and the lock detector output during the AFC process, and the locations of V_ctrl and lock detector output nodes are described in Figure 17. The coarse code calibration time is set by the AFC as it finds the appropriate coarse code. Outside the frequency threshold, the coarse code transitions faster than the V_ctrl. Inside the threshold, V_ctrl quickly moves and saturates near ground while the coarse code transitions. The measured frequency calibration time at target frequency 5.8 GHz with K_AFC,High = 2² and K_AFC,Low = 2⁰ is 5.28 µs. Once the coarse code reaches the target code, the loop enters linear phase lock, and the linear V_ctrl lock time is mainly determined by the loop bandwidth as V_ctrl moves from ground to the target analog voltage. The total calibration lock time (coarse code calibration time + linear V_ctrl lock time) is 12.5 µs. Figure 21b presents the average calibration time based on 30 measurements for each K_AFC setting. The results are comparable to the theoretical calculation in Figure 11, and calibration is completed within an average of 5–6 μs for K_AFC,High = 2² and K_AFC,Low = 2⁰. Figure 21c shows the average calibration time measured across various output frequency bands using two separately implemented boards. The measured results show that the average calibration time remains consistently at 5–6 μs for both boards, regardless of the PLL output frequency. The consistency arises because, within the 5.3–6.2 GHz operating range, the sampling period of the internal counter in the gain selector remains constant, while the VCO frequency is divided by the ratio N.F (132–155) to generate the UPDATE pulse that drives the AFC. As a result, the AFC operates at a nearly identical update rate across various frequencies, ensuring consistent calibration speed throughout various frequency bands. Figure 21d presents the average calibration time measured under VT variation conditions at a target frequency of 5.8 GHz, with K_AFC,High = 2² and K_AFC,Low = 2⁰. The measurement results demonstrate that the AFC maintains consistent calibration performance when both the supply voltage and temperature vary. This stable behavior is mainly attributed to the fully digital implementation of the AFC, which makes it inherently less sensitive to voltage and temperature fluctuations. The UPDATE pulse that drives the calibration process is generated from the reference clock and divider output clock at relatively low frequencies, further contributing to the stability of the AFC operation across various frequency conditions. Figure 22 presents the lock recovery behavior of the synthesizer during the frequency drift event. The test condition was emulated by rapidly changing the reference clock frequency, and the results demonstrate that as the output frequency deviates from the lock state, the AFC searches within several adjacent coarse-tuning codes to find a new coarse VCO code and successfully recovers the lock quickly and smoothly.

Table 2. Comparison of synthesizer performance and automatic frequency calibration techniques.

	[2]	[3]	[4]	[8]	[16]	[17]	This Work
Technology (nm)	28	65	40	600	65	180	65
Supply	1.05	1.2	1.1	3	1	1.8	1.2
Power (mW)	9.85	NA	15.92	7.5	2.2–2.8	NA	21.5
Output frequency (GHz)	2.9–3.5	1–2.1	4.5–5.4	0.8–1	0.84–1.12	NA	5.3–6.2
REF frequency (MHz)	40	40	80	0.125	40	NA	40
Phase noise (dBc/Hz) @1MHz	−118.03	NA	−124.6	−102 *	−105.5	−120	−107.02
Integrated jitter (ps)	0.331	NA	NA	NA	1.43–1.82	NA	2.733
Reference spur (dBc)	−64.72	NA	NA	−55	−57	NA	−71.17
Search algorithm	Hybrid	Adaptive	Binary	Linear	Binary	Linear	Variable gain
Detection scheme	FDC	FDC	FDC	Vctrl monitoring	FDC	TCFE **	Cycle slip detector
Loop state during calibration	Open	Open	Open	Closed	Open	Closed	Closed
Number of coarse bit	7	5	5	3	3	4	5
Calibration time (μs)	<4.74	4.03	<13.75	<2000	<3.6	<80	5–6 ***
Total calibration lock time **** (μs)	11.8	NA	NA	NA	NA	NA	12.5
Active area (mm2)	0.761	NA	NA	0.7	0.031	NA	0.603

* 100 kHz offset frequency, ** tuning curve feature extraction, *** average calibration time, **** coarse code calibration time + linear V_ctrl lock time.

compares the implemented frequency synthesizer performance and designed AFC technique with prior arts. The designed AFC maintains the closed-loop state during calibration, enabling comparable real-time tracking and correction of frequency drift as the other AFC scheme with closed-loop state. The AFC maintains closed-loop operation during calibration; the measured average calibration time of 5–6 µs is still modest, being comparable to that of open-loop AFC schemes. In the case of the open-loop AFC, when a frequency drift occurs, the loop must be disconnected and a full binary search repeated, leading to re-locking latency. In contrast, designed AFC corrects the deviation by updating only several adjacent coarse code values, enabling stable re-locking without frequency overshoot.

6. Conclusions

A cycle slip-based AFC scheme for fractional-N frequency synthesizer has been presented. The AFC uses a cycle slip to effectively detect a frequency error with a simple structure and integrates it to successfully find a coarse code closest to the target frequency. The gain selector logic applies to a variable gain calibration algorithm, ensuring calibration stability while reducing the calibration time. By combining cycle slip detection with a variable gain-controlled calibration algorithm, the presented AFC unifies the convergence speed characteristic of open-loop AFCs with the stable locking behavior of closed-loop systems during frequency drift. The AFC operates in a closed loop and continuously monitors the frequency offset, enabling real time tracking and the correction of frequency drifts caused by operation environment changes to maintain stable PLL lock. Measurement results demonstrate an average calibration time of 5–6 μs. The prototype has been fabricated in a 65 nm CMOS process and consumes 21.5 mW while occupying 0.603 mm² of active area.