A Study on Exploiting Temporal Patterns in Semester Records for Efficient Student Dropout Prediction
Abstract
1. Introduction
- Existing studies discussing the problem of SDP were summarized and compared from the perspective of data characteristics, machine-learning algorithms, and prediction performance (Section 2).
- The need for a new solution to exploit patterns in the students’ semester records was first discussed. Regarding this, we discussed that RNN algorithms can effectively be used to capture the patterns, and presented the structure of the SDP model using RNNs with attention mechanisms, including self-attention and multi-head attention (Section 3).
- Through experiments on real student data, we showed that the proposed SDP model using RNN variants or TCN provides better performance than the existing summary-based approaches, demonstrating that the semester records exhibit temporal patterns (Section 4).
- We also conducted experiments using a CNN model to investigate whether spatial patterns exist in the semester records (Section 4).
2. Related Work
2.1. Course-Level Prediction
| Ref# | Dataset | Drop Rate | Algorithms | F1 Score |
|---|---|---|---|---|
| [13] | KDDCup2015 | 79.3% | CNN, LSTM | 0.900 |
| [14] | KDDCup2015 | 79.3% | CNN, LSTM | 0.949 |
| [15] | KDDCup2015 | 79.3% | CNN, LSTM | 0.980 |
| [24] | KDDCup2015 | 79.3% | CNN | 0.864 |
| [25] | KDDCup2015 | 79.3% | CNN | 0.925 |
| [26] | KDDCup2015 | 79.3% | CNN, Attention | 0.929 |
| [27] | KDDCup2015 | 79.3% | CNN, LSTM | 0.899 |
| [28] | KDDCup2015 | 79.3% | CNN-Autoencoder, LSTM | 0.924 |
| [29] | KDDCup2015 | 79.3% | Faster R-CNN, Attention | 0.972 |
| [31] | KDDCup2015 | 79.3% | GNN | 0.923 |
| [33] | OULAD | 52.8 | LSTM | 0.808 |
| [34] | OULAD | 52.8 | Sequential LR | 0.860 |
2.2. School-Level Prediction
| Ref# | Dataset | Drop Rate | Algorithms | F1 Score |
|---|---|---|---|---|
| [11] | Dong-Ah University with 60,010 students | 11.6% | LightGBM | 0.790 |
| [12] | Sahmyook University with 20,050 students | 14.0% | LightGBM | 0.840 |
| [35] | Gyeongsang Natl. University with 67,060 students | 5.1% | XGBoost, CatBoost | 0.786 |
| [38] |
A private university in Italy
with 44,875 students | 23.4% | Random Forest | 0.880 |
| [39] | A public university in Kosovo with 4697 students | 23.7% | LR | 0.850 |
| [40] | A private university in Brazil with 40,000 students | 7.59% | ANN, Decision Tree, LR | 0.938 |
| [41] | A public university in Columbia with 6100 students | - | LR | 0.712 |
| [43] |
Roma Tre University
with 6078 students | 40.8% | CNN | 0.650 |
| [44] | A Latin American university with 13,969 students | - | CNN |
0.933
(Accuracy) |
3. Proposed Method
3.1. Data Description
3.2. Feature Extraction
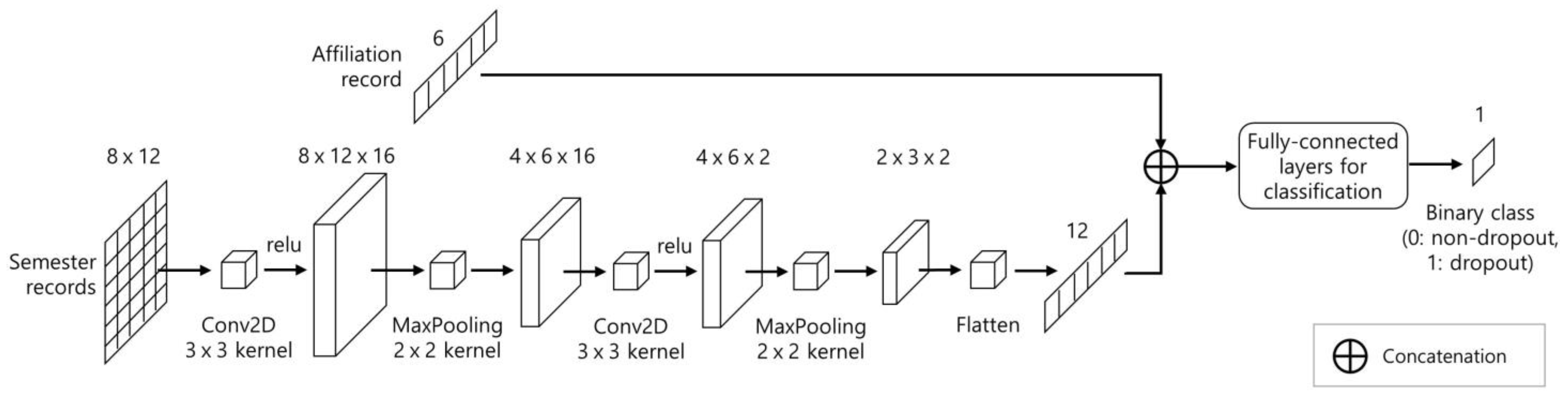
3.3. Model Implementation
4. Experimental Results
4.1. Performance Measure
4.2. Experimental Setup
4.2.1. Configuration for Existing Models
- (1)
- Last semester: choose the value of the last semester as the summary.
- (2)
- Mean: choose the arithmetic mean of the list values as the summary.
- (3)
- Weighted mean: choose the weighted mean as the summary, which gives higher weight to recent semesters. The simple exponential smoothing function [50] can be used to calculate the weighted mean, such that the following applies:
4.2.2. Performance Validation
4.3. Performance Evaluation
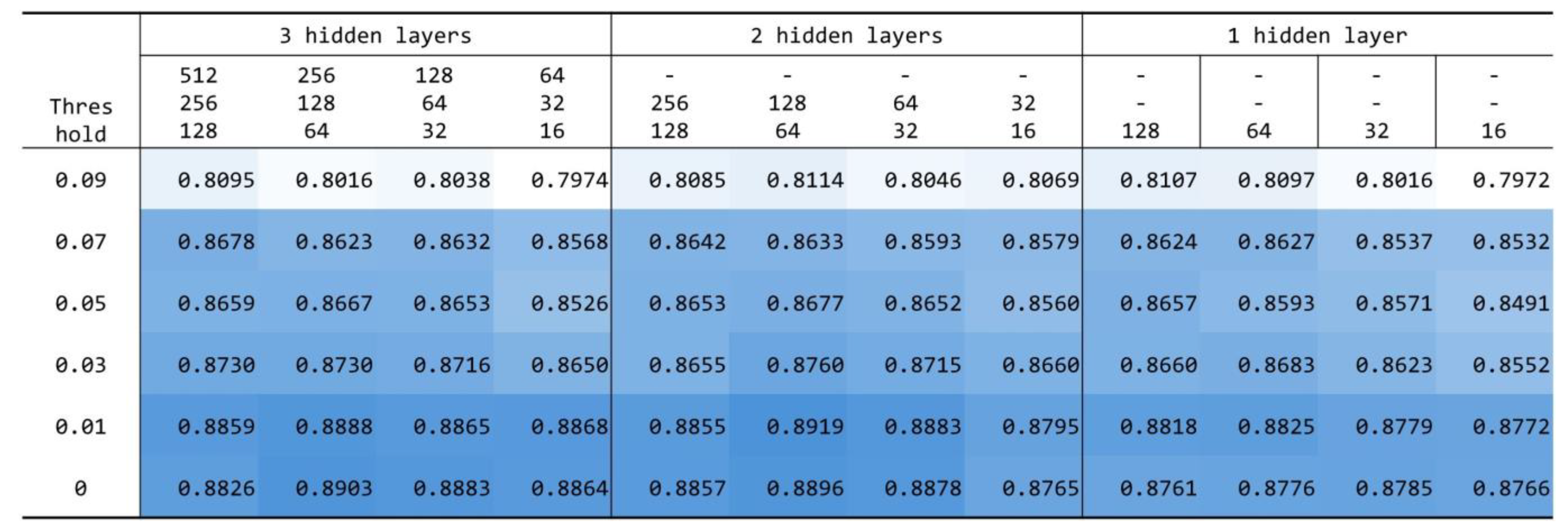
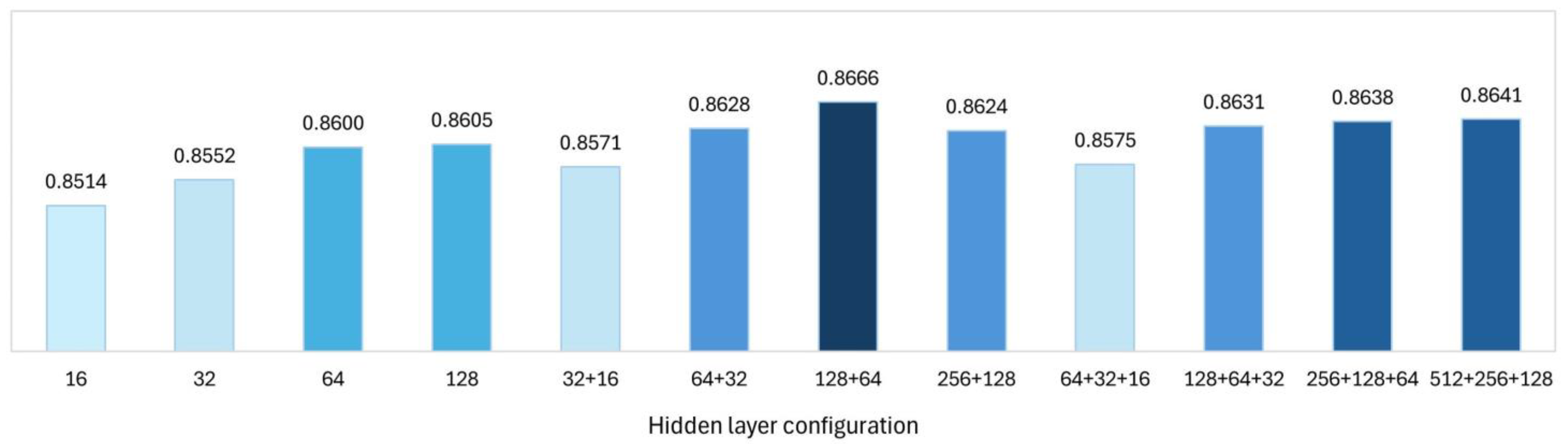
4.3.1. Determination of the Correlation Coefficient Threshold
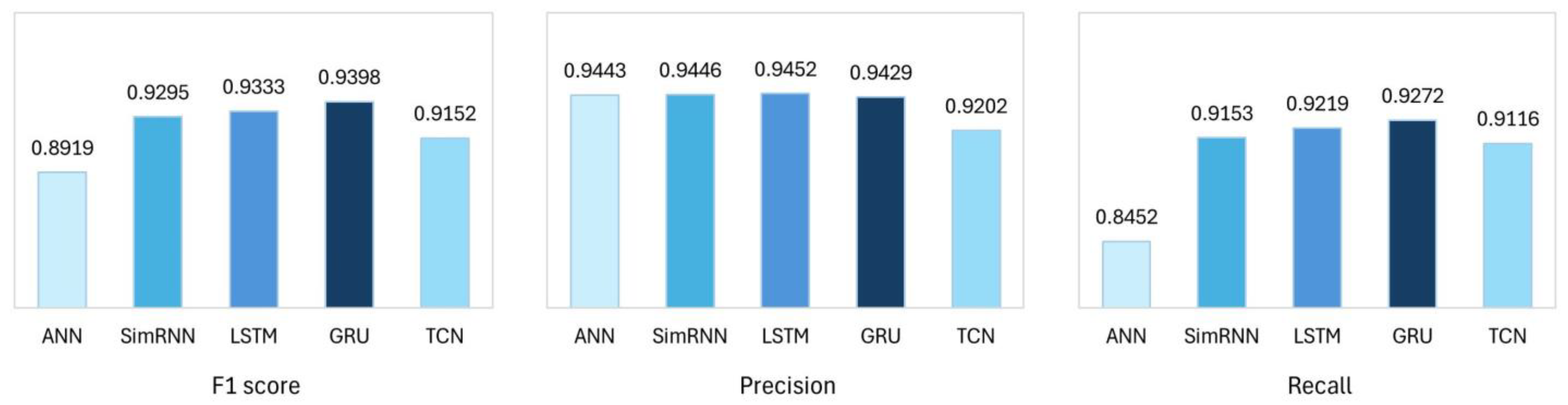
4.3.2. Performance of the Basic RNNs
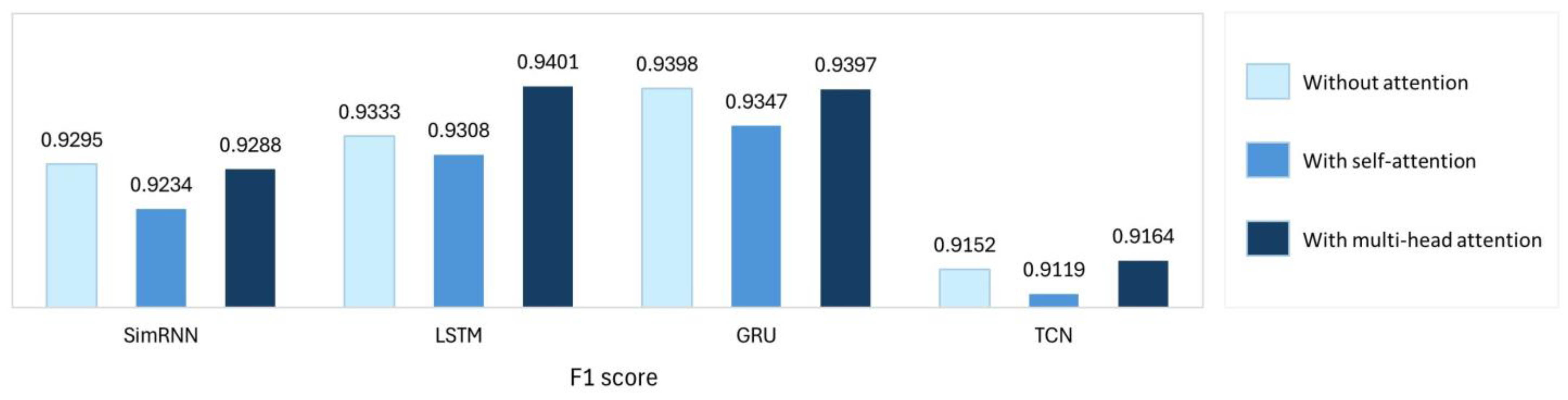
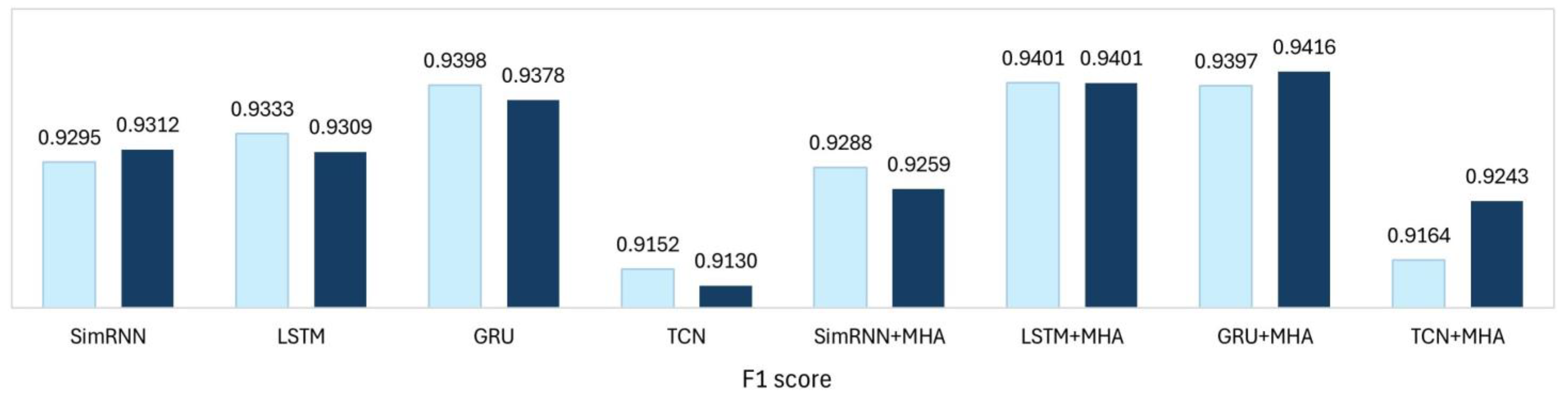
4.3.3. Influence of Attention Mechanisms
4.3.4. Influence of Oversampling
4.3.5. Spatial Temporality in Semester Records
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, D.; Kim, S. Sustainable education: Analyzing the determinants of university student dropout by nonlinear panel data models. Sustainability 2018, 10, 954. [Google Scholar] [CrossRef]
- Mduma, N.; Kalegele, K.; Machuve, D. A survey of machine learning approaches and techniques for student dropout prediction. Data Sci. J. 2019, 18, 14. [Google Scholar] [CrossRef]
- Fierro Saltos, W.R.; Fierro Saltos, F.E.; Elizabeth Alexandra, V.S.; Rivera Guzmán, E.F. Leveraging Artificial Intelligence for Sustainable Tutoring and Dropout Prevention in Higher Education: A Scoping Review on Digital Transformation. Information 2025, 16, 819. [Google Scholar] [CrossRef]
- Pelima, L.R.; Sukmana, Y.; Rosmansyah, Y. Predicting university student graduation using academic performance and machine learning—A systematic literature review. IEEE Access 2024, 12, 23451–23465. [Google Scholar] [CrossRef]
- Alnasyan, B.; Basheri, M.; Alassafi, M. The power of deep learning techniques for predicting student performance in virtual learning environments: A systematic literature review. Comput. Educ. Artif. Intell. 2024, 6, 100231. [Google Scholar] [CrossRef]
- Colpo, M.P.; Primo, T.T.; Aguiar, M.S.; Cechinel, C. Educational data mining for dropout prediction: Trends, opportunities, and challenges. Rev. Bras. Inform. Educ. 2024, 32, 220–256. [Google Scholar] [CrossRef]
- Prenkaj, B.; Velardi, P.; Stilo, G.; Distante, D.; Faralli, S. A survey of machine learning approaches for student dropout prediction in online courses. ACM Comput. Surv. 2020, 53, 1–34. [Google Scholar] [CrossRef]
- Alyahyan, E.; Dustegor, D. Predicting academic success in higher education: Literature review and best practices. Int. J. Educ. Technol. High. Educ. 2020, 17, 3. [Google Scholar] [CrossRef]
- Oriveira, C.F.; Sobral, S.R.; Ferreira, M.J.; Moreira, F. How does learning analytics contribute to prevent students’ dropout in higher education: A systematic literature review. Big Data Cogn. Comput. 2021, 5, 64. [Google Scholar] [CrossRef]
- Mbunge, E.; Batani, J.; Mafumbate, R.; Gurajena, C.; Fashoto, S.; Rugube, T.; Akinnuwesi, B.; Metfula, A. Predicting student dropout in massive open online courses using deep learning models-A systematic review. In Cybernetics Perspectives in Systems. CSOC 2022. Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2022; pp. 212–231. [Google Scholar] [CrossRef]
- Song, Z.; Sung, S.H.; Park, D.M.; Park, B.K. All-year dropout prediction modeling and analysis for university students. Appl. Sci. 2023, 13, 1143. [Google Scholar] [CrossRef]
- Cho, C.H.; Yu, Y.W.; Kim, H.G. A study on dropout prediction for university students using machine learning. Appl. Sci. 2023, 13, 12004. [Google Scholar] [CrossRef]
- Mubarak, A.A.; Cao, H.; Hezam, I.M. Deep analytic model for student dropout prediction in massive open online courses. Comput. Electr. Eng. 2021, 93, 107271. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, H.; Zhang, N.; Yan, H. Dropout rate prediction of massive open online courses based on convolutional neural networks and long short-Term memory metwork. Mob. Inf. Syst. 2022, 2022, 1–11. [Google Scholar] [CrossRef]
- Talebi, K.; Torabi, Z.; Daneshpour, N. Ensemble models based on CNN and LSTM for dropout prediction in MOOC. Expert. Syst. Appl. 2024, 235, 121187. [Google Scholar] [CrossRef]
- Pelletier, C.; Webb, G.I.; Petitjean, F. Temporal convolutional neural network for the classification of satellite image time series. Remote Sens. 2019, 11, 523. [Google Scholar] [CrossRef]
- Yadav, S.P.; Zaidi, S.; Mishra, A.; Yadav, V. Survey on machine learning in speech emotion recognition and vision systems using a recurrent neural network (RNN). Arch. Comput. Methods Eng. 2022, 29, 1753–1770. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- KDDCup2015, Biendata. Available online: https://www.biendata.xyz/competition/kddcup2015/rank/ (accessed on 21 August 2025).
- OULAD, Open University Learning Analytics Dataset, UC Irvine Machine Learning Repository. Available online: https://archive.ics.uci.edu/dataset/349/open+university+learning+analytics+dataset (accessed on 21 August 2025).
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6999–7019. [Google Scholar] [CrossRef]
- Zheng, Y.; Gao, Z.; Wang, Y.; Fu, Q. MOOC dropout prediction using FWTS-CNN model based on fused feature weighting and time series. IEEE Access 2020, 8, 225324–225335. [Google Scholar] [CrossRef]
- Wen, Y.; Tian, Y.; Wen, B.; Zhou, Q.; Cai, G.; Liu, S. Consideration of the local correlation of learning behaviors to predict dropouts from MOOCs. Tsinghua Sci. Technol. 2019, 25, 336–347. [Google Scholar] [CrossRef]
- Feng, W.; Tang, J.; Liu, T.X. Understanding dropouts in MOOCs. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; 33, pp. 517–524. [Google Scholar] [CrossRef]
- Pan, F.; Huang, B.; Zhang, C.; Zhu, X.; Wu, Z.; Zhang, M.; Ji, Y.; Ma, Z.; Li, Z. A survival analysis based volatility and sparsity modeling network for student dropout prediction. PLoS ONE 2022, 17, e0267138. [Google Scholar] [CrossRef]
- Niu, K.; Lu, G.; Peng, X.; Zhou, Y.; Zeng, J.; Zhang, K. CNN autoencoders and LSTM-based reduced order model for student dropout prediction. Neural Comput. Appl. 2023, 35, 22341–22357. [Google Scholar] [CrossRef]
- Kumar, G.; Singh, A.; Sharma, A. Ensemble deep learning network model for dropout prediction in MOOCs. Int. J. Electr. Comput. Eng. Syst. 2023, 14, 187–196. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Roh, D.; Han, D.; Kim, D.; Han, K.; Yi, M.Y. SIG-Net: GNN based dropout prediction in MOOCs using student interaction graph. In Proceedings of the 39th ACM/SIGAPP Symposium on Applied Computing, Ávila, Spain, 4–8 April 2024; pp. 29–37. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef] [PubMed]
- Waheed, H.; Hassan, S.-U.; Nawaz, R.; Aljohani, N.R.; Chen, G.; Gasevic, D. Early prediction of learners at risk in self-paced education: A neural network approach. Expert. Syst. Appl. 2023, 213, 118868. [Google Scholar] [CrossRef]
- Mubarak, A.A.; Cao, H.; Zhang, W. Prediction of students’ early dropout based on their interaction logs in online learning environment. Interact. Learn. Environ. 2022, 30, 1414–1433. [Google Scholar] [CrossRef]
- Kim, S.; Choi, E.; Jun, Y.K.; Lee, S. Student Dropout Prediction for University with High Precision and Recall. Appl. Sci. 2023, 13, 6275. [Google Scholar] [CrossRef]
- Zhang, P.; Jia, Y.; Shang, Y. Research and application of XGBoost in imbalanced data. Int. J. Distrib. Sens. Net. 2022, 18, 6. [Google Scholar] [CrossRef]
- Hancock, J.T.; Khoshgoftaar, T.M. CatBoost for big data: An interdisciplinary review. J. Big Data 2020, 7, 94. [Google Scholar] [CrossRef]
- Zanellati, A.; Zingaro, S.P.; Gabbrielli, M. Balancing performance and explainability in academic dropout prediction. IEEE Trans. Learn. Tech. 2024, 17, 2086–2099. [Google Scholar] [CrossRef]
- Ujkani, B.; Minkovska, D.; Stoyanova, L. Application of logistic regression technique for predicting student dropout. In Proceedings of the 2022 XXXI International Scientific Conference Electronics (ET), Sozopol, Bulgaria, 13–15 September 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Rabelo, A.M.; Zárate, L.E. A model for predicting dropout of higher education students. Data Sci. Manag. 2025, 8, 72–85. [Google Scholar] [CrossRef]
- Nieto, Y.; Gacía-Díaz, V.; Montenegro, C.; González, C.C.; Crespo, R.G. Usage of machine learning for strategic decision making at higher educational institutions. IEEE Access 2019, 7, 75007–75017. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Agrusti, F.; Mezzini, M.; Bonavolontà, G. Deep learning approach for predicting university dropout: A case study at Roma Tre University. J. E-Learn. Knowl. Soc. 2020, 16, 44–54. [Google Scholar] [CrossRef]
- Gutierrez-Pachas, A.; Garcia-Zanabria, G.; Cuadros-Vargas, E.; Camara-Chavez, G.; Gomez-Nieto, E. Supporting decision-making process on higher education dropout by analyzing academic, socioeconomic, and equity factors through machine learning and survival analysis methods in the Latin American context. Edu. Sci. 2023, 13, 154. [Google Scholar] [CrossRef]
- Rehmer, A.; Kroll, A. On the vanishing and exploding gradient problem in gated recurrent units. IFAC-PapersOnLine 2020, 53, 1243–1248. [Google Scholar] [CrossRef]
- Shaw, P.; Uszkoreit, J.; Vaswani, A. Self-attention with relative position representations. arXiv 2018, arXiv:1803.02155. [Google Scholar] [CrossRef]
- Cordonnier, J.B.; Loukas, A.; Jaggi, M. Multi-head attention: Collaborate instead of concatenate. arXiv 2020, arXiv:2006.16362. [Google Scholar] [CrossRef]
- Keras, Google. Available online: https://keras.io/ (accessed on 21 August 2025).
- Keras Self-Attention Project, Google. Available online: https://pypi.org/project/keras-self-attention/ (accessed on 21 August 2025).
- Keras Temporal Convolutional Network Project, Google. Available online: https://pypi.org/project/keras-tcn/2.9.3/ (accessed on 15 October 2025).
- Adam, K.D.B.J. A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Alhudhaif, A. A novel multi-class imbalanced EEG signals classification based on the adaptive synthetic sampling (ADASYN) approach. PeerJ Comput. Sci. 2021, 7, e523. [Google Scholar] [CrossRef] [PubMed]
- Keras Masking and Padding, Google. Available online: https://www.tensorflow.org/guide/keras/understanding_masking_and_padding?hl=en (accessed on 15 October 2025).










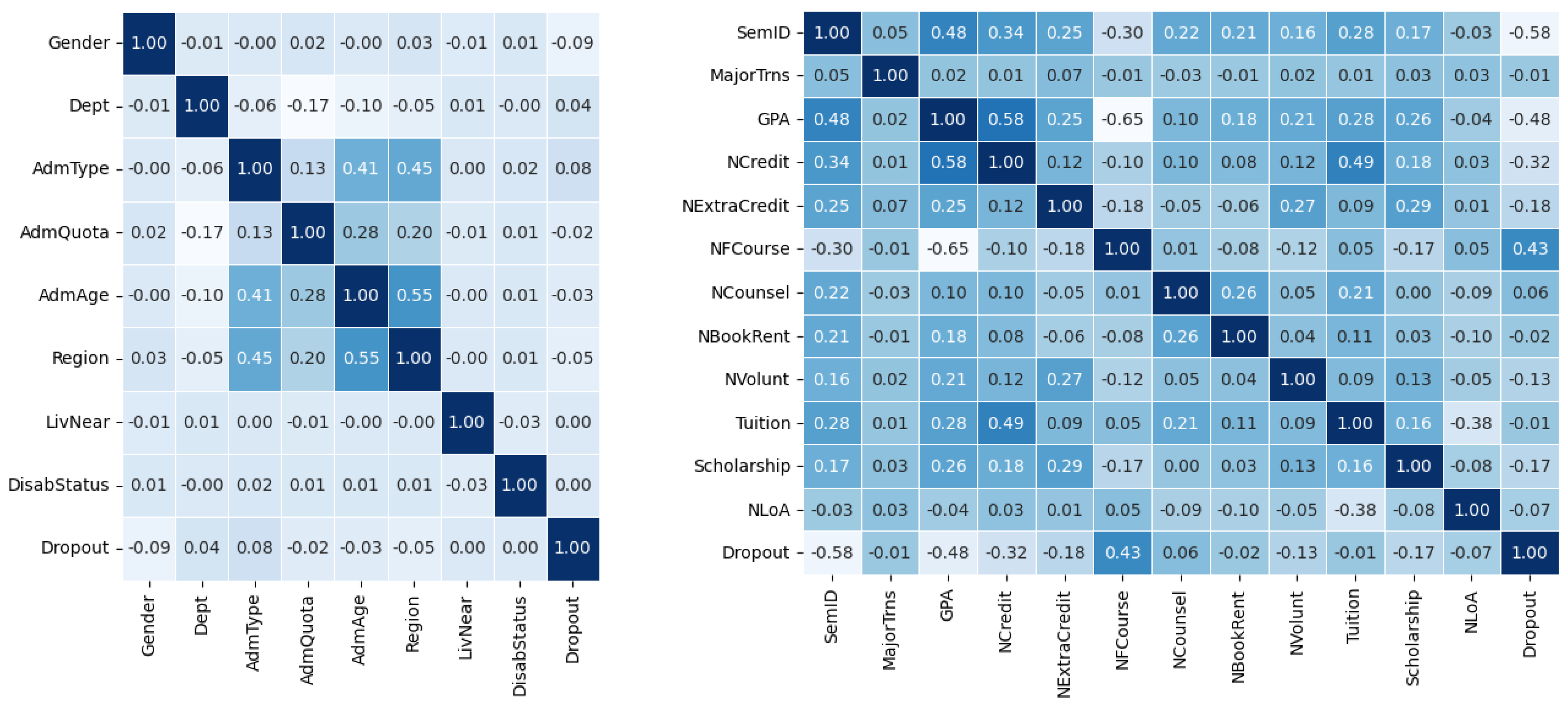
| Name | Description | Format |
|---|---|---|
| SID | Student ID | Number (11 digits) |
| Name | Student name | String |
| Birthdate | Student birth date | Date |
| Gender | Gender: male (0), female (1) | Boolean |
| Dept | Department or division name | String |
| AdmType | Type of admission: new (0), transfer (1) | Boolean |
| AdmQuota | Admission quota: within (0), outside (1) | Boolean |
| AdmAge | Age at the time of admission | Number (2 digits) |
| Region | Region code of the graduated high school | Number (2 digits) |
| LivNear | Living near school: yes (1), no (0) | Boolean |
| DisabStatus | Disability status: yes (1), no (0) | Boolean |
| Dropout | Dropout: yes (1), no (0) | Boolean |
| Name | Description | Format |
|---|---|---|
| SID | Student ID | Number (11 digits) |
| Year | Year enrolled | Number (4 digits) |
| Semester | Semester enrolled | Number (1 or 2) |
| Status |
Enrollment status: admission (0),
enrollment (1), leave-of-absence (2), transfer (3), dropout (4), graduation (5) | Categorical |
| MajorTrns | Major transferred: yes (1), no (0) | Boolean |
| GPA | Grade point average | Number (0~4.5) |
| NCredit | Number of credits earned | Number |
| NExtraCredit | Number of extracurricular credits earned | Number |
| NFCourse | Number of courses receiving an F grade | Number |
| NCounsel | Number of counseling sessions attended | Number |
| NBookRent | Number of book rentals | Number |
| NVolunt | Number of volunteer participations | Number |
| Tuition | Tuition paid | Number |
| Scholarship | Scholarship received | Number |
| SID | Year | Semester | Status | GPA | NCredit | … |
|---|---|---|---|---|---|---|
| 2023xx1003 | 2023 | 1 | admission (0) | 3.43 | 17 | … |
| 2013xx1003 | 2023 | 2 | enrollment (1) | 2.89 | 18 | … |
| 2013xx1003 | 2024 | 1 | leave-of-absence (2) | - | - | … |
| 2013xx1003 | 2024 | 2 | leave-of-absence (2) | … | ||
| 2013xx1003 | 2025 | 1 | enrollment (1) | 3.26 | 21 | … |
| 2013xx1004 | 2023 | 1 | admission (0) | 2.45 | 18 | … |
| 2013xx1004 | 2023 | 2 | leave-of-absence (2) | - | - | … |
| 2013xx1004 | 2024 | 1 | dropout (4) | - | - | … |
| SID | SemID | NLoA | GPA | NCredit | … |
|---|---|---|---|---|---|
| 2023xx1003 | 1 | 0 | 3.43 | 17 | … |
| 2013xx1003 | 2 | 2 | 2.89 | 18 | … |
| 2023xx1003 | 3 | 0 | 3.26 | 21 | … |
| 2013xx1004 | 1 | 1 | 2.45 | 18 | … |
| Category | Attributes |
|---|---|
| Affiliation information | Gender, Dept, AdmType, AdmQuota, AdmAge, Region |
| Academic achievement information | SemID, MajorTrns, GPA, NCredit, NExtraCredit, NFCourse, NCounsel, NBookRent, NVolunt, Tuition, Scholarship, NLoA |
| Algorithm | Parameters | Description | Value | |
|---|---|---|---|---|
| SimpleRNN, LSTM, GRU, and TCN | Layer-1 | units | Dimensionality of the output space | 128 |
| return_sequences | Whether to return the hidden state output for each time step of the input sequence | True | ||
| Layer-2 | units | Dimensionality of the output space | 12 | |
| SeqSelfAttention | Layer-1 | attention_activation | Activation function to calculate output for the next layer | sigmoid |
| MultiHeadAttention | Layer-1 | num_heads | Number of attention heads | 4 |
| key_dim | Size of each attention head for query and key | 32 | ||
| ANN | Layer-1 | units | Dimensionality of the output space | 128 |
| activation | Activation function to calculate output for the next layer | relu | ||
| Layer-2 | units | Dimensionality of the output space | 32 | |
| activation | Activation function to calculate output for the next layer | relu | ||
| Layer-3 | units | Dimensionality of the output space | 1 | |
| activation | Activation function to calculate output for the next layer | sigmoid | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Na, J.; Kim, K.W.; Kim, H.G. A Study on Exploiting Temporal Patterns in Semester Records for Efficient Student Dropout Prediction. Electronics 2025, 14, 4356. https://doi.org/10.3390/electronics14224356
Na J, Kim KW, Kim HG. A Study on Exploiting Temporal Patterns in Semester Records for Efficient Student Dropout Prediction. Electronics. 2025; 14(22):4356. https://doi.org/10.3390/electronics14224356
Chicago/Turabian StyleNa, Jungjo, Kwan Woo Kim, and Hyeon Gyu Kim. 2025. "A Study on Exploiting Temporal Patterns in Semester Records for Efficient Student Dropout Prediction" Electronics 14, no. 22: 4356. https://doi.org/10.3390/electronics14224356
APA StyleNa, J., Kim, K. W., & Kim, H. G. (2025). A Study on Exploiting Temporal Patterns in Semester Records for Efficient Student Dropout Prediction. Electronics, 14(22), 4356. https://doi.org/10.3390/electronics14224356