Dynamic Equivalent Modeling of Distributed Photovoltaic Generation Systems in Microgrid Considering LVRT Active Power Response Difference
Abstract
1. Introduction
- (1)
- Three dominant active power responses are identified by comprehensively characterizing the LVRT response of PV units, and two candidate segmentation thresholds for clustering are identified;
- (2)
- A voltage dip dependency segmentation threshold is approximated, and an additional threshold based on the average pre-fault steady-state active power is incorporated to accurately represent post-fault active power ramp recovery.
- (3)
- A four-machine equivalent modeling method is proposed to replace detailed modeling of all PV units in microgrid, significantly reducing model complexity while maintaining high simulation accuracy.
2. Modeling of a Distributed PV Unit Considering LVRT Control
3. Equivalent Modeling of Distributed PV Generation Systems in Microgrid
3.1. Analysis of Active Power Transient Responses Characteristics
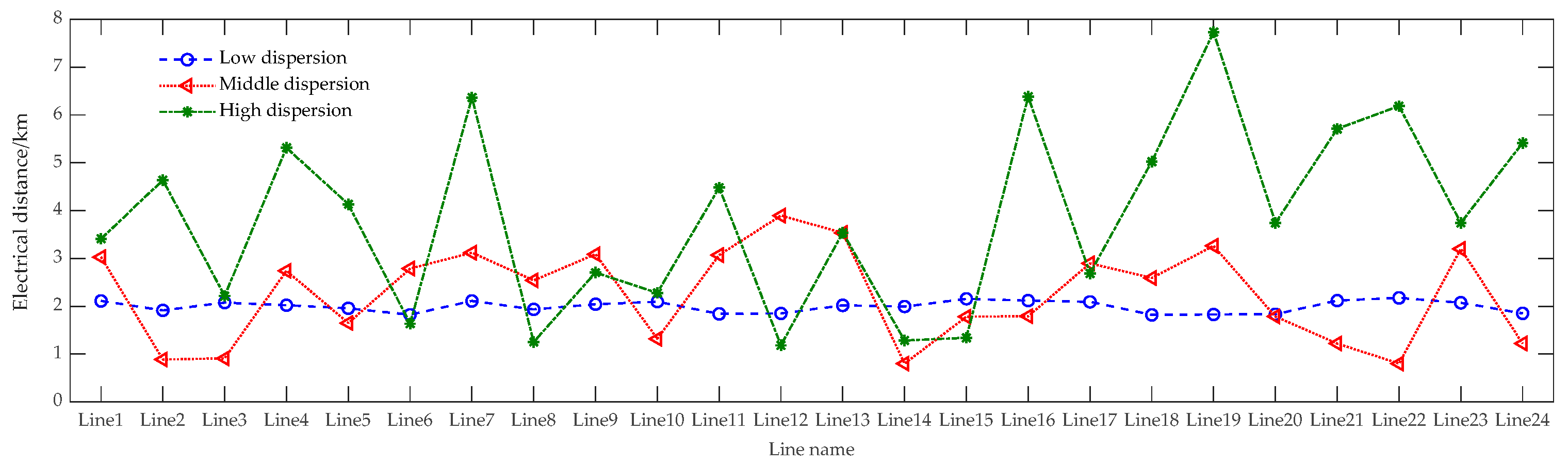
3.2. Clustering Method of Distributed PV Units in Microgrid
3.3. Equivalent Modeling of Distributed PV Generation Systems in Micgrid
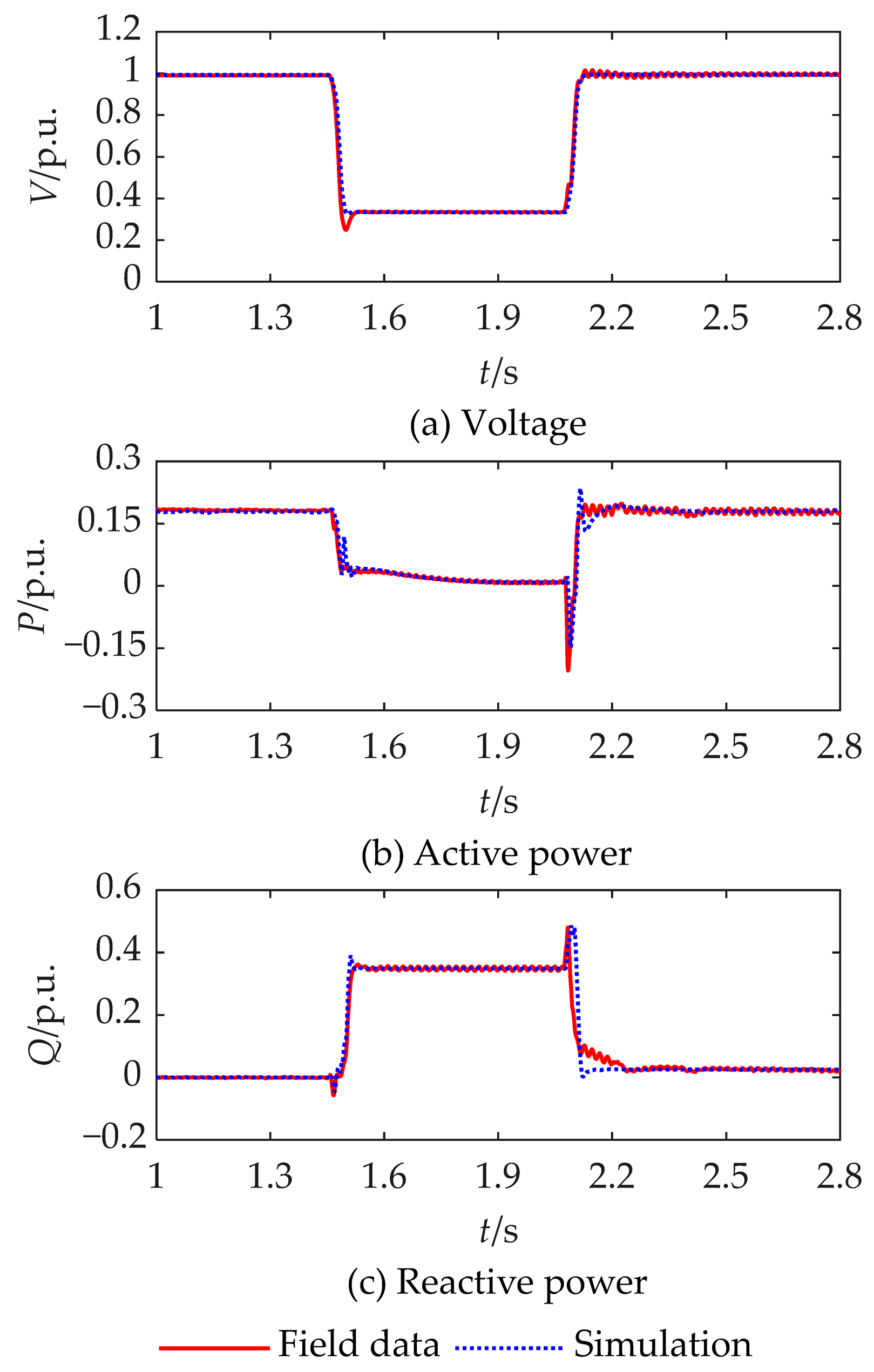
4. Simulation Results
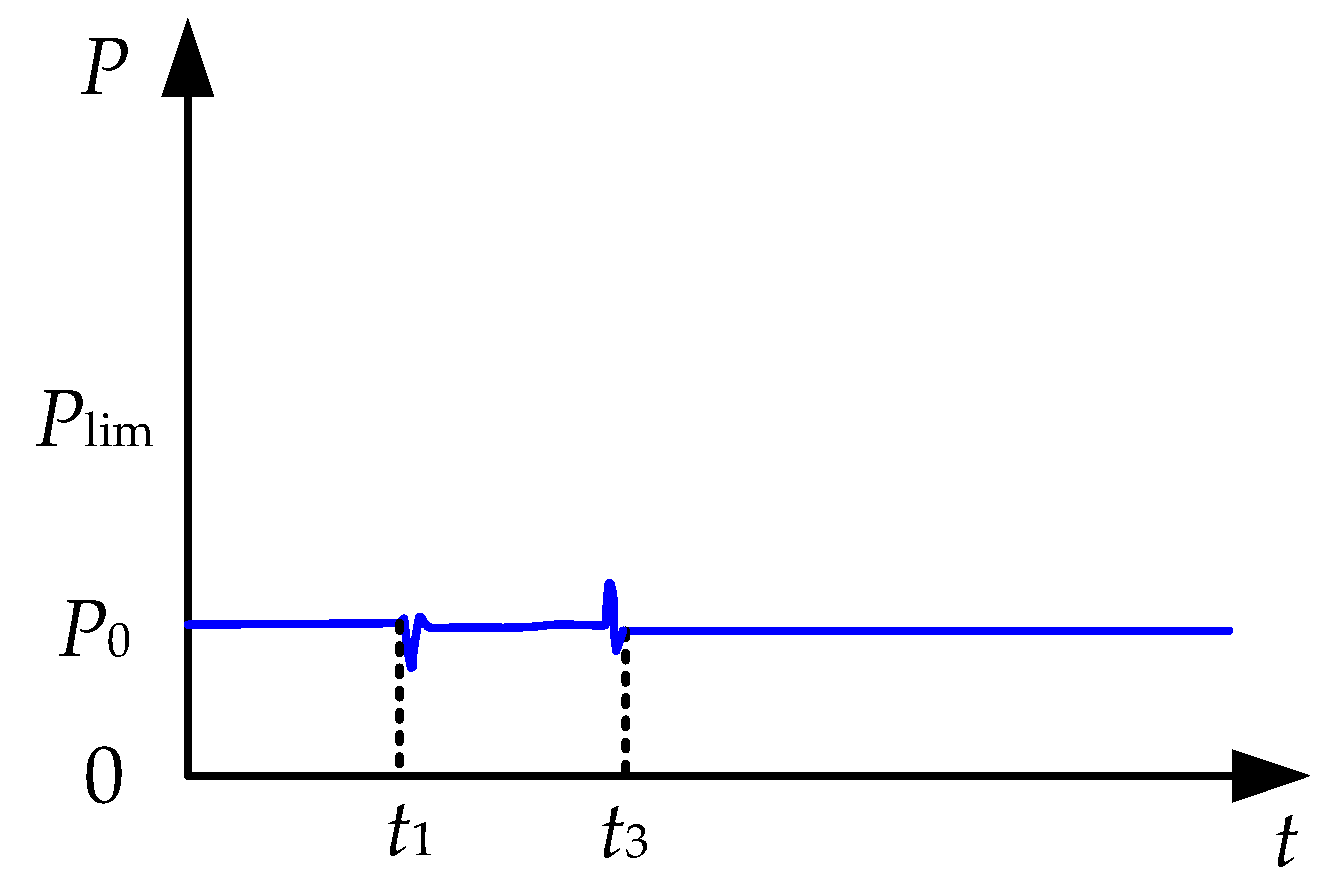
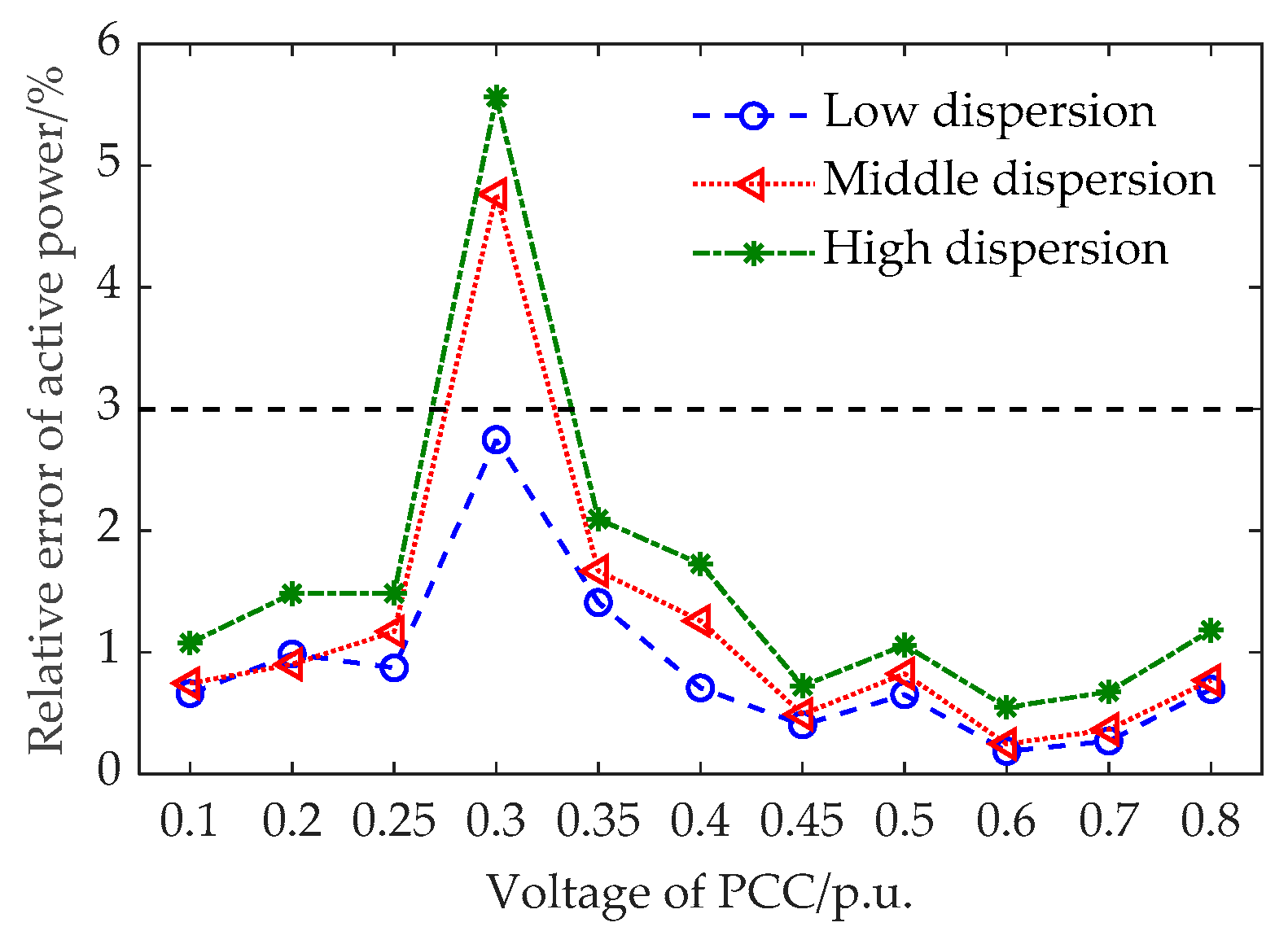
4.1. Error Analysis and Validation of Pfault_avg Approximation
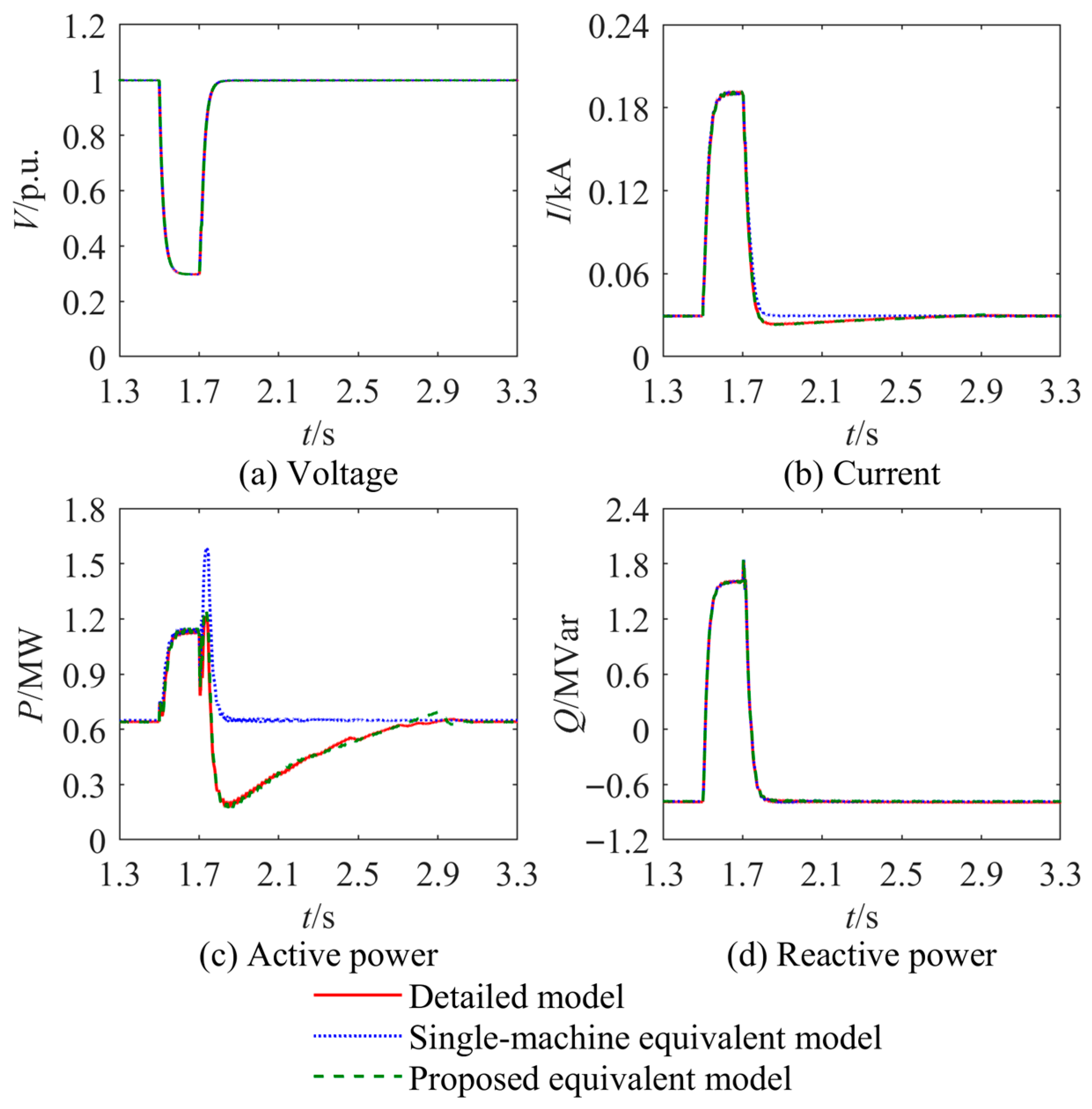
4.2. Effectiveness of Equivalent Modeling Method Under Various Steady-State Operating Conditions
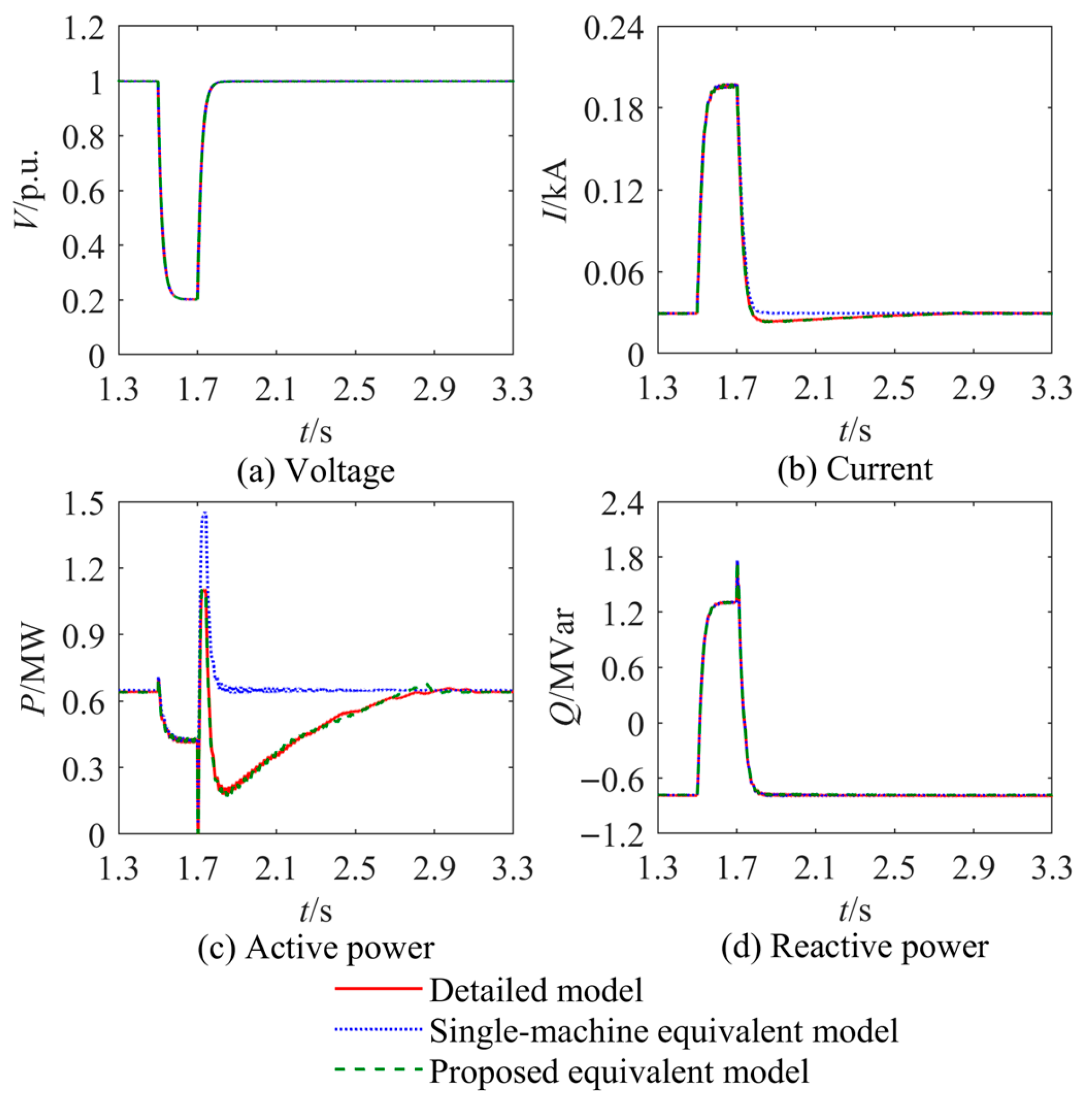
4.3. Effectiveness of Equivalent Modeling Method Under Different Voltage Dip Scenarios
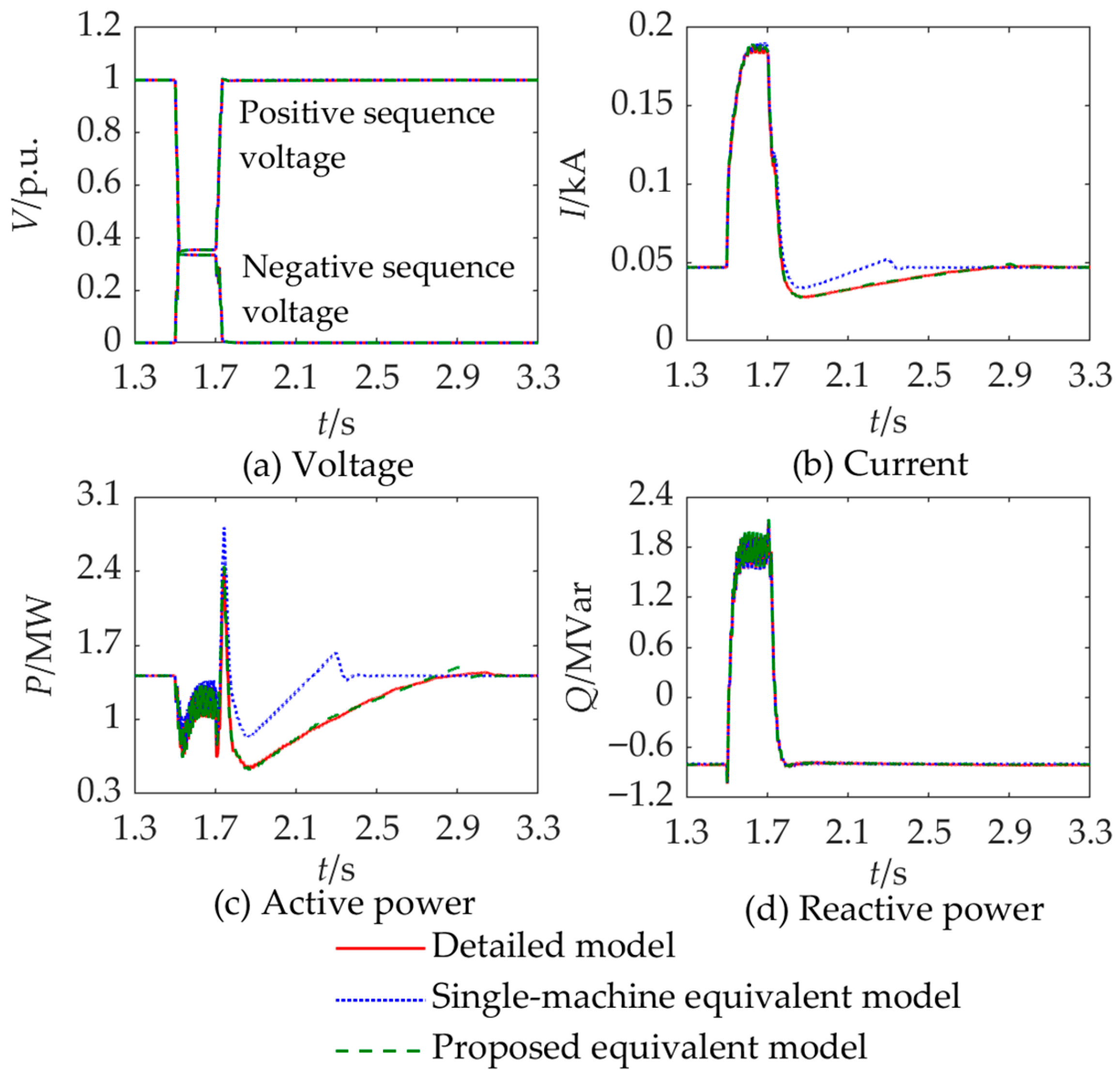
4.4. Effectiveness of Equivalent Modeling Method Under Unbalanced Fault Conditions
4.5. Effectiveness of Equivalent Modeling Method Under Varying Irradiance Conditions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Han, Y.; Zhang, K.; Li, H.; Coelho, E.A.A.; Guerrero, J.M. MAS-based distributed coordinated control and optimization in microgrid and microgrid Clusters: A comprehensive overview. IEEE Trans. Power Electr. 2018, 33, 6488–6508. [Google Scholar] [CrossRef]
- Higashikawa, K.; Ide, A.; Bian, W.; Kiss, T. Development of superconducting cable with energy storage function and evaluation of its functionality in DC microgrid with renewable energy sources. IEEE Trans. Appl. Supercond. 2023, 33, 5400405. [Google Scholar] [CrossRef]
- Badal, F.R.; Das, P.; Sarker, S.K.; Das, S.K. A survey on control issues in renewable energy integration and microgrid. Prot. Control. Mod. Power Syst. 2019, 4, 8. [Google Scholar] [CrossRef]
- Radovanovic, A.; Milanovic, J.V. Equivalent modelling of hybrid RES plant for power system transient stability studies. IEEE Trans. Power Syst. 2022, 37, 847–859. [Google Scholar] [CrossRef]
- Remon, D.; Cantarellas, A.M.; Rodriguez, P. Equivalent model of large-scale synchronous photovoltaic power plants. IEEE Trans. Ind. Appl. 2016, 52, 5029–5040. [Google Scholar] [CrossRef]
- Xie, Y.; He, Y.; Zhou, X.; Zhang, Z. Investigation of the feasibility of the dynamic equivalent model of large photovoltaic power plants in a harmonic resonance study. Electronics 2023, 12, 3746. [Google Scholar] [CrossRef]
- Rahbar, K.; Xu, J.; Zhang, R. Real-time energy storage management for renewable integration in microgrid: An off-line optimization approach. IEEE Trans. Smart Grid. 2015, 6, 124–134. [Google Scholar] [CrossRef]
- Ross, M.; Abbey, C.; Bouffard, F.; Joós, G. Multiobjective optimization dispatch for microgrids with a high penetration of renewable generation. IEEE Trans. Sustain. Energy 2015, 6, 1306–1314. [Google Scholar] [CrossRef]
- Shabanikia, N.; Khajehoddin, S.A. Weighted dynamic aggregation modeling of grid-following inverters to analyze renewable DG integrated microgrids. IEEE Trans. Ind. Electr. 2024, 71, 583–594. [Google Scholar] [CrossRef]
- Radovanovic, A.; Milanovic, J.V. Deep learning-based equivalent modelling of hybrid RES plant for efficient, repetitive power system transient stability studies. IEEE Trans. Power Syst. 2024, 39, 3008–3020. [Google Scholar] [CrossRef]
- Li, H.; Pang, S.; Huang, J. Equivalent modeling and simulation of large photovoltaic station. Appl. Mech. Mater. 2014, 615, 27–30. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, F.; Zhang, L.; Wu, F.; Ma, M.; Zhang, X. Equivalent modeling of distributed photovoltaic power stations based on line impedance clustering. Acta Energiae Sol. Sin. 2022, 43, 312–318. [Google Scholar]
- Wang, J.; Wang, F.; Zhu, J.; Zhou, J. A multi-machine equivalent modeling method of T-connected inverter-interfaced distributed generation suitable for protection setting calculation of distribution network. In Proceedings of the 2024 the 7th International Conference on Energy, Electrical and Power Engineering (CEEPE), Yangzhou, China, 26–28 April 2024. [Google Scholar]
- Ma, Z.; Zheng, J.; Zhu, S.; Shen, X.; Wei, L.; Wang, X.; Men, K. Online clustering modeling of large-scale photovoltaic power plants. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015. [Google Scholar]
- Sheng, W.; Ji, Y.; Wu, M.; Liu, H.; Kou, L. Dynamic clustering modeling of regional centralized photovoltaic power plant based on improved fuzzy c-means clustering algorithm. Power Syst. Technol. 2017, 41, 3284–3291. [Google Scholar]
- Cui, X.; Li, W.; Li, Z.; Fang, Y.; Xue, Y.; Xue, F. An online dynamic equivalent method for large-scale photovoltaic power plant suitable for electromechanical transient stability simulation. Autom. Electr. Power Syst. 2015, 39, 21–26. [Google Scholar]
- Zheng, J.; Ma, Z.; Wang, Z.; Wang, X.; Zhu, S.; Wei, L. Feature distance based online cluster modeling of LVRT controlled PV power plants. Electr. Power Syst. Res. 2018, 154, 223–233. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, J.; Luo, C.; Xu, B. Equivalent modeling of photovoltaic power station based on canopy-FCM clustering algorithm. IEEE Access 2019, 7, 102911–102920. [Google Scholar] [CrossRef]
- Li, F.; Huang, Y.; Wu, F.; Liu, Y.; Zhang, X. Research on clustering equivalent modeling of large-scale photovoltaic power plants. Chin. J. Electr. Eng. 2018, 4, 80–85. [Google Scholar] [CrossRef]
- Ding, M.; Liu, X.; Bi, R.; Hu, D.; Ye, B.; Zhang, J. Method for cluster partition of high-penetration distributed generators based on comprehensive performance index. Autom. Electr. Power Syst. 2018, 42, 47–52+141. [Google Scholar]
- Ye, L.; Shi, Y.; Wang, Q.; Peng, Y.; Pei, M. Multi-step grouping and equivalent modeling of distributed photovoltaic clusters for transient analysis. Autom. Electr. Power Syst. 2023, 47, 72–81. [Google Scholar]
- Li, P.; Gu, W.; Wang, L.; Xu, B.; Wu, M.; Shen, W. Dynamic equivalent modeling of two-staged photovoltaic power station clusters based on dynamic affinity propagation clustering algorithm. Int. J. Electr. Power Energy Syst. 2018, 95, 463–475. [Google Scholar] [CrossRef]
- Wu, H.; Liu, Z.; Chen, Y.; Xu, B.; Qi, X. Equivalent modeling method for regional decentralized photovoltaic clusters based on cluster analysis. CPSS Trans. Power Electr. Appl. 2018, 3, 146–153. [Google Scholar] [CrossRef]
- Pan, X.; Wang, W.; Huang, H.; Liang, W.; Chen, H.; Yong, C. Equivalent modeling of PV station groups considering dynamic interaction between PV and power grid. Electr. Power Autom. Equip. 2023, 43, 80–85+109. [Google Scholar]
- Li, J.; He, G.; Sun, G.; Wang, Y.; Li, J. Clustering analysis method for large-scale photovoltaic with LVRT characteristics. Proc. CSU-EPSA 2023, 35, 1–8. [Google Scholar]
- Han, P.; Lin, Z.; Zhang, J.; Xia, Y.; Wang, L. Equivalent modeling of photovoltaic power plant based on factor analysis and correlation clustering. IEEE Access 2019, 7, 56935–56946. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, X.; Shi, X.; Wang, Z.; Lin, L. Equivalent modeling of distributed photovoltaic clusters with various voltage support functions. In Proceedings of the 2024 IEEE 10th International Power Electronics and Motion Control Conference (IPEMC2024-ECCE Asia), Chengdu, China, 17–20 May 2024. [Google Scholar]
- Meng, H.; Ye, X.; Yang, M.; Song, X.; Su, Z.; Liu, W.; Luo, L.; Zhao, H. Equivalent modeling and simulation for PV system on dynamic clustering equivalent strategy. In Proceedings of the IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017. [Google Scholar]
- Fan, S. Investigation on Equivalent Modeling of Photovoltaic Power Plants. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2016. [Google Scholar]
- Kim, S.-K.; Kim, E.-S. PSCAD/EMTDC-based modeling and analysis of a gearless variable speed wind turbine. IEEE Trans. Energy Convers. 2007, 22, 421–430. [Google Scholar] [CrossRef]
- Han, P.; Lin, Z.; Wang, L.; Fan, G.; Zhang, X. A survey on equivalence modeling for large-scale photovoltaic power plants. Energies 2018, 11, 1463. [Google Scholar] [CrossRef]
- Zhu, Q. Research on Equivalent Modeling of Wind Power Plants for Electromechnical Transients in Power Systems. Doctoral Thesis, Hefei University of Technology, Hefei, China, 2017. [Google Scholar]
- Qi, J.; Li, W.; Chao, P.; Liang, X.; Sun, Y.; Li, Z. Generic EMT modeling method of Type-4 wind turbine generators based on detailed FRT studies. Renew. Energy 2021, 178, 1129–1143. [Google Scholar] [CrossRef]















| Equivalent Method | Reference | Input Variables Required | Cluster Number | Computational Cost | Reported Errors |
|---|---|---|---|---|---|
| Clustering algorithm based method | [12] | Line impedance from PV unit to the PCC | 5 | Middle | Below 2% |
| [14,15,16,17] | PI parameters of inverter controllers | 3~4 | Middle | No reported | |
| [18] | Filter inductance and PI parameters of inverter controllers | 3 | Middle | Below 2% | |
| [19] | Irradiation intensity, temperature, and active power | 3 | Middle | Below 1% | |
| [20] | Electrical distance, active power, and reactive power | 8 | Middle | No reported | |
| [21] | Electrical distance, irradiation intensity, and inverter control parameters | 4 | Middle | No reported | |
| [22] | Waveforms of voltage, current, active power, and reactive power in a period of time | 3 | High | Below 5% | |
| [23] | Feature points extracted from the power response curve | No fixed | Middle | Below 1% | |
| [24] | PV unit’s voltage during fault period | 3 | Middle | No reported | |
| [25] | PV unit’s voltage during fault period and network structure of system | 3~4 | High | No reported | |
| [26] | Pre-fault and fault period data (active power, reactive power, active current, and reactive current) | 4 | Middle | Below 1% | |
| [27] | Reactive power before and after the transient are used for clustering | 3 | Middle | No reported | |
| Threshold-based method | [28] | Pre-fault active power of PV units | 3 | Low | Below 4% |
| [29] | Pre-fault active power of PV units | 3 | Low | Below 5% | |
| Proposed method | Pre-fault active power of PV units | 4 | Low | Below 3% (Error in Section 4) |
| Parameters | Values |
|---|---|
| Rated capacity of a distributed PV unit | 0.32 MW |
| Rated voltage of a distributed PV unit | 0.8 kV |
| DC link voltage | 1.5 kV |
| DC link capacitance | 6000 µF |
| Filter resistance | 0.003 Ω |
| Filter reactance | 0.0001 H |
| Transformer LV/HV ratio | 0.8/20 kV |
| Case | Clusters | Number of PV Units | Pre-Fault Steady-State Active Power of Equivalent Machine |
|---|---|---|---|
| Case 1 | Cluster 1 | 2, 3, 5 | 0.224 MW |
| Cluster 2 | 1, 4, 8 | 0.419 MW | |
| Cluster 3 | 6, 11, 12, 15, 18, 19 | 1.178 MW | |
| Cluster 4 | 7, 9, 10, 13, 14, 16, 17, 20 | 2.010 MW | |
| Case 2 | Cluster 1 | 1, 2, 3, 4, 5, 8, 12 | 0.566 MW |
| Cluster 2 | 6, 11, 15, 18, 19 | 0.710 MW | |
| Cluster 3 | 7, 9, 10, 17 | 0.768 MW | |
| Cluster 4 | 13, 14, 16, 20 | 0.986 MW |
| Case | Voltage Dip | Error of Single-Machine Equivalent Model | Error of Proposed Equivalent Model |
|---|---|---|---|
| Case 1 | 0.3 p.u. | 18.77% | 1.68% |
| Case 2 | 0.3 p.u. | 27.45% | 2.22% |
| Model | Computational Time |
|---|---|
| Detailed model of distributed PV generation system | 852 s |
| Single-machine equivalent model | 12 s |
| Proposed equivalent model | 46 s |
| Case | Voltage Dip | Error of Single-Machine Equivalent Model | Error of Proposed Equivalent Model |
|---|---|---|---|
| Case 1 | 0.2 p.u. | 20.72% | 1.62% |
| Case 2 | 0.2 p.u. | 29.11% | 1.95% |
| Case 1 | 0.4 p.u. | 18.74% | 1.71% |
| Case 2 | 0.4 p.u. | 25.26% | 2.49% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, J.; Guo, Q.; Zhu, Y.; Yu, Y.; Tu, L.; Luo, C.; Sun, C.; Tang, Y.; Liu, Y. Dynamic Equivalent Modeling of Distributed Photovoltaic Generation Systems in Microgrid Considering LVRT Active Power Response Difference. Electronics 2025, 14, 4355. https://doi.org/10.3390/electronics14224355
Qi J, Guo Q, Zhu Y, Yu Y, Tu L, Luo C, Sun C, Tang Y, Liu Y. Dynamic Equivalent Modeling of Distributed Photovoltaic Generation Systems in Microgrid Considering LVRT Active Power Response Difference. Electronics. 2025; 14(22):4355. https://doi.org/10.3390/electronics14224355
Chicago/Turabian StyleQi, Jinling, Qi Guo, Yihua Zhu, Yanxue Yu, Liang Tu, Chao Luo, Chu Sun, Yujia Tang, and Yuyan Liu. 2025. "Dynamic Equivalent Modeling of Distributed Photovoltaic Generation Systems in Microgrid Considering LVRT Active Power Response Difference" Electronics 14, no. 22: 4355. https://doi.org/10.3390/electronics14224355
APA StyleQi, J., Guo, Q., Zhu, Y., Yu, Y., Tu, L., Luo, C., Sun, C., Tang, Y., & Liu, Y. (2025). Dynamic Equivalent Modeling of Distributed Photovoltaic Generation Systems in Microgrid Considering LVRT Active Power Response Difference. Electronics, 14(22), 4355. https://doi.org/10.3390/electronics14224355





