Abstract
Ultra-reliable low-latency communication (URLLC) presents significant challenges in simultaneously guaranteeing stringent latency bounds, ultra-high reliability, and efficient resource utilization under dynamic channel conditions. To address these joint constraints, a novel framework that integrates a reconfigurable intelligent surface (RIS) with cooperative non-orthogonal multiple access (NOMA) is proposed for short-packet communications. Two distinct phase configuration designs for the RIS are considered, i.e., a near-user priority strategy (NUPS) and a far-user priority strategy (FUPS). The NUPS configures the RIS to enhance the received signal power for the near user, while the FUPS optimizes the phase shifts to maximize the received power for the far user. Closed-form expressions that characterize the average block error rate (BLER) of the near and far users under the two proposed strategies in the presence of hardware impairments are derived. Specifically, the analysis for the far user considers both selection combining (SC) and maximum ratio combining (MRC) reception schemes. Based on the average BLER, we then derive a closed-form expression for the effective throughput. Simulation findings reveal the following: (1) The far user in the proposed cooperative NOMA achieves a lower average BLER than in the non-cooperative NOMA. (2) When the RIS is deployed in close proximity to the base station (BS), the NUPS can effectively leverage the RIS to enhance the far user’s signal quality through cooperation, without sacrificing the near user’s priority; and (3) SC serves as a low-complexity alternative that achieves near-optimal performance when inter-user channel conditions are favorable.
1. Introduction
The passive reconfigurable intelligent surface (RIS) has recently garnered significant interest in wireless communications due to its potential to provide high data-rate services for next-generation networks in a remarkably cost- and energy-efficient manner [1,2,3]. Such a passive RIS is a planar structure comprising a large number of passive reflective elements. As a passive device, it operates without power-intensive radio frequency chains. To intelligently reshape the wireless propagation environment, the channel information is first estimated. This information is then converted into control signals for the phase shifts of the RIS, which configures the bias voltages of its tunable elements (e.g., varactor diodes or positive intrinsic negative (PIN) diodes). By smartly adjusting the phase shifts of all its passive elements, the signals reflected from the RIS can coherently combine at the intended receiver, thereby enhancing communication reliability even in challenging channel conditions [4]. The passive nature of its signal reflection enables flexible deployment on facades or indoor walls, as it does not require a power supply to amplify signals. Although a power supply is needed for the control circuit to reconfigure its elements (e.g., using a microcontroller), the overall power consumption remains exceptionally low. This makes it an energy-saving and cost-effective solution that aligns with green communication objectives. Moreover, the integration of the RIS into current network infrastructures is greatly facilitated, as it requires minimal to no hardware modifications to existing base stations (BSs), access points, or end-user devices [5,6].
Due to superior spectral efficiency and massive connectivity capabilities, non-orthogonal multiple access (NOMA) has also attracted significant attention as a pivotal technique for future wireless networks [7,8,9]. To enhance the performance of NOMA networks further, a promising development known as cooperative NOMA was introduced by Ding et al. [10]. The fundamental concept behind cooperative NOMA is that users with stronger channel conditions act as relays to assist the transmission to those with poorer channels. In cooperative NOMA networks, a supplementary cooperative transmission link provides spatial diversity alongside the direct link to help combat signal fading and increase the overall coverage area [11]. This improved reliability significantly boosts the communication performance for the weak users. Consequently, cooperative NOMA enhances the fairness of NOMA transmissions, especially in scenarios where the weak user is located at the cell edge [12].
However, the performance of cooperative NOMA is still limited by the uncontrollable wireless propagation environment. To address this, the integration of a RIS offers a promising solution [13]. By optimizing the RIS’s reflection coefficients, the channel quality for both the direct and cooperative links can be proactively enhanced. This capability introduces new degrees-of-freedom in the system design, enabling RIS-aided cooperative NOMA networks to achieve superior performance. In particular, Zuo et al. [12] introduced an alternating optimization framework for RIS-assisted cooperative NOMA networks to achieve minimal total transmit power. This method jointly optimizes the active beamforming vectors, power allocated for relaying, and phase shifts of the RIS elements. Building on the work in [12], Elhattab et al. [14] extended it to full-duplex (FD) cooperative NOMA networks. When the cooperation between the strong user and weak user was conducted through a device-to-device (D2D) channel, Gu et al. [15] demonstrated that various degrees of diversity gain are achievable in the proposed cooperative RIS-NOMA network by adjusting the number of RIS elements. Zhang et al. [16] explored the use of simultaneous wireless information and power transfer (SWIPT) in RIS-assisted cooperative NOMA networks and derived closed-form expressions for the outage probability. The joint optimization of beamforming coefficients, power splitting factors, and reflection coefficients was addressed by Ren et al. [17] to maximize the achievable rate for the strong user under a strict quality of service requirement for the weak user. In [18], Muhammad et al. proved that combining RIS with cooperative NOMA significantly reduces information age by optimizing power control and RIS phase shifts. Simultaneously transmitting and reflecting RIS (STAR-RIS) was subsequently incorporated into the framework of cooperative NOMA by Toregozhin et al. [19] to improve spectral and energy efficiency.
The rise of the Internet of Things (IoT) and mission-critical control is driving a critical shift in wireless communication paradigms [20,21]. In contrast to traditional scenarios focused on high throughput, these emerging applications rely on frequent short-packet exchanges [22]. This shift necessitates a fundamental re-evaluation of communication theories, as the classical Shannon capacity theorem becomes inadequate and even misleading for characterizing performance in this regime. Shannon’s theory, which provides the fundamental limits of reliable communication, is an asymptotic result that assumes infinitely long codewords. In the short-packet regime, however, finite blocklength and stringent reliability constraints introduce a significant penalty in coding rate [23]. Therefore, new metrics and analytical frameworks are essential. A key performance measure that has emerged is the maximum achievable coding rate at a finite blocklength and a given decoding error probability [24]. Then, a derivation of the average block error rate (BLER) was presented by Vu et al. [25] for RIS-assisted short-packet NOMA networks, demonstrating significant performance gains over orthogonal multiple access (OMA). The interplay between optimal power allocation and minimum common blocklength was investigated by Yuan et al. [26]. To maximize the overall device throughput, Lou et al. [27] constructed an optimization problem to jointly design the blocklength and phase shifts of RIS. Wang et al. [28] addressed the multi-objective problem of joint throughput maximization and blocklength minimization by converting it into a tractable single-objective problem using the Chebyshev method. Given a certain probability of failure for the reflecting elements, Yang et al. [29] derived asymptotic closed-form expressions for the average BLER of NOMA users.
Notably, a key limitation of the approaches proposed in [25,26,27,28,29] is the assumption of ideal transceiver nodes. This assumption does not hold in practice, as all practical nodes are subject to hardware impairments, such as imperfect radio frequency components and phase noise. Lioce et al. [30] revealed the impact of circuit non-idealities on RIS system-level performance. Specifically, Xia et al. [31] examined the average BLER performance of a RIS-assisted NOMA downlink network with short-packet communications, taking into account transceiver hardware impairments. Ren et al. [32] considered the simultaneous presence of both direct and RIS-reflected links from a BS to a pair of NOMA users and accounted for the effects of hardware impairments. In wireless-powered RIS-assisted cognitive NOMA networks, Kumar et al. [33] analyzed the latency and reliability performance under hardware impairments. Imperfect SIC was considered by Ma et al. [34] for RIS-aided short-packet NOMA networks with hardware impairments. The average BLER of active STAR-RIS-assisted NOMA networks with hardware impairments for the short-packet regime was derived by Kumar et al. [35]. The studies in [31,32,33,34,35] focused on conventional NOMA protocols, in which users decode their signals directly from the superimposed transmission. Although NOMA efficiently serves multiple users simultaneously, the weak user often experiences poor channel conditions, which severely limits its data rate and reliability. This problem becomes particularly critical in short-packet communications for ultra-reliable and low-latency communication (URLLC), where the coding gains of traditional infinite blocklength are absent. Consequently, using NOMA without cooperative assistance often fails to meet the ultra-reliability requirements of critical applications. A theoretical analysis was performed by Zheng et al. [36] for cooperative NOMA networks with RIS assistance under the assumption of ideal hardware. However, cooperative NOMA relies on precise successive interference cancellation (SIC), a process highly sensitive to distortion. Hardware impairments can severely degrade the SIC process, causing error propagation and fundamentally limiting the achievable gain for the weak user. Consequently, there is a critical need to holistically and realistically evaluate the reliability of RIS-assisted cooperative NOMA networks, accounting for the practical constraints imposed by hardware imperfections and short-packet transmission.
Inspired by the above observations, in this work, we investigate reliable transmission in cooperative NOMA networks with RIS assistance over Nakagami-m fading channels. To enhance the transmission reliability of a far user, a cooperative decode-and-forward (DF) strategy is utilized, with a near user acting as an intermediate relay node. Besides, we consider a more practical assumption of imperfect hardware at all nodes, i.e., transceivers at a BS and both users are all subject to hardware impairments. The main contributions of this paper are summarized as follows:
- 1.
- We investigate a downlink cooperative NOMA network that utilizes short-packet communications and is enhanced by a RIS. We examine two distinct RIS phase configuration strategies, i.e., a near-user priority strategy (NUPS) and a far-user priority strategy (FUPS). The NUPS configures the RIS to enhance the received signal power for the near user, while the FUPS optimizes the phase shifts to maximize the received power for the far user.
- 2.
- We quantify the average BLER performance for the near and far users under the two proposed strategies through derived closed-form expressions, which incorporate the effects of hardware impairments. Specifically, the reception at the far user is studied for two diversity techniques, that is, selection combining (SC) and maximum ratio combining (MRC). Based on the average BLER, we provide a closed-form expression for the effective throughput of the system.
- 3.
- The numerical simulations confirm the accuracy of the theoretical analysis and demonstrate that the proposed cooperative NOMA provides a lower average BLER for the far user than the non-cooperative NOMA. In addition, deploying the RIS in proximity to the BS enables the NUPS to cooperatively enhance the far user’s signal quality, without sacrificing the near user’s priority. Moreover, under favorable inter-user channel conditions, SC is a low-complexity alternative that achieves near-optimal performance.
Table 1 summarizes the key distinctions between the contributions of this work and those of existing related studies.

Table 1.
Comparison of this work with related papers.
The remainder of this paper is organized as follows. In Section 2, we detail the system model for the RIS-assisted cooperative NOMA network. In Section 3, we derive the closed-form expressions for the average BLER and effective throughput. Finally, simulation results and concluding remarks are provided in Section 4 and Section 5, respectively.
2. System Model
As shown in Figure 1, we consider a RIS-assisted cooperative NOMA network utilizing short-packet transmission with hardware impairments. The system comprises a single-antenna BS, two single-antenna users, i.e., a near user and a far user , and a RIS with M reflecting elements. Similar to [27,37], we assume that obstacles block the direct links between the BS and both users (), thus necessitating the use of the RIS for reliable transmission. This assumption is based on the negligible impact of the direct links when the number of RIS elements is large [38]. To evaluate the theoretical performance gain and derive meaningful insights regarding the interplay between RIS and cooperative NOMA, we assume that the BS possesses perfect channel state information (CSI) for all communication links. Although achieving perfect CSI is generally challenging, numerous studies have recently introduced effective channel estimation techniques suitable for RIS-assisted wireless networks, which can be incorporated into our system to obtain accurate CSI [39,40]. For example, Wei et al. [39] proposed an alternating least squares method to achieve continuous and low-complexity estimation of all channels. Moreover, compressive sensing and deep learning were used by Taha et al. [40] to develop two new channel estimation schemes for RIS-assisted wireless systems. The data transmission procedure consists of two phases. In the first phase, BS broadcasts a superimposed signal x containing bits for and bits for with power P over blocklength L. Subsequently, serves as a DF relay, processing, and retransmitting signals intended for in the second phase.
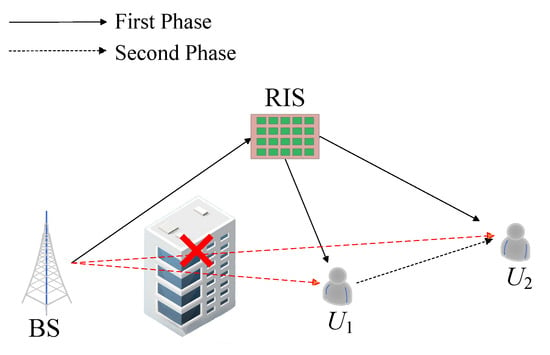
Figure 1.
System Model.
According to NOMA scheme [31], the signal x can be expressed as
where and are the signals intended for and , and and are the power allocation factors for and , respectively. Furthermore, the power allocation factors are constrained by and . Thus, the signals received at and are given by
and
where is the channel vector for the link, and is the channel coefficient from the BS to the l-th reflecting element of the RIS, is the channel vector for the link, and is the channel coefficient from the l-th reflecting element of the RIS to , is the channel vector for the link, and is the channel coefficient from the l-th reflecting element of the RIS to . The diagonal phase shifting matrix of the RIS is denoted by , where is the phase shift applied at the l-th reflecting element of the RIS. In addition, is the transmission distortion at the BS, is the reception distortion at and is the reception distortion at . and are the additive white Gaussian noise (AWGN) at and , respectively. All channels undergo Nakagami-m fading, i.e., , , . Here, , , and denote the corresponding distribution parameters, and , , and represent the corresponding fading means.
According to (2), the instantaneous signal-to-interference-plus-noise ratio (SINR) received to decode at in the first phase is given by
where is the transmit signal-to-noise ratio (SNR). Following the finite blocklength analysis in [24], the instantaneous BLER for decoding at can be formulated as
where , and . After successfully decoding and removing via SIC, then decodes its own signal . Thus, the instantaneous SINR received to decode at in the first phase can be expressed as
Then, the instantaneous BLER at is expressed as
where .
According to (3), the instantaneous SINR received to decode at in the first phase can be given by
During the second phase, the signal is cooperatively sent by to with the transmit power , where . Thus, the received signal at is given by
where is the Nakagami-m fading channel coefficient from to . Here, is the distribution parameter, and is the fading mean. Besides, is the transmission distortion at , is the reception distortion at , and is the AWGN at . Therefore, the instantaneous SINR received to decode at in the second phase is given by
To improve signal detection at , we consider both SC and MRC schemes to combine the received signals during the first and second phases. For the SC scheme, the instantaneous SINR received to decode at is given by
For the MRC scheme, we have
Thus, the instantaneous BLER for decoding at using the SC scheme is expressed as
and the instantaneous BLER for decoding at using the MRC scheme is expressed as
3. Performance Analysis
In this section, we consider the NUPS and FUPS. For the NUPS, the RIS phase shifts are configured to enhance the channel conditions for the near user, i.e., . For the FUPS, the RIS phase shifts are configured to enhance the channel conditions for the far user, i.e., . Then, we conduct a comprehensive performance analysis for the near and far users. To characterize the fundamental performance limits of RIS, we assume that the phase shifts can be adjusted continuously within [0, ), whereas in practical applications they are typically chosen from a discrete set of values ranging from 0 to for simpler hardware implementation. The configuration of RIS utilizing discrete phase shifts will be addressed in future research.
3.1. Preliminaries
According to (4), the cumulative distribution function (CDF) of under the NUPS can be expressed as
where , , , , , and .
Proof.
See Appendix A.
Using a method similar to that described in Appendix A, the CDF of under the NUPS can be expressed as
According to [41], can be approximated by a Rayleigh distribution, i.e., . Then, through straightforward mathematical derivations, the CDF of under the NUPS can be formulated as
Due to the independence between the relay and reflection links, the CDF of is identical for both the FUPS and NUPS. Since the CDF of can be expressed as , thus, the CDF of can be expressed as
Under the FUPS, can be approximated as an exponential distribution with mean . Thus, the CDFs of and under the FUPS can be, respectively, expressed as
and
Based on (8) and following a derivation similar to Appendix A, the CDF of under the FUPS is given by
where , , . □
3.2. Near-User Priority Strategy
The closed-form expression of the average BLER at under the NUPS is given by
where denotes the expectation operator, and are given by
and
with , , , , , , , , , , , , , and N being a parameter for the complexity accuracy tradeoff.
Proof.
See Appendix B.
For the SC scheme, the closed-form expression of the average BLER at under the NUPS is given by
where is expressed as
with , ,
and . □
Proof.
See Appendix C.
Note that directly computing is intractable. Inspired by [42], we can use as an approximation for . Based on (18), following a similar procedure to Appendix B, can be derived as
with , and .
For the MRC scheme, the closed-form expression of the average BLER at under the NUPS is given by
According to the approximation method in [43], can be approximated as . Following a similar procedure to Appendix C, we can express and as
and
with , and . □
3.3. Far-User Priority Strategy
The closed-form expression of the average BLER at under the FUPS is given by
, ,
, and .
For the SC scheme, the closed-form expression of the average BLER at under the FUPS is given by
Similar to the analysis for the NUPS, can be expressed as
and can be approximated as the product of and .
For the MRC scheme, the closed-form expression of the average BLER at under the FUPS is given by
Employing the same method as applied to the NUPS, can be approximated as the product of and , where is given by
with .
3.4. Effective Throughput
Effective throughput is defined as the average number of information bits successfully decoded per channel use. For the RIS-assisted cooperative NOMA network, the effective throughput is expressed as
where , , and represent the information rates of and , and and are the reliabilities of and , respectively. It can be observed that as L increases, the information rate decreases while the user reliability increases. Therefore, there exists an optimal L at which the effective throughput reaches its maximum. However, due to the complexity of the effective throughput expression, an explicit closed-form solution for the optimal blocklength L is difficult to obtain. Nevertheless, a gradient-based search method can be employed to numerically determine the optimal L.
4. Numerical Results
In this section, we present comprehensive simulation results to evaluate the performance of the RIS-assisted cooperative NOMA network. The system’s performance is primarily measured in terms of the average BLER and effective throughput, which are derived from the analytical expressions in the previous sections. Unless otherwise specified, the simulation parameters are given in Table 2. The following figures aim to provide key insights into the interplay between RIS configuration, hardware impairments, and the requirements of finite blocklength. The accuracy of our theoretical analysis is validated by the close alignment between the Monte Carlo simulation results and the analytical curve, as evidenced in these figures. The simulations in this work are conducted using a baseband-equivalent model, which is a common methodology for analyzing the fundamental performance of communication systems independent of a specific carrier frequency. This approach allows us to study the core relationship between SNR and BLER, as it is the most direct and critical measure for assessing reliability in short-packet communications. It is important to note that the choice of a carrier frequency in a practical implementation would directly impact the absolute path loss and fading characteristics. However, in our model, these frequency-dependent propagation effects are implicitly captured by the SNR value at the receiver and the statistical channel model (e.g., Nakagami-m fading) we employ. The presented SNR-BLER curves illustrate the fundamental trade-offs and performance trends. For a specific real-world deployment (e.g., at a sub-6 GHz or millimeter wave frequency bands), the absolute SNR required for a target BLER would be determined by the total link budget, including the frequency-specific path loss, but the relative shape and trends of the curves would remain valid.

Table 2.
List of simulation parameters.
Figure 2 plots the average BLER under the NUPS and FUPS versus . For comparison, the average BLER of the far user in the conventional non-cooperative NOMA network is also provided, denoted as . As increases, the average BLER decreases for the near and far users, which is attributed to the corresponding rise in received SNR. Moreover, the average BLER of the far user under the NUPS and FUPS is lower than that in the conventional non-cooperative NOMA network. In the NUPS, MRC demonstrates a clear performance advantage over SC.
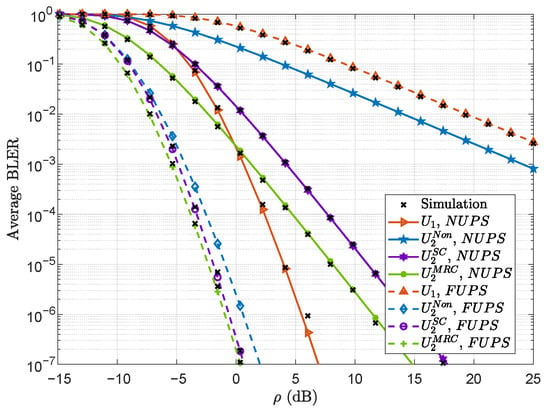
Figure 2.
Average BLER under the NUPS and FUPS versus .
Figure 3 plots the average BLER under the NUPS and FUPS versus M. We first observe that as M increases, the average BLER of both users decreases, indicating that employing more RIS elements can improve transmission reliability. When the NUPS is adopted, the BLER of the nerar user decreases more pronouncedly than that of the far user. In contrast, when the FUPS is adopted, the opposite is true. These results collectively demonstrate that the network can dynamically prioritize and enhance the performance of either the near or far user by strategically allocating the reflective resources of the RIS.
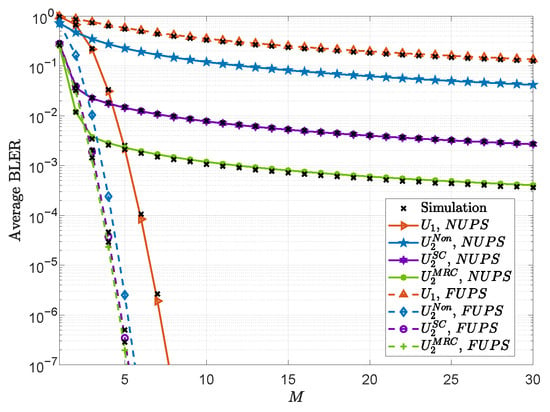
Figure 3.
Average BLER under the NUPS and FUPS versus M.
Figure 4 plots the average BLER under the NUPS and FUPS versus with , and . It can be observed that as increases, the average BLER of the near and far users increases and eventually approaches 1. This inevitable convergence to an error-saturated state is fundamentally due to the distortion noise caused by hardware impairments, which imposes a finite ceiling on the achievable SNR, regardless of the transmit power. In addition, the performance gap between SC and MRC narrows as increases. This indicates that the advantage of sophisticated combining techniques diminishes under severe hardware impairments, as the system performance becomes limited by hardware-induced distortions rather than by the quality of the combined signal. Therefore, in severely impaired hardware environments, simpler techniques like SC can offer a more complexity-effective solution.
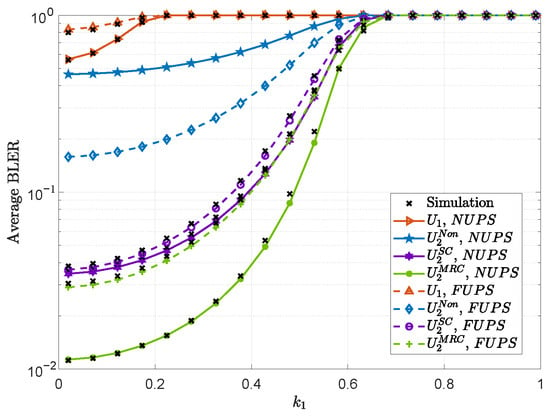
Figure 4.
Average BLER under the NUPS and FUPS versus with , and .
Figure 5 plots the average BLER under the NUPS and FUPS versus . We observe that enhancing the link quality from the BS to the RIS can significantly improve the overall system reliability for all users, which demonstrates the critical role of the RIS in establishing a high-quality communication link. Moreover, it is noteworthy that the near user under the NUPS exhibits a more pronounced performance improvement with increasing compared to the near user under the FUPS. This suggests that when the RIS is deployed in close proximity to the BS, the NUPS can effectively leverage the RIS to enhance the far user’s signal quality through cooperation, without sacrificing the near user’s priority.
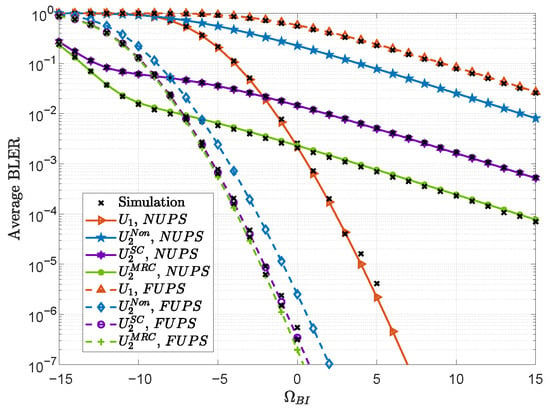
Figure 5.
Average BLER under the NUPS and FUPS versus .
Figure 6 plots the average BLER under the NUPS and FUPS versus with , and . As increases, the average BLER for all cooperative schemes (SC and MRC) under the NUPS and FUPS decreases significantly. This trend confirms that a high-quality inter-user channel is crucial for enabling effective user cooperation, which is a cornerstone of the proposed system’s reliability enhancement. In addition, when is small, the performance of SC for the far user reduces to the conventional non-cooperative NOMA, while it approaches the performance of MRC under large . Therefore, SC demonstrates remarkable adaptability, serving as a low-complexity alternative that achieves near-optimal performance when inter-user channel conditions are favorable.
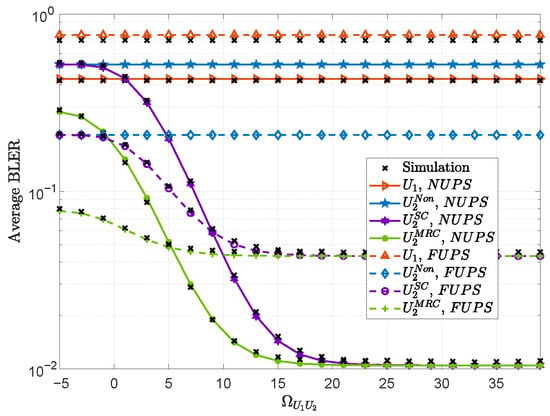
Figure 6.
Average BLER under the NUPS and FUPS versus with , and .
Figure 7 plots the effective throughput under the NUPS and FUPS versus L with . It can be observed that an optimal blocklength exists which maximizes the effective throughput. This phenomenon arises from a fundamental trade-off in the finite blocklength regime. Specifically, shorter packets incur a higher error rate, thereby reducing the effective throughput. Conversely, longer packets introduce greater transmission latency, which can similarly degrade the overall effective throughput performance. In addition, the optimal blocklength for MRC scheme is smaller than that for SC scheme. This finding suggests that MRC is not only more reliable but also inherently better suited for latency-critical applications where shorter packets are required.
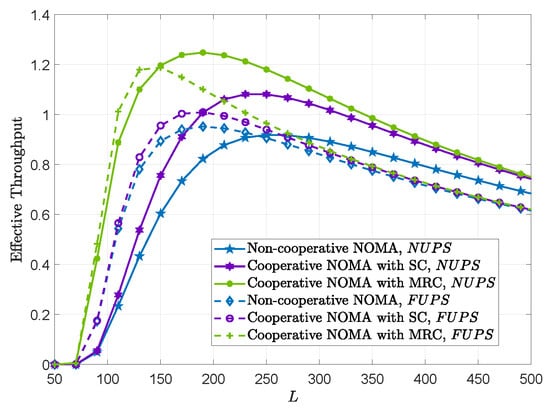
Figure 7.
Effective throughput under the NUPS and FUPS versus L with .
Figure 8 plots the effective throughput under the NUPS and FUPS versus with dB. For all schemes, the effective throughput increases significantly with improving in the low-to-medium range. This is expected, as a stronger BS-to-RIS link enhances the overall transmission reliability. However, when is high, the effective throughput for all schemes begins to saturate, as the system becomes limited by the transmission rates. In addition, cooperative NOMA schemes consistently outperform the non-cooperative NOMA, particularly in the low-to-medium region. This gain is attributed to the diversity advantage offered by cooperation, which mitigates the effects of fading and improves reliability.
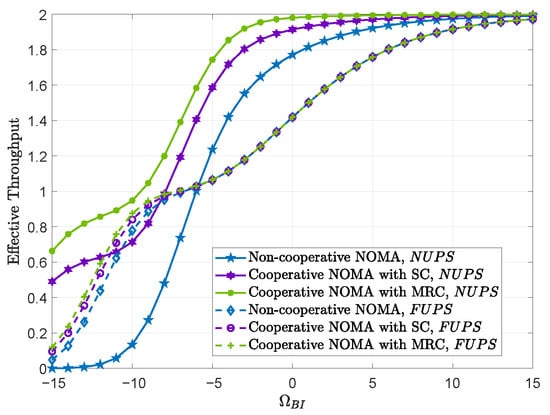
Figure 8.
Effective throughput under the NUPS and FUPS versus with dB.
5. Conclusions
This paper presented an investigation of the RIS-assisted cooperative NOMA network for short-packet communications in the presence of hardware impairments. To characterize the average BLER of the near and far users, closed-form expressions were derived for the NUPS and FUPS. Specifically, the analysis for the far user considered both SC and MRC reception schemes. Simulation results demonstrated that the proposed cooperative NOMA framework achieved a lower average BLER for the far user than the benchmark. In addition, when the RIS was deployed in close proximity to the BS, the NUPS effectively leveraged the RIS to enhance the far user’s signal quality through cooperation without compromising the near user’s priority. Moreover, SC provided a low-complexity alternative that attained near-optimal performance under favorable inter-user channel conditions. Future work can explore the integration of a STAR-RIS, which would enable unified phase-shift protocols for full-space coverage and necessitate a new performance analysis for users in the transmission and reflection regions.
Author Contributions
Formal analysis, W.S., D.C., J.L., X.Z. and Z.W.; writing—original draft preparation, W.S., D.C. and J.L.; writing—review and editing, W.S., D.C., J.L., X.Z. and Z.W.; supervision, D.C., J.L., X.Z. and Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Key Scientific Research Projects of Colleges and Universities in Henan Province of China under Grant 23A520027 and 24A520032, in part by the Philosophy and Social Sciences Research Planning Program of Henan Province under Grant 2024ZZX024, in part by the Natural Science Foundation of Henan under Grant 252300421813, in part by the Young Backbone Teachers of Nanyang Normal University under Grant 2023-QNGG-7, and in part by the Scientific Research Project on the Development of Educational Informatization under Grant 2025KT01005.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
This article is a revised and expanded version of a paper entitled Performance Analysis of RIS-Assisted Cooperative NOMA Systems with Finite Blocklength, which was presented at the Seventeenth International Conference on Wireless Communications and Signal Processing, 2025 [44].
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
In the NUPS, the RIS is configured to maximize the SINR for the near user. Under this configuration, the combined channel gain can be rewritten as . Let , and the first moment and the second moment of can be expressed as
Following [41], is well approximated by a Gamma distribution , where the shape and scale parameters are expressed as
After applying mathematical transformations, the CDF of is given by
and the CDF of is given by (15).
Appendix B
From (7), the average BLER at under the NUPS is given by
where step is based on the fact of characteristically negligible error rates observed in short-packet communications systems [31]. According to (4), can be derived as
where represents an approximation of the instantaneous BLER and represents the probability density function (PDF) of . Then, three specific cases are investigated to determine the closed-form expression of .
Case 1: When , we have .
Case 2: When , can be expressed as
where step derives from applying partial integration and step is calculated through Gaussian-Chebyshev quadrature.
Case 3: When , using a similar analytical method as implemented for Case 2, can be expressed as
Appendix C
According to (8), can be expressed as
Then, we consider three specific cases to derive the closed-form expression for .
Case 1: When , we have .
Case 2: When , can be expressed as
where step is derived from [45], 3.351.4.
Case 3: When , we apply an analytical method similar to that used for Case 2 to express as
The closed-form solution for , which combines the three aforementioned cases, is given in (26).
References
- Liu, Y.; Mu, X.; Liu, X.; Renzo, M.D.; Ding, Z.; Schober, R. Reconfigurable Intelligent Surface-Aided Multi-User Networks: Interplay Between NOMA and RIS. IEEE Wirel. Commun. 2022, 29, 169–176. [Google Scholar] [CrossRef]
- Li, X.; Liu, M.; Dang, S.; Luong, N.C.; Yuen, C.; Nallanathan, A.; Niyato, D. Covert Communications With Enhanced Physical Layer Security in RIS-Assisted Cooperative Networks. IEEE Trans. Wirel. Commun. 2025, 24, 5605–5619. [Google Scholar] [CrossRef]
- Zeng, M.; Hao, W.; Peng, Z.; Chu, Z.; Li, X.; You, C.; Pan, C. Resource Allocation for Ris-Empowered Wireless Communications: Low-Complexity and Robust Designs. IEEE Wirel. Commun. 2024, 31, 68–75. [Google Scholar] [CrossRef]
- Yang, H.; Kim, S.; Kim, H.; Bang, S.; Kim, Y.; Kim, S.; Park, K.; Kwon, D.; Oh, J. Beyond Limitations of 5G with RIS: Field Trial in a Commercial Network, Recent Advances, and Future Directions. IEEE Commun. Mag. 2024, 62, 132–138. [Google Scholar] [CrossRef]
- Li, X.; Zhao, J.; Chen, G.; Hao, W.; Da Costa, D.B.; Nallanathan, A.; Shin, H.; Yuen, C. TAR-RIS Assisted Covert Wireless Communications with Randomly Distributed Blockages. IEEE Trans. Wirel. Commun. 2025, 24, 4690–4705. [Google Scholar] [CrossRef]
- Zhang, Y.; Guan, X.; Wu, Q.; Zhang, R.; Ma, Y.; Miao, C.; Wu, W.; Cai, Y. Minimize Age of Information for IRS-Aided Sensor Systems: How Many IRS Elements Are Needed? IEEE Sens. J. 2025, 25, 14099–14111. [Google Scholar] [CrossRef]
- Li, X.; Wang, Q.; Zeng, M.; Liu, Y.; Dang, S.; Tsiftsis, T.A.; Dobre, O.A. Physical-Layer Authentication for Ambient Backscatter-Aided NOMA Symbiotic Systems. IEEE Trans. Commun. 2023, 71, 2288–2303. [Google Scholar] [CrossRef]
- Zhang, Y.; Guan, X.; Ding, G.; Yang, W.; Yu, B.; Zhang, R.; Wu, W.; Cai, Y. Optimizing Age of Information for IRS-Assisted NOMA-Based Short Packet Communication Systems. IEEE Trans. Cogn. Commun. Netw. 2025. early access. [Google Scholar] [CrossRef]
- Xiang, Z.; Yang, W.; Cai, Y.; Ding, Z.; Song, Y.; Zou, Y. NOMA-Assisted Secure Short-Packet Communications in IoT. IEEE Wireless Commun. 2020, 27, 8–15. [Google Scholar] [CrossRef]
- Ding, Z.; Peng, M.; Poor, H.V. Cooperative Non-Orthogonal Multiple Access in 5G Systems. IEEE Commun. Lett. 2020, 27, 8–15. [Google Scholar] [CrossRef]
- Dinh, P.; Arfaoui, M.A.; Sharafeddine, S.; Assi, C.M.; Ghrayeb, A. A Low-Complexity Framework for Joint User Pairing and Power Control for Cooperative NOMA in 5G and Beyond Cellular Networks. IEEE Trans. Commun. 2020, 68, 6737–6749. [Google Scholar] [CrossRef]
- Zuo, J.; Liu, Y.; Al-Dhahir, N. Reconfigurable Intelligent Surface Assisted Cooperative Non-Orthogonal Multiple Access Systems. IEEE Trans. Commun. 2021, 69, 6750–6764. [Google Scholar] [CrossRef]
- Fu, S.; Wang, Y.; Feng, X.; Di, B.; Li, C. Reconfigurable Intelligent Surface Assisted Non-Orthogonal Multiple Access Network Based on Machine Learning Approaches. IEEE Netw. 2024, 38, 272–279. [Google Scholar] [CrossRef]
- Elhattab, M.; Arfaoui, M.A.; Assi, C.; Ghrayeb, A. Reconfigurable Intelligent Surface Enabled Full-Duplex/Half-Duplex Cooperative Non-Orthogonal Multiple Access. IEEE Trans. Wirel. Commun. 2022, 21, 3349–3364. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, G.; Zhuo, B.; Duan, W.; Wang, J.; Wen, M.; Ho, P.H. On the Performance of Cooperative NOMA Downlink: A RIS-Aided D2D Perspective. IEEE Trans. Cogn. Commun. Netw. 2023, 9, 1610–1624. [Google Scholar] [CrossRef]
- Zhang, G.; Gu, X.; Duan, W.; Wen, M.; Choi, J.; Gao, F.; Ho, P.H. Hybrid Time-Switching and Power-SPlitting Relaying -Ris-Noma Downlink. IEEE Trans. Cogn. Commun. Netw. 2023, 9, 146–158. [Google Scholar] [CrossRef]
- Ren, J.; Lei, X.; Peng, Z.; Tang, X.; Dobre, O.A. RIS-Assisted Cooperative NOMA With SWIPT. IEEE Wirel. Commun. Lett. 2023, 12, 446–450. [Google Scholar] [CrossRef]
- Muhammad, A.; Elhattab, M.; Arfaoui, M.A.; Assi, C. Optimizing Age of Information in RIS-Empowered Uplink Cooperative NOMA Networks. IEEE Trans. Netw. Serv. Manag. 2024, 21, 897–907. [Google Scholar] [CrossRef]
- Toregozhin, T.; Shaikh, M.; Almagambetov, A.; Nauryzbayev, G. Performance of STAR-RIS-aided cooperative NOMA networks under Nakagami-m fading. Ad Hoc Netw. 2024, 156, 103399. [Google Scholar] [CrossRef]
- Zhang, Z.; Lung, C.-H.; Wei, X.; Chen, M.; Chatterjee, S.; Zhang, Z. In-Network Caching for ICN-Based IoT (ICN-IoT): A Comprehensive Survey. IEEE Internet Things J. 2023, 10, 14595–14620. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, M. Deep Learning Empowered Real-Time Haptic Communications for IoT. IEEE Trans. Consum. Electron. 2025, 71, 5606–5618. [Google Scholar] [CrossRef]
- Ma, R.; Yang, W.; Guan, X.; Lu, X.; Song, Y.; Chen, D. Covert mmWave Communications With Finite Blocklength Against Spatially Random Wardens. IEEE Internet Things J. 2024, 11, 3402–3416. [Google Scholar] [CrossRef]
- Shirvanimoghaddam, M.; Mohammadi, M.S.; Abbas, R.; Minja, A.; Yue, C.; Matuz, B.; Han, G.; Lin, Z.; Liu, W.; Li, Y.; et al. Short Block-Length Codes for Ultra-Reliable Low Latency Communications. IEEE Commun. Mag. 2019, 57, 130–137. [Google Scholar] [CrossRef]
- Polyanskiy, Y.; Poor, H.V.; Verdu, S. Channel Coding Rate in the Finite Blocklength Regime. IEEE Trans. Inf. Theory 2010, 56, 2307–2359. [Google Scholar] [CrossRef]
- Vu, T.-H.; Nguyen, T.-V.; Costa, D.B.D.; Kim, S. Intelligent Reflecting Surface-Aided Short-Packet Non-Orthogonal Multiple Access Systems. IEEE Trans. Veh. Technol. 2022, 71, 4500–4505. [Google Scholar] [CrossRef]
- Yuan, L.; Du, Q.; Yang, N.; Fang, F.; Yang, N. Performance Analysis of IRS-Aided Short-Packet NOMA Systems Over Nakagamim Fading Channels. IEEE Trans. Veh. Technol. 2023, 72, 8228–8233. [Google Scholar] [CrossRef]
- Lou, Y.; Zou, Y.; Wang, H.; Zhai, L.; Li, Y. Joint Phase Shifts and Blocklength Resources Optimization in RIS-Assisted NOMA Short-Packet Systems. IEEE Trans. Veh. Technol. 2024, 73, 12132–12136. [Google Scholar] [CrossRef]
- Wang, H.; Fu, Y.; Shi, Z.; Feng, Y. Joint Throughput and Blocklength Optimization for RIS-Aided Hybrid Multi-Access Short-Packet System. IEEE Wirel. Commun. Lett. 2024, 13, 2787–2791. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, L.; Ding, J.; Ding, Z. Performance Analysis of Short-Packet NOMA Systems Assisted by IRS With Failed Elements. IEEE Trans. Veh. Technol. 2024, 73, 5959–5964. [Google Scholar] [CrossRef]
- Lioce, S.; Avitabile, G.; Florio, A.; Saucez, D.; Dabbous, W. The Impact of the Circuit Non-Idealities on the System-Level Communication Metrics in Reconfigurable Intelligent Surfaces. In Proceedings of the 2025 IEEE 16th Latin America Symposium on Circuits and Systems (LASCAS), Sao Paulo, Brazil, 25–28 February 2025. [Google Scholar]
- Xia, C.; Xiang, Z.; Su, B.; Liu, H.; Meng, J.; Pan, G. RIS-NOMA-Assisted Short-Packet Communication With Hardware Impairments. IEEE Internet Things J. 2024, 11, 2990–3002. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, J.; Zhang, X.; Lv, T.; Lin, S.; Lu, G. RIS Assisted Short-Packet NOMA Systems with Discrete Phase Shifts and Hardware Impairments. IEEE Internet Things J. 2025. early access. [Google Scholar] [CrossRef]
- Kumar, S.; Kumbhani, B. Wireless-Powered Reconfigurable-Intelligent-Surface-Aided Cognitive NOMA Network With Hardware Impairments: IBL and FBL Analysis. IEEE Internet Things J. 2025, 12, 17473–17486. [Google Scholar] [CrossRef]
- Ma, R.; Li, Y.; Deng, H.; Zhang, J. Performance of RIS-Aided Short-Packet NOMA Networks with Hardware Impairments and Imperfect SIC. In Proceedings of the 2024 7th International Conference on Information Communication and Signal Processing (ICICSP), Zhoushan, China, 21–23 September 2024; pp. 253–258. [Google Scholar]
- Kumar, S.; Kumbhani, B. Performance Analysis of Active STAR-RIS-assisted NOMA with Hardware Impairments at Finite Blocklength. Digit. Signal Process. 2025, 163, 105206. [Google Scholar] [CrossRef]
- Zheng, J.; Wu, T.; Yao, J.; Yuen, C.; Ding, Z.; Adachi, F. Exploring the Impact of RIS on Cooperative NOMA URLLC Systems: A Theoretical Perspective. IEEE Trans. Wirel. Commun. 2025, in press. [Google Scholar] [CrossRef]
- Yue, X.; Song, M.; Ouyang, C.; Liu, Y.; Li, T.; Hou, T. Exploiting Active RIS in NOMA Networks With Hardware Impairments. IEEE Trans. Veh. Technol. 2024, 73, 8207–8221. [Google Scholar] [CrossRef]
- Björnson, E.; Sanguinetti, L. Rayleigh fading modeling and channel hardening for reconfigurable intelligent surfaces. IEEE Wirel. Commun. Lett. 2021, 10, 830–834. [Google Scholar] [CrossRef]
- Wei, L.; Huang, C.; Alexandropoulos, G.C.; Yuen, C.; Zhang, Z.; Debbah, M. Channel estimation for RIS-empowered multi-user MISO wireless communications. IEEE Trans. Commun. 2021, 69, 4144–4157. [Google Scholar] [CrossRef]
- Taha, A.; Alrabeiah, M.; Alkhateeb, A. Enabling large intelligent surfaces with compressive sensing and deep learning. IEEE Access 2021, 9, 44304–44321. [Google Scholar] [CrossRef]
- Tahir, B.; Schwarz, S.; Rupp, M. Analysis of Uplink IRS-Assisted NOMA Under Nakagami-m Fading via Moments Matching. IEEE Wirel. Commun. Lett. 2021, 10, 624–628. [Google Scholar] [CrossRef]
- Lai, X.; Zhang, Q.; Qin, J. Cooperative NOMA Short-Packet Communications in Flat Rayleigh Fading Channels. IEEE Trans. Veh. Technol. 2019, 68, 6182–6186. [Google Scholar] [CrossRef]
- Vu, T.-H.; Nguyen, T.-V.; Nguyen, T.-T.; Bao, V.N.Q.; Kim, S. Short-Packet Communications in NOMA-CDRT IoT Networks With Cochannel Interference and Imperfect SIC. IEEE Trans. Veh. Technol. 2022, 71, 5552–5557. [Google Scholar] [CrossRef]
- Song, W.; Chen, D.; Li, J.; Zhang, X.; Wang, Z. Performance Analysis of RIS-Assisted Cooperative NOMA Systems with Finite Blocklength. In Proceedings of the 2025 International Conference on Wireless Communications and Signal Processing, Chongqing, China, 23–25 October 2025. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals Series, and Products; Zwillinger, D., Ed.; Elsevier: New York, NY, USA, 2014. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).