Batch Cyclic Posterior Selection Particle Filter and Its Application in TRN
Abstract
1. Introduction
1.1. Motivation
- ➢
- It first generates one-step transition particles based on the particles representing the posterior distribution at the previous time step using the deterministic part of the state transition function.
- ➢
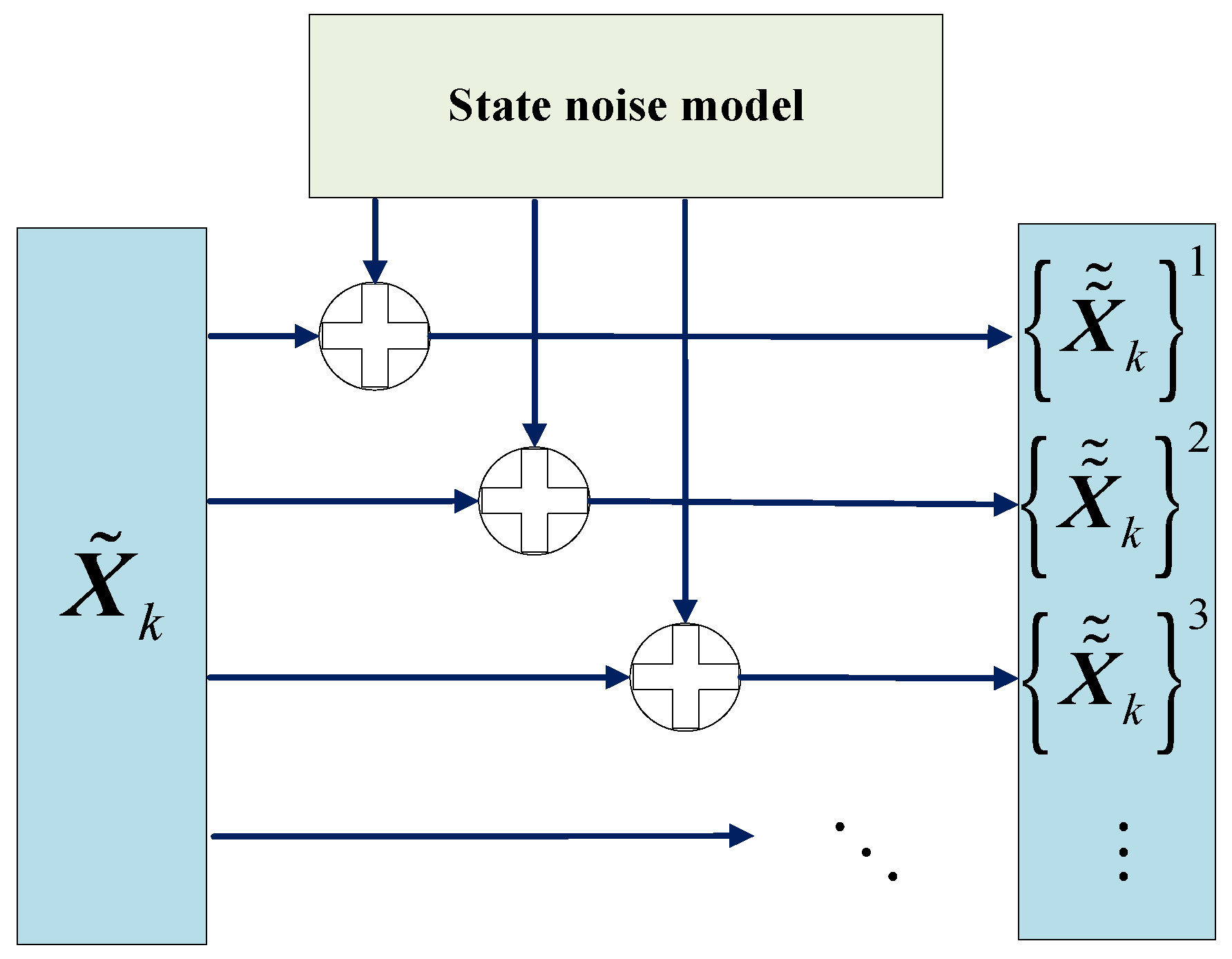
- Subsequently, it adds a noise sequence generated from the state noise model to each one-step transition particle in a cyclic manner, thus continuously generating a large batch of proposed particles that correctly conform to the prior distribution.
- ➢
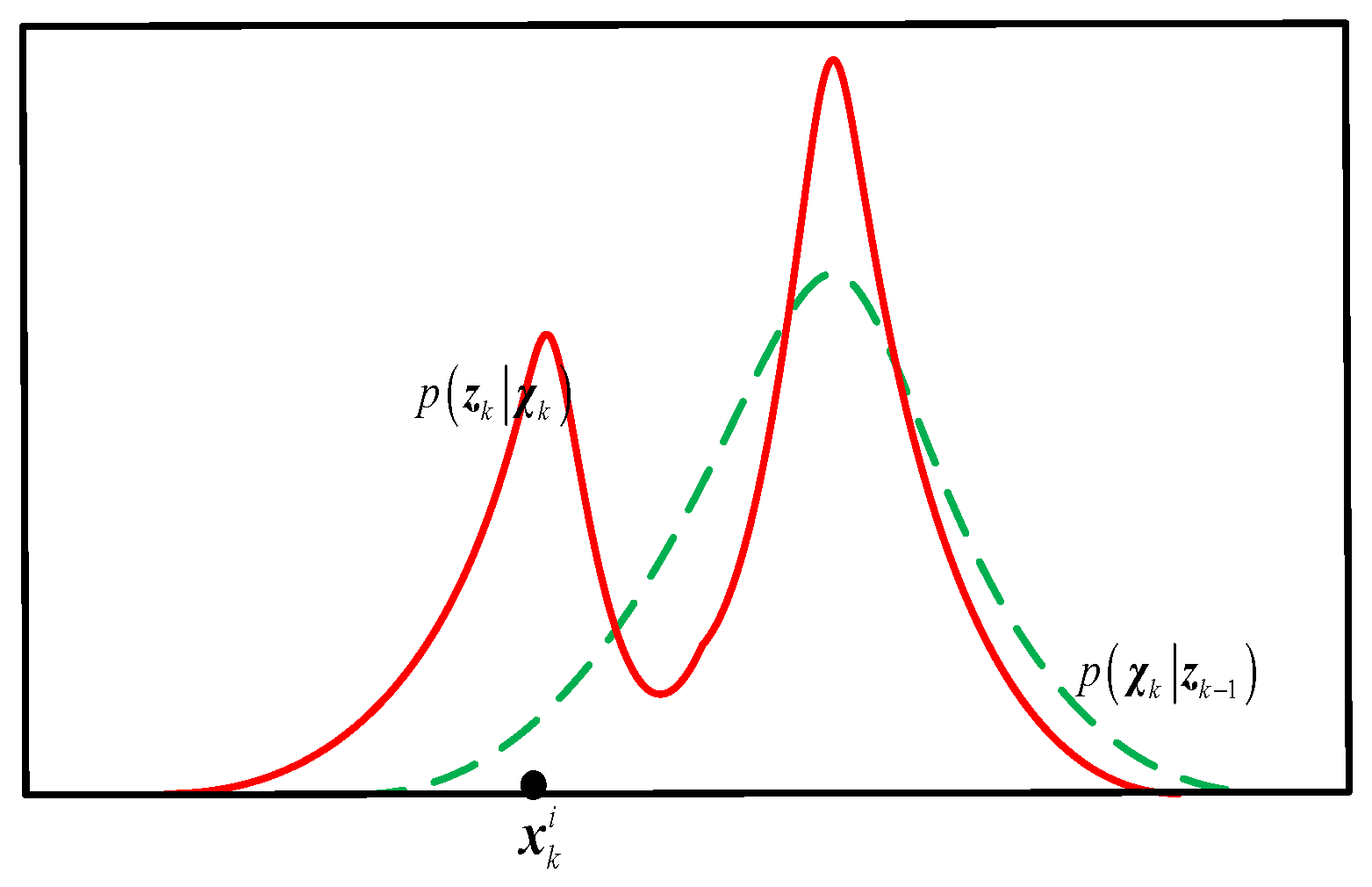
- It first matches the batch cycle particles with the digital elevation map (DEM) and calculates the likelihood weights by combining the observation and observation noise model.
- ➢
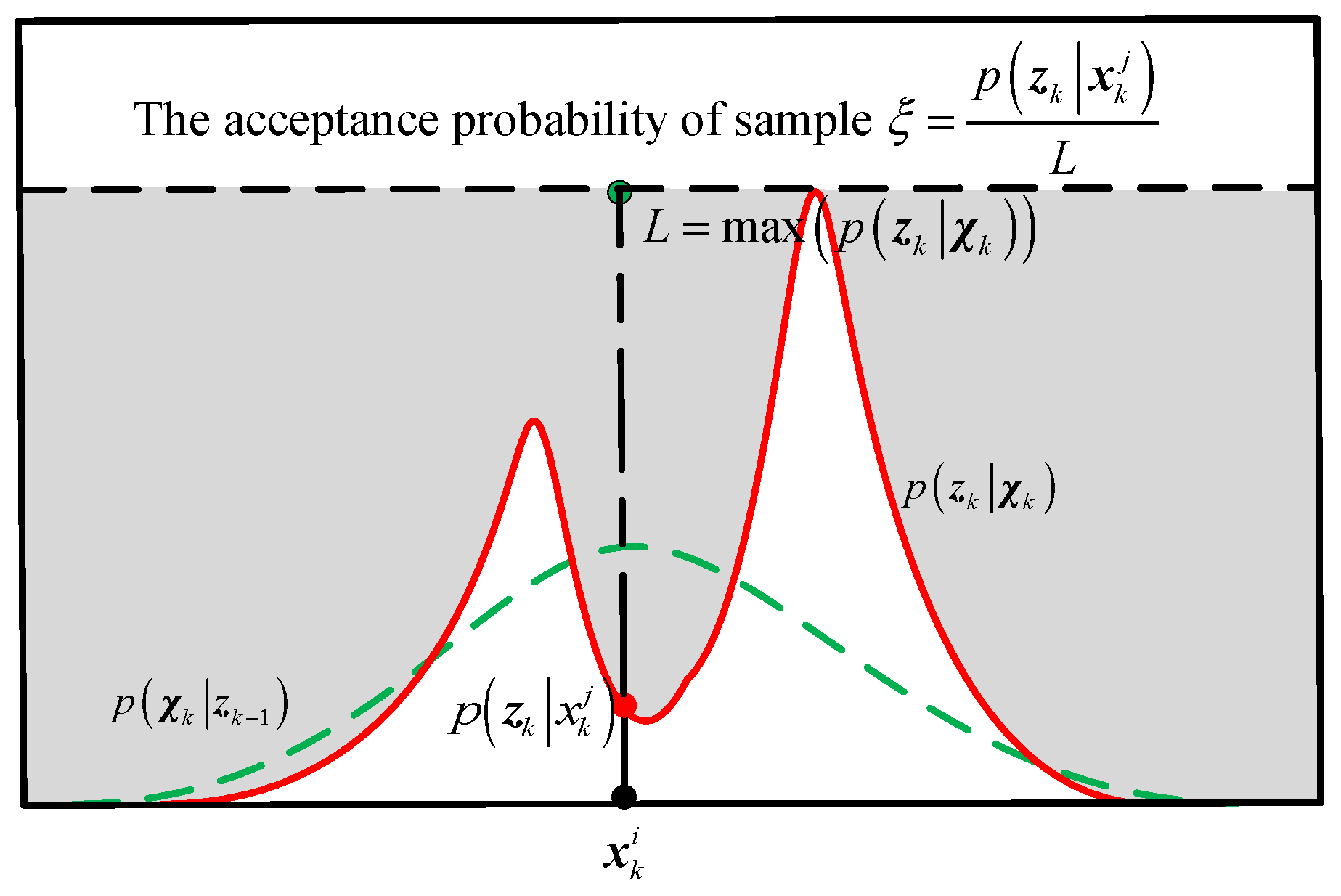
- Then, it performs acceptance/rejection sampling on the batch cycle particles based on the magnitude of the likelihood weights. This selection mechanism effectively completes the fusion of prior and likelihood information and obtains a new particle set that statistically conforms to the posterior distribution.
1.2. Related Works
1.3. Our Contributions
- (1)
- Developing a mechanism to generate batch cycle particles that form cyclic continuous batches conforming to the prior distribution. This involves decomposing the state model into a state transition function and a state noise model. The state transition function transfers particles, while the state noise model ensures particle diversity, resulting in batch cycle particles that describe the prior distribution.
- (2)
- Designing a particle selection mechanism that integrates the update step in the fusion process with the RS technique, obtaining selected particles that conform to the posterior distribution.
- (3)
- Proposing the BCPS-PF algorithm, which indirectly uses the posterior distribution as the proposal distribution, avoiding the need for resampling and recursive weight transmission, thus effectively balancing degeneracy and impoverishment problems, ensuring filter accuracy and stability.
- (4)
- Evaluating the algorithm in inertial measurement units (IMUs) with TRN fusion positioning scenarios, demonstrating significant performance improvements.
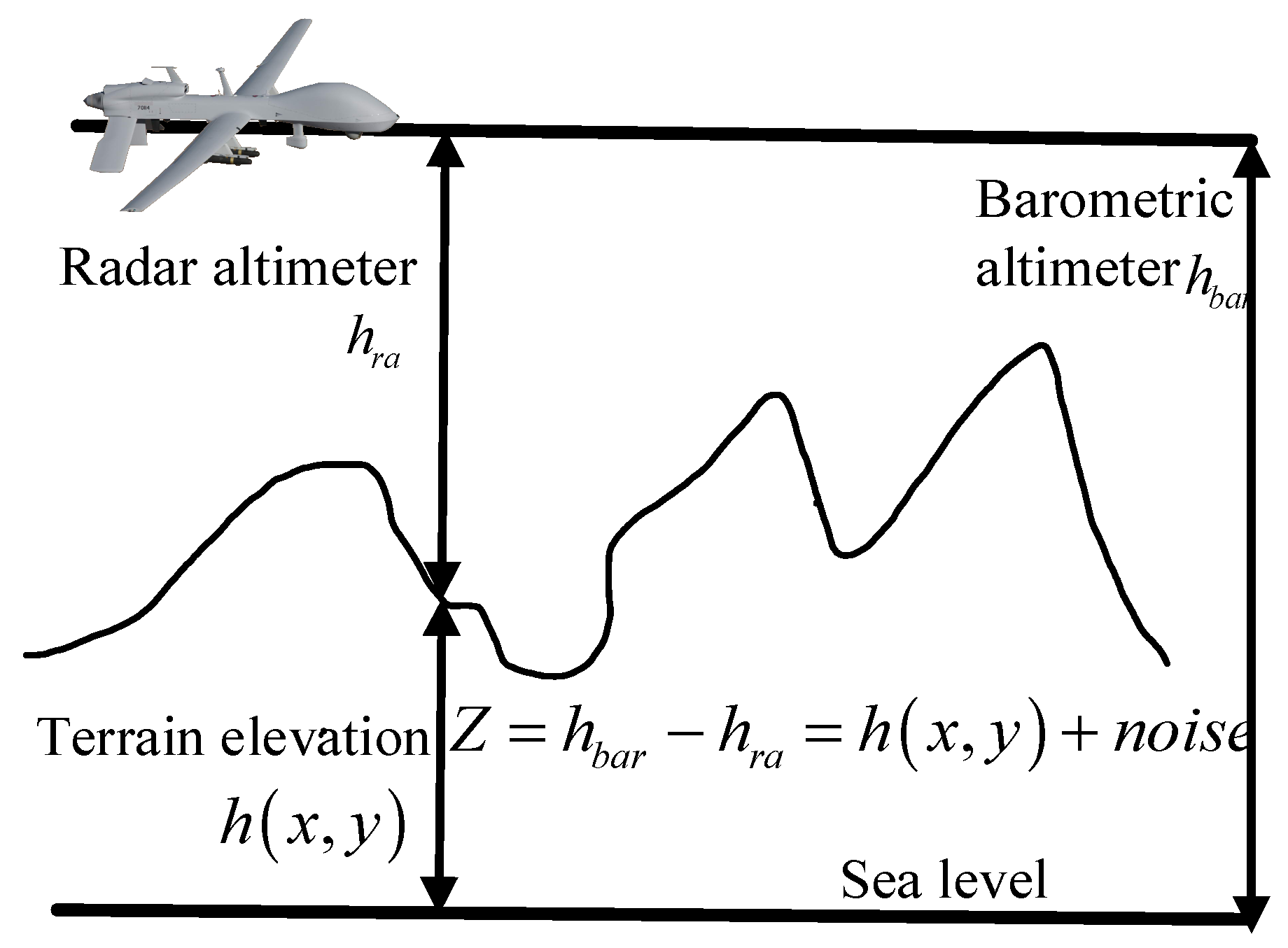
2. TRN Principle and System Model
3. From Bayesian Estimation to Particle Filter
| Algorithm 1. Particle filter algorithm. |
| Initialization: Particle sampling is performed according to the pdf of the initial position. and obtain observation |
| //Overall time steps: For to do (1): Draw according to (2), respectively; (2): are matched with the DEM to generate the predicted observations . (3): Calculate the deviation (4): Calculate , respectively; (5): Normalization of the weights: , respectively; (6): Resampling [11], and obtain (7): State estimation: End |
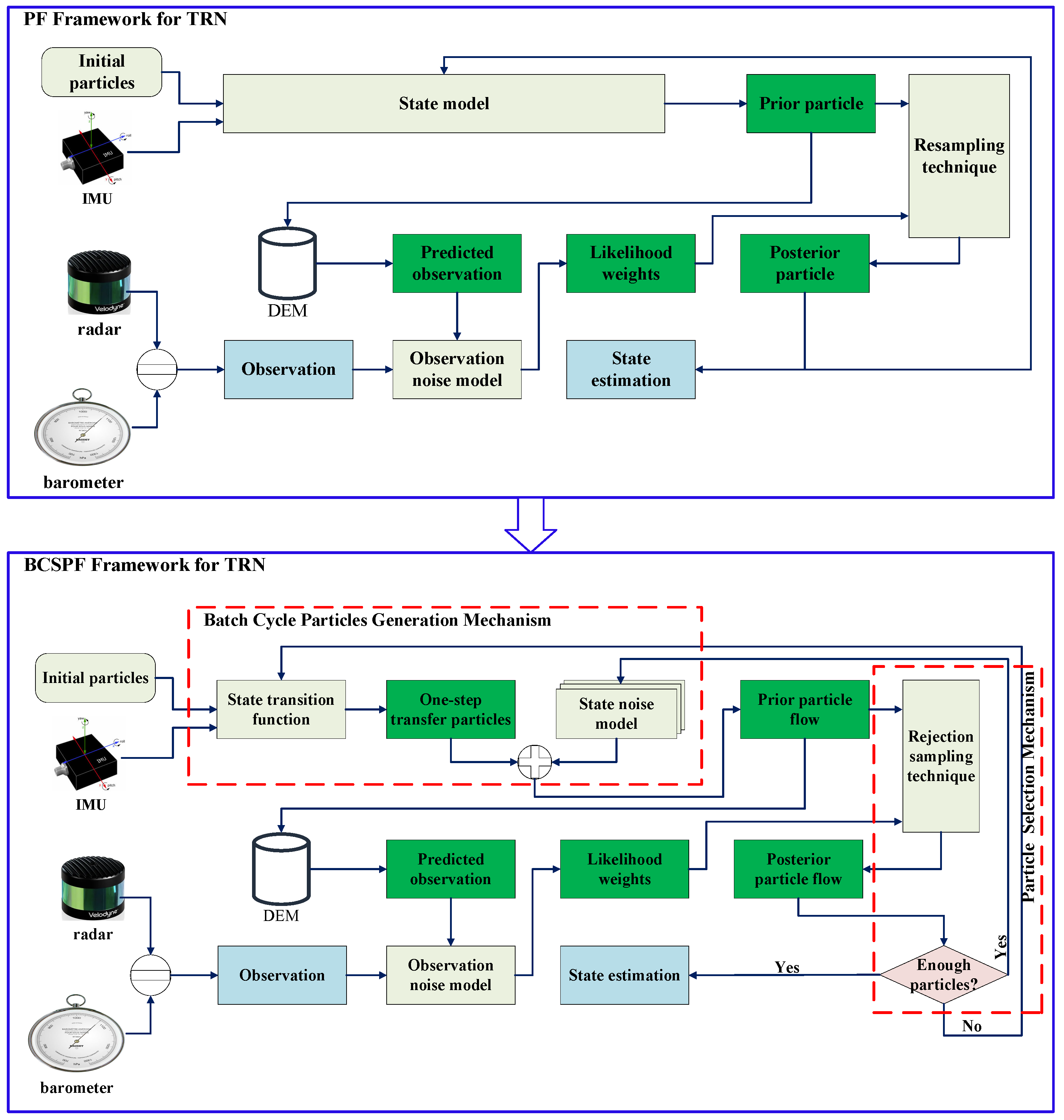
4. The BCPS-PF Algorithm
4.1. Batch Cycle Particle Generation Mechanism in Prediction Step
4.2. Particle Selection Mechanism in Update Step
| Algorithm 2. The BCPS-PF algorithm. |
| Initialization: Set sample number Generate the initial sample according to the initial PDF |
| //Overall time steps: For to do (1): Obtain the prior particles without state noise model according to ; (2): Set While : (3): Obtain a batch of prior particles according to Equation (4); (4): are matched with the DEM to generate the predicted observations ; (5): Calculate the deviation ; (6): Calculate the likelihood weights of each particle according to (10); (7): Generate random number where ; For to (8): if : , ; End End (9): State estimation according to Equation (13). End |
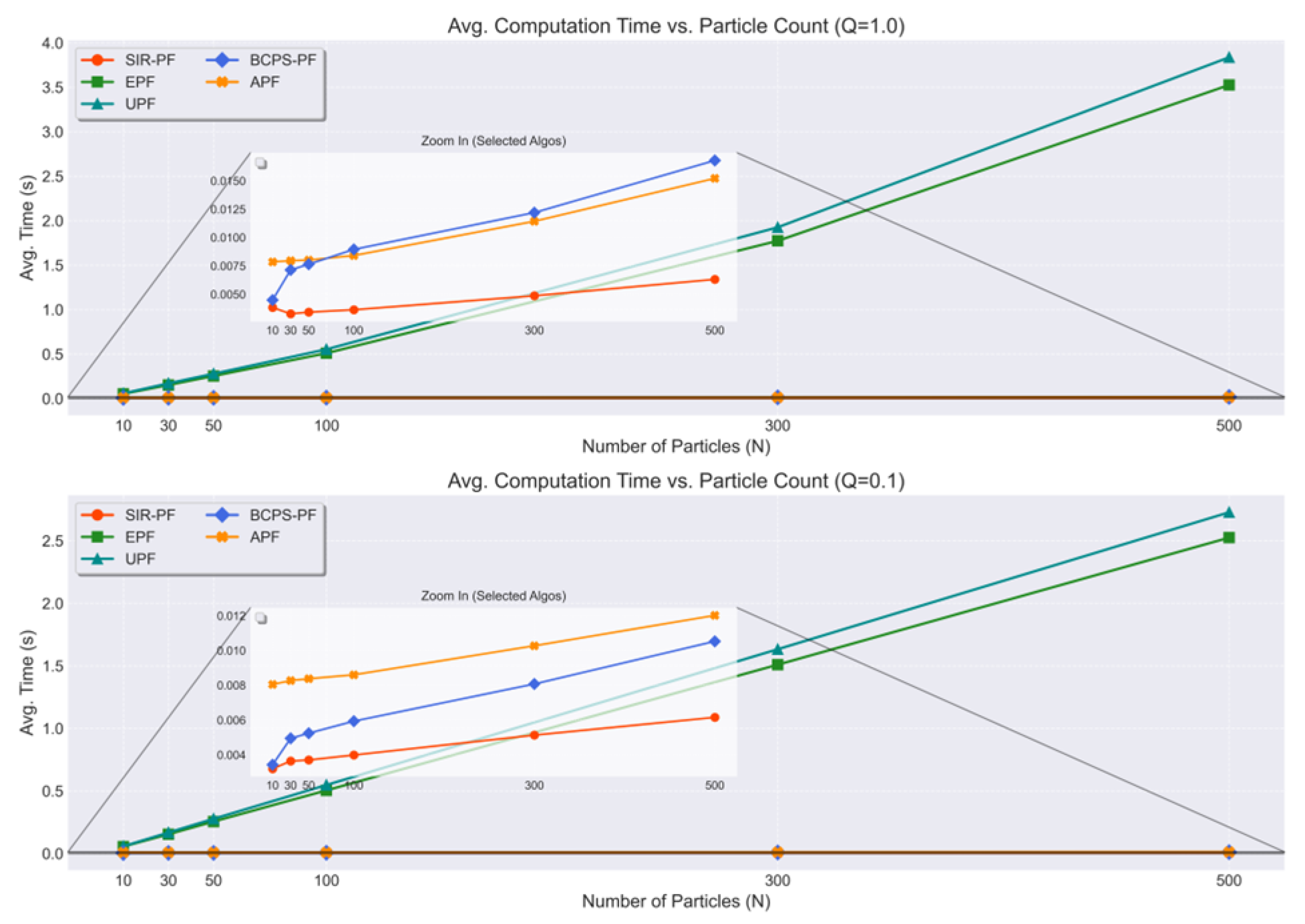
4.3. Computational Complexity Analysis
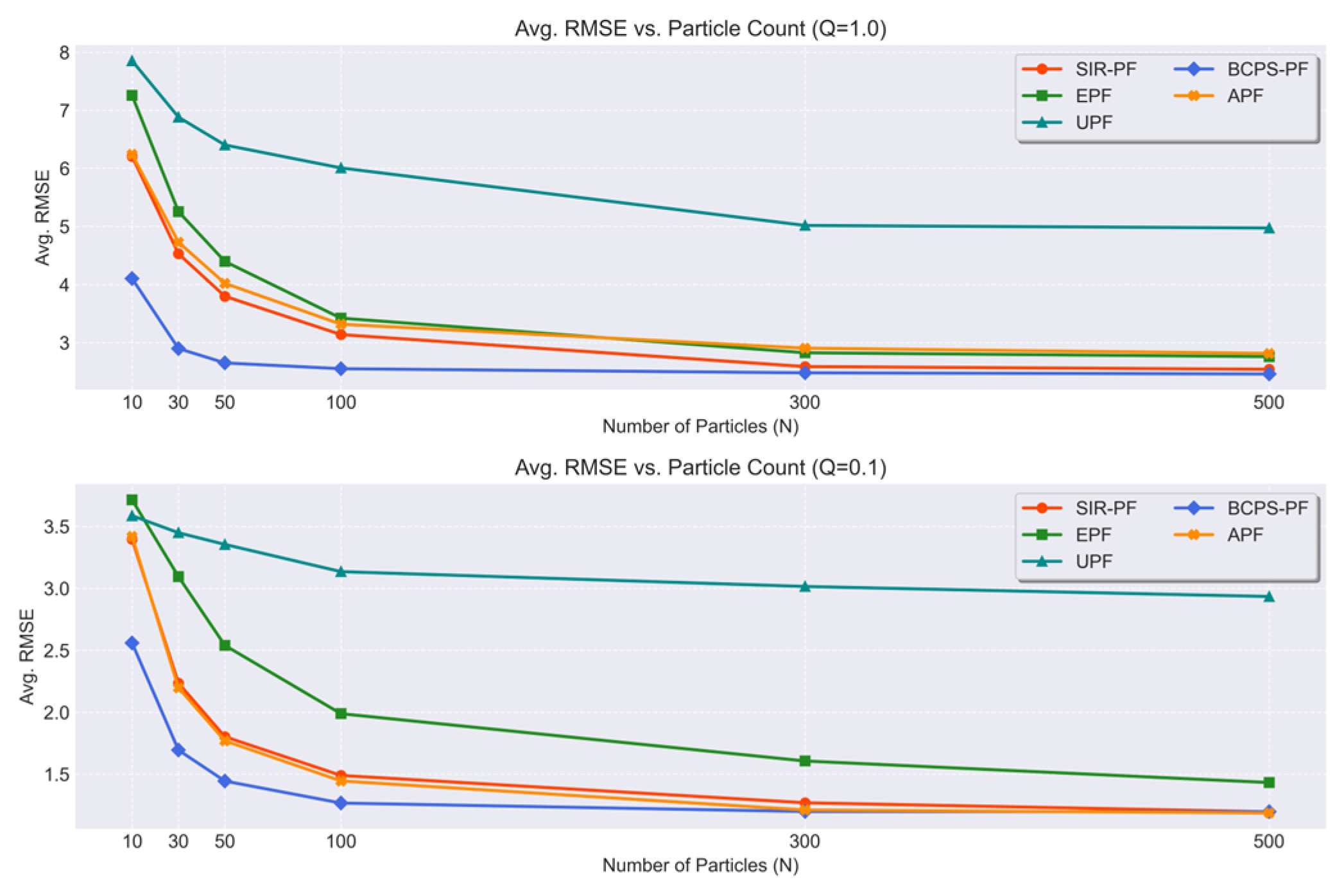
5. Simulation Experiment
5.1. Kitagawa’s Nonlinear Model
5.2. TRN Scenarios
5.2.1. Simulation Model and Condition
- (1)
- DEM data: The scenario utilizes a pre-loaded DEM with a resolution of 30 m (DEM) [37]. These DEM data are represented by a 4801 × 1000 matrix. The UAV’s initial position for the flight is set at row 87, column 94 within this matrix.
- (2)
- IMU data: As detailed in Section 2, the mathematical model incorporates errors associated with the IMU’s position and velocity estimations. These errors are modeled as zero-mean Gaussian distributions.
- (3)
- TRN observation: The TRN observation is obtained by subtracting the barometer altimetry reading from the radar altimetry reading. During this process, independent zero-mean Gaussian distributed errors are introduced for both barometer and radar altimetry measurements.
- (4)
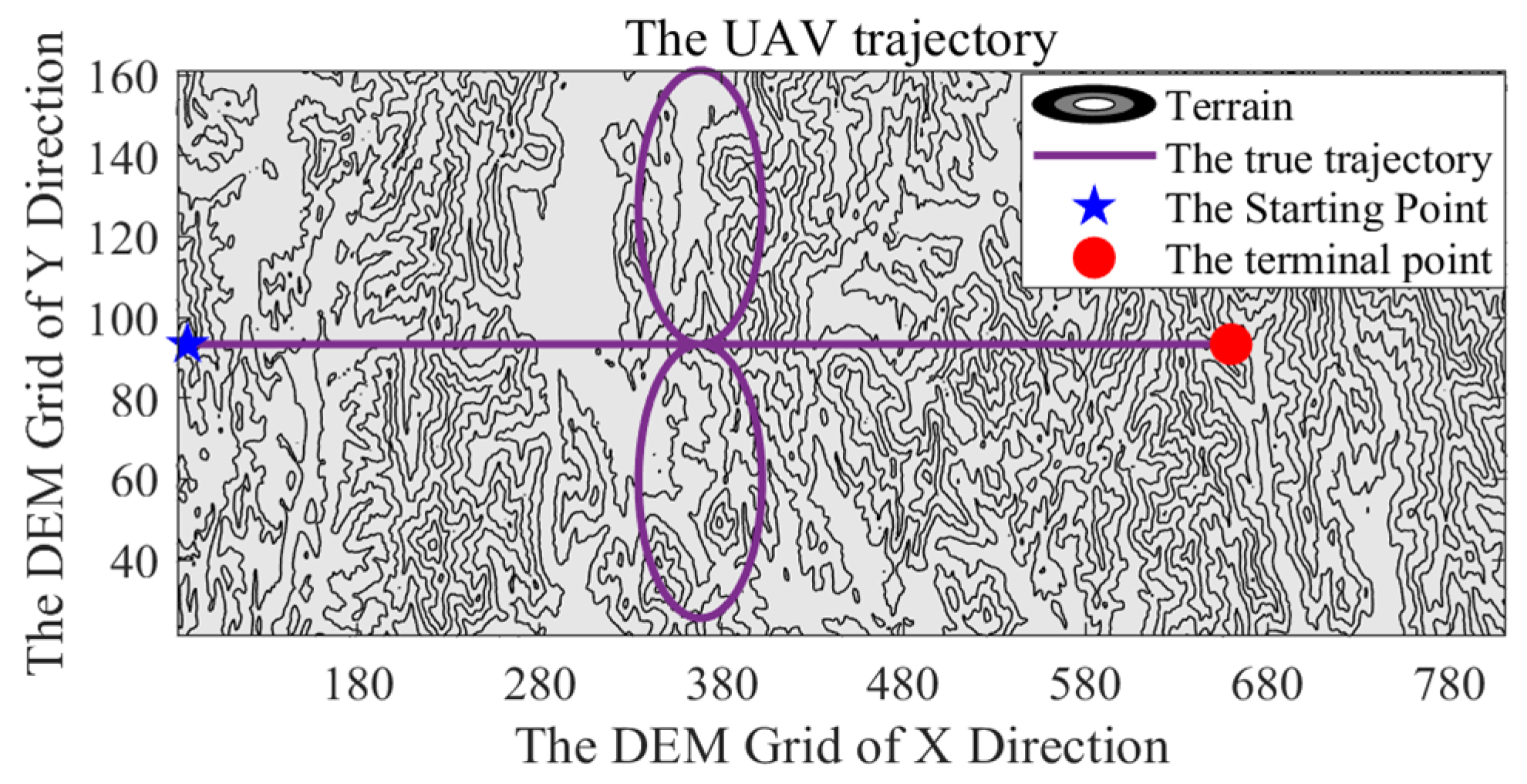
- UAV trajectory: The UAV commences its flight from the designated starting point, traveling due east for 86 s at a constant speed. It then performs a northward circular flight for 43 s. Furthermore, it executes another southward circular flight for 43 s. Finally, it flies straight towards the east for 128 s. The total flight time is 300 s. Throughout the entire flight, the UAV maintains a constant speed. The trajectory of the UAV flying over the DEM is shown in Figure 10. The relevant parameters are shown in Table 1.
5.2.2. Method
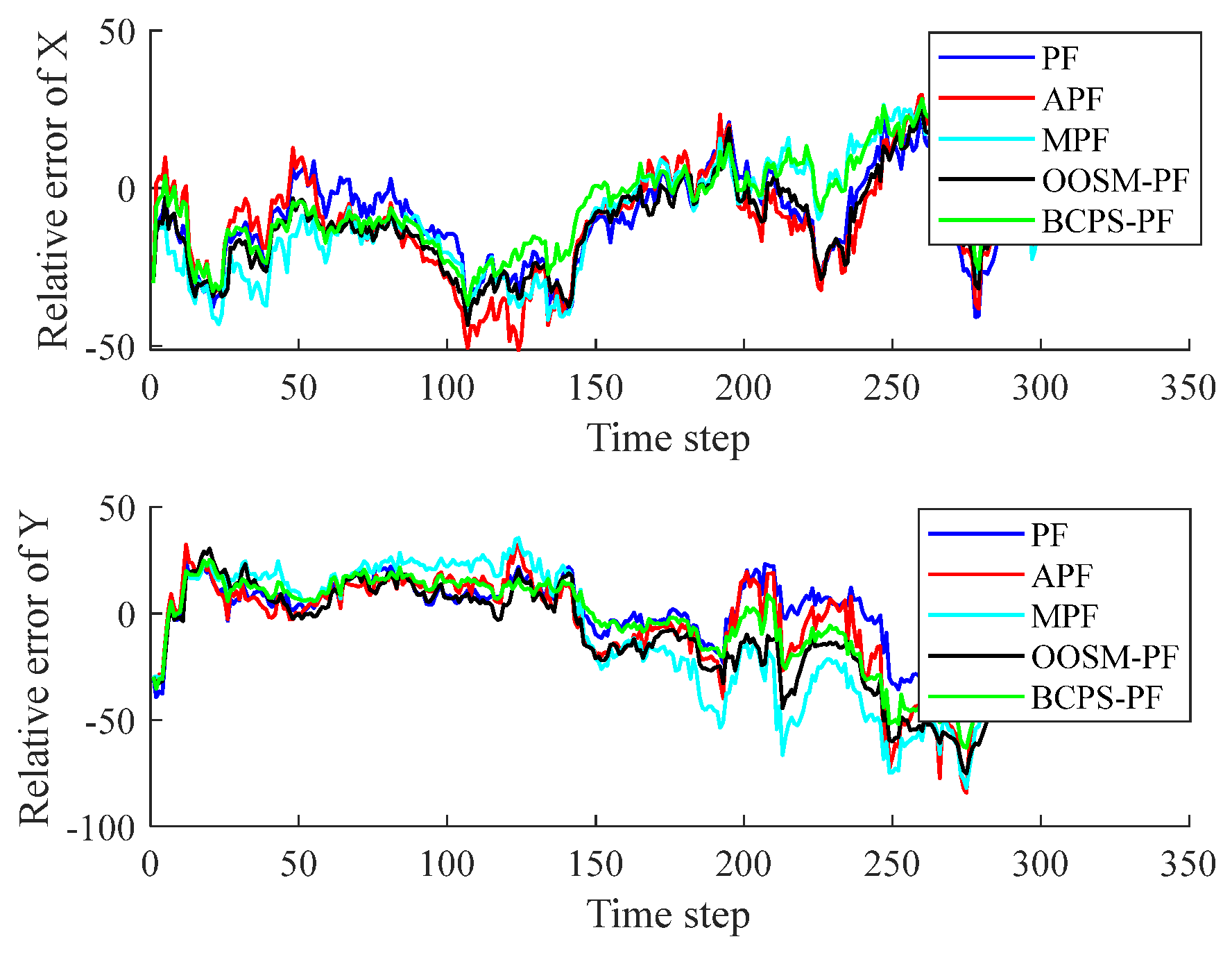
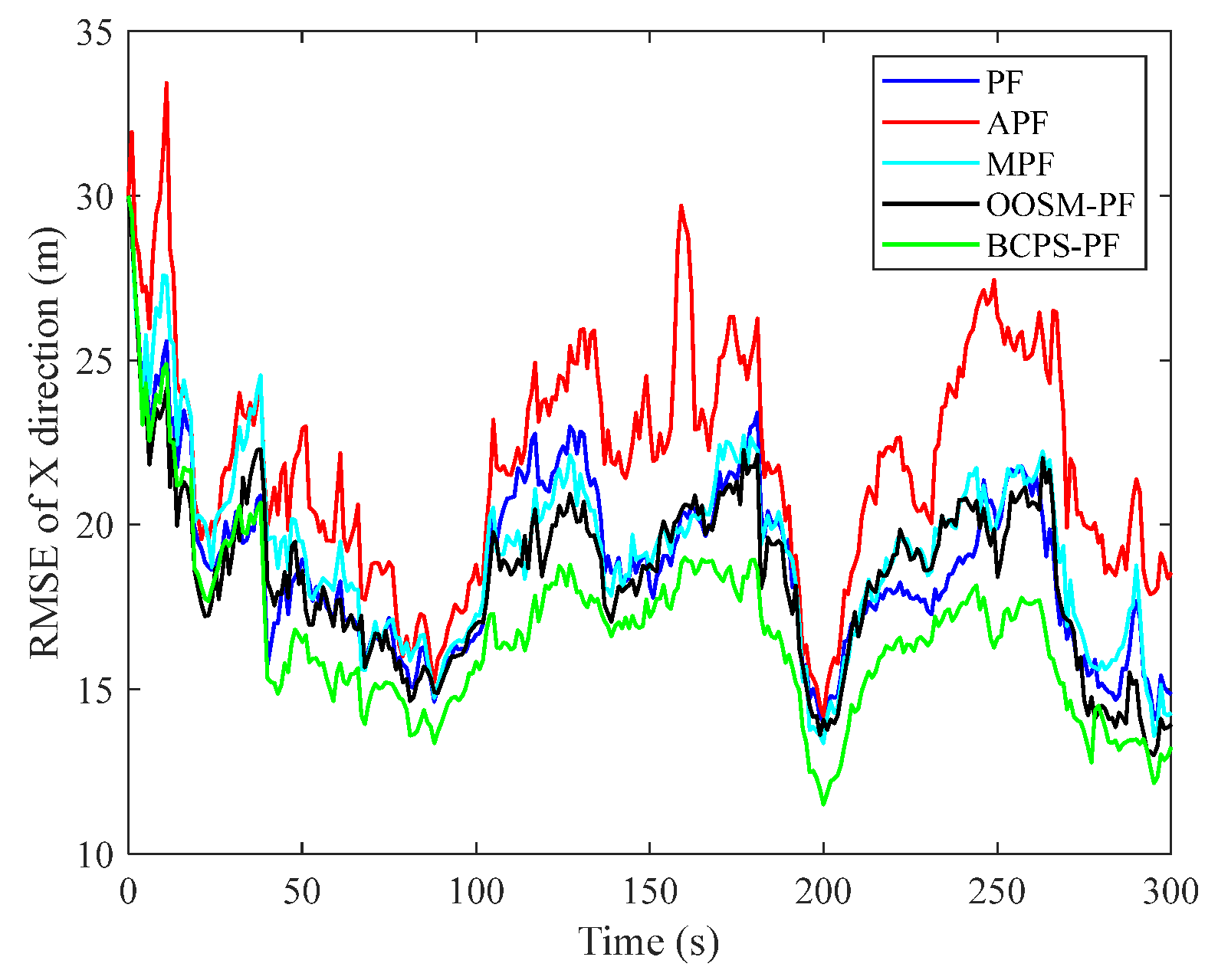
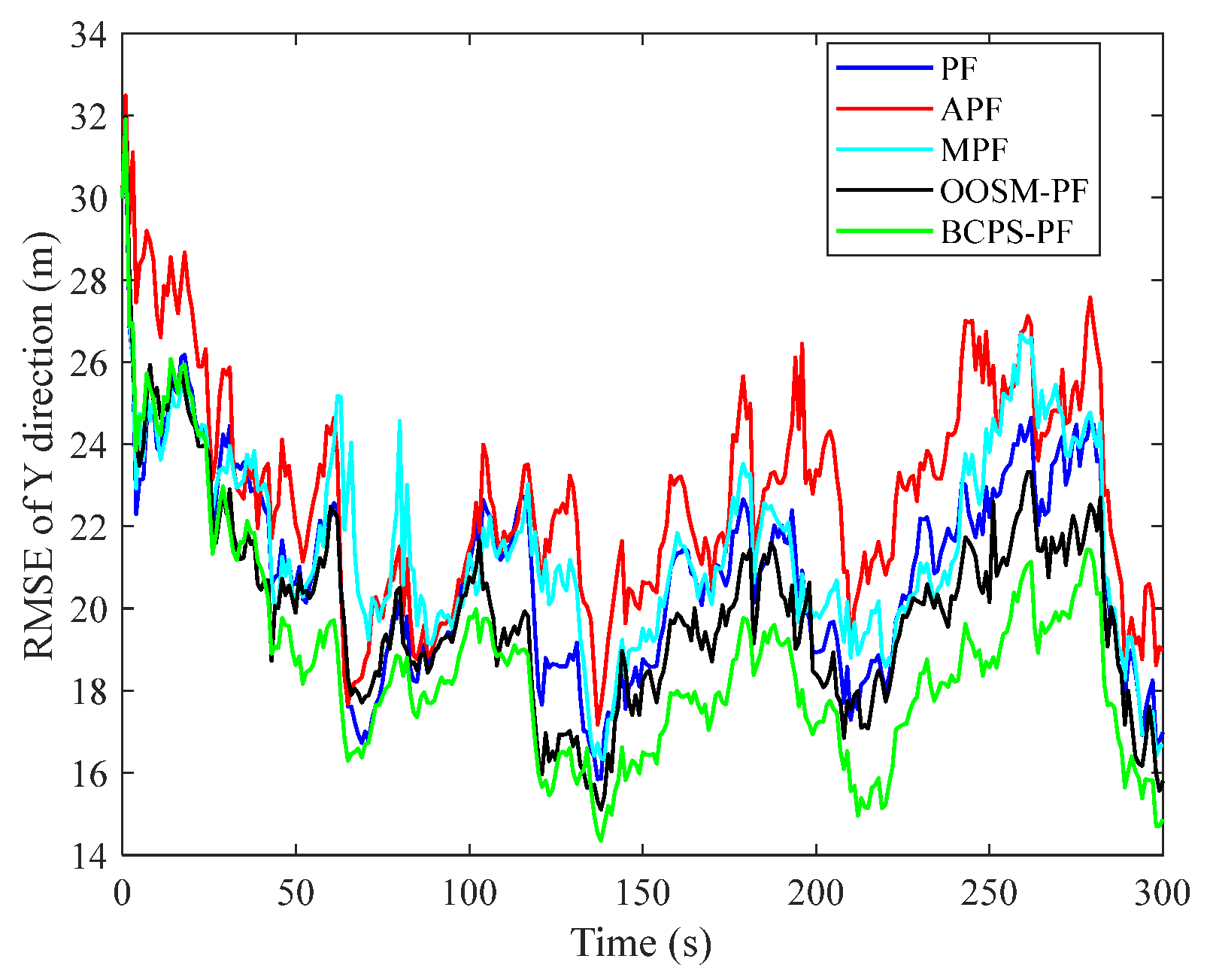
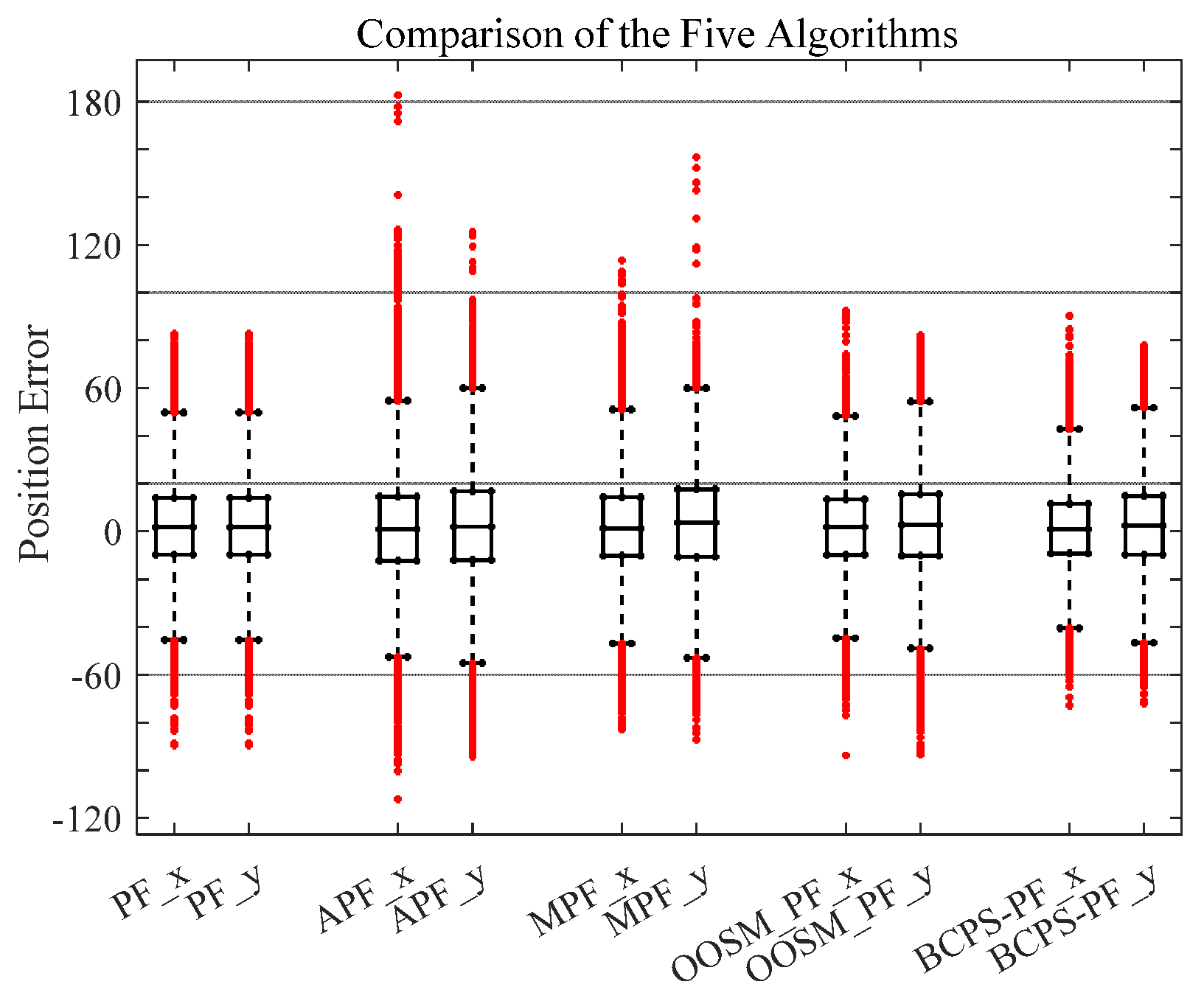
5.2.3. Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vaman, D. TRN history trends and the unused potential. In Proceedings of the IEEE/AIAA 31st Digital Avionics Systems Conference, Williamsburg, VA, USA, 14–18 October 2012; pp. 1A3-1–1A3-16. [Google Scholar]
- Kim, Y.; Park, J.; Bang, H. Terrain-referenced navigation using an interferometric radar altimeter. Navigation 2018, 65, 157–167. [Google Scholar] [CrossRef]
- Carroll, J.D.; Canciani, A.J. Terrain-referenced navigation using a steerable-laser measurement sensor. Navigation 2021, 68, 115–134. [Google Scholar] [CrossRef]
- Yin, J.; Zhang, J.; Klaas, M. The Marginal Rao-Blackwellized Particle Filter for Mixed Linear/Nonlinear State Space Models. Chin. J. Aeronaut. 2007, 20, 346–352. [Google Scholar] [CrossRef]
- Copp, B.; Subbarao, K. Nonlinear adaptive filtering in terrain-referenced navigation. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 3461–3469. [Google Scholar] [CrossRef]
- Choe, Y.; Park, C.G. Point-mass filtering with boundary flow and its application to terrain referenced navigation. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 3600–3613. [Google Scholar] [CrossRef]
- Liu, D.; Chen, X.; Liu, X. A novel optimal data fusion algorithm and its application for the integrated navigation system of missile. Chin. J. Aeronaut. 2022, 35, 53–68. [Google Scholar] [CrossRef]
- Ahwiadi, M.; Wang, W. An adaptive particle filter technique for system state estimation and prognosis. IEEE Trans. Instrum. Meas. 2020, 69, 6756–6765. [Google Scholar] [CrossRef]
- Zhu, N.; Zhao, H.; Feng, W.; Wang, Z. A novel particle filter approach for indoor positioning by fusing WiFi and inertial sensors. Chin. J. Aeronaut. 2015, 28, 1725–1734. [Google Scholar] [CrossRef]
- Wan, X.; Shao, Y.; Zhang, S.; Li, S. Terrain aided planetary UAV localization based on geo-referencing. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Qiang, X.; Zhu, Y.; Xue, R. SVRPF: An Improved Particle Filter for a Nonlinear/Non-Gaussian Environment. IEEE Access 2019, 7, 151638–151651. [Google Scholar] [CrossRef]
- Zhao, L.; Gao, N.; Huang, B.; Wang, Q.; Zhou, J. A novel terrain-aided navigation algorithm combined with the TERCOM algorithm and particle filter. IEEE Sens. J. 2014, 15, 1124–1131. [Google Scholar] [CrossRef]
- Talebi, S.P.; Mandic, D.P. Distributed Particle Filtering of-Stable Signals. IEEE Signal Process. Lett. 2017, 24, 1862–1866. [Google Scholar] [CrossRef]
- Golden, J.P. Terrain contour matching (TERCOM): A cruise missile guidance aid. In Image Processing for Missile Guidance; SPIE: Bellingham, WA, USA, 1980; Volume 238, pp. 10–18. Available online: https://www.spiedigitallibrary.org/conference-proceedings-ofspie/0238/0000/Terrain-Contour-Matching-TERCOM-A-Cruise-Missile-Guidance-Aid/10.1117/12.959127.full (accessed on 29 September 2025).
- Baker, W.; Clem, R. Terrain Contour Matching [TERCOM] Primer; Technical Report ASP-TR-77-61; Aeronautical Syst. Division, Wright-Patterson AFB, Wright-Patterson Air Force Base: Dayton, OH, USA, 1977. [Google Scholar]
- Hollowell, J. Heli/SITAN: A Terrain Referenced Navigation Algorithm for Helicopters. January 1990. Available online: https://www.osti.gov/biblio/5127167 (accessed on 29 September 2025).
- Boozer, D.D.; Fellerhoff, J.R. Terrain-aided navigation test results in the AFTI/F-16 aircraft. Navigation 1988, 35, 161–175. [Google Scholar] [CrossRef]
- Wei, E.; Dong, C.; Yang, Y.; Tang, S.; Liu, J.; Gong, G.; Deng, Z. Arobust solution of integrated SITAN with TERCOM algorithm: Weightreducing iteration technique for underwaterVehicles’ gravity-aided inertial navigation system. Navigation 2017, 64, 111–122. [Google Scholar] [CrossRef]
- Peng, H.Z.; Jun, Y.; Wei, W.W.; Zhi, M.B. An algorithm of terrain matching aided navigation forUAVs. In Proceedings of the IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China, 10–12 August 2018; pp. 1–6. [Google Scholar]
- Cowie, M.; Wilkinson, N.; Powlesland, R. Latest development of the TERPROM digital terrain system (DTS). In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Monterey, CA, USA, 5–8 May 2008; pp. 1219–1229. [Google Scholar]
- Yuan, G.; Zhang, H.; Yuan, K.; Zhu, L. Improved SITAN algorithm in the application of aided inertial navigation. In Proceedings of the International Conference on Measurement, Information and Control, Vinnytsia, Ukraine, 9–11 October 2012; Volume 2, pp. 922–926. [Google Scholar]
- Oh, J.; Sung, C.K.; Lee, J.; Lee, S.W.; Lee, S.J.; Yu, M.J. Accurate measurement calculation method for interferometric radar altimeter-based terrain referenced navigation. Sensors 2019, 19, 1688. [Google Scholar] [CrossRef]
- Enns, R.; Morrell, D. Terrain-aided navigation using the Viterbi algorithm. J. Guid. Control Dyn. 1995, 18, 1444–1449. [Google Scholar] [CrossRef]
- Ånonsen, K.B. Advances in Terrain Aided Navigation for Underwater Vehicles. Ph.D. Thesis, Department of Engineering Cybernetics, Norwegian University of Science and Technology, Trondheim, Norway, 2010. [Google Scholar]
- Bergman, N.; Ljung, L.; Gustafsson, F. Terrain navigation using Bayesian statistics. IEEE Control Syst. 1999, 19, 33–40. [Google Scholar]
- Park, Y.-G.; Park, C.G. Grid support adaptation for point mass filter-based terrain referenced navigation using mutual information. IEEE Sens. J. 2018, 18, 7603–7610. [Google Scholar] [CrossRef]
- Zhang, K.; Li, Y.; Zhao, J.; Rizos, C. A Study of Underwater Terrain Navigation based on the Robust Matching Method. J. Navig. 2014, 67, 569–578. [Google Scholar] [CrossRef]
- Ma, T.; Ding, S.; Li, Y.; Fan, J. A review of terrain aided navigation for underwater vehicles. Ocean. Eng. 2023, 281, 114779. [Google Scholar] [CrossRef]
- Ristic, B.; Arulampalam, S.; Gordon, N. Beyond Kalman Filter: Particle Filters for Tracking Applications; Artech House: Norwood, MA, USA, 2003. [Google Scholar]
- Gustafsson, F.; Gunnarsson, F.; Bergman, N.; Forssell, U.; Jansson, J.; Karlsson, R.; Nordlund, P.J. Particle filters for positioning, navigation, and tracking. IEEE Trans. Signal Process. 2002, 50, 425–437. [Google Scholar] [CrossRef]
- Nordlund, P.-J.; Gustafsson, F. Marginalized particle filter for accurate and reliable terrain-aided navigation. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1385–1399. [Google Scholar] [CrossRef]
- Turan, B. Comparison of nonlinear filtering methods for terrain referenced aircraft navigation. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 144–149. [Google Scholar]
- Turan, B.; Kutay, A.T. Particle filter studies on terrain referenced navigation. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium (PLANS), Savannah, GA, USA, 11–14 April 2016; pp. 949–954. [Google Scholar]
- Salavasidis, G.; Munafò, A.; McPhail, S.D.; Harris, C.A.; Fenucci, D.; Pebody, M.; Rogers, E.; Phillips, A.B. Terrain-aided navigation with coarse maps—Toward an Arctic crossing with an AUV. IEEE J. Ocean. Eng. 2021, 46, 1192–1212. [Google Scholar] [CrossRef]
- Palmier, C.; Dahia, K.; Merlinge, N.; Del Moral, P.; Laneuville, D.; Musso, C. Adaptive approximate Bayesian computational particle filters for underwater terrain aided navigation. In Proceedings of the 22th International Conference on Information Fusion (FUSION), Ottawa, ON, Canada, 2–5 July 2019; pp. 1–8. [Google Scholar]
- Li, X.; Zhong, Y.; Han, Y. Constrained cubature particle filter for vehicle navigation. Sensors 2024, 24, 1228. [Google Scholar] [CrossRef] [PubMed]
- Jia, K.; Pei, Y.; Gao, Z.; Zhong, Y.; Gao, S.; Wei, W.; Hu, G. A Quaternion-Based Robust Adaptive Spherical Simplex Unscented Particle Filter for MINS/VNS/GNS Integrated Navigation System. Math. Probl. Eng. 2019, 2019, 8532601. [Google Scholar] [CrossRef]
- Zhou, T.; Wang, T.; Gao, J.; Guo, Q.; Yan, Z. Particle filter underwater terrain-aided navigation based on gradient fitting. Meas. Sci. Technol. 2022, 33, 105009. [Google Scholar] [CrossRef]
- Qiang, X.; Xue, R.; Zhu, Y. Bayesian filter based on grid filtration and its application to Multi-UAV tracking. Signal Process. 2022, 190, 108305. [Google Scholar] [CrossRef]
- Dissanayaka, D.; Wanasinghe, T.R.; De Silva, O.; Jayasiri, A.; Mann, G.K.I. Review of Navigation Methods for UAV-Based Parcel Delivery. IEEE Trans. Autom. Sci. Eng. 2024, 21, 1068–1082. [Google Scholar] [CrossRef]

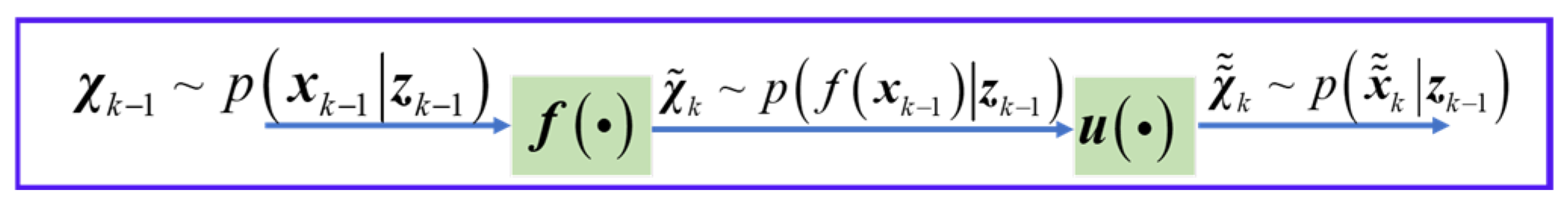

| Condition | Value |
|---|---|
| Simulation duration | 300 s |
| Velocity | 100 m/s |
| The flight altitude | 900 m |
| Initial position error | 40 m |
| The std of position error estimated by the IMU | 5 |
| The std of velocity error estimated by the IMU | 2 |
| IMU sampling frequency | 1 Hz |
| The flight altitude | 900 m |
| Observation sampling frequency | 1 Hz |
| The std of observation error obtained by barometer altimetry | 15 |
| The std of observation error obtained by radar altimetry | 4.71 |
| Method | RMSE | Times(s) | ||
|---|---|---|---|---|
| -- | ||||
| PF | 22.5276 | 25.0796 | 33.7886 | 0.0463 |
| APF | 26.2716 | 27.4077 | 38.0666 | 0.0924 |
| MPF | 23.0830 | 25.8360 | 34.7122 | 0.9856 |
| OOSM | 22.0741 | 24.0055 | 32.6898 | 0.0736 |
| BCPS-PF | 20.0280 | 22.4909 | 30.1838 | 0.0838 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, Z.; Qiang, X.; Shi, W.; Gong, Y.; Wu, L. Batch Cyclic Posterior Selection Particle Filter and Its Application in TRN. Electronics 2025, 14, 4257. https://doi.org/10.3390/electronics14214257
Lyu Z, Qiang X, Shi W, Gong Y, Wu L. Batch Cyclic Posterior Selection Particle Filter and Its Application in TRN. Electronics. 2025; 14(21):4257. https://doi.org/10.3390/electronics14214257
Chicago/Turabian StyleLyu, Zhiqiang, Xingzi Qiang, Wenwu Shi, Yingkui Gong, and Longxing Wu. 2025. "Batch Cyclic Posterior Selection Particle Filter and Its Application in TRN" Electronics 14, no. 21: 4257. https://doi.org/10.3390/electronics14214257
APA StyleLyu, Z., Qiang, X., Shi, W., Gong, Y., & Wu, L. (2025). Batch Cyclic Posterior Selection Particle Filter and Its Application in TRN. Electronics, 14(21), 4257. https://doi.org/10.3390/electronics14214257








