Abstract
Accurate walking trajectory estimation is critical for monitoring activity levels in healthcare and occupational safety applications. Ultra-Wideband (UWB) technology has emerged as a key solution for indoor human activity and trajectory tracking. However, its performance is fundamentally limited by Non-Line-of-Sight (NLOS) errors and kinematic drift during turns. To address these challenges, this study introduces a novel integrated IMU-UWB framework for walking trajectory estimation in NLOS scenarios involving turning gait. The algorithm integrates an error-state Kalman filter (ESKF) and a phase-aware turning correction module. Experiments were carried out to evaluate the effectiveness of this framework. The results show that the presented framework demonstrates significant improvements in walking trajectory estimation, with a smaller mean absolute error (7.0 cm) and a higher correlation coefficient, compared to the traditional methods. By effectively mitigating both NLOS-induced ranging errors and turn-related drift, this system enables reliable indoor tracking for healthcare monitoring, industrial safety, and consumer navigation applications.
1. Introduction
A person’s walking trajectory is a vital metric for quantifying activity levels, with applications in healthcare and occupational safety [1]. In clinical settings, such as hospitals and assisted living facilities, tracking the movement patterns of patients and the elderly helps monitor mobility declines and assess rehabilitation progress [2]. Similarly, in hazardous environments like construction sites and factories, trajectory analysis estimates worker exertion levels, reduces fatigue-related risks, and optimizes task efficiency [3,4].
Wearable sensor technologies have been widely used for walking trajectory estimation. Traditionally, these sensors relied on satellite positioning systems, such as the Global Positioning System (GPS), to track human movement [5]. However, GPS is primarily suited for outdoor environments and is not effective for indoor tracking of human activities. Additionally, human walking speeds are generally slower than those of vehicles, leading to significant distance detection errors in GPS technology [6]. This limitation complicates the accurate estimation of human activities, highlighting the need for alternative tracking solutions in indoor settings.
In recent years, Ultra-Wideband (UWB) technology has emerged as a key solution for indoor human activity and trajectory tracking, thanks to its high positioning accuracy, low power consumption, and strong resistance to multipath effects [7]. For instance, UWB can effectively track movements in harsh environments where other technologies struggle [8,9]. Compared to indoor tracking solutions like Bluetooth Low Energy (BLE) using Angle-of-Arrival (AoA) or Angle-of-Departure (AoD) algorithms, or Wi-Fi-based tracking relying on signal strength (RSSI) or channel state information (CSI), UWB offers superior centimeter-level accuracy, near-instantaneous response, and robust performance in cluttered settings [10].
While Ultra-Wideband (UWB) technology has become prevalent for indoor human trajectory estimation, its accuracy remains fundamentally constrained by two systematic error sources, i.e., the Non-Line-of-Sight (NLOS) propagation effects and turning-induced kinematic errors. NLOS errors occur when obstacles like walls or furniture block direct signals. It resulted in distorting signal strength (RSSI) and forcing reliance on reflected paths that increase time-of-flight measurements and introduce distance overestimations [11]. Turning-induced errors arise when body-mounted tags rotate during movement [12]. This could alter antenna polarization and radiation patterns relative to fixed anchors [13].
The NLOS scenarios can be mitigated by integrating IMU sensors with UWB positioning systems. For example, Ali et al. [14] introduced a tightly coupled approach that enhances indoor localization by integrating UWB ranging with foot-mounted IMU data. The fusion results showed improved accuracy and resilience against typical indoor localization challenges, such as multipath effects. Naheem and Kim [15] present a low-cost solution that mitigates IMU drift, allowing for continuous and accurate tracking of pedestrian movements. The study highlights the importance of balancing cost and performance. Feng et al. [16] combined IMU and UWB through the extended Kalman filter (EKF) and unscented Kalman filter (UKF) to improve the robustness and accuracy. While UWB provides precise location data in Line of Sight (LOS) conditions, IMUs can help maintain a stable estimate of position during brief interruptions in UWB signal. However, IMUs estimate position and orientation based on accelerometer and gyroscope data. Over time, small measurement errors accumulate, leading to drift from the actual position [17]. This problem can be exacerbated when individuals make turns. More importantly, during turning gait, the rapid changes in direction can amplify the drift errors in IMUs, leading to significant inaccuracies in tracking the walking trajectory [18,19]. The combination of angular velocity and accumulated errors can result in substantial deviations from the actual path, making precise monitoring more challenging. However, previous studies have not adequately addressed this issue. The impact of turning gait on IMU drift remains underexplored, leaving a gap in understanding how to optimize tracking accuracy during dynamic movements.
To address this research gap, this study proposes a novel walking trajectory estimation algorithm that fuses UWB and IMU data. The algorithm integrates an error-state Kalman filter (ESKF) and a turning correction module. This algorithm was designed to mitigate the effect of NLOS scenarios and turning. The hypothesis to be tested is that this algorithm significantly improves walking trajectory estimation accuracy compared to conventional UWB-only systems, particularly in challenging indoor environments with frequent obstructions and path curvature. The algorithm’s potential applications include elderly fall detection in smart homes and worker safety monitoring in industrial warehouses.
The novelties of this study are:
This study shows that the ESKF, which directly incorporates UWB ranging errors into IMU state estimation, can improve the accuracy of trajectory estimation in challenging environments.
This study presents a novel integrated framework with an ESKF model and turning correction module. This framework can significantly improve trajectory estimation accuracy.
Our solution demonstrates that careful modeling of specific gait events (like turns) can yield disproportionate improvements in human trajectory estimation.
2. Materials and Methods
2.1. The Implementation of the Integrated Framework
The proposed algorithm employs an integrated framework (Figure 1). An ESFK model was used to dynamically compensate for UWB positioning errors in NLOS conditions through IMU data fusion, and a gait-phase-aware turning correction model was used to correct the walking trajectory during directional changes.
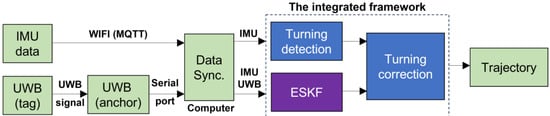
Figure 1.
The block diagram of the presented walking trajectory estimation algorithm.
Importantly, this approach requires time-synchronized UWB and IMU data. Therefore, we developed a customized wearable sensor that integrates both IMU and UWB modules (Figure 2a). The IMU module (Figure 2b) consists of a 9-axis inertial sensor chip (BNO055, Bosch Sensortec GmbH, Kusterdingen, Germany), which combines a three-axis 14-bit accelerometer, a three-axis 16-bit gyroscope, and a three-axis magnetometer. A microcontroller unit (ESP32-WROOM-32, Espressif Systems Co., Ltd., Shanghai, China) was employed to enable real-time wireless data transmission without delay. For the UWB, we utilized an off-the-shelf module (LD150, Haoru Technology Co. Ltd., Dalian, China) (Figure 2b). This module features the DecaWave’s DW1000 as its core UWB chip and is equipped with an STM32 as the microcontroller unit. The LD150 module can function flexibly as either an anchor or a tag in the UWB system.
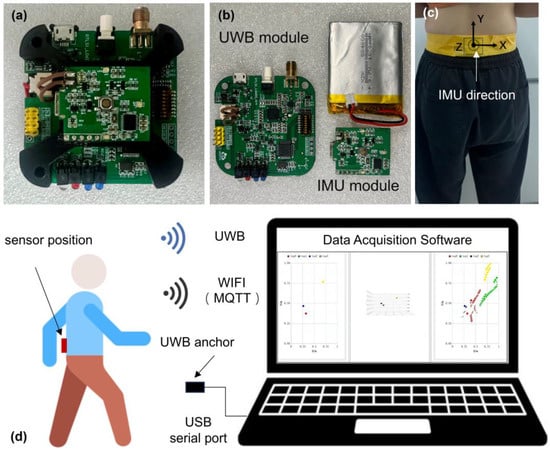
Figure 2.
(a) the customized wearable sensor that integrates both IMU and UWB modules. (b) the breakdown of the wearable sensor; (c) wearable sensor placement. (d) schematic plot of data acquisition system.
To ensure algorithm adaptability, the sensor was designed to be worn on the lower back, with the IMU required to maintain a fixed orientation during use (Figure 2c). For data acquisition, a computer-based software was developed based Qt application development framework (Version 5.15) (Figure 2d). For the IMU data, we utilized wireless data transmission via WIFI using the MQTT (Message Queuing Telemetry Transport) protocol (QoS level 1). For UWB data transmission, a UWB anchor (LD150 module) was connected to the computer via the USB serial port. This UWB anchor establishes wireless communication with those LD150 modules (e.g., the one integrated in the wearable sensor) through UWB signaling, and sends the received data to the computer via serial port.
When processing algorithms simultaneously using IMU and UWB sensors, there is a difference in the Output Data Rate (ODR) between the two sensors, necessitating initial data processing to address the temporal alignment of their data. The UWB has an ODR of 10 Hz, meaning the time interval between data frames is 100 ms. In contrast, the IMU has an ODR of 100 Hz, resulting in a 10 ms interval between data frames. The data from both sensors must be unified under the same time reference to guarantee that each frame of data corresponds precisely on the timeline. To address this issue, this study proposes a data fusion algorithm capable of dynamically adjusting the time stamps of the IMU and UWB, achieving temporal synchronization and one-to-one correspondence between the two data streams. Specifically, the temporal information of the lower-ODR UWB data was used as the reference, and an interpolation alignment was used to derive new temporal information corresponding to the IMU data. The algorithm took the following steps.
First, the data from the IMU and UWB are placed into separate virtual “data containers”. Since the data in these containers are time-series data, each “data container” maintains its own independent temporal information. Second, a “data indexing” approach was used to map the timestamps of UWB data to their corresponding locations within the IMU sensor’s time sequence. More specifically, a time stamp of the UWB frame () was assigned between two adjacent IMU time stamps, ( which satisfy that . Lastly, a new synchronized IMU data was estimated by the linear-interpolation as,
2.2. Error State Kalman Filter (ESKF) Model
This study employs the ESKF, a variant of the Kalman filter. Compared to traditional Kalman filtering, ESKF is specifically designed as a nonlinear filter for time-varying systems [20]. By estimating state errors, ESKF enables faster updating of state estimations. The system block diagram of the implemented ESKF model is illustrated in Figure 3, with the main algorithmic steps outlined below.
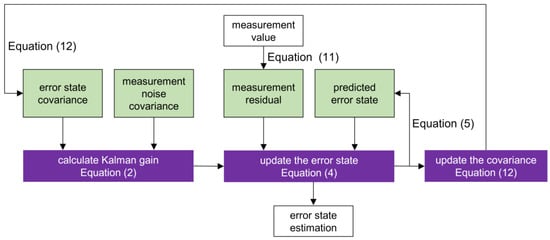
Figure 3.
The block diagram of the ESKF model.
First, the Kalman gain is calculated based on the measurement noise covariance (i.e., measurement error) and error-state covariance (i.e., estimation error). This common gain dynamically adjusts error weights according to the relative magnitudes of measurement and estimation errors (e.g., assigning greater weight to values with smaller errors).
After computing the common gain, the model updates the predicted error state. This update requires three variables: the common gain, measurement residual, and predicted error state. The core concept is that the calculated common gain determines whether the error state estimation should place more trust in the measured error or predicted error. Following the update, the model outputs the error state estimation and uses it to predict the next cycle’s error state.
Finally, based on the updated error state, the model recalculates its error by updating the covariance), then uses this updated covariance to compute the error-state covariance for the next cycle. This process iterates through multiple cycles.
The model’s specific computations proceed as follows. First, the common gain is expressed through the Kalman gain matrix (). The estimation error is represented by error-state covariance (). The measurement error is characterized by the measurement noise covariance matrix (). represents the statistical uncertainty in the measurement readings. Given that a high confidence in the accuracy of the UWB measurements, was set as a 1 × 1 unit vector, with a small value 0.1. It helps in minimizing the initial estimation error during the filter’s startup phase. It also allows the filter to rely more on the available measurements, which is crucial when prior estimates may be less accurate. We also adopted fixed value Kalman gain tuning strategy, where pre-defined values for measurement noise covariance matrix (R) and the process noise covariance matrix (Q) based on known noise characteristics of the sensors were used. These components are mathematically represented as,
where is the measurement matrix which serves to align the dimensionality of the error-state covariance matrix with that of the measurement noise covariance matrix. is calculated as,
where
- is the state transition matrix.
- is the estimated covariance matrix at time k-1.
- is the control input matrix.
- is the process noise covariance matrix.
Here, the process noise covariance matrix () was estimated by the noise and bias of the IMU sensor (i.e., BNO055). Specifically, according to the sensor data sheet, the noise of the accelerometer and gyroscope was 0.01 m/s2 and 0.3 dps, respectively. And the bias of the accelerometer and gyroscope was 0.001 m/s2 and 0.03 dps, respectively.
The Kalman gain matrix () was then used to update the error state through the state update equation,
where
- is the error state estimation at time k.
- is the measurement residual.
- is the predicted error state at time k.
In the state update equation, the calculation for the predicted error state is as follows,
The initial predicted errors were obtained from the IMU sensor. They include position error (), velocity error (), misalignment angles (), accelerometer bias error (), and gyroscope bias error (), which are expressed in vector form as follows,
It should be noted that all these error states are 3 × 1 vectors, with each element corresponding to a specific spatial direction (X, Y, Z), i.e.,
Here, the position error (), velocity error (), misalignment angles () are estimated as,
where
- is the earth rotation rate components,
- is the geodetic latitude at the measurement site,
- is the body-frame components of the gyroscope bias.
- is body-to-navigation frame transformation matrix for IMU.
- is the navigation-frame representation of IMU force (acceleration).
On the other hand, the measurement residual in the state update equation is calculated as,
where is the observation noise. Both and are unit transformation matrix.
Finally, following the state estimate update, the error state covariance matrix is updated through the covariance update equation
The ESFK model is observable, given that the current state can all be determined based on the measurement. Therefore, no additional stability validation was conducted. The inconsistencies or sudden jumps in UWB measurements could suggest NLOS interference. However, we trusted the ESKF model to inherently manage NLOS interference without additional attenuation strategies such as the piecewise relinearization.
2.3. Turning Correction Module
This model consists of two parts, turning detection and gait-phase-aware turning correction. Previous research has found that during turning movements, the orientation of the torso changes, leading to variations in waist-worn gyroscope data [18]. Analysis of the IMU raw data in this study also confirmed this pattern. During left turns, the angular velocity data of the gyroscope, rotating around the vertically upward axis exhibits a positive peak, while during right turns, a negative peak appears. The magnitudes of these peak values exceed those observed during foot strikes and the elevation of the body’s center of mass during straight-line walking. Therefore, this study employs the vertical-axis gyroscope data (GyroZ) and a threshold-based method to determine the start and end of turning. As illustrated in the flowchart (Figure 4a), when an increase in the vertical-axis angular velocity is detected, the moment before the positive peak where the absolute angular velocity exceeds 40 dps is identified as the start of a left turn, and the moment after the positive peak where the absolute angular velocity falls below 40 dps is marked as the end of the left turn. Similarly, when a decrease in the vertical-axis angular velocity is detected, the moment before the negative peak where the absolute angular velocity exceeds 40 dps is identified as the start of a right turn, and the moment after the negative peak where the absolute angular velocity drops below 40 dps is marked as the end of the right turn. This threshold was determined iteratively based on experimental data, to ensure that the turnings can be distinguished, even when they might be obscured by stride signals. Figure 4b shows an example of the turning detection during the experiment.
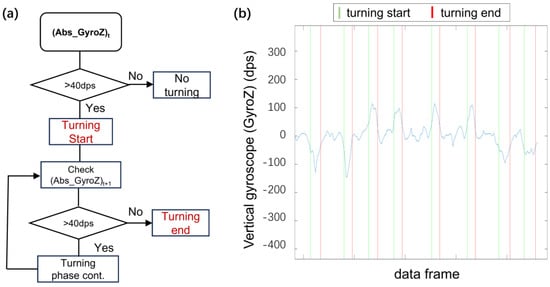
Figure 4.
(a) The flowchart of turning detection. (b) an example of the turning detection results.
Based on the starting and ending point of turning, a phase-aware turning correction was designed to dynamically adjust the walking trajectory during the pre-turn and post-turn phase. The pre-turn phase refers to the gait cycle prior to the turning start point, whereas the post-turn phase refers to the gait cycle following the turn end point. The underlying principle of the trajectory correction approach involves preserving the forward-motion trajectory components during pre-turn and post-turn phases, while compensating for estimation errors induced by non-forward directional movements, as follows
where is the non-forward directional movements. is the correction coefficient, which is dynamically computed as the ratio of forward-direction displacement magnitude to total displacement magnitude, serving as a real-time metric accounting for turn intensity.
2.4. Experimental Study
Eighteen young participants were involved in the experiment (10 male: age = 21.0 ± 1.2 years, mass = 65.2 ± 6.2 kg, height = 174.3 ± 5.5 cm; 8 female: age = 22.3 ± 2.1 years, mass = 46.6 ± 6.0 kg, height = 162.1 ± 6.4 cm). A post hoc power analysis was performed using G*Power software (Version 3.1.9.6) to assess the adequacy of the sample size. The results indicated that, for a Wilcoxon signed-rank test, the sample size was sufficient with a statistical power of 87% and a significance level of 5%. All participants self-reported their right foot as the dominant foot and were free from any diseases or medical conditions that would affect their gait patterns. The participants signed an informed consent form before the experiment. This study complied with the Declaration of Helsinki and was reviewed and approved by the Institutional Review Board of Shenzhen University.
The experiment was conducted in a gait laboratory. Four UWB anchors were secured at the top of the tripods (height = 1.8 m), placed at the four corners of a walking platform (Figure 5). The UWB anchors formed a 4-m by 7-m rectangular area. Two foldable blocking panels, 1.6 m in length and 2 m in height, were placed in the center area. They were used to simulate the NLOS scenarios, such as the office cube in the occupational settings. The walking path was marked by colored tapes adhered to the ground, guiding the participants to make 90-degree turns.
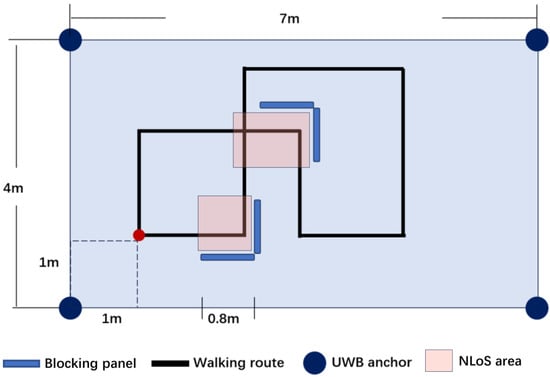
Figure 5.
The experimental set-up.
At the beginning of the experiment, clear instructions and sufficient practice time were given to the participants so that they could learn to walk along the defined turning path. They were instructed to follow the trajectory as closely as possible while avoiding deliberate alterations to their natural walking gait. After practice, the participants were asked to start from the designated point and walk along the prescribed trajectory. The experimenters conducted a visual inspection to ensure the participants followed the predefined walking path.
The total length of one full lap of the walking path was 16.2 m, including four left turns and four right turns. Each participant was required to walk eight laps along the trajectory, covering a total walking distance of approximately 129.6 m, with a walking duration of about 3–5 min. The actual walking trajectory (i.e., the ground truth) was defined as the predetermined walking path with the manual color-tape marking, which was later represented as a series of two-dimensional coordinates on the transverse (top-view) plane, spaced at one-centimeter intervals [21].
The walking trajectories were calculated based on UWB-only data, IMU-UWB with ESKF only (without turning correction model) method, and the presented integrated framework. The Mean Absolute Error (MAE) and Spearman correlation coefficient were calculated between the estimated walking trajectories and the actual walking trajectory, i.e., the “ground truth”. Lower MAE and higher correlation coefficient indicate better estimation accuracy. The Wilcoxon signed-rank test was conducted to compare the MAE and correlation coefficient across different methods. Additionally, the 95% confidence interval (CI) was calculated based on the differences between the 5th and 95th percentile values.
3. Results
Figure 6 illustrates an example of synchronized data obtained from the IMU and UWB (i.e., the tag). Notably, during the turning events, the gyroscope readings along the vertical axis (GyroZ) exhibit distinct peaks. Corresponding data frames reveal significant variations in the UWB raw data, attributed to NLOS scenarios and the impact of the turning maneuvers.
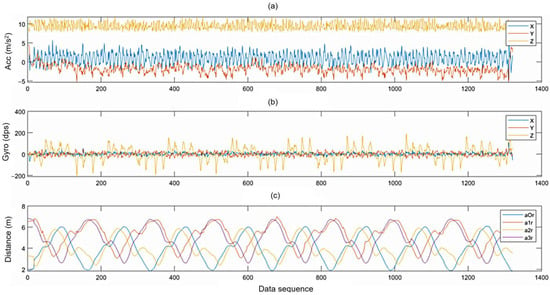
Figure 6.
An example of (a) IMU acceleration data used for ESKF; (b) IMU gyroscope data used for detection and ESKF; (c) the UWB data (the data received by the tag from the four anchors).
Figure 7 demonstrates the effectiveness of our algorithm in improving trajectory tracking accuracy, particularly during turns. While the UWB-alone and IMU-UWB trajectory exhibits noticeable deviations from the actual path, the trajectory estimated by the presented algorithm, closely follows the ground truth. The turning correction is especially effective, as seen in the sharp reduction of positional error during directional changes.
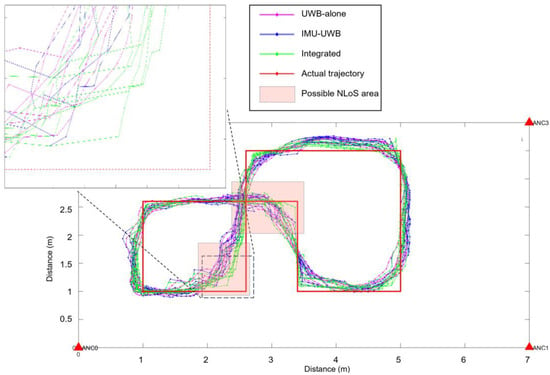
Figure 7.
An example of the estimated walking trajectories by different methods.
It is worth noting that all the estimated trajectories appeared smoother than the actual trajectory. This smoothing effect is likely because the participant did not make sharp 90-degree turns at the corners. However, we observed that the trajectories estimated by the integrated method were closer to the actual trajectories (i.e., the ground truth) compared to other methods.
The implementation of the presented integrated framework demonstrates significant improvements in walking trajectory estimation (Table 1). The mean absolute error (MAE) decreased from 22.2 cm to 7.0 cm (integrated), corresponding to a reduction in error percentage from 17.1% to 5.4%. On average, the presented algorithm demonstrated an 11.7% improvement in accuracy across all participants, compared to the UWB-alone method. Individual people’s data showed consistent enhancements, with error reductions ranging from 7.5% to 15.4%, highlighting the robustness of this algorithm accounting for individual differences (Table 1). UWB-IMU fusion with ESKF can reduce the MAE to 16.9 cm, with a 4% improvement over UWB alone. In contrast, the integrated framework significantly outperforms the UWB-IMU fusion, indicating the importance and effectiveness of the turning correction model. The Wilcoxon signed-rank test confirmed that the integrated framework resulted in significantly smaller MAE (z = −3.724, p-value = 0.0002, 95% CI: 9.8–20.0 cm) compared to the UWB-alone and UWB-IMU fusion with ESKF methods (Figure 8a). UWB-IMU fusion with the ESKF method also significantly improved the estimation over the UWB-alone method (z = −3.724, p-value = 0.0002, 95% CI: 1.5–12.5 cm).

Table 1.
The comparison of the MAE obtained from different methods.
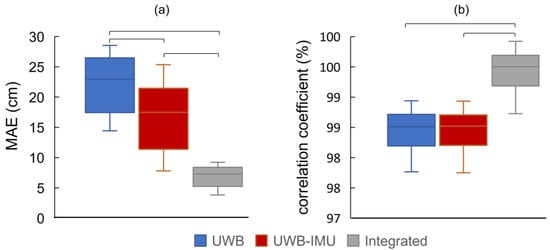
Figure 8.
The boxplot of the (a) mean absolute error (MAE), and (b) correlation coefficient, with the indication of significant differences found between groups based on the Wilcoxon signed-rank test.
This algorithm also resulted in a higher correlation coefficient, with improvements ranging from 0.49% to 1.16% (Figure 8b). Notably, the highest correlation (99.9%) was observed in participant 6, demonstrating near-perfect alignment with ground truth. These results confirm that the IMU-UWB fusion enhances tracking reliability and precision, reducing drift and noise inherent in IMU-only systems. The Wilcoxon signed-rank test confirmed that the integrated framework resulted in a significantly higher correlation coefficient (z = −3.724, p-value = 0.0002, 95% CI: 0.98–0.99) compared to the UWB-alone and UWB-IMU fusion with ESKF methods. However, no significant difference was found between the UWB-alone and UWB-IMU fusion with the ESKF method (z = −0.879, p-value = 0.379, 95% CI: 0–0.11).
4. Discussion
This study presents a novel walking trajectory estimation algorithm that addresses two critical challenges in indoor pedestrian tracking., i.e., the NLOS errors in UWB based trajectory tracking, and drift accumulation in IMU-based tracking, particularly during turning motions. By integrating an ESFK model with a gait-phase-aware turning correction module, our framework demonstrates significant improvements in trajectory estimation accuracy compared to UWB-only and conventional UWB-IMU fusion with the ESFK only method. The mean absolute error (MAE) decreased from 22.2 cm (UWB-only) to 7.0 cm (integrated framework), representing a 68.5% improvement (percentage reduction in MAE) in accuracy. Notably, the error percentage dropped from 17.1% to 5.4%. Such relative error reduction confirms the robustness of our approach in mitigating drift and NLOS-induced errors. The high correlation coefficients between the estimated and ground-truth trajectories further validate the framework’s reliability. These improvements are particularly evident during turning maneuvers, where traditional UWB-IMU fusion struggles due to accumulated IMU drift. Our algorithm’s ability to maintain sub-10 cm accuracy even in dynamic scenarios highlights its superiority over existing methods.
The ESKF model plays a critical role in enhancing trajectory estimation by dynamically adjusting error weights based on measurement reliability. Unlike traditional Kalman Filters or Extended Kalman Filters, the ESKF offers several key advantages. Firstly, The ESKF separates error dynamics from nominal state propagation, allowing faster convergence and reduced computational complexity. By estimating only the error state (rather than the full state), it minimizes linearization errors, which are common in EKF-based fusion [22]. Secondly, The ESKF dynamically adjusts Kalman gain based on real-time measurement noise covariance [23]. This can ensure that unreliable UWB data (e.g., during NLOS) are down-weighted, and in favor of IMU predictions when the UWB data is noisy. This adaptability is crucial for our application to have improvement under the NLOS scenario. Lastly, unlike prior works that use loosely coupled Kalman [24], the ESKF model directly integrates UWB ranging errors into IMU state estimation, which can further improve its robustness under NLOS [14].
On the other hand, the gait-phase-aware turning correction module addresses a critical limitation of IMU drift amplification during turning gait. Traditional UWB-IMU integration suffers from compounded drift during turns due to the integration of angular velocity errors. Without turning correction, IMU drift leads to exponential error growth during curved paths. Our results show that ESKF-based fusion alone reduced MAE by 4% compared to UWB-only, but the full framework (with turning correction) achieved 11.7% further improvement. A novelty of this model is that it cannot only detect the occurrence of the turning, but also distinguish between pre-turn, turning, and post-turn gait phases. The results demonstrated that the threshold-based turn detection reliably identifies turning initiations and terminations, and applying corrections only where needed. This phase-aware correction preserves straight-path trajectory components before and after turns. This dual-phase approach can prevent overcorrection while effectively mitigating turn-induced drift.
The true novelty of our approach lies in the tight coupling between the ESKF and turning correction systems. The ESKF provides robust baseline tracking during straight-line walking and brief NLOS events, while the turning module intervenes specifically during high-drift turning maneuvers. This integrated error correction strategy ensures that our framework outperforms conventional UWB-IMU fusion. While foot-mounted IMUs with Zero Velocity Update (ZUPT) can achieve high accuracy [25], they are still prone to possible sensor drift, especially in dynamic environments and during various gait scenarios, such as turning. The combination of IMU and UWB allows for cross-validation of both sensor output. This redundancy helps to identify and mitigate errors that may arise from either sensor, leading to a more robust state estimation.
While demonstrating superior accuracy, several practical limitations warrant discussion. The fixed 40 dps turn detection threshold, though effective in our experiments, may require adaptation for populations with different gait characteristics (e.g., elderly users or clinical cases). More importantly, such turning detection, more specifically, the determination of the starting and ending the turning action can possibly affect the turning correction approach. Therefore, future research could include conducting a comprehensive sensitivity study, varying the threshold from 20 to 80 dps, to better understand the impact of different thresholds on turn detection. Additionally, comparing our turning detection method against alternative detectors such as adaptive filters, gait phase hidden Markov models (HMMs), or cadence-based rules would provide deeper insights into the effect of turning detection on the accuracy of turning trajectory estimation. Additionally, the computational overhead of real-time ESKF updates and turn detection could challenge deployment on low-power wearable devices. Future work should explore adaptive thresholding and hardware optimization to enhance generalizability. The experiment was conducted in a controlled laboratory setting with healthy young individuals, which may restrict the generalizability of our findings to older adults or real-world environments. Furthermore, in industrial applications, several challenging scenarios could impact the performance of our method. For instance, continuous curves and turns greater than 90° may present difficulties in accurately detecting turns. Navigating stairs or uneven surfaces could introduce variability. Exploring these factors in future work would enhance the applicability and reliability of our findings in re-al-world scenarios. Utilizing a public dataset that includes raw signals and turn annotations could also allow for more comprehensive testing across diverse conditions and populations.
This work has significant practical implications. The sub-10 cm tracking accuracy enables applications like fall detection systems that demand precise motion capture, while the NLOS resilience makes it suitable for complex industrial environments. Perhaps most importantly, our solution demonstrates that careful modeling of specific gait events (like turns) can yield disproportionate improvements in human trajectory estimation. This insight can inform future pedestrian tracking research.
5. Conclusions
This study presents a novel UWB-IMU fusion framework that combines ESKF-based error compensation and gait-phase-aware turning correction to achieve unprecedented accuracy in walking trajectory estimation. By addressing both NLOS errors and turning-induced drift, our method outperforms existing approaches. Future work will focus on adaptive thresholding and edge-computing optimization to broaden applicability. The framework can be implemented for reliable indoor tracking in healthcare, industrial, and consumer navigation systems.
Author Contributions
Conceptualization, H.J., W.Z. and X.H.; methodology, X.H. and W.Z.; validation, T.P. and X.H.; formal analysis, Z.Z. and Q.F.; investigation, H.J., T.P. and X.H.; writing—original draft preparation, T.P. and X.H.; writing—review and editing, H.J., W.Z., X.H. and H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Shenzhen Science and Technology Program [JCYJ20210324093005015].
Data Availability Statement
Data are available upon reasonable inquiries and can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| K | Kalman Gain Matrix |
| F | State Transition Matrix |
| B | Control Input Matrix |
| H | Measurement Matrix |
| Q | Process Noise Covariance Matrix |
| δP | Position Error |
| δV | Velocity Error |
| δϕ | Misalignment Angles |
References
- Wei, L.; Wang, S.J. Motion tracking of daily living and physical activities in health care: Systematic review from designers’ perspective. JMIR Mhealth Uhealth 2024, 12, e46282. [Google Scholar] [CrossRef]
- Seifallahi, M.; Galvin, J.E.; Ghoraani, B. Curve walking reveals more gait impairments in older adults with mild cognitive impairment than straight walking: A Kinect camera-based study. J. Alzheimer’s Dis. Rep. 2024, 8, 423–435. [Google Scholar] [CrossRef] [PubMed]
- Duan, P.; Zhou, J.; Qiao, Y.; Guo, P. Block-based construction worker trajectory prediction method driven by site risk. Autom. Constr. 2024, 167, 105721. [Google Scholar] [CrossRef]
- Stirling, L.; Acosta-Sojo, Y.; Dennerlein, J.T. Defining a systems framework for characterizing physical work demands with wearable sensors. Ann. Work Expo. Health 2024, 68, 443–465. [Google Scholar] [CrossRef]
- Miola, L.; Muffato, V.; Sella, E.; Meneghetti, C.; Pazzaglia, F. GPS Use and Navigation Ability: A Systematic Review and Meta-Analysis. J. Environ. Psychol. 2024, 102417. [Google Scholar] [CrossRef]
- Hamadi, A.; Latoui, A. An accurate smartphone-based indoor pedestrian localization system using ORB-SLAM camera and PDR inertial sensors fusion approach. Measurement 2025, 240, 115642. [Google Scholar] [CrossRef]
- Al-Okby, M.F.; Junginger, S.; Roddelkopf, T.; Thurow, K. UWB-Based Real-Time Indoor Positioning Systems: A Comprehensive Review. Appl. Sci. 2024, 14, 11005. [Google Scholar] [CrossRef]
- Zhang, K.; Gao, S.; Lv, J.; Lin, T.; Chen, P. UWTrack: Clustering Assisted Multi-person Passive Indoor Tracking via IR-UWB. IEEE Trans. Instrum. Meas. 2024, 73, 5038914. [Google Scholar] [CrossRef]
- Pardhu, T.; Kumar, V.; Kumar, P.; Deevi, N. Advancements in UWB Based Human Motion Detection Through Wall: A Comprehensive Analysis. IEEE Access 2024, 12, 89818–89835. [Google Scholar] [CrossRef]
- Qiao, J.; Yang, F.; Liu, J.; Huang, G.; Zhang, W.; Li, M. Advancements in Indoor Precision Positioning: A Comprehensive Survey of UWB and Wi-Fi RTT Positioning Technologies. Network 2024, 4, 545–566. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, D.; Gui, L.; Sheng, B.; Cai, H.; Xiao, F.; Han, J. UWTracking: Passive human tracking under LOS/NLOS scenarios using IR-UWB radar. IEEE Trans. Mob. Comput. 2024, 23, 11853–11870. [Google Scholar] [CrossRef]
- Xu, L.; Chen, Y.; Fan, B.; Yang, C.; Yang, W. Wearable Continuous Gait Phase Estimation During Walking, Running, Turning, Stairs, and Over Uneven Terrain. IEEE Trans. Med. Robot. Bionics 2024, 6, 1135–1146. [Google Scholar] [CrossRef]
- Ge, Y.; Li, W.; Farooq, M.; Qayyum, A.; Wang, J.; Chen, Z.; Cooper, J.; Imran, M.A.; Abbasi, Q.H. Logait: Lora sensing system of human gait recognition using dynamic time warping. IEEE Sens. J. 2023, 23, 21687–21697. [Google Scholar] [CrossRef]
- Ali, R.; Liu, R.; Nayyar, A.; Qureshi, B.; Cao, Z. Tightly coupling fusion of UWB ranging and IMU pedestrian dead reckoning for indoor localization. IEEE Access 2021, 9, 164206–164222. [Google Scholar] [CrossRef]
- Naheem, K.; Kim, M.S. A low-cost foot-placed UWB and IMU fusion-based indoor pedestrian tracking system for IoT applications. Sensors 2022, 22, 8160. [Google Scholar] [CrossRef] [PubMed]
- Feng, D.; Wang, C.; He, C.; Zhuang, Y.; Xia, X.G. Kalman-filter-based integration of IMU and UWB for high-accuracy indoor positioning and navigation. IEEE Internet Things J. 2020, 7, 3133–3146. [Google Scholar] [CrossRef]
- Cardarelli, S.; Mengarelli, A.; Tigrini, A.; Strazza, A.; Di Nardo, F.; Fioretti, S.; Verdini, F. Single IMU displacement and orientation estimation of human center of mass: A magnetometer-free approach. IEEE Trans. Instrum. Meas. 2019, 69, 5629–5639. [Google Scholar] [CrossRef]
- Novak, D.; Goršič, M.; Podobnik, J.; Munih, M. Toward real-time automated detection of turns during gait using wearable inertial measurement units. Sensors 2014, 14, 18800–18822. [Google Scholar] [CrossRef]
- Fino, P.C.; Frames, C.W.; Lockhart, T.E. Classifying step and spin turns using wireless gyroscopes and implications for fall risk assessments. Sensors 2015, 15, 10676–10685. [Google Scholar] [CrossRef]
- Del Rosario, M.B.; Khamis, H.; Ngo, P.; Lovell, N.H.; Redmond, S.J. Computationally efficient adaptive error-state Kalman filter for attitude estimation. IEEE Sens. J. 2018, 18, 9332–9342. [Google Scholar] [CrossRef]
- Sagawa, K.; Ohkubo, K. 2D trajectory estimation during free walking using a tiptoe-mounted inertial sensor. J. Biomech. 2015, 48, 2054–2059. [Google Scholar] [CrossRef]
- Liu, W.; Song, D.; Wang, Z.; Fang, K. Comparative analysis between error-state and full-state error estimation for KF-based IMU/GNSS integration against IMU faults. Sensors 2019, 19, 4912. [Google Scholar] [CrossRef] [PubMed]
- Chhabra, A.; Venepally, J.R.; Kim, D. Measurement noise covariance-adapting Kalman filters for varying sensor noise situations. Sensors 2021, 21, 8304. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.; Fu, Z. An adaptive Kalman filter loosely coupled indoor fusion positioning system based on inertial navigation system and ultra-wide band. Measurement 2025, 244, 116412. [Google Scholar] [CrossRef]
- Bi, J.; Wang, J.; Yu, B.; Yao, G.; Wang, Y.; Cao, H.; Xing, H. Precise Step Counting Algorithm for Pedestrians Using Ultra-Low-Cost Foot-Mounted Accelerometer. Eng. Appl. Artif. Intell. 2025, 150, 110619. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).