Replacing Batch Normalization with Memory-Based Affine Transformation for Test-Time Adaptation

Abstract

Batch normalization (BN) has become a foundational component in modern deep neural networks. However, one of its disadvantages is its reliance on batch statistics that may be unreliable or unavailable during inference, particularly under test-time domain shifts. While batch-statistics-free affine transformation methods alleviate this by learning per-sample scale and shift parameters, most treat samples independently, overlooking temporal or sequential correlations in streaming or episodic test-time settings. We propose LSTM-Affine, a memory-based normalization module that replaces BN with a recurrent parameter generator. By leveraging an LSTM, the module produces channel-wise affine parameters conditioned on both the current input and its historical context, enabling gradual adaptation to evolving feature distributions. Unlike conventional batch-statistics-free designs, LSTM-Affine captures dependencies across consecutive samples, improving stability and convergence in scenarios with gradual distribution shifts. Extensive experiments on few-shot learning and source-free domain adaptation benchmarks demonstrate that LSTM-Affine consistently outperforms BN and prior batch-statistics-free baselines, particularly when adaptation data are scarce or non-stationary.

1. Introduction

Normalization layers—most notably batch normalization (BN)—have become a cornerstone of modern deep neural networks, stabilizing optimization and improving generalization by controlling the distribution of intermediate features during training [1]. Despite its success, BN implicitly relies on the availability and reliability of batch-level statistics, an assumption that is often violated at test time. In particular, few-shot learning (FSL) and source-free domain adaptation (SFDA) operate under restricted data regimes or distribution shift, where batch composition is small, imbalanced, or even sequential [2,3,4]. Under such non-i.i.d. conditions, the mismatch between training and testing statistics can degrade performance as running estimates fail to represent new input distributions accurately.

We revisit BN from the perspective of feature-wise affine modulation: beyond computing batch statistics, BN effectively applies a learned scale and shift to features. Prior analysis shows that BN’s benefit largely arises from smoothing the optimization landscape rather than merely mitigating internal covariate shift [5]. This motivates a complementary direction—retain the representational benefits of BN’s affine transform while removing explicit dependence on batch moments, and make the modulation adapt over time as test inputs evolve. Concretely, we seek a module that (i) is batch-statistics-free, (ii) adapts per instance without backpropagation at test time, and (iii) can be dropped into standard backbones with minimal changes to the training recipe.

To this end, we propose LSTM-Affine, a memory-driven affine transformation that replaces BN’s fixed affine part with parameters generated by a lightweight LSTM conditioned on the temporal context of features [6]. By maintaining hidden states across samples, LSTM-Affine captures slow distribution drift and stabilizes predictions in streaming or episodic evaluations. Unlike approaches that update BN statistics or require test-time optimization, LSTM-Affine performs purely feed-forward adaptation: for each incoming sample, it predicts channel-wise scale and shift and immediately modulates the features—no batch moments, moving averages, or test-time backpropagation are needed. The design is drop-in: in convolutional networks, we place the module after each convolutional block and before activation; in fully connected architectures, we place it before the final classifier.

Our empirical study targets two regimes where non-i.i.d. effects are prominent: (i) FSL on Omniglot, MiniImageNet, and TieredImageNet [2,3,4], and (ii) SFDA on digits (MNIST, USPS, and SVHN) and Office-31. For SFDA, we adopt a unified SHOT protocol to isolate the contribution of the normalization/affine component: the adaptation pipeline is kept fixed, and we only swap the BN-based affine part for different variants, including our LSTM-Affine. This organization enables like-for-like comparisons while avoiding confounds due to protocol changes. We also relate LSTM-Affine to batch-statistics-free designs that learn affine modulation without explicit whitening [5,7], and to recurrent normalization paradigms that insert temporal modeling into normalization [8]; in contrast, we produce normalization-free, temporally conditioned affine parameters expressly for test-time robustness. In this paper, non-i.i.d. refers to test conditions that deviate from the i.i.d. training assumption, including domain shift (as in SFDA), temporally correlated or streaming inputs, few-shot episodic evaluation with very small or imbalanced batches, and single-instance/small-batch inference where batch statistics are unreliable.

The main contributions of this work are as follows: (1) LSTM-Affine: We introduce a batch-statistics-free, memory-driven affine transformation that replaces BN’s affine part and predicts per-instance (γ, β) from a temporal feature context via a lightweight LSTM [6]. (2) Drop-in rule and procedures: We provide a simple integration rule (after each conv block and before activation) and formalize the training and SFDA test-time inference workflows (Algorithms 1 and 2 in Section 1). (3) Unified evaluation and gains: Under a unified SHOT protocol for SFDA—and on standard FSL benchmarks [2,3,4]—LSTM-Affine consistently improves over BN and adaptive baselines, while requiring no test-time backprop or batch statistics. (4) Analysis of temporal memory: We analyze hidden-state design and reset policies, showing how temporal memory improves stability and robustness under distribution shifts.

Algorithm 1: LSTM-Affine—Training/Forward Integration (for FSL and supervised training)

Input: Training set $D_{tr}$, validation set $D_{val}$; feature extractor ${\theta }_F$ with $L$ target layers; LSTM-Affine generators ${\left\{{\theta }_{\mathrm{L}\mathrm{S}\mathrm{T}\mathrm{M},i}\right\}}_{i=1}^L$ (output $\gamma ,\beta$); classifier ${\theta }_C$; epochs $T$; mini-batch size $m$; learning rate $\eta$; hidden size $d$; state reset policy (when to reset $\left\{h_i\right\}$). Output: Trained parameters ${\theta }_F^{\ast }$, ${\left\{{\theta }_{LSTM,i}^{\ast }\right\}}_{i=1}^L$, ${\theta }_C^{\ast }$. 1.    for epoch $t\leftarrow 1$ to $T$ do 2.     Sample a mini-batch $B_m={\left\{{(x_j,y}_j)\right\}}_{j=1}^m\subset D_{tr}$. 3.     Apply the state reset policy to initialize/keep hidden states ${\left\{h_i\right\}}_{i=1}^L$. 4.     ${Z\leftarrow B}_m$ # current tensor traveling through the network 5.     for layer $i\leftarrow 1$ to $L$ do 6.        $U_i\leftarrow {\theta }_{F,i}\left(Z\right)$ # backbone convolution/FC block output 7.        ${(\gamma }_i,{\beta }_i,h_i) \leftarrow {\theta }_{\mathrm{L}\mathrm{S}\mathrm{T}\mathrm{M},i}(GAP\left(U_i\right),h_i)$ # temporal parameter generation 8.        $U_i\leftarrow {\gamma }_i\odot U_i+{\beta }_i$ # channel-wise affine modulation (no batch statistics) 9.        $Z\leftarrow Activation\left(U_i\right)$ # e.g., ReLU (follow the backbone design) 10.     end for 11.    $\widehat{y}\leftarrow {\theta }_C\left(Z\right)$; 12.      $L \leftarrow CE(\widehat{y},y)$; # compute loss 13.      Validate on $D_{val}$ and keep the best checkpoint. 14.    end for 15.    return ${\theta }_F^{\ast }$, ${\left\{{\theta }_{LSTM,i}^{\ast }\right\}}_{i=1}^L$, ${\theta }_C^{\ast }$.

Algorithm 2: LSTM-Affine—SFDA/SHOT-Style Test-Time Inference (No Backprop)

Input: Pretrained feature extractor ${\theta }_F$ with $L$ target layers; classifier ${\theta }_C$; LSTM-Affine generators ${\left\{{\theta }_{\mathrm{L}\mathrm{S}\mathrm{T}\mathrm{M},i}\right\}}_{i=1}^L$; unlabeled target-domain stream $X_t$ (single instance or mini-batches); hidden size; state reset policy (episode-/batch-wise). Output: Target predictions $\left\{{\widehat{y}}_t\right\}$ (and carried hidden states). 1.    Initialize/keep hidden states ${\left\{h_i\right\}}_{i=1}^L$ according to the reset policy. 2.    for each incoming target sample or mini-batch $x_t\in X_t$ do 3.    $Z\leftarrow x_t$ 4.    for layer $i\leftarrow 1$ to $L$ do 5.       $U_i\leftarrow {\theta }_{F,i}\left(Z\right)$  # backbone block output 6.       ${(\gamma }_i,{\beta }_i,h_i) \leftarrow {\theta }_{\mathrm{L}\mathrm{S}\mathrm{T}\mathrm{M},i}(GAP\left(U_i\right),h_i)$  # temporal parameter generation 7.       ${ U}_i\leftarrow {\gamma }_i\odot U_i+{\beta }_i$ # channel-wise affine modulation (no batch stats) 8.         $Z\leftarrow Activation\left(U_i\right)$  # e.g., ReLU (follow backbone) 9.    end for 10.     ${\widehat{y}}_t\leftarrow arg {max}_k{\theta }_C\left(Z\right)\left[k\right]$ # feed-forward prediction (no test-time backprop) 11. end for

2. Related Work

Batch-normalization-based approaches normalize activations using batch moments and then apply a learnable affine transform, yielding faster training and improved generalization [1]. However, their dependency on reliable batch statistics can be problematic under non-i.i.d. or low-batch scenarios, especially at test time. Here, non-i.i.d. refers to test conditions that deviate from the i.i.d. training assumption, including domain shift (e.g., SFDA), temporally correlated streams/online inference, few-shot episodic evaluation with small or imbalanced batches, and single-instance or small-batch inference where batch statistics are unreliable. Alternatives such as Group Normalization (GN), Instance Normalization (IN), and Layer Normalization (LN) reduce batch dependence but do not explicitly exploit temporal continuity [9,10,11].

A complementary line removes explicit whitening and instead adapts normalization parameters through conditional modulation, such as FiLM [12] and AdaBN [13]. AdaBN replaces the source-domain batch statistics in BN with those computed from target test data, which still requires batch-level moments [5,7,14] at test time—making it incompatible with instance-wise or online adaptation. Yet these designs often overlook cross-sample temporal structure, limiting adaptation to evolving distributions. Recurrent or memory-based mechanisms introduce temporal modeling into normalization/modulation modules—e.g., Recurrent Batch Normalization—to capture long-term dependencies and maintain adaptation states for continual or online learning [8,15]. Nevertheless, many such methods still rely on explicit statistical normalization, making them sensitive when accurate moment estimates are unavailable.

Meta-learning has also been used to adapt normalization behavior across tasks and domains. MetaBN [2], for instance, meta-parameterizes statistics or affine parameters to improve transfer. Our earlier MetaAFN [16] removes the dependence on batch moments and generates input-adaptive affine parameters from the current instance, but it does not explicitly model temporal memory. Beyond these normalization-centric directions, test-time adaptation (TTA) methods have emerged; a representative BN-based approach is TENT, which minimizes prediction entropy at test time and updates BN-related parameters via backpropagation [17]. In our evaluations, we focus on a unified SHOT protocol for SFDA and isolate the effect of the normalization/affine component by swapping BN for different variants—keeping the rest of the pipeline unchanged—to enable like-for-like comparison.

3. Method: LSTM-Affine

Building on the limitations identified in prior normalization and feature modulation methods, we propose LSTM-Affine, a batch-statistics-free, memory-driven affine transformation mechanism that integrates temporal context into parameter generation.

In this section, we introduce LSTM-Affine, a novel approach designed to replace traditional batch normalization (BN) with a memory-based affine transformation module. The key idea is to eliminate the dependency on batch statistics by learning a dynamic function that generates affine parameters conditioned on the temporal context of input features. This is particularly useful in scenarios such as test-time adaptation, online inference, or few-shot learning, where reliable batch-level normalization is either infeasible or suboptimal.

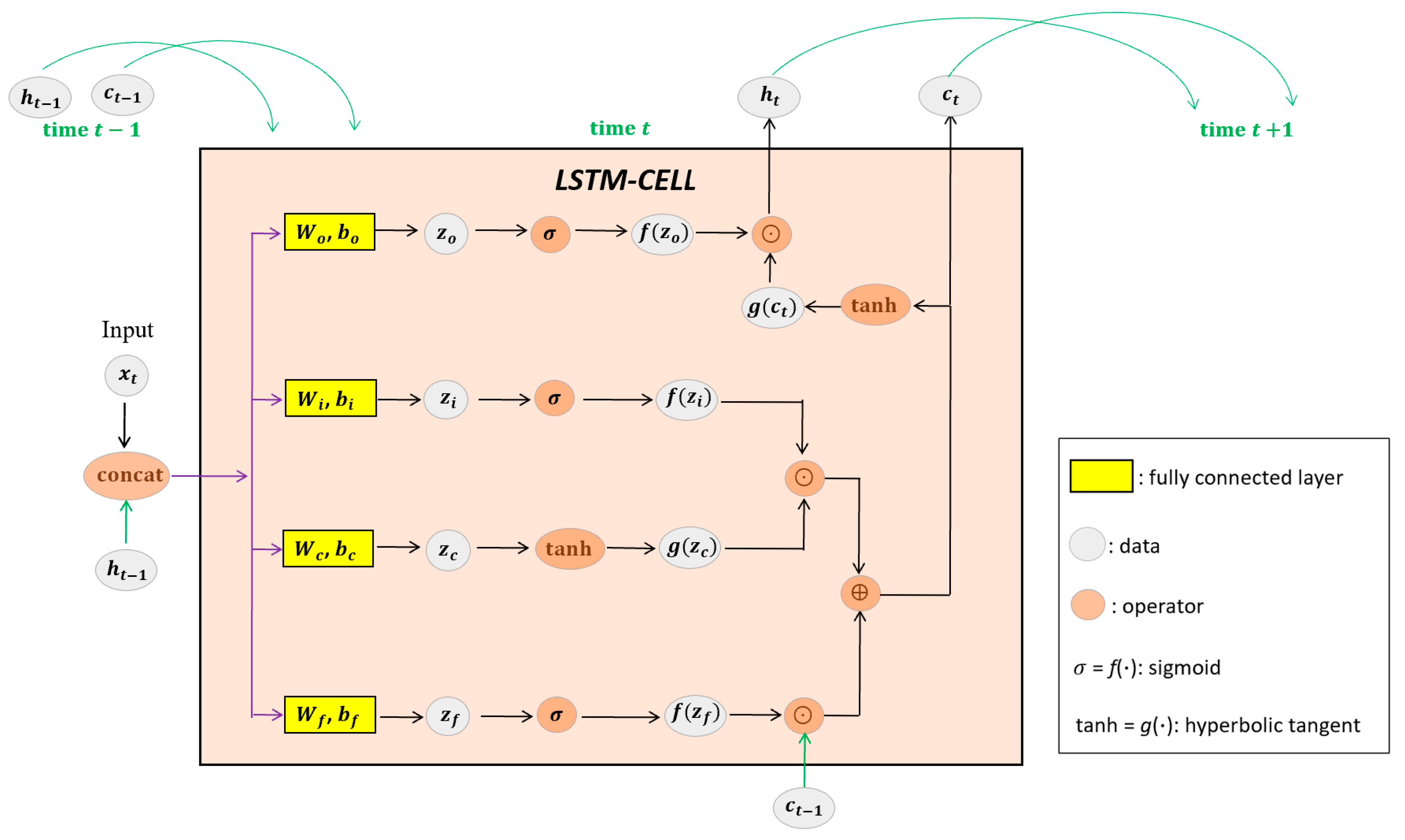
LSTM-Affine leverages the sequential modeling capability of Long Short-Term Memory (LSTM) [6] networks to maintain a hidden memory state that accumulates information from previously seen features. Instead of normalizing the input using batch-level mean and variance, we directly apply an LSTM-predicted affine transformation to the incoming feature map, thereby achieving the same representational modulation effect while remaining independent of batch composition.

We will now describe the architecture and mechanisms of LSTM-Affine in detail, starting with a conceptual overview, followed by the design of the LSTM-based affine generator, training objectives, and comparisons with traditional BN-based approaches.

3.1. LSTM-Affine: Overview and Architecture

We propose LSTM-Affine, a batch-statistics-free, memory-driven affine transformation that replaces the fixed affine part of batch normalization (BN) with parameters generated from temporal context. Unlike BN—which relies on mini-batch moments followed by a learnable affine transform—LSTM-Affine directly predicts channel-wise scale and shift for each incoming sample via a lightweight LSTM, enabling per-instance, feed-forward adaptation without batch statistics, moving averages, or test-time backpropagation. In convolutional networks, the module is inserted after each convolutional block and before the activation; in fully connected architectures, it is placed before the final classifier layer. This placement keeps downstream nonlinearities unchanged while allowing the affine modulation to reshape intermediate features analogously to BN’s affine step but without requiring batch moments. Each target layer is paired with its own LSTM-Affine submodule and maintains independent recurrent states so that temporal information can be captured locally per depth. Unless otherwise specified, we set the hidden size to $d =128$ across experiments, which balances adaptation capacity and efficiency.

Let $x_t\in R^{C\times H\times W}$ denote the channel-wise feature map at time $t$. The module predicts channel-wise scale and shift parameters ${\gamma }_t,{\beta }_t\in R^C$ and applies a feature-wise affine multiplication, as shown in (1), where ⊙ denotes channel-wise multiplication.

For comparison, standard batch normalization (BN), defined in (2), can be reformulated into an equivalent affine form as in (3). In this formulation, $\mu$ and ${\sigma }^2$ denote the batch mean and variance, $\epsilon$ is a small constant for numerical stability, and $\gamma ,\beta$ are learnable affine parameters. The resulting ${\gamma }^{\prime }$ and ${\beta }^{\prime }$ represent the induced affine parameters. This reformulation highlights that BN essentially modulates input features through affine scaling and shifting, with parameters derived from batch statistics—making it a form of statistically driven affine transformation.

In contrast, our LSTM-Affine module retains the affine modulation structure in (1), but eliminates the reliance on batch moments. Instead, it generates the affine parameters $({\gamma }_t,{\beta }_t)$ dynamically from the temporal context, enabling more adaptive and sequence-aware modulation.

$${\widehat{x}}_t={\gamma }_t\odot x_t+{\beta }_t$$

(1)

$$BN\left(x\right)={\displaystyle \frac{x}{\sqrt{{\sigma }^2+\epsilon }}}\ast \gamma +\left(-{\displaystyle \frac{\mu }{\sqrt{{\sigma }^2+\epsilon }}}\ast \gamma +\beta \right)$$

(2)

$$BN\left(x\right)={\gamma }^{\prime }\ast x+{\beta }^{\prime },\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} {\gamma }^{\prime }={\displaystyle \frac{\gamma }{\sqrt{{\sigma }^2+\epsilon }}}, {\beta }^{\prime }=-{\displaystyle \frac{\mu }{\sqrt{{\sigma }^2+\epsilon }}}\ast \gamma +\beta$$

(3)

To enable context-aware affine modulation, we generate the scale and shift parameters using a lightweight LSTM. Given the input feature map x_t, we first apply global average pooling (GAP) to obtain a compact channel descriptor ${\overline{x}}_t$, as shown in (4). This descriptor ${\overline{x}}_t$ is then fed into an LSTM that maintains temporal states $(h_{t-1},c_{t-1})$ and produces updated hidden and cell states $(h_t,c_t)$, as shown in (5).

$${\overline{x}}_t={\displaystyle \frac{1}{H·W}}{\sum }_{i=1}^H{\sum }_{j=1}^W{x}_t[:,i,j]$$

(4)

$$h_t,c_t=LSTM({\overline{x}}_t,h_{t-1},c_{t-1};\mathsf{\Theta })$$

(5)

We then use a linear projection with parameters $W_p\in R^{2C\times d}$ and $b_p\in R^{2C}$ to map the hidden state to the affine parameters, as shown in (6). The resulting modulation is applied channel-wise to every spatial location, as shown in (7).

$$[{\gamma }_t,{\beta }_t]=W_p{h}_t+b_p$$

(6)

$${\widehat{x}}_t\left[:,i,j\right]={\gamma }_t\odot x_t\left[:,i,j\right]+{\beta }_t$$

(7)

Training proceeds end-to-end together with the backbone using the task loss, and no special regularizers beyond standard weight decay are required. At inference, test samples (or mini-batches) are processed sequentially; recurrent states are carried over across samples—or reset according to a specified policy (episode-wise or batch-wise)—to encode temporal context and track gradual distribution shifts, thereby enabling purely feed-forward test-time adaptation without computing or updating batch statistics and without any optimization at test time. Conceptually, LSTM-Affine can be seen as retaining BN’s beneficial affine modulation while replacing batch-moment estimation with a temporally conditioned parameter generator; empirically, the temporal memory stabilizes predictions under continuous distribution shifts and alleviates the fragility of batch statistics in non-i.i.d. or low-batch regimes (e.g., FSL, SFDA, and streaming/online settings).

3.2. Network Design

Following the formulation and core ideas introduced in Section 3.1, this section focuses on the practical architecture and implementation details of the proposed LSTM-Affine module, particularly how it integrates into deep neural networks for adaptive feature modulation.

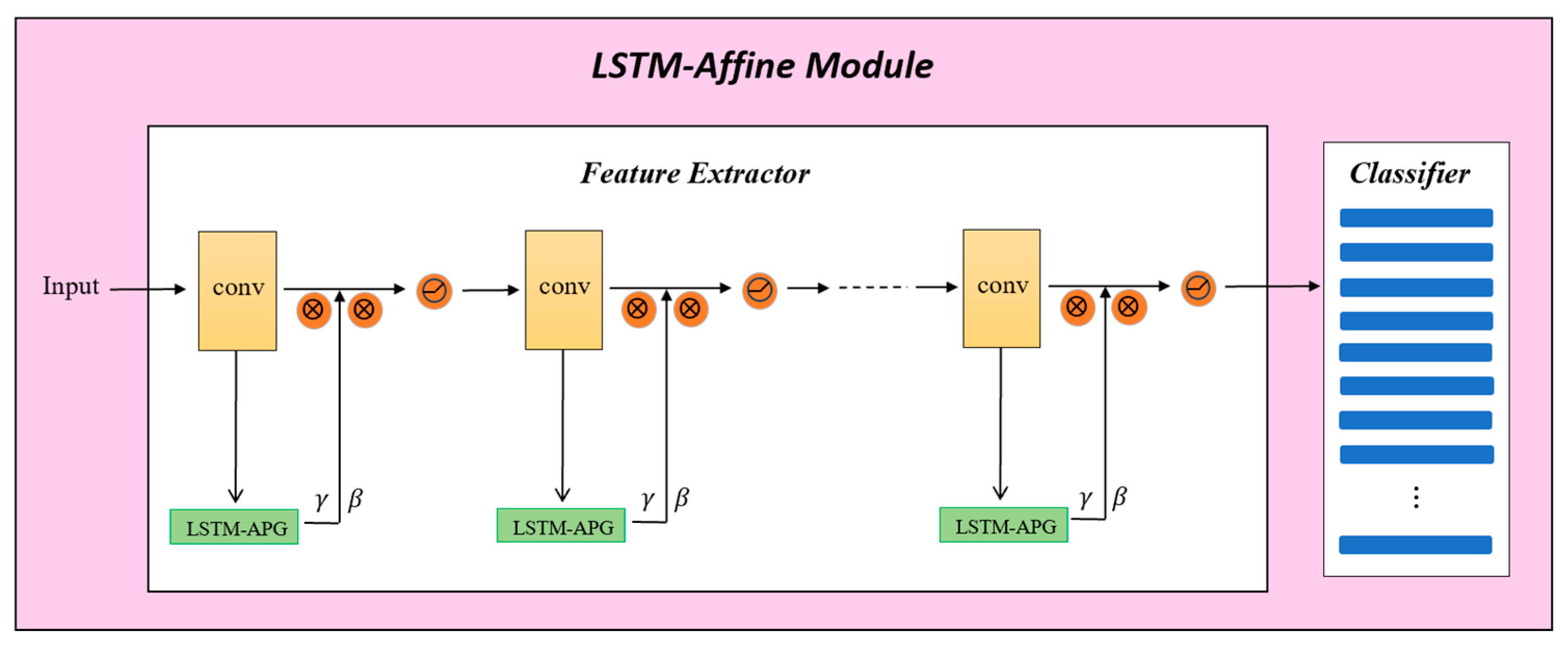
Each LSTM-Affine unit is inserted into the network as a standalone module assigned to a specific layer—typically after a convolutional block and before the activation function. Rather than applying batch-based normalization followed by a fixed affine transformation, the LSTM-Affine module dynamically generates the affine parameters based on the temporal context encoded in an LSTM. This design allows the model to adapt feature distributions across time, especially in settings where input data are non-i.i.d., such as streaming or episodic test-time scenarios.

To process the input, the feature map is first compressed into a compact representation through global average pooling, producing a channel-wise descriptor that serves as the input to the LSTM. The LSTM maintains its own hidden and cell states across time, capturing contextual patterns and enabling sequential awareness. The output hidden state is then projected through a fully connected layer to produce the channel-wise scale and shift parameters. These parameters are used to perform affine modulation directly on the original feature map, effectively reshaping it in a context-aware manner.

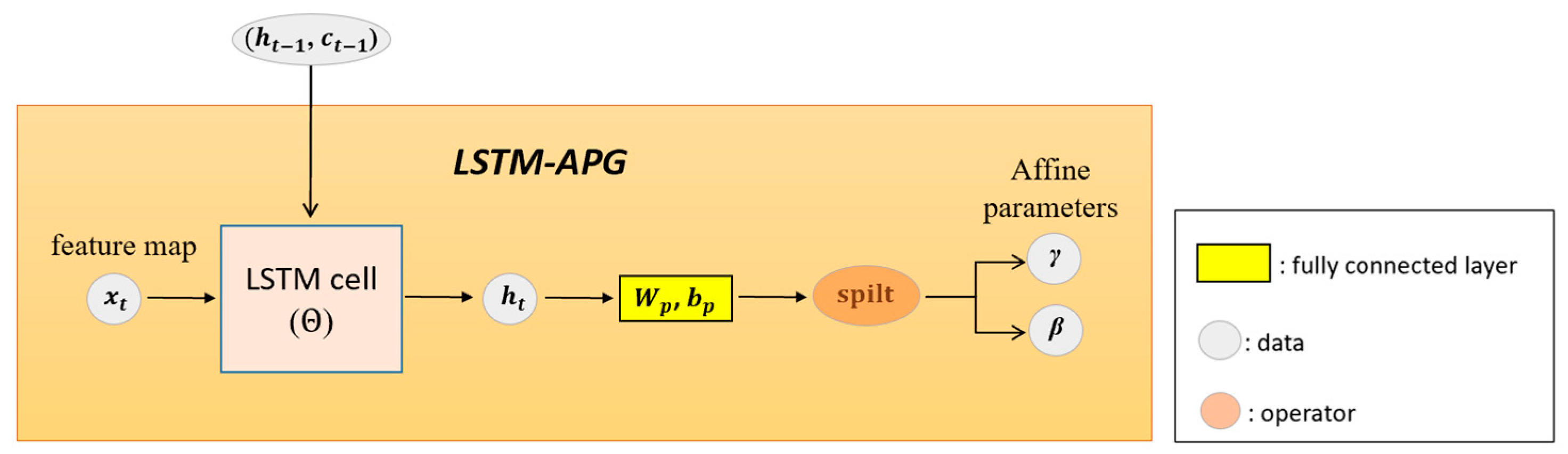
The entire operation is visualized in Figure 1, Figure 2 and Figure 3. Figure 1 illustrates the internal structure of the LSTM cell, which governs how the current input descriptor interacts with the memory from previous inputs. Figure 2 shows the overall architecture of the affine parameter generator, including how the input descriptor is processed and projected. Figure 3 provides an end-to-end view of the complete data flow: the feature map is pooled, passed through the LSTM-Affine module, and modulated with generated parameters—all achieved without computing any normalization statistics.

By assigning a separate LSTM-Affine generator to each layer, the model can maintain independent temporal memory across network depth. This prevents interference between semantically different layers and improves adaptation fidelity. During training, the modules are updated jointly with the backbone using the same task objective, requiring no additional supervision. At inference, test samples are processed sequentially, and the LSTM states are propagated across inputs—enabling efficient, purely feed-forward adaptation without test-time optimization or backpropagation. This makes the method well-suited for real-time or resource-constrained scenarios where batch normalization and online learning are impractical.

The precise training and test-time procedures are detailed in Algorithm 1 and Algorithm 2, respectively.

The complete operation is summarized in Figure 3: the feature map is pooled into ${\overline{x}}_t$, processed by the LSTM-APG using both the current descriptor and its memory states, projected into ${\gamma }_t$ and ${\beta }_t$, and applied to the feature map. Each LSTM-APG is assigned to a specific layer, maintaining its own memory to avoid interference between semantically distinct features. Training is performed end-to-end with the same task loss as the baseline. During inference, test samples are processed sequentially, carrying forward LSTM states to adapt to evolving input distributions without relying on batch statistics, moving averages, or backpropagation. For clarity, the pooling step is omitted in Figure 2 and Figure 3, but is applied in all experiments.

Implementation details and the step-by-step procedures are provided in Algorithm 1 (training) and Algorithm 2 (SFDA inference).

4. Experimental Results

We evaluate the proposed LSTM-Affine on few-shot learning (FSL) and source-free domain adaptation (SFDA) benchmarks, including digit recognition and Office-31 datasets. Unless otherwise noted, results are averaged over five independent runs. Ablation studies are additionally conducted to analyze the contributions of temporal memory and hidden states.

4.1. Datasets and Experimental Settings

For the FSL experiments, we use three standard benchmarks: Omniglot [18], MiniImageNet [19], and TieredImageNet [20], following the 5-way 5-shot classification protocol [3]. Each model is trained on the respective training split and evaluated on unseen classes from the test split.

For SFDA, we adopt two settings: (1). Digits SFDA: MNIST [21], USPS [22], and SVHN [23], with domain adaptation across U → M, S → M, and M → U tasks. (2). Office-31 SFDA: Amazon (A), Webcam (W), and DSLR (D) domains [24], with adaptation across A → D, A → W, W → D, W → A, D → A, and D → W tasks.

For LSTM-Affine, the LSTM hidden size $d$ is set to 128, determined empirically to balance adaptation capacity and efficiency. A sensitivity study for $d\in \{64, 128, 256\}$ shows minor variation in performance (see also [2,16]). Each LSTM-Affine module is inserted after each convolutional block and before the activation (or before the final classifier in fully connected networks), and maintains its own hidden and cell states $(h_i,c_i)$ per layer. These states are carried across samples to support temporal adaptation during test time, unless explicitly reset in ablation experiments.

4.2. Few-Shot Learning

We first evaluate LSTM-Affine on the 5-way 5-shot classification task.

Table 1. Experimental results (%) on the 5-way 5-shot few-shot learning (FSL) tasks. Each value is the average accuracy over five runs.

Method	Omniglot	MiniImageNet	TieredImageNet	Avg.
BN	94.8	67.5	72.4	79.4
MetaBN	95.2	70.2	75.5	80.3
MetaAFN	96.7	72.3	77.0	82.0
LSTM-Affine (ours)	99.0	74.5	79.4	84.3

compares our method against BN, MetaBN [2], and MetaAFN [16]. The results show that LSTM-Affine, being batch-statistics-free and memory-driven, achieves the best accuracy, surpassing MetaAFN by 2–3%. It is also worth noting that the reported accuracy on Omniglot is much higher than on MiniImageNet and TieredImageNet. This is expected and consistent with prior studies, since Omniglot contains simple handwritten characters with clear structural patterns, making it easier for models to generalize in few-shot settings. In contrast, MiniImageNet and TieredImageNet consist of natural images with high intra-class variability and fine-grained distinctions, which present greater challenges. The performance gap therefore reflects the intrinsic differences in dataset difficulty rather than limitations of the proposed method.

4.3. Source-Free Domain Adaptation (Digits)

We further evaluate our method on digit classification with domain shifts (MNIST, USPS, and SVHN). Following the clarification in Section 4.1, all SFDA baselines in

Table 2. Comparison of source-free domain adaptation (SFDA) results (%) on digit classification tasks with domain shifts among USPS, MNIST, and SVHN. Each method is evaluated using the SHOT protocol, and results are averaged over all domain pairs.

Method	U → M	S → M	M → U	Avg.
SHOT (BN)	97.71	99.05	98.17	98.31
SHOT (MetaBN)	97.66	98.82	98.17	98.22
SHOT (MetaAFN)	97.61	99.09	98.17	98.29
SHOT (LSTM-Affine)	98.04	99.10	98.66	98.60

and

Table 3. Comparison of source-free domain adaptation (SFDA) results (%) on the Office-31 dataset across three transfer tasks under the SHOT protocol. Reported values are average accuracies over five runs.

Method	A → D	A → W	W → D	W → A	D → A	D → W	Average
SHOT (BN)	90.29	92.24	99.90	72.82	73.39	97.78	87.74
SHOT (MetaBN)	92.21	92.20	99.80	71.14	73.77	98.03	87.86
SHOT (MetaAFN)	93.52	90.25	99.60	76.75	75.21	98.10	88.91
SHOT (LSTM-Affine)	94.05	92.26	99.90	77.94	76.14	98.37	89.78

are implemented within the same SHOT protocol, differing only in the normalization/affine component. Table 2 reports average accuracy across all domain pairs. LSTM-Affine consistently outperforms all baselines. Unlike optimization-based test-time adaptation methods such as SHOT, which require backpropagation during inference and incur additional computational and memory overhead, LSTM-Affine performs purely feed-forward adaptation through its recurrent generator, maintaining efficiency comparable to standard BN inference.

4.4. Source-Free Domain Adaptation (Office-31)

We also evaluate our method on the Office-31 dataset (A → D, A → W, W → D, W → A, D → A, D → W). Table 3 shows that LSTM-Affine achieves the best average accuracy among all compared methods.

4.5. Ablation Study

To better understand the roles of temporal memory and hidden states in LSTM-Affine, we perform ablation experiments by selectively removing these components (

Table 4. Ablation study of LSTM-Affine. Average accuracy (%) across all benchmarks when removing temporal memory (“No memory”) or hidden state (“No hidden state”). Both ablations reduce performance compared to the full model, yet still outperform MetaAFN, indicating that recurrent modeling—even when partially disabled—offers stronger adaptation than meta-learning alone.

Method	Few-Shot	Digits SFDA	Office-31 SFDA	Average	Gap to Full
Full	84.3	98.6	89.8	90.9	—
No memory	83.1	98.2	89.3	90.2	−0.7
No hidden state	83.5	98.3	89.4	90.4	−0.5
MetaAFN	82.0	98.3	88.9	89.7	−1.2

). Resetting the LSTM for each sample (“No memory”) prevents the model from accumulating contextual information, which slows adaptation to gradual distribution shifts and increases sensitivity to abrupt changes. Eliminating the hidden state (“No hidden state”) removes short-term dependency, resulting in noisier affine parameters and less stable predictions. Both ablations lead to performance degradation relative to the full model, yet still outperform MetaAFN. This observation highlights that recurrent modeling—even when partially disabled—provides more effective adaptation than relying solely on meta-learning, while maintaining the batch-statistics-free nature of the framework.

5. Conclusions and Future Work

This paper introduced LSTM-Affine, a memory-based affine transformation module that serves as a drop-in replacement for batch normalization (BN) in deep neural networks. By leveraging an LSTM conditioned on historical input features, the module dynamically generates scale and shift parameters without relying on batch-level statistics or moving averages. This batch-statistics-free design enables robust adaptation to distributional shifts in settings where conventional normalization is unreliable, such as single-instance, streaming, or test-time inference.

Extensive experiments on few-shot learning and source-free domain adaptation benchmarks—including Omniglot, MiniImageNet, TieredImageNet, digit datasets, and Office-31—demonstrated that LSTM-Affine consistently outperforms or matches strong baselines such as BN and MetaBN. The method achieves competitive accuracy even under severe domain shifts, while maintaining efficiency by avoiding test-time backpropagation.

Beyond accuracy, LSTM-Affine offers architectural simplicity, full differentiability, and temporal awareness through its built-in memory mechanism, making it a compelling alternative to traditional normalization layers. Future work will investigate meta-learning-based training strategies, such as episodic optimization or gradient-based meta-updates, to further improve adaptability to unseen domains and extend applicability to continual learning scenarios.