Robust Denoising of Structure Noise Through Dual-Diffusion Brownian Bridge Modeling and Coupled Sampling
Abstract
1. Introduction
- We propose a novel structured noise denoising framework based on the Diffusion Brownian Bridge Model (DBBM), marking the first application of the DBBM to structured image denoising tasks.
- We jointly model clean images and structured noise using two conditional Brownian bridge diffusion processes, formulating the denoising task as two mutually coupled posterior sampling procedures.
- We introduce a gradient refinement strategy wherein residuals from the image and noise models are used to dynamically update each other during sampling, leading to an optimized denoising trajectory.
- Extensive experiments on diverse datasets with various types of structured noise demonstrate that our model achieves robust and superior denoising performance compared to state-of-the-art methods.
2. Related Works
Image Denoising
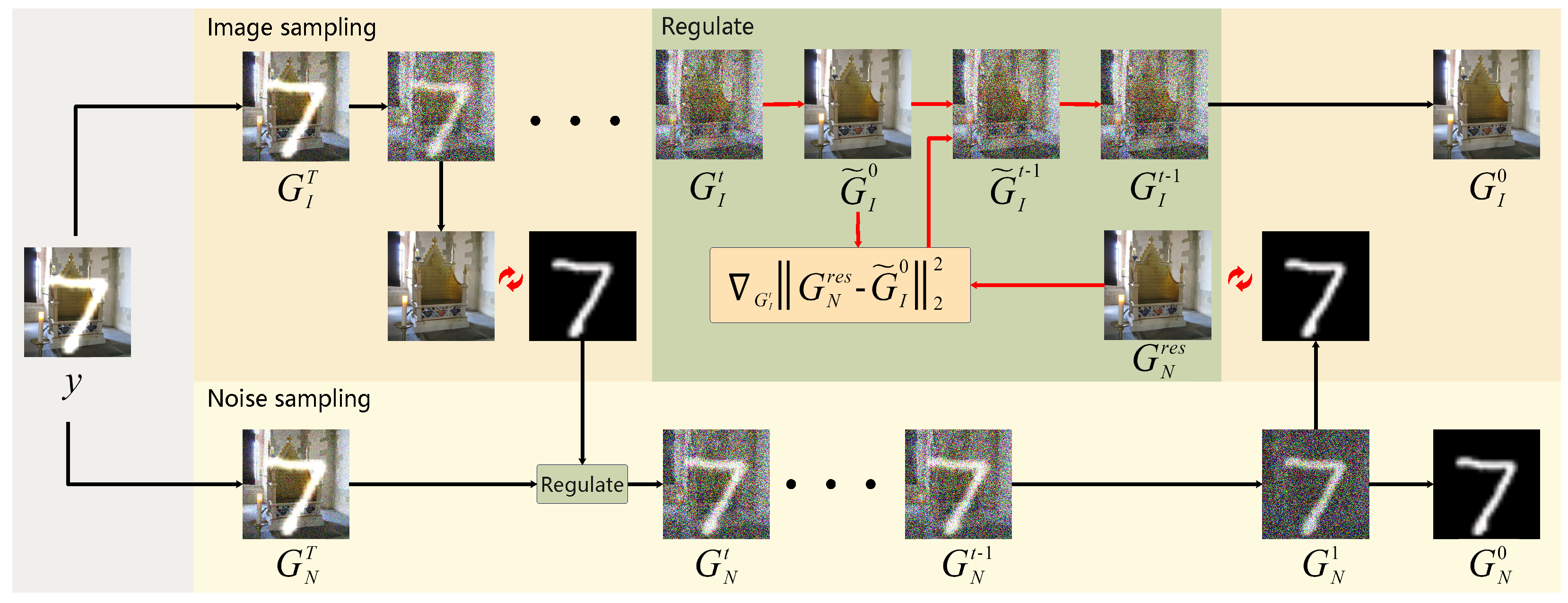
3. Method
3.1. Problem Definition
3.2. Preliminaries
3.3. Diffusion Brownian Bridge Model
3.4. Noise Addition Process
3.5. Denoising Process
3.6. Objective Function
| Algorithm 1 Training and |
| Require: Image , Structural noise , Time step , Gaussian noise Ensure: Image model , Noise model
|
3.7. DBBCS Denoising
| Algorithm 2 Structural noise denoising |
Require: T, y, ,
|
4. Experiments
4.1. Datasets
4.2. Implementation Details
4.3. State-of-the-Art Methods
4.4. Quantitative Comparison
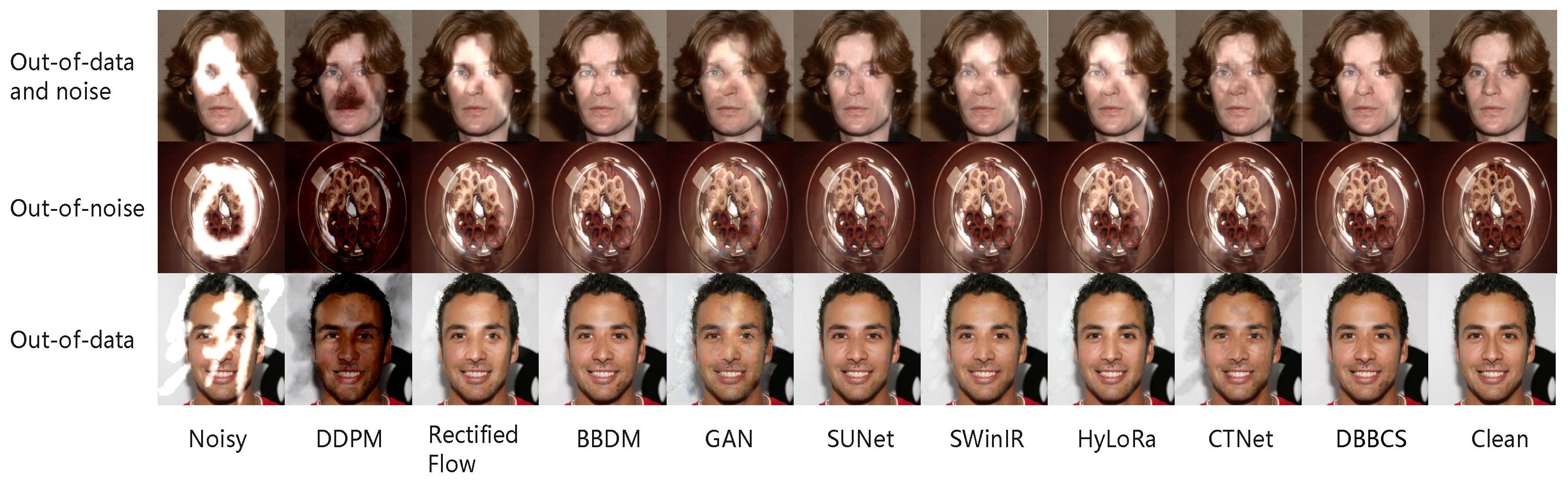
4.5. Qualitative Comparison
4.6. Robustness Analysis
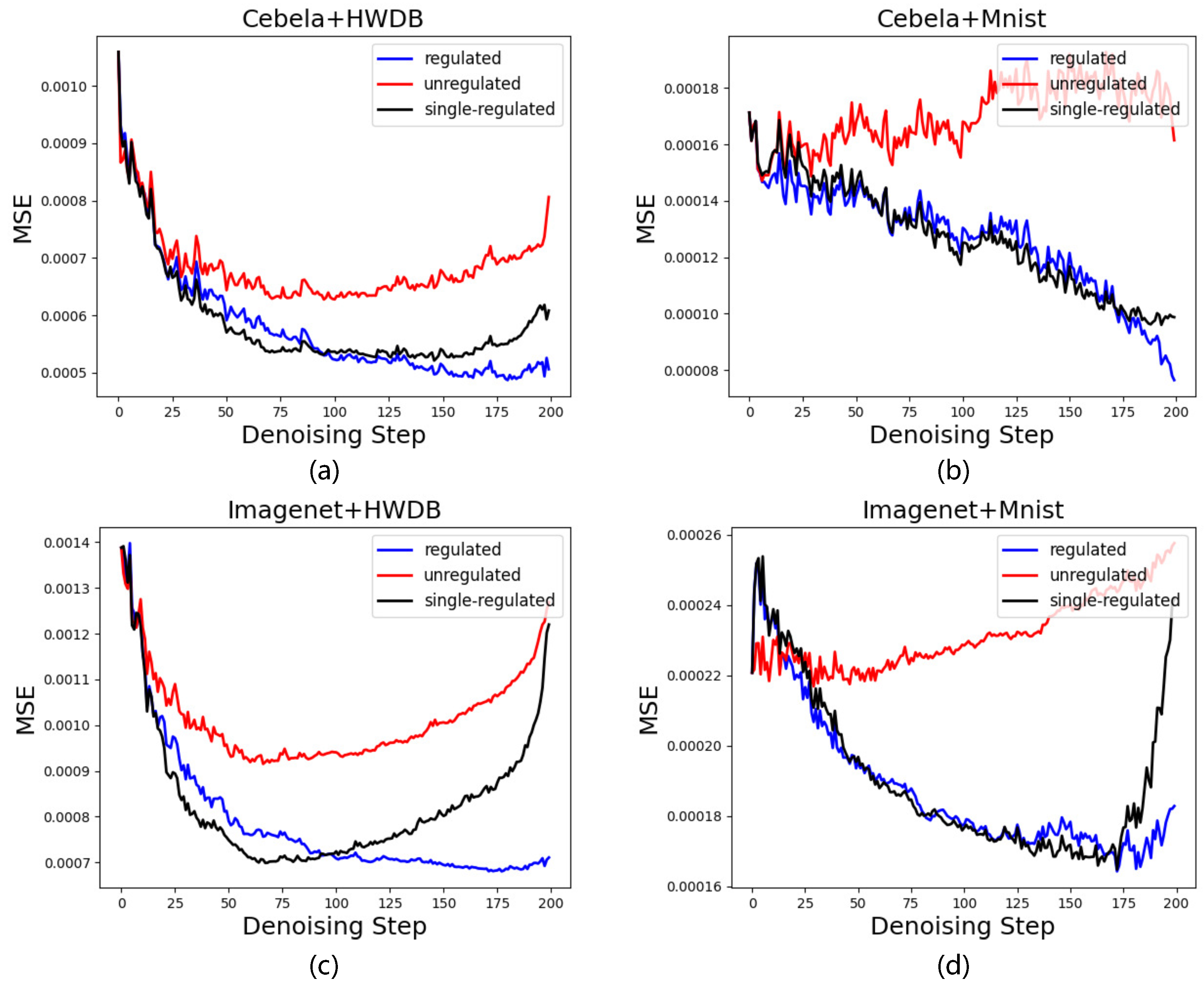
4.7. Ablation Analysis
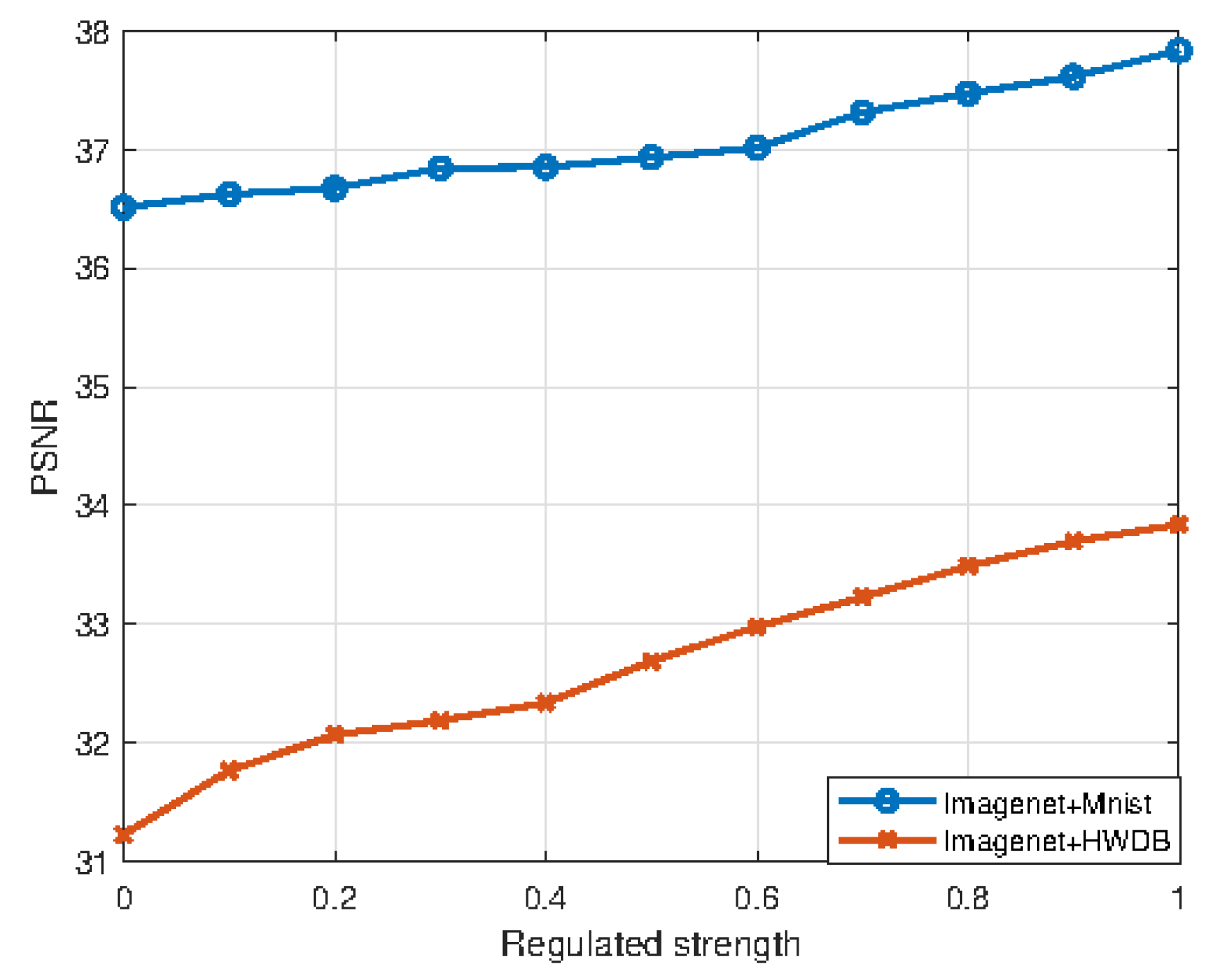
4.8. Impact of Regulated Strength
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. The Derivation Process of Equations (6) and (8)
- Write the exponential parts of two Gaussian distributions:
- -
- First item:
- -
- Second item:
- Merge the items:
- Expand the square term:
- Extract the quadratic and linear terms of :
- -
- Quadratic coefficient:
- -
- Primary coefficient:
Appendix A.2. The Derivation Process of Equations (20)–(23)
Appendix A.3. Symbols Used in This Paper
| Symbol | Description | Equation |
| y | Noisy observation image with structural noise | Equations (1) and (2) |
| x / | Clean image | Equations (1) and (2) |
| Gaussian noise | Equation (8) | |
| T | Total number of diffusion steps | Equation (10) |
| Noise intensity at the t-th forward diffusion step | Equation (4) | |
| Predefined coefficient | Equation (5) | |
| Cumulative retention coefficient up to the t-th diffusion step | Equation (5) | |
| Single-step probability distribution of forward diffusion | Equation (4) | |
| Multi-step probability distribution of forward diffusion (from to ) | Equation (5) | |
| Posterior conditional probability distribution of forward diffusion | Equation (6) | |
| Mean of the reverse diffusion distribution (learned by the neural network) | Equation (7) | |
| Clean image predicted by the neural network | Equation (7) | |
| Noise term predicted by the neural network | Equation (9) | |
| Simple loss function of the diffusion model (noise prediction MSE) | Equation (9) | |
| Endpoint state of the diffusion Brownian bridge process (set to in denoising) | Equation (10) | |
| Time weighting factor of the diffusion Brownian bridge process | Equation (11) | |
| Noise standard deviation at the t-th step of the diffusion Brownian bridge process | Equations (11) and (12) | |
| s | Scaling parameter for the noise intensity of the diffusion Brownian bridge process | Equation (12) |
| Standard deviation of the single-step transition probability of the diffusion Brownian bridge process | Equation (15) | |
| Parameterized conditional distribution of the reverse denoising process in the diffusion Brownian bridge | Equation (16) | |
| Variance of the reverse denoising process | Equation (16) | |
| ELBO | Evidence lower bound (used for optimizing the diffusion Brownian bridge model) | Equation (17) |
| KL divergence (measures the distance between two probability distributions) | Equation (17) |
Appendix A.4. The Effects of Different Experimental Settings
| Datasets | Cebela+Mnist | Imagenet+HWDB | ||||
| Metrics | MSE | PSNR | SSIM | MSE | PSNR | SSIM |
| batch = 8, patch = 256 × 256, iterations = 100,000, lr = 0.0002 | 0.0001 | 39.96 | 0.994 | 0.0005 | 33.84 | 0.975 |
| batch = 4, patch = 256 × 256, iterations = 100,000, lr = 0.0002 | 0.0001 | 39.93 | 0.991 | 0.0005 | 33.80 | 0.971 |
| batch = 8, patch = 256 × 256, iterations = 10,000, lr = 0.0002 | 0.0002 | 38.46 | 0.985 | 0.0007 | 31.27 | 0.947 |
| batch = 8, patch = 512 × 512, iterations = 100,000, lr = 0.0002 | 0.0001 | 39.90 | 0.992 | 0.0005 | 33.79 | 0.970 |
| batch = 8, patch = 256 × 256, iterations = 100,000, lr = 0.001 | 0.0001 | 39.85 | 0.986 | 0.0006 | 33.70 | 0.961 |
Appendix A.5. The Parameters and FLOPs Information of Each Model
| Model | FLOPs (G) | Parametres (M) |
| DBBCS | 398 | 12 |
| DDPM | 360 | 47 |
| Rectified Flow | 672 | 56 |
| BBDM | 288 | 15 |
| GAN | 968 | 64 |
| SUNet | 458 | 31 |
| SwinIR | 788 | 11 |
| HyLoRa | 516 | 34 |
| CTNet | 512 | 35 |
References
- Huo, Y.; Deng, Z.; Zhang, P.; Lu, Z.; Zhang, F.; Li, M.; Hou, Y.; Xi, P.; Huang, W.; Zhang, Y. DMF-SIM: Dual-Model Framework for super-resolution reconstruction and denoising in Structured Illumination Microscopy. Pattern Recognit. 2025, 169, 111865. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, W.; Guo, C.; Qiu, Q.; Xie, Z. PyramidPCD: A novel pyramid network for point cloud denoising. Pattern Recognit. 2025, 161, 111228. [Google Scholar] [CrossRef]
- Li, S.; Wang, F.; Gao, S. New non-local mean methods for MRI denoising based on global self-similarity between values. Comput. Biol. Med. 2024, 174, 108450. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, L.; Fu, X.; Ng, M.K.; Bioucas-Dias, J.M. Hyperspectral image denoising based on global and nonlocal low-rank factorizations. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10438–10454. [Google Scholar] [CrossRef]
- Sheng, J.; Lv, G.; Wang, Z.; Feng, Q. SRNet: Sparse representation-based network for image denoising. Digit. Signal Process. 2022, 130, 103702. [Google Scholar] [CrossRef]
- Xu, W.; Zhu, Q.; Qi, N.; Chen, D. Deep sparse representation based image restoration with denoising prior. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 6530–6542. [Google Scholar] [CrossRef]
- Li, P.; Liang, J.; Zhang, M.; Fan, W.; Yu, G. Joint image denoising with gradient direction and edge-preserving regularization. Pattern Recognit. 2022, 125, 108506. [Google Scholar] [CrossRef]
- Pleschberger, M.; Schrunner, S.; Pilz, J. An explicit solution for image restoration using Markov random fields. J. Signal Process. Syst. 2020, 92, 257–267. [Google Scholar] [CrossRef]
- Zhang, L.; Rao, A.; Agrawala, M. Adding conditional control to text-to-image diffusion models. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 4–6 October 2023; pp. 3836–3847. [Google Scholar]
- Xie, Y.; Yuan, M.; Dong, B.; Li, Q. Diffusion model for generative image denoising. arXiv 2023, arXiv:2302.02398. [Google Scholar] [CrossRef]
- Izadi, S.; Sutton, D.; Hamarneh, G. Image denoising in the deep learning era. Artif. Intell. Rev. 2023, 56, 5929–5974. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Timofte, R.; Van Gool, L.; Tu, Z.; Du, K.; Wang, H.; Chen, H.; Li, W.; Wang, X.; et al. NTIRE 2023 challenge on image denoising: Methods and results. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 1905–1921. [Google Scholar]
- Gkillas, A.; Ampeliotis, D.; Berberidis, K. Connections between deep equilibrium and sparse representation models with application to hyperspectral image denoising. IEEE Trans. Image Process. 2023, 32, 1513–1528. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Guo, Y.; Ying, Y.; Liu, Y.; Peng, Q. Fast non-local algorithm for image denoising. In Proceedings of the 2006 International Conference on Image Processing, Atlanta, GA, USA, 8–11 October 2006; IEEE: New York, NY, USA, 2006; pp. 1429–1432. [Google Scholar]
- Elad, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Anwar, S.; Zheng, L.; Tian, Q. Gradnet image denoising. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 508–509. [Google Scholar]
- Amini, M.; Ahmad, M.O.; Swamy, M. Image denoising in wavelet domain using the vector-based hidden Markov model. In Proceedings of the 2014 IEEE 12th International New Circuits and Systems Conference (NEWCAS), Trois-Rivieres, QC, Canada, 22–25 June 2014; IEEE: New York, NY, USA, 2014; pp. 29–32. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In Proceedings, Part I 13, Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 818–833. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Croitoru, F.A.; Hondru, V.; Ionescu, R.T.; Shah, M. Diffusion models in vision: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10850–10869. [Google Scholar] [CrossRef] [PubMed]
- Burger, H.C.; Schuler, C.J.; Harmeling, S. Image denoising: Can plain neural networks compete with BM3D? In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RL, USA, 16–21 June 2012; IEEE: New York, NY, USA, 2012; pp. 2392–2399. [Google Scholar]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef] [PubMed]
- Tai, Y.; Yang, J.; Liu, X.; Xu, C. Memnet: A persistent memory network for image restoration. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4539–4547. [Google Scholar]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual dense network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2472–2481. [Google Scholar]
- Liu, X.; Suganuma, M.; Sun, Z.; Okatani, T. Dual residual networks leveraging the potential of paired operations for image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7007–7016. [Google Scholar]
- Anwar, S.; Barnes, N. Real image denoising with feature attention. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3155–3164. [Google Scholar]
- Cheng, S.; Wang, Y.; Huang, H.; Liu, D.; Fan, H.; Liu, S. Nbnet: Noise basis learning for image denoising with subspace projection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 4896–4906. [Google Scholar]
- Tian, C.; Zheng, M.; Zuo, W.; Zhang, S.; Zhang, Y.; Lin, C.W. A cross Transformer for image denoising. Inf. Fusion 2024, 102, 102043. [Google Scholar] [CrossRef]
- Wang, M.; Yuan, P.; Qiu, S.; Jin, W.; Li, L.; Wang, X. Dual-Encoder UNet-Based Narrowband Uncooled Infrared Imaging Denoising Network. Sensors 2025, 25, 1476. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Chen, J.; Chao, H.; Yang, M. Image blind denoising with generative adversarial network based noise modeling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 3155–3164. [Google Scholar]
- Yue, Z.; Zhao, Q.; Zhang, L.; Meng, D. Dual adversarial network: Toward real-world noise removal and noise generation. In Proceedings, Part X 16, Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 41–58. [Google Scholar]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10684–10695. [Google Scholar]
- Xiang, T.; Yurt, M.; Syed, A.B.; Setsompop, K.; Chaudhari, A. DDM2: Self-Supervised Diffusion MRI Denoising with Generative Diffusion Models. arXiv 2023, arXiv:2302.03018. [Google Scholar]
- Chung, H.; Lee, E.S.; Ye, J.C. MR image denoising and super-resolution using regularized reverse diffusion. IEEE Trans. Med. Imaging 2022, 42, 922–934. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Xie, Y.; Liu, C.; Cheng, J.; Diao, S.; Tan, S.; Liang, X. Diffusion probabilistic priors for zero-shot low-dose CT image denoising. Med. Phys. 2025, 52, 329–345. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Zhang, W.; Hu, X.; Jiang, T.; Chen, Z.; Wang, H. Prompt-SID: Learning Structural Representation Prompt via Latent Diffusion for Single Image Denoising. Proc. AAAI Conf. Artif. Intell. 2025, 39, 4734–4742. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, K.; Liang, J.; Cao, J.; Wen, B.; Timofte, R.; Van Gool, L. Denoising diffusion models for plug-and-play image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 1219–1229. [Google Scholar]
- Teng, H.; Quan, Y.; Wang, C.; Huang, J.; Ji, H. Fingerprinting Denoising Diffusion Probabilistic Models. In Proceedings of the Computer Vision and Pattern Recognition Conference, Nashville, TN, USA, 11–15 June 2025; pp. 28811–28820. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Li, B.; Xue, K.; Liu, B.; Lai, Y.K. Bbdm: Image-to-image translation with brownian bridge diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 1952–1961. [Google Scholar]
- Lee, S.; Lin, Z.; Fanti, G. Improving the training of rectified flows. Adv. Neural Inf. Process. Syst. 2024, 37, 63082–63109. [Google Scholar]
- Fan, C.M.; Liu, T.J.; Liu, K.H. SUNet: Swin transformer UNet for image denoising. In Proceedings of the 2022 IEEE International Symposium on Circuits and Systems (ISCAS), Austin, TX, USA, 28 May–1 June 2022; pp. 2333–2337. [Google Scholar]
- Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Van Gool, L.; Timofte, R. Swinir: Image restoration using swin transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 1833–1844. [Google Scholar]
- Tan, X.; Shao, M.; Qiao, Y.; Liu, T.; Cao, X. Low-Rank Prompt-Guided Transformer for Hyperspectral Image Denoising. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–15. [Google Scholar] [CrossRef]



| Datasets | Cebela+Mnist | Imagenet+HWDB | Cebela+HWDB | Imagenet+Mnist | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metrics | MSE | PSNR | SSIM | MSE | PSNR | SSIM | MSE | PSNR | SSIM | MSE | PSNR | SSIM |
| DDPM | 0.0010 | 30.43 | 0.908 | 0.0215 | 19.00 | 0.744 | 0.0190 | 19.89 | 0.788 | 0.0201 | 19.56 | 0.764 |
| Rectified Flow | 0.0004 | 33.99 | 0.976 | 0.0016 | 28.95 | 0.937 | 0.0012 | 29.58 | 0.934 | 0.0004 | 35.48 | 0.984 |
| BBDM | 0.0002 | 37.49 | 0.991 | 0.0009 | 32.31 | 0.971 | 0.0009 | 31.49 | 0.961 | 0.0003 | 36.89 | 0.990 |
| RDGAN | 0.0079 | 21.51 | 0.782 | 0.0042 | 24.43 | 0.829 | 0.0019 | 27.91 | 0.889 | 0.0020 | 27.23 | 0.891 |
| SUNet | 0.0003 | 35.55 | 0.974 | 0.0006 | 33.19 | 0.964 | 0.0007 | 32.84 | 0.961 | 0.0003 | 37.50 | 0.985 |
| SwinIR | 0.0004 | 34.38 | 0.978 | 0.0012 | 29.94 | 0.937 | 0.0020 | 27.70 | 0.902 | 0.0003 | 36.30 | 0.985 |
| HyLoRa | 0.0004 | 34.56 | 0.974 | 0.0006 | 32.89 | 0.967 | 0.0009 | 30.68 | 0.947 | 0.0013 | 29.36 | 0.943 |
| CTNet | 0.0009 | 30.65 | 0.971 | 0.0024 | 26.87 | 0.899 | 0.0007 | 32.18 | 0.953 | 0.0009 | 31.47 | 0.962 |
| DBBCS | 0.0001 | 39.96 | 0.994 | 0.0005 | 33.84 | 0.975 | 0.0006 | 33.04 | 0.970 | 0.0002 | 37.83 | 0.994 |
| Datasets | Out-of-Data | Out-of-Noise | Out-of-Data and Noise | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Metrics | MSE | PSNR | SSIM | MSE | PSNR | SSIM | MSE | PSNR | SSIM |
| DDPM | 0.0346 | 16.71 | 0.579 | 0.0310 | 16.92 | 0.604 | 0.0408 | 16.80 | 0.602 |
| Rectified Flow | 0.0021 | 27.22 | 0.916 | 0.0084 | 21.68 | 0.922 | 0.0073 | 22.00 | 0.915 |
| BBDM | 0.0007 | 32.36 | 0.966 | 0.0031 | 25.77 | 0.956 | 0.0031 | 25.61 | 0.952 |
| RDGAN | 0.0039 | 24.67 | 0.810 | 0.0073 | 22.11 | 0.875 | 0.0050 | 23.61 | 0.883 |
| SUNet | 0.0005 | 33.76 | 0.967 | 0.0028 | 25.51 | 0.960 | 0.0026 | 25.79 | 0.952 |
| SwinIR | 0.0005 | 33.81 | 0.970 | 0.0049 | 23.76 | 0.936 | 0.0039 | 24.50 | 0.946 |
| HyLoRa | 0.0013 | 29.35 | 0.931 | 0.0064 | 22.57 | 0.932 | 0.0057 | 22.80 | 0.939 |
| CTNet | 0.0027 | 26.29 | 0.880 | 0.0038 | 25.07 | 0.930 | 0.0028 | 25.99 | 0.932 |
| DBBCS | 0.0005 | 33.84 | 0.972 | 0.0025 | 26.32 | 0.961 | 0.0025 | 26.54 | 0.961 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Yuan, C.; Xu, H.; He, Y.; Jiang, J. Robust Denoising of Structure Noise Through Dual-Diffusion Brownian Bridge Modeling and Coupled Sampling. Electronics 2025, 14, 4243. https://doi.org/10.3390/electronics14214243
Chen L, Yuan C, Xu H, He Y, Jiang J. Robust Denoising of Structure Noise Through Dual-Diffusion Brownian Bridge Modeling and Coupled Sampling. Electronics. 2025; 14(21):4243. https://doi.org/10.3390/electronics14214243
Chicago/Turabian StyleChen, Long, Changan Yuan, Huafu Xu, Ye He, and Jianhui Jiang. 2025. "Robust Denoising of Structure Noise Through Dual-Diffusion Brownian Bridge Modeling and Coupled Sampling" Electronics 14, no. 21: 4243. https://doi.org/10.3390/electronics14214243
APA StyleChen, L., Yuan, C., Xu, H., He, Y., & Jiang, J. (2025). Robust Denoising of Structure Noise Through Dual-Diffusion Brownian Bridge Modeling and Coupled Sampling. Electronics, 14(21), 4243. https://doi.org/10.3390/electronics14214243





