DCPRES: Contrastive Deep Graph Clustering with Progressive Relaxation Weighting Strategy
Abstract
1. Introduction
- We introduce a novel contrastive deep graph clustering model featuring a PRES. To improve feature representation, our model concurrently processes both sample attributes and graph structures and establishes a two-tiered contrastive learning framework at both the instance and cluster levels.
- The progressive relaxation weight strategy implements an “easy-to-hard” learning curriculum. It guides the model to initially train on high-confidence samples to build a strong feature foundation, before gradually incorporating more challenging, lower-confidence samples. This approach enhances the model’s capacity for distinguishing between positive and negative pairs.
- Extensive experiments on six benchmark datasets validated the superiority of our proposed model, which set new state-of-the-art results across several key quantitative metrics against competing methods.
2. Related Work
2.1. Contrastive Deep Graph Clustering
2.2. Semi-Supervised Clustering Based on Self-Paced Learning
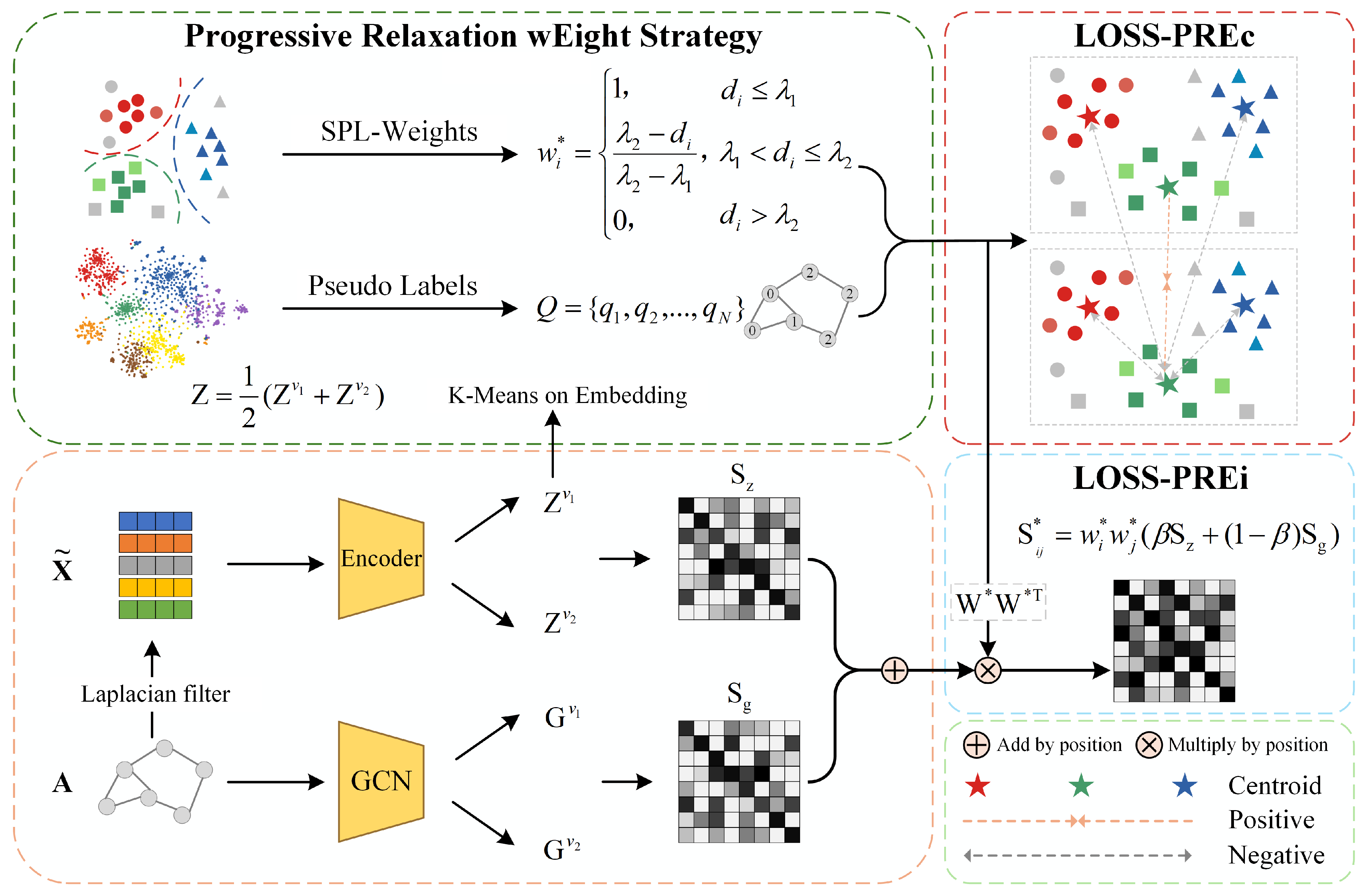
3. Method
3.1. Overview of the Framework
3.2. Attribute and Structural Feature Encoding
3.3. Progressive Relaxation Weight Strategy
3.4. Progressive Relaxation Weighted Instance-Level Contrastive Loss (LOSS-PREi)
3.5. Progressive Relaxation Weighted Cluster-Level Contrastive Loss (LOSS-PREc)
| Algorithm 1 CPRES algorithm flow. |
|
4. Experiment
4.1. Dataset
4.2. Experimental Environment and Hyperparameter Settings
4.3. Comparative Experiments
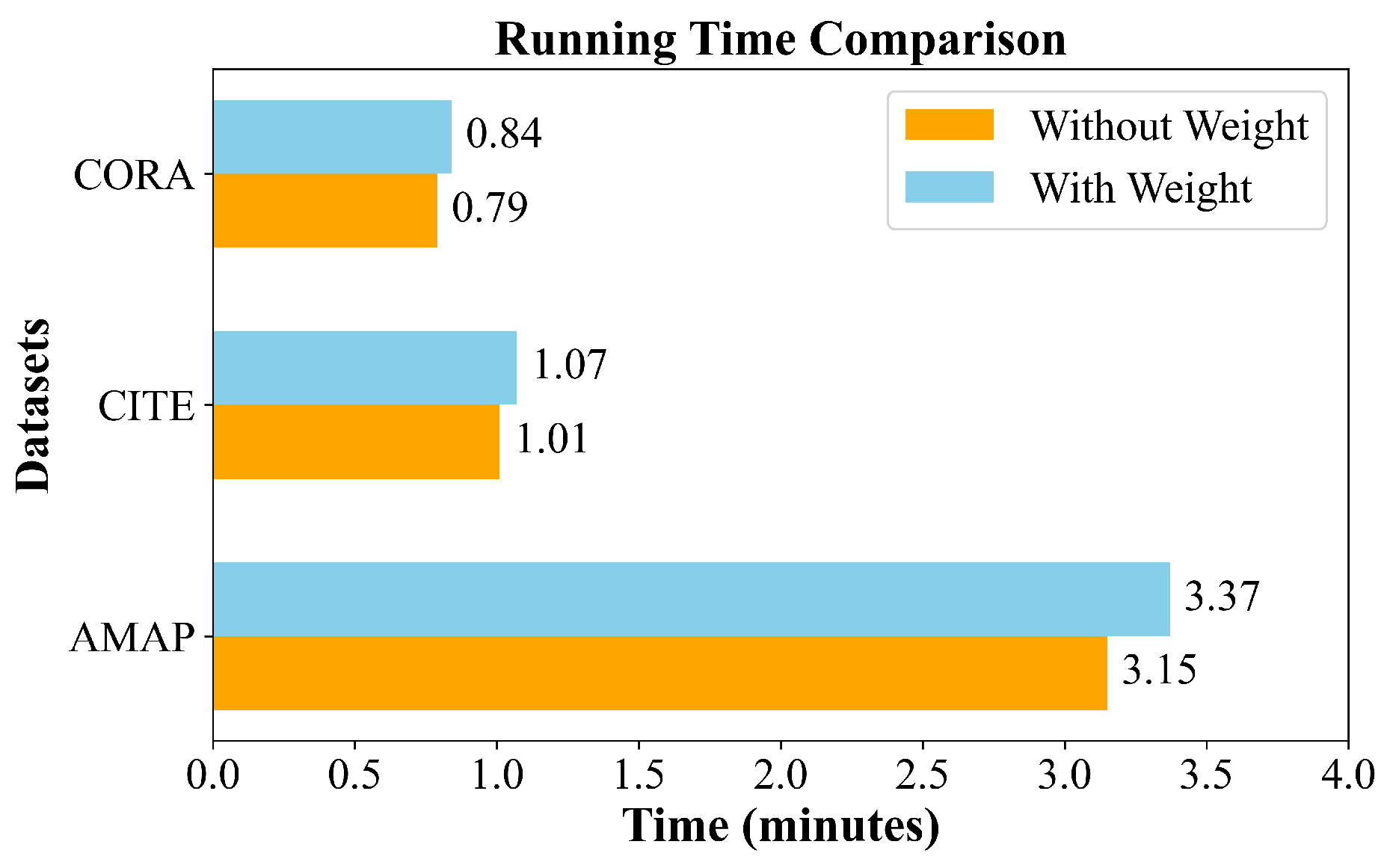
4.4. Ablation Experiments
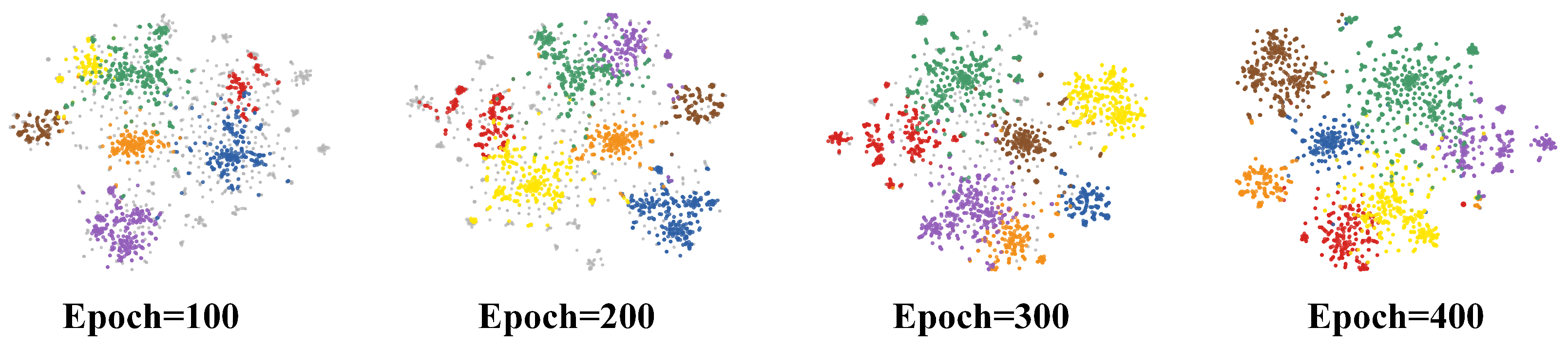
4.5. Visual Analytics
4.6. Hyperparameter Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Y.; Xia, J.; Zhou, S.; Yang, X.; Liang, K.; Fan, C.; Zhuang, Y.; Li, S.Z.; Liu, X.; He, K. A survey of deep graph clustering: Taxonomy, challenge, application, and open resource. arXiv 2022, arXiv:2211.12875. [Google Scholar]
- Ren, Y.; Pu, J.; Yang, Z.; Xu, J.; Li, G.; Pu, X.; Yu, P.S.; He, L. Deep clustering: A comprehensive survey. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 5858–5878. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Hu, R.; Fung, S.; Long, G.; Jiang, J.; Zhang, C. Learning graph embedding with adversarial training methods. IEEE Trans. Cybern. 2019, 50, 2475–2487. [Google Scholar] [CrossRef] [PubMed]
- Qin, X.; Yuan, C.; Jiang, J.; Chen, L. Deep semi-supervised clustering based on pairwise constraints and sample similarity. Pattern Recognit. Lett. 2024, 178, 1–6. [Google Scholar] [CrossRef]
- Hong, S.; Yue, T.; You, Y.; Lv, Z.; Tang, X.; Hu, J.; Yin, H. A Resilience Recovery Method for Complex Traffic Network Security Based on Trend Forecasting. Int. J. Intell. Syst. 2025, 2025, 3715086. [Google Scholar] [CrossRef]
- Jaiswal, A.; Babu, A.R.; Zadeh, M.Z.; Banerjee, D.; Makedon, F. A survey on contrastive self-supervised learning. Technologies 2020, 9, 2. [Google Scholar] [CrossRef]
- Hassani, K.; Khasahmadi, A.H. Contrastive multi-view representation learning on graphs. In Proceedings of the International Conference on Machine Learning, Virtual Event, 13–18 July 2020. [Google Scholar]
- Yang, X.; Liu, Y.; Zhou, S.; Wang, S.; Tu, W.; Zheng, Q.; Liu, X.; Fang, L.; Zhu, E. Cluster-guided contrastive graph clustering network. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023. [Google Scholar]
- Liu, Y.; Yang, X.; Zhou, S.; Liu, X.; Wang, Z.; Liang, K.; Tu, W.; Li, L.; Duan, J.; Chen, C. Hard sample aware network for contrastive deep graph clustering. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023. [Google Scholar]
- Li, Y.; Hu, P.; Liu, Z.; Peng, D.; Zhou, J.T.; Peng, X. Contrastive clustering. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual Event, 2–9 February 2021. [Google Scholar]
- Dang, Z.; Deng, C.; Yang, X.; Wei, K.; Huang, H. Nearest neighbor matching for deep clustering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual Event, 19–25 June 2021. [Google Scholar]
- Huang, D.; Deng, X.; Chen, D.H.; Wen, Z.; Sun, W.; Wang, C.D.; Lai, J.H. Deep clustering with hybrid-grained contrastive and discriminative learning. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 9472–9483. [Google Scholar] [CrossRef]
- Yong, Q.; Chen, C.; Zhou, X. Contrastive Learning Subspace for Text Clustering. arXiv 2024, arXiv:2408.14119. [Google Scholar] [CrossRef]
- Chen, M.; Wang, B.; Li, X. Deep contrastive graph learning with clustering-oriented guidance. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024. [Google Scholar]
- Kulatilleke, G.K.; Portmann, M.; Chandra, S.S. SCGC: Self-supervised contrastive graph clustering. Neurocomputing 2025, 611, 128629. [Google Scholar] [CrossRef]
- van der Oord, A.; Li, Y.; Vinyals, O. Representation learning with contrastive predictive coding. arXiv 2018, arXiv:1807.03748. [Google Scholar]
- Zhang, X.; Xu, H.; Zhu, X.; Chen, Y. Deep contrastive clustering via hard positive sample debiased. Neurocomputing 2024, 570, 127147. [Google Scholar] [CrossRef]
- Kumar, M.; Packer, B.; Koller, D. Self-paced learning for latent variable models. Adv. Neural Inf. Process. Syst. 2010, 23, 1189–1197. [Google Scholar]
- Gu, N.N.; Sun, X.N.; Liu, W.; Li, L. Semi-supervised classification method based on self-paced learning and sparse self-expression. Syst. Sci. Math. 2020, 40, 191–208. [Google Scholar]
- Jiang, Y.Y.; Tao, C.F.; Li, P. Deep subspace clustering algorithm with data augmentation and adaptive self-paced learning. Comput. Eng. 2023, 49, 96–103. [Google Scholar]
- Zhang, C.; Fan, W.; Wang, B.; Chen, C.; Li, H. Self-paced semi-supervised feature selection with application to multi-modal Alzheimer’s disease classification. Inf. Fusion 2024, 107, 102345. [Google Scholar] [CrossRef]
- Wang, C.; Pan, S.; Hu, R.; Long, G.; Jiang, J.; Zhang, C. Attributed graph clustering: A deep attentional embedding approach. arXiv 2019, arXiv:1906.06532. [Google Scholar] [CrossRef]
- Zhu, P.; Wang, Q.; Wang, Y.; Li, J.; Hu, Q. Every node is different: Dynamically fusing self-supervised tasks for attributed graph clustering. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 17184–17192. [Google Scholar]
- Zhang, J.; Peng, H.; Sun, L.; Wu, G.; Liu, C.; Yu, Z. Unsupervised graph clustering with deep structural entropy. In Proceedings of the 31st ACM SIGKDD Conference on Knowledge Discovery and Data Mining, V.2, Toronto, ON, Canada, 3–7 August 2025; pp. 3752–3763. [Google Scholar]
- Zhao, H.; Yang, X.; Wang, Z.; Yang, E.; Deng, C. Graph debiased contrastive learning with joint representation clustering. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Montreal, QC, Canada, 21–26 August 2021. [Google Scholar]
- Liu, Y.; Li, J.; Chen, Y.; Wu, R.; Wang, E.; Zhou, J.; Chen, L. Revisiting modularity maximization for graph clustering: A contrastive learning perspective. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Barcelona, Spain, 25–29 August 2024; pp. 1968–1979. [Google Scholar]
- Wan, X.; Liu, J.; Liang, W.; Liu, X.; Wen, Y.; Zhu, E. Continual multi-view clustering. In Proceedings of the 30th ACM International Conference on Multimedia, Lisbon, Portugal, 10–14 October 2022. [Google Scholar]
- Liu, Y.; Yang, X.; Zhou, S.; Liu, X.; Wang, S.; Liang, K.; Tu, W.; Li, L. Simple contrastive graph clustering. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 13789–13800. [Google Scholar] [CrossRef] [PubMed]
- Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]


| Dataset | Type | #Nodes | #Edges | #Classes | Feature Dim |
|---|---|---|---|---|---|
| CORA | Graph | 2708 | 5278 | 7 | 1433 |
| CITE | Graph | 3327 | 4552 | 6 | 3703 |
| AMAP | Graph | 7650 | 119,081 | 8 | 745 |
| BAT | Graph | 131 | 1038 | 4 | 81 |
| EAT | Graph | 399 | 5994 | 4 | 203 |
| UAT | Graph | 1190 | 13,599 | 4 | 239 |
| Dataset | Metrics | DAEGC | DyFSS | DeSE | GDCL | DCHD | MAGI | CCGC | HSAN | DCPRES |
|---|---|---|---|---|---|---|---|---|---|---|
| CORA | NMI | 52.89 ± 0.69 | 54.58 ± 0.51 | 57.27 ± 0.38 | 56.30 ± 0.36 | 60.13 ± 0.99 | 59.71 ± 0.12 | 56.45 ± 1.04 | 59.21 ± 1.03 | 61.18 ± 0.61 |
| ACC | 70.43 ± 0.36 | 72.08 ± 0.37 | 75.31 ± 0.61 | 70.83 ± 0.47 | 78.67 ± 0.87 | 76.03 ± 0.21 | 73.88 ± 1.20 | 77.07 ± 1.56 | 78.65 ± 0.63 | |
| ARI | 49.63 ± 0.43 | 49.33 ± 0.44 | 54.89 ± 0.49 | 48.05 ± 0.72 | 59.60 ± 1.62 | 57.31 ± 0.11 | 52.51 ± 1.89 | 57.52 ± 0.70 | 59.54 ± 0.76 | |
| F1 | 68.27 ± 0.57 | 67.37 ± 0.34 | 72.29 ± 0.34 | 52.88 ± 0.97 | 76.84 ± 0.79 | 73.92 ± 0.26 | 70.98 ± 2.79 | 75.11 ± 1.40 | 76.87 ± 0.62 | |
| CITE | NMI | 36.41 ± 0.86 | 43.96 ± 0.65 | 44.68 ± 0.31 | 39.52 ± 0.38 | 44.97 ± 1.20 | 45.24 ± 0.28 | 44.33 ± 0.79 | 45.06 ± 0.74 | 45.89 ± 0.40 |
| ACC | 64.54 ± 1.39 | 70.34 ± 0.92 | 69.88 ± 0.51 | 66.39 ± 0.65 | 71.13 ± 1.00 | 70.65 ± 0.32 | 69.84 ± 0.94 | 71.15 ± 0.80 | 72.31 ± 0.30 | |
| ARI | 37.78 ± 1.24 | 45.37 ± 0.54 | 45.35 ± 0.46 | 41.07 ± 0.96 | 46.87 ± 1.09 | 46.83 ± 0.15 | 45.68 ± 1.80 | 47.05 ± 1.12 | 48.38 ± 0.54 | |
| F1 | 62.20 ± 1.32 | 64.01 ± 0.75 | 64.58 ± 0.46 | 61.12 ± 0.70 | 62.71 ± 2.08 | 64.82 ± 0.24 | 62.71 ± 2.06 | 63.01 ± 1.79 | 66.53 ± 0.62 | |
| AMAP | NMI | 65.25 ± 0.45 | - | - | 37.32 ± 0.28 | 67.08 ± 0.88 | - | 67.44 ± 0.48 | 67.21 ± 0.33 | 67.85 ± 0.40 |
| ACC | 75.96 ± 0.23 | - | - | 43.75 ± 0.78 | 77.81 ± 0.68 | - | 77.25 ± 0.41 | 77.02 ± 0.33 | 77.74 ± 0.44 | |
| ARI | 58.12 ± 0.24 | - | - | 21.57 ± 0.51 | 58.71 ± 1.47 | - | 57.99 ± 0.66 | 58.01 ± 0.48 | 58.79 ± 0.56 | |
| F1 | 69.87 ± 0.54 | - | - | 38.37 ± 0.29 | 72.37 ± 1.41 | - | 72.18 ± 0.57 | 72.03 ± 0.46 | 75.49 ± 1.35 | |
| BAT | NMI | 21.43 ± 0.35 | - | - | 31.70 ± 0.42 | 54.30 ± 1.54 | - | 50.23 ± 2.43 | 53.21 ± 0.93 | 56.04 ± 0.58 |
| ACC | 52.67 ± 0.00 | - | - | 45.42 ± 0.54 | 78.85 ± 1.08 | - | 75.04 ± 1.78 | 77.15 ± 0.72 | 80.00 ± 0.46 | |
| ARI | 18.18 ± 0.29 | - | - | 19.33 ± 0.57 | 52.75 ± 2.02 | - | 46.95 ± 3.09 | 52.20 ± 1.11 | 54.97 ± 0.86 | |
| F1 | 52.23 ± 0.03 | - | - | 39.94 ± 0.57 | 78.80 ± 1.03 | - | 74.90 ± 1.80 | 77.13 ± 0.76 | 79.98 ± 0.41 | |
| EAT | NMI | 05.57 ± 0.06 | - | - | 13.22 ± 0.33 | 34.87 ± 0.54 | - | 33.85 ± 0.87 | 33.25 ± 0.44 | 35.90 ± 0.40 |
| ACC | 36.89 ± 0.15 | - | - | 33.46 ± 0.18 | 57.84 ± 0.49 | - | 57.19 ± 0.66 | 56.69 ± 0.34 | 58.45 ± 0.29 | |
| ARI | 05.03 ± 0.08 | - | - | 04.31 ± 0.29 | 28.03 ± 0.49 | - | 27.71 ± 0.41 | 26.85 ± 0.59 | 28.92 ± 0.17 | |
| F1 | 34.72 ± 0.16 | - | - | 25.02 ± 0.21 | 58.16 ± 0.46 | - | 57.09 ± 0.94 | 57.26 ± 0.28 | 58.60 ± 0.22 | |
| UAT | NMI | 21.33 ± 0.44 | - | - | 25.10 ± 0.01 | 27.33 ± 1.66 | - | 28.15 ± 1.92 | 26.99 ± 2.11 | 29.28 ± 1.01 |
| ACC | 52.29 ± 0.49 | - | - | 48.70 ± 0.06 | 56.78 ± 1.17 | - | 56.34 ± 1.11 | 56.04 ± 0.67 | 58.39 ± 0.83 | |
| ARI | 20.50 ± 0.51 | - | - | 21.76 ± 0.01 | 24.85 ± 1.91 | - | 25.52 ± 2.09 | 25.22 ± 1.96 | 28.19 ± 1.00 | |
| F1 | 50.33 ± 0.64 | - | - | 45.69 ± 0.08 | 55.93 ± 1.84 | - | 55.24 ± 1.69 | 54.20 ± 1.84 | 57.23 ± 0.89 |
| Dataset | Metrics | PREc | PREi | GCN + PREc | GCN + PREi | PREi + PREc | DCPRES |
|---|---|---|---|---|---|---|---|
| CORA | NMI | 58.01 ± 0.46 | 59.48 ± 0.51 | 60.95 ± 0.42 | 61.07 ± 0.47 | 61.22 ± 0.37 | 61.18 ± 0.61 |
| ACC | 74.47 ± 0.38 | 75.84 ± 0.46 | 77.49 ± 0.63 | 77.88 ± 0.71 | 78.41 ± 0.90 | 78.65 ± 0.63 | |
| ARI | 55.67 ± 0.56 | 56.85 ± 0.65 | 58.35 ± 0.68 | 58.68 ± 0.68 | 59.47 ± 0.61 | 59.54 ± 0.76 | |
| F1 | 73.51 ± 0.27 | 74.00 ± 0.59 | 75.75 ± 0.70 | 76.09 ± 0.71 | 76.52 ± 0.98 | 76.87 ± 0.62 | |
| CITE | NMI | 43.97 ± 0.99 | 43.48 ± 1.00 | 44.37 ± 0.53 | 44.95 ± 0.35 | 45.02 ± 0.44 | 45.89 ± 0.40 |
| ACC | 68.86 ± 0.97 | 69.78 ± 0.78 | 70.35 ± 0.49 | 70.73 ± 0.57 | 70.90 ± 0.58 | 72.31 ± 0.30 | |
| ARI | 42.90 ± 1.45 | 44.22 ± 1.17 | 45.21 ± 0.83 | 45.94 ± 0.58 | 46.14 ± 0.82 | 48.38 ± 0.54 | |
| F1 | 64.83 ± 0.68 | 64.71 ± 0.80 | 65.29 ± 0.69 | 65.45 ± 0.53 | 65.62 ± 0.31 | 66.53 ± 0.62 | |
| AMAP | NMI | 65.86 ± 0.39 | 65.91 ± 0.39 | 66.31 ± 0.32 | 66.86 ± 0.39 | 67.57 ± 0.40 | 67.85 ± 0.40 |
| ACC | 74.73 ± 0.44 | 75.78 ± 0.39 | 75.39 ± 0.19 | 76.73 ± 0.44 | 77.41 ± 0.52 | 77.74 ± 0.44 | |
| ARI | 55.78 ± 0.54 | 56.92 ± 0.56 | 56.58 ± 0.26 | 57.78 ± 0.54 | 58.75 ± 0.54 | 58.79 ± 0.56 | |
| F1 | 73.71 ± 1.19 | 72.92 ± 1.03 | 73.90 ± 1.15 | 75.71 ± 1.19 | 74.62 ± 1.58 | 75.49 ± 1.35 | |
| BAT | NMI | 52.38 ± 0.51 | 53.21 ± 0.46 | 54.59 ± 0.70 | 54.43 ± 0.78 | 53.52 ± 0.51 | 56.04 ± 0.58 |
| ACC | 76.71 ± 0.67 | 77.48 ± 0.51 | 78.93 ± 0.61 | 78.63 ± 0.68 | 77.71 ± 0.46 | 80.00 ± 0.46 | |
| ARI | 50.23 ± 0.81 | 50.95 ± 0.61 | 53.11 ± 0.91 | 52.79 ± 1.05 | 51.27 ± 0.65 | 54.97 ± 0.86 | |
| F1 | 76.66 ± 0.65 | 77.44 ± 0.48 | 78.90 ± 0.60 | 78.51 ± 0.70 | 77.67 ± 0.43 | 79.98 ± 0.41 |
| Thresholds | CORA | AMAP | ||||||
|---|---|---|---|---|---|---|---|---|
| NMI | ACC | ARI | F1 | NMI | ACC | ARI | F1 | |
| Fixed | 56.99 ± 1.19 | 73.02 ± 2.25 | 52.44 ± 3.25 | 72.20 ± 2.44 | 66.37 ± 0.40 | 76.55 ± 0.34 | 56.67 ± 0.43 | 74.57 ± 1.32 |
| Single | 59.85 ± 0.60 | 75.93 ± 0.47 | 56.20 ± 0.58 | 73.92 ± 0.30 | 66.86 ± 0.37 | 77.15 ± 0.39 | 57.82 ± 0.53 | 75.02 ± 0.88 |
| DCPRES | 61.18 ± 0.61 | 78.65 ± 0.63 | 59.54 ± 0.76 | 76.87 ± 0.62 | 67.85 ± 0.40 | 77.74 ± 0.44 | 58.79 ± 0.56 | 75.49 ± 1.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, X.; Peng, L.; Qin, Z.; Yuan, C. DCPRES: Contrastive Deep Graph Clustering with Progressive Relaxation Weighting Strategy. Electronics 2025, 14, 4206. https://doi.org/10.3390/electronics14214206
Qin X, Peng L, Qin Z, Yuan C. DCPRES: Contrastive Deep Graph Clustering with Progressive Relaxation Weighting Strategy. Electronics. 2025; 14(21):4206. https://doi.org/10.3390/electronics14214206
Chicago/Turabian StyleQin, Xiao, Lei Peng, Zhengyou Qin, and Changan Yuan. 2025. "DCPRES: Contrastive Deep Graph Clustering with Progressive Relaxation Weighting Strategy" Electronics 14, no. 21: 4206. https://doi.org/10.3390/electronics14214206
APA StyleQin, X., Peng, L., Qin, Z., & Yuan, C. (2025). DCPRES: Contrastive Deep Graph Clustering with Progressive Relaxation Weighting Strategy. Electronics, 14(21), 4206. https://doi.org/10.3390/electronics14214206






