Optimized FreeMark Post-Training White-Box Watermarking of Tiny Neural Networks

Abstract

Neural networks are powerful, high-accuracy systems whose trained parameters represent a valuable intellectual property. Building models that reach top level performance is a complex task and requires substantial investments of time and money so protecting these assets is an increasingly important task. Extensive research has been carried out on Neural Network Watermarking, exploring the possibility of inserting a recognizable marker in a host model either in the form of a concealed bit-string or as a characteristic output, making it possible to confirm network ownership even in the presence of malicious attempts at erasing the embedded marker from the model. The study examines the applicability of Opt-FreeMark, a non-invasive post-training white-box watermarking technique, obtained by modifying and optimizing an already existing state-of-the-art technique for tiny neural networks. Here, “Tiny” refers to models intended for ultra-low-power deployments, such as those running on edge devices like sensors and micro-controllers. Watermark robustness is also demonstrated by simulating common model-modification attacks that try to eliminate it from the model while preserving performance; the results presented in the paper indicate that the watermarking scheme effectively protects the networks against these manipulations.

1. Introduction

Recently, deep neural networks (DNNs) reached state-of-the-art performances across many applications [1], including speech recognition, natural language processing (NLP), and even autonomous and agentic systems. Developing these models however is extremely costly and requires access to large-scale datasets, significant computational power, and a deep expertise in both architecture design and hyperparameter optimization. Due to the substantial amount of resources invested in their development, DNNs are considered highly valuable forms of Intellectual Property (IP) [2], and ensuring their protection is a crucial concern for both industrial and academic stakeholders.

Up until recently, DNN inference was carried out mainly on high-performance cloud servers. However, as the number of connected devices rapidly increased, this cloud-focused model revealed limitations in terms of scalability, cost, and privacy. Thanks to the TinyML (Tiny Machine Learning) movement [3] and its investment in edge AI, it has become possible to run lightweight neural networks (NNs) directly on micro-controllers (MCUs) and other low-power hardware such as sensors. Furthermore, through techniques like weight pruning and quantization (usually down to 8-bit integers or even less), TinyML has enabled ultra-low-power on-device intelligence, opening the door to applications ranging from wearable health monitors to real-time assistance in sensor-based systems [4].

Distributing intelligence across numerous tiny neural networks (NNs) rather than a single centralized model raises the likelihood of IP exposure, as each standalone binary encapsulates a fully trained model that is vulnerable to extraction or reverse engineering [5]. To mitigate these risks, an optimization of the FreeMark Neural Network Watermarking (NNW) approach by Chen et al. [6] has been developed for the tiny NN use case, serving both as a safeguard against unauthorized use and as a mechanism for asserting model ownership. Optimizing the original watermarking method proved essential for applying it to the tiny neural network (NN) domain because state-of-the-art watermarking techniques are generally designed for larger models that can absorb additional watermark information without degrading their performance. Furthermore the vast number of parameters available in large NNs enables them to preserve high performance despite intense model alterations aimed at eliminating the embedded watermark (WM) (e.g., weight pruning) or overwriting it (e.g., fine-tuning). The role of over-parameterization in enabling a model to “forget” specific learned information while maintaining high accuracy on the main task is discussed in [7]. Since networks can also be trivially copied, measures that only protect against tampering or verify integrity are insufficient; watermarks must also be resilient to a wide range of transformations.

Generally, watermarking techniques rely on storing a large amount of WM information in the model parameters, thus porting them to tiny networks is not an easy task: the lower number of available parameters, and the need to operate under strict latency and resources constraints, reduces the capacity of the model to store longer watermarks and makes removal attacks more likely to succeed.

This manuscript explores the applicability of FreeMark, a state-of-the-art NNW technique presented by Chen et al. [6], to tiny NNs, devising and evaluating an optimized version, Opt-FreeMark, that leverages Singular Value Decomposition (SVD) and Error-Correcting Codes (ECC) to enhance the robustness of the watermarking method enabling its use on tiny NNs. Additionally, the robustness against four attacks, Gaussian noise addition, weight pruning, quantization, and fine-tuning, has been extensively evaluated.

The study shows that with the applied optimizations, Opt-FreeMark maintains its performance and remains resilient against malicious tampering, offering an effective solution for protecting tiny NNs deployed in real edge scenarios.

The paper is organized as follows: Section 2 presents a review of the state-of-the-art, where different white-box and black-box watermarking methods are presented. Section 3 examines the deployability of the watermarked models on a standard low-power MCU. Section 4 offers a technical explanation of the optimized watermarking method. Section 5 is where the two use cases and experimental results are presented and analyzed. Finally in Section 6, the conclusions are discussed.

2. State of the Art

Depending on how a watermark (WM) is inserted into a NN, watermarking approaches are typically divided into training-based, fine-tuning-based, or post-training-based [8]. Early research on DNN watermarking focused on embedding watermarks during the original training process, embedding the WM without degrading model performance on the primary task. However, this is not always practical: training large-scale networks requires a considerable amount of resources. For this reason, many researchers have investigated watermark insertion pipelines via fine-tuning of already-trained models, which makes the process much faster and cheaper [9]. Beyond training and fine-tuning approaches, post-training watermarking has recently emerged as a compelling, very low-cost alternative; the method described in [10] is among the first examples of this class of embedding methods. Watermarking schemes are also distinguished based on the data used to detect the WM: techniques are categorized as white-box (WB) if they require internal model information, or black-box (BB) if they rely only on the inputs–outputs relationships [11].

2.1. White-Box Watermarking

A watermarking technique is called “white-box” if the WM is inserted in the network’s internal parameters and recovered by reading those otherwise hidden parameters. These can be either static, like the network weights, or dynamic, like the neuron activations produced in response to a selected set of inputs. The work by Uchida et al. [12] is one of the first attempts at static white-box NN watermarking, and it validated the possibility of encoding a bit-string into one or more target layers by introducing a dedicated regularizer to the loss function. Regarding dynamic white-box watermarking, in the work by Rouhani et al. [13], they used a tailored loss function, modified by adding two regularization terms to the original loss function, altering the feature distributions produced by the target layers.

2.2. Black-Box Watermarking

A watermarking technique is called “black-box” if the WM is encoded in the input–output behavior of the network, since only the output of the model is accessible; therefore, WM extraction is performed by querying the network on a predetermined set of samples and inspecting the final output. Networks may be trained to produce distinctive outputs for particular “triggers”, generating anomalous behaviors that an unmodified model would not exhibit, which is the basis for many backdoor-style black-box watermarking methods. An example is given by the work by Zhang et al. [14] where the trigger information is embedded into the training samples, creating in this way trigger-based watermarks. A different approach was proposed by Ong et al. [15], who encouraged the model to generate watermarked images in response to specific triggers by creating a mapping between each trigger and the corresponding output.

3. Deployability on MCU

To evaluate the deployability of the watermarked models, the NUCLEO-STM32H743ZI2 board was used as a reference MCU; the specifics of the board are shown in

Table 1. NUCLEO-STM32H743ZI2 board hardware specifics.

Board Name	Flash (KiB)	RAM (KiB)	Freq. (MHz)
NUCLEO-STM32H743ZI2	1024	2048	400

.

The assessment of the memory size required by the two models and their latency was carried out using ST Edge AI Developer Cloud (https://stedgeai-dc.st.com/home, accessed on 2 October 2025), an online platform that enables the deployment of pre-trained NNs onto specific STM boards, offering an automated optimization and benchmarking pipeline, directly on real MCUs.

Table 2. Memory footprint and inference time of the models when deployed on the NUCLEO-STM32H743ZI2 board; model inputs and outputs are in FP32 precision.

Model (FP32)	Flash (KiB)	RAM (KiB)	Inference Time (ms)
ResNet8	323	140	122.30
MobileNetV1	855	160	109.20

presents the measurements obtained after deploying the models on the board.

Since neither FreeMark nor Opt-FreeMark required changing the baseline model topologies, the watermarked NNs exhibited identical memory usage (both flash and RAM), inference time, and per-inference energy consumption of the baseline networks.

4. Post-Training Non-Invasive White-Box Watermarking

The FreeMark post-training non-invasive NNW pipeline, presented by Chen et al. in [6], is based on the idea of indirectly watermarking a model without modifying its parameters by carefully learning its behavior over a set of trigger inputs, extracted from the original training data. The model is queried on a subset of the training data $\Gamma$, which is used to generate a series of activations computed over a target layer l. These are the features $f_l$ that will be used to tie the model behavior on the trigger inputs to the WM message. Applying the state-of-the-art approach to the two tiny NNs adopted in this work led to some difficulties in guaranteeing reasonable WM robustness to attacks and model modifications due to the limited number of features that can be extracted from such tiny models. Two modifications were devised and applied to the FreeMark pipeline to enhance its robustness for the “tiny” use case: (I) Applying redundancy to the watermarking message through hamming encoding/decoding, making it more resistant to noise. (II) Instead of simply averaging the $f_l$ features extracted from the lth layer using the triggers, Singular Value Decomposition (SVD) is computed over the $f_l$ matrix, and the $to{p}_k$ singular values $Sig{n}_k$ are kept for further processing. SVD is a mathematical technique that factorizes a real or complex matrix into a rotation followed by a scaling operation that is then followed by another rotation, which is done by decomposing the matrix into three components, U, $\Sigma$, and $V^T$, where U and $V^T$ are the matrices containing the left-singular vectors and right-singular vectors, respectively. $\Sigma$ is the matrix that contains the singular values representing the intrinsic strength of different data directions. By only keeping the largest singular values, SVD captures the most significant structural information while filtering out minor variations caused by noise. This property makes SVD inherently robust to perturbations. As shown in Section 5, through these two additional processing steps, the new Opt-FreeMark version becomes much more robust to even the most intense attacks. The same mathematical notation of [6] is used for the unmodified section of the watermarking and detection flows. Since many objects are created and used during the watermarking process, the main parameters are listed here for clarity:

• b: The randomly generated WM vector with length N, b$\in {\{0,1\}}^N$.
• $b_{red}$: The redundant WM vector with length $N_{red}$ obtained by applying hamming encoding to b.
• ${\tilde{b}}_{red}$: The extracted redundant WM vector with length $N_{red}$.
• $\tilde{b}$: The extracted WM vector obtained by applying hamming decoding to ${\tilde{b}}_{red}$.
• $\Gamma$: The subset of trigger inputs extracted from the training data.
• $f_l$: The activations computed over $\Gamma$ from the lth layer, $f_l\in {\mathbb{R}}^{M\times S}$ where M is the number of features extracted from the layer l, and S is the number of samples in $\Gamma$.
• $Sig{n}_k$: Signature computed from the $to{p}_k$ singular values extracted from $f_l$ using SVD.
• $\mu$: An auxiliary vector sampled from a normal distribution $\mathcal{N}(0,1)$, $\mu \in {\mathbb{R}}^K$, where K is the number of singular values kept.
• $(A,d)$: A pair of secret keys, with $A\in {\mathbb{R}}^{N_{red}\times K}$, and $d\in {\mathbb{R}}^K$.
• $\theta$: A predetermined threshold, where $\theta \in [0,1]$.

4.1. Embedding the Watermark

Given a host model H, a trigger set $\Gamma$ is extracted from the training data, so that it contains at least one sample from each class. By querying the model H on $\Gamma$, the feature matrix $f_l$ is extracted from the target layer l. SVD is computed over $f_l$ obtaining the singular values matrix, among all the singular values computed through SVD, the top k are kept as the signature of the model $Sig{n}_k$ while the rest are discarded. The model owner then generates a random binary WM b of length N applying hamming encoding to it, obtaining the redundant WM $b_{red}$.

A thresholding function $\Delta (·)$ can be defined as

$$\Delta \left(x\right)=Thresholding\left({\displaystyle \frac{1}{1+e^{-x}}}\right)$$

with

$$Thresholding\left(z\right)=\left\{\begin{array}{cc}\hfill 1& \hfill \mathrm{if} z\ge 0.5,\\ \hfill 0& \hfill \mathrm{if} z<0.5.\end{array}\right.$$

Given a vector $x=(x_1,\dots ,x_n)$, the thresholding function is applied as follows:

$$\Delta \left(x\right)=(\Delta \left(x_1\right),\dots ,\Delta \left(x_n\right)).$$

A random auxiliary vector $\mu$ of length K is sampled from a normal distribution $\mathcal{N}(0,1)$. The WM b is encoded through hamming encoding, obtaining the redundant WM $b_{red}\in {\{0,1\}}^{N_{red}}$. The next step is to generate a secret matrix $A\in {\mathbb{R}}^{N_{red}\times K}$, such that

$$b_{red}=\Delta (A·\mu ).$$

This is achieved by randomly initializing $A^{\left(0\right)}$, then for each iteration $t\in [1,T]$, the matrix A is updated by solving the following optimization problem:

$${\mathcal{L}}_t=\Delta (A^{\left(t\right)}·\mu )-b_{red}$$

$$A^{(t+1)}=A^{\left(t\right)}-\lambda ·{\displaystyle \frac{\partial {\mathcal{L}}_t}{\partial A^{\left(t\right)}}}.$$

where $\lambda$ is the learning rate. After having generated the secret matrix $A^T$, a second secret key $d\in {\mathbb{R}}^K$ is generated by computing the following:

$$d=\alpha Sig{n}_k-\mu .$$

where $\alpha \in \mathbb{R}$ is a scaling factor that solves the following equation:

$${∥\Delta (A·d)-b∥}_1\ge \theta N.$$

This process ensures the robustness of the WM, as $\theta$ is a hyperparameter that can be arbitrarily tuned by the model owner. The secret key generation process is concluded by saving the secret keys $(A,d)$, the scaling factor $\alpha$, and the subset of trigger inputs $\Gamma$. The secret key generation process is shown in Figure 1.

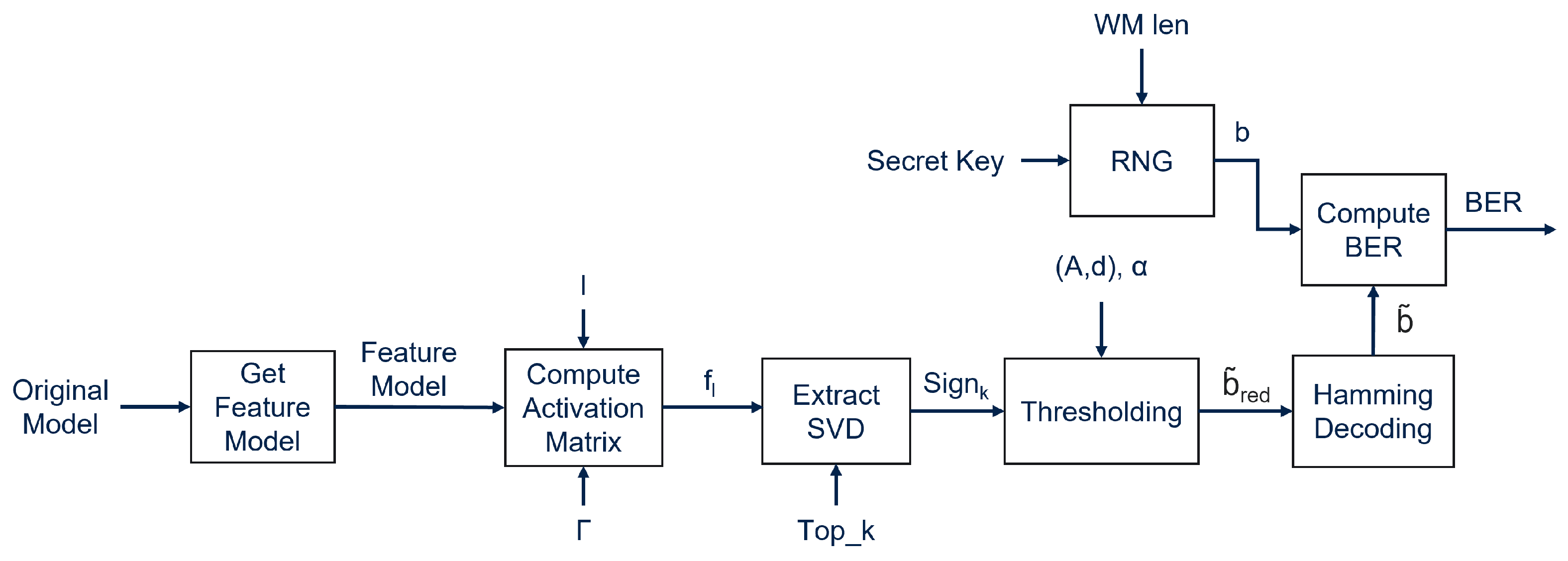
4.2. Extracting the Watermark

To verify if a model is watermarked, the owner of the model can use the trigger set $\Gamma$ to query the model, extracting the features $f_l$ generated by the lth layer. Now the $to{p}_k$ singular values $Sig{n}_k$ are computed by applying SVD on the features $f_l$, and the extracted WM ${\tilde{b}}_{red}$ is computed as follows:

$${\tilde{b}}_{red}=\Delta (A·(\alpha Sig{n}_k-d)).$$

Finally, the extracted WM $\tilde{b}$ is obtained by applying hamming decoding to ${\tilde{b}}_{red}$. The Bit Error Rate (BER), the percentage of bits differing between two messages, is computed between the original WM b and the extracted WM $\tilde{b}$ in order to verify the correctness of the extracted WM. If the BER is below the predetermined threshold $\theta$, then the WM is considered successfully extracted. The extraction process is shown in Figure 2.

5. Experiments and Results

5.1. Use Cases

The experiments carried out in this work considered two MLCommons [16] Tiny benchmarking use cases, Image Classification (IC) and Visual Wake Word (VWW), explored in Section 5.1.1 and Section 5.1.2, respectively. Although this work evaluates only these two use cases, Opt-FreeMark is model and task agnostic: the watermarking procedure does not depend on the host model’s architecture or on its training protocol. Consequently, the results reported for these two scenarios are expected to be accurate indicators of the method’s broader behavior and should generalize well to other tiny NN settings, such as speech recognition or sensor data applications, and to other common network architectures.

Opt-FreeMark is non-invasive and leaves model weights untouched. Runtime is therefore dominated by (1) evaluating the trigger set, N forward passes, where N is the number of triggers used in the process, and (2) secret matrix optimization, giving an overall time complexity linear in those two costs. Memory is dominated by the $N\times F$ activation matrix used for SVD; the complexity is given by $\mathcal{O}(N\times F)$ where F is the number of features of the target layer. For typical tiny NN values, this corresponds to only a few dozen to a few hundred kilobytes of RAM, making the method practical on many modern MCUs.

5.1.1. Image Classification

The dataset used for the IC task is the CIFAR-10 dataset [17]. The dataset is composed of 60k 32 × 32 RGB images; the samples are divided into training and testing subsets following an 80:20 ratio, with each image belonging to one of ten possible classes. The NN deployed for the IC task is a custom ResNet8 made up of less than 90K parameters [18] provided by MLCommons, with the number of residual blocks of the model being reduced to three. After processing the 32 × 32 × 3 sized inputs, the ResNet outputs a n length probability vector where n is the number of labels in the dataset; in this case, n is equal to 10. The ResNet8 model is very light and only requires 96 KiB of memory after 8 bit post-training quantization using Tensorflow Lite (TFL).

For the IC task, a WM of length equal to 128 bits was used, where the secret matrix A was generated using a number of iterations $T=500$ and a learning rate $\lambda =0.001$. The secret key d was generated using a trigger set $\Gamma$ composed of 200 samples, the threshold $\theta$ was set to $0.2$ (BER threshold = 0.2), and the number of singular values K was set to 20.

5.1.2. Visual Wake Words

VWW applications aim at detecting the presence of a person in an image [19]. The dataset used to train the models on this task is obtained by filtering the much larger COCO dataset [20], and provides 115K 96 × 96 RGB images divided into “person” or “non-person” classes. The network trained on this task is a MobileNetV1 [21], also provided by the MLCommons benchmarking suite, composed of a total of 220K parameters; the model performs multiple depth-wise convolutions producing the two-class output. While being larger than the ResNet8, the MobileNetV1 is suited for human detection on edge devices, requiring only 320 KiB of storage after 8-bit post-training quantization.

For the VWW task, the length of the WM was changed to 256 bits while all the other parameters were kept the same as in the IC case.

5.2. Attacks

Robustness evaluation of the WM embedded in the models was carried out by applying a number of different model modification attacks to the watermarked models; the results on the IC task are shown in

Table 3. Attack outcomes on the IC models are reported, with cells colored green when values exceed the threshold, and shaded yellow or red as performance declines.

WMK Method		Opt-FreeMark
WM Len		128
Atk. Type	Atk. Power	Dataset Acc.	WM Acc.
Threshold		1%	80.00%
No Attack		86.50%	100.00%
G. Noise	S = 0.001	86.44%	100.00%
	S = 0.01	86.00%	100.00%
	S = 0.1	72.20%	91.50%
	S = 1	12.30%	62.50%
L1 Pruning	P = 0.1	86.40%	100.00%
	P = 0.2	82.70%	100.00%
	P = 0.3	67.40%	97.70%
	P = 0.4	27.00%	75.00%
	P = 0.5	23.30%	83.00%
Quant.	B = 8	86.50%	100.00%
	B = 7	86.20%	100.00%
	B = 6	85.20%	98.50%
	B = 5	84.30%	96.00%
	B = 4	67.00%	93.75%
Fine-tune *	E = 5	87.20%	100.00%
	E = 10	87.15%	100.00%

* LR = 0.0001.

, while the one obtained on the VWW task is shown in

Table 4. Attack outcomes on the VWW models are reported, with cells colored green when values exceed the threshold, and shaded yellow or red as performance declines.

WMK Method		Opt-FreeMark
WM Len		256
Atk. Type	Atk. Power	Dataset Acc.	WM Acc.
Threshold		1%	80.00%
No Attack		82.50%	100.00%
G. Noise	S = 0.001	82.50%	100.00%
	S = 0.01	82.40%	100.00%
	S = 0.1	76.70%	96.00%
	S = 1	50.30%	33.00%
L1 Pruning	P = 0.1	82.40%	100.00%
	P = 0.2	82.30%	99.30%
	P = 0.3	77.30%	90.30%
	P = 0.4	72.50%	89.00%
	P = 0.5	61.50%	88.00%
Quant.	B = 8	82.50%	100.00%
	B = 7	82.50%	100.00%
	B = 6	82.00%	100.00%
	B = 5	81.40%	98.00%
	B = 4	80.60%	93.00%
Fine-tune *	E = 5	82.20%	98.00%
	E = 10	82.30%	98.00%

* LR = 0.0001.

. The tested attack pipelines included fine-tuning, quantization, pruning, and Gaussian noise addition. It is extremely important to verify that watermarks remain reliable under such attacks, since techniques like fine-tuning and quantization are often applied for purposes other than watermark removal. This is particularly relevant in embedded systems, where these methods are standard optimization strategies used to reduce the memory footprint of deep neural networks on MCUs. To study the behavior of the model when attacked, different intensity values were used for each attack type:

• Additive Gaussian Noise: Random samples were drawn from a Gaussian distribution defined as $\mathcal{N}(0,S·\sigma )$, where S denotes the intensity of the attack and $\sigma$ is the standard deviation. These samples were added to each weight parameter of the neural network.
• L1 Pruning: Within every layer of the model, the lowest $P\times 100\%$ of weights (based on their $L^1$ norm) was pruned by setting them to zero.
• Quantization: Model parameters were compressed by applying quantization with a precision of B bits.
• Fine-tuning: The network was retrained with a learning rate of $LR=0.0001$ over E epochs to adjust its weights.

Each row in Table 3 and Table 4 refers to a specific combination of attack type and attack intensity. Each model’s performance was assessed by measuring its accuracy computed on both the original dataset and the WM, both prior to the attacks $\left(ac{c}_{ref}\right)$ and after the attacks $\left(ac{c}_{atk}\right)$. In Table 3 and Table 4, different cell colors are used to emphasize results relative to threshold values, defined to evaluate the accuracy on the main task and on the watermark.

• Original Dataset: The attacked model’s accuracy is color-coded as follows: green when $ac{c}_{atk}\ge ac{c}_{ref}-1\%$, yellow when $ac{c}_{ref}-1\%>ac{c}_{atk}\ge ac{c}_{ref}-4\%$, and red for all other cases. These thresholds were chosen based on practical insights from field trials on edge devices, where drops in accuracy of up to $4\%$ were found to be acceptable.
• Watermark: For the watermark results, two colors are applied: green indicates successful detection of the watermark after the attack, while red marks cases where the watermark was not reliably identified. The thresholds used for watermark recognition are specified in the Threshold row of the tables. Watermark accuracy is calculated as $(1-BER)\%$.

For a quantitative comparison between the results achieved by Opt-FreeMark and other state-of-the-art watermarking techniques, we refer the reader to our previous work [22], where we analyzed the applicability of DeepSigns and TATTOOED to tiny neural networks using the same attack pipelines adopted in this study.

5.3. Results of the Attacks on the Image Classification Task

The results in Table 3 confirm the robustness of the watermarking technique, even against the most powerful attacks. In every case in which the attacked model retained a high level of accuracy on the main task, the WM was correctly identified, demonstrating the ownership of the model.

5.4. Results of the Attacks on the Visual Wake Word Task

The results shown in Table 4 confirm and validate the results obtained on the VWW task. The watermarking method achieved positive results on both tasks confirming the capability of Opt-FreeMark to successfully WM the VWW model; the only cases in which the WM is not reliably verified, red colored cells in the table, are the ones in which the model has been modified up to the point of being unusable.

5.5. Watermark Extraction with Forged Keys

As demonstrated in [6], FreeMark’s WM extraction is correctly carried out only by using a subset of keys $\Gamma$ that belongs to the training set on which the model has been pre-trained, guaranteeing robustness against ambiguity attacks. It is thus paramount to verify that this remains true also for Opt-FreeMark. Two different cases should be addressed:

• WM extraction using randomly forged keys: A subset of images generated by recursively composing each image with geometrical shapes and colors, as shown in Figure 3, was used to test this case.
• WM extraction using keys that are similar to the ones in $\Gamma$, thus keys on which the model performs well on; to test this case, a subset of the test-split of the dataset on which the model has not been trained on was used.

The experiments on WM extraction with forged keys was carried out on the IC use case using the Resnet8 as described in Section 5.1.1. The results on the two sets of forged keys, obtained by averaging the accuracies achieved by the model over 10 different subset of forged keys, are presented in

Table 5. Results of WM extraction using keys that do not belong to the training set $\Gamma$.

Key Type	Avg. Acc. on WM	Highest	Lowest
Randomly forged keys	54.50%	54.70%	53.90%
Keys belonging to the test set	75.80%	78.10%	71.20%

; in the table, the lowest and highest accuracy values obtained on the different subsets are also present. From Table 5, it can be observed how the accuracy values are always below the threshold ($(1-BER)\%=80.00\%$) used to verify the presence of the WM in the results presented in Section 5.2. It can be thus stated that Opt-FreeMark is indeed reasonably robust to ambiguity attacks, even against keys that belong to the same dataset, but on which the model has not been watermarked on.

5.6. Optimization for the Tiny Use Case

Table 6. Comparison between the average results achieved against Gaussian noise addition attack by FreeMark and Opt-FreeMark on the IC task. The attacks have been repeated 10 times for each setting; 95% confidence intervals are also shown.

Atk.	Atk. Str.	Avg. FreeMark WM ac.	Avg. Opt-FreeMark WM ac.
G. Noise	S = 0.001	78.17% ± 0.16%	100.00% ± 0.00%
G. Noise	S = 0.01	69.41% ± 0.62%	99.91% ± 0.08%
G. Noise	S = 0.1	51.07% ± 1.06%	91.26% ± 0.58%

shows the comparison between the results obtained by attacking two IC models using the same Gaussian noise addition pipeline used in Section 5.3. The models have been watermarked respectively with the baseline, non-optimized FreeMark NNW technique and the version optimized to guarantee robustness in tiny NNs, Opt-FreeMark. The attacks have been repeated 10 times for each modality; in the table, the average values and their 95% confidence intervals are displayed. By looking at the results presented in Table 6, it can be observed that on the models watermarked with the FreeMark technique, the WM is not reliably detected, while the WM accuracy computed on the models watermarked using Opt-FreeMark is much higher. These results demonstrate the efficacy of the proposed solution in enhancing FreeMark’s robustness in the “tiny” use case.

6. Conclusions

This work explored the applicability of Opt-FreeMark, an optimized version of FreeMark for tiny NN watermarking. Two optimizations have been devised: model signature computation through SVD, and the creation of a noise-resistant watermarking message through ECC. The optimizations are aimed at improving the robustness of the state-of-the-art method when applied to tiny NNs. The proposed technique has been extensively evaluated on four common malicious model modification attacks, Gaussian noise addition, weight pruning, quantization, and fine-tuning, ensuring that the WM remains correctly identifiable even after the models have been subject to powerful modifications. This paper also verified the capability of Opt-FreeMark to withstand ambiguity attacks by using multiple subsets of different types of forged keys and evaluating the accuracy on the WM obtained using them. The results presented in the work confirm the robustness of Opt-FreeMark for tiny NNs against all the attack pipelines explored in the paper, confirming its capability of guaranteeing the model’s IP protection. Future research should address the applicability of Opt-FreeMark to other typical tiny NN domains, such as speech recognition or sensor data analysis, while also exploring other model architectures. The results achieved in the work also underline the importance of designing specialized watermarking techniques for tiny NN architectures.