A Calculation Methodology for Short-Circuit Currents Under High Penetration of Renewables and VSC-HVDC

Abstract

The increasing integration of power-electronic devices, such as voltage source converter-based high-voltage direct current (VSC-HVDC) systems and inverter-interfaced renewable energy sources (RESs), has rendered conventional short-circuit current (SCC) calculation methods inadequate. This paper proposes a novel analytical model that explicitly incorporates the current-limiting control dynamics of voltage source converters to accurately determine SCCs. The key contribution is a simplified yet accurate formulation that captures the transient behavior during faults, offering a more realistic assessment compared to traditional quasi-steady-state approaches. The proposed model was rigorously validated through electromagnetic transient (EMT) simulations and large-scale case studies. The results demonstrate that the method reduces the SCC calculation error to below 4%. Furthermore, when applied to the real-world provincial power grids of ZJ and JS, all computations converged within 10 iterations, confirming its robust numerical stability. These findings offer valuable insights for protection coordination studies and verify the model’s effectiveness as a reliable tool for planning future power systems with high power-electronics penetration.

1. Introduction

The calculation of SCC constitutes a fundamental aspect of power system analysis, underpinning critical activities such as system planning, relay protection coordination, and verification of electrical equipment ratings. The global pursuit of carbon peaking and carbon neutrality goals is driving a significant transformation of power systems, marked by the growing integration of renewable energy sources, particularly wind and solar power. Concurrently, the need for large-scale renewable energy transmission has led to the widespread adoption of VSC-HVDC technology, owing to its inherent advantages [1,2]. These developments have resulted in an increasing proportion of power-electronic devices on the grid’s supply side, whose distinct characteristics in contributing to SCC can no longer be neglected [3]. Crucially, the high controllability of power-electronic devices leads to SCC characteristics that are fundamentally different from those of traditional synchronous machines. This critical difference necessitates dedicated research into SCC calculation methods specifically tailored for modern power systems integrating VSC-HVDC and a significant share of renewable energy.

Extensive research has investigated the SCC contribution from VSC-HVDC systems. A novel SCC calculation method based on discrete-time modeling was proposed in [4], which demonstrated the capability to accurately track current evolution during a short-circuit fault given the initial state. However, this work focused exclusively on internal faults of modular multilevel converters (MMCs) and did not address the broader system-level SCC contribution of MMCs within an interconnected grid. A detailed analysis of the mechanism by which VSC-HVDC adds SCC to AC systems during AC faults was conducted in [5], which also proposed supplementary control strategies to suppress SCC under both symmetrical and asymmetrical conditions. Despite these contributions, the analysis in [5] was limited to a single-machine infinite-bus system, and a generalized SCC calculation method for power systems incorporating VSC-HVDC was not developed. Research efforts in [6,7,8] have analyzed the inner- and outer-loop control strategies and corresponding response processes of VSC-HVDC converters. While valuable for understanding converter behavior, these studies primarily concentrate on the SCC contribution from the VSC-HVDC itself and generally overlook the significant influence of low-voltage ride-through (LVRT) strategies on the overall SCC characteristics. The SCC response characteristics of VSC-HVDC, considering different fault ride-through strategies and control methods, were analyzed in [9]. This work led to derived expressions for both the transient and steady-state SCC during the current-limiting stage and proposed an SCC calculation method based on a hybrid parameter matrix. Nevertheless, the applicability and convergence of this method in large-scale power grids remain unvalidated and require further investigation. An analysis of MMC output SCC characteristics under a dual-loop voltage-frequency (VF) control strategy was presented in [10], which noted that the converter may exhibit either current-source-like or voltage-source-like behavior post-fault. However, the associated calculation process is acknowledged to be complex, and the analysis does not yield an SCC calculation method suitable for practical application in large-scale power grids, thereby limiting its engineering utility.

The SCC characteristics contributed by distributed renewable energy resources and large-scale renewable energy stations have also attracted considerable research attention. An expression for the SCC from inverter-interfaced distributed renewable energy, incorporating current limiters, was derived in [11]. However, the complexity of the modeling process and its reliance on experimental data hinder the general applicability of this method. Research on doubly fed induction generator (DFIG)-based wind turbines solved the transfer function between the stator steady-state voltage and current under asymmetrical short-circuit faults [12]. This approach utilized the initial and final value theorems of the transfer function to compute the initial and steady-state components of the SCC during the current-limiting stage. Additionally, ref. [13] explored the inclusion of negative-sequence control loops in both the rotor-side and grid-side converters of DFIGs, providing steady-state negative-sequence current expressions under asymmetrical faults for various control objectives and strategies. Notably, both [12,13] concentrate their analysis on single DFIG units and do not extend their methodologies to address the aggregated SCC characteristics of entire wind farms. For renewable energy power stations incorporating energy storage, studies such as [14,15] analyze the SCC contribution characteristics of energy storage stations. These studies treat the stations as current sources during LVRT and propose a short-circuit power calculation method for grids based on the superposition theorem. However, the approach for modeling large-scale energy storage stations in these works relies on a simple per-unit multiplication method, failing to account for the distributed nature and potential interactions of resources within the station. A method for calculating the SCC during the current-limiting stage for renewable energy stations under symmetrical faults, derived from analyzing the inner-loop response of inverters, was proposed in [16]. Importantly, this method calculates the SCC at the station level and does not consider its integration into the SCC calculation for the entire power grid. Analyses of SCC calculation for distributed distribution networks containing renewable energy are presented in [17,18]. However, due to the inherently smaller scale of such distribution networks compared to transmission systems, the methods proposed therein are generally not applicable to large-scale power grids.

The main differences and contributions of our method compared with previous studies are as follows:

(1)

For the calculation of SCC in renewable energy stations, the single-machine multiplication method is commonly used, which does not take into account the variability of the numerous renewable units within the station, leading to increased calculation errors. Existing methods mostly consider only the reactive power current injected by renewable energy, neglecting the contribution of active power current to short-circuit current.

(2)

Previous approaches have rarely been applied to large-scale power systems, and their algorithmic convergence has not been thoroughly validated.

In contrast, the proposed method in this paper offers the following novelties:

(1)

It employs the short-circuit current–voltage (SCC–V) curve, derived from electromagnetic transient (EMT) simulations, as the equivalent port characteristic of renewable energy stations, thereby significantly enhancing the accuracy of SCC calculation.

(2)

The accuracy of the method is validated through comparative analysis with EMT simulation results on the WSCC 3-machine, 9-bus test system.

(3)

The method is successfully applied and tested on a real-world large-scale power grid comprising over 10,000 nodes. More than 400 SCC calculations performed on 525 kV buses all converged within 10 iterations, demonstrating both robust numerical convergence and strong practical engineering applicability.

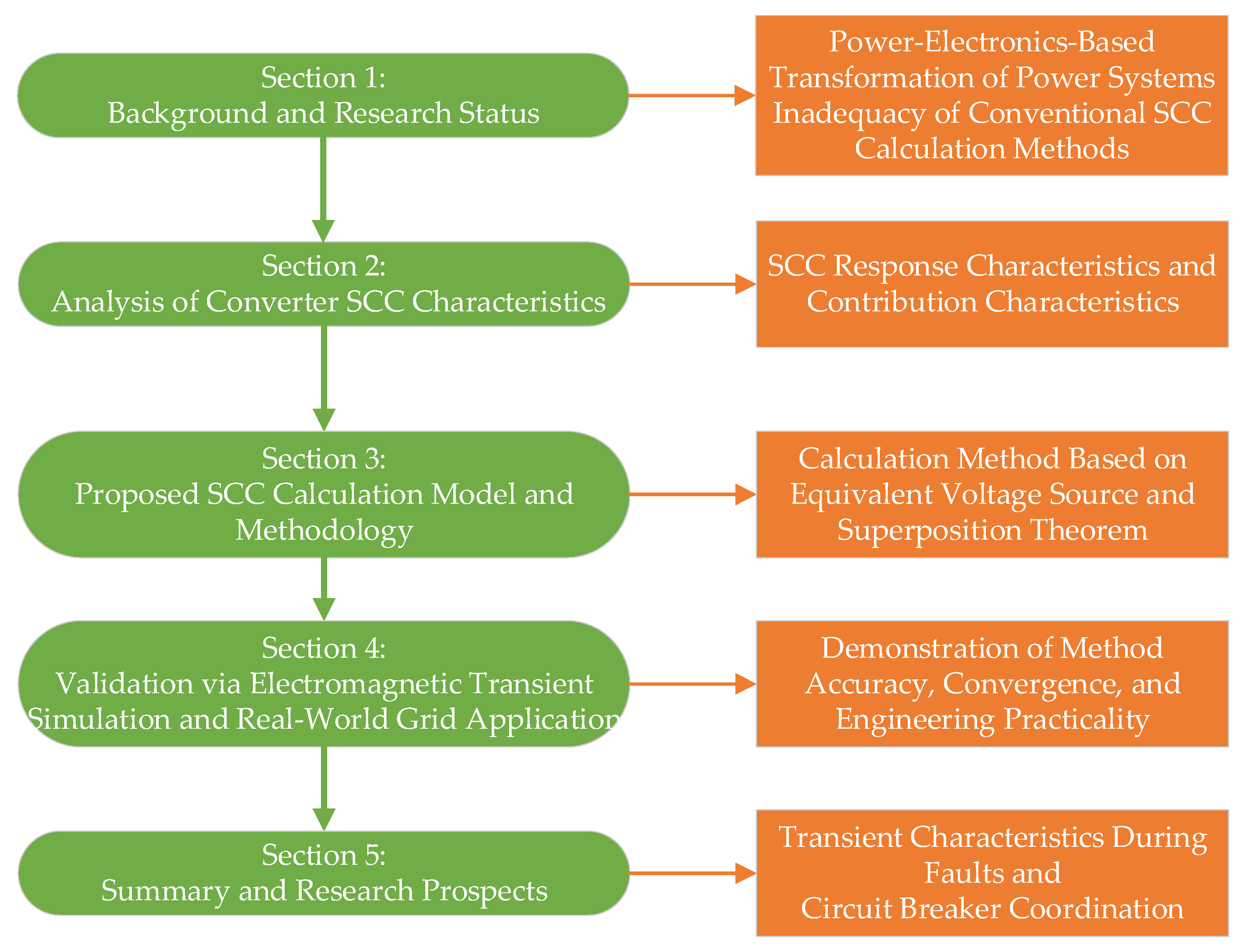
The organization of the paper is as follows:

(1)

Section 2 analyzes the control principles of grid-connected inverters and their SCC response characteristics, establishes the assumption that the current-limiting stage is reached before circuit breaker operation, develops SCC calculation models for the current-limiting stage under various LVRT strategies, and investigates the influence mechanism of inverters on AC system SCC.

(2)

Section 3 introduces a novel SCC calculation model for power systems integrating VSC-HVDC and RESs.

(3)

Section 4 validates the proposed approach through EMT simulations and comprehensive case studies on the ZJ and JS power grids.

(4)

Section 5 summarizes the key findings and outlines directions for future research.

The logic between each section of this paper and the conclusions is shown in Figure 1.

2. Analysis of SCC Characteristics in Converters

2.1. Control Principles and SCC Response Characteristics

2.1.1. Internal and External Loop Control Strategy of the Converter

Various types of non-synchronous machine sources (NSMS) are integrated into power systems, including photovoltaic systems, permanent magnet synchronous generator-based wind turbines, doubly fed induction generator-based wind turbines, energy storage systems, static var generators (SVGs), and voltage source converter-based high-voltage direct current (VSC-HVDC) systems. Although their machine-side operational principles differ, all these systems are connected to the grid through power electronic converters, thereby exhibiting similar power-electronic interface characteristics. Consequently, their control strategies and underlying principles are fundamentally consistent. This section will therefore focus on introducing typical control principles that are applicable to most NSMS.

Modern power electronic systems widely adopt direct current control, which utilizes fast current feedback to achieve high-quality current response. This control strategy has become the mainstream approach for grid-connected converters. However, when a voltage source converter (VSC) is connected to an AC system with a relatively low short-circuit ratio (SCR) (e.g., below 1.3), the direct current control strategy may fail to maintain stable operation at rated power. 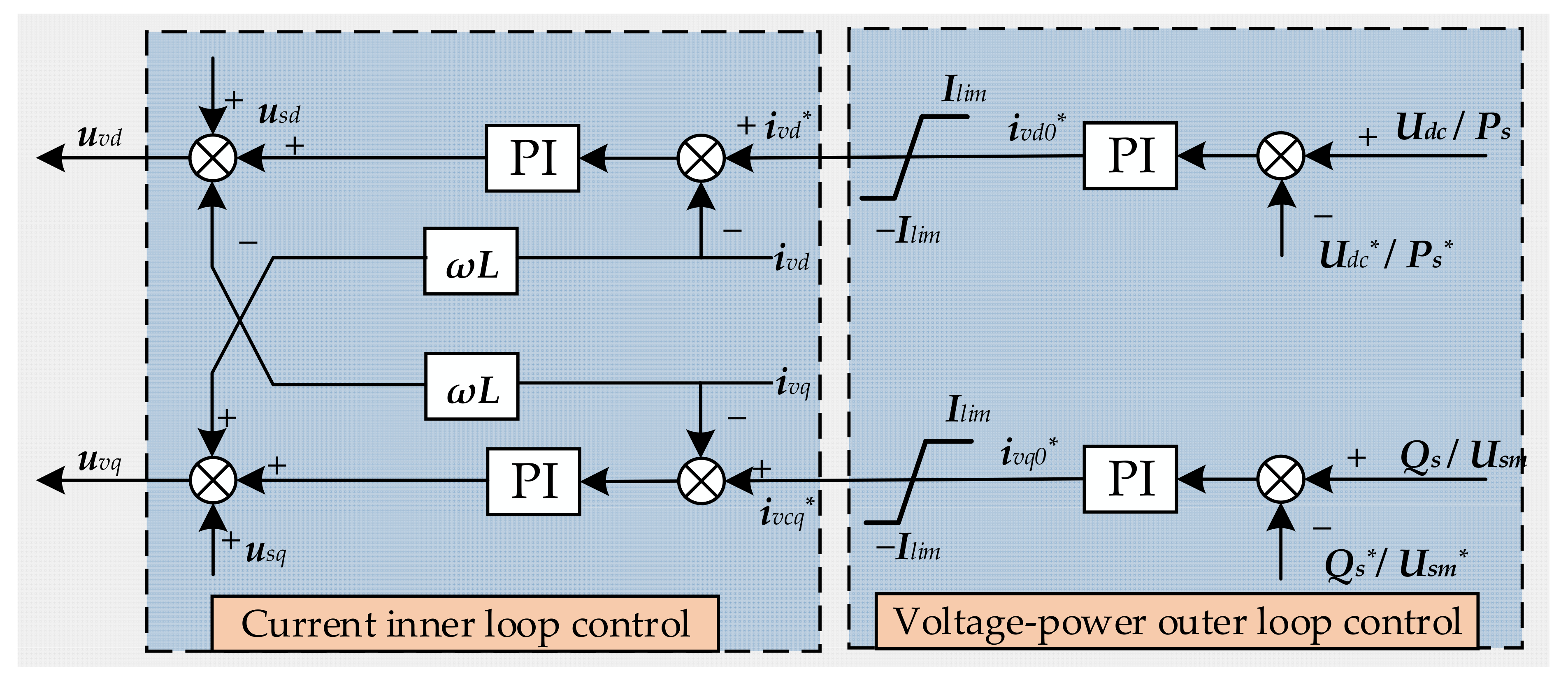To address this issue, power synchronization control (PSC) has been proposed in the literature [19]. The primary distinction between these two control strategies lies in the grid synchronization method: direct current control employs a phase-locked loop (PLL), whereas PSC utilizes a power synchronization loop (PSL) for phase modulation. Despite this difference, both strategies share a common structure of inner and outer control loops, where the outer loop generates current reference commands and the inner loop produces corresponding voltage reference signals. A typical block diagram of the inner- and outer-loop control structure is presented in Figure 2 [20].

As shown in Figure 2, the control objectives of the voltage-power outer loop controller are divided into two categories: the first category is active power control objectives, and the second category is reactive power control objectives. P_s* and U_dc* are the command values for the active power control objectives, representing the active power on the AC side and the DC voltage on the DC side, respectively. Q_s* and U_sm* are the command values for the reactive power control objectives, representing the reactive power and the AC side voltage on the AC side, respectively. Note that only one command value from each category can be selected for control at any given moment.

The output of the outer loop power controller consists of the d-axis current command value, i_vd0*, and the q-axis current command value, i_vq0*, for the inner loop current controller. These two values are the command values before current limiting. I_lim represents the current limit of the converter. After current limiting, the command values become i_vd* and i_vq*. When vector control is applied, the active power control objectives and the reactive power control objectives can be decoupled from each other. Specifically, the active power control objective and the d-axis current command value, i_vd*, of the inner loop current controller form an independent control loop, while the reactive power control objective and the q-axis current command value, i_vq*, of the inner loop current controller form another independent control loop.

2.1.2. Converter Output Current Response Characteristics

During a grid fault, the variation in outer-loop controller parameters induces corresponding changes in the current reference values of the inner loop. Owing to the dynamic response of multiple control loops, the SCC exhibits a transient response process. Similar to the SCC from synchronous machines, the SCC contributed by NSMS also contains fundamental frequency components. To simplify the analysis while accounting for the operating time of circuit breakers, it is essential to characterize the transient response of the SCC. Therefore, this study analyzes the influence of the power-voltage outer loop and the current inner loop on the SCC transient behavior by examining their time-domain characteristics [21].

Based on the control block diagram in Figure 2, the open-loop transfer function of the power outer loop can be expressed as follows:

$$G_{\mathrm{q}}(s)={\displaystyle \frac{K_{\mathrm{Qp}}(s+\frac{K_{\mathrm{Qi}}}{K_{\mathrm{Qp}}})K_{\mathrm{PWM}}{K}_{\mathrm{iP}}(s+\frac{K_{\mathrm{ii}}}{K_{\mathrm{ip}}})}{sL(s+R/L)(s{T}_{\mathrm{PWM}}+1)+K_{\mathrm{PWM}}{K}_{\mathrm{ip}}(s+\frac{K_{\mathrm{ii}}}{K_{\mathrm{ip}}})}}{U}_{\mathrm{g}}$$

(1)

where K_Qp + K_Qi/s represents the transfer function of the power outer loop PI controller, where K_Qp and K_Qi are the proportional and integral coefficients, respectively. K_ip + K_ii/s represents the transfer function of the current inner loop PI controller, where K_ip and K_ii are the proportional and integral coefficients, respectively. K_PWM/(T_PWM/s + 1)is the transfer function of the converter, representing a first-order inertia term, where K_PWM is the converter gain, and T_PWM is the inertia time constant. 1/(Ls + R) is the transfer function of the machine-side filter circuit, where L and R are the inductance and resistance of the machine side, respectively, connected to the external grid. The main control elements include the PI control loop, the converter inertia loop, and the filter circuit loop.

Typical control parameters are as follows [21]: K_Qp = 0.51, K_Qi = 0.10, K_ip = 0.25, K_ii = 0.2475, K_PWM = 3.17, T_PWM = 0.2992, L = 0.43368, R = 0.

Based on (1), the closed-loop transfer function can be derived. The unit step response settling time is then calculated to be 12 ms. Response time is not solely dependent on T_PWM and L, but is influenced by multiple factors. Specifically, the controller parameters (K_Qp, K_Q) are key adjustable design variables. K_Qp primarily governs the initial response speed and disturbance rejection, while K_Q plays a dominant role in eliminating the current-limiting stage error and determining the final convergence behavior. While T_PWM and L are important system constraints and fundamental parameters, the analysis in the paper focuses more on the system constraints and basic parameters to determine the upper limits of the settling time, given the adjustability of the controller parameters. When both parameters are increased by a factor of three, the response time reaches approximately 25 ms, as shown in

Table 1. Voltage–power loop parameter sensitivity analysis.

TPWM	Response Time/ms	L	Response Time/ms
0.2992	12	0.4336	12
0.6	18.3	0.8	19.4
0.9	25.6	1.2	24.2

. Additionally, simulation using a typical non-synchronous machine model shows that the SCC reaches the current-limiting stage around 15 ms.

Based on the above analysis, considering the average response time of SF₆ circuit breakers is between 40 ms and 100 ms, it can be assumed that the current reaches the current-limiting stage before the circuit breaker operates. From an engineering perspective, it is reasonable to calculate only the SCC during the current-limiting stage.

2.2. SCC Calculation Model of the Converter During Current-Limiting Operation

According to the preceding analysis, NSMS typically operate in PV or PQ control mode under steady-state conditions. When an AC fault occurs, the voltage at the point of common coupling (PCC) drops. If the voltage drop is severe, PV or PQ control may generate a current reference that exceeds the rated value of the IGBT devices. To address this, a current-limiting function is generally incorporated into the control system. In this scheme, the current reference calculated by the outer loop is passed through a limiter before being sent to the inner current loop. Under such conditions, the non-synchronous machine source can be modeled as a current source.

The output current characteristics of NSMS are determined by their LVRT strategies. Common LVRT strategies include: reactive power priority limiting, active power priority limiting, and proportional limiting [15].

These strategies are described in more detail below.

(1) Reactive Power Priority Limiting Strategy

In this case, the NSMS prioritizes the delivery of reactive current to support the system voltage, while the remaining capacity is used to deliver active current. The active and reactive current command values are given as follows:

$$\begin{array}{l}{i_{\mathrm{vd}}}^{*}=\left\{\begin{array}{cc}\sqrt{{I_{\lim }}^2-{i_{\mathrm{vq}}}^{*2}}& \left|i_{\mathrm{v}0}*\right|<\left|I_{\lim }\right|\\ 0& \left|i_{\mathrm{v}0}*\right|\ge \left|I_{\lim }\right|\end{array}\right.\\ i_{\mathrm{vq}*}=\left\{\begin{array}{cc}{i}_{\mathrm{vq}0*}\hfill & \left|i_{\mathrm{v}0}*\right|<\left|I_{\lim }\right|\hfill \\ I_{\lim }\hfill & \left|i_{\mathrm{v}0}*\right|\ge \left|I_{\lim }\right|\hfill \end{array}\right.\end{array}$$

(2)

where i_v0* represents the magnitude of the current command before current limiting.

When the reactive current reference exceeds the limit, the limiter saturates at the limit value, and the active current reference is reduced to zero. However, if the reactive current reference remains within the limit, the limiter remains inactive, and the remaining capacity is utilized to deliver active current.

(2) Active Power Priority Limiting Strategy

In this case, the NSMS prioritizes the delivery of active current to avoid causing significant active power shocks to the system. The remaining capacity is used to deliver reactive current. The active and reactive current command values are given as follows:

$$\begin{array}{l}{i}_{\mathrm{vd}}*=\left\{\begin{array}{cc}{i}_{\mathrm{vd}0}*\hfill & \left|i_{\mathrm{v}0}*\right|<\left|I_{\lim }\right|\\ I_{\lim }\hfill & \left|i_{\mathrm{v}0}*\right|\ge \left|I_{\lim }\right|\end{array}\right.\\ i_{\mathrm{vq}}*=\left\{\begin{array}{cc}\sqrt{{I_{\lim }}^2-{i_{\mathrm{vd}}}^{*2}}& \left|i_{\mathrm{v}0}*\right|<\left|I_{\lim }\right|\\ 0& \left|i_{\mathrm{v}0}*\right|\ge \left|I_{\lim }\right|\end{array}\right.\end{array}$$

(3)

When the active current reference exceeds its limit, the limiter saturates at the threshold value and the reactive current reference is set to zero. Conversely, if the active current reference remains within the permissible range, the limiter remains inactive, allowing the remaining capacity to be utilized for reactive current delivery.

(3) Proportional Limiting Strategy

In this case, the NSMS delivers active and reactive current based on a fixed power factor. The active and reactive current command values are given as follows:

$$\begin{array}{l}{i}_{\mathrm{vd}}*=\left\{\begin{array}{cc}{i}_{\mathrm{vd}0}*& \left|i_{\mathrm{v}0}*\right|<\left|I_{\lim }\right|\\ I_{\lim }{\displaystyle \frac{i_{\mathrm{vd}0}*}{i_{\mathrm{vd}0}*+i_{\mathrm{vq}0}*}}& \left|i_{\mathrm{v}0}*\right|\ge \left|I_{\lim }\right|\end{array}\right.\\ i_{\mathrm{vq}}*=\left\{\begin{array}{cc}{i}_{\mathrm{vq}0}*& \left|i_{\mathrm{v}0}*\right|<\left|I_{\lim }\right|\\ I_{\lim }{\displaystyle \frac{i_{\mathrm{vq}0}*}{i_{\mathrm{vd}0}*+i_{\mathrm{vq}0}*}}& \left|i_{\mathrm{v}0}*\right|\ge \left|I_{\lim }\right|\end{array}\right.\end{array}$$

(4)

When the magnitude of the total current reference exceeds the limit, the active and reactive current components maintain their pre-limiting ratio. Otherwise, the limiter remains inactive.

2.3. Influence Mechanism of the Converter on the AC System SCC

2.3.1. Impact of LVRT Strategies on SCC

In AC synchronous power grids, the reactance of high-voltage transmission lines significantly exceeds their resistance, indicating that the SCC is predominantly reactive. As established in the previous section, only the SCC during the current-limiting stage needs to be considered for NSMS. Therefore, the SCC contribution from NSMS equals the current reference value under the LVRT strategy.

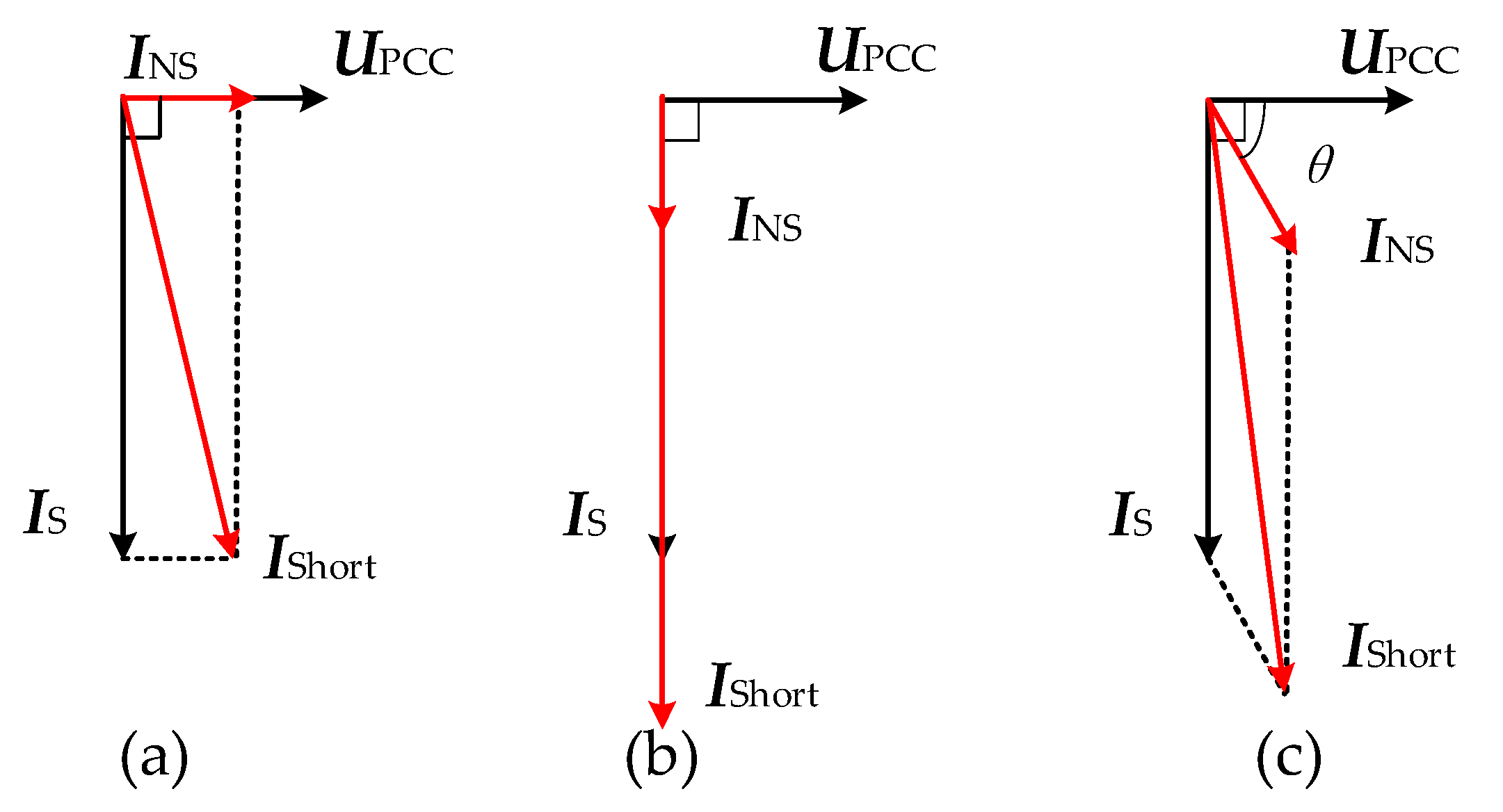
The mechanism by which NSMS contributes to SCC is illustrated in Figure 3.

In Figure 3, I_NS represents the SCC contribution from the NSMS, I_S represents the SCC contribution from the synchronous machine, U_PCC is the voltage at the PCC point, and I_Short is the total SCC. When the NSMS only provides active current, its contribution to the AC system’s SCC is minimal, as shown in Figure 3a. When the NSMS only provides reactive current, its contribution to the AC system’s SCC is maximal, as shown in Figure 3b. When the NSMS simultaneously provides both active and reactive current, its contribution to the AC system’s SCC falls between the two previous cases, as shown in Figure 3c.

2.3.2. SCC of VSC-HVDC Output Under Symmetrical and Asymmetrical Faults

The preceding analysis is based on the positive-sequence network, implying that it only addresses symmetrical faults. For asymmetrical faults, the sequence network analysis method should be applied. Currently, NSMS typically employs control strategies to suppress negative-sequence short-circuit currents. In such cases, the negative-sequence component is modeled as an equivalent impedance, while the zero-sequence component is considered open-circuited due to transformer blocking. Therefore, the mechanism of SCC contribution from NSMS remains consistent under both symmetrical and asymmetrical faults. Specifically, the positive-sequence SCC injected by NSMS is determined by the PCC voltage and the implemented control strategy, whereas no contribution is provided to the negative-sequence and zero-sequence SCC components.

2.4. Challenges in SCC Calculation for Power Systems with VSC-HVDC and RESs

Under steady-state conditions or prior to the activation of LVRT, NSMS can be classified according to their grid interconnection type as PQ-type or PV-type. PQ-type sources are modeled as power sources whose output current varies with the voltage at the PCC. PV-type sources are represented as voltage sources that maintain a constant terminal voltage. Once LVRT is activated, and in accordance with the previously analyzed voltage and current behavior of NSMS during AC faults, all such sources are represented as voltage-controlled current sources.

The aforementioned calculation model presents two principal challenges that must be resolved.

The first challenge originates from the coupling between voltage and current in the voltage-controlled current source model, which necessitates an iterative computational approach. The proposed method initially uses the PCC voltage—without any NSMS connected—as the starting voltage, and then calculates the corresponding SCC. This procedure is iteratively repeated until a converged solution is obtained. Detailed computational steps will be provided in a subsequent section.

The second challenge concerns the large number of NSMS units present in renewable energy stations. If the single-machine multiplication method is employed for equivalence, the distributed arrangement of sources within the station introduces significant errors in the SCC calculation. To address this, this paper proposes using the aggregate voltage–current characteristic curve of the renewable energy station as an interface for iterative interaction with the main grid. This aspect of the methodology will be examined in greater detail in a later section.

3. SCC Method for Power Systems with VSC-HVDC and RESs

Based on the preceding analysis, a SCC calculation method for power systems incorporating VSC-HVDC and RESs is developed. This method builds upon the equivalent voltage source principle [22]. The computational procedure is as follows: First, NSMS are initially neglected, and the SCC at the fault location is calculated using conventional AC system SCC methods. Subsequently, the residual voltage at the node where the NSMS is connected is determined. Based on the SCC-V characteristic of the NSMS, the active and reactive current components injected by the NSMS at that node are then obtained. Finally, the influence of the NSMS injection current on the fault point voltage is incorporated, and the accurate SCC is achieved through iterative computation. The specific steps are detailed below:

(1) Form the node impedance matrix needed for fault component calculation. The node admittance matrix can be obtained first from the power flow data, and the node impedance matrix is obtained by inverting this matrix.

(2) For the fault component network, write the node voltage equations.

$$\left[\begin{array}{c}\Delta \stackrel{.}{U_1}\\ ⋮\\ \Delta \stackrel{.}{U_f}\\ ⋮\\ \Delta \stackrel{.}{U_n}\end{array}\right]=\left[\begin{array}{ccccc}{Z}_{11}& \dots & Z_{1f}& \dots & Z_{1n}\\ ⋮& & ⋮& & ⋮\\ Z_{f1}& \dots & Z_{ff}& \dots & Z_{fn}\\ ⋮& & ⋮& & ⋮\\ Z_{n1}& \dots & Z_{nf}& \dots & Z_{nn}\end{array}\right]\left[\begin{array}{c}0\\ ⋮\\ -\stackrel{.}{I_f}\\ ⋮\\ 0\end{array}\right]=-{\dot{I}}_f^{″}\left[\begin{array}{c}{Z}_{1f}\\ ⋮\\ ⋮\\ Z_{ff}\\ ⋮\\ ⋮\\ Z_{nf}\end{array}\right]$$

(5)

where

Z_ij(i, j = 1,2, …, n and i≠j) represents the mutual impedance between nodes i and j in the node impedance matrix;

Z_ii represents the self-impedance of node i;

$\Delta \stackrel{.}{U_i}$ represents the voltage deviation of node i;

$\stackrel{.}{I_f}$ represents the emitted fault current at the fault point.

(3) According to the boundary conditions, the boundary condition is that the fault point voltage is zero. The SCC calculation equation is written as:

$${\dot{U}}_f={\dot{U}}_f^{(0)}+\Delta \stackrel{.}{U_f=}{\dot{U}}_f^{(0)}-{\dot{I}}_f^{″}{Z}_{ff}=0$$

(6)

The SCC at the fault point (initial sub-transient current) is obtained as:

$${\dot{I}}_f={\displaystyle \frac{{\dot{U}}_f^{(0)}}{Z_{ff}}}$$

(7)

where ${\dot{U}}_f^{(0)}$ represents the pre-fault voltage at the fault point, which can be chosen based on the power flow calculation method for the SCC.

(4) Based on the node impedance matrix and the SCC, the residual voltage at each node can be calculated using the following method:

$${\dot{U}}_i={\dot{U}}_i^{(0)}+\Delta {\dot{U}}_i={\dot{U}}_i^{(0)}-Z_{if}{{\dot{I}}^{″}}_f$$

(8)

where ${\dot{U}}_i$ represents the residual voltage at node i, and ${\dot{U}}_i^{(0)}$ represents the pre-fault voltage at node i.

(5) For the NSMS connection node, the residual voltage is substituted into the NSMS SCC-V curve, and the SCC emitted by the NSMS is obtained. The active and reactive current components are calculated separately.

$$\begin{array}{l}{I_{\mathrm{d}}}_i=f({\dot{U}}_i)\\ I_{qi}=f({\dot{U}}_i)\end{array}$$

(9)

where I_di, I_qi represent the active and reactive currents emitted by the NSMS at node i, and f is the linearized SCC-V function.

(6) Using the node impedance matrix, the impact of the current emitted by the NSMS on the fault point voltage is calculated. With the new boundary conditions, the SCC at the fault point is recalculated.

$${\dot{U}}_f={\dot{U}}_f^{(0)}+\Delta \stackrel{.}{U_f=}{\dot{U}}_f^{(0)}-{\dot{I}}_f^{″}{Z}_{ff}+{\displaystyle \sum Z_{fi}{{\dot{I}}^{″}}_i}=0$$

(10)

where

$${{\dot{I}}^{″}}_i={I_{\mathrm{d}}}_i-j{I}_{qi}$$

(11)

where ${{\dot{I}}^{″}}_i$ represent the current vector emitted by the NSMS at node i.

The SCC at the fault point (initial sub-transient current), considering the NSMS, is obtained as:

$${\dot{I}}_f={\displaystyle \frac{{\dot{U}}_f^{(0)}+{\displaystyle \sum Z_{fi}{{\dot{I}}^{″}}_i}}{Z_{ff}}}$$

(12)

At this point, the SCC, considering the NSMS has been obtained. By setting the convergence accuracy and iterating steps (4) to (6), the SCC with the specified accuracy can be determined.

The convergence of the proposed iterative algorithm is governed by two criteria: the iteration process terminates when either the maximum voltage change across all nodes between consecutive iterations falls below the threshold of |ΔV| < 0.001 p.u., or when the number of iterations reaches the predefined maximum limit of 15. A valid solution is considered converged only if the voltage tolerance criterion is satisfied within the maximum allowed iterations; otherwise, the result is classified as non-convergent. A smaller voltage tolerance threshold improves computational accuracy at the cost of increased iterations and computational resources.

Regarding initialization, the initial voltage profile can be set either to a flat start at the rated value (1.0 p.u.) or based on a pre-converged power flow solution, depending on whether the algorithm operates with or without prior power flow analysis.

The d-axis and q-axis current components are derived from the SCC-V characteristic curves using piecewise linear function fitting. Specifically, in accordance with LVRT requirements, the relationships for both d- and q-axis components are approximated as three-segment piecewise linear functions. The current components corresponding to a specific node voltage are obtained by evaluating these fitted functions. This approach maintains a balance between computational simplicity and accuracy, though more sophisticated fitting methods can be employed for higher precision requirements.

4. Results

To validate the proposed methodology, the initial step involves obtaining the SCC–V characteristic curves of NSMS. Unlike renewable energy power plants that comprise numerous NSMS units, VSC-HVDC systems contain relatively few internal power electronic devices. Therefore, the SCC–V curve for VSC-HVDC can be derived directly from its LVRT control strategy. For renewable energy stations with extensive NSMS deployments, however, obtaining accurate SCC–V curves requires detailed modeling and EMT simulation in PSCAD/EMTDC.

Subsequently, a comparative analysis was conducted between the simulation results and those calculated using the single-machine equivalent multiplication method. Furthermore, a modified WSCC three-machine nine-bus test system was implemented in PSCAD/EMTDC to evaluate the computational outcomes of the proposed method against EMT simulation results. Finally, the proposed methodology was employed to perform comprehensive short-circuit current analysis in two large-scale power grids, namely the ZJ and JS systems.

4.1. Obtaining the SCC-V Curve of the Renewable Energy Station

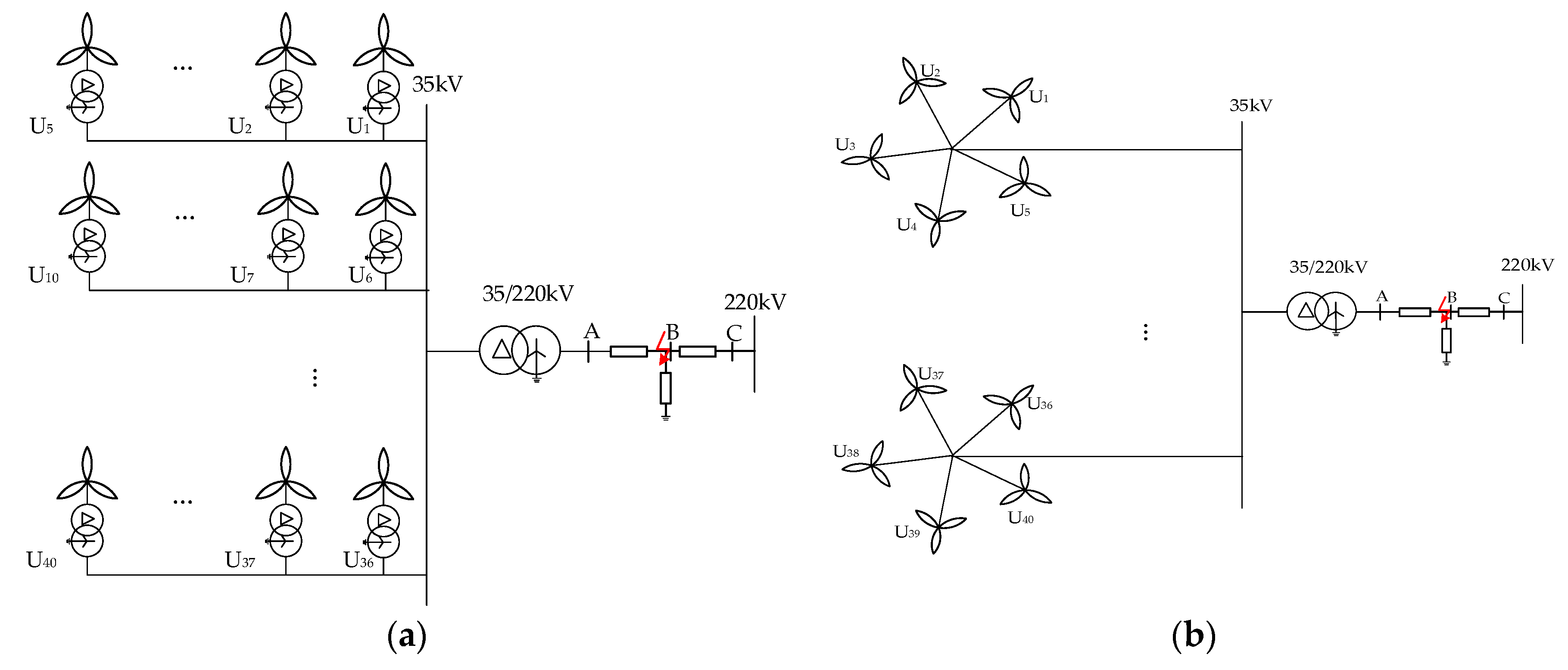
An EMT model was developed in PSCAD/EMTDC based on actual wind farm configuration data. Simulations were performed using PSCAD/EMTDC v5.0.1 with a fixed time step of 50 μs. The wind farm topology is illustrated in Figure 4, with case studies conducted for both chain and radial configurations. The total installed capacity of the wind farm is 200 MW, configured as 8 collector lines × 5 turbines per line × 5 MW per turbine. A three-phase short-circuit fault was applied at point B with a duration of 100 ms, as shown by the red arrow in Figure 4. By varying the fault impedance, different voltage conditions at the PCC were obtained. The turbine spacing was set to 1 km, and the baseline wind speed was maintained at 10 m/s. Key parameters of the wind farm are provided in Appendix A,

Table A1. Main component parameters of permanent magnet wind field.

Type	Parameter	Value
35 kV line	Impedance	0.13 + 0.23 j Ω/km
Main transformer	Transformation ratio	35/220 kV
	Capacity	240 MW
	Impedance	13.54%

.

Under full generation conditions with the PCC voltage dropping to 0.9 pu, the wind farm operates under LVRT control with a fixed power factor (PF) strategy. The active and reactive current outputs during LVRT were evaluated at PF of 0, 0.33, 0.67, and 1, where the power factor is calculated using (13). This approach enables flexible control of the reactive-to-active current ratio, facilitating the implementation of different LVRT strategies. The SCC-V characteristic curves were subsequently derived from these simulations.

$$PF={\displaystyle \frac{i_{vd}*}{\sqrt{{i_{vd}}^{*2}+{i_{vq}}^{*2}}}}$$

(13)

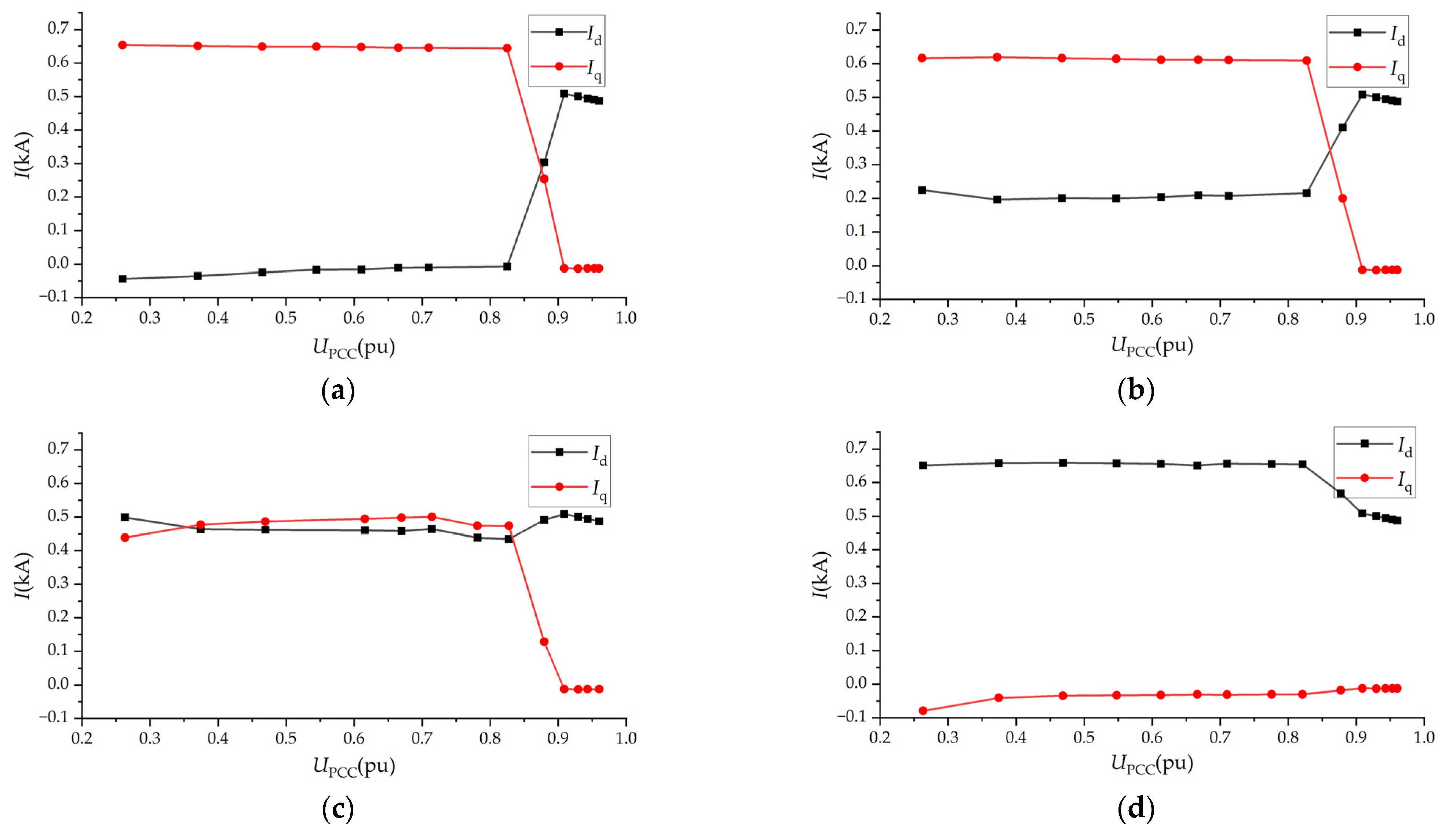
The SCC simulation results and the SCC-V curve for chain topology are shown in Figure 5. The data in Figure 5 was obtained by simulating the system with the short-circuit impedance at Bus B (Figure 4) varied from 0.5 Ω to 9 Ω. This variation resulted in a U_PCC voltage range of 0.26 pu to 0.96 pu, thereby revealing the relationship between U_PCC and the active and reactive currents (I_d, I_q) of the wind farm. This empirical relationship corresponds to the functional form expressed in (9) in Section 3.

Analysis of the characteristic curves reveals that at a U_PCC (PCC voltage) of 0.85 pu, the terminal voltages of individual wind turbines in the chain topology exhibit significant variation. This voltage disparity causes some turbines to experience voltages below the 0.9 pu threshold and enter LVRT mode, while others remain above this threshold and continue normal operation. Consequently, the I_d-U_PCC and I_q-U_PCC curves, are represented using three-segment piecewise functions. Each voltage interval corresponds to a distinct functional relationship.

For the radial topology, the SCC characteristics exhibit a similar pattern to those shown in Figure 5. However, since all wind turbines in this configuration share the same terminal voltage, their LVRT activation occurs simultaneously. Therefore, the I_d–U_PCC and I_q-U_PCC curves are described using two-segment piecewise functions, with different functional expressions applied within specific voltage ranges.

4.2. Comparison with the Single-Machine Multiplication Method

In contemporary large-scale power grids, the SCC contribution from renewable energy stations is typically calculated using the single-machine multiplication method. However, due to the distributed nature of NSMS within a station, the terminal voltages of individual turbines may differ, introducing calculation errors. The magnitude of these errors depends on the station’s collection topology and the control strategies implemented before and after entering LVRT mode. Owing to its distributed configuration, the chain topology exhibits greater voltage variation among turbines than the radial topology, consequently resulting in larger errors when compared with the single-machine multiplication method. Generally, under steady-state conditions, NSMS only injects active current into the grid. If an active-priority control strategy is employed during LVRT, the associated error remains minimal. In contrast, reactive-priority control strategies tend to produce substantially larger errors.

To further investigate the impact of collection topology on SCC characteristics, single-machine multiplier models were developed in PSCAD/EMTDC based on the chain and radial topology wind farms established in Section 4.1. In these models, the 200 MW wind farm was represented by four equivalent wind turbines. By varying the short-circuit impedance, the SCC was calculated under different voltage dip levels, and the results from the single-machine multiplier model were compared with those from the detailed chain and radial topology models. Since significant discrepancies primarily occur within the U_PCC range of 0.8–0.9 pu,

Table 2. Comparison of SCC simulation results between the single-machine multiplication method, the chain topology detailed model and the radial topology detailed model.

Method	Voltage	SCC
		PF = 0		PF = 0.33		PF = 0.67		PF = 1
Single-machine multiplication	Upcc/pu	Id/kA	Iq/kA	Id/kA	Iq/kA	Id/kA	Iq/kA	Id/kA	Iq/kA
	0.82	0.00	0.68	0.24	0.64	0.48	0.50	0.70	−0.02
	0.88	−0.01	0.67	0.24	0.64	0.46	0.50	0.66	−0.02
	0.91	0.54	−0.01	0.54	−0.01	0.54	−0.01	0.54	−0.01
Chain topology detailed model	Upcc/pu	Id/kA	Iq/kA	Id/kA	Iq/kA	Id/kA	Iq/kA	Id/kA	Iq/kA
	0.82	−0.01	0.64	0.22	0.61	0.43	0.47	0.65	−0.03
	0.88	0.30	0.25	0.41	0.20	0.49	0.13	0.57	−0.02
	0.91	0.51	−0.01	0.51	−0.01	0.51	−0.01	0.51	−0.01
Radial topology detailed model	Upcc/pu	Id/kA	Iq/kA	Id/kA	Iq/kA	Id/kA	Iq/kA	Id/kA	Iq/kA
	0.82	−0.01	0.67	0.21	0.65	0.46	0.51	0.72	−0.02
	0.88	−0.01	0.66	0.24	0.63	0.42	0.45	0.63	−0.02
	0.91	0.52	−0.01	0.52	−0.01	0.52	−0.01	0.51	−0.01
Chain topology relative error	/	0.0%	6.3%	9.1%	4.9%	11.6%	6.4%	7.7%	−33.3%
	/	−103.3%	168.0%	−41.5%	220.0%	−6.1%	284.6%	15.8%	0.0%
	/	5.9%	0.0%	5.9%	0.0%	5.9%	0.0%	5.9%	0.0%
Radial topology relative error	/	0.0%	1.5%	14.3%	−1.5%	4.3%	−2.0%	−2.8%	0.0%
	/	0.0%	1.5%	0.0%	1.6%	9.5%	11.1%	4.8%	0.0%
	/	3.7%	0.0%	3.7%	0.0%	3.7%	0.0%	5.6%	0.0%

presents the comparative results for this critical range. To emphasize the topological differences, relative errors between the single-machine multiplication results and both detailed topology models were also calculated. Larger relative errors indicate greater inaccuracy in the single-machine multiplication method for the corresponding topology.

As shown in Table 2, the single-machine multiplication method and the radial topology calculation both avoid the complication of staggered LVRT activation among different turbines within the farm. Consequently, the relative error between the single-machine multiplication method and the radial topology remains relatively small, demonstrating that the single-machine multiplication approach can meet accuracy requirements for SCC calculation in radial-topology renewable energy stations. In contrast, for chain topologies, particularly when the grid connection voltage is approximately 0.9 pu, the single-machine multiplication method produces substantial errors, revealing its limitations under such configurations. In these cases, the I_d-U_PCC and I_q-U_PCC curves provide a more accurate alternative to the multiplication method.

For chain topologies, multiple factors influence the internal voltage distribution among renewable energy units, including variations in collector line impedance and non-uniform wind conditions. The characteristic curve method effectively accounts for these distributed parameters, and the standard curves can be further calibrated to address specific site conditions.

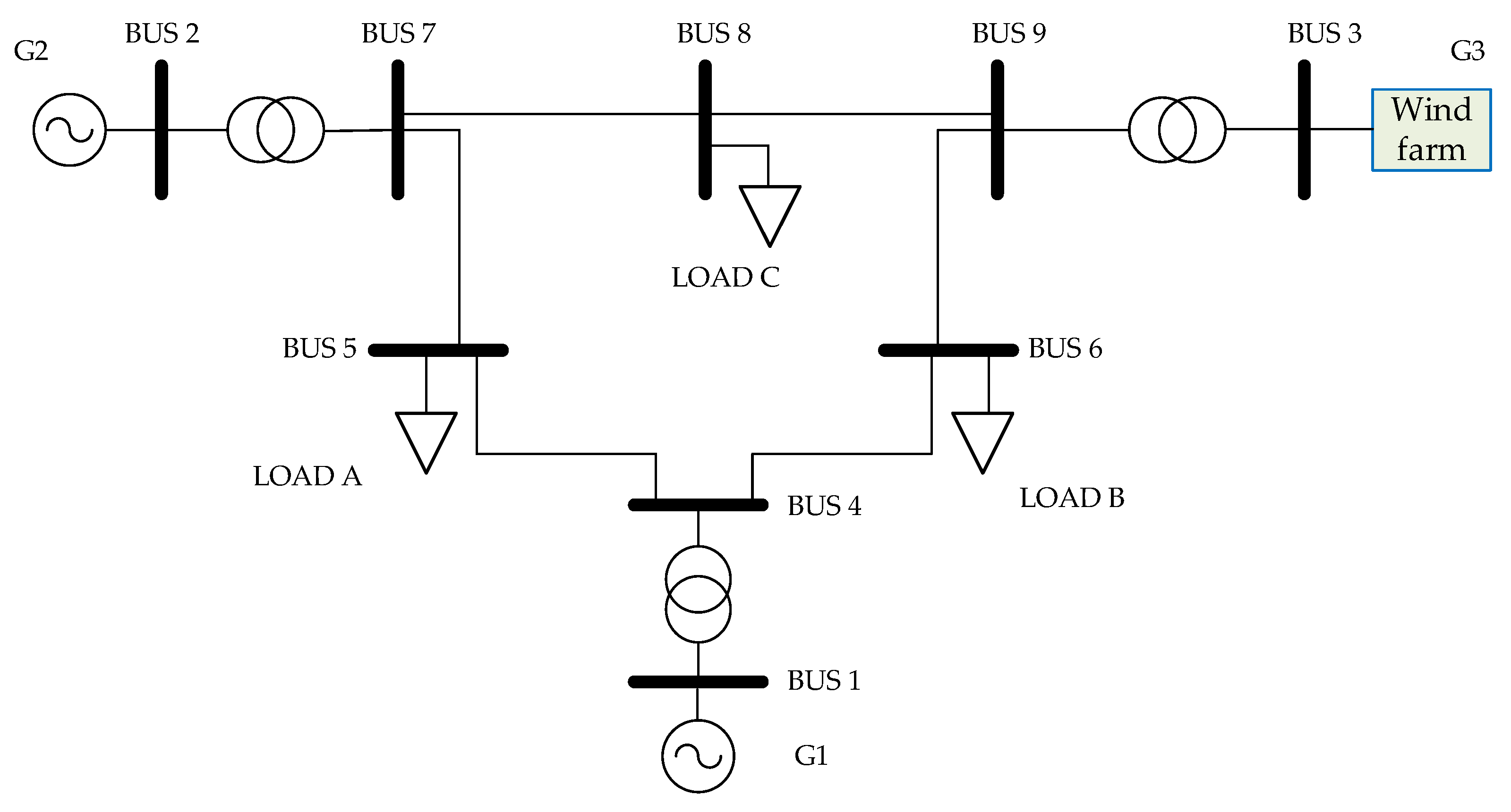
4.3. Case Study on the WSCC 3-Machine, 9-Bus System

Within the same PSCAD/EMTDC simulation environment, a modified WSCC three-machine nine-bus system was implemented. In this configuration, the synchronous generator at bus G3 (originally supplying 85 MW of active power) was replaced with a wind farm while maintaining identical power flow conditions across the system. Detailed system parameters are provided in Reference [23]. All wind turbines in the farm employ the reactive-power-priority control strategy defined by (2), corresponding to a power factor of zero (PF = 0). The resulting system topology is depicted in Figure 6.

The SCC for the system in Figure 6 was calculated using the method presented in Equations (5)–(12) of Section 3. A comparison with the results from detailed PSCAD/EMTDC simulations was conducted, followed by the calculation of relative errors. The comparative results are summarized in

Table 3. SCC calculation results for the modified WSCC 3-machine, 9-bus system.

Bus Number	PSCAD		The Method Proposed in This Study		Error Relative to the PSCAD Simulation Results
	Id/kA	Iq/kA	Id/kA	Iq/kA	Id/kA	Iq/kA
1	18.42	−54.93	18.68	−55.78	1.42%	1.54%
2	15.55	−45.96	15.18	−45.25	−2.37%	−1.53%
3	19.65	−58.03	20.37	−58.88	3.66%	1.45%
4	1.32	−3.92	1.35	−3.82	1.83%	−2.76%
5	1.26	−3.65	1.28	−3.76	1.08%	2.77%
6	1.27	−3.59	1.23	−3.68	−3.27%	2.37%
7	1.28	−3.76	1.27	−3.64	−0.81%	−3.24%
8	1.24	−3.61	1.22	−3.69	−1.47%	2.30%
9	1.26	−3.68	1.26	−3.76	−0.02%	2.20%

. The results indicate maximum calculation errors of 3.66% for active current and 3.24% for reactive current. These error levels fall within acceptable engineering tolerances, thus validating the effectiveness of the proposed methodology.

4.4. SCC Calculation Using the Curve Method in a Real Power Grid

Leveraging the Python 2.7 programming capabilities of PSS/E 33, this study utilizes the SCC-V characteristic curves of renewable energy stations derived in previous sections as representative profiles to model the port characteristics of all renewable energy stations in the ZJ and JS power systems.

The practical application of this method requires the same fundamental data as conventional short-circuit current calculations: system topology, line impedance parameters, synchronous generator subtransient reactances, generator capacities, and load profiles. For implementations based on power-flow calculations, converged power flow results are additionally required. The characteristic curve method specifically demands SCC-V curves for both renewable energy stations and VSC-HVDC systems, which can typically be provided by equipment manufacturers for different grid-connected devices.

Both RESs and VSC-HVDC systems employ identical LVRT strategies. This research implements the proportional current-limiting strategy, where during LVRT conditions, active and reactive currents are injected according to fixed ratios corresponding to power factors of 0, 0.33, 0.67, and 1.

The first case study utilizes the ZJ power grid dataset, which comprises over 10,000 nodes including more than 80 nodes operating at 500 kV and above. Using the proposed algorithm, the SCC calculation achieved convergence within 10 iterations. The contribution of NSMS to the SCC at 525 kV buses under different LVRT strategies was evaluated, with selected results presented in

Table 4. SCC calculation results of ZJ power grid.

Bus Number	PSS/E-ASCC		The Method Proposed in This Study
			No NSMS		PF = 0		PF = 0.33		PF = 0.67		PF = 1
	Id/kA	Iq/kA	Id/kA	Iq/kA	Id/kA	Iq/kA	Id/kA	Iq/kA	Id/kA	Iq/kA	Id/kA	Iq/kA
9190	2.09	−68.02	2.09	−68.02	3.49	−80.05	7.61	−79.26	11.93	−77.02	15.31	−68.17
9251	1.81	−47.42	1.81	−47.42	3.37	−50.08	4.27	−49.85	5.29	−49.29	6.02	−47.50
9639	1.46	−48.71	1.46	−48.71	2.80	−54.18	4.70	−53.79	6.66	−52.80	8.20	−48.72
9661	1.45	−46.45	1.45	−46.45	3.01	−48.23	3.63	−48.12	4.30	−47.77	4.83	−46.61
9925	1.95	−46.91	1.95	−46.91	3.52	−48.99	4.26	−48.85	5.03	−48.45	5.62	−46.94

.

The PSS/E-ASCC (automated short-circuit current) results in Table 4 were obtained using the short-circuit analysis function within the PSS/E software, configured to exclude NSMS. The exact agreement between these results and those computed by the proposed method ((5)–(12)) provides a primary validation of our approach. Additionally, Table 4 presents the SCC calculations under four different PF conditions: PF = 0, 0.33, 0.67, and 1.

As the PF increases, the active current component in the SCC progressively increases while the reactive component decreases—a trend consistent with theoretical expectations. Notably, the calculations for all four PF scenarios achieved convergence predominantly within a single iteration, demonstrating excellent numerical efficiency.

As evidenced in Table 4, Bus 9190 exhibits the most substantial impact from NSMS SCC contributions. This observation is attributed to its connection configuration—linked to the grid interface of an 8000 MW VSC-HVDC system through four transmission lines with relatively shorter electrical distance. In contrast, Bus 9639 connects to the same VSC-HVDC interface through only two transmission lines with a longer electrical distance, resulting in comparatively less influence. These findings confirm that the impact of NSMS on SCC is strongly correlated with electrical distance.

Subsequently, a sensitivity analysis was conducted by removing the 8000 MW VSC-HVDC link to quantify its specific contribution.

Table 5. The sensitivity of the NSMS’s contribution to SCC.

Bus Number	With VSC-HVDC		Without VSC-HVDC
	PF = 0		PF = 0
	Id/kA	Iq/kA	Id/kA	Iq/kA
9190	3.49	−80.05	3.42	−70.90
9251	3.37	−50.08	2.72	−49.78
9639	2.80	−54.18	2.80	−51.04
9661	3.01	−48.23	2.69	−48.22
9925	3.52	−48.99	3.17	−48.97

compares the SCC at various nodes with and without the VSC-HVDC link, under the power flow condition of PF = 0. The comparative results in Table 5 demonstrate that Buses 9190 and 9639 experience the most significant changes in SCC levels, while other nodes remain relatively unaffected. This further validates that the contribution of NSMS to system short-circuit current is predominantly determined by electrical proximity.

The second validation case employs the JS power grid dataset, which similarly comprises over 10,000 nodes including more than 120 nodes operating at 500 kV or higher. Applying the same analytical methodology previously used for the ZJ system, the computational results are summarized in

Table 6. SCC calculation results of JS power grid.

Bus Number	PSS/E-ASCC		The Method Proposed in This Study
			No NSMS		PF = 0		PF = 0.33		PF = 0.67		PF = 1
	Id/kA	Iq/kA	Id/kA	Iq/kA	Id/kA	Iq/kA	Id/kA	Iq/kA	Id/kA	Iq/kA	Id/kA	Iq/kA
2228	0.38	−14.88	0.38	−14.88	1.34	−15.10	1.43	−15.08	1.52	−15.03	1.58	−14.90
2229	2.82	−53.21	2.82	−53.21	6.00	−53.94	6.29	−53.86	6.65	−53.68	6.92	−53.23
2257	0.70	−18.43	0.70	−18.43	2.25	−20.62	3.00	−20.44	3.82	−20.01	4.41	−18.44
2258	2.24	−55.56	2.24	−55.56	4.35	−61.33	6.30	−60.89	8.46	−59.69	10.03	−55.60
2564	0.65	−16.11	0.65	−16.11	1.83	−16.19	1.86	−16.18	1.91	−16.15	1.95	−16.15

. Table 6 presents the SCC results obtained using the PSS/E-ASCC method alongside those calculated by the proposed method across five different operating conditions. All calculations demonstrated efficient convergence within 10 iterations, further validating the method’s applicability to large-scale power systems with high penetration of power-electronic interfaces.

The ZJ and JS provincial power grids both feature substantial renewable energy integration, rendering them highly representative test systems. The proposed methodology demonstrates robust numerical convergence across these large-scale practical cases, underscoring its practical engineering utility for power system planning and operation.

5. Conclusions

This paper first analyzes the control principles of NSMS and examines the response characteristics of inner and outer control loops using transfer functions. For typical inverter-based resources, the control system transition time ranges between 12–25 ms, confirming that the SCC reaches steady-state conditions before circuit breaker operation. This finding justifies the engineering practice of calculating only the current-limiting stage SCC.

Based on different LVRT strategies, an improved SCC calculation model is developed, with subsequent analysis of the underlying contribution mechanisms. The study reveals that reactive current serves as the determining factor in SCC calculation—higher proportions of reactive current during LVRT conditions result in greater SCC contributions from NSMS.

Building upon these foundations, this research proposes a comprehensive SCC calculation framework incorporating VSC-HVDC systems and renewable energy sources. The methodology introduces SCC-voltage characteristic curves as the interface for modeling NSMS behavior and demonstrates its advantages over conventional single-machine multiplication methods. This curve-based approach enables more accurate SCC calculations for renewable energy power plants.

Validation proceeds through two phases: EMT simulations of a small-scale test system verify methodological effectiveness, while subsequent application to the ZJ and JS provincial power grids (each exceeding 10,000 nodes) demonstrates practical utility. For these large-scale systems, all SCC calculations for 525 kV buses converged within 10 iterations, confirming both robust numerical performance and engineering applicability.

The proposed methodology effectively quantifies NSMS contributions to SCC. With the ongoing development and integration of renewable energy and VSC-HVDC technologies, their application to increasingly large-scale power systems becomes increasingly valuable. Particularly in contexts of high-penetration wind, solar, and distributed energy resources, where NSMS impacts grow more complex, this SCC calculation model can provide crucial support for grid operation, protection coordination, and fault analysis.

Future research should address dynamic transient characteristics of SCC, which remain critical for protection system design yet are insufficiently explored in this study. Subsequent work will include detailed electromagnetic transient modeling and investigation of impacts on circuit breaker operation and relay coordination, enabling more comprehensive fault response assessment and protection system design.