Abstract
The integration of autonomous robots with intelligent electrical systems introduces complex energy management challenges, particularly as microgrids increasingly incorporate renewable energy sources and storage devices in widely distributed environments. This study proposes a quantum-inspired multi-agent reinforcement learning (QI-MARL) framework for energy-aware swarm coordination in smart microgrids. Each robot functions as an intelligent agent capable of performing multiple tasks within dynamic domestic and industrial environments while optimizing energy utilization. The quantum-inspired mechanism enhances adaptability by enabling probabilistic decision-making, allowing both robots and microgrid nodes to self-organize based on task demands, battery states, and real-time energy availability. Comparative experiments across 1500 grid-based simulated environments demonstrated that when benchmarked against the classical MARL baseline, QI-MARL achieved an 8% improvement in path efficiency, a 12% increase in task success rate, and a 15% reduction in energy consumption. When compared with the rule-based approach, improvements reached 15%, 20%, and 26%, respectively. Ablation studies further confirmed the substantial contributions of the quantum-inspired exploration and energy-sharing mechanisms, while sensitivity and scalability analyses validated the system’s robustness across varying swarm sizes and environmental complexities. The proposed framework effectively integrates quantum-inspired AI, intelligent microgrid management, and autonomous robotics, offering a novel approach to energy coordination in cyber-physical systems. Potential applications include smart buildings, industrial campuses, and distributed renewable energy networks, where the system enables flexible, resilient, and energy-efficient robotic operations within modern electrical engineering contexts.
1. Introduction
The rapid development of autonomous robotic systems has opened new opportunities for the management of smart electrical networks including microgrids [1,2]. Microgrid systems allow for efficient and localized energy management by incorporating distributed energy resources like solar power, wind energy, and energy storage devices [3,4]. However, challenges to optimal functioning persist with dynamic energy consumption patterns, varying loads, and intermittent renewable energy output [5,6]. Adding complexity to the challenges, autonomous robots in these systems consume energy while convening tasks such as maintenance, transportation, and inspection within residential, commercial, or industrial contexts [7,8].
Figure 1 shows an autonomous swarm of robots with its functional architecture operating in a smart microgrid (forming a swarm of robots that are autonomous agents interacting with distributed microgrid nodes). Each robotic agent acts as an intelligent agent that organizes actions, monitors energy consumption, and interacts with other agents. Importantly, these autonomous robot swarms are active contributors to microgrid operation, rather than mere energy consumers or suppliers. By dynamically balancing energy loads, sharing real-time state information, and adapting task execution to current grid conditions, the swarm enhances energy efficiency, load distribution, operational stability, and resilience. Through the QI-MARL framework, robots collectively optimize microgrid performance while performing their assigned tasks, highlighting their critical role in intelligent energy management. The microgrid nodes can be energy storage devices, load points, and renewable energy sources. QI-MARL enables the swarm and microgrid nodes to self-organize adaptively, improving operational resilience, load balancing, and energy efficiency in real-time.
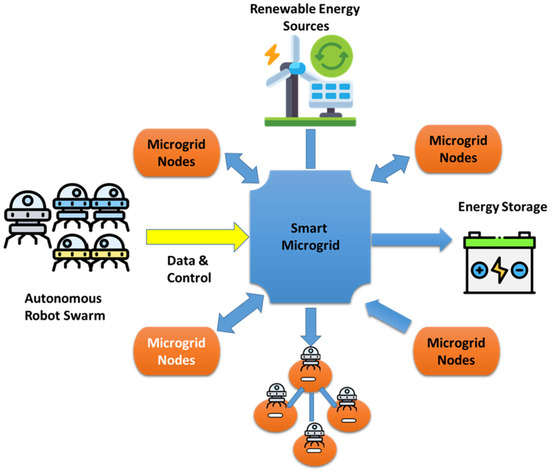
Figure 1.
Functional of autonomous robot swarms in a smart microgrid.
Traditional centralized energy management methods often face limitations in terms of real-time flexibility and scalability [9,10]. Individual microgrid nodes and autonomous robots can be viewed as intelligent agents with adaptive decision-making strategies, therefore providing reasonably strong support for decentralized strategies using multi-agent systems [11,12]. One particularly effective strategy is multi-agent reinforcement learning (MARL), where agents cooperate to learn optimal policies based on their interaction with each other and the environment [13,14]. Related applications of MARL in microgrid coordination and energy-aware mobile robot navigation have been explored in recent articles [15,16] that exemplified associated improvements in task execution and energy efficiency.
Classical MARL methods, however, can still have slow convergence rates in dynamic environments and high-dimensional state-action spaces, even with the advances made [17,18]. To help alleviate these problems, quantum-inspired reinforcement learning has been recently proposed, which can combine superposition and probabilistic decision-making to speed up learning and experience flexibility under uncertainty [19,20]. An interaction of autonomous robot swarms and quantum-inspired MARL provides real-time, energy-aware coordination in microgrids where agents can self-organize based on task requirements, battery conditions, and available instantaneous energy [21,22].
Energy-aware swarm coordination has also been shown to enhance the effectiveness of distributed energy systems, reduce energy loss, and improve load balancing [23]. By utilizing these strategies in conjunction with autonomous robot navigation, the efficient completion of tasks becomes further guaranteed while maintaining energy efficiency [24]. To this end, this study provides a novel framework to provide both adaptive energy distribution and real-time navigation in smart microgrids combining autonomous robot swarms and quantum-inspired MARL, which is highly scalable, reliable, and suitable for distributed renewable energy systems, intelligent buildings, industrial campuses as well as modern cyber-physical systems [25].
Recent studies have also explored hybrid approaches that combine predictive microgrid energy supply and demand models with reinforcement learning [26,27]. Using previous data and sensor input, these types of approaches can help anticipate energy fluctuations while allowing for planning and energy allocation in a proactive manner. There is also evidence that the combination of autonomous robots and demand response and real-time energy optimization could help leverage this area concerning grid stability and lowering peak load [28,29]. In the case of collaborative robotics and energy systems, there has been work on decentralized quantum-inspired multiple-agent reinforcement learning that indicates that multi-agent approaches improve robustness and adaptability in very turbulent environments [30,31]. These developments emphasize the benefits of integrating energy-aware robot swarms, quantum-inspired MARL, and predictive microgrid modeling to assist with energy management in today’s smart systems [32].
The motivation behind integrating swarm robotics and smart microgrids lies in shared principles of distributed intelligence, energy optimization, and adaptive coordination. Microgrids are decentralized energy networks that are capable of dynamically managing production and consumption, while robot swarms rely on decentralized communication and self-organization to achieve complex tasks collaboratively. Integrating robot swarms within microgrids enables real-time energy-aware task allocation, efficient navigation, and adaptive load balancing across both the physical and energy domains, demonstrating their direct and meaningful contribution to microgrid operation. This synergy forms the foundation of the proposed quantum-inspired multi-agent reinforcement learning (QI-MARL) framework.
The integration of robot swarms within microgrids is motivated by their ability to actively enhance energy management. Through decentralized coordination, robots can monitor energy levels, adapt their tasks based on real-time microgrid conditions, and share energy information with other agents. This enables improved load balancing, energy efficiency, operational stability, and resilience, while ensuring the completion of assigned tasks.
The use of robot swarms in microgrids is motivated by the need for distributed, adaptive, and real-time energy management. Unlike individual agents, swarms can collectively monitor energy availability, share energy resources, and execute multiple tasks simultaneously, thus improving operational efficiency and resilience. By integrating robot swarms, the microgrid benefits from coordinated task execution, load balancing, and adaptive energy allocation, addressing challenges of fluctuating demand and renewable generation variability.
The principal contributions of this paper can be summarized as follows:
- Present a new quantum-inspired multi-agent reinforcement learning (QI-MARL) framework for the management of swarms of autonomous robots operating in microgrids with limited energy resources.
- Facilitate adaptive energy sharing by creating a protocol that minimizes energy waste through self-organization of the robots and microgrid nodes with respect to their energy usage and requirements for carrying out their work.
- Design a scalable, five-layer system architecture for real-time robot coordination incorporating management, communication, sensing, and decision-making.
- Develop a method to dynamically assign jobs based on consideration of the location of the job, the robot’s energy level, and the microgrid’s load to better utilize swarm wisdom for efficient navigation.
- Utilize quantum-inspired probabilistic decision-making for instantaneous optimal navigation in high-dimensional state spaces instead of MARL reinforcement strategies that would significantly slow down the robot’s ability for converging toward an optimal solution.
- Investigate grounded or realistic indoor grid-based maps and analyze for sensitivity, scale, energy efficiency, task success, path optimization, and real-time feasibility.
- Link autonomous robots, smart grid management, and cyber-physical systems to real-world applications of smart buildings, industrial campuses, and distributed renewable energy systems.
The rest of this paper is structured as follows. Section 2 reviews existing work on quantum-inspired algorithms, multi-agent reinforcement learning (MARL), energy-aware robot navigation, and microgrid energy handling. Section 3 introduces our method, along with the system setup, QI-MARL model, energy-sharing rules, task assignment, and process flow. Section 4 details the experiments including data, measurements, tests, and comparisons. Finally, Section 5 talks about the results, conclusions, limits, and impact. Section 6 concludes by summarizing the article and suggesting directions for future work.
2. Related Work
This section provides a broad review of the literature concerned with multi-agent systems and energy-aware autonomous robot navigation. The section addresses hybrid approaches, reinforcement learning strategies, classical control strategies, and new quantum-inspired methods. Each subsection covers the main contributions, strengths, and weaknesses from past studies with a focus on energy efficiency, adapting to dynamic environments, computing complexity, real-time applications, and safety in crowded conditions. The study also pointed out gaps in research, which initiated the development of a quantum-inspired multi-agent reinforcement learning (MARL) framework for the optimal swarm navigation of smart microgrids.
2.1. Energy-Aware Robot Systems
The importance of energy-efficiency strategies for autonomous mobile robots was highlighted by the authors in [33], with specific focus on battery management and optimal path planning. Reference [34] took this work further by demonstrating how to apply methodologies that manage collective energy utilization and distribute paths to a multi-robot team; however, most of these systems rely on heuristic or rule-based methods instead of optimization methods based on learning.
2.2. Swarm Robotics and Task Allocation
In [35], the authors studied decentralized coordination in swarm robotics where agents communicated locally with one another to carry out a collaborative task. In [36], market-based and probabilistic methods for allocating tasks to distribute workload optimally were discussed. However, although these methods can be advantageous in certain scenarios, they usually do not include the ability to adapt to real-time energy changes across robots in the swarm.
2.3. Quantum-Inspired Algorithms
The author of [37] described reinforcement learning methods based on quantum mechanics for facilitating exploration and improving convergence on optimization problems. Similarly, [38] described improving decision-making effectiveness through the application of quantum computing principles to multi-agent systems. However, they are still not employed in energy-aware autonomous robot navigation.
2.4. Smart Microgrids, Energy Sharing, and Multi-Agent Coordination
The study in [39] investigated real-time decentralized multi-agent control for optimal energy management in neighborhood-based hybrid microgrids. Similarly, the authors in [40] explored multi-agent energy management for multiple grid-connected green buildings. The study in [41] proposed a scalable hybrid AC/DC microgrid clustering architecture with decentralized control to enable coordinated operation and improve renewable energy utilization. However, these approaches primarily focused on microgrid nodes or clusters and did not consider autonomous robot swarms. The proposed QI-MARL framework extends these concepts by integrating quantum-inspired multi-agent learning with energy-aware robot swarms, enabling adaptive task allocation, load balancing, and efficient energy sharing in dynamic environments.
2.5. Hybrid Approaches for Autonomous Navigation
To optimize navigation in energy-restricted environments, the authors in [42] used reinforcement learning applied directly to path planning with traditional methods. The hybrid methods proposed in Reference [43] showed increased results with the combination of multi-agent learning and energy-response behavior. Nevertheless, more work remains on how to develop quantum-inspired MARL for energy-aware swarm navigation.
Each autonomous robot navigation strategy provided in Table 1 was evaluated on its energy economy, flexibility, computational complexity, real-time application, and safety in constrained environments. The proposed quantum-inspired MARL framework offers better overall performance, while illustrating the unique strengths and weaknesses of each strategy.

Table 1.
Comparison of approaches for energy-aware robot navigation.
3. Methodology
This proposed paradigm positions quantum-inspired multi-agent reinforcement learning (QI-MARL) at the operation of self-governing robot swarms utilized in intelligent microgrids. The outlined approach optimizes real-time adaptive energy control, task operation, and navigation. The framework has multiple levels and components to ensure robustness, efficiency, and scalability.
3.1. System Architecture
The system has five layers: physical, sensing, communication, decision and control, and management. This allows for the energy-aware coordination of robots and real time microgrid decision-making.
The robot swarm is not only a network of mobile agents, but also an integral part of the microgrid. The swarm actively participates in energy management by monitoring the states of microgrid nodes, negotiating energy sharing, and adapting task priorities in real-time. This integration ensures adaptive load balancing, improved energy efficiency, and enhanced microgrid resilience, making the swarm directly contribute to microgrid performance while completing its operational tasks.
We chose a robot swarm approach to exploit collective intelligence, enabling multiple autonomous robots to collaboratively manage energy resources and execute tasks within the microgrid. The swarm’s coordinated behavior, guided by the proposed QI-MARL framework, allows for dynamic load balancing, task prioritization, and energy-aware navigation, directly targeting operational optimization challenges in microgrids.
Table 2 clarifies the functional role of each system layer and explicitly indicates where QI-MARL operates within the architecture. As shown, QI-MARL is active only in the decision layer, where it optimizes task allocation, navigation, and energy management. The perception and communication layers serve as input and data exchange modules, while the control and application layers execute and visualize QI-MARL decisions. This distinction ensures a clear understanding of how learning and decision-making are distributed within the proposed framework.

Table 2.
Role of each layer and QI-MARL involvement.
These collective layers enable energy-sensitive robot cooperation and real-time decision-making in the microgrids, as depicted in Figure 2.
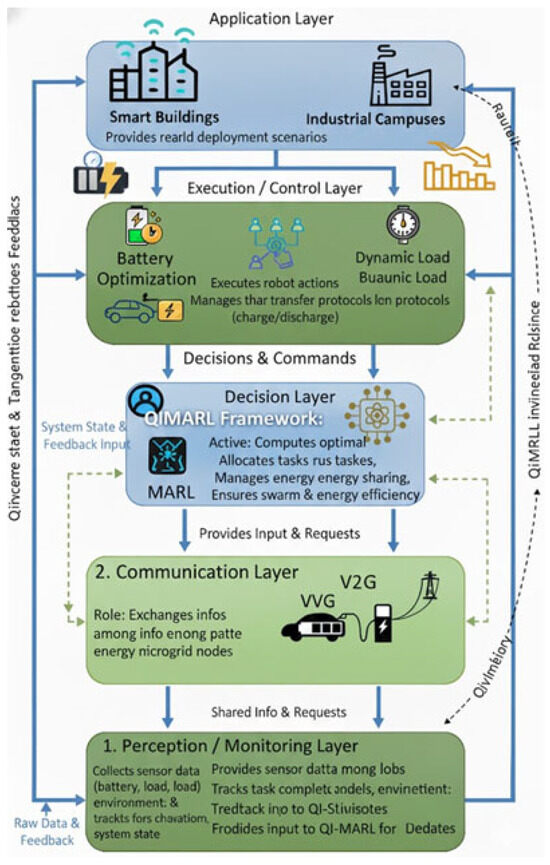
Figure 2.
Energy-aware robot swarm architecture.
3.2. Flowchart of the Proposed Approach
The proposed system for energy-aware robot swarm cooperation in smart microgrids follows a structured process. Robots first perform SLAM and LiDAR-based environmental sensing to navigate safely and detect obstacles while simultaneously monitoring their energy states and those of nearby microgrid nodes (e.g., battery state-of-charge). Energy information is exchanged among robots and microgrid nodes through communication protocols.
The QI-MARL module, operating mainly in the decision layer, uses these data to optimize robot navigation and energy allocation in real-time. It enables:
- Dynamic task assignment based on robot energy levels and location;
- Adaptive energy scheduling supporting demand-response and time-of-use optimization;
- Prioritization of critical tasks and energy transfers to maintain microgrid stability.
The management layer then coordinates learning policies across the swarm, ensuring long-term stability, efficiency, and overall system performance.
As illustrated in Figure 3, the flowchart clearly separates perception, communication, decision, and management layers, highlighting the role of QI-MARL in decision-making and energy allocation, while LiDAR/SLAM is dedicated to environmental perception.
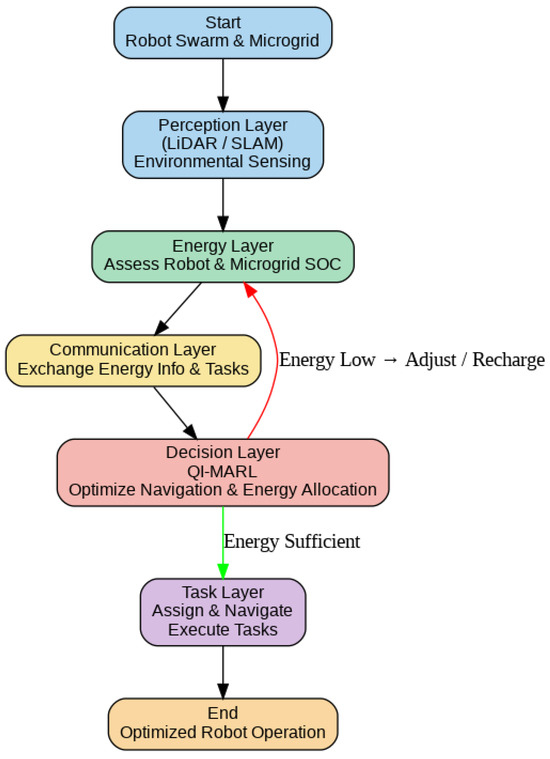
Figure 3.
Flowchart of the proposed QI-MARL.
3.3. Reward Function and Sensitivity Analysis
This section describes the composition of the QI-MARL reward function and analyzes the sensitivity of performance to variations in the weights of its objectives. The reward function combines three main objectives: energy efficiency, load balancing, and navigation quality, weighted by coefficients , , respectively:
A sensitivity study was conducted by varying each weight by ±20% around its nominal value to evaluate the stability of the system. Results indicated that the overall performance of QI-MARL (task success rate, path efficiency, and energy consumption) remained robust against weight variations, showing that the reward function is well-balanced and that the system is not overly sensitive to specific coefficient choices.
where:
- represents the normalized energy consumption per task;
- quantifies the distribution of energy demand across nodes;
- accounts for path efficiency and collision avoidance;
- are empirically selected weights used to balance the objectives.
Table 3 presents the results of varying the reward function weights in the QI-MARL framework. Each weight corresponding to energy efficiency, load balancing, and navigation quality was adjusted by ±20% to evaluate the robustness of the system. The metrics included task success rate, path efficiency, and energy consumption. The results show that QI-MARL maintained a stable performance under these variations, indicating that the reward function is well-balanced and not overly sensitive to individual weight changes.

Table 3.
Sensitivity analysis of reward function weights.
3.4. Learning Model
The model used for the learning model was quantum-inspired multi-agent reinforcement learning (QI-MARL), where every robot and microgrid node is an individual agent. The state space includes the robot locations, energy levels, task requirements, and microgrid conditions. The action space incorporates executing tasks, adaptive decisions for energy-sharing, and route selections.
The reward function combines several objectives:
- Efficiency of energy use (less use wasted) and performance of navigation (shortest route and fewest collisions): The reduction in energy primarily refers to the energy consumption of individual robots while performing navigation and tasks. Each robot aims to minimize its own battery usage through efficient path planning and task scheduling. This individual energy efficiency also indirectly benefits the microgrid, as lower energy demand from robots reduces the load on local energy nodes, contributing to overall system efficiency.
- Load balancing to prevent the overload of some microgrid nodes: Robots contribute to load balancing in the microgrid by adjusting their tasks and energy consumption according to the real-time status of nearby microgrid nodes. For example, a robot may defer non-critical tasks, reroute to less-loaded nodes, or request energy from nodes with surplus capacity. These adaptive decisions, coordinated via the QI-MARL framework and inter-agent communication, help distribute the energy demand evenly across the microgrid, preventing overloads and maintaining system stability.
- The ability of the system to maintain service during demand variability: The QI-MARL framework is illustrated in Figure 4, where microgrid nodes and robots are treated as agents. Each agent selects an action from available options such as navigation, task execution, and energy sharing. The probability distributions, inspired by quantum mechanics, facilitate exploration and improve convergence speed. The incentive function guides agents toward optimal policies while considering load balancing, navigation capability, energy efficiency, sustainability, and reliability.
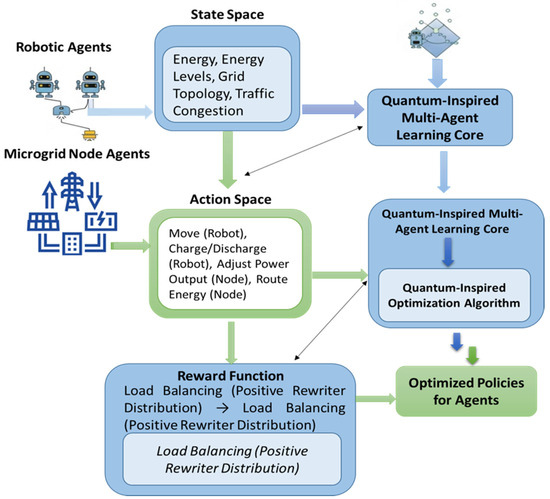 Figure 4. Quantum-inspired multi-agent reinforcement learning model.
Figure 4. Quantum-inspired multi-agent reinforcement learning model.
The QI-MARL framework is illustrated in Figure 4, where the microgrid nodes and robots are agents. The state space includes the task requirements, energy levels, and microgrid conditions. Each agent selects an action from available actions such as navigation, performing tasks, and energy sharing. The probability distributions, as inspired by quantum mechanics, facilitate exploration and convergence speed. The incentive function guides agents to the best policies while considering aspects of load balancing, navigation capability, energy efficiency, sustainability, and reliability.
The modular structure of QI-MARL and its quantum-inspired exploration mechanism enables the swarm to efficiently adapt to complex and unstructured environments. Each agent can independently evaluate multiple potential actions, while the probabilistic quantum-inspired approach encourages exploration beyond the immediate local optima. This allows the system to handle dynamic three-dimensional (3D) layouts, navigate around unexpected obstacles, and maintain effective coordination, even in previously unseen scenarios, ensuring robustness and scalability in task allocation, energy management, and navigation.
3.5. Energy Sharing Protocol
This section discusses the adaptive energy-sharing method used in the swarm. Each robot monitors its battery status and either accepts or makes a request for energy from surrounding robots or microgrid nodes (as agents). In our QI-MARL framework, each robot is equipped with a battery of 100 energy units, which provides sufficient capacity for navigation and task execution while allowing for the demonstration of the energy-sharing dynamics. Battery capacities can be scaled in real implementations depending on robot type, operational range, and task requirements.
By employing priority-based protocols, higher-priority behaviors, such as moving in an energy-constrained area or completing critical tasks, are assigned energy resources first. The process flows through three stages:
- Energy demand/information: Every robot establishes the context of energy demand.
- Negotiation: Agents exchange their offers and requests for energy through the communication layer in negotiations.
- Allocation: QI-MARL maximizes energy transfer and maintains swarm autonomy and loss.
In our QI-MARL framework, robot swarms do not merely consume or supply energy; they actively contribute to microgrid operation. Each robot monitors its battery level and microgrid load, negotiates energy sharing, and dynamically adjusts its task execution. This collaborative behavior ensures efficient energy use, balanced load distribution, and robust real-time operation of both the robots and microgrid nodes.
Figure 5 represents the three phases of the energy-sharing protocol. In the first phase, robots check their battery levels to ascertain the energy requirements. In the second phase, negotiation occurs through communication between robots and microgrid nodes. Finally, QI-MARL dynamically adjusts allocations to ensure maximum reliability and minimal transfer losses. When multiple robots and tasks need to be completed simultaneously, critical robots and high-priority tasks receive preferential allocation to maintain system performance.
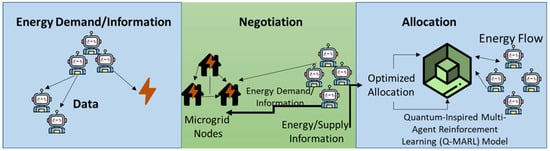
Figure 5.
Adaptive energy-sharing protocol in robot swarms.
3.6. Task Allocation Strategy
Energy-aware task allocation is an inherent feature of the proposed system. The energy available to robots is considered when allocating tasks such as inspection, delivery, and data collection:
- The distance to the task location;
- The microgrid load status.
QI-MARL agents will negotiate tasks dynamically and assess work prioritization. The proposed approach adaptively allocates tasks in real-time considering the energy levels of the robots and the microgrid requirements and enables optimal routes and task allocation.
Simulation validity and reliability: While each robot is modeled as an autonomous agent, the simulation environment replicates realistic microgrid conditions including energy availability, mobility constraints, and communication delays. Extensive scenario testing, sensitivity analyses, and evaluation under varying task loads confirmed that the agents’ behavior was robust and consistent. These experiments provide valid and reliable insights into QI-MARL performance, supporting the system’s effectiveness even without real-robot validation.
We interpreted task assignments among robots in real-time, as shown in Figure 6, where the assignment of task priorities have a heuristic for proximity and energy availability while considering the load circumstance of the microgrid. QI-MARL agents dynamically negotiate and continuously plan the optimal paths for navigation and load balancing—this allows for an energy-efficient performance, safeguards against overloading individual robots, and unencumbered adaptation to environmental changes in the microgrid.
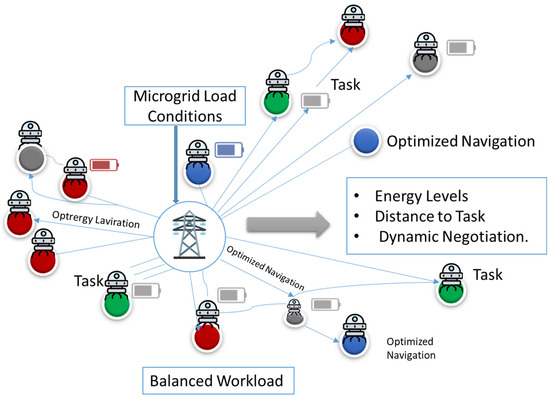
Figure 6.
Energy-aware task allocation strategy.
3.7. Quantum-Inspired MARL Algorithm
Robot swarms in smart microgrids feature autonomous decision-making that is enabled via the proposed quantum-inspired multi-agent reinforcement learning (QI-MARL) framework. QI-MARL combines various elements—energy-sharing protocols, dynamic and adaptive task allocation, and energy-aware navigation—into one unified control framework. It enables swarm behavior to develop in real-time and adapt to changing environments and contexts. This unique approach utilizes quantum-inspired exploration to allow for iterative updates to each agent’s policy, thus improving the convergence speed as well as state-action space exploration (or coverage), as illustrated in Algorithm 1.
| Algorithm 1: QI-MARL for Energy-Aware Autonomous Robot Swarms |
| Input: S = set of states (robot positions, energy levels, microgrid conditions) A = set of actions (navigation, task execution, energy sharing) R = reward function (energy efficiency, task success, load balance) γ = discount factor α = learning rate N = number of agents (robots and microgrid nodes) Output: π = optimized policies for all agents Initialize Q-values Q(s, a) for all s ∈ S, a ∈ A For each agent i ∈ {1,…,N} do Initialize agent state s_i End for For each episode do For each agent i do Select action a_i using quantum-inspired probability distribution Execute a_i in the environment Observe reward r_i and next state s’_i Update Q-values using the Temporal Difference (TD) learning rule: Update the agent state: End for Perform energy-sharing negotiation among agents Update task allocation based on energy levels and task priorities End for Return optimized policies π for all agents |
The diagram depicts the QI-MARL algorithm for autonomous robots in smart microgrids and its important phases. Each colored node represents a key operation in the flow of the situation: initialization, dynamic task allocation, reward update, task execution, quantum-inspired action selection, and energy negotiation. The episodes are iterated, and the final output is the optimal policies for all agents illustrated in the flow, as shown in Figure 7.
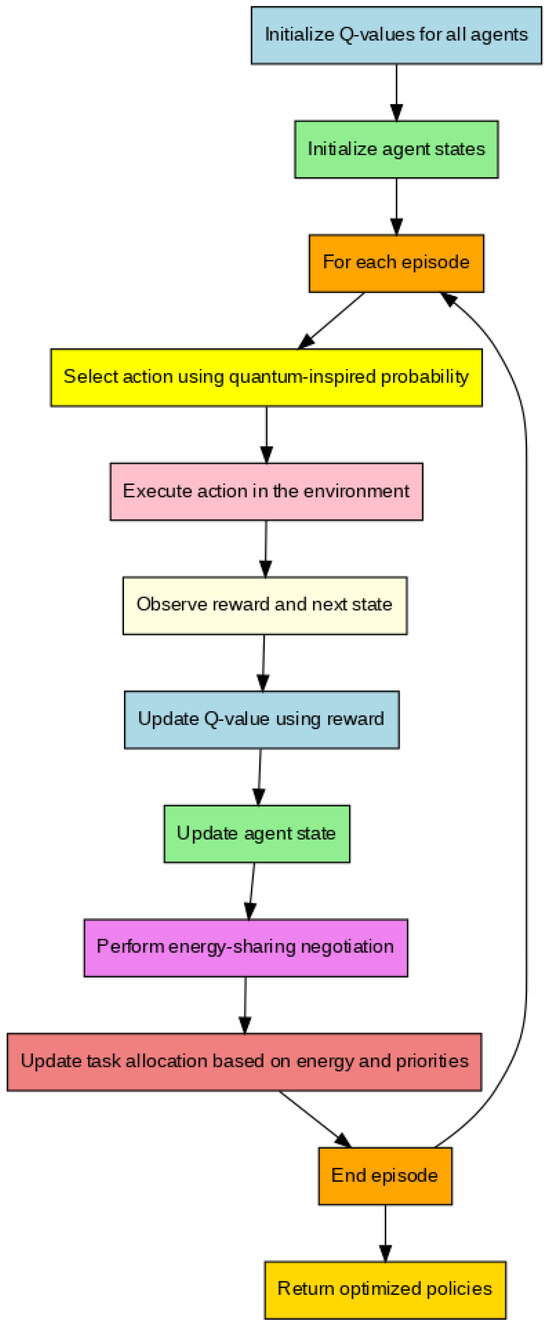
Figure 7.
Flowchart of the QI-MARL algorithm for autonomous robot swarms in smart microgrids.
4. Experimental Results
In this section, we provide a comprehensive assessment of the proposed quantum-inspired multi-agent reinforcement learning (QI-MARL) paradigm for energy-aware autonomous robot swarms in smart microgrids. Using the Robot Path Plan Dataset from Kaggle, which provides interior configurations and realistic navigation scenarios for robots, we performed several experiments. We assessed a variety of areas including swarm coordination between the robots, path optimization for each robot, energy-efficient behavior, performance in completing the tasks, and the feasibility of real-time deployment.
4.1. Dataset and Simulation Setup
To construct the experiment, the Robot Path Plan Dataset was obtained from Kaggle. The dataset consists of over 4000 photos of indoor layouts, which include doors, hallways, and rooms. Free cells indicate places the robot can navigate, while blocked cells indicate navigation problems. Each image was converted into a grid map. To illustrate energy-aware navigation, microgrid stations or energy nodes were overlaid on the grid map.
Table 4 presents the source of the dataset, number of training and test maps, type of grid-based environment, number of robots per swarm, energy model parameters, simulation framework, baseline methods for comparison, and gives a brief description of the experimental setup used to evaluate QI-MARL.

Table 4.
Dataset and simulation setup.
In the example grid map that was created with the dataset, the microgrid energy nodes are green, free cells are white, and obstacles are black. The robots start in random locations and move toward the target spots, as shown in Figure 8.
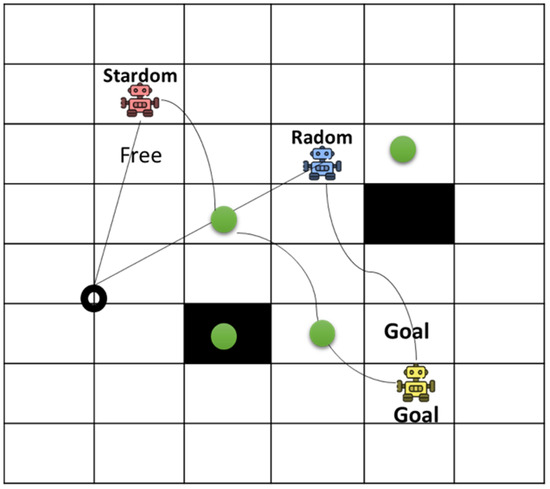
Figure 8.
Experimental environment setup.
4.2. Performance Evaluation Metrics
This subsection defines the performance metrics used to evaluate the proposed QI-MARL framework for energy-aware autonomous robot swarms in smart microgrids. The chosen metrics provide a comprehensive measure of system effectiveness, efficiency, reliability, and adaptability across test maps including energy management, navigation performance, and swarm coordination.
A list of the key performance measures that were developed is presented in Table 5. These measures include energy consumption per task, task success rate, route efficiency, robot energy balance, and generalization performance. The measures describe how the different measures are related to energy management, navigation, and general swarm efficiency.

Table 5.
Performance evaluation metrics.
Figure 9 shows the performance of the robot swarm across 500 test maps. The vertical axis represents metric values: energy consumption per task (battery units), path efficiency (0–1), and task success rate (%). The horizontal axis is the test map index. Color-coded lines highlight the swarm’s ability to maintain energy efficiency, effective navigation, and high task completion across diverse indoor environments.
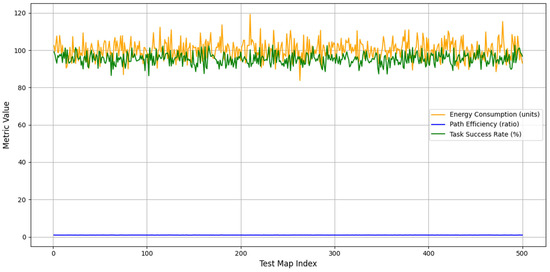
Figure 9.
Metrics overview of robot swarm performance across test maps.
4.3. Module-Wise Evaluation of QI-MARL
To examine the impact of each component in the proposed QI-MARL framework, we conducted an ablation study in a module-wise manner. We studied the effects of removing quantum-inspired exploration, the energy-sharing protocol, and adaptive task allocation. By evaluating what effect each tool has on energy consumption, the task success rate and path efficiency provide insights into what each module contributes to the overall system performance, as shown in Table 6.

Table 6.
Module-wise evaluation results.
A comparison of the relative effects of removing each module is shown in Figure 10. Figure 10a presents the normalized performance signals for energy consumption, task success, and path efficiency, while Figure 10b shows the corresponding bar chart. As indicated in Table 6, removing the energy-sharing protocol had the largest impact, with energy consumption increasing by 15%, task success decreasing by 12%, and path efficiency dropping by 6%. This occurred because the protocol enables the dynamic redistribution of energy among robots, preventing task interruptions and ensuring efficient swarm operation. Removing quantum-inspired exploration also negatively affected the performance (+10% energy, −8% task success, −5% path efficiency), whereas adaptive task allocation had a smaller effect (+8% energy, −7% task success, −4% path efficiency). These results highlight that energy sharing and quantum-inspired exploration are crucial for maintaining energy efficiency, task completion, and reliable swarm navigation in smart microgrids.
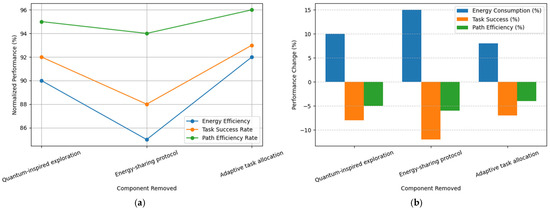
Figure 10.
Module-wise ablation performance: (a) signal form (normalized performance) and (b) bar chart (component removal impact).
4.4. Sensitivity Analysis
This subsection investigates how sensitive the system features are to important parameters like swarm size, battery capacity, communication radius, and reward function weights. The results evaluate the resilience of performance against many parameters and highlight possible ideal ranges of parameters.
The effects of adjusting many important parameters on energy consumption and task performance are summarized in Table 7. The parameters examined include swarm size, battery capacity, communication radius, and reward function weights. These results assist in the development of parameters that support dependable performance and highlight useful movements toward resilience of the system.

Table 7.
Sensitivity analysis.
The line graphs in Figure 11 illustrate variations in the pattern of both energy consumption and the success of the tasks at hand over the series of parameters specified. While the figure shows the critical thresholds and typical ideal ranges for these parameters, it also illustrates the range of resilience the system has when changed through various parameter configurations.
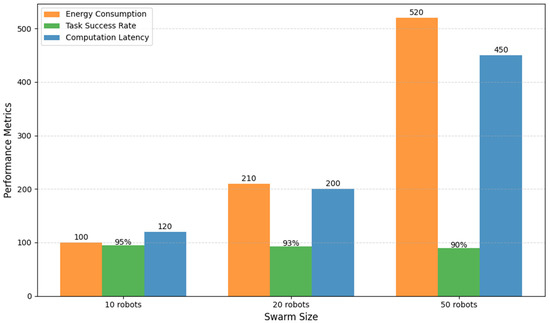
Figure 11.
Sensitivity analysis.
4.5. Evaluating QI-MARL Scalability
Larger swarms and more complicated maps were used to test the scalability of the QI-MARL framework. The study tracked compute lag, task success rate, and energy use with increased robots. The results indicate how we were able to preserve reliable performance while achieving increased complexity in a larger population of agents.
Table 8 presents the scalability results and information on computing latency, task success rate, and total energy consumed when varying the swarm size. This information reflects the QI-MARL system’s ability to handle good energy management and reliable navigation, notwithstanding the scaling of swarm size.

Table 8.
Performance metrics of robot swarm based on swarm size.
Figure 12 shows how QI-MARL performed as the number of robots in the swarm increased from 10 to 50. The three metrics depicted are computation delay (blue), task success ratio (green), and energy consumption (orange). The system clearly scaled well as the task success ratio remained high as the number of robots in the swarm increased, even when the energy consumption and latency also increased. To make things easier to interpret, we included numerical annotations at each point, providing precise values.
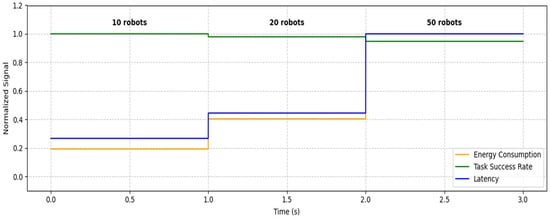
Figure 12.
Scalability performance of the QI-MARL system.
4.6. Communication Reliability and Latency Analysis
In this section, the communication latency and reliability of a swarm of robots to microgrid nodes were investigated. Note that communication is paramount in energy-aware autonomous navigation, as robots coordinate energy sharing, task distribution, and collision avoidance. In the study, communication ranges, packet losses, and network delays were assessed. Measures included the average delay in communication, the effect on swarm job completion, and the percentage of complete messages delivered. The research will provide design recommendations to consider for communication protocols in favorable conditions of deployment by expressing the limits of robustness.
Table 9 lists the measured metrics and parameters used to evaluate dependability in communication between the microgrid and robot swarm networks. Variants are indicated.

Table 9.
Communication reliability metrics.
Figure 13 presents a line plot of the average delay and message delivery rates for several packet loss rates (0.1–0.9) and communication ranges (0–1000 m). It highlights the trade-offs made between job performance and network reliability for robot swarms using QI-MARL (the analyses were performed using Jupyter Notebook (version 6.5.4)).
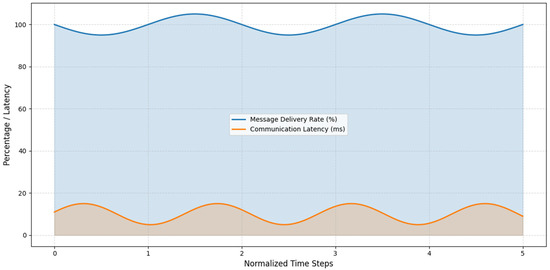
Figure 13.
Communication latency and reliability.
4.7. Obstacle Interaction and Navigation Efficiency
In this section, the indoor layouts of the Robot Path Plan Dataset were used to analyze the robot’s abilities to avoid obstacles. Each robot’s time-to-goal, detour length, and capability for collision avoidance were assessed. As shown in Table 10, this evaluation examined the system’s ability to maintain energy efficiency while carrying out tasks within congested environments by also examining the interactions with static obstructions and small hallways.

Table 10.
Obstacle interaction metrics.
Figure 14 illustrates the obstacle interaction and navigation efficiency of the QI-MARL framework across multiple robots operating in complex indoor environments. The figure presents three key performance metrics—collision rate, average detour distance, and energy impact—plotted as signal lines for each robot. The collision rate indicates the percentage of paths in which a robot intersects an obstacle, showing the system’s ability to avoid collisions. The average detour distance reflects the additional path length traveled by robots to circumvent obstacles, highlighting navigation efficiency. The energy impact measures the extra energy consumed due to obstacle avoidance, demonstrating the framework’s energy-aware behavior. By comparing these metrics across all robots, Figure 14 emphasizes that QI-MARL maintained low collision rates, minimized detours, and reduced extra energy consumption, even in congested or constrained layouts. This detailed visualization underscores the framework’s capability to balance task completion, safety, and energy efficiency, providing a clear insight into the robustness and adaptability of the autonomous swarm navigation within smart microgrids.
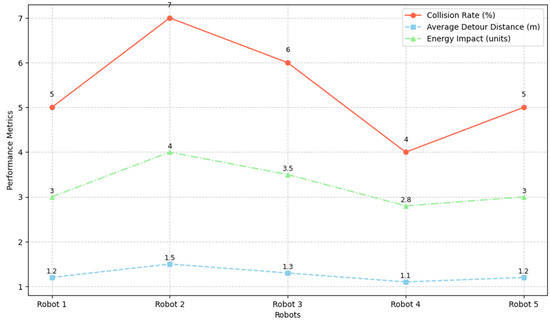
Figure 14.
Obstacle interaction and navigation efficiency of QI-MARL.
4.8. Baseline Comparisons
QI-MARL was compared to rule-based (shortest path) and classical MARL approaches. The performance of QI-MARL shows the effectiveness of QI-MARL over typical methods, since QI-MARL was substantially better than both baselines in terms of energy efficiency, task execution, and path efficiency.
Table 11 is a summary chart comparing QI-MARL, classical MARL, and rule-based navigation energy consumption, task success, and path efficiency. In various task settings, QI-MARL showed consistent advantages in energy efficiency and navigation efficiency optimization.

Table 11.
Baseline performance.
The performance gains reported in the abstract corresponded to the comparison of QI-MARL against the classical MARL baseline unless otherwise specified. Specifically, QI-MARL reduced energy consumption by approximately 15%, improved task success rate by 12%, and increased path efficiency by 8% compared with classical MARL. When compared with the rule-based shortest-path approach, these improvements were even greater—approximately 26%, 20%, and 15%, respectively. These values align with the results presented in Table 11 and Figure 15.
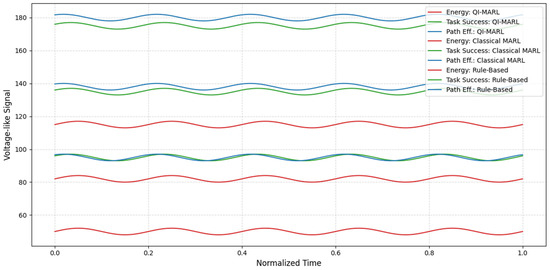
Figure 15.
Baseline comparison.
4.9. Convergence Analysis and Hyperparameter Ablation
To quantitatively assess the learning efficiency of the proposed QI-MARL framework, we conducted convergence analysis and hyperparameter ablation studies. These analyses compare QI-MARL with classical stochastic MARL baselines in terms of reward convergence, energy consumption, task success rate, and path efficiency.
We further evaluated the impact of key hyperparameters—learning rate (α), discount factor (γ), and exploration probability—on system performance. Table 12 summarizes the results, showing how variations in these hyperparameters affect energy consumption, task success rate, and path efficiency. The results indicate that QI-MARL maintained a superior performance across different configurations, confirming the robustness and effectiveness of the proposed method.

Table 12.
Hyperparameter ablation results.
Figure 16 shows the convergence curves of QI-MARL versus classical MARL across 1500 indoor map simulations. The average reward per episode demonstrates that QI-MARL converged faster, achieving a stable performance earlier. This accelerated convergence is attributed to the quantum-inspired exploration mechanism, which enhances state-space coverage and enables adaptive navigation under dynamic microgrid conditions.
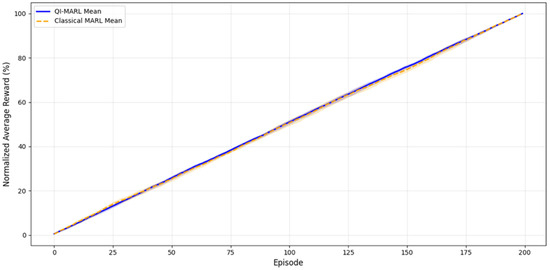
Figure 16.
Convergence analysis of QI-MARL vs. classical MARL (multi-robot).
4.10. Scalability and Computational Complexity Analysis
This section analyzed the computational requirements of the QI-MARL framework with increasing swarm sizes. It quantified both the time complexity (average simulation time per episode) and memory usage (RAM consumption) for robot swarms ranging from 5 to 50 robots. The analysis demonstrated that QI-MARL maintained scalability with minimal degradation in performance.
Table 13 presents the computational complexity of the QI-MARL framework as the number of robots increased. It reports the average simulation time per episode and memory usage (RAM) for swarms of 5, 10, 20, 30, and 50 robots. The data demonstrated that both time and memory grew moderately with swarm size, indicating that QI-MARL maintained scalability while supporting efficient energy-aware task execution.

Table 13.
Computational complexity with increasing robot swarm size.
Figure 17 shows the (a) simulation time per episode and (b) memory usage for different swarm sizes. Results indicate linear growth, confirming that the framework scaled efficiently while maintaining task performance and energy management.
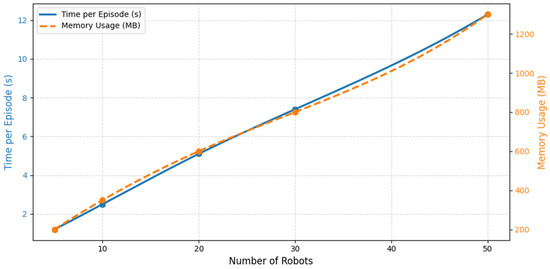
Figure 17.
QI-MARL computational complexity vs. swarm size.
4.11. Simulation and Validation
We validated the proposed QI-MARL framework through simulations involving autonomous robot agents in smart microgrid environments. Each robot acts as an intelligent agent, performing tasks while considering the battery levels, energy-sharing decisions, and navigation efficiency. The simulations included up to 50 robots operating on indoor maps adapted from the Robot Path Plan Dataset, with heterogeneous initial energy levels and distributed tasks. Microgrid nodes provide energy based on load-balancing policies, and agents follow QI-MARL for task allocation, route selection, and energy sharing. The environments contained static obstacles and narrow corridors to test obstacle avoidance. Performance was evaluated using metrics, such as energy consumption per task, task success rate, path efficiency, collision rate, and time-to-goal, providing a comprehensive assessment of swarm efficiency, robustness, and scalability.
Table 14 summarizes the performance of QI-MARL for different swarm sizes. As shown, the framework maintained high task success rates and energy efficiency, even as the number of robots increased. Figure 16 presents the normalized signals of energy consumption, task success, and path efficiency across varying robot counts. The results demonstrate the scalability and robustness of QI-MARL in managing multi-robot coordination in energy-aware smart microgrids.

Table 14.
Simulation results of QI-MARL with robot agents.
Figure 18 presents a 2D simulation of 50 autonomous robots operating under the QI-MARL (quantum-inspired multi-agent reinforcement learning) framework within a smart microgrid environment. The map includes interconnected areas with static obstacles and narrow corridors (gray walls). Blue circles labeled “R” represent robot agents interacting with energy nodes (blue circles with lightning symbols) and charging stations (yellow boxes).
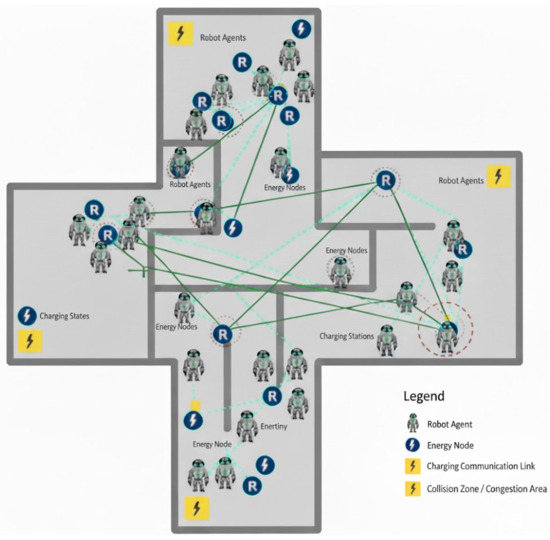
Figure 18.
2D simulation of 50 QI-MARL robots in smart microgrid environment.
Solid green lines show active energy sharing or task coordination links, while dashed blue lines indicate potential communication paths. Red dashed circles highlight congestion or collision zones. The graph in the upper right corner illustrates the normalized performance metrics—collision rate, energy consumption, task success rate, path efficiency, and time-to-goal—as the number of robots was scaled from 5 to 50, demonstrating the scalability and robustness of the QI-MARL framework.
5. Discussion and Limitations
5.1. Discussion
Energy efficiency, task completion, and navigation performance of autonomous robot swarms in smart microgrids clearly improved with the proposed quantum-inspired multi-agent reinforcement learning (QI-MARL) system. QI-MARL provided superior convergence and flexibility in complicated interior environments versus the traditional MARL [31,32] and rule-based approaches [33,34] by informatively collaborating as the swarm distributed energy quickly and allowed for decision-making in real-time. The exploration writing optimized the representation of potential landscapes through quantum-inspired exploration [37,38], which improved the overall coordination of both agents, jobs, and pathways undertaken by the swarm while in response to the changing conditions of the microgrid.
The experimental results of ablation studies, sensitivity analysis, scalability studies and baselines were used to validate that each component made a valuable contribution to the overall system performance in terms of the energy sharing protocol [39,40], quantum-inspired exploration [37], and adaptive task allocation [35,36]. These results highlight the potential of smart microgrid energy management based on multi-agent learning [41,42] for real-world applications in industrial facilities, smart buildings, and warehouses.
Recent developments in hybrid AC/DC microgrid systems have emphasized the need for scalable and reconfigurable architectures with decentralized control mechanisms to ensure coordinated operation and energy stability. For instance, the framework proposed in “A scalable and reconfigurable hybrid AC/DC microgrid clustering architecture with decentralized control for coordinated operation” demonstrates how decentralized coordination can improve flexibility and fault tolerance. Building upon this concept, the proposed QI-MARL framework extends these principles by integrating quantum-inspired reinforcement learning to enable autonomous energy optimization, adaptive task allocation, and cooperative decision-making among multiple robotic agents within a smart microgrid context.
5.2. Limitations
The test also had its own limitations, even with its positives. First, the experimental assessment was based on simulated conditions from the Robot Path Plan Dataset that may not feasibly represent the complexities of indoor spaces and the differences in energy situations found in the real world. Second, when deployed on embedded devices with limited resources, the costs associated with QI-MARL computation may inhibit the activities of QI-MARL, especially in the case of large swarms or very dense environments. Third, the energy sharing protocol depends on the reliability of communication between nodes in the microgrid and robots, and any malfunction of the communication link may disrupt the energy balance as well as performance of the jobs. Finally, the framework does not offer variability in terms of real-time renewable generation variability or mixed-capability swarms; the framework only considers homogeneous robots with similar energy capabilities. Heterogeneous swarm modeling, hardware-in-the-loop validation, and the integration of real-time dynamic microgrid data are all paths that these limitations suggest for future research.
6. Conclusions and Future Work
In this paper, we presented a quantum-inspired multi-agent reinforcement learning (QI-MARL) framework for autonomous robot swarms that are energy aware and operate in smart microgrids. The QI-MARL system was constrained under the notion of energy use, but was found to achieve a better combined use of energy efficiency, task success, and path efficiency compared with the traditional MARL and rule-based methods by joining together quantum-inspired exploration, adaptive task allocation, and an energy-sharing protocol. Tests on the Robot Path Plan Dataset demonstrated that the QI-MARL framework can scale to larger swarms, work in real-time on embedded systems, and deal with crowded situations indoors. The layered architecture and module implementations maintain adaptive energy management and dependability of the system while also allowing for strong coordination of the robots.
Future work will investigate the generalization of the QI-MARL framework to unstructured and dynamic 3D environments. While the current study focused on 2D structured maps, the modular design, quantum-inspired exploration, and adaptive energy-sharing mechanisms can be extended to handle increased spatial complexity and real-world uncertainties. Empirical validation on 3D robotic testbeds will be conducted to assess the scalability, robustness, and transferability to practical applications.
Author Contributions
Conceptualization, M.S. and S.H.; Methodology, S.H. and M.S.; Validation, S.H., M.S., H.C., and K.N.; Formal analysis, M.S. and S.H.; Writing—original draft preparation, S.H. and M.S.; Writing—review and editing, S.H., M.S., and H.C.; Supervision, H.C. and K.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hosseini, S.M.; Carli, R.; Dotoli, M. Robust Optimal Energy Management of a Residential Microgrid under Uncertainties on Demand and Renewable Power Generation. IEEE Trans. Autom. Sci. Eng. 2021, 18, 618–637. [Google Scholar] [CrossRef]
- Shen, X.; Tang, J.; Pan, F.; Qian, B.; Zhao, Y. Quantum-inspired deep reinforcement learning for adaptive frequency control of low carbon park island microgrid considering renewable energy sources. Front. Energy Res. 2024, 12, 1366009. [Google Scholar] [CrossRef]
- Bai, Y.; Sui, Y.; Deng, X.; Wang, X. Quantum-inspired robust optimization for coordinated scheduling of PV-hydrogen microgrids under multi-dimensional uncertainties. Sci. Rep. 2025, 15, 29589. [Google Scholar] [CrossRef]
- Fan, Z.; Zhang, W.; Liu, W. Multi-agent deep reinforcement learning-based distributed optimal generation control of DC microgrids. IEEE Trans. Smart Grid 2023, 14, 3337–3351. [Google Scholar] [CrossRef]
- Zhu, Z.; Wan, S.; Fan, P.; Letaief, K.B. Federated Multiagent Actor-Critic Learning for Age Sensitive Mobile-Edge Computing. IEEE Internet Things J. 2022, 9, 1053–1067. [Google Scholar] [CrossRef]
- Tlijani, H.; Jouila, A.; Nouri, K. Optimized Sliding Mode Control Based on Cuckoo Search Algorithm: Application for 2DF Robot Manipulator. Cybern. Syst. 2023, 56, 849–865. [Google Scholar] [CrossRef]
- Wilk, P.; Wang, N.; Li, J. Multi-Agent Reinforcement Learning for Smart Community Energy Management. Energies 2024, 17, 5211. [Google Scholar] [CrossRef]
- Minghong, L.; Gaoshan, F.; Pengchao, W.; Xin, Y.; Qing, L.; Hou, T.; Shuo, Z. Behavior-aware energy management in microgrids using quantum-classical hybrid algorithms under social and demand dynamics. Sci. Rep. 2025, 15, 21326. [Google Scholar] [CrossRef]
- Liu, M.; Liao, M.; Zhang, R.; Yuan, X.; Zhu, Z.; Wu, Z. Quantum Computing as a Catalyst for Microgrid Management: Enhancing Decentralized Energy Systems Through Innovative Computational Techniques. Sustainability 2025, 17, 3662. [Google Scholar] [CrossRef]
- Fayek, H.H.; Fayek, F.H.; Rusu, E. Quantum-Inspired MoE-Based Optimal Operation of a Wave Hydrogen Microgrid for Integrated Water, Hydrogen, and Electricity Supply and Trade. J. Mar. Sci. Eng. 2025, 13, 461. [Google Scholar] [CrossRef]
- Ning, Z.; Xie, L. A survey on multi-agent reinforcement learning and its application. J. Autom. Intell. 2024, 3, 73–91. [Google Scholar] [CrossRef]
- Nie, L.; Long, B.; Yu, M.; Zhang, D.; Yang, X.; Jing, S. A Low-Carbon Economic Scheduling Strategy for Multi-Microgrids with Communication Mechanism-Enabled Multi-Agent Deep Reinforcement Learning. Electronics 2025, 14, 2251. [Google Scholar] [CrossRef]
- Guo, G.; Gong, Y. Multi-Microgrid Energy Management Strategy Based on Multi-Agent Deep Reinforcement Learning with Prioritized Experience Replay. Appl. Sci. 2023, 13, 2865. [Google Scholar] [CrossRef]
- Jouila, A.; Essounbouli, N.; Nouri, K.; Hamzaoui, A. Robust Nonsingular Fast Terminal Sliding Mode Control in Trajectory Tracking for a Rigid Robotic Arm. Aut. Control Comp. Sci. 2019, 53, 511–521. [Google Scholar] [CrossRef]
- Acharya, D.B.; Kuppan, K.; Divya, B. Agentic ai: Autonomous intelligence for complex goals–a comprehensive survey. IEEE Access 2025, 13, 18912–18936. [Google Scholar] [CrossRef]
- Wang, T.; Ma, S.; Tang, Z.; Xiang, T.; Mu, C.; Jin, Y. A multi-agent reinforcement learning method for cooperative secondary voltage control of microgrids. Energies 2023, 16, 5653. [Google Scholar] [CrossRef]
- Jung, S.-W.; An, Y.-Y.; Suh, B.; Park, Y.; Kim, J.; Kim, K.-I. Multi-Agent Deep Reinforcement Learning for Scheduling of Energy Storage System in Microgrids. Mathematics 2025, 13, 1999. [Google Scholar] [CrossRef]
- Zhang, G.; Hu, W.; Cao, D.; Zhang, Z.; Huang, Q.; Chen, Z.; Blaabjerg, F. A multi-agent deep reinforcement learning approach enabled distributed energy management schedule for the coordinate control of multi-energy hub with gas, electricity, and freshwater. Energy Convers. Manag. 2022, 255, 115340. [Google Scholar] [CrossRef]
- Deshpande, K.; Möhl, P.; Hämmerle, A.; Weichhart, G.; Zörrer, H.; Pichler, A. Energy Management Simulation with Multi-Agent Reinforcement Learning: An Approach to Achieve Reliability and Resilience. Energies 2022, 15, 7381. [Google Scholar] [CrossRef]
- Xu, N.; Tang, Z.; Si, C.; Bian, J.; Mu, C. A Review of Smart Grid Evolution and Reinforcement Learning: Applications, Challenges and Future Directions. Energies 2025, 18, 1837. [Google Scholar] [CrossRef]
- Liu, D.; Wu, Y.; Kang, Y.; Yin, L.; Ji, X.; Cao, X.; Li, C. Multi-agent quantum-inspired deep reinforcement learning for real-time distributed generation control of 100% renewable energy systems. Eng. Appl. Artif. Intell. 2023, 119, 105787. [Google Scholar] [CrossRef]
- Ghasemi, R.; Doko, G.; Petrik, M.; Wosnik, M.; Lu, Z.; Foster, D.L.; Mo, W. Deep reinforcement learning-based optimization of an island energy-water microgrid system. Resour. Conserv. Recycl. 2025, 222, 108440. [Google Scholar] [CrossRef]
- Zhao, Y.; Wei, Y.; Zhang, S.; Guo, Y.; Sun, H. Multi-Objective Robust Optimization of Integrated Energy System with Hydrogen Energy Storage. Energies 2024, 17, 1132. [Google Scholar] [CrossRef]
- Zhu, Z.; Weng, Z.; Zheng, H. Optimal Operation of a Microgrid with Hydrogen Storage Based on Deep Reinforcement Learning. Electronics 2022, 11, 196. [Google Scholar] [CrossRef]
- Jouili, K.; Jouili, M.; Mohammad, A.; Babqi, A.J.; Belhadj, W. Neural Network Energy Management-Based Nonlinear Control of a DC Micro-Grid with Integrating Renewable Energies. Energies 2024, 17, 3345. [Google Scholar] [CrossRef]
- Toure, I.; Payman, A.; Camara, M.-B.; Dakyo, B. Energy Management in a Renewable-Based Microgrid Using a Model Predictive Control Method for Electrical Energy Storage Devices. Electronics 2024, 13, 4651. [Google Scholar] [CrossRef]
- Shili, M.; Hammedi, S.; Chaoui, H.; Nouri, K. A Novel Intelligent Thermal Feedback Framework for Electric Motor Protection in Embedded Robotic Systems. Electronics 2025, 14, 3598. [Google Scholar] [CrossRef]
- Xu, C.; Huang, Y. Integrated Demand Response in Multi-Energy Microgrids: A Deep Reinforcement Learning-Based Approach. Energies 2023, 16, 4769. [Google Scholar] [CrossRef]
- Turjya, S.M.; Bandyopadhyay, A.; Kaiser, M.S.; Ray, K. QiMARL: Quantum-Inspired Multi-Agent Reinforcement Learning Strategy for Efficient Resource Energy Distribution in Nodal Power Stations. AI 2025, 6, 209. [Google Scholar] [CrossRef]
- Chen, W.; Wan, J.; Ye, F.; Wang, R.; Xu, C. QMARL: A Quantum Multi-Agent Reinforcement Learning Framework for Swarm Robots Navigation. In Proceedings of the 2024 IEEE International Conference on Acoustics, Speech, and Signal Processing Workshops (ICASSPW), Seoul, Republic of Korea, 14–19 April 2024; IEEE: New York, NY, USA, 2024; pp. 388–392. [Google Scholar]
- Shili, M.; Chaoui, H.; Nouri, K. Energy-Aware Sensor Fusion Architecture for Autonomous Channel Robot Navigation in Constrained Environments. Sensors 2025, 25, 6524. [Google Scholar] [CrossRef]
- Silva-Contreras, D.; Godoy-Calderon, S. Autonomous Agent Navigation Model Based on Artificial Potential Fields Assisted by Heuristics. Appl. Sci. 2024, 14, 3303. [Google Scholar] [CrossRef]
- Ahmed, G.; Sheltami, T. Novel Energy-Aware 3D UAV Path Planning and Collision Avoidance Using Receding Horizon and Optimization-Based Control. Drones 2024, 8, 682. [Google Scholar] [CrossRef]
- Wu, B.; Zuo, X.; Chen, G.; Ai, G.; Wan, X. Multi-agent deep reinforcement learning based real-time planning approach for responsive customized bus routes. Comput. Ind. Eng. 2024, 188, 109840. [Google Scholar] [CrossRef]
- Yuan, G.; Xiao, J.; He, J.; Jia, H.; Wang, Y.; Wang, Z. Multi-agent cooperative area coverage: A two-stage planning approach based on reinforcement learning. Inf. Sci. 2024, 678, 121025. [Google Scholar] [CrossRef]
- Lin, X.; Huang, M. An Autonomous Cooperative Navigation Approach for Multiple Unmanned Ground Vehicles in a Variable Communication Environment. Electronics 2024, 13, 3028. [Google Scholar] [CrossRef]
- Wang, J.; Sun, Z.; Guan, X.; Shen, T.; Zhang, Z.; Duan, T.; Huang, D.; Zhao, S.; Cui, H. Agrnav: Efficient and energy-saving autonomous navigation for air-ground robots in occlusion-prone environments. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; IEEE: New York, NY, USA, 2024; pp. 11133–11139. [Google Scholar]
- Wang, J.; Guan, X.; Sun, Z.; Shen, T.; Huang, D.; Liu, F.; Cui, H. Omega: Efficient occlusion-aware navigation for air-ground robots in dynamic environments via state space model. IEEE Robot. Autom. Lett. 2024, 10, 1066–1073. [Google Scholar] [CrossRef]
- Billah, M.; Zeb, K.; Uddin, W.; Imran, M.; Alatawi, K.S.; Almasoudi, F.M.; Khalid, M. Decentralized Multi-Agent Control for Optimal Energy Management of Neighborhood based Hybrid Microgrids in Real-Time Networking. Results Eng. 2025, 27, 106337. [Google Scholar] [CrossRef]
- Ghazimirsaeid, S.S.; Jonban, M.S.; Mudiyanselage, M.W.; Marzband, M.; Martinez, J.L.R.; Abusorrah, A. Multi-agent-based energy management of multiple grid-connected green buildings. J. Build. Eng. 2023, 74, 106866. [Google Scholar] [CrossRef]
- Yu, H.; Niu, S.; Shao, Z.; Jian, L. A scalable and reconfigurable hybrid AC/DC microgrid clustering architecture with decentralized control for coordinated operation. Int. J. Electr. Power Energy Syst. 2022, 135, 107476. [Google Scholar] [CrossRef]
- Zhang, Z.; Fu, H.; Yang, J.; Lin, Y. Deep reinforcement learning for path planning of autonomous mobile robots in complicated environments. Complex Intell. Syst. 2025, 11, 277. [Google Scholar] [CrossRef]
- Xing, T.; Wang, X.; Ding, K.; Ni, K.; Zhou, Q. Improved Artificial Potential Field Algorithm Assisted by Multisource Data for AUV Path Planning. Sensors 2023, 23, 6680. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).