ANT-KT: Adaptive NAS Transformers for Knowledge Tracing
Abstract
1. Introduction
- Proposes ANT-KT, an adaptive neural architecture search architecture based on Transformer for Knowledge Tracing tasks. ANT-KT integrates an innovative Transformer variant and an improved evolutionary algorithm to enhance model performance and architecture search efficiency.
- Designs an enhanced encoder–decoder architecture that strengthens the modeling of local and global dependencies. The encoder introduces state vectors combined with convolution operations to capture short-term knowledge state transitions, while the decoder employs a novel linear attention mechanism for efficient fusion of long-term global information, enabling more accurate modeling of students’ learning dynamics over time.
- Designs an improved evolutionary algorithm to further enhance search efficiency. An optimization efficiency objective in the model is introduced to establish a balanced optimization objective function between performance and computational efficiency. Additionally, a dynamic reduction strategy is adopted to dynamically adjust the search space during the search process, enabling a more efficient discovery of neural network architectures that are both high-performance and computationally efficient.
- Conducts extensive experiments on two large-scale real-world datasets, EdNet and RAIEd2020, and compares with multiple existing methods. The results demonstrate that the proposed method achieves improvements across multiple evaluation metrics while also enhancing search efficiency, confirming the framework’s advantages in both performance and efficiency.
2. Related Work
3. Methodology
3.1. Problem Definition
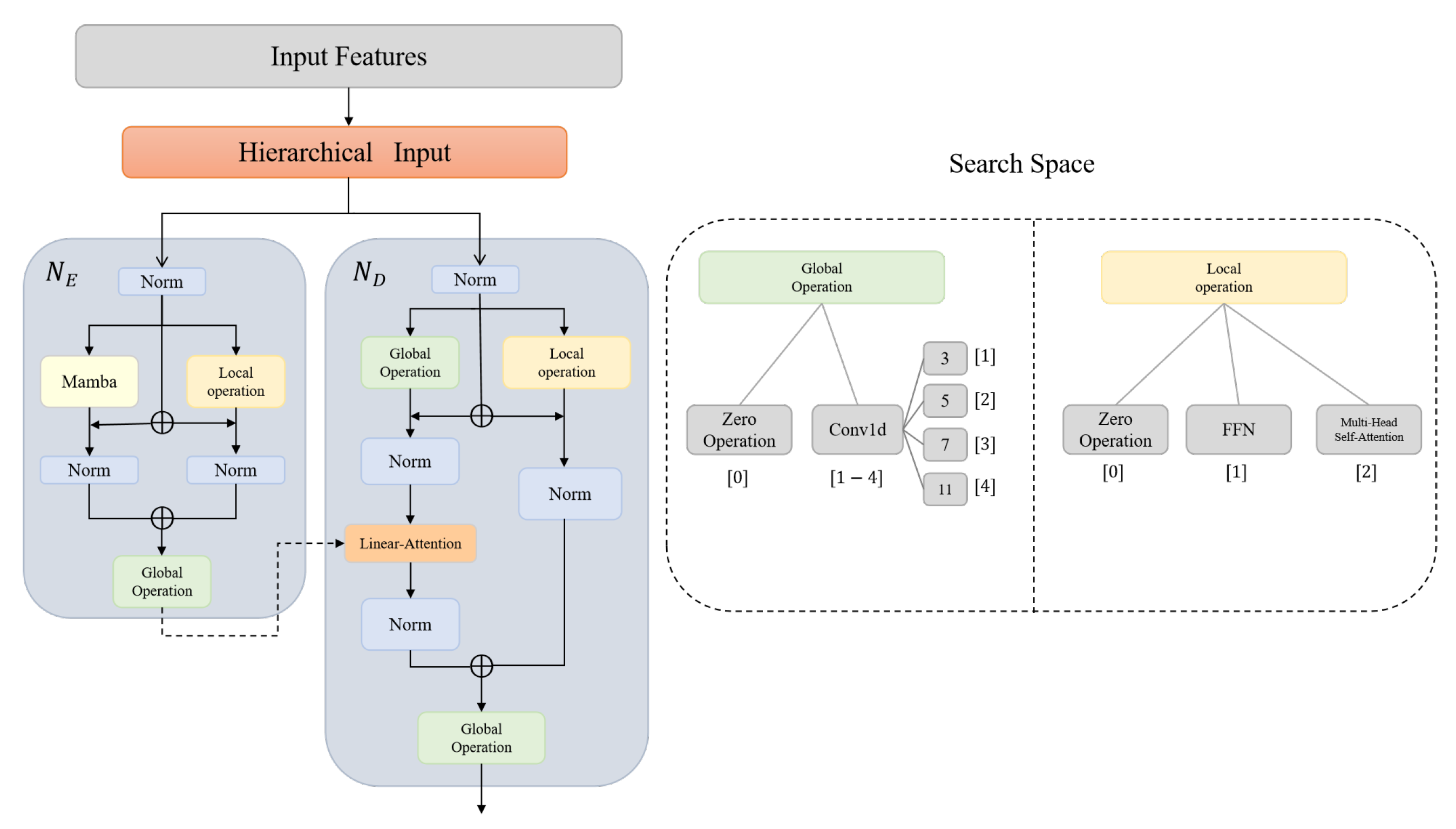
3.2. Proposed Method: ANT-KT Framework
3.3. Adaptive Embedding Selection Module
3.3.1. Enhanced Encoder
3.3.2. Optimized Decoder
3.4. Neural Architecture Search
3.4.1. Objective Function
3.4.2. Search Strategies
- Weighted Combination of Operations: Each operation is assigned an importance weight :This allows flexible combination of different structural elements, improving generalization.
- Weight Sharing: Certain parameters are shared across different architectural configurations, significantly reducing computational overhead.
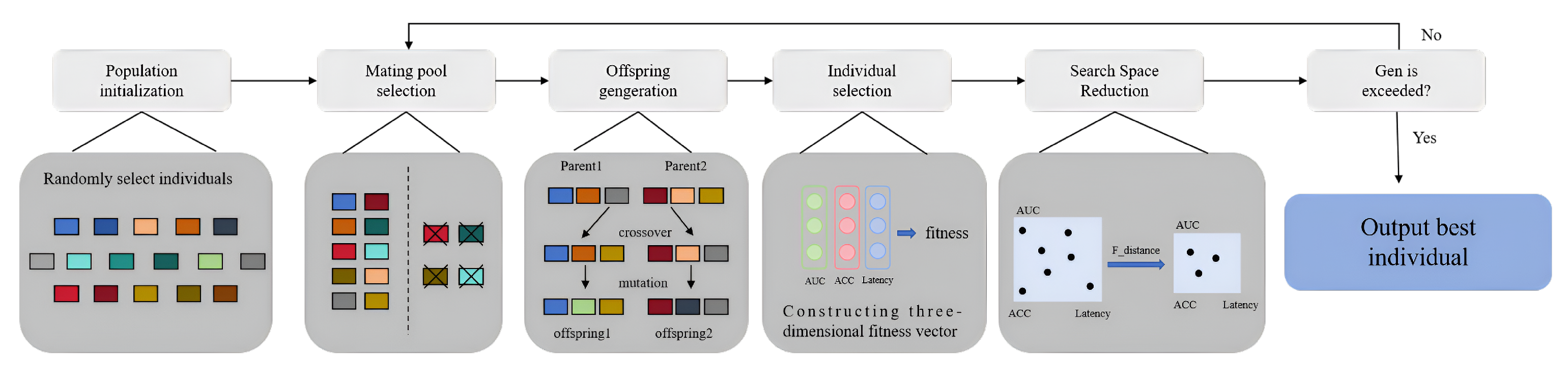
3.4.3. Improved Evolutionary Algorithm
3.4.4. Alternating Optimization
4. Experiments
4.1. Datasets
4.2. Baseline Models
- DKT [8]: The DKT model is the first KT method leveraging deep neural networks, commonly used as a baseline model. It focuses only on concept labels, ignoring exercise-level information.
- HawkesKT [31]: This model uses Hawkes processes to model the temporal dynamics in student interactions, enabling more accurate predictions of knowledge states by capturing the time-sensitive effects of prior responses.
- CT-NCM [32]: The CT-NCM method incorporates a continuous-time neural cognitive model that captures knowledge forgetting and learning progress through time-aware neural architectures.
- SAKT [10]: A self-attentive Knowledge Tracing model that utilizes attention mechanisms to model relationships among exercises, capturing dependencies without relying on sequence order.
- AKT [24]: The AKT method employs context-aware representations and Rasch embeddings to dynamically link students’ historical responses with their future interactions.
- SAINT [11]: This model adopts a Transformer-based encoder–decoder structure to integrate both student and exercise interactions for more comprehensive Knowledge Tracing.
- SAINT+ [33]: Building on SAINT, SAINT+ incorporates additional temporal features such as elapsed time and lag time, enhancing its ability to model temporal dependencies in student learning.
- NAS-Cell [28]: This method applies reinforcement learning to optimize RNN cell structures for Knowledge Tracing tasks, achieving architectures superior to manually designed ones.
- DisKT [34]: The DisKT model addresses cognitive bias in Knowledge Tracing by disentangling students’ familiar and unfamiliar abilities through causal intervention, using a contradiction attention mechanism to suppress guessing/mistaking effects and integrating an Item Response Theory variant for interpretability.
- ENAS-KT [12]: An evolutionary neural architecture search method tailored for KT, which designs a search space specialized for capturing Knowledge Tracing dynamics effectively.
- AAKT [35]: The AAKT model reframes Knowledge Tracing as a generative autoregressive process, which alternatively encodes question–response sequences to directly model pre- and post-response knowledge states, and incorporates auxiliary skill prediction and extra exercise features by enhancing sequences through state-of-the-art Natural Language Generation (NLG) techniques.
4.3. Implementation Details
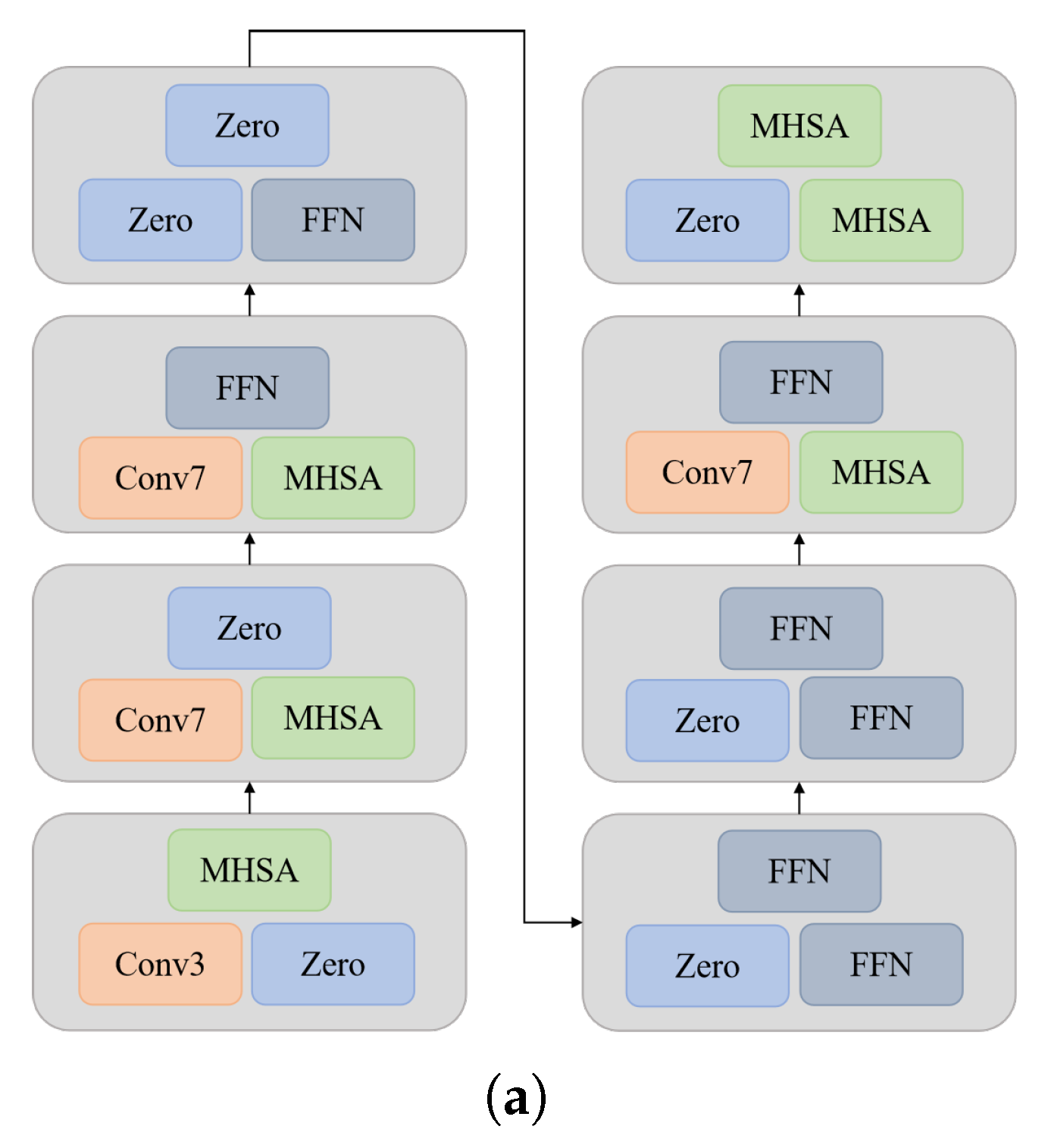
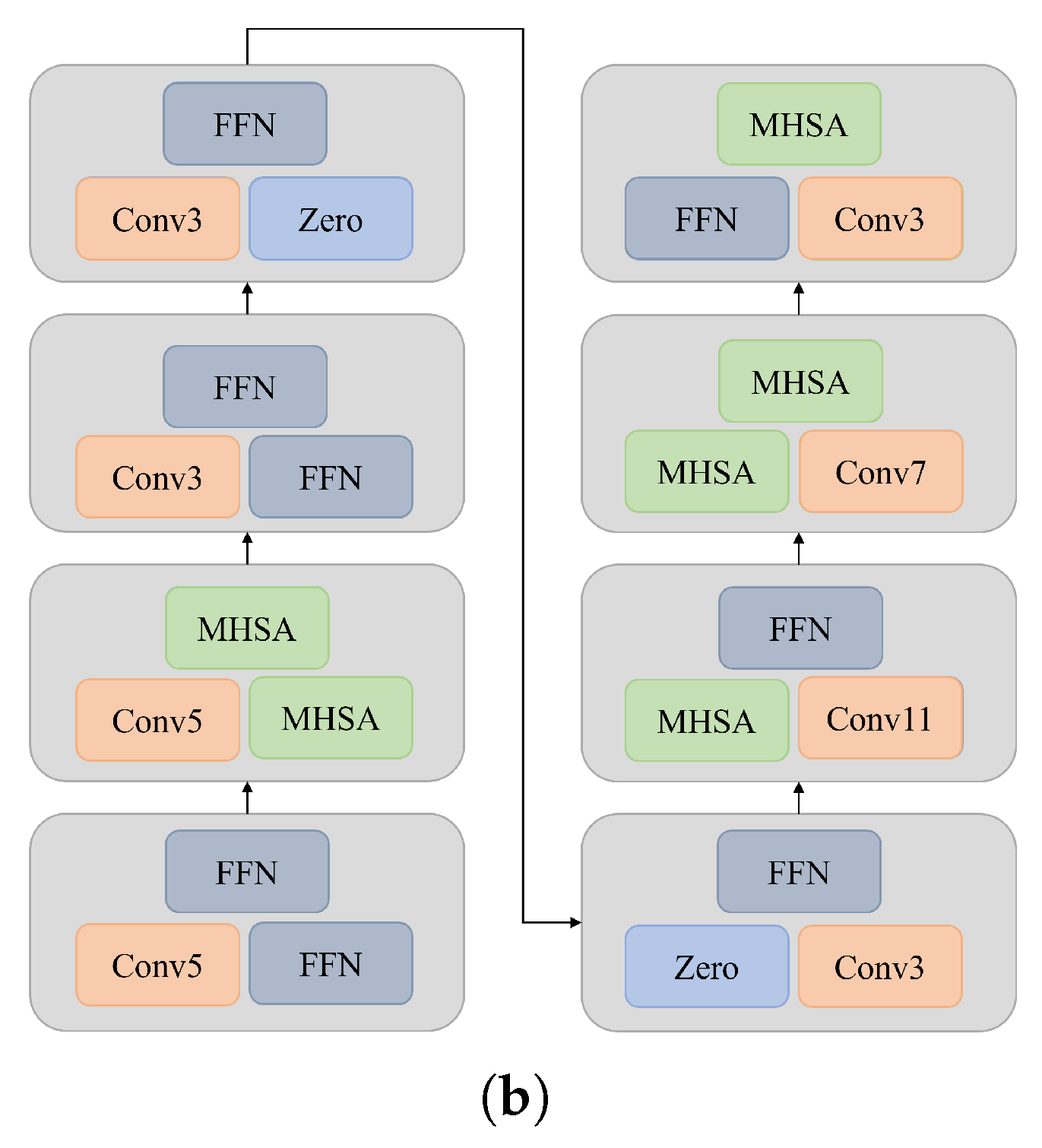
4.4. Main Results
4.5. Ablation Studies
4.6. Analysis of Search Optimization Strategies and Training Efficiency Comparison
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Algorithm A1 Dynamic Multi-Objective Evolutionary Algorithm with Adaptive Search Space |
|
Appendix B. Limitation Analysis
Appendix B.1. Dataset Generalization and Low-Resource Scenarios
Appendix B.2. Deployment Feasibility
References
- Abdelrahman, G.; Wang, Q.; Nunes, B. Knowledge Tracing: A Survey. ACM Comput. Surv. 2023, 55, 1–37. [Google Scholar] [CrossRef]
- Dowling, C.; Hockemeyer, C. Automata for the assessment of knowledge. IEEE Trans. Knowl. Data Eng. 2001, 13, 451–461. [Google Scholar] [CrossRef]
- Geigle, C.; Zhai, C. Modeling MOOC Student Behavior with Two-Layer Hidden Markov Models. In Proceedings of the Fourth (2017) ACM Conference on Learning @ Scale, Cambridge, MA, USA, 20–21 April 2017; pp. 205–208. [Google Scholar]
- Anderson, A.; Huttenlocher, D.; Kleinberg, J.; Leskovec, J. Engaging with massive online courses. In Proceedings of the 23rd International Conference on World Wide Web, Seoul, Republic of Korea, 7–11 April 2014; pp. 687–698. [Google Scholar]
- Corbett, A.T.; Anderson, J.R. Knowledge tracing: Modeling the acquisition of procedural knowledge. User Model.-User-Adapt. Interact. 2005, 4, 253–278. [Google Scholar] [CrossRef]
- Yudelson, M.V.; Koedinger, K.R.; Gordon, G.J. Individualized Bayesian Knowledge Tracing Models. In Proceedings of the Artificial Intelligence in Education, Memphis, TN, USA, 9–13 July 2013; pp. 171–180. [Google Scholar]
- Baker, R.S.J.d.; Corbett, A.T.; Gowda, S.M.; Wagner, A.Z.; MacLaren, B.A.; Kauffman, L.R.; Mitchell, A.P.; Giguere, S. Contextual Slip and Prediction of Student Performance after Use of an Intelligent Tutor. In Proceedings of the User Modeling, Adaptation, and Personalization, Big Island, HI, USA, 20–24 June 2010; pp. 52–63. [Google Scholar]
- Piech, C.; Bassen, J.; Huang, J.; Ganguli, S.; Sahami, M.; Guibas, L.J.; Sohl-Dickstein, J. Deep Knowledge Tracing. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; Volume 28. [Google Scholar]
- Zhang, J.; Shi, X.; King, I.; Yeung, D.Y. Dynamic Key-Value Memory Networks for Knowledge Tracing. In Proceedings of the 26th International Conference on World Wide Web, Perth, Australia, 3–7 April 2017; pp. 765–774. [Google Scholar]
- Pandey, S.; Karypis, G. A Self-Attentive model for Knowledge Tracing. arXiv 2019, arXiv:1907.06837. [Google Scholar] [CrossRef]
- Choi, Y.; Lee, Y.; Cho, J.; Baek, J.; Kim, B.; Cha, Y.; Shin, D.; Bae, C.; Heo, J. Towards an Appropriate Query, Key, and Value Computation for Knowledge Tracing. In Proceedings of the Seventh ACM Conference on Learning @ Scale, Virtual, 12–14 August 2020; pp. 341–344. [Google Scholar]
- Yang, S.; Yu, X.; Tian, Y.; Yan, X.; Ma, H.; Zhang, X. Evolutionary Neural Architecture Search for Transformer in Knowledge Tracing. In Proceedings of the 37th International Conference on Neural Information Processing Systems, Orleans, LA, USA, 10–16 December 2023. [Google Scholar]
- Elsken, T.; Metzen, J.H.; Hutter, F. Neural architecture search: A survey. J. Mach. Learn. Res. 2019, 20, 1997–2017. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Dao, T.; Gu, A. Transformers are SSMs: Generalized Models and Efficient Algorithms Through Structured State Space Duality. In Proceedings of the International Conference on Machine Learning (ICML), Vienna, Austria, 21–27 July 2024. [Google Scholar]
- Real, E.; Aggarwal, A.; Huang, Y.; Le, Q.V. Regularized evolution for image classifier architecture search. In Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence and Thirty-First Innovative Applications of Artificial Intelligence Conference and Ninth AAAI Symposium on Educational Advances in Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; AAAI Press: Washington, DC, USA, 2019. AAAI’19/IAAI’19/EAAI’19. [Google Scholar] [CrossRef]
- Xiong, X.; Zhao, S.; Inwegen, E.G.V.; Beck, J.E. Going deeper with deep knowledge tracing. In Proceedings of the International Educational Data Mining Society, Raleigh, NC, USA, 29 June–2 July 2016. [Google Scholar]
- Shen, S.; Huang, Z.; Liu, Q.; Su, Y.; Wang, S.; Chen, E. Assessing Student’s Dynamic Knowledge State by Exploring the Question Difficulty Effect. In Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval, Madrid, Spain, 11–15 July 2022; SIGIR ’22, pp. 427–437. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Q.; Chen, J.; Huang, S.; Gao, B.; Luo, W.; Weng, J. Enhancing Deep Knowledge Tracing with Auxiliary Tasks. In Proceedings of the ACM Web Conference 2023, Austin, TX, USA, 30 April–4 May 2023; WWW ’23, pp. 4178–4187. [Google Scholar] [CrossRef]
- Yeung, C.K.; Yeung, D.Y. Addressing two problems in deep knowledge tracing via prediction-consistent regularization. In Proceedings of the Fifth Annual ACM Conference on Learning at Scale, London, UK, 26–28 June 2018. L@S ’18. [Google Scholar] [CrossRef]
- Nakagawa, H.; Iwasawa, Y.; Matsuo, Y. Graph-based Knowledge Tracing: Modeling Student Proficiency Using Graph Neural Network. In Proceedings of the IEEE/WIC/ACM International Conference on Web Intelligence, Thessaloniki, Greece, 14–17 October 2019; WI ’19, pp. 156–163. [Google Scholar] [CrossRef]
- Yang, Y.; Shen, J.; Qu, Y.; Liu, Y.; Wang, K.; Zhu, Y.; Zhang, W.; Yu, Y. GIKT: A Graph-Based Interaction Model for Knowledge Tracing. In Proceedings of the Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2020, Ghent, Belgium, 14–18 September 2020; Proceedings, Part I. Springer: Berlin/Heidelberg, Germany, 2020; pp. 299–315. [Google Scholar] [CrossRef]
- Miller, A.; Fisch, A.; Dodge, J.; Karimi, A.H.; Bordes, A.; Weston, J. Key-Value Memory Networks for Directly Reading Documents. In Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing, Austin, TX, USA, 1–5 November 2016; pp. 1400–1409. [Google Scholar] [CrossRef]
- Ghosh, A.; Heffernan, N.; Lan, A.S. Context-Aware Attentive Knowledge Tracing. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual, 6–10 July 2020; pp. 2330–2339. [Google Scholar]
- Cheng, K.; Peng, L.; Wang, P.; Ye, J.; Sun, L.; Du, B. DyGKT: Dynamic Graph Learning for Knowledge Tracing. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Barcelona, Spain, 25–29 August 2024; KDD’24, pp. 409–420. [Google Scholar] [CrossRef]
- Fu, L.; Guan, H.; Du, K.; Lin, J.; Xia, W.; Zhang, W.; Tang, R.; Wang, Y.; Yu, Y. SINKT: A Structure-Aware Inductive Knowledge Tracing Model with Large Language Model. In Proceedings of the 33rd ACM International Conference on Information and Knowledge Management, Boise, ID, USA, 21–25 October 2024; CIKM ’24, pp. 632–642. [Google Scholar] [CrossRef]
- Pardos, Z.A.; Bhandari, S. Learning gain differences between ChatGPT and human tutor generated algebra hints. arXiv 2023, arXiv:2302.06871. [Google Scholar] [CrossRef]
- Ding, X.; Larson, E.C. Automatic RNN Cell Design for Knowledge Tracing using Reinforcement Learning. In Proceedings of the Seventh ACM Conference on Learning @ Scale, Virtual, 12–14 August 2020; pp. 285–288. [Google Scholar]
- Choi, Y.; Lee, Y.; Shin, D.; Cho, J.; Park, S.; Lee, S.; Baek, J.; Bae, C.; Kim, B.; Heo, J. EdNet: A Large-Scale Hierarchical Dataset in Education. In Proceedings of the Artificial Intelligence in Education, Ifrane, Morocco, 6 July 2020; pp. 69–73. [Google Scholar]
- Howard, A.; bskim90; Lee, C.; Shin, D.M.; Jeon, H.P.T.; Baek, J.J.; Chang, K.; kiyoonkay; Heffernan, N.; seonwooko; et al. Riiid Answer Correctness Prediction. 2020. Available online: https://www.kaggle.com/competitions/riiid-test-answer-prediction (accessed on 8 October 2025).
- Wang, C.; Ma, W.; Zhang, M.; Lv, C.; Wan, F.; Lin, H.; Tang, T.; Liu, Y.; Ma, S. Temporal Cross-Effects in Knowledge Tracing. In Proceedings of the 14th ACM International Conference on Web Search and Data Mining, Virtual, 8–12 March 2021; pp. 517–525. [Google Scholar]
- Ma, H.; Wang, J.; Zhu, H.; Xia, X.; Zhang, H.; Zhang, X.; Zhang, L. Reconciling Cognitive Modeling with Knowledge Forgetting: A Continuous Time-aware Neural Network Approach. In Proceedings of the Thirty-First International Joint Conference on Artificial Intelligence, IJCAI-22, Vienna, Austria, 23–29 July 2022; pp. 2174–2181. [Google Scholar]
- Shin, D.; Shim, Y.; Yu, H.; Lee, S.; Kim, B.; Choi, Y. SAINT+: Integrating Temporal Features for EdNet Correctness Prediction. In Proceedings of the LAK21: 11th International Learning Analytics and Knowledge Conference, Irvine, CA, USA, 12–16 April 2021; pp. 490–496. [Google Scholar]
- Zhou, Y.; Lv, Z.; Zhang, S.; Chen, J. Disentangled knowledge tracing for alleviating cognitive bias. In Proceedings of the ACM on Web Conference 2025, Sydney, Australia, 28 April–2 May 2025; pp. 2633–2645. [Google Scholar]
- Zhou, H.; Rong, W.; Zhang, J.; Sun, Q.; Ouyang, Y.; Xiong, Z. AAKT: Enhancing Knowledge Tracing With Alternate Autoregressive Modeling. IEEE Trans. Learn. Technol. 2025, 18, 25–38. [Google Scholar]
- Liu, H.; Simonyan, K.; Yang, Y. DARTS: Differentiable Architecture Search. arXiv 2018, arXiv:1806.09055. [Google Scholar]
- Pham, H.; Guan, M.; Zoph, B.; Le, Q.; Dean, J. Efficient Neural Architecture Search via Parameters Sharing. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Dy, J., Krause, A., Eds.; Proceedings of Machine Learning Research (PMLR): Brookline, MA, USA, 2018; Volume 80, pp. 4095–4104. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Liu, S.; Wu, D.; Sun, H.; Zhang, L. A Novel BeiDou Satellite Transmission Framework With Missing Package Imputation Applied to Smart Ships. IEEE Sens. J. 2022, 22, 13162–13176. [Google Scholar] [CrossRef]
- Liu, S.; Wu, D.; Zhang, L. CGAN BeiDou Satellite Short-Message-Encryption Scheme Using Ship PVT. Remote Sens. 2023, 15, 171. [Google Scholar] [CrossRef]
- Nielsen, J. Usability Engineering; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1994. [Google Scholar]

| Datasets | # of Interactions | # of Students | # of Exercises | # of Skills |
|---|---|---|---|---|
| (# of Tags) | (# of Tag-Sets) | (# of Bundles) | (# of Explanations) | |
| EdNet | 95,293,926 (302) | 84,309 (1792) | 13,169 (9534) | 7 (-) |
| RAIEd2020 | 99,271,300 (189) | 393,656 (1520) | 13,523 (-) | 7 (2) |
| Model | EdNet | RAIEd2020 | ||||
|---|---|---|---|---|---|---|
| RMSE | ACC | AUC | RMSE | ACC | AUC | |
| DKT | 0.4653 | 0.6537 | 0.6952 | 0.4632 | 0.6622 | 0.7108 |
| HawkesKT | 0.4475 | 0.6888 | 0.7487 | 0.4453 | 0.6928 | 0.7525 |
| CT-NCM | 0.4364 | 0.7063 | 0.7743 | 0.4355 | 0.7079 | 0.7771 |
| SAKT | 0.4405 | 0.6998 | 0.7680 | 0.4381 | 0.7035 | 0.7693 |
| AKT | 0.4399 | 0.7016 | 0.7686 | 0.4368 | 0.7076 | 0.7752 |
| SAINT | 0.4322 | 0.7132 | 0.7825 | 0.4310 | 0.7143 | 0.7862 |
| SAINT+ | 0.4285 | 0.7188 | 0.7916 | 0.4272 | 0.7192 | 0.7934 |
| NAS-Cell | 0.4345 | 0.7143 | 0.7796 | 0.4309 | 0.7167 | 0.7839 |
| DisKT | 0.4592 | 0.6863 | 0.7384 | - | - | - |
| ENAS-KT | 0.4209 | 0.7295 | 0.8062 | 0.4196 | 0.7313 | 0.8089 |
| AAKT | 0.4064 | 0.7554 | 0.7827 | - | - | - |
| ANT-KT | 0.4062 | 0.7553 | 0.8387 | 0.4122 | 0.7438 | 0.8239 |
| Improve | −1.47% | 0% | 3.25% | −0.74% | 1.25% | 1.50% |
| Dataset | Metric | Baseline | Encoder | Decoder | ANT-KT |
|---|---|---|---|---|---|
| EdNet | RMSE | ||||
| ACC | |||||
| AUC | |||||
| RAIEd2020 | RMSE | ||||
| ACC | |||||
| AUC |
| Model | Supernet Training Time (h) | Evolutionary Search Time (h) | Final Architecture Training Time (h) | AUC | ACC |
|---|---|---|---|---|---|
| Saint+ | NAN | NAN | 2.381 | 0.7934 | 0.7192 |
| ENAS-KT | 41.863 | 12.8 | 8.784 | 0.8089 | 0.7313 |
| ANT-KT (Encoder) | 41.438 | 8.65 | 6.066 | 0.7993 | 0.7243 |
| ANT-KT (Decoder) | 39.767 | 8.921 | 17.85 | 0.8208 | 0.7424 |
| ANT-KT | 39.288 | 8.81 | 5.39 | 0.8387 | 0.7553 |
| ANT-KT (Search optimization) | 39.288 | 7.42 | 4.357 | 0.8228 | 0.7439 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, S.; Song, Y.; Liu, Y.; Chen, J.; Zhao, D.; Wang, X. ANT-KT: Adaptive NAS Transformers for Knowledge Tracing. Electronics 2025, 14, 4148. https://doi.org/10.3390/electronics14214148
Yao S, Song Y, Liu Y, Chen J, Zhao D, Wang X. ANT-KT: Adaptive NAS Transformers for Knowledge Tracing. Electronics. 2025; 14(21):4148. https://doi.org/10.3390/electronics14214148
Chicago/Turabian StyleYao, Shuanglong, Yichen Song, Ye Liu, Ji Chen, Deyu Zhao, and Xing Wang. 2025. "ANT-KT: Adaptive NAS Transformers for Knowledge Tracing" Electronics 14, no. 21: 4148. https://doi.org/10.3390/electronics14214148
APA StyleYao, S., Song, Y., Liu, Y., Chen, J., Zhao, D., & Wang, X. (2025). ANT-KT: Adaptive NAS Transformers for Knowledge Tracing. Electronics, 14(21), 4148. https://doi.org/10.3390/electronics14214148






