An Adaptive JPEG Steganography Algorithm Based on the UT-GAN Model

Abstract

Adversarial examples pose severe challenges to information security, as their impacts directly extend to steganography and steganalysis technologies. This scenario, in turn, has further spurred the research and application of adversarial steganography. In response, we propose a novel adversarial embedding scheme rooted in a hybrid, partially data-driven approach. The proposed scheme first leverages an adversarial neural network (UT-GAN, Universal Transform Generative Adversarial Network) to generate stego images as a preprocessing step. Subsequently, it dynamically adjusts the cost function with the aid of a DCTR (Discrete Cosine Transform Residual)-based gradient calculator to optimize the images, ensuring that the final adversarial images can resist detection by steganalysis tools. The encoder in this scheme adopts a unique architecture, where its internal parameters are determined by a partially data-driven mechanism. This design not only enhances the capability of traditional steganography schemes to counter advanced steganalysis technologies but also effectively reduces the computational overhead during stego image generation.

1. Introduction

Steganography is a technology that hides confidential digital information in carrier media in an imperceptible way. In recent years, most steganography methods have adopted a framework centered around minimizing distortion [1]. Within this paradigm, the precise formulation of embedding cost is essential, as it quantifies the level of alteration or impairment introduced when concealing data within fundamental units of the image, including pixels or discrete cosine transform (DCT) coefficients. Typically, regions with complex image textures are assigned higher embedding costs, while those with simple and flat textures incur lower costs. These spatially varying embedding costs have a significant impact on the security performance of image steganography methods. Once the embed costs are defined, the Syndrome Trellis Codes (STC) [2] can be used to embed secret messages, aiming to minimize the total embedding cost. Over the years, numerous conventional steganographic techniques have been introduced, including HUGO, WOW, HILL, S-UNIWARD, MiPOD, and CMD [3,4,5,6,7,8]. To illustrate, WOW employs directional high-pass filters to establish spatial additive distortion, whereas HILL designs customized filter sets to better manage the dispersion of distortions in areas with complex textures.

In contrast, steganalysis focuses on detecting stego images that may carry concealed data. Classical detection approaches, like SPAM [9] and SRM [10], commonly convert input images into multiple residual domains and derive high-dimensional statistical [11] attributes to identify alterations caused by steganographic operations. More recently, convolutional neural network (CNN)-based steganalysis techniques [12], including Xu-Net [13], Yedrouj-Net [14], SRNet [15], and CovNet [16], have demonstrated substantial advancements compared to conventional methods. Steganography and steganalysis complement each other, engaged in a continuous technological arms race. While conventional feature-based steganalyzers (e.g., DCTR) exhibit limitations in handling adversarial embeddings due to their non-end-to-end architecture and manually designed features, recent studies have attempted to adapt them to adversarial environments by incorporating advanced training strategies or hybrid frameworks. Recent advances have shown that neural network models mimicking feature-based steganalyzers offer an effective solution to this limitation.

Researchers have recently proposed some deep learning-based steganography methods, mainly categorized into adversarial attack-based [17,18,19,20,21,22] and GAN-based [23,24,25] approaches. Drawing inspiration from the Fast Gradient Sign Method [6], a number of adversarial attack-driven techniques—including adva-emb [17], JS-IAE [18], MAE [19], minmaxstrategy [26], and Back-pack [27,28] —have been developed to optimize initial embedding costs through the use of pretrained convolutional neural network steganalyzers. Early studies on steganographic cost functions also laid a foundation for these methods. The advent of generative artificial intelligence has catalyzed the emergence of an entirely new paradigm. DBS [29] represents a fundamental shift toward a generative framework, wherein secret information is embedded by conditioning the denoising process of a diffusion model to directly synthesize a photorealistic stego image concealing the embedded data, rather than modifying a pre-existing cover medium.

However, although these adversarial and generative approaches incorporate advanced steganographic cost functions and deep learning-based detectors, they have not yet demonstrated substantial performance improvements over conventional steganography techniques in terms of empirical security. With the emergence of GANs, researchers have started integrating them into image steganography to seek breakthroughs. As a pioneering work in this field, ASDL-GAN pioneered the integration of generative adversarial networks into the domain of image steganography, yet its security performance still lags behind traditional methods such as HILL [30]. Recent advances in steganalysis metrics [31] further validate this performance gap. UT-GAN improves on ASDL-GAN [24] to achieve significant performance gains over traditional steganography methods, despite sharing the same end-to-end, data-driven paradigm.

This paper presents a novel adversarial embedding scheme based on steganalysis features, which employs a hybrid (partially data-driven) approach. While the UT-GAN network used for preprocessing is trained in a data-driven manner, the core adversarial gradient generation mechanism—i.e., the gradient calculator—operates in a non-data-driven fashion. Specifically, the linear mapper within the gradient calculator derives its internal parameters by solving equation systems built from individual cover–stego pairs, instead of training on large-scale datasets. This structure reduces the dependency on voluminous data, enhances the resistance to steganalytic detection, and strengthens adversarial stego images by minimizing their feature-space divergence from cover images, as quantified by the NN-DCTR metric. The key contributions of this study are outlined below.

• Combining non-data-driven gradient generation with UT-GAN preprocessing, the scheme reduces reliance on datasets and enhances the robustness of adversarial stego images.
• Presenting a new gradient calculator that computes adversarial gradients in place of steganalyzers based on deep learning. The gradient calculator is tailored to DCTR steganalysis, serving as an approximate neural network for the extraction of stego features.
• Striking a balance between security and implementation efficiency. The UT-GAN adversarial framework is utilized to generate adversarial stego images. To achieve optimal results, the embedding cost function is iteratively refined through the use of an embedding simulator.

2. Related Work

With the swift advancement of deep learning methodologies, its applications have significantly expanded, thereby propelling the development of image steganography. Recently, the application of adversarial attacks to image steganography has emerged as a focus of interest, stemming from similarities in technical implementation to adversarial sample generation. Using the Fast Sparse Symbol Method, Zhang et al. [21] suggested creating adversarial examples from cover images, which complicates the task for steganalyzers to distinguish between cover and secret images. Zhou et al. [23] introduced a framework for efficiently generating large-scale adversarial cover images by training a generator to convert cover images into adversarial samples via simple forward propagation, which are subsequently used for steganography. While these approaches have incorporated adversarial attack techniques into image steganography, they mainly focus on converting cover images into adversarial samples rather than achieving end-to-end image steganography.

AdvSGAN [32], inspired by the adversarial perturbation generation model known as AdvGAN, employs a deep neural network architecture with a constrained neural encoder to advance image steganography learning frameworks. The architecture integrates two adversarial components: a discriminator co-trained with the encoder, and a pretrained target model. They collaboratively develop the steganography from first principles. Mirroring the adversarial training dynamic between generators and discriminators in GANs, steganography and steganalysis exhibit mutual improvement. This collaborative dynamic has driven the broad adoption of GAN frameworks in contemporary steganography to strengthen security. Next, we present a brief summary of ASDL-GAN and UT-GAN.

Early studies pioneered the integration of GANs into steganography. For example, one framework [33] incorporates a Kirchhoff–Volterra (KV) high-pass filter kernel into the embedding process, with the kernel defined based on steganographic distortion criteria. The KV kernel is expressed as

$$K_{\mathrm{kv}}=\left(\begin{array}{ccccc}-1& 2& -2& 2& -1\\ 2& -6& 8& -6& 2\\ -2& 8& -12& 8& -2\\ 2& -6& 8& -6& 2\\ -1& 2& -2& 2& -1\end{array}\right)$$

(1)

This framework adjusts probability mappings for the backpropagation process within the GAN structure. The generator’s loss function directly influences the discriminator’s decision-making logic. Nevertheless, ASDL-GAN’s security performance still lags behind methods like those proposed in [34], which adopts a more optimized architecture for steganographic embedding.

Furthermore, a trainable Double-Tanh function was developed to replace the TES subnet as an embedding simulator. This modification eliminates the need for pretraining and significantly reduces computational overhead. In terms of security performance, when facing detection by advanced steganalyzers such as SRM and maxSRMD2, UT-GAN’s error rate is approximately 0.16% lower than that of ASDL-GAN, indicating stronger resistance to detection. In terms of adaptability, UT-GAN can better learn content-adaptive features during training: complex texture regions in images have higher embedding probabilities, meaning secret messages can be embedded more effectively and securely in areas less likely to attract steganalytic attention. This characteristic makes UT-GAN more effective in practical applications, such as scenarios where information concealment must be maintained while preserving the integrity of the carrier image. Given these outstanding performance improvements, UT-GAN was selected as the adversarial network model in this study.

3. Proposed Approach

3.1. Optimal Selection of Compliant Stego Images

Derived from the Fast Gradient Sign (FGS) technique [35], the ADV-EMB approach serves as a significant framework for producing adversarial samples extensively utilized in tasks related to image classification. FGS operates by applying subtle perturbations to input data, generating adversarial instances that deceive neural network models—including convolutional neural networks (CNNs)—into producing erroneous outputs, into misclassifying images. Its application, for instance, entails creating an adversarial example K that can cause a CNN to incorrectly categorize an image X as the wrong label y, despite minimal perturbations.

However, the FGS technique requires adaptation for adversarial embedding tasks, especially when altering the steganographic content. The key adaptation involves regulating steganographic modifications based on the sign of adversarial gradients, implemented through ±1 cost adjustments. The primary goal of ADV-EMB is to synthesize a stego image Z from a cover image C capable of misleading a convolutional neural network (CNN)-based steganalysis system.

Firstly, this section compares ADV-EMB [36] with the proposed adversarial embedding scheme SE, highlighting their shared non-data-driven nature and two key differences. The first lies in the adversarial model employed in their design; the second relates to the criteria for selecting optimal samples. SE utilizes a gradient calculator, while ADV-EMB employs a CNN-based steganalysis model. It serves as a form of steganalysis despite not being used explicitly for such purposes. Its architecture comprises NN-DCTR as a feature extractor and a linear mapper as a classifier, inspired by feature-based steganalysis to eliminate dataset dependency. The internal weights of NN-DCTR are manually configured based on DCTR settings, while those of the linear mapper adapt dynamically to the processed cover–stego pair. DCTR was selected for its balance of low computational complexity and adequate detectability. Alternative feature extractors like GFR [37] and PHARM [38], could also implement the gradient calculator, although at a higher computational cost. Furthermore, the transferability of adversarial examples further improves robustness against diverse steganalysis systems. Despite being an empirically designed adversary, the gradient calculator significantly strengthens the anti-detection ability of traditional feature-based steganographic methods.

Secondly, the criteria for optimal sample selection differ between SE and ADV-EMB. ADV-EMB’s security performance is directly governed by adjustment cost parameters through a two-phase process: (1) generating multiple adversarial stego images with varying adjustment costs, and (2) selecting the optimal sample that simultaneously maximizes adversarial deception while minimizing adjustment costs. This selection process is illustrated in Figure 1, where the optimal sample is chosen to be as close as possible to cover image C. As depicted in Figure 1a, among candidate stego images (e.g., Z1, Z2, and Z3), Z1 is chosen as the optimal output Z because it resides within the adversarial camouflage region (ensuring misclassification) while maintaining the closest proximity to the hyperplane (minimizing adjustment costs).

By contrast, SE uses universal selection criteria instead of relying on steganalyzer-specific knowledge or dataset-dependent parameters. SE’s criteria focus on minimizing the feature–space distance between stego and cover images. Specifically, the weights of the linear mapper in SE are computed using individual cover–stego images. Among candidate stego images (Z1, Z2, and Z3), Z1 is selected as it minimizes ‖Z-C‖, adhering to the statistical principle that distribution proximity correlates with higher likelihood.

A summary of the key differences between ADV-EMB and SE is provided in

Table 1. Comparison between ADV-EMB and SE.

Aspect	ADV-EMB	SE (Proposed)
Adversarial model	CNN-based steganalyzer	Gradient calculator
Data dependency	Dataset-specific	Non-data-driven
Selection criterion	Minimize cost	Minimize cover–stego distance
Gradient source	Pretrained CNN	Feature-based (DCTR-inspired)
Transferability	Limited to known models	High (generalizable)
Training overhead	High (requires labeled data)	Low (no dataset training)

.

While the architectural and methodological distinctions between ADV-EMB and SE are clearly outlined in Table 1 and the preceding discussion, it is important to address the absence of direct experimental comparison between the two approaches. This omission stems primarily from practical implementation challenges rather than conceptual oversight.

The original ADV-EMB publication presents a theoretical framework for adversarial embedding but does not provide a complete, reproducible implementation with specified hyperparameters and adjustment strategies. This lack of standardized implementation makes a fair and consistent comparison problematic, as results could be significantly influenced by implementation-specific choices rather than fundamental methodological differences.

To alleviate this limitation, while still being able to provide a meaningful performance context, the following measures were taken.

• Indirect Performance Benchmarking: The security performance of our SE method is thoroughly evaluated against a comprehensive suite of modern steganalyzers (DCTR, SRM, GFR, XuNet, SRNet, CovNet) in Section 4. The consistently high error rates ($P_e$) achieved across these diverse detectors demonstrate SE’s robust anti-detection capability, which conceptually surpasses the security level anticipated from the ADV-EMB framework given its dataset-dependent nature.
• Theoretical Superiority Validation: The fundamental advantages of SE’s design—particularly its non-data-driven gradient calculator and universal selection criterion—provide theoretical grounding for its superior generalizability and robustness compared to ADV-EMB’s model-specific approach.
• Future Comparative Commitment: We acknowledge the value of empirical comparison and commit to conducting a comprehensive experimental analysis against ADV-EMB in subsequent work, pending the development of a standardized implementation benchmark.

This multi-faceted approach ensures a rigorous evaluation of SE’s capabilities while maintaining scientific integrity in the absence of directly comparable benchmarks.

3.2. Gradient Calculator

The gradient calculator is designed as a function that maps images to feature vectors. By integrating NN-DCTR with a linear mapper, it generates gradients that are both adversarial and structured to challenge steganalytic models that rely on frequency-based patterns or spatial anomalies. Specifically, $f^{NNDCTR}:{\{-1023,-1022,\dots ,1024\}}^{H\ast W}\to R^{1\ast 8000}$. The linear mapper then further maps these vectors to scalars, i.e., $R(1\ast 8000)\to R$. Figure 2 illustrates the process of constructing the gradient calculator. Initially, $f^{NNDCTR}\left(C\right)$ and $f^{NNDCTR}\left(S\right)$ are extracted from C and S, respectively. Subsequently, the weights of the linear mapper are computed using $f^{NNDCTR}\left(C\right)$ and $f^{NNDCTR}\left(S\right)$.

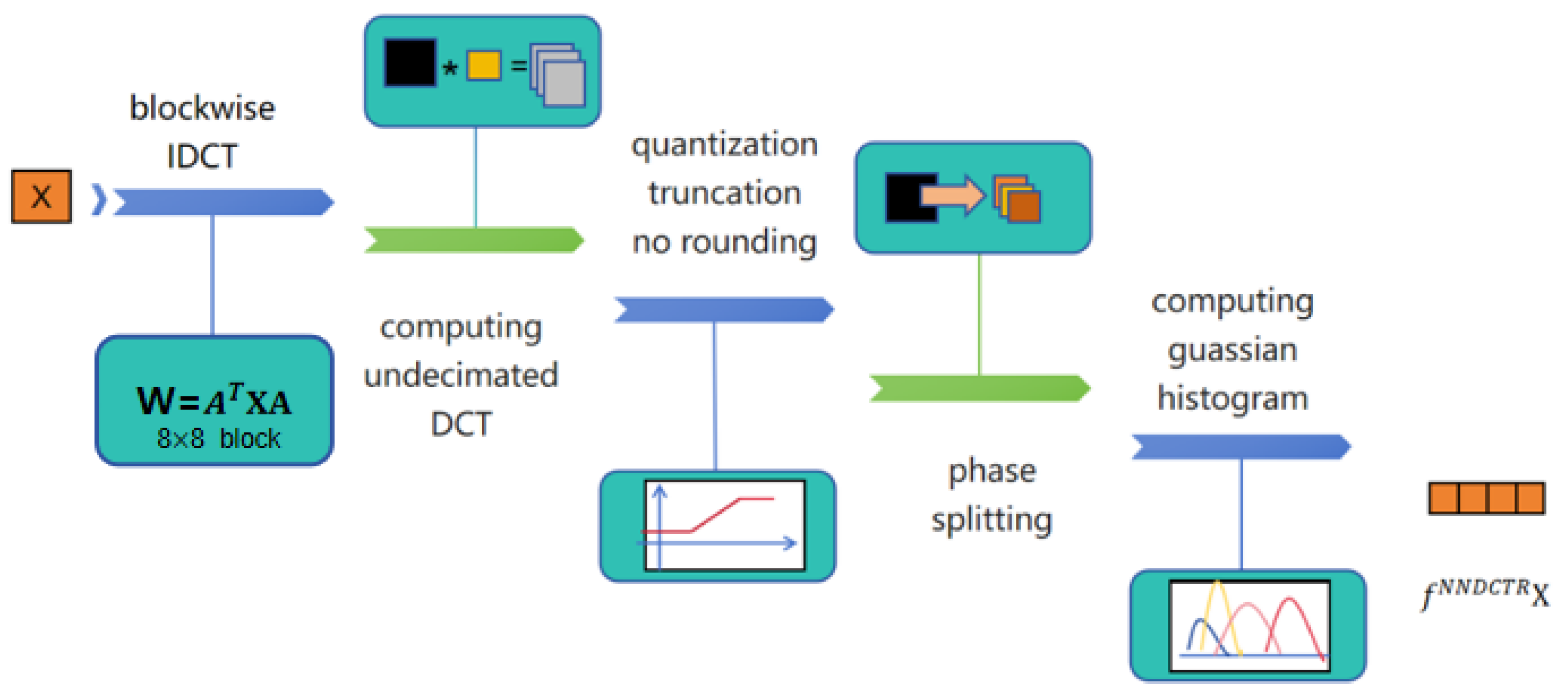
3.3. NN-DCTR

NN-DCTR is a neural network-based approximation of DCTR (Discrete Cosine Transform Representation), designed to be fully differentiable, which allows for the calculation of adversarial gradients. Each operation in NN-DCTR mirrors or approximates a corresponding operation in DCTR, ensuring alignment with the core processing steps of the original DCTR method. NN-DCTR replicates the structure of DCTR through five core operations, each of which aligns with its DCTR counterpart, maintaining consistency in feature extraction while enabling differentiability. Figure 3 illustrates the block diagram of NN-DCTR.

Step 1: 8 × 8 Block IDCT

This step mirrors the transformation procedure utilized in DCTR, wherein the matrix of DCT coefficients, denoted as X, is inversely transformed to produce a corresponding spatial domain representation, designated as W. Ignoring direct current bias and dequantization, Equation (2) defines the function for the 8 × 8 Discrete Cosine Transform block transformation.

$$w_{i,j}=c\sum _{u=0}^7\sum _{v=0}^7{x}_{u,v}cos\left[{\displaystyle \frac{(2i+1)u\pi }{16}}\right]cos\left[{\displaystyle \frac{(2j+1)v\pi }{16}}\right]$$

(2)

where $x_{u,v}$ represents the elements of the 8×8 block DCT coefficient matrix $X_8$, and $w_{i,j}$ denotes the elements of the 8 × 8 spatial matrix $W_8$. Parameter c, determined by Equation (3), defines a constant value.

$$c\left(u\right)=\left\{\begin{array}{cc}{\displaystyle \frac{\sqrt{2}}{4}},\hfill & u=0\hfill \\ {\displaystyle \frac{1}{2}},\hfill & u\ne 0\hfill \end{array}\right.$$

(3)

This translation clarifies the mathematical process of transforming DCT coefficients into spatial domain matrices within the context of DCTR.

Since the inverse Discrete Cosine Transform operates on discrete 8 × 8 blocks independently within the DCT coefficient matrix X, it is particularly suitable for designing adversarial gradients. The gradient of each 8 × 8 block in the DCT coefficient matrix X is denoted as ${\displaystyle \frac{\partial J}{\partial X_8}}$, with each element represented by ${\displaystyle \frac{\partial J}{\partial x_{uv}}}$. Similarly, the spatial matrix $W_8$ has its gradient represented as ${\displaystyle \frac{\partial J}{\partial W_8}}$, with individual elements denoted as ${\displaystyle \frac{\partial J}{\partial w_{ij}}}$. According to the chain rule of differentiation, ${\displaystyle \frac{\partial J}{\partial w_{uv}}}$ can be derived from Equation (4):

$${\displaystyle \frac{\partial J}{\partial w_{uv}}}=\sum _{i,j}\left({\displaystyle \frac{\partial w_{ij}}{\partial x_{uv}}}{\displaystyle \frac{\partial J}{\partial w_{ij}}}\right)$$

(4)

To enable gradient propagation through the IDCT step, we apply the chain rule of differentiation.

Step 2: Non-matching DCT Calculation

In this step, the non-matching Discrete Cosine Transform (DCT) is computed from the spatial matrix W. This operation is functionally equivalent to convolving the residual signal with a set of 64 distinct DCT kernels, each 8 × 8 in size, within the DCT domain. These kernels originate from the core DCT basis functions defined in Equations (2) and (4). The kernel corresponding to frequency coordinates (u,v) is formally represented as $B^{uv}$, and its elements are calculated using Equation (5):

$$B_{i,j}^{u,v}=c\left(u\right)c\left(v\right)cos\left({\displaystyle \frac{(i+0.5)\pi }{8}}u\right)cos\left({\displaystyle \frac{(j+0.5)\pi }{8}}v\right)$$

(5)

The DCT basis kernels are used to compute residuals in the DCT domain, adopting convolutional operations similar to those in CNNs, where the kernel is fixed on $B^{uv}$.

Step 3: Residual Filtering

This step applies a filtering operation to the residuals in order to enhance the discriminative capability of histogram features within the NN-DCTR framework, as formally expressed in Equation (6). The operation yields a filtered output residual r’.

$$r^{\prime }=\mathrm{truncT}\left(\mathrm{round}\left({\displaystyle \frac{r}{q}}\right)\right)$$

(6)

where round(·) is the rounding function, truncT(.) is the truncation function (defined in Equation (7)), and q is the quantization step (set to 8, as shown in Equation (7)).

$$q=8u(2-{\displaystyle \frac{Q}{50}}),Q\in \{50,51,\dots ,99\}$$

(7)

Since the rounding function is non-differentiable, we replace it with a continuous approximation, Equation (8), to enable gradient flow during backpropagation:

$$r^{\prime }=\mathrm{truncT}\left(\left({\displaystyle \frac{r}{q}}\right)\right)$$

(8)

Step 4: Phase Splitting

This step splits the filtered residual matrix into 64 sub-matrices 8 × 8 in size (consistent with DCT operations in DCTR). The unmodified residual matrix is denoted as U, and the sub-matrix at position $(k,l)$ of the $(a,b)$-th phase is denoted as $U_{(a,b)}^{(k,l)}$. Equation(9) defines the splitting function, where $a,b,k,l,i,j\in \{0,1,\dots ,7\}$:

$$\begin{array}{cc}\hfill & {\mathrm{U}}_{a,b}^{k,l}(i,j)={\mathrm{U}}^{(k,l)}(i+8\times a,j+8\times b)\hfill \end{array}$$

(9)

Step 5: Gaussian Histogram Calculation

This step involves approximating histogram features for the extracted sub-matrices from the previous operation. Since direct histogram computation is non-differentiable and cannot be directly applied to fully differentiable structures, a Gaussian histogram layer is utilized. Introduced in [32], the Gaussian histogram layer is an integral component of neural network architectures designed to optimize the PSRM kernel [39]. It employs cumulative Gaussian functions to approximate histogram distributions.

3.4. Linear Mapper

The core component of the gradient calculator is the linear mapping function, defined by Equation (10).

$$w{\left(f^{\mathrm{NNDCTR}}\left(X\right)\right)}^{\mathbf{T}}+b$$

(10)

where w (weight vector) and b (bias term) are parameters of the linear mapper. Since $f^{NNDCTR}\left(X\right)\in {\mathbb{R}}^{18000}$, it follows that $w\in {\mathbb{R}}^{18000}$. To establish the decision boundary between cover and stego images, the bias term b is determined using Equation (11), ensuring the hyperplane passes through the midpoint of $f^{NNDCTR}\left(C\right)$ and $f^{NNDCTR}\left(S\right)$:

$$\begin{array}{cc}\hfill & w=f^{\mathrm{NNDCTR}}\left(C\right)-f^{\mathrm{NNDCTR}}\left(S\right)\hfill \\ \hfill & b=-w\left({\left({\displaystyle \frac{f^{\mathrm{NNDCTR}}\left(C\right)+f^{\mathrm{NNDCTR}}\left(S\right)}{2}}\right)}^T\right)\hfill \end{array}$$

(11)

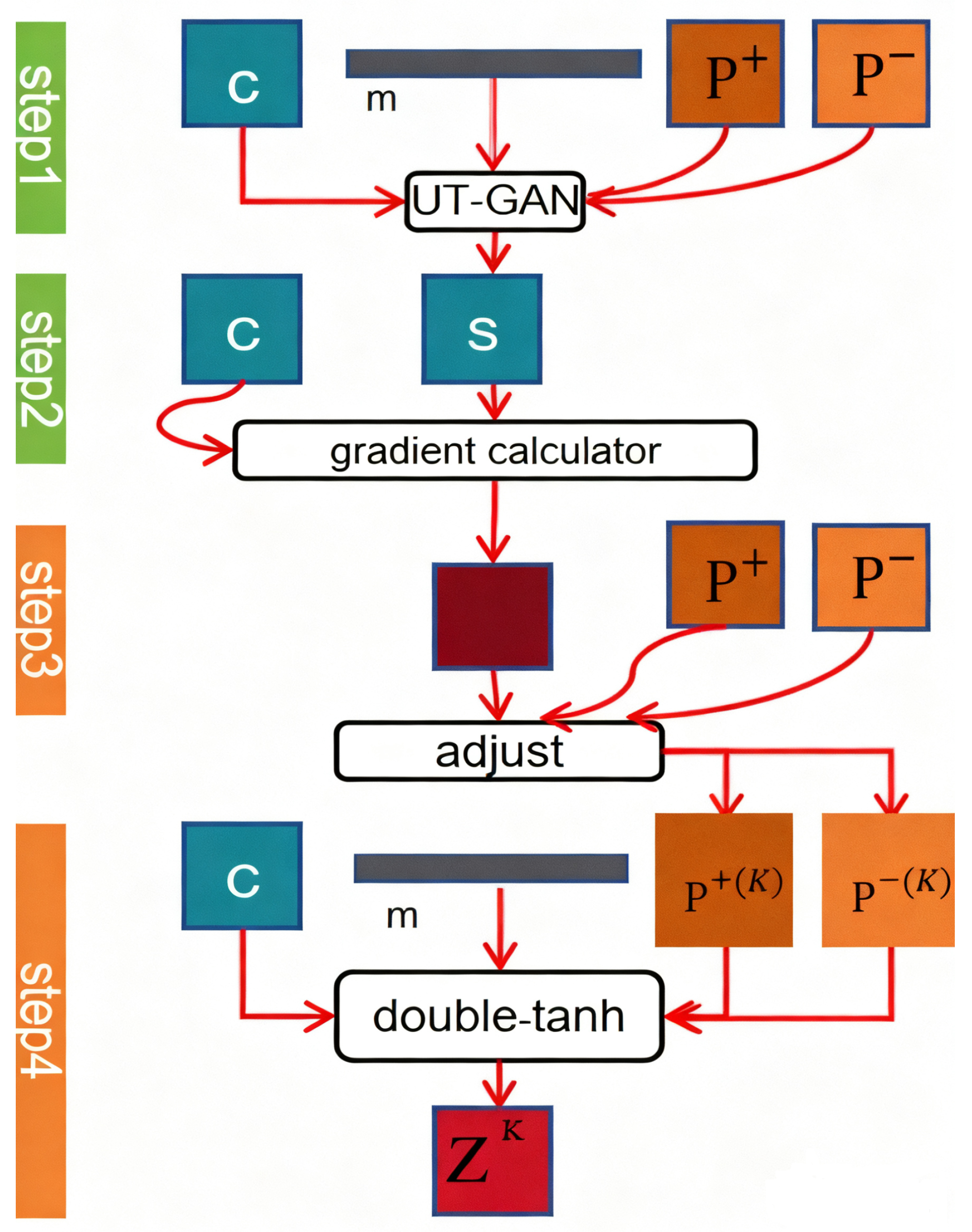
3.5. The SE Implementation

In typical image steganography, multiple candidate stego images are first generated using different embedding costs, after which the solution minimizing the distance to the cover image is selected as optimal. The proposed adversarial steganography algorithm SE first utilizes the UT-GAN adversarial network for pretraining to generate adversarial stego images with relatively enhanced security performance. Subsequently, adversarial gradients are computed multiple times based on different embedding rates. Additionally, it replaces the TES subnet with a Double-Tanh function as an embedding simulator, eliminating the need for pretraining, significantly reducing training time, and improving security performance. The SE process comprises four steps, as illustrated in Figure 4.

Step 1: Generating Adversarial Stego Images with UT-GAN

Inspired by ASDL-GAN, we adopted UT-GAN, an improved version that offers enhanced security performance and shorter training times. We refined its network architecture by adding additional convolutional layers to the existing network and expanding the preprocessing filter bank to improve detection accuracy.

Step 2: Adversarial Gradient Generation

In this step, the adversarial gradient matrix G is generated. G is computed with reference to C and the stego image S generated in Step 1, specifically $G={\nabla }_{C}J(C,c,{\phi }_{(c,s)})$.

Step 3: Cost Adjustment

Cost adjustment is performed using Equation (12), where $p_{i,j}^{+1}$ and $p_{i,j}^{-1}$ represent the embedding costs for +1 and −1 modifications, respectively, and $p_{i,j}^0$ (cost for no modification) is set to 0:

$$\begin{array}{cc}\hfill & \left\{\begin{array}{cc}\hfill p_{i,j}^{+1}& =ln({\displaystyle \frac{1}{p_{i,j}^1}}-2)\hfill \\ \hfill p_{i,j}^{-1}& =ln\left({\displaystyle \frac{1}{p_{i,j}^{-1}}}-2\right)\hfill \\ \hfill p_{I,j}^0& =0\hfill \end{array}\right.\hfill \\ \hfill \end{array}$$

(12)

Step 4: Embedding Simulator

Using the adjusted cost from Step 3, we further generate adversarial stego images. Initially, a random matrix r (with elements $r_{i,j}\sim \mathrm{Uniform}(0,1)$) is generated, where all $r_{i,j}$ are independent and identically distributed. The modification mapping $m_{i,j}$ (indicating +1, −1, or 0 modifications) is determined by Equation (13):

$$\begin{array}{c}\hfill m_{i,j}=\left\{\begin{array}{cc}-1\hfill & \mathrm{if}{r}_{i,j}<p_{i,j}^{-1}\hfill \\ +1\hfill & \mathrm{if}{r}_{i,j}>1-p_{i,j}^{+1}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.\end{array}$$

(13)

Due to the non-differentiability of the step function in Equation (13), we adopt a continuous approximation (proposed in [33]) to replace the discrete step function, enabling backpropagation, as shown in Equation (14):

$$m_{i,j}={\displaystyle \frac{1}{2}}tanh\left(\lambda \left(p_{i,j}^{(+1)}-r_{i,j}\right)\right)-{\displaystyle \frac{1}{2}}tanh\left(\lambda \left(p_{i,j}^{(-1)}-(1-r_{i,j})\right)\right)$$

(14)

where $m_{i,j}$ represents the simulated modification, and $\lambda$ (set to 60) controls the approximation accuracy of the step function. Finally, we use the Double-Tanh function for message embedding. During the above steps, multiple iterated stego images ($Z^1,Z^2,\dots ,Z^K$) are generated. From these candidates, we select the optimal stego image Z that minimizes the total embedding cost, with the cost measured as the feature–space distance between the cover image and the stego image (standardized by Equation (15)):

$$Z=\underset{Z\in \left\{Z^K\right\}}{min}\mathrm{d}\left(f^{\mathrm{NNDCTR}}\left(C\right),f^{\mathrm{NNDCTR}}\left(Z\right)\right)$$

(15)

4. Experiments

4.1. Experimental Setup

All experiments were implemented using Python 3.9.13 and TensorFlow 2.10.0 for deep learning-based components (e.g., the CNN steganalyzer, implemented with TensorFlow and Keras), while traditional steganographic algorithms and feature-based steganalyzers were implemented using MATLAB R2021b. We used 10 image datasets (denoted as C) for experiments, each containing 10,000 natural images. Each image was adjusted to a fixed pixel size (512 × 512) using a scaling factor of 1.9, and then split into two subsets: CTRN (training set) and CTRT (test set), each with 5000 images. These subsets were used exclusively for training and testing steganalyzers, respectively. Specifically, adversarial stego images generated by the UT-GAN network are denoted as $S_1$, while those optimized through cost adjustment are denoted as $Z_j$. To evaluate the resilience of the SE scheme under different compression conditions, we extended our experiments to multiple JPEG quality factors (QFs: 50, 75, 85, and 95). The security performance was tested at an embedding rate of 0.4 bits per non-zero AC coefficient (bpnzac) against representative steganalyzers. The experiment involved the following key parameters and metrics:

(1) Steganalyzers: Five types of steganalyzers were used, including three traditional feature-based methods (DCTR, SRM, GFR) and three modern CNN-based methods (XuNet, SRNet, CovNet). These were categorized into non-adversarial and adversarial steganalyzers. Non-adversarial steganalyzers: Do not assume prior knowledge of adversarial embedding and may use adversarial stego images for retraining. Adversarial steganalyzers: Assume the analyst knows the samples are adversarial and are trained on adversarial stego images.

(2) Comparison Methods: We benchmarked the SE (Steganographic Embedding) scheme against four representative steganographic methods:

• J-UNIWARD: A traditional steganographic algorithm that adopts the Syndrome Trellis Code (STC) method for information embedding.
• UT-GAN: A GAN (Generative Adversarial Network)-based steganographic model, which is mainly used for preprocessing in the SE (Steganography/Steganalytic Evaluation, adjust based on specific context) task.
• SPAR-RL: An adaptive steganographic method designed based on reinforcement learning, enabling dynamic adjustment of embedding strategies.
• DBS: A generative steganographic method built on diffusion models, leveraging the iterative denoising process of diffusion for hidden information transmission.

(3) Detection Criteria: A pretrained binary classifier was used as the steganalyzer. Two types of errors were defined. False negatives ($P_{md}$): Misclassifying stego images as cover images. False positives ($P_{fa}$): Misclassifying cover images as stego images. The overall steganalytic error rate $P_e$ was computed as the average of $P_{md}$ and $P_{fa}$, as shown in Equation (16):

$$P_e^{(⌀C,S)}=\left(P_{\mathrm{md}}^{(⌀C,S)}+P_{\mathrm{fa}}^{(⌀C,S)}\right)/2$$

(16)

where $P_{\mathrm{md}}^{({⌀}_C,S)}$ denotes the false negative rate, and $P_{\mathrm{fa}}^{({⌀}_C,S)}$ denotes the false positive rate. The design goal of steganographic algorithms is to maximize $P_e$, whereas the design goal of steganalyzers is the opposite.

4.2. Performance Evaluation of NN-DCTR Detection

The NN-DCTR framework builds upon the DCTR foundation, implementing optimizations and upgrades to enhance performance. Experimental tests in this section compare NN-DCTR with DCTR. The results in

Table 2. Comparison of detection performance between DCTR and NN-DCTR.

Steganalyzer	Steganography	0.1	0.2	0.3	0.4
		Pe	Pe	Pe	Pe
NN-DCTR	J-UNIWARD	48.7	46.1	41.6	38.7
	UERWARD	45.3	43.5	41.1	37.4
DCTR	J-UNIWARD	48.2	47.1	43.1	39.8
	UERWARD	46.0	44.2	42.2	38.8

show that when traditional steganography algorithms J-UNIWARD and UERD are used, NN-DCTR exhibits a slightly higher overall error rate compared to DCTR, indicating a slight decrease in detection performance. In DCTR, rounding operations and histogram calculations are non-differentiable, leading to discrepancies in the differentiation of NN-DCTR from its original version and resulting in performance degradation. However, NN-DCTR remains an effective alternative to DCTR.

4.3. Feature–Space Distance Analysis

The feature–space distance between cover and stego images (quantified by $d(f^{NNDCTR}\left(C\right),f^{NNDCTR}\left(Z\right))$) is a crucial metric for evaluating the SE scheme. By varying the parameter k (controlling the intensity of adversarial perturbations), we selected the optimal stego image based on minimizing this distance. In this experiment, the embedding rate was fixed at 0.4 bpnzac, and each scheme (SE, J-SE, U-SE) included nine adjustable k values (0.1, 0.2, …, 0.9). A representative image from the CTRT dataset was used as the cover image, with the embedding rate set to 0.4 bpnzac. As shown in Figure 5, SE achieves the minimum feature–space distance—represented by the shortest red bar compared to J-SE and U-SE—demonstrating its superiority in minimizing the distance between cover and stego images. Additionally, SE exhibits lower average steganographic distances across different k values than J-SE and U-SE. A smaller distance indicates more “accurate” generation of adversarial gradients, confirming that the SE scheme generates more effective adversarial gradients for resisting steganalytic detection.

4.4. Performance Under Different Quality Factors

The security performance under different JPEG quality factors is summarized in

Table 3. Security performance ($P_e$) under different JPEG quality factors (embedding rate: 0.4 bpnzac).

Steganalyzer	Method	Quality Factor
		50	75	85	95
SRNet	J-UNIWARD	25.1	22.1	20.5	18.9
	UT-GAN	35.8	33.1	31.7	29.2
	SPAR-RL	36.5	34.1	32.8	30.5
	DBS	37.1	34.5	33.2	31.6
	SE	38.5	35.2	34.0	30.8
XuNet	J-UNIWARD	36.2	39.0	40.1	41.5
	UT-GAN	40.5	39.8	39.2	38.5
	SPAR-RL	41.8	40.8	38.4	39.3
	DBS	42.0	40.5	39.8	39.0
	SE	41.2	40.4	40.3	39.5
CovNet	J-UNIWARD	28.5	28.7	29.2	30.1
	UT-GAN	31.2	29.9	30.5	31.8
	SPAR-RL	33.8	32.5	31.9	32.4
	DBS	34.5	33.2	32.8	33.1
	SE	35.1	33.8	33.5	33.9

Note: Bold values indicate the maximum and optimal $P_e$ values under each quality factor.

. A general observation is that the detection error rate $P_e$ for all methods tends to decrease with decreasing QF, implying that stronger compression facilitates detection. This is expected because more aggressive compression introduces more artifacts that can interfere with both the embedding process and the steganalytic features. Nonetheless, the proposed SE method outperforms all comparison methods across all QFs and steganalyzers. This highlights the robustness of our adversarial embedding scheme under a wide range of compression conditions.

4.5. Non-Adversarial Steganalysis Testing

In this study, the steganalyst was aware of the structure of the steganalyzer, while the steganalyzer remained unaware of adversarial embedding operations, thus qualifying it as a non-adversarial steganalyzer. The experiment employed DCTR, SRM, and GFR steganalyzers as target models trained on the image sets $\{C_J,S_J\}$. The SE algorithm utilized an embedding simulator to compute gradient-modified embedding costs, thereby generating an adversarial stego image dataset $Z_J$. To assess the transferability of adversarial stego images, experiments were also conducted under conditions testing non-adversarial steganalyzers, as shown in

Table 4. The security performance of non-adversarial steganalyzers (denoted as $P_e$).

Steganalyzer	Steganography	Embedding Rate (%)
		0.1	0.2	0.3	0.4	Average
DCTR	J-UNIWARD	47.2	41.7	35.2	28.2	38.1
	ASDL-GAN	41.4	38.7	34.3	28.4	35.7
	UT-GAN	58.2	53.1	49.4	44.6	51.3
	SPAR-RL	59.3	54.5	50.6	46.7	52.8
	DBS	59.5	54.0	50.9	46.2	52.7
	SE	58.7	57.9	51.1	47.3	53.8
SRM	J-UNIWARD	42.3	33.8	27.4	22.1	31.4
	ASDL-GAN	37.0	32.1	27.0	22.5	29.7
	UT-GAN	46.8	43.5	38.3	33.1	40.4
	SPAR-RL	48.1	44.8	39.1	34.1	41.5
	DBS	48.1	45.2	38.5	34.9	41.6
	SE	47.8	44.3	39.7	35.2	41.8
GFR	J-UNIWARD	45.2	37.7	29.3	21.6	33.5
	ASDL-GAN	41.5	32.1	28.7	19.7	30.5
	UT-GAN	47.2	42.2	35.6	31.8	39.2
	SPAR-RL	49.1	43.4	36.1	33.6	40.6
	DBS	48.8	44.3	35.4	33.5	40.4
	SE	48.5	44.1	37.4	32.9	40.7

Note: Bold values are the optimal security performance (highest $P_e$ in respective experimental settings.

below.

4.6. Adversarial Steganalysis Testing

In adversarial steganalysis, the steganalyst knows both the steganalyzer’s architecture and the existence of adversarial embedding operations. We used XuNet, SRNet, and CovNet steganalyzers as adversarial steganalyzers, trained on the image sets $\{C_J,S_J\}$. The SE algorithm utilizes an embedding simulator to compute gradient-modified embedding costs, thereby generating an adversarial stego image dataset $Z_J$. To assess the transferability of adversarial stego images, experiments were conducted under conditions testing adversarial steganalyzers, as shown in

Table 5. The security performance of adversarial steganalyzers (denoted as $P_e$).

Steganalyzer	Steganography	Embedding Rate (%)
		0.1	0.2	0.3	0.4	Average
XuNet	J-UNIWARD	47.4	45.1	42.8	39.0	43.6
	ASDL-GAN	43.0	40.2	37.1	33.3	38.4
	UT-GAN	48.9	46.3	43.5	39.8	44.6
	SPAR-RL	48.7	47.2	43.7	40.8	45.1
	DBS	49.0	47.5	44.3	40.5	45.1
	SE	49.6	47.0	44.8	40.4	45.5
SRNet	J-UNIWARD	48.1	39.2	34.7	32.6	38.7
	ASDL-GAN	48.2	32.3	29.0	27.6	34.3
	UT-GAN	49.0	40.1	37.3	33.4	40.0
	SPAR-RL	49.3	37.5	35.6	33.4	39.0
	DBS	49.5	38.8	35.2	33.7	39.2
	SE	48.6	39.9	38.1	34.2	40.2
CovNet	J-UNIWARD	36.0	32.1	30.1	28.7	31.7
	ASDL-GAN	32.4	26.9	23.9	22.9	26.5
	UT-GAN	36.3	33.1	32.5	29.9	33.0
	SPAR-RL	38.1	33.4	29.9	28.5	32.4
	DBS	37.9	33.8	30.3	30.0	33.0
	SE	37.7	34.1	31.1	30.8	33.4

Note: Bold values are the optimal security performance (highest $P_e$) in respective experimental settings.

below.

4.7. Computational Cost Analysis

To quantitatively evaluate the efficiency and scalability of the SE method, we conducted a comprehensive empirical study following the methodology suggested in the recent literature [40,41]. We compared its computational overhead against several benchmark algorithms, including J-UNIWARD, UT-GAN, SPAR-RL, and the diffusion-based DBS. All experiments were performed on a unified system equipped with an NVIDIA GeForce RTX 3080 GPU and an Intel Core i9-10900K CPU. The evaluation metrics included:

• Training Time (GPU Hours): The total time required to train the models to convergence.
• Inference Time (ms per image): The average time required to process a single image ($256\times 256$), including both the UT-GAN preprocessing and the gradient calculator optimization.
• Computational Complexity (GFLOPs): Measured using a deep learning profiler (TensorFlow Profiler).
• Peak GPU Memory Usage (GB): The maximum GPU memory consumed during the inference phase.

The results are summarized in

Table 6. Comparative analysis of computational cost and complexity.

Method	Training Time (GPU hrs)	Inference Time (ms/img)	Complexity (GFLOPs)	GPU Memory (GB)
J-UNIWARD	-	12.5	0.02	0.1
UT-GAN	48.2	15.3	0.85	1.8
SPAR-RL	62.5	18.7	1.12	2.2
DBS	105.4	125.6	15.32	4.5
SE (Ours)	48.2	22.1	1.05	2.1

Note: “-” indicates that the method is non-trainable.

.

The results reveal a clear trade-off between security performance and computational cost, which aligns with findings in related studies on efficient steganographic frameworks [40]:

• J-UNIWARD, as a conventional non-trainable method, exhibits the lowest overhead but also the lowest security performance (as shown in previous sections).
• DBS, the diffusion-based generative method, achieves high security but at an extremely high computational cost, making it less practical for real-time applications due to its iterative denoising process.
• Our SE method strikes an effective balance. It inherits the same training cost as UT-GAN since it uses the same pretrained network. More importantly, its inference overhead is only marginally higher than that of UT-GAN and SPAR-RL (22.1 ms vs. 15.3/18.7 ms). This is because the gradient calculator, despite its powerful optimization capability, is a relatively lightweight network. The complexity (GFLOPs) and memory usage of SE are also on par with other GAN-based adaptive methods.

Recent advances in adversarial image ste [41].Our empirical cost analysis demonstrates that the performance gain of the SE algorithm is achieved with a reasonable and manageable increase in computational cost, offering a far more efficient solution compared to other high-security paradigms like DBS. This makes the proposed method suitable for practical applications where both security and efficiency are concerned.

5. Conclusions

This study presents a novel adversarial steganographic embedding scheme (SE) that outperforms traditional feature-based steganalyzers and their deep learning-based counterparts. Since DCTR steganalyzers are heuristically designed, SE remains independent of any specific dataset. Additionally, the criterion for selecting optimal adversarial steganographic images is minimizing their distance to cover images in the steganalysis space, thus avoiding reliance on dataset-specific knowledge. Unlike traditional feature-based adversarial steganography algorithms, this study introduces an adversarial network and develops a novel gradient calculator. This calculator computes gradients directly from the steganographic features of images, significantly decreasing the time required to generate adversarial stego images. Experiments confirm that SE improves the security of traditional adaptive steganography.

As the gradient calculator serves as the core of this approach, future optimizations to its architecture could lead to better performance. In particular, an ablation study comparing the performance of NN-DCTR against conventional DCTR or CNN-based gradient estimators would provide further validation of its effectiveness. Such a study is of significant research value and will be conducted in our subsequent work.

Furthermore, while the current implementation of SE is tailored for JPEG steganography due to its reliance on DCT coefficient manipulation and quantization-aware operations, the hybrid (partially data-driven) approach underlying our scheme holds potential for generalization to other domains, such as spatial steganography or other compression formats. Future work will explore the adaptability of SE beyond JPEG, addressing domain-specific challenges such as spatial redundancy management and format-specific feature extraction.

To adapt SE to handle large-scale images. Moreover, experiments conducted across multiple JPEG quality factors confirm that the superiority of the SE method is consistent and not limited to specific compression settings, highlighting its practical robustness. Future work will explore the effectiveness of segmentation strategies. Additionally, refining the selection of optimal adversarial steganographic samples remains a key focus for future research.