Abstract
The classification of urban residential settlements through Machine Learning (ML) and Deep Learning (DL) remains a complex task due to the intrinsic heterogeneity of urban environments and the scarcity of large, accurately labeled training datasets. To overcome these limitations, this study introduces a novel GIS-based unsupervised classification framework that exploits Fuzzy C-Means (FCM) clustering for the detection and interpretation of urban morphologies. Compared to unsupervised classification approaches that rely on crisp-based clustering algorithms, the proposed FCM-based method more effectively captures heterogeneous urban fabrics where no clear predominance of specific building types exists. Specifically, the method applies fuzzy clustering to census units—considered the fundamental scale of urban analysis—based on construction techniques and building periods. By grouping census areas with similar structural features, the framework provides a flexible, data-driven approach to the characterization of urban settlements. The identification of cluster centroids’ dominant attributes enables a systematic interpretation of the spatial distribution of the built environment, while the subsequent mapping process assigns each cluster a descriptive label reflecting the prevailing building fabric. The generated thematic maps yield critical insights into urban morphology and facilitate evidence-based planning. The framework was validated across ten Italian cities selected for their diverse physical, morphological, and historical characteristics; comparisons with the results of urban zone classifications in these cities conducted by experts show that the proposed method provides accurate results, as the similarity to the classifications made by experts, measured by the use of the Adjusted Rand Index, is always higher than or equal to 0.93; furthermore, it is robust when applied in heterogeneous urban settlements. These results confirm the effectiveness of the method in delineating homogeneous urban areas, thereby offering decision makers a robust instrument to guide targeted interventions on existing building stocks. The proposed framework advances the capacity to analyze urban form, to strategically support renovation and urban regeneration policies, and demonstrates a strong potential for portability, as it can be applied to other cities for urban scale analyses.
1. Introduction
Knowledge of the distribution of morphological characteristics of urban settlements today plays a fundamental role for decision makers and urban planners in designing resilient actions and strategies to address climate and environmental issues.
Studies on urban settlement classification play a crucial role in multiple disciplines, supporting applications such seismic vulnerability modeling, energy planning and urban retrofitting strategies aimed at the reducing of carbon emissions. In particular, the analysis of the distribution of residential buildings is significant for identifying the distinctive characteristics of the building fabric and guiding targeted interventions of adaptation and mitigation applied to residential buildings.
Traditionally, the activity of classifying urban settlements based on building characteristics has relied on manual classification methods, which are time-consuming and labor-intensive.
The rapid and heterogeneous urban development of contemporary cities further complicates the reading and understanding of the built environment configuration.
Conventional image-based mapping approaches become impractical metropolitan scale studies due to the extensive manual effort required [1]. This underscores the need for automated methods capable of efficiently analyzing complex urban fabrics.
The growing integration of AI Machine Learning (ML) and Deep Learning (DL) computer vision techniques into urban studies has introduced innovative methods for analyzing and interpreting city structures [2]. This approach has opened a better understanding of the complexities of urban settlements, allowing researchers to explore urban forms and patterns with greater precision and depth.
ML techniques are widely used in urban studies to analyze and classify spatial structures, detect patterns, and model complex relationships within the built environment [2,3]. These approaches enable the automated extraction of relevant features from large-scale urban datasets, facilitating the understanding of urban growth, density, and functionality. DL techniques extend the capability of feature extraction and pattern recognition ML methods in analyzing urban structures, by employing hierarchical feature learning structures for the automatic identification of complex urban patterns from large-scale imagery.
Despite the increasing use of ML and DL models in urban settlement studies, several critical research gaps persist:
- Dependence on labeled training data: ML and DL models require high-quality training datasets, meaning large amounts of precisely labeled data, a resource that is often expensive and time-consuming to produce. This dependency represents a major challenge in applying these methods effectively.
- Limited Portability of classification models: since ML and DL methods rely heavily on locally trained datasets, their applicability is often limited to specific urban settlements. This dependence on local training data reduces the adaptability of these classification models, limiting their ability to accurately analyze the building fabric in diverse urban settlements.
- Heterogeneity and Complexity of Urban Settlements: Cities exhibit highly diverse configurations due to their unique historical, economic, and socio-political development processes. This diversity makes it difficult to apply rigid ML/DL models, which typically require homogeneous and well-labeled datasets, thus restricting their usability to specific local conditions.
These limitations impact the usability of ML and DL models in large-scale urban studies and necessitate alternative approaches better suited for complex urban morphologies.
To overcome the above issues, this study introduces an unsupervised urban settlement classification framework based on Fuzzy C-Means (FCM) clustering for partitioning an urban settlement in urban patterns, which represent urban agglomerations with specific building characteristics.
The proposed framework ensures high scalability and portability, enabling its application across different urban settlements, without the need for model recalibration. Indeed, unlike ML and DL urban settlement classification models, the proposed model does not require training set samples, which are often not readily available. Furthermore, it is highly portable and scalable across different urban settlements, as it only requires census data relating to residential building characteristics. The use of a fuzzy unsupervised classification model based on FCM allows for a more nuanced representation of the built environment by capturing gradual transitions between different residential building characteristics, an aspect often overlooked by rigid classification models.
The framework categorizes urban structures by analyzing construction techniques and building eras, providing a structured and adaptable method to classify the built environment.
The aim of the research is to provide a method for classifying urban residential structures that guarantees:
- -
- High portability across different urban settlements, without requiring massive training sets that are difficult to replicate in complex urban settlements. The proposed method, in fact, uses only census data; the urban settlement is initially divided into subzones, given by census units with homogeneous urban characteristics, which serve as the atomic unit for urban analysis.
- -
- Better accuracy in classifying different types of urban patterns than that obtained with other unsupervised methods; in fact, the use of FCM allows for the identification and capture of mixed urban pattern typologies more effectively than approaches based on crisp-based clustering algorithms.
- -
- Effective representability and interpretability of the results, achieved through a fuzzification process that facilitates optimal interpretation of the urban form typology identified by the cluster. The classification result is displayed in final thematic maps of the urban settlement which provide a spatial visualization of the distribution and significance of the identified clusters. These maps serve as a powerful tool for urban planners, policymakers, and stakeholders, facilitating data-driven decision-making for urban redevelopment and conservation strategies.
The proposed framework has been validated through its application to ten Italian cities, representing diverse urban morphologies.
The analysis of cluster centroids allowed for the identification of recurring patterns and significant differences between the studied cities, demonstrating the reliability of the method in characterizing different urban residential typologies.
Comparative tests were conducted on random samples of subzones in the ten cities, comparing the classification determined using the proposed method with that defined by experts in urban technologies and urban planning. The results show, for each of the cities analyzed, a high degree of similarity between the classification obtained using the proposed method and that determined by the experts, highlighting the performance benefits of the proposed method in terms of accuracy and scalability to different urban settlements.
The remainder of this paper is organized as follows:
Section 2 presents a literature review on related works centered around urban typo- form classification studies. Section 3 introduces the proposed framework for the urban subzone classification. Section 4 describes the experiment settings and then presents the results. Section 5 concludes the paper and discusses its contribution.
2. Related Work
The classification of urban form has traditionally relied on empirical and cartographic analyses based on direct observation, field surveys, and interpretation of morphological and socio-economic data [4,5].
These studies provided valuable insights into spatial organization but were inherently time-consuming and difficult to scale to large or rapidly changing metropolitan areas. Traditional typological classifications based on morphological attributes also required expert interpretation, limiting their reproducibility and applicability to extensive datasets [6,7].
The integration of Artificial Intelligence (AI) and Machine Learning (ML) techniques has transformed urban morphology analysis, enabling data-driven and automated approaches for classifying and interpreting complex urban structures [8,9]. ML encompasses a range of algorithms designed to identify patterns within geospatial data, extract meaningful insights, and adapt to heterogeneous contexts [10,11,12].
Supervised Learning (SL) methods, which rely on labeled datasets, have been extensively applied in urban analysis for tasks such as land-use classification, built-up area detection, and urban change monitoring [13,14].
Among these, Support Vector Machines (SVM), Decision Trees (DT), and Random Forests (RF) have achieved notable results.
SVMs can delineate complex boundaries between urban typologies using spectral and morphological features [15], while DTs and RFs leverage hierarchical rules to classify spatial data derived from satellite imagery, LiDAR, or census datasets [16,17,18,19]. These approaches have proven effective in distinguishing residential, industrial, and commercial areas, but they depend heavily on the quality and representativeness of training data.
Deep Learning (DL) methods—particularly Convolutional Neural Networks (CNNs) and Deep Neural Forests (DNFs)—extend ML capabilities by learning hierarchical spatial features from high-resolution satellite imagery and multispectral data [20,21].
DL techniques, such as Convolutional Neural Networks (CNNs) and Deep Neural Forests (DNFs), have demonstrated significant potential in remote sensing and urban analysis. These methods leverage high-resolution satellite imagery and multi-source geospatial data for tasks including land-use classification, semantic segmentation, and change detection. CNNs, in particular, excel at extracting spatial features for urban mapping, while DNFs enhance classification accuracy by integrating hierarchical decision processes [22]. Among DL architectures, Convolutional Neural Networks (CNNs) and Deep Neural Forests (DNFs) have demonstrated particular effectiveness in urban and remote sensing applications [22].
However, despite their strengths, DL models face several critical challenges. First, they require large, well-labeled training datasets, which are costly and time-consuming to build [23,24]. Second, the quality of input data significantly affects their performance: atmospheric distortions, sensor limitations, and preprocessing errors can lead to blurred or low-resolution imagery, reducing model accuracy. Third, the strong dependency of DL models on locally trained datasets restricts their transferability to different urban contexts, limiting their scalability and generalization capacity [25]. Consequently, although DL has greatly advanced the field of land-use and urban mapping, these models often remain constrained to surface or spectral classification, failing to fully capture the morphological and structural complexity of the urban fabric.
To overcome these constraints, unsupervised learning (UL) has emerged as a powerful alternative, allowing for pattern discovery in unlabeled urban datasets [26,27,28].
UL algorithms such as K-Means [29], Hierarchical Clustering, Gaussian Mixture Models (GMM), Density-Based Spatial Clustering of Applications with Noise (DBSCAN), and Spectral Clustering (SC) have been applied to classify urban areas based on morphological, infrastructural, or socioeconomic indicators.
For instance, Zhou et al. [30] applied hierarchical clustering and Principal Component Analysis (PCA) to classify over 8900 global urban street networks, while Bai et al. [31] proposed an ensemble clustering framework combining multiple algorithms to improve robustness and reliability.
Building upon these early approaches, recent studies have sought to refine unsupervised clustering techniques to better capture the complexity of urban morphology and overcome the limitations of traditional partitioning methods. Among these, density-based algorithms such as DBSCAN have proven particularly effective in identifying irregular or non-convex urban forms and distinguishing compact from fragmented built-up areas. Unlike classical algorithms such as K-Means or hierarchical clustering, DBSCAN does not require specifying the number of clusters a priori and can automatically separate dense urban cores from peripheral or noisy samples, thereby offering a more realistic representation of heterogeneous urban fabrics. Zhou et al. [32] demonstrated the potential of this approach by embedding DBSCAN within a pre-clustering active learning framework for building structure classification, exploiting its ability to detect both dense and sparse regions while excluding noise and consequently improving the accuracy of subsequent supervised learning phases.
Probabilistic approaches, such as the Gaussian Mixture Model (GMM), further extend clustering flexibility by representing each cluster as a Gaussian distribution and thus accommodating overlapping and non-linear data structures. GMMs provide a powerful way to describe gradual transitions between urban classes [33]. In the urban context, Batista et al. [34] successfully applied GMMs to segment city networks into homogeneous regions for traffic analysis, showing that this method produces spatially coherent and continuous urban partitions that outperform traditional hard-clustering approaches.
Beyond geometric or density-based methods, Spectral Clustering (SC) has been employed to identify clusters based on topological connectivity rather than simple geometric proximity. Patt [35] demonstrated that SC can reveal hidden spatial structures and transitional zones within complex urban grids, offering a graph-based perspective particularly useful for capturing spatial relationships that conventional clustering methods often overlook.
Together, these unsupervised approaches have significantly expanded the analytical toolkit available for urban studies by uncovering spatial regularities, density gradients, and network-based structures. However, they still rely on crisp partitions that impose hard class boundaries and fail to fully represent the gradual transitions and overlapping typologies typical of urban morphology. These limitations motivate the adoption of fuzzy clustering methods such as FCM, which allow partial class memberships and thus provide a more nuanced, continuous representation of the urban fabric.
Fuzzy clustering methods, particularly Fuzzy C-Means (FCM), address the above-mentioned shortcomings by allowing each spatial unit to belong to multiple clusters with varying degrees of membership. The fuzzy partitioning mechanism enables a more realistic representation of gradual morphological transitions, such as those between historical centers and post-war expansions, typical of heterogeneous urban environments.
Recent studies have demonstrated the potential of FCM for environmental and urban applications. For instance, Wicaksono et al. [36] applied FCM to classify urban park quality using land surface temperature data, highlighting its suitability for handling soft spatial boundaries. Cafaro et al. [37] used an FCM-based approach to detect urban heat islands, confirming its robustness in modeling spatial continuity and overlapping phenomena. Other studies have integrated FCM within GIS frameworks for classification purposes [38], showing the flexibility of fuzzy clustering in handling spatial uncertainty and non-linear relations among features.
Despite these advances, applications of FCM to morphological urban classification remain limited. Most existing works rely on remote-sensing or environmental parameters, neglecting structural and temporal dimensions such as construction techniques and building periods. Compared to traditional clustering methods like K-Means or DBSCAN, FCM better captures the continuity of urban form by accommodating mixed typologies within the same urban area. Its fuzzy membership structure enhances both analytical precision and interpretability of results, offering a means to classify transitional zones where distinct urban fabrics coexist.
Existing literature highlights the growing interest in unsupervised methods for urban classification, yet few studies have fully exploited the potential of FCM to represent the intrinsic heterogeneity of the built environment. The combination of FCM with GIS-based census data remains underexplored, particularly for analyzing residential building structures through their temporal and construction attributes. The present study addresses this gap by proposing a GIS-integrated unsupervised framework based on FCM clustering. By incorporating validity indices to determine the optimal number of clusters and using census-derived features related to building typologies and construction periods, the proposed approach offers a flexible and transferable tool for classifying urban settlements. Our method advances beyond previous studies by providing a fuzzy-based interpretation of urban morphology that captures both the structural diversity and the gradual spatial transitions characteristic of contemporary cities.
The following sections detail the workflow of the proposed framework, including the dataset preparation, the clustering algorithm configuration, and the visualization of results through GIS-based thematic mapping. This process allows for the identification of urban clusters while capturing gradual transitions between different building characteristics, an aspect often overlooked by rigid classification models.
3. Material and Methods
To overcome the limitations of the ML and DL approaches discussed earlier, this study introduces a replicable unsupervised classification framework based on FCM. Unlike supervised ML and DL techniques, which rely on labeled datasets, and traditional partitioning clustering methods, which require a predefined number of clusters, the proposed framework, illustrated in the flow diagram in Figure 1, offers a more flexible and adaptive approach to urban classification.
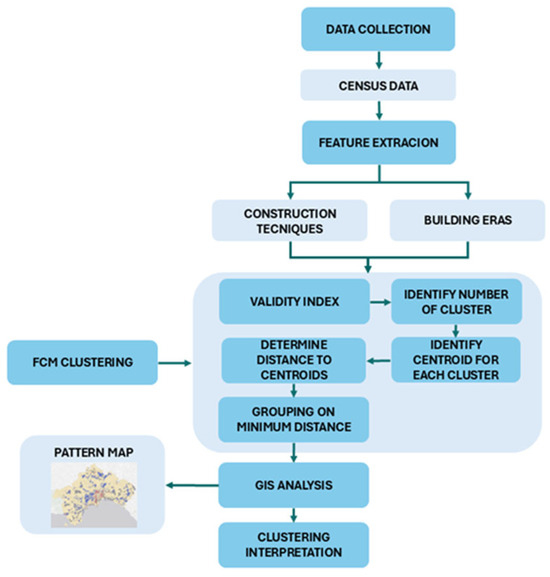
Figure 1.
Flow diagram of the proposed method.
The urban area of study is partitioned into subzones, consisting of urban areas with homogeneous characteristics. A subzone represents the atomic area on which the building census is carried out.
After acquiring from institutional sources census data collected by subzones, the framework performs a subzone classification based on the characteristics of the buildings being censused.
The objective of this classification process is to identify significant patterns that typify the urban area under study. This process is achieved by running FCM and subsequently mapping each cluster to a pattern that represents a typology of urban form. The framework is designed to be adaptable, allowing researchers and urban planners to select any relevant set of features related to subzones for clustering, based on their specific objectives and available data.
The proposed framework is structured into multiple sequential phases, where FCM was encapsulated within a geo-computational framework.
The Framework Processess
The methodological process consists of the following five phases:
- (a)
- Data Collection and Preprocessing
The proposed methodology starts with census data collection, which serves as the foundation for the classification process. This data provides essential spatial and demographic information, including administrative boundaries, population distribution, and building characteristics, that defines the spatial configuration of the study area. Census areas represent the subzones and serve as the primary analytical units, ensuring a systematic and standardized basis for classification.
- (b)
- Feature Selection and Dataset Construction
A feature selection step is conducted to identify the most relevant building variables for classification. The framework is designed to be flexible, imposing no constraints on feature choice, thus allowing researchers to tailor the selection according to the specific objectives and context of the study. The selected variables are then standardized and normalized in the interval [0, 1] to ensure consistency in data representation.
- (c)
- Clustering Process
The clustering process represents the core of the framework. Through the implementation of FCM, each subzone is assigned a membership degree to multiple clusters, capturing the continuous and gradual transitions that characterize urban morphology.
A critical aspect of partition-based clustering approaches in urban form classification concerns the selection of the optimal number of clusters. Defining a fixed number of clusters can introduce portability issues, as urban form characteristics may vary significantly from city to city. This variability requires adapting the number of clusters to the specific morphology of each urban settlement, which, if not properly addressed, can reduce the model’s adaptability and generalizability. To overcome this limitation, the proposed framework determines the optimal number of clusters by computing multiple cluster validity indices, which jointly evaluate the compactness within clusters and the separability between them. Specifically, three widely adopted fuzzy validity metrics are employed: the Xie–Beni Index, the Partition Coefficient, and the Fuzzy Silhouette Index. Using multiple indices ensures a robust estimation of the optimal number of clusters, as different metrics may yield divergent results when cluster separability is weak or ambiguous. The most frequent optimal value across indices is therefore selected as the final number of clusters, providing a reliable balance between intra-cluster cohesion and inter-cluster distinction.
This process consists of the following steps:
- -
- Validity Index Calculation: To determine the optimal number of clusters, the three validity metrics are computed. Using multiple indexes ensures the accuracy of the optimal value of the class number.
- -
- Execute FCM: Once the optimal number of clusters is established, the algorithm assigns each subzone to each detected cluster with a fuzzy membership degree. Each subzone is assigned to the cluster to which it belongs with the highest member degree. Each cluster is represented by a centroid, which encapsulates the average features of the subzones most strongly associated with it and thus represents a specific urban typology.
- (d)
- Cluster Labeling
After each subzone is assigned to the cluster for which it exhibits the highest membership degree, a mapping process is performed by analyzing the centroids of each cluster. To execute this process a fuzzification of the values of the features in each centroid is executed in which a Ruspini fuzzy partition [39] on the domain [0, 1] of the features is built, where the Ruspini condition ensures that the sum of the degrees of membership of a subzone to the clusters is equal to 1. The cluster is classified by assigning to each feature the label of the fuzzy set to which the cluster’s centroid feature value belongs. The fuzzy partition is given by the three triangular fuzzy sets in Figure 2.
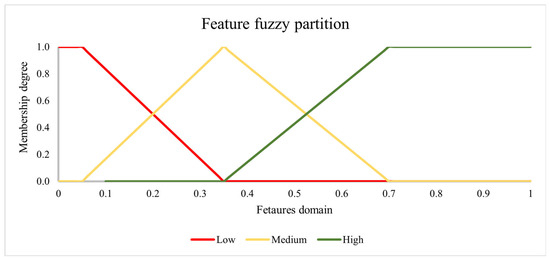
Figure 2.
Example of triangular Ruspini Fuzzy partition.
As an example, let us consider a set of 6 features, called:
f1: Percentage of residential buildings constructed in load-bearing masonry
f2: Percentage of residential buildings constructed in reinforced concrete
f3: Percentage of residential buildings constructed in laminated timber
f4: Percentage of residential buildings constructed before 1960
f5: Percentage of residential buildings constructed between 1960 and 2000
f6: Percentage of buildings constructed after 2000.
In the example in Table 1 the values of the features of a cluster centroid are assigned.

Table 1.
Example of values of the features of a cluster’s centroid.
Then, to each feature is assigned the label of the fuzzy set to whom it belongs with greatest membership degree. Table 2 shows the labels with which the features of the cluster centroid are assigned.

Table 2.
Fuzzification of the cluster centroid in the example.
Analyzing the result of this process we can deduce that the subzones belonging to this cluster are rubicund areas specifically characterized by recently formed building settlements built mainly using cross-laminated timber technology.
To avoid interpretive evaluations and to avoid generating imprecise or confusing semantic labels, it is necessary that the assignment of cluster labels follows the broadest possible consensus of experts. Thus, this cluster identifies an urban pattern that could be labeled, with the consensus of experts: Contemporary Eco-Residential Zone.
- (e)
- Subzones Dissolving and Thematic Map Generation
Finally, spatially contiguous subzones that belong to the same cluster are dissolved to form an urban area representing the pattern identified by the cluster.
The outcome of this process is a thematic map in which the urban settlement is partitioned in urban residential patterns, where each pattern is given by neighborhood subzones belonging to the same cluster.
The proposed method was implemented in the GIS-based suite ESRI ArcGIS PRO 3.5. The algorithm was implemented in Python 3.11.11 using the ESRI ARCPy library for ArcGIS PRO 3.5 and encapsulated in the GIS platform.
In the next section are show the results obtained by applying our method on a set of different Italian urban settlements. The case study is discussed in Section 4, Section 4.1 describes the preprocessing phase used to build the input datasets including residential building characteristics grouped by subzone. The results of the tests are shown and discussed in Section 4.2.
4. Results and Discussion
For testing the framework were selected ten Italian cities: Bari, Bologna, Bolzano, Cagliari, Florence, Genoa, Naples, Palermo, Turin, Trieste.
These cities were chosen to test how the framework performs in cities with different urban features. In fact, the selected cities have different histories, building types, and environments, which made them a good test to see how adaptable the method is.
For each city, a structured dataset was compiled based on census data from the 2011 population and building census dataset provided by the Italian National Statistical Institute (ISTAT). These data, collected at the level of subzones as the smallest territorial units used for statistical purposes, provided detailed information on population distribution, household composition, building typologies, and residential structures.
Population and building census data are collected every 10 years and released by the ISTAT; the last census dataset was carried out in 2021, but it does not include information on buildings due to the limited urban-residential development in Italian cities in the last decade. This led to the choice to use the previous census dataset from 2011. Since there have been no significant changes in residential built-up areas in Italian cities, urban changes since 2011 do not impact the framework’s applicability.
4.1. Dataset Preprocessing
To construct the datasets to be used for evaluating the performances of the proposed clustering model, urban subzones without residential buildings were excluded from the analysis. This methodological choice allows us to work on a homogeneous sample, composed exclusively of comparable residential urban areas, in order to ensure greater consistency and reliability in the classification results.
To support the clustering process, a set of census-derived variables was selected, capturing both the construction period and the structural characteristics of residential buildings. Specifically, the 2011 ISTAT population and building census dataset provides detailed information on the structural typologies of residential buildings, such as load-bearing masonry, reinforced concrete and other materials (e.g., wood, steel), and on their construction periods, divided into twelve distinct time classes (e.g., pre-1919, 1919–1945, 1946–1960, etc.). These features provide valuable information on the evolution and stratification of the built urban environment over time. Table 3 summarizes the selected variables used in the clustering analysis.

Table 3.
ISTAT variables used for clustering analysis.
To enable meaningful comparisons across subzones of varying sizes, all variables were transformed by dividing the raw value of each variable by the area of the corresponding subzone. This process ensures that the dataset captures the density of each building characteristic per unit area, rather than absolute quantities, allowing the clustering algorithm to more effectively detect structural and temporal patterns in the urban fabric. Following normalization, all variables were finally scaled using a Min-Max normalization to project feature values onto a [0, 1] interval. This ensures that each variable contributes equally to the clustering process, avoiding dominance by variables with inherently larger numeric ranges.
The variance threshold technique was used to select the features. The final dataset is given by twelve features related to construction techniques and construction periods, corresponding to the variables in Table 3; it was then used as input for the FCM clustering algorithm.
4.2. Cluster Characterization and Centroid Analysis
After determining the optimal number of clusters using the six validity indices described previously; FCM is executed, and each subzone was assigned to the cluster for which it had the highest membership value. To assign a building specificity to each cluster, a fuzzification was applied to the feature values of the cluster centroid. This process uses the Ruspini fuzzy partition in Figure 3. given by three overlapping fuzzy numbers, called Low, Medium, and High.
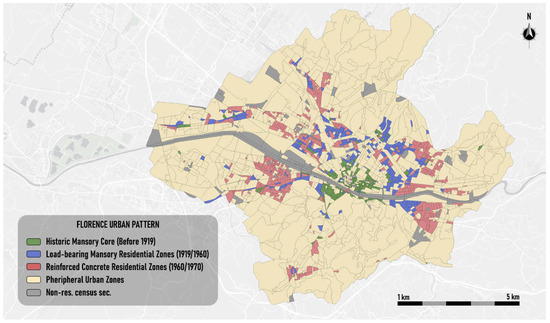
Figure 3.
Thematic map of cluster distribution in Florence.
Each feature value in the centroid was then assigned to the fuzzy set (Low, Medium or High) corresponding to the highest membership degree.
This fuzzy labeling process allows each cluster to be semantically described through the identification of the dominant building typologies and historical construction periods.
For example, a centroid with high values in load-bearing masonry and early construction periods is indicative of a historic urban fabric, while high values in reinforced concrete construction and recent construction periods suggest the presence of recent residential developments.
The cluster labeling process provides a detailed understanding of the spatial articulation of the built environment. Based on the combination of dominant features, each cluster was assigned a descriptive label that captures its most representative urban characteristics. The labels assigned to the clusters were assigned with the broad consensus of experts who participated in the testing activities.
Labels such as “Historical masonry residential area”, “Post-war reinforced concrete area” or “Contemporary reinforced concrete residential area” were adopted to summarize the results and facilitate the communication of spatial patterns to stakeholders and professionals. These semantic labels enrich both the interpretability of the clustering results and their subsequent cartographic representation through GIS-based thematic mapping, allowing for a deeper understanding of the urban morphology in the cities under study.
Finally, the Subzone dissolving process is performed; neighborhood subzones belonging to the same cluster are dissolved in an urban pattern; the thematic map of the urban patterns is generated.
Now the details obtained applying the proposed method to the city of Florence are shown and discussed. The city was segmented into four clusters; analyzing the values of the centroids of each cluster were assigned specific labels which semantically summarize the urban characteristics of each cluster.
Below, for each cluster, the results of the clustering and fuzzification processes are shown.
As can be seen from the results in Table 4, Cluster 1 is predominantly characterized by high values both in E5—Residential buildings in load-bearing masonry (value: 0.2958, membership degree: High)—and E8—Buildings constructed before 1919 (value: 0.2803, membership degree: High)

Table 4.
Fuzzification of Cluster 1 centroids: Historic Masonry Core.
At the same time, all other construction period variables (E9–E16) and structural typologies (E6: reinforced concrete, E7: other materials) fall within the Low fuzzy set, with very small or null values.
This suggests that Cluster 1 corresponds to the Historic masonry center of Florence, where the architectural fabric is primarily composed of masonry buildings built before the 1919th.
The results in Table 5 indicate that all building features in Cluster 2 fall within the Low fuzzy membership set.

Table 5.
Fuzzification of Cluster 2 centroids: Peripheral Urban Zones.
This suggests that this cluster corresponds to sparse or transitional residential development with low residential building density.
Table 6 presents the fuzzy labeling of the centroid for Cluster 3. This cluster shows a clear predominance of both E6—Reinforced concrete buildings with a High fuzzy membership (value: 0.2118) and E10 (1946–1960) and E11 (1961–1970) with Medium fuzzy memberships, indicating concentration of buildings constructed during the post-war period. All other variables fall within the Low fuzzy category.

Table 6.
Fuzzification of Cluster 3 centroids: Reinforced Concrete Residential Zone.
This suggests a residential urban fabric developed primarily in the 1950s–1970s, dominated by reinforced concrete structures.
The fuzzification results of the features of Cluster 4, shown in Table 7, reveal a clear predominance of buildings constructed with load-bearing masonry techniques, with a high degree of membership to the variable E5 (value: 0.1965). Furthermore, the most representative construction period is 1919–1945, as indicated by the high degree of membership associated with E9 (value: 0.3029), followed by the period 1946–1960 with a medium degree of membership, suggesting some post-war additions. These variables define the primary characteristics of this cluster, indicating a built environment composed largely of masonry structures developed during the interwar period and up to 1960. The remaining periods (from E11 to E16) and the structural categories show a low influence.

Table 7.
Fuzzification of Cluster 4 centroids: Load-bearing Masonry Residential Zone.
These urban features are located just beyond the historic center, forming a first suburban ring that preserves a compact and coherent morphological structure.
Given the structural and temporal attributes observed in the centroid, Cluster 4 was semantically labeled as Suburban Residential Area.
To better visualize the distribution of urban typologies across the city of Florence, Figure 3 presents the final thematic map of the urban patterns, classified based on its cluster labels.
The map illustrates the spatial distribution of the four urban patterns identified in the city of Florence, based on the results of the fuzzy classification model.
In the map each cluster is associated with the corresponding semantic label; the spatial distribution of the patterns highlights the morphological differentiation within the urban fabric.
The Historic Masonry Nucleus (in green), located mainly in the central part of the city, delineates the oldest portion of the urban fabric. This cluster includes subzones where buildings constructed before 1919 with load-bearing masonry techniques are particularly widespread, reflecting the oldest portions of the urban settlement.
Adjacent to this area, the Residential Zone in Load-bearing Masonry (in blue) extends towards the eastern and north-eastern portions of the city. This zone includes buildings constructed mainly between 1919 and 1960, also with masonry techniques, and corresponds to development phases subsequent to those of the historic center.
The Reinforced Concrete Residential Zone (in red) is mainly located in the outer areas, particularly in the southern and south-eastern portions of the city. The buildings in this cluster were generally built between the 1940s and the 1970s and are characterized by the use of reinforced concrete, in line with post-war building practices.
The remaining areas of the city, assigned to the Peripheral Urban Zones cluster (in beige), are generally located at the urban fringes. These areas show lower values in all structural and temporal indicators of the buildings, suggesting a more heterogeneous or non-predominant pattern in terms of construction techniques and periods.
The results reflect the city’s urban development. Indeed, the subzones identified as Historic Masonry Core correspond to the city’s historic center, and the areas classified as Reinforced Concrete Residential zones are the areas of subsequent development that arose from the building boom following the end of World War II.
This process was performed for all the ten Italian cities; thematic maps of the urban patterns were generated for each city to spatially represent their spatial distribution. These maps allow for an immediate and intuitive reading of the morphological structure of urban settlements, providing visual insight into the spatial extent and concentration of homogeneous building typologies.
For brevity, below are shown the results obtained for three others Italian cities: Genoa, Naples and Turin. Figure 4, Figure 5 and Figure 6 show, respectively, the urban pattern thematic maps obtained for the cities of Genoa, Naples and Turin. In each map, the classified urban patterns are displayed using a distinct color scheme, with legends reflecting the semantic labels derived from the fuzzy centroid analysis. These visualizations serve as practical tools for identifying areas with similar construction characteristics and can support targeted urban regeneration strategies, especially in contexts marked by complex stratifications of building age and technique.
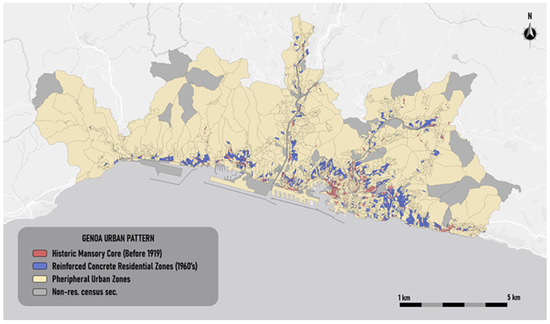
Figure 4.
Thematic map of the urban patterns of Genoa.
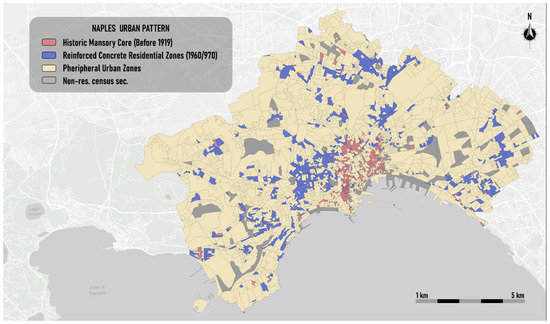
Figure 5.
Thematic map of the urban patterns of Naples.
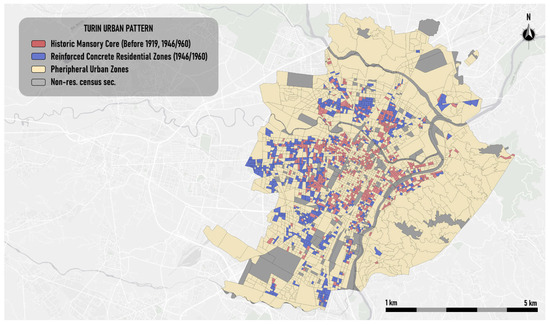
Figure 6.
Thematic map of the urban patterns of Turin.
Figure 4 visualizes the spatial distribution of urban pattern of Genoa, in which each cluster is associated with a semantic label that synthetically captures its predominant construction characteristics. The Historic Masonry Core (in red) is distributed mainly along the coastal strip, the subzones that identify this pattern are aligned along the central valleys and hillsides of the city. This cluster includes subzones characterized by buildings constructed before 1919 with load-bearing masonry techniques. The Reinforced Concrete Residential Zones (in blue) appear more dispersed and fragmented, following the post-war urban expansion that occurred in the 1960s. The remaining areas are classified as Peripheral Urban Zones (in beige), located mostly in peripheral or less consolidated parts of the municipality. These zones do not show a predominance of any specific building technique or historical period, suggesting a more heterogeneous urban structure.
The thematic map of the urban patterns of Genoa highlights the development of the city, which is a typical port city and former maritime republic. Development began in the port area and subsequently spread along the coast and into neighboring inland areas. The subzones classified as Peripheral Urban Zones are areas further from the port, where residential construction has been less intense.
Figure 5 displays the spatial distribution of the urban patterns identified in the city of Naples. The classification highlights the structural and historical layering of the built environment.
Like the thematic map of urban patterns for the city of Genoa, the one for the city of Naples highlights that the areas belonging to the Historic Mansory Core (in red) are those is concentrated in the oldest part of the city, particularly around the central and coastal areas. This cluster includes buildings mostly constructed before 1919 and built using traditional load-bearing masonry methods, reflecting the city’s historical urban core. The Reinforced Concrete Residential Zones (in blue) extend across various parts of the city, particularly in areas that underwent expansion during the 1960s and 1970s. The Peripheral Urban Zones (in beige) represent the rest of the city, often located in the outer margins of the urban territory. These zones exhibit a more mixed or less clearly defined building composition, without strong dominance of either specific structural types or time periods.
Unlike Genoa, where the areas distant from the city center are predominantly Peripheral Urban Zones, a significant number of peripheral areas of the city of Naples are classified as Concrete Residential Zones, Unlike Genoa, where the areas distant from the city center are predominantly Peripheral Urban Zones, a significant number of peripheral areas of the city of Naples are classified as X, as they underwent residential development during the decades of Italy’s economic boom in the 1960s and 1970s.
The spatial distribution of urban patterns in Turin is presented in Figure 6.
The classification outlines three distinct urban typologies: the Historic Masonry Core (in red) extends concentrically from the central part of the city and includes portions of the built environment dating back to before 1919, as well as to the 1946–1960 period. This dual component reflects both the historical center and the masonry-based expansion that followed World War II. The fact that these subzones refer to two different time periods indicates that the buildings constructed in load-bearing masonry refer to two different construction periods, a time interval that reaches 1919 and a subsequent period between 1946 and 1960. Unlike other cities, Turin underwent a building evolution in the post-war period in the central areas but always adopted the load-bearing masonry construction technique.
What is most striking about the thematic map of the urban patterns of Turin is the fact that, unlike Florence and the two port cities of Naples and Genoa, Turin does not have a well-located ancient historic center, but rather a large central zone in which subzones belonging to the Historic Masonry Core are mixed with subzones classified as Reinforced Concrete Residential Zones (in blue) which underwent subsequent building development from 1946 to 1970. These subzones are widely distributed across the municipality. Finally, the Peripheral Urban Zones (in beige) comprise subzones with no dominant structural typology or construction period. They are mainly located in the eastern part of the city and may include mixed or less consolidated residential areas.
4.3. Comparison Results
Unlike DL and ML classification models, which cannot be used without massive training sets, the proposed unsupervised method does not require labeled datasets and is easily scalable and reproducible across different urban settlements. Indeed, it provides the classification of urban residential areas using building census data, which are available for each type of urban settlement. Furthermore, it facilitates better interpretation of the classification results through appropriate user-defined cluster labeling.
Then, since ML and DL algorithms are not applicable in these case studies as they require appropriate training sets that would be very expensive to build, the comparative tests were performed against urban form classifications carried out directly by pools of experts. To this end, a pool of domain experts, made up of two urban technology experts and two urban planners, was asked to assign the correct class from the set of classes obtained after the mapping process to a sample of different subzones in each city, given by about 10% of the residential sections, selected randomly. In order to compare the classifications obtained with those assigned by the experts, for each of the cities studied it was necessary to present the experts with the set of urban form classes obtained after mapping the resulting clusters. This was performed so that the experts’ assessments could be made starting from the same set of classes.
To evaluate the method’s performance, we used the Adjusted Rand Index (ARI) [37], a measure that evaluates the similarity between cluster-based classifications of data points. The Cohen’s Kappa concordance index was used to measure the agreement between the classifications made by experts; it provides a value of 0.95, which implies significant agreement among experts and justifies the use of the ARI to assess the accuracy of the proposed method.
The ARI is calculated from the contingency table of the two classifications.
Let n be the sample size and L1, L2,…, LC be the class labels obtained after the mapping process applied on the C clusters. The contingency table of two classifications is given by (Table 8):

Table 8.
Example of contingency table.
The ARI is given by
where nij is the number of objects in the sample assigned to the ith class by the first classifier and to the jth class by the second classifier. In the table, ai represents the total number of objects assigned by the first classifier to the ith cass, and bj represents the total number of objects assigned by the second classifier to the jth cass.
- where in general, . It represents a measure of mean binary classification accuracy over pairs of object. The value of ARI oscilates between −1 and 1. The closer it is to 1, the better the similarity between the two classifications.
Table 9 shows the ARI values calculated for all 10 Italian cities analyzed.

Table 9.
ARI measured for the ten Italian cities.
The results in Table 9 show that the classification performed by the proposed FCM-based method is very similar to that performed by experts, regardless of the type of urban settlement analyzed. The ARI values range in all cases between 0.93 and 1.00.
4.4. Final Discussions
The results of tests demonstrate that the proposed unsupervised method for classifying urban subzones based on building characteristics provides high accuracy and is highly scalable, adapting to different types of urban settlements.
Comparative tests performed on subsets of subzones for all 10 cities confirmed that the model provides classifications consistent with expert assessments, regardless of the type of urban settlement analyzed.
The proposed framework could therefore be a valuable tool to support decision makers and urban planners in designing effective strategies and actions to adapt to and mitigate environmental and climate risks. For example, it could provide assessments of the most critical areas of urban settlements for climate retrofitting of residential buildings or indicate which urban residential areas are affected by high energy loss from buildings.
The main critical aspect of the model is its spatial scale; in fact, it refers to the atomic scale of the subzone. Finer spatial scales, where the focus is on specific areas of the city, would require more in-depth knowledge of the urban settlement and the use of tools more suited to fine-scale spatial study. Furthermore, census data are not frequently updated, and the census data accuracy can be affected by measurement errors or by incomplete or inaccurate data. In addition, surveyed building characteristics may be insufficient to correctly classify informal areas, consisting of unstructured urban settlements, or mixed-use areas, where functional diversity exists. The acquisition of more detailed data on structural and functional built elements would allow for further refinement of the unsupervised classification process of residential building types; the use of a larger number of features corresponding to detailed characteristics of the built environment would lead to the identification of building subclasses and a more refined classification of urban settlements.
5. Conclusions
This study presents an innovative and replicable approach to classify urban settlements based on building characteristics, using the FCM clustering algorithm integrated into a GIS environment. The proposed methodology overcomes the limitations of traditional supervised Machine Learning and Deep Learning approaches, which strongly depend on massive, labeled datasets and are often not transferable between different urban contexts.
Starting from building census data summarized by subzones, where a subzone represents the minimum spatial unit of analysis, and applying a fuzzification process to the final clusters, the framework allows to identify urban patterns referring to the construction characteristics of residential buildings. They consist of urban areas with a prevalence of residential buildings built in a specific period and with a specific construction technique.
Thanks to the fuzzy nature of the method, it is possible to represent gradual transitions between different urban morphologies, offering a more nuanced view of the built structure. In fact, unlike crisp-based urban settlements classification methods, the proposed model adopts a fuzzy-based approach that allows us to detect urban forms in which there is no clear prevalence of residential buildings with specific construction characteristics and typologies, and there are also, but not negligible, urban forms with different construction characteristics. For example, a cluster could identify areas in the historic center that may have undergone significant recent residential development; this differs from historic center areas where no recent residential development has occurred. Another cluster could identify residential areas with predominantly reinforced concrete buildings constructed from the post-war period to the 1980s; buildings in these urban areas, especially if in seismic zones, may require prioritized seismic retrofitting. Residential areas belonging to clusters that identify areas with residential buildings constructed mostly in reinforced concrete in more recent periods, between the 1980s and the first decade of the 2000s, could be given particular attention for energy efficiency interventions.
The methodology has been tested on ten Italian cities, chosen for their morphological and historical variety, proving to be robust, flexible and easily adaptable. The identified urban patterns reflect the construction evolution over time and the technologies used, offering, along with the usability and portability of the model, useful insights for urban analysts and decision makers for planning and urban diagnosis purposes.
The method’s main performance limitations are its spatial scale, where data is aggregated by census areas, and the infrequent updating of census data. Acquiring more detailed data with more frequent updates, while very costly, would improve the accuracy of the results.
In future research we intend to test the framework to enrich the classification and to detail it on specific problems, testing its performance in classifying types of urban residential areas based on the issue at hand. For example, the use of socioeconomic variables such as household size, unemployment rate and average per capita income could be significant in determining which urban residential areas are most critical, similarly the use of climate and environmental variables could impact the determination of the urban areas most exposed to environmental and climate-related risks.
Furthermore, the application of the framework in international urban settlements will allow us to further test its adaptability and refine its effectiveness.
In summary, the proposed framework is configured as a powerful and scalable tool for supporting decision makers in the analysis of urban patterns and in planning interventions in the fields of regeneration, energy retrofit and resilient planning. In fact, the framework can serve as a tool to support decision makers in analyzing the distribution of residential urban zone types to determine which retrofit actions or urban planning strategies are best suited for assigned urban zones classified as having a specific residential urban form typology referring to the characteristics of residential buildings.
Author Contributions
Conceptualization, R.C., B.C., V.D., F.D.M. and V.M.; methodology, R.C., B.C., V.D., F.D.M. and V.M.; software, R.C., B.C., V.D., F.D.M. and V.M.; validation, R.C., B.C., V.D., F.D.M. and V.M.; formal analysis, R.C., B.C., V.D., F.D.M. and V.M.; investigation, R.C., B.C., V.D., F.D.M. and V.M.; resources, R.C., B.C., V.D., F.D.M. and V.M.; data curation, R.C., B.C., V.D., F.D.M. and V.M.; writing—original draft preparation, R.C., B.C., V.D., F.D.M. and V.M.; writing—review and editing, R.C., B.C., V.D., F.D.M. and V.M.; visualization, R.C., B.C., V.D., F.D.M. and V.M.; supervision, R.C., B.C., V.D., F.D.M. and V.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study and the source code created to implement the proposed method are available on request from the corresponding author.
Acknowledgments
The article has been developed within the context of the project RETURN (Multi-Risk sciEnce for resilienT commUnities undeR a changiNg climate)—the extended partnership that aims to strengthen research chains on environmental, natural and anthropogenic risks at national level and promote their participation in strategic European and global value chains.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Thakur, G.; Fan, J. MapSpace: POI-Based Multi-Scale Global Land Use Modeling. In Proceedings of the GIScience 2021 Short Paper Proceedings, Poznań, Poland, 27–30 September 2021. [Google Scholar] [CrossRef]
- Cai, Z.; Demuzere, M.; Tang, Y.; Wan, Y. The characteristic and transformation of 3D urban morphology in three Chinese mega-cities. Cities 2022, 131, 103988. [Google Scholar] [CrossRef]
- Chen, W.; Wu, A.N.; Biljecki, F. Classification of urban morphology with deep learning: Application on urban vitality. Comput. Environ. Urban Syst. 2021, 90, 101706. [Google Scholar] [CrossRef]
- Batty, M.; Longley, M. Fractal Cities—A Geometry of Form and Function; Academic Press: London, UK, 1994; p. 394. [Google Scholar]
- Whitehand, J.W.R.; Samuels, I.; Conzen, M.P.; Conzen, M.R.G. 1960: Alnwick, Northumberland: A study in town-plan analysis. Prog. Hum. Geogr. 2009, 33, 859–864. [Google Scholar] [CrossRef]
- Caniggia, G.; Maffei, G.L. Composizione architettonica e tipologia edilizia 1. In Lettura Dell’edilizia di Base; Marsilio: Padova, Italy, 1979. [Google Scholar]
- Whitehand, J.W.R. British Urban Morphology: The Conzenian Tradition. Urban Morphol. 2001, 5, 103–109. [Google Scholar] [CrossRef]
- Koutra, S.; Ioakimidis, C.S. Unveiling the Potential of Machine Learning Applications in Urban Planning Challenges. Land 2023, 12, 83. [Google Scholar] [CrossRef]
- Arditi, A.; Toch, E. Evaluating Package Delivery Crowdsourcing Using Location Traces in Different Population Densities. Comput. Environ. Urban Syst. 2022, 96, 101842. [Google Scholar] [CrossRef]
- Wang, J.; Biljecki, F. Unsupervised Machine Learning in Urban Studies: A Systematic Review of Applications. Cities 2022, 129, 103925. [Google Scholar] [CrossRef]
- Casali, Y.; Nazli Yonca, A.; Comes, T. Machine Learning for Spatial Analyses in Urban Areas: A Scoping Review. Sustain. Cities Soc. 2022, 97, 101842. [Google Scholar] [CrossRef]
- Wu, C.; Wang, J.; Wang, M.; Kraak, M.-J. Machine Learning-Based Characterisation of Urban Morphology with the Street Pattern. Comput. Environ. Urban Syst. 2024, 109, 102078. [Google Scholar] [CrossRef]
- Foody, G.M.; Mathur, A. Implementation of Machine-Learning Classification in Remote Sensing: An Applied Review. Int. J. Remote Sens. 2018, 39, 8803–8825. [Google Scholar] [CrossRef]
- Panđa, L.; Radočaj, D.; Milošević, R. Methods of Land Cover Classification Using WorldView-3 Satellite Images in Land Management. Tech. J. 2024, 18, 142–147. [Google Scholar] [CrossRef]
- Vakula, C.S.V.; Anitha, P. Building Footprint Extraction from LIDAR Data Using SVM Classification. Int. J. Sci. Res. Eng. 2019, 7, 1–11. [Google Scholar]
- Samardžić-Petrović, M.; Dragićević, S.; Bajat, B.; Kovačević, M. Exploring the Decision Tree Method for Modelling Urban Land Use Change. Geomatica 2015, 69, 313–325. [Google Scholar] [CrossRef]
- Kim, J. Building Classification Using Random Forest to Develop a Geodatabase for Probabilistic Hazard Information. Nat. Hazards Rev. 2022, 23, 3. [Google Scholar] [CrossRef]
- Ruiz Hernández, I.E.; Shi, W. A Random Forests Classification Method for Urban Land-Use Mapping Integrating Spatial Metrics and Texture Analysis. Int. J. Remote Sens. 2018, 39, 1175–1198. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, M.; Shi, W.; Sun, Z. Detailed Urban Land Use Land Cover Classification at the Parcel Level: A Comparison of Decision Tree, Random Forest, and Support Vector Machine. Sensors 2019, 19, 3120. [Google Scholar] [CrossRef]
- Rewhel, E.M.; Li, J.Q.; Hamed, A.A.; Keshk, M.H.; Mahmoud, A.S.; Sayed, S.A.; Samir, E.; Zeyada, H.H.; Mohamed, S.A.; Moustafa, M.S.; et al. Deep Learning Methods Used in Remote Sensing Images: A Review. J. Environ. Earth Sci. 2023, 5, 33–64. [Google Scholar] [CrossRef]
- Qi, Y. Evaluation of Urbanization Quality Based on Deep Learning and Intelligent Algorithms. Int. J. High Speed Electron. Syst. 2024, 33, 2540144. [Google Scholar] [CrossRef]
- Feilin, L.; Sharma, A.; Liu, X.; Yang, X. Deep Learning for Urban and Landscape Mapping from Remotely Sensed Imagery. In Urban Remote Sensing; Yang, X., Ed.; Wiley: Hoboken, NJ, USA, 2021; Chapter 8. [Google Scholar] [CrossRef]
- Grekousis, G. Artificial neural networks and deep learning in urban geography: A systematic review and meta-analysis. Comput. Environ. Urban Syst. 2019, 74, 244–256. [Google Scholar] [CrossRef]
- Ullah, Z.; Al-Turjman, F.; Mostarda, L.; Gagliardi, R. Applications of Artificial Intelligence and Machine Learning in Smart Cities. Comput. Commun. 2020, 154, 313–323. [Google Scholar] [CrossRef]
- Li, Z.; Xia, L.; Tang, J.; Xu, Y.; Shi, L.; Xia, L.; Yin, D.; Huang, C. UrbanGPT: Spatio-Temporal Large Language Models. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Barcelona, Spain, 25–29 August 2024; pp. 5351–5362. [Google Scholar] [CrossRef]
- Park, J.Y.; Ryu, D.J.; Nam, K.W.; Jang, I.; Jang, M.; Lee, Y. DeepDBSCAN: Deep density-based clustering for geo-tagged photos. ISPRS Int. J. Geo-Inf. 2021, 10, 548. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation Learning: A Review and New Perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef]
- Choi, C.; Hong, S.Y. MDST-DBSCAN: A density-based clustering method for multidimensional spatiotemporal data. ISPRS International J. Geo-Inf. 2021, 10, 391. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-means Clustering Algorithm. J. R. Stat. Soc. Ser. C (Appl. Stat.) 2019, 28, 100–108. [Google Scholar] [CrossRef]
- Zhou, Q.; Bao, J.; Liu, H. Mapping urban forms worldwide: An analysis of 8910 street networks and 25 indicators. ISPRS Int. J. Geo-Inf. 2022, 11, 370. [Google Scholar] [CrossRef]
- Bai, L.; Liang, J.; Du, H.; Guo, Y. An Information-Theoretical Framework for Cluster Ensemble. IEEE Trans. Knowl. Data Eng. 2019, 31, 1464–1477. [Google Scholar] [CrossRef]
- Zhou, P.; Zhang, T.; Zhao, L.; Qi, Y.; Chang, Y.; Bai, L. Pre-clustering Active Learning Method for Automatic Classification of Building Structures in Urban Areas. Eng. Appl. Artif. Intell. 2023, 123 Pt C, 106382. [Google Scholar] [CrossRef]
- Zhou, L.; Ye, W.; Plant, C.; Böhm, C. Knowledge Discovery of Complex Data Using Gaussian Mixture Models. In Big Data Analytics and Knowledge Discovery, DaWaK 2017; Bellatreche, L., Chakravarthy, S., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2017; Volume 10440. [Google Scholar] [CrossRef]
- Batista, S.F.A.; Lopez, C.; Menéndez, M. On the Partitioning of Urban Networks for MFD-Based Applications Using Gaussian Mixture Models. In Proceedings of the 7th International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS), Heraklion, Greece, 16–17 June 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Patt, T. Spectral Clustering for Urban Networks. CAADRIA Bangk. 2020, 91–100. [Google Scholar]
- Wicaksono, A. Public Urban Park Quality Assessment Using Fuzzy C Means Classification of Land Surface Temperature and Social Function. In Proceedings of the International Conference on Radioscience, Equatorial Atmospheric Science and Environment and Humanosphere Science, Padang, Indonesia, 20–22 September 2021; Springer Proceedings in Physics, Series; Yulihastin, E., Abadi, P., Sitompul, P., Harjupa, W., Eds.; Springer: Singapore, 2021; Volume 275. [Google Scholar] [CrossRef]
- Cafaro, R.; Cardone, B.; D’Ambrosio, V.; Di Martino, F.; Miraglia, V. A New GIS-Based Detection Technique for Urban Heat Islands Using the Fuzzy C-Means Clustering Algorithm: A Case Study of Naples, (Italy). Algorithms 2025, 18, 228. [Google Scholar] [CrossRef]
- Pérez-Sánchez, I.; Medina-Pérez, M.A.; Monroy, R.; Loyola-González, O.; Gutierrez-Rodríguez, A.E. New Evaluation Method for Fuzzy Cluster Validity Indices. IEEE Access 2025, 13, 22728–22744. [Google Scholar] [CrossRef]
- Ruspini, E.H. A new approach to clustering. Inf. Control 1969, 15, 22–32. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).